Ambiguity Coding Allows Accurate Inference of Evolutionary Parameters from Alignments in an Aggregated State-Space

Abstract

How can we best learn the history of a protein’s evolution? Ideally, a model of sequence evolution should capture both the process that generates genetic variation and the functional constraints determining which changes are fixed. However, in practical terms the most suitable approach may simply be the one that combines the convenience of easily available input data with the ability to return useful parameter estimates. For example, we might be interested in a measure of the strength of selection (typically obtained using a codon model) or an ancestral structure (obtained using structural modeling based on inferred amino acid sequence and side chain configuration).

But what if data in the relevant state-space are not readily available? We show that it is possible to obtain accurate estimates of the outputs of interest using an established method for handling missing data. Encoding observed characters in an alignment as ambiguous representations of characters in a larger state-space allows the application of models with the desired features to data that lack the resolution that is normally required. This strategy is viable because the evolutionary path taken through the observed space contains information about states that were likely visited in the “unseen” state-space. To illustrate this, we consider two examples with amino acid sequences as input. We show that 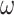, a parameter describing the relative strength of selection on nonsynonymous and synonymous changes, can be estimated in an unbiased manner using an adapted version of a standard 61-state codon model. Using simulated and empirical data, we find that ancestral amino acid side chain configuration can be inferred by applying a 55-state empirical model to 20-state amino acid data. Where feasible, combining inputs from both ambiguity-coded and fully resolved data improves accuracy. Adding structural information to as few as 12.5% of the sequences in an amino acid alignment results in remarkable ancestral reconstruction performance compared to a benchmark that considers the full rotamer state information. These examples show that our methods permit the recovery of evolutionary information from sequences where it has previously been inaccessible. [Ancestral reconstruction; natural selection; protein structure; state-spaces; substitution models.]

The evolution of protein sequences is driven by a combination of forces that influence both what types of mutation occur and which of them are allowed to fix by natural selection. The former process operates at the level of the nucleotide sequence and manifests at the amino acid level through the structure of the genetic code. Functional and structural constraints then determine the probability of survival of the mutants. A wide variety of computational tools to make inferences about different layers of this process are available, considering observations from nucleotide, codon or amino acid sequences, and (occasionally) protein structure. Models that take data from one of these state-spaces as input typically use transition probabilities between these same character states to compute outputs, such as phylogenies, selective constraints, or ancestral states. Being able to obtain certain types of information about evolution is therefore usually contingent on having access to observations in the relevant state-spaces.

Given the abundance of available genome sequences, access to interesting data is ordinarily not a problem. Codon sequences, for example, are commonly used to quantify the strength of natural selection, measured by 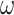, the relative rate of nonsynonymous to synonymous substitutions. Variants of the standard codon model estimate constraints on specific sites, branches, or different types of amino acid substitutions (Yang et al. 1998; Yang 2014; Weber and Whelan 2019). Empirical amino acid models, which work with amino acid sequences and are often used to estimate phylogenies, consider how “exchangeable” different residues are (Whelan and Goldman 2001; Le and Gascuel 2008). This allows them to capture some functional constraints and therefore reconstruct plausible amino acid trajectories and ancestral sequences.

A subset of models go beyond sequence alone and incorporate elements of structure. This can either take the form of mixture models describing site- or partition-specific amino acid propensities (Koshi and Goldstein 1995; Le et al. 2008a,b; Le and Gascuel 2010), or explicitly modeling observed changes in the protein’s three-dimensional organization. Recently, an extended version of the empirical amino acid model was introduced that additionally accounts for rates of exchange between amino acid side chain configurations (Perron et al. 2019). How suited a given amino acid is to a particular sequence and structural context is not only influenced by the biochemical properties of its side chain, but also by its spatial orientation. This includes the rotation of the 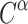– bond, or the 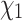rotational isomer (“rotamer”) configuration, which can be discretized into up to three states per residue, resulting in a state-space with 55 characters (see Methods and (Perron et al., 2019) for details). The empirical rotamer-aware model therefore allows reconstruction of ancestral amino acid sequences that include side chain configurations (Perron et al. 2019)—provided structural information is available for the extant descendants of the protein of interest. Reconstructed side chain configurations are of practical interest as they can provide a plausible prior for structure prediction for a variety of applications. For example, structural models are widely used for in silico functional annotation of genes and variants, prediction of protein-protein interactions and docking (Zhang et al. 2012; Vakser 2014; Waterhouse et al. 2018).

Given the variety of options, the choice of model for a study might be guided by the research question and which aspects of the evolutionary process are most interesting. In some cases, data availability may limit the range of suitable models. For example, given a set of amino acid sequences, models operating in codon- or rotamer space cannot be straightforwardly applied. Scenarios where one might encounter this mismatch include selection analyses incorporating protein sequences from ancient specimens or databases where corresponding nucleotide sequences are not retrievable, or studies where access to complete high-quality protein structures is limited. Attempts to bridge the gap between available input and desired model output have, thus far, been limited—at least as far as conventional observable character states are concerned. For example, Yang et al. (1998) formulated an amino acid model that merges synonymous codons into a single amino acid state, with substitution rates computed as an average of the codon rates. This model can estimate transition–transversion bias from amino acids. However, it is unable to provide a measure of the strength of selection.

Nevertheless, there are well-established methods that allow the handling of data for which only part of the state-space information is available. This is achieved by encoding observed states as ambiguous representations of characters in a larger state-space. This application of standard statistical theory for missing data has been used previously in phylogenetics (e.g., (Yang 2014), p. 110–112). A notable example are covariotide models, conceptualized by Fitch and Markowitz (1970), where each nucleotide may be in an “on” or “off” state that cannot be directly observed (Tuffley and Steel 1998; Galtier 2001; Huelsenbeck 2002). Can the principles employed by these methods be applied more broadly to allow substitution models to take “partial” observations as input?

In this article, we present a proof of principle, demonstrating that it is possible to infer information about evolutionary processes that occurred in an expanded state-space using only the aggregated data, taking advantage of an established method for handling ambiguity in sequence alignments. The ability to model sequences in a state-space with a larger set of characters allows us to obtain outputs that would otherwise be unavailable. For example, we can capture relative selective constraints on nonsynonymous versus synonymous substitutions from amino acid sequences. The path through amino acid space hence helps reveal the path evolution takes through codon space. The same method can be applied to reconstructing ancestral amino acid rotamer configurations using only amino acid sequences. Using input data consisting of a mixture of rotamer and amino acid sequences further allows us to refine these reconstructions and obtain a useful starting point for homology modeling.

Materials and Methods

Inferring Model Parameters from Data in an Aggregated State-Space using Ambiguity

Our framework is maximum likelihood (ML) inference on phylogenetic trees, based on alignments of observable characters that evolve independently according to a Markov process. We consider cases where the characters at the tips of a phylogenetic tree are only available in an “aggregated” state-space 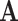with 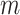states. Each state 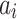in 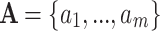corresponds to one or more “separate” states 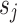in a larger state-space 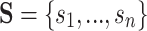(where 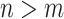). Meanwhile, each state in 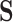maps to a single state in 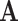. For example, where 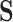describes the set of 61 sense codons, 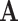might describe the 20 amino acid states: each codon codes for one specific amino acid, while a given amino acid can be represented by multiple codons. Similarly, each amino acid (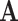) can represent multiple rotamer configurations (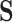; see Perron et al. (2019), Table 1). If we only have access to amino acid sequences rather than codon or rotamer sequences, but modeling the data in 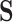would be more informative, we can take advantage of these mappings.

In order to estimate phylogenetic models under ML when the data do not match the model state-space, we modify an established method for handling alignment gaps and ambiguity characters. The conditional probability vector 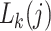is a crucial part of phylogenetic likelihood calculations. It records the probability of the observed data descended from node 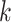conditional on the presence of state 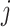at node 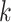. There is one such vector for each combination of alignment position (not indicated in this notation, for simplicity) and node 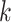, with one element for every permitted state 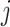. The iterative calculation of the likelihood is initialized at the tips of the tree: if 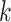is a tip with state 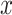recorded in the alignment, the element 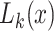is set to 1 and 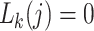for all other 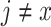(Felsenstein 2004)—the data are recorded as having been correctly observed with certainty. When data are missing, or when there is a gap at a site in the alignment, the corresponding 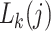are set to 1 for all 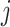, representing total absence of knowledge of the true character states and effectively removing node 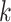from the likelihood calculation for the site.

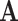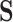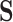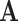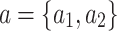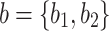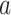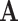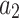In the case where the observed data are in the aggregated state-space , and we are interested in modeling in the separate state-space , we can proceed in a similar manner. Consider a simple four-state () model with the aggregated () states and . If we observe state in , which could represent either or in 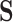, the corresponding conditional probability vector 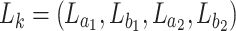is set to 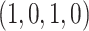. Hence, our observation is ambiguous with respect to the character in 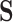. We use the term “ambiguous” to refer to instances where incomplete information about the state at a given site is available, but the character is not missing. Where data are completely absent (missing) for an alignment position, the same vector is encoded by 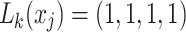. Once 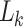has been set at all tips according to this modification, the calculation of the likelihood proceeds as normal following Felsenstein’s pruning algorithm (Felsenstein 1981).

Treating data observed in 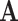as ambiguous states in 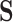is similar to the “covariotide” model of Huelsenbeck (2002), which assigns each nucleotide an ambiguous “on” or “off” state. Ambiguity has also been used to encode population allele frequencies using small samples as input (De Maio et al. 2015), and to handle sequence error and uncertainty (Kozlov 2018). Our approach differs from that presented in Yang et al. (1998), where all synonymous codons for an amino acid are combined into one state and substitution rates between amino acids represent averages over codons.

Description of the Codon Model

The codon model considered here follows the standard M0 model as implemented in PAML (Yang 2007); see also (Goldman and Yang 1994; Yang et al. 2000), with parameters 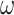= 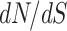, representing the ratio of transition mutations to transversions, and 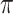representing the codon equilibrium frequencies. The instantaneous rate matrix is given by:

(1)

We implemented the model (now available in PAML as M5) and likelihood calculations in a standard ML framework, encoding the conditional probability vector 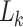in codon space (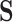) using observed amino acids (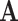), as outlined above. We make the simplifying assumption that the vector of equilibrium frequencies is fixed at 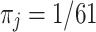for all codons 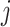. The codon frequencies cannot be directly observed and examining their identifiability is beyond the scope of this work.

Codon Sequence Simulations and Inference

We used evolver (Yang 2007) to generate a single random unrooted tree with 20 tip nodes using a birth–death process (Yang and Rannala 1997) with a tree height of 0.5 (see Supplementary Fig. S1A available on Dryad at http://dx.doi.org/10.5061/dryad.tx95x69sm). We next simulated sequences under M0 over a range of parameters generating 100 replicates with 3000 codons for each combination of configurations (unless stated otherwise). We then analyzed the simulated sequences using codeml from the PAML package, fitting M5 to the translated amino acid sequences and fitting M0 to the original codon sequences, both assuming equal codon frequencies (Yang 2007). We also recorded the standard errors for the parameters (option getSE = 1).

Description of the Rotamer Model

The empirical rotamer-aware model (RAM55) follows the structure of a standard empirical amino acid model and is fit to alignment data in the same manner. The instantaneous rate matrix, 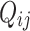, is defined by the exchangeabilities between states derived from a database of sequences of proteins with known 3D structure and their equilibrium frequencies. Rather than the usual 20 amino acid states, the rotamer model considers 55 discrete states determined by the 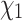dihedral angle between the side chain’s first two covalently linked carbons, the rotamer configuration. Each amino acid can be categorized into up to three distinct states based on an observed protein structure; for example, state L3 denotes a leucine residue in conformational state 3. The exchange rates likely capture the effect of local steric constraints on side chain orientation. RAM55 is described in detail by Perron et al. (2019), along with RUM20, a conventional 20-state empirical amino acid model computed from the same data set.

Rotamer Sequence Simulation and Ancestral Side Chain Configuration Reconstruction

To generate sequences in rotamer space with known phylogenies and ancestral states, we used a set-up similar to the one described by Perron et al. (2019). Briefly, we randomly generated a 32-tip tree using a Yule process and scaled the branches by 0.1–1 (Supplementary Fig. S2 available on Dryad). We then performed a continuous-time Markov chain simulation along the branches for 1000 replicates of 200 sites each using the RAM55 exchangeabilities and equilibrium frequencies. Simulated alignments use a custom encoding format which expresses both amino acid states and rotamer states (i.e., a mixed alignment) using a common alphabet of single-character symbols (see https://bitbucket.org/uperron/ambiguity_coding).

To emulate cases where structural information is not available for some of the terminal nodes, we generated mixed alignments by “masking” a proportion of the terminal rotamer sequences, leaving only amino acids. Amino acid states are then treated as ambiguous rotamer state assignments in the inference step (see below). Further, sequences can be removed from the simulated alignment to illustrate the loss of information caused by discarding sequences entirely when no structure is available. This is done by replacing a specific proportion of the alignment’s sequences with gap characters. Both the masking and discarding operations are performed over a set of sequences selected independently for each replicate according to a uniform distribution.

To reconstruct ancestral states, we modified the approach described by Perron et al. (2019), encoding each amino acid (state-space 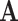) observed in the alignment as ambiguous in rotamer space (state-space 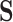) in the conditional probability vector. This procedure allows us to use the RAM55 model to infer rotamer sequences at internal nodes using amino acid or rotamer sequences and the tree that was used for simulation as input. To compute posterior probabilities for reconstructions (Yang et al. 1995), we applied the marginal reconstruction algorithm of Koshi and Goldstein (1996). A joint reconstruction algorithm (Pupko et al. 2000) gives qualitatively similar results. To assess the accuracy of the reconstructions, we examined the proportion of sites with matching characters in rotamer space. That is, we require both the amino acid and its rotamer configuration to be identical.

The same reconstruction approach can be modified to predict side chain configurations for extant homologous proteins in a given family (i.e., tip nodes of the tree). Specifically, each terminal rotamer sequence is, in turn, masked and its side chain configurations are reconstructed conditioned on the observed amino acid states by treating the terminal node as if it were an internal node. This permits us to infer rotamer configurations for extant proteins with known sequences but unknown structures, based on the known sequences and structures of their homologs. To illustrate this, we considered two manually curated empirical data sets, consisting of 16 ADK structures and 30 RuBisCO structures from PDBe (wwPDB consortium 2018), respectively. For each data set, a multiple amino acid sequence alignment was generated using MAFFT (Katoh et al. 2002). Rotamer configuration was then assigned to each amino acid in the alignment, generating a rotamer sequence alignment (see Perron et al. (2019) Methods for details). The tree for the reconstruction was estimated from the rotamer sequence alignment using RAxML-NG under the RAM55 model (Kozlov et al. 2019; Perron et al. 2019). We then masked, in turn, each terminal rotamer sequence in the alignment and predicted each amino acid’s 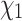configuration using RAM55 and the marginal reconstruction algorithm as described above. Here, the extant amino acid sequence is known and the rotamer state prediction is thus constrained to the observed amino acid. Prediction accuracy can be computed against the original rotamer sequence; in order to benchmark our method’s accuracy we first established a baseline accuracy by assigning the 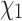configuration either according to a uniform probability distribution (we denote this by “Unif”) or using the relative equilibrium frequencies of each possible configuration according to RAM55 (“RelFreq”).

A widely used strategy to predict side chain configurations in unresolved structures consists of assigning to each amino acid the same configuration found at the corresponding site in the nearest homologous neighbor’s structure (Sutcliffe et al. 1987; Waterhouse et al. 2018); we refer to this approach as “Nearest Neighbor Configuration” (NNC). NNC is only applicable to sites where the amino acid is conserved in the template, and so our implementation of NNC falls back to a RelFreq strategy for nonconserved sites. We also evaluated a scenario where no structural information is available for the nearest sequence [“Masked Nearest Neighbor” (MNN)]. Here, RAM55 can make use of mixed data (both amino acid-only and rotamer sequences) using the ambiguity coding described above.

Results

Substitutions in the Aggregated State-Space Contain Information about the Path Taken through the Larger State-Space

We first consider how it might be feasible to extract information about a process operating in a separate state-space 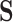from data in 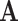. This will naturally depend on the relationships between the structures of the state-spaces. Where some states in the aggregated space are only accessible via multiple steps in the separate space, it is possible to gather information about which states might have been visited. To illustrate this concept, we examine an example where sequences evolve in codon space and are observed in amino acid space. For simplicity, we disregard transition-transversion bias (i.e., we assume 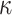= 1). Given an alignment and phylogeny that strongly suggest an evolutionary trajectory W 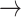L 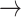H, the most direct path through codon space in single nucleotide steps requires at least two synonymous substitutions (Fig. 1). Hence, knowledge of amino acid sequence evolution can reveal information about codon changes. In practice, many different routes through codon space may be compatible with the observed data; each is assessed by standard likelihood calculations and the embedded information about codon changes weighted appropriately.

Figure 1.

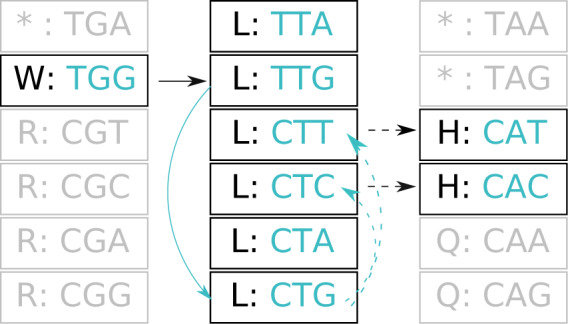
The path of a sequence through amino acid space contains information about which codons may have been visited. We illustrate a W (tryptophan) L (leucine) 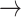H (histidine) trajectory that requires multiple synonymous substitutions. Amino acid states representing the trajectory are shown in dark font. Compatible corresponding (unobserved) codons are shown in lighter font. Faded out boxes represent neighboring states in the genetic code. Solid arrows indicate changes required for the trajectory with the minimum number of steps, while dashed arrows indicate substitutions associated with multiple compatible paths. Black arrows denote nonsynonymous substitutions, and lighter arrows indicate synonymous substitutions.

Where the separate state-space model disallows many transitions (as with the codon model in equation 1), it is easy to see how inferred moves through the aggregated space can give information about the separate states. However, even when the model of interest in is described by a -matrix that does not contain zeros, similar principles apply. Here, none of the routes through the unobserved space are prohibited by the exchangeabilities, but each is more or less probable. We can therefore distinguish between different routes without directly observing them. For example, given an alignment that implies the amino acid trajectory L F Y, the RAM55 model has several available routes through rotamer space. However, considering the relative empirical exchangeabilities between states, we observe marked differences in how probable each path is (Fig. 2). This, in turn, should allow us to infer, for example, the most probable rotamer sequence at an ancestral node, using the ambiguity approach. Note that, in some cases, the aggregated state-space will not retain sufficient information about paths through the separate space to estimate parameters. One example would be a nucleotide model with 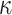applied to a (fully) RY-coded alignment, where all transitions become unobservable and transversions provide direct routes between both aggregated states.

Figure 2.

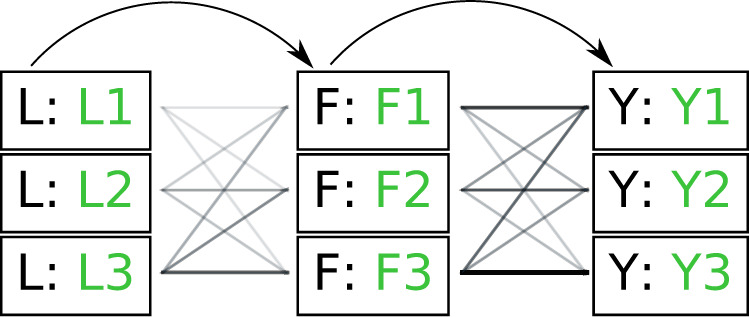
Illustration of paths through amino acid and rotamer space, given an implied trajectory L (leucine) F (phenylalanine) Y (tryptophan). Dark font indicates observed amino acid states. Light font indicates unobserved rotamer configurations. Arrows show observed path through amino acid space. Lines connecting rotamer states indicate transition probabilities between states, with darker shading indicating more probable substitutions according to the RAM55 matrix. L3 F3 Y3 is the most likely trajectory.

Selection can be Inferred from Amino Acid Data Alone

Next, the question arises whether ambiguity coding extracts enough signal to allow meaningful inferences to be made. We therefore asked whether the ambiguity approach permits inference about codon evolution from amino acid data, considering the M5 variant of the standard M0 codon model (see Methods section). To determine if M5 is capable of detecting the relative strength of selection under which a sequence evolved, we require data for which this parameter is known. The most straightforward way of obtaining this is to simulate sequences under a model identical to the one used in the estimation step.

We therefore considered translated sequences that were evolved on a randomly generated 20-taxon tree under the codon model M0. As an initial benchmark, we generated 100 alignments with 3000 codons with the simulation parameters 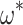= 0.3 and 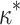= 2, and obtain accurate and unbiased estimates of both (median 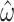= 0.304; median 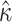= 1.99). Analyzing the original codon sequences using M0 with identical settings gives similar results (median 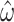= 0.299; median 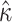= 2.00). We note that M5 tends to be noisier, presumably due to its inability to directly observe synonymous changes. This observation holds across a range of 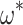and 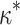values, with high 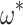values being somewhat prone to overestimation, although a strong linear relationship between true and estimated parameters is maintained (Fig. 3). There is little interaction between 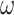and 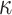(see Supplementary Fig. S3 available on Dryad). In the following, we therefore consider only the combination 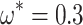and 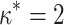, unless otherwise noted.

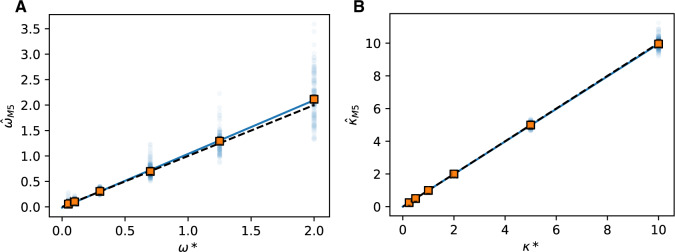
Figure 3.

Estimation of codon model parameters from amino acid data. A) Simulation (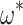) and estimated (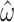) values of 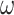show a strong linear relationship ( 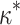= 2 for all simulations shown). Squares represent the median 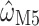for each 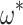; points show estimates from individual alignments. Dashed line indicates 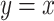; solid line shows the line fit for the medians, with high values of 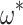slightly prone to overestimation (slope = 1.07, intercept = 0.0083, 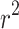= 0.92, 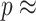0). B) Estimates of 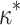show a similar pattern ( 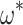= 0.3; slope = 1.00, intercept = 0.0009, 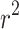= 1.0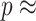0, 0).

The parameter 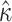shows a relatively modest increase in variance under M5 compared to M0 (standard deviation 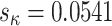under M5; 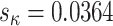under M0), presumably due to its direct, and thus inferable, impact on nonsynonymous substitution patterns. The results obtained for 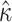under M5 are similar to those for M6 ( 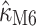= 2.00 with 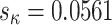), which estimates the parameter from amino acid sequences by averaging over synonymous codons rather than gathering information from ambiguity coding while traversing the tree (Yang et al. 1998). This suggests that can be robustly estimated from amino acid sequences, even using coarse-grained approaches.

However, as expected, discarding codon information does lead to a loss of signal primarily affecting , which displays a markedly higher variance under M5 than under M0 (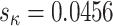 vs. 0.0056, respectively). Why might this be? A comparison of the estimates for 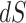tree length versus 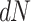tree length suggests that M5 has more difficulty estimating the former, with variation in 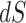tree length accounting for almost all of the variation in overall tree length (see Supplementary Fig. S4 available on Dryad). This is consistent with the fact that synonymous changes are not directly represented in amino acid sequences, whereas nonsynonymous changes are (as long as sufficiently short timescales are considered). We therefore next consider how much information about 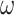is retained by M5, compared to M0.

How Much Information Loss Does Discarding Codons Cause?

The ability of M5 to capture information that is directly “seen” by M0 can be measured by comparing the variances in parameter estimates on alignments with varying amounts of evolutionary signal. The most straightforward way to add information to a phylogeny given a codon model is to increase the number of codons in the alignment. Since both M0 and M5 give rise to unbiased estimates of 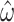and 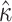(Fig. 3), we compared the variance in the parameter estimates for alignments of varying lengths. Given 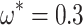and 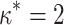across 1000 replicates, we find that the median standard error of 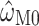, as estimated by codeml, is consistently lower than that of 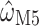. Across the range, the standard error is approximately 10 times higher for M5 (Fig. 4), indicating an information loss of 98.7% (see Fig. 4A for details). By comparison, the equivalent loss for is only 38.8% (Fig. 4B). Nevertheless, the estimates of are reasonably accurate given a sufficiently long alignment (Fig. 3).

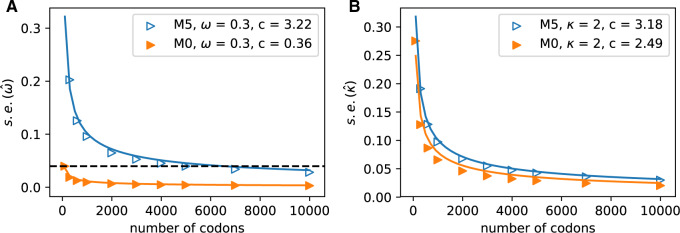
Figure 4.

Increasing the number of columns allows us to quantify how much information is retained in amino acid sequences (M5) relative to codon sequences (M0). The median standard errors of A) 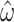and B) 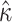decrease for both models as codons are added. The dashed horizontal line in a) indicates the observed median standard error of 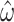for 100 codons under M0, and illustrates that M5 requires a substantially longer alignment to reach a comparable standard error. Fitting functions of the form 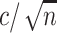to the median standard errors, with 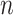equaling the number of alignment columns, allows us to quantify the difference in information content. Equating 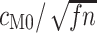with 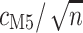indicates equivalent information content for 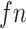codons in M0 and 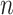codons in M5: hence M5 recovers a fraction 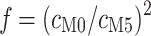of the information available to M0. Alternatively, M5 has lost 100(1 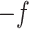)% of the information available to M0.

It is perhaps counter-intuitive that acceptable estimates of 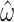can still be obtained with M5 in these circumstances. However, the relative magnitude of the error may remain relatively small. For example, given 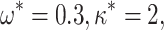and 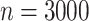, the interquartile range for 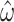is 0.296–0.304 under M0 and 0.270–0.344 under M5. Note that the information loss seems to vary with 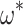. We observe a larger ratio of standard errors when 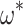= 0.1 (approximately 12–20 times), with an information loss of about 99.2% (results not shown).

Tree Depth and Taxon Number Impact M5 Information Loss

Our results show estimates of to be noise-prone for short alignments. Because increasing alignment length is not a viable solution to reduce variance for real amino acid sequence data, we also considered how other features of the alignment impact M5’s ability to accurately infer 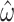. For example, it may be possible to select sequences with higher divergence or include additional taxa in the phylogeny, hence adding more information. Scaling-up the branch lengths of the tree in the simulations gives an initial improvement in the standard error of 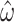. The greatest reduction is observed for a tree length of approximately 4 times the length of the original tree (around 20), followed by a decline for longer trees (see Fig. 5). This is a consequence of the increased number of substitution events from which the model can infer parameters, which is advantageous until the sequences become too divergent, the true number of substitutions is underestimated, and the data become too noisy.

Figure 5.

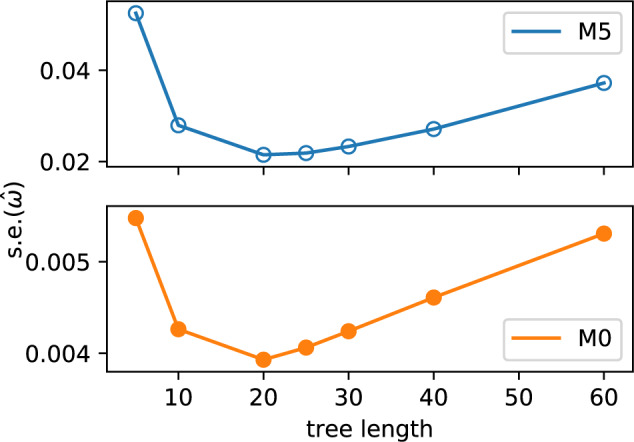
Tree length influences variance in estimates 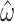for both M5 and M0, with intermediate values producing the lowest standard errors. Points show the median value across replicates. Note the difference in scale on the y-axis between M5 and M0.

The trajectory of the change in variance observed across different tree lengths is broadly comparable for M0 and M5, with the variance for M5 remaining consistently higher for all lengths. In the case of M0, this is due to saturation at synonymous sites (Yang 2014). For M5, it is easy to see that multiple substitutions at a site along a single branch make it more difficult to infer the path through codon space (see Fig. 1). This confirms that the model is behaving as expected.

Adding additional taxa has a similar effect on the variance. When we examine a tree of comparable height (0.5) with twice as many tips (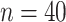, see Supplementary Fig. S1B available on Dryad), the standard error of 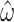decreases compared to the smaller tree (median = 0.0223 vs. 0.0396 for 1000 replicates of 5000 codons and 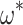= 0.3; equivalent values for M0 are 0.0030 vs. 0.0043). As above, this behavior is expected as the additional tips add information, provided the branches are not exceedingly long.

Given these observations, we conclude that estimating the strength of selection from amino acids is a feasible strategy where nucleotide sequences may be difficult or impossible to obtain (e.g., where amino acid sequences from databases or publications cannot be reliably mapped back to the underlying codons). Although there is an appreciable loss of signal, M5 is statistically consistent and approaches the correct parameter estimates given enough amino acid sequence data.

Accurate Reconstruction of Ancestral Side Chain Configuration from Amino Acids

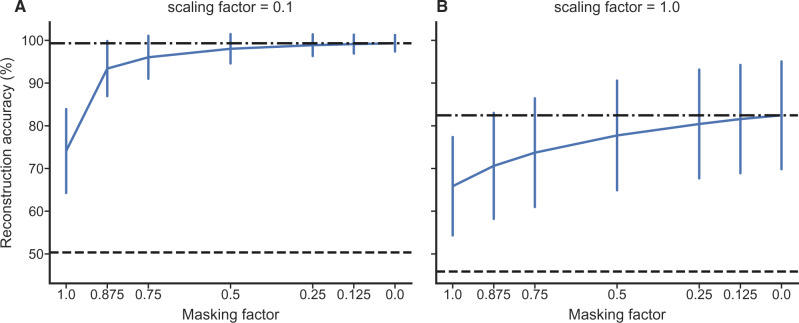
We next ask whether the strategy of treating characters that are not directly observable as ambiguous is also informative when the instantaneous rate matrix underlying the substitution model is not sparse (i.e., does not contain transitions with probabilities equal to 0). To examine how ambiguity coding performs given an empirical rotamer-aware model, we simulated data with 55 states under the RAM55 model on a 32-taxon tree (Supplementary Fig. S2 available on Dryad, see Methods section), and subsequently reconstructed the ancestral sequences under the same model. We opted to benchmark the model using reconstruction accuracy, as ancestral side chain configurations represent an output that would be otherwise unobtainable from amino acid data alone. Varying the proportion of masked sequences in the alignment (see Methods section) allows us to compare scenarios where structures are available for some of the sequences of interest, or none at all, similar to what would be observed for real empirical data. The reconstruction accuracy for the data where rotamer information is available for all of the tips provides a benchmark for the performance of ambiguity coding.

There is a relatively modest reduction in overall rotamer state reconstruction accuracy between simulations where rotamer configurations are known for all taxa, and simulations where this information is not available for any of the taxa (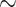15% difference for the unscaled tree, Fig. 6, scaling factor = 1.0). Reconstruction under RAM55 using only amino acid sequences is markedly more accurate than the only alternative approaches of using a conventional empirical amino acid model to reconstruct the protein sequence and randomly assigning (“guessing”) rotamer states (Fig. 6, dashed line), or assigning them based on the equilibrium frequencies of the RAM55 model (Supplementary Fig. S5 available on Dryad). Hence, it is advantageous to reconstruct under the rotamer-aware model, even when the input data are only available in the aggregated state-space.

Figure 6.

The accuracy of ancestral rotamer sequence reconstruction from mixed data under RAM55 increases and shows lower variance when more rotamer configuration information is available. The x-axis shows the fraction of rotamer configuration information removed (i.e., masked). The vertical bars show the standard deviation of the reconstruction accuracies, centered around the median. The black dash-dot lines represent the maximum accuracy reached on full (unmasked) alignments; black dashed lines show the accuracy achieved by reconstructing the amino acids under RUM20 and randomly assigning (“guessing”) the rotamer configuration. A) Results when all branches of the tree (Supplementary Fig. S2 available on Dryad) are multiplied by 0.1, showing greater overall accuracy in this case. B) Results for the standard simulation tree (see Methods section).

As expected, the overall accuracy depends on how difficult the ancestral sequence reconstruction problem is, with a shallower tree showing higher sequence identity between simulated and reconstructed characters (Fig. 6A). Interestingly, the greatest increase in performance appears between alignments with no rotamer configuration information present and 12.5% of sequences containing that information (Fig. 6). This suggests that little structural information is required in order to achieve ancestral reconstruction of rotamer states with acceptable accuracy. Intuitively, the fraction of correctly inferred states declines with increasing distance from the tips of the tree (Spearman’s rank correlation coefficient 0.537, 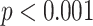; details not shown). We also considered how the certainty with which the model assigns the correct ancestral state responds to rotamer information being masked at the tips of the tree. Unsurprisingly, the marginal posterior probability for the correct state declines as information is removed (see Supplementary Fig. S6 available on Dryad). We observe a drop in the certainty of the reconstruction preceding the drop in accuracy.

To examine the robustness of our approach, we also assessed ancestral sequence reconstruction accuracy under a simple model violation scenario, simulating data under RAM55 with gamma-distributed rates (Yang 1994) and reconstructing under RAM55 without rate heterogeneity. When rotamer configuration is masked, we observe a larger decline in accuracy compared to a scenario with no violation, which is expected given that the amino acid sequence contains less signal (Supplementary Fig. S7 available on Dryad).

Gains Associated with using Amino Acid Sequences to Infer Rotamer Configuration in Absence of Structure

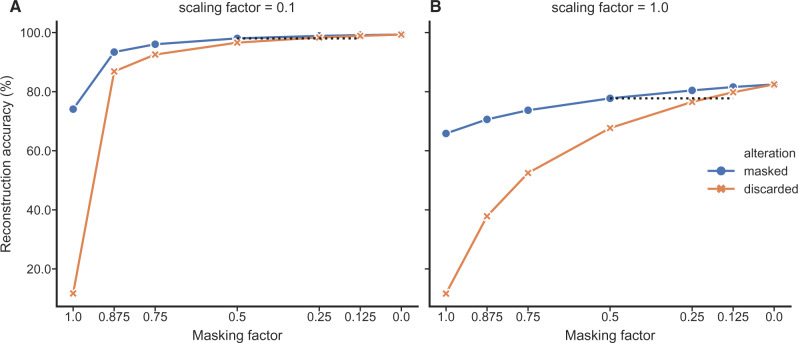
As with the codon model example, we would like to quantify the loss of information associated with using aggregated state-space data for inference in the separate state-space. Given that the output of the empirical model we are studying is not a parameter estimate (as opposed to our mechanistic codon model/selection example) but the percentage of correctly reconstructed residues, extending the alignment is not informative. Instead, we compared the accuracy of reconstructions under two scenarios: (a) all state information (amino acid and rotamer configuration) is discarded from a proportion of sequences and (b) masking is used so that amino acid, but not rotamer, sequences are available for a proportion of the alignment. This provides a measure of the advantage gained by considering additional amino acid sequences where no structural information is available.

For the unscaled tree, masking 50% of the rotamer configurations produces ancestral reconstructions that are comparable in accuracy to trees where 12.5% of taxa have gaps (Fig. 7A), indicating a noticeable advantage for including amino acid sequences where full rotamer state information is unavailable. In other words, augmenting half of the amino acid sequences with rotamer configuration information is approximately as informative as having 87.5% of the full rotamer information. Further, removing all rotamer information and reconstructing with ambiguity is equivalent to retaining 50% of the original information. These results suggest that it can be very valuable to consider amino acid sequences that lack structures.

Figure 7.

The accuracy of ancestral rotamer sequence reconstruction from mixed data under RAM55 increases when masked sequences, which lack rotamer states, are not discarded. The x-axis shows the fraction of information available under two scenarios. The dark circles reflect the amount of rotamer information that has been masked (i.e., replaced with amino acids), and the light crosses represent the amount of rotamer sequences that has been replaced with gaps (discarded). Masking half of the rotamer configurations produces accuracies comparable with those obtained by replacing 1/8–1/4 of sequences in the alignments with gaps (see black dashed lines). Reconstructions with ambiguity always outperform discarding an equivalent fraction of amino acid sequences. As before, the shallower tree, A), shows higher overall accuracy.

Improved Prediction of Side Chain Configurations in Homologous Structures

Considering its robust performance, how might ambiguity coding be put to practical use in the context of reconstructing side chain configurations? Prediction of side chain conformations is an important part of protein structure modeling and interaction modeling. For a given protein sequence of unknown structure, it is possible to construct a model of the target protein from its amino acid sequence and experimentally determined structures of related homologous proteins. This homology modeling strategy aims to predict both the main chain geometry and side chain configurations. In conserved regions, side chains can be modeled starting from configurations observed at corresponding sites in the nearest homologous structure (NNC: see Methods section). Further steps are then required, particularly to model nonconserved side chain configurations (Waterhouse et al. 2018). Side chain configurations could be predicted for an extant amino acid sequence using RAM55 and a modified ancestral reconstruction algorithm by constraining the 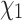configuration prediction to the set of configurations that are possible given the observed amino acid at any given site. Another realistic homology modeling scenario might involve our target’s nearest homolog also lacking a resolved structure and only being available as an amino acid sequence (MNN: see Methods section). In this context, RAM55 can use a mixed alignment (amino acid sequences and rotamer sequences) to inform its predictions rather than relying exclusively on available structures, which ought to improve reconstruction accuracy as seen above (Fig. 7).

To evaluate our approach to side chain configuration prediction, we considered two empirical protein family data sets (RuBisCO and ADK, see Methods section) composed of amino acid sequences from a range of species and their corresponding rotamer configuration information. We investigated two scenarios: (i) a rotamer sequence is available for the nearest neighbor of each terminal node or (ii) only a masked amino acid sequence is available for the nearest neighbor. Predicting 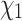side chain configurations using RAM55 is more accurate ( 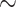11% median improvement for both data sets) than NNC (see Methods section) when the nearest neighbor’s structure is available (Supplementary Figs. S8, S9 available on Dryad). Further, RAM55 can make use of all the available rotamer sequence information, as well as the nearest neighbor’s amino acid information, when the nearest neighbor’s structure is not available. Meanwhile, the traditional approach would instead rely on the second-nearest structure (MNN: see Methods section). This results in improved reconstruction accuracy for RAM55 (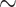9% and 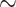12% median improvement, respectively) over MNN (Supplementary Figs. S8, S9 available on Dryad). For both NNC and MNN analyses, the improvements with RAM55 are driven by strongly increased accuracy at nonconserved sites (results not shown).

Our method provides plausible predictions of 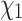configurations using a strategy that, as opposed to NNC or MNN, explicitly models the evolutionary process along the branches of the phylogeny and can make use of amino acid information when structures are not available. RAM55-based predictions could speed up the side chain homology modeling process by creating an informed prior to constrain the search space, particularly where close homologs with unresolved structures might otherwise be discarded by traditional strategies.

Discussion

We have demonstrated that treating characters in an aggregated state-space 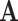as ambiguous versions of characters in a larger state-space 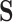allows us to obtain information that would otherwise not be accessible from data in 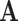. Our examples show that this is true for estimating the strength of natural selection under a codon model, and for reconstructing ancestral side chain configurations under an empirical model, both from amino acid sequences alone.

Naturally, where data are available in a larger state-space matching the internal structure of the preferred model it is advantageous to make use of them. The codon model example provides a particularly clear illustration: completely discarding codon information leads, for obvious reasons, to increased variance in estimates of 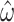. We nevertheless find it remarkable that selection parameter estimates ordinarily derived from comparisons of synonymous and nonynonymous substitutions can be obtained given sufficient amino acid data.

It has previously been argued that modeling coding sequence evolution at the codon level rather than the amino acid level is generally preferable because it offers a more detailed description of the process that generated the data (Ren et al. 2005; Seo and Kishino 2008; Kosiol and Goldman 2011; Whelan et al. 2015; Weber and Whelan 2019). On the other hand, the ambiguity approach may be useful to obtain an approximate estimate of the strength of natural selection in cases where amino acid sequences are more readily obtainable. For example, the supplementary materials accompanying phylogenetic studies often only provide amino acid alignments, and as many as 17% of nucleotide sequences corresponding to proteins in Pfam (El-Gebali et al. 2018) have been previously reported unrecoverable (Whelan et al. 2003). The ability to perform a preliminary screen to determine whether a sequence of interest is under weak or strong evolutionary constraint might therefore be convenient. However, we caution against over-interpreting the results returned by M5, particularly when individual sequences are being considered or codon usage may be biased (violating model assumptions).

The absence of high-quality structures for many extant proteins provides more practical applications for ambiguity coding. In the case of the RAM55 empirical rotamer model, we have shown the utility of using amino acid sequences alone, and “mixed” inputs where even a limited amount of structural information leads to considerable improvements in the accuracy of 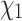configuration prediction. Being able to use information from amino acid sequences improves prediction accuracy over modeling side chains based on the nearest available structure alone. This approach could benefit homology modeling strategies, specifically the steps involving modeling both conserved side chains based on a known template structure, and nonconserved side chain modeling achieved by searching a rotamer library and minimizing an energy function (Xu 2005; Krivov et al. 2009; Shapovalov and Dunbrack Jr 2011). In this context, RAM55’s predictions constrain the rotamer configuration sampling space. This could result in a reduction of the number of energy refinement cycles required.

In addition, using RAM55 and the marginal ancestral reconstruction algorithm makes it possible to obtain posterior probabilities for each of the possible configurations at a given site. This distribution might provide a more robust prior for further refinement, compared to using the single most likely reconstructed configuration or the nearest homolog’s configuration at that site. Further work would be required to quantify improvements in speed and accuracy.

Given the advantage of including mixed input data demonstrated in our rotamer sequence reconstruction analyses, we expect combining amino acid and DNA sequences to be promising, as well as straightforward to implement. This would address some of the current limitations of M5 with respect to analyzing phylogenetic data sets with some missing codon sequences. For example, accurate estimates of codon frequencies would be more readily obtainable. A more speculative and potentially intriguing application would be estimating selection or structural information from ancient protein sequences. Proteins can persist for longer in the environment than DNA under certain conditions (Schweitzer et al. 2007; Wadsworth and Buckley 2014; Cappellini et al. 2019), enabling phylogenetic inferences to be made based on substantially older specimens such as dinosaurs and other extinct organisms (Schroeter et al. 2017; Schweitzer et al. 2019; Welker et al. 2019). Our methods permit the use of a mixture of all available DNA and protein sequences to maximize signal, extending analyses that are normally only possible with DNA sequences to incorporate additional data sources. In the absence of any compelling available ancient protein data sets, we do not attempt to provide a benchmark here.

The proof of principle described here using two relatively simple models should not be taken as a substitute for carefully stress-testing the ambiguity coding approach for specific applications. As is the case with all models, with or without ambiguous inputs, making overly simple assumptions about the data can lead to misspecification and therefore inaccurate results. We recommend performing appropriate benchmarks and specifying models accordingly. As illustrated by our rate heterogeneity model violation scenario, we expect model misspecifications to have similar effects with ambiguity coding as they would in general: Estimates will become more noisy. Due to the information loss inherent to relying on the aggregated state-space, a somewhat greater decline is naturally to be expected. However, we note that our empirical analysis, which demonstrates that rotamer states can be reconstructed using real sequences as input, suggests that more complex scenarios can be captured. One could conceive of a variety of extensions to our implementations, including gamma-distributed rate variation or mixture models of codon evolution. Assessing them all thoroughly is beyond the scope of this manuscript.

In this work, we have shown that ambiguity coding allows evolutionary inference from partially “hidden” data under phylogenetic models with both sparse (e.g., mechanistic) and nonsparse (e.g., empirical) exchangeability matrices. Thus, the principles underlying likelihood analysis of missing data (Felsenstein, 2004; Yang, 2014) and covariotide models (Huelsenbeck 2002) can be applied more broadly, allowing us to estimate selection and reconstruct aspects of protein structure given input data that are not fully resolved. Finally, ambiguity coding could conceivably be applied to other state-spaces beyond amino acids, codons, and rotamer states, provided there is reason to believe that movement through the aggregated space contains info about the separate space.

Supplementary Material

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.tx95x69sm.

Model Availability

The M5 codon model is available as model 5 in codeml (PAML version 4.9h) (Yang, 2007) and is run with the sequence type set to amino acids (seqtype = 2). The program overrides the codon frequency setting specified in the control file and resets the CodonFreq variable to 0 (1/61). Rotamer sequence simulation and ancestral sequence reconstruction code is available at https://bitbucket.org/uperron/ambiguity_coding.