External bone size identifies different strength-decline trajectories for the male human femora

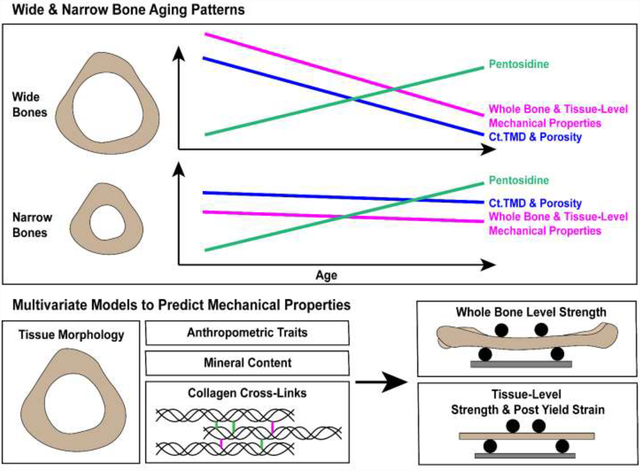
Abstract

Understanding skeletal aging and predicting fracture risk is increasingly important with a growing elderly population. We hypothesized that when categorized by external bone size, the male femoral diaphysis would show different strength-age trajectories which can be explained by changes in morphology, composition and collagen cross-linking. Cadaveric male femora were sorted into narrow (n = 15, 26–89 years) and wide (n = 15, 29–82 years) groups based upon total cross-sectional area of the mid-shaft normalized to bone length (Tt.Ar/Le) and tested for whole bone strength, tissue-level strength, and tissue-level post-yield strain. Morphology, cortical TMD (Ct.TMD), porosity, direct measurements of enzymatic collagen cross-links, and pentosidine were obtained. The wide group alone showed significant negative correlations with age for tissue-level strength (R² = 0.50, p = 0.002), tissue-level post-yield strain (R² = 0.75, p < 0.001) and borderline significance for whole bone strength (R² = 0.14, p = 0.108). Ct.TMD correlated with whole bone and tissue-level strength for both groups, but pentosidine normalized to enzymatic cross-links correlated negatively with all mechanical properties for the wide group only. The multivariate analysis showed that just three traits for each mechanical property explained the majority of the variance for whole bone strength (Ct.Area, Ct.TMD, Log(PEN/Mature; R² = 0.75), tissue-level strength (Age, Ct.TMD, Log(DHLNL/HLNL); R² = 0.56), and post-yield strain (Age, Log(Pyrrole), Ct.Area; R² = 0.51). Overall, this highlights how inter-individual differences in bone structure, composition, and strength change with aging and that a one-size fits all understanding of skeletal aging is insufficient.

Graphical Abstract:

Introduction:

Identifying individuals that are susceptible to fracturing and predicting bone fracture risk remain critical unmet needs in musculoskeletal health. In 2010, there were approximately 158 million individuals worldwide at high risk of osteoporotic fracture and this figure is estimated to double by 2040 (Odén et al., 2015). The economic burden and costs associated with bone fracture are also expected to rise concurrently. The costs of treating osteoporotic fractures for women alone in the US are projected to increase from $57 billion in 2018 to $95 billion by 2040 (Lewiecki et al., 2019). The current clinical “gold-standard” to assess fracture risk is measurement of bone mineral density (BMD) using dual X-ray absorptiometry (DXA). The patient’s BMD combined with fracture probability algorithms like FRAX® can help clinicians assess fracture risk and make treatment decisions (Leslie and Lix, 2014). However, DXA-based measurements only take into account the tissue density, which helps predict bone strength but provides no insight into the structural and material changes responsible for strength-declines (Burr, 2019; Saito and Marumo, 2015). DXA identifies some, but not all (Nguyen et al., 2005), high-risk individuals; and has not kept pace with the introduction of treatments that target parameters beyond BMD (Choksi et al., 2018). Thus, there is a need to develop new fracture risk predictors that provide insight into bone strength and the material-basis of the age-related strength decline. Identifying critical structural and material factors contributing to fracture risk may help clinicians tailor treatment options to mitigate the strength decline on an individual basis.

In previous work, we reported external size-specific differences in the association between the strength of cadaveric male radii and age. After dividing the sample cohort into wide and narrow subgroups, wide radii showed a significant negative correlation between whole bone strength and age, whereas narrow radii showed no association between strength and age (Bigelow et al., 2019). The femoral midshaft differs from the radius in terms of its daily loading scheme, fracture occurrence (Court-Brown and Caesar, 2006) and pattern of age-related bone loss. For example, the radius shows a uniform increase in porosity around the circumference of the endocortical surface with age, whereas the femoral midshaft exhibits increases in porosity predominantly along the anterior-posterior axis (Thomas et al., 2005).

Expanding upon our previous work in the radius, we hypothesize that in the femoral diaphysis, wide bones will exhibit sharper age-related strength declines than narrow bones at the whole-bone and tissue-levels, and that morphological, structural and compositional characteristics can explain the differences in mechanical behavior. Bone is a hierarchically organized composite tissue that can be examined on several length scales. Of particular interest at the tissue-level are the enzymatic and non-enzymatic collagen cross-links which contribute to the strength, toughness and fracture resistance of bone. Whereas enzymatic cross-links are thought to favorably impact mechanical properties, advanced glycation end products (AGEs) are considered detrimental (Saito and Marumo, 2015, 2010). Lysyl hydroxylases (LH), and lysyl oxidases (LOX) are responsible for the formation of enzymatic cross-links. These enzymatic cross-links include the immature divalent cross-links dehydro-dihydroxylysinonorleucine (deh-DHLNL) and dehydro-hydroxylysinonorleucine (deh-HLNL), which are experimentally reduced ex vivo and measured as DHLNL and HLNL, and the mature trivalent cross-links pyridinoline (PYD), deoxypyridinoline (DPD) and pyrroles. Non-enzymatic cross-links or AGEs form via glycation with age or diseases like diabetes. Pentosidine (PEN) is commonly measured as a surrogate for total AGE content (Saito and Marumo, 2010). Including a thorough characterization of collagen cross-links alongside mineral and morphological changes could improve our understanding of changes in bone strength with aging.

The objectives of this study were: (1) to determine how wide vs. narrow femoral diaphyses differ in terms of strength, structure, and composition with age and (2) to determine which combination of factors best models whole bone and tissue-level strength and tissue-level ductility.

Methods:

Samples:

Whole bone strength was reported previously (Patton et al., 2019), but is being used in this study in a novel analysis comparing whole bone mechanical parameters to previously unreported morphology, composition, and tissue-level mechanical parameters. Samples were processed similarly to previous studies (Bigelow et al., 2019; Patton et al., 2019), but procedures are outlined below briefly. Paired fresh-frozen cadaveric femora (n = 33, 26–89 years) of white males were acquired from the University of Michigan Anatomical Donations Program (Ann Arbor, MI, USA), Science Care (Phoenix, AZ, USA), and Anatomy Gifts Registry (Hanover, MD, USA). All tissue use and handling was approved by the University of Michigan Institutional Biosafety Committee and deemed exempt by the Institutional Review Board. Donor age and height were known, and any individual with a disease known to impact bone metabolism was excluded. Donor demographics and anthropometric data are reported in Supplemental Table 1. Distribution of tissues for characterization is shown in Figure 1. Left femora underwent pQCT imaging for bone morphology and length measurements, followed by whole bone mechanical testing. Right femora were cut with a diamond-coated saw (Exakt 312; Exakt Technologies, Oklahoma City, OK, USA) into multiple sections. A 60-mm long annulus was sectioned from the mid-diaphysis. From this annulus, a 5-mm long proximal section was used for high-resolution porosity imaging. The 5-mm section was then sectioned into sextants to isolate the anterior region for ash composition analysis. The remaining 55-mm long section was used for tissue-level mechanical testing and cross-link composition.

Figure 1:

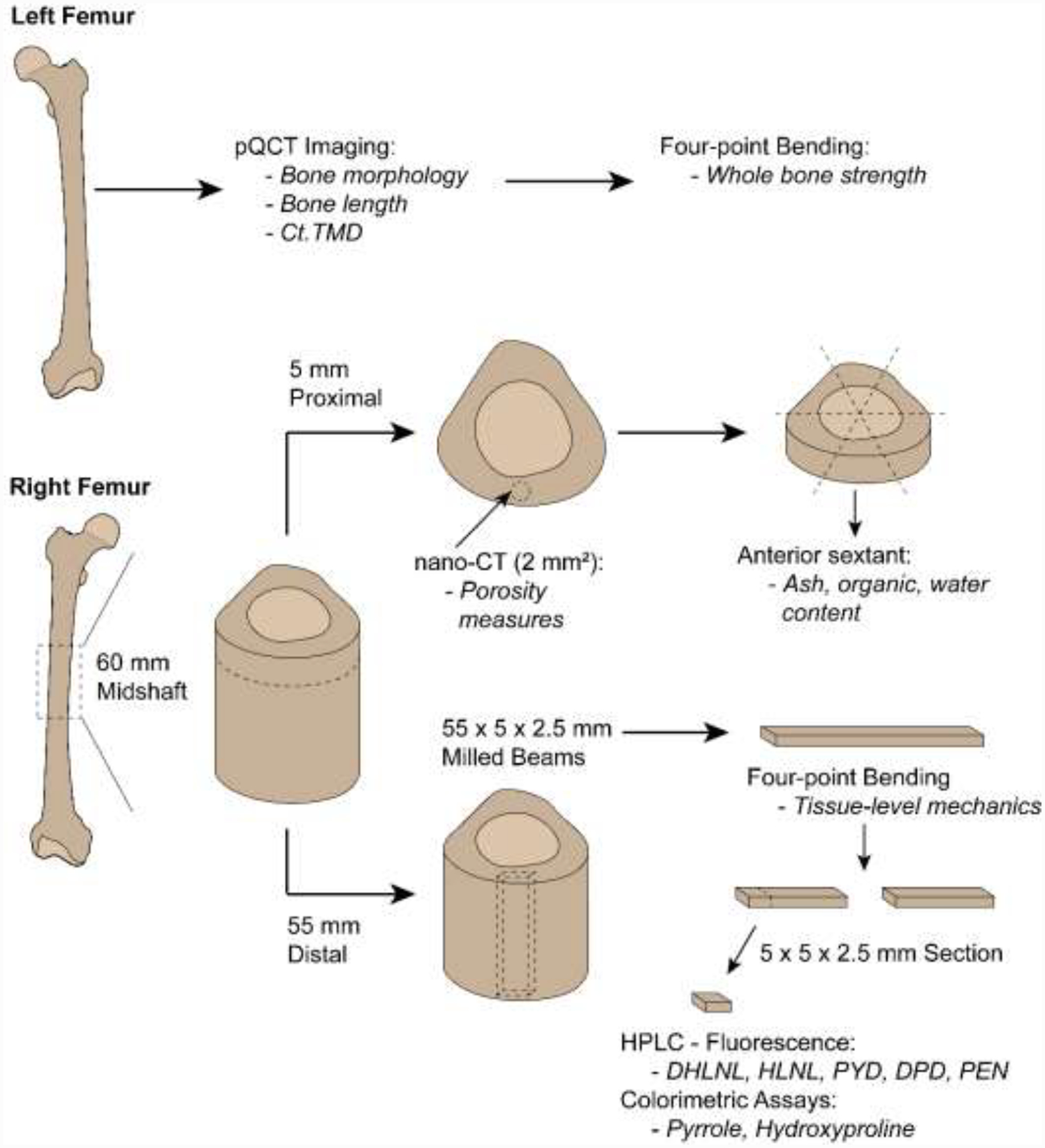
Distribution of tissue from left and right femora for each characterization method. Output(s) from each characterization technique are italicized. Milled beams and cut sections are presented as L × W × H. Not drawn to scale.

Cross-sectional Morphology:

The mid-shaft of the femur was imaged at 161 μm in-plane pixel size using a pQCT system (XCT 2000L, Stratec Medizintechnik, Pforzheim, Germany). Daily calibration scans of a standard phantom of known densities, as well as a cortical bone phantom (Bone Diagnostic LLC, Spring Branch TX, USA) were completed to ensure quality and consistency of scans. Morphological traits were quantified from 2D images using ImageJ (Schneider et al., 2012) and MomentMacroJ (www.hopkinsmedicine.org/fae/mmacro.htm) (Bigelow et al., 2019) and included total area (Tt.Ar), cortical area (Ct.Ar), marrow area (Ma.Ar), circumference, and tissue mineral density (Ct.TMD). Maximum (I_max) and minimum (I_min) second moment of area were calculated. Bone length (Le.) was measured from the distal articular surface of the condyles to the superior side of the femoral neck. The samples were rank ordered by Tt.Ar/Le and then sorted into two external size subgroups: narrow (n = 15) and wide (n = 15) groups. Tt.Ar/Le refers to the continuous variable, and external bone size refers to the narrow and wide categorization. One outlier and two boundary cases were excluded following a sensitivity analysis (see Statistics).

Mechanical Testing:

For whole bone-mechanical testing, the metaphyses of the left femur were potted in an acrylic resin square channel (Ortho-Jet BCA, Lang Dental, Wheeling, IL, USA) with a custom alignment fixture. The hardened acrylic resin blocks prevented sample rotation during testing. Following three pre-yield load-unload conditioning cycles, the femora were loaded to failure in four-point bending at 0.1mm/s in the posterior to anterior direction (anterior surface in tension) using a materials testing system (Model 8511, Instron, Inc., Norwood, MA, USA). The loading points were adjusted for each sample so the lower loading points were located at 25% and 75% of bone length and the upper points were located at 33% and 67% of the lower span length. Load-deflection curves (Supplemental Fig. 4) were adjusted for test fixture span lengths to calculate maximum bending moment hereafter referred to as whole-bone strength. This regimen was validated by testing aluminum cylinders under the same loading conditions which resulted in calculated material modulus levels within 1% of textbook values (Patton et al., 2019).

The 60-mm long section extracted from the right femur was used to quantify tissue-level mechanical properties (Fig. 1). Rectangular beams (55 mm × 5 mm × 2.5 mm) were milled from the anterior quadrant using a customized computer numerical controlled (CNC) mill (Velox VR-1414 CNC; Velox CNC, Orange, CA, USA). Each beam was loaded to failure in four-point bending at 0.05 mm/sec while submerged in a 37°C bath of phosphate buffered saline solution (PBS) with added calcium as described previously (Bigelow et al., 2019). The upper and lower span lengths were 18 and 42 mm, respectively. Load and deflection were converted to stress and strain using bending equations, taking yielding into consideration (Tommasini et al., 2005). Yield was determined using the 0.2% offset method where the offset modulus regression line intersects with the stress-strain curve. Tissue-level strength (referring to maximum stress for each beam) and post-yield strain (strain from yield point to failure) were then calculated from the stress-strain curve.

Porosity & Ash Content Measures:

Porosity was directly measured from high-resolution images of the right femora. A 5-mm thick cross section proximal to the midshaft was cleaned using a warm solution of oxidative detergent (OxiClean, Church & Dwight Co., Trenton, NJ, USA), rinsed and sonicated in PBS, then dried to a constant weight at 37°C. The section was imaged at 13μm voxel size using a nanotom m(Waygate Technologies LP, Pasadena, TX, USA) with scan settings of 150kV, 320μA, 500ms, 3 averages, filtering of 0.653 mm aluminum and 0.07 mm brass, 108 minute scan time. Daily calibration scans of a standard phantom of known densities, as well as a cortical bone phantom (Bone Diagnostic LLC, Spring Branch TX, USA) were completed to ensure quality and consistency of scans. Scans were reconstructed with datos|x (Version 2.6.1). Two slices were extracted from each image volume for analysis in ImageJ (Schneider et al., 2012). Each digital section was thresholded to segment bone pixels from pores and background. A 2mm² circular region of interest (ROI) was identified for the mid-cortex of the anterior quadrant, centered along the anterior-posterior axis, coinciding with the location the beams were milled from. Each ROI was analyzed to quantify pore number and area. Pores not entirely within the ROI were still included in the analysis but only the portion of the pore within the ROI was included in the calculations. Porosity was defined as the total pore area divided by the area of the ROI. Pore density was defined as the number of pores divided by the area of the ROI.

Ash, water, and organic content were measured for the anterior sextant as previously described [7]. Briefly, samples were defatted and then hydrated with a volume measurement taken, centrifuged and hydrated weight measured, dried to a constant weight in a 80°C oven and dried weight measured, ashed in a 600°C oven for 18 hours with an ashed weight measured. All measurements were normalized to hydrated weight (Bigelow et al., 2019; Tommasini et al., 2008).

Cross-link Measurements:

The distal end of the rectangular beams used for tissue-level mechanical testing was cut using a low-speed diamond circular saw (Buehler, Inc, Lake Bluff, IL USA). Each section (5 mm × 5 mm × 2.5 mm) was decalcified in Cal-Ex (CS510, Fisher, Waltham, MA) for two days at 4°C under constant agitation, replacing solution daily. Sample processing and HPLC detection of cross-links were similar to methods previously published (McNerny et al., 2015). Decalcified specimens were washed several times with distilled water, and phosphate buffered saline before dicing and sodium borohydride reduction. After rinsing again with distilled water, samples were denatured and then digested with TPCK-treated trypsin in a shaking water bath for 38 hours at 37°C. An aliquot of the trypsin digest was set aside for pyrrolic cross-link quantification and the remaining amount was subjected to acid hydrolysis in a 1:1 volume ratio with 12M HCl and hydrolyzed for 24 hours at 110°C. The pyrrole content was quantified using a colorimetric assay (Roberts et al., 2007). An aliquot of the acid hydrolysate was diluted and a colorimetric assay was performed to quantify the amount of hydroxyproline present (Brown et al., 2001). Another aliquot of the acid hydrolysate was cleaned using an SPE column (Bond Elut-Cellulose, 12102095, Agilent, Santa Clara, CA) eluted, lyophilized, and reconstituted to match initial flow conditions with pyridoxine added as an internal standard.

Cross-link quantification of DHLNL, HLNL, PYD, DPD, and PEN was executed on a Waters 1525 Binary Pump (Waters Corp., Milford, MA, USA), with an Atlantis T3 Column (Waters, PN: 186003728) kept at 30°. With a flow rate of 1 mL/min, the solvent gradient was held at 85% A (Solvent A = 0.12% heptafluorbutyric acid) 15% B (Solvent B = 50% acetonitrile) for 10 minutes, linearly changed from 85% A:15% B to 75%A:25% B from 10 to 30 minutes, and held from 30 to 60 minutes. The first injection with that gradient scheme detected PYD, DPD, PEN and a second injection with a post-column reaction detected DHLNL and HLNL. This post-column reaction was the addition of opthaldialdehyde solution via. a high pressure syringe pump (Nexus 5000, Chemyx, Stafford, TX, USA) at a rate of 0.25 mL/min (McNerny et al., 2015). See representative chromatogram in Supplemental Fig. 3. All cross-link concentrations were calculated from a standard curve, corrected for dilution and normalized to collagen content determined by hydroxyproline content. Standards of PYD, DPD (Quidel, San Diego, CA) and PEN (Cayman Chemical, Ann Arbor MI) were purchased from commercial vendors while DHLNL and HLNL were a generous gift from Simon Robins (University of Aberdeen). Each individual cross-link was quantified by integrating each representative peak and grouped for total immature (DHLNL + HLNL), total mature (PYD + DPD + pyrroles), total pyridinolines (PYD + DPD), and total enzymatic cross-links (total immature + total mature). Cross-link measurement ratios included DHLNL/HLNL, PYD/DPD, (total pyridinolines)/pyrroles, immature/mature, immature/(total pyridinolines), PEN/(total enzymatic), PEN/(total mature), and PEN/(total pyridinolines).

Statistics:

All statistical analyses were carried out using the R code (R Core Development Team. 2011. R: a language and environment for statistical computing. Vienna, Austria., n.d.) and data provided in the supplemental material. Any trait failing the Shapiro-Wilk normality test was log transformed. Pearson correlation coefficients were calculated for all variables against each other for the pooled data and for the wide and narrow groups. Those values not highlighted in the main body of text are included in the complete Pearson coefficient table in the supplementary material (Supplemental Table 2). Femora were assigned to narrow and wide groups (n = 15 each) based upon Tt.Ar/Le, excluding one outlier and two boundary cases. The supplemental material also includes a rank-ordered scatterplot of all Tt.Ar/Le values and their assigned subgroup (Supplemental Fig. 5). A sensitivity analysis was conducted to determine if splitting the dataset into two groups affected the outcomes. The sensitivity analyses were conducted with no borderline samples (primary analysis) and then after excluding the middle 2, 4, and 6 samples of the rank-ordered data. This sensitivity analysis demonstrated similar results for all conditions, the middle 2 were ultimately excluded since their Tt.Ar/Le values scores differed by less than 1%. Linear regression analyses were performed for the pooled, narrow, and wide groups, (Fig. 2–4) for age, Ct.TMD, and log(PEN/Matures) vs. mechanical properties, reporting adjusted R² and p-values. An ANCOVA was performed to determine if there were differences in slope or intercept for the wide and narrow linear regressions. A partial regression analysis was also performed to remove the common effects of age on mechanical properties, morphology, and composition. The added variable plots are included in the supplemental data (Supplemental Fig. 1).

Figure 2:

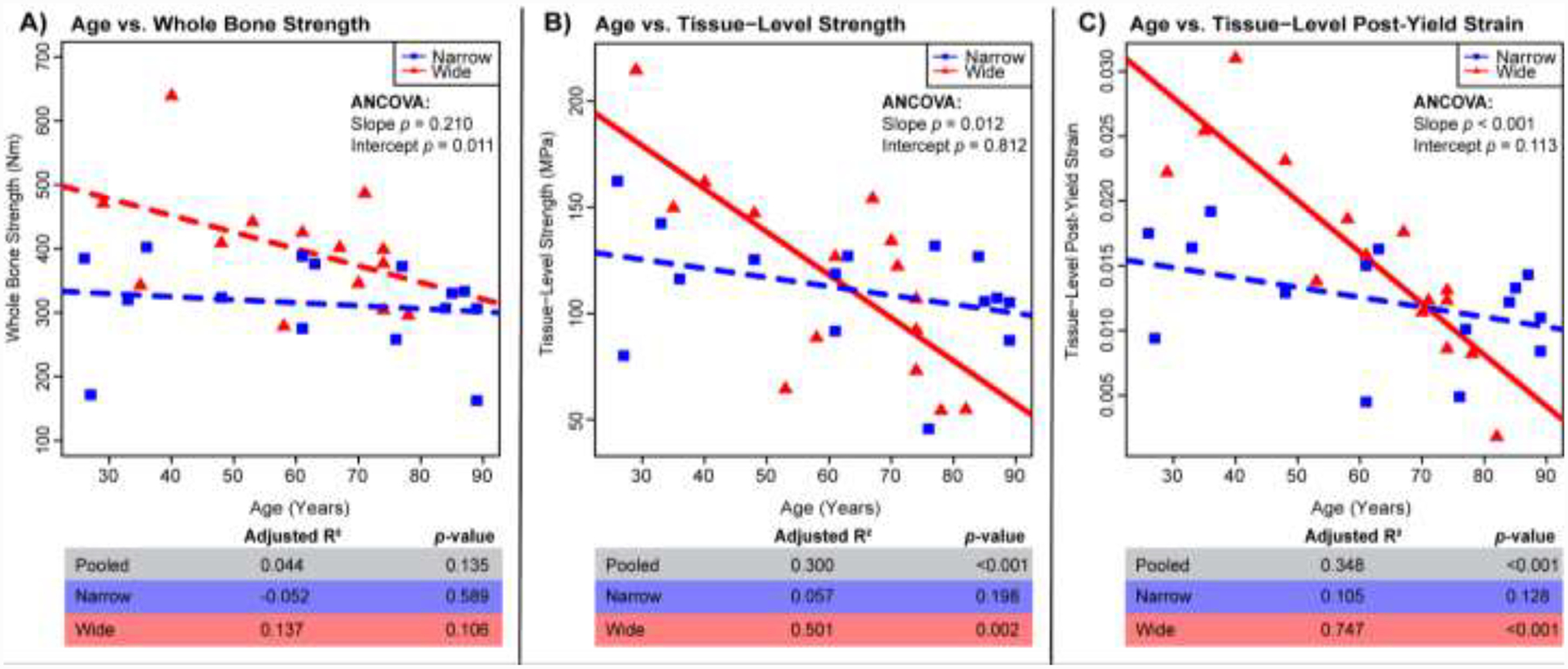
Regressions for age vs. mechanical properties: A) whole bone strength, B) tissue-level strength, C) tissue-level post-yield strain. Adj. R², and p-values for all samples pooled (n=33), wide (n=15), and narrow (n=15). Solid lines represent a significant regression (p-value < 0.05) and dashed lines represent a non-significant regression.

Figure 4:

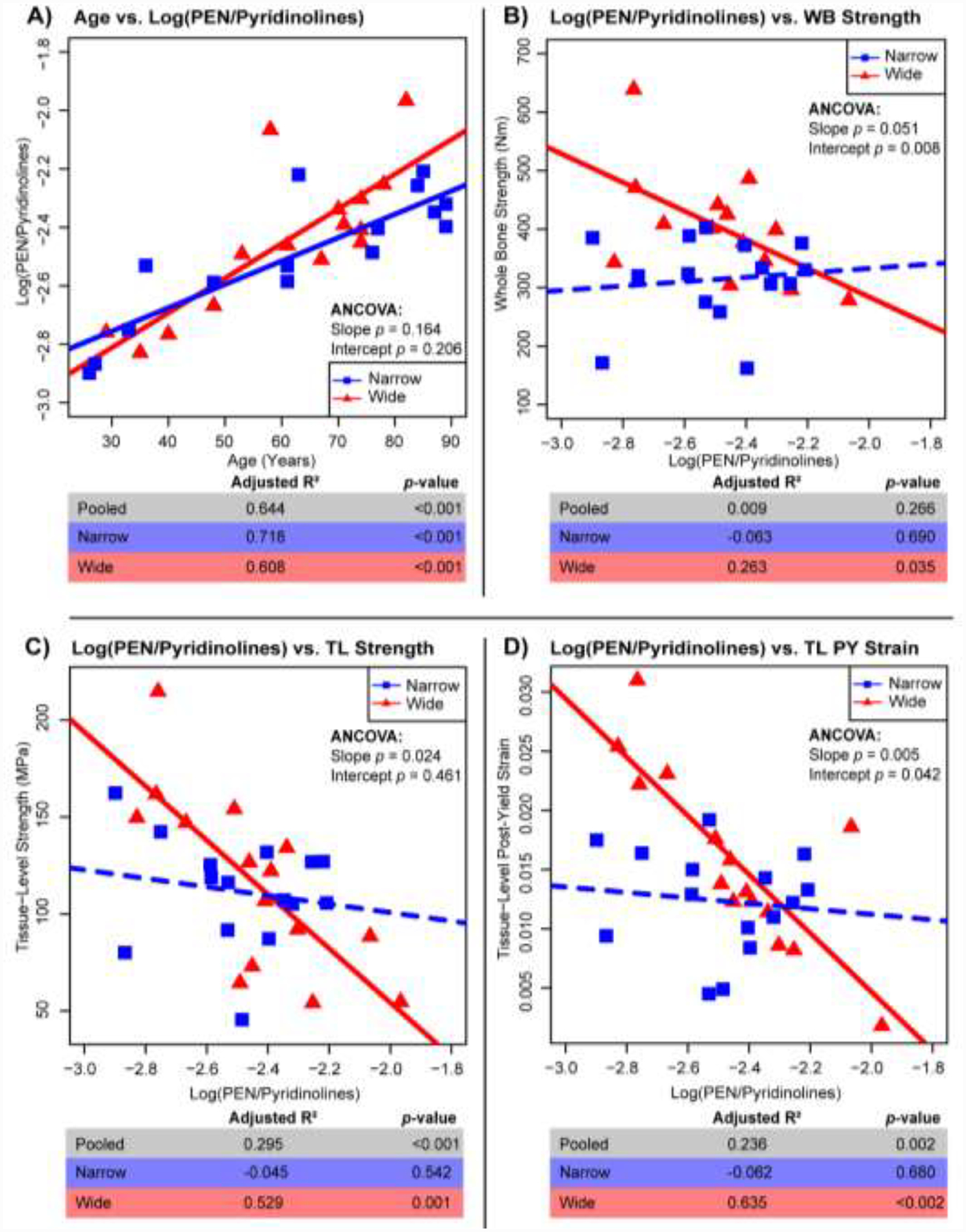
Regressions for Log(PEN/Pyridinolines) vs. age (A) and mechanical properties of whole bone (WB) strength (B), tissue-level (TL) strength (C) and tissue-level (TL) post-yield (PY) strain (D). Adj. R², and p-values for all samples pooled (n=33), wide (n=15), and narrow (n=15). Solid lines represent a significant regression (p-value < 0.05) and dashed lines represent a non-significant regression.

For the multivariate regressions, all traits (morphological, inorganic/organic/water content, cross-link measures) were initially selected using a Lasso regression (Engebretsen and Bohlin, 2019). This technique assigns a penalty to each parameter than can be driven to zero to minimize the sum of the squared error of the model. An automated backwards stepwise regression was then carried out followed by a manual stepwise regression to eliminate traits that were less significant (higher p-value) to the model in order to simultaneously minimize the number of variables and variance inflation factor (VIF). The lower the maximum VIF, the less collinearity exists between independent variables (O’brien, 2007). The goal was to simplify the model to 3 or 4 parameters. This limitation to 3–4 variables was decided upon due to the general “rule of ten” for multivariate regression that for every 10 data points there should be 1 explanatory parameter (Peduzzi et al., 1996). The adjusted R², p-value, and max(VIF) are reported for each manual elimination of traits.

Results:

Wide Femora Show Greater Declines in Mechanical Properties with Age than Narrow Femora

Mechanical parameters were regressed against age for all of the data (pooled) and for the wide and narrow groups separately (Fig. 2). Graphical outcomes show regressions for the wide and narrow groups. R² and p-values are reported for the regressions of the pooled data for comparison purposes. The wide group showed significant negative correlations with age for tissue-level strength (Adj. R² = 0.501, p = 0.002), tissue-level post-yield strain (Adj. R² = 0.747, p < 0.001) and borderline significance for whole bone strength (Adj. R² = 0.137, p = 0.108). In contrast, narrow bones showed non-significant associations between all mechanical parameters and age. Further, the associations differed between the narrow and wide groups for tissue-level strength (p = 0.012 for slope, ANCOVA), tissue-level post-yield strain (p < 0.001 for slope, ANCOVA) and whole bone strength (p = 0.011 for y-intercept, ANCOVA). For the tissue-level mechanical parameters, a cross-over of the narrow and wide regression lines occurred at approximately 63 years for tissue-level strength and approximately 70 years for tissue-level post-yield strain. When examining all of the data pooled, the correlations with age were non-significant for whole bone strength (Adj. R² = 0.044, p = 0.135), and significantly negative for both tissue-level strength (Adj. R² = 0.300, p < 0.001) and tissue-level post-yield strain (Adj. R² = 0.348, p < 0.001).

Correlations Between Bone Quality and External Size

Pearson correlation coefficients were calculated to identify which mechanical, compositional, and structural parameters correlate with external size (Table 1). Morphological measures of bone length, circumference, total area, marrow area, cortical area, and second moment of area correlated significantly and positively with Tt.Ar/Le, which was expected given their shared morphological associations. Whole bone strength, age, log(PEN), log(PEN/X) (where X = total mature, total pyridinolines or total enzymatic cross-links) and PYD/DPD were all significantly positively correlated with Tt.Ar/Le, whereas Ct.TMD was negatively correlated.

Table 1:

Pearson correlation coefficients between external size (Tt.Ar/Le) and mechanical parameters, morphology mineral content and cross-link measures. Significant correlations are shaded and marked with an asterisk.

	Mechanics			Morphology											Content
	Whole Bone Strength	Tissue-Level Strength	Tissue-Level Post-Yield Strain	Age	Height	Bone Length	Circumference	Total Area	Marrow Area	Cortical Area	Log(Porosity)	Pore Density	I.Max	I.Min	Ct.TMD	Water Content	Ash Content	Organic Content
Not Controlled for Age	0.45*	−0.32	−0.07	0.38*	0.38*	0.37*	0.92****	0.96****	0.52**	0.83****	0.30	−0.03	0.90****	0.93****	−0.52**	0.06	0.06	−0.18
Controlled for Age	0.55**	−0.13	0.22	NA	0.40*	0.37*	0.91****	0.96****	0.49**	0.81****	0.14	−0.04	0.91****	0.92****	−0.46**	0.19	−0.02	−0.27
	Cross-Link Measures
	Log(Pyrrole)	Log(DPD)	Log(PYD)	DHLNL	HLNL	Log(PEN)	Total Immature	Log(Total Pyridinolines)	Total Mature	Total Enzymatic	Log(DHLNL/HLNL)	PYD/DPD	Log(Pyridinoline/Pyrrole)	Log(Immature/Mature)	Immature/Pyridinoline	Log(PEN/Total Enzymatic)	Log(PEN/Total Mature)	Log(PEN/Total Pyridinolines)
Not Controlled for Age	−0.15	−0.15	0.01	−0.26	−0.12	0.35*	−0.23	−0.04	−0.09	−0.17	−0.13	0.38*	0.07	−0.16	−0.26	0.43*	0.42*	0.42*
Controlled for Age	−0.05	−0.23	−0.02	−0.15	−0.13	0.10	−0.16	−0.08	−0.06	−0.12	−0.04	0.51**	−0.04	−0.10	−0.14	0.22	0.20	0.20

p value:

^*< 0.05,

^**< 0.01,

^***< 0.001,

^****< 0.0001.

Two parameters stood out in the associations with Tt.Ar/Le in (Table 1) as measures of mineral quantity and collagen quality that prompted further examination: Ct.TMD and log(PEN/Pyridinolines). Log(PEN/Pyridinolines) was examined instead of other pentosidine measures (log(PEN), log(PEN/X) ratios) because it was the simplest AGE measure that still accounted for some enzymatic cross-link formation. All pentosidine measures showed similar correlations with mechanical properties (Supplemental Table 2). The wide (R²=0.218, p=0.045) but not the narrow group showed a significant negative correlation between Ct.TMD and age (Fig. 3). Ct.TMD correlated significantly with whole bone strength, tissue-level strength and tissue-level post-yield strain for both the narrow and wide groups. The only exception being a nonsignificant association between Ct.TMD and whole bone strength for the narrow group. However, sorting the data into these groups revealed novel differences for these associations. The wide group showed greater whole bone strength (p<0.001, ANCOVA), tissue-level strength (p=0.061, ANCOVA) and tissue-level post-yield strain (p<0.001, ANCOVA) compared to the narrow group for any Ct.TMD value.

Figure 3:

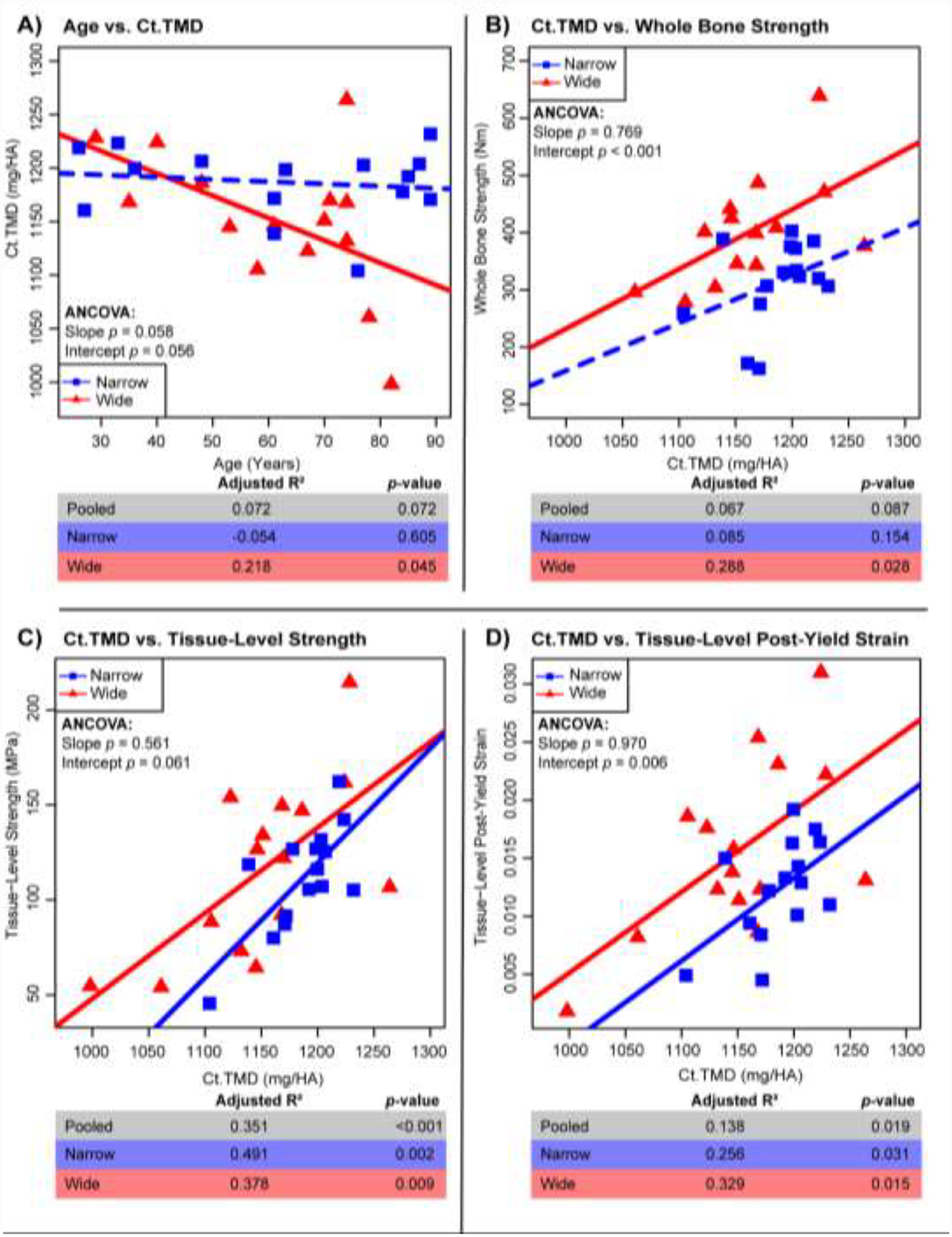
Regressions for Ct.TMD vs. age (A) and mechanical properties of whole bone strength (B), tissue-level strength (C) and tissue-level post-yield strain (D). Adj. R², and p-values are shown for pooled samples (n=33), the wide group (n=15), and the narrow group (n=15). Solid lines represent a significant regression (p-value < 0.05) and dashed lines represent a non-significant regression.

Both wide and narrow groups showed significant positive correlations between age and log(PEN/Pyridinolines) (Fig. 4A). However, only the wide group showed significant correlations between log(PEN/Pyridinolines) and whole bone strength (R² = 0.283; p < 0.035), tissue-level strength (R2 = 0.529; p < 0.001), and tissue-level post-yield strain (R² = 0.635; p < 0.002) (Fig. 4B–D). All mechanical correlations with log(PEN/Pyridinolines) for the wide group were negative, indicating that accumulation of pentosidine relative to pyridinoline cross-links was associated with weaker and more brittle bones at both the whole bone and tissue levels. Importantly, these associations were not observed for the narrow group despite showing similar ranges of log(PEN/Pyridinolines) ratios.

The Aging Pattern Differs Between Narrow and Wide Bones

The findings that the age-related change in Ct.TMD (Fig. 3A), but not log(PEN/Pyridinolines) (Fig. 4A), differed between wide and narrow bones raised the question of what other traits are different in the aging profile between the wide and narrow bones. The Pearson’s correlation coefficient for each morphological group (pooled, wide, and narrow) for age vs. all parameters was determined (Table 2). For numerous parameters, the Pearson’s correlation coefficient for age associations was significant for pooled and either narrow or wide, but often not all three. The narrow group showed significant increases with age for Tt.Ar/Le, cortical circumference, Tt.Ar, Ma.Ar, I_min and significant decreases for log(DHLNL/HLNL) and immature/pyridinolines. In contrast, the wide group showed significant decreases in Ct.TMD and significant increases in log(Porosity) with age. Log(PEN) and all log(PEN/x) ratios increased significantly with age for wide, narrow and pooled samples. The majority of the correlation coefficients did not exceed ~0.3–0.5, suggesting that there are multiple traits changing between the narrow and wide phenotypes, and a combination of traits might be more suitable for predicting the mechanical properties.

Table 2:

Pearson correlation coefficients showing age-association for mechanical properties, morphology, mineral content and cross-link measures and stratified into pooled (n=33), wide (n=15), and narrow (n=15) groups. Significant correlations are shaded and marked by an asterisk;

	Mechanics			Morphology											Content
	Whole Bone Strength	Tissue-Level Strength	Tissue-Level Post-Yield Strain	(Total Area/Length)	Height	Bone Length	Perimeter	Total Area	Marrow Area	Cortical Area	Log(Porosity)	Pore Density	I.Max	I.Min	Ct.TMD	Water Content	Ash Content	Organic Content
Pooled	−0.27	−0.57***	−0.61***	0.38*	0.03	0.06	0.41*	0.33	0.2	0.28	0.47**	0.02	0.20	0.36*	−0.32	−0.33	0.23	0.21
Narrow	−0.15	−0.35	−0.41	0.68**	0.03	0.39	0.74**	0.73**	0.56*	0.21	0.49	0.15	0.49	0.69**	−0.15	−0.35	0.24	0.32
Wide	−0.45	−0.73**	−0.87****	0.24	−0.13	−0.41	0.07	−0.05	−0.39	0.26	0.53*	−0.36	−0.13	0.22	−0.52*	−0.35	0.12	0.37
	Cross-Link Measures
	Log(Pyrrole)	Log(DPD)	Log(PYD)	DHLNL	HLNL	Log(PEN)	Total Immature	Log(Total Pyridinolines)	Total Mature	Total Enzymatic	Log(DHLNL/HLNL)	PYD/DPD	Log(Pyridinoline/Pyrrole)	Log(Immature/Mature)	Immature/Pyridinoline	Log(PEN/Total Enzymatic)	Log(PEN/Total Mature)	Log(PEN/Total Pyridinolines)
Pooled	−0.27	0.15	0.06	−0.34	0	0.77****	−0.21	0.09	−0.08	−0.15	−0.3	−0.2	0.29	−0.2	−0.36*	0.84****	0.84****	0.81****
Narrow	0.02	0.4	0.25	−0.47	0.17	0.87****	−0.2	0.3	0.25	0.02	−0.60*	−0.33	0.31	−0.36	−0.54*	0.85****	0.87****	0.86****
Wide	−0.4	−0.26	−0.29	−0.15	−0.17	0.63*	−0.19	−0.28	−0.36	−0.31	0.09	−0.13	0.07	0.2	0.15	0.81***	0.82***	0.80***

p-value:

^*< 0.05,

^**< 0.01,

^***< 0.001,

^****< 0.0001.

Predictors of Whole Bone Strength

To create a multivariate model for each mechanical property for the entire dataset, the number of parameters were reduced using Lasso regression, automatic backwards stepwise regression, and then manually removed to minimize the number of model variables and minimize the maximum VIF while maintaining a comparable Adj. R² (Tables 3–5). The final model for whole bone strength (Table 3) using only three traits - Ct.Ar, Ct.TMD, log(PEN/Mature) - had strong predictive value (Adj. R² = 0.749, p < 0.001, Max. VIF = 1.04) and the Adj. R² is greater than any of those three parameters as individual linear regressions. Apart from Ct.Ar, the Adj. R² for this model’s variables when regressed against whole bone strength independently are below 0.1 and non-significant. This demonstrates that some combination of optimized parameters that may not hold individual regressive power, can be combined to provide better prediction of whole bone strength.

Table 3:

Multivariate analysis to create a model for whole bone strength using all pooled samples (n = 31, some parameters were not complete across the dataset and unable to be included). Each column represents a model using all non-grayed out parameters, with reported β-coefficients for each parameter and each model’s Adj. R², p-value, and maximum VIF. Moving left to right, a backwards stepwise regression is performed. The final model with three parameters is highlighted, and each individual variable for the final model is also presented alone.

Whole Bone Strength Multivariate Regression
	β-Coefficient
Ct.Area	0.861	0.918	0.926	1.08	1.14	1.12	1.07	1.08
Ct.TMD	0.639	0.755	0.561	0.484	0.475	0.492	0.586		0.624
Log(PEN/Matures)	−54.2	−67.4	−88.7	−97.2	−111	−124				−97.91
Log(Pyrrole)	283	273	360	310	206
HLNL	−602	−497	−648	−454
Height	372	323	273
Log(Pyridinolines/Pyrrole)	−119	−127
Log(Porosity)	−37.5
Adj. R2	0.868	0.861	0.850	0.820	0.791	0.749	0.667	0.590	0.067	0.022
p -value	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.087	0.207
Max(VIF)	2.51	2.50	1.73	1.45	1.07	1.04	1.00

Table 5:

Multivariate analysis to create a model for tissue-level post-yield strain using all pooled samples. Each column represents a model using all non-grayed out parameters, with reported β-coefficients for each parameter and each model’s Adj. R², p-value, and maximum VIF. Moving left to right, a backwards stepwise regression is performed. The final model with three parameters is highlighted, and each individual variable for the final model is also presented alone

Tissue-Level Post-Yield Strain Multivariate Regression
	β-Coefficient (× 10−3)
Age	−0.118	−0.131	−0.148	−0.175	−0.2	−0.181	−0.161	−0.192
Log(Pyrrole)	29.3	30.9	30.6	31.7	28.5	26.5	22.9		31.8
Ct.Area	0.0276	0.027	0.0341	0.0348	0.0295	0.0215				0.00054
PYD/DPD	−6.01	−5.8	−5.41	−4.96	−3.57
Organic Congent	−177	−187	−166	−124
Log(Porosity)	−6.42	−4.81	−3.54
Height	19.2	15.8
Pore Density	−0.328
Adj. R2	0.652	0.626	0.612	0.596	0.522	0.505	0.451	0.348	0.218	−0.032
p -value	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.004	0.970
Max(VIF)	1.93	1.84	1.63	1.47	1.48	1.13	1.08

Predictors of Tissue-Level Strength

For tissue-level strength, the final model (Table 4), with explanatory parameters of age, Ct.TMD and log(DHLNL/HLNL), predicted a majority of the variance (Adj. R² = 0.561, p < 0.001, Max. VIF = 1.19). Similarly, to whole bone strength, the model with all three variables performed better than any parameter individually. Log(DHLNL/HLNL) did not show a significant association with tissue-level strength, while the Adj. R² for age (0.300) and Ct.TMD (0.351) were both significant but less than the Adj. R² for the multivariate model.

Table 4:

Multivariate analysis to create a model for tissue-level strength using all pooled samples. Each column represents a model using all non-grayed out parameters, with reported β-coefficients for each parameter and each model’s Adj. R², p-value, and maximum VIF. Moving left to right, a backwards stepwise regression is performed. The final model with three parameters is highlighted, and each individual variable for the final model is also presented alone

Tissue-Level Strength Multivariate Regression
	β-Coefficient
Age	−0.956	−0.889	0.256	−9.832	−1.14
Ct.TMD	0.350	0.327	0.340	0.345		0.440
Log(DHLNL/HLNL)	−15.9	−15.8	−16.2				−7.69
Log(Pyrrole)	89.5	74.4
Ct.Ar	0.0956
Adj. R2	0.602	0.579	0.561	0.495	0.300	0.351	−0.014
p-value	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.464
Max(VIF)	1.29	1.26	1.19	1.11

Predictors of Tissue-Level Post-Yield Strain

Of the mechanical property models, tissue-level post-yield strain had the lowest Adj. R², but the model still predicted a majority of the variance. The final three variables in the model used were age, Ct.Ar, and log(Pyrrole) (Table 5; Adj. R² = 0.510, p < 0.001, Max. VIF = 1.13). Both age and log(Pyrrole) were significant contributors when examined alone (Age: Adj. R² = 0.348, p < 0.001, log(Pyrrole) Adj. R² = 0.218, p = 0.003) whereas Ct.Ar regressed against tissue-level post-yield strain was non-significant.

Discussion:

The novelty of these results are two-fold. First, the age-related deterioration in mechanical properties varies with external bone size (wide or narrow) even when taken at a tissue-level (milled beams) in the male femoral diaphysis. Secondly, a thorough characterization of bone morphology, composition, and mechanics combined with multivariate models highlights the main contributors to whole-bone and tissue-level mechanical properties. This work supports our hypothesis that wide human male femora show greater age-related declines in whole bone and tissue-level mechanical properties than narrow femora and that the mechanical declines are dependent on compositional properties. Although the mechanical properties of the wide group were greater at a younger age, the age-related decline in mechanical properties was more pronounced in the wide group (Fig. 2) and more distinct at the tissue-level (Fig. 2B,C). The distinction between wide and narrow was masked when examining the pooled data, which exhibited intermediate declines in strength with age (Fig 2). Thus, the age-related deterioration in mechanical properties varies with external bone size, even for local and tissue-level mechanical properties. The whole bone strength of the wide and narrow groups converged and had equivalent mechanical properties around 60–70 years of age (Fig. 2). Beyond this age, tissue-level properties were greater in the narrow group. Overall, this outcome motivated the examination of additional traits such as structure, composition, and collagen cross-links to explain this differential decline in tissue-level strength.

Traits such as Ct.TMD, PYD/DPD and log(PEN/Pyridinolines) correlated with Tt.Ar/Le (Table 1). When sorted into wide and narrow groups, Ct.TMD, log(Porosity), log(DHLNL/HLNL), and log(Immature/Pyridinolines) correlated with age for exclusively the narrow or the wide groups (Table 2, Fig. 3A). This suggested that there are age-related changes that are unique to each bone morphology that are impacting composition, structure and ultimately mechanical performance. When examining the relationship between age, log(PEN/Pyridinolines), and mechanical properties, distinguishing whether age or log(PEN/Pyridinolines) is the driver of mechanical properties can be difficult since log(PEN/Pyridinolines) strongly correlates with age (Fig. 4A). When the common effects of age were removed by partial correlation analysis (Supplemental Fig. 1, Supplemental Table 3), the negative trends for the wide group remained and were non-significant, whereas the narrow group showed positive associations between log(PEN/pyridinolines) and whole bone strength, tissue-level strength, and tissue-level post-yield strain but were still non-significant.

Sorting the samples into narrow and wide subgroups provided evidence that there are important inter-individual differences in how bone composition and tissue-level strength and ductility change with aging. When pooling the data and treating the population as being homogenous, an important parameter for the multivariate regressions of both whole bone strength (Table 3) and tissue-level post-yield strain (Table 5) was Ct.Ar,, a measure of the amount of bone. This emphasis on Ct.Ar does not invalidate the earlier conclusions that a bone’s mechanical performance with age differs between the wide and narrow subgroups. The initial reduction of variables by Lasso regression is not well suited to distinguish relative importance between co-linear variables and many of these cross-sectional morphology measures correlate strongly with one another. The multivariate regressions show that simplified models with 3–4 variables, incorporating aspects of morphological and compositional measures better predict mechanical outcomes than any individual trait alone when all the data are pooled.

For the tissue-level mechanical properties basic biomechanical theory suggests porosity as a very important parameter. There was a significant correlation between log(Porosity) vs. tissue-level strength and post-yield strain (Pearson correlation coefficients = −0.59, and −0.49, respectively; Supplemental Table 2). However, log(Porosity) also significantly correlated with Ct.TMD (−0.64). Therefore, when used in the multivariate models, log(Porosity) may contribute to the strong predictive value of Ct.TMD in tissue-level strength. For the multivariate model of tissue-level post-yield strain, elimination of log(Porosity) did not significantly reduce the amount of variance explained (0.612 vs. 0.596). While porosity is physically important, in this study porosity was redundant with Ct.TMD as a covariate and did not add substantial explanation to the multivariate model. Clinically, this redundancy between Ct.TMD and porosity may be useful since such a high resolution scan for porosity measurements is impractical. Many of these traits in the final predictive models, including Ct.TMD and Ct.Ar can be measured non-invasively.

Adding collagen cross-link measures to the models, the predictive capacity is increased. Often, AGEs alone are used in fracture risk prediction as an estimate of collagen quality (Abraham et al., 2015; Granke et al., 2015), however, our data highlights the importance of combinatorial measures of enzymatic collagen cross-links. The final multivariate models included Ct.Ar., Ct.TMD, log(PEN/Matures) for whole bone strength; age, Ct.TMD, log(DHLNL/HLNL) for tissue-level strength; and age, log(Pyrrole), Ct.Ar. for tissue-level post-yield strain. The importance of log(PEN/Matures) for whole bone strength, log(DHLNL/HLNL) for tissue-level bone strength, and log(Pyrrole) for tissue-level post-yield strain, provides insight into the relative mechanical contribution of different collagen cross-link species across different length scales. The log(DHLNL/HLNL) ratio raises the question of how lysine hydroxylase or hydroxylation impacts tissue-level strength. Of these three relationships, the only collagen cross-link parameter that significantly correlated with its respective mechanical property alone was log(Pyrrole) vs. tissue-level post yield strain. But, the inclusion of log(PEN/Matures) for whole bone strength and log(DHLNL/HLNL) for tissue-level strength did improve the predictive ability each respective model. It has also been established that PEN negatively impacts post-yield behavior (Saito et al., 2015), but these results suggest it is an important factor for decreasing strength at the whole bone level as well. Given that many of these parameters correlate (e.g., age and PEN (Table 2); Ct.TMD and porosity), the multivariate regression results should be interpreted with a degree of caution and understanding that in a larger dataset, which factors are the main contributors may be different. Ideally, when using a Lasso regression, a training set is used to develop the model and a testing set is used to evaluate the efficacy of the model. Due to the sample size of this study and efforts to maximize statistical power, we were unable to divide the data into a training and testing set. Additionally, while PEN was measured as a surrogate marker for total AGE content here, a thorough characterization of all AGEs (Thornalley et al., 2003) found in human bone and their relative abundance is needed to isolate which AGEs are contributing most to the age-related decline in mechanical performance.

Previous studies suggest that femora change their shape by periosteal or endosteal expansion (Ruff et al., 1998). However, this paradigm breaks down when examining subgroups within a population, like wide or narrow. When examining the Pearson correlation coefficients (Supplemental Table 2) for the pooled dataset: circumference, Tt.Ar/Le, and log(Porosity) significantly increase with age. When just examining the narrow group: circumference, Tt.Ar/Le, Tt.Ar, and Ma.Ar significantly increase with age. While, for the wide group only log(Porosity) significantly increased with age. Suggesting that there was periosteal expansion and endosteal resorption in the narrow group only, while the wide group became more porous. The physical activity history and health status of each donor were unknown, except that the none of the femora showed evidence of a prior fracture. Exercise and loading affect cross-sectional bone morphology (Daly and Bass, 2006; Ferry et al., 2011; Rantalainen et al., 2015), and the appearance of wide or narrow phenotypes occurs in early adolescence (Bhola et al., 2011) but it remains unclear what are the exact determinants of bone morphology. There is evidence that earlier lifetime physical activity may impact morphology later in life. Differences between throwing vs. non-throwing arms show differences in cross-sectional morphology of the humerus within the same individual that can persist after years of detraining (Warden et al., 2014). Likewise, elderly men who exercise early in life show lasting impacts on cortical morphology independent of current physical status (Nilsson et al., 2014). While loading may play a role, it remains unclear how underlying osteoblast, osteoclast or osteocyte behavior affect total cross-sectional area morphology, especially at the periosteal or endosteal surfaces. Correlations exist between Tt.Ar/Le and osteon area, resorption, and formation (Goldman et al., 2014) suggesting that the cellular behavior between bone morphologies may be different.

The tissue-level analysis was carried out on the anterior beams and future work should establish whether there are regional differences in composition. Predictive models to assess the contribution of morphology, structure, and composition to bone mechanical properties have mostly been focused to the proximal femur (Boehm et al., 2008; Johannesdottir et al., 2017; Le Corroller et al., 2012). However, the proximal femur has a complex morphology and loading scheme. The results presented herein for the femoral diaphysis may guide future experimental or computational models that may be better suited to the complex morphologies and loading schemes at other anatomical locations with high age-related fractures, including but not limited to the proximal femur, pelvis, and proximal humerus (Court-Brown and Caesar, 2006). This study was also limited to male donor femora. Further collections and analyses will be carried out on female specimens to determine if similar external size dependent differences exist for mechanical, structural, and morphological properties, and to test for sex-specific differences in aging structure and composition (Djonic et al., 2011; Patton et al., 2019).

The distinction between wide and narrow begins to explain why certain individual’s bones might show an age-related decline in strength whereas others maintain strength. While the division into wide versus narrow groups identified different aging patterns for bone composition, bisecting the samples into just two groups may be too blunt of a tool. Aging is a continuum, of which it appears that individuals may follow different patterns of bone loss. Our results suggest that fracture risk prediction tools could be more personalized when incorporating static measures, by utilizing several variables besides just Tt.Ar/Le or the current clinical usage of DXA-based measurements to better identify those at greatest risk of fracture.

Conclusions

This study investigates two morphological phenotypes of human femoral midshafts - wide and narrow – which show different trajectories in mechanical, morphological, and compositional properties with age. This unbalanced aging process may explain why use of DXA alone is insufficient to predict all individuals at risk of fracture. Wide bones exhibit initially greater mechanical properties than narrow bones, but have sharper declines in all mechanical properties with age than narrow bones. This decline may be explained by a detrimental increase in AGEs, porosity, and decrease in Ct.TMD. These traits have limited predictive power alone. Therefore, multiple parameters should be investigated to generate predictive models for fracture risk. A comprehensive characterization of collagen, mineral and morphology allowed for multivariate analysis which produced strong predictive models of mechanical properties. The final multivariate models included Ct.Ar, Ct.TMD, log(PEN/Matures) for whole bone strength; age, Ct.TMD, log(DHLNL/HLNL) for tissue-level strength; and age, log(Pyrrole), Ct.Ar for tissue-level post-yield strain. Modeling of these changes may help inform future studies, better predict the aging process for an individual and open doors for new intervention or therapies.

Highlights:

• Cortical midshaft morphology predicts age-related declines in mechanical properties

• Wide bones exhibit greater declines in mechanical properties than narrow bones

• Cortical area, mineral density, and collagen glycation predict whole bone strength

• Age, mineral density, and immature cross-links predict tissue-level strength

• Age, cortical area, and mature cross-links predict tissue-level post-yield strain

• Personalized view of traits that contribute to fragility is warranted

Abbreviations:

Ct.TMD

Cortical tissue mineral density

DHLNL

dihydroxylysinornorleucine

HLNL

hydroxylysinonorleucine

PYD

pyrdinoline

DPD

deoxypyridinoline

PEN

pentosidine

BMD

bone mineral density

DXA

dual X-ray absorptiometry

LH

lysyl hydroxylases

LOX

lysyl oxidases

AGEs

advanced glycation end products

Tt.Ar

total area

Ct.Ar

cortical area

Ma.Ar

marrow area

VIF

variance inflation factor