Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Dec 1;5(49):31880–31890. doi: 10.1021/acsomega.0c04724

Interactions Between Hydrated Cerium(III) Cations and Carboxylates in an Aqueous Solution: Anomalously Strong Complex Formation with Diglycolate, Suggesting a Chelate Effect

Masahito Oh-e †,*, Akira Nagasawa ‡
PMCID: PMC7745448  PMID: 33344842

Abstract

graphic file with name ao0c04724_0012.jpg

Interactions between hydrated Ce3+ and various carboxylates are of fundamental interest. Anomalously strong interactions with Ce3+ occur when diglycolic acid (DGA) is added into a Ce3+ aqueous solution, unlike various other carboxylic acids. Herein, the complex-formation constants of Ce3+ with these acids are evaluated via absorption and emission spectra. Hydrated Ce3+ emits fluorescence with unity quantum yield; however, addition of various carboxylates statically quenches the fluorescence when Ce3+–carboxylate complexes form because the fluorescence lifetime is constant irrespective of the carboxylate concentration. In the observed static quenching, the complex-formation constants obtained from the absorption and emission spectra (Kabs and Kem) agree well. The binding of Ce3+ by the conjugate Lewis bases, i.e., carboxylates, is approximately inversely proportional to the pH. Adding DGA into the system also statically quenches the fluorescence, but far more efficiently, even in a much weaker solution. We rigorously deduce Kabs and Kem of Ce3+ with DGA without any approximation using comparable concentrations. Careful fittings provide equivalent Kem and Kabs values, and by varying the pH and ionic strength, we confirm that this equivalence is an inherent property of the Ce3+−DGA system. The Lewis acid–base theory cannot explain why DGA binds to Ce3+ ∼1000 times more strongly than the other carboxylates. This anomalously strong binding may be due to a chelate effect caused by the DGA’s central oxygen atom, which forms a five-membered ring with the conjugate Lewis bases of DGA; double chelate rings can also form, while bis-deprotonated DGA binds to Ce3+, facilitated by the central oxygen. Therefore, DGA enables efficient quenching through the chelate effect when it binds to Ce3+.

Introduction

Highly coordinated lanthanoid cations have attracted considerable attention for their optical, magnetic, and catalytic properties, and therefore, lanthanoid cations play an important role in many interesting applications such as phosphors and sensors.1−3 Owing to their luminescent nature, lanthanoid cations have often been incorporated into inorganic phosphors for luminescent applications.4−6 Trivalent lanthanoid cations have also been used for sensor applications,7 e.g., a sensor for detecting physiological phosphates and phosphate-containing biomolecules.8 Among rare-earth elements, cerium is the most abundant and is thus an inexpensive, accessible raw material. In addition, its trivalent cation, Ce3+, exhibits some biologically important properties such as antiseptic and virus-removal characteristics9−11 and potential anticancer activities,12 and it promotes the proliferation of fibroblasts and osteoblasts.13 Because Ce3+ is similar to Ca2+ in terms of its outermost electron configuration, Ce3+ is expected to provide various biological effects, which enables replacing biomolecules in vivo.14,15 Therefore, understanding the fundamental properties of Ce3+ and its interactions with other molecules is extremely important, especially from the viewpoint of potential applications.

Hydrated Ce3+ doped into a host material has been studied, and its absorption and emission bands are well assigned.16,17 For Ce3+ doped into lanthanum(III) ethylsulfate nonahydrate (Ce:LaES), five absorption bands appear in the region between 37 and 51 × 103 cm–1(196–270 nm) at room temperature, whereas at the liquid-nitrogen temperature, two resolved fluorescence bands appear at 30 and 32 × 103 cm–1 (313–333 nm). Nine aqua ligands in [Ce(H2O)9]3+ are arranged around the center Ce3+, defining the vertices of a triaugmented triangular prism with a tricapped trigonal prismatic molecular geometry. The radius of Ce3+ is similar to that of La3+; thus, Ce3+ can be doped into LaES without significantly changing its structure. The ground 2F(4f1) multiplet is split into 2F5/2 and 2F7/2 by the spin-orbit coupling of a cerium 4f electron, while the excited state 2D(5d1) is also separated into five Kramers doublets by the ligand–field interactions and spin-orbit coupling of a cerium 5d electron.

In an aqueous solution, hydrated Ce3+ cations exhibit five absorption bands, which coincide with those observed using Ce:LaES. However, an additional absorption band appears at 34 × 103 cm–1 (294 nm), which is attributed to a partially dissociated species of the coordinated aqua ligands, i.e., [Ce(H2O)8]3+, which is in equilibrium with [Ce(H2O)9]3+.18−20 Increasing the temperature of the aqueous solution changes the absorption spectrum, except at some isosbestic points, and increases the intensity of the absorption band at 34 × 103 cm–1. In the Ce:LaES crystal, even if the amount of doped Ce3+ is increased or the crystal is thickened, the absorption band near 34 × 103 cm–1 does not appear. In addition, adding an acid such as HClO4 does not change the absorption spectrum, which suggests that the additional absorption band cannot be attributed to chemical species that can be created by the proton dissociation of the coordinated water molecules such as [Ce(H2O8(OH))]2+. The 2D Kramers doublet does not split into more than five states. In this way, [Ce(H2O)8]3+ can coexist with [Ce(H2O)9]3+ in the aqueous solution.

According to X-ray scattering studies on the structures of hydrated lanthanoid metal ions in aqueous solutions,21−23 the partial dissociation of a water ligand out of [Ce(H2O)9]3+ is not necessarily anomalous. The lanthanoid ions from La3+ to Nd3+ have nine-water coordinate structures, and Nd3+ to Tb3+ have both nine-water and eight-water coordinate structures.

When Ce3+ is in an aqueous solution, the fluorescence shifts to 28 × 103 cm–1(357 nm), which is a lower wavenumber (longer wavelength) than that from Ce3+ in Ce:LaES. The fluorescence excitation spectra of the aqueous Ce3+ solution are in good agreement with the absorption spectra. Even if the hydrated Ce3+ cations in the aqueous solution are excited in the five absorption bands of [Ce(H2O)9]3+ or in that of [Ce(H2O)8]3+, i.e., 34 × 103 cm–1, the fluorescence maximum remains unchanged at 28 × 103 cm–1 with unity quantum yield.16,19 These observations suggest that when [Ce(H2O)9]3+ is photoexcited, one water molecule is dissociated in 100% yield to become *[Ce(H2O)8]3+, i.e., the fluorescence of the aqueous solution is due to the excited [Ce(H2O)8]3+.

The fluorescence lifetime of Ce3+ in an aqueous solution is 45 ns, whereas Ce3+ in Ce:LaES decays in 27 ns. A very fast aqua ligand dissociation of [Ce(H2O)9]3+ in the excited state was previously investigated;19 one water molecule dissociates from [Ce(H2O)9]3+ in an aqueous solution within the short time of 0.4 ns and produces the excited-state ion, *[Ce(H2O)8]3+. Because the water molecules rearrange in the coordination sphere faster than they dissociate, the eight-water coordinate structure would be favorable in the excited state.19

Along with the structure and fluorescence of Ce3+ in an aqueous solution, interactions (and hence complexes) between Ce3+ and the anions of organic compounds such as carboxylates, which are the conjugate Lewis bases, have become increasingly important.24 This importance is rooted in the potential applications of trivalent lanthanoid ions in diverse areas such as optoelectronics,25 biology,26,27 and pharmaceutical sciences.28 Probing the change in fluorescence from Ce3+ enables understanding the interactions between Ce3+ and other chemical species such as carboxylates because the luminescence is highly sensitive to the environment.29 Generally, the fluorescence of Ce3+ is known to be normally quenched upon complexation with carboxylates.30,31 This suppression of the fluorescence is explained by an electron transfer from the excited 5d electron of Ce3+ to a closely lying π* orbital of a ligand. An electron can also be completely transferred from the excited Ce3+ to persulfate anions via photooxidation.32 However, some carboxylates do not suppress the fluorescence of Ce3+, for example, tris(pyrazine-2-carboxylato)cerium(III) is known to be emissive.33,34 The metal-to-ligand charge transfer occurs predominantly from Ce3+ to the ligand’s pyrazine moiety, which is strongly electron accepting. The interactions between trivalent metal ions including Ce3+ and polymethacrylates in aqueous solutions have also been investigated.35

In this study, we discover anomalously strong interactions between hydrated cerium(III) cations (Ce3+) and diglycolic acid (DGA), also known as 2-(carboxymethyloxy)acetic acid, while studying the complex formation of hydrated Ce3+ with a series of carboxylic acids in aqueous media. Remarkably, a DGA solution more efficiently quenches the fluorescence from Ce3+ than the other carboxylic acid solutions, even though it is two to three orders of magnitude less concentrated. These interactions can be observed by adding different carboxylic acids to the solutions and then observing the changes in the absorption and fluorescence of hydrated Ce3+. We carefully determine the constants of complex formation from the absorption and emission spectra, Kabs and Kem, when hydrated Ce3+ ions interact with the various types of carboxylic acids. The focus is on how the constants of complex formation between Ce3+ and DGA can be rigorously determined, and whether the individual complex-formation constants, Kabs and Kem, obtained from the absorption and emission spectra are the same or different. We also analyze the obtained Kabs and Kem in the aqueous Ce3+–DGA system to separate the apparent complex-formation constants, Kabs and Kem, into those of individual species in equilibrium. Comparing Kabs and Kem, which depend on the type of carboxylate, enables interpreting the interactions between Ce3+ and various carboxylates. Understanding the fundamental behavior of Ce3+ in aqueous media with carboxylic acids remains extremely important from the viewpoint of applications that use Ce3+.

Results and Discussion

As the concentration of carboxylic acid increases, the absorption spectra of Ce3+ in aqueous solutions gradually change shape, except at some isosbestic points. Some new peaks appear with the increasing DGA concentration, while others decrease in intensity. The spectrum of a pure Ce3+ solution has an absorption maximum (εmax) of 726 M–1 cm–1 at 40 × 103 cm–1 (250 nm). Figure 1a shows how the absorption spectra of Ce3+ change as a function of the concentration of DGA. Figure 1b shows the difference spectra between the Ce3+−DGA solutions and their Ce3+ counterpart, thus representing only the changes in the spectra.

Figure 1.

Figure 1

Open in a new tab

(a) Changes in the absorption spectra of hydrated Ce3+ ions when diglycolic acid (DGA) aqueous solutions with various concentrations are added at room temperature (I = 0.1 M, pH 3.00); [Ce3+]0 = 1.10 × 10–3 M. (b) Difference spectra of (a).

The isosbestic points indicate that the solution system includes two Ce3+-related species that are equilibrated at a constant pH. Therefore, the apparent complex-formation constant can be given by

graphic file with name ao0c04724_m001.jpg 1

where ∑[CeL] and ∑[L] represent the total concentrations of all one-to-one complexes and all ligand species, respectively. With the total concentrations of Ce3+ and ligands L, namely, [Ce3+]0 = [Ce3+] + ∑[CeL] and [L]0 = ∑[L] + ∑[CeL], the absorbance A is given by

graphic file with name ao0c04724_m002.jpg 2

with P = [Ce3+]0 + [L]0 + Kabs–1 and Q = P2 – 4[Ce3+]0[L]0, where εCe and εCeL are the apparent absorption coefficients of Ce3+ and its complex species, respectively. Therefore, the complex-formation constants Kabs of Ce3+ with DGA can be analytically deduced from the absorption spectra using the nonlinear least-squares method with eq 2 without any approximation. Equation 2 is explicitly derived in the Supporting Information (SI).

Meanwhile, the changes in the fluorescence emission, however, also enable deducing the complex-formation constants, Kem. Ce3+ emits fluorescence with a quantum yield of unity, and the fluorescence lifetime is 45 ns. Figure 2 shows changes in the fluorescence of Ce3+ and the excitation spectrum when DGA is added at different concentrations. Regardless of the concentration, the shape of the excitation spectra is in good agreement with that of the absorption spectra. According to this excitation spectrum, only Ce3+ emits fluorescence, and its lifetime is still 45 ns. Thus, the fluorescence of Ce3+ is statically quenched by DGA.

Figure 2.

Figure 2

Open in a new tab

Changes in the emission and excitation spectra of hydrated Ce3+ ions when DGA aqueous solutions at various concentrations are added at room temperature (I = 0.1 M, pH 3.00); [Ce3+]0 = 2.20 × 10–4 M.

When fluorescence is statically quenched by the added ligand species, the complex-formation constant Kem can also be deduced from changes in the emission spectra. Thus, Kem of Ce3+ is defined in the same way as Kbs in eq 1 as

graphic file with name ao0c04724_m003.jpg 3

With [Ce3+] = [Ce3+]0/(1 + Kem∑[L]), ∑[CeL] = [Ce3+]0Kem∑[L]/(1 + Kem∑[L]), and [L]0 = ∑[L] +∑[CeL], the quadratic equation in terms of ∑[L] can be derived, which is given by

graphic file with name ao0c04724_m004.jpg 4

with R = Kem[Ce3+]0 – Kem[L]0 + 1, and S = R2 + 4Kem[L]0.

Therefore, the relative quantum yield with and without ligand quenchers can be given by

graphic file with name ao0c04724_m005.jpg 5

Equation 5 is explicitly derived in the SI.

In the Ce3+–DGA system, Stern–Volmer plots for ϕ0/ϕ – 1 are not proportional to [DGA]0 because [DGA]0 is comparable to [Ce3+]0. With eq 5, however, the complex-formation constants, Kem, of Ce3+ with DGA can be analytically deduced from the changes in the emission spectra using the nonlinear least-squares method without any approximation.

With eqs 2 and 5, we deduce the values of Kabs and Kem, respectively, obtained at some of the adjusted pH points by performing nonlinear curve fittings. Table 1 compares the values of Kabs and Kem at various pH in the Ce3+–DGA system. Note that the form of hydrated Ce3+ is not affected by hydrolysis or condensation in this pH range,36,37 and therefore, the proton ambiguity in this system can be ignored. For Kabs, we fit the data using the large change in absorption at 37 × 103 cm–1. Figure 3 shows how the absorbance of Ce3+ changes when DGA is added at different concentrations to solutions with different pH as well as analytical fits for each pH. An iterative procedure is employed that minimizes the reduced chi-square value to attain the optimal parameter values. The process is complete when the difference between reduced chi-square values of two successive iterations is less than the tolerance value of 1 × 10–9. All of the fits were carefully performed and converged under these procedures with εCeL = 595–615 M–1 cm–1. In the same way, Kem can also be deduced, which is more straightforward because there is only one unknown parameter. Figure 4 shows the change in quantum yield (ϕ) as a function of the concentration of DGA, and the analytical fits are of good quality. As a result, the values of Kem agree with those of Kabs within the range of accuracy from ∼0.5 through ∼15%. To carefully compare these values, we calculated a relative uncertainty, |Kabs – Kem|/Kabs × 100, as shown in Table 1. Assuming the estimated Kem is more reliable than Kabs because of the smaller number of unknown parameters, the accuracy of the best estimated value of Kabs can be evaluated using this relative uncertainty, which varies from ∼0.5 to ∼15%. Presumably, this variation arises because another unknown parameter must be handled in addition to Kabs. Even under these conditions, Kabs and Kem can be expected to agree within the attained accuracy from the fact that the fluorescence of Ce3+ is statically quenched by DGA. Accordingly, the fluorescence lifetime is constant, irrespective of the amount of DGA.

Table 1. Complex-Formation Constants, Kabs and Kem, between Ce3+ and DGA at Various pH in Aqueous Solutionsa Obtained Using Absorption and Emission Spectra, Respectively,b with the Relative Uncertainty of Kabs with Respect to Kem.

pH Kabs /103 M–1 Kem /103 M–1 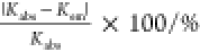Inline graphic
2.00 2.06 2.05 0.49
2.50 10.3 11.8 14.6
3.00 53.7 46.6 13.2
3.70 114 112 1.75
4.70 199 192 3.52
Open in a new tab
a

Ionic strength I = 0.1 M at room temperature (∼20 °C).

b

Acid dissociation constants of DGA: pKa1DGA = 2.79, pKa2 = 3.93 at 20 °C.54

Figure 3.

Figure 3

Open in a new tab

Changes in the absorbance of Ce3+ as a function of the DGA concentration and analytical fits for each pH. For comparison purposes, these plots are merged in Figure S1 of the SI.

Figure 4.

Figure 4

Open in a new tab

Changes in the quantum yield (ϕ) of Ce3+ as a function of the DGA concentration and analytical fits for each pH. For comparison purposes, these plots are merged in Figure S2 of the SI.

The same experiments were carried out with other carboxylic acids to validate how Kabs and Kem are obtained. The changes in the absorption spectra with some isosbestic points are the same as those in the case of DGA. However, changes in the absorption spectra only appear when the concentration of each carboxylic acid is much higher than that of [Ce3+]0. When [L]0 ≫ [Ce3+]0, the Benesi–Hildebrand approximation can be used as ∑[CeL] ≈ [Ce3+]0[L]0/([Ce3+]0 + [L]0 + Kabs–1), which is valid if (∑[CeL])2 ≪ [Ce3+]0[L]0.38,39 We can then deduce

graphic file with name ao0c04724_m006.jpg 6

where A0 = εCe[Ce3+]0 and A∞ = εCeL[L]0. In the case of the other carboxylic acids besides DGA, the plots of [Ce3+]0/(A – A0) vs ([Ce3+]0 + [L]0) yield straight lines, as shown in Figure 5, which validates eq 6. In addition, Kabs obtained from eq 6 using the approximation coincides with that obtained from the original equation, i.e., eq 2, in a series of carboxylic acids. Thus, the Kabs values of Ce3+ with other carboxylic acids are determined by the linear least-squares fit using eq 6, as shown in Figure 5.

Figure 5.

Figure 5

Open in a new tab

Plots of [Ce3+]0/(A – A0) vs [Ce3+]0 + [L]0 for various carboxylic acids other than DGA. Solid lines are analytical fits. For comparison purposes, these plots are merged in Figure S3 of the SI.

The fluorescence of Ce3+ is also statically quenched when carboxylic acids are added, similar to the case with DGA because the fluorescence lifetime is independent of the concentration of carboxylic acids. Figure 6 shows Stern–Volmer plots for quenching with carbonic acids. Unlike the cases with DGA, owing to the excess concentration of carboxylic acid relative to that of Ce3+, the proportional relation, i.e., (ϕ0/ϕ – 1) vs [L]0, holds. Therefore, Kem can be derived from the slope of the Stern–Volmer plots.

Figure 6.

Figure 6

Open in a new tab

Stern–Volmer plots, (ϕ0/ϕ – 1) vs [L]0, for various carboxylic acids excluding DGA. [L]0 is the total concentration of each carboxylic acid. Solid lines are analytical fits. For comparison purposes, these plots are merged in Figure S4 of the SI.

Table 2 compares Kabs and Kem of the various carboxylic acids other than DGA. For the measurements, each pH value was set to be approximately the acid dissociation constant, pKa, except for glutaric acid (GLA), also known as pentanedioic acid. Note again that the form of hydrated Ce3+ is not affected by hydrolysis or condensation in this pH range.36,37 As expected for static quenching, as in the case of DGA, the values of Kabs agree well with those of Kem within the accuracy from ∼0.7 to ∼9%. This agreement clearly indicates that Ce3+ forms a complex with carboxylates, and these complexes are not emissive, which is the typical static quenching. Therefore, Kabs should be equivalent to Kem. The range of the relative uncertainties, |Kabs – Kem |/Kabs × 100, in Table 2 is smaller than that in Table 1, which indicates better agreement between Kabs and Kem in these systems than that in the Ce3+–DGA system. For deducing Kabs for the Ce3+–carboxylate systems other than DGA, eq 6 is more straightforward than eq 2 because it does not require two unknown parameter fittings. These results are consistent with the previously obtained cases in which Kabs and Kem are equivalent in the Ce3+–DGA system. Notably, however, the values of Kabs and Kem in the Ce3+–DGA system are anomalously large; indeed, they are two to three orders of magnitude larger than those in the series of carboxylic acids, which prompted us to further investigate the interactions between Ce3+ and DGA.

Table 2. Complex-Formation Constants, Kabs and Kem, between Ce3+ and Carboxylic Acids Other Than DGA in Aqueous Solutions Obtained from Their Absorption and Emission Spectra, Respectively, with the Relative Uncertainty of Kabs with Respect to Kema.

ligand pH Kabs/M–1 Kem/M–1 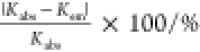Inline graphic
CH3COOH 4.73 (4.56)b 42.0 40.7 3.10
CH3CH2COOH 4.87 (4.67)b 44.6 44.9 0.67
ClCH2COOH 2.87 (2.68)b 8.32 8.63 3.73
CF3COOH 0.60 (0.0)b ∼0 ∼0  
CH3OCH2COOH 3.53 (3.57)b 36.8 40.2 9.24
CH2(CH2COOH)2c : GLA 3.50 21.9 23.4 6.85
4.00 48.2 46.1 4.36
4.50 116 119 2.59
Open in a new tab
a

Ionic strength I = 0.1 M at room temperature (∼20 °C).

b

Note that each solution involving a monocarboxylic acid was set to a particular pH to attain equal rates of protonation and deprotonation, such that each value of the adjusted pH became equivalent to that of pKa at 20 °C in parentheses.54

c

Acid dissociation constants of GLA: pKa1GLA = 4.34, pKa2 = 5.41 at 20 °C.54

When Ce3+ forms a complex with carboxylate, the carboxylate donates a lone pair of electrons to the ion, which is true for all carboxylates in our experiments. According to Lewis’s definition of acids and bases, the carboxylate serves as a base, whereas Ce3+ behaves as an acid, and hence, they form a Werner-type complex. In addition, Ce3+ and carboxylates are categorized into hard acids and bases,40,41 respectively, and therefore, Ce3+ can form complexes with carboxylates, which are the conjugates of Lewis bases, through bonding that is mostly governed by Coulombic interactions. Similarly, however, the protonation of the carboxylates can also be regarded as a hard acid–hard base complex-formation reaction. The mechanism underlying the association and dissociation of Werner-type complexes is compatible with the association and dissociation of carboxylates and protons. This suggests that stronger carboxylic acids, which have a stronger tendency to release protons, are also preferable for avoiding the formation of complexes with Ce3+. Figure 7 exhibits the relationship between pKa and Kabs (or Kem) in the series of monocarboxylic acids in Table 2. The relation between pKa and Kabs including Kem can be seen to yield a straight line; weaker acids, which indicate a larger pKa and associate more strongly with protons, also easily bind to Ce3+. The slope of the line is close to one, which indicates a typical relationship between hard acids and hard bases. However, note that the slope of the line cannot be determined accurately because trifluoroacetate is unlikely to form a complex with Ce3+, i.e., the antilogarithm is not allowed to be exactly zero. Here, we approximate Kabs (or Kem) of Ce3+ with trifluoroacetate to a number that can be regarded as zero within experimental accuracy while recognizing ambiguity. The slope of the relation between pKa and Kabs (or Kem) directly depends on how the carboxylates interact with Ce3+ in comparison with H+; the influential factors are the size of Ce3+, the distance between Ce3+ and the carboxylates, and the charge-shielding effect caused by the inner electrons of Ce3+. The aqua ligands surrounding Ce3+ can also cause the shielding effect if the carboxylates can react with Ce3+ in its outer-sphere region. Nevertheless, our results with monocarboxylic acids clearly suggest that a Lewis base that easily binds to a Lewis acid H+ also easily binds to a central ion Ce3+, which is another Lewis acid. We conclude that this finding is consistent with the conventional theory on the relationship between the basicity of ligands and complex formation.42−45

Figure 7.

Figure 7

Open in a new tab

Relationship between pKa and Kabs (or Kem) of Ce3+ with the series of aqueous monocarboxylic acid solutions.

Now let us consider dicarboxylic acids, i.e., GLA in Table 2 and DGA in Table 1, which cannot be compared by extrapolating the line in Figure 7. Figure 8 shows how the complex-formation constants, Kabs and Kem, increase as a function of pH. Specifically, for the case of GLA, both KabsGLA and Kem (which are equivalent) increase proportionally to the pH. At pH = pKa1GLA, however, Kabs (or KemGLA) can be compared with Kabs (or Kem) of monocarboxylates, which allows us to observe that Kabs (or KemGLA) is near the trend line in Figure 7. This finding suggests that in the case of GLA, other interactions beyond the strength of Lewis bases seem not to significantly influence the formation of complexes with Ce3+. Beyond the case of GLA, however, we can clearly recognize how the complex-formation constants of DGA, Kabs and KemDGA, are anomalously larger than those of the dicarboxylic acid GLA. Surprisingly, Kabs and KemDGA are three orders of magnitude larger than Kabs and KemGLA, respectively.

Figure 8.

Figure 8

Open in a new tab

Kabs and Kem of Ce3+ with two different dicarboxylic acids (DGA and GLA, as indicated by superscripts) as a function of pH. The solid line for GLA is the least-squares fit, whereas the solid line for DGA is a visual guide for pH ≤ 3.0. The vertical dotted lines are visual guides for the pKa values of DGA and GLA.

Besides the Lewis base property, the molecular structures of the dicarboxylic acids might also influence the complex formation, as multidentate ligands potentially lead to interactions, owing to a chelate effect.45−47 Both GLA and DGA can be dissociated successively with two protons, thereby changing their forms, i.e., the deprotonated GL– and DG– and bis-deprotonated GL2–, DG2– species. The dianionic species GL2– and DG2– are well known as bidentate and tridentate ligands, respectively,47,48 which can then form ring structures with Ce3+, i.e., chelate-ring structures. The ether oxygen of DG2– was already discovered to have a strong stabilizing effect in chelate rings.47,48 In fact, DG2– forms complexes with various metallic cations such as Eu(III),49 Co(II),50 Cu(II),51 Ca(II), and Ba(II),52 with the ether oxygen stabilizing the chelate structure. This property of DGA has been exploited to remove rare-metal ions from an aqueous solution via the interactions of polymer-functionalized DGA with Ce3+ and Nd3+.53 The findings of those studies support the anomalous KabsDGA and Kem in our series of measurements and analyses.

The chelate effect is known to stabilize complexes, owing to increased entropy. GL2– can indeed form an eight-membered ring while forming complexes with Ce3+; however, the chelate effect of GL2– does not seem significant, presumably because of the eight-membered ring, which provides such a large multimembered ring that the distortion is large. By contrast, in addition to its two carboxyl groups, DGA has an oxygen atom that can donate a lone pair of electrons to the center ion, which suggests DG2– can work as a tridentate ligand while interacting with Ce3+. Therefore, DG2–and Ce3+ can form two five-membered rings, which results in a double chelate effect. The chelate effect can be amplified when a five-membered ring is formed and when the number of rings increases. Furthermore, the tripod-bonding structures formed by Ce3+ and DG2– would have shape flexibility in three dimensions because Ce3+ is highly coordinated by nine ligands. The double chelate effect with five-membered rings could plausibly explain why KabsDGA and Kem are so much larger than those of other ligands. In Figure 8, the magnitudes of KabsDGA and Kem vastly differ from those of KabsGLA and Kem; this difference may be caused by the oxygen atom in the DGA molecule, which produces the chelate effect. When the pH surpasses pKa2DGA, the values of Kabs and KemDGA begin to level off, indicating that DG2– becomes the major component and is saturated.

Figure 9 shows how the ionic strength affects KabsDGA and Kem, which are determined at several pH values. Because KabsDGA and Kem are equivalent, only KemDGA is represented in the figure. Clearly, Kem decreases with the increasing ionic strength only in the region of the low ionic strength, especially KemDGA at high pH. This initial decreasing trend is due to the decreased activities of the ion species, which do not change much in the region of high ionic strength. The activity coefficient is largely determined by the charge of the ion, and therefore, at higher pH, the increasing ionic strength considerably affects the activity because DG2– becomes more important and plays a crucial role in forming complexes.

Figure 9.

Figure 9

Open in a new tab

KemDGA as a function of the ionic strength for various pH. The solid lines are visual guides.

In principle, the apparent complex-formation constants, KabsDGA and Kem, of the Ce3+–DGA system can be separated into those of individual reaction steps. In fact, the pH dependence of KabsDGA and Kem is an obvious consequence of the protolytic equilibria of DGA and its complex species with Ce3+. Figure 10 shows a plausible mechanism of complex formation between Ce3+ and DGA, assuming that they interact on a one-to-one basis. DGA dissociates into two pH-equilibrated, conjugate Lewis bases, i.e., DG– and DG2– with equilibration constants of KLH2 = 1/Ka1DGA and KLH = 1/Ka2, respectively. The values of pKa1DGA and pKa2 are 2.79 and 3.93, respectively.54 Ce3+ can form complexes with DG2–, DG–, and neutral DGA0. Each DGA ligand forms CeDG+, CeDG2+, and CeDGA3+ with complex-formation constants of KML, KMLH, and KMLH2, respectively. The apparent complex-formation constants, KabsDGA and Kem, are then rewritten as

graphic file with name ao0c04724_m007.jpg 7

With this equation, measuring KabsDGA or Kem with varying pH values at a fixed ionic strength enables us to obtain the complex-formation constants KML, KMLH, and KMLH2. Here, we use the values of KemDGA because Kabs and KemDGA are equal.

Figure 10.

Figure 10

Open in a new tab

Plausible mechanism underlying the complex formation between Ce3+ and DGA.

Throughout the series of experiments on the Ce3+–DGA system with various pH and ionic strength conditions, the values of KabsDGA and Kem in this system are indeed equivalent, although they are much larger than those in the other carboxylic acid systems. Unfortunately, however, decomposing KabsDGA or Kem into KML, KMLH, and KMLH2 for each ionic strength with eq 7 can only be successful while constraining one of three unknown parameters, suggesting that freely optimizing three parameters at a time with only five data points for each ionic strength would be very difficult. Nevertheless, Figure 9 allows us to assume that KMLH2 ≈ 10–1000 M–1 would be reasonable orders of magnitude because the major species at pH 2.00 would be DGA0. Additionally, we noticed that the optimized KML and KMLH values hardly vary within the assumed range of KMLH2. For the ionic strength I = 0.1, values of KML ≈ 2.18–2.19 × 105 M–1 and KMLH ≈ 5.23–5.30 × 104 M–1 are attained. Table 3 summarizes the decomposed values of KML and KMLH from KemDGA for each ionic strength. In the cases of I = 0.01 and 0.05, a further constraint is required to improve KML and KMLH, which are optimized within the possible range of KMLH in addition to the constraint on KML2. Interestingly, however, KML hardly varies within the wide range of KMLH and KML2. Therefore, the results for KML are roughly more reliable than the others. Indeed, we can reliably recognize that dicarboxylate DG2– exhibits an anomalously larger KML than the other carboxylates.

Table 3. Decomposed Complex-Formation Constants, KML and KMLH, of Ce3+ with DG2– and DG–, Respectivelya.

ionic strength I/M KML/105 M–1 KMLH/104 M–1
0.01 50.7–51.3 6.00–20.0b
0.05 2.98–3.20 4.00–9.00b
0.1 2.18–2.19 5.23–5.30
0.2 2.03–2.04 3.23–3.30
0.7 1.31–1.32 1.75–1.83
Open in a new tab
a

Note that KMLH2 ≈ 10–1000 M–1 is assumed, as described in the text.

b

Range of KMLH is also assumed to have high-quality fits.

Further, we can directly compare the value of KML for the Ce3+–DG2– complex with those of all its Ce3+–carboxylate counterparts. Using the same stepwise-formation scheme, we can deduce KML for all of the other carboxylates while assuming that only the deprotonated carboxylates are capable of binding to Ce3+. For the monocarboxylates, each KML can be simply calculated using Kabs or Kem with the pH and pKa, whereas nonlinear fits using three pH values enable deducing KML and KMLH for GL2–. Table 4 summarizes the values of KML and KMLH for all of the other carboxylates besides DG2–. The value of KML for acetate is in good agreement with that in the previous work,55 indicating the reliability of our way to obtain KML. Therefore, determining KML for Ce3+ bound by the series of carboxylates is meaningful. The anomaly of DG2– and DG– becomes more pronounced when comparing KML values between DG2– and the other carboxylates. Presumably, as discussed above, the oxygen atom in the DG2– carboxylate can stabilize the Ce3+–DG2– complexes by creating two five-membered rings, thus demonstrating the chelate effect.

Table 4. Decomposed Complex-Formation Constants, KML and KMLH, of Ce3+ with the Carboxylates Other Than DG2–a,b.

carboxylates KML/M–1 KMLH/M–1
CH3 COO– 68.2–70.4 0
CH3CH2COO– 72.7–73.2 0
ClCH2COO– 13.7–14.3 0
CF3COO– ∼0 0
CH3OCH2COO– 77.2–84.3 0
CH2(CH2COO–)2: GL2– 577–673 132–139
Open in a new tab
a

Ionic strength I = 0.1 M at room temperature (∼20 °C).

b

Note that KMLH = 0 M–1 for monocarboxylates and KMLH2 = 0 M–1 for GL2– are assumed, as described in the text.

Conclusions

While exploring the interactions between hydrated Ce3+ and various types of carboxylates, we discovered anomalously strong interactions between Ce3+ and DGA. Presumably, a chelate effect plays an important role in forming a complex between these species in an aqueous solution. The complex-formation constants of Ce3+ with various carboxylates are determined through the changes in the absorption and emission spectra. Although hydrated Ce3+ emits fluorescence with unity quantum yield, when Ce3+ forms complexes with carboxylates, it becomes nonemissive, which means that the fluorescence of Ce3+ is statically quenched by carboxylates, including DGA. This behavior is supported by the good agreement between the Kabs values obtained from the absorption spectra and those Kem obtained from the emission spectra. In the investigated series of monocarboxylates, the binding strength between Ce3+ and the conjugate Lewis bases, i.e., carboxylates, is inversely proportional to the acidity strength. Similarly, the conjugate Lewis bases of DGA, i.e., DG– and DG2–, bind to Ce3+ in an aqueous solution; however, the rigorously deduced Kabs and Kem values of Ce3+ with DGA are three to five orders of magnitude larger than those obtained with other carboxylates as well as another typical dicarboxylate, namely, glutarate. These constants suggest interactions beyond those explained by the Lewis acid–base theory. We propose that this anomalously strong binding between Ce3+ and DGA is caused by a chelate effect because of the central oxygen atom in DGA molecules. Specifically, the two conjugate Lewis bases of DGA, i.e., DG− and DG2−, enable forming a five-membered ring with the help of this central oxygen atom. Moreover, double chelate rings can form, which can be created by DG2– and stabilized by its central oxygen. We have also attempted to decompose the apparent complex-formation constants, KabsDGA and Kem, of the Ce3+–DGA system into individual complex-formation constants. Unfortunately, however, optimizing three unknown parameters made it difficult to find solutions without constraining one or two parameters. A large amount of data would be required to deduce more reliable individual complex-formation constants through the fittings. Nevertheless, our analysis allows us to conclude that the conjugate Lewis bases, DG2– and DG–, bind to Ce3+ three to five orders of magnitude more strongly than the other carboxylates. Further efforts should be devoted to revealing the double chelate structure of the complex between Ce3+ and DG2– and its properties in a solution, such as the temperature-dependent equilibria of the chelate formation.

Methods

Materials

Cerium(III) perchlorate nonahydrate Ce(ClO4)39H2O was synthesized from Ce2(SO4)38H2O and Ba(ClO4)23H2O19 (Sigma-Aldrich, reagent grade). Ce2(SO4)38H2O (7.12 g, 9.99 × 10–3 mol) was dissolved in water (100 mL), and the solution was stirred while being kept cool for 2–3 h. Insoluble Ce2(SO4)38H2O was removed with a pleated filter. Ba(ClO4)23H2O (11.7 g, 3.00 × 10–2 mol) in water (50 mL) was gently added to the filtrate, which produced white precipitates. The solution was sufficiently stirred and allowed to sit still overnight. The precipitates were removed by decantation and filtering, and 1 M H2SO4 was gradually added 1 μL at a time to the solution while stirring to precipitate the excess Ba2+ dissolved in the solution. The Ce(ClO4)39H2O solution was adequately concentrated and used as a stock solution.

Ce(C2H5SO4)39H2O (CeES) was obtained using the method reported by Ketelaar.56 CeES was synthesized from Ce2(SO4)38H2O and Ba(C2H5SO4)32H2O (BaES). (C2H5)2SO4 (27.2 g, 1.80 × 10–1 mol) was added into an adequate quantity of water containing BaCO3 (200 g, 1 mol), and the mixture was vigorously stirred overnight until it homogenized. Excess BaCO3 was removed by decantation and filtration. The solvent was distilled off using an evaporator, and BaES (12 g) was obtained in 32% yield.

Ce2(SO4)38H2O (4.80 g, 6.74 × 10–3 mol) dissolved in water (100 mL) was stirred for 2–3 h while being kept cool. After excess Ce2(SO4)38H2O was removed, BaES (9.07 g, 2.14 × 10–2 mol) in water was added into this solution, which precipitated white BaSO4. The solution was decanted after allowing the BaSO4 precipitate to settle, which was completely filtered off. The solvent was distilled, and CeES was recrystallized in water. White CeES crystals (5.05 g) were obtained in 55% yield. The total yield based on (C2H5)2SO4 was 18%.

Solutions with a definite quantity of dissolved [Ce(ClO4)3·9H2O] and a desired amount of the various carboxylates were prepared to measure the absorption and emission spectra and lifetime. These carboxylates used as quenchers were of the best quality commercially available: i.e., sodium acetate (≥99%), sodium propionate (≥99%), methoxyacetic acid (98%), sodium chloroacetate (98%), sodium trifluoroacetate (98%), DGA (98%), and GLA (99%), all of which were purchased from Sigma-Aldrich. Because [Ce(ClO4)3·9H2O] is too deliquescent to be quantitatively prepared in a solution, the concentration was determined by comparing its absorption spectra with that of a standard solution of weighed nondeliquescent CeES. The ionic strength of the solutions was controlled with NaClO4 (ACS reagent, >98%), and the pH was adjusted with HClO4 (ACS reagent, >70%) and NaOH (ACS reagent, >97%) in the range between 0.6 and 4.7. These chemicals were also obtained from Sigma-Aldrich.

Characterization

Absorption spectra were recorded on a Hitachi 330 spectrophotometer, and emission and excitation spectra were acquired on a Hitachi 850 spectrofluorometer equipped with a Hamamatsu Photonics R928 photomultiplier. The spectra were calibrated using a concentrated solution of rhodamine B (8 g/dm3) in ethylene glycol.57 Fluorescence lifetimes were measured by means of photon counting on a PRA nanosecond fluorometer system. Samples were irradiated by pulses with a duration of 2 ns from a PRA model 510B hydrogen gas lamp through a Jobin Yvon model H10 monochromator. Photon emission was detected on a Hamamatsu Photonics R928 photomultiplier and counted on a Norland model 5300 multichannel analyzer.

All processes, from preparing each sample solution to measuring the absorption and emission spectra, were performed in replicate; specifically, the experiments for the Ce3+–DGA system and the Ce3+ systems with other carboxylates were performed at least five and three times, respectively. The average of raw data was taken for each data point and used for further analysis. The accuracy of the two values being compared is evaluated using their relative uncertainty, which is defined as |δK|/Kbest, where Kbest is the best estimated value and δK is the uncertainty associated with each measurement

Acknowledgments

This work was supported by grants from the Ministry of Science and Technology (MOST), Taiwan, under Grant MOST 108-2221-E-007-094-MY2, as well as Grants MOST 108-2622-M-007-006-CC1 and 109-2622-M-007-007-CC1 for industrial–academic collaborations jointly funded by MOST and Profound Material Technology Co., Ltd., in Taiwan.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c04724.

  • Explicit derivation of eqs 2 and 5 and plots merged separately from Figures 3–6 in the main text (PDF)

Author Contributions

This manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ao0c04724_si_001.pdf (642.3KB, pdf)

References

  1. Comby S.; Surender E. M.; Kotova O.; Truman L. K.; Molloy J. K.; Gunnlaugsson T. Lanthanide-Functionalized Nanoparticles as MRI and Luminescent Probes for Sensing and/or Imaging Applications. Inorg. Chem. 2014, 53, 1867–1879. 10.1021/ic4023568. [DOI] [PubMed] [Google Scholar]
  2. Allen M. J. Aqueous Lanthanide Chemistry in Asymmetric Catalysis and Magnetic Resonance Imaging. Synlett 2016, 27, 1310–1317. 10.1055/s-0035-1561363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Yang X.; Lin X.; Zhao Y.; Zhao Y. S.; Yan D. Lanthanide Metal–Organic Framework Microrods: Colored Optical Waveguides and Chiral Polarized Emission. Angew. Chem., Int. Ed. 2017, 56, 7853–7857. 10.1002/anie.201703917. [DOI] [PubMed] [Google Scholar]
  4. Werts M. H. V. Making Sense of Lanthanide Luminescence. Sci. Prog. 2005, 88, 101–131. 10.3184/003685005783238435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Escribano P.; Julián-López B.; Planelles-Aragó J.; Cordoncillo E.; Viana B.; Sanchez C. Photonic and Nanobiophotonic Properties of Luminescent Lanthanide-Doped Hybrid Organic-Inorganic Materials. J. Mater. Chem. 2008, 18, 23–40. 10.1039/B710800A. [DOI] [Google Scholar]
  6. Zhou J.; Leaño J. L.; Liu Z.; Jin D.; Wong K. L.; Liu R. S.; Bünzli J. C. G. Impact of Lanthanide Nanomaterials on Photonic Devices and Smart Applications. Small 2018, 14, 1801882 10.1002/smll.201801882. [DOI] [PubMed] [Google Scholar]
  7. Gomez G. E.; Afonso M. D. S.; Baldoni H. A.; Roncaroli F.; Soler-Illia G. J. A. A. Luminescent Lanthanide Metal Organic Frameworks as Chemosensing Platforms towards Agrochemicals and Cations. Sensors 2019, 19, 1260. 10.3390/s19051260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Qin J.; Li D.; Miao Y.; Yan G. Detection of Phosphate Based on Phosphorescence of Mn Doped ZnS Quantum Dots Combined with Cerium(III). RSC Adv. 2017, 7, 46657–46664. 10.1039/C7RA07991E. [DOI] [Google Scholar]
  9. Lansdown A. B.; Myers S. R.; Clarke J. A.; O’Sullivan P. A Reappraisal of the Role of Cerium in Burn Wound Management. J. Wound Care 2003, 12, 113–118. 10.12968/jowc.2003.12.3.26480. [DOI] [PubMed] [Google Scholar]
  10. De Gusseme B.; Du Laing G.; Hennebel T.; Renard P.; Chidambaram D.; Fitts J. P.; Bruneel E.; Van Driessche I.; Verbeken K.; Boon N.; et al. Virus Removal by Biogenic Cerium. Environ. Sci. Technol. 2010, 44, 6350–6356. 10.1021/es100100p. [DOI] [PubMed] [Google Scholar]
  11. Anastasiou A. D.; Nerantzaki M.; Gounari E.; Duggal M. S.; Giannoudis P. V.; Jha A.; Bikiaris D. Antibacterial Properties and Regenerative Potential of Sr2+ and Ce3+ Doped Fluorapatites; a Potential Solution for Peri-Implantitis. Sci. Rep. 2019, 9, 14469 10.1038/s41598-019-50916-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Palizban A. A.; Sadeghi-Aliabadi H.; Abdollahpour F. Effect of Cerium Lanthanide on Hela and MCF-7 Cancer Cell Growth in the Presence of Transferring. Res. Pharm. Sci. 2010, 5, 119–125. [PMC free article] [PubMed] [Google Scholar]
  13. Schmidlin P. R.; Tchouboukov A.; Wegehaupt F. J.; Weber F. E. Effect of Cerium Chloride Application on Fibroblast and Osteoblast Proliferation and Differentiation. Arch. Oral Biol. 2012, 57, 892–897. 10.1016/j.archoralbio.2012.01.010. [DOI] [PubMed] [Google Scholar]
  14. Stephen Inbaraj B.; Chen B.-H. An Overview on Recent in Vivo Biological Application of Cerium Oxide Nanoparticles. Asian J. Pharm. Sci. 2020, 15, 558–575. 10.1016/j.ajps.2019.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Heckman K. L.; Estevez A. Y.; DeCoteau W.; Vangellow S.; Ribeiro S.; Chiarenzelli J.; Hays-Erlichman B.; Erlichman J. S. Variable in Vivo and in Vitro Biological Effects of Cerium Oxide Nanoparticle Formulations. Front. Pharmacol. 2020, 10, 1599 10.3389/fphar.2019.01599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Okada K.; Kaizu Y.; Kobayashi H. Aqualigand Dissociation of 5d←4f Excited [Ce(OH2)9]3+ in Aqueous Solution. J. Chem. Phys. 1981, 75, 1577–1578. 10.1063/1.442197. [DOI] [Google Scholar]
  17. Okada K.; Kaizu Y.; Kobayashi H.; Tanaka K.; Marumo F. The 5d←4f Excited States of [Ce(OH2)9]3+. Mol. Phys. 1985, 54, 1293–1306. 10.1080/00268978500101011. [DOI] [Google Scholar]
  18. Jørgensen C. K.; Brinen J. S. Far Ultra-Violet Absorption Spectra of Cerium(III) and Europium(III) Aqua Ions. Mol. Phys. 1963, 6, 629–631. 10.1080/00268976300100731. [DOI] [Google Scholar]
  19. Kaizu Y.; Miyakawa K.; Okada K.; Kobayashi H.; Sumitani M.; Yoshihara K. Aqualigand Dissociation of [Ce(OH2)9]3+ in the 5d ←4f Excited State. J. Am. Chem. Soc. 1985, 107, 2622–2626. 10.1021/ja00295a010. [DOI] [Google Scholar]
  20. Miyakawa K.; Kaizu Y.; Kobayashi H. An Electrostatic Approach to the Structure of Hydrated Lanthanoid Ions. [M(OH2)9]3+ versus [M(OH2)8]3+. J. Chem. Soc., Faraday Trans. 1 1988, 84, 1517–1529. 10.1039/F19888401517. [DOI] [Google Scholar]
  21. Habenschuss A.; Spedding F. H. The Coordination (Hydration) of Rare Earth Ions in Aqueous Chloride Solutions from X-Ray Diffraction. I. TbCl3, DyCl3, ErCl3, TmCl3, and LuCl3. J. Chem. Phys. 1979, 70, 2797–2806. 10.1063/1.437866. [DOI] [Google Scholar]
  22. Habenschuss A.; Spedding F. H. The Coordination (Hydration) of Rare Earth Ions in Aqueous Chloride Solutions from X-Ray Diffraction. II. LaCl3, PrCl3, and NdCl3. J. Chem. Phys. 1979, 70, 3758–3763. 10.1063/1.437928. [DOI] [Google Scholar]
  23. Habenschuss A.; Spedding F. H. The Coordination (Hydration) of Rare Earth Ions in Aqueous Chloride Solutions from X-Ray Diffraction. III. SmCl3, EuCl3, and Series Behavior. J. Chem. Phys. 1980, 73, 442–450. 10.1063/1.439895. [DOI] [Google Scholar]
  24. Azenha M. E.; Burrows H. D.; Fonseca S. M.; Ramos M. L.; Rovisco J.; Seixas de Melo J. S.; Sobral A. J. F. N.; Kogej K. Luminescence from Cerium(III) Acetate Complexes in Aqueous Solution: Considerations on the Nature of Carboxylate Binding to Trivalent Lanthanides. New J. Chem. 2008, 32, 1531–1535. 10.1039/b800105g. [DOI] [Google Scholar]
  25. Zheng X.-L.; Liu Y.; Pan M.; Lü X.-Q.; Zhang J.-Y.; Zhao C.-Y.; Tong Y.-X.; Su C.-Y. Bright Blue-Emitting Ce3+ Complexes with Encapsulating Polybenzimidazole Tripodal Ligands as Potential Electroluminescent Devices. Angew. Chem. Int. Ed. 2007, 46, 7399–7403. 10.1002/anie.200702401. [DOI] [PubMed] [Google Scholar]
  26. Gupta A.; Das S.; Neal C. J.; Seal S. Controlling the Surface Chemistry of Cerium Oxide Nanoparticles for Biological Applications. J. Mater. Chem. B 2016, 4, 3195–3202. 10.1039/C6TB00396F. [DOI] [PubMed] [Google Scholar]
  27. Pulido-Reyes G.; Martín E.; Gu; Coronado J. L.; Leganes F.; Rosal R.; Fernández-Piñas F. Physicochemical and Biological Interactions between Cerium Oxide Nanoparticles and a 1,8-Naphthalimide Derivative. J. Photochem. Photobiol., B 2017, 172, 61–69. 10.1016/j.jphotobiol.2017.05.009. [DOI] [PubMed] [Google Scholar]
  28. Jakupec M. A.; Unfried P.; Keppler B. K.. Pharmacological Properties of Cerium Compounds. In Reviews of Physiology, Biochemistry and Pharmacology, Amara S. G.; Bamberg E.; Jahn R.; Lederer W. J.; Miyajima A.; Murer H.; Offermanns S.; Schultz G.; Schweiger M., Eds.; Springer-Verlag: Berlin, Heidelberg, 2005; Vol. 153, pp 101–111. [DOI] [PubMed] [Google Scholar]
  29. Hazin P. N.; Lakshminarayan C.; Brinen L. S.; Knee J. L.; Bruno J. W.; Streib W. E.; Folting K. Luminescence Spectra and Lifetimes of Cerium(III) Compounds as Indicators of Solution Behavior and Radiative Efficiency. Inorg. Chem. 1988, 27, 1393–1400. 10.1021/ic00281a019. [DOI] [Google Scholar]
  30. Marques E. F.; Burrows H. D.; da Graca Miguel M. The Structure and Thermal Behaviour of Some Long Chain Cerium(III) Carboxylates. J. Chem. Soc., Faraday Trans. 1998, 94, 1729–1736. 10.1039/a800326b. [DOI] [Google Scholar]
  31. Blasse G.; Schipper W.; Hamelink J. J. On the Quenching of the Luminescence of the Trivalent Cerium Ion. Inorg. Chim. Acta 1991, 189, 77–80. 10.1016/S0020-1693(00)80392-8. [DOI] [Google Scholar]
  32. Matthews R. W.; Sworski T. J. Photooxidation and Fluorescence of Cerium(III) in Aqueous Sulfuric Acid Solutions. J. Phys. Chem. A. 1975, 79, 681–686. 10.1021/j100574a003. [DOI] [Google Scholar]
  33. Kunkely H.; Vogler A. Optical Metal-to-Ligand Charge Transfer in Tris(pyrazine-2-carboxylato)cerium(III): Absorption and Emission. J. Photochem. Photobiol. A Chem. 2002, 151, 45–47. 10.1016/S1010-6030(02)00171-5. [DOI] [Google Scholar]
  34. Vogler A.; Kunkely H. Excited State Properties of Lanthanide Complexes: Beyond ff States. Inorg. Chim. Acta 2006, 359, 4130–4138. 10.1016/j.ica.2006.05.025. [DOI] [Google Scholar]
  35. Kogej K.; Fonseca S. M.; Rovisco J.; Azenha M. E.; Ramos M. L.; Seixas de Melo J. S.; Burrows H. D. Understanding the Interaction between Trivalent Lanthanide Ions and Stereoregular Polymethacrylates through Luminescence, Binding Isotherms, NMR, and Interaction with Cetylpyridinium Chloride. Langmuir 2013, 29, 14429–14437. 10.1021/la4036024. [DOI] [PubMed] [Google Scholar]
  36. Kragten J.; Decnop-Weever L. G. Hydroxide Complexes of Cerium(III). Talanta 1978, 25, 147–150. 10.1016/0039-9140(78)80103-9. [DOI] [PubMed] [Google Scholar]
  37. Teksöz S.; Acar Ç.; Ünak P. Hydrolytic Behavior of Th4+, UO22+, and Ce3+ Ions at Various Temperatures. J. Chem. Eng. Data 2009, 54, 1183–1188. 10.1021/je800601m. [DOI] [Google Scholar]
  38. Rossotti F. J. R.; Rossotti H.. The Determination of Stability Constants and Other Equilibrium Constants in Solution; McGraw-Hill: New York, 1961. [Google Scholar]
  39. Nagasawa A.; Diebler H. Interactions of Ni2+ Ion with Inosine and Inosine 5'-Monophosphate. Equilibriums and Dynamics. J. Phys. Chem. B. 1981, 85, 3523–3528. 10.1021/j150623a031. [DOI] [Google Scholar]
  40. Pearson R. G. Hard and Soft Acids and Bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. 10.1021/ja00905a001. [DOI] [Google Scholar]
  41. Klopman G. Chemical Reactivity and the Concept of Charge- and Frontier-Controlled Reactions. J. Am. Chem. Soc. 1968, 90, 223–234. 10.1021/ja01004a002. [DOI] [Google Scholar]
  42. Schwarzenbach G.; Willi A.; Bach R. O. Komplexone IV. Die Acidität Und Die Erdalkalikomplexe Der Anilin-Diessigsäure Und Ihrer Substitutionsprodukte. Helv. Chim. Acta 1947, 30, 1303–1320. 10.1002/hlca.19470300524. [DOI] [PubMed] [Google Scholar]
  43. Schwarzenbach G.; Ackermann H.; Ruckstuhl P. Komplexone XV. Neue Derivate Der Imino-Diessigsäure Und Ihre Erdalkalikomplexe. Beziehungen Zwischen Acidität Und Komplexbildung. Helv. Chim. Acta 1949, 32, 1175–1186. 10.1002/hlca.19490320403. [DOI] [Google Scholar]
  44. Irving H.; Rossotti H.; et al. Some Relationships among the Stabilities of Metal Complexes. Acta Chem. Scand. 1956, 10, 72–93. 10.3891/acta.chem.scand.10-0072. [DOI] [Google Scholar]
  45. Ohtaki H.; Tanaka M.; Funahashi S.. Chemistry of Solution Reaction (in Japanese); Gakkai-Syuppan Center: Tokyo, 1977. [Google Scholar]
  46. Schwarzenbach G.; Senn H.; Anderegg G. Komplexone XXIX. Ein Grosser Chelateffekt Besonderer Art. Helv. Chim. Acta 1957, 40, 1886–1900. 10.1002/hlca.19570400640. [DOI] [Google Scholar]
  47. Schwarzenbach G. The General, Selective, and Specific Formation of Complexes by Metallic Cations. Adv. Inorg. Chem. Radiochem. 1961, 3, 257–285. 10.1016/S0065-2792(08)60242-3. [DOI] [Google Scholar]
  48. Motekaitis R. J.; Martell A. E. New Multidentate Ligands. XXV. the Coordination Chemistry of Divalent Metal Ions with Diglycolic Acid, Carboxymethyltartronic Acid and Ditartronic Acid. J. Coord. Chem. 1984, 13, 265–271. 10.1080/00958978408073876. [DOI] [Google Scholar]
  49. Kirby A. F.; Richardson F. S. Optical Excitation and Emission Spectra of Eu3+ in Microcrystalline Samples of Trigonal Na3[Eu(ODA)3]·2NaClO4·6H2O. J. Phys. Chem. C. 1983, 87, 2557–2563. 10.1021/j100237a019. [DOI] [Google Scholar]
  50. Li J. X.; Du Z. X.; Zhu B. L.; An H. Q.; Dong J. X.; Hu X. J.; Huang W. P. A Bimetallic CoII–DyIII Complex Bridged by Oxydiacetate Ligand: Synthesis, Structure, Magnetic, Spectral and TG Properties of {[DyCo(oda)3]4[Co(H2O)6]2·6H2O}n. Inorg. Chem. Commun. 2011, 14, 522–525. 10.1016/j.inoche.2011.01.012. [DOI] [Google Scholar]
  51. Siddiqi Z. A.; Sharma P. K.; Shahid M.; Khalid M.; Kumar S. Synthesis, Spectral Characterizations and Biological Studies of Transition Metal Mixed Ligand Complexes: X-Ray Crystal Structures of [Cu(oda)(Bipy)(H2O)]·4H2O and [VO(oda)(Bipy)]·2H2O. J. Mol. Struct. 2011, 994, 295–301. 10.1016/j.molstruc.2011.03.036. [DOI] [Google Scholar]
  52. Soumya Mol U. S.; Drisya R.; Satheesh Chandran P. R.; Sudarsanakumar M. R.; Prathapachandra Kurup M. R. Synthesis, Structural, Spectral and Photoluminescent Studies of New Polymorphs of Ca(II) and Ba(II) Complexes of Diglycolic Acid. Main Group Chem. 2017, 16, 291–305. 10.3233/MGC-170244. [DOI] [Google Scholar]
  53. Pereao O.; Laatikainen K.; Bode-Aluko C.; Kochnev I.; Fatoba O.; Nechaev A. N.; Petrik L. Adsorption of Ce3+ and Nd3+ by Diglycolic Acid Functionalised Electrospun Polystyrene Nanofiber from Aqueous Solution. Sep. Purif. Technol. 2020, 233, 116059 10.1016/j.seppur.2019.116059. [DOI] [Google Scholar]
  54. Appendix 1: Dissociation Constants (pKa) of Organic Acids (at 20 °C). In Applications of Ion Chromatography for Pharmaceutical and Biological Products; Bhattacharyya L.; Rohrer J. S., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp 449–453. [Google Scholar]
  55. Devine C. D.The Stability Constants of Some Carboxylate Complexes of the Trivalent Lanthanons. Ph.D. Dissertation, Iowa State University of Science and Technology: Ames, Iowa, 1969. [Google Scholar]
  56. Ketelaar J. A. A. The Crystal Structure of the Ethyl Sulphates of the Rare Earthes and Yttrium. Physica 1937, 4, 619–630. 10.1016/S0031-8914(37)80158-5. [DOI] [Google Scholar]
  57. Melhuish W. H. Calibration of Spectrofluorimeters for Measuring Corrected Emission Spectra. J. Opt. Soc. Am. 1962, 52, 1256–1258. 10.1364/JOSA.52.001256. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c04724_si_001.pdf (642.3KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES