Development of Europe-Wide Models for Particle Elemental Composition Using Supervised Linear Regression and Random Forest

Abstract

We developed Europe-wide models of long-term exposure to eight elements (copper, iron, potassium, nickel, sulfur, silicon, vanadium, and zinc) in particulate matter with diameter <2.5 μm (PM_2.5) using standardized measurements for one-year periods between October 2008 and April 2011 in 19 study areas across Europe, with supervised linear regression (SLR) and random forest (RF) algorithms. Potential predictor variables were obtained from satellites, chemical transport models, land-use, traffic, and industrial point source databases to represent different sources. Overall model performance across Europe was moderate to good for all elements with hold-out-validation R-squared ranging from 0.41 to 0.90. RF consistently outperformed SLR. Models explained within-area variation much less than the overall variation, with similar performance for RF and SLR. Maps proved a useful additional model evaluation tool. Models differed substantially between elements regarding major predictor variables, broadly reflecting known sources. Agreement between the two algorithm predictions was generally high at the overall European level and varied substantially at the national level. Applying the two models in epidemiological studies could lead to different associations with health. If both between- and within-area exposure variability are exploited, RF may be preferred. If only within-area variability is used, both methods should be interpreted equally.

1. Introduction

Exposure to particulate matter (PM) is associated with adverse health outcomes.^1,2 PM is a complex mixture of components that differ spatially and temporally. Identifying which components are main contributors to adverse health effects is important for targeted policymaking. Multiple studies have attempted to associate health effects with PM components including metals, organic compounds, inorganic carbonaceous material, and inorganic secondary aerosols.³⁻⁵ Findings, however, are inconsistent. Epidemiological studies have been limited because of the scarcity of air quality monitors that routinely measure PM composition. In Europe, a PM monitoring campaign was conducted in 20 ESCAPE (European Study of Cohorts for Air Pollution Effects) study areas following a common sampling protocol.⁶ Most study areas consisted of a metropolitan area with some small towns around the main city. The PM samples were analyzed for elemental composition.⁷ Based on the measurements from 20 sites in each study area, area-specific land use regression (LUR) models were developed to assess long-term exposure to elemental composition.⁸ The models were applied to cohorts within the study areas to assess health effects related to particle composition.⁹

The geographical extent of the study-area-specific ESCAPE models is limited and predictions from these models cannot reliably be used for other cohorts, such as large multicenter studies. The models were furthermore developed on 20 sites per area. Methodological studies suggested that more stable models can be developed based on larger number of sites in the model training dataset.^10,11 In addition, the ESCAPE study-area specific models had rather good performance for traffic-related elements such as copper (Cu) and iron (Fe), but had poor performance for elements such as sulfur (S), nickel (Ni), and vanadium (V) for which spatial variation was limited within areas and key predictors were missing.⁸ The lack of large-scale European models for particle elemental composition hampers large-area epidemiological studies. Our previous studies showed the possibility to develop European LUR models with good performance using a combined dataset from the ESCAPE study areas for PM with diameter <2.5 μm (PM_2.5), black carbon (BC) and nitrogen dioxide (NO₂).^12,13

The supervised linear regression (SLR) algorithm is often used in air pollution modeling,^14,15 and was used to develop ESCAPE models of elemental composition⁸ and European models of PM_2.5, NO₂, and BC.¹² The SLR algorithm shows good predictive ability and interpretability but has strong statistical assumptions such as linearity. SLR models can, however, take into account nonlinear relationships by offering a priori transformed predictor variables (e.g., inverse distance to a source), include only predictor variables following plausible direction of effect (e.g., a positive traffic slope) and add interaction terms. A number of more flexible algorithms including machine-learning algorithms have increasingly been applied in air pollution exposure assessment.^16,17 Random forest (RF) has been widely used in recent years.^18,19 RF is a classification tree analysis. It can model potentially complex relationships including nonlinearity and interactions within data but gives little information regarding the prediction process.²⁰ A key feature of RF is the “bagging” procedure adopted in both observation and variable selection: this allows even marginally important predictors to contribute, even in the presence of high multicollinearity. A previous study found RF outperformed linear regression in modeling spatial variation of particle elemental composition.²¹

LUR models for multiple particle components are more useful for epidemiological studies if they include more specific predictors. Developments in satellite and chemical transport modeling and availability of industrial point source data have made it possible to develop more specific models.

The aim of this study was to assess the performance of Europe-wide models for particle elemental composition, developed using SLR and RF algorithms. The models have been developed in the “Effects of Low-Level Air Pollution: A Study in Europe” (ELAPSE), a Europe-wide project investigating long-term health effects of low-level air pollution.

2. Materials and Methods

2.1. Air Pollution Data

The PM_2.5 elemental composition concentration data originated from the ESCAPE monitoring campaigns conducted in 19 study areas across Europe (Figure S1). PM sampling and analysis methods have been described previously.^6,7 Briefly, measurements were made at 20 sites in each study area (40 in the large Catalunya and Netherlands/Belgium areas) for three 2-week periods in a 1-year period between October 2008 and April 2011. Monitoring sites were selected to represent pollution levels at regional background, urban background, and street locations using a common sampling protocol. PM_2.5 samples were collected on Teflon filters using Harvard Impactors and analyzed for elemental composition using energy-dispersive X-ray fluorescence. Annual average concentrations were calculated based on three 14-day average measurements spread over the seasons (warm, cold, and intermediate) with temporal adjustment from a reference background site in each study area. Our measurement campaign was restricted temporally, as previous sampling campaigns used to develop LUR models.²² While this design does not formally estimate absolute annual average concentrations as in regulatory monitoring, it has been shown to be useful to assess spatial contrast of long-term average concentrations because of specific design elements.^6,22,23 We performed temporal adjustment, using a continuous reference site located at a regional or urban background location (not directly influenced by local sources), where measurements were made for the full 12-month period. Three 14-day average samples were taken in different seasons at all locations, which are less sensitive to the very short-term variations caused by daily variation in weather. Five sites and the reference site were measured simultaneously representing all different site types (regional background, urban background, and street).^6,23

Eight elements were a priori selected within ESCAPE to represent major pollution sources: Cu, Fe, and Zn representing nontailpipe traffic emissions, S representing long-range transport, Ni and V representing mixed oil burning/industry, silicon (Si) representing crustal material, and potassium (K) representing biomass burning.^7,8

2.2. Potential Predictor Variables

2.2.1. Traffic, Population, Altitude, and Land Use Variables

We used the same road density, population, and elevation variables as in our previous exposure modeling paper for PM_2.5, NO₂, ozone (O₃), and BC across Europe.¹² In short, road data were extracted from the 1:10,000 EuroStreets digital road network (version 3.1 based on TeleAtlas MultiNet TM, year 2008), classified into “all” and “major” roads, and road density calculated in a 100 × 100 m grid. Population density in 1 × 1 km grid for 2011 were obtained from Eurostat.²⁴ Elevation was obtained from the SRTM Digital Elevation Database²⁵ version 4.1 with a resolution of 3 arc second (approximately 90 m) with vertical error of <16 m. X and/or Y coordinates were offered to represent the east–west/north–south gradient.

Land use variables were newly extracted from an updated European CORINE Land Cover surface in 100 × 100 m grid.²⁶ The initial 44 land cover classes were grouped to six main classes: residential, industry, ports, urban green space, total built up land, and natural land.

2.2.2. Additional Component/Source-Specific Variables

Special attention was taken in obtaining specific potential predictor variables representing different sources of the eight selected elements. We hypothesized that this would allow us to develop better and more specific models, such that the independent associations of the different elements with health could be studied better. For each component, only plausible variables were offered for model development. The restrictions of offering specific potential predictors are specified in Table S1.

Satellite-model (SAT) estimates of 2010 annual average sulfate (SO₄^2–), organic matter (OM), BC, and mineral dust (SOIL) in PM_2.5 were extracted from a gridded surface (0.01° × 0.01°, ∼1.11 km) over Europe. These estimates are an application of simulated relative composition to the total PM_2.5 estimates produced by the methods described elsewhere,²⁷ and do not incorporate compositional ground-based measurements over Europe. In brief, PM_2.5 mass estimates were produced by relating a combined aerosol optical depth (AOD) retrieval involving multiple satellite products and simulation to near-surface PM_2.5 concentrations using the spatiotemporally varying geophysical relationship simulated by the GEOS-Chem chemical transport model (CTM). Ground-based observations of total PM_2.5 were then incorporated into these initial values using geographically weighted regression, and the resulting total mass estimates partitioned into chemical composition using their relative contributions according to the GEOS-Chem CTM simulations.

CTM estimates of BC AOD, Sulphate AOD, total column SO₂, and sea-salt AOD were obtained from the European Centre for Medium-Range Weather Forecasts.²⁸ Daily estimates in 2010 were extracted from a gridded surface (0.125° × 0.125°, ∼13.9 km) produced by the MACC-II ENSEMBLE model,²⁹ and then aggregated to derive the annual average.

In addition to the unspecific industry land-use category, information on major industrial point sources was obtained including facility location, pollutant, and emission amount from the European Pollutant Release and Transfer Register.³⁰ The industrial facility points were intersected with a 100 m base polygon, and then the number of facility sites and emissions were summed within each 100 × 100 m cell. Density of general industries and industries emitting specific aerosols (metal, Cu, Ni, PM₁₀, SO_x, and Zn) were calculated accordingly. Sum of emissions were calculated for PM₁₀, Cu, Ni, SO_x, and Zn.

All predictor variables were integrated into a 100 m gridded GIS database covering Europe. For the road density, land use and industrial information, a moving window procedure was used to calculate the sum of values for selected buffers (focal statistics using sum within a circle). The influence of industrial point sources was calculated by inverse distance weighting (1/d). The processing of variable surfaces was done in ArcMap 10.6.

2.3. Model Development

The number of monitoring sites available for particle composition ranged from 400 to 414 because of failed PM composition measurements.⁸ We used both SLR and RF algorithms to develop models.

The SLR approach has been described in detail before.¹² Briefly, a univariate linear regression model was applied for each potential predictor to find the predictor that explained the maximum variance in the measurements. At each subsequent step, the significant predictor variable (P < 0.1) that generated the highest increase in the model adjusted coefficient of determination (adjusted R²) was added. Predictors only entered the model if they adhered to the plausible direction of the effect (Table S1). This process was repeated until the model adjusted R² could not be increased anymore. Predictor variables with variance inflation factor larger than 3 were removed from the model to avoid multicollinearity.

RF is an ensemble machine learning technique based on decision trees.³¹ It builds independent trees in parallel, each based on a random sample drawn from the full set of measurements. At each node, a random subset of potential predictors is split. The final predictions are derived by averaging predictions from all decision trees. RF does not perform variable selection. It produces variable importance, calculated as percentage increase in mean squared errors after a random permutation of the values of a variable. We used the R package “randomForest” to develop the RF models.

One-step and two-step modeling processes were used to offer geographical coordinates (X and Y) to the models. Following our previous exposure modeling procedure,¹² for SLR we used a 2-step approach, in which we first developed a SLR model without offering X or Y, then added X and Y only if they increased the model adjusted R². The rationale for the 2-step procedure is that we preferred spatial variation to be explained first by specific predictor variables and the residual variation to be further explained by the X, Y coordinates added in the second step. In RF, we applied one-step modeling as our primary approach: X and Y were offered together with the other predictor variables. This allowed us to take advantage of the possibilities of RF algorithm to model the potential interactions between coordinates and other predictors. For comparison, we also developed one-step models for SLR and 2-step models for RF: we first developed a RF model without offering X or Y, then developed a second RF model with X, Y coordinates only, explaining variations in the residuals of the step1 RF model. The predictions of these two RF models were later added together. We further performed a sensitivity analysis offering a few nonlinear transformations of the X- and Y-coordinates to the SLR model, including X², Y², √X, √Y, and XY, to allow more flexible functions of the coordinates than the linear function. We were not able to perform kriging because of the clustered nature of the monitoring data.¹²

2.4. Model Evaluation and Comparison

For each model, we calculated model r² (squared Pearson correlation) and root-mean-square error (RMSE) by comparing main model predictions to the measurements.

We performed five-fold hold-out validation (HOV). The full set of measurements were randomly divided into five groups (20% each), stratified by site type (street, rural, and urban background) and region (north, west, central, and south). For each element-model combination, five additional HOV models were built, each based on 80% of the monitoring sites, with the remaining 20% for validation. HOV regression-based r² and RMSE were computed by comparing the stacked predictions at the five HOV test sets to the corresponding measurements. We also calculated mean square error-based R² (MSE-R²), defined as

where y̅ is the average of the measurements. MSE-R² can be seen as a rescaling of MSE. It measures fit about the 1:1 line rather than fit about the best fit line in regression-based r². The HOV r² and RMSE are relevant for multicity studies that exploit both within and between city variability of air pollution contrasts.

To test how the European models predict within-area variability, we calculated within-area r² and RMSE by comparing the stacked HOV predictions and measurements within each individual study area. Because the monitors are spatially clustered over Europe and nearby locations might have auto-correlations in their measurements, we additionally performed leave-one-area-out cross-validation (LOAOCV).^32,33 We developed Europe-wide models by excluding all observations from one study area at a time and applied the models to the sites that were left out. Therefore, 19 additional models were developed for each pollutant-algorithm combination. Within-area r² and RMSE were computed by comparing the predictions and measurements in the area that was excluded from model development. We focus interpretation on the average of the within-area r²s and RMSEs because the performance statistics of the individual study areas may be affected strongly by random error because they were based on only 20 sites in each study area.

For each main model, predictor variables selected in SLR models and the 15 most important variables in RF models were compared.

Each main model was mapped at a 100 × 100 m resolution across the whole study area, allowing for visual comparison between maps. Additionally, we compared predictions from models at 41,936 random locations across Europe used previously.¹² Comparisons of model predictions were made for the entire study area and at the national scale reporting the Pearson correlation coefficient (r) and RMSE. Truncations were performed to deal with unrealistic predictions of the SLR approach: predictions at the high end were truncated to the maximum final two-step modeled value, calculated by fitting the model with the maximum predictor values at monitoring sites for positive slopes (or the minimum predictor values for negative slopes); the negative predictions were set to zeros.

3. Results and Discussion

3.1. Distribution of PM_2.5 Component Measurements

Boxplots of the annual mean concentration for PM_2.5 components in the full dataset and in individual study areas are shown in Figure S2. For the majority of pollutants, pollution concentrations varied substantially within and between study areas. A positive north–south gradient was observed with higher pollution levels in southern study areas. A more detailed interpretation of the measured concentrations can be found elsewhere.⁷

3.2. Model Performance

Performance of models across Europe is shown in Table 1. Models for most components had moderate to good performance based upon HOV. Model performance was almost the same evaluating by regression-based r² or MSE-based R² (Table S2), consistent with the observation that the fitted regression slopes between observed versus predicted values are close to the 1–1 line (Figure S3). Models with the highest HOV r²s were developed for PM_2.5 S, having large between-area concentration variability for which large-scale predictor variables from CTM were available to explain the contrast. Sulfate (represented by S) is a secondary pollutant formed by the oxidation of sulfur dioxide for which the ratio of between- and within-area variability is larger than for the other elements.⁷ RF models consistently outperformed SLR models for all elements. This agrees with a previous study, which found more accurate exposure assessed for elemental components by RF than SLR, based on 24 monitoring sites.²¹ The better performance of RF is different from two previous comparisons,^16,17 where similar performance of spatial models was observed for SLR and RF. One study compared Europe-wide models for PM_2.5 and NO₂ developed using similar predictor variables as in the current study,¹⁶ the second study compared LUR models for ultrafine particles based upon mobile monitoring.¹⁷ One possible explanation for the difference in findings is that there might be more complex relationships between predictors and elemental composition than with the mass of PM_2.5, NO₂, and UFP. RF can capture unknown nonlinear relationships and interactions not predefined in SLR, without introducing overfitting of the data. Another important difference is that in the current study, the data were clustered within Europe, whereas in the earlier study on PM_2.5 and NO₂, models were developed based upon routine monitoring, with a more even distribution of sites across Europe. We hypothesize that the RF model accounted for spatial trends across Europe better than the linear model.

Table 1. Performance of PM_2.5 Composition Models over Europe^a.

		component	Cu	Fe	K	Ni	S	Si	V	Zn
	inclusion of X, Y coordinates	no. of sites	414	413	414	402	404	400	402	413
Model Building
SLR	one-step	model r2	0.56	0.55	0.61	0.62	0.79	0.52	0.70	0.48
		model RMSEb	3.3	65.5	64.6	0.9	146.5	59.7	1.7	11.8
	two-step, step1	model r2	0.52	0.53	0.52	0.56	0.80	0.48	0.66	0.47
		model RMSE	3.4	67.4	71.1	1.0	142.2	61.9	1.8	11.9
	two-step, step2	model r2	0.56	0.53	0.60	0.60	0.82	0.50	0.69	0.48
		model RMSE	3.3	67.4	65.0	0.9	135.4	61.1	1.7	11.8
RFc	one-step	model r2	0.95	0.95	0.97	0.95	0.98	0.95	0.97	0.95
		model RMSE	1.1	20.8	16.8	0.3	40.2	19.9	0.5	3.5
	two-step, step1	model r2	0.95	0.95	0.97	0.95	0.98	0.94	0.97	0.96
		model RMSE	1.1	20.9	17.4	0.3	41.8	20.3	0.5	3.4
	two-step, step2	model r2	0.98	0.98	0.99	0.98	0.99	0.98	0.99	0.99
		model RMSE	0.6	12.4	9.5	0.2	27.0	12.2	0.3	1.8
HOV
SLR	one-step	HOV r2	0.47	0.48	0.58	0.57	0.76	0.50	0.63	0.41
		HOV RMSE	3.6	70.5	66.4	1.0	156.4	60.8	1.8	12.5
	two-step, step1	HOV r2	0.44	0.46	0.50	0.51	0.76	0.46	0.60	0.42
		HOV RMSE	3.7	71.7	72.6	1.0	154.9	63.4	1.9	12.4
	two-step, step2	HOV r2	0.48	0.48	0.59	0.56	0.79	0.46	0.63	0.41
		HOV RMSE	3.6	70.5	66.1	1.0	147.0	62.9	1.8	12.5
RF	one-step	HOV r2	0.60	0.60	0.82	0.74	0.91	0.62	0.85	0.68
		HOV RMSE	3.2	61.7	44.1	0.7	97.0	52.9	1.2	9.3
	two-step, step1	HOV r2	0.59	0.59	0.79	0.74	0.90	0.60	0.84	0.68
		HOV RMSE	3.2	62.4	47.4	0.7	102.1	54.2	1.2	9.2
	two-step, step2	HOV r2	0.59	0.61	0.80	0.76	0.90	0.62	0.86	0.71
		HOV RMSE	3.2	61.3	45.8	0.7	99.5	53.1	1.1	8.7

^aSLR = supervised linear regression; RF = random forest; r² = squared Pearson correlation; RMSE = root-mean-square error; HOV = fivefold hold-out validation.

^bUnit of RMSE: ng/m³.

^cPerformance of RF on training set cannot be interpreted.

For most components, HOV r²s were similar for the one-step model and the final two-step model and higher than for the first step of the two-step model, documenting that spatial trends account for the residual variance not explained by the available predictors. Offering a priori transformed X- and Y-coordinates did not further improve performance for SLR models. The differences between model r² and HOV r² in SLR models were small, suggesting the models do not overfit. The perfect performance on training set (model r²) for RF models is “by design” and basically meaningless. This is because the RF algorithm generally does not prune the individual trees, relying instead on the ensemble of trees to control overfitting.²⁰

While the models performed well to explain overall variability across Europe, models performed less well in explaining variation within individual study areas (Table 2). Results are similar by performing fivefold HOV and LOAOCV, suggesting the model performance is stable regardless of CV methods. The better overall performance is explained by a combination of larger variability of concentrations between areas than within areas and the better availability of predictor variables for describing between- compared to within-area variability. Specifically, the addition of large-scale satellite and CTMs has contributed to assess the study-area background. The average within-area r²s were moderate for Cu and Fe and relatively poor for other components. Cu and Fe represent mechanically generated traffic-related particles and thus their particle size distribution within PM_2.5 is skewed toward coarse particles.^7,34 Therefore, Cu and Fe do not travel far and may show large within-area variation. The better within-area performance for Cu and Fe is thus possibly because of the combination of higher within-area variation of the concentrations in most areas and the availability of data on traffic networks within individual areas. Within-area r²s were poor for components that have limited within-area variation such as S. S represents secondary inorganic aerosols (sulfates) produced by atmospheric chemistry of precursor gases (sulfur oxides) originating from combustion of sulfur-containing fossil fuels (e.g., in power plants).³⁵ Much of transported sulfate are in the submicron range and travel far, resulting in fairly uniform spatial variation in the scale of cities. Ni and V are often emitted from coal, oil, or residual oil burning in buildings and ships. The emission height of buildings and ships are relatively low so that within-city variation can be observed. Despite the consistently better performance of RF models than SLR models in overall HOV, the average within-area r²s were similar across models for each element. This further supports our hypothesis that the RF model accounted for spatial trends across Europe better than the SLR model. Within-area r²s varied substantially across study areas and were low in areas with small contrasts in measured concentrations shown by low RMSE (Figure S4).

Table 2. Performance of PM_2.5 Composition Models to Assess within-Area Variation: Average within-Area r^2a.

avg. WA r2	inclusion of X, Y coordinates	evaluation method	Cu	Fe	K	Ni	S	Si	V	Zn
SLR	one-step	five-fold HOV	0.34	0.35	0.09	0.18	0.14	0.18	0.21	0.20
		LOAOCV	0.37	0.38	0.09	0.15	0.22	0.21	0.23	0.18
	two-step, step1	five-fold HOV	0.34	0.34	0.08	0.17	0.14	0.20	0.18	0.21
		LOAOCV	0.35	0.35	0.09	0.15	0.22	0.20	0.20	0.18
	two-step, step2	five-fold HOV	0.35	0.36	0.07	0.17	0.14	0.20	0.19	0.19
		LOAOCV	0.36	0.36	0.09	0.15	0.22	0.20	0.21	0.18
RF	one-step	five-fold HOV	0.31	0.31	0.05	0.21	0.21	0.19	0.27	0.24
		LOAOCV	0.35	0.35	0.12	0.18	0.21	0.17	0.27	0.18
	two-step, step1	five-fold HOV	0.31	0.30	0.06	0.21	0.22	0.17	0.27	0.24
		LOAOCV	0.34	0.34	0.07	0.16	0.21	0.16	0.23	0.19
	two-step, step2	five-fold HOV	0.29	0.29	0.07	0.21	0.23	0.17	0.29	0.25
		LOAOCV	0.34	0.34	0.07	0.16	0.21	0.16	0.23	0.20

^aSLR = supervised linear regression; RF = random forest; r² = squared Pearson correlation; avg. WA r² is the average of 19 study area-specific r²s (area-specific r²s evaluated by five-fold HOV are shown in Figure S4); HOV = hold-out validation; LOAOCV = leave-one-area-out cross-validation.

In summary, the generally moderate within-area performance of the developed models is likely related to a combination of limited availability of predictor variables, for example, targeting especially nonexhaust traffic emissions, the clustered nature of the monitoring data and the lack of exposure contrasts within specific areas. Especially predictor variables at the local scale are insufficient.

3.3. Model Structure

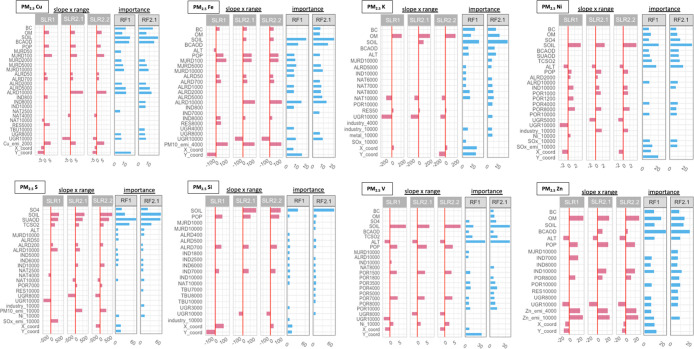
Predictor variables selected in SLR models and the 15 most important variables in RF models are shown in Figure 1. For each element, some consistency was found between SLR models and RF models in terms of the variable categories that were included. To some extent, however, different buffer sizes were included. Variables within each algorithm were very similar. X, Y coordinates usually contributed to the models when offered and were considered relatively important variables in the one-step RF.

Figure 1.

Regression slopes (shown in red) of predictors selected in SLR and relative variable importance (shown in blue) of the 15 most important predictors in RF.

The major predictors in the models differed substantially between the eight elements, broadly reflecting the different sources.

In Cu and Fe models, traffic-related predictor variables dominated the other source categories in SLR models while they were also considered relatively important in RF models. This is consistent with previous LUR models of Cu and Fe where a large proportion of the variability in the measured concentrations was explained by traffic-related variables.^8,36,37 Some of the industrial point sources were picked up in the SLR models for Cu and Fe, possibly reflecting emission released by metallurgic industries.³⁵ A previous study suggested that industrial sources were major predictors for Cu and Fe models in PM with diameter <1 μm (PM₁).³⁸

In Zn models, predictors representing industrial Zn emission and combustion sources contributed a large proportion to the overall r². This is consistent with LUR models in other studies.³⁶⁻³⁸ In ESCAPE modeling, specific industrial predictors were not available.⁸ The large contribution of industrial point sources to the Zn models is consistent with results of source apportionment analyses in MESA (Multi-Ethnic Study of Atherosclerosis) showing that Zn-rich features were indicative of incinerators at nearby fixed locations.³⁴ Previous studies have used Zn as a tracer for metallurgic industries and nonmetallurgic industries for frit production.³⁵

In Ni and V models, ports were important predictors, as a proxy for shipping emissions. Density of Ni-emitting industries and more general industrial density predictors were included in the SLR model for Ni and V, consistent with the identification that Ni and V shared the same mixed industrial/fuel-oil combustion source.³⁹ Large-scale SAT dust showed a large contribution in the Ni and V models, which possibly accounts for the observed north–south trend in the absence of a specific large-scale Ni and V CTM or satellite predictors. We offered SAT dust to all elements as windblown dust can be a source for all components.

In S models, variation in the measured concentrations was predominantly explained by large-scale satellite and CTM estimates and predictors in large buffers. Sulfate from the CTM and SAT dust were virtually equally important in the models. SAT sulfate did not enter the model possibly because sulfate from the CTM was in the model and they are highly correlated. SAT dust likely accounts for the observed north–south trend in concentration. In area-specific ESCAPE models, less well performing models were developed for S mainly because of the small within-study area variability.⁸ Predictors representing industrial point sources also contributed to the S models, indicative of the transformation of emissions from combustion.³⁴

In K models, SAT estimates for OM explained a large proportion of the variation, indicative of the main source of biomass burning for fine particle K.³⁵ Small-scale variables contributed little to K models, resulting in limited ability in explaining within-area variability. In our current models, we are still missing fine spatial scale biomass burning source terms because of the lack of reliable predictor variables.

Si models were dominated by SAT dust estimates and the population density, reflecting its crustal dust source.³⁵ Road length and industry areas from CORINE land cover also contributed to the models. These variables contributed a large fraction also in models for Si in PM₁.³⁸ In a previous study in New York, Si was strongly associated with an indicator for areas of industrial structures. This indicator includes a wide range of industrial, manufacturing, and commercial activities, thus it is difficult to identify the main source.³⁶

Values between two algorithms are not quantitatively comparable. Regression slopes in SLR were multiplied by the range of each predictor to allow comparison across predictors. Relative variable importance in RF was calculated as percentage increase in mean squared errors after a random permutation of the values of a variable. SO₄ = satellite sulfate, OM = satellite organic matter, SOIL = satellite dust; BC = satellite black carbon; BCAOD = CTM black carbon, SUAOD = CTM sulphate, TCSO₂ = CTM SO₂, POP = population, ALT = altitude, MJRD = major roads, ALRD = all roads, TBU = total build up, NAT = natural land, IND = industry, POR = ports, UGR = urban green, RES = residential, Cu_emi = Cu emission amount, PM₁₀_emi = PM₁₀ emission amount, SO_x_emi = SO_x emission amount, Zn_emi = Zn emission amount, industry = number of total industrial sites, Ni = number of industrial sites emitting Ni, X_coord = east–west gradient, and Y_coord = north–south gradient. Number in subscript depicts the buffer size SLR1 = one-step SLR; SLR2.1 = two-step SLR, step one; SLR2.2 = two-step SLR, step two; RF1 = one-step RF; RF2.1 = two-step RF, step one.

3.4. Maps and Prediction at Random Locations

The truncation frequency for prediction at random locations is shown in Table S3. A large number of negative SLR predictions were truncated to zero for some elements—for example, 41.3% of the 41,936 random locations across Europe for Cu in the final two-step SLR model predictions. Most of the negative values were located in the low population density areas of Northern Europe, covered mostly by natural land. When we applied the final two-step SLR models to a large Europe-wide pooled dataset of ESCAPE cohorts with 393,064 subjects (including a Swedish and Danish cohort), truncation frequencies were much smaller: 10.5% for PM_2.5 Cu, 0.5% for PM_2.5 Fe, 11.3% for PM_2.5 Ni, 14.2% for PM_2.5 V, and 2.7% for PM_2.5 Zn. Therefore, we do not expect this to be a big issue when applying the SLR models to participants in epidemiological studies. No truncation was needed for RF models.

Although we a priori considered one-step RF models as our main RF models, we observed large concentration jumps along horizontal or vertical lines in several maps (Figure S5). This counterintuitive pattern possibly reflects the role of the X, Y coordinates in RF modeling and relative importance attributed to these variables. Using X and Y in RF introduces strong boundary effects because, depending on the value where trees are split, large difference in predictions will be produced below and above that value. The concentration jumps were also observed in the final two-step RF model maps with X, Y coordinates. The RF models without offering X, Y coordinates produced clearly different maps while the HOV r²s were marginally lower than for the RF models with coordinates (Table 1). We, therefore, prefer the first step in the two-step RF and the final two-step SLR (maps in Figure 2), and show maps deriving from the other procedures in the appendix (Figure S5). The maps showing strong boundary effects might require smoothing before application in epidemiological studies. Our results clearly indicate the value in evaluating plausibility of maps as an important last step in air pollution exposure assessment studies. Comparing models solely by HOV statistics is not sufficient. We did not observe sharp gradients in the SLR model maps.

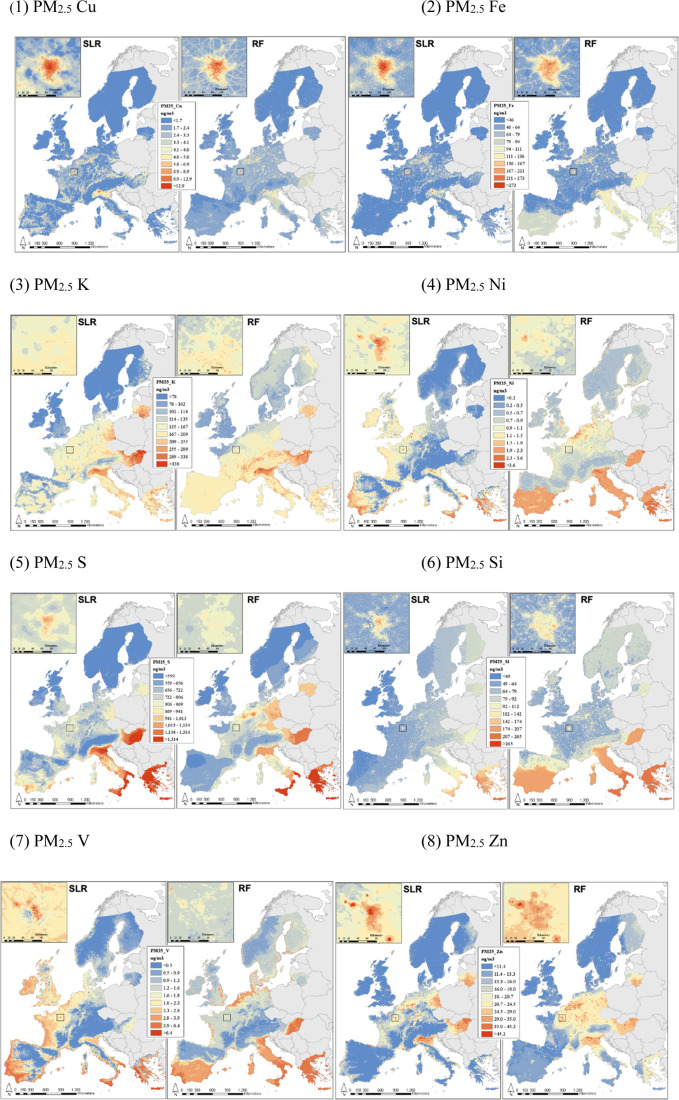
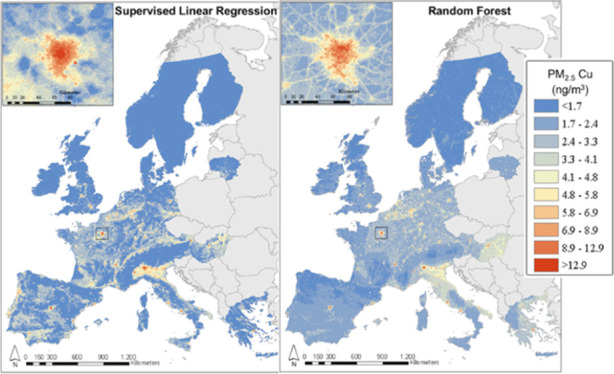
Figure 2.

Maps of PM_2.5 components developed by our main SLR (two-step, step2) and RF (two-step, step1) models.

There are clear agreements between maps produced by our main SLR and RF for some elements and differences for other elements (Figure 2). In both maps for Cu, high levels of pollution are shown in big cities, and transport networks can be clearly seen in the inset map of the area around Paris. Maps for PM_2.5 S are broadly similar with higher pollution levels in the south and east, while quite different patterns were observed for East Germany and Spain. Both maps for Zn show high concentrations close to industrial sites. The same industrial sites were picked up in the area around Paris shown in the inset. Comparing the predictions at a total of 41,936 random locations, agreement was high at all European countries-level and the ELAPSE countries combined-level for PM_2.5 Cu, PM_2.5 K, PM_2.5 S, PM_2.5 Zn (r > 0.7), and moderately high for other elements (Table 3). Correlation between all model predictions at the ELAPSE countries combined-level is presented in Figure S6. For most components, correlations were high for predictions derived from the same algorithm, and lower for predictions derived from different algorithms.

Table 3. Correlations between Predictions by Our Main SLR (Two-Step, step2) and RF (Two-Step, step1) Models at 41,936 Random Locations^a.

	PM2.5 Cu		PM2.5 Fe		PM2.5 K		PM2.5 Ni		PM2.5 S		PM2.5 Si		PM2.5 V		PM2.5 Zn
region	r	RMSEb	r	RMSE	r	RMSE	r	RMSE	r	RMSE	r	RMSE	r	RMSE	r	RMSE	N
all European countries	0.72	1.1	0.66	20.5	0.75	51.3	0.56	0.5	0.88	162.6	0.56	22.8	0.64	1.0	0.73	7.1	41,936
ELAPSE Countries
combined	0.79	1.0	0.77	19.1	0.70	56.1	0.53	0.5	0.89	142.0	0.75	12.5	0.66	0.8	0.73	7.0	27,411
Austria	0.77	1.1	0.80	16.2	0.80	35.0	0.28	0.1	0.95	69.5	0.08	9.5	0.82	0.2	0.89	4.4	1051
Belgium	0.82	0.9	0.89	11.9	0.05	21.0	0.83	0.4	0.79	47.4	0.71	8.2	0.76	0.8	0.70	11.4	355
Switzerland	0.80	1.1	0.89	13.1	0.76	24.1	0.36	0.1	0.48	95.0	0.38	9.2	0.49	0.2	0.65	5.8	500
Germany	0.74	1.0	0.80	14.9	0.43	30.6	0.66	0.3	0.67	60.1	0.59	8.2	0.80	0.4	0.58	6.9	4233
Denmark	0.77	0.3	0.77	9.3	0.68	15.0	0.21	0.2	0.73	36.0	0.45	7.2	0.24	0.3	0.49	2.0	522
France	0.62	1.1	0.75	14.2	0.31	26.9	0.39	0.4	0.72	69.0	0.48	9.0	0.77	0.6	0.59	6.8	6476
Italy	0.72	1.3	0.53	23.2	0.69	33.6	0.51	0.6	0.83	183.0	0.70	19.5	0.63	1.3	0.67	9.0	3550
Netherlands	0.74	0.9	0.83	14.2	0.55	17.2	0.64	0.4	0.60	45.0	0.68	8.9	0.48	0.7	0.66	14.2	451
Norway	0.37	0.0	0.61	5.6	–0.68c	8.6	0.43	0.2	0.25	104.9	0.03	4.3	0.80	0.3	0.46	4.0	2649
Sweden	0.56	0.2	0.77	5.8	–0.68c	22.6	0.68	0.1	0.88	86.7	0.31	4.9	0.73	0.4	0.38	3.6	4786
United Kingdom	0.85	0.6	0.87	12.0	–0.74c	25.9	0.59	0.3	0.86	72.1	0.12	9.6	0.57	0.5	0.68	4.1	2838
Non-ELAPSE Countries
Greece	0.55	1.0	0.57	16.8	0.38	28.7	0.44	0.8	0.18	123.5	0.34	25.6	0.46	1.9	0.54	7.0	1541
Finland	0.25	0.3	0.58	7.4	0.49	28.7	0.48	0.1	0.85	67.3	0.28	4.9	0.33	0.3	0.55	4.2	3208
Hungary	0.68	0.9	0.61	11.7	0.74	29.0	0.34	0.2	0.60	87.4	0.57	8.2	0.67	0.3	0.79	5.0	1123
Ireland	0.52	0.3	0.65	5.8	–0.70c	16.9	0.46	0.2	0.45	48.5	–0.08	4.8	0.41	0.4	0.26	1.8	844
Lithuania	0.63	0.8	0.68	7.0	0.65	25.3	0.26	0.1	0.16	52.5	0.59	4.7	0.29	0.2	0.89	1.8	783
Luxembourg	0.76	0.8	0.83	8.4	–0.08	16.2	0.82	0.1	0.82	26.5	0.77	4.9	0.80	0.2	0.83	2.1	33
Portugal	0.41	1.6	0.01	21.0	–0.03	23.5	0.71	0.4	0.72	72.9	0.22	7.3	0.80	0.7	0.60	6.6	1021
Spain	0.59	1.2	0.34	17.2	0.06	32.7	0.41	0.6	0.59	102.0	0.49	10.7	0.59	1.1	0.56	8.0	5972

^ar = Pearson correlation coefficient; RMSE = root-mean-square error.

^bUnit of RMSE: ng/m³.

^cWe do not have clear explanations of these high negative correlations. These values possibly reflect the poor performance of both models at low concentrations. Scatter plots documented the poor agreement between predictions by the two models with lots of scatters.

While correlations between predictions derived from SLR and RF were moderate to high at the European level, they are lower than the very high correlations (r generally >0.9) reported previously for Europe-wide models of PM_2.5 and NO₂.¹⁶ Agreement between predictions from the two algorithms at the national level varied substantially across countries (Table 3). There was no consistently good agreement between predictions for a specific country. Poor agreement between predictions were observed for area-component combinations that had small contrasts in measured concentrations shown by low RMSE (e.g., most components in Norway and Sweden).

Computation time for mapping differed substantially for RF and SLR—around 40 h for RF and less than 1 h for SLR to map pollution concentrations across Europe on a standard office computer.

3.5. Strengths and Limitations

With the development of Europe-wide models, we are able to assess long-term exposures to PM_2.5 components in a large European project, which consists of several nation-wide cohorts and smaller cohorts in which participants were recruited in specific study areas. The use of a single harmonized model allows a standardized exposure assessment in international multicenter studies.

Our Europe-wide models had the advantage of a large training dataset with large contrasts in measured concentrations by combining measurements from individual ESCAPE study areas. In contrast, the previous ESCAPE area-specific models could not be developed for some composition-area combinations because of missing data (e.g., in Lugano), small within-area variability (e.g., S) and poor precision of the measurements in areas with low concentrations (Ni and V).⁸ The moderate to good performance of our models across Europe suggests that the models would perform well in multicenter studies that exploit both within and between area variability of air pollution contrasts.

Another strength of our study is that we made efforts in collecting specific large-scale predictors, from satellites and CTMs, representing different pollution sources such as soil, industrial sources, and biomass burning, which could not be applied in prior area-specific models. The availability of these predictors increased the specificity of our models, which is useful to study associated health effects of specific single components.

While inclusion of industrial point source data was an improvement over the simple land use categories available in CORINE land cover, a dispersion model for point sources would have been the method of choice. We did not have the possibility to use Europe-wide small-scale dispersion modeling, and we did not have information on chimney height and wind direction around chimneys. We therefore used inverse distance weighting to create variables from industrial point sources, which can lead to overestimation of pollution levels in areas very close to the industrial sites.⁴⁰ The misclassification is expected to be minimal given that it is unlikely that many people live very close to the large point source chimneys included in the European Pollutant Release and Transfer Register databases. The small truncation frequency (<0.1%) above the maximum values in a total of around 42,000 random locations across Europe suggested the overestimation might not have a large impact.

The prediction ability of our Europe-wide model at small-scale, however, is limited, especially in areas without main sources present. The lack of specificity of the small-scale land use predictors might have contributed to the poor predictive ability for some elements. The poor within-area predictive ability suggests our Europe-wide models should be applied with caution in small-scale individual study areas, with the possible exception of the Cu and Fe models. Our model is more suited for multicenter studies.

Moderate to high overall correlations between our Europe-wide SLR and previous area-specific ESCAPE model predictions at monitoring sites were observed except for K and Zn (Table S4). The within-area correlations between SLR and ESCAPE varied considerably and the average correlations were high for Cu and Fe. The results suggested applying the newly developed Europe-wide models in epidemiological studies could lead to different findings from the ESCAPE study. The leave-one-out-cross-validation (LOOCV) r²s of the area-specific ESCAPE models are not quantitatively comparable with the within-area fivefold cross-validation r²s in this study as the LOOCV is based on a small number of sites and tends to overestimate predictive ability.^10,11

Given the discrepancies in predictions derived from the two methods, applying the two sets of models in epidemiological studies could lead to different associations with health. SLR and RF model performances were similar for the within-area concentration variability, while RF model explained overall concentration variability (including between-area variability) better than SLR. In SLR, we did not add fixed or random intercepts for study area as such models could not be applied outside the specific study areas. In a previous study on PM_2.5 and NO₂,³³ we found that adding indicators for study area or the measured regional background in each study area, improved the overall explained variability. Therefore, when applied in epidemiological studies, it depends on the contrast exploited in the epidemiological study which method is the preferred method. If both between- and within-area variability are exploited, RF would be the method of choice based on the cross-validation statistics. If an epidemiological study only includes within-area exposure contrast, then both methods should be interpreted equally, without a prior preference for one of the methods. Given the moderate performance of both models, it would be important to observe robustness of the findings in epidemiological studies. If health effects are found with only one model, this should be interpreted cautiously.

Because of the lack of external validation data, we cannot draw strong conclusions about the preferred method. We note that RF models might be more difficult to interpret in terms of how predictor variables act in the models, although the “importance” statistics provide useful information on the relative importance of individual predictors. The classification nature of RF led to visible boundary effects in some exposure maps, which might require smoothing before application in epidemiological studies. On the other hand, SLR might fail to capture some complex nonlinear relationships and/or interactions between predictors and pollutants, or might induce overfitting if multiple nonlinear and interaction terms were added to the model. Despite the discrepancies in predictions, we believe our models are stable and the results are robust, as different cross-validation methods and several sensitivity analyses showed moderate to good performance, especially at the overall Europe-wide scale and similar results.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.0c06595.

• Overview of potential predictor variables; performance of PM2.5 composition models over Europe; truncation frequency for model predictions at random locations; correlation of predictions at monitoring sites; distribution of 416 ESCAPE monitoring sites; boxplots of annual mean concentrations for PM2.5 composition; scatter plots of the stacked predictions at five held-out sites versus measurements; within-area r²s and RMSEs of PM2.5 composition models; maps of PM2.5 components; and Pearson correlation between model predictions at random locations across ELAPSE countries (PDF)

The authors declare no competing financial interest.