Coherent optical nanotweezers for ultracold atoms

Abstract

There has been a recent surge of interest and progress in creating subwavelength free-space optical potentials for ultracold atoms. A key open question is whether geometric potentials, which are repulsive and ubiquitous in the creation of subwavelength free-space potentials, forbid the creation of narrow traps with long lifetimes. Here, we show that it is possible to create such traps. We propose two schemes for realizing subwavelength traps and demonstrate their superiority over existing proposals. We analyze the lifetime of atoms in such traps and show that long-lived bound states are possible. This work allows for subwavelength control and manipulation of ultracold matter, with applications in quantum chemistry and quantum simulation.

Coherent manipulation of atoms using light is at the heart of cold-atom-based quantum technologies such as quantum information processing and quantum simulation [1,2]. The most commonly used methods to trap atoms optically are based on the ac-Stark shift induced in a two-level system by an off-resonant laser field, which provides a conservative potential that is proportional to laser intensity. The spatial resolution of such a trapping potential is diffraction limited, unless operated near surfaces [3–8]. In contrast, a three-level system with two coupling fields offers more flexibility and can generate a subwavelength optical potential even in the far field: although the intensity profiles of both laser beams involved are diffraction limited, the internal structure of the state can change in space on length scales much shorter than the wavelength λ of the lasers [9–20]. Such a subwavelength internal-state structure can lead to subwavelength potentials either by creating spatially varying sensitivity to a standard ac-Stark shift [21–23] or by inducing a conservative subwavelength geometric potential [24–26].

Subwavelength traps can be useful in atom-based approaches to quantum information processing [27,28], anyon braiding [29], and quantum materials engineering, as well as for efficient loading into traps close to surfaces [3–8]. The use of dynamically adjustable subwavelength tweezers [30,31], in which atoms can be brought together and apart, can also enable controlled ultracold quantum chemistry [32–34].

To trap atoms on a subwavelength scale, the optical potential must provide a local minimum. The geometric scalar potential associated with a laser-induced internal-state structure is always repulsive and increases in magnitude as its spatial extent is reduced. This repulsive contribution must be considered when engineering attractive subwavelength optical potentials. A trap based on the combination of ac-Stark shift and subwavelength localization [9–16,35–55] within a three-level system was proposed in Ref. [21], but the geometric potentials arising from nonadiabatic corrections to the Born-Oppenheimer approximation [24,25] were not considered. In this paper, we show that even with the repulsive nonadiabatic corrections, attractive subwavelength potentials are still possible. We also propose two alternative schemes for the generation of traps that offer longer trapping times as compared to the approach of Ref. [21]. We analyze the performance of all three approaches and show that 14-nm-wide traps offering 100-ms trapping times are feasible. Compared with near-field methods, our far-field approach not only avoids losses and decoherence mechanisms associated with proximity to surfaces, but also provides more flexibility in time-dependent control of the shape and position of the trapping potentials [56] and, additionally, works not only in one and two dimensions but also in three dimensions.

I. MODEL

We start with a single-atom Hamiltonian,

$$H=H_{\text{al}}(x)+\frac{p^2}{2m},$$ (1)

where m is the mass, p is the momentum, and H_al describes the atom-light interaction. We consider three schemes shown in Fig. 1: (a) electromagnetically induced transparency (EIT), (b) blue-detuned ac-Stark, and (c) red-detuned ac-Stark [21]. For the EITscheme $(\hslash =1)$,

$$H_{\text{al}}=\left(\begin{array}{ccc}{\delta }_r& 0& {\mathrm{\Omega }}_c(x)\\ 0& 0& {\mathrm{\Omega }}_p\\ {\mathrm{\Omega }}_c(x)& {\mathrm{\Omega }}_p& \mathrm{\Delta }\end{array}\right)$$ (2)

in the basis of bare atomic states {|r〉, |g〉 |e〉}, where 2Ω_p and 2Ω_c(x) are Rabi frequencies of a spatially homogeneous probe field and a spatially varying control field, respectively. For the two ac-Stark schemes, in the limit of large single-photon detuning |Δ| ≫ Ω_c(x), Ω_p, |δ| [see Figs. 1(b) and 1(c)], the intermediate state |e〉 can be adiabatically eliminated, resulting in an effective two-state Hamiltonian,

$$H_{\text{al}}=\left(\begin{array}{cc}\delta -\frac{{\mathrm{\Omega }}_c^2(x)}{\mathrm{\Delta }}& {\mathrm{\Omega }}_p\\ {\mathrm{\Omega }}_p& 0\end{array}\right),$$ (3)

in the {|r〉, |g〉} basis.

FIG. 1.

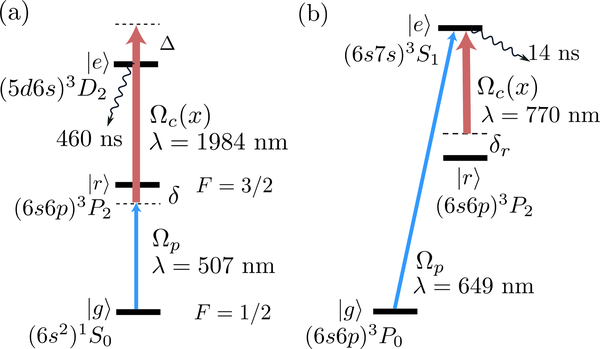
(a) Level diagram for the EITscheme, showing a spatially homogeneous field Ω_p (solid blue bar) and a spatially varying field ${\mathrm{\Omega }}_c(x)={\mathrm{\Omega }}_0{(1-e^{-x^2/{\sigma }^2})}^{1/2}$ (red bar with gradient). Γ is the linewidth of the excited state. (b) Level diagram for the blue-detuned ac-Stark scheme. The intermediate state |r〉 is dressed by coupling it to the excited state |e〉 with a spatially dependent ${\mathrm{\Omega }}_c(x)={\mathrm{\Omega }}_0{(1-e^{-x^2/{\sigma }^2})}^{1/2}$ and a large detuning Δ ≫ Ω_c, which gives rise to a light shift ${\mathrm{\Omega }}_c^2(x)/\mathrm{\Delta }$ of state |r〉. The ground state |g〉 is coupled to state |r〉 with a spatially uniform Ω_p and detuning δ = 0. (c) Level diagram for the red-detuned ac-Stark scheme [21]. The difference from panel (b) is that ${\mathrm{\Omega }}_c(x)={\mathrm{\Omega }}_0{e}^{-x^2/\left(2{\sigma }^2\right)}$ is maximal at x = 0 and that |Δ|≫ Ω_c, δ now indicates the amount of red detuning. Moreover, the detuning $\delta ={\mathrm{\Omega }}_0^2/\mathrm{\Delta }$ is chosen to exactly compensate for the light shift of |r〉 at x = 0. (a’, b’) Sketches of the relevant eigenstates (an atom depicted by a green ball is trapped in the blue potential): (a’) for the (a) scheme; (b’) for the (b) scheme, which for x < w is equivalent to the (c) scheme. Although E_± are diffraction limited, E₀ has a subwavelength shape characterized by the width w, which can be expressed using the enhancement factor defined as s = σ/w.

Within the Born-Oppenheimer approximation, we first diagonalize H_al, which leads to position-dependent eigenstates. Nonadiabatic corrections give rise to geometric scalar U and vector A potentials, defined as $U=R^{†}{\partial }_x^{2}R$ and $A=i{R}^{†}{\partial }_{x}R$, where R is a unitary operator diagonalizing H_al [24,25]. The resulting Hamiltonian is given by $H^{\prime }=R^{†}HR=R^{†}{H}_{\text{al}}R+U(x)+\frac{p^2}{2m}-\frac{A(x)p}{m}$. Below, we focus on the potential R^†H_alR + U(x) experienced by three-level atoms under three different schemes.

II. EIT SCHEME

In Refs. [24–26], subwavelength barriers were considered in the EITconfiguration assuming two-photon resonance, i.e., δ_r = 0 in Fig. 1(a). The approximate dark state |D〉 ∝ Ω_c(x)|g〉 − Ω_p|r〉 then experiences only a repulsive geometric potential 〈D|U|D〉. On the other hand, in the presence of a finite detuning δ_r for state |r〉, the dark state |D〉 can acquire a negative energy shift E₀(x) with an absolute value greater than the positive geometric potential. Moreover, we see that, as we move from large to small x, the state |D〉 changes its character from |g〉 to |r〉 at x = w defined via Ω_c(w) = Ω_p. Therefore, for Ω₀ ≫ Ω_p, we can engineer subwavelength traps with width w ≪ σ. However, at first glance, it is not obvious whether the additional contribution from the repulsive geometric potential would cancel the attractive potential. Moreover, the approximate dark state experiencing the trapping potential can have a significant admixture of state |e〉, leading to loss. Below, we address these two issues.

In the following, for simplicity, we set Δ = 0 because, for a single trap in the EITconfiguration, nearly all results (except the tunneling losses to the lower dressed-state |−〉) are Δ independent. For |δ_r +U(x)| ≪ Ω_p, the bright states |±〉 are well separated from the dark state. In this case, the ground state is composed of the dark state with a small admixture of bright states, so that the geometric potential and the energy shift E₀ can be calculated separately [see Fig. 1(a’)]. Note that, for all schemes, we take into account the decay Γ of state |e〉 perturbatively. We are interested in a spatially dependent [57] control Rabi frequency ${\mathrm{\Omega }}_c(x)={\mathrm{\Omega }}_0{(1-e^{-x^2/{\sigma }^2})}^{1/2}$. For small x, Ω_c ≈ Ω₀x/σ, so that the total effective potential V_tot = |〈D|r〉|²δ_r + U_D is equal to

$$V_{\text{tot}}=\frac{{\delta }_r}{1+x^2/w^2}+\frac{1}{2m{w}^2}\frac{1}{{\left(1+x^2/w^2\right)}^2},$$ (4)

where we use $U_D=\langle D|U|D\rangle =\frac{1}{2m}{(\frac{{\mathrm{\Omega }}_p{\partial }_x{\mathrm{\Omega }}_c(x)}{{\mathrm{\Omega }}_p^2+{\mathrm{\Omega }}_c^2(x)})}^2$ and w = σΩ_p/Ω₀. We see explicitly that the trapping potential has the subwavelength width w, which can be characterized by the enhancement factor s = σ/w, and that U_D is always repulsive. In addition, we note that 〈D|A(x)|D〉 = 0 (see Ref. [25]).

To compare all three schemes, we start by considering traps that have a specific width w and support a single bound state. Furthermore, we assume that our maximum Rabi frequency Ω_c(x) is limited to Ω₀. In that case, if we drop factors of order unity, our scheme supports a single bound state when the kinetic energy E_w = 1/(2mw²) is equal to the depth of the potential V_tot.

The leading source of loss comes from the admixture of the short-lived state |e〉. There are two processes leading to this admixture: (1) imperfect EIT due to δ_r ≠ 0 and (2) nonadiabatic off-diagonal corrections. Both processes admix |D〉 with |±〉, which in turn have significant overlap with |e〉. Within second-order perturbation theory, the loss rates from processes (1) and (2) are ${\mathrm{\Gamma }}_D^{(1)}\sim \mathrm{\Gamma }{V}_{\text{tot}}^2/{\mathrm{\Omega }}_p^2$ and ${\mathrm{\Gamma }}_D^{(2)}\sim \mathrm{\Gamma }\frac{{\left|U_{D\pm }\right|}^2}{{\mathrm{\Omega }}_p^2}\sim \mathrm{\Gamma }\frac{E_w^2}{{\mathrm{\Omega }}_p^2}$, respectively. Here U_D± = 〈D|U|±〉 and we use the fact that, for a trap with a single bound state, the off-diagonal [25] terms of U are of the same order as E_w. Thus, up to factors of order unity, the total losses are ${\mathrm{\Gamma }}_D\sim {\mathrm{\Gamma }}_D^{(1)}+{\mathrm{\Gamma }}_D^{(2)}\sim \mathrm{\Gamma }{E}_w^2/{\mathrm{\Omega }}_p^2$. We would like to note that we can modify the EITsetup so that nonadiabatic corrections are further suppressed (see Appendix A) and the only (and unavoidable) losses come from imperfect EIT. The decay rate for the bound state can be expressed using E_σ, Ω₀, and s as Γ_D ∼ Γs⁶(E_σ/Ω₀)², where E_σ ~ 1/(2mσ²). An additional constraint on available widths w comes from the fact that our perturbative analysis holds only for |V_tot| and E_w much smaller than the gap to the bright states |±〉, leading to E_w ≪ Ω_p, which is equivalent to s³ ≪ Ω₀/E_σ. Another source of losses is tunneling from the subwavelength-trapped state [22] to state |−〉, which, based on a Landau-Zener-like estimate (see Appendix B), is negligible for s³ ≪ Ω₀/E_σ. The specific experimental parameters are analyzed after the presentation of all three schemes.

III. BLUE-DETUNED ac-STARK SCHEME

The second scheme we propose is shown in Fig. 1(b) and is described by the Hamiltonian (3) with δ = 0. Here, the intermediate state |r〉 is dressed by coupling it to the excited state |e〉 with a spatially dependent Rabi frequency ${\mathrm{\Omega }}_c(x)={\mathrm{\Omega }}_0{(1-e^{-x^2/{\sigma }^2})}^{1/2}$. Together with a large blue detuning |Δ| ≫ Ω_c(x), this leads to a light shift ${\mathrm{\Omega }}_c^2(x)/\mathrm{\Delta }$ of state |r〉. At large x, state |0〉 is equal to |g〉, whereas, at x = 0, it is proportional to |g〉 − |r〉. The light shift E₀ describing the trapped state |0〉 is equal to

$$E_0(x)={\mathrm{\Omega }}_p\left(\frac{1}{2}{\left(\frac{x}{w}\right)}^2-\sqrt{1+\frac{1}{4}{\left(\frac{x}{w}\right)}^4}\right),$$ (5)

where the width w equals σ/s with

$$s=\sqrt{\frac{{\mathrm{\Omega }}_0^2}{\left|\mathrm{\Delta }\right|{\mathrm{\Omega }}_p}}.$$ (6)

Intuitively, the width w is equal to the distance at which the ac-stark shift is equal to the coupling Ω_p.

For this scheme, the nonadiabatic potential U is equal to

$$U=\left(\begin{array}{cc}\alpha & -\beta \\ \beta & \alpha \end{array}\right),$$ (7)

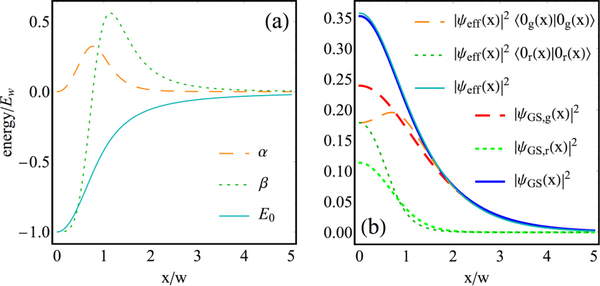
with $\alpha =E_w\frac{4w^2{x}^2}{{\left(4w^4+x^4\right)}^2}$ and $\beta =E_w\frac{6x^4-8w^4}{{\left(4w^4+x^4\right)}^2}$. Note that the off-diagonal terms are significantly greater than the diagonal ones (i.e., α < |β|), especially for x ≲ w, as shown in Fig. 2(a). For Ω_p = E_w, which leads to a single bound state, we obtain β on the order of the energy E₀(x). Note that our derivation works for arbitrary fractional probabilities f_r = |ψ_r(x)/ψ(x)|, whereas the method in Ref. [21] works only for fractional probabilities f_r ≪ 1, where ψ_r = 〈r|ψ〉 is the r component of the ground-state wave function ψ.

FIG. 2.

Analysis of the blue-detuned ac-Stark scheme [Fig. 1(b)]. (a) The light shift E₀(x), as well as the diagonal and off-diagonal couplings coming from the nonadiabatic potential U in Eq. (7) parametrized by α and β. (b) Properties of the ground state obtained from the effective Hamiltonian and from the full Hamiltonian (see main text for details). Figures are shown in units of w and E_w, making them applicable to all s ≫ 1.

In order to analyze the impact of U, we compare the ground state of the effective Hamiltonian $H_{\text{eff}}=E_0(x)-\frac{{\partial }_x^2}{2m}$ without U with the exact solution of the full Hamiltonian given by Eqs. (1) and (3). Even though |〈0|U|+〉| ~ E_w ~ Ω_p is large and on the order of the energy difference E₊ − E₀ ~ Ω_p, we see in Fig. 2(b) that the probability densities (and therefore the widths) of the ground states ψ_eff of H_eff and ψ_GS of the full Hamiltonian are nearly the same. However, from the comparison of components |g〉 and |r〉 of the ground state in Fig. 2(b), we see that the trapped atoms are not exactly in the eigenstate |0〉. This partially explains why the nonadiabatic corrections do not influence the width of the ground state: the components of the true ground state are smoother (spatial gradients are smaller) than those of the ground state |0〉 of H_al, which leads to weaker nonadiabatic corrections for the true ground state. In summary, even though the nonadiabatic potential U can be on the order of E_w for subwavelength traps, the width of the ground state is only very weakly influenced by U.

We now turn to the analysis of the trap lifetime. The leading contribution to losses comes from the admixture P_e of the short-lived state |e〉. P_e is determined by the characteristic coupling strength Ω_c(w) ≈ Ω₀/s within the trapped region and by the detuning Δ as P_e ∼ [Ω₀/(Δs)]2 ∼ s⁶(E_σ/Ω₀)². In principle, the condition Δ > Ω₀ might give an upper limit on s, which, based on Eq. (6), for Ω_p = E_w, is s⁴ < Ω₀/E_σ. However, this is not a constraint for any of the results considered here.

IV. RED-DETUNED ac-STARK SCHEME

Finally, we analyze the third scheme, which was proposed in Ref. [21], where we take into account nonadiabatic corrections for arbitrary fractional probabilities. This scheme differs from the blue-detuned ac-Stark scheme in that, first, the control Rabi frequency is ${\mathrm{\Omega }}_c(x)={\mathrm{\Omega }}_0{e}^{-x^2/\left(2{\sigma }^2\right)}$ which, for small x, is ≈Ω₀[1 − x²/(2σ²)]; second, the detuning $\delta ={\mathrm{\Omega }}_0^2/\mathrm{\Delta }$ is chosen to exactly compensate for the ac-Stark shift at the center of the trap [60]; and third, the detuning Δ now indicates the amount of red detuning. The resulting E₀ w, and s are identical to those in the blue-detuned ac-Stark scheme, Eqs. (5) and (6). We find that, for x ≲ w, the nonadiabatic corrections have nearly exactly the same form as in the blue-detuned ac-Stark scheme and differ only in the sign of the off-diagonal terms: $U=\left(\begin{array}{cc}\alpha & \beta \\ -\beta & \alpha \end{array}\right)$.

To derive the lifetime of this trap, we can set Ω_c(x) to Ω₀ within the trapped region, which leads to $P_e\sim \left({\mathrm{\Omega }}_0^2/{\mathrm{\Delta }}^2\right)={\left(s^2{\mathrm{\Omega }}_p/{\mathrm{\Omega }}_0\right)}^2=s^8{\left(E_{\sigma }/{\mathrm{\Omega }}_0\right)}^2$. This expression is identical to the one in the EITand blue-detuned ac-Stark schemes, except for the more favorable scaling with s (s⁶ vs s⁸). The intuition behind the difference between the two schemes based on the ac-Stark shift is the following: in the red-detuned ac-Stark scheme, the atoms are trapped in the region of maximal scattering from state |e〉, whereas, in our blue-detuned ac-Stark scheme, atoms are trapped in the region of minimal scattering from state |e〉.

V. ATOMIC LEVELS

Very well-isolated three-levels systems (either ladder type or Λ type) are required for efficient implementation of these subwavelength trapping schemes. The strong Ω_c(x) beam can off-resonantly couple |g〉 and |r〉 to states outside the three-level system and can limit lifetimes in addition to providing undesired additional confinement for the atoms in these subwavelength lattices [26,61]. This can significantly reduce the upper bound on the magnitude of Ω_c(x) [56,61] and therefore limit the width of the traps that can be realized. Here, in order to mitigate the issues discussed above, we propose using metastable states ³P₀ and ³P₂ in Yb atoms for the implementation of subwavelength trapping schemes.

For the blue- and red-detuned ac-Stark schemes, we use |g〉 = |(6s²) ¹S₀, F = 1/2〉, |r〉 = |(6s6p) ³P₂, F = 3/2〉, and |e〉 = |(5d6s) ³D₂〉 in ¹⁷¹Yb, as shown in Fig. 3(a). The hyperfine structure should not play a crucial role as Ω_p only couples | ¹S₀, F = 1/2〉 with | ³P₂, F = 3/2〉 as allowed by dipole selection rules and Ω_c (x) is blue- or red-detuned relative to the entire fine-structure manifold ³D₂. Note that the transition (6s²) ¹S₀ ↔ (6s6p) ³P₂ is a weak, forbidden transition [62,63] and requires a narrow, stable laser to address it.

FIG. 3.

(a) Atomic levels for the blue- and red-detuned ac-Stark schemes in ¹⁷¹Yb. (b) Atomic levels for the EITscheme in bosonic Yb atoms. In all schemes, the main limitation comes from the admixture of levels outside the three-level system.

For the EIT scheme, we use |g〉 = |(6s6p) ³P₀〉, |r〉 = |(6s6p) ³P₂〉, and |e〉 = |(6s7s) ³S₁〉 in bosonic Yb atoms, as shown in Fig. 3(b). High-polarization purity of the light fields is required for proper implementation of this scheme. In addition, the lifetime of atoms in the subwavelength traps for this scheme may be limited by fine-structure changing collisions of atoms in ³P₂ [64]. We note that all three schemes can be generalized to two dimensions, whereas blue- and red-detuned ac-Stark trapping schemes can be extended to three dimensions.

VI. ACHIEVABLE TRAP PARAMETERS

We showed above that, for fixed Ω₀, the two schemes proposed here provide superior performance to the red-detuned ac-Stark scheme due to the s⁶ vs s⁸ scaling of the losses. We now discuss what widths of the trapping potentials are achievable when we include fundamental limitations imposed on the magnitude of Ω₀. We set the trapping time T to be equal to 100 ms. Depending on the scheme and on σ (equal to λ/2π for the lattice, and to 3 μm for the tweezer; denoted by subscripts λ and 3μm, respectively), we find maximal Ω₀ and s such that the off-resonant position-dependent light shifts are less than 0.1E_w and that TΓP_e ~ 1:

Setup	$\frac{{\mathbf{\Omega }}_{\mathbf{0},\mathit{\lambda }}}{\mathbf{2}\mathit{\pi }\mathbf{GHz}}$	$\frac{{\mathit{w}}_{\mathit{\lambda }}}{\mathbf{nm}}$	sλ	$\frac{{\mathbf{\Omega }}_{\mathbf{0},\mathbf{3}\mathit{\mu }\mathbf{m}}}{\mathbf{2}\mathit{\pi }\mathbf{GHz}}$	$\frac{{\mathit{w}}_{\mathbf{3}\mathit{\mu }\mathbf{m}}}{\mathbf{nm}}$	s3 μm
EIT	7.0	14.0	7.0	1.5	68.0	44.0
Blue-ac	2.3	16.0	20.0	0.75	48.0	63.0
Red-ac	0.85	42.0	7.0	0.19	190.0	16.0

We see that the EITand the blue-detuned ac-Stark schemes allow for greater Ω₀, which translates into narrower traps. Note that narrower traps can be achieved, however, at the cost of reducing the lifetime of atoms in these traps. We would like to note that the presented results—for the sake of clarity and brevity—are based on the estimates neglecting factors on the order of the unity.

VII. APPLICATIONS

We now make a few remarks related to the applications pointed out in the introduction. Note that, if one’s goal is simply to use the expansion of a control field Ω_c(x) around its nodes to create traps with tight bound states with minimal scattering, then our EITscheme has no advantages over a simple two-level blue-detuned trap. Indeed, in our case, up to an additive constant, the potential near a node is given by $V(x)\approx {\delta }_r{\mathrm{\Omega }}_c{(x)}^2/{\mathrm{\Omega }}_p^2$, while the population of the excited state is given by $P_e(x)\approx {\delta }_r^2{\mathrm{\Omega }}_c^2(x)/{\mathrm{\Omega }}_p^4$. On the other hand, if one uses the same field Ω_c(x) to create a simple two-level blue-detuned trap (with detuning Δ), one obtains $V(x)\approx {\mathrm{\Omega }}_c^2(x)/\mathrm{\Delta }$ and $P_e(x)\approx {\mathrm{\Omega }}_c^2(x)/{\mathrm{\Delta }}^2$. In other words, our scheme is identical to the two-level scheme provided one replaces Δ with ${\mathrm{\Omega }}_p^2/{\delta }_r$.

However, our goal is not only to create a tight bound state in a trap of subwavelength width w but also to make the trapping potential nearly constant for |x| > w so that we can make and possibly independently move several traps, or a full lattice of traps, with subwavelength separations. In that case, a simple two-level scheme will not work. Instead, one has to use one of the subwavelength schemes we discuss here.

Recently, lattices of repulsive subwavelength barriers and subwavelength spacings were proposed [56,65] and realized [61] by time-averaging over different configurations of a dynamically applied optical Kronig-Penney potential. By extending the stroboscopic protocol [56,65] to lattices of subwavelength traps, it may be possible to “paint” arbitrary time-averaged potential landscapes for atoms with subwavelength resolution.

APPENDIX A: MODIFIED EIT SCHEME

Here, we show how to suppress nonadiabatic corrections in the EITscheme. The idea is that Ω_c(0) does not necessarily have to go to zero and that the gradient of Ω_c(x) around x = w can be smaller than for linear Ω_c(x) ~ x₀/σ. Nonadiabatic corrections can then be suppressed by using the following control field [66]: Ω_c(x) = Ω₀[1 + ν − cos(kx)], which does not go to zero as deeply and as sharply as the linear Ω_c(x).

Expanding Ω_c(x) around a minimum for ν > 0, we find

$${\mathrm{\Omega }}_c(x)={\mathrm{\Omega }}_p[\eta +{(x/w)}^2],$$ (A1)

with η = ν Ω₀/Ω_p and $w=\frac{1}{k}\sqrt{2{\mathrm{\Omega }}_p/{\mathrm{\Omega }}_0}$, and which gives rise to

$$V_{\text{tot}}=\frac{{\delta }_r}{{[\eta +{(x/w)}^2]}^2+1}+\frac{4E_w{(x/w)}^2}{{\{{[\eta +{(x/w)}^2]}^2+1\}}^2},$$

whose depth can be tuned to accommodate one or more bound states. By operating at η > 0, we can use appropriate |δ_r| ~ E_w to engineer trapping potentials with negligible nonadiabatic potential U. Therefore, when it comes to losses, this modified EIT scheme allows us to gain up to a factor of ~2.

APPENDIX B: LANDAU-ZENER ESTIMATES OF LOSSES TO LOWER DRESSED STATES

Another source of losses is tunneling from the single bound state we consider to state |−〉. Note that, due to the conservation of energy, atoms in |−〉 will have large kinetic energy. Following Ref. [22], the loss rate Γ_LZ can be estimated using a Landau-Zener-like argument, which, in our setup, leads to

$${\mathrm{\Gamma }}_{\text{LZ}}\sim E_w{e}^{-v{\mathrm{\Delta }}_{0-}/E_w},$$ (B1)

where ν is a factor of order unity, and Δ₀₋ is the energy difference between two dressed states involved in the tunneling.

In the EIT scheme, we have Δ₀₋ ∼ |E₋(0)| ∼ Ω_p because the tunneling occurs around x ∼ 0, where the gap between E_D and E₋ is smallest and where the atoms are trapped. This leads to the condition 1 ≪ Ω_p/E_w = Ω_c/(E_σs³). Note that we obtained the same condition from the requirement E_w ≪ Ω_p, which enabled us to treat nonadiabatic potentials and light shifts separately and perturbatively. We can further suppress tunneling losses by working at Δ ≠ 0.

In the blue-detuned ac-Stark scheme, Δ₀₋ ∼ |E₋| ∼ |Δ|, so this tunneling loss rate is strongly suppressed as exp[−|Δ|/E_w].

In the red-detuned ac-Stark scheme, there is no state below the state of interest and therefore no tunneling.