Abstract
A bottom-up multi-scale modeling approach is used to develop an Integrated Computational Materials Engineering (ICME) framework for carbon fiber reinforced polymer (CFRP) composites, which has the potential to reduce development to deployment lead time for structural applications in lightweight vehicles. In this work, we develop and integrate computational models comprising of four size scales to fully describe and characterize three types of CFRP composites. In detail, the properties of the interphase region are determined by an analytical gradient model and molecular dynamics analysis at the nano-scale, which is then incorporated into micro-scale unidirectional (UD) representative volume element (RVE) models to characterize the failure strengths and envelopes of UD CFRP composites. Then, the results are leveraged to propose an elasto-plastic-damage constitutive law for UD composites to study the fiber tows of woven composites as well as the chips of sheet molding compound (SMC) composites. Subsequently, the failure mechanisms and failure strengths of woven and SMC composites are predicted by the meso-scale RVE models. Finally, building upon the models and results from lower scales, we show that a homogenized macro-scale model can capture the mechanical performance of a hat-section-shaped part under four-point bending. Along with the model integration, we will also demonstrate that the computational results are in good agreement with experiments conducted at different scales. The present study illustrates the potential and significance of integrated multi-scale computational modeling tools that can virtually evaluate the performance of CFRP composites and provide design guidance for CFRP composites used in structural applications.
Keywords: Integrated Computational Materials Engineering (ICME), Multi-scale modeling, Carbon fiber reinforced polymer (CFRP) composites, Lightweight applications
1. Introduction
With the growing attention on energy conservation and environmental protection, lightweight design for automobiles is becoming increasingly attractive in the automotive industry. Generally speaking, material replacement, structural optimization, and application of new manufacturing technology can be adopted in the lightweight design process, among which material replacement is arguably the most effective approach [1]. Carbon fiber reinforced polymer (CFRP) composites, with a density of 1.55 g/cm3 and a tensile strength of up to 2000 MPa along the fiber direction, stand as one of the most promising classes of materials to replace the engineered metals for automotive structural components. In particular, chopped carbon fiber sheet molding compound (SMC) and woven composites have great potential in automotive manufacturing due to their excellent mechanical performance, moderate cost, and easier fabrication compared to unidirectional (UD) CFRP composites [2–4]. In order to fully exploit the potential of these CFRP composites, we need to target increasing the accessibility of CFRP component designs, improving the robustness of initial designs, and most importantly, reducing the development to deployment lead time of CFRP components. These targets will eventually help mitigate greenhouse gas emissions from passenger vehicles and improve national energy independence [5].
The typical material design (or replacement) cycle consists of appropriate material selection followed by component size, shape design, and optimization [6]. In woven and chopped SMC CFRP composites, material selection also involves the size of representative element selection at the microstructure level. For instance, changing the size and/or angle of fiber tows for woven composites or changing the chip orientation for SMC composites significantly alter the anisotropic behavior of the material as well as its failure mechanisms, which in turn influence failure strength and fracture toughness of the material [3]. Thus, material design is not only limited to the size and geometry of constituents but also closely connected to the microstructural design. Traditionally, characterization of materials is done by carrying out expensive and time-consuming material tests to establish stiffness (elastic modulus) as well as strength properties in all material coordinates. With the advancements in computational materials science and engineering as well as multi-scale modeling, the “validation through simulation” approach has been increasingly adopted to decrease the time and cost of applying new materials to automotive components. Integrated Computational Materials Engineering (ICME) is the integration of materials information captured through computational tools with engineering product performance analysis and manufacturing process simulation [7]. This concept was first described by the U. S. National Materials Advisory Board Committee in 2008. Since then, ICME has become a fast-growing discipline within materials science and engineering and has been successfully employed in the design of metallic metals [8–10]. Compared to advanced metallic systems, the CFRP composites have the unique features of anisotropic and heterogeneous multi-scale microstructures and even larger variations in the material properties induced by the unique injecting/compression molding processes. Currently, there still exist two major challenges in developing ICME tool for CFRP composites: (1) development of high fidelity computational models; and (2) integration of the validated models and computational tools into one automated workflow so that the material processing, microstructure, and component structure can be optimized simultaneously [11].
In line with the overarching goal of ICME to reduce the time and the cost in the discovery and development of novel CFRP composites structures, multi-scale computational models have been established and embraced in our previous work and those of other researchers [12–24]. A majority of those models deliver the concerned information embedded in equations and parameters from lower-scale simulations to higher-scale, which is termed as the bottom-up hierarchical approach [17]. These previous studies on multi-scale model development have addressed the first challenge to a large extent. The primary objective of the present work is to address the second challenge, i.e., to integrate the multi-scale computational models and demonstrate an ICME framework of CFRP composites for lightweight vehicles, with a particular focus on three types of widely-used thermoset epoxy based CFRP composites in structural parts: long fiber UD composites, chopped short fiber SMC composites, and woven composites.
2. Synopsis of ICME framework
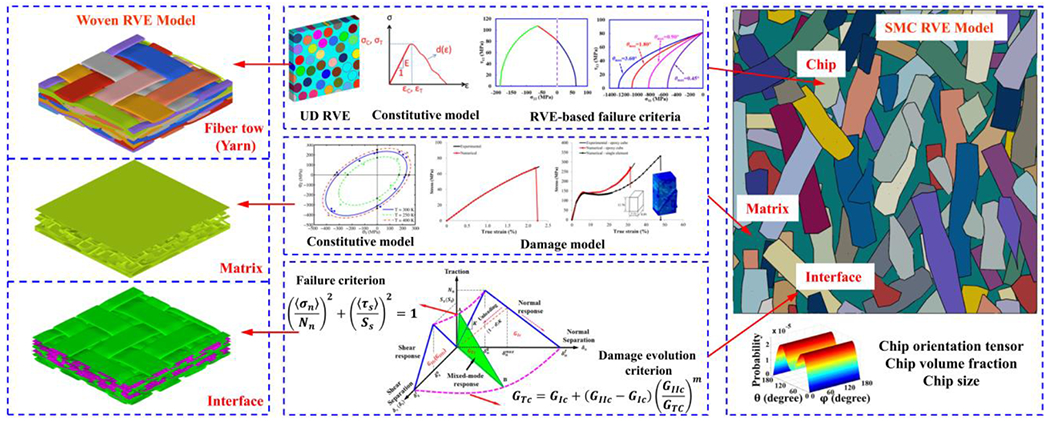
In the ICME framework considered in the present work, the intrinsic relationship between material microstructure (i.e., the fiber volume fraction of UD CFRP composites, woven yarn angle, SMC chip orientation, and size, etc.) and the mechanical performance of CFRP composites will be systematically developed by a bottom-up multi-scale modeling approach with the aim of structural design and failure analysis. As shown in Fig. 1, we use a four-scale model to describe the cured CFRP composites: properties of constituents (e.g. resin matrix and interphase region) at the nano-scale, UD representative volume element (RVE) at the micro-scale, chopped SMC as well as woven RVE at the meso-scale, and lastly the structural part at the macro-scale.
Figure 1.
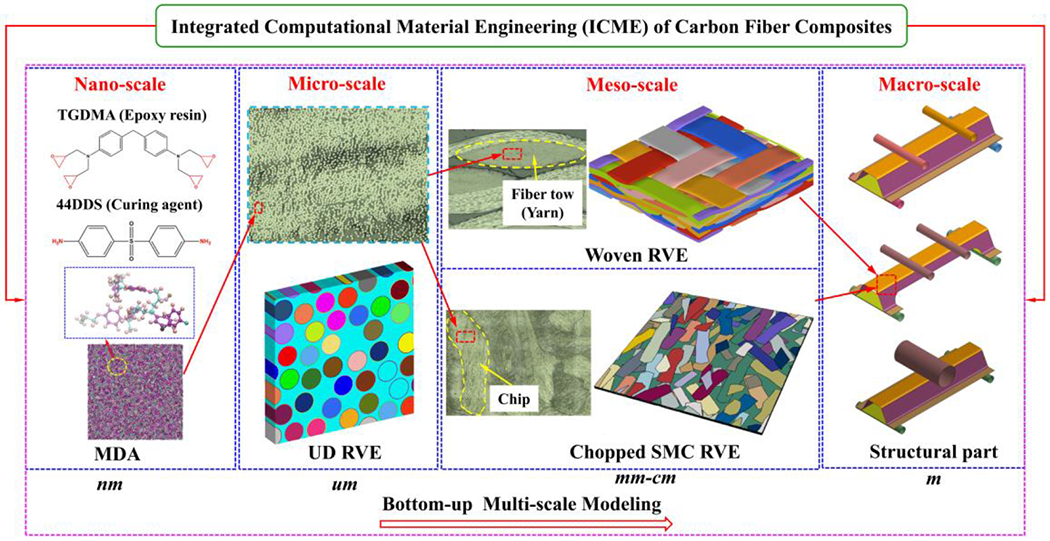
Schematic of the ICME framework with the bottom-up multi-scale modeling.
In the proposed bottom-up approach, the information obtained at lower scales will be passed on to higher scales. Specifically, molecular dynamics analysis (MDA) will be utilized as it offers a promising way to determine the material properties of constituents depending on molecular structures [25, 26]. In this work, MDA is used to quantify the influence of material gradient on mechanical property within the interphase region [12], which is an important input for micro-scale UD RVE. The UD RVE is then used to investigate the mechanical properties and failure envelopes of UD CFRP composites under multiple loading conditions, which inform us to propose an effective elasto-plastic constitutive law with damage evolution for homogenized UD composites. Chips in meso-scale SMC RVE and fiber tows (yarns) in meso-scale woven RVE have very similar properties as UD RVE [16]. Therefore, the elasto-plastic-damage material law and results from UD RVE are used to describe the properties of chips and fiber tows, which are basic structures of meso-scale SMC and woven RVE. Furthermore, meso-scale woven and SMC RVE models are constructed to gain in-depth insight into their complex failure mechanisms under various loading conditions. Finally, the effective properties of meso-scale SMC and woven RVE are used to predict the homogenized mechanical performance of a hat-section-shaped part at the macro-scale. Along the way, the accuracy of the proposed multi-scale models developed by the bottom-up approach is validated by comparing with the corresponding experimental results at different size scales. In essence, the ICME framework integrates four size scales by communicating information from lower scale to upper scale, and simultaneously, achieves the capability of designing and optimizing the global and local structures and constituents down to the micro- and nano-scale.
3. Nano-scale model of the interphase region based on MDA
Down to the nano-scale level, the carbon fiber surface is quite rough, partially due to the treatments applied to the carbon fibers during the fiber manufacturing process [27]. In addition, there is a significant nano-confinement effect from the carbon fibers on matrix resins [28–30]. As a result, a submicron-thick interphase region exists between carbon fibers and the matrix, as shown schematically in Fig. 2(a). It has been demonstrated that the interphase property has a significant influence on the composite mechanical performance [12, 31]. For CFRP composites specifically, the thickness of the interphase region has been evaluated to be about 200 nm [27]. To achieve a good balance of accuracy and simplicity, we have assumed the interphase region as a cylindrical shell adjacent to fiber, with the inner radius (rf) being the same as fiber radius. In the following text and Fig. 2, sub-indices f, i, and m denote fiber, interphase region, and matrix, respectively.
Figure 2.
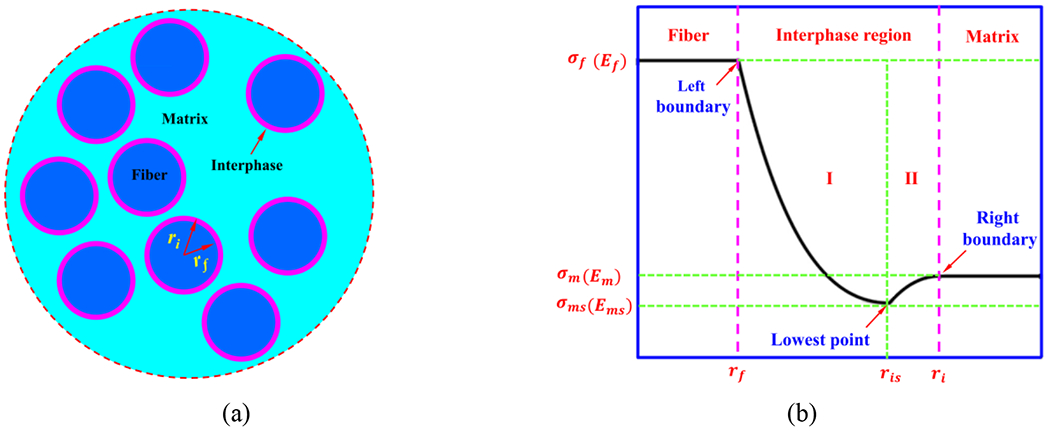
(a) Schematic of the cross-section of UD CFRP composites including the interphase region. (b) Variation of Young’s modulus or strength inside the interphase region.
To characterize the average properties of the interphase region, we adopted an analytical gradient model in our previous study [12] to describe the modulus and strength profile inside the interphase region. The key features of the gradient model are discussed here, while more detailed information is included in the Supplemental Information (SI). First, we assume the interphase region has isotropic properties, and the boundary values of the interphase are consistent with fiber and bulk matrix properties accordingly. Second, the modulus value of the fiber is taken as the average modulus in three dimensions. We formulate the strength boundaries according to the tensile strength of the fiber and the matrix. Third, the proposed gradient model includes two parts. In the first part (from rf to ris, and ris locates at three-quarters of the interphase width away from the fiber surface), Young’s modulus and strength decrease from fiber values to the lowest value, i.e., Ems or σms. The reason is due to the attenuation of the fiber confinement effect and possible incompatibility between fiber surface treatment and bulk matrix. In the second part, the mechanical properties increase from the lowest value to that of the matrix.
MDA has been used to characterize Ems and σms inside the interphase region. The effect of the degree of crosslinking on mechanical properties such as Young’s modulus and intrinsic yield and maximum stress of epoxy resin has been investigated. Epoxy resin, commercially denoted as 3501-6, utilized in the present work consists of TGDMA as the resin and 44DDS as the curing agent (see Fig. 3(a) for details of atomic structure). The above epoxy resin shares similar chemical features with the epoxy XPR-0273-31 used in this study [25]. The MDA results in Fig. 3(b) show an increasing trend of Young’s modulus and strength with an increasing degree of crosslinking. The results indicate that an insufficient crosslinking process leads to deleterious mechanical properties. The difference in Young’s modulus between under-cured epoxy (~70% degree of crosslinking) and fully cured epoxy (95% degree of crosslinking) is about 20%, and the difference in the strengths between them could be up to 50%. These MDA predicted results provide reasonable lower bounds of interphase mechanical properties due to insufficient curing, and the ratio between the lower bounds and matrix values have been selected as: Ems/Em = 0.8, σms/σm = 0.5.
Figure 3.
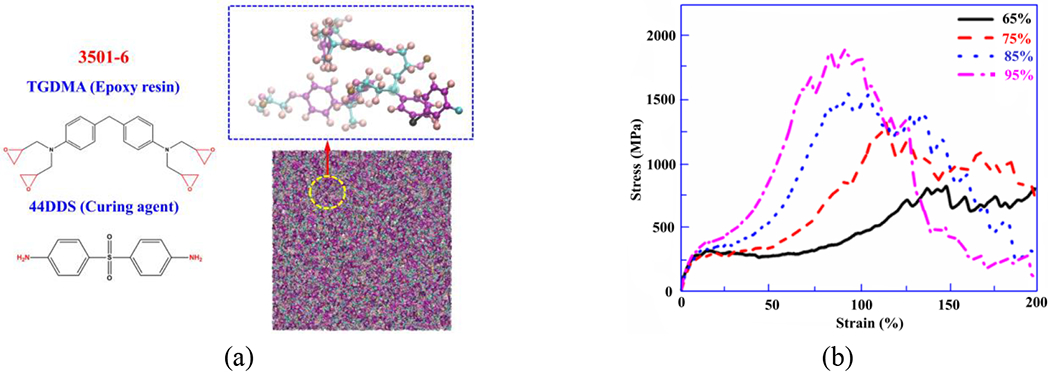
(a) Molecular structures of epoxy resin 3501-6 and the cross-linked resin model used in MD simulations. (b) Effect of degree of crosslinking onstress-strain behavior by using epoxy 3501-6 as a model system[25].
The resulting average modulus and strength of the interphase region are 22.5 GPa and 670 MPa respectively. Comparing these values to the modulus (3.8 GPa) and tensile strength (68 MPa) of the bulk resin matrix as measured from experiments, the average Young’s modulus and strength of the interphase region are higher about 5 and 9 times respectively. As a result, the interphase region shows an obvious stiffened response on average compared to the bulk matrix, although a portion of the interphase region is weaker due to insufficient crosslinking. This also demonstrates that the confinement effect by the fiber surface plays a dominant role in the interphase region. We note that as we assume isotropic properties to the interphase, this results in a modulus of the interphase larger than the transverse modulus of the carbon fiber (Table 1). However, our previous studies indicate that the failure behaviors and failure strengths of the composites have minor dependence on the elastic properties assigned to the interphase region, and it is mainly the interfacial properties between fiber and interphase that influence the failure strength of the UD composites [12]. We note that improvement can be made to the model by considering the transversely isotropic behavior of the interphase, with different moduli in the longitudinal and transverse directions [32].
Table 1.
Constituent properties used in the micro-scale UD RVE model.
| Carbon fiber | E11 (GPa) | E22=E33 (GPa) | G12=G13 (GPa) | G23 (GPa) | v12 | σT (GPa) | ||||||||||
| 245 | 19.8 | 29.191 | 5.922 | 0.28 | 3.46 | |||||||||||
| Epoxy matrix [12] | Em (GPa) | vm | vp | σft (MPa) | σfc (MPa) | GIC (J/m2) | ||||||||||
| 3.8 | 0.38 | 0.3 | 61.6 | 300 | 334.1 | |||||||||||
| Interphase region [12] |
Ei (GPa) | σi (MPa) | ||||||||||||||
| 22.5 | 670 | |||||||||||||||
| Fiber/interphase region interface [12] | K (MPa/mm) | σ1 (MPa) | σ2, σ3 (MPa) | GIC (J/m2) | GIIC, GIIIC (J/m2) | |||||||||||
| 108 | 70 | 80 | 2 | 32 | ||||||||||||
A recent study adopted a similar analytical function to represent the interphase region in fiber-reinforced composites [33]. The study also showed the capability to represent different types of interphase regions by adjusting ris and boundary values. For instance, imperfect adhesion between fiber and interphase, imperfect interphase region with impurities or damages, and imperfect cross-linking between interphase and matrix can be all adequately represented by replacing Ef, Em, Ems (or σf, σm, σms) with lower values. Additionally, the effect of ris has been investigated systematically and it was found that increasing ris from 0 to 1, both the effective Young’s and shear modulus of the interphase region increases. In sum, the analytical gradient function used in this study is versatile to represent the interphase regions in other fiber or even particle reinforced composites systems.
4. Micro-scale model development for UD CFRP composites
4.1. UD RVE model and constitutive laws for constituents
For model development, a cross-section of the microstructure of the UD RVE model with cylindrical fibers randomly distributed in the matrix is obtained using an algorithm proposed by Melro et al. [34]. The average fiber diameter of 7 μm and fiber volume fraction (Vf) of 51.4% are utilized based on experimental material characterization. In addition to the fiber and matrix phase, the UD RVE model includes a finite thickness (~200 nm) interphase region adjacent to fibers, consistent with the nano-scale model of the interphase region in the earlier Section 3. The details of the UD RVE model can be found in our previous study [12].
In the UD RVE model, carbon fibers are assumed to be transversally isotropic and linearly elastic. The five independent material constants of AKSACA carbon fibers and fiber tensile strength (σT) are listed in Table 1. The matrix adopted in this study is developed by the Dow Chemical company. Uniaxial tensile, compressive, and Mode I fracture toughness tests are conducted according to ASTM D638 [35], ASTM D695 [36], and ASTM E399 [37], respectively. Table 1 summarizes the basic epoxy properties obtained through experiments, where Em is Young’s modulus; vm is Poisson’s ratio in the elastic region; vp refers to the Poisson’s ratio in the plastic region; σft is tensile strength; σfc is compressive strength; and GIC represents the Mode I fracture toughness. The polymeric matrix of epoxy is modeled as an isotropic elasto-plastic solid and it follows the isotropic damage law proposed by Melro et al. [38]. The latter is implemented as a VUMAT user subroutine in the finite element commercial software Abaqus [39]. The interphase region is represented by a homogenous layer between fiber and matrix, with stiffened properties compared to the bulk matrix. In this study, the constitutive behavior and damage model of the interphase are assumed to be similar to those of the matrix material [12].
In addition to the three phases (fiber, matrix, and interphase), we also add a zero-thickness interface between the fiber and interphase region, which plays a key role in stress transferring between constituent materials and functions as the initiation site for the debonding failure. We add the interface between the fiber and the interphase while not the interphase and matrix based on two reasons. First, the failure of the matrix and interphase has been well described in the constitutive model and the interphase is treated as a mechanically enhanced matrix region. Second, there are pieces of experimental evidence showing that the interfacial debonding more likely occur towards the fiber side [40]. We have previously found that the interfacial parameters are crucial to accurately capture the failure strength of UD CFRP compared to experimental results. More details about constitutive law calibration and material property selection can be found in our previous study [12]. Recently, an analytical method in Ref. [41, 42] has been proposed to predict interfacial debonding under an arbitrary load with the input of only the transverse tensile strength and the components’ properties of UD composite. This approach has the advantage of avoiding errors due to the transformation of scales. Compared to this approach, the cohesive zone model (CZM) has been more extensively used among the available computational methods for the investigation of interfacial debonding [43]. In this work, we adopt the CZM approach, where interfacial debonding is considered by inserting cohesive elements at the interface between fiber and interphase region, with a constitutive response defined by a bilinear mixed-mode softening law [12].
Table 2 summarizes the key mechanical properties of UD composites predicted from UD RVE models. We also include a table in the SI that compares the experimentally measured properties with these predicted from RVE models under different uniaxial loading conditions.
Table 2.
Summary of the properties of UD composites predicted from UD RVE model
|
E11 (GPa) |
E22= E33 (GPa) |
G12= G13 (GPa) |
G23 (GPa) |
v12= v13 | v23 |
|---|---|---|---|---|---|
| 125.9 | 8.6 | 4.86 | 2.74 | 0.32 | 0.606 |
4.2. Failure analysis of UD CFRP composites under uniaxial stress state
The failure modes of UD CFRP composite are quite complex, and different failure mechanisms exist depending on the loading conditions. Pure transverse tensile loading causes debonding between the fiber/interphase region interface, which leads to matrix micro-cracking and matrix yielding, and subsequently results in a transverse crack perpendicular to the loading axis. As for the case of transverse compressive loading, the final failure of the UD CFRP composite takes place through the development of a matrix shear band, with an angle of inclination of 57.12° with respect to the plane perpendicular to the loading axis. This angle of the fracture surface orientation is very close to experimental data (56.15°). In the case of in-plane shear, interfacial debonding starts at different positions on the front surface of the UD RVE. The debonded regions link up with matrix cracks leading to complete rupture. We note that matrix cracks are not parallel to the fibers but having an angle of about 45° with the fiber direction. For out-of-plane shear, failure is trigged by interfacial debonding, and through the process of damage accumulation, these local failures coalesce to form an interface dominated crack orientated at 45° to the applied shear load. Longitudinal compression failure of the UD CFRP composite can be very sensitive to the initial fiber waviness angle introduced during the manufacturing process, which will lead to a localized hinge zone of fibers (kink-band). It is, however, difficult to determine the exact initial fiber misalignment angle since manufacturing defects appear stochastically. Recently, Bai et al. [44] presented a 3D RVE investigation of the formation of kink-band under longitudinal compression of the composites. Here, we further extend that work in the fiber longitudinal direction by considering local fiber waviness with a cosine wave shape following the work by Bishara and coworkers [42, 43]. The maximum waviness angle (θmax) locates at the deflection point between the trough and adjacent crest of the cosinoidal waveform. We would like to note that due to computational limitation, we only introduce this simple yet representative form in the computational model to present the initial fiber misalignment angle, but θmax should be pertinent to the averaged misalignment angle outlined and discussed in Yurgartis’s paper [45]. A parametric study relating the mechanical properties of longitudinal compression and θmax has been conducted in our previous work [14]. The predicted values of fiber rotation angle and bandwidth are in good agreement with experimental results [14].
4.3. Failure envelopes of UD CFRP composites under multi-axial stress state
We have also characterized the failure envelopes under multi-axial loading conditions from UD RVE analysis, and based on these failure envelopes, a new set of failure criteria of σ22-τ12, σ22-τ23, and σ11-τ12 has been proposed [13]. We have identified three dominant failure mechanisms or modes from the computational UD RVE analyses under multi-axial loading conditions of σ22-τ12 and σ22-τ23, which are tension, shear, and compression dominated failure modes. The failure envelopes of σ22-τ12 and σ22-τ23 show that the maximum shear strength increases by applying transverse compressive stress up to a transition point, before which it indicates a hardening effect of shear strength under moderate transverse compression. In this regime, the failure is shear dominated. With further increasing the magnitude of the transverse compression, failure of the matrix under compression loading starts to dominate the failure process of composites, and the shear strength starts to decrease. Basically, the transition point is defined as the transition between compression dominated and shear dominated failure. In the transverse tension side, we observe that the shear strength decreases with the magnitude of transverse tension monotonically, as shown in Fig. 4(a) and (b). The same transition point is expected to appear in the σ33-τ12 and σ33-τ23 stress space as the transverse directions (direction 2 and 3) are identical. These three dominant failure mechanisms resemble those proposed by the NU-Daniel failure criteria [46, 47]. As such, we propose a new set of failure criteria for σ22-τ12 and σ22-τ23 based on the NU-Daniel failure criteria. For the multi-axial loading case of σ11-τ12, the shape of the failure envelope in σ11-τ12 space will be different as the main failure mechanism changes to fiber kinking, as investigated in our previous studies [14]. We modify Tsai-Wu’s failure criterion [48] by considering the dependence of compressive strength on the maximum waviness angle θmax. All of the proposed failure criteria based on UD RVE model results are summarized in Eqn. (1)–(5).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where and are transverse normal and in-plane shear strengths of the transition point; Vf is fiber volume fraction, which is 51.4% in our case; Gm is matrix shear modulus; α and β are material-based parameters, and is the in-situ in-plane shear strength of the composite considering the in-situ constraining effect, which can be theoretically calculated by the model proposed by Camanho et al [49]. By changing τ12 and SL to τ23 and ST in the Eqn. (1)–(3), we can obtain the failure criteria for σ22-τ23. Material properties in Eqn. (1)–(5) are listed in Table. 3.
Figure 4.
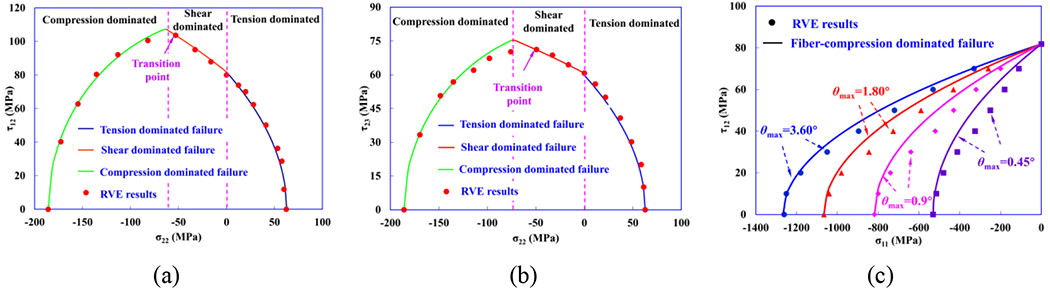
Comparison of the failure envelopes obtained from the computational RVE model and the proposed failure criteria under multi-axial stress states: (a) σ22-τ12, (b) σ22-τ23, and (c) σ11-τ12.
Table 3.
|
XT (MPa) |
XC (MPa) |
YT (MPa) |
YC (MPa) |
SL (MPa) |
(MPa) |
ST (MPa) |
(MPa, MPa) |
(MPa, MPa) |
|---|---|---|---|---|---|---|---|---|
| 2022.44 | 1066.26 | 64.95 | 182.32 | 81.4 | 113.3 | 60.1 | (53, 103.7) | (49, 71) |
A comparison of computational results and the proposed failure criteria for several stress states are shown in Fig. 4. We can see that the proposed failure criteria are in good agreement with computational UD RVE results. The present work demonstrates that more accurate failure criteria can be developed using more realistic computational models such as the one shown in the present work.
4.4. Elastic-plastic-damage model for homogenized UD CFRP composites
For meso-scale SMC and woven structures, of which the basic elements-chips and fiber tows (yarns) need to be treated as homogenized UD CFRP composites to enable more efficient characterization of these larger-scale structures. As such, we need to epitomize the failure behaviors and failure envelopes obtained in previous sections to construct the constitutive material laws and damage behaviors for homogenized UD CFRP composites. In this section, the homogenized UD composites are described by an elastic-plastic-damage model combining the Liu-Huang-Stout (LHS) yield criterion [50] and the UD RVE-based failure criteria.
LHS yield criterion is used to describe the elasto-plastic behavior of UD CFRP composites. The yield criterion is defined as:
| (6) |
where F, G, H, L, M, N I, J, and K are parameters characterizing the current state of anisotropy. These parameters can be simplified and defined as follows:
| (7) |
where σ1t and σ1c are longitudinal tensile and compressive yield stresses respectively; σ2t (σ3t) and σ2c (σ3c) are the transverse tensile and compressive yield stresses respectively; ) and are the in-plane and out-of-plane shear stresses respectively.
An associative flow rule is adopted to describe the yield surface evolution:
| (8) |
where ∅ has been previously defined in Eqn. (6), represents the plastic multiplier, determined by the Newton-Raphson method, σd is the stress tensor, and the partial derivation represents the gradient vector.
RVE-based failure criteria incorporating various damage mechanisms are adopted to describe the damage initiation. The damage evolution of homogenized UD CFRP composites is defined as a reduction in the stiffness matrix C(D), expressed as:
| (9) |
where Cij (i=1-6, j=1-6) are the components of undamaged stiffness matrix, and the parameters di are defined as following:
| (10) |
where dL and dT are denoted as:
| (11) |
In Eqn. (11), εLf is the tensile/compressive failure strain along fiber direction, εL0 is the tensile/compressive initial damage strain along fiber direction, εTf is the tensile/compressive failure strain along the transverse direction, and εT0 is the tensile/compressive initial damage strain along the transverse direction. The damage initiation strains (εL0, εT0) are defined by appropriate failure criteria (Eqn. (1)–(5)), which are only related to stress state. The post-failure behavior is governed by the damage evolution law, which is associated with the fracture toughness, element stress and element characteristic length Lc. To avoid the element size effect, the ultimate failure strains (εLf, εTf) are determined by the fracture toughness based on smeared formulation [51]:
| (12) |
where GL and GT are the fracture toughness in longitudinal and transverse direction respectively, which are adopted from the results of for UD CFRP composites from Pinho [52] with similar material used in this study, GL = 91.6 N/mm, GT = 0.022 N/mm. XT,C and YT,C are tensile (T)/compressive (C) strength in longitudinal and transverse direction respectively.
The above damage model is implemented at the integral point in every element of homogenized UD CFRP composites through the user a VUMAT subroutine in ABAQUS [39]. We have systematically evaluated and validated the proposed elastic-plastic-damage model by comparing the computational results with the experimental tests on open-hole off-axial tension/compression and four-point bending. More details can be found in the SI. The proposed elastic-plastic-damage constitutive model has been shown to sufficiently capture the failure mechanisms in UD CFRP composites.
5. Meso-scale model development for chopped SMC and woven composites
5.1. Chopped SMC and woven composites description
Chopped SMC and woven fabric composites are produced using the same DowAksa A42 carbon fiber and Dow thermoset epoxy as the UD CFRP composites. The fiber diameter and fiber volume fraction of chips for SMC as well as fiber tows (yarns) for woven are 7 um and 51.4% respectively, which are the same as for UD CFRP composites.
For chopped SMC composites, long continuous UD prepregs are chopped into sections approximately 25 mm in length, which are then distributed onto a resin film to create an SMC prepreg. Prepregs are stacked to achieve the appropriate nominal thickness and are then compression molded. The material flow during the compression molding process results in a spatially-variant chip orientation distribution in the molded structure. Fiber chips of different sizes are stochastically distributed in the matrix in the in-plane section, and a layered structure is formed by stacks of fiber chips in the through-thickness direction, as shown in Fig. 5(a). Chip volume fraction of SMC is about 80%, thus the total fiber volume fraction in SMC composites is about 51.4% × 80% = 41%. The fiber aspect ratio (length over to diameter) is about 3571. For woven composite, 2×2 twill weave plaques of 300×300 mm2 are formed by hot compression with 4 prepreg plies in the same lay-up direction to obtain a nominal thickness of 2.5 mm. The prepregs have an area density of 660 g/m2 and weave density of 4 picks/cm. Both warp and weft yarns have the same bundle size of 12K (number of fibers in a bundle). As shown in Fig. 5(b), the twill composite illustrates a complex initial configuration. Both warp and weft yarns have a quasi-elliptical shape. Due to the weaving processing, the yarns in two directions also have different cross-section geometries. Meanwhile, yarns in the warp direction show less undulation (crimp ratio) than those in the weft direction [53].
Figure 5.

Typical initial microstructures of SMC and woven composites; (a) raw UD prepregs cut into chips (left), planar view of chips set in a resin matrix (middle), and through-thickness view of chips set in a resin matrix (right) of a typical SMC microstructure, and (b) initial microstructures along warp and weft directions of the woven composite.
5.2. Meso-scale RVE model and constitutive and damage law
The details of the RVE model generation for SMC and woven composites have been introduced in our recent studies [16, 54] and are further included in the SI. We have generated SMC RVE models with six different fiber orientation tensors (a11). The details of model construction are included in SI. The size of the RVE model for SMC is 50 mm × 50 mm × 0.8 mm (8 layers in the thickness direction). The size of the RVE model for woven composites is 12.5 mm × 12.5 mm × 2.5 mm (4×4 yarns in-plane and 4 layers in the thickness direction), and yarn volume fraction is 87%. Two representative RVE models are shown in Fig. 6.
Figure 6.
Constitutive and damage laws of RVE models of SMC and woven composites.
In addition to well-constructed meso-scale RVE models, constitutive and damage laws for each constituent are required for failure analysis. A comprehensive schematic diagram of the constitutive and damage law for each constituent is presented in Fig. 6. The matrix constitutive law is established using a paraboloidal yield criterion and an isotropic damage model, the same as the UD RVE model. The material parameters of the epoxy matrix are listed in Table 1. The chips of SMC RVE and fiber tows of woven RVE are modeled by the proposed elastic-plastic-damage model combining LHS yield criterion and UD RVE-based failure criteria as discussed earlier in Section 4.4. The chip splitting in SMC RVE is caused by matrix failure in the chips based on different dominated failure states using Eqn. (1)–(3). Critical parameters of chips of and fiber tows in these meso-scale RVE models are obtained from the previous UD RVE model as described in Section 4.2 and listed in Table 2. The interface between matrix and chip (or fiber tow) is modeled using cohesive elements with a bilinear mixed-mode traction-separation law. The interfacial parameters are listed in Table 4.
Table 4.
Interfacial parameters for SMC and woven RVE model
5.4. Failure behaviors of SMC composites
We have previously validated the SMC RVE models by comparing the predicted modulus and strength values with the experimental results. Good agreement can be observed between the computational and experimental results in general. The comparison can be found in the SI. Through virtual tests conducted on the constructed SMC RVE models, the failure process of the SMC composites can be further analyzed A sequence of damage development stages resulting in ultimate failure for a representative SMC RVE model (a11 = 0.2) under uniaxial tension are presented in Fig. 7(a). It is observed that cracks initiate at the stress concentration locations, such as chip ends, chip-matrix interface, and chip-chip interface. As the load increases, the cracks start to propagate in the matrix. When a crack reaches another chip, it begins to propagate along the interfaces. Chip splitting and chip breakage also occur during crack propagation. Finally, interfacial cracks at different locations are connected through matrix cracks and spread through the entire SMC RVE causing ultimate fracture path perpendicular to the loading axis, as shown in Fig. 7(a).
Figure 7.
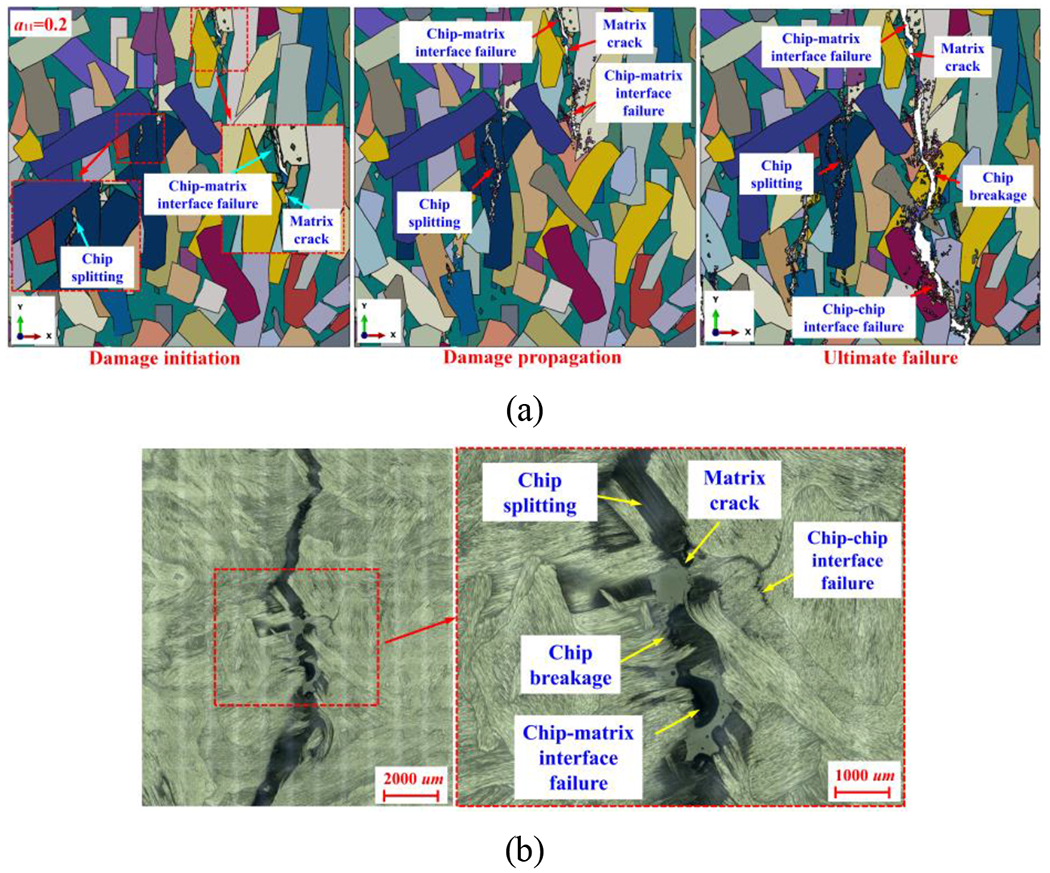
Failure processes in SMC RVE models and experiments under tension load (X-direction) for: (a) SMC RVE with a11=0.2; (b) experimental failure modes.
Comparing ultimate failure modes observed in the experiments (Fig. 7(b)), the proposed SMC RVE models successfully reproduce all failure modes (matrix cracking, chip splitting, chip breakage, chip-chip interface, and chip-matrix interface debonding) of SMC composites under tensile load. The failure behaviors under compression and in-plane shear are further included in the SI, which both show excellent agreement with experimental results.
5.5. Failure behaviors of woven RVE composites
Our recent studies have demonstrated that the RVE model of woven composites can adequately conserve the mechanical properties of woven composites, including stress-strain curves depending on loading directions and elastic moduli, as summarized in the SI. We use Table 5 to summarize the elastic properties of woven composites obtained from woven RVE models under uniaxial loading conditions.
Table 5.
Summary of the elastic properties predicted from woven RVE model
|
E11 (GPa) |
E22 (GPa) |
E33 (GPa) |
G12 (GPa) |
G13 (GPa) |
G23 (GPa) |
v21 | v31 | v32 |
|---|---|---|---|---|---|---|---|---|
| 62.6 | 59.1 | 12.89 | 4.63 | 4.56 | 4.56 | 0.6 | 0.04 | 0.12 |
In this section, we focus on using the RVE model to analyze the failure behaviors of woven composites, during which experimental validations are also discussed (details on experimental characterization can be found in the SI). The damage initiation and propagation points of constituents (weft tows, matrix, the interface between fiber tows and matrix, warp tows) have been added to the stress-strain curves for clarity. The damage in weft and warp tows (dWeft and dWarp), in the matrix (dMatix), and in the interface between fiber tows and matrix (dInterface) appear and gradually accumulate with applied loading. A similar failure process is observed in warp and weft tension. Specifically, a detailed sequence of failure initiation and propagation under tension along the warp direction based on the woven RVE model is shown in Fig. 8. Since the transverse strength of fiber tows (62.1 MPa) and tensile strength of matrix (61.6 MPa) are similar and relatively low, the inter-fiber tows’ transverse cracks and matrix cracks initiate first at a strain of 0.40%, and then propagate along a path perpendicular to the loading axis, as shown in Fig. 8(b)–(c). Subsequently, the interfacial cracks between fiber tows and matrix are triggered at a strain of 0.75% (Fig. 8(d)). The damage fraction of transverse/matrix cracks as well as interfacial cracks accumulate extensively and lead to an inflection point in the stress-strain curve. Finally, the longitudinal fiber damage initiates in the fiber tows parallel to loading direction at a strain of about 1.35% and results in the final failure of the woven RVE (Fig. 8(e)), causing a sudden drop in stress. Comparing the computational and experimental results, the predicted failure behaviors show good agreements with the experimental observations for tension along warp direction. Similar behavior is also observed in tension along weft direction. The failure process under compression is further discussed in the SI. In sum, this proposed woven RVE model can provide reliable predictions of failure strengths under tension and compression, and capture the realistic damage mechanisms of the woven composites under different loading conditions.
Figure 8.
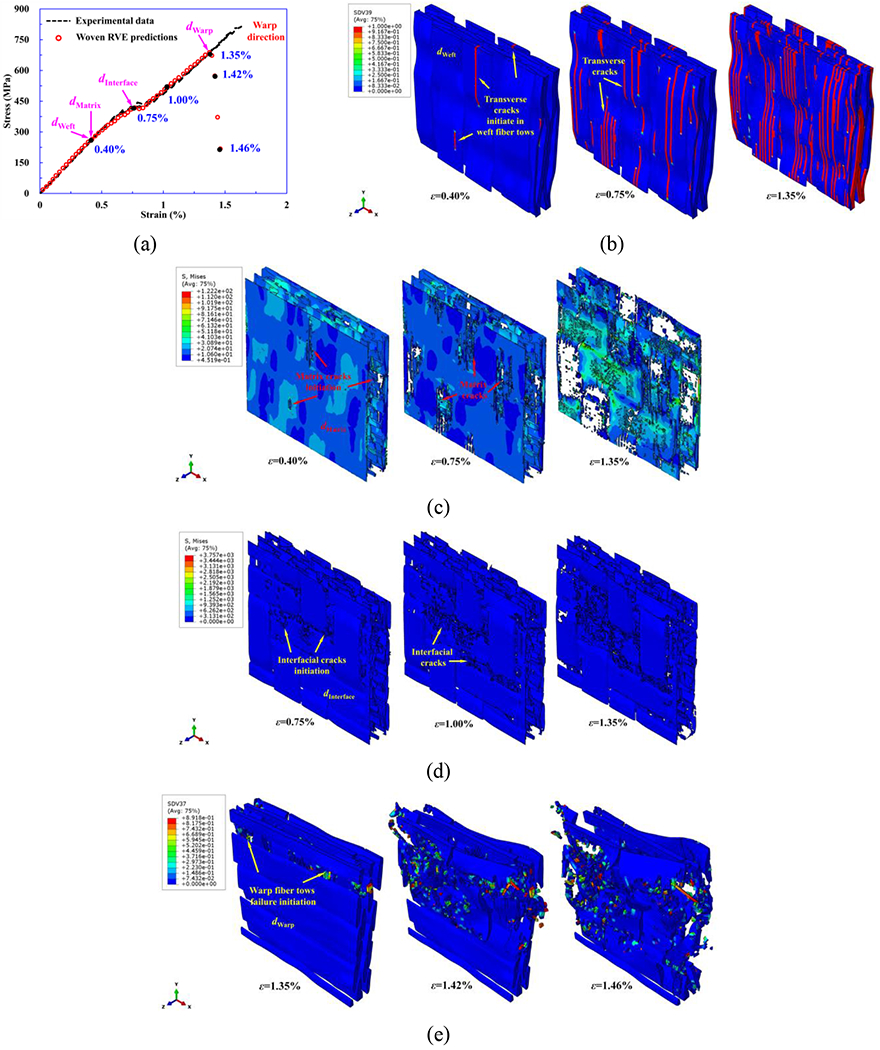
A detailed sequence of failure initiation and propagation informed from woven RVE model under tensile load in warp direction (X-direction): (a) damage initiation and propagation points (solid black points) marked on the strain-stress curve; (b) transverse cracks initiation and propagation in fiber tows along weft direction; (c) matrix damage initiation and propagation; (d) interfacial debonding initiation and propagation; (e) fiber breakage initiation and propagationin fiber tows along warp direction. SDV39 and SDV37 represent transverse and longitudinal tensile damage evolution indices, respectively.
6. Macro-scale bending model of hat-section-shaped parts made of UD and Woven CFRP composites
In this section, we use a hat-section-shaped part subjected to four-point bending load to demonstrate the final stage of the proposed bottom-up multi-scale ICME framework. The detailed geometry of the hat-section-shaped part is shown in Fig. 9(a). The UD CFRP hat-section-shaped part is made up of [0/90/90/0/0/0]s and [0/60/−60/0/60/−60]s layup with 12 layers (noted as UD 0-90 and UD 0-60, respectively), and the layups of woven CFRP hat-section-shaped part are [90/0/90/0]s and [45/−45/45/−45]s with 4 layers (noted as woven 0-90 and woven 45-45, respectively). The warp yarn orientation of 0° is parallel to the length direction of the hat section sample. For the experimental setup, a backplate of the same layup and thickness is glued to the bottom of the hat section sample at the location of the lower roller. The testing setup of the four-point bending is shown in Fig. 9(b). The specimen is tested at a constant displacement rate (or speed) of 0.2 mm/min. The experimental load-displacement curves and failure modes are obtained for comparison with the computational predictions. Fig. 9(c) shows the macro-scale model of a hat-section-shaped sample under four-point bending load in LS-DYNA [56] with 12 layers (UD)/4 layers (woven) of thick shell elements. The thick shell element is an 8-noded element with the kinematics of shell theory but with added strain component through the thickness. Each layer of thick shell element represents one ply. The mesh size is 4 mm. A layer of cohesive elements of 0.01 mm thickness is inserted between two layers to simulate the delamination. A linear-elastic composite material model MAT_54 [57] in LS-DYNA for the thick shell element combined with Chang/Chang failure criteria [58] is adopted to model the ply property.
Figure 9.
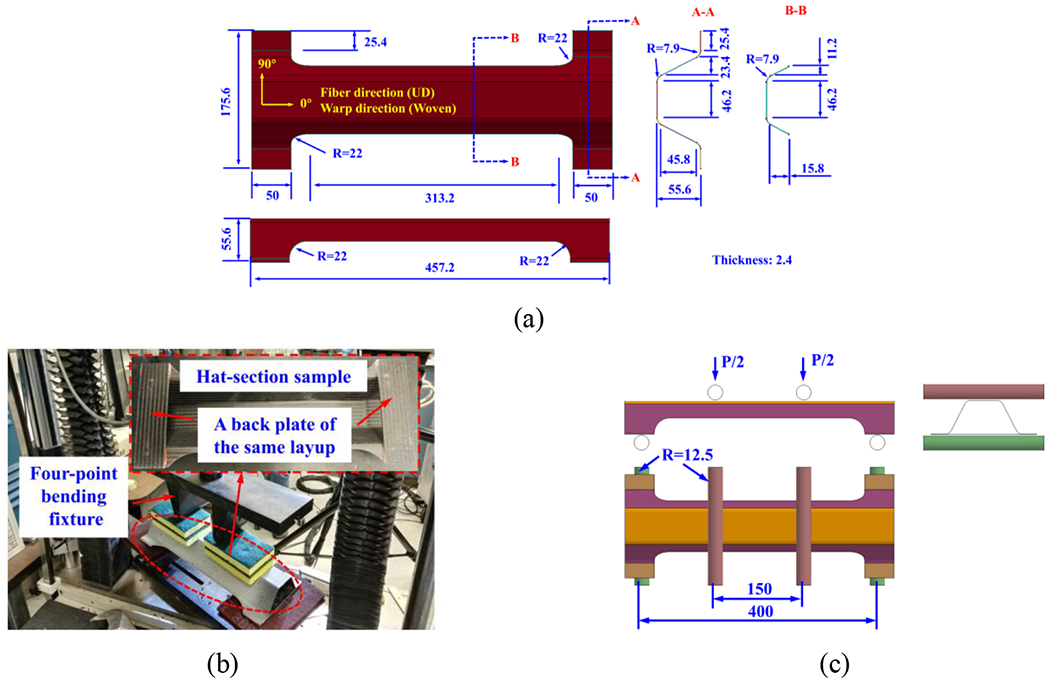
(a) Geometry and dimension of the hat-section-shaped part (unit: mm). (b) Schematic of the testing setup. (c) Macro-scale model of the hat-section-shaped sample under four-point bending load.
We note that the input parameters of the LS-DYNA model are informed from the micro-scale and meso-scale models and computational results discussed in earlier sections. The input material parameters including elastic properties and strength predicted from UD and woven RVE models are listed in Table 2, Table 5, Table S1, and Table S3. A cohesive material model considering strain rate effect, i.e., MAT_240 [59], in LS-DYNA is adopted to simulate the delamination. A bi-linear traction-separation law with a quadratic yield and damage initiation criterion in mixed-mode is included. The damage evolution is governed by a power-law formulation. The input parameters of cohesive elements for different modes are obtained from experimental and computational results in our previous work [15]. The interfacial parameters between adjacent plies are listed in Table 6.
Table 6.
Interfacial parameters between adjacent plies [15]
| K (MPa/mm) | σ1 (MPa) | σ2, σ3 (MPa) | GIc (J/m2) | GIIc(J/m2) |
|---|---|---|---|---|
| 105 | 17 | 60 | 550 | 913 |
Fig. 10(a)–(b) show the comparisons of load-displacement curves from computational modeling and experimental testing of UD 0-90, UD 0-60, woven 0-90 as well as woven 45-45 specimens. The present model captures the overall behaviors reasonably well for all the hat-section-shaped samples. For UD CFRP hat-section-shaped samples, the load increases linearly at first and then becomes slightly non-linear towards the final failure stage, while for woven CFRP hat-section-shaped sample, non-linear behavior occurs rather early, especially for woven 45-45.
Figure 10.
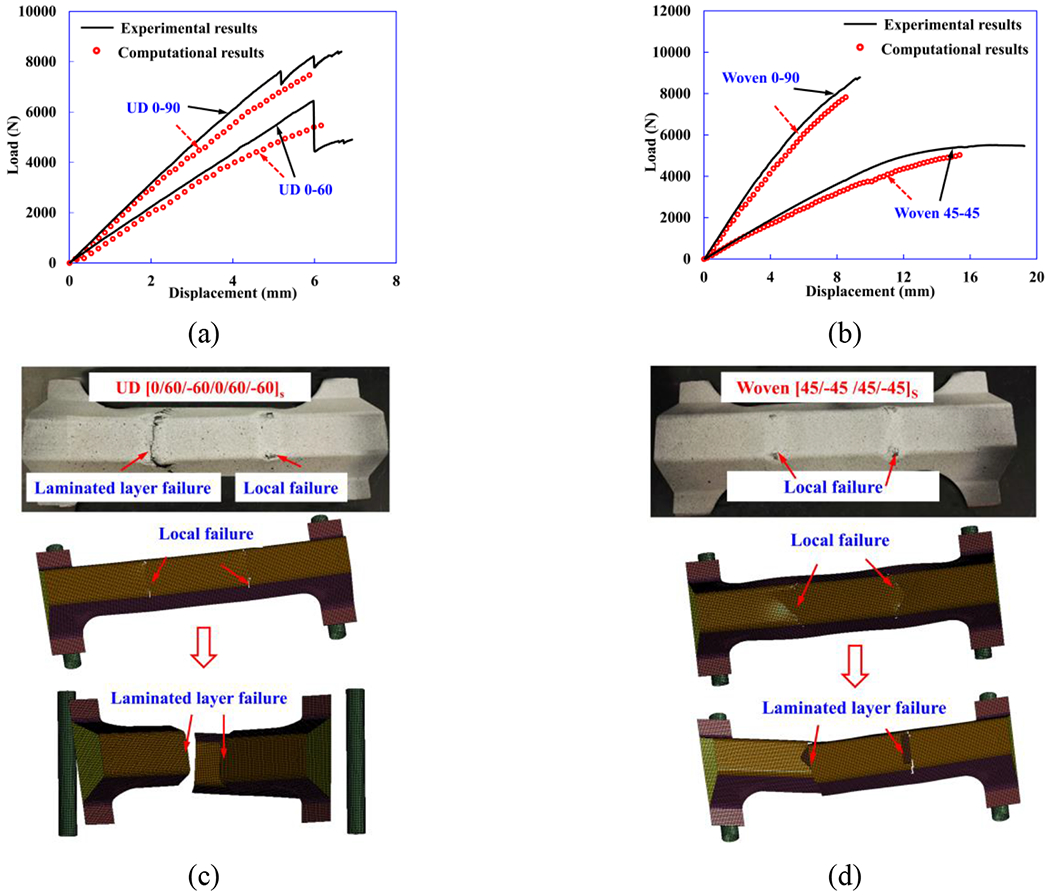
Comparison of load-displacement curves between computational modeling and experimental testing of (a) UD and (b) woven CFRP hat-section-shaped samples. Comparison of experimentallyobserved and computational predicted failure modes of (c) UD 0-60 and (d) woven 45-45 under four-point bending load.
For both UD 0-60 and woven 45-45 samples, the failure is concentrated around the direct loading locations. All the samples show significant corner failure (local failure) due to stress concentration during deformation. As the corner failure becomes more severe, there is greater fiber direction failure/fiber breakage, which results in a dramatic load drop and catastrophic laminated layer failure of the UD CFRP hat-section-shaped samples, as shown in Fig. 10(c)–(d). Due to the slight deviation of the location of the lower and upper rollers during the testing setup, the experimental observed failure stage of UD 0-60 at the two loading points (Fig. 10(c)) are different. Compared to experiments, the computational model has the advantage to clearly reveal the failure initiation and evolution process of UD 0-60 and woven 45-45 under four-point bending load. The symmetric local failure first occurs at the corners of the sample contacted with upper rollers where the stress concentration is higher, and the final failure of laminated layers takes place when the load increases to a critical value, as shown in Fig. 10(c)–(d). Comparing with experimentally observed failure modes, the proposed macro-scale models of the hat-section-shaped part agree well with experimental observations.
7. Conclusions
This study presents a systematic investigation into the failure behaviors of UD, woven, and chopped SMC CFRP composites at different scales by developing an ICME framework with a bottom-up multi-scale modeling approach. The multi-scale models combine MDA at the nano-scale, UD RVE model at the micro-scale, chopped SMC, and woven RVE models at the meso-scale, and hat-section-shaped parts at the macro-scale. The major insights/conclusions are summarized below.
(1) At the nano-scale, the average mechanical properties of the interphase region are obtained from an analytical gradient model and MD simulations. The average Young’s modulus and strength of the interphase region increase by about 5 and 9 times, compared to the bulk epoxy resin matrix.
(2) A micro-scale UD RVE model has been adopted to investigate the failure mechanisms and failure criteria of UD CFRP composites under uniaxial and multi-axial stress states. Based on the computational results and analyses, a new elasto-plastic constitutive law with damage evolution for homogenized UD CFRP composites is proposed. The newly proposed elastic-plastic-damage model shows significant improvement in efficiency to model fiber tows of the woven composites as well as chips in SMC composites.
(3) Conforming model/mesh generation methods are adopted to construct meso-scale SMC and woven RVE models. The complex failure mechanisms of woven and SMC composites under various loading conditions are captured by these meso-scale computational models. Current work also presents an effective computational approach to analyze the complex failure behaviors of woven and SMC composite, which is of significant interest in the design and optimization of CFRP composites based structural components.
(4) A macro-scale hat-section-shaped part consisting of UD or woven CFRP composites under four-point bending is presented building upon the models and results at nano-, micro-, and meso-scales. The macro-scale model shows good agreements with test results and captures the failure strengths and behaviors. This demonstration provides a promising solution to the grand challenge of modeling failure of composites used in structural applications by integrating lower scale structural and mechanical attributes.
In conclusion, the validated ICME framework with well-integrated multi-scale models and tools presented in this work has been demonstrated to effectively and accurately link the structures and mechanical properties from different levels and predict the failure behaviors of CFRP composites including, but not limited to, UD, chopped SMC, and woven CFRP composites. The ICME framework has the potential to significantly shorten the time from composite development to deployment.
Supplementary Material
Acknowledgments
The authors acknowledge support from the Ford Motor Company with funding from the U.S. Department of Energy’s Office of Energy Efficiency and Renewable Energy (EERE), under Award Number DE-EE0006867. Q. Sun acknowledges support from the China Scholarship Council (CSC). Z. Meng would like to acknowledge startup funds from Clemson University and SC TRIMH support (P20 GM121342).
References
- [1].Liu Q, Lin Y, Zong Z, Sun G, Li Q. Lightweight design of carbon twill weave fabric composite body structure for electric vehicle. Composite Structures. 2013;97:231–8. [Google Scholar]
- [2].Xu J, Lomov SV, Verpoest I, Daggumati S, Van Paepegem W, Degrieck J. A comparative study of twill weave reinforced composites under tension–tension fatigue loading: Experiments and meso-modelling. Composite Structures. 2016;135:306–15. [Google Scholar]
- [3].Tang H, Chen Z, Zhou G, Li Y, Avery K, Guo H, Kang H, Zeng D, Su X. Correlation between failure and local material property in chopped carbon fiber chip-reinforced sheet molding compound composites under tensile load. Polymer Composites. 2019;40(S2):E962–E74. [Google Scholar]
- [4].Zhou G, Sun Q, Fenner J, Li D, Zeng D, Su X, Peng Y. Crushing behaviors of unidirectional carbon fiber reinforced plastic composites under dynamic bending and axial crushing loading. International Journal of Impact Engineering. 2020;140:103539. [Google Scholar]
- [5].Kim HC, Wallington TJ. Life-cycle energy and greenhouse gas emission benefits of lightweighting in automobiles: review and harmonization. Environmental science & technology. 2013;47(12):6089–97. [DOI] [PubMed] [Google Scholar]
- [6].Shaik A, Kalariya Y, Pathan R, Salvi A, editors. ICME based hierarchical design using composite materials for automotive structures Proceedings of the 4th World Congress on Integrated Computational Materials Engineering (ICME 2017); 2017: Springer. [Google Scholar]
- [7].Engineering CoICM. Integrated computational materials engineering: a transformational discipline for improved competitiveness and national security: National Academies Press; Washington, DC; 2008. [Google Scholar]
- [8].Thapliyal S, Komarasamy M, Shukla S, Zhou L, Hyer H, Park S, Sohn Y, Mishra RS. An integrated computational materials engineering-anchored closed-loop method for design of aluminum alloys for additive manufacturing. Materialia. 2020;9:100574. [Google Scholar]
- [9].Ghosh S, Weber G, Pinz M, Bagri A, Pollock TM, Lenthe W, Stinville J-C, Uchic MD, Woodward C. Multi-scale Microstructure and Property-Based Statistically Equivalent RVEs for Modeling Nickel-Based Superalloys Integrated Computational Materials Engineering (ICME): Springer; 2020. p. 55–90. [Google Scholar]
- [10].Wang WY, Li J, Liu W, Liu Z-K. Integrated computational materials engineering for advanced materials: A brief review. Computational Materials Science. 2019;158:42–8. [Google Scholar]
- [11].Xu H, Li Y, Zeng D. Process Integration and Optimization of ICME Carbon Fiber Composites for Vehicle Lightweighting: A Preliminary Development.SAE International Journal of Materials and Manufacturing. 2017;10(3):274–81. [Google Scholar]
- [12].Sun Q, Meng Z, Zhou G, Lin S-P, Kang H, Keten S, Guo H, Su X. Multi-scale computational analysis of unidirectional carbon fiber reinforced polymer composites under various loading conditions. Composite Structures. 2018;196:30–43. [Google Scholar]
- [13].Sun Q, Zhou G, Meng Z, Guo H, Chen Z, Liu H, Kang H, Keten S, Su X. Failure criteria of unidirectional carbon fiber reinforced polymer composites informed by a computational micromechanics model. Composites Science and Technology. 2019;172:81–95. [Google Scholar]
- [14].Sun Q, Guo H, Zhou G, Meng Z, Chen Z, Kang H, Keten S, Su X. Experimental and computational analysis of failure mechanisms in unidirectional carbon fiber reinforced polymer laminates under longitudinal compression loading. Composite Structures. 2018;203:335–48. [Google Scholar]
- [15].Sun Q, Zhou G, Guo H, Meng Z, Chen Z, Liu H, Kang H, Su X. Failure mechanisms of cross-ply carbon fiber reinforced polymer laminates under longitudinal compression with experimental and computational analyses. Composites Part B: Engineering. 2019;167:147–60. [Google Scholar]
- [16].Chen Z, Tang H, Shao Y, Sun Q, Zhou G, Li Y, Xu H, Zeng D, Su X. Failure of chopped carbon fiber Sheet Molding Compound (SMC) composites under uniaxial tensile loading: Computational prediction and experimental analysis. Composites Part A: Applied Science and Manufacturing. 2019;118:117–30. [Google Scholar]
- [17].Gao J, Shakoor M, Domel G, Merzkirch M, Zhou G, Zeng D, Su X, Liu WK. Predictive multiscale modeling for Unidirectional Carbon Fiber Reinforced Polymers. Composites Science and Technology. 2020;186:107922. [Google Scholar]
- [18].Tao W, Zhu P, Xu C, Liu Z. Uncertainty quantification of mechanical properties for three-dimensional orthogonal woven composites. Part II: Multiscale simulation. Composite Structures. 2020;235:111764. [Google Scholar]
- [19].Ullah Z, Zhou X-Y, Kaczmarczyk L, Archer E, McIlhagger A, Harkin-Jones E. A unified framework for the multi-scale computational homogenisation of 3D-textile composites. Composites Part B: Engineering. 2019;167:582–98. [Google Scholar]
- [20].Tang H, Chen Z, Avinesh O, Guo H, Meng Z, Engler-Pinto C, Kang H, Su X. Notch insensitivity in fatigue failure of chopped carbon fiber chip-reinforced composites using experimental and computational analysis. Composite Structures. 2020:112280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Tang H, Zhou G, Chen Z, Huang L, Avery K, Li Y, Liu H, Guo H, Kang H, Zeng D. Fatigue behavior analysis and multi-scale modelling of chopped carbon fiber chip-reinforced composites under tension-tension loading condition. Composite Structures. 2019;215:85–97. [Google Scholar]
- [22].LLorca J, González C, Molina-Aldareguía JM, Segurado J, Seltzer R, Sket F, Rodríguez M, Sádaba S, Muñoz R, Canal LP. Multiscale modeling of composite materials: a roadmap towards virtual testing. Advanced Materials. 2011;23(44):5130–47. [DOI] [PubMed] [Google Scholar]
- [23].Zheng T, Guo L, Huang J, Liu G. A novel mesoscopic progressive damage model for 3D angle-interlock woven composites. Composites Science and Technology. 2020;185:107894. [Google Scholar]
- [24].Omairey SL, Dunning PD, Sriramula S. Multiscale surrogate-based framework for reliability analysis of unidirectional FRP composites. Composites Part B: Engineering. 2019;173:106925. [Google Scholar]
- [25].Meng Z, Bessa MA, Xia W, Kam Liu W, Keten S. Predicting the macroscopic fracture energy of epoxy resins from atomistic molecular simulations. Macromolecules. 2016;49(24):9474–83. [Google Scholar]
- [26].Vu-Bac N, Bessa M, Rabczuk T, Liu WK. A multiscale model for the quasi-static thermo-plastic behavior of highly cross-linked glassy polymers. Macromolecules. 2015;48(18):6713–23. [Google Scholar]
- [27].Wu Q, Li M, Gu Y, Li Y, Zhang Z. Nano-analysis on the structure and chemical composition of the interphase region in carbon fiber composite. Composites Part A: Applied Science and Manufacturing. 2014;56:143–9. [Google Scholar]
- [28].Shao C, Keten S. Stiffness enhancement in nacre-inspired nanocomposites due to nanoconfinement. Scientific reports. 2015;5(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Xia W, Song J, Meng Z, Shao C, Keten S. Designing multi-layer graphene-based assemblies for enhanced toughness in nacre-inspired nanocomposites. Molecular Systems Design & Engineering. 2016;1(1):40–7. [Google Scholar]
- [30].Li T, Meng Z, Keten S. Interfacial mechanics and viscoelastic properties of patchy graphene oxide reinforced nanocomposites. Carbon. 2020;158:303–13. [Google Scholar]
- [31].Zhao W, Singh RP, Korach CS. Effects of environmental degradation on near-fiber nanomechanical properties of carbon fiber epoxy composites. Composites Part A: Applied Science and Manufacturing. 2009;40(5):675–8. [Google Scholar]
- [32].Kiritsi C, Anifantis N. Load carrying characteristics of short fiber composites containing a heterogeneous interphase region. Computational materials science. 2001;20(1):86–97. [Google Scholar]
- [33].Wang B, Fang G, Liu S, Liang J. Effect of heterogeneous interphase on the mechanical properties of unidirectional fiber composites studied by FFT-based method. Composite Structures. 2019;220:642–51. [Google Scholar]
- [34].Melro A, Camanho P, Pinho S. Generation of random distribution of fibres in long-fibre reinforced composites. Composites Science and Technology. 2008;68(9):2092–102. [Google Scholar]
- [35].Standard A. D638: Standard test method for tensile properties of plastics. West Conshohocken (PA): ASTM International; 2010. [Google Scholar]
- [36].Standard A. D695-15.Standard test method for compressive properties of rigid plastics. 2015. [Google Scholar]
- [37].Fatigue AICEo, Mechanics FSEoF. Standard Test Method for Linear-elastic Plane-strain Fracture Toughness K [Ic] of Metallic Materials: ASTM International; 2013. [Google Scholar]
- [38].Melro A, Camanho P, Pires FA, Pinho S. Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part I–Constitutive modelling. International Journal of Solids and Structures. 2013;50(11-12):1897–905. [Google Scholar]
- [39].Hibbitt, Karlsson, Sorensen. ABAQUS/Explicit: user’s manual: Hibbitt, Karlsson and Sorenson Incorporated; 2001. [Google Scholar]
- [40].Vajari DA, Sørensen BF, Legarth BN. Effect of fiber positioning on mixed-mode fracture of interfacial debonding in composites. International Journal of Solids and Structures. 2015;53:58–69. [Google Scholar]
- [41].Zhou Y, Huang ZM, Liu L. Prediction of interfacial debonding in fiber-reinforced composite laminates. Polymer Composites. 2019;40(5):1828–41. [Google Scholar]
- [42].Huang Z-M. On micromechanics approach to stiffness and strength of unidirectional composites. Journal of Reinforced Plastics and Composites. 2019;38(4):167–96. [Google Scholar]
- [43].Heidari-Rarani M, Shokrieh M, Camanho P. Finite element modeling of mode I delamination growth in laminated DCB specimens with R-curve effects. Composites Part B: Engineering. 2013;45(1):897–903. [Google Scholar]
- [44].Bai X, Bessa MA, Melro AR, Camanho PP, Guo L, Liu WK. High-fidelity micro-scale modeling of the thermo-visco-plastic behavior of carbon fiber polymer matrix composites. Composite Structures. 2015;134:132–41. [Google Scholar]
- [45].Yurgartis S Measurement of small angle fiber misalignments in continuous fiber composites. Composites Science and Technology. 1987;30(4):279–93. [Google Scholar]
- [46].Daniel IM, Daniel SM, Fenner JS. A new yield and failure theory for composite materials under static and dynamic loading. International Journal of Solids and Structures. 2018;148:79–93. [Google Scholar]
- [47].Daniel IM. Yield and failure criteria for composite materials under static and dynamic loading. Progress in Aerospace Sciences. 2016;81:18–25. [Google Scholar]
- [48].Liu K-S, Tsai SW. A progressive quadratic failure criterion for a laminate. Composites Science and Technology. 1998;58(7):1023–32. [Google Scholar]
- [49].Camanho PP, Dávila CG, Pinho ST, Iannucci L, Robinson P. Prediction of in situ strengths and matrix cracking in composites under transverse tension and in-plane shear. Composites Part A: Applied Science and Manufacturing. 2006;37(2):165–76. [Google Scholar]
- [50].Liu C, Huang Y, Stout M. On the asymmetric yield surface of plastically orthotropic materials: a phenomenological study. Acta materialia. 1997;45(6):2397–406. [Google Scholar]
- [51].Pinho S, Iannucci L, Robinson P. Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation. Composites Part A: Applied Science and Manufacturing. 2006;37(5):766–77. [Google Scholar]
- [52].Pinho ST. Modelling failure of laminated composites using physically-based failure models. 2005. [Google Scholar]
- [53].Zhou G, Sun Q, Meng Z, Li D, Peng Y, Zeng D, Su X. Experimental investigation on the effects of fabric architectures on mechanical and damage behaviors of carbon/epoxy woven composites. Submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Zhou G, Sun Q, Li D, Meng Z, Peng Y, Chene Z, Zeng D, Su X. Meso-scale Modeling and Damage Analysis of Carbon/Epoxy Woven Fabric Composite under In-plane Tension and Compression Loadings. International Journal of Mechanical Sciences. 2020:105980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Turon A, Davila CG, Camanho PP, Costa J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Engineering fracture mechanics. 2007;74(10):1665–82. [Google Scholar]
- [56].Murray YD. Users manual for LS-DYNA concrete material model 159. United States: Federal Highway Administration. Office of Research; …, 2007. [Google Scholar]
- [57].Wade B, Feraboli P, Osborne M, Rassaian M. Simulating laminated composite materials using LS-DYNA material model mat54: single-element investigation,”. Federal Aviation Administration DOT/FAA/TC-14; 2015;19:1–36. [Google Scholar]
- [58].Chang F-K, Chang K-Y. A progressive damage model for laminated composites containing stress concentrations. Journal of composite materials. 1987;21(9):834–55. [Google Scholar]
- [59].Sønstabøa JK, Morina D, Langsetha M. A Cohesive Element Model for Large-Scale Crash Analyses in LS-DYNA®. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


