Supplemental Digital Content is available in the text.
Keywords: acute respiratory distress syndrome, computational model, lung elastance, mechanical ventilation, recruitment and derecruitment, ventilator-induced lung injury, volutrauma
Abstract
Objectives:
Elucidate how the degree of ventilator-induced lung injury due to atelectrauma that is produced in the injured lung during mechanical ventilation is determined by both the timing and magnitude of the airway pressure profile.
Design:
A computational model of the injured lung provides a platform for exploring how mechanical ventilation parameters potentially modulate atelectrauma and volutrauma. This model incorporates the time dependence of lung recruitment and derecruitment, and the time-constant of lung emptying during expiration as determined by overall compliance and resistance of the respiratory system.
Setting:
Computational model.
Subjects:
Simulated scenarios representing patients with both normal and acutely injured lungs.
Measurements and Main Results:
Protective low-tidal volume ventilation (Low-Vt) of the simulated injured lung avoided atelectrauma through the elevation of positive end-expiratory pressure while maintaining fixed tidal volume and driving pressure. In contrast, airway pressure release ventilation avoided atelectrauma by incorporating a very brief expiratory duration (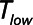 ) that both prevents enough time for derecruitment and limits the minimum alveolar pressure prior to inspiration. Model simulations demonstrated that
) that both prevents enough time for derecruitment and limits the minimum alveolar pressure prior to inspiration. Model simulations demonstrated that  has an effective threshold value below which airway pressure release ventilation is safe from atelectrauma while maintaining a tidal volume and driving pressure comparable with those of Low-Vt. This threshold is strongly influenced by the time-constant of lung-emptying.
has an effective threshold value below which airway pressure release ventilation is safe from atelectrauma while maintaining a tidal volume and driving pressure comparable with those of Low-Vt. This threshold is strongly influenced by the time-constant of lung-emptying.
Conclusions:
Low-Vt and airway pressure release ventilation represent markedly different strategies for the avoidance of ventilator-induced lung injury, primarily involving the manipulation of positive end-expiratory pressure and 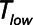 , respectively.
, respectively. 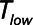 can be based on exhalation flow values, which may provide a patient-specific approach to protective ventilation.
can be based on exhalation flow values, which may provide a patient-specific approach to protective ventilation.
Ever since the publication of the acute respiratory distress syndrome (ARDS) net trial of low tidal volume (Vt) ventilation, the critical care community in the United States has been dominated by the notion that a Vt of 6-mL/kg ideal body weight should be used in ARDS (1). However, this prescription has not been adopted universally without reservation. The reason for this is not simply lack of attention to the message by the medical community. The ARDS network trial compared only two interventions—a Vt of 6 versus 12 mL/kg—and thus, it cannot possibly have settled on the global optimum. In addition, even if it had, what is best for the population on average may be very far from best for an individual patient when it comes to a condition as heterogeneous as ARDS (2). In the face of these obvious shortcomings, the search for the best way to ventilate ARDS patients continues.
Motivated by the above considerations, numerous studies have sought to optimize various aspects of the mechanically ventilated breath, including the choice of positive end-expiratory pressure (PEEP), minimization of driving pressure, and use of extremely small Vt in high-frequency oscillatory ventilation (3–5). None of these approaches has reduced mortality in large clinical trials. Indeed, the only recent addition to the evidence-based management of ARDS is prone-positioning (6), which is a manipulation of the lung itself rather than of ventilation strategy. Such a paucity of positive outcomes is curious given how much is apparently understood about the mechanistic underpinnings of ventilator-induced lung injury (VILI). In particular, it is well accepted that breath-by-breath recruitment of closed lung units is extremely damaging to the lung parenchyma (7, 8) and that this can be mitigated by PEEP (5, 9), so why is the choice of PEEP still not firmly evidence based? We therefore ask the following questions:
1) What has been missed in the search for the level of PEEP that minimizes VILI?
2) What other ventilation parameters can provide patient-specific means for protective ventilation?
The premise of the present study is that the answers to these questions lie in the dynamic nature of lung recruitment and derecruitment. That is, recruitment and derecruitment do not occur as soon as pressure thresholds have been crossed; they take time to manifest, and the amount of time required depends on the nature and degree of lung injury in addition to the applied airway pressure (1, 10). This means that the fraction of the lung that is open at any point in time is determined not only by the current pressure but also by its recent history, which is defined by the prior pattern of ventilation (11, 12). However, alveolar ventilation is determined by an airway pressure profile acting on the mechanical properties of the lung, which themselves change with recruitment and derecruitment (12). Therefore, intrabreath changes in the fraction of open lung, which are what give rise to atelectrauma, are determined by two interacting time-dependent processes. These processes are governed by two time-constants:
1) The respiratory system time-constant,
 , accounting for passive emptying of the lungs during expiration.
, accounting for passive emptying of the lungs during expiration.2) The recruitment and derecruitment time-constant,
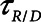 , accounting for the rate of opening and closing of lung units, that is associated with atelectrauma.
, accounting for the rate of opening and closing of lung units, that is associated with atelectrauma.
In this article, we develop a first-order model of lung mechanics that encapsulates both these processes in order to investigate how they interact, the goal being to identify conditions under which atelectrauma and/or volutrauma might be minimized.
MATERIALS AND METHODS
Following Hamlington et al (13), we represent the lung as a single alveolar compartment that can expand in two orthogonal directions, as illustrated in Figure 1. Vertical expansion corresponds to distension of the open lung, whereas horizontal expansion corresponds to an increase in the open lung fraction (i.e., recruitment of closed lung units). Parameters of this model are provided in Table 1.
Figure 1.
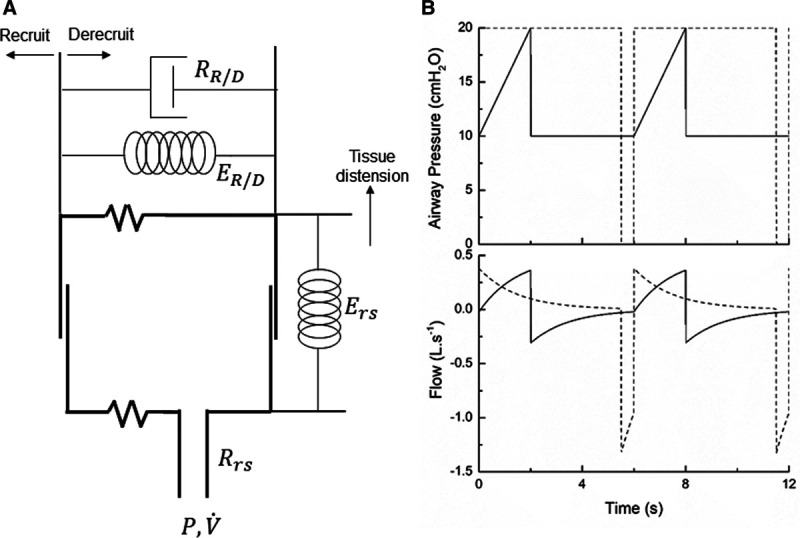
Model schematic and example behavior. A, Single-compartment model of the lung; the alveolar compartment expands vertically to represent tissue distension and horizontally to represent recruitment. B, Simulated profiles of airway pressure and flow during pressure-controlled low-Vt ventilation (solid lines) and airway pressure release ventilation (dashed lines).
TABLE 1.
Description of Symbols and Acronyms
| Symbol | Description |
|---|---|
| ARDS | Acute respiratory distress syndrome |
| VILI | Ventilator-induced lung injury |
| PEEP | Positive end-expiratory pressure |
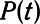 |
Airway pressure |
 |
Airway flow |
| Vt | Tidal volume |
| Low-Vt | Low tidal volume ventilation |
| APRV | Airway pressure release ventilation |
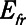 |
Elastance of the respiratory system when the lung is fully recruited |
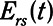 |
Elastance of the respiratory system at any level of recruitment |
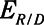 |
Elastance associated with recruitment and decrecruitment |
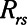 |
Resistance of respiratory system |
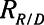 |
Resistance associated with recruitment and decrecruitment |
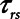 |
Time-constant of patent region of respiratory system (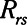 / /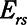 ) ) |
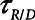 |
Time-constant associated with recruitment and derecruitment (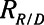 / /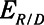 ) ) |
 |
Fraction of open (nonderecruited) lung |
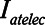 |
Atelectrauma index (change in  during a breath) during a breath) |
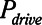 |
Driving pressure (difference between end-inspiratory and end-expiratory pressures) |
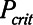 |
Critical airway pressure for recruitment and derecruitment |
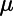 |
Mean of Gaussian distribution of 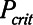 values throughout the lung values throughout the lung |
 |
sd of Gaussian distribution of 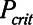 values throughout the lung values throughout the lung |
The intrinsic mechanical properties of the respiratory system tissues are represented by a spring with stiffness 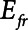 . The elastance of the respiratory system,
. The elastance of the respiratory system, 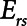 , is equal to
, is equal to 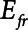 when the lung is fully recruited. As the lung derecruits, its open fraction,
when the lung is fully recruited. As the lung derecruits, its open fraction, 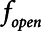 , becomes less than unity. This causes
, becomes less than unity. This causes 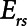 to increase above
to increase above 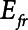 according to
according to 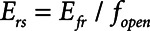 . The alveolar compartment is served by a conduit representing respiratory system resistance
. The alveolar compartment is served by a conduit representing respiratory system resistance 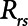 . This resistance contains a component from the lung and chest wall tissues as well as the airways themselves (14), but in a mechanically ventilated patient, the effective value of
. This resistance contains a component from the lung and chest wall tissues as well as the airways themselves (14), but in a mechanically ventilated patient, the effective value of 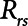 includes significant contributions from the endotracheal tube and the ventilator circuit, which are not affected by recruitment and derecruitment. Accordingly, we assume in our model that
includes significant contributions from the endotracheal tube and the ventilator circuit, which are not affected by recruitment and derecruitment. Accordingly, we assume in our model that 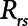 remains fixed regardless of the state of the lung. The time-constant of the respiratory system that governs how rapidly the patent regions of the lung empty during passive expiration is given by
remains fixed regardless of the state of the lung. The time-constant of the respiratory system that governs how rapidly the patent regions of the lung empty during passive expiration is given by 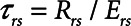 , which shows that the time required for lung deflation decreases as
, which shows that the time required for lung deflation decreases as 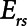 increases.
increases.
The rate at which the model recruits and derecruits is governed by the two parameters 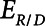 and
and 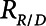 that together determine a time-constant of recruitment and derecruitment,
that together determine a time-constant of recruitment and derecruitment, 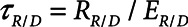 . If airway pressure is held constant, it will eventually equilibrate with alveolar pressures, and the fraction of open lung will eventually approximate a steady-state value determined by the stiffness
. If airway pressure is held constant, it will eventually equilibrate with alveolar pressures, and the fraction of open lung will eventually approximate a steady-state value determined by the stiffness 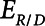 of the horizontal spring in Figure 1A. The horizontal dashpot with resistance
of the horizontal spring in Figure 1A. The horizontal dashpot with resistance 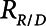 in Figure 1A prevents the steady-state open fraction from being attained immediately following a change in airway pressure and is related to the resistance provided by the motion of a plug of airway fluid or the peeling open of a collapsed airway that is required for airflow (15). Instead, the steady-state value is approached asymptotically as the dashpot slides under the force exerted by the spring.
in Figure 1A prevents the steady-state open fraction from being attained immediately following a change in airway pressure and is related to the resistance provided by the motion of a plug of airway fluid or the peeling open of a collapsed airway that is required for airflow (15). Instead, the steady-state value is approached asymptotically as the dashpot slides under the force exerted by the spring. 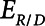 and
and  together thus imbue the model with dynamic recruitment/derecruitment behavior, whereby the fraction of open lung at any point in time is determined by prior excursions in alveolar pressure, in addition to its current value. Note that the time taken for the dashpot to approach its steady-state value may be substantially longer than the duration of a single breath, depending on the value of
together thus imbue the model with dynamic recruitment/derecruitment behavior, whereby the fraction of open lung at any point in time is determined by prior excursions in alveolar pressure, in addition to its current value. Note that the time taken for the dashpot to approach its steady-state value may be substantially longer than the duration of a single breath, depending on the value of 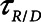 .
.
Although the model is represented as having a single alveolar compartment in Figure 1, this compartment corresponds to a distribution of alveolar units each of which is either open or closed at any point in time. Those units that are open are distended to an identical extent by alveolar pressure, but the number of open units changes with time as recruitment or derecruitment occurs. It is well accepted that the pressure that causes a closed lung unit to open during inflation is higher than the pressure at which it closes during a subsequent expiration (16). In the interests of keeping the model of the present study as simple as possible, however, we assume here that the opening and closing pressures are equal to a single critical pressure, 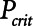 , that determines whether the steady-state condition of a particular lung unit is to be open or closed at the current value of airway pressure,
, that determines whether the steady-state condition of a particular lung unit is to be open or closed at the current value of airway pressure,  . Thus, if a unit is closed and
. Thus, if a unit is closed and 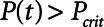 , then the unit will start to open, and conversely, if the unit is open and
, then the unit will start to open, and conversely, if the unit is open and  , then the unit will start to close. Following our previous modeling work and that of others (12, 16), we assume that
, then the unit will start to close. Following our previous modeling work and that of others (12, 16), we assume that 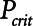 is a Gaussian function of airway pressure with mean
is a Gaussian function of airway pressure with mean 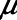 and sd
and sd
 . The mean of the Gaussian,
. The mean of the Gaussian,  , varies with lung injury, increasing monotonically with surface tension at the air-liquid interface (i.e., with the increasing surfactant dysfunction that accompanies VILI) (17).
, varies with lung injury, increasing monotonically with surface tension at the air-liquid interface (i.e., with the increasing surfactant dysfunction that accompanies VILI) (17).
We simulated mechanical ventilation by driving the model with a prescribed airway pressure profile, 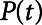 , producing a calculated airway flow profile,
, producing a calculated airway flow profile, 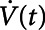 . Two modes of protective mechanical ventilation, both delivered at a rate of 12 breaths/min, were investigated with this model:
. Two modes of protective mechanical ventilation, both delivered at a rate of 12 breaths/min, were investigated with this model:
1) Low tidal volume ventilation (Low-Vt) generated using a ramp in airway pressure during inspiration and an inspiratory:expiratory ratio of 1:2. A set value of PEEP was used to maintain airway/alveolar patency at end-expiration, whereas peak airway pressure was adjusted to target a desired Vt.
2) Airway pressure release ventilation (APRV) in which pressure has a defined maximum airway pressure (
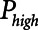 ) applied over the duration (
) applied over the duration ( ) with a short exhalation defined by the duration (
) with a short exhalation defined by the duration (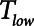 ) over which a constant low pressure (
) over which a constant low pressure (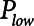 ) is applied with no applied PEEP.
) is applied with no applied PEEP. 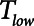 is the key parameter that may be tuned based on a measured expiratory flow profile to maintain airway/alveolar patency.
is the key parameter that may be tuned based on a measured expiratory flow profile to maintain airway/alveolar patency.
The two modes of ventilation were thus adjusted to be as comparable as possible, although this is impossible in every respect (e.g., compared with Low-VT, APRV had a somewhat greater mean airway pressure because of its greater inspiratory duration). We explore these modes and how they affect the level of atelectasis in a time-dependent breath-by-breath analysis.
Examples of simulated airway flow and pressure waveforms with each mode are shown in Figure 1B. Each simulation was initialized with the lung fully open (open fraction = 1.0) and was continued until the model reached steady state (which took only a few breaths in each case). Once steady state had been reached, we calculated tidal volume (Vt) as well as the driving pressure (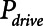 ) given by the difference between end-inspiratory and end-expiratory alveolar pressures. As a measure of the rate of formation of atelectrauma, we calculated an atelectrauma index (
) given by the difference between end-inspiratory and end-expiratory alveolar pressures. As a measure of the rate of formation of atelectrauma, we calculated an atelectrauma index (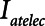 ) defined as the total change in the fraction of open lung taking place per breath.
) defined as the total change in the fraction of open lung taking place per breath.
The equations defining the model are given in the Supplement Digital Content (http://links.lww.com/CCX/A453). The five free parameters in the model are 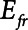 ,
, 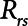 ,
, 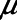 ,
,  , and
, and 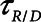 (Table 1). When these parameters are given the values
(Table 1). When these parameters are given the values 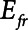 = 20 cm H2O.mL–1,
= 20 cm H2O.mL–1, 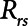 = 15 cm H2O.s.mL–1,
= 15 cm H2O.s.mL–1, 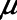 = 2 cm H2O,
= 2 cm H2O,  = 6 cm H2O, and
= 6 cm H2O, and 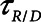 = 10 s, the model is able to recapitulate our previously observed the dynamics of recruitment and derecruitment in normal mice. We modeled an ARDS lung by increasing
= 10 s, the model is able to recapitulate our previously observed the dynamics of recruitment and derecruitment in normal mice. We modeled an ARDS lung by increasing 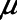 to 7.5 cm H2O, which produces behavior corresponding to mice receiving intratracheal instillations of hydrochloric acid to simulate aspiration injury (10, 12), as illustrated by
to 7.5 cm H2O, which produces behavior corresponding to mice receiving intratracheal instillations of hydrochloric acid to simulate aspiration injury (10, 12), as illustrated by 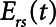 as a function of PEEP in Figure 2.
as a function of PEEP in Figure 2.
Figure 2.
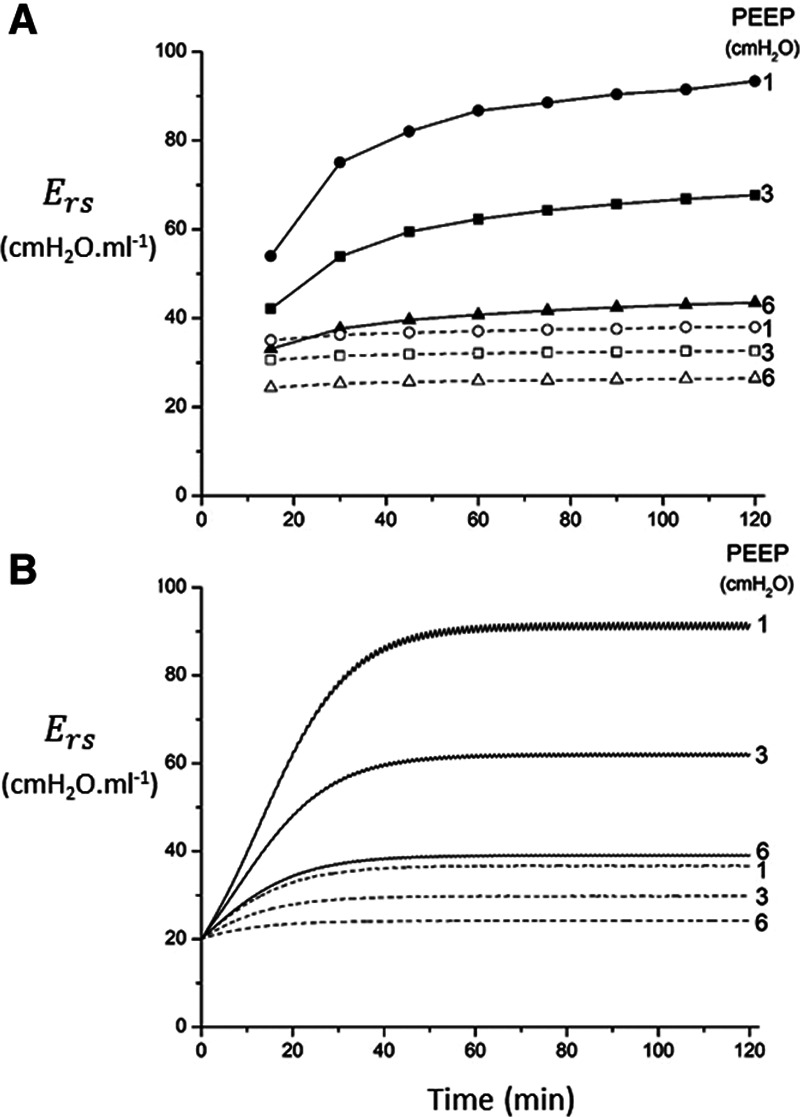
Calibration of model to experimental data. A, Respiratory system elastance versus time in mice following recruitment maneuvers given at t = 0 at three different positive end-expiratory pressure (PEEP) levels (adapted from a previous study [10] with permission from the American Physiologic Society). Open symbols: baseline conditions; closed symbols: lung injury; circles: PEEP = 1 cm H2O; squares: PEEP = 3 cm H2O; triangles: PEEP = 6 cm H2O. B, Elastance profiles simulated using the model. Solid lines: baseline conditions; dashed lines: lung injury.
In order to model mechanically ventilated patients, we used the human scale value of 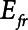 = 10 cm H2O.L–1 to represent the elastance of a typical fully open adult human respiratory system. We thus assumed that any increases in elastance (decreases in compliance) due to lung injury occurred entirely as a result of lung derecruitment. We also used
= 10 cm H2O.L–1 to represent the elastance of a typical fully open adult human respiratory system. We thus assumed that any increases in elastance (decreases in compliance) due to lung injury occurred entirely as a result of lung derecruitment. We also used 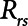 = 15 cm H2O.s.L–1 to represent the total series flow resistance of the airway tree, the endotracheal tube, and the ventilator tubing. This gave a time-constant for emptying of the respiratory system during expiration of
= 15 cm H2O.s.L–1 to represent the total series flow resistance of the airway tree, the endotracheal tube, and the ventilator tubing. This gave a time-constant for emptying of the respiratory system during expiration of 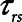 = 1.5 s when the lung was fully open. There is little in the literature to guide the choice of
= 1.5 s when the lung was fully open. There is little in the literature to guide the choice of 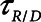 in humans, however, so we performed simulations using both
in humans, however, so we performed simulations using both 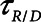 = 10 s derived from the above mouse data as well as the shorter time-constant of
= 10 s derived from the above mouse data as well as the shorter time-constant of 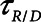 = 2 s based on previous experimental observations in a rat model of lung injury created by lavage (1). Per the above calibration of the model in our previous mouse study (12), we modeled the normal human lung using
= 2 s based on previous experimental observations in a rat model of lung injury created by lavage (1). Per the above calibration of the model in our previous mouse study (12), we modeled the normal human lung using 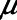 = 2 cm H2O and
= 2 cm H2O and  = 6 cm H2O, with
= 6 cm H2O, with 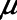 = 7.5 cm H2O to simulate lung injury. Since these studies involve only a computational model, no ethics review of the protocol was required.
= 7.5 cm H2O to simulate lung injury. Since these studies involve only a computational model, no ethics review of the protocol was required.
RESULTS
The primary adjustable parameter in Low-Vt is PEEP, since the value of PEEP determines the plateau airway pressure via the requirement to achieve a particular Vt. Accordingly, we determined 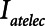 ,
, 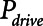 , and Vt as PEEP increased from 5 to 25 cm H2O when the model was ventilated with Low-Vt ventilation. At the same time, the plateau airway pressure increased from 15 to 35 cm H2O so that Vt remained close to 400 mL in all cases. Figure 3 shows
, and Vt as PEEP increased from 5 to 25 cm H2O when the model was ventilated with Low-Vt ventilation. At the same time, the plateau airway pressure increased from 15 to 35 cm H2O so that Vt remained close to 400 mL in all cases. Figure 3 shows 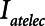 ,
, 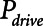 , and Vt versus PEEP for slow (
, and Vt versus PEEP for slow (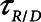 = 10 s) and rapid (
= 10 s) and rapid ( = 2 s) rates of recruitment for both a healthy lung (dashed lines) and an injured lung (solid lines). In both cases,
= 2 s) rates of recruitment for both a healthy lung (dashed lines) and an injured lung (solid lines). In both cases, 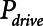 and Vt remain roughly constant with PEEP above about 20 cm H2O. As PEEP decreases below this level, the increasing degree of derecruitment causes
and Vt remain roughly constant with PEEP above about 20 cm H2O. As PEEP decreases below this level, the increasing degree of derecruitment causes 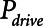 to increase and Vt to decrease modestly. Iatelec, on the other hand, is highly PEEP-dependent, being close to zero above about 20 cm H2O but increasing dramatically as PEEP descends to impinge on the Gaussian distribution of
to increase and Vt to decrease modestly. Iatelec, on the other hand, is highly PEEP-dependent, being close to zero above about 20 cm H2O but increasing dramatically as PEEP descends to impinge on the Gaussian distribution of 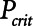 values. Note that
values. Note that 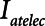 is also strongly dependent on
is also strongly dependent on 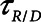 ; shorter time-constants allow for more intratidal recruitment and derecruitment to occur within the breath.
; shorter time-constants allow for more intratidal recruitment and derecruitment to occur within the breath.
Figure 3.

Atelectrauma index ( ), driving pressure (Pdriving), and tidal volume as a function of positive end-expiratory pressure (PEEP) for Low-Vt ventilation for (A)
), driving pressure (Pdriving), and tidal volume as a function of positive end-expiratory pressure (PEEP) for Low-Vt ventilation for (A) 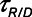 = 10 s and (B)
= 10 s and (B)  = 2 s. Peak airway pressure was 10 cm H2O above PEEP in all cases. Dashed lines: healthy lung; solid lines: injured lung. Note that
= 2 s. Peak airway pressure was 10 cm H2O above PEEP in all cases. Dashed lines: healthy lung; solid lines: injured lung. Note that  remains relatively high until PEEP reaches approximately 15 cm H2O.
remains relatively high until PEEP reaches approximately 15 cm H2O.
We also explored 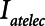 ,
, 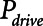 , and Vt when the model was ventilated with APRV, which is characterized by four parameters—the duration (
, and Vt when the model was ventilated with APRV, which is characterized by four parameters—the duration (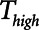 ) at which a constant inspiratory pressure (
) at which a constant inspiratory pressure (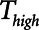 ) is applied to the airways to inflate the lungs and the duration (
) is applied to the airways to inflate the lungs and the duration (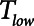 ) at which a constant low pressure (
) at which a constant low pressure (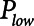 ) is applied to the airways to allow for expiration to occur (as exemplified in Fig. 1B). It is typical to set
) is applied to the airways to allow for expiration to occur (as exemplified in Fig. 1B). It is typical to set 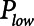 = 0, because this maximizes the pressure drop that drives expiratory flow and thus maximizes minute ventilation, but the remaining three parameters are all subject to adjustment. During weaning, for example,
= 0, because this maximizes the pressure drop that drives expiratory flow and thus maximizes minute ventilation, but the remaining three parameters are all subject to adjustment. During weaning, for example, 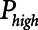 is progressively decreased while
is progressively decreased while 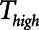 is progressively increased (18). Arguably, the parameter most critically in need of careful attention, however, is
is progressively increased (18). Arguably, the parameter most critically in need of careful attention, however, is  , which keeps expiration brief.
, which keeps expiration brief. 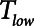 can be as low as 0.2 s when APRV is first applied to lungs that are severely injured and can increase somewhat as they become inflated and stabilized (19, 20). As a rule of thumb,
can be as low as 0.2 s when APRV is first applied to lungs that are severely injured and can increase somewhat as they become inflated and stabilized (19, 20). As a rule of thumb, 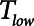 should rarely exceed about 0.5 s, although the specific value should be set in a patient-specific manner based on the exhalation flow profile to prevent derecruitment and the associated damage from atelectrauma that occurs with rerecruitment.
should rarely exceed about 0.5 s, although the specific value should be set in a patient-specific manner based on the exhalation flow profile to prevent derecruitment and the associated damage from atelectrauma that occurs with rerecruitment.
To explore the critical nature of 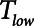 , we repeated a similar set of simulation experiments as in Figure 2 but this time determining how
, we repeated a similar set of simulation experiments as in Figure 2 but this time determining how 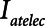 ,
,  , and Vt varied as
, and Vt varied as 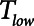 was varied between 0.2 and 2.0 s, again for
was varied between 0.2 and 2.0 s, again for  = 10 and 2 s and for a healthy (dashed lines) and an injured (solid lines) lung. The results in Figure 4 show that
= 10 and 2 s and for a healthy (dashed lines) and an injured (solid lines) lung. The results in Figure 4 show that 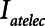 ,
, 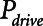 , and Vt all exhibit strong positive dependencies on
, and Vt all exhibit strong positive dependencies on 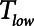 .
.
Figure 4.
Atelectrauma index ( ), driving pressure (Pdriving), and tidal volume as a function of
), driving pressure (Pdriving), and tidal volume as a function of  for low-Vt ventilation for (A)
for low-Vt ventilation for (A)  = 10 s and (B)
= 10 s and (B) 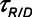 = 2 s. Peak airway pressure was 10 cm H2O above positive end-expiratory pressure in all cases. Dashed lines: healthy lung; solid lines: injured lung. Note that
= 2 s. Peak airway pressure was 10 cm H2O above positive end-expiratory pressure in all cases. Dashed lines: healthy lung; solid lines: injured lung. Note that  is low until
is low until 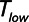 reaches approximately 0.5 s, after which it rises dramatically as
reaches approximately 0.5 s, after which it rises dramatically as  is further increased.
is further increased.
Finally, we examined how the potential for atelectrauma during APRV is affected by the rate of lung emptying governed by value of 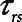 , given by the ratio of
, given by the ratio of 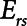 to
to 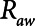 . The baseline value of
. The baseline value of 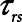 = 1.5 s used in the above simulations represents what one might expect in a typical ventilated patient, but we explored the effect of its reduction by, for example, the absence of an endotracheal tube as might be the case during noninvasive ventilation. Figure 5 shows that
= 1.5 s used in the above simulations represents what one might expect in a typical ventilated patient, but we explored the effect of its reduction by, for example, the absence of an endotracheal tube as might be the case during noninvasive ventilation. Figure 5 shows that 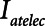 increases substantially as
increases substantially as 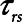 decreases and the lungs empty more rapidly duration expiration. These differences are greatest in relative terms at low values of
decreases and the lungs empty more rapidly duration expiration. These differences are greatest in relative terms at low values of 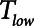 but are essentially unaffected in relative terms by the value of
but are essentially unaffected in relative terms by the value of 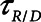 . In absolute terms, however,
. In absolute terms, however, 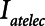 has a substantial inverse dependence on
has a substantial inverse dependence on 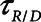 as is seen in Figure 4. Thus, the degree of atelectrauma produced in the injured lung during a fixed pattern of APRV is largely dictated by the two time-constants
as is seen in Figure 4. Thus, the degree of atelectrauma produced in the injured lung during a fixed pattern of APRV is largely dictated by the two time-constants 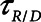 and
and 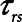 .
.
Figure 5.
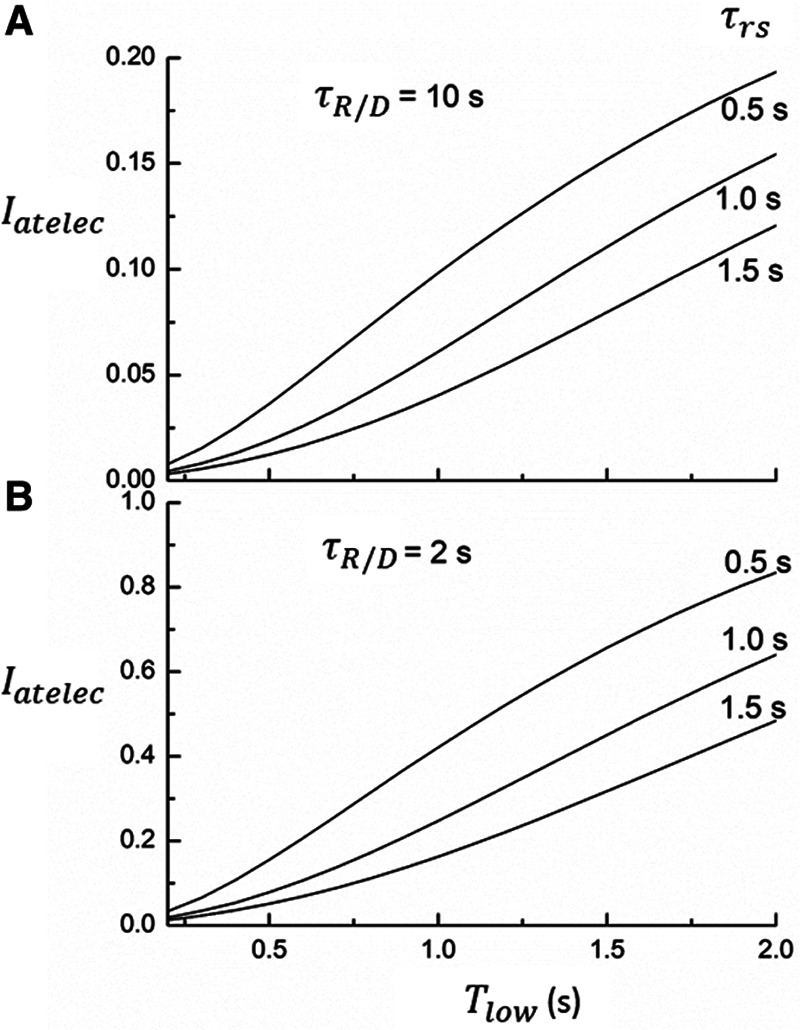
Model predictions of the atelectrauma index ( ) as a function of
) as a function of 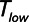 during ventilation of the injured lung with airway pressure release ventilation for (A)
during ventilation of the injured lung with airway pressure release ventilation for (A) 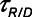 = 10 s and (B)
= 10 s and (B) 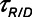 = 2 s, showing the effects of reducing the time-constant of emptying of the lung achieved by varying airway resistance (Raw).
= 2 s, showing the effects of reducing the time-constant of emptying of the lung achieved by varying airway resistance (Raw).
DISCUSSION
The search for better ways to ventilate patients with ARDS has been an ongoing focus of critical care research for decades, with the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic only increasing motivation to improve upon current approaches (21, 22). It seems self-evident that this search will be most efficient if it is based on an understanding of the biophysical mechanisms that give rise to VILI, the primary evil afflicting the ventilated ARDS patient. Ideally, one would like to identify the most clinically advantageous ventilation strategy for a given patient. Despite its obvious appeal, however, personalized ventilation for ARDS has so far proven elusive, presumably because key aspects of how ventilators cause VILI have yet to be taken into account in a quantifiable manner to design optimal ventilation strategies.
We hypothesize that critical among the missing considerations is recognition of the importance of the dynamic nature of recruitment and derectruitment. That is, collapse of alveoli and small airways in the injured lung is not only determined by the applied inflation pressure; collapse takes time to manifest, and the rate at which it manifests varies with the nature and severity of lung injury (10). This means that atelectrauma, perhaps the most insidious of VILI mechanisms (8, 23), depends not only on the pressure and volumes that are applied to the lungs during mechanical ventilation but also on how these pressure and volumes vary with time.
In the current study, we present a simple mathematical model of lung mechanics that incorporates the temporal nature of recruitment and derecruitment. We set the physiologic parameters (functional residual capacity, 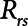 , and
, and 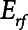 ) of the model to correspond approximately to a 70-kg human patient connected to a standard ventilator circuit. We imposed acute lung injury on the model by increasing the mean of the critical opening/closing pressure distribution (μ) so that the model mimicked time courses of respiratory system elastance observed experimentally during derecruitability tests (Fig. 2A). This allowed us to explore how two canonical modes of mechanical ventilation, Low-Vt and APRV, are compared in terms of measures of intratidal recruitment (
) of the model to correspond approximately to a 70-kg human patient connected to a standard ventilator circuit. We imposed acute lung injury on the model by increasing the mean of the critical opening/closing pressure distribution (μ) so that the model mimicked time courses of respiratory system elastance observed experimentally during derecruitability tests (Fig. 2A). This allowed us to explore how two canonical modes of mechanical ventilation, Low-Vt and APRV, are compared in terms of measures of intratidal recruitment (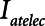 ) and tissue distension (Vt and
) and tissue distension (Vt and 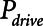 . Our results show that Low-Vt and APRV can each avoid atelectrauma if their respective parameters are chosen appropriately, but the strategies employed are very different. For the particular example of lung injury examined here (simulated by increasing
. Our results show that Low-Vt and APRV can each avoid atelectrauma if their respective parameters are chosen appropriately, but the strategies employed are very different. For the particular example of lung injury examined here (simulated by increasing 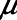 from 2 to 7.5 cm H2O), similar reductions in
from 2 to 7.5 cm H2O), similar reductions in 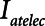 are achieved if PEEP is elevated to about 15 cm H2O in the case of Low-Vt, and if
are achieved if PEEP is elevated to about 15 cm H2O in the case of Low-Vt, and if 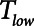 is reduced to about 0.5 s in the case of APRV (Figs. 3 and 4, respectively). Vt,
is reduced to about 0.5 s in the case of APRV (Figs. 3 and 4, respectively). Vt, 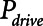 , and mean airway pressure are similar at these two respective thresholds implying that, under the particular injury condition we have simulated here, the two modes of mechanical ventilation are essentially equal in their abilities to avoid VILI.
, and mean airway pressure are similar at these two respective thresholds implying that, under the particular injury condition we have simulated here, the two modes of mechanical ventilation are essentially equal in their abilities to avoid VILI.
The above results might seem to suggest Low-Vt and APRV can each be set so as to achieve similar levels of avoidance of both atelectrauma and volutrauma. The situation is not quite this simple, however, because of the following tradeoffs:
1) Low-Vt: Figure 3 shows that further reductions in
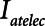 can be achieved with Low-Vt without incurring an increase in Vt by increasing PEEP above 15 cm H2O. However, if PEEP is increased to the point that lung volume starts to impinge on the upper curvilinear portion of the pressure-volume curve of the respiratory system, this may come at the expense of an increase in mean intrathoracic pressure.
can be achieved with Low-Vt without incurring an increase in Vt by increasing PEEP above 15 cm H2O. However, if PEEP is increased to the point that lung volume starts to impinge on the upper curvilinear portion of the pressure-volume curve of the respiratory system, this may come at the expense of an increase in mean intrathoracic pressure.2) APRV: Figure 4 shows that further reductions in
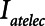 can be achieved with APRV by decreasing
can be achieved with APRV by decreasing 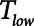 below 0.5 s, but at the expense of a reduced Vt (and hence minute ventilation).
below 0.5 s, but at the expense of a reduced Vt (and hence minute ventilation).
The implications of these differences depend on which of atelectrauma versus volutrauma is considered to be the principle culprit behind VILI and also on hemodynamic factors that might be impacted by high intrathoracic pressures.
In addition, Crotti et al (16) have shown that the values of mean and sd of opening and closing pressure distributions in the injured lung are hugely variable between the patients. For example, in those cases where these distributions do not extend up to excessively high pressures, the plateau pressures resulting from the PEEP required to avoid atelectrauma with Low-Vt may pose no danger to the patient. However, this may not be the case in the cases of very severe lung injury in which the opening pressures can extend to well above 20 cm H2O (16). In such a case, the use of APRV may be advantageous if it can be employed with a 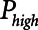 that is substantially lower than the plateau pressure required of Low-Vt.
that is substantially lower than the plateau pressure required of Low-Vt.
Figures 3 and 4 also highlight the potential dangers of both Low-Vt and APRV. Obviously, using excessive peak airway pressures in either mode of ventilation poses risk of causing mechanical damage to the lungs. What is also clear, however, is that both modes have the potential to cause substantial atelectrauma due to significant intratidal recruitment and derecruitment (23).
In the case of Low-Vt (Fig. 3), this risk increases as PEEP decreases, because it allows for an increasing fraction of the lung to derecruit during expiration, only to be forced to recruit again during the subsequent inspiration. Because the duration of expiration in Low-Vt is invariably a few seconds or more, there is usually plenty of time for derecruitment to occur even though, as we have established, this is a process that does not take place immediately upon the lowering of airway pressure.
In contrast, the dangers of atelectrauma with APRV manifest when 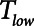 increases (Fig. 4), because this allows more time for derecruitment to occur. Furthermore, since the rate of derecruitment depends on how far airway pressure has been allowed to fall below the critical closing pressure (10–12), the rapid emptying of the lungs during the early stages of
increases (Fig. 4), because this allows more time for derecruitment to occur. Furthermore, since the rate of derecruitment depends on how far airway pressure has been allowed to fall below the critical closing pressure (10–12), the rapid emptying of the lungs during the early stages of  mitigates in favor of rapid derecruitment. Thus, as demonstrated in Figure 4, although short durations of
mitigates in favor of rapid derecruitment. Thus, as demonstrated in Figure 4, although short durations of 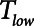 (below about 0.5 s) can protect against atelectrauma, lengthening
(below about 0.5 s) can protect against atelectrauma, lengthening 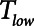 by a relatively small amount above the safe range rapidly leads to large values of
by a relatively small amount above the safe range rapidly leads to large values of 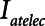 and thus substantial atelectrauma. Studies with porcine models of ARDS provide dramatic confirmation of these model predictions (16) and support the potential for personalized mechanical ventilation based on targeting end-expiratory flows.
and thus substantial atelectrauma. Studies with porcine models of ARDS provide dramatic confirmation of these model predictions (16) and support the potential for personalized mechanical ventilation based on targeting end-expiratory flows.
The above considerations might be taken as a support for the practice of keeping 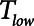 in the region of half a second when applying APRV. However, as Figure 5 makes clear, this is the only case when the combined resistance of an endotracheal tube and its associated ventilator tubing elevates the time-constant of lung emptying from its normal value of 0.5 s or less in a free-breathing human to the 1.5 s
in the region of half a second when applying APRV. However, as Figure 5 makes clear, this is the only case when the combined resistance of an endotracheal tube and its associated ventilator tubing elevates the time-constant of lung emptying from its normal value of 0.5 s or less in a free-breathing human to the 1.5 s 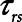 we have assumed here for the ventilated patient. Slowing the rate of emptying slows the rate at which derecruitment occurs throughout
we have assumed here for the ventilated patient. Slowing the rate of emptying slows the rate at which derecruitment occurs throughout 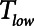 , but it also reduces minute ventilation, an effect that is relatively insensitive to the rate at which derecruitment occurs as governed by
, but it also reduces minute ventilation, an effect that is relatively insensitive to the rate at which derecruitment occurs as governed by 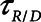 (Fig. 5).
(Fig. 5).
Another very important clinical source of variation in 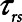 arises from the changes in lung compliance that take place as the mechanical status of the lung changes over time. In particular, when severely injured patients are first intubated and started on mechanical ventilation, their lungs may be very stiff due to a high degree of derecruitment and so
arises from the changes in lung compliance that take place as the mechanical status of the lung changes over time. In particular, when severely injured patients are first intubated and started on mechanical ventilation, their lungs may be very stiff due to a high degree of derecruitment and so 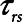 may be small. If the patient is being ventilated with APRV, they will require a very short
may be small. If the patient is being ventilated with APRV, they will require a very short 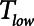 , possibly substantially less than 0.5 s, in order to avoid high values of
, possibly substantially less than 0.5 s, in order to avoid high values of 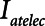 , as illustrated in Figure 5. If Low-Vt is being employed, the patient will require a high airway plateau pressure in order to deliver the target Vt. Once mechanical ventilation is underway, the lungs often become progressively more compliant as derecruited regions open up. This process can take hours and is not incorporated into the computational model of the present study, but it causes
, as illustrated in Figure 5. If Low-Vt is being employed, the patient will require a high airway plateau pressure in order to deliver the target Vt. Once mechanical ventilation is underway, the lungs often become progressively more compliant as derecruited regions open up. This process can take hours and is not incorporated into the computational model of the present study, but it causes 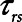 to increase.
to increase. 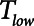 can then be lengthened accordingly in the case of APRV, or inflation pressure reduced if Low-Vt is being used. In either case, this highlights the importance of allowing mechanical ventilation to be adaptable so that ventilation parameters can be adjusted in the face of changing lung mechanics (19, 24, 25).
can then be lengthened accordingly in the case of APRV, or inflation pressure reduced if Low-Vt is being used. In either case, this highlights the importance of allowing mechanical ventilation to be adaptable so that ventilation parameters can be adjusted in the face of changing lung mechanics (19, 24, 25).
The results of our model analysis thus point to significant differences in the way that Low-Vt versus APRV can be used to manage the potential mechanisms of VILI. Which mode is more advantageous depends on the particular dynamics and pressure dependencies of recruitment and derecruitment that pertain to a given patient, since both characteristics vary substantially with the nature and severity of lung injury (10, 16). Accordingly, the practical implementation of a personalized ventilation strategy is almost certainly going to rely on a means of accurately determining these characteristics in a patient-specific manner. If this was done using either the capability of modern ventilators to estimate lung mechanics or alternatively an ancillary technique such as oscillometry to measure respiratory system impedance (26), the model we present here could potentially be fit to the mechanical characteristics of a given patient. The model could then be interrogated computationally by subjecting it to a wide range of ventilatory regimens and identifying the least injurious strategy for the patient in question.
Nevertheless, our model has some immediate implications for the management of ARDS patients, including those whose primary affliction is infection with the SARS-CoV-2 virus. Reports are that at least some of these patients first present with the somewhat puzzling picture of hypoxemia in the presence of relatively normal lung mechanics (27, 28). A possible explanation for this scenario is that the pulmonary edema that forms early in coronavirus disease 2019 (COVID-19) infection is confined to the interstitium where it interferes with gas exchange by thickening the blood-gas barrier, but this does not stiffen the lung tissue more than modestly. The major effects on lung mechanics, especially significantly decreased lung compliance, do not manifest until the epithelial barrier is breached. When this happens, plasma-derived fluid and proteins enter the airspaces, disrupt surfactant function, and increase surface tension, thereby altering alveolar mechanics. This leads to alveolar instability, which is a primary mechanism of VILI via atelectrauma (29). Ventilation strategies that are not adjusted to restabilize alveoli increase the tissue stress and damage caused by mechanical ventilation (23). In this sense, the lung epithelium functions as a last line of defense against the worst clinical manifestations of COVID-induced ARDS, suggesting that keeping it intact is paramount.
This, in turn, highlights the importance of preemptively ventilating in a way that avoids atelectrauma, even if COVID patients do not appear to be in full-blown ARDS when they are first placed on mechanical ventilation. Both Low-Vt and APRV are potentially capable of meeting this goal, but the short 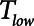 employed with APRV prevents derecruitment in two ways: 1) limiting the fall in lung volume during expiration so that it remains above the level at which derecruitment starts to occur and 2) not giving epithelial surfaces enough time to come into apposition before the next inspiration begins even if end-expiratory pressure (PEEP) falls to levels at which derecruitment would eventually occur if given enough time. Low-Vt, in contrast, only exploits the first of these mechanisms through its use of PEEP. To our knowledge, there are no published studies using APRV in COVID-19 patients. The efficacy of mechanical ventilation, however, in this disease has so far been disappointing, with mortalities among individuals 18–65 and greater than 65 years old being 74.6% and 97.2%, respectively (21). This suggests that a more personalized approach to mechanical ventilation in SARS-CoV-2 is needed (30).
employed with APRV prevents derecruitment in two ways: 1) limiting the fall in lung volume during expiration so that it remains above the level at which derecruitment starts to occur and 2) not giving epithelial surfaces enough time to come into apposition before the next inspiration begins even if end-expiratory pressure (PEEP) falls to levels at which derecruitment would eventually occur if given enough time. Low-Vt, in contrast, only exploits the first of these mechanisms through its use of PEEP. To our knowledge, there are no published studies using APRV in COVID-19 patients. The efficacy of mechanical ventilation, however, in this disease has so far been disappointing, with mortalities among individuals 18–65 and greater than 65 years old being 74.6% and 97.2%, respectively (21). This suggests that a more personalized approach to mechanical ventilation in SARS-CoV-2 is needed (30).
In terms of ARDS in general, the fact that recruitment and derecruitment depend on time as well as pressure means that APRV is not simply a means for producing auto-PEEP. Certainly, limiting the duration of expiration does produce auto-PEEP, but not all lung units have enough time to actually close as they would if the lung equilibrated against an equivalent level of static PEEP. This has implications for the clinical use of recruitment maneuvers; the key questions are not whether they should be used at all, but rather how frequently they should be given and long should each maneuver last. Indeed, there is experimental evidence that there is an optimal frequency of application for recruitment maneuvers that balance the tissue stresses wrought by their application to the temporary relief of stress produced by a subsequent period of more open lung (31).
The model of the present study might possibly serve as a vehicle for achieving this end. Nevertheless, the simplicity of this model brings with it numerous limitations. We designed the model to be the simplest that still retains the essential elements necessary to account for basic lung mechanics as well as the dynamics of recruitment and derecruitment. Application of this model to a patient, however, might require incorporation of more realistic representations of physiology, such as a nonlinear pressure-volume relationship for the lung tissues rather than the linear relationship we assumed here. It is also clear that the dynamics of recruitment and derecruitment themselves are substantially more complex than the linear first-order representation we used in our simple model (see Supplement Digital Content, http://links.lww.com/CCX/A453). For example, although Crotti et al (16) found evidence that Pcrit remains roughly Gaussian in injured lungs, they also showed that the distributions of opening and closing pressures can be quite widely separated, rather than being identical as we assumed in the present model. Incorporating such details would inevitably improve the model’s ability to serve as a useful platform for finding optimal ventilation strategies (13). In addition, we implemented Low-Vt in the model using a ramp in inspiratory pressures; there are other ways in which 6 mL/kg can be achieved, such as with a constant inspiratory pressure of the appropriate level. Despite these various limitations, however, our study clearly demonstrates that in order to develop personalized strategies for mechanical ventilation in ARDS, it is going to be necessary to assess the dynamics of recruitment and derecruitment taking place in the lungs of an individual patient. Only with this information in hand will it be possible to optimize the timing as well as the magnitudes of the pressures that are applied to the airways during mechanical ventilation.
CONCLUSIONS
We conclude that the generation of atelectrauma during mechanical ventilation is critically determined not only by how lung recruitment and derectruitment depend on pressure but also by how they depend on time. Our simulation results confirm conventional wisdom that avoidance of atelectrauma during Low-Vt is achieved primarily by manipulating pressure through adjustment of PEEP. In contrast, avoidance of atelectrauma during APRV is achieved by manipulating time through adjustment of 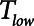 . Our simulation studies further show that the efficacy of APRV is determined by the relative values of two time-dependent processes that, in our model, are represented by the time-constant of lung emptying (
. Our simulation studies further show that the efficacy of APRV is determined by the relative values of two time-dependent processes that, in our model, are represented by the time-constant of lung emptying (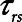 ) and the time-constant of recruitment and derecruitment (
) and the time-constant of recruitment and derecruitment (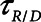 ). Model simulations also demonstrated that
). Model simulations also demonstrated that 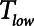 has an effective threshold value below which APRV is safe from atelectrauma while maintaining a tidal volume and driving pressure comparable with those of Low-Vt. This threshold is strongly influenced by the time-constant of lung emptying. The relative advantages of Low-Vt versus APRV for the avoidance of VILI thus depend on the dynamics of recruitment and derecruitment in a given patient and on whether the primary mechanism of lung damage is volutrauma or atelectrauma. Critical to this consideration is the underappreciated fact that the timing of expiration is as important as the applied levels of airway pressure in avoiding atelectrauma. Bedside use of our computational model could potentially help in the optimization of these parameters in a patient-specific manner.
has an effective threshold value below which APRV is safe from atelectrauma while maintaining a tidal volume and driving pressure comparable with those of Low-Vt. This threshold is strongly influenced by the time-constant of lung emptying. The relative advantages of Low-Vt versus APRV for the avoidance of VILI thus depend on the dynamics of recruitment and derecruitment in a given patient and on whether the primary mechanism of lung damage is volutrauma or atelectrauma. Critical to this consideration is the underappreciated fact that the timing of expiration is as important as the applied levels of airway pressure in avoiding atelectrauma. Bedside use of our computational model could potentially help in the optimization of these parameters in a patient-specific manner.
Supplementary Material
Footnotes
Dr. Bates developed and coded the computational model. Dr. Bates, Dr. Gaver, and Mr. Nieman conceived and drafted the article. Dr. Habashi related the modeling results to clinical practice. All authors participated in multiple editing and revision steps, and approved the final draft.
Supplemental digital content is available for this article. Direct URL citations appear in the printed text and are provided in the HTML and PDF versions of this article on the journal’s website (http://journals.lww.com/ccxjournal).
Supported, in part, by R01 grant HL142702 from the National Institutes of Health.
Dr. Bates is a consultant for and shareholder in Oscillavent and LLC (Iowa), and a coapplicant on the patent “Variable ventilation as a diagnostic tool for assessing lung mechanical function” PCT Application WO2015127377 A1, Filed on February 23, 2014 (C538); Mr. Nieman has an Unrestricted Educational Grant from Dräger Medical; Dr. Habashi is founder of Intensive Care On-line Network, lectured at symposia sponsored in part by an unrestricted educational grant from Dräger Medical, holds patents that have not been commercialized, licensed or produced royalties on a method of initiating, managing and/or weaning airway pressure release ventilation, and controlling a ventilator in accordance with the same. Dr. Gaver has disclosed that he does not have any potential conflicts of interest.
REFERENCES
- 1.Albert SP, DiRocco J, Allen GB, et al. The role of time and pressure on alveolar recruitment. J Appl Physiol (1985). 2009; 106:757–765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Shaver CM, Bastarache JA. Clinical and biological heterogeneity in acute respiratory distress syndrome: Direct versus indirect lung injury. Clin Chest Med. 2014; 35:639–653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ferguson ND, Cook DJ, Guyatt GH, et al. ; OSCILLATE Trial Investigators; Canadian Critical Care Trials Group. High-frequency oscillation in early acute respiratory distress syndrome. N Engl J Med. 2013; 368:795–805 [DOI] [PubMed] [Google Scholar]
- 4.Young D, Lamb SE, Shah S, et al. ; OSCAR Study Group. High-frequency oscillation for acute respiratory distress syndrome. N Engl J Med. 2013; 368:806–813 [DOI] [PubMed] [Google Scholar]
- 5.Cavalcanti AB, Suzumura ÉA, Laranjeira LN, et al. ; Writing Group for the Alveolar Recruitment for Acute Respiratory Distress Syndrome Trial (ART) Investigators. Effect of lung recruitment and titrated positive end-expiratory pressure (PEEP) vs low PEEP on mortality in patients with acute respiratory distress syndrome: A randomized clinical trial. JAMA. 2017; 318:1335–1345 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Guérin C, Reignier J, Richard JC, et al. ; PROSEVA Study Group. Prone positioning in severe acute respiratory distress syndrome. N Engl J Med. 2013; 368:2159–2168 [DOI] [PubMed] [Google Scholar]
- 7.Neto AS, Simonis FD, Barbas CS, et al. ; PROtective Ventilation Network Investigators. Lung-protective ventilation with low tidal volumes and the occurrence of pulmonary complications in patients without acute respiratory distress syndrome: A systematic review and individual patient data analysis. Crit Care Med. 2015; 43:2155–2163 [DOI] [PubMed] [Google Scholar]
- 8.Seah AS, Grant KA, Aliyeva M, et al. Quantifying the roles of tidal volume and PEEP in the pathogenesis of ventilator-induced lung injury. Ann Biomed Eng. 2011; 39:1505–1516 [DOI] [PubMed] [Google Scholar]
- 9.Webb HH, Tierney DF. Experimental pulmonary edema due to intermittent positive pressure ventilation with high inflation pressures. Protection by positive end-expiratory pressure. Am Rev Respir Dis. 1974; 110:556–565 [DOI] [PubMed] [Google Scholar]
- 10.Allen G, Bates JH. Dynamic mechanical consequences of deep inflation in mice depend on type and degree of lung injury. J Appl Physiol (1985). 2004; 96:293–300 [DOI] [PubMed] [Google Scholar]
- 11.Bates JH, Irvin CG. Time dependence of recruitment and derecruitment in the lung: A theoretical model. J Appl Physiol (1985). 2002; 93:705–713 [DOI] [PubMed] [Google Scholar]
- 12.Massa CB, Allen GB, Bates JH. Modeling the dynamics of recruitment and derecruitment in mice with acute lung injury. J Appl Physiol (1985). 2008; 105:1813–1821 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hamlington KL, Smith BJ, Allen GB, et al. Predicting ventilator-induced lung injury using a lung injury cost function. J Appl Physiol (1985). 2016; 121:106–114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bates JH, Brown KA, Kochi T. Respiratory mechanics in the normal dog determined by expiratory flow interruption. J Appl Physiol (1985). 1989; 67:2276–2285 [DOI] [PubMed] [Google Scholar]
- 15.Fujioka H, Takayama S, Grotberg JB. Unsteady propagation of a liquid plug in a liquid-lined straight tube. Phys Fluids (1994). 2008; 20:62104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Crotti S, Mascheroni D, Caironi P, et al. Recruitment and derecruitment during acute respiratory failure: A clinical study. Am J Respir Crit Care Med. 2001; 164:131–140 [DOI] [PubMed] [Google Scholar]
- 17.Gaver DP, 3rd, Samsel RW, Solway J. Effects of surface tension and viscosity on airway reopening. J Appl Physiol (1985). 1990; 69:74–85 [DOI] [PubMed] [Google Scholar]
- 18.Zhou Y, Jin X, Lv Y, et al. Early application of airway pressure release ventilation may reduce the duration of mechanical ventilation in acute respiratory distress syndrome. Intensive Care Med. 2017; 43:1648–1659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nieman GF, Gatto LA, Andrews P, et al. Prevention and treatment of acute lung injury with time-controlled adaptive ventilation: Physiologically informed modification of airway pressure release ventilation. Ann Intensive Care. 2020; 10:3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Habashi NM. Other approaches to open-lung ventilation: Airway pressure release ventilation. Crit Care Med. 2005; 33:S228–S240 [DOI] [PubMed] [Google Scholar]
- 21.Richardson S, Hirsch JS, Narasimhan M, et al. ; the Northwell COVID-19 Research Consortium. Presenting characteristics, comorbidities, and outcomes among 5700 patients hospitalized with COVID-19 in the New York City area. JAMA. 2020; 323:2052–2059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marini JJ, Gattinoni L. Management of COVID-19 respiratory distress. JAMA. 2020; 323:2329–2330 [DOI] [PubMed] [Google Scholar]
- 23.Gaver DP, 3rd, Nieman GF, Gatto LA, et al. The POOR Get POORer: A hypothesis for the pathogenesis of ventilator-induced lung injury. Am J Respir Crit Care Med. 2020; 202:1081–1087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Andrews PL, Shiber JR, Jaruga-Killeen E, et al. Early application of airway pressure release ventilation may reduce mortality in high-risk trauma patients: A systematic review of observational trauma ARDS literature. J Trauma Acute Care Surg. 2013; 75:635–641 [DOI] [PubMed] [Google Scholar]
- 25.Kollisch-Singule MPA, Satalin J, et al. The time-controlled adaptive ventilation protocol: Mechanistic approach to reducing ventilator-induced lung injury. European Respiratory Review. 2019; 28:180126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bates JH, Irvin CG, Farré R, et al. Oscillation mechanics of the respiratory system. Compr Physiol. 2011; 1:1233–1272 [DOI] [PubMed] [Google Scholar]
- 27.Gattinoni L, Chiumello D, Caironi P, et al. COVID-19 pneumonia: Different respiratory treatments for different phenotypes? Intensive Care Med. 2020; 46:1099–1102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lang M, Som A, Carey D, et al. Pulmonary vascular manifestations of COVID-19 pneumonia. Radiol: Cardiothorac Imaging. 2020; 2:e200277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kollisch-Singule M, Emr B, Smith B, et al. Mechanical breath profile of airway pressure release ventilation: The effect on alveolar recruitment and microstrain in acute lung injury. JAMA Surg. 2014; 149:1138–1145 [DOI] [PubMed] [Google Scholar]
- 30.Matta S. Dilemmas in Covid-19 respiratory distress: Early vs late intubation; high tidal volume and low PEEP vs traditional approach? J Intensive Critical Care. 2020; 6:7 [Google Scholar]
- 31.Allen GB, Suratt BT, Rinaldi L, et al. Choosing the frequency of deep inflation in mice: Balancing recruitment against ventilator-induced lung injury. Am J Physiol Lung Cell Mol Physiol. 2006; 291:L710–L717 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


