Summary
The antibody repertoire possesses near limitless diversity, enabling the adaptive immune system to accommodate essentially any antigen. However, this diversity explores the antigenic space unequally, allowing some pathogens like influenza virus to impose complex immunodominance hierarchies that distract antibody responses away from key sites of virus vulnerability. We developed a computational model of affinity maturation to map the patterns of immunodominance that evolve upon immunization with natural and engineered displays of hemagglutinin (HA), the influenza vaccine antigen. Based on this knowledge, we designed immunization protocols that subvert immune distraction and focus serum antibody responses upon a functionally conserved, but immunologically recessive, target of human broadly neutralizing antibodies. We tested in silico predictions by vaccinating transgenic mice in which antibody diversity was humanized to mirror clinically relevant humoral output. Collectively, our results demonstrate that complex patterns in antibody immunogenicity can be rationally defined and then manipulated to elicit engineered immunity.
In brief
Antibodies against the hemagglutinin (HA) spike protein of influenza virus naturally target immunodistractive features rather than conserved sites that confer broad neutralization. Amitai et al. resolve drivers of immunodominance computationally and then apply this knowledge in vivo to refocus humoral responses against a ‘universal’ vaccine target.
Graphical Abstract
Introduction
Many effective vaccines program humoral immunity to occlude incoming pathogens through antibody responses (Chaplin, 2010; Crotty, 2015). In this programing scheme, vaccine antigens are first recognized by germline B cell receptors (BCRs), the surface displayed precursors to antibodies bearing appropriate complementarity, which are then subjected to affinity maturation (AM) within B cell germinal centers (GCs). The result is the generation of recallable B cell memory and antibody-secreting plasma cells bearing high affinity for cognate antigen. The memory cells and antibodies can last for the lifetime of an individual, providing long-lasting immunity. However, some pathogens such as influenza virus and HIV ‘resist’ conventional vaccination approaches as their surface antigens display hypervariable regions that are often immunodominant and therefore preferentially targeted by the responding B cell repertoire (Abbott et al., 2018; Altman et al., 2015; Dosenovic et al., 2018; McGuire et al., 2014; Peterhoff and Wagner, 2017; Sangesland et al., 2019). As a result, responses to these hypervariable regions naturally distract the B cell response from conserved sites of vulnerability, thus inhibiting the generation of broadly neutralizing antibodies (bnAbs) that can offer protection against the evolving virus population (Altman et al., 2018; Altman et al., 2015; Angeletti et al., 2017; Kwong and Mascola, 2018; Montefiori et al., 2018; Nabel and Fauci, 2010; Peterhoff and Wagner, 2017; Zost et al., 2019). Hence some viruses appear to tune immunogenicity so as to ensure that conserved epitopes and bnAb targets remain immunologically recessive.
Influenza A viruses (IAV) remains a significant public health burden and represents a major source of pandemic threats and severe disease (Paules and Subbarao, 2017; Petrie and Gordon, 2018). Diversity in IAVs is genetically and antigenically categorized into two phylogenetic groups (Group 1 and Group 2) encompassing the various subtypes of the viral spike protein hemagglutinin (HA) (Nabel and Fauci, 2010). Structurally, HA is a trimer comprised of a hypervariable and immunologically dominant globular head region, and a relatively conserved but immunologically recessive, stem or stalk region (Krammer et al., 2018; Nabel and Fauci, 2010; Wu and Wilson, 2017). The discovery of human bnAbs that target conserved epitopes within the HA stem, and thus can neutralize strains across HA Group 1 and Group 2 diversity, has spurred efforts to promote their elicitation by designing appropriate vaccination strategies and antigens (Cho and Wrammert, 2016; Krammer et al., 2018; Nabel and Fauci, 2010; Wu and Wilson, 2017). However, the immunological recessive nature of these responses remains a major impediment to achieving this goal (Krammer et al., 2018; Tan et al., 2019; Wu and Wilson, 2017; Zost et al., 2019).
Operationally defining the rules governing epitope immunodominance hierarchies would be a critical asset in subverting this property. However, immunogenicity, or the strength of an antibody response against a given epitope, depends on a complex set of interactions during the humoral response and has consequently proven difficult to computationally delineate or predict (Mahanty et al., 2015; Rockberg and Uhlen, 2009; Van Regenmortel, 2002, 2011). B cell epitope prediction is further confounded by the fact that antibody paratopes are enriched in aromatic side chains that recognize conformational protein epitopes through interaction with backbone atoms and side-chain carbons, physiochemical features that are common to all protein surfaces (Peng et al., 2014; Sun et al., 2011). This means that antibody targets are engaged via features that can be difficult to distinguish from a typical protein surface, a fact that has prevented the development of accurate B cell epitope prediction algorithms, even for the most simple protein antigens (Rockberg and Uhlen, 2009; Sela-Culang et al., 2013).
In this study, we sought to define antibody immunodominance hierarchies elicited by various influenza vaccine immunogens by reconstructing B cell selection and AM within the GC in silico. To do so, we combined Molecular Dynamics (MD) simulations that account for differential access to antigenic epitopes due to the geometry of HA immunogens presented in different ways with an agent-based stochastic model of GC reactions. The GC simulations are based on rules derived from past experimental studies with model antigens (Amitai et al., 2018; Victora and Nussenzweig, 2012; Wang et al., 2015). Using the influenza trimer hemagglutinin (HA) and key seasonal flu vaccine antigen as a model immunogen, we generated ‘immunogenicity heatmaps’ that illustrate how and why the antigenic space is explored unevenly across the surface of this key glycoprotein. The immunogenicity heatmaps helped define how reengineered nanoparticle displays of HA, along with specific human germline-endowed B cell responses, can be harnessed to alter immunodominance hierarchies in favor of targeting a normally immunologically recessive bnAb/’universal’ vaccine target. In all cases, we validated the predictions of our in silico model experimentally by vaccinating mice that have been specifically engineered to elicit humanized Ig responses that emanate from a germline antibody repertoire with similar diversity to that of humans (Sangesland et al., 2019). Collectively, our results demonstrate that immunodominance hierarchies of antibody responses against HA can be rationally defined, and then manipulated and re-oriented to elicit unnatural or engineered immunity.
Results
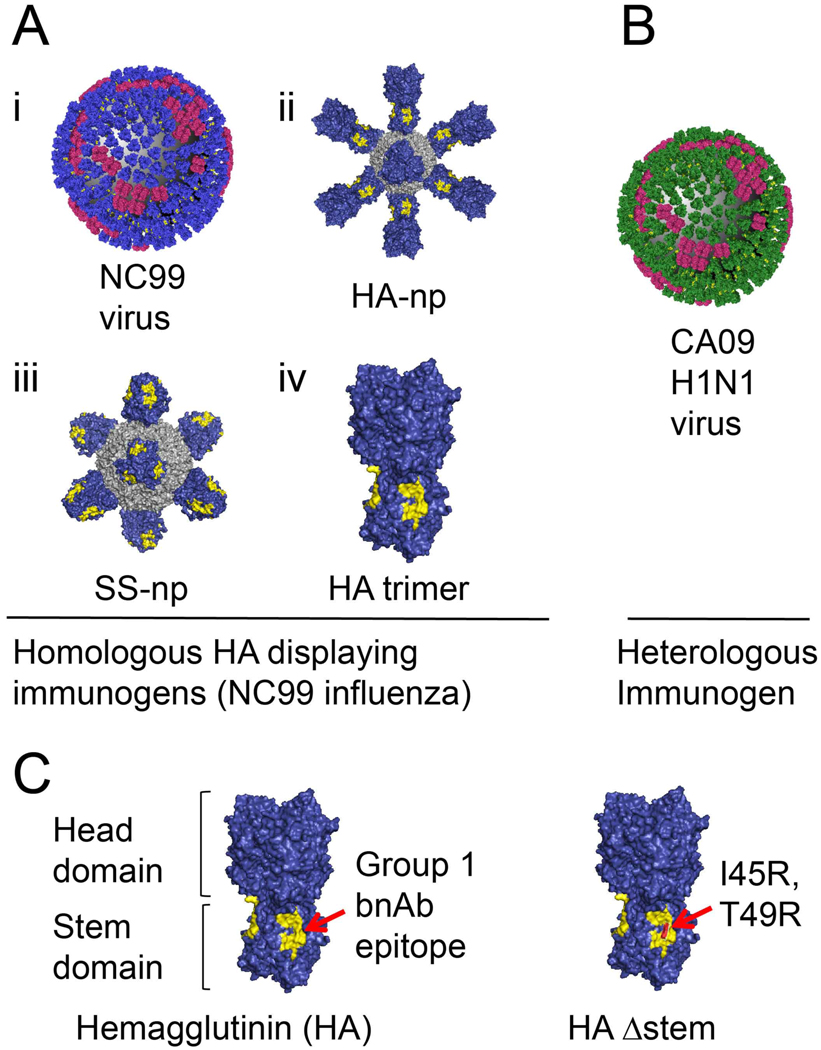
Vaccination in silico: geometry-dependent on-rates of BCRs for HA epitopes
We employed MD simulations to define how BCR on-rate, and hence affinity, could be modulated by the steric constraints imposed by various HA immunogens. We studied four geometrically distinct and structurally defined HA immunogens: 1) HA presentation within H1N1 influenza A viruses (Figure 1A–i) [A/New Caledonia/20/1999 (NC99) or A/California/09/2009 (CA09) (Figure 1B)]; 2) HA presentation as a full length HA trimer arrayed as an 8mer on a ferritin nanoparticle support (HA-np, NC99) (Figure 1A–ii) (Kanekiyo et al., 2013); 3) the trimeric stalk-only region of HA trimer arrayed as an 8mer on the same ferritin nanoparticle support (SS-np, NC99) (Figure 1A–iii) (Sangesland et al., 2019; Yassine et al., 2015); and 4) HA presentation as soluble full-length HA trimer (NC99) (Figure 1A–iv) (Lingwood et al., 2012; Sangesland et al., 2019; Villar et al., 2016; Weaver et al., 2016). Based on structural considerations we computed the on-rate for BCRs engaging different glycoprotein epitopes on each HA immunogen (Figure 2A–E). The events occurred in the following sequence: 1] a single BCR arm first engages a target epitope; 2] the BCR molecule continues to fluctuate, and when the immunogen geometry is favorable, allows the second arm to target a second epitope. Binding then occurs with a high rate, resulting in bivalent interaction.
Figure 1. Antigens presenting distinct hemagglutinin (HA) geometries.
(A) A/New Caledonia/20/1999 (NC99) H1N1 influenza virus with hemagglutinin (blue) and neuraminidase (red) (i). Ferritin nanoparticles presenting either full length HA (ii) or stem only trimer (iii), and free HA trimer (iv) (all are derived from NC99). (B) The 2009 H1N1 pandemic Influenza virus A/California/09/2009 (CA09). (C) The hemagglutinin ectodomain is composed of two domains: a globular head and narrowing stalk or stem region. The HA stalk-bnAb epitope (referred throughout as the “Group 1 bnAb epitope”) is depicted in yellow. HAΔstem contains the I45R, T49R substitutions that sterically present access to this site.
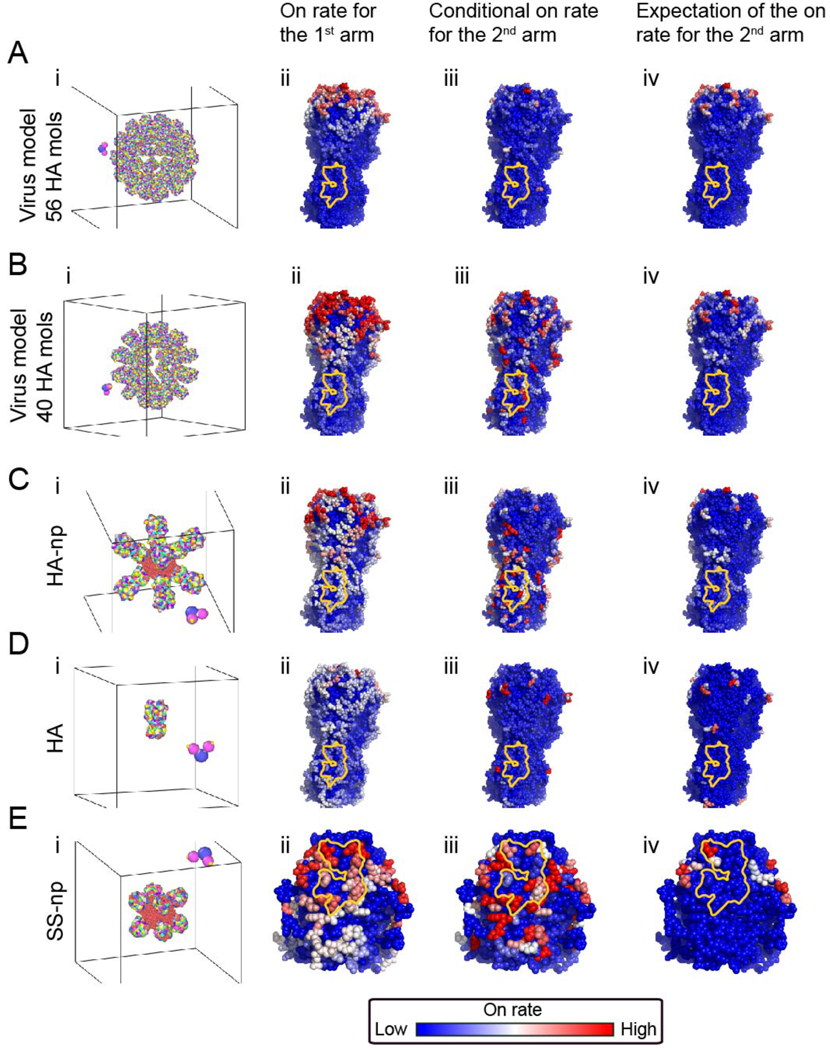
Figure 2. B cell receptor on-rate to HA epitopes in silico.
(A) Influenza virus. The virus model has 56 HA molecules at a spike spacing of 12.5 nm. (B) The virus has 40 HA molecules at a spike spacing of 14.8 nm. [Measured spike spacing on influenza is 14 nm (Harris et al., 2013)]. (C) HA-np. (D) HA trimer alone. (E) SS-np. For each immunogen geometry (A-D), a detailed atomistic structure of the immunogen is coarse-grained and presented in rainbow colors (panels i). Here every colored bead on the immunogen is a residue, representing a different HA epitope (184 different possible sites on trimeric HA and 67 possible sites on the trimeric stem). The B cell receptor structure is presented as the Fc (blue bead), and two antigen binding sites (magenta beads) Panels ii-iv within A-D, depict coarse-grained simulations of BCR first arm followed by second BCR arm binding to these residues. The on-rate to red sites is high, intermediate to white sites, and low for blue sites and was the average of multiple simulations (see Eq.(5)). Second arm binding was measured as on-rate to the second site, given that the first site is already bound (see Eq.(6)) and the expectation of the 2nd binding on-rate (see Eq.(7))(= total rate for the binding of the second arm from the beginning of the simulation, multiplied by the probability of such an event). The Group 1 bnAb epitope is marked in yellow. Germinal center formation and B cell proliferation require threshold affinity to the Ag which allows its capture and downstream MHCII presentation to T cells. The on-rates shown in panels ii, iii are used, along with the binding energy of each B cell, to compute the probability of this process for each immunogen, and each B cell clone targeting an epitope (see “Antigen Capture” section in the SI and Figure S7). Thereby, the on-rate is translated to the physiologically relevant quantity as the amount of captured antigen. Intuitively, low on-rate = small amount of captured Ag; high on-rate = large amount of captured Ag.
In order for germinal centers to form and for B cells to proliferate therein, the B cells require a threshold affinity to the antigen that would allow for antigen capture and MHCII presentation to T cells. The on-rates estimated from the MD simulations are used to compute the probability of this process. Furthermore, the initial affinity of the B cells was chosen such that some B cells manage to capture antigen. The on-rates estimated from the MD simulations are used to compute the probability of a B cell clone to capture antigen (see “Antigen Capture” section in the SI). In this way, the physiologically relevant quantity, the on-rate, can be translated to the amount of captured antigen. In this view, low on-rate = small amount of captured Ag while high on-rate = large amount of captured Ag (see “Antigen Capture” section in the SI).
For influenza virus (Figure 2A–i, B–i), we found that the on-rate for the first BCR arm was high to head epitopes (Figure 2A–ii, B–ii), and because of the small spacing/tight packing between adjacent HAs, some head-targeting BCRs were capable of rapidly forming bivalent interactions (Figure 2A–iii, B–iii). As a result, the average rate for such bivalent interactions at the head was high (Figure 2A–iv, B–iv), consistent with previous reports for Abs targeting the receptor-binding site on HA (Ekiert et al., 2012; Lee et al., 2012). The tight packing of surface glycoproteins also severely reduced the ability of the first BCR arm to penetrate and interact with epitopes on the stem domain, particularly the Group 1 bnAb target, lowering the BCR on-rate for this site (Figure 2A–ii). However, when the first arm of the BCR did engage the bnAb epitope (on-target), we found that the second arm then gained a high on-rate for an adjacent stem bnAb epitope (Figure 2B–iii). This occurred when the HA spacing matched the natural value reported for the influenza virus (14 nm) (Harris et al., 2013) (Figure 2B–i). Hence, the overall on-rate to the Group 1 bnAb epitope was small compared to other epitopes on virally displayed HA, but our model also indicated that viral geometry at this spike spacing promoted bivalent interactions if the first arm of the BCR was able to first engage the target (Figure 2B–iii).
Upon comparison with HA-np (Figure 2C–i), which is an octameric HA display that was in part engineered to promote steric access to the HA stem region (Kanekiyo et al., 2013), we found that the corresponding on-rate for bnAb epitope targeting was indeed elevated for the first BCR arm (Figure 2C–ii). However, accessibility of the head epitopes on HA-np resulted in higher first arm engagement on-rates for these sites compared to those BCRs targeting the HA stem (compare Figure 2A–ii and C–ii). As with the viral display of HA, second arm binding was actually faster for the stem specific BCRs (Figure 2B–iii, Figure 2C–iii).
We also found similar targeting biases for the free HA trimer (Figure 2D–i), where BCR on-rates were elevated for the HA head domain (Figure 2D–ii). All epitopes in the free trimer are sterically accessible and this was reflected by near-uniform first arm on rates across the surface of HA. The slight preference for the head epitopes was due to the convex shape of the head, compared to the concave stem bnAb epitope. Also, the HA head domain has a higher cross-sectional area due to the geometry of this protein, resulting in increased opportunities for second arm contact, the formation of bivalent interactions, and second arm-driven preference for the HA head region (Figure 2D–iii). Note that the HA trimer contains 15 different epitopes that can be bivalently targeted, HA-np contains an additional 63 epitopes where bivalent interactions occur between different HA trimers (Figure 2C–iii vs. Figure 2D–iii). The geometry of the HA trimer is such that on-target BCRs specific to the bnAb epitope cannot form bivalent interactions on the same HA trimer. Hence, when presented on the FDC it will be more difficult for bivalent binding to occur for HA trimers as compared to the multimerized immunogens.
MD simulations using SS-np (Figure 2E–i) revealed that the absence of the HA head domain had two key consequences for epitope presentation in the nanoparticle context (Figure 2E ii–iv): 1] the preferential engagement of the first arm of the BCR to head epitopes was now not a factor, allowing for near-uniform engagement of essentially all stem epitopes by the first arm of the BCR; and 2] the rapid second arm contacts to stem epitopes, especially to the Group 1 bnAb epitope remained as before. Hence the antigen display geometry of SS-np is predicted to redirect immunogenicity upon HA stem epitopes, and through bivalent interactions, now favor engaging the Group 1 bnAb epitope (Figure 2E–iv).
Immunogenicity heat maps generated by vaccination in silico predict immunodominance hierarchies in vivo
We next studied how antibodies evolved following sequential immunization with our HA antigen geometries. For this, we generated immunogenicity heat maps for HA-epitope targeting on these antigens using our computational model for GC reactions and AM (Figure 3; see also Method Details). In this model, BCRs mutate, interact with FDCs, and can internalize antigens depending upon their free energy for antigen binding. B cells that internalize antigen then compete with other B cells for positive selection. The probability for positive selection depends upon the amount of antigen a given B cell has internalized relative to other B cells. However, BCR mutations alter biochemistry, and hence the intrinsic binding free energy for target epitopes, with mutations more likely to be deleterious. The intrinsic binding free energy changes are further modulated by differential steric effects for B cells targeting different HA epitopes. The results of our MD simulations (Figure 2) are used to incorporate these steric effects into our simulations of GC reactions and AM. We note that our model does not introduce biases in T cell help or skew the efficacy of any one T cell epitope for presentation by MHCII.
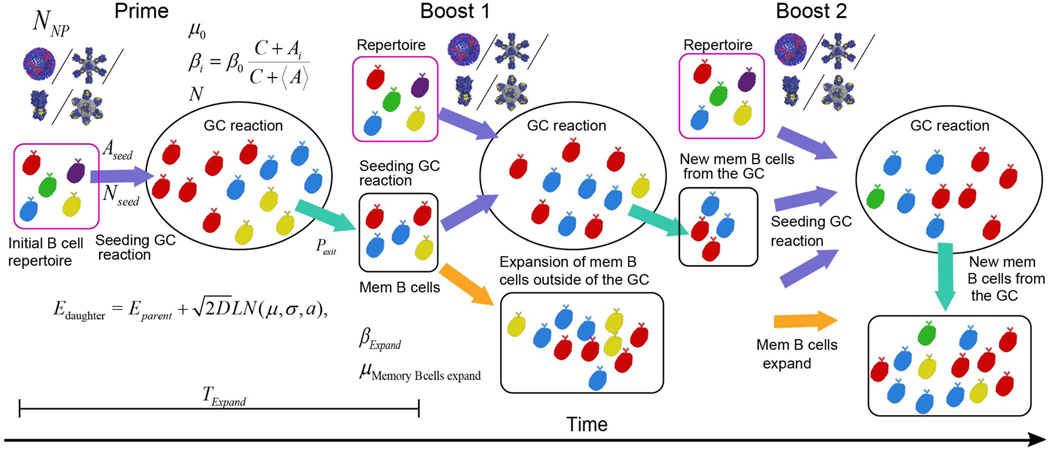
Figure 3. Schematics of the B cell response in silico.
Following a priming vaccination where NNP immunogens are being administered, germinal center reaction (GCR) is elicited. A number Nseed B cells from the repertoire (pink square) seeds (purple arrow) a germinal center (ellipse). Cells must capture at least Aseed Ag molecules to attempt entry. Different B cell clones targeting different epitopes (different colors) compete over Ag for 16 days (TExpand ). The GC has B cells capacity of N (see Eq.(9)). B cells proliferate at a rate βi that depends on the amount of Ag they capture (see Eq.(8)), and die with a death rate μ (see Eq.(9)). Following each cellular division, B cells acquire mutations that change their binding energy to the Ag (see Eq.(1)). The difference between the daughter binding energy (Edaughter) and the parent binding energy (Eparent) is drawn from a log-normal distribution (see Method Details, section “Vaccination in silico”). During the GCR, memory B cells are created as they mature from the GC (cyan arrow). The constant flux of memory B cells depends on their exit probability Pexit. These cells, along with cells from the naïve repertoire, seed the following GC which is elicited following a boost vaccine with an immunogen. Memory B cells which are left outside of the GC expand in an Ag dependent manner with a birth rate βExpand and die with rate μMemory Bcells expand. B cells created at this stage, memory B cells created from the second GC, and cells from the naïve repertoire seed the next GC elicited following the 2nd boost.
We first explored how antigen geometry shaped antibody targeting of different HA epitopes upon using various immunization regimens. To establish the baseline rules by which antigen geometry may regulate on-target BCR responses, we first set the precursor frequency equal for all epitopes, allowing us to investigate the effects of this parameter in an unbiased manner (Part A; Figure 4A–i, B–i, C–i, D–i). We then studied how the resultant immunodominance hierarchies were influenced by the precursor frequency and affinity of the responding germline B cells (Part B; Figure 4A–ii,iii, B–ii,iii, C–ii,iii, D–ii,iii). We then performed the corresponding immunization regimens in vivo, within IGHV1–69 mice (Figure 4A–iv, B–iv, C–iv, D–iv). These animals use the human VH sequence IGHV1–69 but have unconstrained and humanized diversity in the centrally positioned CDRH3 antigen binding loop, mirroring that of humans (Sangesland et al., 2019). The hypervariable CDRH3 provides the majority of diversity (and thus antigen binding potential) to the germline antibody repertoire (Kuroda et al., 2008; Morea et al., 1998; Schroeder and Cavacini, 2010; Shirai et al., 1999; Xu and Davis, 2000).
Figure 4. Immunogenicity heatmaps developed in silico predict immunodominance patterns in vivo.
(A) Influenza virus. (B) HA-np. (C) HA trimer alone. (D) SS-np. HA heatmaps were developed in silico for each HA presentation geometry where the Group 1 bnAb epitope is marked in yellow. (panels i). To account for geometric effects alone, the B cell precursor frequency was made uniform for every epitope on the surface of HA (A-C), or over the stem surface (D) (panels i, left). Next, we report heatmaps following sequential immune challenge in silico, where fi of memory B cells targeting different residues created post-prime (i, box, left), post-boost1 (i, box, middle), and post-boost 2 (i, box, right). To increase the visibility of residue targeted by a small fraction of B cells, the color shows fi1/2 where red sites are targeted by the largest number of B cells color bar. White sites are targeted by an intermediate number, and blue sites are targeted by few or no B cells. (Panels ii-iii). The magnitude of the on-target response elicited by different HA geometries as a function of precursor frequency and affinity (= geometry effect + precursor frequency and affinity consideration). The initial fraction of on-target precursors was expressed as the ratio of on-target germline clones (specific for Group 1 bnAb target), to HA-specific off-target germline clones (=on/off ratio) (see also Method Details “Setting clonal precursor frequency”, Eq.(21), Figure S1D), or stem-specific off-target germline clones (Eq.(20)). The result of sequential immunization in silico plotted as a function of: the average on-target germline affinity (off-rate) relative to the off-target germlines affinity (x-axis), the on/off ratio(y-axis), and on-target antibody response titer (z-axis). The color map (blue to red) corresponds to the number of memory B cells targeting the conserved epitopes elicited by the immunogen. influenza virus (A-ii), HA-np (B-ii), HA-trimer (C-ii), and SS-np (D-ii). (Panel iii) The fraction of B cells targeting the conserved epitopes compared to all memory B cells created during the simulation. (Panels iv) Experimental validation in mice. To test our predictions in vivo, we sequentially immunized with homologous preparations of these same HA presentations within IGHV1–69 humanized mice bearing human-like CDRH3 diversity (Sangesland et al., 2019). Mice were sequentially immunized or infected with NC99 virus (A-iv) or HA-np (B-iv) or HA trimer (C-iv), or SS-np (D-iv) at weeks 0, 3, and 6 and sampled for blood at weeks 2 (post-prime), 5 (post-boost 1), and 8 (post-boost 2). Epitope-targeting was assessed by the binding of serum IgG to HA (black line) vs HAΔstem (red line). Mean and SEM values for reactivity to HA vs HAΔstem are shown for each time point (n=5 animals per regimen). Area under the curve (AUC) values were compared using the AUC comparison method of Hanley and McNeil (Hanley and McNeil, 1983) which includes a correction for curves derived from the same subject and was applied to test the two-sided null hypothesis that the there is no difference between the curve areas (**P<0.03, A-C, or **P<0.002 D).
Part A. Geometry effects in silico.
We initially performed computer simulations of AM using influenza virus or HA-np as immunogens. We studied a sequential immunization regimen using the same HA immunogens and vaccination regimens that we performed previously in vivo (Sangesland et al., 2019) and could be readily evaluated experimentally. To first isolate the role of immunogen geometry in directing AM, we set the number of germline precursors to be equal for all epitopes. Thus, the number of B cells targeting an area was proportional to its surface area (Figure 4A–i left). In this AM computation, antigen specific B cells exiting the prime reaction were able to, as memory B cells, re-seed the GCs formed following sequential antigen exposure, or expand in an Ag-dependent manner outside of the GC. Secondary GCs could also be seeded by the naïve B cell repertoire, consistent with experimental data (Mesin et al., 2020; Shlomchik, 2018). We found that sequential vaccination with influenza virus or HA-np increasingly selected for B cells engaging the off-target (non-Group 1 bnAb epitope) regions of HA upon boosting (Figure 4A–i, B–i). This is presented as the fraction of the B cell response targeting different residues as an immunogenicity heat-map superimposed on HA (Figure 4A–i, B–i). Stem-specific B cells were out-selected in the process, consistent with a first arm BCR on-rate that was preferentially directed against head epitopes (Figure 2A–ii, C–ii). AM simulation with the free HA trimer similarly showed that sequential vaccination with the trimer gradually selected for head specific B cells (Figure 4C–i). Stem-specific B cells were not selected in these in silico GC reactions because lowered antigen valency reduced the probability of B cells engaging in bivalent stem interactions (Figure 2D–iii), and because off-target B cells showed a slight preference in the on-rate of the first arm (Figure 2D–ii).
For sequential immunization with SS-np, we again evaluated immunogen geometry effects by setting B cell precursor frequency equal for all epitopes (Figure 4D–i left) (see Method Details “Setting clonal precursor frequency”). We now observed enhanced targeting of B cell clones with specificity to the stem epitopes (Figure 4D–i), which elevated the number of BCRs specific for the Group 1 bnAb epitope (on-target). In the absence of distracting HA head epitopes, the bnAb epitope comprises a larger area fraction of the stem-only immunogen as compared to immunogens bearing full length HA. As a result, the on-target B cell clones now comprised an effectively larger relative precursor frequency as compared to off-target stem-specific (non-bnAb epitope-targeting) clones (compared to full length HA), and therefore had a higher chance of being recruited to and then positively selected within GC reactions. Furthermore, on-target bnAb specific B cells have an advantage due to their rapid engagement in bivalent stem interactions because of geometric effects (Figure 2E–iii–iv). These effects resulted in refocusing the antibody responses upon the bnAb epitope, which is illustrated in the immunogenicity heat map of the HA stem (Figure 4D–i). Thus, in contrast to the other structural presentations of HA, sequential immunization with SS-np was predicted to focus the serum antibody responses against the Group 1 bnAb site on the HA stem (Figure 4D–i).
Part B. B cell precursor frequency and affinity effects in silico.
Experimentally the strength of an antibody response against a given epitope depends on both the frequency and affinities of the engaging antibody precursors within the germline BCR repertoire (Abbott et al., 2018; Dosenovic et al., 2018; Dosenovic et al., 2019; Sangesland et al., 2019). We performed computer simulations to define how the antigen geometry effects described above are integrated with the effects of these parameters to modulate the immunogenicity of target epitopes on HA.
We found that, for viral HA, HA-np, and HA trimer alone, there was a naturally high frequency of germline B cells specific for epitopes on the HA head, resulting in the immunodominance of this domain (Figure 4A–ii, B–ii, C–ii). Notably, this immunodominance was not offset by on-target B cells even if there was an advantage in germline binding free energy for the on-target clones that engage the Group 1 bnAb epitope. In the case of HA-np (and to a lesser extent viral HA), the fraction of bnAbs emerging from the GC reaction did increase due to strengthened germline affinity of on-target clones (Figure 4B–iii). Our simulations predicted that strengthened affinity to the bnAb epitope alone would not be sufficient to offset immunodistraction by head epitopes due to the high number of head-specific B cell clones [accounting for ~70% of the total number of HA-specific germline B cells (Sangesland et al., 2019)] (Figure 4B–iii). For example, our model suggests that to elicit stem targeting bnAbs at 15% of total antibody response using HA-np, the precursor frequency of on-target stem germline B cells would need to be ~1/4 of the antigen specific B cells to overcome the immunodominance of the head (Figure 4B–iii, boost 2). This suggests that for realistic precursor frequencies, immunization with full length HA-bearing immunogens is unlikely to elicit substantial titers of stem directed bnAbs.
Our computational model indicated the successful elicitation of bnAbs could be achieved upon vaccination with SS-np (Figure 4D–ii–iii), depending upon germline precursor frequency and the affinity for cognate antigen. A minimum threshold affinity for forming a productive GC in vivo has also recently been measured as ~100nM (Mesin et al., 2020). In our model, B cells need to capture a minimal amount of Ag to attempt to seed the GC (see Table S3). We found that the model was qualitatively robust for a range of seeding thresholds (Figure S3). At very high values of that threshold, GCs were not seeded by B cells and no memory B cells were formed.
Part C. Validation in vivo and prediction of bnAb elicitation in humans.
To test our computational predictions, we sequentially immunized IGHV1–69 animals bearing humanized CDRH3 diversity (Sangesland et al., 2019) with these same HA immunogen geometries. The human VH gene IGHV1–69 provides a natural source of germline BCR affinity to the Group 1 bnAb epitope (Sangesland et al., 2019). We found that sequential immunization with both influenza virus and HA-np preferentially boosted antibodies that were off-target (i.e. did not engage the Group 1 bnAb epitope). This was defined as the fraction of IgG in the serum that bound HA but not HAΔstem (I45R, T49R), where I45R + T49R in the latter are substitutions that prevent access to the Group 1 bnAb site (Sangesland et al., 2019; Weaver et al., 2016). We observed a fraction of the post-prime antibody response that was specific for the bnAb target upon immunizing with influenza virus or HA-np (Figure 4A–iv-prime, B–iv-prime), but this specificity was lost upon repeat exposure to our HA immunogens, consistent with our computational model and previous data (Sangesland et al., 2019). These initial on-target responses were not observed for the free HA trimer (Figure 4C–iv). These results are therefore consistent with the computational predictions (Figures 3A–i, B–i, C–i) where a lowered ability to form bivalent interactions on the stem of the free HA trimer, may explain why this immunogen did not show significant post-prime bnAb antibody responses.
We then sequentially immunized IGHV1–69 and WT C57Bl/6 mice with SS-np (Figure 4D–iv, see also Figure S4). We observed refocusing of the serum antibody response upon the otherwise immunologically recessive Group 1 bnAb epitope (~50% of the antigen specific response) in IGHV1–69 animals, but not in WT C57Bl/6 mice, consistent with the prediction of our AM model in silico and our previous work (Sangesland et al., 2019). The harmony between the in vivo data for the IGHV1–69 mice and geometry only predictions in silico results (Figure 4D–i) suggests that immunogen geometry is an important factor, outside precursor frequency considerations. However, the fact that SS-np elicited an off-target response within WT C57Bl/6 mice and an on-target response in IGHV1–69 animals suggested that B cell antibody precursor differences were also deterministic for epitope-targeting by the polyclonal antibody response (Figure S4). We previously noted that the on-target responses observed post prime with influenza virus or HA-np were also IGHV1–69-dependent (Sangesland et al., 2019). Indeed VH usage of IGHV1–69, naturally increases the number of germline B cells specific for the Group 1 bnAb epitope within these animals (Sangesland et al., 2019). To account for this, we used the experimentally measured Group 1 bnAb precursor frequencies within WT C57Bl/6 and IGHV1–69 mice in our computational model of AM [0.82±0.083 % of IgM B cells in WT C57Bl/6 mice and 1.45±0.22 % of IgM B cells in IGHV1–69 mice (Sangesland et al., 2019)]. Our model indicated that the number of mature bnAb-epitope targeting B cells that emerged from the GC reaction depended directly upon germline precursor frequency and affinity for cognate antigen and that bnAbs would be more likely to be elicited in IGHV1–69 than WT C57Bl/6 mice (Figure 4D–ii–iii).
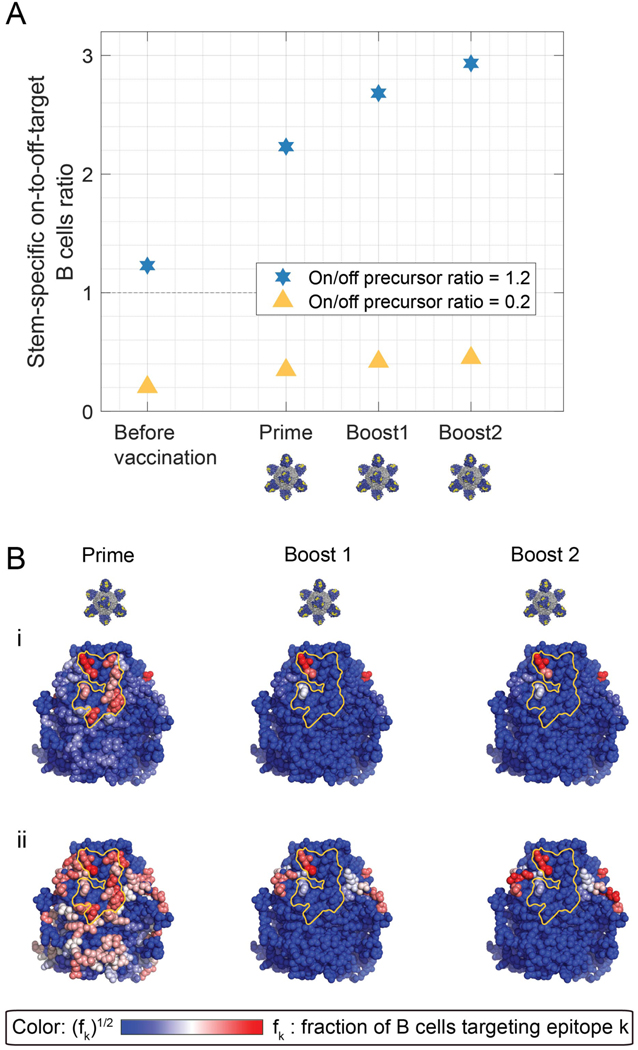
Importantly, we also employed our computational model of AM to account for the Group 1 bnAb precursor frequency recently measured for humans (1.15 ±0.079% IgM B cells) (Sangesland et al., 2019). Notably, our model predicts bnAb elicitation by SS-np at this precursor frequency, as depicted in the corresponding immunogenicity heat maps (Figure 4D–ii–iii, Figure 5).
Figure 5. The Group 1 bnAb B cell frequency in the human antibody repertoire predicts bnAb elicitation by SS-np.
(A) The on-to-off stem-specific ratio of mature B cells (a proxy for Ab titers). The stem-specific on/off ratio was 1.2 (blue hexagram), similar to the stem-specific on/off ratio measured in humans, which is 1.15 (see text “Results - Part C. Validation in vivo”), or 0.2 (yellow triangle). The germline relative affinity was 1. (B) Immunogenicity heatmaps developed in silico. (i) The stem-specific on/off ratio was 1.2. fi is the fraction of memory B cells targeting an epitope of all stem specific memory B cells. To increase the visibility of residue targeted by a small fraction of B cells, the color bar shows fi1/2. (ii) The stem-specific on/off ratio was 0.2. The Group 1 bnAb epitope is marked in yellow.
Influenza virus pre-exposure and the effects of antigen geometry shape the evolution of HA stem specific responses through a ‘vertical’ immunodominance principle
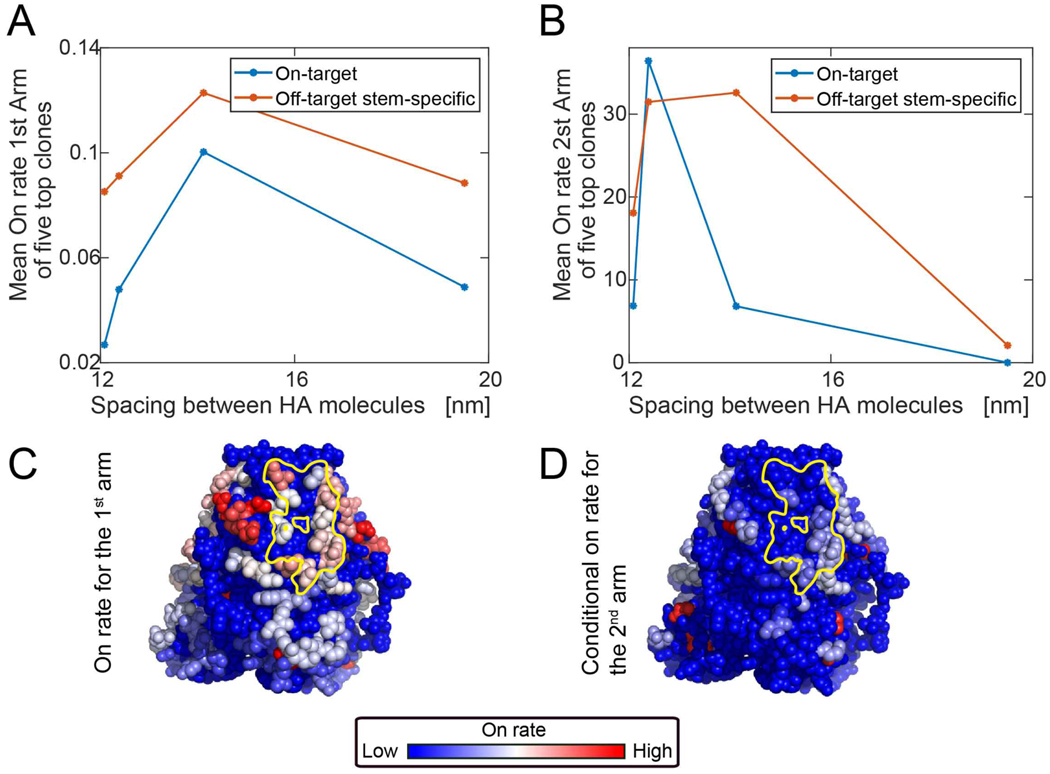
Most adults have already been exposed to the influenza virus, which typically results in B cell memory against off-target or non-neutralizing HA targets (Guthmiller and Wilson, 2018; Henry et al., 2018; Raymond et al., 2018). Avoiding memory recall of these off-target antibody specificities remains a challenge to universal vaccine design (Andrews et al., 2015; Erbelding et al., 2018). To seed B cell memory against HA as imposed by the geometry of influenza virus, we employed MD simulations to generate BCR on-rates for stem bnAb versus non-bnAb targets for increasingly dense arrays of HA at the viron surface. We studied average spacings ranging from 12 to 19.5 nm, where the average spike spacing on influenza virus has been reported as 14 nm (Harris et al., 2013) (Figure 6A–B). We then computed the mean on-rates of the first arm binding for the five highest on-rate B cell clones that engaged either on-target (Group 1 bnAb site) or off target epitopes on HA stem. At low HA density/large HA spacing, the first arm on-rate is low because of the small number of target epitopes (Figure 6A). We found that above a threshold level, decreasing the lateral spacing between HA spikes reduced the accessibility of BCRs targeting the stem region (Figure 6A). We then computed the on-rate for the second arm binding for those highest on-rate clones and found that at more sparse spike spacing, group 1 bnAb site specific clones were incapable of forming bivalent interactions because the distance between the neighboring trimers is too large, while at a tighter spacing, steric constraints prevented most BCR clones from binding bivalently (Figure 6B). Hence, we predict that Group 1 bnAb epitope targeting would be optimal at intermediate spacing between adjacent spikes (Figure 6A–B). Notably, we found that within the stem region, off-target responses near the top of the stem had an affinity advantage over the those engaging the bnAb epitope, which is more proximal to the membrane surface of the viron (Figure 6C–D). We then employed these parameters for on-rates for targeting different epitopes that are pertinent for the virion geometry into our computational model for AM following sequential immunization schemes (Figure 7). We first noted that the sterically imposed immunodominance hierarchy due to virion geometry resulted in a reduced fraction of on-target B cells that could be expanded by subsequent boosting with SS-np (Figure 7A, B–i). Parallel simulations revealed that this ‘vertical gradient’ in affinity advantage on stem epitopes was dampened when the same HA was reconfigured as HA-np and used as the priming antigen (Figure 7A). The open configuration of HA in this immunogen enabled a greater number of bnAb-epitope-targeting B cell clones to participate in the GC reaction following sequential immunization with SS-np in silico (Figure 7B–ii).
Figure 6. On-rate of the BCR to the epitopes for different HA spacing on influenza virus.
Coarse-grained MD simulation to estimate the mean first passage time of the antibody to different HA residues by varying spike spacing at the viron surface. [reported value is 14 nm (Harris et al., 2013)] (A) The average on-rate for the first arm for the five clones with the highest first-arm on-rate Average for the top five on-target clones (blue). Average for top five off-target clones (red). (B) The average on-rate for the second arm, given that the first arm is bound for the five clones with the highest first-arm on-rate. On-target (Group 1 bnAb-epitope targeting; blue curve) and off-target (red curve). (C,D) BCR on-rates within the stem region (full virus with 56 HA surface molecules with spike spacing of 12.5 nm). The on-rate of the first arm to red sites is high, intermediate to white sites, and low for blue sites and was the average of multiple simulations (see Eq.(5)). The Group 1 bnAb epitope is marked in yellow. Second arm binding was measured as on-rate to the second site, given that the first site is already bound (see Eq.(6)).
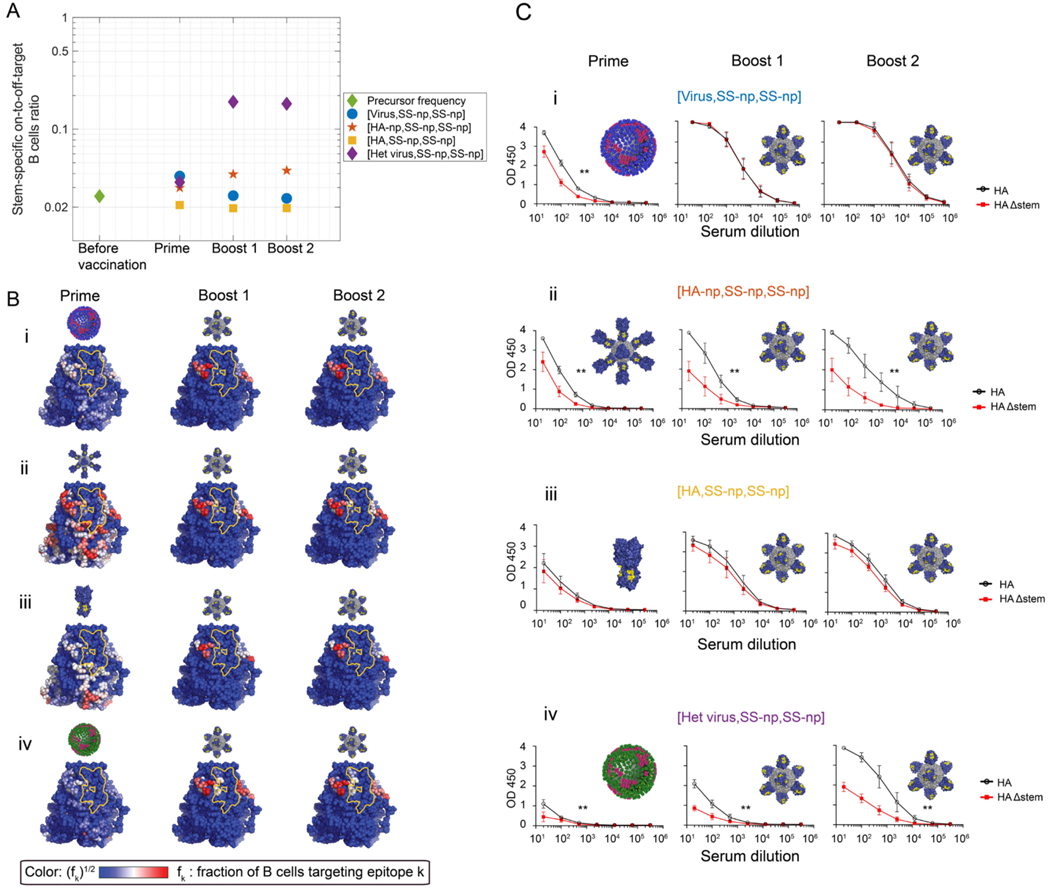
Figure 7. The geometry of influenza virus shapes the pre-existing immunity by establishing a ‘vertical’ immunodominance effect, which can be overcome by the presence of human B cell memory to the 2009 H1N1 pandemic influenza virus.
(A) In silico immune exposure schemes where the prime is one of the following: NC99 H1N1 virus (strain matched to SS-np) (blue full circles); HA-np (red pentagram); HA trimer (yellow squares); or heterologous virus (CA09) (purple diamond). SS-np was then sequentially immunized (boost 1 and then boost 2) following this prime. Depicted is the on-to-off stem-specific ratio of mature B cells (a proxy for Ab titers) elicited following each regimen. This ratio is also shown prior to immune challenge (green diamond). (B) Immunogenicity heatmaps for the 67 available stem epitopes when the following priming agents preceded sequential immunization with SS-np: (i) NC99 virus (strain matched to SS-np); (ii) HA-np; (iii) HA trimer (yellow squares); and (iv) the heterologous 2009 H1N1 pandemic virus (CA09). The stem-specific on-to-off-target ratio was 1.2, similar to the stem-specific on/off ratio measured in humans which is 1.15 (see text “Results - Part C. Validation in vivo”) (Sangesland et al., 2019). is the fraction of memory B cells targeting an epitope of all stem specific memory B cells. To increase the visibility of residue targeted by a small fraction of B cells, the color bar shows (blue = low, white = intermediate, red=high). The Group 1 bnAb epitope is marked in yellow. (C) Performing these same immunization regimens in IGHV1–69 mice. Mice were primed with NC99/CA09 virus or HA-np or HA trimer at week 0, and then sequentially immunized with SS-np at weeks 3 and 6. Blood was collected at weeks 2 (post-prime), 5 (post-boost 1), and 8 (post-boost 2). Epitope-targeting By the serum antibody response at each time point was measured by the binding of serum IgG to HA (black line) vs HAΔstem (red line); mean and SEM are shown. Mean and SEM values for reactivity to HA vs HAΔstem are shown for each time point (n=5 animals per regimen) and AUC values were compared using the method of Hanley and McNeil (Hanley and McNeil, 1983) which was applied to test the two-sided null hypothesis that the there is no difference between the curve areas (**P<0.02).
To experimentally test the prediction that the influenza virus restricts access to the Group 1 bnAb epitope through a geometrically-imposed vertical gradient in affinity advantage, we primed our IGHV1–69 animals with either NC99 virus or HA-np and then sequentially immunized with SS-np, as we had studied in silico (Figure 7C–i–ii). After priming, both NC99 virus and HA-np stimulated a fraction of bnAb-epitope targeting B cells. We reasoned that if the vertical gradient in affinity advantage was meaningful in vivo then there should be differences in the capacity of subsequent sequential immunization with SS-np (which is matched to the NC99 stem domain) to boost the antibody responses specific for the bnAb site. Notably, we found that SS-np expanded the bnAb-epitope targeting responses primed by HA-np, but not those primed by NC99 virus. In the latter case, SS-np was only able to expand off-target antibody responses on the HA stem (non-bnAb epitope targeting) indicating that the geometry of the virus not only disfavors access to the stem domain (Figures 2,4) but that even within the stem region, a vertical immunodistractive effect further disfavors access to the Group 1 bnAb epitope, as predicted by our in silico studies (Figure 7B–i–ii).
Recent reshaping of the human pre-immune repertoire can be manipulated to offset immunodistractive effects imposed by the geometry of influenza virus.
The 2009 influenza pandemic (CA09) was a critically important event in shaping current human B cell memory to IAV (Guthmiller and Wilson, 2018; Raymond et al., 2018). Due to its dissimilarity to seasonal IAV, CA09 ‘reset’ much of the human B cell memory population, such that HA CA09 remains a major immunodominant antigen in current memory recall responses in humans (Guthmiller and Wilson, 2018; Raymond et al., 2018). We and others have demonstrated that sequential exposure to divergent forms of the same antigen can boost antibody responses against conserved features of that antigen (Guthmiller and Wilson, 2018; Krammer et al., 2018; Wang et al., 2015). Given that much of human immune memory remains specific for CA09 epitopes (Guthmiller and Wilson, 2018; Raymond et al., 2018), we reasoned that subsequent exposure to the stem-only region from a divergent HA displayed as SS-np may be able to overcome the viral geometry-induced effects on memory recall as the shared residues between CA09 and SS-np are primarily restricted to the Group 1 bnAb footprint. Our AM simulations demonstrated that this heterologous immunization approach indeed resulted in enhanced on-target memory B cells specific to the Group 1 bnAb epitope following sequential boosting with SS-np (Figure 7B–iv, C–iv). Upon boosting with SS-np, competition occurred between memory and germline on-target clones and the stem-specific off-target germline precursors specific to the NC99 strain. On-target responses are thus more likely to win this competition, and so priming by CA09 and subsequent boosting with the NC99 SS-np now favored elicitation of bnAbs.
We tested this prediction by first priming our IGHV1–69 animals with a sublethal dose of CA09 and then sequentially immunizing with SS-np (Figure 7C–iv). In contrast to the scenario where we primed with NC99 (matched virus, Figure 7C–i), we now found that SS-np expanded the IGHV1–69-dependent bnAb-epitope targeting response that was initially primed by CA09. Importantly, we have previously shown that CA09 priming followed by SS-np boosting fails to expand Group 1 bnAbs in WT mice, where IGHV1–69 endowed on-target precursors are absent (Sangesland et al., 2019). Collectively our results indicate that an immunoreactive fraction of current human B cell memory (Guthmiller and Wilson, 2018; Raymond et al., 2018) may be poised to enable expansion of IGHV1–69-dependent Group 1 bnAbs via vaccination with SS-np, and overcome the vertical immunodistractive effects otherwise imposed by influenza virus.
The in silico model does not distinguish between different GC seeding scenarios.
Currently, the degree to which memory versus germline B cells seed secondary GCs following sequential antigen exposure is under study (Mesin et al., 2020; Shlomchik, 2018). We find that our computational model flexibly accounts for all modes of GC seeding and memory B cells expansion wherein GCs are seeded by both memory and naïve B cells, with or without memory B cell expansion, and by naïve cells alone with memory B cells expansion (Figure S5, S6) (see also “Method Details”, subsection “Vaccination in Silico”). For certain parameter regimes, all the models yield similar qualitative results.
Discussion
The antibody repertoire is equipped with diversity that enables complementarity to essentially any antigen (Schroeder and Cavacini, 2010; Xu and Davis, 2000). However, humoral immunity is often underscored by dominant versus recessive responses to different epitopes on the same antigenic surface, a feature that some pathogens, including influenza virus, appear to have manipulated to ensure immune-distraction away from conserved sites of vulnerability (Altman et al., 2018; Altman et al., 2015; Peterhoff and Wagner, 2017). In these cases, the physicochemical basis for low-frequency targeting has been unclear, meaning that the resultant immunodominant off-target antibody responses have proven difficult to redirect through vaccination (Krammer et al., 2018; Tan et al., 2019; Wu and Wilson, 2017; Zost et al., 2019). In this study, we combined a computational model of antibody AM and MD simulations to define the molecular basis for immunodominance hierarchies that underscore humoral responses against natural and engineered displays of influenza HA, the current seasonal vaccine antigen. We applied this model to generate ‘immunogenicity heat maps’ that accurately predicted patterns of immune-distraction in vivo. This knowledge then provided a framework for rationally applying immunogen presentation and display principles to refocus antibody responses upon a normally immunologically recessive but functionally conserved bnAb target on Group 1 IAVs.
Our immunogenicity heat maps depend upon three key parameters: steric accessibility, BCR affinity, and antibody precursor frequency within the germline B cell repertoire. Beginning with the structure of influenza virus, we found HA presentation by this format favored germline recognition and memory recall of non-bnAb targeting antibody sequences, which was consistent with the immunological subdominance of the HA stem observed following infection by influenza virus (Altman et al., 2015; Angeletti et al., 2017; Jegaskanda et al., 2013; Tan et al., 2019). Experimentally manipulating antibody precursor frequencies within the germline repertoire can alter downstream antibody targeting profiles (Abbott et al., 2018; Dosenovic et al., 2018). However, when precursor frequency was increased for the Group 1 bnAb target (as endowed by the usage of the human antibody VH gene IGHV1–69 (Sangesland et al., 2019)), immunodistraction by virally displayed HA remained in force and prevented the productive vaccine-induced expansion of the VH endowed bnAb precursors following sequential exposure to this antigen geometry. This was consistent with our previous findings (Sangesland et al., 2019) and indicates that the virus imposes an immunodominance hierarchy that overwhelms BCRs bearing specify for this bnAb target. Computationally, we found that immune distraction was supported by viral geometry effects that favored BCR on-rates for ‘off-target’ epitopes of the HA head domain which were seeded by first-arm directed antibody interactions. HA spacing on the virus allows group 1 bnAbs to form bivalent interaction. However, because its first-arm on-rate to the epitope was low, its average rate of binding bivalently was also low. By contrast, we found that BCRs targeting the HA head were capable of rapidly forming bivalent interactions. These results are consistent with experimental observations where the BCR is known to engage the epitopes in HA head domain with bivalency as a way to enhance neutralization activity (Ekiert et al., 2012; Lee et al., 2012) whereas such enhancement not been described for engaging epitopes on the HA stem. Notably, the sterically accessible hemagglutinin trimer displayed by HA-np recapitulated these effects both computationally and within IGHV1–69 animals, indicating that the high density of the viral spike protein was not the only component of the immune-distraction principle. Our model indicated that the relatively high number of off-target head-specific precursors is a second factor leading to immune-distraction by the HA head. Computationally, we found that the distraction would be difficult to off-set by increasing precursor affinity for the bnAb target and that a more effective means was to physically remove the distractive residues on HA, a potentially important principle for universal vaccine concepts.
To test this further, we removed the HA head domain in the form of SS-np. As predicted, sequential immunization with this immunogen resulted in the refocusing of serum antibody responses upon the bnAb target, both in silico and in vivo. In both cases, epitope refocusing was dependent on the frequency of the on-target germline B cells, where in vivo this was demonstrated by its reliance on IGHV1–69 endowed bnAb target solutions within the antibody repertoire, as previously described (Sangesland et al., 2019). Collectively, these results provide proof of concept that antibody immunodominance hierarchies can be both modeled and then manipulated to redirect humoral responses upon otherwise immunologically recessive epitopes. Importantly, our computational model of AM further predicted that the bnAb precursor frequency measured within humans would support similar vaccine expansion of this bnAb response, suggesting that SS-np is poised to elicit broadly neutralizing/protective humoral responses from the germline antibody repertoire of humans.
Previous work has suggested that immunological dominance of antibody responses to the HA head region may also be enforced by immunodominant peptides from this domain which intrinsically limits Tfh help to B cells with different target specificities, including to the HA stem (Cassotta et al., 2020; Tan et al., 2019). This same principle is likely an additional factor that is in operation in our system and is not inconsistent with our results. However, our findings also resolve immunodominance effects that are independent of T cell help and have been experimentally validated as causal for group 1 bnAb epitope targeting in vivo. Notably, we have previously exchanged the IGHV1–69 gene for a different human antibody VH sequence (IGHV1–2*02) within our transgenic mice, a manipulation that only changes germline BCR input to antigen recognition (Sangesland et al., 2019). This results in the loss of Group 1 bnAb stem epitope-targeting by the serum antibody response, as elicited by SS-np (where the HA head is absent) and by the full-length HA immunogens of the present study. Hence, we can assign a causal relationship between the vaccine-elicited immunodominance hierarchies and BCR input to antigen recognition in our system. Nevertheless, we stress that both our experimental and computational results do not preclude a contribution of Tfh to immunodominance patterns, particularly when the HA head is present.
Influenza virus has long been predicted to enforce immunological subdominance of HA stem via a dense array of spike proteins presented at the virion surface (Nabel and Fauci, 2010). We found that this HA spacing parameter imparted a geometric effect that was critical in shaping the pre-immune repertoire and subsequent memory recall in response to SS-np. This is important because most adults bear pre-existing B cell memory to HA that was imprinted by prior infection and/or vaccination, a complicating factor that can profoundly alter the immune response against a subsequent influenza vaccine (Andrews et al., 2015; Andrews et al., 2017). Our computational model of AM showed that in contrast to the pre-immunity seeded by sterically accessible HA-np, pre-exposure to virally displayed HA generated B cell memory that was both globally biased for HA head epitope specificities, and also target-biased within the remaining subdominant anti-stem responses. Within the stem domain, the dense lateral packing of viral HA predisposed responses toward the more vertically accessible stem epitopes, which were situated further away from the membrane proximal bnAb target. As a result, subsequent immunization with SS-np expanded off-target stem responses from virally seeded immune-memory. These data were observed both in silico and within our IGHV1–69 vaccine model, demonstrating that even within the immunologically recessive anti-stem immunity, the virus geometry favors off-target memory recall.
Importantly, we also found that the current structure of human pre-existing immune memory to influenza virus may also impart solutions to this geometry-based immune distraction phenomenon. The virally seeded off-target recall response was observed when HA-sequences were strain matched (both the virus and SS-np displayed HA from NC99). By contrast, the pre-existing immune repertoire of humans has been shaped by non-matching influenza viruses, in particular the 2009 H1N1 pandemic strain (CA09). Due to its antigenic dissimilarity, this pandemic strain has partially reset current clinical pre-immunity such that HA from CA09 still represents an immunodominant target within human B cell memory (Guthmiller and Wilson, 2018; Raymond et al., 2018). We and others have also demonstrated that sequential exposure to sequence-variant forms of the same antigen can promote boosting on conserved antigenic features, including otherwise immunorecessive vaccine targets (Guthmiller and Wilson, 2018; Krammer et al., 2018; Wang et al., 2015). Accordingly, we hypothesized that B cell memory seeded by CA09 may be dissimilar enough from NC99 in sequence space to enrich memory recall on only the ultraconserved features (namely the group 1 stem bnAb epitope) when immunized with SS-np. Our computational model of AM, followed by animal experiments to test predictions, demonstrated that this was indeed the case, where an IGHV1–69-dependent serum bnAb response could now be expanded through SS-np-elicited recall of on-target memory that was originally seeded by infection with CA09, consistent with previous results (Sangesland et al., 2019). We therefore suggest that SS-np may also be effective as a selective booster of stem bnAb responses in adult humans bearing immunological memory to influenza virus, provided the SS-np is chosen appropriately.
Fundamentally, IGHV1–69 usage provides an intrinsic predisposition to engage the group 1 bnAb epitope, and its frequency within the human repertoire can be considered a proxy for the germline B cells specific for this site. Interestingly, BCR sequencing of several humans showed that their relative fraction of IGHV1–69-on target B cells was similar (Sangesland et al., 2019). VDJ recombination processes could theoretically create endless diversity, thus it is noteworthy that BCR repertoires of different individuals are statistically similar and exhibit convergence. Indeed, some BCRs arise with a much higher probability than random in the repertoires of different zebrafish (Jiang et al., 2011; Weinstein et al., 2009). Similar phenomena have also been noted for TCR repertoires in humans (Elhanati et al., 2018; Pogorelyy et al., 2017). This could suggest that the elicitation probability of stem bnAbs may behave relatively uniformly across the human population if the influenza-reacting BCR repertoire was shown to have such similarities on a population scale.
In summary, our work demonstrates that computational modeling of AM can be applied to define the immunodominance hierarchies enforced by the influenza vaccine antigen hemagglutinin, where the immunological recessive nature of bnAb targets has hampered universal vaccine design efforts. We find that compiling this information into immunogenicity heat maps provides a framework for understanding the molecular nature of the immunodistractive principles in operation, such that they can then be subverted through rational vaccine design. We provide proof of concept for vaccine elicitation of influenza bnAbs in mice bearing human-like antibody diversity. Human vaccine studies will ultimately be needed to test our predictions in vivo. Importantly, our approach is not antigen specific and could in principle be applied to other pathogens.
STAR METHODS
RESOURCE AVAILABILITY
LEAD CONTACT
Further information and requests for reagents should be directed to and will be fulfilled by Daniel Lingwood (dlingwood@mgh.harvard.edu).
MATERIALS AVAILABILITY
There are restrictions on the availability of the IGHV1–69 mice due to an MTA with Bristol-Myers Squibb.
DATA AND CODE AVAILABILITY
Source data are not provided in this paper but are available from the Lead Contact on request.
Original code is publicly available at https://github.com/amitaiassaf/B-cell-Immunodominance-Hierarchies
Scripts used to generate the figures presented in this paper are not provided in this paper but are available from the Lead Contact on request.
Any additional information required to reproduce this work is available from the Lead Contact.
EXPERIMENTAL MODEL
Transgenic Mice
The mice used were of a previously established transgenic model in which VH usage is constrained to user-defined gene segments, while allowing for normal and random recombination with diverse human D and J segments, which generates an antibody CDRH3 repertoire that is similar to humans, both in relation to length distribution and amino acid usage (Sangesland et al., 2019). In this study, either wildtype C57Bl/6 or transgenic mice constrained to the human VH gene IGHV1–69*01 (Sangesland et al., 2019) were deployed. The animals were maintained within Ragon Institute’s HPPF barrier facility and all experiments were conducted with institutional IACUC approval (MGH protocol 2014N000252). In this study, both male and female animals, aged 6–10 weeks, were used.
Methods Details
HA antigen geometries.
We studied four geometrically distinct structurally defined HA ectodomain geometries (Figure 1A–B): 1) HA presentation within H1N1 influenza A viruses (Figure 1A–i) [A/New Caledonia/20/1999 (NC99) or A/California/09/2009 (CA09) (Figure 1B)]; 2) HA presentation as a full length HA trimer arrayed as an 8mer on a ferritin nanoparticle support (HA-np, NC99) (Figure 1A–ii) (Kanekiyo et al., 2013); 3) the trimeric stalk-only region of HA trimer arrayed as an 8mer on the same ferritin nanoparticle support (SS-np, NC99) (Figure 1A–iii) (Sangesland et al., 2019; Yassine et al., 2015); and 4) HA presentation as soluble full-length HA trimer (NC99) (Figure 1A–iv) (Lingwood et al., 2012; Sangesland et al., 2019; Villar et al., 2016; Weaver et al., 2016).
The HA-np and SS-np multivalent 8mers nanoparticles were built to promote B cell crosslinking and antibody immunogenicity. These immunogens were developed and evaluated previously in preclinical models (Kanekiyo et al., 2013; Sangesland et al., 2019; Yassine et al., 2015) and are currently being tested as influenza vaccine candidates within Phase 1 clinical trials [Trial Identifiers: NCT03186781 and NCT03814720].
Deploying the NC99 virus enabled the opportunity to model and then experimentally evaluate how viral geometry vs structurally reconfigured HA geometries/presentations modulated antibody immunodominance hierarchies with respect to a functionally conserved and structurally defined site of vulnerability, the Group 1 bnAb epitope; one of the candidate targets of current universal influenza vaccine efforts (Figure 1). The CA99 virus strain was chosen as it was the most recent influenza immune challenge that reshaped much of the existing human B cell memory to flu (Guthmiller and Wilson, 2018; Raymond et al., 2018).
Vaccination in silico: geometry of HA immunogens and epitope targeting
The first input to our model was an atomistic description of the geometry of our HA immunogens, which we generated from available structural information and pdb files (Gallagher et al., 2018; Weaver et al., 2016). For HA, HA-np, and SS-np, solvent-accessible residues were identified using PyMOL script “findSurfaceResidues” (https://pymolwiki.org/index.php/FindSurfaceResidues), which identifies atoms with a solvent accessible area greater than or equal to 20 Ang2. This procedure results in a uniformly distributed set of residues on the face of the HA surface (Figure S1A). Overall, we identified 184 solvent-accessible epitopes on HA, where 67 were present on the trimeric stem. We applied this epitope identification scheme to all the HA immunogens, and separated the epitopes into three classes (Figure 1): 1] the stem bnAb epitope [targeted by antibodies that are pan-neutralizing for Group 1 IAV (Avnir et al., 2014; Ekiert et al., 2009; Lerner, 2011; Lingwood et al., 2012; Pappas et al., 2014; Sui et al., 2009; Wheatley et al., 2015; Whittle et al., 2014) - yellow patch in Figure 1]; 2] non-neutralizing or off-target residues on the HA stem domain (blue area in Figure 1); 3] off-target on the HA head domain (Figure 1).
We also constructed a simplified model of the influenza virus, in which multiple HA molecules are arranged in a fixed conformation on a sphere of radius equal to 16nm (a value chosen for computational tractability). We then constructed virus models with different number of HAs on their surface to explore the effect of HA spacing, which ranged from 12 to 19.5 nm. The average spacing between adjacent HA on the influenza viral surface has been reported as ~14 nm (Harris et al., 2013).
For each virus model, we computed the spacing between adjacent HA as follows. We first estimated the great-circle distance between the center of a chosen spike at its top to the center-top of other spikes (denoting “average-neighbor-distance”). The HA spike height is 14.2nm (Yamaguchi et al., 2008) and our virus model has a radius of 16 nm. Hence, this is the distance along the sphere of a radius of 30.2 nm. We then computed the average distance to six closest neighboring spikes of the chosen spike. We then choose different spikes and computed the mean of their average-neighbor-distance. At the top of the spike (the head of HA), the average distance between the center of the HAs molecules was 21nm (56 spikes model, Figure 2A) or 23.3nm (40 spikes model, Figure 2B). The diameter of HA is about 8.5nm (Tran et al., 2016). Hence the characteristic spacing between HAs around the head is 14.8nm (40 spikes), or 12.5 nm (56 spikes). We similarly computed HA spacing for the results shown in Figure 6A–B.
We used MD simulations to compute the relative extent to which immunogen geometry affects access to different epitopes for each of the immunogens. This relative access factor becomes an input to the simulations of GC reactions, as it corrects for intrinsic affinities of BCR/antibodies for different epitopes.
The reported packing of spikes on both filamentous influenza (Einav et al., 2020) and spherical influenza (H1N1) is roughly similar with around 1 spike per 100 nm2 (for a spherical virion (Yamaguchi et al., 2008), for a filamentous virus (Tran et al., 2016). Hence, to the first order, our results should be consistent for both forms. The difference in membrane curvature may slightly modify the relative accessibility of BCRs to the stem epitopes.
Vaccination in silico: generation of Immunogenicity ‘heat maps’
Each memory B cells created by the GC simulation targets one of the 117 solvent-accessible epitopes on the HA head or one of the 67 epitopes on the stem. The number of B cells specific for an epitope that evolve during AM is used as a proxy for the magnitude of the immune response against that epitope. To create the immunogenicity ‘heat maps’, we colored each epitope on HA proportionally to the magnitude of the immune response against it. Red residues are highly targeted, while blue ones are targeted by few or no memory B cells. Thus, the heatmaps provide a visual depiction of immunodominance hierarchies, and how they are differentially manipulated by different immunogens and vaccination protocols.
Vaccination in silico: a coarse-grained model of the antibody and the immunogens
To estimate the encounter probability and rate of different residues on the surface on the NP by the BCR, we employed coarse-grained MD simulations. The B cell receptor is represented using 8 beads (see Figure S1). We used a coarse-grained model of the Ag and BCR (see Figure S1). In (De Michele et al., 2016), a model of the BCR was suggested, built from ellipsoids and spheres. Here, we built our BCR model using spheres of different sizes to approximate the same dimension and flexibility of the Ab. The MD simulation system is composed of different beads (see Table S1). This size of the beads was chosen such that the distance between the two Fabs is approximately 15nm and the length of the BCR arm is 7nm (Klein and Bjorkman, 2010). The size of the Fc region is chosen to be 5nm (Leake, 2013) (see Table S1). To construct the 7nm arm we use 3 beads (types 4,5,6 – Figure S1B–C, Table S1), where nearest-neighbor beads are connected with rigid bonds of length 1.75nm. Bead type 4 (arm hinge) is connected to bead 3 (Fc hinge) by a rigid bond of length 1.75nm. The epitope bead (type 7, Table S1) was chosen to have the same size as the Fab beads (1.75nm) (Table S1). The beads along the arm (type 4,5,6) are on a straight line (no kink), and the middle bead (type 6) is larger, to approximate the elongated ellipsoid shaped arm of the BCR (De Michele et al., 2016).
The average angle between the two arms of the BCR fluctuate with a mean of 120 degrees and obeys the harmonic potential
| (1) |
with θ0 =0.66radians and κ=10kb T/ radian2, resulting in a relatively rigid model of the BCR (De Michele et al., 2016).
The system is integrated using a Langevin thermostat under “fix nve” to perform performs Brownian dynamics simulations (see https://lammps.sandia.gov/doc/fix_langevin.html).
The Fab bead interacts with the respective epitope bead via the Morse potential
| (2) |
where r0 =1.75nm which is the distance between the Fab bead and an epitope bead at which the LJ energy between them is zero, and the cutoff radius rc = 2.2nm. D0 = 50 is the energy and the bond fluctuation scale α=1nm−1 : the Morse potential only serves to anchor the 1st arm to the epitope allowing the second arm to search for a second epitope. The binding energies of the BCR and the epitope during the AM simulation are determined as described in (“The binding energy of the germline clones”, ”Binding energy to the antigen”, and “Vaccination in silico: B cell epitope targeting and affinity maturation (AM)”).
The beads interact with the Lennard-Jones potential
| (3) |
where ε =1, σi,j is the interaction distance between beads i and j, and the cutoff radius is rc =21/6σi, j. The values of σi,j are detailed in Table S2. The LJ interaction distance σi,j between all beads composing the BCR arm (types 4,5,6), and the epitope bead (type 7) is 1.75nm to construct the 7nm long arm. The LJ self-interaction distance of the BCR arm bead (type 6) was taken to be 4.2nm (Table S1) to maintain an angle of approximately 120 degrees between the arms. The interaction distance of other pairs of beads is the sum of their radii (Table S2).
Estimating the on-rates to the epitopes
The on-rate to each of the residues is estimated using MD simulations. Each simulation runs for a predetermined amount of time and we find the diffusion-limited first passage time of one of the Fabs to the neighborhood of the target residue. The on-rate for the first arm to find an epitope is given by
| (4) |
where kon,1arm,Ep.i is the on-rate estimated from simulation, i, for the BCR to find epitope Ep, and NSim is the number of independent simulations we perform. In a simulation where the BCR does not find its respective epitope we take kon,1arm,Ep.i =0. We perform independent MD simulations to estimate kon,1arm,Ep. for each epitope (28 independent simulations for the HA trimer, 12 for each virus model shown in Figure 6, 14 for the HA-np runs, 14 for the SS-np). To measure the convergence of the on-rates estimated by the MD simulations, we considered the virus model used for the AM simulations (56 HA molecules). For each epitope, we computed the student’s t-test between the on rate computed when taking all MD simulations results, and that estimated when taking only a random subset of half of the MD results . Averaging over all epitopes, we find mean t value of 0.24 for all clones 184 targeting the virus, and a value of 0.32 when taking on the stem clones. In most simulations, the BCR finds its target epitope. We plot the distribution of the number of epitopes as a function of the fraction of simulations where the epitope was found (Figure S1). For HA-np, the BCR finds its target in all simulations for 150 epitopes. In the AM simulation, we take the estimated on-rate for the epitopes to be of kon,1arm,Ep.
The on-rate for the binding of the second arm is given by
| (5) |
where in a simulation where the BCR does not find its epitope we take kon,2arm,Ep,i=0.
We also compute the expectation of the 2nd arm on-rate. This is the inverse of the total time until the 2nd binds from the beginning of the simulation, times the probability of this event occurring
| (6) |
where P1arm,Ep and P2arm,Ep are, respectively, the probability of the first arm and the second arm to find its epitope, as estimated from the simulation.
Vaccination in silico: B cell epitope targeting and affinity maturation (AM)
Numerous computational models of GC reactions and AM have been formulated in the past (Amitai et al., 2018; Chaudhury et al., 2014; Childs et al., 2015; Figge, 2005; Kepler and Perelson, 1993; Meyer-Hermann et al., 2012; Oprea and Perelson, 1997; Wang et al., 2015; Zhang and Shakhnovich, 2010). Our model is a coarse-grained representation of GC reactions, which is aimed toward revealing qualitative mechanistic insights into the effects of different immunogen geometries, germline precursor frequencies, affinities, and pre-exposure to influenza on antibody responses generated upon vaccination. Our predictions are then tested experimentally.
Using rules derived from past experimental studies with single model antigens (Amitai et al., 2018; Victora and Nussenzweig, 2012) we created a computational model of a GC reaction where B cells need to capture a minimum threshold amount of Ag to enter the GC and participate in AM (see Method Details “AM simulation algorithm”). While in the GC, B cells undergo a process of mutation and selection. The AID gene introduces mutations into the B cell receptor (BCR) at a high rate. We modeled the effect of mutation as a change in the interaction energy upon cell division, where one of the daughter cells has the parent affinity and the other daughter has binding energy, which is the summation of its parent’s plus a random number with a given distribution. The changes in intrinsic affinity due to mutations were described as follows
| (7) |
where the affinity of the daughter cell, Edaughter, can be different from the affinity of the parent B cell, Eparent, due to mutation. LN is a log-normal distribution with mean μ, standard deviation σ, and an offset a. It is scaled by with D determining the magnitude of affinity change. The log-normal distribution was selected since mutations are more likely to reduce the free energy of the Ab towards the Ag rather than be beneficial (Kumar and Gromiha, 2006; Zhang and Shakhnovich, 2010). The changes in affinity due to mutation described by Eq.(7) pertain to the intrinsic affinity determined by biochemistry. We assumed that affinity changes due to mutation principally affect the off-rate.
Steric constraints affect the access of antibodies to epitopes and this modifies the on-rate, thus modulating the affinity. To compute the relative magnitude of this effect for different epitopes presented by immunogens with different geometries, we employed MD simulations. In these simulations, a Lennard-Jones potential describes the interactions of antibodies with the immunogen atoms, and a separate Morse-potential is used to model interactions of the antigen binding region of the BCR to its specific cognate epitope (see Table S1). To estimate the steric effects alone, we first assumed that the affinity of Abs to all HA epitopes was equal in the absence of steric constraints. We then used MD simulations (Lammps software) (Plimpton, 1995) to compute the average time for the BCR antigen-binding region (Figure S1B) to find the target epitope for the first time, which is called a “first passage time”. By running simulations multiple times, and then averaging over many simulations, we could estimate the mean first passage time to the epitope. In most of the simulations, the antibody found its target (HA-np 89%, intermediate density virus model 74%, high-density virus 49%, SS-np 84%) (Figure S2). For the HA timer, because of the small number of targets (3 of each epitope, compared to 24 on the nanoparticles), only in 35% of the simulations the BCR finds its target. This translates to a relatively small on-rate for the HA trimer (Eq.(4)). The inverse of the mean first-passage time is the on-rate, and thus we computed the relative on-rates for BCR binding to different epitopes for different immunogen geometries. Taken together with the off-rates and their evolution by mutation as per Eq.(7), we were able to compute how the affinity evolves due to mutations for each epitope when presented in the context of different immunogen geometries (i.e. full virus, HA-np, and SS-np).
During AM, B cells capture Ag that is displayed on follicular dendritic cells (FDC) (Tam et al., 2016; Vinuesa et al.). How much Ag is captured by a B cell was computed by taking account of the BCR affinity and the estimated pulling force of the B cell (Amitai et al., 2018; Wang et al., 2015) (see “Antigen Capture”, Figure S7). After Ag internalization, B cell selection/proliferation in the GC is mediated by T follicular helper cells (Tfhs) (Amitai et al., 2018; Victora and Nussenzweig, 2012; Vinuesa et al.; Wang et al., 2015). The proliferation rate of a B cell depends on the amount of Ag internalized relative to the average number of Ag internalized by other B cells. This reflects competition between B cells for receiving survival signals from Tfhs (Amitai et al., 2018; Wang et al., 2015). If Tfhs are very abundant, all B cells that internalized antigen proliferate at the same rate as there is no competition, as observed in experiments (Victora and Nussenzweig, 2012). We explicitly accounted for the fact that Ag capture gradually depletes Ag from the FDCs. Since B cells need Ag to compete for survival signals from Tfhs and proliferate, fewer B cells receive survival signals at later stages of the GC simulation when Ag is scarce. Hence, Ag depletion provides a natural time scale for the GC reaction to end. For all simulations, the GC reaction was stopped after 16 days. In our model, the mutation and selection process of AM was described by simulating a birth-death process (see Eqs.(8),(9)). The death rate of B cells was fixed because GC B cells are apoptotic without survival signals (Victora and Nussenzweig, 2012).
Using the above approach, we studied how antibodies evolve after priming with an immunogen followed by two boosts (Figure 3). A traditional view of humoral responses is that memory B cells that emerge from primary GCs would be able to reseed GCs upon repeat exposure to antigen (Chaplin, 2010; Crotty, 2015). The net result would be that B cell memory directly contributes to selective pressure within a secondary GC, enabling the further accumulation of antibody mutations and AM. However recent B cell lineage tracing/ B cell experiments in mice indicate that the majority of IgG memory B cells do not re-enter the GC upon sequential antigen exposure (Mesin et al., 2020; Shlomchik, 2018). This data does not preclude reseeding of germinal centers by memory B cells, but only that the proportion of memory and naïve B cells within secondary GCs are likely determined by various factors. These factors would include the frequency of naïve B cells for a particular epitope, the affinity advantage of memory B cells over naïve B cells, etc. Thus, we studied three different scenarios (Figure 3): 1] Both memory B cells and naïve B cells can seed the GC formed during the boost, depending upon their relative Ag affinities and precursor frequencies. Memory B cells can also expand outside the GC in an Ag-dependent manner, where memory B cells that internalize more Ag proliferate faster. 2] Only naïve B cells seed the GC and memory B cells can expand outside the GC in an Ag-dependent manner. 3] The GC is seeded by both naïve and memory B cells, as in model 1 above, but memory B cells do not proliferate outside the GC.
Our GC simulations were carried out with different choices for the precursor frequencies of germline B cells targeting different epitopes, and these choices are described in the context of the results.
We now describe the full, most general, simulation algorithm. In model 3 we take the birthrate and death rate of memory B cells outside the GC to be both zero (see Table S3).
AM simulation algorithm
In the GC, B cells undergo cycles of selection and mutation that result in B cells with receptors that have a higher affinity towards the pathogen. This receptor later becomes an Ab if the B cell differentiates into an antibody-secreting plasma cell. The initial set of B cells that seed the GC is small (up to a few hundred clones (Tas et al., 2016)) comparing to the full size of the B cell repertoire (measured in millions). Since B cell clones target different locations (epitopes) on the antigen (Ag), the initial GC reaction is very diverse in its clonality.
GC formation: A B cell needs to capture at least ASeed Ag molecules to be considered for entry. This reflects the fact that entry to the GC depends on T follicular helper cell (TfhC) mediated signaling. Given that a B cell captured at least this amount, it will compete for entry to the GC with probability PSeed =min{Nseed / NBcell Agcap,1}, where NBcell Agcap is the total number of B cells that managed to capture at least ASeed Ag molecules, and the GC is seeded on average with Nseed cells. The type of cells seeding the GC (memory/naïve) depends on which of the models described in the main text is studied.
Growth phase: B cells proliferate without competition according to a stochastic birth-death process. At each time step (Δt), a B cell proliferates with probability β0Δt and dies with probability μ0Δt. This phase lasts Tgrowth days. The values of these parameters are detailed in Table S3.
- Competitive phase: Our model does not have an explicit transition between the dark and light zone (Victora and Nussenzweig, 2012)– only birth and death rates, which give rise to stochastic dynamics. Thus, B cells proliferate and die with competition according to a stochastic birth-death process. Ag capture determines the proliferation rate while the death rate is Ag independent, and reflects the basal apoptotic state of GC B cells (Table S3). B cells are selected to proliferate based on the amount of Ag they capture. The competitive phase lasts Tcomp days, during which there are many rounds of mutation and selection. In the stochastic simulation, at each time step:
- Ag capture by B cells: At each round of selection/proliferation, a B cell attempts to capture Ag. In the GC, B cells capture antigen by forming a transient immune synapse with follicular dendritic cells (FDCs) (Batista et al., 2001). When a synapse is formed, GC B cells send small protrusions, each containing a small cluster of BCRs (Nowosad et al., 2016) directed at the immune complex (IC) presenting the Ag on the surface of the FDCs (Park and Choi, 2005). The probability of Ag capture success depends on the binding energy to the epitope (Amitai et al., 2018). At the beginning of each GC reaction, the ICs are seeded with a total of NNP nanoparticles, divided equally amongst NIC different immune synapses. Ag that was successfully captured is removed from the immune complexes. Hence, the Ag on the ICs is depleted over time.
- B cell proliferation: The proliferation rate of a B cell i is a function of the number Ai of captured Ag molecules, further modulated through competition for T follicular helper cell (TfhC) signaling. We assume that B cells have to capture at least a threshold amount of Ag (AThrs) to attempt proliferation (B cells that do not capture enough Ag have zero birth rate). It was shown that TfhCs would preferentially interact with B cells that captured more Ag, presumably giving them a stronger proliferation signal. To mimic this competition we assume the birthrate of B cell i to be :
where 〈A〉 is the average amount of Ag consumed by all B cells that captured an amount of Ag larger or equal to AThrs; β0 is the basal birthrate, and C is a proxy for the availability of TfhCs. Hence, the proliferation rate is proportional to the amount of Ag B cells capture and thus to their affinity. The model assumes that the amount of T cell help given to antigen-specific B cells is similar for all the immunogens and is not biased for MHCII presentation of any one particular T cell epitope.(8) - B cell death: To account for the limited capacity of a GC during the competitive phase, we employed a variant of the stochastic logistic growth process (Nåsell, 2001), in which the death rate increases with the overall population size, from a basal rate of μ0 as
Here, N is the population capacity; n=(n1, n1, …, nM) is the vector of cell numbers ni for the M clones such that is the total number of B cells in the GC. 〈β〉 is the average birth rate of B cells that proliferate – those that capture enough Ag. The competitive phase lasts about 16 days in mice (Tas et al., 2016).(9) - B cell mutation: The progeny of a B cell mutates, thus affecting its BCR affinity (see “Vaccination in silico: B cell epitope targeting and affinity maturation (AM)”).
- Exit of memory B cells from the GC: During the simulation of the GC reaction, cells leave the GC with a certain probability Pexit. The cells that exit constitute the memory B cells pool.
- The positively selected can B cells become memory B cells (those that exited the GC – with probability Pexit) and join the B cell repertoire which contains now both germline precursors and mature B cells. Memory B cells expansion (only for models 1,2): Memory B cells that do not participate in the GC reaction would react to Ag by an exponential growth outside the GC in an Ag dependent manner. To model Ag capture, we assume it is presented to the memory B cells by Ag presenting cells and use the same capture model as that we developed for the GC B cells. Memory B cells that have a higher affinity (capture more Ag) and have a higher chance of proliferating, but the process does not depend on TfhCs signaling. Hence, B cells stochastically proliferate, given that they capture at least 100 Ag molecules, with their birth rate given by:
Importantly, memory B cells do not acquire mutations when they expand outside of the GC hence their affinity does not change. These B cells stochastically die with rate μMemory Bcells expand. The expansion phase lasts TExpand days and occurs in parallel to the GC process. The values of these parameters are detailed in Table S3.(10) Antibody titer estimation: We sample the existing B cell population to estimate the amount of antibodies against different epitopes or the number of different memory B cells of different clones.
A random fraction Nseed from the naïve and/or memory pools of B cells is chosen to seed the next GC (see point 1.). Cells that capture more Ag are more likely to seed the next GC reaction. The chosen cells will begin again in the Growth phase (point 2).
The vaccination protocol is composed of three Ag injections: “Prime”, “Boost1”, “Boost2”.Memory B cells that exit “Prime” seed “Boost1”, and memory B cells that exit “Boost1” seed “Boost2”. Thus, we have three consecutive GC reactions.
The binding energy of the germline clones
The initial energies of the clones were taken from the following distributions
| (11) |
where f is the on-target germline relative affinity: binding energy difference compared to the off-target germline B cell clones. f is a free parameter in our model that we vary (see Figure 4A–D panels ii-iii).
Antigen capture
In order for germinal centers to form and for B cells to proliferate therein, the B cells require a threshold affinity to the antigen that would allow for capture and downstream MHCII presentation to T cells. The on-rates estimated from the MD simulation are used to compute the probability of this process. To allow germinal center formation in the simulation, we choose the initial affinity of the B cells so that some B cells manage to capture antigen. Hence, the physiologically relevant quantity, the on-rate, can be translated as the amount of captured antigen. In this view, low on-rate = small amount of captured Ag while high on-rate = large amount of captured Ag.
Antigen encounter and binding by the BCR
We assume here that an arm of a BCR at the tip of a B cell protrusion has a characteristic time τ to find an Ag molecule, after which the protrusion retracts empty. The probability that an arm of a BCR at the tip of a B cell protrusion finds Ag before time τ is
| (12) |
where kon,1arm,Ep is the on-rate for one arm of the BCR to the epitope computed from the MD simulations. This leads to
| (13) |
where p0 is the probability that no Ag is encountered, while p1 is the probability that one of the arms encounters an Ag molecule in this time period.
Binding energy to the antigen
The binding affinity of the BCR to a surface residue on the NP is the ratio between the on-rate, which is estimated from MD simulation and the off-rate which is related to the binding energy with the Ag (EBCR–Ag) through Kramer’s escape from a potential barrier formula: with β = (kBT)−1: kB the Boltzmann constant, T the temperature. K is a coefficient that depends on the shape of the interaction potential (Schuss, 2009). We take K =1, and note that in writing the equation for roff we have assumed that the activation barrier to form the bond is much smaller than the energy gained upon binding. In our AM maturation model, we assume that beneficial mutation contributes to increasing the binding energy.
To capture the Ag, the BCR attached to a protrusion of the B cell applies a pulling force that works against the interactions of the BCR with Ag. We denote the interaction energy required to extract the Ag from the IC by EAg–mem.
The characteristic rupture time depends on the force applied by the B cell (Bell, 1978). The force F does work xbF on the bond, reducing its free energy and increasing the rupture rate to , where roff is the characteristic rate for bond disassociation when no force is present, xb is the distance at which the bond ruptures. The intrinsic rupture rate with no force is estimated by Kramer’s escape from a potential barrier as
| (14) |
where K is a coefficient that depends on the shape of the interaction potential (61). We take K =1, and note that in writing equation (14) we have assumed that the activation barrier to form the bond is much smaller than the energy gained upon binding (EBCR–Ag). F is typically of the order of a few pico-Newtons (Tolar and Spillane, 2014). We assume that each B cell has 20 BCRs. When the immune complex is extracted it contains 100 Ag molecules. Hence, a B cell can extract between 0 and 2000 Ag molecules.
Estimating the antigen capture probabilities
To calculate the result of a capture attempt, we define the capture process of Ag by the BCR as an absorbing Markov chain and estimate the probabilities of the different outcomes (Figure S7A, B). We describe the process with four bits. The first bit corresponds to the bound state of the first arm to the immunogen, the second to the bound state of the second arm with the immunogen, the third to the bound state between the piece of the immunogen to which the first arm is bound to and the IC, and the fourth to the bound state between the piece of the immunogen to which the second arm is bound to and the IC. Thus, 1111 is a state where both arms are connected to the immunogen and all elements of the immunogen are attached to the IC. 0111 is a state where only one arm is connected to the immunogen, while the immunogen is firmly attached to the IC (Figure S7B), 0011 is a state where none of the arms are connected to the immunogen, while the immunogen is fully attached to the IC, 1100 is a state where both arms extracted antigen from the IC, etc. All states are illustrated in Figure S7C. We define the transition probabilities between all states as:
Transition states
where the transition probabilities are
| (15) |
| (16) |
| (17) |
Here, ξ is the off-rate of the Ag from the membrane when two arms are bound and λ is the off-rate when one arm is bound. If we take to be the off-rate when no force is applied, the two off-rates are
| (18) |
k is the arm rupture rate when two arms are bound and r is the arm rupture rate when one arm is bound
| (19) |
where .
The absorbing states are: 1100,1001,0110,0011.
Setting clonal precursor frequency
The simulations estimate the fraction of memory B cells targeting different epitopes depending on the initial clonal frequency. We assume that there are 184 different B cell clones in the mouse which are HA-specific, each targeting a different residue on HA. Figure 4A–i shows all the sites (in white) we consider as epitopes on HA in our model. 13 of the clones bind to different conserved residues (“on-target”). The other 171 clones (“off-target”) bind other residues on the head and stem.
The on-to-off-target ratio represents the relative abundance of cells belonging to the “on-target” clones compared to cells belonging to the “off-target” group. It is computed by dividing the total number of Ag-specific “on-target” germline cells with a total number of Ag-specific “off-target” germline cells.
The stem is targeted by 67 clones, 10 of which are on-target (see Figure 4D–i). The ratio is given by
| (20) |
where #Stem-specific-off-target is the number of germline cells targeting the stem, but not the conserved residues (namely the Group 1 bnAb target). Hence, when the mouse has one copy of each germline, the stem-specific on-to-off-target ratio is 10/ 57 = 0.1754. In the computation for the on-target response for a vaccination with SS-np, we take 7 copies per clone for the on-target clone and change the copy number of off-target clones.
In computing the result of vaccination with the full HA, we make use of the estimated onto-off target ratio of stem specific IgM germline cells in IGHV1–69 mice, which is 1.2 (Sangesland et al., 2019): we assume that there are 7 copies of each on-target clones, and 1 copy of each stem-specific off-target clones. This gives an in-silico on-to-off stem-specific ratio of 1.27. Hence, the ratio of on-to-off-stem-specific clones is fixed, while we manipulate the number of clones targeting the head. We study the result of vaccination as a function of the number of B cells targeting the head
| (21) |
For the number of on-target, off-target stem-specific, and head clones in each simulation, refer to Table S3.
Generation of HA antigen geometries for experimental use
All virus preparations for NC99 and CA09 were grown within ten-day-old embryonated chicken eggs and purified as before (Sangesland et al., 2019) and the HA nanoparticle and trimer immunogens were expressed and purified as described previously (Kanekiyo et al., 2013; Weaver et al., 2016; Yassine et al., 2015). ELISA reagents used to measure the fraction of polyclonal serum IgG responses targeting the Group 1 bnAb epitope versus other epitopes on HA consisted of recombinant HA ectodomain trimers: wildtype HA or and HAΔstem (I45R, T49R), where these amino acid mutations occlude antibody access to the Group 1 bnAb epitope (Sangesland et al., 2019; Weaver et al., 2016) (Figure 1C).
Briefly, 293F cells grown in Freestyle media were transfected with 500 μg/L of plasmids encoding HA, HAΔstem, HA-np, or SS-np using 293fectin™ Reagent. After five days, the culture supernatant was collected, filtered, and gravity-loaded on either Ni Sepharose resin (GE Healthcare) for HA trimers, or Erythrina cristagalli Gel-ECA-Immobilized Lectin (EY Laboratories) for HA-np and SS-np. For purification of HA trimers, the Ni resin was then washed with 20mM imidazole and the protein was eluted in 500mM imidazole. For purification of HA nanoparticles, the ECA resin was washed in PBS and the particles were eluted in 0.2M lactose. All proteins were then separated by size exclusion chromatography (SEC) using an AKTA pure protein purification system (GE Healthcare). HA trimers were then buffer exchanged to PBS via separation on a Superdex 200 10/300 column while HA-np and SS-np were buffer exchanged into PBS via separation on Superose 6 10/300 column.
Immune challenges in mice
For NC99 infection, mice were sequentially infected sublethally (105.4 TCID50 units/ml) and intranasally at weeks 0, 3, and 6 with the virus (Glaser et al., 2007; Sangesland et al., 2019). Blood was collected 14 days after each infection time point. For protein immunogens, the animals were immunized intraperitoneally with 15ug of SS-np or equimolar HA-np or HA in a 100ul inoculum containing 50% w/v Sigma adjuvant, as described previously (Kanekiyo et al., 2013; Sangesland et al., 2019; Yassine et al., 2015). Immunization regimens with geometrically heterologous immunogens were also performed where we first immunized with HA-np and then boosted with SS-np. Similarly, mice were first infected with NC99 (105.4 TCID50 units/ml) or a sublethal dose of the H1N1 pandemic strain A/California/04/2009 (CA09) (105.8 TCID50/ml) at week 0 followed by sequential immunization with SS-np at weeks 3 and 6.
ELISA
Epitope specific antibody responses in the polyclonal vaccine responses of our mice were measured as previously described (Sangesland et al., 2019). Briefly, we coated HA, HAΔstem (I45R/T49R), SS-np, and HA-np protein antigens onto 96 well Nunc MaxiSorp plates at 200ng per well. The plates were blocked (2% BSA in PBS for 1 hour) and then washed with PBST (PBS containing 0.05% Tween 20). The immune sera were then added to each well following initial dilution in PBS at 1:20 and subsequent serial dilution at 1:5. Plates were then washed with PBST and incubated with anti-IgG-HRP (GE Healthcare) following 1:5000 of the secondary antibody in PBS. The plates were again washed and then developed using TMB substrate. After 10 minutes the reaction was quenched with 1N sulphuric acid and then read at 450nm using the Teacan Infinite m1000 Pro microplate absorbance reader (Männedorf, Switzerland). The loading of HA and HAΔstem (NC99 versions) was standardized by reactivity to CH65, an RBS-specific mAb (Whittle et al., 2011). To quantify mAb or serum IgG reactivity to HA vs HAΔstem, area under the curve was calculated using GraphPad PRISM software. The IgG binding to HA but not HAΔstem was defined as the fraction of the polyclonal antibody response specific for the Group 1 bnAb epitope on the HA stem (Sangesland et al., 2019).
Quantification and Statistical Analysis
All statistical analysis was performed using Prism Graphpad software. Sample sizes of animals and specific tests to determine the statistical significance used are indicated in the methods and corresponding figure legends. Data were considered statistically significant at P<0.05.
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Sheep Anti-IgG-HRP | GE Healthcare | Cat#NA931 |
| Bacterial and Virus Strains | ||
| A/New Caledonia/20/1999 (H1N1) | International Reagent Resource | FR-395 |
| A/California/04/2009 (H1N1)pdm09 | International Reagent Resource | FR-371 |
| Biological Samples | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| H1 HA Trimer (NC99) | Produced in house (Weaver et al., 2016) | N/A |
| H1 HA TrimerΔstem (NC99) | Produced in house (Weaver et al., 2016) | N/A |
| H1 HA-np (NC99) | Produced in house (Kanekiyo et al., 2013) | N/A |
| SS-np (NC99) | Produced in house (Yassine et al., 2015) | N/A |
| 293fectin Reagent | Invitrogen | Cat#12347019 |
| Ni-Sepharose excel Affinity Medium | GE Healthcare | Cat#GE17-3712-02 |
| Erythrina Cristagalli (ECA) Immobilized Lectin | EY Laboratories | Cat#A-5901-2 |
| Sigma Adjuvant System | Sigma-Aldrich | Cat#S6322 |
| Tetramethylbenzidine (TMB) | Sigma | Cat#T0440 |
| Critical Commercial Assays | ||
| Deposited Data | ||
| Experimental Models: Cell Lines | ||
| Human: FreeStyle 293F | Thermo Fisher | Cat#R79007; RRID: CVCL_D603 |
| Human: Expi293F | Thermo Fisher | Cat#A14527; RRID: CVCL_D615 |
| Experimental Models: Organisms/Strains | ||
| Mouse: IGHV1-69*01+/+ IgH Restricted Mouse Model with Diverse Human CDRH3 (C57Bl/6 Strain) | Sangesland et al. 2019 | N/A |
| Mouse: C57BL/6 | The Jackson Laboratory | RRID: IMSR_JAX:000664 |
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and Algorithms | ||
| Prism 7 | GraphPad | https://www.graphpad.com; RRID: SCR_002798 |
| Matlab | Mathworks | http://www.mathworks.com/products/matlab/RRID:SCR_001622 |
| PyMol Molecular Graphics System 1.8 | Schrodinger, LLC | http://www.pymol.org/RRID:SCR_000305 |
| LAMMPS: MD simulations work was performed using the LAMMPS molecular dynamics software | Plimpton, 1995 | https://lammps.sandia.gov/ |
| Other | ||
| Superdex 200 10/300 Column | GE Healthcare | Cat#17517501 |
| Superose 6 10/300 Column | GE Healthcare | Cat#17517201 |
| SPF Embryonated Chicken Eggs | Charles River Laboratories | Cat#10100335 |
| 96 well microtiter plates | Fisher Scientific | Cat#439454 |
Highlights.
MD simulations and germinal center modeling map B cell immunodominance hierarchies.
Immunodominance is determined by germline frequency, affinity and antigen geometry.
Distractive pre-existing immunity to influenza virus is shaped by viral geometry.
HA immunogens can be applied to subvert immune-distraction in humanized mice.
Acknowledgments
A.A. and A.K.C. acknowledge support from NIH, grant number 2U19AI057229-16. D.L. was supported by the NIH (R01AI137057, DP2DA042422, R01AI124378), the Harvard University Milton Award, and the Gilead Research Scholars Program. M.S. was supported by the NSF Graduate Research Fellowship Program and an NIH fellowship (F31Al138368).
Footnotes
Declaration of interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abbott RK, Lee JH, Menis S, Skog P, Rossi M, Ota T, Kulp DW, Bhullar D, Kalyuzhniy O, Havenar-Daughton C, et al. (2018). Precursor Frequency and Affinity Determine B Cell Competitive Fitness in Germinal Centers, Tested with Germline-Targeting HIV Vaccine Immunogens. Immunity 48, 133–146 e136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altman MO, Angeletti D, and Yewdell JW (2018). Antibody Immunodominance: The Key to Understanding Influenza Virus Antigenic Drift. Viral Immunol 31, 142–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altman MO, Bennink JR, Yewdell JW, and Herrin BR (2015). Lamprey VLRB response to influenza virus supports universal rules of immunogenicity and antigenicity. eLife 4, e07467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amitai A, Chakraborty AK, and Kardar M. (2018). The low spike density of HIV may have evolved because of the effects of T helper cell depletion on affinity maturation. PLoS Comput Biol 14, e1006408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews SF, Huang Y, Kaur K, Popova LI, Ho IY, Pauli NT, Henry Dunand CJ, Taylor WM, Lim S, Huang M, et al. (2015). Immune history profoundly affects broadly protective B cell responses to influenza. Sci Transl Med 7, 316ra192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews SF, Joyce MG, Chambers MJ, Gillespie RA, Kanekiyo M, Leung K, Yang ES, Tsybovsky Y, Wheatley AK, Crank MC, et al. (2017). Preferential induction of cross-group influenza A hemagglutinin stem-specific memory B cells after H7N9 immunization in humans. Sci Immunol 2, eaan2676. [DOI] [PubMed] [Google Scholar]
- Angeletti D, Gibbs JS, Angel M, Kosik I, Hickman HD, Frank GM, Das SR, Wheatley AK, Prabhakaran M, Leggat DJ, et al. (2017). Defining B cell immunodominance to viruses. Nat Immunol 18, 456–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avnir Y, Tallarico AS, Zhu Q, Bennett AS, Connelly G, Sheehan J, Sui J, Fahmy A, Huang CY, Cadwell G, et al. (2014). Molecular signatures of hemagglutinin stem-directed heterosubtypic human neutralizing antibodies against influenza A viruses. PLoS Pathog 10, e1004103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batista FD, Iber D, and Neuberger MS (2001). B cells acquire antigen from target cells after synapse formation. Nature 411, 489–494. [DOI] [PubMed] [Google Scholar]
- Bell GI (1978). Models for the specific adhesion of cells to cells. Science 200, 618. [DOI] [PubMed] [Google Scholar]
- Cassotta A, Paparoditis P, Geiger R, Mettu RR, Landry SJ, Donati A, Benevento M, Foglierini M, Lewis DJM, Lanzavecchia A, et al. (2020). Deciphering and predicting CD4+ T cell immunodominance of influenza virus hemagglutinin. J Exp Med 217, e20200206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaplin DD (2010). Overview of the immune response. J Allergy Clin Immunol 125, S3–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhury S, Reifman J, and Wallqvist A. (2014). Simulation of B Cell Affinity Maturation Explains Enhanced Antibody Cross-Reactivity Induced by the Polyvalent Malaria Vaccine AMA1. J. Immunol. 193, 2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Childs LM, Baskerville EB, and Cobey S. (2015). Trade-offs in antibody repertoires to complex antigens. Philos Trans R Soc Lond B Biol Sci 370, 20140245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho A, and Wrammert J. (2016). Implications of broadly neutralizing antibodies in the development of a universal influenza vaccine. Curr Opin Virol 17, 110–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crotty S. (2015). A brief history of T cell help to B cells. Nat Rev Immunol 15, 185–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Michele C, De Los Rios P, Foffi G, and Piazza F. (2016). Simulation and Theory of Antibody Binding to Crowded Antigen-Covered Surfaces. PLoS Comput. Biol 12, e1004752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenovic P, Kara EE, Pettersson AK, McGuire AT, Gray M, Hartweger H, Thientosapol ES, Stamatatos L, and Nussenzweig MC (2018). Anti-HIV-1 B cell responses are dependent on B cell precursor frequency and antigen-binding affinity. Proc. Natl. Acad. Sci. U.S.A. 115, 4743–4748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenovic P, Pettersson AK, Wall A, Thientosapol ES, Feng J, Weidle C, Bhullar K, Kara EE, Hartweger H, Pai JA, et al. (2019). Anti-idiotypic antibodies elicit anti-HIV-1-specific B cell responses. J Exp Med 216, 2316–2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einav T, Gentles LE, and Bloom JD (2020). SnapShot: Influenza by the Numbers. Cell 182, 532–532.e531. [DOI] [PubMed] [Google Scholar]
- Ekiert DC, Bhabha G, Elsliger MA, Friesen RH, Jongeneelen M, Throsby M, Goudsmit J, and Wilson IA (2009). Antibody recognition of a highly conserved influenza virus epitope. Science 324, 246–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekiert DC, Kashyap AK, Steel J, Rubrum A, Bhabha G, Khayat R, Lee JH, Dillon MA, O’Neil RE, Faynboym AM, et al. (2012). Cross-neutralization of influenza A viruses mediated by a single antibody loop. Nature 489, 526–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elhanati Y, Sethna Z, Callan CG Jr., Mora T, and Walczak AM (2018). Predicting the spectrum of TCR repertoire sharing with a data-driven model of recombination. Immunol Rev 284, 167–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erbelding EJ, Post D, Stemmy E, Roberts PC, Augustine AD, Ferguson S, Paules CI, Graham BS, and Fauci AS (2018). A Universal Influenza Vaccine: The Strategic Plan for the National Institute of Allergy and Infectious Diseases. J Infect Dis 218, 347–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figge MT (2005). Stochastic discrete event simulation of germinal center reactions. Physical Review E 71, 051907. [DOI] [PubMed] [Google Scholar]
- Gallagher JR, McCraw DM, Torian U, Gulati NM, Myers ML, Conlon MT, and Harris AK (2018). Characterization of Hemagglutinin Antigens on Influenza Virus and within Vaccines Using Electron Microscopy. Vaccines (Basel) 6, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaser L, Conenello G, Paulson J, and Palese P. (2007). Effective replication of human influenza viruses in mice lacking a major alpha2,6 sialyltransferase. Virus Res 126, 9–18. [DOI] [PubMed] [Google Scholar]
- Guthmiller JJ, and Wilson PC (2018). Harnessing immune history to combat influenza viruses. Curr Opin Immunol 53, 187–195. [DOI] [PubMed] [Google Scholar]
- Hanley JA, and McNeil BJ (1983). A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 148, 839–843. [DOI] [PubMed] [Google Scholar]
- Harris AK, Meyerson JR, Matsuoka Y, Kuybeda O, Moran A, Bliss D, Das SR, Yewdell JW, Sapiro G, Subbarao K, et al. (2013). Structure and accessibility of HA trimers on intact 2009 H1N1 pandemic influenza virus to stem region-specific neutralizing antibodies. Proc. Natl. Acad. Sci. U.S.A. 110, 4592–4597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry C, Palm AE, Krammer F, and Wilson PC (2018). From Original Antigenic Sin to the Universal Influenza Virus Vaccine. Trends Immunol 39, 70–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jegaskanda S, Weinfurter JT, Friedrich TC, and Kent SJ (2013). Antibody-dependent cellular cytotoxicity is associated with control of pandemic H1N1 influenza virus infection of macaques. J Virol 87, 5512–5522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang N, Weinstein JA, Penland L, White RA, Fisher DS, and Quake SR (2011). Determinism and stochasticity during maturation of the zebrafish antibody repertoire. Proc. Natl. Acad. Sci. U.S.A. 108, 5348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanekiyo M, Wei CJ, Yassine HM, McTamney PM, Boyington JC, Whittle JR, Rao SS, Kong WP, Wang L, and Nabel GJ (2013). Self-assembling influenza nanoparticle vaccines elicit broadly neutralizing H1N1 antibodies. Nature 499, 102–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepler TB, and Perelson AS (1993). Cyclic re-entry of germinal center B cells and the efficiency of affinity maturation. Immunol Today 14, 412–415. [DOI] [PubMed] [Google Scholar]
- Krammer F, Garcia-Sastre A, and Palese P. (2018). Is It Possible to Develop a “Universal” Influenza Virus Vaccine? Potential Target Antigens and Critical Aspects for a Universal Influenza Vaccine. Cold Spring Harb. Perspect. Biol. 10:a028845, a028845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar MDS, and Gromiha MM (2006). PINT: Protein–protein Interactions Thermodynamic Database. Nucleic Acids Res 34, D195–D198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuroda D, Shirai H, Kobori M, and Nakamura H. (2008). Structural classification of CDR-H3 revisited: a lesson in antibody modeling. Proteins 73, 608–620. [DOI] [PubMed] [Google Scholar]
- Kwong PD, and Mascola JR (2018). HIV-1 Vaccines Based on Antibody Identification, B Cell Ontogeny, and Epitope Structure. Immunity 48, 855–871. [DOI] [PubMed] [Google Scholar]
- Lee PS, Yoshida R, Ekiert DC, Sakai N, Suzuki Y, Takada A, and Wilson IA (2012). Heterosubtypic antibody recognition of the influenza virus hemagglutinin receptor binding site enhanced by avidity. Proc. Natl. Acad. Sci. U.S.A. 109, 17040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerner RA (2011). Rare antibodies from combinatorial libraries suggests an S.O.S. component of the human immunological repertoire. Mol Biosyst 7, 1004–1012. [DOI] [PubMed] [Google Scholar]
- Lingwood D, McTamney PM, Yassine HM, Whittle JR, Guo X, Boyington JC, Wei CJ, and Nabel GJ (2012). Structural and genetic basis for development of broadly neutralizing influenza antibodies. Nature 489, 566–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahanty S, Prigent A, and Garraud O. (2015). Immunogenicity of infectious pathogens and vaccine antigens. BMC Immunol 16, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuire AT, Dreyer AM, Carbonetti S, Lippy A, Glenn J, Scheid JF, Mouquet H, and Stamatatos L. (2014). HIV antibodies. Antigen modification regulates competition of broad and narrow neutralizing HIV antibodies. Science 346, 1380–1383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mesin L, Schiepers A, Ersching J, Barbulescu A, Cavazzoni CB, Angelini A, Okada T, Kurosaki T, and Victora GD (2020). Restricted Clonality and Limited Germinal Center Reentry Characterize Memory B Cell Reactivation by Boosting. Cell 180, 92–106.e111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer-Hermann M, Mohr E, Pelletier N, Zhang Y, Victora, Gabriel D, and Toellner K-M (2012). A Theory of Germinal Center B Cell Selection, Division, and Exit. Cell Rep. 2, 162–174. [DOI] [PubMed] [Google Scholar]
- Montefiori DC, Roederer M, Morris L, and Seaman MS (2018). Neutralization tiers of HIV-1. Curr Opin HIV AIDS 13, 128–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morea V, Tramontano A, Rustici M, Chothia C, and Lesk AM (1998). Conformations of the third hypervariable region in the VH domain of immunoglobulins. J Mol Biol 275, 269–294. [DOI] [PubMed] [Google Scholar]
- Nabel GJ, and Fauci AS (2010). Induction of unnatural immunity: prospects for a broadly protective universal influenza vaccine. Nat Med 16, 1389–1391. [DOI] [PubMed] [Google Scholar]
- Nåsell I. (2001). Extinction and Quasi-stationarity in the Verhulst Logistic Model. J. Theor. Biol. 211, 11–27. [DOI] [PubMed] [Google Scholar]
- Oprea M, and Perelson AS (1997). Somatic mutation leads to efficient affinity maturation when centrocytes recycle back to centroblasts. J. Immunol. 158, 5155–5162. [PubMed] [Google Scholar]
- Pappas L, Foglierini M, Piccoli L, Kallewaard NL, Turrini F, Silacci C, Fernandez-Rodriguez B, Agatic G, Giacchetto-Sasselli I, Pellicciotta G, et al. (2014). Rapid development of broadly influenza neutralizing antibodies through redundant mutations. Nature 516, 418–422. [DOI] [PubMed] [Google Scholar]
- Paules C, and Subbarao K. (2017). Influenza. Lancet 390, 697–708. [DOI] [PubMed] [Google Scholar]
- Peng HP, Lee KH, Jian JW, and Yang AS (2014). Origins of specificity and affinity in antibody-protein interactions. Proc. Natl. Acad. Sci. U.S.A. 111, E2656–2665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterhoff D, and Wagner R. (2017). Guiding the long way to broad HIV neutralization. Curr Opin HIV AIDS 12, 257–264. [DOI] [PubMed] [Google Scholar]
- Petrie JG, and Gordon A. (2018). Epidemiological Studies to Support the Development of Next Generation Influenza Vaccines. Vaccines (Basel) 6, pii: E17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plimpton S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. [Google Scholar]
- Pogorelyy MV, Elhanati Y, Marcou Q, Sycheva AL, Komech EA, Nazarov VI, Britanova OV, Chudakov DM, Mamedov IZ, Lebedev YB, et al. (2017). Persisting fetal clonotypes influence the structure and overlap of adult human T cell receptor repertoires. PLoS Comput. Biol 13, e1005572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raymond DD, Bajic G, Ferdman J, Suphaphiphat P, Settembre EC, Moody MA, Schmidt AG, and Harrison SC (2018). Conserved epitope on influenza-virus hemagglutinin head defined by a vaccine-induced antibody. Proc. Natl. Acad. Sci. U.S.A. 115, 168–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockberg J, and Uhlen M. (2009). Prediction of antibody response using recombinant human protein fragments as antigen. Protein Sci 18, 2346–2355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sangesland M, Ronsard L, Kazer SW, Bals J, Boyoglu-Barnum S, Yousif AS, Barnes R, Feldman J, Quirindongo-Crespo M, McTamney PM, et al. (2019). Germline-Encoded Affinity for Cognate Antigen Enables Vaccine Amplification of a Human Broadly Neutralizing Response against Influenza Virus. Immunity 51, 735–749 e738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder HW Jr., and Cavacini L. (2010). Structure and function of immunoglobulins. J Allergy Clin Immunol 125, S41–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuss Z. (2009). Diffusion and Stochastic Processes An Analytical Approach (New York, NY: Springer-Verlag; ). [Google Scholar]
- Sela-Culang I, Kunik V, and Ofran Y. (2013). The structural basis of antibody-antigen recognition. Front Immunol 4, 302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirai H, Kidera A, and Nakamura H. (1999). H3-rules: identification of CDR-H3 structures in antibodies. FEBS Lett 455, 188–197. [DOI] [PubMed] [Google Scholar]
- Shlomchik MJ (2018). Do Memory B Cells Form Secondary Germinal Centers? Yes and No. Cold Spring Harb. Perspect. Biol. 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sui J, Hwang WC, Perez S, Wei G, Aird D, Chen LM, Santelli E, Stec B, Cadwell G, Ali M, et al. (2009). Structural and functional bases for broad-spectrum neutralization of avian and human influenza A viruses. Nat Struct Mol Biol 16, 265–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Xu T, Wang S, Li G, Wu D, and Cao Z. (2011). Does difference exist between epitope and non-epitope residues? Analysis of the physiochemical and structural properties on conformational epitopes from B-cell protein antigens. Immunome Res 7, 1–11. [Google Scholar]
- Tam HH, Melo MB, Kang M, Pelet JM, Ruda VM, Foley MH, Hu JK, Kumari S, Crampton J, Baldeon AD, et al. (2016). Sustained antigen availability during germinal center initiation enhances antibody responses to vaccination. Proc. Natl. Acad. Sci. U.S.A. 113, E6639–E6648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan HX, Jegaskanda S, Juno JA, Esterbauer R, Wong J, Kelly HG, Liu Y, Tilmanis D, Hurt AC, Yewdell JW, et al. (2019). Subdominance and poor intrinsic immunogenicity limit humoral immunity targeting influenza HA stem. J Clin Invest 129, 850–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tas JMJ, Mesin L, Pasqual G, Targ S, Jacobsen JT, Mano YM, Chen CS, Weill JC, Reynaud CA, Browne EP, et al. (2016). Visualizing antibody affinity maturation in germinal centers. Science 351, 1048–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolar P, and Spillane KM (2014). Chapter Three - Force Generation in B-Cell Synapses: Mechanisms Coupling B-Cell Receptor Binding to Antigen Internalization and Affinity Discrimination In Adv. Immunol, Ploegh HL, ed. (Academic Press; ), pp. 69–100. [DOI] [PubMed] [Google Scholar]
- Tran EEH, Podolsky KA, Bartesaghi A, Kuybeda O, Grandinetti G, Wohlbold TJ, Tan GS, Nachbagauer R, Palese P, Krammer F, et al. (2016). Cryo-electron Microscopy Structures of Chimeric Hemagglutinin Displayed on a Universal Influenza Vaccine Candidate. mBio 7, e00257–00216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Regenmortel MH (2002). Reductionism and the search for structure-function relationships in antibody molecules. J Mol Recognit 15, 240–247. [DOI] [PubMed] [Google Scholar]
- Van Regenmortel MH (2011). Limitations to the structure-based design of HIV-1 vaccine immunogens. J Mol Recognit 24, 741–753. [DOI] [PubMed] [Google Scholar]
- Victora GD, and Nussenzweig MC (2012). Germinal centers. Annu. Rev. Immunol. 30, 429–457. [DOI] [PubMed] [Google Scholar]
- Villar RF, Patel J, Weaver GC, Kanekiyo M, Wheatley AK, Yassine HM, Costello CE, Chandler KB, McTamney PM, Nabel GJ, et al. (2016). Reconstituted B cell receptor signaling reveals carbohydrate-dependent mode of activation. Sci Rep 6, 36298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinuesa CG, Linterman MA, Goodnow CC, and Randall KL T cells and follicular dendritic cells in germinal center B-cell formation and selection. Immunol Rev 237, 72–89. [DOI] [PubMed] [Google Scholar]
- Wang S, Mata-Fink J, Kriegsman B, Hanson M, Irvine DJ, Eisen HN, Burton DR, Wittrup KD, Kardar M, and Chakraborty AK (2015). Manipulating the selection forces during affinity maturation to generate cross-reactive HIV antibodies. Cell 160, 785–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver GC, Villar RF, Kanekiyo M, Nabel GJ, Mascola JR, and Lingwood D. (2016). In vitro reconstitution of B cell receptor-antigen interactions to evaluate potential vaccine candidates. Nat Protoc 11, 193–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinstein JA, Jiang N, White RA, Fisher DS, and Quake SR (2009). High-Throughput Sequencing of the Zebrafish Antibody Repertoire. Science 324, 807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheatley AK, Whittle JR, Lingwood D, Kanekiyo M, Yassine HM, Ma SS, Narpala SR, Prabhakaran MS, Matus-Nicodemos RA, Bailer RT, et al. (2015). H5N1 Vaccine-Elicited Memory B Cells Are Genetically Constrained by the IGHV Locus in the Recognition of a Neutralizing Epitope in the Hemagglutinin Stem. J Immunol 195, 602–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittle JR, Wheatley AK, Wu L, Lingwood D, Kanekiyo M, Ma SS, Narpala SR, Yassine HM, Frank GM, Yewdell JW, et al. (2014). Flow cytometry reveals that H5N1 vaccination elicits cross-reactive stem-directed antibodies from multiple Ig heavy-chain lineages. J Virol 88, 4047–4057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittle JR, Zhang R, Khurana S, King LR, Manischewitz J, Golding H, Dormitzer PR, Haynes BF, Walter EB, Moody MA, et al. (2011). Broadly neutralizing human antibody that recognizes the receptor-binding pocket of influenza virus hemagglutinin. Proc. Natl. Acad. Sci. U.S.A. 108, 14216–14221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu NC, and Wilson IA (2017). A Perspective on the Structural and Functional Constraints for Immune Evasion: Insights from Influenza Virus. J Mol Biol 429, 2694–2709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu JL, and Davis MM (2000). Diversity in the CDR3 region of V(H) is sufficient for most antibody specificities. Immunity 13, 37–45. [DOI] [PubMed] [Google Scholar]
- Yamaguchi M, Danev R, Nishiyama K, Sugawara K, and Nagayama K. (2008). Zernike phase contrast electron microscopy of ice-embedded influenza A virus. J Struct Biol 162, 271–276. [DOI] [PubMed] [Google Scholar]
- Yassine HM, Boyington JC, McTamney PM, Wei CJ, Kanekiyo M, Kong WP, Gallagher JR, Wang L, Zhang Y, Joyce MG, et al. (2015). Hemagglutinin-stem nanoparticles generate heterosubtypic influenza protection. Nat Med 21, 1065–1070. [DOI] [PubMed] [Google Scholar]
- Zhang J, and Shakhnovich EI (2010). Optimality of mutation and selection in germinal centers. PLoS Comput Biol 6, e1000800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zost SJ, Wu NC, Hensley SE, and Wilson IA (2019). Immunodominance and Antigenic Variation of Influenza Virus Hemagglutinin: Implications for Design of Universal Vaccine Immunogens. J Infect Dis 219, S38–S45. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source data are not provided in this paper but are available from the Lead Contact on request.
Original code is publicly available at https://github.com/amitaiassaf/B-cell-Immunodominance-Hierarchies
Scripts used to generate the figures presented in this paper are not provided in this paper but are available from the Lead Contact on request.
Any additional information required to reproduce this work is available from the Lead Contact.