Dynamic Instability from Non-Equilibrium Structural Transitions on the Energy Landscape of Microtubule

SUMMARY

Microtubules are the backbone of the cytoskeleton and vital to numerous cellular processes. The central dogma of microtubules is that all their functions are driven by dynamic instability, but its mechanism has remained unresolved for over thirty years due to conceptual difficulties inherent in the dominant GTP-cap framework. We present a physically rigorous structural mechano-chemical model: dynamic instability is driven by non-equilibrium transitions between the bent (B), straight (S) and curved (C) forms of tubulin monomers and longitudinal interfaces in the two-dimensional lattice of microtubule. All the different phenomena (growth, shortening, catastrophe, rescue and pausing) are controlled by the kinetic pathways for B↔S↔C transitions and corresponding energy landscapes. Different kinetics at minus-end are due to different B↔S↔C pathways imposed by the polarity of microtubule lattice. This model enables us to reproduce all the observed phenomena of dynamic instability of purified tubulins in kinetic simulations.

Graphical Abstract

In Brief

We present a structural mechano-chemical model that explains all the phenomena of dynamic instability of microtubules, including growth, shortening, catastrophe, rescue and pausing at both plus- and minus-ends. This model is based on the hypothesis that all these phenomena are driven by bent-to-straight-to-curved conformational changes of tubulins monomers and interfaces.

INTRODUCTION

Microtubules (MT) are crucial for numerous essential cellular processes, such as mitosis, morphogenesis, and neurogenesis (Akhmanova and Steinmetz, 2015, Desai, 1997, Kirschner and Mitchison, 1986, Liu, 2007). All functionality of MTs is driven by dynamic instability, but its mechanism has remained unresolved despite intensive experimental and modeling efforts of the past three decades (Akhmanova and Steinmetz, 2015, Bowne-Anderson et al., 2013). This has been the bottleneck to further understanding the cytoskeletal MT network, whose mechanism is built on the mechanism of dynamic instability (Akhmanova and Steinmetz, 2015).

Microtubules are hollow cylindrical polymers of α,β-tubulin heterodimers arranged head-to-tail in thirteen protofilaments (PFs), with the plus and minus ends marked by β- and α-tubulins, respectively. Dynamic instability refers to the spontaneous stochastic switching of a MT end between steady-states of growth and shortening (Desai, 1997, Mitchison and Kirschner, 1984), featuring four key phenomena: 1) catastrophe (growth to shortening), 2) rescue (shortening to growth), 3) a metastable pause state (neither growth nor shortening) (Desai, 1997, Walker et al., 1988), and 4) plus/minus-end asymmetry: the plus and minus ends both show full-range dynamic instability, but with very different kinetics (Walker et al., 1988). Characteristic time scales of these phenomena, from the fast shortening (10⁻³ s) to the slow and rare catastrophe (10³ s), span a range of 10⁶. Efforts since the discovery of dynamic instability in 1984 (Mitchison and Kirschner, 1984) have focused on plus-end catastrophe alone, but its mechanism remains unclear (Akhmanova and Steinmetz, 2015, Bowne-Anderson et al., 2013, Desai, 1997, Hill, 1984).

The current conceptual framework on plus-end catastrophe centers on GTP hydrolysis (Hill, 1984, Hill and Carlier, 1983, Mitchison and Kirschner, 1984): GTP-tubulins adopt the straight conformation (S form) observed in stable MTs and GDP-tubulins prefer the curved conformation (C form) observed during rapid shortening. Thus a MT dominated by GDP-tubulins suffers high mechanical stress and is unstable, requiring a cap of GTP-tubulins at the tip (i.e. a GTP-cap) to hold it together (Desai, 1997, Mitchison and Kirschner, 1984). When hydrolysis overtakes growth and eliminates the GTP-cap, catastrophe occurs. Alternatively, the structural cap model identifies the GTP-cap with the slightly curved sheet structures observed at growing plus-ends (Chretien et al., 1995), and the conformational cap model postulated a metastable intermediate state of straight GDP-tubulins (Tran et al., 1997a, Tran et al., 1997b).

Experimental efforts on determining the size and nature of GTP-cap have led to conflicting conclusions (Drechsel and Kirschner, 1994, Caplow et al., 1994, Zhang et al., 2015, Duellberg et al., 2016, Gardner et al., 2011, Odde et al., 1995, Schek, 2007, Caplow and Shanks, 1996, Walker et al., 1991). Early experiments measured the number of GMPCPP-tubulins binding to a MT end, showing that up to three layers of GMPCPP-tubulins is sufficient to prevent catastrophe independent of MT length (Drechsel and Kirschner, 1994, Caplow and Shanks, 1996). This was counter-intuitive because a long MT should require a longer GTP-cap, as the mechanical stress should increase with MT length. In contrast, recent experiments based on growth against an artificial barrier and measurement of EB1-comets suggested long GTP-caps (Duellberg et al., 2016, Schek, 2007). Since these experimental observations are indirect, as it is not yet possible to directly determine the number of GTP-tubulins at a growing plus-end, the length of GTP-cap remains an open question. In addition, recent experiments identified catastrophe as a multi-step process that features aging—the increase of propensity to catastrophe with growth time (Gardner et al., 2011, Odde et al., 1995). In the meantime, structural studies suggested tight coupling between dynamic instability and conformations of tubulin (Nogales et al., 1998, Ravelli et al., 2004, Chretien et al., 1995, Muller-Reichert et al., 1998, Wang and Nogales, 2005, Brouhard and Rice, 2014, Rice et al., 2008, Wu et al., 2009), as articulated in refs. (Kueh and Mitchison, 2009, Rice et al., 2008, Brouhard and Rice, 2014, Zhang et al., 2015), but the mechanism has remained unclear.

Computational models built under the GTP-cap framework have led to diverse mechanisms for plus-end catastrophe (Bowne-Anderson et al., 2013, Bayley et al., 1990, Brun et al., 2009, Flyvbjerg et al., 1994, Hill, 1984, Janosi et al., 1998, Li and Kolomeisky, 2013, Li and Kolomeisky, 2014, Margolin et al., 2012, Molodtsov, 2005, VanBuren, 2005, Zong, 2006). Some assumed spatial patterns that signal catastrophe through the loss of GTP-cap, and ad hoc rules for hydrolysis (Bowne-Anderson et al., 2013). Consequently, catastrophe often appears sensitive to the specific GTP-cap patterns that are difficult to interpret physically (Bowne-Anderson et al., 2013, Brun et al., 2009), whereas the ad hoc rules for hydrolysis often contradict our understanding of chemical kinetics (Bowne-Anderson et al., 2013). The mechanical model by VanBuren et al attributed catastrophe to increase in the tapering of tip structure with growth time (Coombes et al., 2013, VanBuren, 2005), whereas Zakharov et al attributed catastrophe to stochastic fluctuations of the conformation and composition of protofilament extensions at a plus-end (Zakharov et al., 2015). With currently available experimental results, it is not possible to decide which one of these mechanisms might be correct, or if there are other alternatives.

Consequently, all four key phenomena of dynamic instability has remained unclear: plus-end catastrophe is poorly understood (Akhmanova and Steinmetz, 2015); rescue has seen little systematic investigations (Dimitrov et al., 2008); pausing and minus-end dynamic instability have been rarely explored (Strothman et al., 2019). The difficulty encountered by models under the GTP-cap framework originates from their neglect of an essential factor in dynamic instability—the conformational changes of tubulins.

Existing models of dynamic instability assumed that a tubulin dimer changes into the C form instantly after hydrolysis—VanBuren et al argued that it should complete within 10⁻¹² s (VanBuren, 2005). The physical picture underlying this assumption is the induced-fit hypothesis for ligand-induced protein conformational changes (Koshland, 1958). In this hypothesis, a protein exists in the apo form in the ligand-free state (e.g. the C form of GDP-tubulin), but changes to the holo form after ligand binding due to protein-ligand interactions (Fig. 1a). The essence is that a protein exists only in one conformation in each condition: apo form in the ligand-bound state and holo form in the ligand-free state are both unstable. This picture was favored when no experimental techniques can detect protein conformations with small populations, but has been refuted by the overwhelming evidence from NMR relaxation dispersion and single molecule FRET experiments that accumulated since late 1990’s (Boehr et al., 2009, Boehr et al., 2006a, Henzler-Wildman et al., 2007a, Lerner et al., 2018, Henzler-Wildman and Kern, 2007b, Seo et al., 2014). Textbook examples for induced-fit (David L. Nelson, 2004), dihydrolate reductase and adenylate kinase, were shown to populate both apo and holo forms in both ligand-bound and ligand-free states (Henzler-Wildman et al., 2007b, Boehr et al., 2006b, Boehr et al., 2009), directly contradicting the induced-fit picture.

Figure 1:

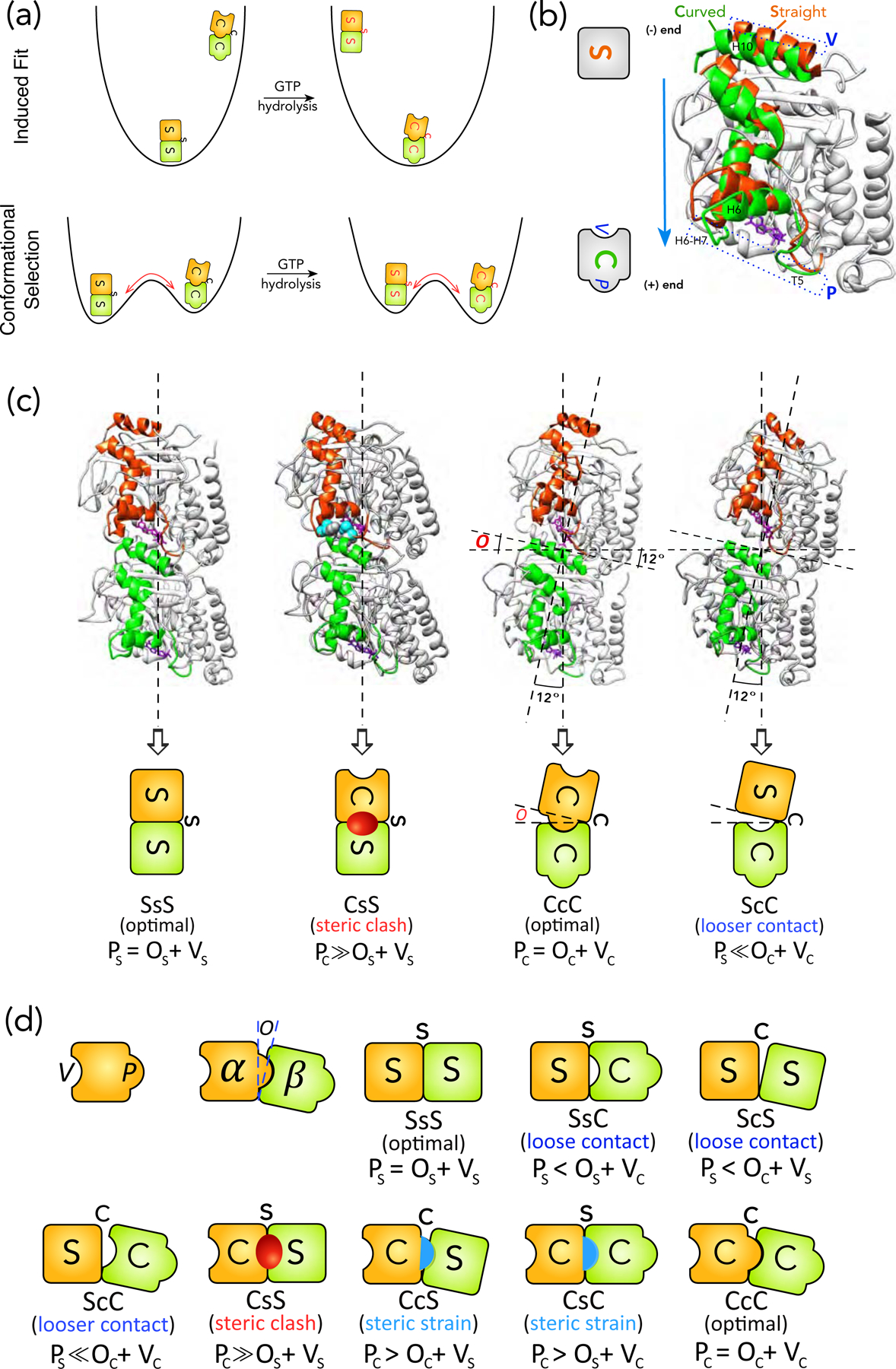
Schematics of structural intermediates in S→C transition. (a) Comparison of the physical pictures of induced-fit and population shift using the energy landscape for S→C transition of a tubulin dimer in a MT as an example. The induced-fit hypothesis suggests that, in the GTP state, the only stable state (i.e. a basin in the energy landscape) is the S form, whereas the C form is unstable. After GTP-hydrolysis, the C form becomes the stable state, whereas S form becomes unstable and will convert into the C form within one vibrational cycle. This is the physical picture behind the assumption by VanBuren et al. The red arrow points to the direction of conformational change. In contrast, the population shift hypothesis suggests that both S and C forms are stable in both GTP and GDP states, but their stabilities change with the nucleotide state. The transition between S and C forms in both nucleotide states need to surmount a free energy barrier and the barrier height determines the time scale of the corresponding transition. (b) Definition of the protrusion (P) and cavity (V) based on comparison between the S and C forms of a tubulin monomer. The S (PDB 1jff) and C (PDB 1sa0) forms of a β-monomer are aligned by their NTD and CTD, following the procedure by Ravelli et al. The structural elements that moves significantly in S→C transitions are highlighted in Orange (S form) and Green (C form) respectively. The rest are colored light Grey. The movement of loops T5 and H6–H7 towards the plus-end side of the monomer leads to P (Blue dashed rectangle at the bottom). The movement of helix H10 leads to V (Blue dashed rectangle at the top). The GDP is shown as stick representation in Purple. The cartoon representations for S and C forms are shown on the left, with both P and V marked. (c) The structures for SsS (PDB 1jff), CcC (PDB 1sa0), CsS and ScC conformations of tubulin dimer and their corresponding cartoon representations (video S3). We use upper case for monomer (i.e. S, B, C) and lower case for interface (i.e. s, b, c) conformations: SsS denotes a dimer or an intra-dimer interface in S form, with the minus-end side on the left. To distinguish an inter-dimer interface, we put hyphens on its two sides: S-s-S indicates an inter-dimer interface. Since hydrolysis only modifies the nucleotide of β-monomer, we use a superscript for the nucleotide state of the β-monomer when necessary: T for GTP and D for GDP (e.g. S-s-S^D represents an inter-dimer interface with a GDP-bound β-monomer). For the two types of lateral bonding, we use “e” for sheet-like and “t” for tube-like bonds respectively (e.g. BeB means two monomers in B form sharing a sheet-like lateral bond). The opening (O) is defined by the angle between the major axes of the two monomers in a dimer, which is 12° for CcC and 0° for SsS conformation. The CsS conformation is created by replacing the α-monomer in a SsS dimer with an α-monomer in C form by aligning their NTDs and CTDs. The residues that have steric clashes with each other (their van der Waals radii significantly overlap) are shown in sphere representation in light Blue (α-monomer) and dark Grey (β-monomer) respectively. In the cartoon for CsS conformation, the Red oval represents the steric clashes. The ScC conformation is created by replacing the α-monomer in a CcC dimer with an α-monomer in C form by aligning their NTDs and CTDs. (d) The cartoon representations for all the eight possible structural intermediates for S→C transition of a tubulin dimer. The Red oval and Blue half oval represent steric clashes and strains between two monomers respectively.

Currently, the prevalent view on ligand-induced protein conformational changes, emerged from intensive experimental and theoretical studies over the past two decades, is population shift on the free energy landscape (Frauenfelder et al., 1991, Boehr et al., 2009, Henzler-Wildman et al., 2007a, Bryngelson et al., 1995). In this picture, apo and holo forms are both stable and in equilibrium with each other even in the ligand-free state (Fig. 1a), but apo form has a higher population (i.e. lower free energy). Ligand binding shifts the stability of these two conformations, so that the holo form has higher population in the ligand-bound state (Fig. 1a). The time scale for inter-conversion between apo and holo forms is determined by the energy barrier separating them. It ranges from microseconds to seconds (Henzler-Wildman et al., 2007a, Benkovic and Hammes-Schiffer, 2003), on par with the time scales of other events (e.g. dimer association, hydrolysis) in dynamic instability. Therefore, it is important to explicitly consider the details of tubulin conformational changes in modeling of dynamic instability.

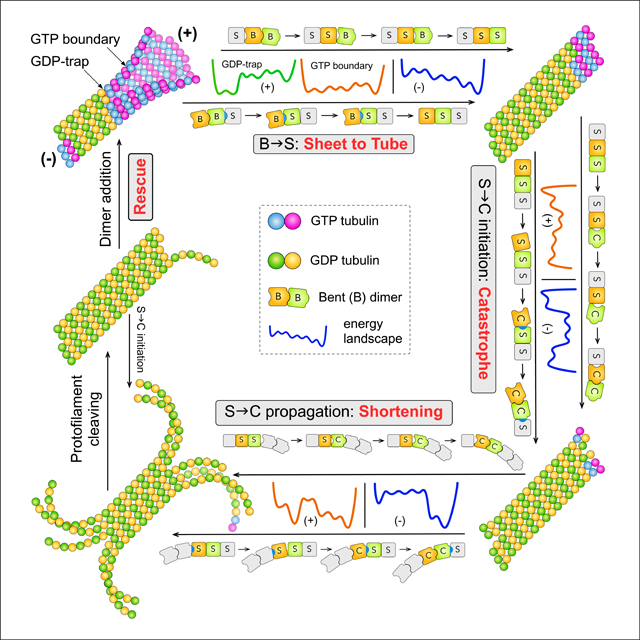
Motivated by this perspective, we developed a structural mechano-chemical model (Fig. 2): dynamic instability is driven by transitions between three polymer structures—bent (B) sheet, straight (S) tube and curved (C) PFs (i.e. B↔S↔C transitions) fueled by GTP hydrolysis, each consisting of monomers and tubulin-tubulin interfaces in matching conformation (i.e. B, S and C forms). Transitions between polymer structures are ordered sequences of conformational transitions of monomers and interfaces. The kinetics of these transitions are controlled by the topology (i.e. the sequence of basins and the ranking of their energies) of the energy landscapes (ELs) of the repeating unit of MT lattice—a dimer with lateral bonds on one side and an inter-dimer longitudinal interface. The sequence of basins on an EL is determined by its corresponding transition pathway (e.g. B→S or S→C), which was inferred from steric constraints of monomer structures and lattice geometry (Figs.1,3). The topology of an EL is determined by the steric rules we inferred from dimer structures (Fig. 1; Table 1).

Figure 2:

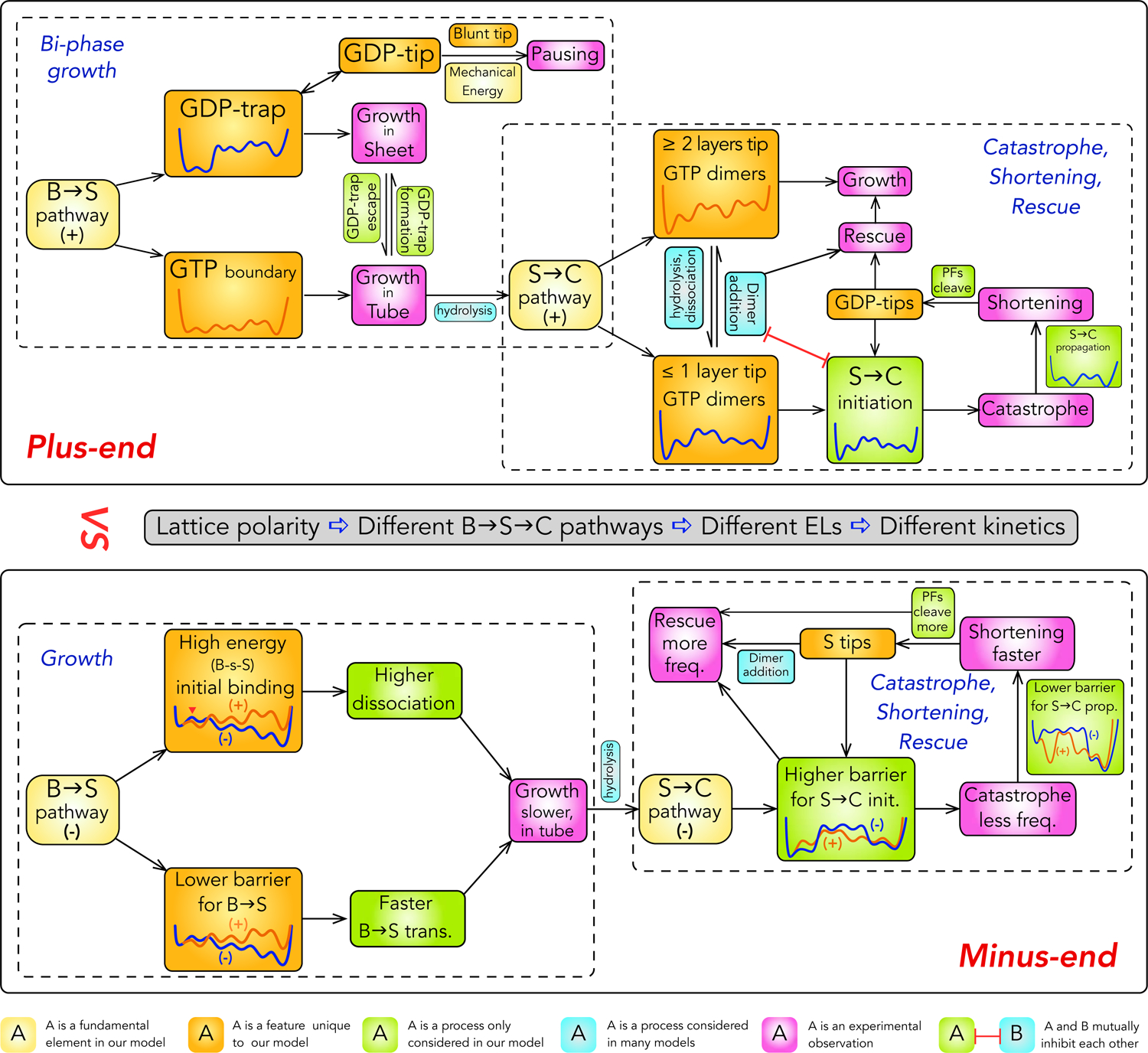
An overview of the current model of dynamic instability. The schematics show the relationships between mechanistic elements and different phenomena of dynamic instability. Curves in boxes are the ELs for the corresponding condition.

Figure 3:

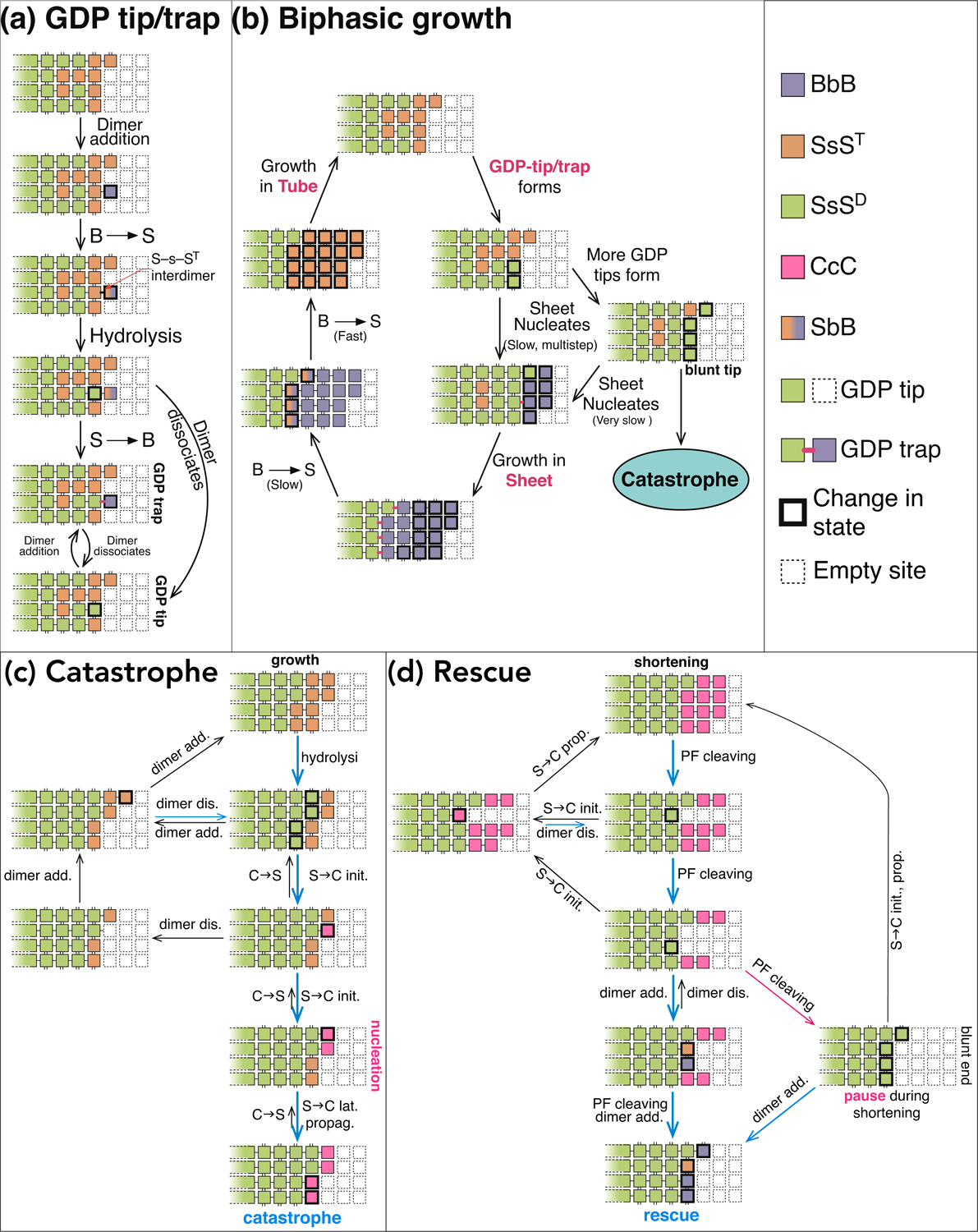
Mechanisms for bi-phase growth, catastrophe and rescue. (a) Schematics for the mechanism for GTP-trap/tip formation. (b) Schematics for the detailed mechanism of bi-phase growth. (c) Schematics for the detailed mechanism of plus-end catastrophe. (d) Schematics for the detailed mechanism of plus-end rescue.

Table 1:

Parameters for the energies of different conformations of monomer and longitudinal and lateral interfaces. E_forbid is an arbitrary large number so that transition from any state to a state with energy of E_forbid has vanishing rate. Since there are no experimental measurements on these properties, they are assumed with two considerations: 1) they need to be in physically reasonable range for the relevant process, 2) they satisfy a list of constraints based on physical principles and relevant experimental observations detailed in the STAR Methods. Within these constraints, they are adjusted to reproduce experimentally measured kinetic data of dynamic instability in Fig. 4.

Monomer or Interface State	Energy of Monomer or Interface State (kcal/mol)	Monomer or Interface State	Energy of Monomer or Interface State (kcal/mol)
B	−10.7	ScSD	−6.8
S	−4.6	ScCT, ST-c-C, ScCD, SD-c-C	−6.1
C	−6.4	CD-c-S, CcSD	−4.9
SsST, ST−s−S, SsSD	−7.4	CcCT, CT-c-C, CD-c-C, CcCD	−8.6
SD−s−S	−5.1	BtB	−2.9
SsBT, ST-s-B, SD-s-B	−1.4	StB	−2.7
SsCT, ST-s-C, SsCD	−7.1	StS	−3.2
SD-s-C	−4.7	BeB	−1.7
SbST, ST-b-S	−5.7	SeB	−1.0
SbBT, ST-b-B, SD-b-B	−1.2	SeS	−2.2
BbST, BT-b-S	−0.74	CeB, CeS, CtB, CtS	0.36
BbBT, BT-b-B	−2.0	(All other states)	Eforbid
ScST, ST-c-S, SD-c-S	−5.0

At the plus-end, the B→S pathway invokes two ELs depending on the nucleotide state at the tube-sheet boundary (Fig. 2). A GDP-bound boundary (i.e. a GDP-trap) causes slow B→S transition and growth in sheet; a GTP-bound boundary causes fast B→S transition and growth in tube (Fig. 3). In addition, a blunt growing tip populated with GDP-tips (i.e. GDP-bound tip dimers; Fig. 3a) leads to pausing due to barrier from mechanical energy. When there is at most one layer of GTP-dimers at a growing end, tip dimers can undergo S→C transition (i.e. S→C initiation) while competing with dimer addition (Fig. 3c). Catastrophe ensues when all tip dimers are in C form, triggering fast shortening enabled by the low energy barriers of S→C propagation (i.e. S→C transitions within PFs). Cleaving of curved PFs during shortening exposes GDP-tips, which leads to either rescue when dimer additions outcompete S→C initiations or resumption of shortening when it is the other way around (Fig. 3d).

At the minus-end, polarity of the MT lattice leads to different B→S→C pathways (Fig. 2). The B→S pathway features a high energy initial state upon binding of a new dimer, causing both higher dissociation rate and faster subsequent B→S transitions, which in turn leads to slower and tube-only growth. The S→C pathway features higher barrier for S→C initiation but lower barrier for S→C propagation, leading to less catastrophe, faster shortening and more rescues.

Further enabled by technical innovations (see Methods), we quantitatively reproduced in simulation all phenomena of dynamic instability for purified tubulins (Fig. 4). The great variability in results across different labs suggests that quantitative kinetics of dynamic instability are sensitive to experimental conditions (Chretien et al., 1995, Gardner et al., 2011, Walker et al., 1988). For a rigorous test, a model should reproduce results from a consistent experimental setup. We simulated the classic experiment by Walker et al (Walker et al., 1988) because it remains the first and only comprehensive quantification of all phenomena of dynamic instability in one experimental setup. Simulations based on our model reproduced all the results in ref. (Walker et al., 1988).

Figure 4:

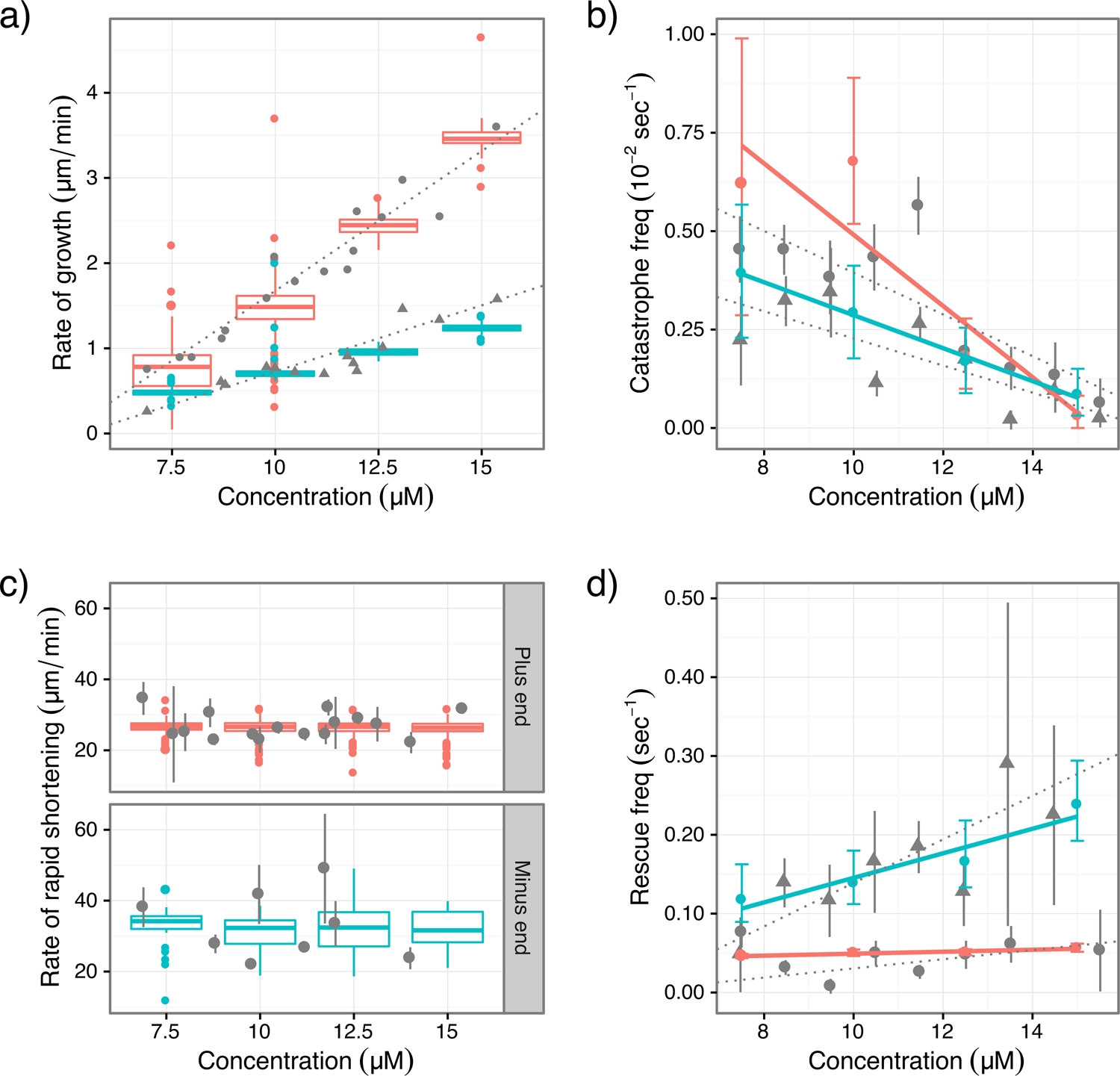
Comparison between results of simulations and experiments in ref. (Walker et al., 1988). The experimental data are obtained by digitization of figures in ref. (Walker et al., 1988). Experimental data are in gray; triangles denote plus-end data and dots denote minus-end data; vertical lines are error bars and dotted lines are linear fitting from ref. (Walker et al., 1988). For simulation results, plus-end is red and minus-end is cyan. Growth and shortening rates are presented as standard box plots; frequencies for catastrophe and rescue are presented as error bars. Simulations are carried out at tubulin concentration of 7.5, 10.0, 12.5 and 15.0 μM. Linear regression (solid lines) was conducted on catastrophe and rescue frequencies. (a) growth rates; (b) catastrophe frequencies; (c) shortening rates; (d) rescue frequencies.

RESULTS

We first introduce our model assumptions inferred from tubulin structures. The basis is the three stable polymer structures observed during different stages of dynamic instability and the steric constraints they impose, which become evident when details of inter-conversions between polymer structures are examined. The three polymer structures, in the temporal order that they appear during dynamic instability, are: 1) the bent sheet at a growing plus-end, 2) the straight tube structure of a stable MT, and 3) the highly curved PFs at a depolymerizing end. This order suggests an ordered transition from one polymer structure to another (i.e. B→S→C) when dynamic instability progresses from growth to shortening, thus each phenomenon of dynamic instability is determined by a polymer structural transition. The mechanism of dynamic instability is embedded in the mechanisms of these transitions.

Each of the three polymer structures has a matching tubulin structure. Change of tubulin structures leads to a polymer structural transition, in which a MT has to go through a series of structural intermediates, each contains a mixture of tubulins structures that match the initial and final polymer structures respectively. Each process of dynamic instability is governed by a polymer structural transition, which is in turn controlled by the energies of the structural intermediates that it goes through. The energies of different structural intermediates are determined by the steric rules that we inferred from structures of tubulin.

Steric Rules for Energy of Longitudinal Interface

The most important hypothesis in our model is the steric rules for the energies of longitudinal interfaces in different conformations, which are essential for determining the energies of structural intermediates during polymer structural transitions. Monomer and longitudinal interface are the basic units of the B→S→C transitions of tubulins. The energy of longitudinal interface is more important because it changes in every step of B→S→C transitions. Conformational change of a monomer simultaneously changes the energies of the two longitudinal interfaces on its plus- and minus-end sides; conformational change of a longitudinal interface changes its own energy.

The energy of a longitudinal interface is determined by three factors: conformations of the two monomers and the interface itself. The conformation of a monomer is characterized by two structural features: 1) the size of its protrusion (P) in its plus-end surface, and 2) the size of its cavity (V) in its minus-end surface (Fig. 1b). The conformation of a longitudinal interface is characterized by one feature: the size of its opening (O) (Fig. 1c).

The concepts of P, V and O were inferred from the structural differences between straight (S) and curved (C) tubulin dimers, shown by Ravelli et al (Ravelli et al., 2004). They found that the change from S to C form of a monomer is a rigid body motion of the intermediate domain (ID), whereas the N-terminal (NTD) and C-terminal (CTD) domains essentially remain the same (video S1).

Following Ravelli et al, we aligned two monomers in S and C forms by their NTDs and CTDs in Fig. 1b (Ravelli et al., 2004). This alignment clarified the essential features of the change from S to C form. At the plus-end surface, loops T5 and H6–H7, and helix H6 moved more into the longitudinal interface; these are the structural elements of P (Fig. 1b). At the minus-end surface, helix H10 moved more into the interior of the monomer; the void created by this movement is V (Fig. 1b). While H6, H6–H7 and H10 belong to the ID, T5 belongs to the junction between NTD and ID.

From the discussion above, we inferred that: 1) the size of P and V changes with monomer conformation; 2) P_c > P_s and V_c > V_s (Fig. 1b). Here we used monomer conformation to label the size of a structural feature (e.g. P_c is the size of P for a monomer in C form).

Moreover, the two monomers in a dimer in C form undergo a 12° rigid body rotation relative to each other around a hinge region. This rotation loosened the longitudinal interface (contact area decreased from 3000 Ų in S to 2200 Ų in C (Ravelli et al., 2004)). We inferred that this rotation opened up the longitudinal interface and called it the opening. The size of O is defined by the angle of rotation (Fig. 1c).

From this we inferred that: 1) O_c > O_s (Fig. 1c), 2) larger O leads to reduced interface area; 3) P_c > V_c, because the interface needs to open up to avoid unfavorable interactions, indicating that V_c itself cannot accommodate P_c; 4) the energy of an interface is determined by the size of P and the size of the pocket formed by O+V, because in a stable conformation the change in O and V are coordinated, suggesting that their combined size determines the optimal interactions.

Based on the above discussion, the energy of a given interface x-y-z ((x, y, z) ∈ (S, C); e.g. S-s-S means x=y=z=S) is determined by the size of P_x and O_y + V_z. In general, there are five possibilities: 1) P_x ≫ O_y + V_z; 2) P_x > O_y + V_z; 3) P_x = O_y + V_z; 4) P_x < O_y + V_z; and 5) P_x ≪ O_y + V_z. The steric rules specify how each possibility is determined by the values of x, y and z.

Our basic assumption is that the three structural features P, V and O have optimal match in a stable tubulin conformation. This assumption leads to: P_s = O_s + V_s and P_c = O_c + V_c. From this, we inferred one foundation of the steric rules: i) P_x = O_y + V_z if x=y=z.

The other logical foundation of the steric rules is based on a structural analysis by Ravelli et al (Ravelli et al., 2004). They replaced the α-monomer in a S dimer by an α -monomer in C form. This procedure led to a CsS (or C-s-S) structure (notation in Fig. 1c). They found that loops T5 and H6–H7 of the α-monomer in C form had steric clashes with helix H10 of the β-monomer in S form (Fig. 2b). From this we inferred that: P_c ≫ O_s + V_s, since T5 and H6–H7 form the P of the α-monomer and H10 forms the V of the β-monomer. From this we formulated the other foundation of the steric rules: ii) P_x ≫ O_y + V_z if x > y and x > z. Conformations rank as: C > S.

By interpolation between the two rules above, we inferred another steric rule: iii) P_x > O_y + V_z if (x > y and x=z, or x=y and x > z).

The rules above are for situations where P is larger than V+O. Following similar logic, we inferred the steric rules for situations where P is smaller than V+O, by reversing the relation between x and y, z in rules (ii) and (iii). The resulting rules are: iv) P_x < O_y + V_z if (x < y and x=z or x=y and x < z); v) P_x ≪ O_y + V_z if x < y and x < z.

The next step is to translate the relationships between P and V+O into interface energies. Since P_x = O_y + V_z only exists in stable conformations, we reasoned that it means optimal interaction. In contrast, P_x ≫ O_y + V_z leads to steric clashes (e.g. CsS). We reasoned that such conformations have prohibitively high energy and cannot be part of any viable kinetic pathway for S→C transition. By interpolation between these two cases, P_x > O_y + V_z means a conformation with high energy due to steric strain, but the energy is not too high so that it can exist, though with small population.

On the other side of the spectrum, CcC has significantly reduced interface area compared to SsS. We reasoned that smaller P will further reduce the interface area. Therefore, we assume P_x < O_y + V_z and P_x ≪ O_y + V_z mean reduced interface, to a mild and severe level respectively. If we equate interface area with interaction strength, then reduced interface means weakened interaction. This completes our steric rules for longitudinal interfaces involving S and C forms, which determine the energetics of S→C transition. Since each of x, y and z can be C or S, there are 2³ = 8 possibilities, corresponding to the 8 structural intermediates listed in Fig. 1d.

The B form appears to be an intermediate between S and C because the opening angle of the S, B and C interfaces increases in the order of 0°, 6° and 12° (Muller-Reichert et al., 1998, Nogales et al., 1998, Ravelli et al., 2004). Consequently, the steric rules for B→S transition are analogous to those for S→C transition. By substituting B for C in the rules for S→C transition, we obtained the steric rules for structural intermediates in B→S transition.

Mechanical Energy of the MT Lattice

Since a MT is a two-dimensional polymer, deviations from its equilibrium structure have long-range effects, which alter the reaction kinetics of monomers and tubulin-tubulin interfaces over many rows. Thus the energy landscape of MT has both chemical and mechanical components. The chemical component accounts for changes in local chemical states (i.e. conformations, bonding) of individual monomers and interfaces, while the mechanical component accounts for long-range effects that conformational changes impose on global polymer structure. The two energy components form a feedback loop: the global chemical state of the polymer dictates the mechanical energy and the mechanical energy affects the changes in local chemical states. For example, when a monomer in sheet converts into S form, its equilibrium geometry no longer agrees with the surrounding monomers in B form. Its longitudinal and lateral bonds with its neighbors create a mechanical strain that is distributed over many monomer-monomer interactions via a process similar to intra-molecular vibrational energy redistribution (Nesbitt and Field, 1996), affecting their conformational changes. The net result is to favor conformational changes that reduce mechanical strain and disfavor those that increase it, with the extent determined by Boltzmann weighting (details in STAR method).

Nucleotide Affects Interface Energy

The nucleotide at an inter-dimer longitudinal interface can affect the structure and energy of: 1) the β-subunit that it binds to, or 2) the longitudinal interface, or 3) both. If it is case (1), hydrolysis should change only the structure of the β-subunit. If it is case (2), hydrolysis should change only the structure of the α-subunit across the interface. If it is case (3), both should change. Structural data excluded case (1) but cannot distinguish between the other two (Alushin et al., 2014, Zhang et al., 2015, Roostalu et al., 2020). For simplicity purpose, we assume that hydrolysis only affects the interface energy to minimize the number of parameters. Since GDP-tubulins prefer the C form, we assumed that GDP state favors interface conformations with larger O (Nogales et al., 1998, Ravelli et al., 2004, Zhang et al., 2015). In this way, the monomer energy is the sum of a monomer’s self-interactions and its interactions with the part of the nucleotide unaffected by hydrolysis. The interface energy is the interaction between two monomers on the opposite sides of the interface, together with the interaction between the part of the nucleotide that changes upon hydrolysis and the monomer on the other side. This treatment of monomer and interface energies is uniform and additive.

GTP-Hydrolysis

We assume random hydrolysis, but explicitly consider how tubulin conformation influences hydrolysis, as enzyme catalysis requires precise arrangements of residues at the active site. The inter-dimer interface is looser in B form than in S form, so will be the catalytic E-site. Consequently, hydrolysis should be slower in the B form. This is consistent with the fact that catastrophe never occurs in a sheet structure; it always occurs at a tube end. To reduce number of adjustable parameters, we assume that hydrolysis only occurs at S^T-s-S interfaces (Nogales et al., 1998).

e) A GTP-tubulin in a PF without lateral bonds adopts B form. This is based on the observation that isolated PFs of GMPCPP-tubulins are bent (Muller-Reichert et al., 1998).

Lateral Bonding

Based on observations by Wang et al (Wang and Nogales, 2005), lateral bonds on the two sides of a PF in the sheet are different. One is the same as those in tube (tube-like); the other is weaker (sheet-like). Converting sheet-like lateral bonds into tube-like, which occurs during sheet closure into tube, requires rotating a dimer around its longitudinal axis and is only feasible for the S form.

From the steric rules and constraints of lattice geometry, we infer B↔S↔C transition pathways, which determine the ELs and consequently the mechanism of dynamic instability (Figs. 2,S4). In the following, we discuss the detailed mechanisms for dynamic instability at the plus-end.

Plus-end Growth

In the growing phase, a new dimer adopts the B form after binding to an MT (assumption (e)) (Muller-Reichert et al., 1998). It then forms lateral bonds with neighboring dimers and integrates into a sheet (Chretien et al., 1995, Wang and Nogales, 2005), which closes into tube via B→S transitions (Chretien et al., 1995). After dimers adopt the S form, GTP hydrolysis starts (assumption (d)) (Nogales et al., 1998), enabling the S→C transitions required for catastrophe. After C forms swept the tip, they propagate along the PFs in rapid shortening.

There are three key phenomena in this period (Chretien et al., 1995, Mitchison and Kirschner, 1984, Walker et al., 1988) (Fig. 3): 1) bi-phase behavior: a growing plus-end alternates between sheet and tube; 2) pausing; and 3) catastrophe is a rare event, and its frequency decreases with increasing tubulin concentration. The first two phenomena are determined by B→S transition; catastrophe is determined by S→C transition.

B→S Pathway and EL during Growth

The directionality of the B→S transition of a monomer—its intermediate domain moves towards its minus-end side—imposes strict directionality and order on B→S transitions in the MT lattice. For a dimer in BbB conformation (Figs. 5a), if the β-monomer converts to S form first, a BbS interface ensues, which has steric strain (P_B > V_S+O_B). If the interface converts next, a BsS conformation follows, which has steric clashes (P_B ≫ V_S + O_S) and is forbidden. Thus the B→S transition cannot start from the β-monomer. In contrast, if the α-monomer adopts S form first, an SbB (P_S ≪ V_B+O_B) interface ensues, which has loose contact. The interface converts next, resulting in SsB (P_S < V_B+O_S), which has tighter contact and is more stable than SbB. Then the β-monomer changes, resulting in SsS (P_S = V_S+O_S), an optimal conformation. Finally, the two SeS lateral bonds of the dimer change to StS, making the final state (SsS) of lower energy than the initial state (BbB) (Figs. 5a, S5a). By the same logic, B→S transition in the MT lattice must start at the tube sheet boundary and proceed sequentially towards the plus-end, as otherwise BsS conformations will occur due to the lattice geometry (Fig. 5b). Therefore, B→S transitions always occur on the tube-sheet boundary.

Figure 5:

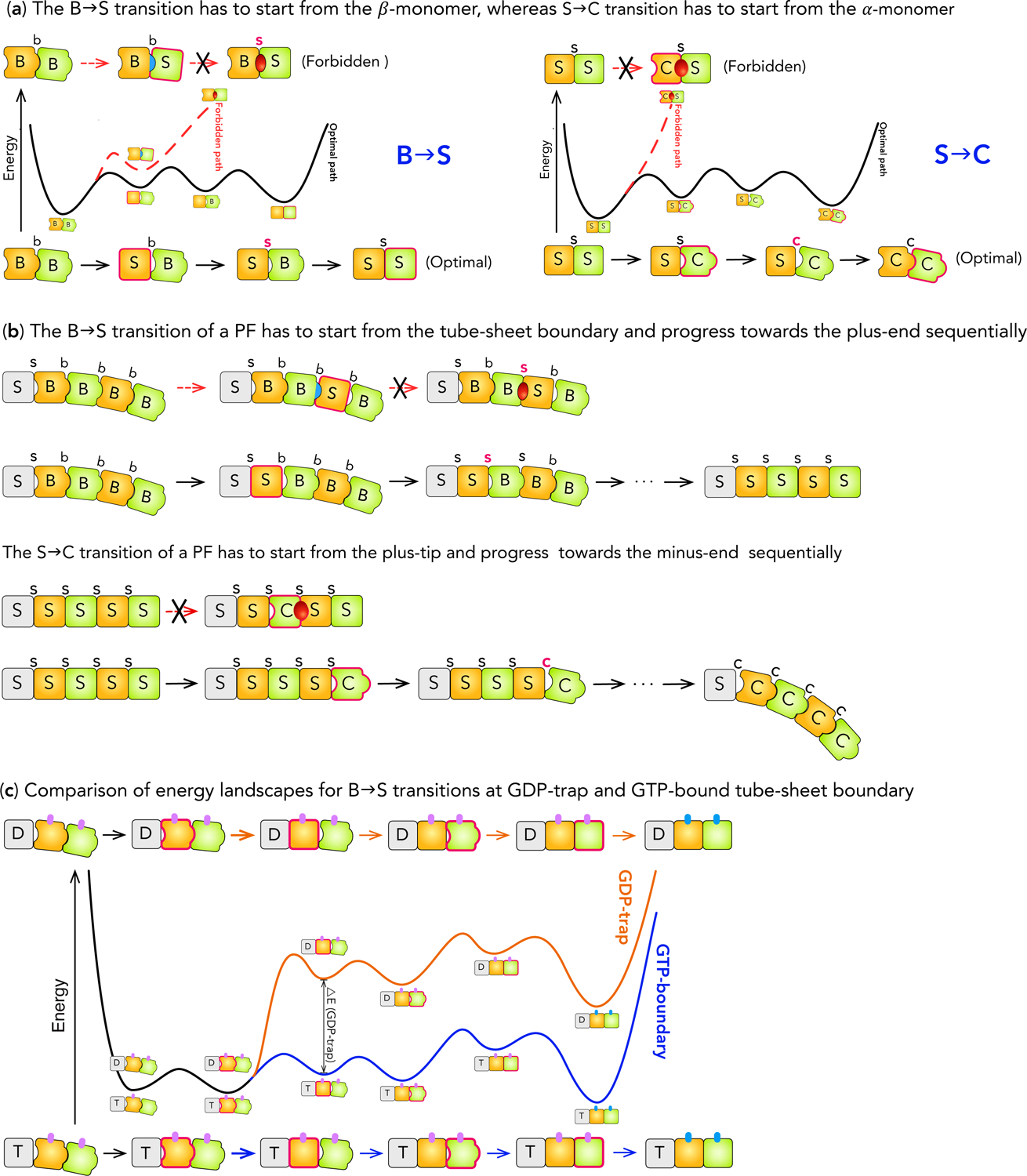
Kinetic pathways for B→S→C transitions at the plus-end. (a) Comparison of the kinetic pathways for the B→S and S→C transitions of a tubulin dimer. The energy landscapes are shown in the middle; the sequences of conformational changes in the forbidden and optimal pathways are shown at the top and the bottom respectively. The monomer or longitudinal interface that changes its conformation at a step is highlighted by a thick borderline or bold face. The color of the arrows in a sequence matches that of the corresponding energy landscape. For the B→S transition, the pathway that starts with the β-monomer (top) quickly leads to the BsS conformation, which has steric clashes and infinitely high energy (Red dashed line). This pathway is forbidden. In contrast, the pathway starting with the α-monomer (bottom) has relatively small changes in energy along the way (Black solid line) to the final conformation. This is the optimal pathway. For S→C transition, the pathway that starts with the α-monomer (top) immediately leads to the CsS conformation, which has steric clashes (Red dashed line). In contrast, the pathway starting with the β-monomer (bottom) has relatively small changes in energy along the way (Black solid line) to the final conformation.

(b) Comparison of pathways for B→S and S→C transitions along a PF. For the B→S transition, one pathway starts from the middle of the PF (top) and the other starts from the tube-sheet boundary (bottom) and progresses sequentially towards the plus-end. The former quickly leads to the B-s-S conformation that has steric clashes. The monomer in Grey represents the remaining of the PF. For the S→C transition, one pathway starts from the middle of the PF (top) and the other starts from the tube-sheet boundary (bottom) and progresses sequentially towards the plus-end. The former quickly leads to the C-s-S conformation that has steric clashes and is forbidden based on the steric rules.

(c) Comparison of the energy landscapes for B→S transition at GDP-trap (Orange) and GTP-bound tube-sheet boundary (Blue). The portion of the energy landscape common to both situations is colored Black. The layout is similar to panel (a). A small vertical bar represents a lateral bond, with Magenta for sheet-like and Cyan for tube-like bond respectively. The difference in the energy barriers at GDP-trap and GTP-boundary tube-sheet boundary, ΔE GDP-trap is marked on the energy landscape.

The nucleotide state at the tube-sheet boundary (i.e. S^T-s-B or S^D-s-B) leads to two barriers for B→S transition (Figs. 5c), whose first step (BbB→SbB) causes a concurrent S-s-B→S-s-S transition at the tube-sheet boundary. While S^D-s-B→S^D-s-S consumes energy (assumption (c)), S^T-s-B→S^T-s-S releases energy to compensate the cost of BbB→SbB, leading to high and low barriers for the respective B→S transitions (Fig. 5c). The energy compensation effect of S^T-s-B→S^T-s-S resembles the allostery in the T→R transition of hemoglobin (Perutz, 1970, Szabo and Karplus, 1972), where the energy gained from interface changes compensates the cost of tertiary structural changes.

Bi-Phase Growth

Plus-end growth shows two phases (Fig. 3b) because the two barriers for B→S lead to two rates: S^T-s-B→S^T-s-S is faster than growth at high tubulin concentrations whereas S^D-s-B→S^D-s-S is slower than growth at low concentrations. At a GDP-bound tube-sheet boundary (i.e. “GDP-trap”, Figs. 5c, 3a), dimers are trapped in B form by the slow S^D-s-B→S^D-s-S transition. All the subsequent dimers are also trapped in B form because B→S transition must proceed sequentially, and the MT grows in sheet. Once the MT escapes the GDP-trap (i.e. S^D-s-B→S^D-s-S completes) after adequate waiting, subsequent B→S transitions assume the fast rate and overtake the front of sheet—the MT exits sheet to enter the tube phase.

In tube phase, a newly added dimer converts to S form before another dimer binds to it, so the growing tip remains in tube until GDP-traps form via fluctuation. After binding to a GTP-bound tip dimer in S form, a new dimer can start the fast B→S transition even before forming lateral bonds. When the inter-dimer interface between the new dimer and the original tip becomes S-s-S, GTP hydrolysis is enabled (Fig. 3a). After hydrolysis, if the new tip dimer fluctuates backward (i.e. S→B) and lateral bonds form in this process, dissociation at the S^D-s-B interface is prevented and a GDP-trap forms. Alternatively, lateral bonds do not form and the tip dimer dissociates easily at the less stable S-b-B or S-s-B interface, exposing the original tip as a GDP-tip (i.e. GDP-bound tip dimer in S form, Fig. 3a). When a dimer binds to the GDP-tip and forms lateral bonds, a GDP-trap forms. Afterwards, growth proceeds as a sheet and the MT leaves tube phase.

The duration of tube phase is determined by the time it took to form GDP-traps; the duration of sheet phase is determined by two factors: 1) the time it took to escape the GDP-trap, 2) the relative rates of S^T-s-B→S^T-s-S transition and sheet growth. Our simulations reproduced the bi-phase behavior (Fig. S1) and the plus-end growth rates (Fig. 4a) in ref. (Walker et al., 1988).

Catastrophe

Catastrophe can only happen when there are no GTP dimers in MT lattice except the tip row and it requires all tip dimers in C form. The critical step is for a stable core of tip dimers that all have undergone S→C initiation (i.e. S→C transition of a tip dimer) (Fig. 5b). This is analogous to the critical nucleus in gas-to-liquid phase transition. Afterwards, lateral propagation of C form through the tip is much easier. Thus the main barrier for catastrophe is the barrier for forming the stable core, which is a cascade of barriers for S→C initiations.

S→C Pathway during Catastrophe

Unlike B→S, the S→C transition of a dimer cannot start from the α-monomer because it would create a CsS interface (Fig. 5a), which has steric clashes and is energetically forbidden (Ravelli et al., 2004). Instead, the optimal pathway starts from the β-monomer at the plus-end and propagates sequentially backward towards the minus-end—the same direction and ordering as plus-end shortening (Fig. 5b).

EL for S→C Initiation

The barrier for S→C initiation is not determined by the nucleotide bound to a tip dimer, but instead the nucleotide at the inter-dimer interface behind the tip dimer (assumption (c)). When this interface is GDP-bound, the first two steps (SsS→SsC→ScC) (Figs. 6a, S7) need to climb substantial barriers, but steps afterwards are energetically downhill. When this interface is GTP-bound, the S^T-s-C→S^T-c-C step faces another steep barrier, which diminishes S→C initiation. Therefore, Catastrophe can only happen when there are no GTP dimers in MT lattice except the tip row.

Figure 6:

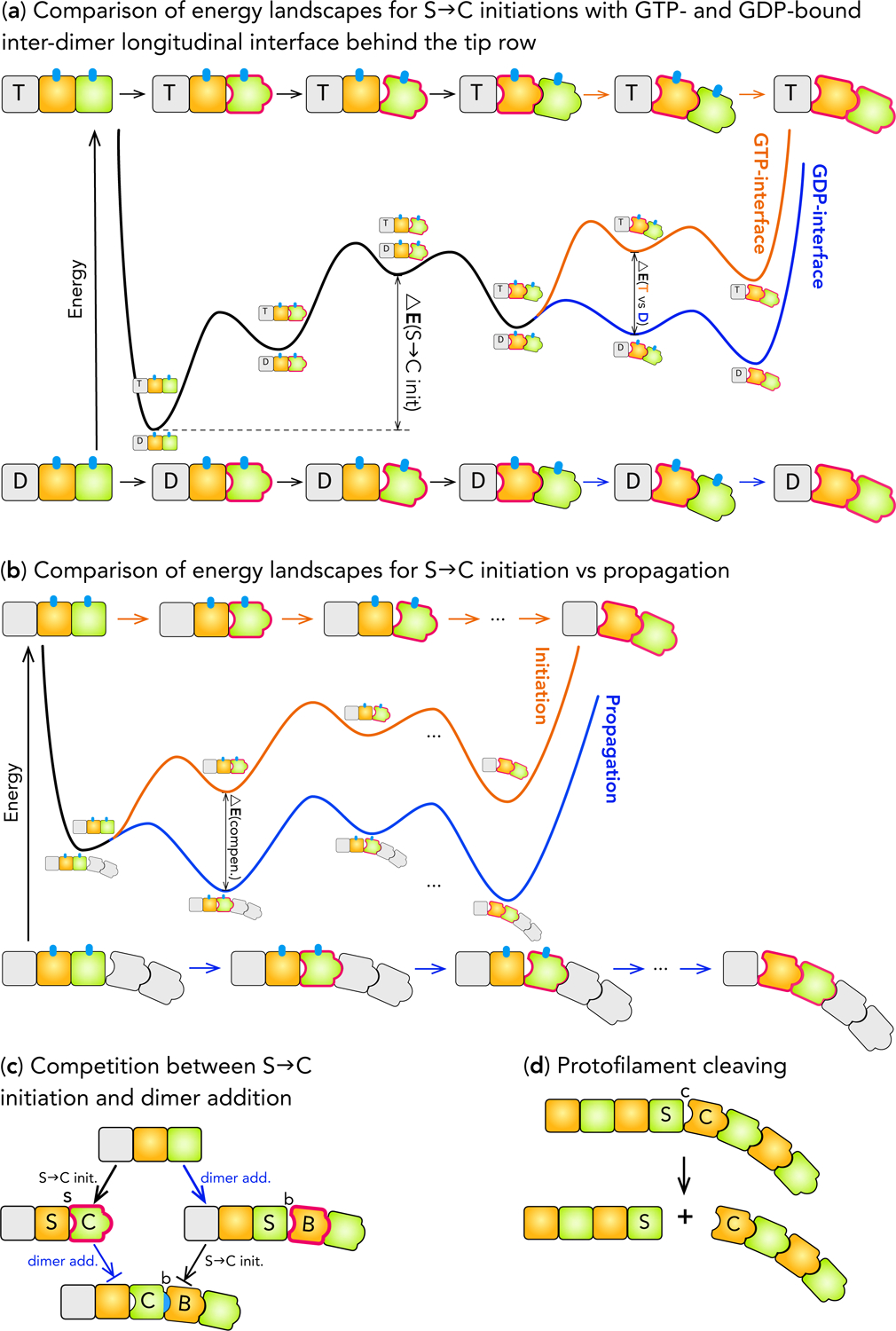
ELs for S→C initiation and propagation at the plus-end. (a) The energy landscapes for S→C initiation at plus-end with GTP- (Orange) and GDP-bound (Blue) inter-dimer longitudinal interface behind the tip row. The major energy barrier for GDP-bound interface, ΔE (S→C init.), and the extra energy required at GTP-bound interface,, are marked. (b) Comparison of the energy landscapes for S→C initiation (Orange) ΔE (T vs. D) and propagation (Blue). The decrease in the energy barrier for propagation due to the energy compensation effect, (ΔE compen.), is marked. (c) Schematic showing that S→C initiation and dimer addition compete with each other and are mutually exclusive. A block-end arrow (⇥) indicates that a reaction is inhibited and unlikely to occur. (d) Schematic showing PF cleaving during shortening.

Forming the Stable Core of Curved Dimers for Catastrophe

Forming the stable core requires multiple S→C initiations, which need to compete with two processes. First, individual S→C initiations need to compete against dimer additions (Fig. 6c): a tip dimer, after binding a new dimer, cannot undergo S→C initiation due to the ordering of S→C transition. This competition increases the effective barrier for S→C initiation. Second, lateral propagation of S→C initiations needs to compete against C→S transitions. After converting into C form, a tip dimer has CtS lateral interface and high energy; it either reverts to S form (i.e. C→S) or breaks its lateral bonds. In the latter case, it makes S→C initiation of its neighbor easier by reducing the latter’s lateral bonding, enabling S→C initiation to laterally propagate.

Once an extended segment of laterally neighboring dimers are all in C form, C→S within the segment diminishes because forming lateral bonds between two C dimers is too costly and C→S without lateral bonds has a high barrier. Moreover, dimer addition to tip dimers in C form is minimal because they form less stable C-b-B (P_C ≫ V_B+O_B) or C-c-B (P_C > V_B+O_C) interface and dissociate quickly (Fig. 6c). The immunity to both C→S transition and dimer addition makes this segment of C dimers a stable core. They also help to reduce dimer additions to adjacent tip dimers because newly added dimers cannot form lateral bonds with them and become stabilized, effectively enhancing S→C initiation of these tip dimers. Consequently, S→C initiation laterally propagates, eventually leads to catastrophe (Fig. 3c, S7).

Catastrophe Frequency

The probability of catastrophe is controlled by the competition between S→C initiation and dimer addition. The former does not depend on tubulin concentration, but the latter increases with it. Thus dimer addition outcompetes S→C initiation more often with increasing tubulin concentration, making catastrophe frequency decrease with it. Our simulations (Fig. 4b) reproduced catastrophe frequencies in ref. (Walker et al., 1988).

Plus-end Shortening

The most distinctive features during shortening are (Mitchison and Kirschner, 1984, Walker et al., 1988): 1) shortening is 10⁶ times faster than catastrophe, even though both processes require S→C transition; 2) rescue is much more frequent than catastrophe despite fast shortening. These arise from the difference between S→C propagation (S→C transition of dimers in the middle of PFs) and S→C initiation (Fig. 6b).

The main process of shortening is S→C propagation; its first step is almost identical to S→C initiation: the β-monomer converts to C form. But this step causes two concerted changes (Figs. 6b, S7b): 1) SsS→SsC, and 2) S-c-C→C-c-C, whereas initiation only has the first one. While the first change is energetically uphill, the second is downhill, thus energy gained from the second change compensates the cost of the first. This energy compensation mechanism (Fig. 6b) makes the barrier for S→C propagation much lower than that for initiation. Moreover, S→C propagation does not need to compete against dimer addition, explaining why catastrophe is rare and slow but shortening is fast. Our simulations (Fig. 4c) reproduced shortening rates in ref. (Walker et al., 1988).

Rescue is the Inverse of Catastrophe

The final step of S→C propagation of a dimer creates a S-c-C interface with the next dimer in the PF (Fig. 6d)—an easy-to-break longitudinal bond due to the loose interaction (P_S ≪ V_C+O_C). As rapid shortening proceeds, breaking S-c-C bond directly competes with S→C propagation. If the S-c-C bond breaks, the curved portion of a PF cleaves (video S3) and exposes a GDP-bound dimer in S form (i.e. a GDP-tip), which mirrors the growing tip in tube phase (Fig. 3d). Thus starts the same competition between dimer addition and S→C initiation that controls catastrophe. If the latter prevails, shortening continues. Otherwise, shortening temporarily halts at this PF. If adjacent PFs cleave in the meantime, a cluster of S dimers forms (i.e. a stable core for “rescue”). They are more resistant to S→C initiations due to lateral bonding between them. They effectively enhance cleaving of neighbor PFs by hampering S→C propagation via their lateral bonds with these PFs. They also assist dimer additions to cleaved neighbor PFs by forming lateral bonds with dimers newly added to them. Consequently, PF cleaving laterally propagates and new dimers add, eventually leads to rescue. Since rescue occurs on GDP-tips, it often renews growth in sheet or occasionally leads to pause during shortening (Figs. 3a,d) (Walker et al., 1988).

In rescue, growth competes against S→C initiation rather than propagation. The high barrier for initiation (Fig. 6b) leads to high probability for resuming growth, which explains the puzzlingly high frequency of rescue despite that shortening is much faster than growth (Fig. 4). Two factors are key to rescue: 1) the rate that a depolymerizing PF cleaves, 2) the chance that a new dimer binds the GDP-tip exposed by PF cleavage and becomes stabilized by lateral bonding. The first determines how often a PF qualifies for rescue; the second determines how likely a qualified PF rescues. Our simulations (Fig. 4d) reproduced rescue results in ref. (Walker et al., 1988).

In essence, catastrophe and rescue are determined by the same processes, but at growing and shortening tips respectively and with opposite definitions for success. If S→C initiations outcompete dimer additions, the result is catastrophe. Otherwise, the result is rescue. This mirror symmetry manifests in two aspects. 1) The high barrier for S→C initiation favors rescue but hampers catastrophe, making recue 80 times more frequent than catastrophe. 2) Dimer addition increases with tubulin concentration, thus rescue increases but catastrophe decreases with it.

DISCUSSION

We have presented a structural mechano-chemical model in which the mechanism for dynamic instability is specified by the B→S→C pathways and their corresponding ELs. Topologies of the Els are determined by constraints inferred from monomer structures and lattice geometry, their quantitative details by varying model parameters to simultaneously reproduce kinetic data of all the phenomena of dynamic instability (see Methods for mechanisms of minus-end dynamic instability) of purified tubulins under a consistent experimental setup.

Our model provided a mechanism for plus-end catastrophe that: 1) provided a unified perspective on important ideas such as structural cap and GTP-cap and clarified their relationship, 2) provided physically coherent solution to open questions such as short GTP-cap and mechanical stress in GDP MT lattice, and 3) specifies the multi-step nature of catastrophe.

In our model, a MT cannot catastrophe during sheet phase because there is no GTP-hydrolysis in the sheet. This is consistent with the structural cap idea (Chretien et al., 1995). However, in our model sheet closure into tube does not induce catastrophe. Instead, it starts the tube phase of growth. This differs from the idea in structural cap that sheet closure itself prompts catastrophe.

When a MT grows in tube phase, two layers or more GTP-tubulins at the tip are sufficient to prevent catastrophe. This is because tip dimers cannot undergo S→C transition when the inter-dimer longitudinal interface behind the tip row is GTP-bound, due to high energy barriers on the kinetic pathway (Fig. 6a). Therefore, GTP tubulins at plus-ends act as a GTP-cap that protects a MT from catastrophe, and a cap of two layers of GTP-tubulins is sufficient, independent of MT length. This is consistent with the observations by Drechsel et al (Drechsel and Kirschner, 1994). However, GTP-tubulins at growing tip do not prevent catastrophe by providing a constraining force that counter-balances the mechanical stress in the GDP-tubulin lattice. Instead, they only prevent S→C transition of tip dimers, which in turn prevents S→C transition of dimers in the lattice because S→C transitions must start from the plus-tip and progress towards the minus-end sequentially, as otherwise conformations with steric clashes (e.g. C-s-S) will occur (Fig. 4b). Consequently, all the dimers in the lattice, whether GTP- or GDP-bound, must remain in S form before S→C transition occurred at the tip—there is no mechanical stress in the MT lattice.

Therefore, in our model both sheet structure and GTP-tubulins act as GTP-cap, with the former being an early stage of it. Moreover, two layers of GTP-tubulins is sufficient for preventing catastrophe, thus long GTP-cap is unnecessary, though not excluded. Moreover, the energy from GTP-hydrolysis is stored in the GDP-tubulins as their conformational energy, not as mechanical stress in the MT lattice. The conformational energy of GDP-tubulins will only be released when they convert into C form during shortening, one dimer at a time. The point of energy release is at the depolymerizing plus-end. Therefore, a cellular structure (e.g. a kinetochore) can utilize this energy with high efficiency if it can track the depolymerizing end effectively. This energy release process is analogous to the release of chemical energy: it is released one reaction at a time and each reaction needs to cross an energy barrier before the energy in the reactant can be released. This is because protein conformational changes follow the laws of chemical kinetics.

Finally, GTP-cap is a sufficient but not necessary condition for preventing catastrophe. When there is only one layer of GTP-tubulins or less at the tip, catastrophe is determined by the competition between S→C transition of tip dimers and addition of new dimers to the tip (Fig. 3c). This is a stochastic multi-step process, consistent with aging. The critical step is to form a large enough core of curved tip dimers. Because the rate of dimer addition increases with tubulin concentration, catastrophe frequency decreases with it. Therefore, higher dimer addition rate slows down catastrophe by both prolonging the lifetime of GTP-cap and decreasing the success rate of S→C initiation, with the latter being more significant.

Our model also provides a mechanism for rescue that does not require remnant GTP-tubulins in MT lattice, an idea that is interesting but faces serious practical challenges upon close examination. Based on random hydrolysis, the number of GTP-tubulins decays exponentially from the plus-tip towards the interior of the MT lattice. At the time of catastrophe, the number of GTP-tubulins at the tip has to be minimal, let alone remnants in the lattice. Moreover, the high shortening rate means that the rescue location is far from the tip, thus the chance of remnants at the rescue location is diminishingly small. Even more challenging, rescue would require significant number of remnant GTP-tubulins to cluster together. Together, these factors make a mechanism that hinges on remnant GTP-tubulins formidably difficult in practice. In contrast, our model suggests that rescue is simply the inverse of catastrophe--it is precisely the same factors that make catastrophe difficult and rare that enables rescue.

We conclude with brief comments on the differences between the current model and other existing models on dynamic instability. Existing models were focused on growth, shortening and catastrophe at plus-ends, with the central assumption that hydrolysis is the rate-limiting step and the mechanical stress in GDP-dimers is the driving force for catastrophe. In contrast, our model was built on the hypothesis that the B→S→C transitions of tubulins control growth, shortening, catastrophe, rescue and pausing at both plus- and minus-ends, providing coherent mechanism for all of them.

METHODS

Pausing

Pausing (Walker et al., 1988, Tran et al., 1997b) is a rare situation during tube-to-sheet transition (Fig. 3b), when a blunt tube end has many GDP-tips and cannot form tube-sheet boundary, due to the high barrier for forming lateral bonds caused by mechanical penalty (Figs. 2, S6). Dimers added to GDP-tips lead to GDP-traps and cannot transition into S form easily. Neither can they form lateral bonds easily due to mechanical penalty: sheet-like lateral bonds require dimers to adopt an orientation that is different from the orientation of dimers on the tube side (assumption (f) (Wang and Nogales, 2005, Wu et al., 2012), Fig. S12). This mismatch causes the longitudinal bonds between the tube and sheet dimers to twist, increasing mechanical energy and inhibiting lateral bond formation. Due to cooperative effects, the difficulty in forming lateral bonds increases with the number of GDP-tips. Lack of lateral bonding leads to high dissociation at the unstable S-b-B interface (P_S ≪ V_B+O_B), thus growth stalls and the MT pauses. A MT can escape pausing when, by chance, a pair of adjacent dimers associate and form lateral bonds before either dissociates, so they are stabilized and can initiate growth in sheet. On the other hand, a growing end with few GDP-tips can initiate a sheet with no observable pause, thus pausing is rare.

Minus-End Dynamic Instability

Minus-end grows slower and catastrophes less, but shortens faster yet rescues more (Walker et al., 1988). These processes are controlled by B→S→C transitions, which follow different pathways (Figs. S2,3) because the directionality of plus-end pathways conflicts with the symmetry of minus-end. Different pathways lead to different B→S→C barriers, consequently different kinetics for growth, catastrophe, shortening and rescue at minus-end.

EL for B→S and Growth at Minus-End

The polarity of MT lattice imposes two constraints on B→S transition at minus-end. 1) To match the direction of minus-end growth, B→S transition should propagate from plus towards minus-end—the opposite of plus-end direction. 2) The interface between a new dimer and the minus-tip is always GTP-bound, because the nucleotide is brought in by the new dimer and cannot hydrolyze until B→S transition completes. Thus the minus-end has only one rate for B→S transition; it needs to be faster than growth at all tubulin concentrations.

Accordingly, conformational changes in the minus-end B→S transition follow the pathway in Fig. S2 to avoid steric clashes, minimize barriers and conform to the direction of minus-end growth. On this pathway, B-b-S interface has the highest energy due to steric strain (P_B>V_S+O_B). Thus the highest barrier for B→S transition is to form B-b-S interface, which happens to be also the initial step of a new dimer’s binding to minus-end. Thus the highest cost in a new dimer’s B→S transition is paid by its binding energy, making barriers for subsequent steps low and B→S transition fast (Fig. S2). Moreover, new dimers tend to dissociate at the B-b-S interface before forming lateral bonds, making minus-end growth slow—slower than plus-end. Together, they make B→S transition faster than growth at all concentrations. Our simulations (Fig. 4a) reproduced the minus-end growth rates in ref. (Walker et al., 1988).

EL for S→C, Catastrophe, Shortening and Rescue at Minus-end

The S→C pathway of the plus-end is disallowed at the minus-end because it immediately leads to a C-s-S interface that is forbidden due to steric clashes (Fig. S3). Consequently, S→C transition at minus-end follows a different pathway. The C-c-S interface on this pathway has high energy due to steric strain (P_C > V_S+O_C), higher than the energy of S-c-C interface at plus-end, making the barrier for S→C initiation higher than at the plus-end (Fig. S3). Therefore, minus-end catastrophes less frequently. Our simulations (Fig. 4b) reproduced catastrophe results in ref. (Walker et al., 1988).

During the minus-end S→C propagation, each step on the pathway maintains a C-c-S or CcS interface by forming and annihilating C-c-S and CcS interfaces simultaneously (Fig. S3c). Therefore, only tip dimers need to pay the high cost for forming CcS interface, which makes the barrier for minus-end S→C propagation lower than that at the plus-end, leading to faster shortening. After a PF cleaves during shortening, the higher barrier for minus-end S→C initiation makes dimer addition more likely to prevail than at the plus-end, causing more frequent rescues at the minus-end.

In summary, creating the high-energy CcS interface only once at the beginning of minus-end S→C pathway simultaneously increases the barrier for initiation and decreases the barrier for propagation (Fig. S3b,c), leading to lower catastrophe, higher rescue and faster shortening than at the plus-end. Our simulations reproduced (Fig. 4c,d) the minus-end shortening rates and rescue frequencies in ref. (Walker et al., 1988).

The key to the mechanism of dynamic instability at the minus-end is its different kinetic pathways for B→S→C transitions. The main part of these differences lies in the different ordering of conformational changes of monomers in the same dimer, which naturally emerges when monomer is used as the basic unit. In contrast, if dimer is used as basic unit, we found it unfeasible to establish different pathways at minus-end without invoking physically unreliable assumptions.

Simulation Method

The simulation system is a MT of thirteen PFs represented as a two-dimensional lattice. Each non-empty lattice site is a monomer, a longitudinal interface, or a lateral interface. There are three types of chemical reactions: 1) conformational change of a monomer or interface; 2) forming and breaking a longitudinal or lateral bond; 3) GTP hydrolysis. They obey first order kinetics. Except for GTP hydrolysis, which is the energy source that sustains dynamic instability, all the reactions are reversible and obey detailed balance. In particular, S→C transitions obey detailed balance because the chemical step of hydrolysis is much faster than subsequent tubulin conformational changes.

The system energy consists of chemical and mechanical components. Chemical energy accounts for conformations of monomer and interfaces, and nucleotide states; mechanical energy accounts for the mechanical strains caused by coexistence of B and S forms in the MT lattice. The mechanical energy uses harmonic terms to constrain geometric parameters to equilibrium values. There are five geometric coordinates: stretching and bending of a longitudinal or lateral bond, and twisting around a longitudinal bond (details in SI). We developed a strategy to integrate the mechanical energy with the kinetics of chemical reactions so that detailed balance is properly maintained: Gillespie algorithm (Gillespie, 1976, Serebrinsky, 2011) followed by a rejection step (details in SI). A chemical reaction selected by Gillespie algorithm is accepted with a ratio $P_{acc}(i\to j)=\text{min}\left(1,\text{exp}\left(\frac{-\Delta E_m(i\to j)}{k_{B}T}\right)\right)$, where ΔE_m (i → j) is the change in mechanical energy induced by the tentative reaction through its perturbation to the MT structure.

Simulating all the phenomena of dynamic instability is technically challenging. We devised numerical strategies (details in SI) to reduce the computational cost of kinetic simulations immensely, allowing proper sampling of rare events with very slow time scales (e.g. catastrophe) in the context of a sea of frequent events (e.g., dimer association during growth), which makes the conventional Gillespie algorithm formidably expensive (Gillespie, 1976, Gillespie, 2007).

Choice of Parameters

Model parameters are energies of monomer and interface in different conformations. Interface energies are most important because the lateral and inter-dimer longitudinal interfaces give MT its special properties that individual dimers do not have, and dynamic instability is a collective many-body phenomenon unique to the two-dimensional nature of the MT lattice. Model parameters are varied to reproduce experimental results in ref. (Walker et al., 1988). Because the same structural transition controls multiple phenomena and the same interface often affects multiple structural transitions, most parameters affect multiple phenomena. Thus parameters are adjusted iteratively in a coordinated manner, guided by the mechanisms of how structural transitions control different phenomena of dynamic instability discussed in Results. We also adopt two general guidelines for choosing parameter values. (1) We restricted the energy difference between neighboring states on B→S→C pathways to be within 4 k_BT based on observations from single molecule FRET experiments on protein conformational dynamics (Aviram et al., 2018, Borgia et al., 2018). (2) The steric rules provide a guideline on the relative ranking of energies of different conformations of the longitudinal interface. A sensitivity analysis on model parameters is presented in the Data S1.

STAR Methods

Lead Contact:

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Ao Ma (aoma@uic.edu)

Materials Availability:

This study did not generate new materials.

Data and Code availability:

• Simulation data used to generate figures in the paper are deposited at UIC Indigo (https://indigo.uic.edu) and available at: https://doi.org/10.25417/uic.12981158.

• Original code is publicly available at: https://doi.org/10.25417/uic.12981164.

• Scripts used to generate figures in this paper are available at: https://doi.org/10.25417/uic.12981122.

• Any additional information required to reproduce this work is available from the Lead Contact

Method Details

In our model, the only irreversible reaction is GTP hydrolysis. The chemical energy of the phosphate-phosphate bond released by GTP hydrolysis provides the energy source that sustains the non-equilibrium cycle of dynamic instability. All the other reactions are reversible and obey detailed balance. In particular, S→C transitions obey detailed balance because of a time scale separation between the chemical step of hydrolysis and subsequent product release and tubulin conformational changes.

Although the overall catalytic turnover time for enzymes are commonly in the range of milliseconds, the rate-limiting step is usually the product release process (Schramm and Schwartz, 2018, Schwartz and Schramm, 2009). In contrast, the chemical step, in which a bond is broken or formed, is much faster (Schramm and Schwartz, 2018, Schwartz and Schramm, 2009). Consistent with this notion, it has long been known that the release of Pi is the slow step in the GTP hydrolysis by tubulins (Melki et al., 1996). Consequently, the energy released from breaking the phosphate-phosphate bond is quickly re-equilibrated among all the degrees of freedom of the protein molecule by a vibrational relaxation process, with a time scale in the range of tens of picoseconds (Sagnella and Straub, 2001). All the subsequent steps, including the product release and conformational changes, happen via thermal activation under equilibrium or near equilibrium condition, instead of being directly driven by the energy released from bond breaking in a highly non-equilibrium manner. Therefore, detailed balance is expected to hold for these processes. Moreover, due to the sequential ordering of the S→C transition in the MT lattice, a GDP tubulin in MT lattice cannot undergo S→C transition until catastrophe has occurred and the subsequent shortening process has proceeded to it. This places the lifetime of GDP tubulins in S form in the range of tens to hundreds of seconds before it can undergo S→C transition, far exceeding the time scale of any enzyme catalysis, let alone the chemical step of GTP hydrolysis.

In our model, all the reaction rates are calculated with Eq. S1, using the energies of different conformations of monomer and longitudinal/lateral interface (Table 1), and the prefactors that sets the time scale of different types of reactions (Table S2). Therefore, these are the most important parameters in our model. They are estimated subject to the following physical constraints. 1) The maximum accumulated energy change along any optimal pathways for B→S→C transitions (Figs. S5, S7, S10) does not exceed the energy of GTP hydrolysis, which is estimated to be 12.5 kcal/mol =20.3 k_BT in ref. (Desai, 1997). This is because energy from GTP hydrolysis is the energy source to sustain dynamic instability, which provides an upper bound for the energy cost for conformational changes that are the underlying processes of dynamic instability. 2) The relative ranking of energies of different conformational states obeys the steric rules. 3) Linear free energy relationship that relates the rate of a reaction to the energy difference between the reactant and product state. 4) The rate for GTP hydrolysis, $r_{\mathit{\text{hyd}}}=k_{\mathit{\text{hyd}}}\cdot \text{min}\left(1,e^{-\frac{\left[E\left(S^D-s-S\right)-E\left(S^T-s-S\right)\right]}{k_{B}T}}\right)=0.12s^{-1}$ (calculated using Eq. S1), is within the range of experimentally measured rate in ref. (Melki et al., 1996) (0.02 to 0.15 s⁻¹), and similar to the values used in the literature (Coombes et al., 2013, VanBuren, 2005, Zakharov et al., 2015). 5) The difference between the energy of any two neighboring conformational states on an optimal B→S→C pathway is within 4 k_BT based on observations from single molecule FRET experiments on protein conformational dynamics. 6) The association rate we used, $r_{on}=k_{as}\cdot \text{min}\left(1,e^{-\text{E}\left({\text{B}}^{\mathrm{T}}-\text{b}-{\text{B or S}}^{\text{T}}-\text{b}-\text{B}\right)/k_{B}T}\right)=12.5\mu M^{-1}\cdot s^{-1}$, which is related to growth rate but cannot be directly measured, is well within the range used in the literature (Coombes et al., 2013, VanBuren, 2005, Zakharov et al., 2015). 7) The energy of sheet-like lateral bonds should be higher than the energy of tube-like lateral bonds based on cryo-EM observations (Wang and Nogales, 2005). 8) The prefactor that sets the basic time scale for conformational changes of monomer and interface should be similar to the experimentally observed fast protein conformational changes, which is microseconds to tens of microseconds (Benkovic and Hammes-Schiffer, 2003, Henzler-Wildman and Kern, 2007a). Moreover, we have k_mer > k_long > k_lat. This is because a monomer conformational change (k_mer) involves domains within a monomer, a longitudinal interface change (k_long) involves moving a monomer, and a lateral interface change (k_lat) involves moving a dimer as a whole. In this way, when the energy differences between different conformational states are considered, the time scale of the conformational changes considered in our model should correspond to the time scales of slow large-scale conformational changes of proteins. These conditions imposed tight constraints on the model parameters. Within these constraints, model parameters are adjusted to reproduce kinetic data of dynamic instability in Fig. 4. An extensive sensitivity analysis of all the parameters are detailed in Data S1.

Simulation Setup and Simplifying Assumptions to Reduce Number of Parameters

A MT of 13 protofilaments (PFs) is laid out as a two-dimensional lattice in the simulation (Fig. S11). The lattice consists of 26 columns indexed from 0 to 25, alternating between PFs and lateral interfaces. A column with an even index (or 0) represents a PF; a column with an odd index contains lateral interfaces. Along a column representing a PF, each lattice site is either a monomer (odd index) or a longitudinal interface (even index). Along a column representing lateral interfaces, each lattice site is either a lateral interface (odd index) or blank (even index). All lattice sites but blank ones can undergo appropriate chemical reactions depending on their state and the states of the adjacent sites. There are six types of chemical reactions:

1. Conformational change of a monomer (e.g. B→S), which is a first-order reaction.

2. Conformational change of a longitudinal interface (e.g. b→s), which is a first-order reaction.

3. Conformational change of a pair of lateral interfaces (e.g. 2e→2t), which is a first-order reaction.

4. Formation and breaking of a longitudinal bond at an inter-dimer longitudinal interface (association and dissociation of dimers). While association reaction linearly depends on tubulin concentration, dissociation reaction does not.

5. Formation and breaking of a pair of lateral bonds, which is a first-order reaction.

6. GTP hydrolysis, which is a first-order reaction.

Parameterzation of Reaction Rates

Each reaction causes a change in the chemical state of the simulation system, which is the collection of the conformations of all the monomers and interfaces (both longitudinal and lateral) and the nucleotide state of the inter-dimer longitudinal nterfaces. For a given reaction i that causes the system to transition from initial state $S_i^i$ to final state $S_i^f$, its rate is given as:

$$k_i=k_{t,i}\cdot \text{min}\left(1,e^{-\Delta E_c\left(S_i^i\to S_i^f\right)/k_{B}T}\right),$$ (S1)

where k_t,i is a prefactor determined by the type of reaction i (e.g. all monomer conformational change reactions share the same prefactor), and $\Delta E_c\left(S_i^i\to S_i^f\right)=E_c\left(S_i^f\right)-E_c\left(S_i^i\right)$ is the change in the total chemical energy of the system caused by reaction i, T is temperature and k_B is Boltzmann constant.

To derive Eq. S1, we start by treating transitions in the system as first order reactions that follow the standard reaction rate theory (i.e. the transition state theory) (Garcia-Viloca et al., 2004): reactions proceed through a high energy transition state shared by both the forward and reverse reaction. The rate of a reaction from state 1 → 2 is $k=A\cdot e^{-\Delta E_{1\to 2}^{\mathit{\text{act}}}/k_{B}T}$, where $\Delta E_{1\to 2}^{\mathit{\text{act}}}=E_{TS}-E_1$ is the activation energy for the forward reaction 1 → 2. Similarly, $\Delta E_{2\to 1}^{\mathit{\text{act}}}=E_{TS}-E_2$ is the activation energy for the reverse reaction 2 → 1. The activation energy is the difference between the Gibbs free energies of the transition state and the reactant. In general, the variables A, E_TS, and E₁ are determined by microscopic details of the system and differ from reaction to reaction. They are difficult to determine from the information available, and present four adjustable parameters for every pair of forward and backward reactions: A and E_TS are shared between the forward and backward reactions, but each stable state has a separate energy (E₁ and E₂).

We can eliminate one of these parameters by noticing that the observed behaviors of dynamic instability are mainly determined by the time scales of reactions and the ratio between the rates in the forward and backward directions of the same reaction. The ratio between forward and backward reactions statistically determines the direction in which the system is moving; the time scales of reactions determine how fast the system moves. With this in mind, we note that the ratio of forward to backward rates equal their populations at equilibrium, or $K_{eq}=k_{1\to 2}/k_{2\to 1}=\frac{e^{-E_2/k_{B}T}}{e^{-E_1/k_{B}T}}=e^{-\left(E_2-E_1\right)/k_{B}T}$. We then make the following assumptions: 1) the prefactor A depends only on the type of a reaction (e.g., changing a monomer conformation); and 2) the energy of the transition state is a constant energy relative to the less stable state, or E_TS = max(E₁,E₂) + ΔE^‡ = max(E₁ + ΔE^‡,E₂ + ΔE^‡), where ΔE^‡ depends only on the reaction types. Now we can rewrite the rates as:

$$k_{1\to 2}=A{e}^{-\frac{\left(E_{TS}-E_1\right)}{k_{B}T}}=A{e}^{-\frac{\text{max}\left(E_1,E_2\right)+\Delta E^{‡}-E_1}{k_{B}T}}=A{e}^{-\Delta E^{‡}/k_{B}T}{e}^{-\frac{\text{max}\left(E_1,E_2\right)-E_1}{k_{B}T}}$$

and

$$k_{2\to 1}=A{e}^{-\frac{\left(E_{TS}-E_2\right)}{k_{B}T}}=A{e}^{-\frac{\text{max}\left(E_1,E_2\right)+\Delta E^{‡}-E_2}{k_{B}T}}=A{e}^{-\Delta E^{‡}/k_{B}T}{e}^{-\frac{\text{max}\left(E_1,E_2\right)-E_2}{k_{B}T}}$$

Notice that max(E₁,E₂) − E_i is equivalent to max(0, E_j − E_i) for i = 1, j = 2 and i = 2, j = 1. Thus we can rewrite k_1→2 and k_2→1 compactly as

$$k_{1\to 2}=k_p{e}^{-\text{max}\left(0,E_2-E_1\right)/k_{B}T}=k_p\text{\hspace{0.17em}min}\left(1,e^{-\left(E_2-E_1\right)/k_{B}T}\right)$$

$$k_{2\to 1}=k_p{e}^{-\text{max}\left(0,E_1-E_2\right)/k_{B}T}=k_p\text{\hspace{0.17em}min}\left(1,e^{-\left(E_1-E_2\right)/k_{B}T}\right)$$

where $k_p=e^{-\Delta E^{‡}/k_{B}T}$ depends on the type of the reaction. Generalizing the labels gives us Eq. (S1). By imposing that all reactions of the same type share the same k_p, each reaction, counting forward and backward directions together, is essentially determined by the energies of the reactant and the product. With these assumptions, number of parameters in the simulation is tremendously reduced.

Chemical Energy of the System

Because of our specific choice for reaction rate, the stable state energies determine both equilibrium constants and reaction rates. The total chemical energy of the system is a function of the chemical state S of the system:

$$E_c(S)={\sum }_{i=1}^{n_{\text{mer}}(S)}{E}_{\text{mer},i}+{\sum }_{j=1}^{n_{\text{long}}(S)}{E}_{\text{long, }j}+{\sum }_{k=1}^{n_{\text{lat}}(S)}{E}_{\text{lat},k}$$ (S2)

Here n_mer(S) is the number of monomers, n_long(S) and n_lat(S) are the number of longitudinal and lateral interactions in the system, respectively. Each monomer state and interaction has an energy: E_mer,i, E_long,j and E_lat,k are the energies of monomer i, longitudinal interaction j and lateral interaction k, respectively.

The energy of a monomer i (E_mer,i) depends only on the monomer conformation, which can take one of three values S, B, and C. The energy E_long,j of a longitudinal interaction j is determined by four factors: 1) the conformation of the two monomer on each side of the interface, 2) the conformation of the interface itself, which can take one of three values s, b, and c, and 3) nucleotide state. Similarly, the energy E_lat,k of a lateral interface k is determined by the conformations of the two monomer on each side of the lateral interface and the conformation of the interface itself (e or t).

The monomer and longitudinal bonds affect different number of terms in the system energy. A conformational change of either a longitudinal or lateral interface modifies the system chemical energy through the longitudinal or lateral interaction term. In contrast, a conformational change reaction in a monomer introduces changes in one monomer energy, one or two longitudinal interface energy, and zero to two lateral interface energy terms, depending on how many longitudinal and lateral neighbors the monomer has.

The steric rules are implemented through change in chemical state and chemical energy, not the mechanical energy. When a monomer or interface changes its conformation, its chemical energy (i.e. parameters in Table 1) changes. The steric rules specify the ranking of energies of different conformations but do not specify their values. For example, steric rules specify that E(B-b-B) < E(S-b-B), but do not decide the values for E(B-b-B), or E(S-b-B), or E(B-b-B) – E(S-b-B). To decide that, both E(B-b-B) and E(S-b-B) are tuned iteratively to reproduce kinetic data of dynamic instability under the constraint that E(B-b-B) < E(S-b-B).

In contrast, the mechanical energy was intended to capture the effects due to co-existence of monomers and interfaces in B and S forms in the sheet region. Based on the cryo-EM structures of MTs and cold-stable sheets, dimers in S and B forms have different geometric requirements for their longitudinal and lateral bonds. When a B dimer and a S dimer are bonded to each other longitudinally or laterally, these longitudinal and lateral bonds cannot satisfy the geometric requirements of neither B dimer nor S dimer. That is, a bond between a B dimer and a S dimer is different from the bond between 2 B dimers or the bond between 2 S dimers--it will be distorted in comparison to the equilibrium geometry of either. This distortion of the longitudinal or lateral bonds is elastic in nature and can be adequately handled by harmonic terms.

Modified Gillespie Algorithm

With this setup, the rate of each reaction is determined by the instantaneous state of the lattice. The reactions are sampled using Gillespie algorithm (Gillespie, 1976). After a specific chemical reaction is selected by the Gillespie algorithm for trial, the potential change in system mechanical energy due to this reaction ΔE_mech(i → j) is computed and used to determine if this reaction should be accepted or rejected using a Metropolis criterion for acceptance:

$$P_{\mathit{\text{acc}}}(i\to j)=\text{min}\left(1,\text{exp}\left(\frac{-\Delta E_{\text{mech}}(i\to j)}{k_{B}T}\right)\right).$$ (S3)

This combination of the Gillespie algorithm with a rejection step employing the Metropolis acceptance criterion preserves detailed balance (Serebrinsky, 2011).

Simulation Details

Extra care is required in handling lateral interactions at the seam (between PFs 0 and 12). To prevent chemical reactions from attempting to create seam bonds when the MT lattice is mostly sheet, we require that both rows involved in the seam reaction have at least nine StS lateral interactions when forming a seam bond.

Our simulations are run at a constant temperature of T = 37° C, which allows us to keep the evaluation of energies simple: all units of energy are in units of k_BT. Each monomer site on the lattice has a length and width of 4 nm and lateral/longitudinal sites occupy no space. In the mechanical model, each monomer is a sphere of diameter 4 nm. The prefactors of reactions are adjustable parameters with few known constraints. To reduce the number of parameters, we pick one as a reference and set the rates of the others in terms of it. Our reference is τ_mer = 1/k_mer, which is the prefactor used for monomer reactions. Based on the size of the changes necessary for each type of reactions, we assume a hierarchy of rates: τ_mer < τ_long < τ_lat. The fastest experiment event is rapid shortening, which at 27 μm/min requires one dimer S→C transition every 1.36 ms. The S → C transitions involve five reactions: two monomer reactions, two longitudinal reactions, and one lateral pair reaction, thus the maximum value for τ_mer is 0.27 ms. We evaluated various values and found that τ_mer = 10⁻⁵ s provided us with the correct dynamics at reasonable values for the energy barriers.

In our simulations, growth rate is the rate at which the lattice elongates due to addition of new dimers. Sheet and tube are determined by conformations of dimers in the lattice: B form indicates sheet and S form indicates tube. Shortening rate is the rate at which the boundary between the tube and the curved PFs (i.e. PFs consisting of dimers in C form) propagates along the lattice. Catastrophe is determined as when the system changes from growing to shortening, and rescue is determined as when the lattice resumes growth.

Mechanical Energy of the System

Monomers in a MT are connected to each other by longitudinal and lateral bonds. These bonds originate from a combination of different inter-molecular interactions such as electrostatic, von der Waals, hydrogen bonds, salt bridges and hydrophobic effects present at the protein-protein interface between tubulin monomers. Although they are considered non-bonded interactions, their effects are similar to covalent bonding: to keep the polymer from deviating from its equilibrium geometry defined by the collection of local equilibrium geometries of individual longitudinal and lateral bonds. Any deviation from the equilibrium polymer structure causes the total energy of the system to increase, and this effect is best captured by mechanical rather than chemical energy. We build a mechanical energy model of the system to mimic this effect. The mechanical energy is designed to keep each monomer at the position required by the equilibrium structure of the relevant polymer system, either tube or sheet. It has the feature that the mechanical energy for pure tube is zero—only deviation from the equilibrium structure causes mechanical energy to increase.

In the mechanical model, we do not distinguish between α and β tubulins. Each monomer is modeled as a rigid sphere. Each rigid sphere contains a number of particles that interact with adjacent monomers. These particles form a right-handed coordinate system local to a monomer. Below we discuss the details (Fig. S12).

Coordinate System for the Mechanical Model

All coordinate systems are right-handed. In the diagram of Fig. S12, we use a reference coordinate system of (ζ, η, and ξ. This coordinate system is local to the monomer, relating it to the lab frame requires both translation and rotation. Let e be the direction along the PF axis, from minus-end to plus-end. The ξ vector is tangent to the curve of a PF, so it coincides with e for a straight PF. In the frame of a monomer, there are two directions perpendicular to ξ: one that points toward lateral monomers, which we call ζ, and one that is perpendicular to both of these axes, η, which is normal to the curve of the PF. In a tube configuration, η points toward the center of the MT.

Each monomer is a rigid body that consists of five particles: the center of mass and four site particles to define longitudinal and lateral interactions with adjacent monomers. The five particles are:

1. CoM: the center of mass of the monomer.

2. ORI-ζ: particle that is a unit distance from the CoM along the ζ (e.g. lateral) axis.

3. ORI-η: particle that is a unit distance from the CoM along the η axis.

4. β: particle that is a distance of the helical offset from the CoM along the e vector.

5. ORI- η₂: particle that is a unit distance from β along the η axis. It constrains bending and twisting around the lateral bond.

The ζ, η, and ξ coordinates of each monomer are related as follows:

1. Longitudinal bonds are primarily along the ξ -axis. Bent and curved conformations bend along the η-axis.

2. Lateral bonds are in the ζ-η plane, and are described relative to the ORI- ζ and ORI- η particles.

Longitudinal bonds are between the CoMs of the monomers in the same PF, and are directional. The direction of the bond is from the nucleotide interface of one monomer to the non-nucleotide interface of another. The direction is collinear with the e vectors of monomers connected by a straight (S) interface, and has a specific angle with the e vectors monomers connected by curved (C) or bent (B) interfaces.

Energy Terms in the Mechanical Model

Longitudinal bonds have a stretching term that is assumed harmonic: $U\left({\overrightarrow{R}}_{ij}\right)=\frac{1}{2}{k}_{\text{long}}{\left(\left|{\overrightarrow{R}}_{ij}\right|-R_{eq}\right)}^2$, where k_long is the force constant, ${\overrightarrow{R}}_{ij}$ is the vector pointing from the CoM of monomer i to the CoM of monomer j, and R_eq = 4 nm is the equilibrium length of longitudinal bond.

Longitudinal bonds also have a bending term. Two angle potentials are used to confine the direction of longitudinal interactions, each one is harmonic in the bending angle. The first term is applied to the angle between ORI- η and the CoM-CoM longitudinal bond, and enforces the observed angle between monomers in a C, B or S conformation.

$$U(\theta )=\frac{1}{2}{k}_{\theta }{\left(\theta -{\theta }_{eq}\right)}^2$$

Here θ is the angle between the ORI- η and CoM within monomer and the CoM—CoM axis of that monomer with an adjacent monomer (Fig. S12).

$$\text{ORI-}\eta \stackrel{(ori)}{\leftrightarrow }CoM\stackrel{c/b/s}{\leftrightarrow }CoM{\theta }_{eq}=\frac{\pi }{2}+\frac{{\theta }_{\text{c}/\text{b}/\text{s}}}{2}$$

The second term keeps the e vector of each monomer in the plane defined by the CoM—CoM axis and the CoM—ORI- η vector (the yz plane in the diagrams in Fig. S12). It does this by constraining the angle between ORI- ζ and the CoM—CoM longitudinal bond to 90°, which penalizes any motion of the e vector out of the ξη -plane.

$$U\left({\theta }^{\xi \eta }\right)=\frac{1}{2}{k}_{\theta }{\left({\theta }^{\xi \eta }-{\theta }_{eq}^{\xi \eta }\right)}^2$$

$$\text{ORI-}\zeta \stackrel{(\mathit{\text{ori}})}{\leftrightarrow }CoM\stackrel{c/b/s}{\leftrightarrow }CoM{\theta }_{eq}^{\xi \eta }=\frac{\pi }{2}$$

For simplicity, we use the same k_θ for terms that involve θ and θ^ξη.

The third term in longitudinal bonds is for bond twisting. A dihedral potential is applied to the CoM—ORI-η vectors in monomers that share a curved, bent, or straight longitudinal bond. This potential keeps the ORI- η vectors of the same PF aligned (Fig. S12). It penalizes twisting within a PF along the axis of the PF.

$$U(\varphi )=\frac{1}{2}{k}_{\varphi }(1-\text{cos}\varphi )$$

Note that ϕ_eq = 0.

Lateral bonds are between the CoMs of a monomer and the β particle of an adjacent monomer. The β particle is offset along the PF axis by the distance required to obtain a helical pitch of three monomers in a 13-PF MT. Lateral bonds may be either tube or sheet.

Lateral bonds have a harmonic stretching term:

$$U\left({\overrightarrow{R}}_{ij}\right)=\frac{1}{2}{k}_{\text{lat}}{\left(\left|{\overrightarrow{R}}_{ij}\right|-R_{eq}\right)}^2$$

Lateral bonds also has a bending term. Two angle potentials are used to confine the direction of lateral interactions, each one is harmonic in the bending angle. The first maintains the required angle for sheet-like and tube-like lateral interactions (Fig. S12):

$$U(\alpha )=\frac{1}{2}{k}_{\alpha }{\left(\alpha -{\alpha }_{eq}\right)}^2$$

$$\beta \stackrel{tu/sh}{\leftrightarrow }\text{CoM}\stackrel{\text{ (ori) }}{\leftrightarrow }\text{ORI-}\eta {\alpha }_{\text{tu}/\text{sh}}$$

$$\text{ORI-}{\eta }_2\stackrel{\text{ (ori) }}{\leftrightarrow }\beta \stackrel{tu/sh}{\leftrightarrow }\text{CoM\hspace{1em}}{\alpha }_{\text{tu}/\text{sh}}$$

The second enforces the helical pitch by keeping CoM- β–CoM angles at 90°:

$$U(\alpha )=\frac{1}{2}{k}_{\alpha }{\left({\alpha }^p-{\alpha }_{eq}^p\right)}^2$$

$$\beta \stackrel{(\beta )}{\leftrightarrow }\text{CoM}\stackrel{tu/sh}{\leftrightarrow }\text{CoM\hspace{1em}}{\alpha }_{eq}^p=\frac{\pi }{2}$$

$$\text{CoM}\stackrel{tu/sh}{\leftrightarrow }\beta \stackrel{(\beta )}{\leftrightarrow }\text{CoM\hspace{1em}}{\alpha }_{eq}^p=\frac{\pi }{2}$$

For simplicity, we use the same k_α for terms that involve α and α^p.

Finally, we use a lateral twisting term to keep monomers from twisting around the lateral bonds (Fig. S12).

$$U(\psi )=\frac{1}{2}{k}_{\psi }(1-\text{cos }\psi )$$

Note that ψ_eq = 0.

Evaluating the Mechanical Energy

For each configuration evaluated, the mechanical energy was minimized using gradient methods. The initial configuration was first relaxed with several hundred steps of steepest descent minimization, followed by up to 100,000 steps of L-BFGS minimization. The stopping tolerance was set to $|\nabla E_{\text{mech}}(\overrightarrow{x})|/|\overrightarrow{x}|\le {10}^{-6}$, where $\nabla E_{\text{mech}}(\overrightarrow{x})$ is the gradient of the energy for configuration $\overrightarrow{x}$.

Calibration of Mechanical Model

The mechanical model describes the mechanical properties of a MT, therefore experimentally measured mechanical properties can be used to calibrate relevant parameters in the mechanical model. Two types of mechanical properties of MTs have been measured. One is flexural rigidity of MT, which can be measured by either bending a MT with mechanical force or measuring thermal fluctuations of a MT. Many experiments have been performed along this line; the resulting flexural rigidity varies with experimental conditions, as is typical for MT system. Another type of experiment is to use AFM tip to mechanically dent a MT lattice and measure the elastic response.

We simulated bending of MT using the full mechanical model, in which we adjusted parameters in the model (Table S2) to reproduce a flexural rigidity measured in experiments (1.8 × 10⁻²⁴ N · m², details in Data S1) (Felgner et al., 1996, Gittes et al., 1993, Kurachi et al., 1995, Venier et al., 1994). From these simulations, we found that k_long, which is the force constant for the stretching of longitudinal bond, dominates flexural rigidity.

In contrast, there has been only one experiment on denting MTs with AFM by Schimdt and co-workers on taxol-stabilized MTs (Schaap et al., 2006). Wu et al conducted a mechanical simulation of this experiment (Wu et al., 2012). The mechanical model they developed is similar to what we have here, though in a different coordinate system. In addition, their model has an extra term for describing the relative sliding between two laterally bonded monomers under sheering stress. Longitudinal and lateral bonds between tubulin monomers are formed by extensive protein-protein interactions that spread over extended region. When the monomers are under sheering stress, they can slide relative to each other and create deformation in the contact surface between them. However, sliding is a response of a MT to strong external force and would not occur under natural self-assembly of tubulins, which is the situation that we are simulating. Thus we do not include this lateral bond sliding term in our mechanical model to avoid introducing extra parameters that are not essential.

Wu et al found that this lateral bond sliding term is very important for capturing the denting experiment (Wu et al., 2012), and its effects overlap with that of the bending of lateral bonds. On the other hand, the parameter for lateral bond bending they determined by fitting the denting response is similar to the value we used in our full mechanical model. With our full mechanical model, we obtained a spring constant for denting response to be 0.08 N/m, in line with experimental measurements in ref. (Schaap et al., 2006) (details in Data S1).

Semi-Analytic Mechanical Model

Because mechanical energy is used to modulate chemical reactions in the system with Eq. S3, it needs to be evaluated at every time step. This makes the computational cost for numerically evaluating mechanical energy with the model described above too high. On the other hand, the harmonic nature of the bonding energies means the total mechanical energy of the system is essentially elastic, making it feasible to develop a semi-analytic model that can reproduce the energies of the full mechanical model with tremendously reduced computational cost.

The purpose of mechanical energy is to account for the energetic cost of deviating from equilibrium global polymer structure due to conformational changes of individual structural elements (monomers and interfaces), thus mechanical energy of pure tube is zero. Consequently, mechanical energy is focused in the transition region between tube and sheet, so it mostly affects growth of sheet from tube and conversion of sheet into tube. To develop an accurate approximation to the full rigid-body mechanical model, we evaluated the energy of various intermediate structures between the sheet and tube states. We found that the mechanical costs could be decomposed into three major components.

The largest component occurred at the longitudinal interface between tube and sheet, when a pair of dimers on the sheet side had sheet lateral bonds. This introduced considerable strain at this interface due to the torsion caused by the mismatch between the preferred angles of the sheet and tube lateral bonds (Fig. S12). This mismatch forced lateral bonds to be twisted out of their equilibrium position. We found that this cost increased quadratically with each mismatch in the same row. The second largest component is a consequence of this mismatch. Each additional row of sheet after the sheet/tube interface could not immediately relax, as this would introduce another large mismatch at the longitudinal interface. Instead, they relaxed gradually, with each row bearing a constant fraction of the strain of the previous row that depends on the width of the row. This gives the additional energy of each row an effectively exponential decay and makes the total energy resembles a geometric sum. The third component involved lateral interfaces between straight and bent monomers. This cost proved small compared to the first two.

Based on the discussion above, we first need a description of the mechanical strain at the tube-sheet boundary due to the torsion caused by the mismatch between the preferred angles of the sheet and tube lateral bonds. This mechanical strain is determined by the number of sheet and tube lateral bonds on the sheet side. Since all the interactions in the mechanical energy are harmonic terms, the mechanical strain has a quadratic form. Empirically, we found the following form:

$$E_{\mathit{\text{long}}}\left(n_s,n_t\right)=a+b{n}_s+c{\left(n_s\right)}^2+d{n}_t+p{n}_s{n}_t$$ (S4)

where n_s and n_t are the number of sheet and tube lateral bonds on the sheet side respectively. Only n_s appears in the quadratic term because the mechanical strain is caused by the mismatch due to the sheet lateral bonds, whereas a tube lateral bond contributes only because it shares the same dimer with a sheet lateral bond. We fit this to the minimum energies from the full mechanical model for a tube that had 50 dimer-rows of pure tube and a single, partial row of sheet. The width and offset of the sheet was varied to allow us to construct a semi-analytic model that would accurately reproduce the change in mechanical energy from adding a new row of sheet.

We found that a linear regression to Eq. S4 reproduce correct energies for the single row case, but the quadratic terms could over-estimate the cost for forming individual lateral bonds between two disjoint regions of sheet in a single row. To fix this issue, we imposed a penalty on the fit to restrict the maximum cost of combining two disjoint regions of sheet. To derive this penalty, we define:

$$\mathit{\text{Δ}}{E}_{\mathit{\text{bond}}}\left(n_s\right)=\left|E_{\mathit{\text{long}}}(N,N)-\left[E_{\mathit{\text{long}}}\left(n_s,n_s+1\right)+E_{\mathit{\text{long}}}\left(N-n_s,N-n_s\right)\right]\right|$$ (S5)

Squaring this expression, we can find the maximum occurs at $n_s=\frac{1}{4}\left(2N-\frac{p}{c+p}\right)$ and is

$$\text{max}\left(\Delta E_{\mathit{\text{bond}}}\right)=\left|-a-d+c\left(\frac{N^2}{2}-\frac{1}{8}\right)+p\left(\frac{1}{8}-\frac{N}{2}+\frac{N^2}{2}\right)+\frac{c^2}{8(c+p)}\right|$$

We limited max(ΔE_bond) to around 0.7 k_BT by imposing a fitting penalty on values above that. The penalty was imposed by adding a term onto the residuals used for fitting. This term was zero for max(ΔE_bond) <0.7 k_BT and increased to a large value (e.g. 10000) for max(ΔE_bond) > 0.8 k_BT. A cubic spline smoothly interpolated between the two values when 0.7 ≤ max(ΔE_bond) ≤ 0.8. We used the standard R non-linear fitting function “nlm” to fit the resulting function and penalty. Table S3 lists the parameters that were effective in reproducing the full mechanical model while not restricting two regions of sheet from joining.

To establish the strain of additional rows of sheet, we evaluated the following form of the energy of each additional row of sheet:

$$\Delta E_n=r(w)\Delta E_{n-1}+\sigma (w)$$ (S6)

where r(w) is a constant strain retention ratio and σ(w) is a constant strain added for each row of sheet. Both depend on the number of PFs in the previous row w. To fit this form, we rewrite this recursive form into a closed form:

$$\Delta E_n=r(w)\Delta E_{n-1}+\sigma (w)=\left(\Delta E_1-\frac{\sigma (w)}{1-r(w)}\right)r{(w)}^{n-1}+\frac{\sigma (w)}{1-r(w)}$$

To fit the total energy of a sheet of n rows, we sum the energy of each row:

$$E_N=\sum _{n=1}^N\Delta E_n=\left[\frac{\left(\Delta E_1-\frac{\sigma (w)}{1-r(w)}\right)}{1-r}\right]\left(1-r^N\right)+N\left(\frac{\sigma (w)}{1-r(w)}\right)$$

To reduce the covariance of the parameters in the fit, we combine the coefficients and rewrite this as

$$E_N=A\left(1-r^N\right)+N\delta (w)$$

As N increases, the two terms of E_N affect its behavior in different regimes. At small N, the energy 1 − r^N term has the largest effect on the change in energy, while at large N, 1 − r^N ≈ 1 and the N δ (w) term provides a constant, linear change in energy. Accordingly, we determine the δ (w) parameter as the slope of a line fit through the linear region at large N (N > 15), and fit the r (w) parameter using the standard R nonlinear fitting procedure. We fit these two parameters to the minimum energies from the full mechanical model for a tube that had 50 dimer-rows of pure tube 1–25 rows of sheet with 2–13 PFs at different offsets to allow us to accurately recreate the behavior of additional rows of sheet. The results of this fitting procedure show excellent agreement with the mechanical energies from the full model (Fig. S12). To use the original formula, Δ E_n = r(w)ΔE_n−1 + σ(w), the σ(w) parameter is determined by r(w) and δ(w) through the relationship σ(w) = (l − r(w)) δ(w).

We treat the cost of lateral interfaces between straight and bent monomers by fitting specific δ(w) parameters for three kinds of lateral sheet-tube boundaries: 1) no tube; 2) tube on one side of the sheet; and 3) tube on both sides of the sheet. The second configuration has two different δ(w) parameters for the two possible tube/sheet configurations. We fit the δ(w) parameters for all four boundaries, and extract the relevant σ(w) = (l − r(w)) δ(w) using the r(w) parameters determined previously. Parameters for r(w) and σ(w) are shown in Tables S4.

For sheet that has a lateral interface with tube, we found that the relaxation parameter r(w) worked better with an effective width given by the following rules: 1) for situations with lateral interface with tube, the effective width is the width, or w_eff = w; 2) if the lateral tube interface corresponds to the “left” (tube at PF j, sheet at PF j + 1), then the width increases by one, or w_eff = w + 1; 3) if the lateral tube interface corresponds to the “right” (sheet at PF j, tube at PF j + 1), then the effective width increases by two, or w_eff = w + 2; 4) there are two lateral tube interfaces then both rules apply, or w_eff = w + 3; and 5) the maximum effective width is 13.

We describe below the procedure for calculating the semi-analytic mechanical energy at the plus end; the minus end is the same with the directions reversed, so n − 1 becomes n + 1. The plus-end semi-analytic mechanical model energy is calculated as:

1. In each dimer-row, dimers are classified as either tube or sheet.

2. In row n, a dimer that was tube in row n − 1 may become sheet. A dimer that was sheet cannot become tube, as this would require forming interfaces with steric clash (see the steric rules).

3. For row n that contains a sheet dimer, we calculate an energy that this row contributes to the overall mechanical energy. This is split into three quantities that correspond to the three terms described above: regions of sheet that share a longitudinal interface with regions of tube, regions of sheet that can relax from the previous row (which was tube), and lateral interfaces between tube and sheet dimers. These contribute as follows:

   1. We find contiguous runs of sheet in row n. Each contiguous run has a width w that corresponds to the number of dimers in the run.
   2. For each contiguous run, we find the overlap with preceding contiguous segments of sheet. We use this to calculate the total relaxable energy of each segment as follows: for a segment i in row n, the relaxable energy for a segment j in row n − 1 is $\Delta E_{n,i,j}^{\text{relax}}=\frac{n_{\text{ov}}(i,j)}{n_{\text{seg}}(j)}\Delta E_{n-1,j}$, where n_ov(i,j) is the number of overlapping dimers between segments i and j, n_seg(j) is the total number of dimers in segment j, and ΔE_n−1,j is the energy contribution of segment j in row n − 1. The total relaxable energy for segment j is the sum of all the relaxable energies for the segments it overlaps.
   3. For each contiguous run, we also find the new tube/sheet longitudinal interfaces. The contribution $\Delta E_{n,i}^{\text{new }}$ is determined from the new row energies described above.
   4. The lateral interface energy σ_n,_i for each contiguous run is determined using the σ(w) parameters obtained above where w is the effective width of each segment: σ_n,i = σ(w_i)

4. Once $\Delta E_{n,i}^{\text{new }}$, $\Delta E_{n,i}^{\text{relax }}$, and σ_n,i have been determined, the energy of the segment is: $\Delta E_{n,i}=\Delta E_{n,i}^{\text{new }}+r\left(w_i\right)\Delta E_{n,i}^{\text{relax }}+{\sigma }_{n,i}$

5. The energies of each row are equal to the sum of the energies of the row’s contiguous segments of sheet, and the total semi-analytic mechanical energy is the sum of the mechanical energy of all the rows.

Numerical Strategies for Reducing Computational Cost

There are three major computational costs for large, spatially-resolved Gillespie simulations on lattices: 1) determining the reactions allowed by a particular configuration of the lattice, 2) calculating total rate of exit from that configuration, k_tot, and 3) selecting the next reaction proportional to the rate of each reaction.

Each step of a standard Gillespie simulations requires enumerating the possible reactions at each site of the lattice, a costly calculation that grows linearly with the number of occupied sites of the lattice. This cost can be tremendously reduced by recognizing that most changes to the lattice state affect the reactions of a small fraction of sites, all within a fixed distance of the site of the current reaction. To do this, we maintain a list of reactions at each site, and only update the reactions at the sites that are affected by a change in the lattice.

To store the list of reactions, we use a variation of a Fenwick tree (Fenwick, 1994), a data structure that allows for both efficient recalculation of the total reaction rate and an efficient search for the next reaction. The nodes of the tree are organized as a binary tree, where each level of node has the sum of the rates of the levels below. Updating the overall rate of a node requires updating the rates of all the nodes above, an average of a log₂ N operations for N total reactions. Searching the tree for the next reaction is essentially a binary search through the tree, also requiring an average of log₂ N operations for N total reactions.

These optimizations reduce the computational cost of each step of the simulation enormously. In our model, a 50-dimer MT has 3900 sites, but most changes of the lattice only affect sites within a 5×5 square (lattice distance of δ = 2). Thus we reduce the cost by a factor of ~150. Importantly, the cost stays constant as the lattice grows; for a 325-dimer MT, the reduction is a factor of ~1000. The use of a Fenwick tree provides an even more dramatic reduction. There are typically four reactions that must be evaluated at each site. For a 50-dimer lattice, the straightforward prefix sum would involve 15,600 terms, while updating our tree structure involves only log₂ 15600 ≈ 13.9 terms (a factor of ~1000 reduction in cost), with a similar reduction for selecting the specific reaction.

Practical Measures to Reduce Computational Cost

One of the major challenges in simulating this system was managing the computational cost. The events in the system have vastly different time scales: rapid shortening at 27 μm/min requires a dimer to undergo an S→C transition every 1.36 milliseconds. In contrast, the lowest frequency for catastrophe is ~0.0005 sec⁻¹, indicating that a catastrophe on average occurs once every 2,000 seconds. This amounts to a difference of six orders of magnitude, and requires long simulations with extremely high computational cost to sample events on both timescales. As the lattice grows larger, the number of reactions also increases in a highly nonlinear manner, which can drastically slow down the simulation as it progresses. To make the simulations practical, we use two different approaches to reduce the computational cost: a) we avoid recalculating simulation quantities with each step unless they change (Stewman, 2007), and b) we introduce penalty terms to suppress unproductive and irrelevant reactions in the lattice.

The first approach consists of two major optimizations. 1) After each reaction, we only update reactions that have changed. The localized nature of interactions on the lattice presents a simple way to do this: reactions consist of changes in the state of one or more sites. Thus we only need to update the reactions of sites that depend on the sites changed. For most moves, the number of sites that are affected is constant, making updates independent of the size of the lattice and greatly reducing computational cost. 2) We use a tree structure similar to previous lattice simulations (Stewman, 2007, Tchernookov et al., 2009) for updating the total reaction rate and selecting the next reaction. This avoids recalculating most of the sums required for the Gillespie algorithm, and results in much faster simulations.

The second approach is needed to reduce the total number of reactions as the simulation progresses and focus on reactions relevant to experimentally observable phenomena, because number of unproductive and irrelevant reactions grows fast with the size of the lattice. For example, in the middle of the MT, the difference in chemical energy between SeS and StS states makes a single StS → SeS reaction rare but viable. However, the large number of StS states in a tube-like lattice makes the probability of a StS → SeS considerable. Once a StS → SeS reaction is attempted, there are two scenarios: 1) it is rejected because of the high mechanical energy that a SeS state induces in the middle of a tube lattice; or 2) it is immediately followed by the reverse SeS → StS reaction even if the attempt was accepted, due to the high energy of the resulting state. In either case, the system is returned to the state before the StS → SeS reaction was attempted. The net result is a nonproductive reaction and a waste of considerable computational time. The number of such reactions goes up quickly with the lattice due to mass action, thus they are attempted with high frequency. Although they do not impact the actual dynamic trajectories in simulations, they waste computational time tremendously and prevent proper sampling of rare events (i.e. catastrophe, rescue), which requires long simulations.

This situation results from our simulation scheme with the rejection step, which is necessary because pre-calculating the change in system mechanical energy, due to its global nature and the complexity of the semi-analytic model, for every candidate reaction is too expensive. This scheme is effective when the chemical energy alone can provide reasonable estimate of the probability of reactions, but its efficiency decreases significantly for cases similar to the example discussed above.

The key to remedy this situation is to prevent such unproductive reactions from being attempted in the first place, by including penalty terms for them in the chemical energy. There are only three types of nonproductive reactions, all with clear patterns: 1) B- and S-form dimers with two sheet-like lateral bonds, 2) B-form dimers with two tube-like lateral bonds, and 3) ScS conformation, which creates a sharp kink in the tube lattice. Thus we add penalty terms in the chemical energy for reactions that create these patterns in the middle of the lattice (i.e. more than four dimers from either plus or minus end) to prevent them from being attempted.

To control the size of the MT lattice in simulations and avoid interference between plus and minus end behavior, we simulate plus and minus ends separately, and stabilize the opposite ends. This is also in line with the experimental setup in ref. (Walker et al., 1988), where the minus/plus end of a MT with a dynamic plus/minus end is capped by the stable axoneme fragment. We also use separate simulations for growth/catastrophe and shortening/rescue, because both catastrophe and rescue are rare events: simulating them together will lead to inadequate sampling of both. In growth/catastrophe simulations, we start with a small seed MT in S-form either with a B-form sheet for plus-end simulations or a longer S-form tube for minus-end simulations. In shortening/rescue simulations, we start with a long S-form tube and give either the plus or minus end tips two rows of C-form dimers, mimicking the situation right after rapid shortening is initiated, so the MTs will immediately begin to shorten.

In order to have a fair comparison with experimental data, we also made some adjustments in calculating experimentally observed quantities to be in line with how they were measured in experiments. In the experiments of Walker et al (Walker et al., 1988), spatial resolution of the video microscopy has limitations. They do not measure dynamics of MTs shorter than 0.5 μm because the bright edge of the axoneme seed for growing MTs interferes with MT detection. In addition, the resolution of their video microscopy is < 0.25 μm. Together this means they only observe behavior of MTs with a minimum length between 0.5 μm and 0.5 + 0.25 = 0.75 μm. This fact appears to have impacted their measurement of catastrophe, especially at lower concentration, as the catastrophe frequency at 7.5 μm is substantially lower than what the linear fit predicted to be (Fig. 7 of ref. (Walker et al., 1988)). This is understandable because catastrophe frequency is higher and growth rate is lower at lower concentration. Therefore, more MTs catastrophe early and at short length under lower tubulin concentrations. This means more catastrophes at lower concentration will not be observed because they committed catastrophe before reaching the minimum length that can be reliably observed in the experiment.

To account for this factor in our simulation, we only count catastrophes for MTs longer than 0.75 μm in our simulations. We found that catastrophe frequency at 10 μm and higher concentrations is not influenced by the minimal length of MT at the time of its catastrophe. For 7.5 μm, because many MTs catastrophe early in the simulation, filtering out short MTs makes catastrophe frequency lower than what the linear fit predicts, mirroring the situation in experiments by Walker et al.

Similarly, in shortening/rescue simulations, enough MTs would immediately rescue. These rescues are effectively micro-rescues that in a growth/catastrophe simulation would not be counted as catastrophes; they are not experimentally observable either due to the resolution of video microscopy. We thus discarded all MTs that shorten for less than 0.5 μm to ensure we only count real rescues that are observable in experiments.

Supplementary Material

3

Video S1: A movie showing the S→C transition of a tubulin dimer. It was created from a linear interpolation between structures 1JFF and 1SA0 using UCSF Chimera. The α-monomer is on the left and the β-monomer is on the right, with their intermediate domains colored Blue and Green respectively. Although this movie by no means reflect the actual dynamics of S→C transition, it clears illustrates the overall direction and magnitude of the transition that are sometimes difficult to visualize from static structures alone.

4

Video S2: A movie showing the transition of a tubulin dimer from SsS (1JFF) to ScC conformation. It was created from a linear interpolation between these two structures. To construct ScC structure, the α-monomer in CcC structure is replaced by an α-monomer in S form obtained from 1JFF, aligned to the original α-monomer by the N- and C-terminal domains. The loosening of the contacts between the intermediate domains of the two monomers during the transition is very obvious.

5

Video S3: A trajectory showing the evolution of the plus-end lattice states from a simulation at 10 μM. The color convention is: Blue for interfaces (longitudinal or lateral) or monomers in S form; Green for interfaces or monomers in B form; Magenta for monomers in C form; Orange for longitudinal interaces in C form. To facilitate viewing, the whole lattice is shifted to the upper edge of the image window when the plus-tip touches the lower edge of the image window.

Highlights.

• Dynamic instability is fully explained by kinetics of tubulin conformational changes

• Catastrophe and shortening are controlled by straight-to-curved transition of tubulins

• Rescue is the reverse of catastrophe

• Minus-end follows different kinetic pathways for tubulin conformational changes