Nonequilibrium dynamics of magnetic nanoparticles with applications in biomedicine

Abstract

Magnetic nanoparticles are currently the focus of investigation for a wide range of biomedical applications that fall into the categories of imaging, sensing, and therapeutics. A deep understanding of nanoparticle magnetization dynamics is fundamental to optimization and further development of these applications. Here, a summary of theoretical models of nanoparticle dynamics is presented, and computational nonequilibrium models are outlined, which currently represent the most sophisticated methods for modeling nanoparticle dynamics. Nanoparticle magnetization response is explored in depth; the effect of applied field amplitude, as well as nanoparticle size, on the resulting rotation mechanism and timescale is investigated. Two applications in biomedicine, magnetic particle imaging and magnetic fluid hyperthermia, are highlighted.

1. Introduction

In recent years, the use of magnetic nanoparticles (MNPs) for a range of biomedical applications, specifically in the areas of medical imaging, diagnostics, and treatment, has been the focus of significant research. Their small size allows MNPs to infiltrate biological systems, and their magnetic properties allow them to be controlled and detected by externally applied magnetic fields and field gradients, allowing for a wide range of potential clinical uses [1, 2] which include targeted drug delivery [3, 4, 5, 6], stem cell tracking [7, 8, 9, 10, 11, 12], molecular detection through magnetic separation [13, 14, 15, 16, 17, 18, 19, 20], contrast enhancement for magnetic resonance imaging [21, 22, 23, 24, 25, 26], hyperthermia therapy in cancer treatment [27, 28, 29, 30, 31, 32], and magnetic particle imaging [33, 34, 1], among others [1, 2, 35]. For further development of these applications, specifically for those involving the application of alternating magnetic fields, a complete understanding of the dynamics of magnetic nanoparticles under nonequilibrium conditions is required.

1.1. Superparamagnetic nanoparticles

Magnetic nanoparticles, comprised of ferromagnetic, ferrimagnetic, or in some cases antiferromagnetic materials, have a permanent magnetic moment in the absence of an applied magnetic field. When the size of a magnetic nanoparticle is reduced to below the single domain limit (e.g. around 30 nm for iron oxide), it can become superparamagnetic at room temperature, in which case the MNP will have a single net magnetic moment that can spontaneously flip within a defined time period. The MNP will behave as a paramagnet under an applied field, but with a magnetic moment magnitude much larger (by as many as four orders of magnitude) than those of typical paramagnets. The lack of remanent magnetization enables the MNPs to avoid agglomeration and maintain colloidal stability, which is critical for use in biomedical applications, while their large magnetic moment allows them to be manipulated by external magnetic fields and remotely detected even at low concentrations. The motion of the magnetic moment of a superparamagnetic particle under an applied field will be a complex stochastic process, due to coupling of the magnetic moment to the microscopic degrees of freedom of its environment (e.g. conducting electrons, phonons, nuclear spins) resulting in thermal fluctuations. The dynamics can also be affected by macroscopic parameters such as the non-magnetic coatings, often used for biocompatibility or for specific functionalization. Iron oxide, particularly the magnetite phase (Fe₃O₄), is a commonly used material for MNPs for biomedical applications, due to its biocompatibility.

Developments to the chemical synthesis procedure have now enabled superparamagnetic iron oxide nanoparticles (SPIONs) to be synthesized with a high degree of control over their phase, size, size distribution, and shape [36, 37, 38, 39]. SPIONs are typically coated with a surfactant, such as a polymer [40, 41, 42, 43, 44, 45, 46, 47], for stabilization in water. Additional functional groups or targeting molecules can then be added to the surface of the nanoparticle, if required. With proper surface functionalization, SPIONs can bind to proteins, genes, or viruses; interact with single cell-receptors; target cancerous tissue; or penetrate cells [13, 48, 49, 23, 50, 19, 2]. The therapeutic and diagnostic power of SPIONs becomes evident when these functionalities are considered in combination with their ability to be magnetically controlled and detected.

1.2. Applications of MNPs in biomedicine

The biomedical applications of MNPs generally fall into the categories of imaging, sensing, and therapeutics. MNPs are currently used as contrast agents for magnetic resonance imaging [23, 25, 26, 51], but are also the key component of magnetic particle imaging (MPI), a new medical imaging system in the preclinical stage [33, 34, 1]. In MPI, a combination of static gradient and alternating current magnetic fields allows the concentration and distribution of magnetic nanoparticles to be detected, enabling reconstruction of a three-dimensional image [33, 52, 34, 1, 53]. MPI relies on the nonlinearity of the magnetization curve for a superparamagnetic particle and the fact that its magnetization is eventually saturated for any applied magnetic field greater than the saturation field. If the MNPs are subject to an oscillating magnetic field, the magnetization response, M(t), will vary with time. The time-varying magnetization will induce a voltage in the receive coil, which will be proportional to the rate of change of the magnetization, M′(t). The spatial localization of the signal is achieved by superimposing a static magnetic gradient field on top of the alternating field, such that the MNP magnetization is saturated outside of the field-free region [33].

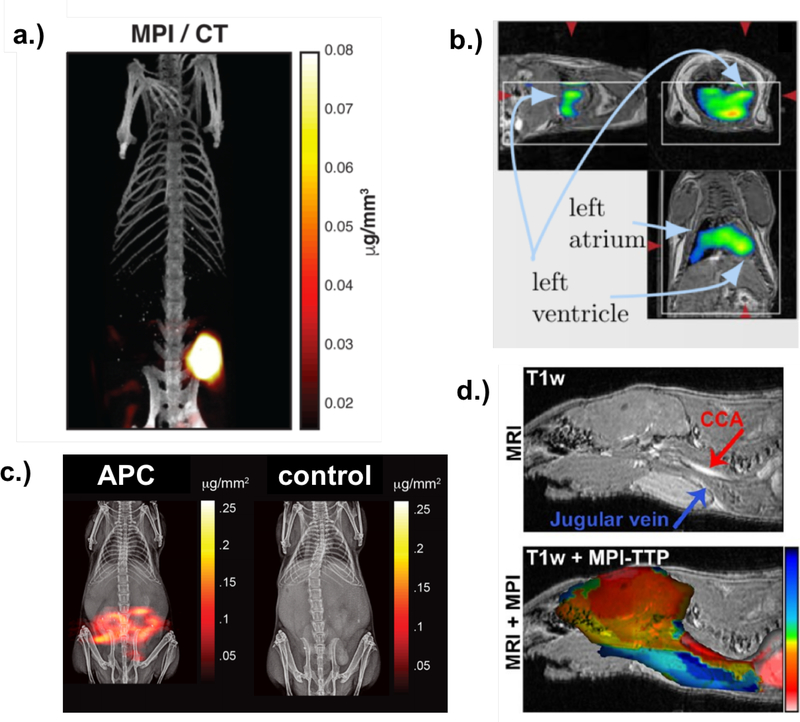
SPIONs are currently used as contrast agents to enhance signal in MRI [54], and so their safety and viability have already been well-tested. However, in MRI, SPIONs generally provide T2 (dark) contrast, whereas they provide positive (bright) contrast in MPI, which is favored by radiologists and clinicians (although it has been shown that bright T1 contrast can be achieved with very small SPIONs 4–7 nm in diameter [51]). Since MPI is a tracer-based imaging system, it produces a quantitative image signal with no background signal from surrounding tissue, since biological tissue is weakly diamagnetic and generates no MPI signal [1]. MPI has high mass sensitivity, and therefore large signal generating efficiency, many orders of magnitude greater per volume than protons detected with MRI, for example, resulting in a high signal-to-noise ratio (SNR) [52] which enables fast image acquisition times. Real-time imaging with MPI over short timescales (on the order of tens of milliseconds) has already been demonstrated [52, 55]. The high SNR also enables MPI to detect very low concentrations (on the order of nanograms [56]) of MNPs, reducing the quantity needed for accurate imaging [57]. The MPI signal is linear with tracer concentration, providing a quantitative image. Furthermore, MPI may be both safer and more cost efficient than other leading medical imaging methods, since it requires only a magnetic field gradient, rather than an expensive highly uniform superconducting magnet, as required for MRI. MPI SPION tracers can be stored for months and are cheaper to produce than radioactive tracers used in positron emission tomography (PET), for example, and are much safer than iodine and gadolinium contrast agents, which are are used in other imaging modalities. Iron oxide magnetic nanoparticle formulations have been approved by the FDA for doses as large as 500 mg/day [58] and shown to have no adverse effects on the body, in contrast to iodine, used for computed tomography (CT), and gadolinium, used in MRI [59], particularly for the small quantities required for MPI. Again due to its high SNR, MPI only requires a very small amount of these tracers, compared to the doses approved. Specific clinical applications for MPI include in vivo cancer imaging [60] (Fig. 1a), real-time cardiovascular imaging [56] (Fig. 1b), gut bleed detection [61] (Fig. 1c), acute stroke detection [62] (Fig. 1d), as well as stem cell tracking [63].

Figure 1:

a. MPI image of a mouse tumor acquired 6 hours after tracer injection with CT underlay. Reproduced with permission from [60]. b. MPI images of nanoparticles passing through a mouse heart with MRI underlay. Reproduced with permission from [56]. c. MPI image of a mouse with GI bleed (left) vs. control (right) with MRI underlay. Reproduced with permission from [61]. d. MPI stroke imaging of a mouse with MRI underlay. Reproduced with permission from [62].

MNP dynamics are highly sensitive to their surrounding environment, which enables the use of MNPs as sensors. For example, changes in viscosity can be detected using the technique of magnetization spectroscopy of nanoparticle Brownian motion (MSB), developed by John Weaver and Adam Rauwerdink [64]. Other biologically relevant parameters, such as temperature, can be detected and even quantified using such a technique [65, 66]. With proper surface functionalization, sensing of specific biomolecules is also possible, due to changes in dynamics that result from differences in the binding state of MNPs, enabling a range of diagnostic applications [67, 68, 69]. These sensing techniques can in principle be combined with imaging, via MPI, to create multi-channel or multicolor images, in which color represents a parameter such as viscosity or temperature, in theory enabling simultaneous real-time imaging and diagnostics.

Another biomedical application of MNPs is magnetic fluid hyperthermia (MFH), in which high-frequency excitation fields are used to induce nonlinear MNP rotations in cancer cells, generating cytotoxic heat [29, 30, 70, 71, 32, 72]. MNPs can be localized in tumors, either with the use of targeting ligands or direct injection. Under application of an alternating magnetic field, magnetic hysteresis losses will result in localized heating of the tumor, triggering the onset of apoptosis under correct conditions. Localized hyperthermia can also be used in conjunction with conventional cancer treatments, such as chemotherapy and radiation, to improve their efficiency [73]. In theory, MFH could also be combined with MPI and temperature sensing to create a combined imaging and therapeutic platform, in which the MNPs and resulting heat generation could be quantitatively tracked. A related use is targeted delivery of chemotherapy drugs, in which antitumor drugs are attached to the nanoparticle surface and then released via thermal activation from application of an external magnetic field. In a similar way, MPI combined with sensing of temperature or binding-state could enable a monitored targeted drug-delivery system.

While the biological applications of MNPs extend beyond these, the above applications have been highlighted because they require a detailed understanding of MNP dynamics in vivo, including their dependence on environmental and particle properties under nonequilibrium conditions. Outlining the current theoretical models of MNP dynamics up to the most recent developments in computational modeling in the context of imaging and therapy will be the focus of this work.

2. Equilibrium and linear models of nanoparticle relaxation

Superparamagnetic nanoparticles are single-domain, and so have a single net magnetic moment. Under an applied magnetic field, the MNP magnetic moment will rotate to align with the field. We define the equilibrium relaxation time constant τ, which refers to the time required for the particle moment to return to equilibrium after an external perturbation. When applying a field, we first consider the equilibrium case, where the timescale of the change in field is large enough that the particle can reach equilibrium at every step. Under an oscillating magnetic field, for example, this condition requires 1/f ≫ τ, where f is the frequency of the applied field. While this condition typically does not apply for biomedical applications of MNPs, it is still instructive to examine the equilibrium case before moving on to nonequilibrium scenarios.

2.1. The Langevin function

Superparamagnetic nanoparticles can be modeled as dipoles with magnetic moment magnitude μ = M_sV_c, where M_s is the saturation magnetization of the material (∼ 420 kA/m for magnetite), and V_c is the volume of the magnetic core. We distinguish this from the hydrodynamic volume, V_h, which includes the non-magnetic ligands that are applied to the surface of the core particle. In an ensemble of isotropic non-interacting magnetic nanoparticles, the equilibrium energy of an individual particle will be:

$$E=-{\mu }_0\mathit{\mu }\cdot \mathbf{H}.$$ (1)

Here, μ is $\mu \widehat{\mathbf{m}}$, with $\widehat{\mathbf{m}}$ a unit vector pointing in the direction of the magnetic moment, μ₀ is the permeability of free space, and H is the applied magnetic field. Without loss of generality, for the remainder of this section we define the field to be applied in the z-direction. With the partition function of an ensemble of such particles, the average particle energy and magnetization in the z-direction can be extracted. The average particle magnetization is proportional to the Langevin function:

$$\langle m_z\rangle =\mu \mathcal{L}(\xi ),$$ (2)

where

$$\mathcal{L}(\xi )=\coth \xi -1/\xi .$$ (3)

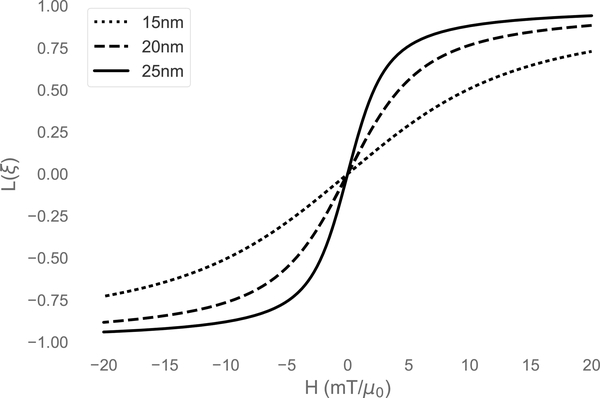
Here, ξ is the unitless field, μ₀μH/k_BT, where T is the temperature and k_B is Boltzmann’s constant. This well-known equation describes the magnetization of an ensemble of isotropic particles at equilibrium, i.e. when the particle dipole moments are allowed to fully relax at every step of the applied field. The Langevin function for three different particle core sizes is shown in Fig. 2. It should be emphasized that the Langevin function does not incorporate particle anisotropy, and so is only applicable as an approximation for small or nearly isotropic particles in a nonequilibrium case.

Figure 2:

The Langevin function for three different particle core diameters, with M_s = 420 kA/m at 300 K. Note that the derivative, dM/dH at H = 0, increases with increasing particle size.

2.2. Anisotropic partition function

In reality, superparamagnetic nanoparticles will have some degree of anisotropy, resulting from combined magnetocrystalline, shape, and surface anisotropies. Typically, uniaxial anisotropy is assumed, indicating that there is a single easy axis $\widehat{\mathbf{n}}$ along which the magnetic moment prefers to align. In that case, we can define σ = KV_c/k_BT, where K is the effective anisotropy constant, incorporating all magnetocrystalline and shape anisotropy. We can then express the energy of a single particle as

$$\frac{E}{k_{B}T}=-\sigma {(\widehat{\mathbf{n}}\cdot \widehat{\mathbf{m}})}^2-\widehat{\mathbf{m}}\cdot \mathit{\xi }.$$ (4)

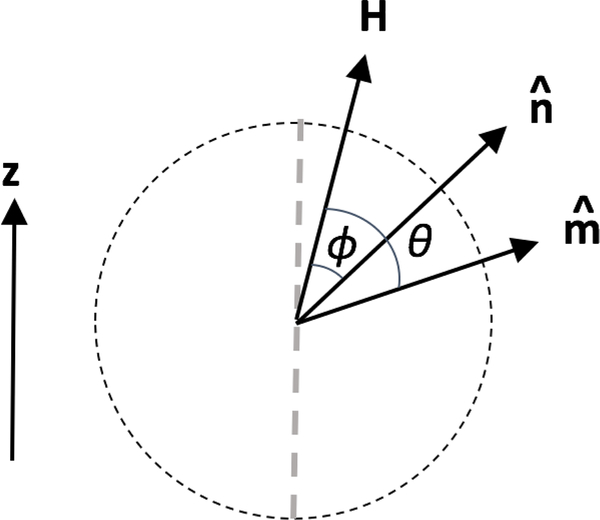
The first term represents the internal anisotropy energy, and the second term represents the energy from the Zeeman interaction with the external applied field. We define θ to be the angle between the moment and ξ (which points in the direction of the applied field), and ϕ to be the angle between the easy axis and ξ (see Fig. 4). If the assumption is made that the easy axis $\widehat{\mathbf{n}}$ is aligned with the magnetic field ξ in the z-direction and lies in the same plane as the magnetization, following Stoner and Wolhfarth [74], the system becomes two-dimensional. The energy, in unitless form, is then:

$$\frac{E}{k_{B}T}=-\sigma {\sin }^2(\theta -\varphi )-\xi \cos \theta .$$ (5)

Figure 4:

Angles defined in the general case. The direction of the applied field is indicated by H, the direction of the easy axis is indicated by $\widehat{\mathbf{n}}$, and the direction of the magnetic moment is indicated by $\widehat{\mathbf{m}}$. In many approximations, the applied field is assumed to lie along the z-direction (not shown here).

To find the equilibrium state of the particle, we take the derivative of the energy with respect to the moment direction θ, which simplifies to

$$\frac{\xi }{\sigma }=-\frac{\sin [2(\theta -\varphi )]}{\sin \theta }.$$ (6)

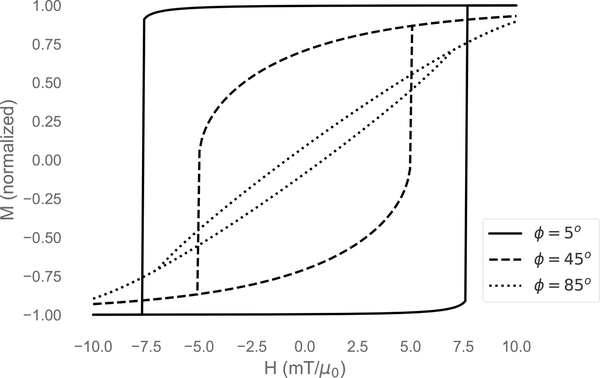
To find a minimum we must also ensure $\frac{{\partial }^{2}E(\theta ,\varphi )}{\partial {\theta }^2}>0$. The Stoner-Wohlfarth hysteresis loop emerges from solving for the magnetization (cosθ) and plotting with respect to the field (see Fig. 3). The width of the hysteresis loop depends on the angle ϕ between the easy axis and the applied field. This model has an advantage over the simple Langevin function in that it accounts for particle anisotropy, but still assumes equilibrium conditions, and therefore does not account for particle relaxation. Furthermore, in this form, the Stoner-Wohlfarth model does not incorporate thermal energy, and is only fully valid at T = 0. Extensions to the Stoner-Wohlfarth model which incorporate temperature dependency have been made [75, 76], but are not discussed here as they still do not incorporate particle relaxation.

Figure 3:

Hysteresis curves calculated from the Stoner-Wohlfarth model at different angles of the easy axis with respect to the applied field.

2.3. Nanoparticle rotation mechanisms and equilibrium timescales

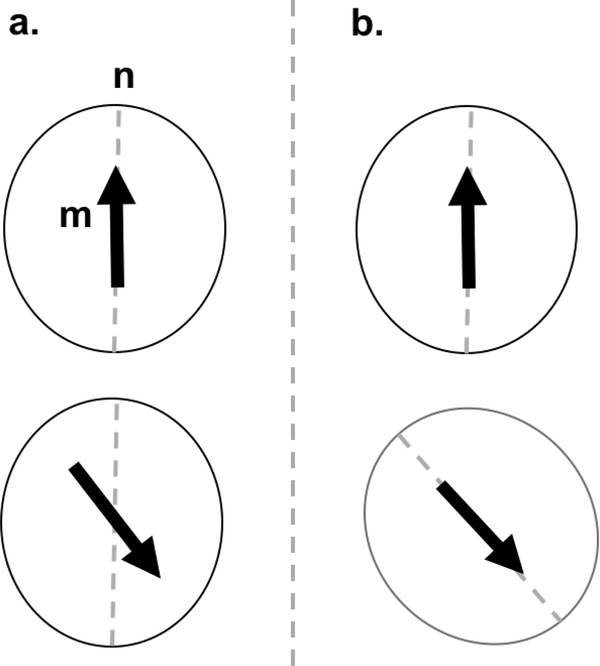
There are two mechanisms by which a superparamagnetic nanoparticle can reverse its magnetic moment. Brownian rotation refers to the physical rotation of the particle to align its magnetic moment with the applied magnetic field, and Néel rotation refers to the reversal of the magnetic moment within the particle itself, assuming that the physical particle remains stationary (see Fig. 5). The particle will rotate via either the Brownian or Néel process or some combination of both, although the faster mechanism will typically dominate. In MPI, nanoparticle dipole moments rotate under the influence of an external oscillating field, generating a measurable signal by induction in a pickup coil resulting from the changing magnetic field. The particle dynamics are typically discussed in terms of timescales of nanoparticle rotations, particularly the equilibrium relaxation time [77, 78, 79].

Figure 5:

Néel (a.) vs. Brownian (b.) rotation mechanisms. With Néel rotation, the easy axis n stays stationary, while only the magnetic moment m rotates. Under Brownian rotation, both the axis and the moment rotate.

Due to the magnetocrystalline anisotropy and shape asymmetry of MNPs, their magnetic moment will preferentially align with a particular crystallographic direction (the easy axis), a result of coupling between the atomic spin and orbital angular moments. The energy required to rotate the magnetization from the easy axis is denoted the anisotropy energy. The anisotropy energy, when uniaxial, has two minima, which correspond to alignment with the easy axis $\pm \widehat{\mathbf{n}}$, separated by an energy barrier KV_c. When this energy barrier is smaller than the thermal energy k_BT, the particle magnetic moment is free to rotate between energy minima. The Néel process occurs when the particle orientation (the easy axis) remains fixed while the magnetic moment flips, and is characterized by the equilibrium Néel relaxation time [80, 32, 81],

$${\tau }_N=\frac{\sqrt{\pi }}{2}{\tau }_0\frac{\exp (\sigma )}{{\sigma }^{1/2}},$$ (7)

where the attempt time τ₀ is equal to M_s/(2αγK). α is a dimensionless damping constant, assumed to be between 0.1 and 1, and γ is the gyromagnetic ratio.

When measuring MNP magnetization, the measurement time τ_M must be defined. The particle is in a superparamagnetic state when τ_M ≫ τ_N. In this state, the magnetization will flip multiple times over the course of the measurement resulting in zero net remanent magnetization. Alternatively, if τ_M ≪ τ_N, then the magnetization will not reverse during the measurement; the particle will be in a blocked state. The blocking temperature is defined as the temperature at which τ_M = τ_N, when the transition between the blocked and the superparamagnetic state occurs [80]. If the particle is in the blocked state, the particle physically rotates along with the magnetic moment, and is then described by the Brownian rotation mechanism. We can similarly quantify the characteristic equilibrium Brownian relaxation time [32, 30]:

$${\tau }_B=\frac{3V_h\eta }{k_{B}T},$$ (8)

where η is the viscosity of the surrounding medium and again V_h is the hydrodynamic volume including any ligands attached to the surface. The mechanism by which the particle reverses its magnetic moment will be determined by the particle anisotropy and size (smaller particles exhibit only Néel rotation, while larger particles exhibit primarily Brownian rotation). The effective magnetic equilibrium relaxation time is often expressed as [32, 30]:

$${\tau }_{\text{eff}}=\frac{{\tau }_B{\tau }_N}{{\tau }_B+{\tau }_N},$$ (9)

from which it can be seen that the mechanism with the lowest relaxation time for a given particle size and anisotropy will dominate. In reality, the two rotation mechanisms are coupled in a non-trivial way, which is not fully described by this effective relaxation time [82, 83]. Furthermore, when a sufficiently large external driving field is applied (ξ > 5), these equilibrium time constants can no longer completely describe the subsequent dynamics [79, 83]. Under a strong applied field, the magnetic moments of the particles will align faster than in the equilibrium case, and so the true timescales of rotation will be shorter than the equilibrium relaxation times.

2.4. Linear response theory

One of the most common models of dynamic MNP magnetization is the Debye/Fannin model [84], which describes the linear response of a dipole to an oscillating field. In linear response theory (LRT), it is assumed that the applied field amplitude is low enough (or that the frequency is high enough) so that magnetic saturation, when all particle moments are fully aligned with the field, is not reached. We define χ to be the magnetic susceptibility, which will be constant with increasing applied field H (so M = χH, where M is the ensemble magnetization in the direction of the field). According to the Langevin model, the equilibrium (or DC) susceptibility, χ₀, of a system of non-interacting MNPs will be [85]:

$${\chi }_0=\frac{M(H)}{H}=\frac{\mu }{H}\mathcal{L}(\xi ),$$ (10)

where $\mathcal{L}(\xi )$ is the Langevin function (Eq. 3). In the Debye model [84, 86], to account for the lag in magnetization with respect to the applied field, the magnetic susceptibility is broken down into real (in-phase) and imaginary (out-of-phase) components:

$$\chi ={\chi }^{\prime }-i{\chi }^{″}={\chi }_0\left(\frac{1}{1+{(\omega \tau )}^2}-i\frac{\omega \tau }{1+{(\omega \tau )}^2}\right).$$ (11)

τ represents the effective magnetic relaxation time, from Eq. 9, and ω is the angular frequency of the applied field. The out-of-phase component will have a maximum at ωτ = 1, at which point the phase shift between the particle’s magnetic moment and the applied field is maximum, resulting in energy loss. The Debye model assumes symmetry in the AC susceptibility spectrum (when plotted vs. log frequency), which is often not seen experimentally. The Havriliak-Negami model [87] provides a phenomenological model for the susceptibility:

$$\chi ={\chi }_{\text{inf}}+\frac{{\chi }_{\text{amp}}}{{(1+{(i\omega \tau )}^{1-\alpha })}^{\beta }}.$$ (12)

Here, χ_inf is the real susceptibility at high frequencies and χ_amp is the amplitude of the remainder of the frequency-dependent regime. The parameter α describes the width of the spectrum, and β incorporates the asymmetry. The model reduces to the Debye model in the limits of α = 0 and β = 1. This model, in addition to incorporating particle size distributions, can be used for more accurate fitting of AC susceptibility spectra to obtain the effective relaxation time.

Finally, the magnetization in the direction of the field is then described by:

$$M(t)=\mu {\int }_0^{\infty }\left(\frac{1}{1+{(\omega \tau )}^2}\mathcal{L}(\xi \cos \omega t)-\frac{\omega \tau }{1+{(\omega \tau )}^2}\mathcal{L}(\xi \sin \omega t)\right)g(d)\text{d}d.$$ (13)

Here we have included a size distribution g(d) for the particles, where d is the particle diameter, typically considered to be a log-normal distribution [88]. This model for the magnetization is theoretically valid as long as linear response theory holds, i.e. for high frequencies or low fields (typically when ξ is less than 10). However, for the frequencies and magnetic field strengths typically employed in MPI and MFH (frequencies on the order of tens or hundreds of kHz, and amplitudes on the order of tens of mT/μ₀), nonlinear behavior will arise. Consequently, while the Debye model is instructive, future sections will focus almost exclusively on nonequilibrium and nonlinear models of nanoparticle dynamics.

3. Nonequilibrium nanoparticle rotation timescales

The magnetic fields required for magnetic particle imaging and magnetic fluid hyperthermia are AC fields with frequencies on the order of tens or hundreds of kilohertz. The short timescales involved give rise to nonequilibrium conditions and resulting nonlinear nanoparticle dynamics. For these clinical applications of MNPs, it is essential to quantify properties of the nanoparticle dynamics as a function of the applied field and characteristics of the nanoparticles and surrounding medium. MNP dynamics are often described in terms of zero-field relaxation timescales; however, the effective rotation timescales have been shown to be highly dependent on field strength (for both AC and DC fields) [89, 79]. Moreover, the physical regime where both Néel rotation and Brownian rotation may occur has yet to be described in any quantitative manner for the relevant field strengths and frequencies required for the above mentioned applications.

Brownian and Néel mechanisms are each characterized by respective timescales. The equilibrium relaxation time constant predicts the time required for thermal fluctuations to reorient the net magnetization to zero after an applied magnetic field is removed. In reality, the Brownian and Néel mechanisms are coupled, and the respective rotation timescales are dependent on parameters like temperature, core and hydrodynamic size, and viscosity. The equilibrium relaxation timescales, which are often used to describe MNP dynamics, ignore applied fields and so have limited applicability for many biomedical applications of MNPs which employ applied magnetic fields. The rotational time constant will change with field and frequency, and for high fields the external magnetic field may dominate over thermal terms.

3.1. Field dependence of rotation timescales

The effective rotation timescale is often expressed as by Eq. 9, which assumes that the rotation mechanism with the lowest rotation timescale will dominate. It should again be emphasized here that τ_N and τ_B refer to zero-field relaxation timescales; once a magnetic field is applied, these equilibrium expressions will no longer hold. We first consider the case of MNPs subjected to a static magnetic field. Brown developed an expression for a DC field-dependent Néel relaxation time [90]:

$${\tau }_{N,H}=\frac{{\tau }_0\sqrt{\pi }}{{\sigma }^{1/2}\left(1-h^2\right)}{[(1+h)\exp (-\sigma {(1+h)}^2)+(1-h)\exp (-\sigma {(1-h)}^2)]}^{-1}$$ (14)

with dimensionless parameter h = H/H_k, with H as the applied magnetic field, the unitless anisotropic field σ = KV_c/k_BT, and H_k = 2K/μ₀M_s. This expression holds as long as the magnetic field is not too large (h < 0.4), and only when the easy axes of the particles are parallel to the field. When σ ≥ 2, Eq. 14 can be approximated as:

$${\tau }_{N,H}={\tau }_0\exp (\sigma {(1-h)}^2).$$ (15)

To properly generalize this expression, averaging over all directions of the easy axis would be necessary, assuming that easy axes in a realistic sample would be randomly oriented. Coffey et al. [91] showed that the Néel rotation timescale under a DC field is highly dependent on the angle between the easy axis and the field. However, to date, no generalized expression has been derived. Furthermore, the above expressions for the Néel rotation timescale are functions of σ, which is expressed in terms of K, the effective uniaxial magnetocrystalline anisotropy constant. For spherical magnetite nanoparticles, the magnetocrystalline anisotropy is cubic rather than uniaxial, and uniaxial anisotropy may not necessarily be an accurate approximation, particularly when considering the relative orientations of the easy axis to the field [92].

Martsenyuk et al. [93] developed the following expressions for the Brownian relaxation time in a static magnetic field, when relaxation is considered parallel and perpendicular to a small probing static field:

$${\tau }_{\text{par}}=\frac{\text{d}\ln \mathcal{L}(\xi )}{\text{d}\ln \xi }{\tau }_B$$ (16)

$${\tau }_{\text{perp}}=\frac{2\mathcal{L}(\xi )}{\xi -\mathcal{L}(\xi )}{\tau }_B$$ (17)

The above expressions are derived by treating the probing field as a small perturbation to the equilibrium field. From Eq. 17, we can find low-field (ξ < 5) and high-field (ξ > 5) approximations [93]:

$${\tau }_{\text{low}}=\left(1-\frac{1}{10}{\xi }^2\right){\tau }_B$$ (18)

$${\tau }_{\text{high}}=\frac{2}{\xi }{\tau }_B$$ (19)

The above expressions hold when ξ ≪ 𝜎 and σ ≥ 10, i.e. when Brownian rotation is clearly dominant and the field strength is still relatively small (compared to the anisotropy energy of the particle). It should be noted that DC magnetization timescales will have limited applicability to AC magnetic fields, except in the adiabatic limit of slowly varying magnetic fields (i.e. when the timescale of rotation is much smaller than the timescale of changes in the magnetic field).

Yoshida and Enpuku [94] derived the following expression for the Brownian rotation timescale under a large DC magnetic field, from fitting to the Fokker-Planck equation:

$${\tau }_{B,H}=\frac{{\tau }_B}{\sqrt{1+0.21{\xi }^2}}$$ (20)

They further determined the following set of equations to describe the dynamics of thermally blocked MNPs under relatively large AC magnetic fields (ξ₀ ≥ 20):

$${\chi }^{\prime }(\omega )=\frac{{\chi }_1}{1+{\left(\omega {\tau }_{B,H}\right)}^2}$$ (21)

and

$${\chi }^{″}(\omega )=k^{″}\frac{{\chi }_1\omega {\tau }_{B,H}}{1+{\left(\omega {\tau }_{B,H}\right)}^2}$$ (22)

where

$${\chi }_1={\chi }_0\left[1-\frac{0.0636{\xi }_0^2}{1+0.18{\xi }_0+0.0659{\xi }_0^2}\right]$$ (23)

and

$$k^{″}=1+\frac{0.024{\xi }_0^2}{1+0.18{\xi }_0+0.033{\xi }_0^2}$$ (24)

Using these expressions, the dynamics of purely Brownian particles under large AC fields can be described. For high DC fields, Eqs. 19 and 20 give similar results [83].

Dieckhoff et al. [89] developed an expression in the form of Eq. 20 for the effective Néel rotation timescale under an AC field, based on fitting to experimental data:

$${\tau }_{N,H}=\frac{{\tau }_N}{\sqrt{1+1.97{\xi }_0^{3.18}}}.$$ (25)

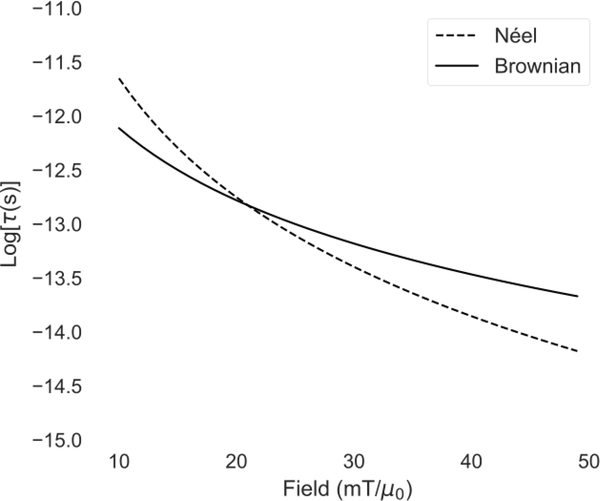
Fig. 6 is a plot of the rotation timescale calculated from Eqs. 20 and 25 as a function of applied field, with parameters d_c = 25 nm, d_h = 40 nm, α = 1, K = 5 kJ/m³, M_s = 420 kA/m, T = 300 K, and η = 1 cp. As can be seen from the figure, the Néel rotation time has a much stronger dependence on field strength. Making the assumption that the rotation mechanism with the shorter associated timescale will typically dominate, it can be inferred that for nanoparticles with these properties, for low fields, the Brownian mechanism will dominate, and for high fields, the Néel mechanism will dominate.

Figure 6:

Brownian and Néel rotation timescales (τ_B,H and τ_N,H from Eqs. 20 and 25) as a function of applied field amplitude, for nanoparticles with 25 nm core diameter and 40 nm hydrodynamic diameter.

The Néel mechanism may be much faster under high applied fields than the Brownian mechanism, even if the zero-field timescales are much higher. For example, with the parameters listed above, the zero-field relaxation timescales τ_N = 354 μs, whereas τ_B = 21.6 μs, a full order of magnitude lower. To understand this, we can look at the internal energy density, when the field is along the z-axis:

$$U(\theta ,\varphi )=K{\sin }^2(\theta -\varphi )-{\mu }_0{M}_{s}H\cos \theta$$ (26)

Again, θ is the angle between $\widehat{\mathbf{m}}$ and H, and ϕ is the angle between $\widehat{n}$ and H (see Fig. 4). The energy is a function of the orientations of the magnetic dipole moment, the crystalline lattice, and the external field. Without an external field, the energy density is symmetric with two minima at the locations of the easy axes. The moment will flip when the thermal energy exceeds the energy barrier, KV_c, and in this case the zero-field relaxation time τ_N will define the magnetization dynamics. When an external field is applied, the energy density will no longer be symmetric. One minimum will be lower, and the energy barrier will be reduced in that direction. For 0 < H < 2K/μ₀M_s, there will be two unequal minima, and for H ≥ 2K/μ₀M_s there will be only one minimum, resulting in a lowered average time to transition. So, for example, there will be only one minimum in the energy density once the magnetic field strength reaches 25 mT/μ₀ for M_s = 420 kA/m and for K = 5 kJ/m³, indicating that for fields above 25 mT/μ₀, the dynamics will be purely driven by the field, since spontaneous flipping of the magnetic moment is not possible.

In applications such as MPI, both static and alternating magnetic fields are employed. As shown above, expressions for field-dependent rotation timescales have been derived for purely Brownian and purely Néel-dominated MNPs, with certain restrictions (particularly, for Néel rotation, that the field is applied parallel to the easy axis). However, as Diessler et al. [79] demonstrated, the Brownian and Néel rotation mechanisms are coupled in a complex way that depends on applied field strength. With increasing field strength, both rotation timescales decrease, but the Néel rotation timescale decreases much more rapidly, as seen in Fig. 6.

Consequently, the zero-field relaxation timescales may indicate that particles are purely Brownian, but for stronger magnetic fields, Néel rotation may dominate the dynamics. This will be especially relevant for high frequency fields, where the period of the AC field is smaller than either the zero-field Néel or Brownian timescales. In that case, the Brownian contribution may be very small, while the amplitude of the field may be strong enough to sufficiently decrease the effective Néel rotation time so that a magnetic response is observed.

3.2. Size dependence of rotation timescales

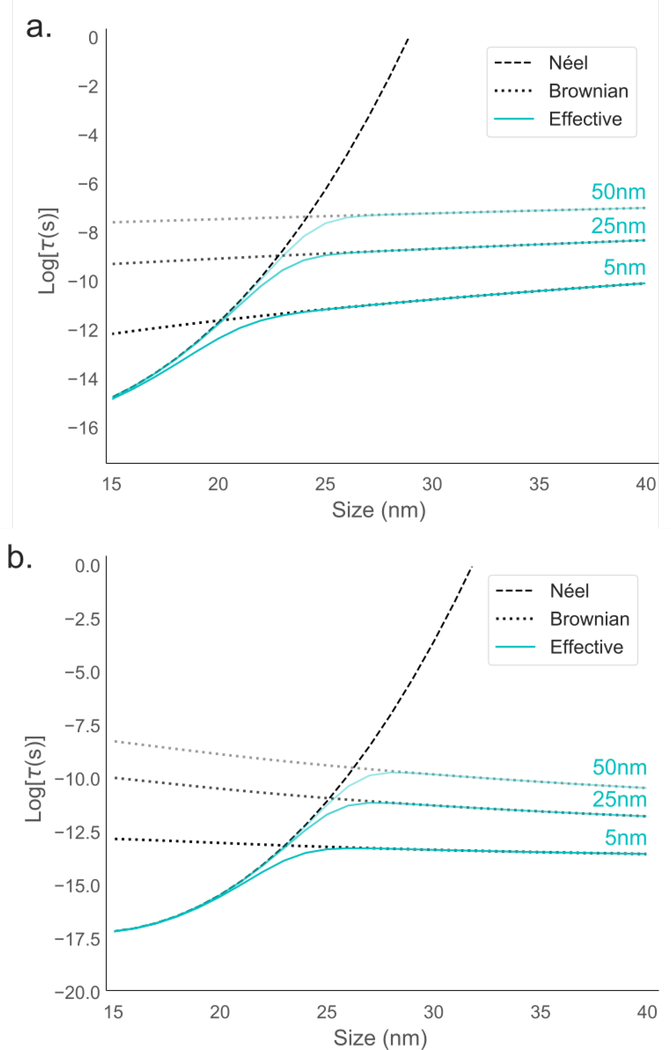
When both rotation mechanisms are considered, the rotation timescale is often described by the reduced relaxation time, τ_eff (Eq. 9). The reduced time implies that the mechanism with the shortest equilibrium relaxation time will dominate. The magnetic core size and hydrodynamic size of the particle will affect which mechanism will dominate, in addition to the field amplitude, as shown in the previous section. The reduced relaxation time τ_eff is plotted as a function of particle core size in Fig. 7a.

Figure 7:

a. τ_N, τ_B, and τ_eff from Eqs. 7, 8 and 9 as a function of core size. b. τ_N,H and τ_B,H from Eqs. 25 and 20 as a function of core size. In both cases, results for three different coating sizes are shown and indicated in cyan. The following parameters were used in both: H₀ = 20 mT/μ₀, K = 5 kJ/m³, M_s = 420 kA/m, T = 300 K, α = 1, and η = 1 cp. It should be noted that as this figure shows calculations for DC fields, it cannot necessarily be generalized to AC fields, such as those used in MPI or MFH.

Since the timescale of the Brownian rotation mechanism is highly dependent on the non-magnetic coating (τ_B scales as V_h), three different coatings have been plotted. The hydrodynamic diameter will be the sum of the core diameter and the non-magnetic coating on each side, so for a core diameter of 20 nm and coating of 5 nm, the hydrodynamic diameter will be 30 nm. For MPI applications, where iron oxide nanoparticles must be dispersed in water, there will always be an additional non-magnetic coating, for hydrophilicity as well as functionalization for in vivo medical purposes, such as long-term blood circulation or cancer targeting. The increase in size due to the added coating is often ignored, and Brownian rotation timescales are often compared to Néel rotation timescales with V_h = V_c [79], which is inaccurate for realistic MPI purposes. While the Néel mechanism is unaffected by added non-magnetic coatings, the Brownian mechanism is dependent on hydrodynamic size.

Using Eqs. 20 and 25, we can plot the field-dependent rotation timescales as a function of size as well. From these, we can also calculate an effective reduced rotation timescale, using the same formula as Eq. 9, but with τ_B,H and τ_N,H substituted for τ_B and τ_N. This is shown in Fig. 7b, also for three different coating sizes.

In the equilibrium (zero-field) case, the relaxation time increases with size. In the field-dependent case, the Néel rotation timescale increases with size, but the Brownian rotation timescale decreases with core size, in contrast to the zero-field case. In both cases, the coating size shifts the intersection point between Brownian and Néel rotation. Larger coatings indicate that the Néel mechanism will dominate through larger sizes. With Eqs. 20 and 25, we can extract the core size at which the two timescales intersect, which indicates the size at which the Brownian mechanism starts to dominate, as a function of field amplitude and coating size. For low field amplitudes (< 7 mT/μ₀) and small coatings (< 5 nm), Brownian rotation starts to dominate when the core size is around 22 nm. As both the field amplitude increases and the coating size increases, Néel rotation remains dominant for increasing core diameters. For high field amplitudes (> 50 mT/μ₀) and large coatings (> 50 nm), Néel rotation dominates up to particles that are larger than 27 nm. It should be emphasized again that these calculations are performed assuming DC fields, rather than AC fields.

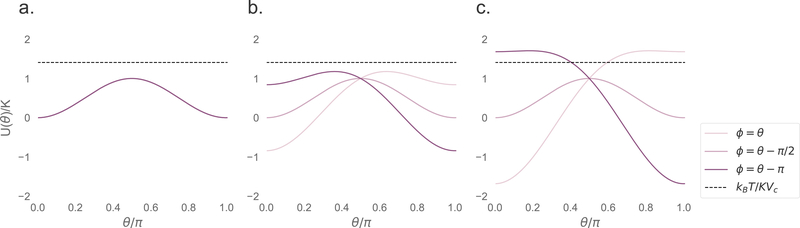
To understand this behavior, we study the energy density, described by Eq. 26. The energy density is shown in Fig. 8 for a range of different AC field strengths at different points in the field cycle, when the axis is aligned with the field (so when ϕ = 0 in Eq. 26). An AC field H = H₀ cos(ωt) is assumed. For small applied fields, the energy density has two minima at all times, and so the particle has enough thermal energy to spontaneously flip. Increasing the particle size will lower the effective thermal energy density k_BT/KV_c, which will increase the rotation timescale. As the field is increased, asymmetry is introduced, lowering the effective energy barrier and shortening the rotation timescale. For high fields, larger particles will no longer have enough thermal energy to spontaneously flip, and the rotation becomes purely driven by the field. The timescale of rotations will become highly dependent on applied field frequency, rather than the core volume.

Figure 8:

Energy density (Eq. 26) for a 10 nm particle as a function of θ, the angle between the particle magnetic moment and the applied field, for different points in the AC field cycle, ωt. The thermal energy density k_BT/KV_c is also shown. a. No external applied field b. 10 mT/μ₀ applied field. c. 20 mT/μ₀ applied field.

4. Nonlinear models of nanoparticle dynamics

The equilibrium and linear models described in the previous section are seriously limited in their ability to describe the dynamics of nanoparticles under the fields employed in MPI and MFH. MPI, for example, relies on nanoparticles reaching magnetic saturation outside of the field-free point, which results in nonlinear behavior outside of the limits of the Debye model. The frequencies used (on the order of tens of kHz for MPI and hundreds of kHz for MFH) are high enough that equilibrium conditions cannot be assumed. Furthermore, the AC field amplitudes used for MPI (on the order of tens of mT/μ₀) result in driven nanoparticle rotation rather than simple relaxation. In this section we proceed to the exploration of nonequilibrium, nonlinear models of nanoparticle dynamics.

4.1. Fokker-Planck equations

The first models we study are the Fokker-Planck equations, which describe the time evolution of the distribution of dipole-moment orientations W(x, t), where x ≡ cosϑ, so that ϑ and the azimuthal angle φ represent the direction of magnetic moment in spherical coordinates. The Fokker-Planck equation was first developed by Brown in 1963 [90]. In this interpretation, a nanoparticle’s magnetization is represented as an arrow pointing to a spot on the unit sphere. The function W(ϑ, φ, t) describes the probability distribution of moments on the surface of the sphere, given the restriction that the total number of particles must be conserved. When the surface density of the magnetization changes, a surface current J(ϑ, φ, t) will arise. The continuity equation will then be enforced:

$$\frac{\partial W(\vartheta ,\phi ,t)}{\partial t}=-\nabla \cdot J(\vartheta ,\phi ,t).$$ (27)

In the absence of thermal fluctuations, J will only depend on the velocity $\left(d\widehat{\mathbf{m}}/dt\right)$ of points. When thermal fluctuations are incorporated, the distribution function acquires a diffusion term, which is manifested as a term proportional to a diffusion constant D. This results in:

$$\frac{\partial W(\vartheta ,\phi ,t)}{\partial t}=-\nabla \cdot \left\{\frac{d\widehat{\mathbf{m}}}{dt}-D\nabla \right\}W(\vartheta ,\phi ,t).$$ (28)

The diffusion constant D is determined by the conditions at equilibrium, where there is no applied field and ∂W/∂t = 0. If we first assume only Brownian rotation, with relaxation time constant τ_B, the velocity of the magnetic moment can be written as a differential equation:

$$\frac{d\widehat{\mathbf{m}}}{dt}=\frac{(\widehat{\mathbf{m}}\times \mathit{\xi })\times \widehat{\mathbf{m}}}{2{\tau }_B}.$$ (29)

Rewriting the numerator using vector identities and inserting the result into Eq. 28 results in:

$$\frac{\partial W}{\partial t}=\nabla \cdot \left[D\nabla -\frac{\mathit{\xi }-\widehat{\mathbf{m}}(\widehat{\mathbf{m}}\cdot \mathit{\xi })}{2{\tau }_B}\right]W.$$ (30)

This equation does not have an analytical solution for general directions of the applied field, but if we assume that the applied magnetic field is aligned with the polar axis $(\mathit{\xi }=\xi \widehat{\mathbf{z}})$, the dependence on the azimuthal angle φ will drop out, and Eq. 30 simplifies to:

$$\frac{\partial W}{\partial t}=\frac{1}{\sin \vartheta }\frac{\partial }{\partial \vartheta }\left[\sin \vartheta \left(D\frac{\partial W}{\partial \vartheta }-\frac{\xi }{2{\tau }_B}\sin \vartheta W\right)\right].$$ (31)

Considering equilibrium conditions (∂W/∂t → 0), we find D = 1/2τ_B. We can then substitute x = cosϑ, and so

$$\frac{\partial }{\partial x}=-\frac{1}{\sin \vartheta }\frac{\partial }{\partial \vartheta }.$$ (32)

Eq. 31 then becomes [95]:

$$2{\tau }_B\frac{\partial W}{\partial t}=\frac{\partial }{\partial x}\left[\left(1-x^2\right)\left(\frac{\partial W}{\partial x}-\xi (t)W\right)\right],$$ (33)

where ξ(t) ≡ μ₀μH(t)/k_BT. The average magnetization is found by integrating the probability distribution W(x, t) over the unit sphere.

To solve this equation, W(x, t) can be expanded in terms of Legendre polynomials:

$$W(x,t)=\sum _{n=0}^{\infty }{a}_n(t)P_n(x).$$ (34)

The coefficients a_n(t) can then be solved recursively, with a₀(t) = 1/2:

$$\frac{2{\tau }_B}{n(n+1)}\frac{\text{d}{a}_n}{\text{d}t}=-a_n+\xi (t)\left[\frac{a_{n-1}}{2n-1}-\frac{a_{n+1}}{2n+3}\right].$$ (35)

Considering Néel rotation only, the corresponding Fokker-Planck equation can be derived in a similar way including an anisotropy term [95]:

$$2{\tau }_N\frac{\partial W}{\partial t}=\frac{\partial }{\partial x}\left[\left(1-x^2\right)\left(\frac{\partial W}{\partial x}-\xi (t)W-{\alpha }_{K}xW\right)\right],$$ (36)

where α_K = 2KV_c/k_BT. This form again assumes azimuthal symmetry, with the easy axis aligned with the applied field in the z-direction. Solutions to this equation are again Legendre polynomials with coefficients a_n(t):

$$\frac{2{\tau }_N}{n(n+1)}\frac{\text{d}{a}_n}{\text{d}t}=-a_n+\xi (t)\left[\frac{a_{n-1}}{2n-1}-\frac{a_{n+1}}{2n+3}\right]$$ (37)

$$+{\alpha }_K\left[\frac{(n-1)a_{n-2}}{(2n-3)(2n-1)}+\frac{n{a}_n}{(2n-1)(2n+1)}-\frac{(n+1)a_n}{(2n+1)(2n+3)}-\frac{(n+2)a_{n+2}}{(2n+3)(2n+5)}\right].$$ (38)

Using the decoupled Fokker-Planck equations (Eq. 33 and Eq. 36), we can extract the rotation timescale separately for pure Brownian or pure Néel rotation. By truncating Eq. 35 or Eq. 37 after N terms, we can write the following matrix equation:

$${\tau }_0\frac{d\mathbf{y}}{dt}=\mathbf{A}\mathbf{y}+\mathbf{b},$$ (39)

where A is an N × N matrix, and b and y are column vectors with N elements. The equilibrium timescales are represented by τ₀, so for Brownian rotation τ₀ = τ_B, and for Néel rotation τ₀ = τ_N. For pure Brownian rotation (Eq. 33), A will be a tridiagonal matrix with components [79]:

$$A_{n,n}=-\frac{n(n+1)}{2}n=1,2,3,\dots ,N,$$ (40)

$$A_{n,n+1}=-\frac{n(n+1)}{2(2n+3)}\xi n=1,2,3,\dots ,N-1,$$ (41)

$$A_{n,n-1}=\frac{n(n+1)}{2(2n-3)}\xi n=2,3,4,\dots ,N.$$ (42)

The remaining components are zero. As before, ξ = μ₀μH/k_BT. The first component of b will be b₁ = ξ/2, with remaining components equal to zero.

For Néel rotation, the components of b are b₁ = ξ/2 and b₂ = α_K/2, and remaining components zero. In this case, A is a pentadiagonal matrix with matrix elements defined by [79]:

$$A_{n,n}=\frac{n(n+1)}{2}\left[-1+\frac{n{\alpha }_K}{(2n-1)(2n+1)}-\frac{(n+1){\alpha }_K}{(2n+1)(2n+3)}\right]n=1,2,3,\dots ,N,$$ (43)

$$A_{n,n+1}=-\frac{n(n+1)}{2(2n+3)}\xi n=1,2,3,\dots ,N-1,$$ (44)

$$A_{n,n-1}=\frac{n(n+1)}{2(2n-3)}\xi n=2,3,4,\dots ,N,$$ (45)

$$A_{n,n+2}=-\frac{n(n+1)(n+2)}{2(2n+3)(2n+5)}{\alpha }_{K}n=1,2,3,\dots ,N-2,$$ (46)

$$A_{n,n-2}=\frac{n(n+1)(n-1)}{2(2n-3)(2n-1)}\xi n=3,4,5,\dots ,N.$$ (47)

Again, the remaining components are zero. For both of these cases, the solution to Eq. 39 will be dominated by the eigenvalue of A with the largest real part, λ^max. We can then find the effective rotation timescale in terms of λ^max and the equilibrium relaxation time [79]. For Brownian rotation, then:

$${\tau }_{B,F}=-\frac{{\tau }_B}{\mathrm{Re}\left\{{\lambda }_B^{\mathit{max}}\right\}},$$ (48)

and for Néel rotation,

$${\tau }_{N,F}=-\frac{{\tau }_N}{\mathrm{Re}\left\{{\lambda }_N^{\mathit{max}}\right\}}.$$ (49)

These solutions can be generated quickly, and provide some analytical information, which makes the Fokker-Planck formulation a useful tool for studying nonlinear nanoparticle dynamics. However, there are two major limitations to this method which must be emphasized. First, these equations are restricted to exclusively either Néel or Brownian rotation, rather than allowing for a combination of both. For nanoparticles with core diameter ∼25 nm, such as those typically used for MPI, there is some indication that both mechanisms play an important role [92] and are coupled in a non-trivial way. Second, the Fokker-Planck equation for Néel rotation assumes that the easy axes of the particles are aligned in the direction of the field. However, this approximation does not generally apply, and the relative angle between the easy axis and the field will significantly affect the nanoparticle dynamics.

Recently, Jürgen Weizenecker derived a Fokker-Planck equation for coupled Néel and Brownian rotation, allowing for full generalization of the direction of the easy axis, moment, and applied field [96]. The results will be presented here, but for the full derivation and additional details, refer to Ref. [96].

The average direction of the particle easy axis is here represented in spherical coordinates as $\widehat{\mathbf{n}}=N_{\rho }{\widehat{\mathbf{e}}}_{\rho }+N_{\theta }{\widehat{\mathbf{e}}}_{\theta }+N_{\varphi }{\widehat{\mathbf{e}}}_{\varphi }$, and the average direction of the particle moment is $\widehat{\mathbf{m}}=E_r{\widehat{\mathbf{e}}}_r+E_{\vartheta }{\widehat{\mathbf{e}}}_{\vartheta }+E_{\phi }{\widehat{\mathbf{e}}}_{\phi }$ (note that here θ and ϕ have been redefined from previous sections to now represent the direction of the easy axis in spherical coordinates). Similarly, the direction of the magnetic field is $\mathbf{H}=H_{\rho }{\widehat{\mathbf{e}}}_{\rho }+H_{\theta }{\widehat{\mathbf{e}}}_{\theta }+H_{\varphi }{\widehat{\mathbf{e}}}_{\varphi }$ in spherical coordinates, and $\mathbf{H}=H_1{\widehat{\mathbf{e}}}_1+H_2{\widehat{\mathbf{e}}}_2+H_3{\widehat{\mathbf{e}}}_3$ in Cartesian coordinates.

This system will have only four degrees of freedom, represented by the four angles, since $\widehat{\mathbf{m}}$ and $\widehat{\mathbf{n}}$ are unit vectors and therefore have fixed unit radial length. The probability density can then be expressed as W(ϑ, φ, θ, ϕ). The fully generalized, coupled Fokker-Planck equation is presented here without derivation:

$$\begin{gathered} \frac{\partial W}{\partial t}=-\frac{1}{2{\tau }_B}\frac{1}{\sin (\vartheta )}\frac{\partial }{\partial \vartheta }\left[\frac{2K{V}_c}{k_{B}T}{E}_r{E}_{\vartheta }\sin (\vartheta )W-\sin (\vartheta )\frac{\partial W}{\partial \vartheta }\right]-\frac{1}{2{\tau }_B}\frac{1}{\sin (\vartheta )}\frac{\partial }{\partial \phi }\left[\frac{2K{V}_c}{k_{B}T}{E}_r{E}_{\phi }W\right] \\ -\frac{1}{2{\tau }_N}\frac{1}{\sin (\theta )}\frac{\partial }{\partial \theta }\left[\frac{M_s{V}_c}{\alpha k_{B}T}\left(\alpha H_{\theta }-H_{\varphi }\right)\sin (\theta )W+\frac{2K{V}_c}{\alpha K_{B}T}{N}_{\rho }\left(\alpha N_{\theta }-N_{\varphi }\right)\sin (\theta )W-\sin (\theta )\frac{\partial W}{\partial \theta }\right] \\ -\frac{1}{{\tau }_N}\frac{1}{\sin (\theta )}\frac{\partial }{\partial \varphi }\left[\frac{M_s{V}_c}{\alpha k_{B}T}\left(\alpha H_{\varphi }+H_{\theta }\right)W+\frac{2K{V}_c}{\alpha k_{B}T}{N}_{\rho }\left(\alpha N_{\varphi }+N_{\theta }\right)W\right] \\ +\frac{1}{2{\tau }_B}\frac{1}{{\sin }^2(\vartheta )}\frac{{\partial }^{2}W}{\partial {\phi }^2}+\frac{1}{2{\tau }_N}\frac{1}{{\sin }^2(\theta )}\frac{{\partial }^{2}W}{\partial {\varphi }^2}. \end{gathered}$$ (50)

Here, α is the dimensionless damping constant which has appeared before, u_i are the direction cosines for the particle moment, and p_i are the direction cosines for the particle axis, defined below:

$$u_1=\cos (\phi )\sin (\vartheta )$$ (51)

$$u_2=\sin (\phi )\sin (\vartheta )$$ (52)

$$u_3=\cos (\vartheta )$$ (53)

$$p_1=\cos (\varphi )\sin (\theta )$$ (54)

$$p_2=\sin (\varphi )\sin (\theta )$$ (55)

$$p_3=\cos (\theta )$$ (56)

Since each component of $\widehat{\mathbf{m}}$ and $\widehat{\mathbf{n}}$ depends on all four angles, the above equation is fully coupled. To find solutions to this equation, we can perform a series expansion into spherical harmonics:

$$W(\vartheta ,\phi ,\theta ,\varphi )=\sum _{l=0}^{\infty }\sum _{m=-l}^l\sum _{r=0}^{\infty }\sum _{q=-r}^r{D}_{l,r}^{m,q}{P}_l^m(\vartheta ){\text{e}}^{im\phi }{P}_r^q(\theta ){\text{e}}^{iq\varphi }:=\sum _{l,m,r,q}{D}_{l,r}^{m,q}{X}_l^m(\vartheta ,\phi )Z_r^q(\theta ,\varphi ).$$ (57)

Here, the expansion coefficients are represented by $D_{l,r}^{m,q}$, and $P_l^m$ and $P_r^q$ are the Legendre polynomials associated with the spherical harmonics $X_l^m$ and $Z_r^q$. The variables l and m are associated with the angular momentum of the particle axis, while r and q describe the angular momentum of the particle moment. It will also be necessary to calculate the derivatives of the spherical harmonics, which will have the effect of raising and lowering the indices, represented by Δ (e.g., l → l + Δl):

$$\sum _{l,m,r,q}\frac{\partial D_{l,r}^{m,q}}{\partial t}{X}_l^m{Z}_r^q=\sum _{l,m,r,q}{D}_{l,r}^{m,q}\sum _{\mathrm{\Delta }l,\mathrm{\Delta }m,\mathrm{\Delta }r,\mathrm{\Delta }q}{g}_{\mathrm{\Delta }r,\mathrm{\Delta }q}(r,q)f_{\mathrm{\Delta }l,\mathrm{\Delta }m}(l,m)X_{l+\mathrm{\Delta }l}^{m+\mathrm{\Delta }m}{Z}_{r+\mathrm{\Delta }r}^{q+\mathrm{\Delta }q}.$$ (58)

Since acting with an operator, such as taking the derivative, can only change the indices by one, our system will be simplified significantly; the operators in the Fokker-Planck equation act a maximum of two times. The full solution to the Fokker-Planck equation can then be written as a system of differential equations:

$$\frac{\text{d}{D}_{L,R}^{M,Q}}{\text{d}t}=\sum _{\mathrm{\Delta }l=-2}^2\sum _{\mathrm{\Delta }m=-2}^2\sum _{\mathrm{\Delta }r=-2}^2\sum _{\mathrm{\Delta }q=-2}^2{f}_{\mathrm{\Delta }l,\mathrm{\Delta }m}(L,M)g_{\mathrm{\Delta }r,\mathrm{\Delta }q}(R,Q)D_{L-\mathrm{\Delta }l,R-\mathrm{\Delta }r}^{M-\mathrm{\Delta }m,Q-\mathrm{\Delta }q},$$ (59)

where $f_{\mathrm{\Delta }l,\mathrm{\Delta }m}(L,M)g_{\mathrm{\Delta }r,\mathrm{\Delta }q}(R,Q)$ represent matrix elements. In the fully general case, there will be 81 coefficients per row, with a total of 131 terms. Since we are only interested in systems where the magnetic field is applied along a single direction, here the z-direction, we can simplify this significantly by imposing azimuthal symmetry, which will send all m, q = 0. The system of differential equations then becomes:

$$\frac{\text{d}{D}_{L,R}^{0,0}}{\text{d}t}=\sum _{\mathrm{\Delta }l=-2}^2\sum _{\mathrm{\Delta }r=-2}^2{f}_{\mathrm{\Delta }l,\mathrm{\Delta }0}(L,0)g_{\mathrm{\Delta }r,\mathrm{\Delta }0}(R,0)D_{L-\mathrm{\Delta }l,R-\mathrm{\Delta }r}^{0,0}.$$ (60)

Now, the matrix elements $f_{\mathrm{\Delta }l,\mathrm{\Delta }0}(L,0)g_{\mathrm{\Delta }r,\mathrm{\Delta }0}(R,0)$ will contain only 11 coefficients with 28 total terms per row. The matrix elements are explicitly listed in Ref. [96]. To generate solutions, the matrix must be truncated, which is done by setting a maximum value for L and R. For simplicity, we will choose the maximum value for both L and R to be represented by L_max. The matrix represented by $f_{\mathrm{\Delta }l,\mathrm{\Delta }0}(L,0)g_{\mathrm{\Delta }r,\mathrm{\Delta }0}(R,0)$ will have dimension N × N, where $N=L_{max}^2$. In a case of L_max = 25, for example, we will have 625 coupled differential equations to solve.

Once the elements of $D_{L,R}^{0,0}$ are determined, we can extract the relevant physical properties, in particular, the average value of the particle magnetization in the z-direction:

$$\begin{gathered} \langle M_z\rangle =M_s\langle E_3\rangle \\ =M_s\langle \cos \vartheta \rangle \\ =M_s\langle X_1^0{Z}_0^0\rangle \\ =M_s\int \int \int \int X_1^0{Z}_0^{0}W(\vartheta ,\phi ,\theta ,\varphi )\text{d}\mathrm{\Omega }\text{d}{\mathrm{\Omega }}^{\prime } \\ =M_s\sum _{l,m,r,q}{D}_{l,r}^{m,q}\int \int X_1^0{X}_l^m\text{d}\mathrm{\Omega }\int \int Z_0^0{Z}_r^q\text{d}{\mathrm{\Omega }}^{\prime } \\ =M_s\frac{{(4\pi )}^2}{3}{D}_{1,0}^{0,0}. \end{gathered}$$ (61)

The time evolution of $D_{1,0}^{0,0}$ will therefore represent the average particle magnetization over time. Again, further details of the derivation and solution can be found in Ref. [96].While the fully general coupled Fokker-Planck equation itself is quite complicated, once azimuthal symmetry is imposed and the required matrix is generated, solutions can be generated fairly easily and quickly, although the time required is highly dependent on L_max, as the number of coupled differential equations scales as $L_{max}^2$.

4.2. Effective field model

For relatively low applied fields, another useful model, that we will mention briefly but not discuss in detail, comes from an approximation to the Fokker-Planck equation, and is called the effective field model. In this model, the frequency of oscillation is assumed to be low enough so the distribution remains in the Maxwell-Boltzmann (equilibrium) form, so that $M(t)=M_s\mathcal{L}\left({\xi }_e(t)\right)$, where ξ_e is an effective field. This is able to produce nonlinear dynamics for the MNP magnetization [97]:

$$\frac{\text{d}M(t)}{\text{d}t}=-\frac{M(t)}{\tau }\left(1-\frac{\xi (t)}{{\xi }_e(t)}\right),$$ (62)

where τ is again the effective rotation timescale. Here, the effective field can be calculated at every time step using the inverse Langevin function, and will change in time but not necessarily be equal to the applied cosinusoidal field. This model is similarly limited in that it assumes that MNPs experience pure magnetic relaxation, rather than driven magnetic reversal. Consequently, this approximation, as well as the Debye model, diverges when the field applied is large (greater than 4K/3M_s).

4.3. Stochastic Langevin equations

To investigate the dynamics of particles which experience both Néel and Brownian rotation, we implement stochastic simulations of Langevin equations. Computational simulations are used to model the magnetic response of nanoparticles exposed to an external magnetic field. The nanoparticles are assumed to be spherical and single-domain, and so can be characterized by a single magnetic moment, as the sizes of particles that we typically consider for biosensing applications (5–30 nm in diameter) are well within the superparamagnetic limit [98]. The size of the nanoparticles as well as the anisotropy constants will vary according to a log-normal distribution, as is typically assumed [99]:

$$g(x)=\frac{1}{\sqrt{2\pi }\sigma x}\exp \left(-\frac{\ln {\left(x/x_0\right)}^2}{2{\sigma }^2}\right),$$ (63)

where x₀ is the median value and σ is the distribution shape parameter. Since some degree of particle agglomeration is common for nanoparticles in liquid suspensions, and particularly in biological environments [100], inclusion of these distributions is necessary to approximate potential agglomeration effects, as well as natural variation among particles from the fabrication process, as observed by TEM images [99, 101]. As nanoparticles are typically coated with a non-magnetic coating as functionalization for specific biomedical purposes, we differentiate between the magnetic core diameter and the hydrodynamic diameter. The particles are able to rotate via both Brownian and Néel rotation. The internal magnetization direction $\widehat{\mathbf{m}}$ will rotate according to the Landau-Lifshitz-Gilbert equation. This differential equation will be coupled with the differential equation describing the general torque exerted on the easy axis $\widehat{n}$ of the particle [102, 82]. The coupled equations for a single particle are as follows:

$$\frac{\text{d}\widehat{\mathbf{m}}}{\text{d}t}=\frac{\gamma }{1+{\alpha }^2}(\mathbf{H}+\alpha \widehat{\mathbf{m}}\times \mathbf{H})\times \widehat{\mathbf{m}}$$ (64)

$$\frac{d\widehat{\mathbf{n}}}{dt}=\frac{\mathrm{\Theta }}{6\eta V_h}\times \widehat{\mathbf{n}},$$ (65)

where γ is the electron gyromagnetic ratio in bulk iron [103], α is the damping coefficient, η is the viscosity of the surrounding medium, and V_h is the hydrodynamic volume. The effective magnetic field, H, and the effective torque, Θ, are determined from the total particle energy:

$$U=-\mu {\mu }_0\widehat{\mathbf{m}}\cdot {\mathbf{H}}_{\text{app}}-K{V}_{\text{c}}{(\widehat{\mathbf{m}}\cdot \widehat{\mathbf{n}})}^2-\sum _i\frac{\mu {\mu }_i{\mu }_0}{4\pi r_i^3}\left(3\left(\widehat{\mathbf{m}}\cdot {\widehat{\mathbf{r}}}_i\right)\left({\widehat{\mathbf{m}}}_i\cdot {\widehat{\mathbf{r}}}_i\right)-\widehat{\mathbf{m}}\cdot {\widehat{\mathbf{m}}}_i\right),$$ (66)

where μ represents the magnitude of the particle’s magnetic moment, equal to M_sV_c, where M_s is the saturation magnetization and V_c is the core volume. K is the effective anisotropy constant, which includes magnetocrystalline and shape anisotropy. Subscript i denotes particle number. Here, the positions r_i are initialized randomly based on the desired nanoparticle concentration, and the positions do not vary in time. The first term in Eq. 66 represents the Zeeman interaction with the applied field, H_app, the second term is the energy contribution from the effective particle anisotropy, and the third term represents the magnetic dipole-dipole interaction with all other particles i in the simulation. The vector r pointing to the center of each particle has magnitude r and direction $\widehat{\mathbf{r}}$. For applications we are considering, the applied field is sinusoidal, with amplitude H₀ and angular frequency ω. We apply the field in the z-direction, and so:

$${\mathbf{H}}_{\text{app}}=H_0\cos (\omega t)\widehat{\mathbf{z}}$$ (67)

The effective magnetic field and torque can then be found by taking derivatives of the energy, and adding thermal fluctuations:

$$\mathbf{H}=-\frac{1}{{\mu }_0\mu }\frac{\partial U}{\partial \widehat{\mathbf{m}}}+{\mathbf{H}}_{\text{th}}={\mathbf{H}}_{\text{app}}+\frac{2K{V}_{\text{c}}}{\mu }(\widehat{\mathbf{m}}\cdot \widehat{\mathbf{n}})\widehat{\mathbf{n}}+\sum _i\frac{{\mu }_i{\mu }_0}{4\pi r_i^3}\left(3\left({\widehat{\mathbf{m}}}_i\cdot {\widehat{\mathbf{r}}}_i\right){\widehat{\mathbf{r}}}_i-{\widehat{\mathbf{m}}}_i\right)+{\mathbf{H}}_{\text{th}}$$ (68)

$$\mathrm{\Theta }=\frac{\partial U}{\partial \widehat{\mathbf{n}}}\times \widehat{\mathbf{n}}+{\mathrm{\Theta }}_{\text{th}}=-2K{V}_{\text{c}}(\widehat{\mathbf{m}}\cdot \widehat{\mathbf{n}})(\widehat{\mathbf{m}}\times \widehat{\mathbf{n}})+{\mathrm{\Theta }}_{\text{th}}$$ (69)

H_th represents the fluctuation field, which accounts for microscopic effects (interactions with nuclear spins, phonons, etc.) that cause fluctuations of the orientation of the magnetic moment. It is generally assumed [104, 105, 82] that this fluctuation field is a Gaussian stochastic process whose components have the following statistical properties:

$$\langle {\mathbf{H}}_{\text{th}}^i(t)\rangle =0$$ (70)

$$\langle {\mathbf{H}}_{\text{th}}^i(t){\mathbf{H}}_{\text{th}}^j\left(t^{\prime }\right)\rangle =\frac{2k_{B}T}{\gamma \mu }\frac{1+{\alpha }^2}{\alpha }{\delta }_{ij}\delta \left(t-t^{\prime }\right),$$ (71)

where k_B is Boltzmann’s constant and T is the temperature. Similarly, Θ_th represents a thermally-generated torque with statistical properties:

$$\langle {\mathrm{\Theta }}_{\text{th}}^i(t)\rangle =0$$ (72)

$$\langle {\mathrm{\Theta }}_{\text{th}}^i(t){\mathrm{\Theta }}_{\text{th}}^j\left(t^{\prime }\right)\rangle =12k_{B}T\eta V_{\text{h}}{\delta }_{ij}\delta \left(t-t^{\prime }\right).$$ (73)

The resulting equations can then be numerically integrated using stochastic calculus; typically, the Stratanovich-Heun scheme is used [92, 104]. Example simulation results using this method (here abbreviated LLG for Landau-Lifshitz-Gilbert), along with comparison to measured magnetic particle spectroscopy (MPS) data, is shown in Fig. 9. Often, significant computational power is required in order to generate solutions for a large number of averages using a sufficiently small time step.

Figure 9:

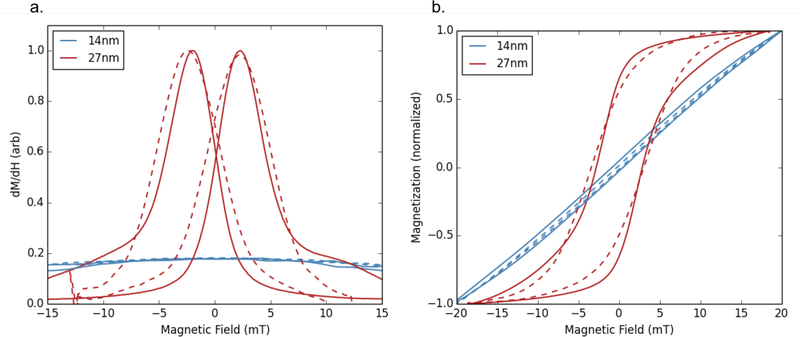
a. Experimental MPS data (solid lines) and simulated data (dashed lines) for two core sizes of nanoparticles. b. Integrated MPS data (solid lines) and simulated LLG data (dashed lines) for two core sizes. Measurements were taken under an applied field of amplitude 20 mT/μ₀ and frequency 26 kHz. The magnetization has been normalized for better comparisons between simulated and measured data. The 14 nm particle shows essentially no MPS signal.

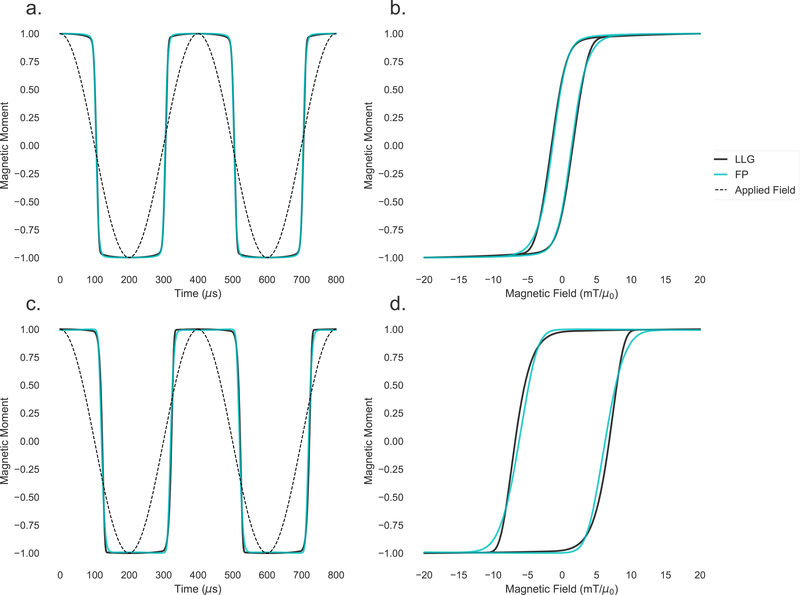
These stochastic simulations, as well as the coupled Fokker-Planck equation, currently represent the most sophisticated methods of modeling nanoparticle dynamics. Fig. 10 shows simulations of the magnetic moment of monodisperse uniaxial particles with identical characteristics, for two different core sizes, plotted against time and applied field. It can be seen that the simulations match very closely, especially for the smaller particles. The remainder of this work will focus on applications of magnetic nanoparticles, specifically MPI and MFH, which both heavily depend on a detailed understanding of nanoparticle rotation dynamics. In both cases, the nonlinear simulation methods described above have been used to improve performance and efficiency.

Figure 10:

Top: simulations of the magnetic moment over time (a.) and plotted against magnetic field (b.) for a 22 nm particle. Bottom: simulations of the magnetic moment over time (c.) and plotted against magnetic field (d.) for a 29 nm particle. Simulations from the stochastic Langevin equations (labeled LLG and shown in black) agree well with simulations of the coupled Fokker-Planck equation (labeled FP and shown in cyan). In the left figures, the applied cosinusoidal field is also shown for reference.

5. Magnetic particle imaging

Although substantial improvements in MPI image quality have been made in recent years, an ongoing challenge in MPI research is improving tracer detection limits and image resolution. The rotation mechanism and magnetization dynamics of MNP tracers plays a significant role in the sensitivity and resolution of the resulting MPI image, and so modeling MNP rotation is critical for optimization in MPI.

5.1. Signal generation in MPI

Although there are different specific setups of current MPI systems, the main principle behind all is the same. A strong static magnetic gradient field, generally called the selection field, is superimposed onto an oscillating drive field. The selection field gradient generates a small well-defined region at its origin where the magnetic field is zero, referred to as the field-free point (FFP). Outside of the FFP, the static field increases in magnitude very rapidly, and therefore the magnetization of the particles is saturated in any region outside of the central point. The FFP can then be scanned across the sample. The resulting induced signal will be nonzero only when the FFP is at the location of the nanoparticle tracers. A tomographic image is formed as the FFP is scanned across the sample, causing any tracers in that voxel to reverse their magnetization and induce a signal in the detection coil. The shape of the differential susceptibility M′(H(t)) determines the point-spread function (PSF) of the MPI imaging system. Understanding the factors that influence the shape of the PSF is key to optimizing the signal and the entire MPI system.

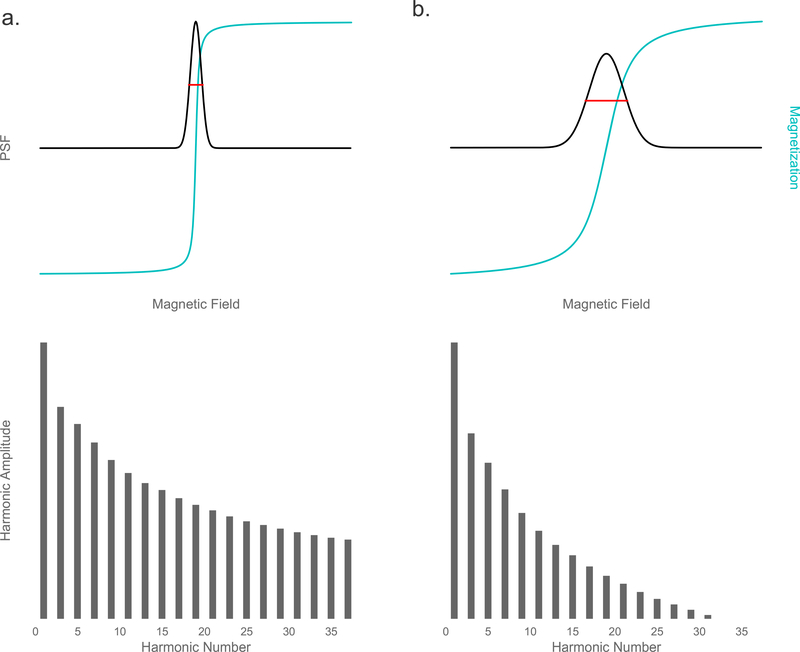
There are two primary MPI system setups currently in development. The first is f-space (frequency-space) MPI, developed by Philips Hamburg, which first measures a harmonic spectrum system function for each sample and reconstructs the image in frequency space [33]. The second is f-space MPI, developed by Goodwill and Conolly at Berkeley, which measures M′(H(t)) directly as the point-spread function (PSF) [106, 34, 53]. The resulting image is then a convolution of the tracer distribution and the PSF. In both methods, the image resolution is defined by the width of the PSF, often described by the full-width at half-maximum (FWHM), and the signal magnitude is defined by the height of the PSF. Resolution is also indicated by the harmonic spectrum (the Fourier transform of M′(H(t))); the wider the PSF, the faster the harmonic amplitudes will drop off (see Fig. 11). For this reason, ratios of the harmonic amplitudes (for example, the ratio of the 5th to the 3rd harmonic, A5/A3) can be used as a concentration-independent measurement of signal quality.

Figure 11:

Nearly ideal (a.) and more realistic (b.) measurements of the point-spread function and resulting harmonics. Top: Particle magnetization (blue) and resulting PSF (black), with FWHM indicated in red. Bottom: Harmonic spectrum.

Magnetic particle spectroscopy (MPS) is functionally a zero-dimensional MPI system that applies an AC field uniformly across the sample and records the inductive signal in a receive coil. With MPS, the PSF of a given sample can be directly extracted. The discussion in this section will be limited to zero-and one-dimensional systems, but the principles apply generally to two- and three-dimensional systems as well. When the particle magnetization is approximated as the Langevin function (Eq. 3), the derivative of the magnetization is given by:

$$M^{\prime }(H(t))=\frac{n{\mu }_0{\mu }^2}{k_{B}T}{\mathcal{L}}^{\prime }(\xi ),$$ (74)

with n as the particle concentration. As expected, the signal scales linearly with concentration. The derivative of the Langevin function is

$${\mathcal{L}}^{\prime }(\xi )=\left(\frac{1}{{\xi }^2}-\frac{1}{{\sinh }^2(\xi )}\right)$$ (75)

for ξ > 0, and equal to 1/3 when ξ = 0. M′(H(t)) therefore has a maximum at ξ = 0, and decreases rapidly for increasing ξ, until it approaches zero in the saturation region. The FWHM here is

$$\mathrm{\Delta }{\xi }^{\text{FWHM}}\approx 4.16$$ (76)

The FWHM of M′(H(t)), which can be used to predict the image resolution that can be obtained by the sample, is then given by:

$$\mathrm{\Delta }{H}^{\text{FWHM}}=\frac{\mathrm{\Delta }{\xi }^{\text{FWHM}}{k}_{B}T}{{\mu }_0\mu }=\frac{4.16k_{B}T}{{\mu }_0\mu }.$$ (77)

The signal-to-noise ratio (SNR) is indicated by the height of the PSF, which is proportional to the concentration and saturation magnetization, as well as the slope of the magnetization. In this idealized case, the peak of the PSF (where the slope of the magnetization is highest) will be given when the field strength is zero:

$$M^{\prime }(0)=\frac{n{\mu }_0{\mu }^2}{3k_{B}T}$$ (78)

The width and height of the PSF (predicting resolution and SNR) are highly affected by properties of the sample itself, the sample environment, and the applied field. To optimize both, highly mondisperse particle sizes are required, as well as strong magnetic gradients.

For the remainder of the discussion, we will examine the one-dimensional case in the x-space formulation, following [34], although the principles apply equally to the Fourier space construction. In a 1D MPI system with linear gradient −G and time-dependent field H₀(t), the magnetic field at a position x will be:

$$H(x,t)=H_0(t)-Gx.$$ (79)

The location of the field-free point, x_s(t), can be found by solving this equation for H(x, t) = 0:

$$x_s(t)=G^{-1}{H}_0(t)$$ (80)

Or equivalently, the magnetic field at position x can be written in terms of the location of the FFP:

$$H(x,t)=G\left(x_s(t)-x\right)$$ (81)

If we assume a continuous distribution of nanoparticles ρ(x) in the adiabatic limit (assuming that the particles’ magnetization reaches equilibrium at every time step of the applied field), the sample magnetization follows the Langevin function:

$$M(x,t)=\mu \rho (x)\mathcal{L}\left[\frac{{\mu }_0\mu }{k_{B}T}G\left(x_s(t)-x\right)\right]$$ (82)

The magnetization flux can be obtained by integrating over x, which can be written as a convolution:

$$\mathrm{\Phi }(t)=-\mu \rho (x)*\mathcal{L}{\left[\frac{{\mu }_0\mu }{k_{B}T}G(x)\right]}_{x=x_s(t)}$$ (83)

The changing magnetic flux will be recorded by an inductive detector that will have some sensitivity, σ_s. The received signal will then be:

$$s_{\text{adiab}}={\sigma }_s\frac{d\mathrm{\Phi }}{dt}={\sigma }_s\mu \rho (x)*\stackrel{.}{\mathcal{L}}{\left[\frac{{\mu }_0\mu }{k_{B}T}Gx\right]}_{x=x_s(t)}\frac{{\mu }_0\mu }{k_{B}T}G{\dot{x}}_f(t)$$ (84)

Defining β ≡ k_BT/σ_sμ₀μ²G and the PSF $h(x)\equiv \stackrel{.}{\mathcal{L}}\left({\mu }_0\mu Gx/k_{B}T\right)$, the signal can be written as a simple spatial convolution (again emphasizing that this is the signal received in the adiabatic limit):

$$s_{\text{adiab}}={\beta {\dot{x}}_s(t)\rho (x)*h(x)|}_{x=x_s(t)}.$$ (85)

The velocity of the FFP, ${\dot{x}}_s(t)$, is simply the scanning rate of the FFP of the system.

5.2. Relaxation effects in image reconstruction

For realistic MPI systems, the adiabatic approximation will not hold. The MNP moments will not align instantaneously with the field; instead, there will be some time required for alignment. This relaxation can be modeled using a Debye (exponential) relaxation kernel r(t) [107]:

$$s(t)=s_{\text{adiab}}\ast r(t)$$ (86)

Plugging in Eq. 85, this becomes

$$s(t)=\beta \left({{\dot{x}}_s(t)\rho (x)\ast h(x)|}_{x=x_s(t)}\right)\ast r(t).$$ (87)

This expression for the total signal now contains two convolutions; the inner convolution here is spatial, and the outer convolution is temporal.

The MPI image $\widehat{\rho }$ can be generated by mapping the signal equation to the spatial location of the FFP. The resulting image will be a convolution of the adiabatic image with the relaxation kernel [108, 107]:

$$\widehat{\rho }\left(x_s(t)\right)=\left({\rho (x)*h(x)|}_{x=x_s(t)}\right)*r(t)$$ (88)

If we assume that the FFP is scanned linearly across the sample with a constant scanning rate v_s, then the location of the FFP can be expressed as x_s(t) = v_st, and so t = x_s(t)/v_s. When this is inserted into Eq. 88, the total MPI image equation, including relaxation, becomes [107]:

$$\widehat{\rho }\left(x_s(t)\right)=\left({\rho (x)*h(x)|}_{x=x_s(t)}\right)*\left(\frac{1}{v_s}\right)r\left(\frac{x_s(t)}{v_s}\right)$$ (89)

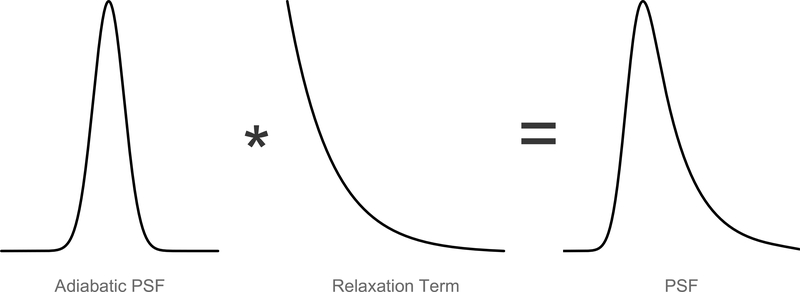
The convolution is now purely spatial, with unit area r(x_s(t)/v_s)/v_s, which allows us to examine the effects of relaxation on the image. As seen in Fig. 12, the particle relaxation increases the width of the PSF, which decreases the image resolution, causing additional blur. The Debye exponential relaxation kernel is:

$$r(t)=\frac{1}{\tau }\exp \left[\frac{-t}{\tau }\right]u(t),$$ (90)

where u(t) is the Heaviside step function (equal to 0 for t < 0, and 1 for t > 0), which serves the function of “turning on” the relaxation at t = 0. As before, τ is the effective relaxation time, which will be a function of particle characteristics as well as properties of the drive field. Again substituting t = x_s(t)/v_s, the relaxation kernel becomes:

$$r(t)=\frac{1}{v_s\tau }\exp \left[-\frac{x_s(t)}{v_s\tau }\right]u\left(x_s(t)\right)$$ (91)

Figure 12:

Non-adiabatic PSF shown as a convolution of the adiabatic PSF and a relaxation term. The effect is a widening of the PSF, resulting in lower image resolution.

Inserting this into Eq. 89 gives the MPI image (where ${\widehat{\rho }}_{\text{adiab}}\left(x_s(t)\right)={\rho (x)\ast h(x)|}_{x=x_s(t)}$):

$$\widehat{\rho }\left(x_s(t)\right)={\widehat{\rho }}_{\text{adiab}}\left(x_s(t)\right)*\left(\frac{1}{v_s\tau }\right)\exp \left(-\frac{x_s(t)}{v_s\tau }\right)u\left(x_s(t)\right)$$ (92)

This important result gives an indication of the trade-offs encountered when attempting to optimize the MPI signal. While the adiabatic signal scales with MNP core size, indicating that increasing particle size should uniformly improve SNR and resolution, the relaxation time τ will monotonically increase with particle size, as indicated by Eqs. 7, 8 and 9. Consequently, increasing particle size will also contribute to increased relaxation effects, causing additional blur in the image. This suggests that there will be an optimal particle core size which maximizes signal and resolution; experimentally, the optimal size has been found to be around 28 nm for magnetite particles [57].

5.3. MNP optimization for performance in vivo

MPI image quality will be dependent on many factors, including hardware parameters (e.g. gradient field strength and coil sensitivity) and tracer properties. Development of highly monodisperse single-phase spherical magnetite MNPs, as well as hardware improvements, has so far resulted in significant improvement in MPI image quality [109, 110, 38]. Controlling drive field conditions (e.g. frequency and amplitude) can minimize particle relaxation behavior, resulting in substantial improvements to MPI signal and resolution [107]. Remaining areas for improvement include optimizing MNP size and monodispersity, as well as optimizing for their specific performance in vivo, which involves an understanding of the physical in vivo environment.

According to Langevin theory, the image resolution should be inversely proportional to the MNP core volume (Eq. 77), and signal strength should be proportional to the square of the volume (Eq. 78) [34, 106]. In this model, then, increasing the nanoparticle core size should result in a dramatic effect on image quality, and so it is often assumed that increasing particle core size will have a unilaterally positive effect on image quality, as long as the particles remain within the superparamagnetic limit. However, as outlined above, relaxation effects increase with core size [109, 111]. Practical limits on performance improvement will therefore arise from increasing core size indefinitely. Previous results have indicated that large core sizes result in image blurring [109, 108, 112, 113, 114] and reduced signal-to-noise ratio (SNR) [57, 115, 108]. Increased interparticle magnetostatic interaction strength and increased polydispersity are additional practical difficulties that arise when increasing MNP core size.

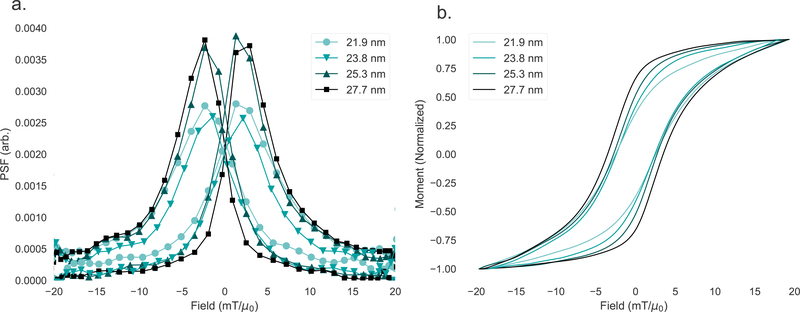
There has been significant recent work into optimizing particles, particularly their size, for MPI, aided by a progressing understanding of nanoparticle rotation dynamics [57, 115]. Examples of measured point-spread functions for different sized MNP tracers are shown in Fig. 13. The two smaller samples (21.9 nm and 23.8 nm) indicate significantly worse signal intensity (indicated by the peak of the PSF) and resolution (indicated by the FWHM of the PSF) than the larger two samples (25.3 nm and 27.7 nm). The differences in magnetization response among the four samples is indicated by the hysteresis loops (M(H)) generated by integrating the time-domain MPS data. Following field reversal, the larger particles’ magnetic moments will take longer to follow the field, resulting in an increased phase lag with size which has the effect of increasing the width of the hysteresis loop. While the PSF for the two smaller samples and two larger samples each look similar, the M(H) curve clearly shows that there is a continuous progression with size, indicated by the increasing steepness of the curve and width of the loop.

Figure 13:

a. The point-spread function for four nanoparticle samples as measured by MPS. The smaller samples show decreased peak height and broader FWHM compared to the larger samples. b. The integrated M(H) magnetization curves.

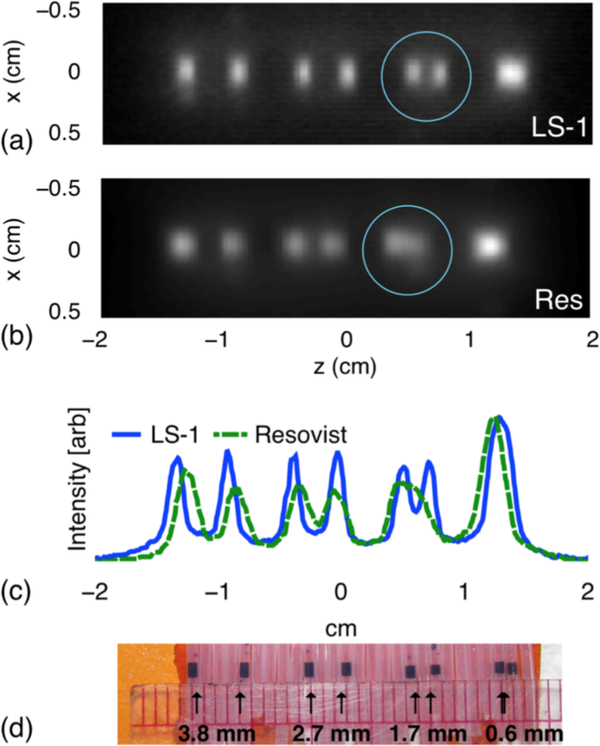
The optimal core size has been found, from experiment and simulation, to be between 27 and 28 nm [110, 116]; larger core sizes result in significant relaxation effects and potential for agglomeration due to interparticle interactions. We can see, for example, that MPI resolution is significantly improved with optimized particles (LS-1) compared to the commercially-available Resovist tracers (Fig. 14). Sensitivity also improves with size-optimized particles; detection of nanogram concentrations of iron oxide has been successfully achieved [56].

Figure 14:

Resolution phantoms. MPI images of phantoms containing LS-1 (a) and Resovist (b); blue circles were overlaid for emphasis. c. Cross sections. d. Photograph of the LS-1 phantom. Reproduced with permission from [116].

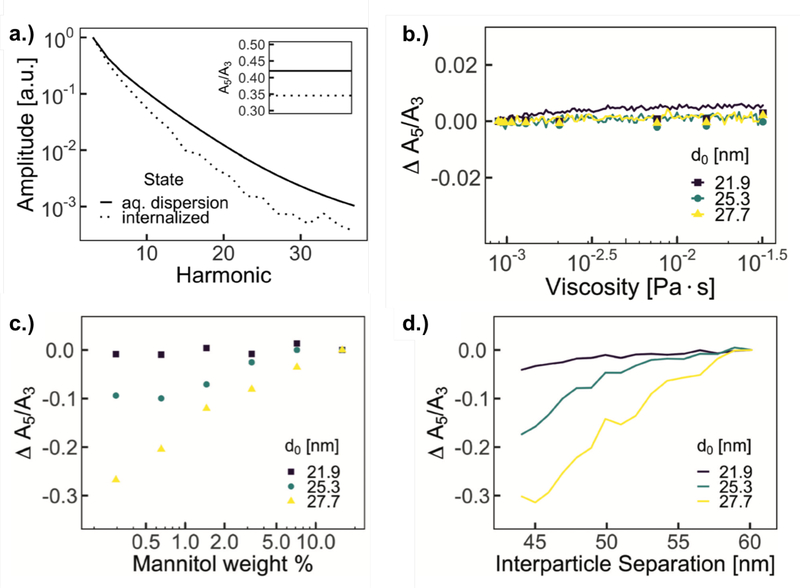
When optimizing for performance in vivo, it is important to understand environmental factors, like viscosity and pH, which may affect MNP dynamics. Brownian rotation, in particular, is influenced by the viscosity of the surrounding medium, as is evident from the equilibrium Brownian relaxation time (Eq. 8). The intracellular magnetic performance of MNPs has been studied [117], and a significant drop in MPI signal quality was found after internalization in cells (Fig. 15a). No evidence of physical degradation of the particles was found.

Figure 15:

a. Comparison of pre- and post-internalization MPS harmonic distribution in cells (with inset A5/A3) b. Magnetic particle spectroscopy performance, A5/A3, as a function of solution viscosity of three different batches of magnetite nanoparticles. Simulation results, shown as lines, of equivalent nanoparticle characteristics show consistent performance over expected range of viscosities. c. Magnetic particle spectroscopy performance, A5/A3, as a function of mannitol weight % of three different batches of MNPs with increasing average core diameters. d. Simulations of A5/A3 of equivalent nanoparticle characteristics for different average interparticle separations. Reproduced with permission from [117].

In Ref. [117], nonlinear simulations of stochastic Langevin equations were performed, with input values of nanoparticle size, size distribution, hydrodynamic size, and saturation magnetization matching measurements of each nanoparticle sample. A range of viscosity values and interparticle separations were input directly into the simulations. For each set of simulations, all other values (e.g. temperature and physical particle characteristics) were assumed to be constant. A minimal dependence on signal quality with viscosity was found, based on experimental measurements of glycerol solutions and simulations of different viscosity values (Fig. 15b). Interparticle interaction strength, however, did have a significant impact on the signal, as studied by mannitol matrix measurements and simulations (Fig. 15c and d). TEM images indicate that MNPs are localized in vesicles within cells, which has the effect of physically bringing particles closer together, compared to when free in solution, which increases average dipole interaction strength, decreasing overall magnetic performance [117]. Minimizing interparticle interactions, then, for example through surface modification, is key to improving performance when internalized in cells, such as required for cell tracking applications in MPI.

5.4. Multicolor imaging and sensing

In conventional MPI, the signal from the nanoparticle tracer response creates a single contrast image, in which the strength of the tracer signal at each spatial location is translated to image intensity of the corresponding pixel during the image reconstruction process. The result of this is a grayscale (or equivalent) image. There have been several recent studies investigating the development multicolor (also referred to as “multi-contrast” or “multi-channel”) MPI, which involves separating the signals generated from different tracers or different environments [118]. If the signal from different particle types or environments can be separately reconstructed on individual channels, a multicolor image can be generated in which each channel corresponds to one color, enabling a new range of therapeutic and diagnostic applications that could function in combination with MPI.

When considering potential theranostic applications of multicolor MPI, a major enabling factor is the wide potential for functionalization of the nanoparticle surface. Iron oxide nanoparticles are particularly versatile. When synthesized via thermolysis of organometallic precursors, superparamagnetic iron oxide nanoparticles (SPIONs) need to be coated with a capping ligand, e.g. oleic acid, which renders them hydrophobic. In order to be dispersed in water for use in biomedical applications, they must undergo a phase transfer process, typically either by ligand exchange [119, 120, 121] or with the addition of a polymer coating, for example, poly(maleic anhydride alt-1-octadecene) (PMAO), which interacts hydrophobically with the capping ligand [122]. Once SPIONs are coated with a polymer, additional molecules can be attached to the surface.

When SPIONs are delivered into the bloodstream, extracellular serum proteins adsorb onto the nanoparticle surface, forming a protein corona [123, 124], which may decrease nanoparticle stability and facilitate nanoparticle removal from the bloodstream and body [125]. To reduce protein adsorption and improve biocompatibility and stability, SPIONs can be coated with poly(ethylene glycol) (PEG) containing co-polymer [38] in addition to PMAO, which enables long term circulation of particles in the blood [126, 61], necessary for applications like cardiovascular imaging. Alternatively, SPIONs can be coated with silica [42, 43], on top of which ligands can be attached, such as ligands for cancer targeting [48, 49, 127, 128, 129]. Cancer targeting ligands include antibodies, oligosaccharides, oligopeptides, and folic acid [130, 131].

In addition to functionalization for long-term blood circulation and cancer targeting, SPIONs can be coated on medical devices; for example, on diagnostic catheters and guide wires used for cardiovascular interventions [132, 133, 134]. A possible application of multicolor MPI, then, would involve distinguishing between particles coated on a catheter and guide wire (used for inserting stents in the heart or diagnosing heart disease) and particles flowing in the blood, on which preliminary studies have been done [134]. This technique could, in theory, replace coronary catheter angiography. Coronary catheter angiograms, which require threading a catheter through the femoral artery, are performed at a rate of approximately 1 million per year in the United States [135]. The catheters are used to inject iodine into the heart, which is then used as a contrast agent in order to allow diagnosis with x-ray imaging or CT. However, iodine can have serious health consequences, particularly for elderly patients or patients with chronic kidney disease. For these patients, the injection of iodine can result in renal failure, and the insertion of the catheter through the femoral artery itself carries a finite risk [135]. Multicolor MPI could therefore provide a significantly safer alternative to coronary angiography.

To create a multi-channel image with MPI, the signal from MNPs of different sizes or in varying chemical, thermal, or viscous environments must be distinguished, in contrast to single-channel MPI which produces a monochromatic image. This is possible due to the sensitivity of the rotation behavior of MNP tracers. Properties that affect the MNP rotation behavior, and therefore resulting MPI signal, as we have seen, include viscosity, interparticle interaction strength, temperature, material, mobility state, core size, and hydrodynamic size. Sensing of any of these properties could in principle be integrated into MPI, and there has already been investigation into many of these [136, 137, 64, 138, 139, 118, 140, 141, 142], including viscosity mapping in [143], and temperature mapping in [144] and [66]. These studies show that the MPI signal is highly sensitive to particle properties and environment, which can enable discrimination based on particle type [118, 140, 142] and in some cases quantification of environmental properties.

Because of this, multicolor MPI could be used to combine medical imaging with disease diagnostics and treatment. For example, quantifying the viscosity of the MNP environment can provide information about nanoparticle binding to or internalization in cells, which would be useful for applications like targeted cancer treatment. Blood viscosity could also be detected as an indication of disease [145], such as a brain hemorrhage, during which blood coagulation occurs [146]. Temperature can be another significant marker of disease; malignant cells have a higher temperature than normal cells, by possibly up to 1 degree Celsius, and general inflammation results in temperature changes [147, 148, 149, 150]. Detecting local temperature changes during an imaging scan could therefore provide information for disease diagnostics, and detection sensitivity of < 1°C should be possible with MPI [66]. Magnetic fluid hyperthermia (MFH), in which magnetic nanoparticles are used to locally heat cancer cells [29, 30, 70, 151, 152, 32, 72], discussed in the following section, could also be combined with active monitoring of temperature with MPI, allowing for a thermally-controlled cancer treatment system. Additionally, cancer detection via protease sensing with MPI could be achieved by detecting changes in interparticle interaction strength using linker peptides that are cleaved in the presence of proteases expressed by malignant cells [69].

To highlight one example, multicolor MPI based on core size discrimination was realized in [142]. As seen in Fig. 13, there is a clear dependence of MPI signal on core size as a result of differing rotation behavior, which enables signal separation. This behavior can be supported and predicted by nonlinear simulations [153], as seen, for example, in Fig. 10, providing a basis for signal separation with MPI based on core size discrimination. Results of a multi-channel reconstruction are shown in Fig. 16. In this example, each particle type could be separately functionalized, e.g. to circulate in the blood or coated on a catheter or guide wire, enabling simultaneous imaging of each element as a replacement for coronary angiography.

Figure 16:

Multi-channel reconstruction with M_avg = 10000 of the multi-sample datasets with all three samples in the field of view. The location of the samples is indicated in the first column. Reconstructions on each channel c_S, c_M, and c_L are shown in the second to fourth columns. Reproduced with permission from [142].

6. Magnetic fluid hyperthermia

In magnetic fluid hyperthermia (MFH), magnetic nanoparticles are dispersed throughout cancerous tissue, either through direct injection [154] or biological targeting [155, 156]. Under subsequent application of an appropriate AC magnetic field, the particles’ magnetic moments will rotate, dissipating energy and transferring heat to the tumor, resulting in cell damage or death. MFH, consequently, provides the benefit of specific localized cancer treatment.

Cytotoxic heat is generated from power losses that result from the lagging of particle magnetizations behind the applied field. As with MPI, iron oxide nanoparticles are typically used because of their magnetic properties and biocompatibility [1, 152]. In order to be effective as a means of therapy, hyperthermia requires heating of tumor cells to between 42° and 45° C from a baseline of 37° C, so tailoring of nanoparticle properties and applied fields for optimal heating is critical [152]. The efficiency of a given nanoparticle sample to generate heat in MFH will be dependent on the MNP concentration, saturation magnetization, and core size [31, 157]. The viability of MFH has been questioned, since most clinical trials have required a high dose of iron oxide nanoparticles [158, 159], and the long-term toxicity of high MNP doses has not yet been thoroughly studied [160]. It is therefore imperative to the success of MFH that particle heating at low iron concentrations be maximized. Understanding the nonlinear magnetization behavior of nanoparticles under an AC magnetic field, which result in power losses, is crucial to this goal.

The mechanism of heat generation in MFH was first studied by Rosensweig [30] in the context of linear response theory. In this model, the power dissipation due to hysteresis losses resulting from the lagging of the magnetization behind the applied field is given by:

$$P=\pi {\mu }_0{H}_0^2{\chi }^{″}f{\int }_0^{\infty }g(R)dR,$$ (93)

where, as before, H₀ is the externally applied field amplitude, f is the applied field frequency, g(R) is the lognormal distribution of particle sizes, and χ′′ is the out-of-phase susceptibility. As χ′′ is strongly dependent on the field frequency and effective MNP rotation timescale, as indicated in Eq. 11, it is evident that particle relaxation effects play a crucial role in determining the power dissipation. In this model, which inherently assumes small anisotropy and core size, the power loss is maximized at:

$$\tau =\frac{1}{2\pi f}.$$ (94)

This would be the theoretically optimal value for the rotation timescale in order to maximize dissipation due to magnetic viscosity, and corresponds to a core size of 14 nm for magnetite, assuming equilibrium relaxation times [30]. If the rotation timescale is shorter than this optimal value, the shorter phase lag will result in a reduction of the area of the hysteresis loop. If τ is longer than 1/2πf, the particle magnetization will rotate too slowly, and will not be able to follow the applied field. While this model is instructive and attractive due to its simplicity, linear response theory is not applicable for all particle core sizes and applied fields, as discussed previously.

Alternatively, heat generation can be predicted directly from the area of simulated (e.g. using the nonlinear methods described in section 4) or measured hysteresis loops. The heat generated from a given nanoparticle during a field-driven rotation process will be equal to the magnetic energy required for magnetic alignment over one cycle of the applied field [161], which is represented by the hysteresis loop M(H). The heat generated will therefore be proportional to the area of the hysteresis loop [76]:

$$A={\int }_{-H_0}^{H_0}{\mu }_{0}M(H)dH.$$ (95)

From this, we can identify the specific loss power (SLP), also called the specific absorption rate (SAR), which indicates the rate of energy loss per unit mass:

$$\text{SLP}=\frac{{\mu }_{0}Af}{\rho },$$ (96)

where ρ is the mass density of the nanoparticles. The SLP can also be expressed in terms of the specific heat capacity c of the surrounding medium (e.g. water):

$$\text{SLP}=\frac{c}{\rho }\left(\frac{\text{d}T}{\text{d}t}\right),$$ (97)

where dT/dt is the measured temperature change over time. This second expression, then, is used to experimentally measure the SLP, while Eq. 96 can be used to predict the SLP from nonlinear simulations, for example.

In MFH, high frequency fields are applied (on the order of hundreds of kHz), and therefore Néel rotation will be the dominant mechanism for nanoparticle rotation. The energy generated will then be related to the anisotropic energy barrier that the particles must overcome, KV_c, and so the heating efficiency will therefore be highly dependent on particle size. As outlined in section 3, however, the effective rotation timescale will also be strongly dependent on the applied field. Biological safety constraints limit the applied field amplitudes and frequencies that can be used for MFH; the “Brezovich-Criterion” requires that H₀·f₀ ≤ 615 kHz·mT/μ₀ in order to limit peripheral nerve stimulation due to induced eddy currents in the body [162].

There have been many studies attempting to optimize nanoparticles for maximal heating rate, particularly investigations into the effect of size [70, 71, 151, 152, 72], structure [161, 163, 164], and aggregates [165, 166]. Stochastic Langevin simulations were used in Ref. [72] to study size and field dependence of heating rate. Results are shown in Fig. 17, with corresponding experimental data. There is a general increase in SLP with increasing field frequency and amplitude, as well as an increase in SLP with core size even up to core sizes as large as 28 nm, in stark contrast to the predictions from linear response theory. From these results, it is clear that nonlinear models, which incorporate field and frequency dependence of nanoparticle rotation dynamics, are necessary in order to accurately model heat generation in MFH.

Figure 17:

Comparison of normalized size-dependent SLP values from experiment (open symbols) and dynamic Monte Carlo simulations (closed symbols) for various frequencies at fixed H₀ = 6 mT/μ₀ (a) and field amplitudes at fixed f = 176 kHz (b). Simulations were performed with an effective anisotropy K = 4 kJ/m³ and damping parameter α = 0.7. The individual fitting parameters (χ²) are shown next to each simulated curve. Reproduced with permission from [72].

7. Conclusion

Here we have presented an overview of the theoretical models describing the dynamics of magnetic nanoparticles, including their applications to magnetic particle imaging and magnetic fluid hyperthermia. The dependence of various factors on nanoparticle magnetization dynamics, such as nanoparticle size and applied field, has been explored. Applied field strength affects the Néel and Brownian rotation mechanisms differently, such that even for Brownian particles (under equilibrium conditions), Néel rotation may dominate for strong field amplitudes. Equilibrium and linear models are useful tools which can be used to gain a basic understanding of the dependence of the rotation timescale on certain parameters, but they are clearly incomplete. Fokker-Planck equations or simulations of stochastic Langevin equations are typically required in order to fully simulate the nonlinear behavior that arises in both MPI and MFH.