Practitioner’s Guide to Latent Class Analysis: Methodological Considerations and Common Pitfalls.

Abstract

Latent Class Analysis (LCA) is a probabilistic modelling algorithm that allows clustering of data and statistical inference. There has been a recent upsurge in the application of LCA in the fields of critical care, respiratory medicine, and beyond. In this review, we present a brief overview of the principles behind LCA. Further, in a stepwise manner, we outline the key processes necessary to perform LCA including some of the challenges and pitfalls faced at each of these steps. The review provides a one-stop shop for investigators seeking to apply LCA to their data.

Syndromic clinical conditions are frequently reliant on rigid, yet broad, definitions. This has led to considerable heterogeneity that is only just beginning to be appreciated across many medical disciplines. The attendant limitations of heterogeneity in poorly-defined clinical syndromes such as sepsis and acute respiratory distress syndrome (ARDS) seem intuitive.(1–4) Emerging evidence, however, indicates that even in seemingly well-defined conditions such as asthma and chronic obstructive pulmonary disease, where comparatively greater clinical and biological uniformity are observed, heterogeneity may be an impediment to delivering effective and targeted therapy.(5–10)

Increasingly, to circumnavigate the “one size fits all” approach to management strategies, researchers are turning to analytic algorithms that allow the use of multiple indicators (variables) to identify homogeneous subgroups within these heterogeneous populations. Many such algorithms exist, and each confers its own unique analytical slant. One such approach, latent class analysis (LCA), has seen a marked increase in its use across many disciplines of medicine.(11–14) As one example, our research group has used LCA to consistently identify two phenotypes of ARDS across five randomized controlled trial (RCT) cohorts. These phenotypes have distinct clinical and biological features and divergent clinical outcomes.(9, 10, 15–17) Further, in secondary analyses of three RCTs, we observed differential treatment responses to randomized interventions in the two phenotypes.(10, 15, 16) Other investigators have used LCA and identified two phenotypes in sepsis associated acute kidney injury (AKI) with divergent clinical outcomes.(18, 19)

The purpose of this review is to describe the application of LCA to clinical research data, with an emphasis on key steps and errors to avoid. It is not intended as a technical treatise but rather as a practical guide. In addition, the manuscript will focus on some specific challenges that are unique to the data types used in clinical research. A recent review by McLachlan, Lee and Rathnayake is an excellent resource for those seeking a more technical review of latent class modelling.(20) A glossary of terms can be found in Table 1 that can be referenced throughout this manuscript.

Table 1.

Glossary of terms and their description (alphabetically ordered)

Terms	Description
Akaike Information Criterion (AIC)	An index of how well a model fits which seeks to balance the complexity of the model against the sample size. The AIC is calculated using the maximum likelihood estimate. The AIC penalizes models as the number of parameters increases. The size of this penalty is constant.
Bayesian Information Criterion (BIC)	An index of how well a model fits which seeks to balance the complexity of the model against the sample size. The BIC is calculated using the maximum likelihood estimate (includes sample-size adjusted BIC). The BIC also penalizes models as the number of parameters increases; however, this penalty increases as the sample size increases.
Entropy	A measure of separation between latent classes. Higher entropy denotes better class separation. It is calculated using sample size, number of classes, and posterior probabilities. Note that an over-fit model will have high entropy so this should not be used for model selection.
Factor Analysis / Complete Factor Analysis	Principal component analysis where the 1’s in the diagonal of the correlation matrix are replaced by an estimate of the communality of the variable.
Full information maximum likelihood (FIML)	A method of finding the maximum likelihood solution in the presence of missing data.
Growth mixture modeling	A form of mixture modeling used to find latent paths in longitudinal data. Growth, as in monotonic increase, is not a requirement.
Hidden Markov Model / Latent Transition Analysis	A form of statistical modeling used to model changes in categories over time where the groups or categories are not directly observed.
Indicators	The variables used in a finite mixture model which generated the observed distribution.
Latent Class Analysis	A form of mixture modeling where all indicator variables are categorical or, in our usage, a mix of categorical and continuous.
Latent Profile Analysis	A form of mixture modeling where all indicator variables are continuous.
Latent Variable	A variable that cannot be directly observed, such as membership in a class.
Local Independence	The concept that variables are independent of each other within a latent class.
Local Maxima	A likelihood value that is not the true likelihood—analogous to mistaking the top of a foothill for the top of the mountain.
Maximum Likelihood	Maximum likelihood estimation/solution is the process of estimating model parameters such that the resultant model generates values that are most likely to represent actual observed values.
Mixture Modeling	A form of statistical modeling that can be used to identify latent groupings within a dataset.
Model Parameter	These are internal component parts of a model that define its composition. Parameters are estimated using the training data, and once estimated, they are constant. The simplest example of a model parameter is coefficients generated in a regression equation.
Monte-Carlo Estimation	Computational algorithms that use repeated and random sampling to estimate expected values in simulated data where direct calculations are not feasible. In LCA, Monte-Carlo simulations studies can be used to determine power or to estimate model performance under varied conditions.
Multiple Imputation	Approach to handling missing data where the missing values are replaced using algorithms that account for the variance of the data and multiple such data sets are imputed. Results from each dataset are combined for the final analysis.
Posterior Probability	The probability of class membership for each observation after the model has been fit.
Principal Components Analysis	A mathematical method of data reduction where N variables are replaced by a smaller set of components.
Salsa Effect	Forcing a single population into separate latent classes which are just spread along a single spectrum or variable.
Vuong- Lo-Mendel-Rubin (VLMR) test	A test of the probability that a k-class model fits the data better than a k-1 class model.

What is Latent Class Analysis?

Finite mixture modeling, of which LCA is one of the most commonly used types, is a set of powerful tools that allow investigators to determine if unmeasured or unobserved groups exist within a population. The unobserved, or “latent”, groups are inferred from patterns of the observed variables or “indicators” used in the modelling.

Latent class analysis (LCA) is the label given to a form of finite mixture modeling where the observed indicators are all categorical.(21) Latent Profile Analysis is the term used for mixture modelling where the indicators are all numerical and continuous in their distribution. Both methods relate to the analysis of cross-sectional data. In instances where combinations of categorical and continuous class-defining indicators have been used, conventional nomenclature remains unestablished. For the sake of ease, we have applied the ‘LCA’ label to such models, as the objectives remain to define class-based phenotypes. For the remainder of this manuscript, unless stated otherwise, the use of the term latent class analysis is applied broadly as a descriptor all forms of cross-sectional finite mixture models where the latent variable is categorical. Application of finite mixture models to longitudinal indicators and continuous latent variables are also well described and are summarized in Table 1.(17)

LCA models work on the assumption that the observed distribution of the variables is the result of a finite latent (unobserved) mixture of underlying distributions (Figure 1). Using a set of observed indicators, LCA models identify solutions that best describe these latent classes within which the indicators follow the same distribution. Whilst Bayesian methods for finite mixture modeling are also described, LCA solutions are often obtained using maximum likelihood estimates and are the primary focus of this review. Viewed simply, LCA is a probabilistic method of unsupervised clustering. Once identified, mathematically, the classes are homogeneous within, but distinct from each other. The basic mathematical principles and algorithms used in LCA modelling are detailed in the supplement.

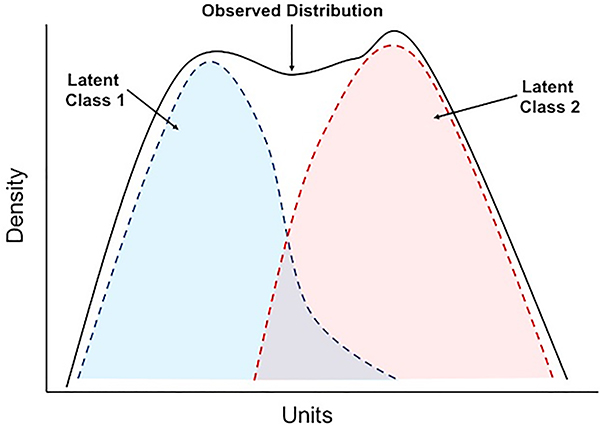
Figure 1.

Illustration of “hidden” or latent classes in a population where the data are normally distributed. The black lines show the density of distribution in the whole population, the dotted lines represent two latent classes (blue and red). The presence of latent classes within a population is a central assumption to the modelling algorithms of latent class analysis.

Once the model has been fitted, the probability of class membership is estimated for each observation in the cohort. These probabilities can then be used to assign class. It is important to emphasize that an LCA model does not assign individuals to latent classes; rather, probabilities are generated for membership in all the identified classes in the model. This distinction, whilst subtle, has important implications when interpreting the findings of the analysis (see section on classify then analyze).

LCA vs Cluster Analysis

Cluster analyses are sets of algorithms that, like LCA, are used to split populations into smaller groups with shared characteristics. Clustering algorithms, of which hierarchal and k-means are two of the most popular, use an arbitrary distance measure to identify clusters. Consequently, determining the appropriate number of clusters is inherently subjective and hypothesis-free.(22–24) Cluster analysis separates the study units into different clusters, whereas LCA estimates the probability that a given study unit belongs to each of the different latent classes. As LCA is model-based, it generates fit statistics, which in turn allows statistical inference when determining the most appropriate number of clusters for a population. In comparison to cluster analyses, LCA is therefore considered a more statistically robust method of clustering.(24, 25)

Interestingly, Magidson and Vermunt studied the accuracy of LCA and k-means clustering in correctly identifying classes where true class membership was known but concealed during analyses. In this simulated study where data were generated preferentially to meet the assumptions for the k-means approach, thereby favouring it over LCA, they found that misclassification rate was approximately four times higher using k-means clustering compared to LCA.(26). A further advantage of a model-based classification algorithm is that the generation of posterior probabilities allows quantitative assessment of uncertainty of class membership. LCA also permits the usage of mixed data types for the class-defining variables, including different scaling, whereas many methods of clustering are limited to numeric and/or a single data type.(27)

A drawback of LCA is that it is computationally demanding.(24) This can be a limitation to how many indicators can be used for the modeling. Currently, the upper limit of how “big” the data can be for LCA remains unknown and is dependent on the processing power available. With current technology, using LCA for clustering large genetic sequencing data, for example, seems unfeasible. The limits of using LCA are, however, constantly being challenged.

Key Steps in Performing Latent Class Analysis

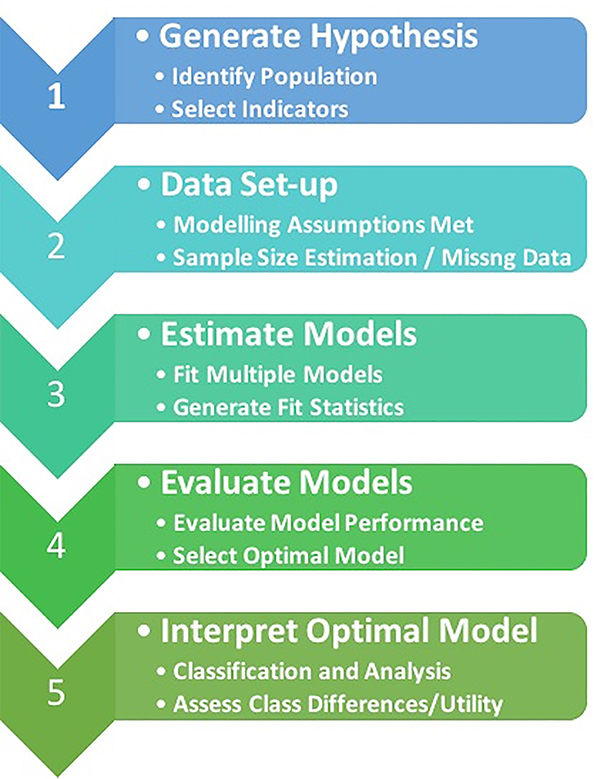
Figure 2 is an outline of the key steps involved in performing LCA. A summary of these steps can be found in Tables 2 – 4.

Figure 2.

Schematic of the stepwise approach for performing latent class analysis.

Table 2.

Summary of key steps and recommendations when setting up the data to perform Latent class analysis.

	Step	Description	Recommendation	Presentation
Study Design & Data Set-up	Indicator Selection	The indicators selected will dictate the nature of the clusters.	- Select indicators based on research question. - Exclude indicators that are composite of other indicators in the model. - Exclude outcome data as indicators.	- Present clear rationale for indicator selection.
	Data Processing	Transforming data to minimize extreme scales is more likely to yield informative classes.	- Categorical variables: Consider collapsing categories with less than 10% of the sample. - Non-parametric data should be transformed such that they are normally distributed and uniformly scaled.	- Clearly describe the procedures used for data transformation and collapsing of categories.
	Local Independence	Assumes that within class, observed indicators are independent.	- Test correlation of indicator variables in the complete dataset and within each class. - Consider removing one or more indicator if there is collinearity. - If a single pair is highly correlated consider relaxing the assumption.(31)	- Present the correlation coefficients of the most highly correlated indicators. - Clearly describe any variables that were excluded from the analysis.
	Sample Size	Power sample to: 1. Determine the true number of classes. 2. Detect pertinent differences between the classes.	- When N < 300 it is recommended to perform Monte Carlo simulation to determine adequacy of sample size.(38) - Standard power calculations should be performed to determine the sample size needed to detect significant inter-class differences.	- Present clear rationale for the sample size and any power calculations performed.
	Handling Missing Data	Approaches for missing data: 1. Full information maximum likelihood 2. Multiple Imputation	- Full information maximum likelihood and multiple imputation are recommended methods of dealing with missing data. - Lower levels of research biomarker assay detection (LLD) impute either LLD, LLD/2, or multiple imputation.(44)	- Present methods used for handling missing data. - Present differences in indicators and outcomes between missing and complete cases. - Sensitivity analysis with missing data / non-imputed data.

Table 4.

Summary of key steps and recommendations when interpreting the final model.

	Step	Description	Recommendation	Presentation
Interpreting Final Model	Convergence	A form of internal validation where the maximum likelihood for each model is generated using random starts.	- Multiple random starts are recommended (minimum 50) to replicate the maximum likelihood at least 20 times. - Increase number of starts with models with increased complexity.(55) - If likelihoods are not replicated evaluate data structure and type. Consider rejecting model if maximum likelihoods are not rejected.	- Confirm that maximum likelihood was replicated at least 20 times for all models in the analysis - Presenting the maximum likelihood is optional as the AIC and BIC are generated using this value
	Classification	Probabilities generated by the model are used to classify each observation to a class.	- Probabilities cut-offs to assign class should be determined a priori. - If the entropy of the model is low with poor class separation, the uncertainty of class membership should be incorporated in the analysis.	- Present the probability distribution of the classes in the optimal model that best describes the population (final model).
	Salsa Effect	This refers to the coercion of classes to fit a population that may not have latent classes.	- Examine the distributions of the indicator variables to see if they suggest a single population has been spread out along a continuum.	- Not applicable.
	Outcome Measures	To demonstrate that the identified classes are of value, certain key variables are shown to differ between the classes.	- A priori key discriminant outcome measures should be described in the analysis plan. - Investigators should be blinded from these outcome measures when determining the best fitting model.	- An a priori analysis plan should describe the likely metric that will be used to determine differences between the latent classes and gauge their clinical utility.

Step 1: Study Design (Table 2)

Observed indicator selection.

Which observed indicators to include in the model is a key decision. The adage of garbage-in-garbage-out holds. A clear rationale for the inclusion of any variable in the models should be presented, as observed indicators are the principal determinants of class characteristics. The indicators used for the analysis should, therefore, largely be dictated by the research question.

For example, Siroux and colleagues used LCA to seek phenotypes of asthma that would allow better assessment of risk factors for asthma.(12) Consequently, they focused on using data pertaining to personal characteristics, disease course and treatment responsiveness as indicators in their model. Whereas, in our work with ARDS, the primary objective of the analysis was to derive subgroups that would enable novel biological and clinical insights. To that end, we selected biological and clinical variables that served as surrogates of biological pathways implicated in the pathogenesis of ARDS (e.g. inflammation, endothelial and epithelial injury) and/or were associated with disease severity in ARDS.(15, 16) It is worth noting that identified classes may not unequivocally link to the underlying biological pathway that the indicators purport to represent. To a large extent, this linkage would depend on the quality of the indicator (i.e. how good it is at separating the classes) and on how specific the indicator is as a surrogate of the biological pathway.

When dealing with critical care data, it is also important to consider the impact of including disease severity scores such as APACHE score or SOFA scores as class-defining variables, as often their component parts are many of the variables that may already be part of the model. For these reasons, in our practice we have not included these summary indicators in the modeling, but use their components instead. Lastly, as the usefulness of novel subgroups using LCA is often demonstrated by differential disease trajectories and clinical outcomes, including information on clinical outcomes as indicators may bias the clustering towards such measures and introduces a certain circularity to the analysis. Inclusion of such data should, therefore, be excluded during discovery-focused LCA.

Step 2: Data Set-up (Table2)

Examine the data.

As in any data analysis, the initial step is to examine the data carefully. One should check for extreme or implausible values. This step is important as LCA models can be sensitive to extreme values. Consider a multivariate distribution with a small but noticeable ‘bump’ at some point. As one keeps increasing the number of latent classes to be fit, the model may, in effect, declare that “bump” a class.

For continuous variables, one needs to examine their univariate distributions and transform those with noticeable non-normality towards a more normal distribution. Which transformation to use is arbitrary. We have used a log-transform but others, such as a square root, may work just as well. Similarly, examine the frequencies of categorical variables. Categories that have low frequencies are difficult to fit into a model, as there is limited distributional information in that space. In that case, one can collapse categories together. In our practice, categories with less than approximately 10% of the sample are excluded from the analysis. This cut-off is arbitrary; however, logically, a small category that is sufficiently unique can increase the probability of identifying a latent class exclusively based on this category. This approach would undermine the “latency” of the identified class. However, in some cases, small categories may be informative, e.g. when studying severe acute hypoxemic respiratory failure, whether a patient is on ECMO may be an infrequent but important predictor variable to consider.

A major challenge faced in our prior work was the wide range of scales used in the observed indicators. For example, age, body-mass index, P/F ratio, bilirubin and Angiopoietin-2 are all measured on widely different scales. In theory, LCA models can accommodate a range of scales, but if the variances measure-to-measure vary widely, it becomes difficult to fit the models. Steinley and colleagues found that models performed best with normally distributed data with equal variance, and unequal variance led to a sharp decrease in accurate cluster identification.(28) Our ‘fix’ for this problem is to standardize all continuous variables by placing them on the same scale, such as a z-scale where the mean is set to zero and the standard deviation to one. Note that any linear standardization which constrains the variances to be similar in size should work. Whilst the standardization process is frequently a necessity for modelling with variables on different physical scales, when interpreting the results, it is worth considering that some informative variance is likely to be dampened due to this procedure. In instances where indicators on the same physical scale are being used of the modelling (e.g. univariate LCA), this standardization may not be necessary.

A critical feature of mixture modeling is that there is an assumption of “local independence” within class.(29) This assumes that within latent classes, observed variables are independent of each other. Violation of this assumption can introduce bias to model parameters and lead to misclassification errors.(30) Simulated studies have shown that violation of this assumption led to lower accuracy of model fit statistics with an overestimation of the true number of classes.(31) The problem, however, is that it is unclear how strong of a correlation is tolerable and what effects bending this assumption has on model fit.

Our advice is to examine the correlation matrix of the candidate variables and serially eliminate one in any pair where strong correlation is observed. It is important to test the correlations in the final form that the variables will enter the model, e.g. after log transformation. Correlation coefficients greater than 0.5 should be examined carefully for their impact on the modelling. Whilst an arbitrary cut-off, in our experience, coefficients > 0.5 can influence the modelling and fit statistics. In particular, multicollinear variables should be minimized to avoid data redundancy, as they are likely to result in emergence of spurious latent classes and poorly converging models.(32) In critical care, multiple colinear variables are frequently encountered; for example, systolic blood pressure is usually correlated with diastolic blood pressure, or C-reactive protein may be correlated with erythrocyte sedimentation rate.

If colinear variables are deemed too important to exclude outright, we conduct sensitivity analyses by excluding each of those variables and repeating the LCA. If this process leads to major changes in class composition or model fit statistics, then we eliminate the least informative variable. Next, to investigate local independence, re-examine the correlations among observed indicators within each of the classes once a model has been selected. Once again, for locally dependent variables, sensitivity analyses should be performed to determine impact of removing each variable. As an alternate strategy, if two locally dependent indicators are felt to be too important to lose, it is possible to relax the assumptions of conditional independence by allowing the two variables to be correlated in the model.(33)

Sample size.

The sample size required to adequately fit an LCA model varies with a number of factors. Broadly speaking, there are two important aspects when considering adequacy of sample size necessary to conduct LCA. First, is the sample adequate to detect the “true” number of latent classes? High-quality indicators, i.e. those that are highly effective at separating the classes (entropy), will necessitate a smaller sample size. Likewise, if the smallest class in the model is relatively big, then less sample size is required. Nylund et al in simulated modelling found that Information Criteria (see section on fit indices below) and likelihood-tests accurately identified the correct models when N = 500 or N = 1000; but not when N = 200.(34) These findings are further supported by the extensive simulation work conducted by Wuprts and Geiser.(35) They found that models with less than an N of 70 were ‘not feasible’ and models based on sample less than 100 should be interpreted with great caution. Lo, Mendell and Rubin showed that their eponymous test for model fit was insufficiently powered when the sample size was less than 300.(36) In summary, LCA can be considered a ‘large sample’ method; with sample sizes of greater than 500, models and fit statistics have been shown to consistently perform with high accuracy.(37) With smaller sample sizes, particularly when N < 300, the results are less reliable.(38) For analyses where N < 300, we would recommend using Monte Carlo simulations to determine adequacy of power.(39) These simulation studies should also be considered in studies where N > 300 but < 500 if there are issues with model fit or convergence.

Second, one must consider whether the sample size within the latent classes will have sufficient statistical power to detect differences in the pre-determined metric of interest (i.e. clinical outcomes) and that the difference is of sufficient magnitude to be meaningfully interpreted. More traditional approaches of power calculations can be used to determine this.

Dealing with Missing Data.

While LCA can be estimated in the presence of missing data, the greater the data sparseness due to missingness, the more difficult the estimation process. The pattern and magnitude of missing data will impact modelling. Swanson et al conducted LCA in a simulation study and found that the accuracy of Information Criteria were worse when the data were not missing at random compared to when missing at random.(31) Similarly, model fit statistics in both missing data patterns were worse when the total missing data was 20% compared to 10%. These errors in identification of the appropriate class were amplified when the sample size was smaller. Similarly, Wolf et al in simulation studies found that in models with 20% missing data required an approximate increase of 50% in their sample size.(40)

Three methods are widely used to deal with missing variables when performing LCA: deletion, multiple imputation, and full information maximum likelihood (FIML). The issue with listwise or pairwise deletion (i.e. complete cases analysis) is that large swathes of data can be lost in the context of sparse and sporadic missingness. In general, this is the least preferred of the three methods and should seldom be used.(41) In relation to LCA, the other two methods have their own inherent advantages and disadvantages, and both approaches work on the assumption that the data are missing at random. Multiple imputation (MI) involves creating several permutations of solutions for the missing variable using the available data. The main advantage of MI is that once the dataset has been generated, it can be used across several models. Further limitations of this approach are that multiple permutations of the dataset are produced, the datasets are generated at random with new each run containing variations in the imputed data compared to the prior, and imputing mixed data types with this method can be complicated.(42)

FIML does not actually impute the data; instead it uses all the data, both complete and incomplete, to estimate parameters of the model. The FIML approach is specific to the model where it is applied and has be shown to be an efficient method for handling missing data for modelling algorithms such as LCA.(43) A limitation of FIML method for dealing with missing data is that it is computationally complex. Having said that, FIML is now available in most software packages that are used for LCA and is our preferred choice for handling missing data. In general, missing data should be kept to a minimum, and the analyst should consider re-fitting models by first removing variables where missing values are high. In addition, difference in population characteristics between missing and non-missing observations should be presented, and a sensitivity analysis should be presented if imputation or deletion are used to handle missing data.

Special case of missing data: Molecular epidemiology.

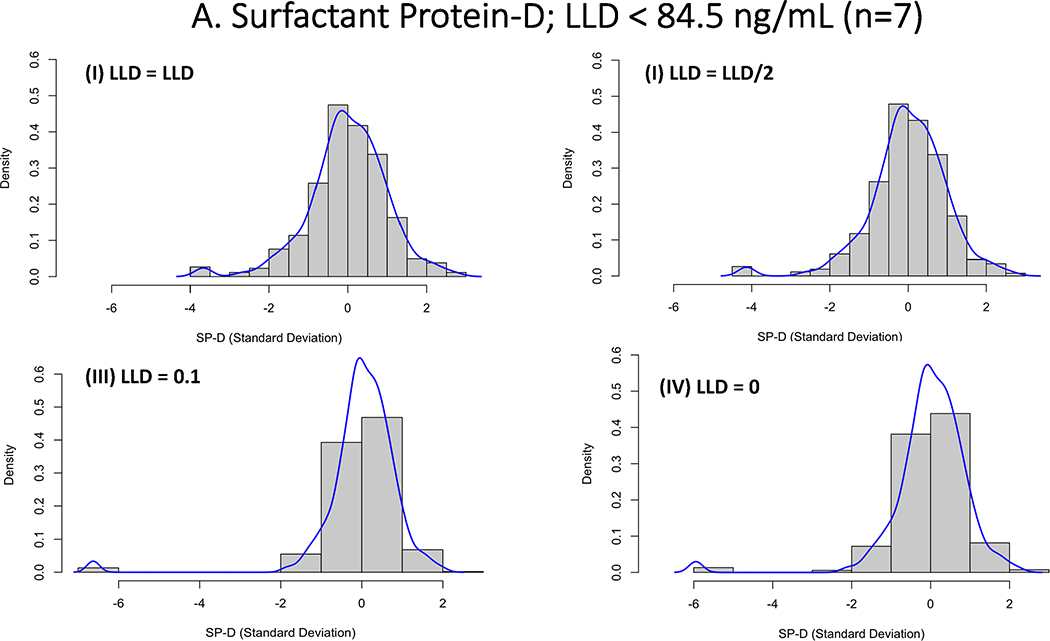
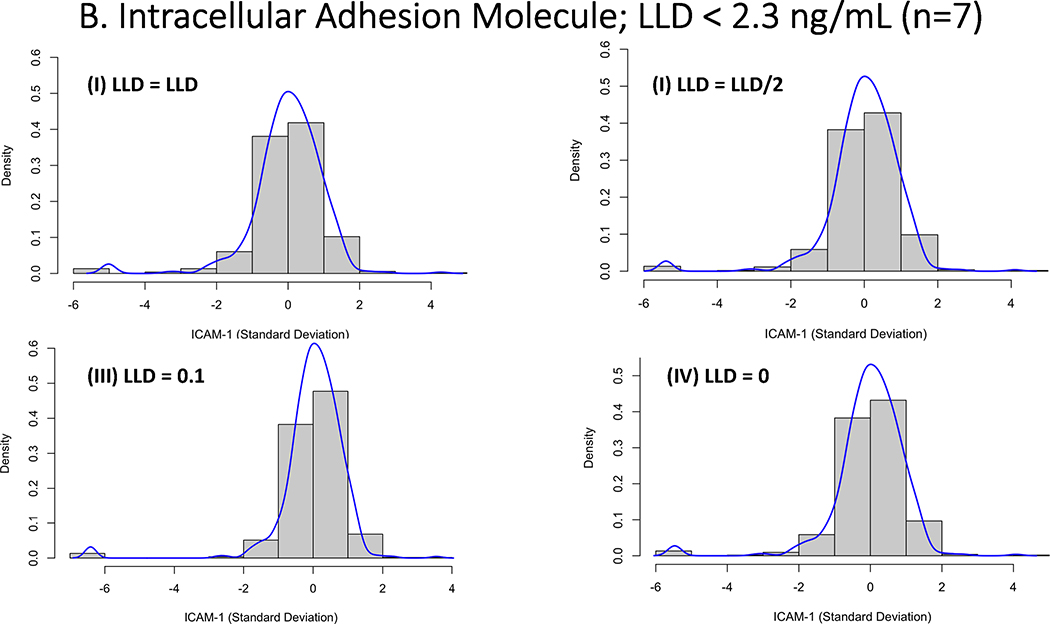
Research biomarkers present a challenge to modeling when there are limits to the level of assay detection, both below and above. One could set such values to missing (as in, we don’t know the value), but that approach discards information unnecessarily. Once an assay has been optimized, there is little to be done when the value in question is “above level of detection” other than to set the value to that limit. When the sample is below the lower limit of detection (LLD), there are several potential options including data truncation where the value is ignored, insert zero or a value just above 0, single imputation with the value to the LLD or LLD/2, use more sophisticated methods of multiple imputation.(44) The strategy used to replace this data are largely driven by the amount of missingness but may have considerable consequences if not approached thoughtfully. In particular with LCA, where model parameters are estimated based on the distribution of an indicator replacing the LLD to extreme values, such as 0 or 0.1, can have profound impact on the models and the cluster they identify. The effect each of these will have depends on the range of values and how far zero is from the lower limit of detection. For example, in values where the lower level of detection is some distance from 0, setting these values to 0 or 0.1 would lead to significant changes in the distribution of the data that may have detrimental effects to model fitting and convergence (see Figure 3a). In contrast, when the lower limit of detection is closer to 0, the same imputation will have a less profound effect (Figure 3b). On the proviso that the levels of censored values are low, for the purposes of LCA modeling, using LLD/2 or LLD would be the more preferable approach to imputation and is known to perform well in setting of low-levels of censored values.(45)

Figure 3.

Histogram demonstrating the impact of imputation strategies for biomarker assay quantification values that were below the lower limit of detection (LLD). For each presented biomarker the values were imputed as either as (I) LLD; (II) LLD/2; (III) LLD = 0 (IV) LLD = 0.1. 3A: Represents z-score transformation and log-transformed data for Surfactant Protein-D, where there were 7 out of 587 values below the LLD (84.5 ng/mL). 3B: Represents z-score transformation and log-transformed data for Intercellular Adhesion Molecule-1, where there were 7 out of 587 values below the LLD (2.3 ng/mL).

A second consideration is about how best to impute missing data when research biomarkers are missing. In particular, as in the case of molecular epidemiological studies where measurements are likely to contain large amounts of data with extreme values, multiple imputation becomes more challenging, and analysis of FIML may be more suitable and in some instances completed case analysis may also be preferable.(46) Uncertainty in imputation of extreme values of protein biomarker that are important in separating the identified classes is likely to lead to misclassification, thereby, undermining the content and construct validity of the said biomarker and its association with the identified latent classes.(47)

Step 3: Fitting Models to the Data

Once the indicators have been selected and processed, the next step is to fit the models to the data. Multiple models consisting of k-classes are fit to the data. Usually, the first model consists of a single class (k = 1) and sequential models, each with one more class than the prior, are fit. Usually, as sample size increases, models with increasing complexity (i.e. greater number of classes) should be fitted to the cohort. As model complexity increases, the number of observations in each class will inevitably get smaller. Further, complex models may become harder to fit, potentially decreasing its generalizability. The correct number of models to fit to the data will largely be dictated by the sample size, number and quality of indicators used in the model, and what an acceptable size may be for the smallest class. For each model that is fit to the data, parameters are estimated based on maximum likelihoods (see Table 1 for definition) and numerous fit statistics are generated. In addition, the algorithm will generate a posterior probability for belonging to all the latent classes in the model for individual observations. There are several key features that may indicate a poorly fit model and require careful analysis of the data. These are summarized in Table 5. It is always worthwhile considering that the studied data may not have underlying latent classes or that the extreme values observed (i.e. classes with small observations) are truly representative of the population. In such instances it is imperative that the investigators repeat their analysis in a second independent cohort to corroborate their findings.

Table 5.

Features that should alert investigators to a potentially poor fitting latent class analysis models and their corresponding trouble-shooting solutions to improve model fit.

Features suggesting poor fitting models	Trouble-shooting
Failure to obtain multiple replications of maximum likelihood	- Increase the number of random starts - Check the scale of the continuous predictor variables are appropriately transformed and uniformly scaled - Check distribution of variables and seek extreme outliers - If models fail to replicate the maximum likelihood consider rejecting the model
Minor perturbation of indicators leading to large changes in the model fit statistics and/or VLMR values	- Check correlation between indicators - Check correlation between indicators within each class - Check if the data transformation/imputation of the continuous indicators has led to extreme scaling of important variables (see Figure 3)
A two class model comprising of a class with less than 15% of the sample or Models comprising three or more classes contain a class(es) with less than 10% of the sample	- Check to ensure that a single indicator is not the pre-dominant determinant of the classes - If a single variable determines the class:  - Check the scale of the continuous predictor variables are appropriately transformed and scaled  - Consider rejecting the model  - Validate the findings in an independent cohort
Models with low entropy	- Assess the quality of the indicators:  - Examine the entropy of individual indicators. The variables may be of insufficient quality to separate the classes  - Consider adding novel, higher quality, indicators to the model

Note: the presented solutions may be helpful in rectifying poor model fit, when interpreting these features, however, it must always be considered that a given population may not have underlying latent classes.

Step 4: Evaluating the Models- Selecting Optimal Number of Classes (Table 3)

Table 3.

Summary of key steps and recommendations when determining the optimal number of classes that best fit the population. AIC, BIC, SABIC, LMR, VLMR, BLMR.

	Step	Description	Recommendation	Presentation
Optimal Class Selection	Fit Indices	AIC, BIC, SABIC	- For most analyses, we recommend using BIC and/or sample adjusted BIC.(32) - For analyses with small sample size (< 300) and/or multiple classes in the final model, use both AIC and BIC.(50)	- All indices used for model selection should be presented in the fit statistics table. - Both AIC and BIC should be presented if N < 300
	Model Testing	LMR, VLMR, BLMR	- VLMR should be used to test if a model with k classes is better than model with k-1 class.(34, 52) - In models with mixed indicator data types the BLMR is not recommended.	- All model statistical tests should be presented with a significance level of p < 0.05. - Clearly present the clinical or biological rationale for selecting a model where the p values may not be significant.
	Model Characteristics	Number of classes, the size of the smallest class and class separation are important determinant of model fit	- Classes with small N’s should be evaluated to determine whether outliers of a single indicator may be determining the class. - Models consisting of numerous small classes are less likely to be externally generalizable than models with fewer, well-distributed, classes.	- Present the fit statistics and the number of observations in each class of all the models used in the analysis - Present the entropy of all the models in the analysis

Once the models are fit, selecting the optimal number of classes is obviously the main decision one has to make in the analysis. The basic approach is to select the model with the fewest number of classes that best fits the data. The trick is deciding what is the “best” fit. There are several factors to consider and, just as a jacket can fit in one dimension, such as sleeve length, but not in another, so too can models fit by one criterion but not in others. The best fitting model may not capture the underlying structure of the data, or the data may not have a clear, well-separated set of underlying distributions. Note that best fit does not always mean a good fit.

The key measures of determining the best model that fits the population are Bayesian information criteria (BIC), sample-size adjusted BIC (SABIC), the Lo-Mendel-Rubin and Vuong- Lo-Mendel-Rubin (p-value), and the size of the smallest class.(48) As one fits more parameters to a model, in this case more classes, the better the model will fit the sample of data but tend towards overfitting. An over-fit model is less generalizable and less likely to replicate.(49) That is, as model complexity increases, it becomes more unique to the sample and less generalizable to the population.

Fit Indices:

The Information Criteria (IC) statistics are derived from maximum likelihood values of a fitted model. The two most frequently used measures, BIC and Akaike Information Criteria (AIC), are designed to strike a balance between accuracy and over-fitting. In both measures, a decreasing value indicates better model fit. A key difference between the two measures is that BIC heavily penalizes the addition of parameters to the model in relation to the sample size, where the larger the sample size the greater the penalty.(50) BIC, therefore, favours simpler models (fewer classes) compared to the AIC. Whereas, as N increases, the AIC has a tendency to select more complex models (more classes), as the best fitting because sample size is not a determining factor in its estimation.(51) To that end, Nylund, et al. (34) using simulations concluded that BIC tends to perform better than AIC especially when N is large. BIC tends to performs poorly when the sample size is modest because of a high probability of extracting too few classes and may be outperformed by the AIC.(52) In these circumstances, when the sample size is known to be small (< 300), it is advisable to present both the AIC and BIC.

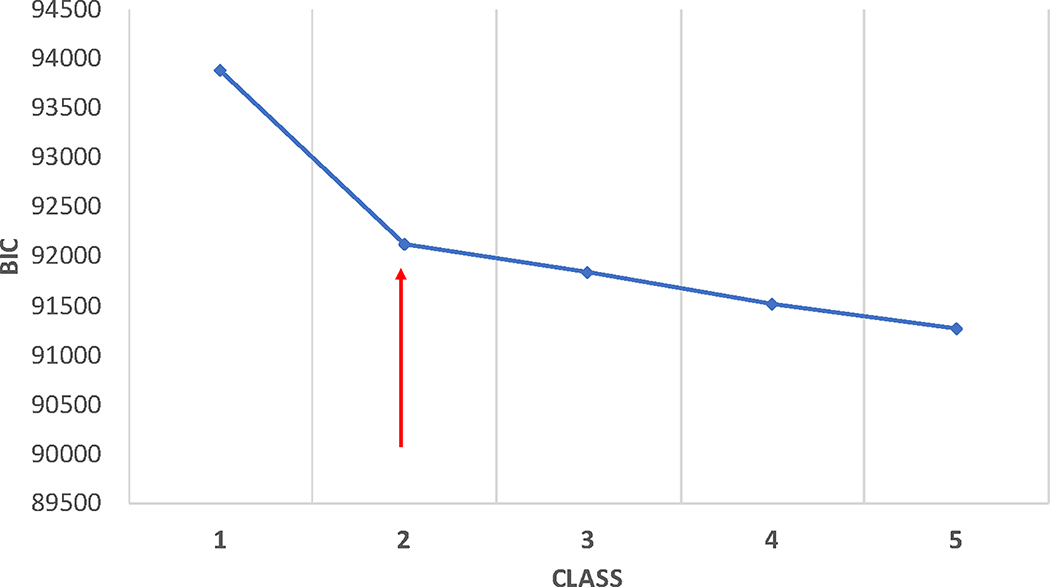
In the case where there is a mix of categorical and continuous variables and the continuous ones are normally distributed, Morgan found that BIC worked best at identifying the correct number of classes when most of the variables are continuous.(53) He also demonstrated that the sample size-adjusted BIC works well in such data types. These findings were in line with Nylund and colleagues.(34) Further, when assessing the best model fit, particularly in large datasets with many indicators, additional classes can often lead to a consistent decrease in the IC, favouring the more complex model. In such instances, it is helpful to plot the IC to seek a point of inflection or plateauing (elbow plot; Figure 4).

Figure 4:

Example of an Elbow plot used for evaluating the Bayesian information criteria (BIC) or other indices of model-fitting. The red arrow indicates the “elbow”, where further increases in model complexity (i.e. more classes) does not yield the same decreases in BIC (lower values suggest a better fitting model. These values are from unpublished data from prior ARDS studies.

Testing for number of classes.

In addition to indexing model fit, there are tests comparing a model with k classes to one with k-1 classes. Developed by Lo, Mendell and Rubin (36) based on work by Vuong (54) the VLMR test assumes multivariate normality, and it is not clear how sensitive the p-value is to violation of that assumption. It is also possible to use a bootstrapped p-value, although its validity outside of normally distributed data remains unknown.(55) In a Monte Carlo simulation of LCA using only categorical indicators, Nylund and colleagues found that the bootstrapped test (BLMR) consistently outperformed the simple Lo-Mendell-Rubin test (LMR).(34) Again in simulation studies with latent profile analysis (continuous indicators), Tein and colleagues found that the BLMR had higher statistical power than LMR, although both tests performed well at detecting the true class.(56) In our practice, across multiple analyses with real-life data consisting of a mixture of categorical and continuous indicators, we have found that the BLMR consistently favours k classes over k - 1 class to the point of being of limited value.

Step 4: Evaluate the Models

Class Numbers, Size and Separation

It is important to remember not to rely too heavily on p-values, as they are only one index of model fit. It is also important to consider the relative size of the smallest latent class. A model with a small class is often a model with too many classes. That is, a small class may be the result of some sort of ‘quirk’ in the data. It is also important to determine the validity of the ‘latency’ of these smaller classes by examining the chief determinants of class-membership, as often they may be driven solely by extreme values of a single-variable rendering the LCA model superfluous for their classification. For example, in a cohort of patients with sepsis, a small class with few observations may be driven almost entirely by neutropenia. Whilst mathematically legitimate, this class provides little additional biological or clinical information that cannot be simply extracted using the neutrophil count. As models with increasing numbers of classes are fit to the data, one also runs the danger of over-extracting classes that may be unique to the dataset. Entropy, a measure of class separation, can be informative of how well the clusters differentiate and should be presented for each model. Again, the model with the highest entropy may not necessarily represent the best fitting model. Theoretically, an over-fit model would have higher entropy, and therefore, the absolute values of entropy should not be used as a metric to determine the optimal model. A low entropy, however, can be informative of a poor class separation and warrants closer inspection of the models and the quality of the indicators used to derive them (see Table 5).

Biological and Clinical Insights

When determining the optimal number of classes in a population, it is important to bring one’s substantive knowledge and expertise to the process. The separation of the classes should be meaningful from either a clinical or a biological stand-point or both. Fundamentally, the utility of the classes identified by the best fitting model often requires the discretion of the investigators. It may be that the biological or clinical insight gleaned from classes identified by a statistically worse fitting model may supersede the primacy of the model with the ‘best’ fit statistics. The best model should, however, be selected prior to linking the outcome variables of interest to the classes identified. Concealing the outcome variable used as a metric to gauge successful clustering from the model selection procedure allows an unbiased approach to model evaluation. Further, it is also important to be mindful that choosing a model that is not statistically the best fitting may compromise the likelihood of replicating the model beyond the data from which they were generated. In such instances, external validation of the identified classes becomes all the more essential. Finally, when evaluating LCA models where the fit statistics suggest that none of the models fit the population or the 1-class model is the best fit, it is important to acknowledge that this may be the ground truth. In such instances, it may be that the studied population does not have “latent” classes or that the indicators are of insufficient quality to distinguish these classes.

Step 5: Interpreting the Final Model

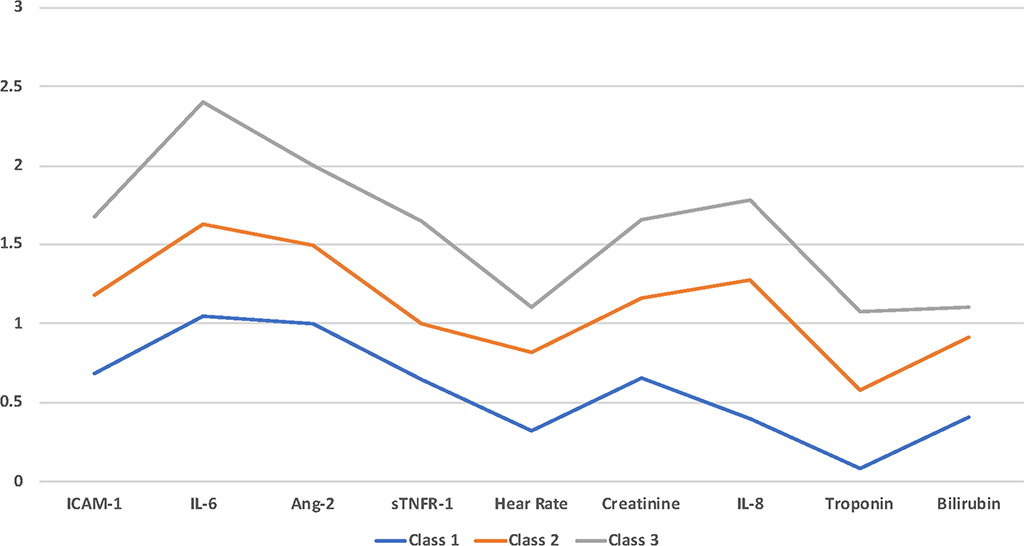
When assessing the validity of the final model, it is important to consider its robustness. Multiple random starts should be used to demonstrate sufficient replication of the maximum likelihood.(57) It is also important to inspect the classes to ensure that they are not merely reflective of scaled groupings of a single observed indicator. If a given dataset has only one class (in other words, there is no underlying mixtures of distributions), there may be some indication that a k-class model fits the data. However, when the profiles are plotted, they roughly form a set of parallel lines (Figure 5). This finding probably suggests that a single sample has been coerced into k levels, such as low, medium and high severity where k is the number of classes one asked the algorithm to fit. This phenomenon is known as the Salsa effect (mild, medium and hot levels of spice). It may still be possible that these classes are distinct, but emergence of such parallel lines should be considered a strong indicator of this phenomenon, and the results should be interpreted cautiously.

Figure 5: Illustration of the “Salsa effect” in latent class analysis using simulated data. The indicators of the identified classes when plotted on a graph they run parallel to each other, suggesting that the identified classes are merely representative of scales of severity of these variables.

ICAM-1 = Intercellular Adhesion Molecule-1, IL = Interleukin Ang-2 = Angiopoetin-2, sTNFR-1 = Soluble tumor necrosis factor receptor-1.

Classify then analyze

When working with LCA models, it is not uncommon to perceive the classifications as absolute and error-free. In reality, individual posterior probabilities for class assignment are estimated. This uncertainty of class membership should be incorporated into analyses that compare differences between classes, particularly when class membership is uncertain. There are several practical advantages to using a classification system rather than probability outputs to determine the validity of the latent class, not least that it simplifies the clinical decision-making process. In our practice, we use a probability cut-off of ≥ 0.5 to assign class. If the model fits well, and the entropy is large enough, the probabilities will be close to 1.0 for one class and close to 0 for the others. In such circumstances, the loss of information introduced by this “classify-analyze” approach will be minimal, limiting the chance of miss-classification. In instances where class-membership carries greater uncertainty, Lanza and Rhoades found this simplistic approach was less conducive to detecting heterogeneous treatment effect compared to more complex model-based approaches, due to high misclassification rates.(58)

Comparing Classes

When interpreting differences between classes, it is important to keep in mind that there is a circularity when doing so based on indicators used to fit the model in the first place. The algorithms used in LCA separate classes using these indicators. Finding that the classes differ on most variables is, therefore, uninformative. What is informative, however, is exploring indicators that are most divergent among the classes, as this helps to characterize the phenotype of each class. Those variables that are not different can, paradoxically, also provide useful insights into the studied population. For example, in LCA in ARDS, common respiratory variables are not important determinants of class-membership, even though clinical outcomes are vastly divergent between the classes.(15) This finding suggests that the classes identified in LCA ARDS populations are based on factors beyond the variables that are used to clinically define the syndrome and that novel prognostic information is captured by these classes that cannot be extracted from respiratory variables on their own.

External Validation:

A key component to demonstrating the validity of classes or subgroups identified using algorithms such as LCA is to demonstrate their reproducibility in external datasets.(59, 60) A study that replicates the findings using the same predictor variables in a second, independent, population that greatly increases generalizability and impact of the identified classes. There are two distinct questions to address when validating LCA models in an external cohort. First, does the best fitting model in the validation cohort have the same number of classes as the best fitting model in the primary analysis? Second, if the same number of classes emerge, are the characteristics of the classes similar to the one identified in the primary model? When assessing similarities between classes across cohorts, frequently the answer may be self-evident. In instances where the similarities are less pronounced or subjective, investigators should consider building parsimonious classifier-models using the a select few top discriminating variables from the primary model and evaluate its performance accuracy in the validation cohort.

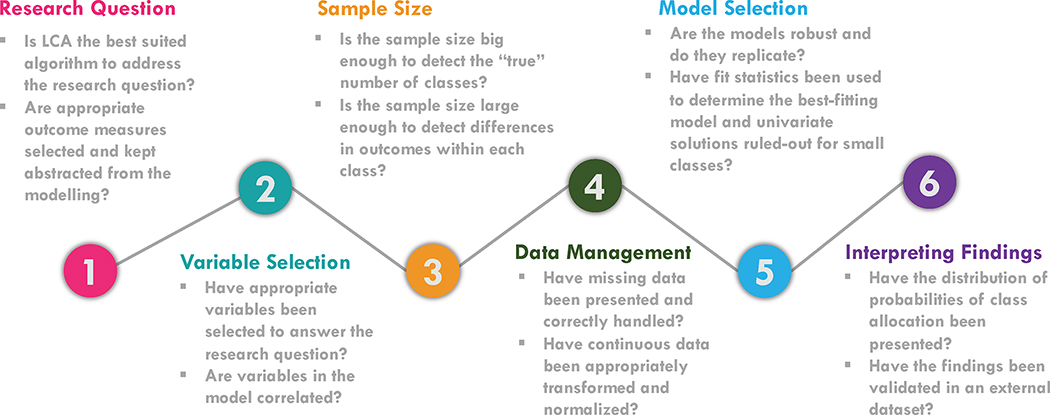
When critically appraising a study using LCA, this reproducibility and robustness of the identified classes should be a key component. Figure 6 is a step-wise framework on the critical appraisal of LCA.

Figure 6.

Key steps and consideration when critically evaluating a latent class analysis study.

Summary

LCA is a powerful analytical tool that allows model-based clustering of heterogeneous populations. Moreover, unlike other methods of clustering, it permits objective testing of model fit. As the field grows with increasing computational power and data complexity, it is likely that LCA will become more commonplace and our understanding of optimal conditions, interpretation and novel application of these algorithms will evolve. In this review, we have presented a brief and current guide on how to approach LCA using clinical and biological data, outlining some of the key steps and pitfalls. It is our hope that it will aid investigators and grow the application of these techniques, further enhancing our understanding of medicine and these powerful analytical tools.