Deep learning toolbox for automated enhancement, segmentation, and graphing of cortical optical coherence tomography microangiograms

Abstract

Optical coherence tomography angiography (OCTA) is becoming increasingly popular for neuroscientific study, but it remains challenging to objectively quantify angioarchitectural properties from 3D OCTA images. This is mainly due to projection artifacts or “tails” underneath vessels caused by multiple-scattering, as well as the relatively low signal-to-noise ratio compared to fluorescence-based imaging modalities. Here, we propose a set of deep learning approaches based on convolutional neural networks (CNNs) to automated enhancement, segmentation and gap-correction of OCTA images, especially of those obtained from the rodent cortex. Additionally, we present a strategy for skeletonizing the segmented OCTA and extracting the underlying vascular graph, which enables the quantitative assessment of various angioarchitectural properties, including individual vessel lengths and tortuosity. These tools, including the trained CNNs, are made publicly available as a user-friendly toolbox for researchers to input their OCTA images and subsequently receive the underlying vascular network graph with the associated angioarchitectural properties.

1. Introduction

Optical coherence tomography (OCT) is a rapid, label-free, high-resolution imaging tool that has been widely used in clinical ophthalmology and is recently becoming increasingly popular and useful for neuroscientific study. OCT angiography (OCTA) is particularly popular for the visualization of cerebral vascular networks, which is based on dynamic scattering in vessels due to moving blood cells. OCT is not only a powerful visualization tool, but can also be leveraged to quantify cerebral blood flow in arterioles and venules using Doppler OCT [1], as well as blood oxygenation levels using visible-light OCT [2,3]. These capabilities make OCT well-suited for the study of various physiological and pathological phenomena in the animal brain cortex, including ischemia [4–6], hemodynamics [7–9], capillary stalling [10,11], and angiogenesis [12,13].

The full 3D nature of OCTA, however, is currently difficult to exploit due to projection artifacts or “tails” underneath vessels in the axial dimension caused by multiple-scattering [8]. In particular, these tails make it challenging to ascertain if two nearby vessels are truly connected, which is important for the graphing of the underlying vascular network and subsequent quantitative analysis. These “tails” have been the major drawback of OCTA for decades, limiting researchers to analyzing only 2D en-face projections and hindering the potential of OCTA for quantitative analysis like vessel connectivity, length, and tortuosity in 3D. Additionally, these “tails” disrupt the tubular or rod-like appearance of vessels, making many traditional techniques for vessel enhancement such as Hessian-based methods yield less than optimal results on OCTAs when compared to two-photon microscopy angiograms (TPMAs) that are free from projection artifacts. This OCTA-specific tail effect, along with the lower signal-to-noise ratio than fluorescence-based TPMA, motivate the need for OCTA-specific image enhancement and graphing techniques.

To suppress the OCTA-specific tail artifact, Leahy et al. combined dynamically-focused OCT with a high-numerical aperture lens such that multiply-scattered photons from the tail are rejected [14]. But this method requires dense scanning in depth to obtain a volumetric image, making it difficult to utilize the Fourier-domain OCT’s strongest advantage that Z-axis scanning is not required over the depth of field. The dense depth scanning with OCT not only wastes the majority of voxels but also is not applicable when one needs rapid volumetric imaging to track dynamic phenomena like neurovascular coupling. Zhang et al. introduced a layer-based subtraction approach to minimize projection artifacts in the choroid layer, but this did not translate well to cortical OCTA images [15]. Alternatively, Vakoc et al. suggested applying a step-down exponential filter beneath vessels to attenuate the signal [16]. More recently, Tang et al. introduced a technique based on autocorrelation (g1-OCTA) to greatly enhance the contrast and mitigate projection artifacts [17]. However, g1-OCTA relies on the injection of a contrast agent like Intralipid and requires 1-2 orders-of-magnitude longer acquisition time and larger data size than traditional OCTA. Therefore, we present a computational approach to efficiently attenuate projection artifacts and significantly enhance image quality of cortical OCTAs, without requiring a contrast agent or additional depth scanning.

Our approach is based on deep learning which has achieved unprecedented results in numerous biomedical and computer vision problems. Convolutional neural networks (CNNs) in particular have proven to be powerful tools in medical diagnosis through effective recognition and localization of objects from images, such as pulmonary nodules from chest CT scans [18] or tumorous regions from MRI scans [19]. CNNs have also proved to be effective at denoising and enhancing CT scans [20] and ultrasounds [21], improving clinical interpretation. In our study, to enhance cortical OCTA images, we specifically drew inspiration from the recent success of encoder-decoders in image denoising and super-resolution [22–24]. The network architecture is described by an encoder which repeatedly down-samples the image, and a decoder which then up-samples the encoded result to the size of the original image. Since the encoder removes noise by extracting relevant features, the decoded result has fewer noise artifacts. In a sense, OCTAs are “corrupted” by noise and projection artifacts, so we investigated whether an encoder-decoder CNN could effectively suppress “tails”. To this end, we developed and trained a 3D CNN on an image pair of a standard (i.e. intrinsic-contrast) angiogram and its manually segmented label such that the trained CNN outputs an enhanced, grayscale, 3D image when applied to any microangiogram. We name this trained network EnhVess.

Along with image enhancement, image segmentation (i.e. assigning labels to each voxel) plays a key role in quantitative analysis of biomedical images. Automated segmentation is considered critical to the unbiased quantification of features and objective comparison between different experimental conditions. For example, the research community concerned with retinal OCT data has long devoted appreciable attention to the automation of segmentation, considering that manual segmentation is a laborious, time-consuming task and often vulnerable to bias. For the segmentation of vessels from angiogram images, deep learning has been shown to achieve unprecedented results on retinal OCTA images [25–27] and cortical TPMAs [28–30]. However, CNNs trained on these image types perform poorly on cortical OCTAs. Thus, we developed and trained another CNN on an image pair of an enhanced angiogram produced by EnhVess and the manually-segmented label. This second network, entitled SegVess, is architecturally simple with only a few hidden layers and one skipped layer. This simple architecture prevents overfitting, while achieving high accuracy [31]. After segmentation, we employ ConVess, a third CNN which is designed to improve connectivity of the segmentation output and therefore reduce effort in correcting gaps during post-processing. This approach is entirely computational, requiring no additional experimental data, and only takes several seconds to process while manual segmentation takes from days to weeks.

Lastly, this paper describes our strategy for graphing the vascular networks from segmented angiograms and quantifying various angioarchitectural properties. Graphing includes the process of reducing each vessel to a single line that passes through its center, which in turn enables the representation of a vascular network as a mathematical graph. From this graph, several parameters can be measured, such as the branching order, vessel length, and vessel diameter. In consequence, this paper presents a complete pipeline of enhancement - segmentation - vessel graphing - property measurement. This pipeline is offered as a toolbox that allows researchers to input their standard OCTA and receive as an output the underlying vascular graph along with the associated angioarchitectural properties.

2. Methods

2.1. OCT system

All OCT measurements were collected with a commercial SD-OCT system (Telesto III, Thorlabs, Newton, NJ, USA). The system uses a large-bandwidth, near-infrared light source (center wavelength, 1310 nm; wavelength bandwidth, 170 nm) which leads to a high axial resolution of 3.5µm in air. The system uses a high-speed 2048-pixel line-scan camera to achieve 147,000 A-scan/s with a relatively large imaging depth (3.6 mm in air; up to 1mm in brain tissue). The transverse resolution is 3.5µm with our 10x objective (NA = 0.26).

2.2. Animal preparation and imaging

Male wild-type mice (n = 2, 20 weeks old, 20-25g in weight, strain C57BL/6, Jackson Laboratories) underwent craniotomy surgeries following the widely used protocol [32]. All animal-based experimental procedures were reviewed and approved by the Institutional Animal Care and Use Committee (IACUC) of Brown University and Rhode Island Hospital. Experiments were conducted according to the guidelines and policies of the office of laboratory animal welfare and public health service, National Institutes of Health.

In detail, the animal was administered 2.5% isoflurane. An area of the skull overlying the somatosensory cortex was shaved, and surgical scrub was applied over the incision site to prevent contamination. A 2-cm midline incision was made on the scalp, and the skin on both sides of the midline was retracted. A 6-mm area of the skull overlying the cortical region of interest was thinned with a dental burr until transparent (100-µm thickness). The thinned skull was removed with scissors while keeping the dura intact. A well was created around the opened area using dental acrylic, filled with a 1% agarose solution in artificial CSF at room temperature, and covered with a small glass cover slip. With this window sealed by agarose and covered by the cover slip, the brain was protected from contamination and dehydration. A metal frame was glued by dental acrylic to the exposed skull, used to hold the head and prevent motion during microscopy measurements. After surgery, the animal was placed under the OCT system for in vivo imaging. The animal was kept under isoflurane anesthesia during imaging. Oxygen saturation, pulse rate, and temperature were continuously monitored with a pulse oximeter and rectal probe for the entire surgical procedure and experiment. Body temperature was maintained at 37 °C and the pulse remained within the normal range of 250-350 bpm. After the acquisition of the first angiogram with intrinsic contrast, an intravenous injection of 0.3-ml Intralipid was administered through the tail vein. We placed the focus about 0.5 mm from the surface of the brain, since we are particularly interested in the enhancement and segmentation of the microvascular bed.

This study used five OCTA datasets. The first two were acquired from the same cortical region, the first being an intrinsic-contrast (“standard”) OCTA while the second one was obtained using Intralipid as a contrast agent to guide the manual annotation. The first standard OCTA was manually labeled; this OCTA and its manual annotation were used for training and testing the three networks. The Intralipid OCTA was not used in training any of the networks. The other three OCTA datasets were used for investigating the performance of the trained networks on different OCTA datasets: one with a larger field of view, one with lower resolution, and another acquired with a different OCT machine by another lab.

2.3. Manual angiogram annotation

We manually labeled vessels in the standard OCTA while using the Intralipid OCTA as a guide. These angiograms are of size (x,y,z) 300 × 300 × 350 um³ or 200 × 200 × 230 voxels.

After acquisition, the images were registered and overlaid, allowing us to use the high-contrast Intralipid image as a guide for manual segmentation of the standard OCTA. We successively examined each slice of these overlaid images to manually label the vasculature using a pen tablet, which took three months, as shown in Fig. 1. The manual annotation was performed using our custom-made user interface which allows for navigating a 3D image both horizontally and vertically by traversing cross-sectional B-scans or en-face slices. We manually annotated vessels with a few criteria: (1) a line of voxels should have higher OCT decorrelation values than its neighboring voxels, when viewed en face; (2) the voxels look highly continuous within the line; and (3) the line of voxels is well connected to one or two neighboring segmented vessels when viewed in 3D space, among other intuitive guides.

Fig. 1.

Manual annotation of OCTA with the aid of external-contrast OCTA. (a) Intrinsic-contrast (“standard”) OCTA. (b) Registered Intralipid-contrast OCTA. (c) Manual segmentation of the standard OCTA under the guidance of Intralipid OCTA. Scale bars, 50µm

2.4. Developing and training EnhVess: OCTA enhancement and “tail” removal

EnhVess is the encoder-decoder employed for image enhancement. This network was trained on the intrinsic-contrast angiogram with the manual annotation as the ground truth, using the mean-squared loss function. We chose this specific loss function because we sought a continuous output and this loss function is most widely used to accomplish this. The input to the encoder is a 3D patch of 32 × 32 × 32 voxels of the intrinsic-contrast angiogram. This size was chosen to facilitate downsampling and subsequent upsampling by factors of 2. The encoder consists of three 3D convolutional layers followed by a max pooling layer. The output of the encoder is then decoded by three transposed convolution layers which upsample the layer inputs and final convolutional layer to produce an output of size 32 × 32 × 32. This network architecture is illustrated in Fig. 2. All convolutional layers employ a rectified linear unit (ReLU) as the activation function, except the final layer which utilizes a clipped ReLU function to produce a continuous output from 0 to 1. To improve performance and stability, we performed batch normalization after each layer. We trained our network using the Adam stochastic optimization for 500 epochs with a learning rate of 1e-4.

Fig. 2.

Architecture of the encoder-decoder used in EnhVess for volumetric image enhancement and “tail” removal.

For training EnhVess, we used 4,000 patches of 32 × 32 × 32 voxels from the single OCTA volume data shown in Figs. 1(a) and 1(c). In detail, from the intrinsic-contrast angiogram with 200 × 200 × 230 voxels, we first reserved about 15% of the data (of size 200 × 32 × 230 [x,y,z]) and did not use it in training either EnhVess or SegVess, allowing the networks to be tested on the unseen data. From the other part of the intrinsic-contrast angiogram (200 × 168 × 230 voxels), 500 patches of 32 × 32 × 32 voxels were randomly obtained. This dataset was augmented by random rotations around the z-axis as well as horizontal flipping, which increased the size of the training data by a factor of 8 (4,000 in total).

When EnhVess was applied to a new, unseen OCTA (512 × 512 × 350 voxels) as shown in the Results, the OCTA was split into 32 × 32 × 32 patches, and each patch was processed by the network.

2.5. Developing and training SegVess: OCTA segmentation

Once EnhVess was fully trained, we trained a second CNN, SegVess, for vessel segmentation using the output of EnhVess (the enhanced image) as the input along with the labeled data as the ground truth. In an attempt to use a much smaller number of learnable parameters compared to large networks such as U-Net that has about 30 million, SegVess consists of 4 hidden layers and one skip connection, as shown in Fig. 3. As a result, this simple architecture has about 1% of the number of learnable parameters. Like EnhVess, we employed 3D convolutions and the ReLU activation function. However, SegVess was designed to produce a binary output (vessel vs background) using the class probabilities determined by the final softmax layer. This network was trained using Adam stochastic optimization and soft Dice loss. The Dice loss has been shown to be effective for imbalanced classes, which is critical here since the vasculature only fills a portion of the total volume (typically less than 10%). To prevent overfitting and improve accuracy, we performed batch normalization after each convolutional layer. Like with EnhVess, we augmented the training data by rotations around the z-axis, as well as horizontal flipping.

Fig. 3.

Architecture of SegVess used for volumetric vessel segmentation. The output of EnhVess is used as the input to SegVess.

To train SegVess, we used 16,000 patches of 16 × 16 × 12 voxels from the enhanced OCTA image shown in Section 3.1 below. In detail, we first split the data into 3 sets for training, validation and testing. The training data was of size 200 × 136 × 230 voxels, the validation data of size 200 × 32 × 230 voxels, and the testing data of size 200 × 32 × 230 voxels. Thus, SegVess was trained with the same ground truth as EnhVess but was tested using data that was unseen to either network during training. Before training SegVess, we determined the optimal input patch size by exploring architectures with different input sizes and evaluating segmentation performance on the validation set. For this optimization step, we trained the network for 100 epochs and quantified the performance by the Dice coefficient. Among ten tested sizes (from [8 8 8] to [32 32 32]), we found the optimal patch size to be [16 16 12] voxels (x,y,z), with the maximum Dice coefficient being 0.48 on the validation data.

Using this patch size, we trained the final network for 500 epochs with a learning rate of 1e-4. To train SegVess, we randomly extracted 2000 patches of size 16 × 16 × 12 from the training set and further augmented this data by random rotations around the z-axis as well as horizontal flipping, which increased the size of the training data by a factor of 8 (16,000 patches in total). Finally, we tested the performance of the network using the reserved test set which was unseen by both EnhVess and SegVess during training.

To demonstrate the result of this network, we applied SegVess to the output of EnhVess on an OCTA image (of size 512 × 512 × 350 voxels) unseen by either network. The enhanced image was divided into patches of size 16 × 16 × 12 and each patch was processed by the network to produce the final segmentation.

2.6. Developing and training ConVess: Improving vessel connectivity in the segmented binary image

To correct any obvious gaps in the segmented binary image (the output of SegVess), we developed and trained another CNN, named ConVess. To obtain training data for ConVess, we corrupted our manual segmentation by randomly deleting small portions of the segmentation, thereby introducing obvious gaps within vessel segments. ConVess was trained to efficiently correct these gaps using both the original and enhanced OCTAs. We opted for this approach as it makes use of the underlying experimental data, unlike other popular gap-correction methods like tensor voting. The structure of this CNN is identical to EnhVess (Fig. 2), but with 3 inputs: the corrupted segmentation, the standard OCTA, and the enhanced OCTA. These inputs are concatenated to produce a 3D image with 3 channels, such that the network could learn features from the gray-scale images on how to correctly connect gaps. We used the same ground truth data as EnhVess and SegVess, and the reserved data for testing the entire pipeline that was unseen by any of the three networks during training.

To train ConVess, we generated about 100 random gaps in the OCTA image (200 × 200 × 230 voxels) such that the center positions of the gaps located within the segmented vessels. The gaps were cubic in shape, the size varied between 1 × 1×1 voxels and 4 × 4×4 voxels, and the edges were smoothed using a Gaussian filter. One-hundred and twenty patches of 32 × 32 × 32 voxels were randomly obtained from this “corrupted” OCTA, and the dataset was augmented by random rotations around the z-axis as well as horizontal flipping, which increased the size of the training data by a factor of 8 (960 in total). Finally, we tested ConVess on another “corrupted” OCTA which was generated from the original, uncorrupted OCTA image by the same method.

The trained connectivity-enhancing network was then applied to the segmented image (the output of SegVess on the new, unseen OCTA) by splitting the image into 32 × 32 × 32 patches and applying the network to each patch.

2.7. Vessel graphing

Our strategy for graphing vessels consists of several steps applied to the output of ConVess. Firstly, we morphologically close the binary image using a 3 × 3×3 kernel to close any further gaps that were not corrected by ConVess, and we remove any connected components smaller than 50 voxels.

This post-processed segmentation is then skeletonized using 3D medial axis thinning. This skeletonization converted the 3D binary segmentation image into a 3D binary image where all vessel-like structures are reduced to 1-voxel wide curved lines. To ensure that the curved line (“skeleton”) passes through the centerline of the vessel, we “recentered” the skeleton using a method inspired by Tsai et al. [33]. In detail, assuming that the intensity of vessels in the enhanced angiogram (the output of EnhVess) is brightest along the centerlines of the vessels, we analyze the local 3 × 3 × 3 voxel neighborhood of each voxel of the skeleton, except for those voxels corresponding to endpoints. The skeleton is recentered by shifting voxels in a three-step hierarchical sequence: (1) A voxel is deleted if doing so does not change the local connectivity. The local connectivity herein was defined by the number of connected objects within a 3 × 3×3 cube around the voxel. (2) If removal is not possible (i.e., if the removal changes the local connectivity), we move this voxel to an unoccupied location that must be within one voxel from the original location, must correspond to a higher intensity in the enhanced angiogram, and must not change the local connectivity. (3) If neither removal nor movement is possible, but if there is an unoccupied neighboring voxel with greater intensity in the enhanced angiogram, we activate that voxel. These steps are repeated for all centerline voxels and iterated until no further changes occur.

Next, we locate all bifurcations in the centerline, and describe each vessel segment as a list of voxel positions in 3D, referred to as edges here. We then extracted the cross-section of the enhanced angiogram perpendicular to the direction of each edge at each voxel position, and fitted each cross-section to a 2D gaussian function, returning the correlation coefficient. The mean correlation coefficient was measured for each edge and served as a measure of how likely each edge represents a “true” vessel. We examine edges with mean correlation coefficients less than 0.5, starting with the edge with the smallest value. If the global connectivity of the skeleton remains unchanged when skeleton voxels are removed at the positions describing the edge, then both the edge and those corresponding skeleton voxels are permanently removed, otherwise the skeleton remains unchanged and the edge is not deleted. The global connectivity herein was defined by the number of endpoints within the skeleton. Finally, we successively remove branches shorter than 7 voxels in length, starting with the shortest branches. Once this process is complete, we manually inspect the results using a custom-made GUI which allows us to delete, create or connect vessel segments.

Any vessels sharing a branchpoint are considered to be connected, such that each vessel is connected to either 2 or 3 other vessels at each end, unless this vessel is at the boundary of the imaging volume in which case only one end of the vessel is connected to other vessels. Therefore, the final result of vessel vectorization is given by a collection of nodes (branching points) and the vessels connected to each node, where each vessel is described by a list of voxel positions in 3D.

2.8. Measurement of angio-architectural properties

The vessel tortuosity was calculated by dividing the vessel length by the straight-line distance between the vessel segment endpoints. To calculate the branching orders, we first chose a depth at which pial vessels were located and classified these vessels as “first-order vessels”. Then, we found the vessel segments connected directly to these vessels and classified them as “second-order vessels” and so on until vessels with terminal endpoints were reached. To measure the vessel diameter, we first extracted the cross-sections of each vessel along the centerline and then fitted a 2D Gaussian to each cross-section. For each vessel, we chose only the cross-sections with the coefficient of determination (R2) above 0.8 and averaged the full width at half maximum of these selected cross-sections.

3. Results

3.1. EnhVess: OCTA enhancement and “tail” removal

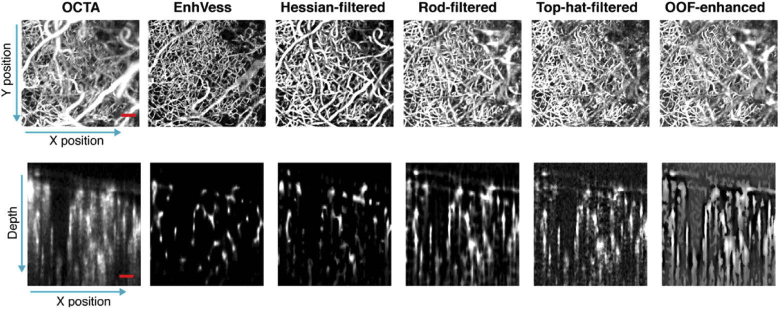
We evaluated the trained EnhVess by applying it to a new standard OCTA image that was unseen during training, and compared the result to common image enhancement techniques: rod filtering [33,34], top-hat filtering [13,35], Hessian-based filtering [36,37], and optimally-oriented flux (OOF) enhancement [38,39]. The enhancement methods were parameterized to provide the best results on capillaries. Rod filtering and top-hat filtering are accomplished by applying a rod filter of diameter and length of 2 voxels and 11 voxels respectively. For Hessian-based filtering and OOF, we chose a diameter range of 1 to 5 voxels in increments of 1 voxel. All methods enhanced visualization of microvessels when viewed from above (en-face projection), but the cross-sectional slices reveal significant distinctions between the methods (Fig. 4). The figure shows that with EnhVess the projection artifacts are significantly diminished, and the image is considerably denoised. The vessels maintain their tube-like shapes such that the vessel cross-sections appear circular instead of elongated as in the case of the other image enhancement techniques. This is tail mitigation is further illustrated in Fig. 5. Among the other techniques, the Hessian-based filtering results in relatively better cross-sectional shapes of vessels, but the shape is still elongated in most vessels when compared to the result of EnhVess.

Fig. 4.

Comparison of EnhVess with common vessel enhancement techniques, viewed as the en-face maximum intensity projection (MIP) (top) and as the cross-sectional slice (bottom). Scale bars, 0.1 mm.

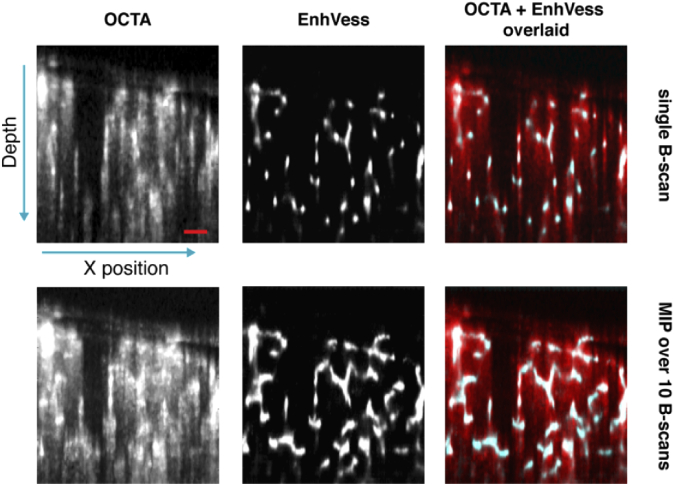
Fig. 5.

Demonstration of projection tail mitigation by overlaying the EnhVess result over the original OCTA. Top row shows a single B-scan, and bottom row shows MIP over 10 B-scans. Scale bar, 0.1 mm.

To assess the performance of EnhVess quantitatively, we compare common metrics of image quality, namely peak signal to noise ratio (PSNR), mean-squared error (MSE) and structural similarity index (SSIM) with respect to the segmented image [40,41]. These metrics are calculated over B-scans and the mean and standard deviation is derived. Higher values for PSNR and SSIM, and lower values for MSE indicate better image quality. As shown in Table 1, EnhVess performs best according to all 3 metrics. All three image quality metrics indicate that every tested technique resulted in statistically significant enhancement compared to the original OCTA; furthermore, EnhVess produced enhancement that was statistically better than every other enhancement technique (p<0.001, one-way ANOVA).

Table 1. Comparison of Image Enhancement Techniques.

	PSNR	SSIM	MSE
OCTA	12.9 ± 0.8	0.013 ± 0.003	0.052 ± 0.010
EnhVess	19.2 ± 1.0	0.776 ± 0.041	0.013 ± 0.003
Hessian-filtered	16.5 ± 1.3	0.711 ± 0.045	0.023 ± 0.007
Rod-filtered	16.1 ± 1.2	0.408 ± 0.068	0.026 ± 0.008
Top-hat filtered	15.8 ± 1.2	0.056 ± 0.004	0.027 ± 0.008
OOF-enhanced	15.3 ± 1.4	0.818 ± 0.046	0.031 ± 0.010

3.2. SegVess: three-dimensional OCTA segmentation

To evaluate SegVess, we used the data reserved for testing, which was unseen to EnhVess and SegVess during training (see Methods), along with the corresponding manual label. The test data was input to EnhVess first, and its output (enhanced OCTA) was input to SegVess. Qualitatively, we observed excellent agreement between the output of SegVess (segmented binary 3D image) and the manual segmentation (Fig. 6). Importantly, the tubularity of vessels was well preserved, implying that the projection artifacts present in the original angiogram were effectively removed by EnhVess and thus negligibly affected the segmentation.

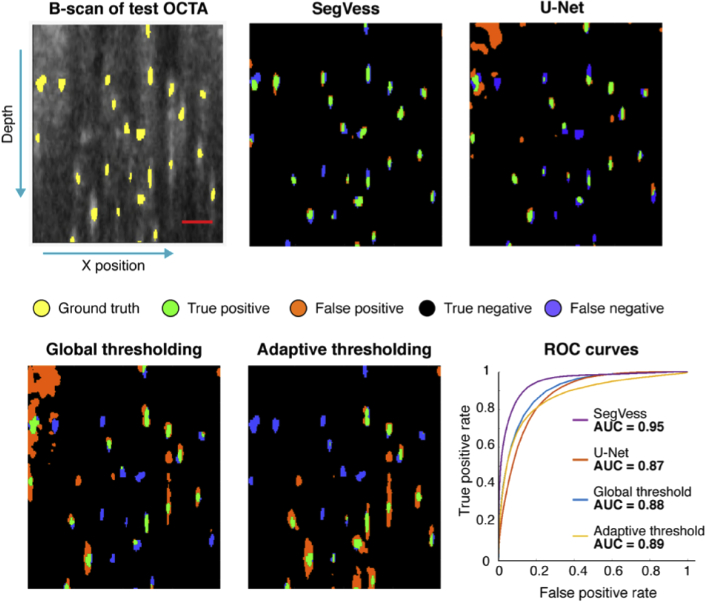
Fig. 6.

Comparison of SegVess with global thresholding, adaptive threshold and U-Net. A B-scan is presented out of the volume with 200 × 32 × 230 voxels (x, y, z). Ground truth is shown in yellow on the first OCTA image, and the true positive, false positive, true negative, and false negative are presented in the segmented images. Scale bar, 50 µm.

To quantitatively assess the performance of SegVess, we used the area under the curve (AUC) of the receiver operating characteristic (ROC), a widely used measure of a model’s capability of accurately classifying different classes. To determine the ROC curve of SegVess, we examined the output of the softmax layer at various thresholds and plotted the true positive rate against the false positive rate. It should be noted that the final segmentation is obtained by thresholding the softmax layer at 0.5, as the network was trained to optimize the probabilities of each voxel belonging to the correct class using the Dice coefficient. We compared the ROC curve of SegVess to those of the widely-used traditional thresholding methods, global and adaptive thresholding as applied to the standard angiogram. For global thresholding, the optimal threshold was determined by calculating the dice coefficient for a range of thresholds. For adaptive thresholding, two parameters are generally chosen: the neighborhood size and the sensitivity. To compare SegVess to the best possible adaptive thresholding result, we chose the neighborhood size that yielded the best AUC score, although this AUC-based optimization is not feasible in the common situation where the ground truth is not given. Also, to further enhance the thresholding results, we removed connected components smaller than 10 voxels and applied gaussian filtering to smoothen the edges. As expected, the adaptive thresholding performed better than the global thresholding (Fig. 6).

Compared to the combination of EnhVess and SegVess, however, the thresholding methods are susceptible to the projection artifacts, producing more false positives. Further, the thresholding methods require the choice of optimal parameters while SegVess does not require any user parameters to be tuned. Lastly, we compared SegVess to U-Net [42] which was trained on the same data with the same patch size and found U-Net to perform similarly to global and adaptive thresholding. Since the U-Net has millions of parameters, we attempted to reduce overfitting by employing drop out layers with a probability of 0.5 after each maxpooling and upsampling layer.

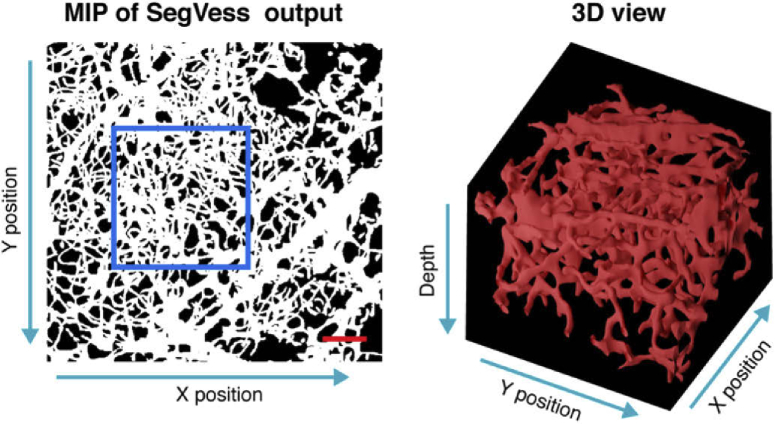
After evaluation, we applied SegVess to the output of EnhVess shown in Fig. 5. Figure 7 displays this segmentation result as an en-face MIP image and a 3D view of a part of the 3D binary image.

Fig. 7.

The output of SegVess. Scale bar, 0.1 mm. The 3D view box shows 0.3 mm x 0.3 mm x 0.5 mm (x, y, z).

3.3. Convess: automated gap correction

Although the segmentation by SegVess is significantly better than the traditional thresholding methods, it is still prone to gaps either within a vessel or between vessels. Such gaps appearing in automated segmentations have been a major source of the need for labor-intensive manual correction in the later vessel-graphing step [43]. Machine-learning approaches other than deep learning were developed and tested to partially automate this manual correction. For example, Kaufhold et al. used a decision tree to identify good candidates for gap correction and spurious branch deletion so as to make the following manual inspection and correction less time-consuming [34]. Here, we used our third network ConVess to automatically identify and correct gaps present in the output of SegVess (the segmented 3D binary image). See Methods for details of the network and its training.

We tested the trained ConVess on an OCTA image with artificially created gaps: we assessed the extent of gap-correction by leveraging the fact that an uncorrected gap in the segmentation leads to a gap in the resulting skeleton. More specifically, we skeletonized the corrected segmentation (output of ConVess) as described in the Methods and examined the region around each of the artificial gaps in the skeleton to determine if the gap had been corrected. As a result, ConVess corrected 94% of the gaps. Figure 8(a) displays a few examples of the gaps appearing in the output of SegVess and how those gaps were corrected by ConVess. The MIP of the output of ConVess is presented in Fig. 8(b).

Fig. 8.

Results of ConVess. (a) Examples of how ConVess corrected gaps. (b) Input and output of ConVess in MIP. SegVess receives the output of SegVess as the input (left) and returns the gap-corrected, 3D binary vessel segmentation image as the output (right). Scale bar, 0.1 mm.

To quantitatively assess the performance of ConVess without artificially adding gaps, we applied ConVess to the output of SegVess shown in Fig. 6 which has the ground truth. ConVess improved the segmentation, as demonstrated by the metrics shown in Table 2. Importantly, the true positive rate increased significantly as well as the dice score. There was only a small change on the false positive rate, although this change is also statistically significant (p<0.001, paired t-tests). The relatively low dice score might be attributed to the difficulties in defining vessel boundaries due to the nature of OCTA imaging. However, the low score would not be problematic in practice because most OCTA studies focus on relative diameters between control and experimental groups than the absolute value while most studies measure the diameter from the gray-scale angiogram, not from the segmented angiogram (see Discussion for details).

Table 2. Quantitative Comparison of ConVess to SegVess only.

	True positive rate	False positive rate	True negative rate	False negative rate	Dice score
SegVess	0.47 ± 0.13	0.01 ± 0.01	0.99 ± 0.01	0.53 ± 0.13	0.52 ± 0.13
SegVess + ConVess	0.59 ± 0.13 a	0.02 ± 0.02 a	0.98 ± 0.01 a	0.41 ± 0.13 a	0.55 ± 0.13 a

^ap < 0.001.

3.4. Graphing the vasculature network and extracting angioarchitectural properties

The gap-corrected, 3D binary vessel segmentation image underwent several processing steps to produce a vascular network graph, including skeletonization, spurious branch detection, and edge re-centering. Figure 9(a) displays the graph obtained from the gap-corrected segmentation shown in Fig. 8.

Fig. 9.

(a) The result of graphing the vessels from the output of ConVess. The top row shows the en-face projection of the vectorized vasculature, where each vessel is displayed with a random color. The middle row displays a 3D view of the region indicated by the white square. The bottom row presents the distribution of vessels in the top row by branching order. b) Each vessel is shown colored according to the mean diameter as averaged along the vessel axis. The histogram in the bottom row shows the distribution of vessels by diameter. c) Each vessel is shown colored according to the length of the vessel. The histogram in the bottom row shows the distribution of vessels by length. d) Each vessel is shown colored according to tortuosity of the vessel. The histogram in the bottom row shows the distribution of vessels by tortuosity. Scale bar, 0.1 mm.

This representation of a vascular network as a graph allows various properties of the angioarchitecture to be easily quantified in an objective manner. In this paper, we demonstrate measurements of branching orders (Fig. 9(a)), vessel lengths (Fig. 9(b)), vessel diameters (Fig. 9(c)), and vessel tortuosity (Fig. 9(d)).

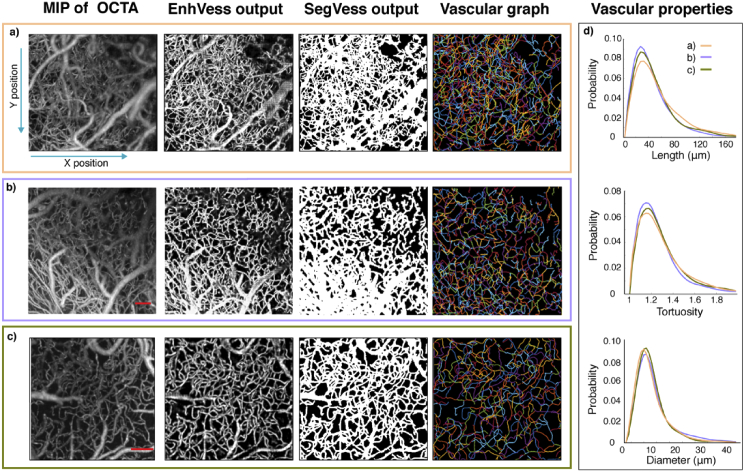
Figure 10(a) summarizes the pipeline presented in this paper, from an OCTA to EnhVess, to SegVess and ConVess, and finally to a vascular graph with associated angioarchitectural properties. This pipeline has been shown to be suitable for images obtained with different resolutions (Fig. 10(b)) and even for images obtained by other labs using a different OCT setup (Fig. 10(c)). The histograms of the angioarchitectural properties for each of these images were similar among these datasets (Fig. 10(d)). The similarity, which should be true when animals were in the physiological condition, supports the generalizability of the developed approach to OCTA images obtained by other researchers.

Fig. 10.

The processing pipeline of OCTA images with examples of the OCTA used in the previous figures (1.5-µm sampling rate) (a), an OCTA with a different sampling rate (3 µm) as obtained in our lab (b), and an OCTA obtained by a different lab (c). (d) The histograms of vessel lengths, diameters and tortuosity extracted from each example. Scale bar, 0.1 mm.

4. Discussion and conclusion

We have presented the pipeline of image processing procedures based on deep learning for the enhancement and segmentation of 3D OCTA images, and subsequent vascular graphing and quantification of angioarchitectural properties. The enhancement and segmentation are achieved using three CNNs: EnhVess, SegVess and ConVess.

EnhVess was designed for image enhancement based on the simple encoder-decoder architecture and was trained using an intrinsic-contrast “standard” 3D OCTA (input) and its manual segmentation (ground truth). This CNN significantly improved the signal-to-noise ratio and more importantly has shown to effectively suppress the OCTA-specific projection artifacts or “tails” caused by multiple scattering, restoring the tubular structure of vessels. EnhVess performed significantly better in this matter than other image enhancement techniques such as Hessian-based filtering, rod filtering, top-hat filtering, and OOF. These common vessel enhancement techniques were not effective in removing the projection artifacts, a unique challenge of OCTA. Because of these “tails”, researchers are often limited to analyzing 2D projections only, as it is challenging to distinguish vessels from background in cross-sectional views. The connectivity between vessels is also challenging to ascertain in cross-sectional views, hindering the accurate segmentation and vessel-graphing of cortical OCTA in 3D. EnhVess, as designed and trained specifically for cortical OCTA, improves vessel contrast and thereby enables the following processes to produce more accurate segmentation and graphing of the vasculature, which are essential for quantitative angioarchitecture analysis.

SegVess was designed for image segmentation based on 3D convolutional layers based on an architecture with fewer learnable parameters than popular segmentation networks like U-Net. SegVess was trained on the output of EnhVess (input) and the manual segmentation (ground truth). SegVess achieved an AUC score of 0.95 while global and adaptive thresholding-based segmentations scored 0.88 and 0.89, respectively, and the U-Net scored 0.87. The distinction was made clearer when assessing the tubularity of vessels in the cross-sectional views. SegVess thus accomplishes automated segmentation of 3D OCTA images with the rigorous AUC score, which is imperative from a practical perspective. While manual segmentation remains the gold standard, it is a subjective, laborious, and time-consuming task which is generally not feasible for large datasets. In this study, the manual segmentation took place over the course of three months for the image of 300 × 300 × 350 um³ or 200 × 200 × 230 voxels (x, y, z). In addition to this long time required, the manual segmentation required an external contrast agent for high confidence in the result, together making manual segmentation impractical for research like our ongoing study that analyzes many OCTA volumes. In contrast, SegVess only takes several seconds and works well without the aid of extrinsic contrast agents. It should be noted that the Intralipid-contrast OCTA had not been used in training any CNN in this paper but was only consulted to guide manual segmentation.

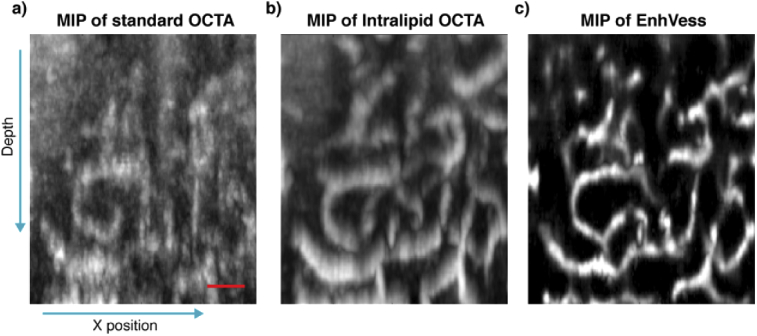
The use of the extrinsic contrast agent was critical in visualizing vertical capillaries for the guidance, because the OCTA contrast depends on the angular orientation of a capillary vessel [44]. It is a known challenge to visualize vertical capillaries in intrinsic-contrast OCTA images, but Intralipid improves this visualization (Figs. 11(a) and 11(b)). We also note that EnhVess is capable of enhancing the visibility of these vertical capillaries without the use of any extrinsic contrast agent (Fig. 11(c)).

Fig. 11.

Enhancement of vertical capillaries using EnhVess. (a) MIP of intrinsic-contrast OCTA image over 32 B-scans. (b) MIP of registered Intralipid-contrast OCTA. (c) MIP of the EnhVess output in response to the input of the intrinsic-contrast OCTA. The Intralipid OCTA (b) was not used in training EnhVess. Scale bar, 50 µm.

ConVess was designed for further improvement of the segmentation, especially with respect to gap correction, based on the same architecture as EnhVess but with 3 input channels. The input consists of the segmentation (output of SegVess) along with the enhanced image (output of EnhVess) and the original OCTA image. We found that the gap-correction is more accurately done when it involves the third input so as to be guided by the grayscale data. This CNN identified and corrected 94% of gaps on the validation data. When applied to the test data, ConVess resulted in fewer gaps in the vascular graph and therefore less manual effort for correcting errors in the following steps in the pipeline.

Finally, the pipeline extracts a network graph representing the vasculature from the gap-corrected, segmented angiogram through moderately improved processes for pruning, loop removal, and re-centering. Such a graph enables the measurement of various angioarchitectural properties, including but not limited to the vessel length, diameter, tortuosity, and branching order. The distributions resulting from our pipeline (Fig. 10) closely resemble those reported using two-photon microscopy in terms of shape as well as value ranges [30]. The distributions shown in Fig. 10 are also similar in shape, as expected for healthy, wild-type mice.

The values of diameters obtained, however, may be inaccurate due to the mechanism of OCTA contrast. The intrinsic contrast of OCTA originates from the movement of RBCs through vessels. This may result in variations in diameter along the centerline of a single vessel, especially in capillaries where RBCs move one by one. The contrast based on RBC movement also makes it unclear which point in the cross-section of a vessel in OCTA exactly indicates the vessel wall. Thus, we measured the diameter by averaging the cross-sections along the centerline, which makes the measurement precise against the variations in diameter. But it is still not accurate depending on the definition of the vessel diameter, due to the uncertainty regarding the vessel wall. Despite this limitation in accuracy, high precision is often sufficient for many studies that focus on relative differences between experimental conditions, rather than absolute diameters.

We have made all of our algorithms in the presented pipeline freely available as a MATLAB toolbox for immediate use https://github.com/sstefan01/OCTA_microangiogram_properties. This toolbox has been implemented to be as user-friendly as possible, such that researchers may simply input an OCTA image and then receive the vascular network graph detailing the connectivity between vessels, as well as the associated angioarchitectural properties of every vessel. We hope that the user-friendly toolbox promotes the utilization of OCTA as a full 3D method for analysis of microvasculature, eventually unlocking the full potential of the imaging tool for neuroscientific research.

Funding

Brown University10.13039/100006418 (Seed); National Eye Institute10.13039/100000053 (R01EY030569).

Disclosures

The authors declare no conflicts of interest.