Abstract
We propose a method that utilizes the trajectory of output polarization states on the Poincaré sphere to derive depth-resolved birefringent information within samples using a fiber-based polarization sensitive optical coherence tomography. The apparent (or intermediate) optic axis and the local phase retardation are first obtained by fitting a plane to the adjacent output polarization states along depths in the Poincare sphere. A sequence of 3D rotation operation determined by the local birefringent property of the upper layers is then applied to the apparent axis to finally determine the local optic axis. This method requires only one input polarization state and is compatible with both free-space and fiber-based PSOCT systems, simplifying the imaging system setup. The theoretical framework is presented to derive the local phase retardation and optic axis from the output polarization states and then demonstrated by mapping local birefringent information of the mouse thigh tissue in vitro.
1. Introduction
In biomedical imaging to determine birefringent properties of a tissue sample, the parameters such as orientation, phase retardation, degree of polarization uniformity and diattenuation are important determinants. These parameters may also be utilized, either alone or combined, to reveal several important physiological processes such as the dynamics of the myocardial fibers [1,2], skin lines of the human body [3] and wound healing process [4].
Polarization-sensitive optical coherence tomography (PS-OCT), an extension of conventional optical coherence tomography (OCT), characterizes cross-sectional anisotropic biological structures, such as tendon, muscle, collagen and nerve fiber bundles non-invasively [5]. This polarization-based three-dimensional (3D) imaging technique has potential applications in ophthalmology, dermatology, and dentistry to investigate relevant disease process. Due to the round-trip measurement, traditional PS-OCT only provides the accumulated polarization results along depth, leading to a difficulty to determine local birefringent information at depth (e.g. orientation of the optic axis and phase retardation).
To derive the local birefringent property and reveal the depth-resolved anisotropic information, algorithms based on Jones matrix have been developed [6,7]. These algorithms require separate measurements of two different incident polarization states to determine the Jones matrix of the sample. While the two distinct input polarization states can often be achieved by assembling a passive optical module [8] or an electro-optic modulator into the PS-OCT system [9], these additional modules complicate the system setup. If the diattenuation of the sample is negligible, Jones matrix-based algorithm can be simplified to map the local birefringent information by using only one incident polarization state in the previous study [10,11]. Another issue of this method is that it assumes that all the possible optic axes lie on the QU-plane of a Poincaré sphere. However, in the PS-OCT system, the overall optic axis may not be constrained to the QU-plane due to the compounding effect of optical fibers used and sample birefringence [12–15], even if the diattenuation is negligible. In this way, the vertical component information is lost by using the Jones matrix-based algorithm in a fiber-based PS-OCT system with only one input polarization state.
Here we propose a Stokes parameter-based polarization state tracing (PST) method to find the exact optic axes of interest in the 3D space in the Poincaré sphere. Different from the Jones matrix method that depends on the matrix calculation, the method we propose here utilizes the geometrical trajectory of the output polarization states on the Poincaré sphere to derive the local birefringent information. The apparent axis and the local phase retardation are first obtained by fitting a plane to the adjacent output polarization states along depth in the Poincare sphere. Then a sequence of 3D rotation operation is applied to the apparent axis to finally determine the local optic axis. This method requires only one input polarization state, which relaxes the PSOCT system setup. In this paper, theoretical derivation to obtain local optic axis and phase retardation is presented, and then demonstrated by imaging the mouse thigh tissue in vitro.
2. Proposed PST method
2.1. Derivation of the local optic axis
In a Poincaré sphere representation, linear polarization can be modeled as a rotation about its optic axis. The amount of rotation is the degree of phase retardation [13]. That is, when a polarized light propagates through a multi-layered material with constant optic axis, the trajectory of the output polarization states of the light beam on the Poincaré sphere are constrained within a plane whose normal vector defines the optic axis. Based on this model, the local optic axis and phase retardation of a multi-layered tissue sample can be obtained by fitting a plane to the output polarization states along depth represented at the Poincare sphere. Here, the output polarization states are directly given by the Stokes parameters determined by the measured quantities of the PS-OCT system [16,17].
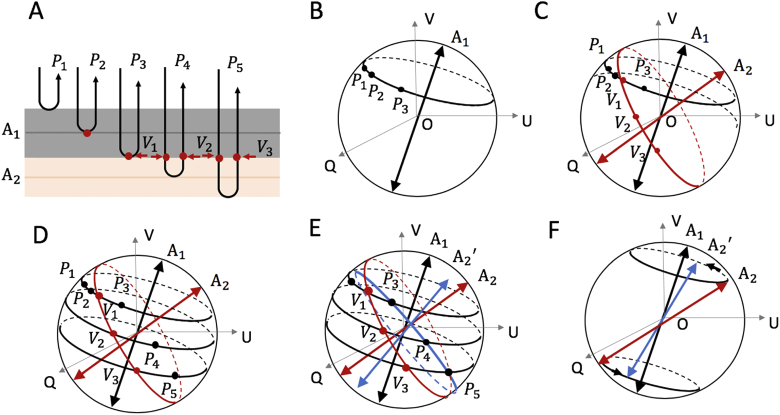
To illustrate, Fig. 1 shows a schematic diagram of the polarization states of the light beams traveling through a simulated birefringent sample with depth-varying optic axis. To simplify, we model the sample to consist of two groups of birefringent material with their optic axes represented by and , respectively [Fig. 1(a)]. The first group is made up of two retarder layers (gray layer) sharing the optic axis of , whereas the 2nd group is also of two retarder layers (yellowish layer) but sharing the optic axis of . With this arrangement when the light beam propagates within this sample, there will be five interfaces that would back-scatter the incoming light to the PS-OCT detector. For the light beams scattered back from the sample surface and the first two gray layers, the output polarization states , and are represented by the black points on the Poincaré sphere as shown in Fig. 1(b). As the first two layers share the same optic axis , , and must be in the same plane whose normal vector is based on the model mentioned above. Hence, by fitting a plane to the output polarization states , and on the Poincaré sphere, the local optic axis of the gray layers can be obtained that equals to the normal vector of that fitted plane.
Fig. 1.
Schematic diagram of the polarization states of the light beams traveling through a simulated birefringent sample with depth-varying optic axis and eventually forming the output polarization states, P1, P2, …, P5, that are detected by the PS-OCT system. (a) A depth scan of a simulated birefringent sample with depth-varying optics axis, where 4 birefringent layers are simulated with the first 2 layers sharing the same optic axis A1, and the last two layers sharing A2. (b) The trajectory of the output polarization states , and on the Poincaré sphere, which forms a plane with a normal vector of A1. (c) The trajectory of the intermediate polarization states , and on the Poincaré sphere, which also form a plane with a normal vector of . (d) The trajectory of the output polarization states , and on the Poincaré sphere, which forms a plane with a normal vector of . (e-f) The geometric relation between the upper optic axes, , the axis of the local fitted plane and the local optic axis .
For the light scattered back from the deeper layers with a differed optic axis of , the resultant output polarization states would be determined by both the layer of interest and all the layers that are on top of that layer due to the round-trip measurement. Here, we discuss in detail the intrinsic geometric relationship among the upper optic axes, the axis of the local fitted plane at the Poincare sphere and the local optic axis of interest, and the use of which to derive the local optic axis in the deeper layers. Figures 1(c)–1(f) illustrate the geometric relationship by presenting the transmission process of the light polarization states in the sample. In these figures, , and indicated by the black points on the Poincaré sphere are the output polarization states scattered back from the interface between the gray and yellowish layers, and the last two yellowish layers as shown in Fig. 1(a). These polarization states are directly represented by the measurements of the PS-OCT system. , and indicated by the red points on the Poincaré sphere [Figs. 1(c)–1(e)] represent the intermediate polarization states of the light beams when they pass through the interface between the yellowish and gray layers as shown in Fig. 1(a). Because the change in the polarization states from to or to is only introduced by the yellowish layers, , and should be in a same plane at the Poincaré sphere. And its normal vector (determined by , and ) represents the local optic axis of the yellowish layers as shown in Fig. 1(c). However, due to the round-trip nature of the OCT measurement, , and are the intermediate states of the light beams and are not measured directly. Hence, the local optic axis in the deeper layer cannot be directly obtained.
Since all of the light beams scattered back from the yellowish layers have to propagate through the same group of the upper gray layers again to reach the PS-OCT system for detection, the intermediate states , and would each experience the same change due to the upper gray layers to form the resultant output polarization states, P3, P4 and P5 for detection as shown in Fig. 1(a). In the Poincaré sphere representation, this change (due to the gray layers) can be viewed as an overall rotation operation that rotates the points , and about the axis by an angle to , and respectively as shown in Fig. 1(d). The angle is determined by the local phase retardations of the first two gray layers. In other words, the output polarization states , and would form a plane (with a normal vector of ) in the Poincaré sphere. This plane can be obtained by rotating the plane determined by , and about axis by an angle - as shown in Fig. 1(e). To summarize, to obtain the local axis , it just needs to rotate about by - as shown in Fig. 1(f). This geometric relationship can be expressed as a matrix rotation in the calculation:
| (1) |
where , and are the 1 × 3 matrices represented by the corresponding Q, U and V values; is the 3D rotation matrix determined by and .
This derivation process can be generalized to the sample with varied optic axes along depth. As the orientation within the biological sample is continuous, we can assume that at least three adjacent OCT pixels in the depth direction of the sample share the same local optic axis, which can compose a plane at the Poincaré sphere. Generally, each of the layers above the layer of interest can rotate the local optic axis to form the final normal vector of the local fitted plane. Each rotation is determined by the local optic axis and phase retardation of the certain layer. Hence, to obtain the local optic axis , a series of rotations are applied:
| (2) |
where is the local phase retardation of the n-th layer, is the normal vector of the local fitted plane, is the 3D rotation matrix determined by and .
2.2. Derivation of the local phase retardation
The local phase retardation can also be evaluated and calculated with the use of the Poincaré sphere. In doing so, one straightforward approach is to calculate the local phase retardation progressively through depth (i.e., layer by layer). Based on the geometric model as discussed above, assuming that the sample has the n homogeneous birefringent layers with each layer having known local input/output polarization states / and its local optic axis , the local phase retardation for the nth layer can then be obtained by
| (3) |
The input/output polarization state at the local layer n can be derived from a series of rotations:
| (4) |
From this treatment, it is trivial to appreciate that the value of the local phase retardation is dependent on the calculated local values of all the layers that are above the layer of interest, which are not from the direct measurements. That is, the errors in the calculation can be propagated and accumulated along the depth. On the other hand, there is also possible errors in the each of the multiple steps in the calculation. Such treatment is clearly not optimal.
To mitigate this issue, here we propose a strategy that calculates the local phase retardation by using two adjacent output polarization states along the depth (that are detected by the PS-OCT system), where the phase retardation of each layer can be simply obtained by:
| (5) |
where is the output polarization state scattered back from the n-th layer, is the normal vector of the local fitted plane as discussed in the last section.
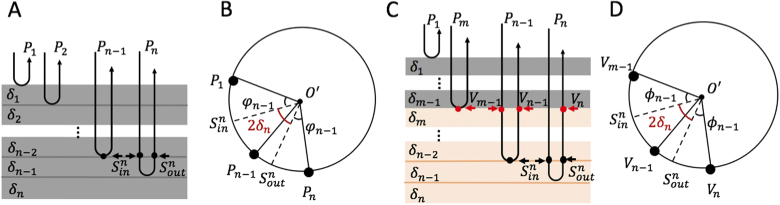
Below, we first prove that this formulation is suitable to the sample with a constant optic axis A as shown in Fig. 2(a), (i).e. a homogenous birefringent sample. In this case, all the output polarization states that are detected by the PS-OCT system are constrained within a defined plane [Fig. 2(b)] and its normal vector of equals to the optic axis A in the Poincaré sphere representation. Consider the n-th layer in Fig. 2(a), the local phase retardation is half the angle that rotates the local input polarization state about A to the local output polarization state as shown in Fig. 2(b), that is, . Note that , where is the sum of the phase retardation of all the upper layers. The local phase retardation can be expressed as , meaning can be calculated using Eq. (5) under this circumstance.
Fig. 2.
Schematic diagram illustrating the relationship between the output polarization states (which are detected by the PS-OCT) and the local phase retardations within a simulated birefringent sample with n layers. (a) A depth-scan of a sample with n discrete layers but with constant optic axis throughout. (b) The plane composed by the output polarization states to within the Poincaré sphere. (c) A depth scan of a simulated birefringent sample with depth-varying optic axis. (d) The plane composed by the to within the Poincaré sphere. is the local phase retardation, is the sum of the phase retardation of all the upper layers, are the local input/output polarization state.
For the sample with varied optic axes along depth [Fig. 2(c)], we consider the plane that is determined by the intermediate polarization states experienced by those layers that share the same optic axis and are located below the upper layers as shown in Fig. 2(c) and Fig. 2(d). In this plane, the local phase retardation of the n-th layer can be expressed as . Consider the round-trip measurement, the angle , and therefore . As discussed in the last section, all the intermediate polarization states would travel back through the same groups of the upper layers again, the same rotation operation should apply to these intermediate polarization states to form the final output polarization states . That is, the plane composed by is the plane determined by after a rigid rotation. Hence, there is a point to point rotational relation between these two planes and their geometric relation within the plane in the Poincare sphere would keep constant before and after rotation. As a consequence, we arrive at , where is the center of the plane composed by in the Poincaré sphere whose normal vector is . That is, the half-angle that rotates about to is equal to the local phase retardation , meaning that Eq. (5) is still valid under this circumstance, and can be generalized to the case with varied optic axis along the depth.
2.3. Fiber-based PS-OCT setup with single incident polarization state
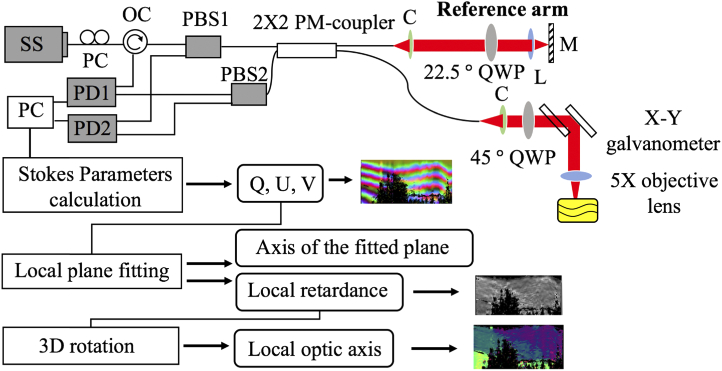
Schematic setup for the fiber-based PS-OCT system with single incident polarization state is shown in Fig. 3, where a swept source configuration is implemented. The system used a 100-kHz MEMS-VCSEL swept laser source (SL1310V1-20048, Thorlabs), providing an output power of 25 mW with a central wavelength of 1310 nm and a spectral tuning range of 100 nm. For PS-OCT imaging, the output of the light source was sent to a polarization controller and became linearly polarized through a polarization beam splitter (PBS 1) (PFC1310A, Thorlabs), and then split into the reference and the sample arms through a PM coupler (PN1310R5A2, Thorlabs) at a split-ratio of 50:50. Note that the use of the PM fibers may induce polarization mode dispersion (PMD) in PS-OCT measurements [9,18,19]. The reference arm was installed with a quarter-wave plate (QWP) with its axis aligned at 22.5° with reference to the input polarization state, ensuring that the reflected light was coupled equally into the vertical and horizontal channels. The sample arm was equipped with a QWP aligned at 45° with respect to the input polarization state, which makes the linearly polarized light to become a circularly polarized light before illuminating the sample. The lights coming back from both the reference and sample arms were recombined and sent to the PBS1 and PBS2, respectively, where the interference light was split into horizontal (Channel 1) and vertical (Channel 2) components. Balanced detection was used for both vertical and horizontal channels to collect the interference signals, upon which to reconstruct the PS-OCT images. In this system, the axial and transverse resolutions were measured at 7.5 µm and 15 µm in air, respectively.
Fig. 3.
Schematic of the fiber-based PS-OCT system. SS: swept source; PC: polarization controller; OC: optical circulator; PBS: polarization beam splitter; PM-coupler: polarization maintaining coupler; QWP: quarter wave plate; PD: photo detector; M: mirror; L: focusing lens; C: collimator. Below: data processing flow chart of the PST method.
The flow chart below the system setup show the processing procedures of the PST method to derive the local phase retardation and optic axis from the PS-OCT measurements. The output polarization states represented by Q, U and V were reconstructed by the Stokes parameters calculation [20]. Before the local phase retardation and axis orientation were calculated, we first applied the color filter to remove the amorphous tissue at the surface which do not alter the input polarization [20]. In this study, we used a sliding window that contains 5 adjacent output polarization states along the depth to do the local plane fitting progressively by using Singular value decomposition. Although each pixel within the sliding window may have a slightly different axis orientation, the axis difference between adjacent pixels should be small when using the muscle as the sample because the orientation of the same muscle group is aligned well. Note that this operation could sacrifice the axial resolution as 5 pixels are used to determine one value. Then the normal vector of each local fitting plane is obtained. The local phase retardations are obtained by Eq. (5). Since , the 3D rotation matrix in Eq. (2) can be calculated layer by layer starting from the surface of the sample. By applying the 3D rotation to the axis of the fitted plane, the local optic axis can be finally obtained.
3. Experimental results and discussions
The proposed PST method was tested on the muscle tissue of a mouse thigh by using the fiber-based PS-OCT system (Fig. 3). The mouse thigh was selected for demonstration because it anatomically consists of multiple muscle groups arranged with different orientations in the shallow depth that are reachable by the OCT imaging. For imaging, we dissected the thigh tissue from a freshly dead mouse that was disposed from another planned project in our lab. Immediately after dissection, the sample was rinsed with PBS saline solution to keep it from dehydration and then placed under the PS-OCT probe for imaging. One B-scan image of the mouse thigh was achieved with 500 A-lines.
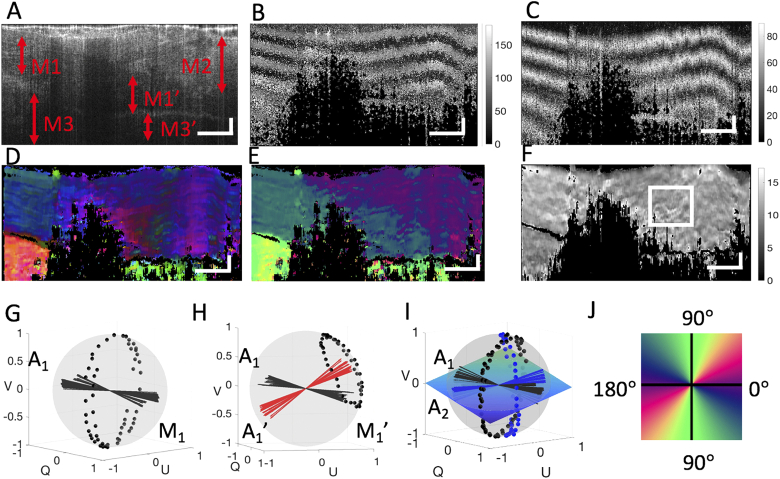
Figure 4(a) shows a representative OCT cross-sectional image, where the anatomical information of the thigh tissue sample is delineated up to an imaging depth of ∼1.5 mm. Notably, there are three different muscle groups (marked as , and ) that can be approximately appreciated. Within this B-scan, there are dark vertical strips that were caused by the probe beam attenuation due to the coagulated blood within the blood vessels situated in the superficial layer. Due to this effect, these dark strips partitioned the appearance of the muscle groups and within this B-scan, where should be part of the muscle group that stretched under the muscle group , and be part of group. Such partitions of the muscle groups in the appearance of the OCT scan provide excellent opportunity to test the proposed algorithm.
Fig. 4.
PS-OCT imaging of the mouse thigh tissue sample that anatomically consists of multiple muscle groups arranged with different orientation. (a) Representative cross-sectional B-scan structural image of the sample where three groups of muscle organizations can be appreciated. The two vertical dark bands are caused by the light attenuation due to the highly absorbing blood clots within vessels situated at the superficial layer. The vertical dark bands partitioned the muscle group and into segments. Segment should belong to , and to . (b) and (c) Corresponding cross-sectional B-scan cumulative optic axis and phase retardation maps where it is difficult to appreciate three muscle groups. (d) Corresponding cross-sectional B-scan map of the optic axis of the local fitted plane, where muscle groups can be appreciated but ambiguous. (e) and (f) Corresponding cross-sectional B-scan maps of the local optic axis and local phase retardation resulted from the proposed PST method, where the three muscle groups are delineated unambiguously. (g) The trajectory of the output polarization states scattered back from the depth extent marked by the two-way red arrow left of label on the Poincaré sphere and the corresponding optic axis determined by plane fitting. (h) The trajectory of the output polarization states scattered back from the depth extent marked by the two-way red arrow left of label on the Poincaré sphere and the corresponding apparent axis and the true optic axis . (i) The trajectories of the output polarization states on the Poincaré sphere that were scattered back from the depth extent marked by the two-way arrows left to the label and right to the label , respectively, where the blue plane is the plane of intermediate optic axes which is fitted by local optic axis and . (j) The colormap used to color-code the maps of the local optic axis. The white lateral and axial scale bars are 1 mm and 0.2 mm, respectively. The units of all the color bars are degrees.
Figures 4(b)–4(f) show the corresponding cross-sectional images of cumulative axis orientation, cumulative phase retardation, axis of the local fitted plane, local axis orientation and local phase retardation images, respectively. From the structural image [Fig. 4(a]), birefringent information of the regions should be the same as that of the region since they are from the same muscle group. And it is also true for the regions of M3’ and M3. As expected, because of the phase accumulation effect, the conventional PS-OCT optic axis map [Fig. 4(b)] and phase retardation map [Fig. 4(c)] are difficult to appreciate the concrete birefringent information of this tissue sample. Figure 4(d) shows the optic axis of the plane directly fitted to the output polarization states (but without applying Eq. (2)). The banded patterns due to the phase accumulation in Fig. 4(b) are removed successfully, however the identification of the three muscle groups are ambiguous because the color of the same muscle group appears quite different. For example, the muscle regions and should have the same optic axis, therefore the same color in this map. However, the color of , which is under appears vastly different from group and varies laterally towards right as the thickness of the is increased. This is because the direction of the axis of the local fitted plane at the region is rotated off the direction of the true local axis of the layer of interest due to the upper layers of muscle group. As discussed in the last section, for the muscle , as the thickness of upper muscle increases, the rotation matrix applied to the local optic axis rotates more and therefore the axis of that local fitted plane of the muscle is off more, leading to the changes in color representation in the Poincare sphere representation.
Figure 4(e) is the corresponding local optic axis map after applying the proposed PST method. The local optic axes of the sample are recovered, and the three groups of the muscle are differentiated without ambiguity. Each color represents an orientation as shown in the colormap in Fig. 4(j). The corresponding map of local phase retardation in Fig. 4(f) appears relatively homogeneous, suggesting a uniform distribution of optical retardance in the sample. These results demonstrate the capability of the PST method to derive correctly the local birefringent information. Note that the local phase retardation in some regions indicated by the white box in Fig. 4(f) exhibits a weak periodic variation. This artifact may be caused by the polarization mode dispersion of the optical components used in the system setup [9,18,19].
To visually show the behavior of the output polarization states backscattered from different muscle groups at localized depth positions, we illustrate their trajectories on the Poincare sphere. The output polarization states scattered back from muscle group [at the depth segment indicated by the two-way red arrow in Fig. 4(a)] are shown in Fig. 4(g) where the trajectory of the output polarization states is constrained within a plane determined by the optic axis A1 as expected. By using a sliding window with 5 adjacent output polarization states to do the plane fitting, the axes of the fitted plane are obtained as indicated by the black axes. These normal vectors represent the axes of the muscle . The slight deviation of the optic axes is the result of the slight local heterogeneous property as expected from the tissue sample. Note also that these optic axes lie in the 3D space at the Poincaré sphere, demonstrating that the vertical component is retained.
Figure 4(h) shows the output polarization states scattered back from muscle group [at the depth segment indicated by the red arrow in Fig. 4(a)]. Affected by the upper muscle , the normal vector [indicated by the red axes in Fig. 4(h)] deviate from the true local axis . By applying Eq. (2) to , the true local optic axes of are obtained as shown in the black axes in Fig. 4(h), which are consistent with the local axes of in Fig. 4(g). In Fig. 4(i), the trajectory of the output polarization states and the local axes of (black points and black axes) and (blue points and blue axes) at the depth segments indicated by red arrows in Fig. 4(a) are presented together. The blue flat plane is the fitted plane of the intermediate optic axes, showing that it is rotated off the QU-plane due to the use of the fiber-based PSOCT system.
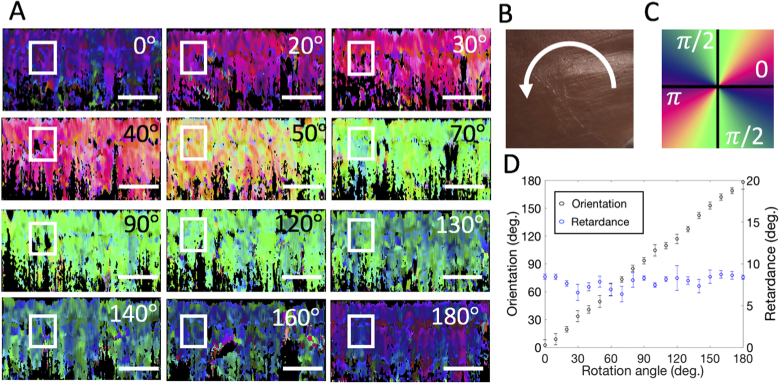
To demonstrate that PST method can extract the relative orientation of the sample, another tissue sample with relatively homogeneous birefringent property was used. The sample was consecutively imaged by the PSOCT system while it was mechanically rotated from 0° to 180° with an increment of ∼10° step. The results are shown in Fig. 5 with a photography of the sample shown together in Fig. 5(b). The 0 deg was defined as the position when muscle orientation was in parallel to the B-scan direction. Figure 5(a) show the representative cross-sectional local optic axis maps of the tissue sample acquired at different angles as shown, where the images of local axis are relatively uniform at each rotation angle but appear different colors. The change trend of the color when the sample was rotated from 0° to 180° is consistent with the colormap in Fig. 5(c), demonstrating that the calculated local axis can retrieve the relative sample orientation. The mean and standard deviation values of the local phase retardation and optic axis in the region enclosed by the white box in Fig. 5(a) were calculated and the curves of these values as a function of the rotation degree are plotted in Fig. 5(d). In Fig. 5(d), the mean local phase retardation values keep relatively constant at different rotation angles, whereas the orientation value increases linearly as the rotation angle increases, showing that the calculated local axis provides correctly the relative orientation of the sample.
Fig. 5.
PS-OCT imaging of a muscle with a homogenous optic axis rotated from 0 to 180 deg. (a) Local orientation images of the same mouse muscle tissue rotated from 0° to 180° with the rotating angle as shown. (b) The photography of the sample and an illustration of the sample rotation. (c) Colormap used to color-code the orientation image. (d) The scatter plots of the local phase retardation and local axis as a function of the rotation angle (from 0° to 180° with a step of 10°). The mean and standard deviation are shown calculated from the region of interest (ROI) marked in the white box in A. The white scale bar is 1 mm.
While we have demonstrated that the PST method can be used to extract the local optic axis and local phase retardance, there are some limitations of this geometric-based method. First of all, at least three depth-measurements are required in the algorithm to fit a plane at the Poincare sphere. This requirement translates to a limitation of minimal mapping resolution of the local optic axis and phase retardance, which equals to a thickness of three-sampling pixels in the OCT depth imaging. For example, if the OCT axial pixel-resolution is 5 µm, then the minimal resolution of local birefringent mapping for our proposed method is 15 µm. Therefore, one way to improve the resolution of the proposed method is to increase the OCT imaging resolution, which is feasible in the current OCT development, but at the expenses of cost.
The 2nd issue is when dealing with the transition from one layer to another layer with a distinct difference in optic axis. Under this circumstance, the fitted plane of this interface region would bear larger errors since the output polarization states at the interface regions would not be constrained to one plane at the Poincare sphere. This results in an error in the determination of the local optic axis and phase retardance at the boundaries of the components within the sample. Again, the improvement of the OCT axial resolution capability may mitigate this issue somehow. Or a new solution to this issue needs to be sought if the birefringent information at the close vicinity of optical interfaces within sample is critical in the research and clinical investigations.
Thirdly, we assumed that the change of the output polarization states is only introduced by the birefringence (i.e. phase retardation and orientation) and neglected the diattenuation of the sample in our current treatment. As the diattenuation is one of important parameters in some ophthalmologic studies to characterize the features of the diseases [21,22], further improvement is required if the diattenuation property of the sample is of concern. Previous studies have shown that when the diattenuation of the sample is not negligible, it can twist the circular curve out of its osculating plane, and hence the trajectory of the output polarization states would become a spiral curve rather than a circular curve at the Poincare sphere [23,24]. One potential solution to evaluate the diattenuation property of the sample is to calculate the torsion value of the trajectory curve and then obtain the degree of the curve twisting out of the plane of the curvature. The bigger the absolute value of the torsion is, the stronger the diattenuation would be.
Finally, the proposed method is only currently suitable to the sample with relatively strong birefringent property such as the muscle. Further improvement and refinement of our proposed framework are required for imaging the sample with relatively weak birefringent property (approximately smaller than 0.6° µm−1) where the output polarization states from the different birefringent groups alter only slightly. In this case, slight differences between the output polarization states from the sample make it difficult to fit a plane accurately at the Poincare sphere. To mitigate this issue, three-dimensional curve interpolation and fitting may be used to fit the curve composed by the output polarization states along the whole depth. While this is a more complicated procedure, such treatment may help suppress errors induced by the noisy points when conducting the plane fitting with the points that are close in space at the Poincare sphere (i.e. slightly altered output polarization states).
Please note that if a linearly polarized light as the single input state is used for the proposed method, there is potentially a caveat that the input state could accidentally align with the optic axis of the sample. In this case, there would be no retardation that could be measured from this linearly polarized input state. This is the reason that we utilized a circularly polarized light as the input state in this study to demonstrate our proposed method.
4. Conclusion
We have proposed and experimentally demonstrated a PST method that utilizes the trajectory of the polarization states on the Poincaré sphere to derive the local birefringent information by using PS-OCT. This method is compatible to the fiber-based PS-OCT system with single incident polarization state. We have described the theoretical framework to derive the local optic axis and phase retardation, and experimentally demonstrated the proposed method by imaging a mouse thigh tissue sample in vitro.
Funding
Research to Prevent Blindness10.13039/100001818; Washington Research Foundation10.13039/100001906; National Heart, Lung, and Blood Institute10.13039/100000050 (R01HL141570).
Disclosures
The authors declare that there are no conflicts of interest.
References
- 1.Whittaker P., Boughner D. R., Kloner R. A., “Analysis of healing after myocardial infarction using polarized light microscopy,” Am. J. Pathol. 134, 879–893 (1989). [PMC free article] [PubMed] [Google Scholar]
- 2.Fan C., Yao G., “Imaging myocardial fiber orientation using polarization sensitive optical coherence tomography,” Biomed. Opt. Express 4(3), 460–465 (2013). 10.1364/BOE.4.000460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sakai S., Yamanari M., Lim Y., Nakagawa N., Yasuno Y., “In vivo evaluation of human skin anisotropy by polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 2(9), 2623–2631 (2011). 10.1364/BOE.2.002623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Park K. S., Choi W. J., Song S., Xu J., Wang R. K., “Multifunctional in vivo imaging for monitoring wound healing using swept-source polarization-sensitive optical coherence tomography,” Lasers Surg. Med. 50(3), 213–221 (2018). 10.1002/lsm.22767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.de Boer J. F., Milner T. E., van Gemert M. J. C., Nelson J. S., “Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography,” Opt. Lett. 22(12), 934–936 (1997). 10.1364/OL.22.000934 [DOI] [PubMed] [Google Scholar]
- 6.Makita S., Yamanari M., Yasuno Y., “Generalized Jones matrix optical coherence tomography: Performance and local birefringence imaging,” Opt. Express 18(2), 854–876 (2010). 10.1364/OE.18.000854 [DOI] [PubMed] [Google Scholar]
- 7.Nam A. S., Easow J. M., Chico-Calero I., Villiger M., Welt J., Borschel G. H., Winograd J. M., Randolph M. A., Redmond R. W., Vakoc B. J., “Wide-Field Functional Microscopy of Peripheral Nerve Injury and Regeneration,” Sci. Rep. 8(1), 14004 (2018). 10.1038/s41598-018-32346-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rivet S., Marques M., Bradu A., Podoleanu A., “Passive optical module for polarization-sensitive optical coherence tomography systems,” Opt. Express 25(13), 14533 (2017). 10.1364/OE.25.014533 [DOI] [PubMed] [Google Scholar]
- 9.Villiger M., Zhang E. Z., Nadkarni S. K., Oh W.-Y., Vakoc B. J., Bouma B. E., “Spectral binning for mitigation of polarization mode dispersion artifacts in catheter-based optical frequency domain imaging,” Opt. Express 21(14), 16353–16369 (2013). 10.1364/OE.21.016353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fan C., Yao G., “Mapping local retardance in birefringent samples using polarization sensitive optical coherence tomography,” Opt. lett. 37(9), 1415–1417 (2012). 10.1364/OL.37.001415 [DOI] [PubMed] [Google Scholar]
- 11.Fan C., o G. J. J., Yao B. O., “Mapping local optical axis in birefringent samples using polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 17(11), 110501 (2012). 10.1117/1.JBO.17.11.110501 [DOI] [PubMed] [Google Scholar]
- 12.Park B., Pierce M., Cense B., Boer J., “Optic axis determination accuracy for fiber-based polarization-sensitive optical coherence tomography,” Opt. lett. 30(19), 2587–2589 (2005). 10.1364/OL.30.002587 [DOI] [PubMed] [Google Scholar]
- 13.Park B. H., Pierce M. C., Cense B., de Boer J. F., “Real-time multi-functional optical coherence tomography,” Opt. Express 11(7), 782–793 (2003). 10.1364/OE.11.000782 [DOI] [PubMed] [Google Scholar]
- 14.Nam A. S., Easow J. M., Chico-Calero I., Villiger M., Welt J., Borschel G. H., Winograd J. M., Randolph M. A., Redmond R. W., Vakoc B. J., “Wide-Field Functional Microscopy of Peripheral Nerve Injury and Regeneration,” Sci. Rep. 8(1), 14004 (2018). 10.1038/s41598-018-32346-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Saxer C., Boer J., Park B., Zhao Y., Chen Z., Nelson J., “High-speed fiber-based polarization-sensitive optical coherence tomography of in vivo human skin,” Opt. lett. 25(18), 1355–1357 (2000). 10.1364/OL.25.001355 [DOI] [PubMed] [Google Scholar]
- 16.de Boer J. F., Milner T. E., Nelson J. S., “Determination of the depth-resolved Stokes parameters of light backscattered from turbid media by use of polarization-sensitive optical coherence tomography,” Opt. Lett. 24(5), 300–302 (1999). 10.1364/OL.24.000300 [DOI] [PubMed] [Google Scholar]
- 17.Boer J., Milner T., “Review of polarization sensitive optical coherence tomography and Stokes vector determination,” J. Biomed. Opt. 7(3), 359–371 (2002). 10.1117/1.1483879 [DOI] [PubMed] [Google Scholar]
- 18.Villiger M., Zhang E. Z., Nadkarni S., Oh W.-Y., Bouma B. E., Vakoc B. J., “Artifacts in polarization-sensitive optical coherence tomography caused by polarization mode dispersion,” Opt. lett. 38(6), 923–925 (2013). 10.1364/OL.38.000923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhang E. Z., Oh W.-Y., Villiger M. L., Chen L., Bouma B. E., Vakoc B. J., “Numerical compensation of system polarization mode dispersion in polarization-sensitive optical coherence tomography,” Opt. Express 21(1), 1163–1180 (2013). 10.1364/OE.21.001163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tang P., Xu J., Wang R. K., “Imaging and visualization of the polarization state of the probing beam in polarization-sensitive optical coherence tomography,” Appl. Phys. Lett. 113(23), 231101 (2018). 10.1063/1.5050208 [DOI] [Google Scholar]
- 21.Huang X.-R., Knighton R. W., “Diattenuation and polarization preservation of retinal nerve fiber layer reflectance,” Appl. Opt. 42(28), 5737–5743 (2003). 10.1364/AO.42.005737 [DOI] [PubMed] [Google Scholar]
- 22.Louis-Dorr V., Naoun K., Allé P., Benoit A.-M., Raspiller A., “Linear dichroism of the cornea,” Appl. Opt. 43(7), 1515–1521 (2004). 10.1364/AO.43.001515 [DOI] [PubMed] [Google Scholar]
- 23.Park J., Kemp N. J., Zaatari H. N., Rylander Iii H. G., Milner T. E., “Differential geometry of normalized Stokes vector trajectories in anisotropic media,” J. Opt. Soc. Am. 23(3), 679–690 (2006). 10.1364/JOSAA.23.000679 [DOI] [PubMed] [Google Scholar]
- 24.Chen C.-L., Wang R. K., “Optical coherence tomography based angiography [Invited],” Biomed. Opt. Express 8(2), 1056–1082 (2017). 10.1364/BOE.8.001056 [DOI] [PMC free article] [PubMed] [Google Scholar]