Choosing the right time granularity for analysis of digital biomarker trajectories

Abstract

Introduction

The use of digital biomarker data in dementia research provides the opportunity for frequent cognitive and functional assessments that was not previously available using conventional approaches. Assessing high‐frequency digital biomarker data can potentially increase the opportunities for early detection of cognitive and functional decline because of improved precision of person‐specific trajectories. However, we often face a decision to condense time‐stamped data into a coarser time granularity, defined as the frequency at which measurements are observed or summarized, for statistical analyses. It is important to find a balance between ease of analysis by condensing data and the integrity of the data, which is reflected in a chosen time granularity.

Methods

In this paper, we discuss factors that need to be considered when faced with a time granularity decision. These factors include follow‐up time, variables of interest, pattern detection, and signal‐to‐noise ratio.

Results

We applied our procedure to real‐world data which include longitudinal in‐home monitored walking speed. The example shed lights on typical problems that data present and how we could use the above factors in exploratory analysis to choose an appropriate time granularity.

Discussion

Further work is required to explore issues with missing data and computational efficiency.

1. INTRODUCTION

Digital biomarker data measure human characteristics that describe a person's behavior or physiology. Common examples include duration of sleep, steps per day, and heart rate. Like other biomarkers, digital biomarkers can be used to potentially identify underlying biological processes, including cognitive function, that may not yet have clear clinical symptoms. ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² Digital biomarker data can be collected at high frequencies using readily available commercial devices. For example, Fitbit (Fitbit Inc, San Francisco, California, USA) activity trackers can measure on the order of seconds to produce daily step counts, sleep quality, and heart rate. Other studies use a system of sensors to record digital biomarker data. In one study, Eby et al. ¹²  measured driving behavior of early stage dementia patients through in‐vehicle technology and sensors that continuously recorded data while subjects were driving. In this study, sensors in the vehicles recorded measurements in interval lengths of no more than 1 second.

Trajectories of high frequency digital biomarker data are increasingly used in health care research to monitor health status in support of disease prevention, treatment, and management. ¹³ Use of digital biomarker data can be extended to disease progression of dementia, which is a process that is currently monitored with limited assessment frequency. For example, neuropsychological (NP) tests used to assess dementia can be administered at most every 6 months to reduce tasking participants and avoid learning and practice effects. As a result, these tests only provide two opportunities for diagnosis of dementia per year. ¹⁴ Trajectories of digital biomarker data can potentially help increase the opportunities for early diagnosis because assessments are made more frequently and can improve precision of person‐specific trajectories.

However, digital biomarkers are noisy in their raw data format. The raw data typically include a series of time stamps with indicators that require processing before they can be used as intelligible measurements. For example, a computer sensor will have a series of indicators for its mouse movements, but those indicators must be translated into comprehensible variables like computer use start time, end time, or duration. ¹ , ¹⁵

In this article we only refer to digital biomarkers that have been pre‐processed into daily measurements. However, one may choose a different starting frequency for measurements if the raw data with finer measurements are available. For example, we may want to examine average hourly heart rate so that we can evaluate a patient's exercise regimen. The approach described in this article can still be applied to data on the hourly scale, or even minute or second scale, but for ease of demonstration, we will assume a daily scale. It is also important to note that the method for processing data may affect aspects of the data, and thus the choice of time granularity.

It is important to remember that as the frequency of measurements increases, the size of the resulting dataset also increases, which then requires a greater amount of computer storage space and computation time for analysis. Thus, it is useful to condense data, such as hourly measurements, to daily, weekly, or monthly summaries, to reduce both data storage demands as well as computation time. At the same time, we would like to maximize the chance of capturing clinically meaningful changes or shifts for each individual. Therefore, it is important to clarify the decision process used to determine the frequency, or time granularity, needed to analyze data.

Determining the appropriate time granularity of data is a complex process, one that has many possible variations. But, regardless of variations, the process to determine time granularity must be explicitly defined before the data are analyzed. It is inappropriate to use statistical significance, ie, P‐values, as a metric for confirming the most appropriate time granularity. Doing so will only serve to inflate the rate of false‐positive findings and may lead one to incorrectly assume that the model with the most statistically significant result is detecting the true underlying signal. Instead, one should make decisions of time granularity in the exploratory portion of analysis, using summary statistics and trajectory plots to help in the decision.

In this article, we will address critical issues to be considered when we decide the level of time granularity to monitor longitudinal digital biomarker trajectories. We will discuss some of the considerations that will help determine the best granularity for analysis, followed by an example, using digital biomarker data collected for dementia research.

RESEARCH IN CONTEXT

1. Systematic review: We searched for publications that included analysis of digital biomarker trajectories in dementia or cognitive aging research. We looked specifically for explanations indicating why certain time granularities were used. We found several publications that use daily, weekly, or monthly time granularities to assess digital biomarker trajectories, but none explained the selection process and/or how selection affected analysis. ¹ , ² , ³ , ⁴ , ⁵ , ⁶

2. Interpretation: We aim to guide researchers through the decision process regarding time granularity selection, so analysis captures the trajectory of digital biomarker data while minimizing the computational burden of the analysis.

3. Future directions: Although we provided an example for choosing an appropriate time granularity, we plan to complement this example with a simulation study to observe different scenarios involving the factors. This will further aid our goal of demonstrating the important factors in the decision of time granularity and give further examples in which we minimize noise while maintaining the true underlying trajectory.

2. FACTORS OF DATA IMPACTING TIME GRANULARITY DECISIONS

When investigating repeated digital biomarker data, one should first consider the statistical model that will be used. For examining trajectories, one typically uses longitudinal data analysis (LDA) to determine how disease progression relates to changes over time in the biomarkers. LDA is the statistical study of repeated measures, and we typically analyze patterns over time with longitudinal analysis through linear mixed effects models (LMMs) or generalized linear mixed effects models (GLMMs). LMMs and GLMMs work to capture information about the population's change over time while accounting for individual differences through random effects. For more information on LMMs, GLMMS, and LDA please refer to statistical textbooks. ¹⁶ , ¹⁷

While fitting a LMM or GLMM, we must look at certain factors that help improve the fit. These factors are: (1) duration of follow‐up, (2) variables of interest in analysis, (3) pattern detection, and (4) signal‐to‐noise ratio (SNR), and each term will be defined in greater detail as it is presented in the following sections. It is important to note that the factors we have listed do not include data management or missing data issues. We assume storing and maintaining the raw data is not an issue, but we understand that this may motivate summarizing data as it is stored.

2.1. Duration of follow‐up

We recommend that readers initially investigate duration of follow‐up, which is the length of time that measurements are recorded for each subject. Follow‐up time will help determine which time granularity is not acceptable for examining trajectories. Time granularities that are close to the total follow‐up time will not provide enough information for analysis because there will not be a sufficient number of data points to accurately model trajectories over time. Thus, these time granularities should not be considered further.

For example, one can measure the weekly estimated fetal weight for pregnant mothers. The maximum follow‐up time for each mother is around 40 weeks, which is limited by the human gestation period. Therefore, we record 40 weekly measurements on fetal weight. If one wanted to condense these measurements into monthly averages, then one would have approximately 9 monthly averages. If one wanted to condense these measurements into trimester averages, then one would have three trimester averages. Last, one may calculate a single gestation average. Thus, there are 40 weekly measurements, 9 monthly averages, three trimester averages, and one gestation average. If trajectory analysis aims to detect fetal weight change over time, then one can immediately eliminate the single gestation average as a feasible time granularity because a single point cannot detect change. The other three time granularities are feasible, in terms of follow‐up time alone, but it is necessary to consider the other factors.

In the case of fetal growth, the duration of follow‐up is short enough that weekly measurements will not be an overwhelming amount of data for analysis, but reduction to monthly, trimester, or gestation averages may greatly reduce power to detect change over time. There is no exact cut‐off for follow‐up time at which reduction of frequent measurements to coarser time granularities becomes appropriate and is context dependent. It is important to remember that we reduce the data by approximately four‐fold when we condense weekly data to monthly averages, so there must be some benefits to analyzing monthly averages to offset this reduction in the number of unique data points.

2.2. Variables in analysis

Variables of interest may influence selection of data granularity. For example, in Dodge et al., ⁴  the authors found that the variability of a subject's walking speed, in addition to walking speed itself, is associated with mild cognitive impairment (MCI). In this example, the data were processed into daily measurements that included average walking speed. The variance was calculated over each week (variability of daily walking speed within each week). Because the authors used a week's worth of data to create the new variance variable, it is no longer viable to model the daily time increments. In this case, using data with weekly time granularity adds an informative variable to analysis that was not available with daily granularity.

Another example is measurement of moderate‐to‐vigorous physical activity (MVPA) using heart rate monitors. Heart rate monitors take time‐stamped measurements of a person's heart rate in beats per minute. These time‐stamped heart rates can stand alone as a measurement of someone's physical activity, but researchers have found a more useful summary of this data to analyze someone's physical activity. ¹⁸ Using established thresholds, heart rate can be categorized into different levels of physical exercise. Moderate exercise is defined as a heart rate within 50% to 70% of an individual's maximum heart rate, and vigorous exercise intensity is 70% to 85%. ¹⁹ From heart rate data, one can summarize the time spent within MVPA in a single day. Within the field of physical exercise tracking, daily MVPA is an established summary, therefore it is often used to analyze trajectories of physical exercise. ²⁰ , ²¹ , ²²

We suggest the reader consult literature in their field to identify evidence for informative variables that may require summaries of their current measurements. These measurements may include peak values, trough values, number of times hitting a threshold, ranges, area under the curve, and other summary statistics. Inclusion of summary variables may elevate the analysis and warrant a reduction in time granularity.

2.3. Pattern detection

Before selecting a time granularity for analysis, one needs to understand the general pattern of outcomes. This should be assisted by clinical and biological knowledge in the field. If an outcome is generally understood to change slowly over time, then we will not lose the signal by condensing the data from daily to weekly, or even monthly. However, if the outcome is generally understood to change rapidly, a coarse time granularity may not capture the pattern. For example, a person's melatonin level, which is associated with sleep, rises during night hours and lowers during day hours. ²³ If we calculated an individual's average daily melatonin level, then we would lose the hourly pattern associated with sleep.

In the case of Alzheimer's disease research, it is understood that clinical evidence of cognitive decline does not change rapidly during pre‐symptomatic stages. ²⁴ Clinical symptoms and changes occur on the order of years. Therefore, if we are examining trajectories of pre‐symptomatic subjects or those with MCI, we believe using condensed time granularities, like weekly or monthly data, is an acceptable approach, but it is important to consider all the factors discussed before making a final decision.

2.4. Signal‐to‐noise ratio

SNR describes the ratio of the underlying signal, or pattern, of the data compared to the noise in the data, which is sample‐to‐sample variability. A higher value of SNR indicates stronger belief that the observed signal is real and not random artifact. For longitudinal analysis including LMMs, SNR for a trajectory is the ratio of (1) the expected pattern over time divided by (2) the standard error for that pattern. For the exploratory analysis in LMMs, we keep our examination of digital biomarkers simple. Often, one will plot the digital biomarker over time. To gauge the linear time pattern, we can fit a simple exploratory model, with time as the independent variable and our digital biomarker as the dependent variable. Thus, the expected pattern is solely dictated by the coefficient for time. If one includes more variables in the model then the expected pattern over time will be a linear combination of those coefficients. In Figure 1, we present a simple LMM ratio as an equation that we break into smaller components. We note that these equations are used to facilitate explanation, and are not meant to be used for actual calculations.

FIGURE 1.

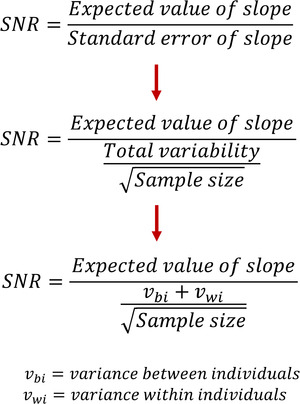
Three simplified representations of the signal‐to‐noise ratio (SNR) equation. For exploratory analysis, in which we investigate the pattern of digital biomarkers over time, our only variable is time. Thus, SNR is the ratio of the expected value of slope over time to the standard error of the slope. The standard error can be broken down further in two steps. Our final equation for SNR includes two important sources of variance (within and between individuals) and the square root of the sample size

In theory, the data at different time granularities are attempting to uncover the same, true pattern, so the expected pattern over time should be the same for each time granularity. However, we do not know the true pattern, so we must compare the signal of each dataset drawn from different time granularities to each other. Typically, one plots a non‐linear fit for data to visually gauge the signal and make comparisons. In general, we want the non‐linear fit of each time granularity to resemble the fit of others. If data quality is good, there should not be major disparities between fits produced by different levels of time granularities. However, data with missing or extreme values are susceptible to biased summaries, leading to different trajectories. Thus, it is important to identify sections of data with missing or extreme values. These sections should not factor into the comparison between non‐linear fits of different time granularities. We will elaborate on data quality in the Discussion section. For now, one should assume that there is no missing data within the dataset.

We will examine standard error further to inform our choice between time granularities. The standard error of the slope is inversely proportionate to the SNR, so a higher standard error will result in a lower, or worse, SNR. We will not make any absolute claims about direct comparison of standard error between time granularities. Instead, we aim to establish an understanding of the trade‐offs for variables of different time granularities by examining the components of the standard error. In the second equation of Figure 1, we see that standard error is the ratio of two components: (1) total variability and (2) the square root of the sample size.

Within total variability, as we saw in the third equation of Figure 1, there are two important sources for repeated measures over time: variability between individuals and variability within an individual. Variability between individuals is how closely the data of one individual resemble that of any other individual. In Figure 2a, we can see a group of individuals that have relatively low between‐individual variability compared to that of Figure 2b. In Figure 2a, individuals have similar slopes and values of their linear fit, while in Figure 2b, the slopes are different for each individual. That is, between‐individual variability is much larger in Figure 2b than that of Figure 2a. Between‐individual variability has limited influence on the decision of time granularity because individual trajectories will generally be maintained across time granularities.

FIGURE 2.

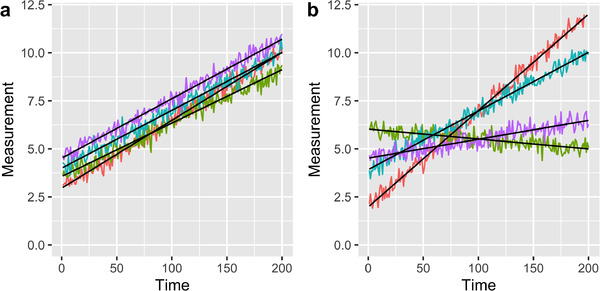
Examples of potential longitudinal data for four subjects. Subjects are represented by different colors. The linear model used to generate the data is displayed in black. Data were generated with equal variation within subjects. (a) Case in which variability between the subjects’ underlying linear model is low, (b) Case in which the variation between subjects’ linear model is high.

Variability within an individual describes the closeness of an individual's data point to any other of the same individual's data points. When one uses summaries from coarse time granularity data, the difference between one individual's digital biomarker values changes, and typically decreases. In Figure 3a, we see that the data closely follow the linear fit for each individual. However, in Figure 3b, we see a larger spread of data around the same individual fits, indicating larger within‐individual variability. For both sources, within and between, if the data are more variable, the support for any estimate replicating the true value is lessened because SNR is smaller.

FIGURE 3.

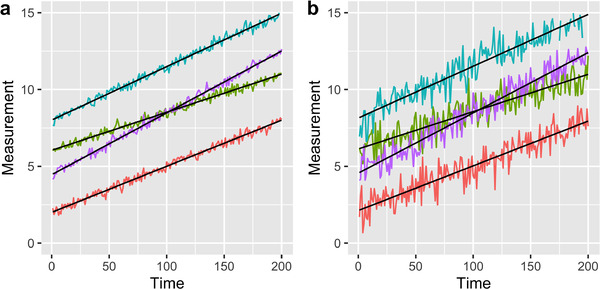
Examples of potential longitudinal data for four subjects. Subjects are represented by different colors. The linear model used to generate the data is displayed in black. Data were generated with same linear model. (a) Case in which variation within subjects is low, (b) Case in which variation within subjects is high

The second important part of standard error is the sample size. With coarser time granularities, the sample size decreases. For example, the sample size for weekly data is seven times less than that of daily data. If we consider weekly and daily data, each having the same total variability, then the standard error for any estimate produced from the weekly data is 2.64 (the square root of 7) times greater than the corresponding estimate produced from the daily data, which leads to a smaller, or worse, SNR for weekly data. This thought process can be applied to the comparison of any two levels of time granularity.

However, the standard error of estimates produced from daily data will not always be smaller than those produced from weekly data because the standard error comprises the variability in the numerator and the square root of the sample size in the denominator. Often, a coarser time granularity reduces the variability of the data in addition to the sample size. The reduction in variability needs to counteract the resulting reduction of the sample size. For example, when condensing daily data to weekly data, the weekly data must have variability that is more than 2.64 (square root of 7) time smaller than the daily data to make the reduced granularity's SNR comparable.

Although one cannot directly compare the standard errors of each time granularity before fitting the models, one can use visualizations of the data to help determine which has less noise. This process will be similar to the one described for Figure 3. This will help direct us toward the more appropriate time granularity, but it is important to keep in mind that more than one time granularity can have low enough noise to strongly detect the signal. It is also important to note that there is no strict cutoff when one compares SNRs; one needs to balance SNR with other factors presented previously.

3. EXAMPLE

To further help readers understand the factors discussed in Section 2, we now examine data from a longitudinal cohort study, the Intelligent Systems for Assessing Aging Change study (ISAAC), which have been collected at the Oregon Center for Aging and Technology (ORCATECH) at the Oregon Health & Science University. More details of this study have been previously published. ³ , ⁶ In the ISAAC study, walking speed was generated using a series of four motion sensors on the ceiling of a narrow hall that were triggered when a subject passed directly underneath. ¹⁴ Walking speed measurements were collected on each participant at multiple time points each day (whenever subjects passed under the series of sensors), and these multiple measures were processed into a daily mean walking speed. We use these daily mean walking speeds in our example. To facilitate discussion about time granularity, we have also summarized the daily measurements into weekly and monthly values. To produce the weekly summaries, we averaged available data over 7‐day consecutive, non‐overlapping windows. The same approach was used to produce monthly summaries, but instead averaging over 30‐day consecutive, non‐overlapping intervals. To simplify our discussion, we have selected the data from four individuals in ISAAC to highlight the factors presented in Section 2. We selected these data simply to illustrate the factors that are important for granularity; it is important to realize that the conclusions in this section are not necessarily generalizable to the remaining data in ISAAC or other studies.

Figure 4 contains two columns of three figures each; both columns contain loess fits. The loess fit is a non‐linear fit produced from overlapping, moving windows of data. Within each window of data, a weighted average is computed such that data closer to the center point are weighted more heavily than points further from the center. The weighted averages give a rough estimate of the smoothed trajectory, or signal, for each individual. The left column contains the loess fit with the data points, and the right column contains the loess fit with confidence bands. We can see that high‐frequency data with high within‐individual variability (Figure 4a) may not help the viewer digest the general pattern over time.

FIGURE 4.

Example longitudinal data from four individuals from the Intelligent Systems for Assessing Aging Change study. Each individual is marked with a different color for clarity. Mean walking speed is the average speed for an individual for the day (in cm/s). All figures have their loess curve in black. The left‐hand column, including (a), (c), and (e), are the plots of the data. (a) is daily data, (c) is the weekly averages of the daily data, and (e) is the monthly average of the daily data. The right‐hand column, including (b), (d), and (f), are plots of their respective average's loess fit with the 95% confidence bands in their respective colors

With regard to the factors presented in Section 2, we first see in Figure 4 that the amount of follow‐up time for the four individuals ranges from 3.8 to 9.2 years. Thus, we could consider reducing the time granularity to weekly or monthly because we would still have a sufficient number of weekly or monthly observations for each individual. Second, for our specific analysis, we want to consider an additional variable that needs to be derived from the data. This additional variable is the amount of variability in walking speed, which has been shown to be associated with cognitive function. ⁴ Because variability, by definition, is based upon several observations of the same quantity, we need to use a level of granularity that would contain several observations in each interval. This again motivates us to reduce the daily walking speeds to weekly or monthly averages to use weekly, or monthly, variance of walking speed in our models. Third, as seen in Figure 4, there is no immediate short‐term change in walking speeds; changes in walking speed occur instead over months or years. Thus, trends in walking speed can be detected from weekly or monthly average data.

Last, we need to consider the SNR, whose exact calculation can occur only after fitting a model. Nonetheless, we can use the exploratory information provided in Figure 4 to roughly compare the relative SNRs resulting from each level of time granularity. We make this comparison through two aspects of each plot: (1) the non‐linear loess fit and (2) the confidence band around the loess fit. Before we further examine the corresponding SNR of each level of granularity, we must address any differences that exist in the loess fits for each time granularity in Figure 4. In theory, with complete data, the loess fit of each time granularity should have similar, if not the same, trajectories. In our example, we see that the loess fits for each follow similar patterns. Therefore, each time granularity is detecting roughly the same underlying signal, and we must inspect the confidence bands to determine the relative SNRs.

The confidence bands will help us understand the relative variability of the data for each level of time granularity. In terms of total variability, all three levels of granularity produce data with relatively similar between‐individual variation. The within‐individual variation decreases as we move from daily granularity to weekly to monthly because the difference in walking speed mean decreases between each individual's data points (Figure 4a,c,e). However, we should look at the individual variability with respect to the sample size, which is incorporated in the plots in right‐hand column through confidence bands (Figure 4b,d,f). As we move from daily to weekly to monthly time granularity, the width of the confidence bands increases, which means we have greater sampling variability with respect to the sample size, which leads to decreased ability to identify significant trends in the data. Most importantly, we would like a level of time granularity that would allow us to detect each individual's pattern as distinct from the others. Thus, in the right‐hand plots of Figure 4, we see that both the daily and weekly levels of granularity produce data that have SNR values that are large enough to detect the underlying signal in the data, relative to the level of sampling variability. Thus, if we can make a good argument for weekly data using the other factors we discussed, then we believe their use for analysis would be beneficial.

Summarizing over all our thoughts for the factors presented in Section 2, we first believe data with monthly granularity do not have a sufficient SNR for analysis, so we will no longer consider that level of granularity. Although the data with daily granularity have the largest SNR, there are a few drawbacks to using daily granularity. First, visualization of the data does not facilitate an understanding of the data pattern because the noise of one subject's trajectory obscures the trajectory of other subjects. Second, daily granularity requires more computation time than data with lower granularity, and daily granularity does not allow for the use of variability in walking speed that can be produced from data with weekly granularity. Third, we believe data with weekly granularity will uncover signals similar to those produced with data with daily granularity. Thus, for this example, reducing the time granularity from daily measurements to weekly summaries is appropriate for assessing longitudinal changes in walking speed.

4. DISCUSSION

The decision of time granularity helps balance computational efficiency and the integrity of data. We discussed factors of the data that one can use to determine whether coarse time granularities maintain the underlying signal of the data. The decision regarding time granularity is a consequence of increased information afforded by digital biomarkers, which allow researchers to assess trajectories more frequently than traditional tests such as pen‐and‐paper–based NP tests or annually collected survey data. While NP tests can be administered at most every 6 months due to learning bias and participant burden, digital biomarker data are collected with much greater frequency.

Due to the high frequency of digital biomarker data collection, there are issues with data management and storage. As mentioned in Section 1, data collection starts with time stamps that can be taken on the order of seconds. This means that one day for one individual can potentially contain 86,400 data points (one per second). Typically, these data are condensed into longer time intervals that are dictated by data storage or available management. Setting aside these hardware issues, we chose to examine time granularities with respect to statistical analysis. If the reader has more concerns about data management issues, we suggest referencing other publications. ²⁵ , ²⁶

Additionally, comparing time granularities, there are issues involving missing data that we did not thoroughly examine in our example. In certain cases, missing data can make the data susceptible to biased averages when looking at different time granularities. This is an issue that can be addressed during model fitting. Assuming missing data occur for completely random reasons (ie, lost data, faulty sensors, etc.), we could implement weighted regression. For example, if a given week has three missing daily measurements, then our weekly average would be calculated from 4 days. If a given week has zero missing daily measurements, then our average would be calculated from 7 days. We could weigh the weekly averaged data by the number of days out of seven that had non‐missing data. That is, weeks with complete data will have greater influence on the model fit. This is just one example, and it should not be taken as an established fitting method. However, there are other options for weighted regression that we encourage readers to explore. ²⁷ , ²⁸ , ²⁹

We also limited our discussion to factors that will strengthen analysis when we fit data using LMMs or GLMMs. Other methods have been used to analyze repeated measures involving dementia, including latent trajectory analysis, path analysis, mixed‐effect model repeat measure models (MMRMs), and functional data analysis (FDA). Readers can approach these forms of analysis using the factors laid out in Section 2, but each method has specific qualities that may require different factors or less emphasis on the ones we mentioned. For example, FDA uses smoothing methods to create continuous functions to represent data. ³⁰ This means that the decision of time granularity, and time as a discrete measurement, is just a processing step before we represent the data as a function and with continuous time. This may lead us to question whether time granularity should even be considered. However, variables of interest like variance of walking speed may still be important in our analysis. Thus, we may want to look at a time granularity that supports summary data like variance.

In this article we addressed factors to be considered when selecting time granularity. We specifically addressed daily data summarized into weekly or monthly data, but this approach is applicable to data summaries of any time length. We also identified factors of the data that are important to consider in the decision of time granularity. In our exploratory procedure we looked at follow‐up time, variables in analysis, pattern detection, and SNR to aid our decision. We showed that these factors of the data are linked to each other, and no single one decides if data reduction is appropriate. Last, we walked through an example of longitudinal data in which weekly time granularity was appropriate for our analysis. In future work, we would like to conduct a simulation study to examine different scenarios for the factors discussed. This simulation study will further explore how our identified factors relate to one another and analysis goals.

CONFLICTS OF INTEREST

The authors have no conflicts of interest.

Supporting information

Supporting Information

Wakim N, Braun TM, Kaye JA, Dodge HH, for ORCATECH. Choosing the right time granularity for analysis of digital biomarker trajectories. Alzheimer's Dement. 2020;6:1–9. 10.1002/trc2.12094