The Actin Cytoskeleton as an Active Adaptive Material

Abstract

Actin is the main protein used by biological cells to adapt their structure and mechanics to their needs. Cellular adaptation is made possible by molecular processes that strongly depend on mechanics. The actin cytoskeleton is also an active material that continuously consumes energy. This allows for dynamical processes that are possible only out of equilibrium and opens up the possibility for multiple layers of control that have evolved around this single protein.Here we discuss the actin cytoskeleton from the viewpoint of physics as an active adaptive material that can build structures superior to man-made soft matter systems. Not only can actin be used to build different network architectures on demand and in an adaptive manner, but it also exhibits the dynamical properties of feedback systems, like excitability, bistability, or oscillations. Therefore, it is a prime example of how biology couples physical structure and information flow and a role model for biology-inspired metamaterials.

INTRODUCTION

The main types of biomolecules in cells are nucleic acids, proteins, lipids, and carbohydrates. When it comes to the physical realization of the information stored in the genes, however, it is mainly the proteins that build the structures making up a biological organism (1, 2). Out of the proteins building the physical structure of the cell, actin is arguably the most important one. A small protein of only 42 kDa molecular weight, actin appeared very early in evolution and afterwards did not change its structure much, so that many other proteins could evolve around it (3, 4). Its main feature is that monomeric actin (globular or G-actin) can readily assemble into polar filaments (filamentous or F-actin), which have two biochemically and structurally distinct ends. These filaments in turn can form different superstructures in cells, including branched networks, cross-linked meshworks, cross-linked bundles, and contractile bundles (5). While actin is essential in all kingdoms of life, it is most prominent in animal cells, where the actin cytoskeleton is the primary determinant of cell shape, mechanics, division, and migration (6, 7). By imaging the actin cytoskeleton of an adherent animal cell, one can easily see the coexistence and complementarity of some of these structures (8, 9) (Figure 1a). The relative extent to which these different structures are formed in a specific cell strongly depends on environmental conditions and in particular on mechanical requirements. For example, cyclic stretch of adherent cells leads to a complete reorganization of the actin cytoskeleton (10–12). Actin is also essential for embryonic development, when the growing organism has to undergo a well-defined sequence of physical changes (13, 14), and in specialized tissues like skeletal, cardiac, or smooth muscle, where molecular motors slide actin filaments past each other during contraction (15). Finally, actin plays an important role when stem cells differentiate into specialized cells, in particular into muscle cells (16–18).

Figure 1.

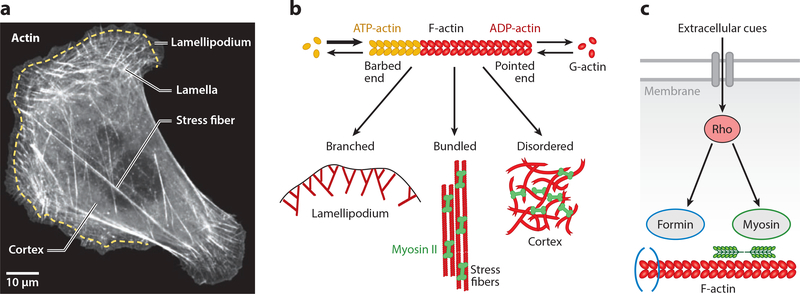
Actin networks organize in distinct architectures and modules in cells. (a) Actin organization in a U2OS cell, visualized by fluorescent actin. The actin cytoskeleton organizes into diverse superstructures in cells, including branched networks in the lamellipodium at the cell front, contractile transverse arcs in the lamella behind the lamellipodium, cross-linked and contractile meshworks in the cortex, and stress fibers stretching toward the cell rear. Scale bar represents 10 μm. Panel adapted from Reference 9. (b) Actin is a living polymer that utilizes energy from ATP-hydrolysis to assemble monomers at the barbed end and to disassemble them from the pointed end. By associating with specific binding partners, actin can assemble the diverse architectures seen in panel a.(c) Flow of information toward actin. Extracellular cues are integrated by membrane receptors to activate signaling pathways, including those that regulate the assembly of actin structures. As an example, here we show the Rho pathway that synchronizes the assembly of the actomyosin system through formin-mediated actin polymerization and myosin II–driven contractility.

Due to its universal role as the cellular building material, actin is increasingly used outside the cellular context to construct new types of materials and systems, in particular synthetic cells that like natural cells can adapt their structures to changing environmental conditions (19, 20). Actin filaments are controlled in cells by more than one hundred proteins directly binding to them (actin-binding proteins, or ABPs). By controlling these processes in the test tube, today one can reconstitute many of the diverse functions and architectures that actin can accomplish in cells, in particular the branched networks of the lamellipodium (21, 22), the contractile bundles of stress fibers (23, 24), and the cross-linked and contractile meshworks of the cell cortex (25, 26) (Figure 1b). Actin and also many of the ABPs require the energy source ATP for their proper function. Therefore, actin-based materials have to be considered as being active (27, 28). In particular, each actin monomer has a binding site for ATP, and an actin filament grows mainly at its plus end (also known as the barbed end) by binding ATP-actin. After hydrolysis by the actin in the filament, the minus end (also known as the pointed end) is characterized by a predominance of ADP-actin, and this marks it for disassembly (29). The combination of association at the barbed end and dissociation at the pointed end leads to the concept of living or treadmilling polymers (Figure 1b), which when anchored to its environment can actively move through space and push against obstacles while keeping its length fixed. In fact, it is exactly this concept (30, 31) that is implemented by the lamellipodium as a whole (cf. Figure 1a) to push itself forward against the plasma membrane (dendritic nucleation/array treadmilling model) (6). Another important example of actin-associated and ATP-driven activity is the action of myosin II molecular motors, which bind to actin filaments of opposing polarity and slide them relative to each other to achieve contraction (32). The ATP-dependent activity of contractile actin networks has been proven by demonstrating experimentally that they break the fluctuation-dissipation theorem at low frequencies (frequencies above 10 Hz are thermal) (33). For reconstitution assays, it is therefore essential to control not only actin and ABP concentrations but also activity in the form of ATP concentration. In this way, the actin system can maintain dynamic features that are not possible in thermodynamic equilibrium.

The activity of the actin system is not only restricted to the requirement of energy influx to maintain conditions of nonequilibrium, but there exists another layer of activity that originates from a higher level of control that has evolved in cells. The proteins that have evolved around actin include not only those that directly bind to actin, but also a large range of signaling molecules that affect several of these processes at once, most importantly the small GTPases from the Rho family (34, 35). This is similar to the control of gene expression, where different genes are switched on together by one operon. The flow of information toward actin and the corresponding control structure is illustrated in Figure 1c, where extracellular cues are integrated by membrane receptors to trigger the Rho-signaling cascade. Rho not only activates formins that recruit new actin monomers to the barbed ends, but it also suppresses their disassembly at the pointed ends, assembles and activates myosin II minifilaments that contract the resulting actin bundles (Figure 1c), and inactivates myosin phosphatase. Other signaling molecules like Rac or Cdc42 bundle activities that are essential to create propulsive networks (lamellipodia) or cross-linked bundles (filopodia), respectively (36). Recently, non-neuronal optogenetics has evolved as a new physics tool to control the actin system with high temporal and spatial resolution by engineering light sensitivity into these regulatory systems (37–42). The evolution of this additional control layer in cells demonstrates the fundamental importance of actin for life and represents new challenges for our physical understanding of how biomolecules can be used to build physical structures.

Here we review the actin cytoskeletal system from the viewpoint of physics as an active adaptive material, with a special focus on the higher control level that is made possible by the signaling molecules controlling the ABPs. We discuss that this system leads to a plethora of intriguing dynamic behaviors, such as bistability, oscillations, waves, and excitable dynamics. In contrast to purely signaling-based systems behavior such as cell proliferation in response to growth factors, the feedback loops in the actin system are strongly coupled to the physical properties of the system. Therefore, signal transduction in the actin system relies not only on diffusion and reaction but also on mechanics and force generation. Thus, the actin system exhibits a particularly close coupling between structure and control, which in the future might be harnessed in novel types of biology-inspired metamaterials.

PHYSICAL PROPERTIES OF ACTIN FILAMENTS AND GELS

Actin monomers are globular proteins that self-assemble into filaments by forming a twisted double helix. In contrast to a linear assembly, the braided architecture provides more stability: Each monomer has multiple binding sites to its neighbors, and therefore opening a single one does not disrupt the mechanical integrity of the filament. The twisted structure results in a chiral and polarized nature of the filament. Very important for the adaptive mechanics of actin, the local twist is variable and can be modulated by ABPs like cofilin and by mechanical tension (43–45). Recently it has been shown that the molecular chirality of actin filaments can manifest itself at the macroscopic level, leading to symmetry-breaking in cells, embryos, and organisms (46–48). The most important symmetry-breaking property of actin filaments, however, is their use of the ATP-binding site in each actin monomer. Most of the polymerizable ATP-actin in cells exists in a binding complex with the small ABP profilin, which makes sure that ATP-actin only binds to the barbed end (49). Because actin monomers in the filament hydrolyze the ATP within seconds and release the inorganic phosphate within minutes, the part of the filament toward the pointed end has very different binding properties and recruits ABPs from the actin-depolymerizing factor (ADF)/cofilin family. Driven by thermal fluctuations, this leads to filament severing, such that the smaller fragments can be depolymerized or recycled for other purposes, including binding to profilin and further growth at the barbed end. Together, these findings show that actin filaments do not simply add and remove monomers at the barbed and pointed ends, respectively. Rather, these kinetic processes are strongly controlled by ABPs that have specifically evolved for this purpose (50), relying on energy consumption and conformational changes provided by ATP-hydrolysis.

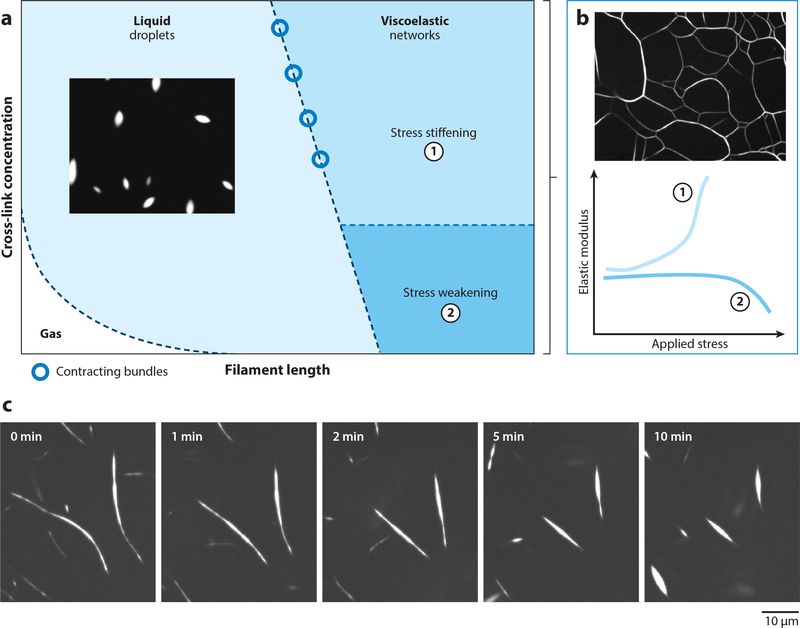
Single actin filaments can generate piconewton forces when growing against an obstacle, but with a persistence length on the order of 10 micrometers they also easily buckle under load (51) and therefore have to be integrated into larger arrays in order to provide mechanical stability to cells. This is achieved by two fundamental processes: branching and cross-linking. Daughter filaments are branched off from mother filaments by the Arp2/3 complex. For cross-linking, a large range of different ABPs exist (including α-actinin, filamin, scruin, and fascin), demonstrating the large importance of mechanical stability in cells. Depending on the physical properties of crosslinks or filamentous units, cross-linked actin can form viscoelastic networks (25, 52) or fluids (53) (Figure 2a). For a given actin density, networks form when the filament contour length is sufficiently long for entanglements (25, 54) and with a kinetically determined architecture (55, 56). Cross-linked actin gels have been extensively investigated and exhibit remarkable tunable materials properties (57, 58). Actin filaments are semiflexible and their mechanics is determined by both stretching and bending modes; together with filament and cross-linking densities, they can result in different force transmission regimes (59). For densely cross-linked networks, filament stretching dominates deformation modes, resulting in a stress-stiffening regime and a highly tunable elastic modulus (52, 57–59) (Figure 2b). As the cross-link density is reduced, filament bending dominates and the networks stress-weaken (57) (Figure 2b). Although typically the strain-stiffening response is reversible (57), recent work shows that F-actin networks cross-linked by filamin can exhibit long-lived mechanical hysteresis effects and can encode multiple hysteretic responses (60). This behavior arises from changes in F-actin nematic order under stress, suggesting a crucial role of actin organization for adaptation to force.

Figure 2.

Materials properties of cross-linked actin networks. (a) State diagram of cross-linked actin networks showing the tunability of mechanical properties by varying cross-link concentration and filament length. When filament lengths are sufficiently long for entanglements, F-actin kinetically arrests to form viscoelastic networks. Short F-actin with sufficiently high cross-linking concentration forms liquid droplets. Gas-like phase appears when both filament length and cross-linking concentration are small. (b) Tunability of elastic modulus of cross-linked F-actin in the viscoelastic phase. F-actin networks stress-stiffen when densely cross-linked and stress-weaken for low cross-linking concentrations. (c) At the boundary between viscoelastic and fluid phases, cross-linked F-actin forms long bundles that contract via surface-tension-like forces. Figure adapted from Reference 53.

Figure 2a also shows that short actin filaments cross-linked by filamin lead to a liquid droplet phase (53). Filamin condenses F-actin into fluid droplets with a characteristic spindle shape (tactoids), which is a signature shape of nematic liquid crystal droplets (61, 62). Size, shape, and coalescence dynamics of the F-actin nematic droplets can be tuned by cross-linking, which controls droplet interfacial tension as well as viscosity. At the boundary between kinetically arrested networks and liquid droplets, liquid-like bundles are found that can contract via surface tension-induced forces (53) (Figure 2c). Thus far, this liquid phase has only been observed for the highly flexible and low-affinity cross-linker filamin; future work is needed to explore how the cross-linker properties support the formation of equilibrated liquid phases of cross-linked actin. For sufficiently short filaments and low cross-link densities, no higher assemblies are found akin to a gas-like phase of individual F-actin (Figure 2a) (53). These results demonstrate that the solid and liquid phases of cross-linked actin can be controlled by tuning the physical properties of cross-linkers or F-actin, and they further demonstrate the central importance of actin mechanics control by ABPs.

GROWTH OF ACTIN FILAMENTS AND NETWORKS

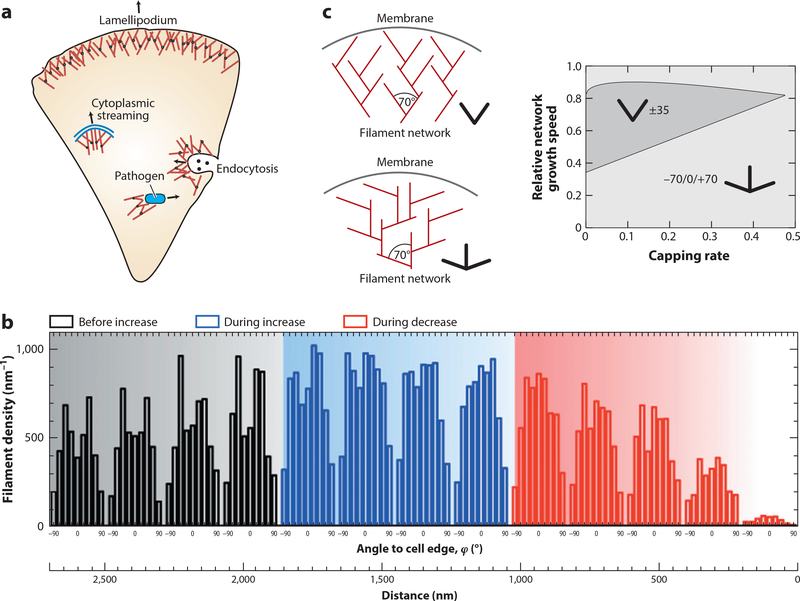
By growing with their barbed ends against obstacles, actin filaments can convert chemical energy into protrusion forces. This is essential for animal cells that have to push against the membrane during spreading and migration, which they do with a dense network of actin filaments called the lamellipodium (Figure 3a). Pushing forces created by branching actin networks are also used to engulf foreign objects during phagocytosis and to push budding vesicles inside cells during endocytosis and during cytoplasmic streaming (63). They are further exploited by certain parasitic bacteria (e.g., Listeria) and viruses (e.g., vaccinia) that nucleate actin comet tails from their surfaces to push themselves forward in the cytoplasm of their host cells (64). The Listeria system has been reconstituted with a minimal set of proteins,first for rigid cargo-like plastic beads (65,66) and later for soft cargo-like vesicles (65, 67). For this system to work, it is essential that new monomers can be added at the barbed end even in close proximity to the obstacle. The main mechanism for this is thermal fluctuations, in particular of the plasma membrane away from the growing actin gels, as described by the different variants of the Brownian ratchet model (30). Mechanical stability of the lamellipodium can be achieved by both branching and cross-linking, but ultrastructural evidence clearly shows that the front part of the lamellipodium is dominated by branching and that cross-linkers are incorporated only toward the back (68). Therefore, the lamellipodium is an intermingled collection of many individual trees, with each tree rattling in a cage defined by the other trees. This observation also implies that excluded volume effects might be relevant for cell migration (69).

Figure 3.

Active growth of F-actin networks. (a) In cells, dendritic actin networks generated by the branching agent Arp2/3 are used to create pushing forces on the objects that nucleate them, for example, on the plasma membrane during migration, on endocytosing vesicles that have to be pushed inside the cell during cytoplasmic streaming and when pathogens push themselves through the cytoplasm. (b) When membrane tension and thus mechanical load on the lamellipodium is first increased and then decreased by micropipette aspiration of migrating keratocytes, filament density first increases and then decreases. At the same time, the orientation distribution changes from two symmetric peaks at ±35° to one peak at 0°. Panel adapted from Reference 75 with permission. (c) These results agree well with the theoretical predictions that the classical ±35° structure (slingshot) competes with a +70/0/−70° structure (trident) depending on the growth kinetics determined by external load. Panel adapted from Reference 77.

Branching is provided by the Arp2/3 complex with a typical branching angle of ~70° that is strongly conserved across species (70). Growing dendritic networks can be reconstituted in vitro by activating the Arp2/3 complex at surfaces facing an actin-solution with the ABPs profilin (for growth from the barbed end) and capping protein (to avoid uncontrolled growth to the sides) (21, 22, 71). By letting such a network grow against an atomic force microscopy (AFM) cantilever, one can probe its response to mechanical force (72, 73). As suggested by the function of the network to distribute force over different filaments, it has been found that its density increases under force, suggesting that the systems design is such that single filaments remain below the buckling threshold. Similar adaptive responses to force have been found for migrating keratocytes in which mechanical load has been changed by changing tension in the plasma membrane by micropipette aspiration (Figure 3b) (74, 75). Strikingly, the adaptive response concerns not only density but also network structure. With the branching angle at 70° and a symmetric arrangement around the direction of protrusion, one might expect the filaments of the lamellipodium to be oriented at ±35° (Figure 3c). Such a configuration is self-reinforcing because +35° filaments would branch into −35° filaments and vice versa; branching in the other directions would lead to ±105° orientations, thus becoming nonproductive for propulsion. While this slingshot configuration has long been thought to be the standard case in growing lamellipodia, computational studies (76, 77) have suggested that an alternative architecture could also be stable: In the trident structure with orientations of 0, +70°, and −70°, the different orientations would also mutually stabilize each other (Figure 3c). Computer simulations and an analytical kinetic theory suggested that the nonconventional trident structure should be favorable for both large and low loads, which correspond to slow and fast velocities, respectively (77) (Figure 3c). Indeed, this prediction was then confirmed in live cell experiments reconstructing the orientation distribution from electron microscopy images (75,78). Together, these results demonstrate that collective effects are essential for the function of branched actin networks and that they dynamically adapt to the mechanical needs of the cell. In fact, it is very likely that more mechanisms of mechanical adaptation exist than currently known. For example, it has been shown that branching is slightly favored on the convex side of curved actin filaments, thus reinforcing the network toward the protruding side (79).

The architecture of branching actin networks is determined not only by mechanical load but also by the availability of actin monomers. It has been suggested that the availability of actin monomers controls the size of filamentous structures in cells (80). In a recent theoretical study, it has been argued that additional control structures are required to make multiple stable filamentous structures (81). Using in vitro reconstitution, it has been shown that two dendritic networks growing next to each other indeed compete for monomers if closer to each other than a typical diffusion length, and that this provides a mechanism for steering lamellipodia through space (71, 82).

CONTRACTILE FORCE GENERATION BY ACTIN NETWORKS

The mechanical properties of actin networks in the cortex of animal cells are controlled by a specific class of molecular motors, namely nonmuscle myosin II. Myosin motors harness chemical energy from ATP hydrolysis to perform mechanical work on actin networks. As individual myosin II motors remain bound to actin filaments only for a small fraction of their ATP-hydrolysis cycle (51), they are incapable of generating appreciable mechanical forces on F-actin as single molecules. Force generation therefore involves myosin motor assembly into bipolar filament structures, called myosin minifilaments, which in nonmuscle animal cells are composed of around 30 myosin molecules (83). As myosin minifilaments translocate along actin filaments, they generate stresses via antiparallel sliding of actin filaments (15, 32). In cells, these stresses are contractile and drive shape changes at the scales of organelles, cells, and tissues for executing diverse physiological functions including cell migration and cell division as well as tissue regeneration and morphogenesis (84–87). For example, in cell division, the actomyosin cytoskeleton assembles into a ring-like structure at the cell equator to locally generate contractile forces (86). In cell migration, contractile stresses are essential for adhesion regulation, cell shape, and mechanosensing (cf. Figure 1a) (88). In development, contractile forces in the cell cortex contribute to tissue morphogenesis (84, 89).

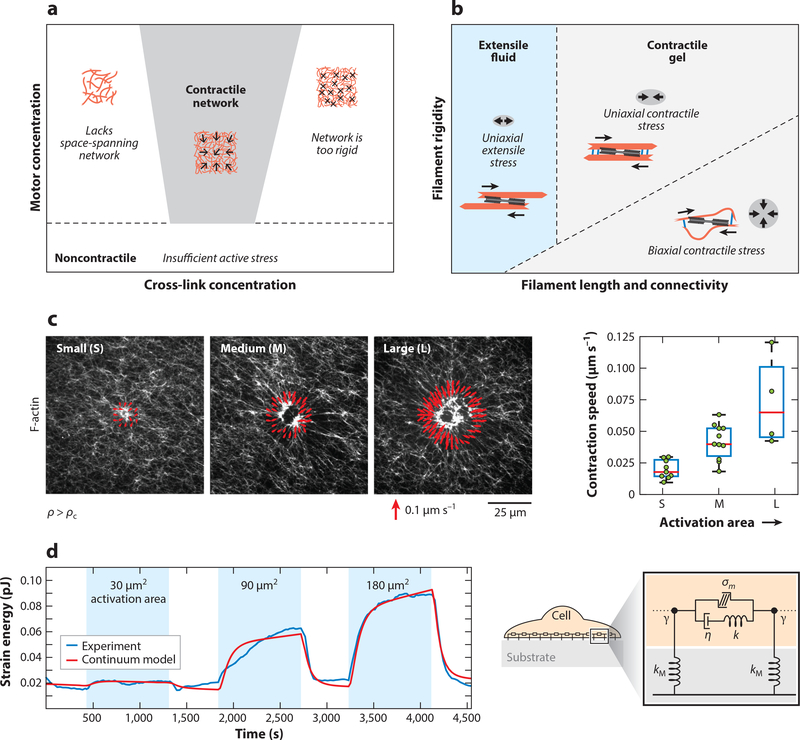
While much is known about the physical interactions between individual actin filaments and myosin motors, far less is understood about how these interactions are integrated within disordered actin networks to generate cell-scale contractile stresses. Understanding the regulatory components for contractile stress generation presents experimental challenges, because cytoskeletal components are coupled by biochemical pathways such that their emergent mechanical roles cannot be easily inferred in isolation from one another. In vitro studies have made major inroads by revealing the minimal set of actuator proteins required to exhibit a wide range of active mechanical behavior by the cytoskeleton, for both microtubule-based (90, 91) and actin-based systems (92–96). These studies have shown that varying the relative amounts and types of myosin motors and actin cross-linking proteins can generate active gels and fluids (26, 97–99). For a given filament concentration, contractility is only observed at sufficiently high motor density and at intermediate cross-linking density (Figure 4a). Inhibited at high and low concentrations of motors and cross-linkers, contractile stresses are able to propagate for intermediate concentrations of motors and cross-linkers (97). Recent work has shown that variations in rigidity and connectivity of actin networks by actin filament bundling and cross-linking proteins can systematically tune the mechanical response of actin networks from extensile to contractile (100) (Figure 4b). This is likely arising from the fluid–gel transition as well.

Figure 4.

Contractile force propagation by actomyosin networks. (a) Phase diagram showing the dependence of macroscopic contractility of F-actin networks on the concentration of cross-linker and myosin II motors. The network contracts for high-enough motor concentration and at intermediate concentration of cross-linkers. Low cross-linking does not yield space-spanning networks, whereas high cross-linking makes the network too rigid to contract. (b) Phase diagram showing the mechanisms for actomyosin contractility by varying network connectivity (cross-link concentration or filament length) or filament rigidity, at high-enough motor concentration. Rigid filaments with low cross-linking yield extensile fluid networks. Panel adapted from Reference 100. (c)(Left) Actomyosin network contraction in vitro for myosin activation regions of varying areas, with red vectors showing the velocity of contraction at the activation boundary. (Right) Contraction velocity of actomyosin scales with myosin activation area. Panel adapted from Reference 120. (d)(Left) Data from live cell experiments showing the dependence of contractile strain energy (measured by traction force microscopy) on the area of RhoA activation by optogenetics. (Right) Schematic of a continuum mechanical model for a contractile adherent cell. Panel adapted from Reference 124.

Contractile behaviors of actin networks for varying rigidity, connectivity,and activity have been reproduced well by agent-based simulation models (100, 101). These models treat the mechanics and dynamics of individual actin filaments and their stochastic interactions with active (motors) and passive (cross-linkers) binding partners. Over the past decade, researchers have developed various mesoscale agent-based models for cytoskeletal dynamics (102–106). While these computational models differ in their implementation, treatment of dynamics, and component features, they share essential similarities, including coarse-grained modeling of polymer mechanics, stochastic biochemistry, active transport, and diffusion. Agent-based frameworks are particularly suited to develop a bottom-up understanding of the collective mechanical behavior of cytoskeletal systems, which remains beyond the scope of current state-of-the-art macroscopic models of active matter (107, 108).

While networks constructed from actin filaments, cross-linkers, and myosin II motors have been found to be robustly contractile (26, 32, 97–100), different microscopic mechanisms can contribute to the macroscopic contractile response. These include contraction driven by relative filament sliding owing to structural asymmetries (100, 109, 110), contractility driven by actin filament turnover (111, 112), and contraction by motor-induced buckling of actin filaments (113, 114). Recently, it was determined that these different mechanisms likely dominate at different levels of filament rigidity (100). To predict whether a network will contract or expand, researchers have developed bottom-up theories of active networks starting from interactions between motors and pairs of filaments (115–119). While this treatment is analytically amenable in the limit of low density of filaments, bottom-up analytical theories for dense networks remain a challenging problem. In a recent study, Belmonte et al.(101) proposed a simple analytical framework to predict contractile behavior of active networks by considering the network-scale effect of pairs of connectors (motors or cross-links) bound to a single filament. The model predicts that the contraction rate scales with the amount of active motors in the network, in agreement with agent-based simulations (101, 120, 121) and continuum active gel models (120). Thus, for a given network size, contraction rate scales linearly with the density of active units. Recent studies, however, show that myosin activity within disordered actin networks is highly cooperative (120). For myosin density ρ below a critical value ρ_c, the network does not contract, whereas for ρ > ρ_c, the contraction rate saturates to a higher value. A critical density threshold for actomyosin contraction suggests a transition in the percolation of actomyosin forces. In the same study, Linsmeier et al. developed a novel in vitro assay to control myosin activity spatiotemporally using light (120; see also 122). By altering the area of myosin activation, they found that actomyosin contraction speed scales with the area of myosin activation (Figure 4c), irrespective of F-actin network organization or rigidity. Thus, disordered actomyosin contracts telescopically with the total size of active units, akin to telescopic contraction in highly ordered sarcomeres or in in vitro apolar bundles that contract at a rate proportional to their lengths (23).

These findings suggest that telescopic contractility may be a generic property of active bundles or networks, and thus it may be predictive of the total contractile force produced by a cell based on its geometric size. Indeed, single cell studies have shown that the contractile work produced by an adherent cell scales with its spread area (123). In a recent study Oakes et al. (124) directly tested telescopic contractility in live cells using optogenetic control of RhoA, the master regulator of contractility. Through temporal activation of RhoA within varying areas, the authors found that the contractile energy of an adherent cell is proportional to the area of the activation region (Figure 4d). This telescopic contractile behavior is well captured by a mechanical model of the cell consisting of contractile active elements (σ_m) in parallel to viscous elements (η) in series with elastic springs (124) (Figure 4d). This model predicted that (in the long time limit) the speed of contraction υ would scale with the area of activation A, υ ~ (σ_m/η)A. Interestingly, the cells returned to the same baseline contractile energy after removal of RhoA activation, consistent with previous reports of tensional homeostasis in cells (125, 126). This suggests that cells actively regulate RhoA and its downstream effectors to maintain a homeostatic level of contractility. Thus, understanding the physics of contractility in cells necessitates a systems-level approach.

ACTOMYOSIN AS A FEEDBACK CONTROL SYSTEM

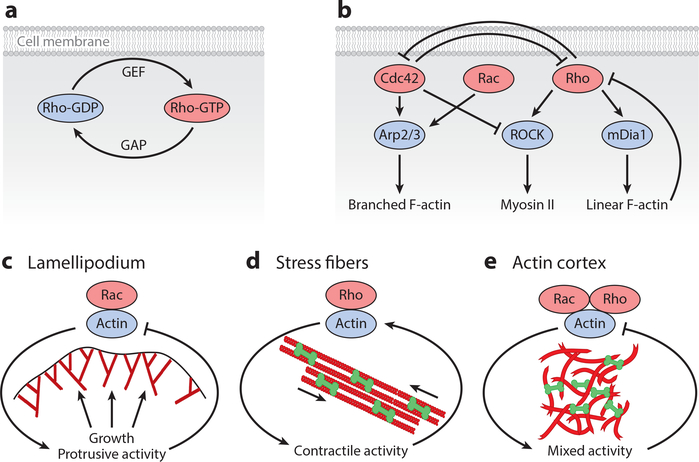
The mechanical activity of F-actin networks during diverse physiological processes is controlled by the small GTPases of the Rho family, most prominently by Rho, Rac, and Cdc42. Cross talks and mutual feedbacks between these proteins lead to the very rich dynamic behavior of the actin cytoskeleton (127). The basic biochemistry of Rho-GTPases is illustrated in Figure 5a. Rho-family proteins act as molecular switches that cycle between an active GTP-bound state on the membrane and an inactive GDP-bound state that is also bound to the membrane or relocalizes to the cytosol (128). The conversion of the inactive GDP-bound state into the active GTP-bound state is promoted by GEFs (guanine nucleotide exchange factors), whereas GTP-to-GDP conversion is driven by GAPs (GTPase-activating proteins). The active forms of Rho-GTPases control the activity of numerous cytoskeletal proteins that are essential for F-actin assembly, disassembly, and contractility. The Rho-GTPases can be considered to be the master regulators of the actin cytoskeleton in cells, which integrate diverse information provided by membrane receptors but also by hundreds of intracellular GEFs and GAPs with different localizations. Not surprisingly, this essential layer of regulation is also powered by energy consumption; in contrast to the cases of actin and myosin II discussed above, here it is GTP rather than ATP that provides the energy used, but the basic physical principle is the same: namely, that energy consumption allows for conformational switches and out-of-equilibrium processes that are not possible in passive systems.

Figure 5.

Feedback control systems in the actin cytoskeleton. (a) Rho-GTPases are localized to the cell membrane and cycle between an active GTP-bound state and an inactive GDP-bound state. The switching rates are determined by a large range of regulators (GEFs for activation and GAPs for inactivation). (b) A simplified diagram of the cross talks and feedback loops in the actin cytoskeleton controlled by the small GTPases of the Rho family. (c) Negative feedback control of protrusive activity in the lamellipodium controlled by the Rac pathway. (d) Positive feedback control of stress fiber assembly and contraction, downstream of the Rho pathway. (e) The actin cortex exhibits a mixture of contractile and protrusive activities downstream of the Rho and Rac pathways. Abbreviations: GAP, GTPase-activating protein; GDP, guanosine diphosphate; GEF, guanine nucleotide exchange factor; GTP, guanosine triphosphate.

Rho-GTP induces formation of contractile actomyosin structures by activating two distinct pathways that are ROCK and mDia1 dependent (Figure 5b) (129). The mDia1 pathway activates formins that nucleate linear F-actin arrays, whereas the ROCK pathway induces the activation of myosin II that associates with linear F-actin to generate contractile forces. Myosin-generated tension can in turn promote F-actin depolymerization (130). Recent studies demonstrate that formin-driven F-actin elongation is force sensitive (131–133), indicating a possible feedback between cell contractility and filament generation. Furthermore, there is recent evidence that F-actin assembly acts as a negative feedback to suppress Rho activity by activating GAPs (134, 135). This negative feedback loop can lead to rich dynamic behaviors such as waves, excitability, and bistability, as discussed in the next section, and demonstrates the close coupling of regulation and physical structure in the actin system.

Formation of branched F-actin structures via the nucleator Arp2/3 is stimulated by the active forms of G-proteins Rac and Cdc42 (Figure 5b) (136). In a polarized migrating cell, there is spatial segregation between Rho and Rac/Cdc42 activity levels (137). While active Rac and Cdc42 concentrations are highest at the front of migrating cells (138), active Rho is found at the rear end of a motile cell (139). These data indicate mutual antagonistic interactions (128) such that Cdc42/Rac activity downregulates Rho and vice versa. Besides upstream feedback between Rho and Rac pathways, there is also downstream feedback between branched and linear F-actin activity due to inter-network competition for the same pool of monomeric actin (140). Thus, the presence of multilevel feedback loops makes the actin cytoskeleton a highly complex mechanical system, challenging existing theoretical approaches (107).

The simplified biochemical feedback system in Figure 5b can be further broken down into three essential mechanochemical feedback modules in the actin cytoskeleton (Figure 5c–e). During cell crawling, active Rac induces Arp2/3-dependent polymerization of branched F-actin in the lamellipodium, which pushes against the cell membrane (Figure 5c). Protrusive force generated by F-actin can lead to an increase in membrane tension by unfolding membrane wrinkles and effecting exocytosis of vesicles (141). Increased tension can then provide a resistive force to prevent further cell spreading. This negative feedback loop between actin polymerization and membrane tension can trigger excitable waves of protrusion and retraction and seems to be at the heart of the oscillations in protrusion speed often observed during cell spreading and migration (142–144). By contrast, the contractile activity of actomyosin stress fibers is induced by active Rho through the ROCK pathway (Figure 5d) (145). Myosin-induced contractile forces are then transmitted to focal contacts, which can turn the mechanical signal into further Rho activation. While the precise molecular mechanism is unknown, it has been proposed that mechanical forces at focal adhesion can initiate conversion of Rho-GDP to Rho-GTP, leading to ROCK activation (146). This positive feedback between Rho and contractility at focal adhesion can lead to a bistable response, as shown theoretically (147, 148). Branched and linear F-actin structures coexist in the actin cortex (149), leading to a mixture of contractile and protrusive activities (Figure 5e). These two structures compete for the same pool of monomeric actin, and their mutual stability is controlled by the feedback from myosin-generated (or polymerization-generated) forces (150). As a result, branched and linear actin structures could spatially segregate, as during cell polarization; they can remain colocalized in space; or one structure can outcompete the other. Thus, the mixture of mechanical activity and mutual feedback systems makes the actin cortex a rich dynamical system, from which new out-of-equilibrium physics can emerge.

ACTIN CYTOSKELETON AS EXCITABLE MEDIA

Mechanochemical feedback modules in the F-actin cytoskeleton (Figure 5c–e), regulated by the active forms of Rho and Rac proteins, can lead to pattern formation or the development of propagating waves that can play a central role in morphogenesis (89, 151–153). The control structure is similar to action potentials in nerve cells (154), cardiac cells (155), or intracellular calcium waves (156), where a fast positive feedback (activator) leads to a rapid upswing of activity, followed by a delayed negative feedback (inhibitor) that brings down the level of activity (157, 158) (Figure 6a). Work in recent years has identified activator-inhibitor feedbacks between F-actin and RhoA signaling (Figure 6d) that drive cortical excitability to direct cleavage furrow positioning in mitotic and meiotic oocytes (134), trigger dynamic instabilities and pulsed contractions in the actomyosin cortex (135, 159), and regulate cross talk between actomyosin contractions and extracellular matrix elasticity (160). Other studies have identified similar feedback modules between Rho-GTPases and F-actin dynamics, elucidating their roles in excitable protrusion dynamics in migrating cells (142, 161–163) or in waves of contraction in oocytes (164, 165).

Figure 6.

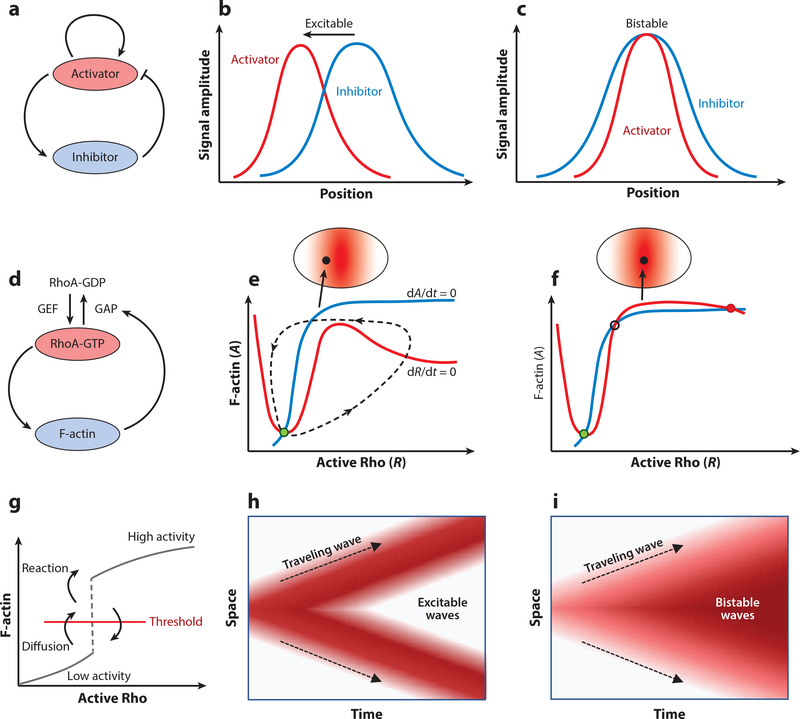
Excitability, bistability, and traveling waves in the actin cortex. (a) Schematic of a typical activator-inhibitor feedback system. (b,c) Spatial profiles of activator (red) and inhibitor (blue) concentrations in a traveling excitable wave (b) and in a static structure (c). Panel adapted from Reference 158. (d) RhoA-actin feedback system in the cortex as an activator-inhibitor system. (e,f) Excitability in the vicinity of the cytokinetic furrow (e) and stable coexistence of high RhoA activity and F-actin concentration in the middle of the furrow (f). GEF concentration is shown in red shading. Phase trajectories are shown for F-actin nullcline (blue curve), Rho nullcline (red curve), an excitable trajectory (dashed curve), and resting steady state of the cortex (green solid circle). Panels e and f adapted from Reference 158. (g) Phase plot in RhoA-actin system illustrating that diffusion can move the F-actin concentration across the threshold for transition to the high-activity state. (h,i) Spatial coupling in the activator-inhibitor system can give rise to excitable (h)orbistable(i) waves. Red shading represents activity. Abbreviations: GAP, GTPase-activating protein; GDP, guanosine diphosphate; GEF, guanine nucleotide exchange factor; GTP, guanosine triphosphate.

To understand the physics underlying pattern formation in excitable media, which has a long tradition in mathematical modeling (166), we focus on a prototypic activator-inhibitor feedback loop (Figure 6d) (158), where an autocatalytic feedback drives the production of activator proteins (RhoA-GTP), leading to fast production of inhibitors (F-actin). A slow negative feedback from the inhibitor limits the spread of the activator profile, bringing down the activator level and thereby triggering the next cycle of autocatalytic reproduction of the activator. This mechanism leads to excitable wave propagation, where the activator spatial profile always precedes the inhibitor (Figure 6b). This pattern of excitable wave propagation has been experimentally observed in the actomyosin cortex of early Caenorhabditis elegans embryos (135, 159) and in mitotic oocytes (134), where the spatial profile of RhoA-GTP peaks ahead of F-actin. By contrast, if the diffusivity of the inhibitor is higher than the diffusivity of the activator, the inhibitor is removed at a fast rate by diffusive transport, leading to spatially colocalized static patterns of activator and inhibitor (Figure 6c). Such immobile pattern formation is indeed observed in the cytokinetic zone, where RhoA-GTP and F-actin ring colocalize in space (134, 158).

From the perspective of dynamical systems, excitable and bistable behaviors of the Rho-actin feedback module can be illustrated using phase trajectories in the Rho(R)–actin(A) plane (Figure 6e,f) (158). Dynamics of Rho and actin concentrations can be described using a simplified set of equations (134, 135),

$$\begin{gathered} dR/dt=S+k_R{R}^2/(R^2+R_0^2)-gR(A+A_0), \\ dA/dt=k_a{R}^2/(R^2+R_1^2)-k_{d}A, \end{gathered}$$

where S is the basal rate of Rho activation; k_R is the rate of actocatalytic production of Rho (controlled by GEF activity); A₀, R₁, and R₀ are constants; g is the strength of negative feedback coupling; and k_a and k_d are the rates of F-actin assembly and disassembly, respectively. On the R—A state space, the nullclines dR/dt = 0 (red curve) and dA/dt = 0 (blue curve) define the points where they A and R do not change with time. The steady state of the dynamical system (fixed point) is given by the point of intersection of the R and A nullclines (green dot), which can be controlled by the threshold of perturbation, S. For a smaller value of S, the system responds to the perturbation (Figure 6e) by performing a burst of activity, in which first the activator R reaches a peak in activity. This is followed by a peak in activity of the inhibitory A, before eventually returning back to the steady state. Such an excitable mode of dynamics can be observed in dividing cells close to the cytokinetic ring, where the GEF concentration is close to its maximum (Figure 6e, inset). For an even higher value of S, the R and A nullclines intersect at three points (Figure 6f), two of which are stable steady states (solid circles) and one is an unstable saddle point (open circle). This implies a bistable system, such that any significant perturbation will push the system into h igh-activity steady state. In this regime Rho and actin profiles stably coexist, as realized in the cytokinetic zone where the GEF concentration is highest (Figure 6f, inset).

The ordinary differential equations for the activator-inhibitor model describe local reactions that exhibit bistability, excitability, or relaxation oscillations depending on the parameters of the model. However, mechanical signal transduction in cells propagates through space-time and is spatially inhomogeneous. Spatial patterns can be generated by coupling the local reactions to diffusion of activators and inhibitors that can lead to propagation of trigger waves (157, 167). For instance, in the case of the bistable system (Figure 6f), diffusion of activators can push the system across a threshold (Figure 6g) such that the reactions can stabilize the system in the high-activity state. In the absence of reactions, the system would eventually return below the threshold to the low-activity state. This mechanism of diffusion-mediated threshold crossing occurs in sequence throughout space, resulting in the generation of trigger waves of bistable switching (Figure 6i). For the excitable case (Figure 6e), coupling of reaction with diffusion can lead to propagating pulsatory waves of Rho and F-actin (Figure 6h), as observed in the actomyosin cortex of the C. elegans embryo (135, 168).

DISCUSSION AND OUTLOOK

Advances on different fronts have led to rapid progress in our understanding of active adaptive actin architectures: cell experiments involving new tools and quantification, reconstitution experiments with minimal sets of proteins,and mathematical models for the kinetics and spatial structure of actin assemblies. Together, these studies have revealed how active stresses in the biopolymer networks and bundles, coupled with mechanochemical feedbacks, can be harnessed to construct spatiotemporally structured responses that are not possible in passive soft matter systems. However, biological cells and their proteins have evolved for billions of years and they might use mechanisms that we have not been able to reveal yet. The recent body of work reviewed here, however, clearly shows that energy consumption, modularity, and feedback are essential elements of how cells achieve these superior functions, and that this leads to a very rich variety of dynamical processes. A current challenge is to understand how actin-based systems trade energy consumption and dissipation to maintain their adaptive functionalities. Recent work has shown that the production of dissipation in actin networks is highly nonmonotonic with the accumulation of active stresses (169), suggesting a trade-off between energy and entropy in maintaining materials stability. Future work is needed to understand how the actin cytoskeleton is able to take varied environmental inputs and then make decisions on how these should impact local stiffness and forces to control cell physiology. Another very rewarding future research direction might be the interplay between active processes in the cytoskeleton and in the plasma membrane, which also has been shown to break the fluctuation-dissipation theorem at low frequencies (170, 171). Capabilities in how to structure such autonomous materials will enable new classes of synthetic cell-like objects. This research direction has strong similarities with the field of metamaterials (172, 173), that is, materials with unusual properties emerging on larger scales from molecular features engineered at the nanoscale. By understanding the forward engineering process, in the future we might be able to reverse engineer the design of desired macroscopic properties from the bottom up (174, 175).