Abstract
Estimates of airborne pollen concentrations at the urban scale would be useful for epidemiologists, land managers, and allergy sufferers. Mechanistic models could be well suited for this task, but their development will require data on pollen production across cities, including estimates of pollen production by individual trees. In this study, we developed predictive models for pollen production as a function of trunk size, canopy area, and height, which are commonly recorded in tree surveys or readily extracted from remote sensing data. Pollen production was estimated by measuring the number of flowers per tree, the number of anthers per flower, and the number of pollen grains per anther. Variability at each morphological scale was assessed using bootstrapping. Pollen production was estimated for the following species: Acer negundo, Acer platanoides, Acer rubrum, Acer saccharinum, Betula papyrifera, Gleditsia triacanthos, Juglans nigra, Morus alba, Platanus x acerfolia, Populus deltoides, Quercus palustris, Quercus rubra, and Ulmus americana. Basal area predicted pollen production with a mean R2 of 0.72 (range: 0.41 – 0.99), whereas canopy area predicted pollen production with a mean R2 of 0.76 (range: 0.50 – 0.99). These equations are applied to two tree datasets to estimate total municipal pollen production and the spatial distribution of street tree pollen production for the focal species. We present some of the first individual-tree based estimates of pollen production at the municipal scale; the observed spatial heterogeneity in pollen production is substantial and can feasibly be included in mechanistic models of airborne pollen at fine spatial scales.
Keywords: allergenic pollen, allergic rhinitis, pollen exposure, street trees
1. INTRODUCTION
Exposure to allergenic pollen can trigger severe allergic reactions, ranging from allergic rhinitis and asthma attacks to allergic conjunctivitis (Bousquet et al. 2008; La Rosa et al. 2013; Linneberg et al. 2002; Salo et al. 2011). For sensitized individuals, exposure can reduce productivity and quality of life (Blaiss et al. 2018; Meltzer 2016; Meltzer et al. 2009), resulting in large economic consequences (Cardell et al. 2016; Nathan 2007).
Pollen monitoring networks, such as the National Allergy Bureau in the United States and the European Aeroallergen Network are the primary source of airborne pollen measurements used by the public and by epidemiologists. However, these networks are not designed to capture urban scale variation in pollen concentrations. Because most epidemiological analyses rely on data from a single pollen monitoring station per city or region, they do not account for spatial variation in pollen concentrations, which routinely span multiple orders of magnitude (Katz and Batterman 2020). This can lead to large measurement errors in the estimates of allergenic pollen exposure used in epidemiological analyses (Katz et al. 2019). Better estimates of airborne pollen concentrations at the urban scale could both improve exposure estimates for epidemiological analyses and lead to spatially resolved forecasts that could potentially help sensitized individuals reduce their exposure (Sofiev and Bergmann 2012).
Airborne pollen concentrations could be estimated at intra-urban scales with mechanistic models. Such models could incorporate pollen production, plant location, the timing of pollen release, and atmospheric dispersion of pollen. A limiting factor for this approach has been the lack of comprehensive maps of individual trees (Lovasi et al. 2013), but improvements in remote sensing data availability are easing that limitation for both trees (Wang et al. 2019; Zhen et al. 2016, Katz et al. 2020, manuscript in prep) and herbaceous plants such as common ragweed (Katz and Batterman 2019). Flowering phenology is also increasingly well quantified and predicted (Gerst et al. 2017; Katz et al. 2019; Taylor and White 2019), and atmospheric dispersion models have been developed for pollen at the relevant spatial scales (Klein et al. 2003; Ye et al. 2016). However, estimates of pollen production remain a key data gap, preventing the development of mechanistic models of airborne pollen (Sofiev and Bergmann 2012). Allometric equations could be applied to tree census datasets or to remote sensing derived maps of trees to estimate pollen production and its spatial distribution.
Pollen production of individual trees can be estimated as the product of the number of flowers per tree, anthers per flower, and pollen per anther (Damialis et al. 2011; Khanduri et al. 2015; Molina et al. 1996; Rojo et al. 2015). Pollen production can then be analyzed as a function of tree size (e.g., canopy area, crown height, or stem diameter) to create allometric equations (e.g., Damialis et al. 2011). However, we are only aware of a few studies that provide equations to estimate total tree pollen production as a function of tree size (i.e., crown area or volume): Corylus avellane, Cupressus sempervirens, Olea europaea, Platanus orientalis (Damialis et al. 2011), Quercus coccifera, Quercus ilex, Pinus heldreichii, Pinus nigra (Charalampopoulos et al. 2013), Olea europaea (Aguilera and Valenzuela 2012; Rojo et al. 2015), and four species of the genus Cupressus (Hidalgo et al. 1999). Such equations are available for one North American tree species, Juniperus ashei (Bunderson et al. 2012).
In this study, we create allometric equations of pollen production for 13 common North American tree species. The models incorporated counts of: flowers per tree, anthers per flower, and pollen grains per anther. The resulting estimates of pollen production at the individual tree level are analyzed as a function of tree canopy area, tree crown height, and stem diameter to produce predictive equations of pollen production. Bootstrap analysis is used to assess how variability at each stage affected the equation coefficient estimates. The allometric equations are then applied to two municipal tree census datasets to calculate the production and spatial distribution of pollen.
2. METHODS
2.1. SITE DESCRIPTION
We conducted our study in Ann Arbor, MI, USA, which has a humid continental climate, an average temperature of 9.3° C, ranging from an average of −4.6° C in January to 22.0° C in July, and an average annual precipitation of 966 mm (National Climate Data Center 2019). Urban tree composition in Ann Arbor is available through both a representative plot-based census and a street tree database. The plot-based survey used the i-Tree Eco sampling framework (www.itreetools.org) to survey 201 randomly located plots (each 405 m2) within Ann Arbor in 2012 (City of Ann Arbor 2013). Based on the 1,872 trees measured, Ann Arbor is estimated to have 1,451,000 trees that cover 32.8% of the city (City of Ann Arbor 2013). The species with the highest percent canopy cover in the city include Quercus rubra L. (8.3%), Acer saccharinum L. (6.7%), Juglans nigra L. (5.3%), Ulmus americana L. (5.2%), Malus spp. (4.9%), and Acer saccharum Marsh. (4.7%). In Ann Arbor’s publicly accessible database of 52,896 street trees (City of Ann Arbor 2019), the species with the highest basal area include: Acer saccharum, Acer platanoides L., Acer saccharinum, Gleditsia triacanthos L., Platanus x acerfolia (Aiton) Willd., and Juglans nigra.
2.2. TREE SELECTION
We conducted transects in Ann Arbor and selected trees of the focal species that were actively flowering, did not show signs of recent or extensive damage, accessible from public areas, and photographable (e.g., their branches did not mingle with those of a conspecific). Trees that spanned the size distribution of Ann Arbor street trees were intentionally selected when available; the size of selected trees are not necessarily representative.
After a tree was selected, we recorded the tree’s species, diameter at breast height (DBH; measured 1.37 m above ground), and coordinates. Data were collected using Collector for ArcGIS 17.0.3 (ESRI, Redlands, CA, USA). Tree coordinates were determined using both GPS and aerial imagery; built in smartphone GPS accuracy is not sufficiently accurate for these purposes (Zandbergen 2009). Species that were measured in both 2017 and 2018 included: Acer negundo L., Betula papyrifera Marsh., Morus alba L., Populus deltoides W. Bartram ex Marsh., Quercus palustris Munchh., and Quercus rubra; Acer platanoides was only measured in 2017, and species that were only measured in 2018 were: Acer saccharinum, Gleditsia triacanthos, Juglans nigra, Platanus x acerfolia, and Ulmus americana. For the selected trees, pollen production was estimated by measuring and multiplying reproductive ratios (e.g., as shown for Q. rubra in Fig. 1, the following ratios were multiplied: pollen per anther, anthers per flower, flowers per catkin, catkins per catkin cluster, and catkin clusters per tree).
Fig. 1.
A) Canopy of a focal Quercus rubra tree (red circle); B) Hemispherical canopy photo; C) zoomed in section of canopy photo showing flower clusters, D) A flower cluster with multiple catkins; E) individual catkin with multiple flowers, each containing anthers; F) Pollen grains.
2.3. FLOWERS PER TREE
The number of inflorescences per tree is generally estimated by assuming that the tree has a fixed geometric shape (e.g., cube, cylinder, or cone) with all pollen production on the periphery; samples of known area are taken from the shape exterior and multiplied by approximate surface area to estimate the number of flowers or branches for the whole tree (Damialis et al. 2011; Gómez-Casero et al. 2004; Molina et al. 1996; Rojo et al. 2015). However, shapes of many urban trees are complex and have poorly distinguished edges. Assuming a particular shape may affect estimates of tissue biomass within the canopy (Karlik and Winer 1999), as does assuming that all flowers occur on the periphery of the crown.
Instead, we use hemispherical photos to estimate the number of flowers on the species that had large and visibly distinct flowers (Populus deltoides) or visibly distinct flower clusters (Acer negundo, Acer platanoides, Acer rubrum, Acer saccharinum, Betula papyrifera, Juglans nigra, Quercus palustris, and Quercus rubra). Photos of each tree were taken after flowers were visible but before leaf out, using a Nikon D750 (Nikon, Tokyo, Japan) with a fisheye lens. Photo angles were chosen to best include the entire tree canopy and reduce overlap between flower bearing branches. The number of flower clusters per tree were estimated by counting the number of flower clusters in a subsection of each photo. Briefly, we selected the best photo of each tree, checked that flower clusters at the top of the tree were visible in the photo, manually delineated the edge of the tree canopy, divided the photo into a grid of 100 photo tiles, and counted all flowers/flower clusters in 10 randomly selected tiles (considering only tiles mostly within the delineated canopy). A grid was superimposed on tiles to aid counting, and the percent of each selected tile that was obscured (e.g., by the tree trunk) was estimated visually and used to adjust the number of flower clusters in that tile. The average number of flower clusters per tile was multiplied by the number of photo tiles within the delineated canopy area to calculate total flower clusters per tree.
For tree species where the flower clusters were too small or indistinct from foliage to easily count in photos (i.e., Ulmus americana, Gleditsia triacanthos, Morus alba, Platanus x acerfolia,), we used manual methods to estimate the number of flower clusters or flowers per tree (Khanduri et al. 2015; Molina et al. 1996). For these species, we selected a branch and counted all flower clusters on that branch. The total number of branches on the entire tree were then counted and the number of flowers was estimated by multiplying those two numbers. This was replicated three times per tree to quantify intra-tree variability.
To estimate the number of flowers per flower cluster, anthers per flower, and pollen per anther, we collected flowers from at least ten trees per species (sample size was slightly higher for Quercus rubra and Acer platanoides). For each tree, we collected 4 twigs from a height of 3 m (± 1 m) and 4 twigs from a height of 6 m (± 1 m) whenever possible (in cases there were not twigs with flowers at both heights). These twigs were collected from each cardinal direction when available, and the twigs were selected haphazardly. Twigs were clipped using a tree trimming pole and were placed in a sealed plastic bag and refrigerated until processed.
2.4. ANTHERS PER FLOWER
The organization of reproductive structures varies considerably between species. For example, some trees have a small number of large flowers (e.g., Platanus x acerfolia) whereas others have many catkins spread across the tree, sometimes occurring in discrete clusters (e.g., Quercus spp.) or spread more evenly across twigs (e.g., Morus alba). Flower processing methods therefore varied between species, but generally we counted the number of inflorescences per visually distinct flower cluster, the number of flowers per inflorescence, and the number of anthers per flower. Most counts were obtained manually, but for some species other approaches were used (e.g., to calculate total anthers per flower for Platanus x acerfolia, we weighed a known number of anthers and then weighed all of the anthers on a flower). The methods for each species are detailed in SI 1.
2.4. POLLEN GRAINS PER ANTHER
A subsample of 5 anthers were cut from flowers using forceps and a dissecting microscope. These anthers were then rinsed in deionized water and placed in 2 mL centrifuge tubes with 1.00 mL of 70% ethanol; one vial was prepared for each sampling height when possible. Several methods have been used to remove pollen from undehisced anthers, including mechanical, chemical and drying. Of these methods, mechanical methods tend to work best for extracting pollen from anemophilous tree anthers (Xiao et al. 2016). We used a glass stir rod to mechanically open the anthers and release pollen. Vials were shaken to homogenize the pollen solution immediately before subsamples were taken. An improved Neubauer hemocytometer was used to count the number of pollen grains in a volume of 0.0009 mL at a magnification of 100 × using an AmScope Plan Infinity microscope (AmScope, Irvine, CA, USA). Two replicates were counted for each vial, and two vials were collected per tree (one for each height).
2.5. TREE CANOPY AREA AND HEIGHT
For each tree, we collected information on both canopy area and median tree height using remote sensing data. To do so, we manually delineated the crown of each focal tree using ArcGIS 7.0 (ESRI, Redland, CA, USA), commercial aerial imagery taken concurrently with our field sampling (Nearmap, Bangaroo, Australia), and a LiDAR normalized digital surface model. LiDAR point cloud data was collected in April 2017 at quality level 2 (RMSE = 6.6 cm) and provided by the Southeast Michigan Council of Governments. A pit-free normalized digital surface model was created from the point cloud data using a triangulated irregular network approach (Khosravipour et al. 2014) that included buffering individual points and Gaussian smoothing, implemented within the R package ‘lidR’ (Roussel and Auty 2017). Median height was extracted for each tree polygon using the R packages ‘sf’ (Pebesma 2018) and ‘raster’ (Hijams and van Etten 2019).
2.7. ANALYSIS
Total pollen production for each focal species was calculated as the product of each reproductive ratio (e.g., flower clusters per tree, flowers per flower cluster, anthers per flower, and pollen per anther). For pollen per anther all measurements were pooled at the species level. For other reproductive ratios, measurements between trees were not pooled in order to account for correlations between reproductive ratios and tree size. Missing reproductive ratio data for particular trees were imputed by using data for a randomly selected individual in each iteration; this approach is conservative because it encompasses the overall variability of the population. Sample sizes for each reproductive ratio (e.g., pollen per anther) are provided in SI 2.
Total pollen production per tree was estimated as a function of tree canopy area and tree diameter. Variability in the measurements for each reproductive ratio affect pollen production estimates for individual trees, which could affect estimates for the relationship between tree size and pollen production. To assess how variability in measurements within individuals affected coefficient estimates for regression slope and intercept, we used the R package ‘boot’ (Canty and Ripley 2019) to create the bootstrap distribution of pollen production for each tree. 1,000 iterations were created, each sampled with replacement from the relevant reproductive ratios and linear models were created for each bootstrap iteration using the lm function in R. While allometric equations for biomass are often created using a different equation form (i.e., M = aDb, where M = tree biomass, D = diameter at breast height, and a and b are estimated empirically; Ter-Mikaelian and Korzukhin 1997) the approach used here allowed for easy reporting of and comparison between results for canopy area, trunk size, and canopy height. Akaike Information Criteria (Akaike 1974) was used to test whether the relationship between pollen production and the independent variable was better described by a linear, quadratic, or exponential fit. These functions were tested because they are simple, have few parameters, and fit the data well. In cases where the best fit was exponential, pollen production was log-transformed. Variability in the coefficients for slope and intercept were calculated by taking the standard deviation among the linear models of each iterations. Because tree canopy area and height are both likely to be extracted from remote sensing data, we also explored models that included both variables; due to the small sample sizes they should be interpreted with caution. To check for correlations between tree size and pollen per anther (which was pooled across individuals), we explored the data and calculated Pearson’s r.
In the case study, we used the equations developed here to calculate pollen production for trees in Ann Arbor, Michigan. We combined the two tree datasets available (a representative plot-based dataset and a street tree dataset; both are described above) with the species-specific equations developed for pollen production as a function of tree basal area (calculated from stem diameter). For the plot-based sample, we calculated total pollen production across the city by multiplying average pollen per km2 in the plots by the city area (72.08 km2). For the street tree data, we calculated total pollen production by summing pollen production of each individual street tree. We also calculated average pollen per m2 produced by street trees by creating a raster for the city of Ann Arbor, summing pollen production within each raster cell, and dividing by the area of each cell. All analyses were conducted in R 3.5 (R Core Team 2018) and data were visualized using ggplot2 (Wickham 2009). Additional maps were created in ArcGIS 10.7 (ESRI, Redlands, CA, USA).
3. RESULTS
3.1. TREE CANOPY
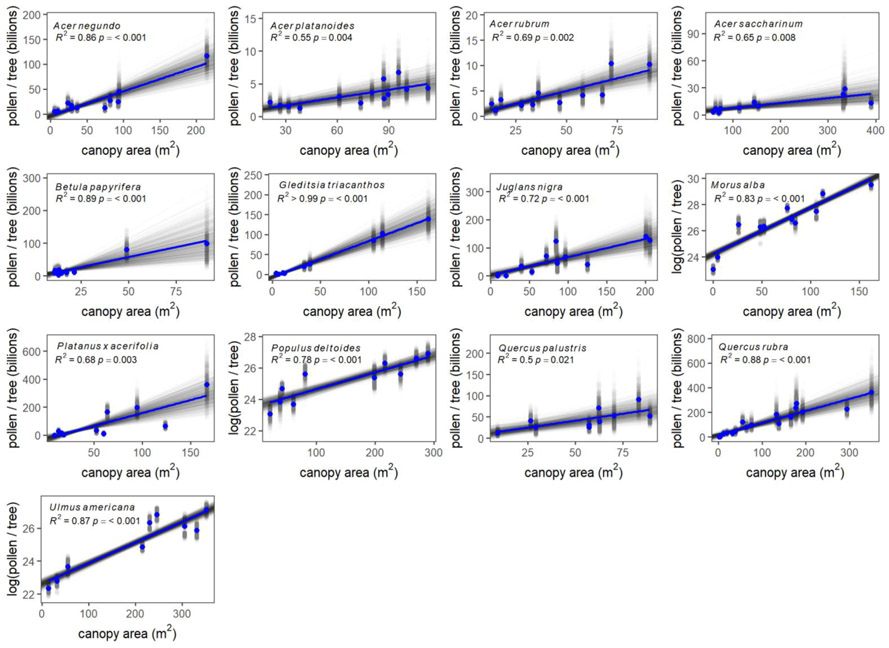
Flower reproductive ratios are provided in Table 1 and variability in pollen per anther is further reported in SI 3. Tree canopy area was an effective predictor of pollen production; across species the R2 averaged 0.79 (Table 2; Fig. 2). Tree canopy area best predicted pollen production for Gleditsia tricanthos (R2 > 0.99), Betula papyrifera (R2 = 0.89), and Quercus rubra (R2 = 0.88) and the species that were least well predicted were Quercus palustris (R2 = 0.50), Acer platanoides (R2 = 0.55), and Acer saccharinum (R2 = 0.65). While the relationship between pollen production and canopy area was best fit by a linear regression for most species, logarithmic relationships provided better fits for Morus alba, Populus deltoides, and Ulmus americana. The estimated standard deviation of the slope which includes variability within each reproductive component was generally small (averaging 20% of the slope).
Table 1:
Flower measurement types and results for each focal species.
| Species | Pollen per anther: mean (SD) |
Reproductive measurement type 1: mean (SD) |
Reproductive measurement type 2: mean (SD) |
Reproductive measurement type 3: mean (SD) |
|---|---|---|---|---|
| Acer negundo | Pollen/anther: 9,932 (2,930) | Anthers/inflorescence: 48.4 (16.2) | Inflorescence/cluster: 8.1 (4.2) | - |
| Acer platanoides | Pollen/anther: 863 (516) | Anthers/flower: 8.0 (0.0) | Flowers/bud: 41.2 (19.0) | - |
| Acer rubrum | Pollen/anther: 1,569 (249) | Anthers/inflorescence 28.2 (6.9) | Inflorescences/cluster: 10.8 (4.6) | - |
| Acer saccharinum | Pollen/anther:1,546 (988) | Anthers/inflorescence 22.4 (4.9) | Inflorescences/cluster: 13.9 (11.2) | - |
| Betula papyrifera | Pollen/anther: 4,697 (1,454) | Anthers/catkin: 5,176.5 (1,936.1) | Catkins/cluster: 2.2 (0.9) | - |
|
Gleditsia triacanthos |
Pollen/anther: 1,924 (911) | Anthers/flower: 5.3 (0.5) | Flowers/catkin: 94.9 (24.1) | - |
| Juglans nigra | Pollen/anther: 2,801 (836) | Anthers/flower: 28.3 (3.7) | Flowers/catkin: 44.2 (7.3) | Catkins/cluster: 3.9 (2.2) |
| Morus alba | Pollen/anther: 52,130 (15,221) | Anthers/flower: 3.9 (0.1) | Flowers/catkin: 26.1 (5.3) | - |
| Platanus x acerfolia | Pollen/anther: 22,741 (8,824) | Anthers/flower: 421.4 (121.9) | - | - |
| Populus deltoides | Pollen/anther: 4,081 (1,173) | Anthers/flower: 4,282.9 (983.4) | - | - |
| Quercus palustris | Pollen/anther: 3,000 (1,846) | Anthers/flower: 4.9 (0.7) | Flowers/catkin: 31.0 (6.0) | Catkins/cluster:18.3 (3.8) |
| Quercus rubra | Pollen/anther: 4,474 (1,428) | Anthers/flower: 5.0 (0.7) | Flowers/catkin: 37.5 (3.9) | Catkins/cluster: 17.8 (4.4) |
| Ulmus americana | Pollen/anther: 3,293 (592) | Anthers/inflorescence: 7.2 (1.5) | Inflorescence/bud: 22.3 (7.1) | - |
Table 2:
Allometric equations for pollen production (; in billions) of each tree of each focal species as a function of tree basal area (B; in m2) or canopy area (A; in m2). Note that pollen production is log transformed for some species and that these equations do not account for sex ratios of diecious species. *The standard deviation of the quadratic term for Morus alba is 2011.79.
| Species | Basal area (B) | Canopy area (A) | ||||||
|---|---|---|---|---|---|---|---|---|
| Equation | Slope standard deviation |
Intercept standard deviation |
R2 | Equation | Slope standard deviation |
Intercept standard deviation |
R2 | |
| Acer negundo | = 253.71B + 0.38 | 47.75 | 3.26 | 0.75 | = 0.49A - 3.16 | 0.09 | 3.72 | 0.86 |
| Acer platanoides | = 25.59B + 1.22 | 7.00 | 0.46 | 0.41 | = 0.04A + 0.53 | 0.01 | 0.42 | 0.55 |
| Acer rubrum | = 62.32B + 1.27 | 13.50 | 0.44 | 0.72 | = 0.10A - 0.10 | 0.02 | 0.64 | 0.69 |
| Acer saccharinum | log() = 2.28B + 21.98 | 0.49 | 0.28 | 0.82 | = 0.05A + 2.59 | 0.02 | 2.33 | 0.65 |
| Betula papyrifera | = 561.16B + 5.03 | 228.86 | 4.42 | 0.94 | = 1.27A - 4.73 | 0.55 | 8.92 | 0.89 |
| Gleditsia tricanthos | = 659.91B - 3.25 | 103.36 | 1.97 | 0.99 | = 0.89A - 6.13 | 0.14 | 2.58 | >0.99 |
| Juglans nigra | = 239.08B + 11.47 | 64.85 | 8.22 | 0.72 | = 0.66A + 1.42 | 0.15 | 8.30 | 0.72 |
| Morus alba | = 6021.57B2 + 1366.09B + 254.06* | 1366.09 | 93.26 | 0.97 | log() = 0.04A + 24.24 | <0.01 | 0.15 | 0.83 |
| Platanus × acerifolia | = 1066.75B + 1.26 | 251.73 | 8.15 | 0.65 | = 1.87A – 26.43) | 0.48 | 16.48 | 0.68 |
| Populus deltoides | log() = 2.01B + 24.17 | 0.24 | 0.19 | 0.47 | log() = 0.01A + 23.57 | <0.01 | 0.21 | 0.78 |
| Quercus palustris | = 327.20B + 14.90 | 100.94 | 7.41 | 0.51 | = 0.65A + 8.30 | 0.19 | 6.88 | 0.50 |
| Quercus rubra | = 423.56B + 36.20 | 85.45 | 11.42 | 0.78 | = 0.97A + 17.02 | 0.16 | 9.54 | 0.88 |
| Ulmus americana | log() = 5.86B + 23.11 | 0.35 | 0.15 | 0.69 | log() = 0.01A + 22.62 | <0.01 | 0.16 | 0.87 |
Fig. 2.
Pollen grains per tree as a function of tree canopy area for each species. Estimates of pollen production for individual trees from each bootstrap iteration are provided in gray and the mean for each tree is provided in blue; this color scheme is also used for regressions. Note that axes scales vary between species. Parameter estimates and their standard deviations are provided in Table 2.
3.2. TRUNK SIZE
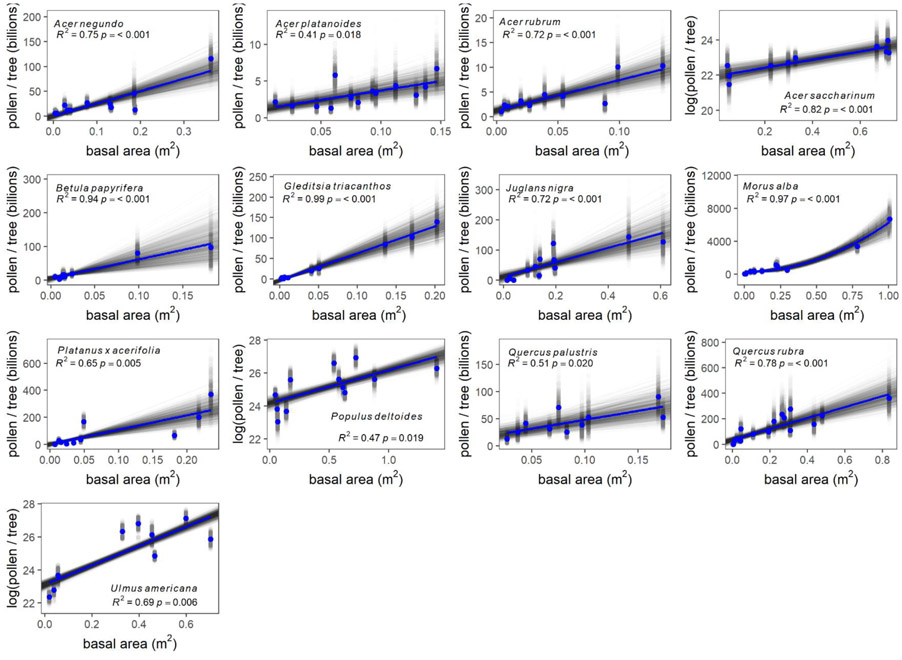
Basal area was a good predictor of pollen production; across species, the R2 averaged 0.72 (Table 2; Fig. 3). The species for which tree canopy best predicted pollen production were Gleditsia triacanthos (R2 = 0.99), Morus alba (R2 = 0.97), and Betula papyrifera (R2 = 0.94), and the species that were least well predicted were Acer platanoides (R2 = 0.41), Populus deltoides (R2 = 0.47), and Quercus palustris (R2 = 0.51). Again, the estimated standard deviation of the slope was generally small (averaging 22% of the slope). Species for which this relationship was best approximated by a logarithmic function were Acer saccharinum, Populus deltoides, while Ulmus americana and Morus alba was best fit by a quadratic function. Trees that were better predicted by canopy area than basal area were: Acer negundo, Acer platanoides, Gleditsia triacanthos, Juglans nigra, Platanus × acerifolia, Populus deltoides, Quercus palustris, Quercus rubra, and Ulmus americana.
Fig. 3.
Pollen grains per tree as a function of tree basal area for each species. Estimates of pollen production for individual trees from each bootstrap iteration are provided in gray and the mean for each tree is provided in blue; this color scheme is also used for regressions. Note that axes scales vary between species.
3.3. HEIGHT
Height was a relatively poor predictor of pollen production; across species the R2 averaged 0.53 (SI ). The only species for which height was a better predictor of pollen production than canopy area were Acer saccharinum (R2 = 0.86 vs R2 = 0.65) and Ulmus americana (R2 = 0.89 vs. R2 = 0.87). The exploratory models that included both crown height and crown area generally only had slightly better explanatory power than models that were just crown height; the average across species were R2 = 0.81 and 0.76, respectively.
3.4. CORRELATIONS BETWEEN REPRODUCTIVE RATIOS
Significant correlation between reproductive ratios and tree size was not uncommon (SI 5). For example, for Gleditsia triacanthos there were correlations between the number of anthers per flower and tree basal area (r = 0.70), tree canopy area (r = 0.69), and tree height (r = 0.68) and between the number of flowers per catkin and tree basal area (r = 0.76), tree canopy area (r = 0.75), and tree height (r = 0.78). Analysis conducted at the individual tree level account for these correlations.
3.5. CASE STUDY: APPLICATION OF POLLEN PRODUCTION
Tree abundance and size distributions varied considerably among the focal species in Ann Arbor, as did their estimated pollen production (Table 3). Based on the representative plot-based survey, the most prolific pollen producing focal tree species in Ann Arbor were Quercus rubra, Ulmus americana, and Morus alba. For a 20 cm DBH tree, the most prolific producers of pollen are expected to be Morus alba, Quercus rubra, and Platanus x acerifolia, while the least prolific are Acer platanoides, Acer rubrum, and Acer saccharinum (Table 3).
Table 3:
Estimated pollen production for trees surveyed in randomly selected and representative plots (the i-Tree Eco census, described in the methods section) and for a street tree database within Ann Arbor, Michigan. Descriptive statistics for tree size and number are provided for each dataset; for the i-Tree Eco total city-wide pollen estimates are calculated by scaling the area surveyed (0.08 km2) to the area of the city (72.08 km2). Total pollen estimates for three species are scaled according to their sex ratio (indicated by “*”; sex ratios are provided in SI 7).
| Taxon | Representative plot-based census | Street tree database | Pollen
production estimate for a 20 cm DBH tree (in billions) |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of trees |
Mean DBH (cm) |
Pollen/ mean tree (in billions) |
Total pollen production in Ann Arbor (in trillions) |
Number of trees |
Mean DBH (cm) |
Pollen/ mean tree (in billions) |
Total pollen produced by street trees in Ann Arbor (in trillions) |
||
| Acer negundo | 63 | 15.3 | 5.1 | 454 | 127 | 29.3 | 17.4 | 3.1 | 8.4 |
| Acer platanoides | 46 | 16.1 | 1.7 | 83 | 5,289 | 34.0 | 3.5 | 21.5 | 2.0 |
| Acer rubrum | 41 | 18.5 | 2.9 | 15* | 3,053 | 17.2 | 2.7 | 1.2* | 3.2 |
| Acer saccharinum | 19 | 52.1 | 5.7 | 136 | 1,818 | 58.0 | 6.4 | 14.7 | 3.4 |
| Betula papyrifera | 4 | 15.3 | 15.4 | 69 | 17 | 17.5 | 18.6 | 0.4 | 22.9 |
| Gleditsia triacanthos | 11 | 27.0 | 34.4 | 491 | 3,649 | 30.5 | 45.0 | 210.9 | 17.5 |
| Juglans nigra | 47 | 19.8 | 18.6 | 959 | 740 | 48.1 | 54.6 | 47.0 | 18.7 |
| Morus alba | 13 | 8.3 | 256.8 | 1,814* | 130 | 26.1 | 344.5 | 37.9* | 486.0 |
| Platanus × acerifolia | 4 | 32.2 | 87.8 | 453 | 1,886 | 33.0 | 92.0 | 247.3 | 34.8 |
| Populus deltoides | 5 | 27.1 | 35.6 | 88* | 206 | 50.0 | 47.0 | 6.6* | 33.8 |
| Quercus palustris | 3 | 35.3 | 46.9 | 180 | 177 | 31.2 | 39.9 | 8.7 | 25.3 |
| Quercus rubra | 78 | 28.9 | 63.9 | 5,929 | 1,264 | 22.8 | 53.4 | 87.6 | 49.4 |
| Ulmus americana | 161 | 11.6 | 11.6 | 1,824 | 776 | 24.6 | 14.4 | 41.2 | 13.1 |
| All focal species | 495 | 18.9 | - | 12,495 | 19,132 | 32.3 | - | 728.1 | - |
| All non-focal species | 1,377 | 15.0 | - | - | 38,406 | 20.9 | - | - | - |
| All trees | 1,872 | 16.0 | - | - | 52,896 | 25.0 | - | - | - |
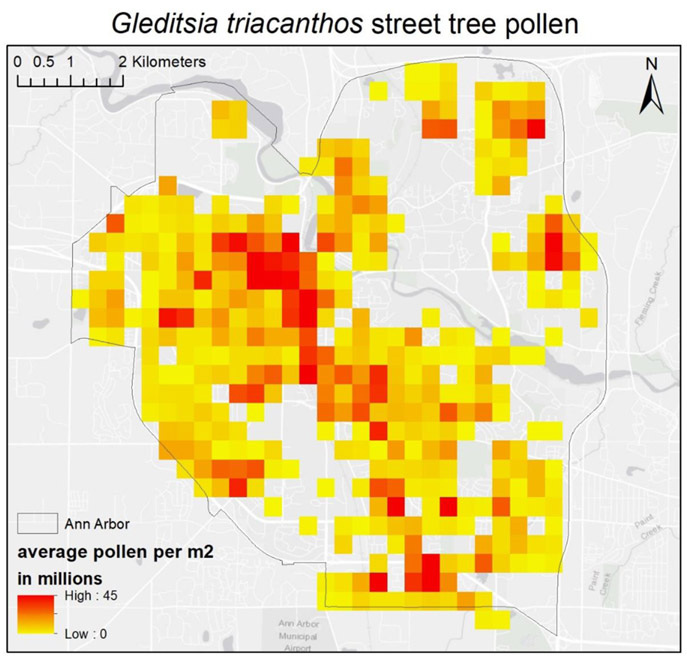
The fraction of pollen produced by street trees (compared to non-street trees) was highest for Gleditsia triacanthos (43%) and Platanus × acerifolia (55%) and moderate for Acer platanoides (26%). Thus, for species such as Gleditsia triacanthos, a pollen emission surface composed of only street trees (Fig. 4) may be of practical use (although the exact percentage should be interpreted with some caution because it is based on small sample sizes in the plot-based census). For other species, street trees will account for only a small fraction of total production (Table 3).
Fig. 4.
Estimated pollen production of Gleditsia triacanthos street trees in Ann Arbor based on tree stem diameter. Note that street trees only comprise a fraction of all trees and the total pollen production by G. triacanthos street trees (2.11 × 1014) are expected to only account for 43% of total pollen production within the city.
4. DISCUSSION
Relationships between tree size and pollen production were characterized for 13 tree species that are common in North American cities. These are some of the first allometric equations for tree pollen production in North America and also the first to quantify the relationship between pollen production and tree trunk diameter. Both trunk diameter and tree canopy area were effective predictors of per capita pollen production. These equations can be combined with other widely available datasets to estimate pollen production at large spatial scales, such as in the municipal case study presented here or with maps of individual trees derived from remote sensing. Such maps of pollen production could be useful for predicting spatial variation in airborne pollen concentrations and for understanding potential pollen exposures in areas without pollen monitoring stations. Since the allergenicity of pollen varies substantially between species, inter-species comparisons of pollen production are not proportional to their allergic importance.
4.1. Pollen production rates
Tree pollen production was well predicted by basal area and canopy area, although the form and fit of these relationships varied substantially among species. Others have found size-based relationships for pollen production as a function of tree canopy surface area (Charalampopoulos et al. 2013; Damialis et al. 2011; Hidalgo et al. 1999; Rojo et al. 2015). Similar allometric scaling relationships have also been developed between tree trunk diameter and stem volume, biomass, total carbon, root mass, and foliage (Forrester et al. 2017; Henry et al. 2013; Ter-Mikaelian and Korzukhin 1997; Zianis et al. 2005). However, reproduction can be more complicated, because the amount and timing of resource allocation to reproduction varies according to plant reproductive strategy (Thomas 1996; Weiner et al. 2009). There is also high natural variability in some reproductive ratios (e.g., inflorescences per cluster for Acer saccharinum) and small subsample size for pollen per anthers could also have introduced additional variability in this study. This may help to explain why the explanatory power of the relationships described here tend to be somewhat lower than those developed for other plant tissues or total biomass (e.g., Ter-Mikaelian and Korzukhin 1997). Our estimates of pollen per anther are roughly similar to the few available reports (Reddi and Reddi 1986); other reproductive ratios (e.g., flowers per catkins) were generally lacking for these study species. Pollen production rates for Gleditsia triacanthos, which is traditionally considered an entomophilous species (Schnabel and Hamrick 1995), was higher than that of many anemophilous species. However, gene flow patterns for this species are similar to wind pollinated plants (Owusu et al. 2016; Schnabel and Hamrick 1995) and we have collected airborne pollen samples where its concentration exceeded 300 grains m−3 (Katz and Batterman 2020) suggesting that some wind pollination may occur for this species.
4.2. Case study
The equations developed here were combined with both a street tree database and with representative vegetation plots to estimate pollen production at a municipal scale. These data types are widely available. Street tree databases generally have coordinates for individual trees, allowing street tree pollen production to be mapped. The overall fraction of pollen that is generated by street trees compared to non-street trees varies between species (Table 3), so for some species (e.g., Gleditsia triacanthos), these maps may include a substantial fraction of total pollen production, whereas for other species (e.g., Acer negundo), street tree derived maps only incorporate a very minor fraction of pollen production. Street trees are owned by cities, and are therefore the trees which governments have both control over and responsibility for. This ratio of street trees to all trees could also inform municipal foresters of whether any potential management actions (e.g., changing tree species selection criteria to include allergenic pollen production) are warranted.
Non-spatial data (e.g., plot-based sampling approaches used in i-Tree Eco or in the Urban FIA data) allow total pollen production to be estimated within a city, which may be useful to understand which local pollen concentrations are driven by local plants. For areas without a pollen monitoring station, city-wide estimates of pollen production would provide insight into which tree species are of potential allergenic concern.
4.3. Limitations
Allometric equations reflect the populations sampled during their development, so coefficient estimates can vary between areas due to differences in environmental conditions or tree genetics (Fortier et al. 2017; Hulshof et al. 2015; Ketterings et al. 2001; Oliveira et al. 2017). Although urban growing conditions and plant communities are relatively similar across large regions of the United States (Groffman et al. 2014; McKinney 2006), applying these equations to trees in other regions could introduce additional variability. Applying these equations to non-urban trees is not advised, as there are often substantial differences between urban and non-urban allometric equations for trees (McHale et al. 2009; McPherson et al. 2016; Yoon et al. 2013), likely due to differences in light availability, fertilization, water availability, air pollutant exposure, salt application, root compaction, physical damage, biotic interactions as well as many other variables.
Flower production can vary substantially between years for some species (Fernández-Martínez et al. 2012; Gómez-Casero et al. 2004; Ranta et al. 2008; Yasaka et al. 2009). In this study, data were collected during either one or two years; for the species that were measured in two years, the relationships between tree size and pollen production were fairly similar across years (SI 6). Even so, pollen production estimates may not be accurate when applied to other years; further data collection is necessary to quantify inter-annual variation in pollen production of urban trees. Ultimately, more data on pollen production need to be collected from different locations, habitats, species, and years.
Even if the total amount of pollen production varies between years, the spatial pattern of relative pollen production may be useful for certain applications (e.g., land use regression models). Where total pollen production is important (e.g., mechanistic models of airborne pollen), it may be possible to scale pollen production by relative annual airborne pollen concentrations. Inter-annual differences in pollen production can be predicted (Ishibashi and Sakai 2019; Tseng et al. 2020), so adjusting predicted annual pollen production to reflect annual patterns is feasible.
4.4. Inter-specific differences
While many of these relationships between area and pollen production were linear (i.e., similar pollen production per m2 of canopy for both small and large trees), some relationships were exponential (i.e. higher pollen production per m2 of canopy for larger trees). This could plausibly be caused by differences in the proportion of resources allocated to reproduction for larger trees (Thomas 1996; Weiner et al. 2009) or simply to higher resource availability. Interestingly, two of the three species that consistently had non-linear relationships (M. alba and P. deltoides) are both diecious and early successional (U. americana is not diecious but is early successional). An alternate explanation could be that these early successional trees were closer to their maximum potential sizes, whereas for other species, few individuals were measured near their maximum potential sizes.
Although our sample sizes were small, we did not observe strong phylogenetic signals. For example, within Acer, pollen per anther varied by an order of magnitude between Acer negundo and Acer platanoides and for a tree with a DBH of 20 cm, total pollen production was over four times higher for A. negundo than for A. platanoides. Reproductive ratios (i.e., pollen per anther, anthers per flower, and flowers per catkin) were more similar for the very closely related Q. palustris and Q. rubra, but for a tree with a DBH of 20 cm, estimated total pollen production was still quite different (25.3 billion vs. 49.4 billion respectively). Our findings suggest that pollen production should be calculated on a per-species basis and not extrapolated between even closely-related species. This conclusion is corroborated by observed differences in pollen production per anther (Reddi and Reddi 1986).
5. Conclusions
We provide the first estimates of pollen production as a function of tree size for these species and capture the shape of the relationship between tree size and pollen production for several taxa of potential concern. These pollen production surfaces could form the basis for mechanistic models of airborne pollen. While such models will require additional data, e.g., the timing of pollen release and the characterization of atmospheric dispersion, they offer the promise of a framework for assessing pollen exposures that is more flexible and robust than the use of data from a regional monitoring station.
Supplementary Material
Acknowledgements
This work was supported by the National Institute of Environmental Health Sciences through a NRSA postdoctoral fellowship (Grant Number F32 ES026477). It was also supported by the Michigan Institute for Clinical Health Research through the Postdoctoral Translational Scholars Program (Grant Number UL1 TR002240). S. Batterman also acknowledges support from grant P30ES017885 from the National Institute of Environmental Health Sciences, National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. We thank the Ann Arbor Department of Public Works for providing i-Tree Eco data. We also thank Victoria Bankowski and John Kost for their contributions to this project.
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
Disclosure statement
No potential conflict of interest was reported by the authors.
WORKS CITED
- Aguilera F, & Valenzuela LR (2012). Microclimatic-induced fluctuations in the flower and pollen production rate of olive trees (Olea europaea L.). Grana, 51(January), 228–239. doi: 10.1080/00173134.2012.659203 [DOI] [Google Scholar]
- Akaike H (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control 19(6), 716–723. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1100705 [Google Scholar]
- Blaiss MS, Hammerby E, Robinson S, Kennedy-Martin T, & Buchs S (2018). The burden of allergic rhinitis and allergic rhinoconjunctivitis on adolescents: A literature review. Annals of Allergy, Asthma and Immunology, 121(1), 43–52.e3. doi: 10.1016/j.anai.2018.03.028 [DOI] [PubMed] [Google Scholar]
- Bousquet J, Khaltaev N, Cruz AA, Denburg J, Fokkens WJ, Togias A, et al. (2008). Allergic Rhinitis and its Impact on Asthma (ARIA) 2008 update (in collaboration with the World Health Organization, GA2LEN and AllerGen). Allergy: European Journal of Allergy and Clinical Immunology, 63(SUPPL. 86), 8–160. doi: 10.1111/j.1398-9995.2007.01620.x [DOI] [PubMed] [Google Scholar]
- Bunderson LD, Wells H, & Levetin E (2012). Predicting and quantifying pollen production in Juniperus ashei forests. Phytologia, 94(December), 417–438. [Google Scholar]
- Canty A, & Ripley BD (2019). boot: Bootstrap R (S-Plus) Functions.
- Cardell LO, Olsson P, Andersson M, Welin KO, Svensson J, Tennvall GR, & Hellgren J (2016). TOTALL: High cost of allergic rhinitis - a national Swedish population-based questionnaire study. Primary Care Respiratory Medicine, 26(15082), 1–5. doi: 10.1038/npjpcrm.2015.82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charalampopoulos A, Damialis A, Tsiripidis I, Mavrommatis T, Halley JM, & Vokou D (2013). Pollen production and circulation patterns along an elevation gradient in Mt Olympos (Greece) National Park. Aerobiologia, 29(4), 455–172. doi: 10.1007/s10453-013-9296-0 [DOI] [Google Scholar]
- City of Ann Arbor. (2013). i-Tree Ecosystem Analysis: Ann Arbor. Ann Arbor, MI. doi: 10.15421/031606 [DOI] [Google Scholar]
- City of Ann Arbor. (2019). Ann Arbor street tree database. https://www.a2gov.org/services/data/Pages/default.aspx. Accessed 10 January 2019 [Google Scholar]
- Damialis A, Fotiou C, Halley JM, & Vokou D (2011). Effects of environmental factors on pollen production in anemophilous woody species. Trees - Structure and Function, 25(2), 253–264. doi: 10.1007/s00468-010-0502-1 [DOI] [Google Scholar]
- Fernández-Martínez M, Belmonte J, & Maria Espelta J (2012). Masting in oaks: Disentangling the effect of flowering phenology, airborne pollen load and drought. Acta Oecologica, 43, 51–59. doi: 10.1016/j.actao.2012.05.006 [DOI] [Google Scholar]
- Forrester DI, Tachauer IHH, Annighoefer P, Barbeito I, Pretzsch H, Ruiz-Peinado R, et al. (2017). Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. Forest Ecology and Management, 396, 160–175. doi: 10.1016/j.foreco.2017.04.011 [DOI] [Google Scholar]
- Fortier J, Truax B, Gagnon D, & Lambert F (2017). Allometric equations for estimating compartment biomass and stem volume in mature hybrid poplars: General or site-specific? Forests, 8(9), 1–23. doi: 10.3390/f8090309 [DOI] [Google Scholar]
- Gerst KL, Rossington NL, & Mazer SJ (2017). Phenological responsiveness to climate differs among four species of Quercus in North America. Journal of Ecology, 1610–1622. doi: 10.1111/1365-2745.12774 [DOI] [Google Scholar]
- Gómez-Casero MT, Hidalgo PJ, García-Mozo H, Domínguez E, & Galán C (2004). Pollen biology in four Mediterranean Quercus species. Grana. 43(March), 22–30. doi: 10.1080/00173130410018957 [DOI] [Google Scholar]
- Groffman PM, Cavender-Bares J, Bettez ND, Grove JM, Hall SJ, Heffernan JB, et al. (2014). Ecological homogenization of urban USA. Frontiers in Ecology and the Environment, 12(1), 74–81. doi: 10.1890/120374 [DOI] [Google Scholar]
- Henry M, Bombelli A, Trotta C, Alessandrini A, Birigazzi L, Sola G, et al. (2013). GlobAllomeTree: International platform for tree allometric equations to support volume, biomass and carbon assessment. IForest, 6(6), 1–5. doi: 10.3832/ifor0901-006 [DOI] [Google Scholar]
- Hidalgo PJ, Galán C, & Domínguez E (1999). Pollen production of the genus Cupressus. Grana, 38(5), 296–300. doi: 10.1080/001731300750044519 [DOI] [Google Scholar]
- Hijams RJ, & van Etten J (2019). raster: Geographic analysis and modeling with raster data, https://cran.r-project.org/web/packages/raster/index.html
- Hulshof CM, Swenson NG, & Weiser MD (2015). Tree height-diameter allometry across the United States. Ecology and Evolution, 5(6), 1193–1204. doi: 10.1002/ece3.1328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishibashi A, & Sakai K (2019). Dispersal of allergenic pollen from Cryptomeria japonica and Chamaecyparis obtusa: characteristic annual fluctuation patterns caused by intermittent phase synchronisations. Scientific Reports, 9(1), 1–9. doi: 10.1038/s41598-019-47870-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlik JF, & Winer AM (1999). Comparison of Calculated and Measured Leaf Masses of Urban Trees. Ecological Applications, 9(4), 1168–1176. [Google Scholar]
- Katz DSW, & Batterman SA (2019). Allergenic pollen production across a large city for common ragweed (Ambrosia artemisiifolia). Landscape and Urban Planning, 190(March), 103615. doi: 10.1016/j.landurbplan.2019.103615 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz DSW, Dzul A, Kendel A, & Batterman SA (2019). Effect of intra-urban temperature variation on tree flowering phenology, airborne pollen, and measurement error in epidemiological studies of allergenic pollen. Science of The Total Environment, 653, 1213–1222. doi: 10.1016/j.scitotenv.2018.11.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz DSW, Batterman SA. Urban-scale variation in pollen concentrations: a single station is insufficient to characterize daily exposure. Aerobiologia (2020). 10.1007/s10453-020-09641-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ketterings QM, Coe R, Van Noordwijk M, Ambagau’ Y, & Palm CA (2001). Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. Forest Ecology and Management, 146(1–3), 199–209. doi: 10.1016/S0378-1127(00)00460-6 [DOI] [Google Scholar]
- Khanduri VP, Kumar KS, & Sharma CM (2015). Role of pollen production in mating success in some tropical tree species. Re\’ista Brasileira de Botanica, 38(1), 107–112. doi: 10.1007/s40415-014-0114-x [DOI] [Google Scholar]
- Khosravipour A, Skidmore AK, Isenburg M, Wang T, & Hussin YA (2014). Generating pit-free canopy height models from airborne LiDAR. Photogrammetric Engineering & Remote Sensing, 80(9), 863–872. doi: 10.14358/PERS.80.9.863 [DOI] [Google Scholar]
- Klein E, Lavigne C, Foueillassar X, Gouyon P, & Laredo C (2003). Corn pollen dispersal: quasi-mechanistic models and field experiments. Ecological Monographs, 73(1), 131–150. http://www.esajournals.org/doi/abs/10.1890/0012-9615(2003)073%5B0131:CPDQMM%5D2.0.CO%3B2 [Google Scholar]
- La Rosa M, Lionetti E, Reibaldi M, Russo A, Longo A, Leonardi S, et al. (2013). Allergic conjunctivitis: a comprehensive review of the literature. Italian Journal of Pediatrics, 39, 18. doi: 10.1186/1824-7288-39-18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linneberg A, Henrik Nielsen N, Frølund L, Madsen F, Dirksen A, & Jørgensen T (2002). The link between allergic rhinitis and allergic asthma: A prospective population-based study. The Copenhagen Allergy Study. Allergy: European Journal of Allergy and Clinical Immunology, 57(11), 1048–1052. doi: 10.1034/j.1398-9995.2002.23664.x [DOI] [PubMed] [Google Scholar]
- Lovasi GS, O’Neil-Dunne JPM, Lu JWT, Sheehan D, Perzanowski MS, Macfaden SW, et al. (2013). Urban tree canopy and asthma, wheeze, rhinitis, and allergic sensitization to tree pollen in a New York city birth cohort. Environmental Health Perspectives, 121(4), 494–500. doi: 10.1289/ehp.1205513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McHale MR, Burke IC, Lefsky MA, Peper PJ, & McPherson EG (2009). Urban forest biomass estimates: Is it important to use allometric relationships developed specifically for urban trees? Urban Ecosystems, 12(1), 95–113. doi: 10.1007/s11252-009-0081-3 [DOI] [Google Scholar]
- McKinney ML (2006). Urbanization as a major cause of biotic homogenization. Biological Conservation, 127(3), 247–260. doi: 10.1016/j.biocon.2005.09.005 [DOI] [Google Scholar]
- McPherson EG, Van Doorn NS, & Peper PJ (2016). Urban Tree Database and Allometric Equations. doi: 10.2737/RDS-2016-0005 [DOI] [Google Scholar]
- Meltzer EO (2016). Allergic rhinitis: Burden of illness, quality of life, comorbidities, and control. Immunology and Allergy Clinics of North America, 36(2), 235–248. doi: 10.1016/j.iac.2015.12.002 [DOI] [PubMed] [Google Scholar]
- Meltzer EO, Blaiss MS, Derebery MJ, Mahr TA, Gordon BR, Sheth KK, et al. (2009). Burden of allergic rhinitis: Results from the Pediatric Allergies in America survey. Journal of Allergy and Clinical Immunology, 124(3 SUPPL. 1), 43–70. doi: 10.1016/j.jaci.2009.05.013 [DOI] [PubMed] [Google Scholar]
- Molina RT, Rodríguez AM, Palaciso IS, & López FG (1996). Pollen production in anemophilous trees. Grana, 35(1), 38–46. doi: 10.1080/00173139609430499 [DOI] [Google Scholar]
- Nathan R (2007). The burden of allergic rhinitis. Allergy and Asthma Proceedings, 28(1), 3–9. doi: 10.2500/aap.2007.28.2934 [DOI] [PubMed] [Google Scholar]
- National Climate Data Center. (2019). Global Summary of the Day. www.ncdc.noaa.gov/. Accessed 8 July 2019
- Oliveira N, Rodríguez-Soalleiro R, Pérez-Cruzado C, Cañellas I, & Sixto H (2017). On the Genetic Affinity of Individual Tree Biomass Allometry in Poplar Short Rotation Coppice. Bioenergy Research, 10(2), 525–535. doi: 10.1007/s12155-017-9818-7 [DOI] [Google Scholar]
- Owusu SA, Schlarbaum SE, Carlson JE, & Gailing O (2016). Pollen gene flow and molecular identification of full-sib families in small and isolated population fragments of Gleditsia triacanthos L. Botany, 94(7), 523–532. doi: 10.1139/cjb-2015-0244 [DOI] [Google Scholar]
- Pebesma E (2018). Simple Features for R: Standardized Support for Spatial Vector Data. The R Journal, 10(1), 439–446. doi: 10.32614/RJ-2018-009 [DOI] [Google Scholar]
- R Core Team. (2018). R: A language and environment for statistical computing. Vienna, Austria, doi: 10.1145/192593.192639 [DOI] [Google Scholar]
- Ranta H, Hokkanen T, Linkosalo T, Laukkanen L, Bondestam K, & Oksanen A (2008). Male flowering of birch: Spatial synchronization, year-to-year variation and relation of catkin numbers and airborne pollen counts. Forest Ecology and Management, 255(3–4), 643–650. doi: 10.1016/j.foreco.2007.09.040 [DOI] [Google Scholar]
- Reddi CS, & Reddi NS (1986). Pollen Production in Some Anemophilous Angiosperms. Grana, 25(April 2015), 55–61. doi: 10.1080/00173138609429933 [DOI] [Google Scholar]
- Rojo J, Salido P, & Perez-Badia R (2015). Flower and pollen production in the Cornicabra olive (Olea europaea L.) cultivar and the influence of environmental factors. Trees - Structure and Function, 29(4), 1235–1245. doi: 10.1007/s00468-015-1203-6 [DOI] [Google Scholar]
- Roussel J, & Auty D (2017). lidR: Airborne LiDAR data manipulation and visualization for forestry applications. https://github.com/Jean-Romain/lidR
- Salo P, Calatroni A, Gergen P, Hoppin J, Sever M, Jaramillo R, et al. (2011). Allergy-related outcomes in relation to serum IgE: Results from the National Health and Nutrition Examination Survey 2005–2006. Journal of Allergy and Clinical Immunology, 127(5), 1226–1235. doi: 10.1016/j.jaci.2010.12.1106.Allergy-related [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnabel A, & Hamrick JL (1995). Understanding the population genetic structure of Gleditsia triacanthos L.: The scale and pattern of pollen gene flow. Evolution, 49(5), 921–931. [DOI] [PubMed] [Google Scholar]
- Sofiev M, & Bergmann K-C (2012). Allergenic Pollen: A Review of the Production, Release, Distribution and Health Impacts. (Sofiev M & Bergmann K-C, Eds.). New York, NY: Springer. [Google Scholar]
- Taylor S, & White EP (2019). Automated data-intensive forecasting of plant phenology throughout the United States. Ecological Applications, 1–25. doi: 10.1002/eap.2025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ter-Mikaelian MT, & Korzukhin MD (1997). Biomass equations for sixty-five North American tree species. Forest Ecology and Management, 97(1), 1–24. doi: 10.1016/S0378-1127(97)00019-4 [DOI] [Google Scholar]
- Thomas SC (1996). Reproductive allometry in Malaysian rain forest trees: Biomechanics versus optimal allocation. Evolutionary Ecology, 10(5), 517–530. doi: 10.1007/BF01237882 [DOI] [Google Scholar]
- Tseng Y-T, Kawashima S, Kobayashi S, Takeuchi S, & Nakamura K (2020). Forecasting the seasonal pollen index by using a hidden Markov model combining meteorological and biological factors. Science of The Total Environment, 698, 134246. doi: 10.1016/j.scitotenv.2019.134246 [DOI] [PubMed] [Google Scholar]
- Wang K, Wang T, & Liu X (2019). A review: individual tree species classification using integrated airborne LiDAR and optical imagery with a focus on the urban environment. Forests, 10(1), 1–18. doi: 10.3390/f10010001 [DOI] [Google Scholar]
- Weiner J, Campbell LG, Pino J, & Echarte L (2009). The allometry of reproduction within plant populations. Journal of Ecology, 97(6), 1220–1233. doi: 10.1111/j.1365-2745.2009.01559.x [DOI] [Google Scholar]
- Wickham H (2009). ggplot2: elegant graphics for data analysis. New York, NY: Springer; http://had.co.nz/ggplot2/book [Google Scholar]
- Xiao L, Yang Q, He H, Zhao J, Ye C, Wu Y, & Han B (2016). An improved method for pollen release from anther: a case study with mangroves. Grana, 55(4), 302–310. doi: 10.1080/00173134.2015.1120775 [DOI] [Google Scholar]
- Yasaka M, Kobayashi S, Takeuchi S, Tokuda S, Takiya M, & Ohno Y (2009). Prediction of birch airborne pollen counts by examining male catkin numbers in Hokkaido, northern Japan. Aerobiologia, 25(2), 111–117. doi: 10.1007/s10453-009-9116-8 [DOI] [Google Scholar]
- Ye R, Huang H, Alexander J, Liu W, Millwood RJ, Wang J, & Stewart CN (2016). Field studies on dynamic pollen production, deposition, and dispersion of glyphosate-resistant horseweed (Conyza canadensis). Weed Science, 64(1), 101–111. doi: 10.1614/WS-D-15-00073.1 [DOI] [Google Scholar]
- Yoon TK, Park CW, Lee SJ, Ko S, Kim KN, Son Y, et al. (2013). Allometric equations for estimating the aboveground volume of five common urban street tree species in Daegu, Korea. Urban Forestry and Urban Greening, 12(3), 344–349. doi: 10.1016/j.ufug.2013.03.006 [DOI] [Google Scholar]
- Zandbergen PA (2009). Accuracy of iPhone locations: A comparison of assisted GPS, WiFi and cellular positioning. Transactions in GIS, 13(SUPPL. 1), 5–25. doi: 10.1111/j.1467-9671.2009.01152.x [DOI] [Google Scholar]
- Zhen Z, Quackenbush LJ, & Zhang L (2016). Trends in automatic individual tree crown detection and delineation-evolution of LiDAR data. Remote Sensing, 8(4), 1–26. doi: 10.3390/rs8040333 [DOI] [Google Scholar]
- Zianis D, Muukkonen P, Mäkipää R, & Mencuccini M (2005). Biomass and stem volume equations for tree species in Europe. Silva Fennica Monographs (Vol. 4). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.