Application of network meta-analysis in the field of physical activity and health promotion

Highlights

• •Network meta-analysis could be a promising method for information synthesis and decision-making processes in the field of physical activity and health promotion.
• •Statistical analysis software and Web-based tools are developing rapidly to provide convenience for carrying out network meta-analysis.
• •Risk of bias and assumptions related to network meta-analysis should be properly considered in order to guarantee the quality of the analysis.

Abstract

Continued advancement in the field of physical activity and health promotion relies heavily on the synthesis of rigorous scientific evidence. As such, systematic reviews and meta-analyses of randomized controlled trials have led to a better understanding of which intervention strategies are superior (i.e., produce the greatest effects) in physical activity-based health behavior change interventions. Indeed, standard meta-analytic approaches have allowed researchers in the field to synthesize relevant experimental evidence using pairwise procedures that produce reliable estimates of the homogeneity, magnitude, and potential biases in the observed effects. However, pairwise meta-analytic procedures are only capable to discerning differences in effects between a select intervention strategy and a select comparison or control condition. In order to maximize the impact of physical activity interventions on health-related outcomes, it is necessary to establish evidence concerning the comparative efficacy of all relevant physical activity intervention strategies. The development of network meta-analysis (NMA)—most commonly used in medical-based clinical trials—has allowed for the quantification of indirect comparisons, even in the absence of direct, head-to-head trials. Thus, it stands to reason that NMA can be applied in physical activity and health promotion research to identify the best intervention strategies. Given that this analysis technique is novel and largely unexplored in the field of physical activity and health promotion, care must be taken in its application to ensure reliable estimates and discernment of the effect sizes among interventions. Therefore, the purpose of this review is to comment on the potential application and importance of NMA in the field of physical activity and health promotion, describe how to properly and effectively apply this technique, and suggest important considerations for its appropriate application in this field. In this paper, overviews of the foundations of NMA and commonly used approaches for conducting NMA are provided, followed by assumptions related to NMA, opportunities and challenges in NMA, and a step-by-step example of developing and conducting an NMA.

Graphical Abstract

1. Introduction

Continual advancement in the field of physical activity and health promotion depends on the accurate and timely synthesis of all available evidence from interventions based on physical activity and lifestyle (e.g., physical activity interventions on children's health).^1,2 In particular, meta-analyses of randomized controlled trials (RCTs) have helped us to better understand the health impact of physical activity promotion interventions and to discern the superiority, or lack thereof, of one intervention strategy over another or of no treatment at all. However, standard meta-analytic techniques only allow for pairwise comparisons (i.e., a direct comparison of one intervention strategy against another or compared to a control condition). Given that levels of physical inactivity and the prevalence of chronic diseases related to physical inactivity remain at epidemic levels (globally, 23% of men and 32% of women aged 18+ years were insufficiently physically active, according to the World Health Organization in 2016), national and global health organizations are seeking quantitative evidence synthesized from simultaneous comparisons of multiple intervention strategies.^3,4

As is recognized, the clinical decision-making process should be based on valid empirical evidence. While RCTs comparing the effects of 2 or more interventions can contribute as direct evidence, systematic reviews show advantages in their abilities to synthesize and analyze all available evidence related to the same clinical question.⁵ Meta-analysis has been employed in clinical practice since the 1980s⁶ and has been one of the most frequently used statistical methods in systematic reviews for data synthesis. The conventional way of carrying out a meta-analysis is through pairwise comparisons between an intervention and a control.⁷ Pairwise meta-analysis is capable of gathering evidence from separate and relatively small studies and, through the combination of their results, may increase statistical power and detect a statistically significant difference between one intervention and another even though not all individual studies observed statistical significance in their results.⁶ However, pairwise meta-analysis is only able to compare head-to-head trials using the same type of intervention, while in practice there are usually more than 2 approaches available. For clinicians, patients, and policy makers to make well-informed decisions, it is necessary to compare all intervention approaches simultaneously. Nonetheless, for various reasons, in some specific areas there may only exist limited direct evidence, making it difficult to carry out head-to-head comparisons for all types of interventions using traditional pairwise meta-analysis. Under these circumstances, the application of network meta-analysis (NMA), also termed multiple treatment comparison (MTC) or multiple treatment meta-analysis, can be very useful for synthesizing all existing evidence simultaneously.⁸

2. Foundations of NMA

2.1. What is NMA?

NMA is a statistical technique that combines both direct (i.e., within-trial) and indirect (i.e., between-trial) comparisons of multiple intervention strategies that may not be directly compared within the same trial.^3,9,10 The most basic requisite for conducting indirect quantitative comparisons using NMA is that there should be at least 1 intervention strategy in common for each chain of comparison. Each type of intervention could serve as a connection to different chains of comparisons as a node. This allows for the construction of a network of trials comparing multiple interventions that can be analyzed using NMA. Therefore, compared with only direct evidence derived from standard pairwise meta-analyses, NMA maximizes the availability of evidence by allowing for the comparison of any pair of interventions linked through the constructed evidence-network, thus increasing the precision of the effect size for a given intervention strategy.^3,11,12

2.2. Advantages of NMA

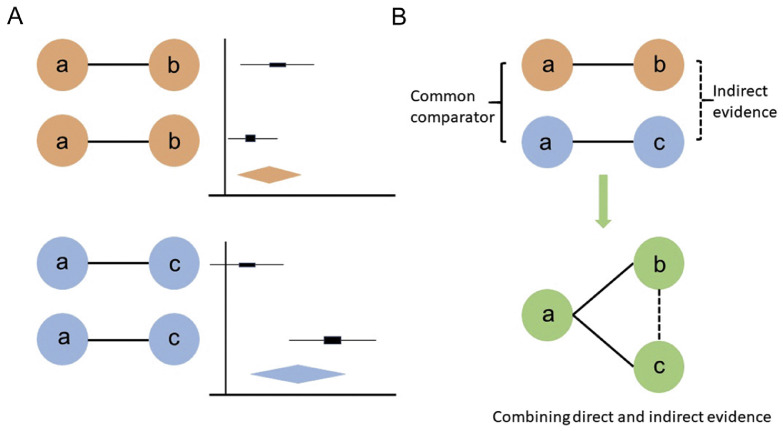
NMA can be seen as an extension of conventional pairwise meta-analysis since they both share similar assumptions and have essentially the same purposes and functions.⁶ In the field of physical activity and health promotion, intervention approaches mainly focus on informational, behavioral, social, environmental, and policy aspects.¹³ More detailed modifiable determinants can be listed under each aspect of approaches that different RCTs carried out by researchers from around the world might address separately. NMA is capable of combining all existing evidence under similar conditions together for analysis, as long as each piece of evidence connects to the network. Not only are direct comparisons from the RCTs taken into account, but every common comparator can contribute to making indirect comparisons as well.5, 6, 7 Using appropriate statistical methods, the direct and indirect evidence can be combined as a weighted average in NMAs. For example, if current clinical trials only compared “a” vs. “b” and “b” vs. “c” directly (i.e., there are no head-to-head trials comparing “a” vs. “c”), as shown in Fig. 1, the NMA is able to estimate the relative effect of “a” vs. “c” using indirect evidence through “a” vs. “b” and “b” vs. “c” under the preceding assumptions. On the other hand, if clinical trials comparing “a” vs. “c” are also available, the relationships of the 3 types of trials could form a closed loop, and the NMA would be able to utilize both direct and indirect sources of information and combine them with an appropriate weight. A visual comparison between pairwise meta-analysis and NMA in the use of direct and indirect evidence is provided below (Fig. 2), featuring the biggest advantage of the NMA. Longer chains of indirect comparisons may also appear under certain circumstances; for example, instead of getting indirect evidence from “a” vs. “c” through “a” vs. “b” and “b” vs. “c”, more common comparators may be needed on the path (i.e., “a” vs. “b”, “b” vs. “d”, and “d” vs. “c”).

Fig. 1.

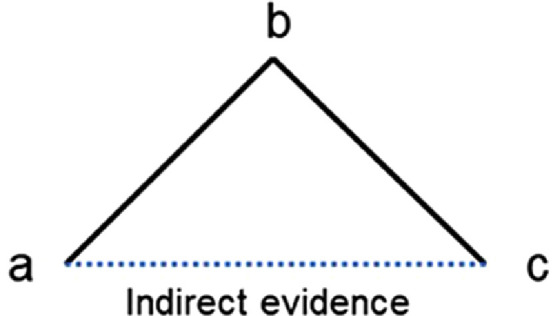
Example of a network of 3 treatments compared in 2 trials (solid black lines), where an indirect comparison can be made using network meta-analysis (dot blue line).

Fig. 2.

Comparisons between pairwise meta-analysis versus network meta-analysis in the use of direct and indirect evidence. (A) Represents an example of pairwise meta-analysis and (B) Shows the biggest advantage for network meta-analysis when a common comparator “a” exists. Solid lines represent direct comparisons and dash lines represent indirect comparisons.⁶

2.3. Assumptions related to NMA and risk of bias

NMA relies on several assumptions that need to be checked prior to conducting the analysis. First, NMA shares the same assumption as pairwise meta-analysis, which is homogeneity.^3,6 This assumption presumes no relevant heterogeneity among trial results, which means that the effect of potential modifiers should be very limited for the included RCTs (apart from sample variability), ensuring that all study-related conditions are homogenous.^3,7 However, in practice, potential modifiers may still exist and sometimes are not measured or even measurable. Examples of common potential effect modifiers include baseline characteristics of recruited participants, personnel choice of measurements, and intervention setting and dosages, to list a few. According to Dias and Caldwell,⁷ an empirical way of checking this assumption is to observe in a general view and see whether the treatments and participants’ characteristics are comparable among all the studies and whether it is suitable to combine them for NMA. If so, then in principle the homogeneity assumption would be satisfied. Specifically, in the field of physical activity and health promotion, one of the most likely ways to bring heterogeneity is due to the complexity of the interventions included across the studies. In practice, interventions in kinesiology studies are very likely to have degrees of flexibility or tailoring of the protocol (intensity, duration, etc.), and the outcomes may appear to be natural variabilities.¹⁴ These could all contribute as characteristics for a complex intervention and might cause the presence of statistical heterogeneity. In their 2016 paper, Caldwell and Welton¹⁵ addressed this issue and concluded that component-based NMA could be a good option for synthesizing complex interventions. Interested readers are referred to their work for detailed information.

Next, the consistency and transitivity assumptions are specific concerns for NMAs since they both involve the proper use of indirect evidence. The assumption of consistency states that there should not be discrepancies between direct and indirect comparisons. In other words, the results obtained from trials providing direct and indirect evidence should essentially agree with each other. Otherwise, there will be network inconsistency. The consistency assumption can only be assessed when both kinds of evidence are available (i.e., a closed loop within the network). In their previous work, Dias et al.,¹⁶ Higgins et al.,¹⁷ and White et al.¹⁸ have all provided detailed descriptions of possible strategies for consistency checking. As mentioned previously, direct comparisons may not be always available. However, the assumption of transitivity should still be assessed whether there is direct evidence or not. Transitivity refers to the assumption that for unobserved head-to-head comparisons, using indirect comparison(s) could provide valid and reliable estimates that are close to a direct comparison if one were available.¹⁹ For example, in a closed loop network among “a”, “b”, and “c”, one should be able to conclude that “a” is better than “c”, knowing that “a” is better than “b”, and “b” is better than “c”. If at the same time there is direct evidence showing that “a” is better than “c”, then the transitivity and consistency assumptions are both met. Dias et al.²⁰ introduced strategies of assessing transitivity in details in the book Network meta-analysis for decision-making. Broadly speaking, transitivity could be achieved by “qualitatively examining relevant clinical and methodological aspects of the relevant intervention comparators”³ to ensure that the potential effect modifiers are distributed evenly across all of the comparators.

Apart from the preceding assumptions that NMAs rely on, it is also important to account for risk of bias of individual studies included in the network. Risk of bias for NMAs shares similarities with conventional pairwise meta-analysis, although risk-of-bias assessment in NMA is far more challenging. First, publication bias or small study effects is one of the most common types of biases faced by meta-analyses since the main data source for second-hand data analyses are usually extracted from published articles. Various statistical methods have been proposed to detect or quantify the magnitude of publication bias.^21,22 Although publication bias is hard to avoid or control, particularly from the perspective of multivariate meta-analyses,²³ including NMAs, it is still necessary to at least be aware of this potential issue. In addition, risk of bias may also commonly occur when individual trials included in the analysis have potential design or execution problems, thus raising concerns regarding the validity and reliability of their results.⁵ More importantly, if there is bias from 1 single trial, it is possible that the findings from this trial may affect several pooled effect estimates in NMAs, whereas only 1 pooled effect estimate will be affected in conventional pairwise meta-analysis.

To evaluate the certainty of the evidence from NMAs, the Grading of Recommendations Assessment, Development, and Evaluation (GRADE) was described by Puhan et al.²⁴ in 2014. The guidance mostly focuses on assessing the confidence and quality of the evidence in an NMA and has been broadly used in a number of studies carrying out NMAs.25, 26, 27 Later in 2018, Brignardello-Petersen et al.²⁸ described recent conceptual advances of the GRADE approach and summarized them into 4 major points, mainly regarding consideration of imprecision, necessity of rating of indirect evidence, and global incoherence. In fact, given the rapidly increasing popularity of NMA in all fields, more challenges are expected to be encountered, and further development of the GRADE criteria is also anticipated through GRADE working-group meetings.

2.4. Theoretical and statistical approaches in NMA

Statistically, one can use either a Bayesian or a frequentist framework to conduct an NMA. When sample size is sufficient, these 2 frameworks should produce similar results despite the fact that the basic concepts of their statistical approaches differ. Essentially, the main difference between these 2 methods is whether prior information is considered when building the model. Frequentist methods do not consider information previously known (prior probability) and estimate the population parameters by infinitely repeating the present data and maximizing its likelihood function under a statistical model. The population parameters are considered as fixed unknown values and are not related to external information under this framework.²⁹ On the other hand, Bayesian methods believe that the interest population parameters should have a posterior distribution that may be affected by prior information since the posterior distribution function can be obtained by multiplying the prior distribution of parameters with the likelihood function.²⁹ Essentially, the observables and parameters in the model are both viewed as random quantities from the Bayesian perspective.^30,31

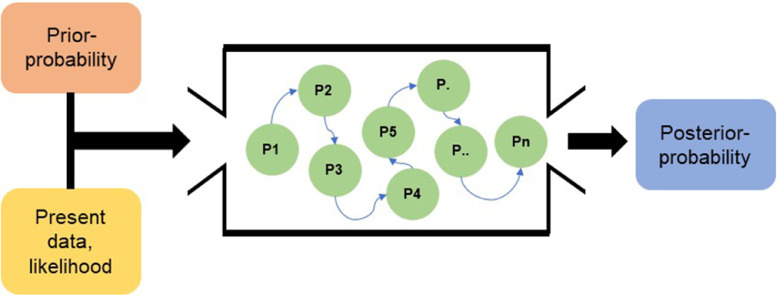
Since the Bayesian method maintains model uncertainty, its posterior distribution does not follow commonly used distributions (i.e., binomial or normal), rendering it difficult to calculate the area under the distribution curve. The Markov Chain Monte Carlo (MCMC) simulation can be used in this case for area calculation, which is essentially Monte Carlo integration using Markov Chains. MCMC emerged as an extremely popular tool for the analysis of complex statistical models for a short period during the 1990s, especially in the field of Bayesian analysis.³¹ The concept of Markov Chains involves calculating the probability of the “next state” of a random variable using an algorithm, where the next state only depends on its current state and transition probability (which is prior information). It is believed that in a Markov Chain, the value of the next state would finally reach a stable distribution with enough repetition of the calculation.²⁹ Monte Carlo simulation aims to predict a targeted value using random sampling methods based on randomness. Basically, it “draws samples from the required distribution and then forms sample averages to approximate expectations”.³² Together, they form the MCMC simulation to determine posterior distribution for relatively complicated statistical models such as the Bayesian model. Fig. 3 shows a simplified schematic of the concept for the MCMC simulation used in the Bayesian approach.

Fig. 3.

The overall concept of the Bayesian approach using a Markov Chain Monte Carlo (MCMC) simulation.²⁹ P = probability.

3. Commonly used approaches for conducting NMA

Besides the differences in theoretical models, there are 2 types of approaches that can be used for NMA. The contrast-based approach is considered by many researchers to be the standard approach for meta-analysis, while arm-based models (discussed later) have more recently been purported to be an intriguing alternative to the understanding of meta-analysis.³³ The main difference between the 2 approaches is the type of information extracted for analysis. For trials, contrast-based models pool information of relative treatment effects, while arm-based models focus on the absolute values of each outcome of interest.³⁴ As an example, absolute measures include treatment-specific event rates, log risks, log odds, and mean outcomes for each arm included. On the other hand, the most commonly reported summary statistics for contrast measures are log-odds ratio (OR)³⁵ and other statistics, such as log relative risks and risk differences for binary outcomes, or mean differences for continuous outcomes between treatments. There is continuing discussion regarding the strengths and weaknesses of the 2 types of models. Zhang et al.³⁵ carried out a series of hypothetical NMA trials as well as reanalysis of published NMAs and compared the results of their self-processed approach using the alternative arm-based methods to the estimations of contrast-based models. They concluded that the arm-based approach outperformed the original contrast-based NMA methods in terms of bias; and for other outcomes the 2 approaches led to different treatment recommendations but shared some similarities as well.³⁵ In general cases, assuming the same OR or relative risk across different baseline risks could lead to different absolute risk differences. Under these circumstances, some researchers believe that arm-based NMA might be preferred because it provides a more straightforward and accurate methodology to assess different intervention effects.³⁴ Moreover, the arm-based methodology can use information contained in single-armed studies and therefore take into account more available treatment groups, while contrast-based studies are not capable of including such studies.³⁴ However, the preference for the arm-based model supported by Zhang et al.³⁵ and Hong et al.³⁶ was criticized by Dias and Ades,³³ who stated that “contrast-based models are to be preferred on both theoretical and practical grounds.” Furthermore, Dias and Ades³³ presented detailed comparisons and arguments supporting their conclusion that advocating for arm-based models is not helpful for the separation of absolute and relative effects, an essential problem that epidemiologists and biostatisticians have been working on for many years. Dias and Ades³³ argued that the use of arm-based models risked biased estimates with over-inflated posterior variance and thus believed that previous studies^35,36 favoring the alternative arm-based method were actually mistaken. The discussion continued when Hong et al.³⁷ published a rejoinder that provided a section-by-section response to Dias and Ades.³³ Hong et al.³⁷ argued that because the assumption requirement for arm-based models is considerably higher than for contrast-based models, the payoffs were worthwhile since arm-based models allowed for significantly higher modeling flexibility, thereby making them more advantageous for model fitting and interpretation. Thus, Hong et al.³⁷ asserted their belief that arm-based models were more complete, and that a fully Bayesian approach was superior for handling missing data. These discussions allowed the researchers to fully explore every aspect of the issue and offered a chance for other analysts to better decide for themselves which model to consider for their own work. A more recent comparison by White et al.³⁸ was carried out specifically targeting the arm-based model supported by Hong et al.³⁶ and the contrast-based model supported by Lu and Ades.³⁹ Four key differences between the 2 models were identified, but the discussion mainly focused on whether the study intercepts were random or fixed effects, which, as White et al.³⁸ suggested, is the most important difference between the models. White et al.³⁸ concluded that both arm-based and contrast-based models are suitable for NMA but pointed out that using random study intercepts requires a strong rationale, while models with fixed study intercepts are useful because they can be implemented with either a contrast-based or arm-based model. Wang et al.⁴⁰ observed that a separation strategy with appropriate priors for the correlation matrix and variances performs better than strategies employing the inverse—Wishart priors used in the original arm-based NMA and can therefore reduce potential biases. Recently, Ma et al.⁴¹ and Lian et al.⁴² have extended arm-based NMA to simultaneously compare multiple diagnostic tests in which absolute measures, such as sensitivities and specificities, are of primary interest.

There are several statistical programs and software available that can carry out the required calculations and simulation steps for NMA. For instance, Statistical Analysis System (SAS) and statistics and data (STATA) are capable of employing NMA based on frequentist methods. Other open-access resources (e.g., Open Bayesian inference Using Gibbs Sampling (OpenBUGS), Windows Bayesian inference Using Gibbs Sampling (WinBUGS), Just Another Gibbs Sample (JAGS)) can help in conducting NMA under the Bayesian framework as an MCMC sampler.⁸ R, a popular open source statistical software, is frequently used among statisticians nowadays. According to the review by Neupane et al.,⁸ until 2014 there were only 3 available R packages developed specifically for performing NMA: gemtc (http://cran.r-project.org/web/packages/gemtc/index.html), pcnetmeta (http://cran.r-project.org/web/packages/pcnetmeta/index.html), and netmeta (http://cran.r-project.org/web/packages/netmeta/index.html). The first 2 packages perform the analysis under the Bayesian framework and the last one performs it using the frequentist framework. According to the comparisons and assessments by Neupane et al.,⁸ the 3 R packages provide different and often complementary features for performing all aspects of NMA. One or more of these packages could be used to plot the network, generate a model, detect heterogeneity and inconsistency in the network, incorporate them into the estimation, and finally generate the estimated effects sizes and rank probabilities. Gemtc and netmeta are comprehensive packages that employ Bayesian and frequentist techniques, respectively, for contrast-based NMA. In comparison, pcnetmeta provides Bayesian analysis for arm-based NMAs, which are generally more robust for the choice of treatments to include in the NMA.⁴³ Table 1 summarizes the features and capabilities of the 3 packages.

Table 1.

Comparison of important features of 3 R packages capable of carrying out an NMA.

Task	Feature	netmeta	gemtc	pcnetmeta
Estimation framework	Bayesian		√	√
	Frequentist	√
Forms of input data	Arm-level data		√	√
	Contrast-level data	√	√
	Accepts multi-arm (≥ 3) trials	√	√	√
Types of outcome data that can be analyzed	Binary	√	√	√
	Count	√	√
	Continuous	√	√	√
	Survival	√	√
Extracts descriptive measures	Total number of studies	√	√
	Total number of multi-arm studies	√	√
	Total number of participants		√
	Total number of treatments	√	√
Network plot and options	Network plot	√	√	√
	Add node labels	√	√	√
	Node size reflects network characteristic			√
	Edge thickness reflects network characteristic	√		√
Assessing heterogeneity	Visual inspection—forest plot	√	√
	Pairwise statistics	√	√
	Global statistics	√	√
Assessing inconsistency	Visual inspection—forest plot of direct vs. indirect		√
	Visual inspection—heat map	√
	Consistency statistics	√	√
	Back-calculation		√
	Node-split/decomposition	√	√
MCMC sampler (when under Bayesian modeling)	WinBUGS	N/A	√
	OpenBUGS	N/A	√
	JAGS	N/A	√	√

Notes: Adapted from Neupane et al. (2014) with premission.⁸ Checks indicate the presence of the feature; otherwise the feature does not apply.

Abbreviations: JAGS = Just Another Gibbs Sample; MCMC = Markov Chain Monte Carlo; N/A = not applicable; NMA = network meta-analysis; OpenBUGS = Open Bayesian inference Using Gibbs Sampling; WinBUGS = Windows Bayesian inference Using Gibbs Sampling.

Recently, a couple of new tools have been created to conduct NMA via the Web. Examples are MetaInsight (https://crsu.shinyapps.io/metainsightc)⁴⁴ and CINeMA (Confidence in Network Meta-Analysis, https://cinema.ispm.unibe.ch/).⁴⁵ Both are Web-based, freely available open-source tools with no requirement for the installment of statistical software. R is used as the “backbone” for both of the tools; however, they only call the routines of R packages on the webserver rather than using the software itself. These newly developed platforms provide a more convenient and reliable source that researchers and nonspecialists can use to perform NMA and get immediate visual feedback during their research.

The software mentioned above can generate network plots, and possible configurations that imitate different situations that might occur in real studies are shown in Fig. 4. Every dot represents an arm of treatment (e.g., control, treatment 1, treatment 2, etc.); the solid lines represent edges or direct comparisons between the 2 treatments or comparators, which are linked by the lines; and the width of the edges has a positive association with the number of direct comparisons that occurred (i.e., the number of articles with this result reported). Generally, the more solid lines that exist, the more precise the estimation of the indirect comparisons would be because any inference should be based on the direct evidence available.

Fig. 4.

Possible configurations of network plots.

4. Opportunities and challenges related to NMA

NMA has most commonly been used in clinical fields where researchers test the effectiveness of different drug interventions. The clinical conditions involving drug interventions most often evaluated by NMA include cardiovascular diseases, oncological disorders, mental health disorders, and infectious diseases.⁶ However, other NMA applications have developed rapidly in the past decade. According to Tonin et al.,⁶ very few systematic reviews containing NMAs were published prior to 2008, yet now there are more than 400 published. NMA is gaining popularity in comparing clinical treatments because there are typically a variety of treatments or drugs targeting similar disease categories, rendering it difficult for clinicians and patients to compare them thoroughly in a pairwise fashion before making informed treatment decisions. Properly conducted NMA studies have the potential to overcome such issues. In fact, using NMA to make indirect comparisons among studies has become a critical component of evidence synthesis and decision making in healthcare.³ In the field of physical activity and health promotion, NMA is gaining attention as a valuable analysis tool and research method. The main trend involves the use of exercise as one of the treatment intervention approaches and comparing this treatment arm with other treatment strategies, or comparing the health benefits of different types of exercise (e.g., aerobic exercise, high-intensity training, resistance training, etc.) in populations with chronic disease or other clinical populations. Specifically, NMA allows for comparisons of the efficacy of behavioral (i.e., physical activity) and biomedical (i.e., pharmacological treatments) intervention strategies on a common health outcome (e.g., weight, body mass index, blood pressure) that would otherwise not have been compared previously in head-to-head trials when they share common comparators, such as a control or placebo group.

In the field of physical activity and health promotion, we identified 11 articles that utilized a physical activity or exercise program as one of the treatment arms within the RCTs. Among the 11 studies, five were carried out in Europe (Austria and UK)^46,47; 4 were carried out in Asia (China and Japan)^45,48,49; and the other 2 studies were carried out in the US⁵⁰ and Brazil.⁵¹ As for software choices for the analysis, it appears that STATA and WinBUGS were most popular. Five of the studies used STATA to either generate network plots as a first step or to perform the full NMA analysis.42, 43, 44, 45, 46, 47, 48^,52,53 The open-source software WinBUGS was used in 5 of the studies to carry out the analysis,^39,46,54,55 and 1 study used the R package “netmeta”.⁴⁹ Most of the studies included in the analysis used a Bayesian approach,^46,47,53, 54, 55, 56 while 2 employed the frequentist approach.^49,50 Six of the studies examined the effects of exercise or other physical-activity-based interventions (e.g., lifestyle interventions) on patients with diseases such as coronary heart disease, type 2 diabetes mellitus (T2DM), and nonalcoholic fatty liver disease, as well as the effects on mortality outcomes.47, 48, 49^,52, 53, 54 Three studies focused on the effect of exercise training on the participants’ change in body weight, adiposity level, or other anthropometric characteristics; all the interventions were moderately effective.^46,50,51 Furthermore, 2 studies focused on less severe chronic diseases such as lower limb osteoarthritis and hypertension.^55,56 Taken together, it is apparent that exercise and physical activity intervention programs are moderately to highly effective for attenuating chronic diseases and obesity-related health problems.

However, kinesiology is a far broader field than exercise science, where most of the focus of NMA currently lies. The promotion of physical activity is needed to improve the health of most populations, given that the prevalence of physical inactivity has become alarmingly higher in the past decade. Numerous studies have reported the use of different approaches for promoting physical activity, and researchers from all over the world are employing various interventions in an effort to find more effective and suitable ways to prevent the incidence of chronic diseases and promote health. Thus, it is important to pool and compare their work in an effort to identify the most effective physical activity and health promotion methods.

Although the use of NMA is spreading rather quickly among various research fields, more methodological research is needed because certain interpretational aspects of the approach are poorly understood. Researchers must consider many different aspects of NMA in order to obtain valid simulations and estimations. These aspects include (1) the strength of evidence and risk of bias for each of the comparisons, (2) the analytical challenges, tools, and opportunities in detecting and exploring heterogeneity within and between comparisons, and (3) the interpretation of widely used statistical models and effect measures. Consideration of these points will help ensure high-quality synthesis of evidence and reasonable analysis when conducting an NMA.

An NMA methodology meeting was held at the Johns Hopkins Bloomberg School of Public Health in May 2010. According to Li et al.,⁵ the attendees discussed the methodological challenges and research opportunities for NMA relevant to each aspect of the systematic review process. The main points addressed included (1) clearly defining the review question and eligibility criteria, (2) searching for and selecting valid and high-quality studies for data analysis, (3) accurately assessing risk of bias and quality of evidence, (4) conducting a quantitative evidence synthesis, and (5) properly interpreting the results and reporting findings. Although the commentary from the meeting is relatively old, most parts of the discussion are still meaningful for guiding the NMA process. However, new software, such as R, has been developed since the 2010 meeting, but much of the meeting discussion indicates that “most network meta-analysis to date use WinBUGs software”, which is limited in functionality and accessibility to the non-statistician. R and other Web-based tools have improved greatly since then. With the rapid growth of NMA studies in the past few years, we have reason to believe that NMA will continue to be a promising analysis technique and will play a significant role in other health-related fields, including physical activity and health promotion.

5. A step-by-step example for developing and conducting an NMA

Pan and collegues⁴⁹ successfully demonstrated how NMA has been applied comparing physical activity interventions that are not usually comprehensively compared with one another directly (Table 2). Main steps used by these authors to conduct the NMA were summarized as below.

Table 2.

Generic steps in planning and executing an NMA.

Step	Aim	Consideration
1	Generate research question	•The research question should be constructed with consideration of both the clinical and methodological characteristics of the studies of interest.
2	Plan systematic review	•This should be guided by the PRISMA extension for an NMA. •A clear definition of the T2DM must be presented, and the associated inclusion and exclusion criteria should allow the inclusion of as many relevant interventions and comparators as possible. •Potential effect modifiers may be identified. •The plan for the systematic review should be registered in PROSPERO and detailed in a study protocol.
3	Conduct search	•In situations where a large body of literature exists and high-quality systematic reviews have been carried out, the search may focus on identifying these because identifying individual studies through a primary search may not be feasible.
4	Select studies	•Ideally, 2 independent reviewers should select the studies according to the inclusion and exclusion criteria. •Studies that involve interventions that are not central to the research question may be included if they are compared to interventions that are central to the research question and provide more useful evidence to the network.
5	Extract data	•This stage will generally focus on extracting the relevant data regarding outcomes and potential effect modifiers. •Risk of bias and evidence quality should be assessed using the tools provided by Cochrane and GRADE because these characteristics also affect transitivity.
6	Build network	•Decisions regarding splitting and lumping are made at this stage, and planned approaches may have to be modified according to the nature of the collected data. For example, if there is a lack of data, some lumping may have to be done. •A network diagram should be constructed, and its geometry should be evaluated, e.g., Fig. 4.
7	Analyze data	•For all comparisons for which there are both direct and indirect evidence, consistency checks should be carried out to ensure that the direct and indirect evidence agree. •Generally, pairwise analyses are conducted first and then NMA models are conducted. •The data should be analyzed as set out in the study protocol.
8	Interpret and report results	•The PRISMA extension for an NMA provides guidance on reporting the results in a clear and comprehensive manner. •Data from individual studies should be summarized in tables. •The estimates of comparative effectiveness are usually presented in tables and sometimes in a rankogram.

Note: Adopted from Molloy et al. (2018) with permission.³

Abbreviations: GRADE = The Grading of Recommendations Assessment, Development, and Evaluation; NMA = network meta-analysis; PRISMA = Preferred Reporting Items for Systematic Reviews and Meta-Analyses; PROSPERO = Prospective Register of Systematic Reviews; T2DM = type 2 diabetes mellitus.

Step 1: The research question for this study was generated to compare the effectiveness of commonly used exercise training modalities on patients with T2DM. The requisite for this process was to properly categorize the training modalities and select representative outcome variables for patients’ health indicator. In this case, Pan et al.⁴⁹ chose to examine the patients’ response in glycemic control, weight loss, and cardiovascular risk factors under 8 types of training conditions.

Step 2: Following the constructs of the Cochrane Handbook Version 5.1.0,⁵⁷ a detailed protocol was developed to guide the study's design, analysis, and reporting of results. This process, which was concurrent with the Population Intervention Comparison Outcome framework, helped to establish (1) a focus on the selected population (adults with T2DM but no other chronic diseases), (2) the interventions included in the studies (physical-activity-based interventions, such as aerobic, anaerobic, resistance-training, flexibility, and combined exercise), (3) comparators (control/standard care), (4) study outcomes (glycemic control, weight loss, and cardiovascular risk factors), and (5) the selection and description of the key search terms used.

Step 3: The study selection process was conducted within available databases. A pilot-literature selection was preformed to ensure reliability among the reviewers. For any grey literature identified, additional standardized strategies were further supplemented.

Step 4: Two researchers involved in the study independently screened the titles and abstracts of potential studies that met the pre-established criteria for inclusion. Conflicted studies were subjected to full-text evaluation and resolved by a third reviewer. The included RCTs were assessed according to the Cochrane Handbook Version 5.1.0⁵⁷ for risk of bias.

Step 5: Two researchers involved in the study independently extracted pre-specified data of interest, including characteristic data (the first author, year of publication, study design,etc.) and data for further use of analysis, for this example study, including hemoglobin A1c, fasting plasma glucose, weight loss, total cholesterol, low-density lipoprotein cholesterol, high-density lipoprotein cholesterol, triacylglycerol, diastolic blood pressure, and systolic blood pressure.

Step 6: The researchers collaborated and used the following categories to divide the intervention arm(s) and control arms within all of the relevant RCTs: supervised aerobic exercise, unsupervised aerobic exercise, anaerobic exercise, supervised resistance exercise, unsupervised resistance exercise, combined exercise, flexibility exercise, and no exercise. Each category was specifically determined in detail to avoid possible heterogeneity across the use of the terms. For example, they defined aerobic training as “a regimen containing aerobic components performed at least 3–5 times per week for at least 4 weeks and performing minimum for 30 min each time.” Also, possible components of aerobic training were listed as “walking, cycling, jogging, and swimming but were not limited to these types” of physical activity. Other definitions of interventions were spelled out as detailed in one of the appendices.

Step 7: The NMA was employed to compare intervention effects of the pre-defined intervention categories on T2DM patients’ glycemic control, weight loss, and cardiovascular risk factors level. Specifically, STATA 15.1 (College Station, TX, USA) was used to generate network plots that described and presented the geometry of different forms of exercise, while R 3.4.0 software was used to perform a frequentist NMA. A random effects NMA was selected to conduct. Instead of using mean difference (MD) or pooled standardized MD, the researchers used the ratio of mean (RoM) to measure the treatment effect between the intervention and control groups. They then presented the results of absolute risk differences calculated through RoM and baseline risk of no exercise. Researchers conducting any NMA would preferably apply models for checking for the presence of consistency; specifically, in this NMA, a node-splitting method was included to evaluate the inconsistency between direct and indirect comparisons among all intervention groups.

Step 8: The NMA, using the available direct and indirect evidence, produced estimates of the effect sizes between each pair of interventions for glycemic control, weight loss, and level of cardiovascular risk factors. These data are presented using a table,⁴⁹ which displays RoMs with their respective effect sizes. These RoMs and effect sizes represent the comparisons between each of the interventions.

Taking these estimates into consideration, the researchers conducting the study concluded that combined exercise would be more efficient in the improvement of hemoglobin A1c (the level to which glycemic control is related) than either supervised aerobic exercise or supervised resistance exercise alone; however, the decrease in some cardiovascular risk factors was less marked with the combined exercise intervention. In terms of weight loss, there were no significant differences among the combined, supervised aerobic, and supervised resistance forms of exercise.

7. Conclusion

The synthesis and quantification of direct evidence has long provided valuable insight into identifying the most effective physical activity intervention strategies in the promotion of physical activity and health behaviors in various populations. However, indirect comparisons allow researchers to maximize the available data concerning specific intervention strategies on various outcomes and allow for unique insights that direct comparisons are unable to provide, given that they are limited to a pairwise structure. Thus, NMA and its variants represent novel and useful synthesis methodologies that are grossly underused in the fields of physical activity and health promotion. We expect that the employment of this statistical methodology will significantly contribute to the continued evolution of the science and practice of physical activity and health in the coming years. Given the rapid growth of studies employing NMA in the past few years, we have reason to believe that this will be a promising technique used within this field of study and will become a significant method of conducting practical analysis in many health-related fields.

Authors’ contributions

XS drafted the manuscript; DJM, HC, and MQ helped to draft the manuscript; ZG conceived the study, and helped to draft the manuscript. All authors have read and approved the final version of the manuscript, and agree with the order of presentation of the authors.

Conflict of interests

The authors declare that they have no competing interests.