A goal-driven modular neural network predicts parietofrontal neural dynamics during grasping

Significance

Grasping objects is something primates do effortlessly, but how does our brain coordinate such a complex task? Multiple brain areas across the parietal and frontal cortices of macaque monkeys are essential for shaping the hand during grasping, but we lack a comprehensive model of grasping from vision to action. In this work, we show that multiarea neural networks trained to reproduce the arm and hand control required for grasping using the visual features of objects also reproduced neural dynamics in grasping regions and the relationships between areas, outperforming alternative models. Simulated lesion experiments revealed unique deficits paralleling lesions to specific areas in the grasping circuit, providing a model of how these areas work together to drive behavior.

Abstract

One of the primary ways we interact with the world is using our hands. In macaques, the circuit spanning the anterior intraparietal area, the hand area of the ventral premotor cortex, and the primary motor cortex is necessary for transforming visual information into grasping movements. However, no comprehensive model exists that links all steps of processing from vision to action. We hypothesized that a recurrent neural network mimicking the modular structure of the anatomical circuit and trained to use visual features of objects to generate the required muscle dynamics used by primates to grasp objects would give insight into the computations of the grasping circuit. Internal activity of modular networks trained with these constraints strongly resembled neural activity recorded from the grasping circuit during grasping and paralleled the similarities between brain regions. Network activity during the different phases of the task could be explained by linear dynamics for maintaining a distributed movement plan across the network in the absence of visual stimulus and then generating the required muscle kinematics based on these initial conditions in a module-specific way. These modular models also outperformed alternative models at explaining neural data, despite the absence of neural data during training, suggesting that the inputs, outputs, and architectural constraints imposed were sufficient for recapitulating processing in the grasping circuit. Finally, targeted lesioning of modules produced deficits similar to those observed in lesion studies of the grasping circuit, providing a potential model for how brain regions may coordinate during the visually guided grasping of objects.

Interacting with objects is an essential part of daily life for primates. Grasping is one of our most complex behaviors, requiring the determination of object features and identity, followed by the execution of the correct temporal sequence of precise muscle patterns in the arm and hand necessary to reach and grasp the object. In macaque monkeys, the circuit formed by the anterior intraparietal area (AIP), the hand area (F5) of the ventral premotor cortex, and the hand area of the primary motor cortex (M1) is essential for grasping. These areas share extensive anatomical connections (1), forming a long-range circuit (Fig. 1A) where AIP receives the largest amount of visual information, and M1 has the largest output to the brainstem and spinal cord. All three areas have been shown to contain grasp-relevant information well before movement (2–7).

Fig. 1.

Frontoparietal grasping circuit and experimental design. (A) Simplified brain schematic of the frontoparietal grasping circuit. Visual information is processed in two parallel streams carrying primarily object features or identity information, both converging on the anterior intraparietal sulcus (AIP). AIP has strong reciprocal connections with the F5 of the ventral premotor cortex, which has strong reciprocal connections to the hand area of the M1. M1 has the majority of subcortical and spinal cord output projections. (B) Location of implanted floating microelectrode arrays, covering the three desired regions. Black dots represent ground and reference electrodes. A, anterior; AS, arcuate sulcus; CS, central sulcus; IPS, intraparietal sulcus; L, lateral; M, medial; P, posterior. (C) Monkeys sat in front of a motorized turntable that presented one of six objects to be grasped on any given trial. Multiple turntables presented in random order across sessions allowed for a total of 42 objects. Gloves with magnetic sensors allowed full tracking of arm and hand kinematics on single trials. Modified from ref. 8, which is licensed under CC BY 4.0. h. and v. correspond to horizontal and vertical cylinders, respectively. (D) Trials began with visual fixation of a red dot for a variable period. Objects were illuminated temporarily, and monkeys were required to withhold movement until a go cue (blinking of fixation dot) instructed them to grasp and lift the object in darkness. Eye fixation was enforced throughout each trial.

Reversible inactivation of AIP (9, 10) or F5 (11) results in a selective deficit in appropriately preshaping the hand during grasping, while M1 lesions lead to profound hand movement deficits (12–14), providing evidence that these areas are required for successful grasping. Additionally, M1 has the largest density of projections directly onto motor neurons for control of the fingers, and precise finger control does not normally recover after lesion (13, 14). So far, models of the grasping system have relied on manually tuning the properties of individual neurons to match the assumed role of a given region (15). No comprehensive model exists of the entire transformation between vision and action, limiting our ability to understand the flexibility of the grasping system.

Goal-driven modeling has emerged as a powerful tool for generating potential neural mechanisms explaining various behaviors (16). The creation of vast datasets of labeled images (Imagenet) (17) opened the door to studying the computational principles underlying object identification using convolutional neural networks (CNNs), such as Alexnet (18). Feed-forward modeling of the ventral stream using CNNs has led to powerful insights into the hierarchy of brain networks (19, 20), revealing that subsequent layers of CNNs trained to classify objects align well with brain regions along the ventral stream. Similar approaches have been used in retinal modeling (21) and recent studies incorporating recurrence into CNNs (22–24). In parallel, advances have been made in understanding motor cortex by modeling it as a dynamical system (25, 26) implemented as a recurrent neural network (RNN) (27–30). In these models, and likely in motor cortex (26), preparatory activity sets initial conditions that unfold predictably to control muscles during reaching.

In the current work, we bridge the gap between previous work in visual processing and motor control by modeling the entire processing pipeline from visual input to muscle control of the arm and hand. First, we recorded neural activity from AIP, F5, and M1 of two macaque monkeys while they grasped a diverse set of 42 objects. Neural activity in AIP during object viewing could be partially explained by visual features extracted from late layers of VGG (Visual Geometry Group) (31), a CNN trained to classify objects, while M1 activity during movement initiation could be partially explained by muscle kinematics (i.e., rate of change of muscle length), and F5 was generally intermediate between the two. Based on these results, we devised several neural network architectures to model the function of this circuit. Primarily, we trained a modular recurrent neural network (mRNN) with sparsely connected modules mimicking cortical areas to use visual features to produce the muscle kinematics required for grasping and found that it could explain large amounts of variance in neural activity (on average 65%), even though no neural activity was used during training. Interestingly, the different modules of the mRNN aligned with brain regions in the grasping circuit, suggesting that the structure of the model combined with the training goals was sufficient to generate interarea differences similar to those observed in the biological circuit. We analyzed the computational mechanisms employed by the network and found that the dynamics could be largely explained by a representation of the object to be grasped that was distributed across all modules and then used as an initial condition for unfolding the necessary motor commands in the final module. Furthermore, alternative models with different inputs, internal structure, or outputs were not able to explain neural data as well as mRNNs that transformed visual features into muscle kinematics. Interestingly, targeted lesioning of modules produced behavioral deficits that varied by module and paralleled deficits observed in previous lesion studies of these cortical areas, providing a potential explanation of how these cortical regions may complete this task in tandem.

Results

Kinematic and Neural Activity Recorded during a Many-Object Grasping Task.

We recorded neural activity in the interconnected AIP, the F5 of ventral premotor cortex, and the M1 using floating microelectrode arrays (Fig. 1 A and B) while two rhesus macaques (monkeys M and Z) performed a delayed grasping task. We presented monkeys with 42 objects composed of shapes of various sizes and orientations on a series of rotating turntables (Fig. 1C). Turntables were presented in random order each session. Experimental and behavioral findings have been presented in previous works (2, 8). Monkeys wore a glove that allowed full joint tracking (32) of the arm, hand, and fingers on single trials, and these data were further transformed into muscle space using a previously described musculoskeletal model (33, 34). On individual trials, monkeys had to fixate a red point just under each object, after which the object was illuminated temporarily. Monkeys then waited for a go cue in darkness, after which they reached to, grasped, and lifted the object (Fig. 1D).

We analyzed the data from 10 recording sessions per monkey (labeled M1 to M10 and Z1 to Z10). On average, each recording session of monkey M consisted of 549 ± 35 (mean ± SD) trials, and 153 ± 8, 179 ± 7, and 215 ± 14 single and multiunits were recorded from AIP, F5, and M1, respectively. On average, each recording session of monkey Z consisted of 490 ± 25 (mean ± SD) trials, and 122 ± 10, 137 ± 6, and 126 ± 9 single and multiunits were recorded from AIP, F5, and M1, respectively.

Previous work using this dataset (2, 8) has shown that this circuit is heavily modulated by the type of object being grasped, containing rich information about objects, both during the presentation and the intervening memory period, and representing temporal information about the kinematic signals required for grasping during movement. Next, we wanted to determine how visual information about grasp targets is used and transformed into the information necessary to execute grasping.

Visual and Kinematic Features Represented across the Grasping Circuit.

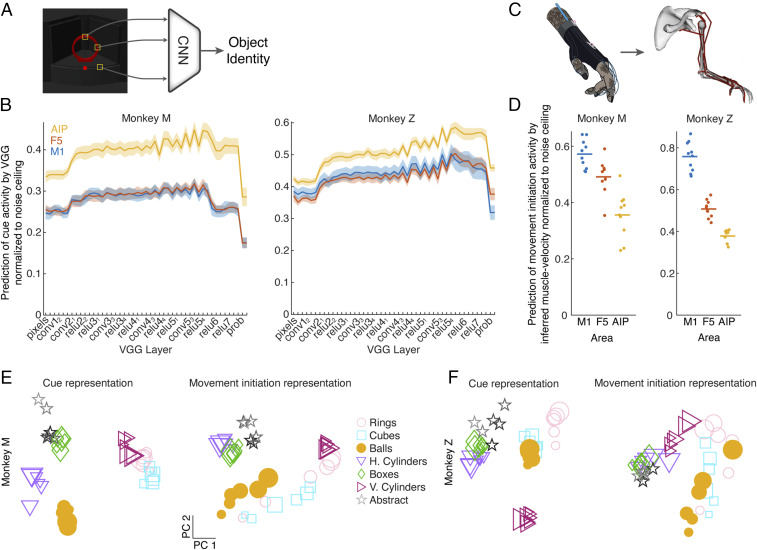
The first step in designing a model of the grasping circuit was determining what information may be available during the planning of grasping movements. Based on the established role of AIP in grasping and its connectivity to areas containing information about the size, shape, orientation, and identity of objects, we hypothesized that later layers of existing CNN models of the ventral stream may match input activity to AIP. We constructed simulated images of the task from the monkey’s perspective (SI Appendix, Fig. S1) and fed them into VGG (31) (Fig. 2A), a feed-forward CNN that was pretrained to classify objects in ImageNet (17). We did not retrain VGG on our stimulus set. We read out the hidden activity from each of the network layers and compared their ability to explain (i.e., predict) neural activity in each brain area averaged over the cue period when the object was visible using single-trial cross-validated regression (Methods). To control for differences in firing rate and recording quality between areas, we calculated a conservative estimate of the noise ceiling in each area (i.e., how reliably single-trial responses correlate to the mean of each condition) (Methods) and normalized the regression results for each unit to that value. Then, we took the median fit across all units within each recording session and plot the mean result across recording sessions in Fig. 2B. A normalized value around one would indicate that a set of predictors captures the condition-dependent neural features as well as can be expected given the single-trial variability of the recorded data.

Fig. 2.

Visual and kinematic features explain neural activity across the frontoparietal grasping circuit. (A) Simulated images of all objects were fed through a multilayer CNN pretrained to classify objects (VGG) (Methods). (B) Single-trial neural activity of each unit averaged during the cue period was regressed (leave one out cross-validated) against the representation of all objects in each layer of the CNN (first 20 PCs), and the median fit was taken over all units within one recording session. The solid lines and error surfaces represent the means and SEMs, respectively, over all recording sessions of each monkey. To ensure that results were not due to varying signal quality or firing rate between areas, regression results were normalized to the noise ceiling of each unit (Methods). conv refers to layers using convolution, relu to layers using rectified linear units, and prob to the probability layer. (C) Joint angles (27 degrees of freedom) recorded while monkeys performed the task were transformed into muscle length space (50 degrees of freedom) using a musculoskeletal model (Methods). For visualization purposes, not all muscles are shown. (D) Single-trial neural activity of each unit averaged during the movement initiation period (200 ms before to 200 ms after movement onset) was regressed (leave one out cross-validated) against the inferred muscle velocity of all grasping conditions averaged over the same time period. As in B, regression results were normalized to the noise ceiling of each unit. Each point represents one recording session of each monkey. (E) Example neural representation (first two PCs) of each object across all three areas during the cue period and during movement initiation (session M7). The size of each marker indicates the relative size of each grasping object. h. and v. correspond to horizontal and vertical cylinders, respectively. (F) Same as E but for session Z9.

As predicted, VGG features better explained single-trial activity in AIP than in F5 or M1 (Fig. 2B, monkey M: F5 and M1, paired t test P < 0.001, P < 0.001; monkey Z: F5 and M1, paired t test P < 0.001, P < 0.001), and the later layers of VGG (e.g., relu5_4 layer) predicted activity in AIP better than the early layers (pixel layer, monkey M: paired t test P < 0.001; monkey Z: paired t test P < 0.001), suggesting that VGG produced features that were more predictive of neural activity in AIP than pure pixel information. Similar results were obtained for nonnormalized values (SI Appendix, Fig. S2A, monkey M: F5 and M1, paired t test P < 0.001, P < 0.001; monkey Z: F5 and M1, paired t test P < 0.001, P < 0.001; relu5_4 vs. pixel layer, monkey M: paired t test P < 0.001; monkey Z: paired t test P < 0.001). Very similar results were obtained by feeding our images through both Alexnet (18) or Resnet (35), two widely used CNN architectures.

Having established that later layers of a CNN trained to classify objects provide natural inputs to AIP, the next step was to determine reasonable outputs of the grasping circuit. As mentioned previously, monkeys wore a tracking glove (32) that allowed the extraction of 27 degrees of freedom of movement information, almost completely capturing reach to grasp movement trajectories. The joint angle signal was further transformed into a 50-dimensional muscle space using a musculoskeletal model of the primate arm and hand (34) (Fig. 2C), allowing detailed access to muscle kinematics in the hand that would be very difficult to obtain using single-muscle recording techniques. While this model does not give us direct access to muscle force or activity, it provides a kinematic signal that bears many similarities to muscle activity, especially during the early portion of the movement before the hand contacts the object. We opted to analyze the rate of change of muscle length (muscle velocity) since it is invariant to starting hand posture. Similar to the analysis of visual features, we used a 50-dimensional muscle velocity signal to predict the single-trial activity of individual units near movement initiation (average activity 200 ms before to 200 ms after movement onset), again normalizing to the noise ceiling of each unit. Muscle features better predicted activity in M1 than F5 or AIP (Fig. 2D, monkey M: F5 and AIP, paired t test P = 0.015, P < 0.001; monkey Z: F5 and AIP, paired t test P < 0.001, P < 0.001), and similar results were obtained for nonnormalized values (SI Appendix, Fig. S2B, monkey M: F5 and AIP, paired t test P = 0.021, P < 0.001; monkey Z: F5 and AIP, paired t test P < 0.001, P < 0.001).

Together, these results suggest a visuomotor gradient from AIP to F5 to M1 that transforms visual features of objects into muscle kinematic signals. In Fig. 2 E and F, we visualize the relationship between the representation of different objects and sizes of objects in the two neural dimensions of largest variability, showing how the relationship between objects is reorganized between the cue and movement periods (SI Appendix, Fig. S3 shows equivalent visualization of all CNN layers). For example, while size does not seem to play a large role in the cue period, some objects are organized by size during movement initiation in both monkeys (balls, cubes, rings). An alternative way to visualize the relationship between conditions is by calculating the Euclidean distance between the mean activity of each pair of conditions in the full neural space of each area (SI Appendix, Fig. S2C) and then correlating this representational similarity matrix between the cue and movement initiation periods. Overall, this analysis revealed that there appears to be changes in the representation of conditions in all areas, with larger shifts occurring in M1 and less so in AIP (mean r value across sessions of monkey M: 0.53 ± 0.17 in M1, 0.55 ± 0.05 in F5, 0.68 ± 0.15 in AIP; mean r value across sessions of monkey Z: 0.27 ± 0.18 in M1, 0.64 ± 0.08 in F5, 0.72 ± 0.10 in AIP). Extending this analysis to show how the similarity between neural activity and either visual or muscle features changed over the course of the trial, it was clear that across the grasping circuit, the similarity to visual features (VGG layer relu5_4) decreased across the course of the trial after the cue period, while the similarity to muscle features increased toward movement onset (SI Appendix, Fig. S2D), reinforcing the finding that representations across the circuit shift from visual to muscle-centric. However, these analyses only provide high-level descriptions of the neural activity and cannot explain the temporal evolution of neural population activity nor the computational mechanisms required to complete the task. One of the goals of the current work is to provide potential explanations of how such activity may be maintained across the grasping circuit and why this representation is useful for movement generation.

A Modular Recurrent Neural Network Model of Vision to Hand Action.

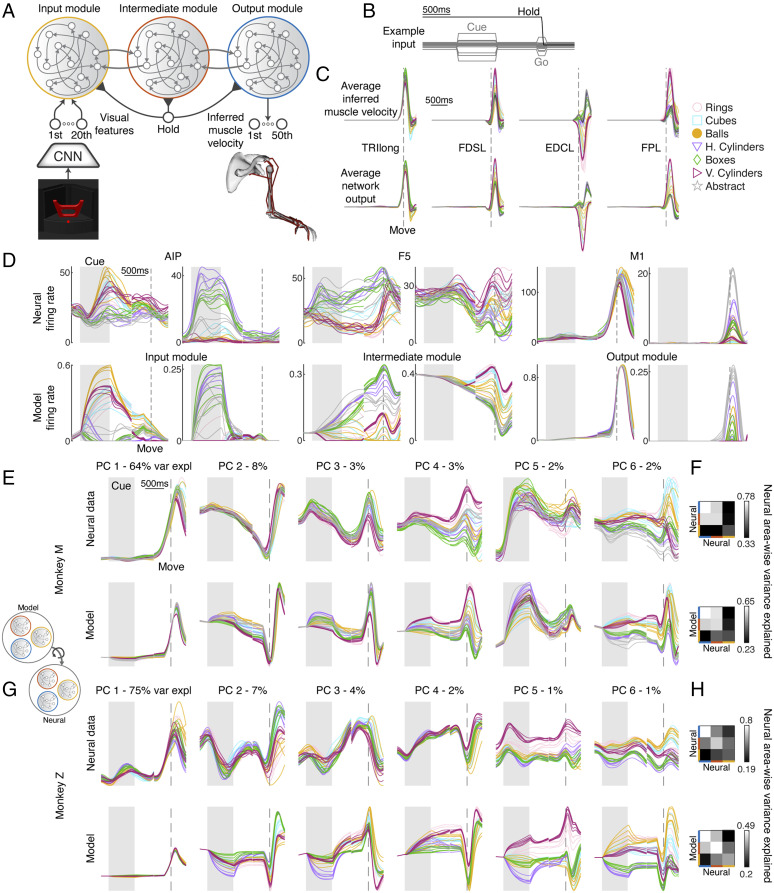
To build a comprehensive model of the grasping circuit incorporating temporal dynamics, we devised an mRNN inspired by the above results and the known anatomical connectivity of the grasping circuit (Methods). The model consisted of three interconnected stages designed to reproduce the muscle dynamics necessary to grasp objects (Fig. 3A). The visual input was a 20-dimensional visual feature signal consisting of the first 20 principal components (PCs) of the features in one of the layers of VGG (relu5_4) that was a good match to AIP activity while viewing the simulated images. This visual signal entered the input module, a fully connected RNN (all modules used a saturating nonlinearity, the rectified hyperbolic tangent ReTanh), that relayed information to the intermediate module through sparse connectivity (10%). Similarly, the intermediate module projected to the output module sparsely, and equally sparse feedback connections existed for each of the feed-forward connections. In order to match kinematic timing, all three modules received a hold signal that cued movements 200 ms before desired movement onset, which was approximately when the monkey’s hand lifted off of a handrest button. The output module was most directly responsible for generating the 50-dimensional muscle velocity signal required to grasp each object up to 400 ms into movement and to suppress movement earlier in the trial. Fig. 3B shows inputs for an example trial, including the visual cue signal and the hold signal. During the fixation, memory, and movement periods only, the fixation point was presented, while during the go cue, the fixation point disappeared for 100 ms.

Fig. 3.

The mRNN model of the frontoparietal grasping circuit. (A) Schematic of neural network model. Visual features of each object (first 20 PCs of relu5_4 layer) were fed into an input module, which is sparsely reciprocally connected to an intermediate module that is similarly connected to an output module. The output module must recapitulate the inferred muscle velocity for every object grasped by the monkey. Every module received a hold signal that was released 200 ms prior to movement onset. (B) Example input for an exemplary trial. (C) Average muscle velocity for four example muscles showing exemplar recorded kinematics and network output (session M2). EDCL, extensor digitorum communis digit 5; FDSL, flexor digitorum superficialis digit 5; FPL, flexor pollicis longus; TRIlong, triceps long head. h. and v. correspond to horizontal and vertical cylinders, respectively. (D) Two example units from each pair of modules and brain regions showing similar properties and highlighting common features of each area. Traces were aligned to two events, cue onset and movement onset, and concatenated together. The shaded gray areas represent the cue period, while the dashed lines represent movement onset. (E) Procrustes analysis (Overall Fit) comparing the dynamics of an exemplar mRNN model (ReTanh activation function, rate regularization: 1e-1; weight regularization: 1e-5; intermodule sparsity, 0.1) with neural data recorded from AIP, F5, and M1 (session M2). For visualization purposes, after model data were fit to neural data it was projected onto the first six PCs defined on the neural data, and percentages show variance explained (var expl) in the neural data per PC. (F) Pairwise Procrustes was performed between each brain region and a resampled version of its own activity (Upper) or between each module and brain region (Interarea Fit; Lower). Individual rows and columns specify from top to bottom and from left to right either the output, intermediate, and input module or M1, F5, and AIP, respectively. (G and H) Same as E and F but for session Z4. For C–E and G, the multiple traces for each type of object represent the different sizes within a turntable.

We used an optimization procedure (Hessian-free optimization) (Methods) to train a series of networks to recapitulate the movement behavior of each monkey while also varying many aspects of the network architecture or regularization (total of 1,760 trained networks, architectures detailed in later sections). Each network was trained to reproduce the average muscle velocity of each condition using a random set of two trials (42 conditions × two examples) where the timing parameters of each example were drawn randomly from the set of timing parameters observed during the monkey experiments (Fig. 1D). It is crucial to emphasize that no neural data were used in any training procedure, allowing us to compare the neural dynamics of the recorded data with the internal dynamics of our model. Trained networks were very successful in reproducing the desired muscle kinematics (Fig. 3C), achieving low levels of normalized error (average of 6% for unregularized networks). In addition to successful recapitulation of muscle kinematics, networks were also able to suppress output before the movement period and maintain an internal representation of the task conditions in the absence of a visual cue.

In addition to the task goal, we tested the effect of common constraints during training via two regularizations (Methods): 1) a cost on the firing rate of all neurons (L2 rate) and 2) a cost in the input and output weights of the network (L2 weight). Hyperparameters for each regularization were tested systematically in a later analysis, and an exemplar network with an L2 rate regularization of 1e-1 and an L2 weight regularization of 1e-5 is analyzed in the following section.

mRNN Model with Visual Feature Input Reproduces Single-Unit, Population-Level, and Area-Wise Neural Dynamics.

To gain an initial intuition of how the hidden state of the regularized mRNN compared with neural data, we plotted the average firing rates of six example units that showcase the similarities between the modules and the brain regions of interest (Fig. 3D). Units in AIP and the input module were often characterized by large responses to the visual cue that were either partially maintained through the memory period into movement or decayed rapidly after the disappearance of the stimulus. Units in F5 and the intermediate module often showed sustained responses throughout the trial that were sensitive to time within the trial. M1 and output module units showed the largest response during movement itself but often had stable or ramping activity earlier in the trial.

While these example units are useful insights into both the simulation and the neural data, a proper characterization requires a full analysis of the neural population dynamics. To capture similarities between the population dynamics of neural and simulated data, we devised a number of metrics based on Procrustes analysis (36). Imagine we have two shapes in front of us (for example, a square and a triangle) consisting of the set of two-dimensional points that make up each shape. If we would like to see if it is possible to overlap the triangle on the square without distorting the overall shapes, Procrustes analysis provides a method for finding the optimal rotation that aligns them in arbitrary dimensionality (Methods). This method is ideal for comparing model and neural data, where the square represents the activity of model data and the triangle of the neural data. Procrustes does not distort the variance structure of either set of data, and similar methods based on dot product similarity have been shown to be ideal for comparing artificial neural networks (37, 38). Other commonly used methods, such as canonical correlation analysis, distort the amount of variance explained by individual units, although this can be alleviated somewhat by first performing PC analysis to constrain the analysis to dimensions of highest variance (27, 39, 40).

Throughout the following sections, we make use of Procrustes in three ways in order to test how well our model was able to capture neural data. Using the condition averaged activity over the course of the trial (same time windows and alignment as in Fig. 3D) for both model data and neural data while pooling across all modules or brain regions, we used Procrustes to find how much variance in the neural data could be explained by the model data across all areas (Methods), terming this Overall Fit. The example mRNN network in Fig. 3 was able to explain 65% of the variance in neural data averaged across recording sessions. We also performed Procrustes where each module was fit to the brain region it was expected to match and then averaged those three variance-explained values to produce the Area-Wise Fit, which was 54% for the example network across recording sessions (SI Appendix, Fig. S4 has an example visualization). Finally, we computed pairwise Procrustes of each module to each brain region and correlated the similarity matrix between all pairs with an estimate of the expected relationship between brain regions using resampled Procrustes (Methods), termed Interarea Fit, yielding an average correlation of 0.91 for the example mRNN across recording sessions.

To help understand these quantitative results, the results of the Overall Fit analysis are visualized in Fig. 3 E and G, comparing the dynamics of an exemplar mRNN with neural data across all brain regions. For visualization purposes, after transforming the model data across all modules onto the neural data across all brain regions (Methods), the resulting model data were projected onto the first six PCs defined by the covariance of the neural data. For both monkeys, there was a striking similarity between the simulations and the neural data, both in terms of temporal properties throughout the trial and how the different grasp conditions were organized. Temporal features were the most dominant, similar to previous work (41), while the more condition-dependent signals were captured by dimensions of relatively small variance. Interestingly, visualizing the similarity matrices for the Interarea Fit analysis (Fig. 3 F and H) shows that the modules within the model best explained the brain regions they were expected to match. Overall, these results suggest that the modules of the mRNN model very well reproduced the unique features of the three brain regions investigated simply by having reasonable inputs, outputs, and modular structure, despite the fact that the modules themselves were not trained to resemble neural activity of any particular region.

In the previous paragraph, we found that a modular network with a saturating nonlinearity (ReTanh), rate and weight regularization, and 10% connectivity between modules was a good match to the neural circuit. To explore how our choice of network parameters affected these results, we systematically tested (SI Appendix, Fig. S5A) the effect of activation function, rate regularization, weight regularization, and intermodule sparsity on the three metrics presented above (SI Appendix, Fig. S5 B–D), additionally generating and training five networks for each choice of hyperparameters and averaging across the five repetitions. The results of these analyses showed small effects of activation function (ReTanh best, in contrast to ref. 42), rate regularization (1e-2 best), and weight regularization (no regularization best) across metrics. Sparsity between modules had the largest effect on Interarea Fit (SI Appendix, Fig. S5E), showing a poor fit when the modules were fully connected and the best fit when modules were 10% connected, suggesting that an intermediate level of sparsity was required to properly model the interarea differences. In many cases, the highest level of weight regularization increased error significantly on the task (SI Appendix, Fig. S6), so these networks were excluded from further analysis. Two example networks illustrate how the fits to neural data were not as good for ReLU (rectified linear unit) networks with no sparsity between modules (SI Appendix, Fig. S5 H and I) or ReTanh networks with 10% sparsity but no regularization (SI Appendix, Fig. S5 J and K) as compared with our exemplar mRNN network (Fig. 3). Overall, this analysis suggests relatively minor differences between choices of hyperparameters. However, later analysis will show that predictions of regularized networks differ significantly from unregularized networks in the case of lesions.

Modular Mechanisms of Memory and Movement Execution within the mRNN Model.

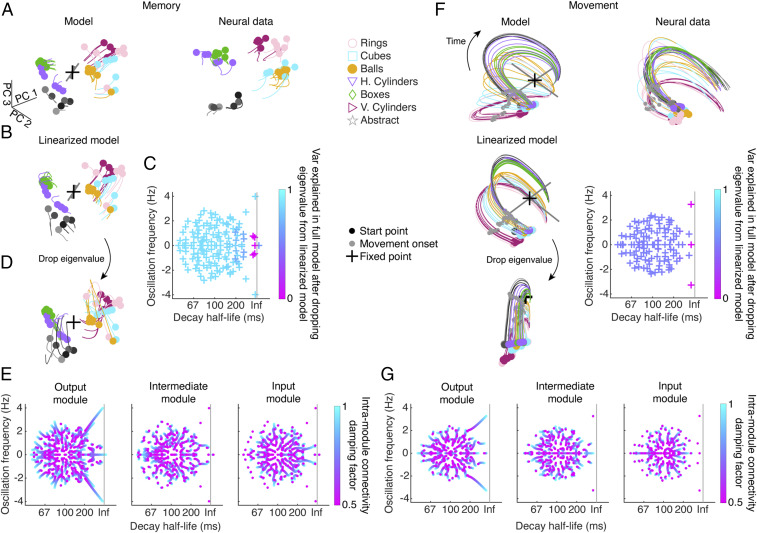
Earlier in Fig. 2, we quantified how the representation of the task conditions within the grasping circuit shifted between visual cue onset and movement onset, posing the question of how this activity is maintained and why this representation is useful for generating muscle activity. Since our models are fully observable, we were able to probe our mRNN networks for explanations of the computations necessary for the task using fixed point analysis (27, 43, 44). In fixed point analysis, we perform an optimization to look for approximate equilibrium points in the activity of the network, linearize the dynamics around these points, and interpret the properties of these linear dynamics to gain insight into what computations govern the network dynamics (Methods). Whenever the input to a system changes, the fixed point structure changes. Therefore, we opted to perform this analysis jointly across all modules of the network during the memory and movement periods when inputs were stable.

During both the memory and movement periods, we generally found a single unique fixed point. By visualizing the activity of the model during the memory period in the first three PCs, we can see that the general effect of the fixed point was to maintain a representation of the task conditions that also evolved slowly (Fig. 4A), similar to the neural data. Next, we could ask how well that fixed point could account for the dynamics of the full model by replacing the network by the linear system around that fixed point (Fig. 4B), showing a strong match (88% variance explained). To understand the precise computational mechanism involved, we performed linear stability analysis on the linearized model, visualizing the complex eigenvalue spectrum (Fig. 4C). Importantly, to figure out which eigenvalues were most responsible for the fit of the linearized to the full model, we removed each complex conjugate eigenvalue pair sequentially and reran the dynamics, showing that when three specific eigenvalue pairs were removed (Fig. 4C, pink and Methods), the fit of the linearization to the full model degraded to zero (Fig. 4 C and D). Interestingly, these were all eigenvalue pairs with real and imaginary parts near zero, which are eigenvalues with very slow dynamics and no oscillatory component, suggesting that the crucial mechanism of the network during the memory period is to keep activity near the location it was set during the cue period, acting like a sheet attractor. In this way, the representation of the conditions is maintained throughout the memory period. Finally, we asked if the underlying dynamics of these slow eigenvalue pairs were localized to a particular module or distributed across the network. To do this, we iteratively damped the intra-area connectivity of each module and then recalculated the linear stability around the fixed point, tracking how the eigenvalues changed (Fig. 4E and Methods) and showing that some eigenvalues decayed when damping a module, while others did not. The results of this analysis showed that each of the three eigenvalue pairs that had been responsible for maintaining memory period activity was localized to each of the three modules, indicating that the overall maintenance of memory period activity was distributed across the three modules.

Fig. 4.

Modular mechanisms of memory and movement execution in the mRNN model. Fixed point analysis was performed to understand the computational mechanism used by the mRNN model to complete the task. (A, Left) The single fixed point of an exemplar mRNN model (same parameters as in Fig. 3) during the memory period (cue offset + 50 ms to cue offset + 500 ms) plotted in the first three model PCs alongside condition average activity. The eigenvectors of the two largest eigenvalues are plotted (gray), scaled by the magnitude of the eigenvalue. (A, Right) Condition average neural data from an example session (M6) over the same time period projected into the activity of the model using Procrustes. h. and v. correspond to horizontal and vertical cylinders, respectively. (B) Replacing the full nonlinear model with the linearized system around the fixed point yields very similar trajectories. (C) The complex eigenvalue spectrum for the fixed point in A and B (Inf corresponds to modes that do not decay). To determine which eigenvalues were essential for the linear dynamics, we removed individual eigenvalues and reran the dynamics (Methods), showing that removing certain eigenvalues decreased the variance explained (var explained) in the full model. (D) An example of removing one of the more important eigenvalues, in this case with a decay close to Inf and an oscillation frequency close to zero. In the equivalent movement period example, the large oscillatory mode was removed. (E) To determine which modules were contributing to the most essential eigenvalues, we damped synaptic weights within each module and recalculated the linear stability of the Jacobian (Methods), showing how the eigenvalues shift. For the memory period, the three most important eigenvalues, which all had slow decay, were distributed across the three modules. (F and G) Same analyses as in A–E for the movement period (150 ms before movement onset to 400 ms after movement onset). For the movement period, the oscillatory mode was localized in the output module, while a slow, nonoscillatory mode was localized mostly in the intermediate module.

We repeated the same analysis during the movement period and found a single fixed point (Fig. 4F) that activity seemed to oscillate around. After linearizing the model around this point, the dynamics were still a good match to the full model (50% variance explained). Performing the same eigenvalue dropping analysis, we found that two eigenvalue pairs were responsible, one with real and imaginary parts close to zero that kept the conditions from collapsing their activity together and one with real part close to zero and a large imaginary part, leading to a stable oscillation around this point. We performed the same damping analysis to disambiguate the contributions of the modules to these important eigenvalue pairs and found that by far the most important contributor was the output module, which was the origin of the oscillatory mode, while the intermediate module contributed to the slow eigenvalue pair somewhat along with the output module, and the input module did not contribute at all (Fig. 4G). The activity that had been set up by the network and maintained during the memory period set the ideal initial conditions for generating the required muscle kinematics during the movement period, suggesting a potential way how desired muscle kinematics may be generated in the grasping circuit following a memory period in the absence of a visual stimulus.

mRNN Model Outperforms Tested Alternative Models in Explaining Neural Data in the Grasping Circuit.

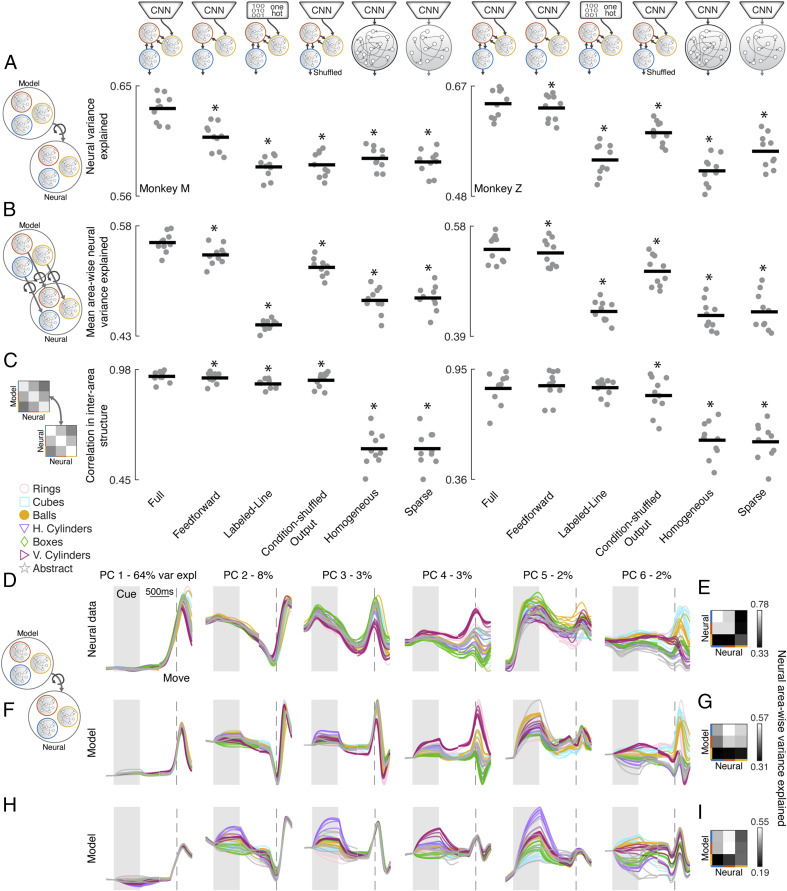
In the previous sections, we have shown that mRNN models with visual feature input from later layers of an object classification CNN and trained to produce the muscle dynamics necessary for grasping were able to explain neural dynamics and interarea differences across the AIP, F5, M1 grasping circuit. However, it was essential to test some alternative models to determine which of these design choices were most essential in producing this result. We tested five alternative models in addition to the Full mRNN model: 1) an mRNN model with only feed-forward connections between modules (Feed Forward) to test the necessity of top-down feedback; 2) an mRNN model receiving a labeled line input, where each condition is represented by a separate input dimension (Labeled Line) to see if equivalent visual inputs could develop by training on motor output alone; 3) an mRNN model with output conditions reassigned between grasping objects (Condition-Shuffled Output) to test if the precise matching between kinematics and neural data was necessary; 4) a fully connected network (Homogeneous) to test if modular processing is necessary; or 5) a sparsely connected network (Sparse) where the sparsity of the input, hidden, and output synaptic weights was matched to the sparsity of the Full model. Therefore, this model did not have explicit modules, but the total number of connections matched the Full mRNN model.

All these alternative models were able to achieve task error similar to the Full model (average 5%) and were trained for the same set of rate and weight regularizations as previous models (SI Appendix, Fig. S5). The results of the best set of regularizations across metrics (chosen separately for each architecture) are shown for each of the three previously introduced metrics in Fig. 5 A–C. Similar results are obtained if instead results are averaged across all sets of regularization parameters. The Overall Fit analysis across all brain regions revealed that all models performed more poorly than the Full model (Fig. 5A) (paired t test, P < 0.01), a result that was replicated when considering Area-Wise Fit (Fig. 5B). Comparing the Interarea Fit between models showed that in general the same result held (Fig. 5C), although not significantly for the Feed Forward and Labeled Line networks in monkey Z. It is important to note that we are not suggesting that a strictly three-module network is necessary for explaining neural data in the grasping circuit but rather, that multimodule networks with distinct modules can explain neural data better than these alternative models. Three were a natural choice based on the anatomical connectivity of AIP, F5, and M1, as well as our access to recordings from all three regions. Two example networks illustrate how the fits to neural data were not as good for Homogeneous models (Fig. 5 F and G) or Condition-Shuffled Output models (Fig. 5 H and I) as compared with our exemplar mRNN network (Fig. 3). Overall, these model comparisons reinforce that the introduction of modules into our network design did in fact improve the ability of the model to fit neural data, suggesting that a modular architecture may be an important feature of the biological network. Furthermore, modular networks that received visual feature input outperformed Labeled Line networks, suggesting that the inputs to AIP cannot simply be understood as optimizing a motor goal but consider the visual features of the objects. Modular networks that included feedback connections between modules performed best, suggesting a role of top-down feedback. Finally, networks that produced the muscle kinematics of grasping outperformed shuffled versions of the kinematic output, suggesting that the precise configuration of the conditions was meaningful, in line with the results of the fixed point analysis showing that a single fixed point could explain movement dynamics that evolved predictably given the right initial conditions for each specific motor plan.

Fig. 5.

mRNN outperforms tested alternative models in explaining neural data in the grasping circuit. (A) Average neural variance explained per recording session for the best set of regularization parameters for each architecture (averaged over five runs) for each of the three proposed metrics, Overall Fit (A), Area-Wise Fit (B), and Interarea Fit (C). Horizontal bars represent the mean, and each dot represents a single session. We tested five alternative models in addition to the Full model: 1) mRNN model with only feed-forward connections between modules; 2) mRNN model receiving a labeled line input (one hot), where each condition is represented by a separate input dimension; 3) mRNN model with output conditions shuffled (objects reassigned); 4) homogeneous, fully connected network; or 5) a single, sparsely connected network with the total number of synaptic connections matched to the Full model. *Significant difference as compared with the Full model (paired t test, P < 0.01). (D, F, and H) Procrustes analysis (Overall Fit) comparing the dynamics of two exemplar models with neural data across all brain regions (session M2). For visualization purposes, after model data were fit to neural data they were projected onto the first six PCs defined on the neural data, and percentages show variance explained (var expl) in the neural data per PC. h. and v. correspond to horizontal and vertical cylinders, respectively. Pairwise Procrustes was performed (E) between each brain region and a resampled version of its own activity or (G and I) between each module and brain region (Interarea Fit). Individual rows and columns specify from top to bottom and from left to right either the output, intermediate, and input module or M1, F5, and AIP, respectively. (F) Exemplar model with the parameters (homogeneous model, ReTanh activation function, L2 rate regularization, 1e-1; L2 weight regularization, 1e-5; intermodule sparsity, 0.1). (H) Exemplar model with the parameters (condition-shuffled output model, ReTanh activation function, rate regularization, 1e-1; weight regularization, 1e-5; intermodule sparsity, 0.1). For D, F, and H, the multiple traces for each type of object represent the different sizes within a turntable.

We repeated the fixed point analysis from Fig. 4 for every network architecture but found only minor differences between fixed point topologies employed by the different models, suggesting that this solution 1) is a parsimonious solution regardless of network architecture and 2) is primarily a function of the task goal being optimized and not the architecture.

Targeted Lesioning of Modules in Rate-Regularized mRNNs Reproduces Behavioral Deficits Observed in the Biological Circuit.

When M1 is lesioned, macaque monkeys lose the ability to shape the digits of the hand (13, 14), movements become smaller in amplitude, and the precise timing of muscle control is severely affected (12). On the other hand, reversible inactivation of either F5 or AIP causes monkeys to generate inappropriate hand shapes for the object they are grasping, mostly maintaining their ability to grasp after making contact with the object (9, 11).

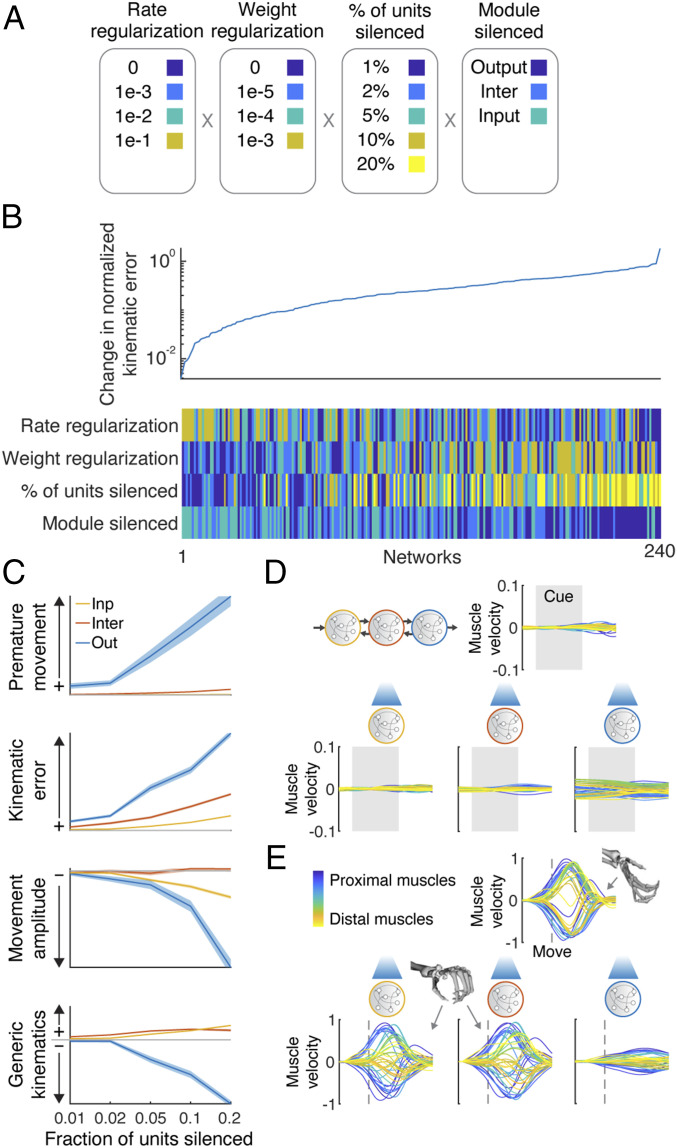
Given the success of the mRNN models in explaining neural dynamics and interarea differences in the grasping circuit, we were curious what behavioral deficits would be predicted from targeted lesioning of each module by silencing random subsets of neurons for the entire trial. We performed silencing with 240 variations, with each experiment additionally repeated 100 times with a different subset of neurons (Fig. 6A). When considering normalized kinematic error (Fig. 6B), it was clear that 1) networks with large amounts of rate regularization performed best and 2) network performance clustered by module silenced, with best to worst ordered from input to output, respectively. To further examine the effect of silencing on the different modules, we examined four behavioral metrics for networks with the highest levels of rate regularization.

Fig. 6.

Targeted lesioning of rate-regularized modular networks produces unique behavioral deficits. (A) Activity within 240 networks was artificially silenced, varying the rate and weight regularizations, percent of units silenced (repeated 100 times with random units), and the module being silenced. (B) Average change in normalized kinematic error after silencing as compared with normal operation. (C) Changes in network behavior as a function of module and number of units silenced for an exemplar network with high robustness to silencing (i.e., high rate regularization). Premature movement refers to the change in variance of output behavior before movement was initiated. Kinematic error refers to the change in normalized kinematic error during the movement period. Movement amplitude refers to the change in absolute movement kinematics during the movement period. Generic kinematics refers to the change in normalized error in output behavior as compared with the mean kinematic behavior across all conditions. Shaded error bars represent SEM over 100 lesion repetitions. (D) Example network output before movement where 20% of the units in each module were silenced (example condition: midsized cylinder). (E) Example network output during the movement without silencing (Upper; midsized cylinder) and when 20% of the units in each module were silenced (Lower), showing that hand shape was not matched to the object (midsized cylinder) when the input or intermediate module was silenced (similar to the grip for the small cube or ball) while being degraded by silencing of the output module.

Silencing the output module increased the kinematic error (normalized variance explained) during the premovement period, while this was not the case for the other modules (premature movement) (Fig. 6 C and D). The effect of silencing on overall kinematic error was graded by module, having the largest effect on the output module and least on the input module. Additionally, the absolute amplitude of movement kinematics was attenuated when the output module was silenced but less so when the other modules were silenced. Finally, we noticed that increasing the number of units silenced in the output module led to degraded behavior that lacked the spatiotemporal dynamics necessary for the task (Fig. 6E). Interestingly, performing the same lesioning to the intermediate and input modules did not degrade behavior but rather, seemed to produce hand shapes that were not appropriate for the target object (Fig. 6E). We quantified this effect by calculating how “generic” kinematics were during the movement period (i.e., what is the normalized error between the output of the network and the mean of the target kinematics across all conditions) (Fig. 6C). Output behavior became more generic for lesions to the input or intermediate module, looking more like the mean kinematics across conditions, in this case most similar to the hand shape required for a small cube or ball. In light of the analysis in Fig. 4, these results suggest that when too many units in the input or intermediate module are silenced, it becomes difficult for the network to maintain the proper representation of the task conditions. However, since the output module is not damaged, the output of the network still resembles correct movements, but the instructions to the output module are more generic and not correctly matching the object presented. Similar results were obtained using rate-regularized feed-forward mRNNs. However, unregularized mRNN models did not show these unique behavioral deficits but rather, showed very similar deficits regardless of module silenced.

Interestingly, silencing all inputs to the output module from the intermediate module immediately after releasing the hold signal produced only minor deficits in the firing rate-regularized mRNN (∼10% normalized error) while catastrophically eliminating behavior in the nonregularized networks. This result suggests that the output module (M1) may be able to produce the required kinematics semiautonomously during movement when firing rates are encouraged to keep from saturating, a hypothesis that has not been tested in the biological circuit.

Overall, these results show that targeted lesioning of modules with rate-regularized mRNNs resembled behavioral deficits observed when lesioning the biological circuit, suggesting that our mRNN may be able to explain specific motor deficits observed in a number of previous studies and that firing rate minimization may be an organizational principle across cortical regions.

Discussion

In this work, we demonstrated that mRNNs trained to complete a complex behavioral task can strongly resemble the processing pipeline for grasping and the inter-area differences observed in the brain, and they can reproduce behavioral deficits caused by lesioning. These mRNNs took in pixel data through a CNN and transformed them into the temporal muscle kinematics necessary to grasp various objects. Importantly, no neural data were involved in the model training procedure.

Visual features of objects, as extracted by a CNN trained to classify objects, provided inputs necessary to complete the task and fit neural data better than tested alternative models, including networks with a simple labeled line code or without modularity. Our results connect the many works on neural networks for object classification in the ventral stream (16, 20, 45) to grasp movement generation by showing that the features extracted by such networks are useful for generating grasping movements to learned objects and that modular network models are useful for understanding the dorsal and ventral streams.

The visual inputs to our model were supplied by a CNN that has been generally compared with the ventral stream. This stream has primarily been implicated in object identity processing, while the dorsal stream is largely implicated in spatial localization (46). Why was this network able to perform so well, despite the fact that AIP lies along the dorsal stream? We propose three reasons. First, AIP is involved in extracting shape information for grasping (47), a process that likely requires the extraction of similar features to those useful for determining object identity. Second, AIP is strongly connected to ventral areas in the inferotemporal cortex, including TEa/m (48, 49), and areas in the temporal cortex essential for three-dimensional (3D) shape perception (50). These areas are thought to interact during 3D object viewing (51) and are possible routes by which AIP could receive object identity information from the ventral stream. Lastly, in this task objects are only in one spatial location, essentially eliminating the need for a “where” code that differs between objects, a dominant feature of the dorsal stream.

We found that architectures containing feedback between modules outperformed architectures with only feed-forward connections at explaining neural data. However, these differences were relatively small, even though strong feedback connections exist in the anatomical circuit. The likely reason for this is that the task modeled in the current study is very feed forward in nature. After the monkeys were trained on all objects, the object presented to the monkey on any given trial uniquely determined the grasp plan required to lift the object. These feedback connections would likely come into play in different tasks, which have rules that determine how an object should be grasped in a given context. The object identity information that is relayed to AIP from TEa/m is also communicated to ventrolateral prefrontal cortex areas 46v (52) and 12r (53), which relay back to F5 and AIP (15, 54, 55). These provide an anatomical substrate for context-dependent motor planning in the AIP–F5 circuit, something not explored in the current study. Future experiments should investigate objects in various locations, with rules and context, and try to close the loop by looking at haptic feedback from S2 (secondary somatosensory cortex) to AIP (49) and F5 (55).

Fixed point analysis revealed that the maintenance of the memory of the different objects in the mRNN networks could be explained by a single fixed point acting as a sheet attractor to keep activity largely in place in the absence of input, similar to models of working memory in LIP/PFC (lateral intraparietal area/prefrontal cortex) (44). Interestingly, all three modules seemed to be involved in the maintenance of this representation, suggesting that the brain may maintain this information in a distributed fashion across areas. The organization of task conditions was appropriate to set the initial conditions required to generate oscillatory patterns for grasping movements, which relied almost entirely on the output module, paralleling results in the arm area of motor cortex (26–28, 56, 57) and suggesting that the initiation of grasping movements can be understood very similarly to reaching movements under the dynamical systems perspective (25).

The fixed point topology of networks with differing architectures tended to be similar, even in nonmodular networks. Previous work has shown that this is often the case in RNNs of differing architectures trained to solve the same task (40). However, this does not preclude different predictions of these networks. For example, we found that modular networks regularized by firing rate predicted the behavioral deficits resulting from lesions to these areas, while nonregularized networks, or networks without modularity, could not. These results seem to suggest that selection of the task goal is vastly more important for the resulting solutions than the architecture, although other studies have shown that particular regularization choices influence the fixed point structure (27). Future work should put heavy emphasis on testing the differential effects of task goal, network architecture, and optimization procedure (58).

The density of long-distance connectivity between areas is predicted to decrease with increasing brain size (59), likely following organizational principles of cortical geometry and an exponential distance rule (60, 61). However, it is not clear what computational benefit is bestowed by increased sparsity in the cortical graph. Communication efficiency appears to be largely conserved between the monkey and the mouse, even though the cortical graph of the mouse is much more dense (62), while some work suggests that modular neural architectures support higher complexity in neural dynamics (63, 64). Overall, the current work is consistent with the notion that connectivity between cortical areas in the macaque may be intermediately sparse, while the computational benefits and potential pitfalls (65) of such connectivity require further study.

Our lesion results provide intriguing evidence of how different behavioral deficits may emerge from lesions to different cortical regions responsible for grasping behavior. One aspect we do not address is potential differences that may emerge in reaching vs. grasping depending on the cortical region lesioned since the reaching behavior in our study was almost identical across conditions. While dexterous movements suffer greatly from lesioning of descending motor pathways, gross movements such as reaching may be less affected (66–68), potentially because of a larger subcortical contribution (69). Future studies could address these differences by examining tasks where reach and grasp behavior are varied in tandem (70).

Our lesion results suggest that motor cortex could potentially act as an autonomous dynamical system during early movement, a question not resolved by previous work in reaching (26). However, it has recently been shown in mice that the motor commands necessary for dextrous control cannot proceed without continuous input from the thalamus (71). These differing results reinforce the need for future models that consider sensory feedback as well as the link between ongoing subcortical (e.g., thalamic) and cortical dynamics. Overall, this work builds on many years of work on goal-driven modeling, dynamical systems, and deep neural networks in the visual and motor systems to present a unified view of grasping from pixels to muscles.

Methods

Experimental design has previously been described in detail (2, 8, 32, 34) and is additionally described in SI Appendix, Experimental setup. Briefly, two rhesus monkeys (Macaca mulatta) participated in this study (monkey Z: female, 7.0 kg; monkey M: male, 10.5 kg). Animal housing, care, and all experimental procedures were conducted in accordance with German and European laws governing animal welfare and were in agreement with the Guidelines for the Care and Use of Mammals in Neuroscience and Behavioral Research (72). Neural recordings are described in SI Appendix, Electrophysiological recordings. The feature regression analysis in Fig. 2 and SI Appendix, Fig. S2 is described in SI Appendix, Visual and muscle feature analysis. The neural network models used are described in SI Appendix, Modular recurrent neural network. The methods for comparing neural and model data are described in SI Appendix, Assessing similarity of model and neural data. The details of the fixed point analysis for evaluating the computations of the models are described in SI Appendix, Fixed point analysis.

Data Availability.

All data discussed in the paper are available in the main text and SI Appendix. The code used to train the network models is available on GitHub (https://github.com/JonathanAMichaels/hfopt-matlab).