Measures of the Degree of Departure from Ignorable Sample Selection

Abstract

With the current focus of survey researchers on “big data” that are not selected by probability sampling, measures of the degree of potential sampling bias arising from this nonrandom selection are sorely needed. Existing indices of this degree of departure from probability sampling, like the R-indicator, are based on functions of the propensity of inclusion in the sample, estimated by modeling the inclusion probability as a function of auxiliary variables. These methods are agnostic about the relationship between the inclusion probability and survey outcomes, which is a crucial feature of the problem. We propose a simple index of degree of departure from ignorable sample selection that corrects this deficiency, which we call the standardized measure of unadjusted bias (SMUB). The index is based on normal pattern-mixture models for nonresponse applied to this sample selection problem and is grounded in the model-based framework of nonignorable selection first proposed in the context of nonresponse by Don Rubin in 1976. The index depends on an inestimable parameter that measures the deviation from selection at random, which ranges between the values zero and one. We propose the use of a central value of this parameter, 0.5, for computing a point index, and computing the values of SMUB at zero and one to provide a range of the index in a sensitivity analysis. We also provide a fully Bayesian approach for computing credible intervals for the SMUB, reflecting uncertainty in the values of all of the input parameters. The proposed methods have been implemented in R and are illustrated using real data from the National Survey of Family Growth.

1. INTRODUCTION

Classical methods of scientific probability sampling and corresponding “design-based” frameworks for making statistical inferences about populations have long been used to advance knowledge about populations. The random selection of elements from a population of interest into a probability sample, where all population elements have a known nonzero probability of selection, ensures that the elements included in the sample are representative of the larger population, mirroring the population in expectation. Random sampling is an example of an ignorable selection mechanism under the theoretical framework for missing data mechanisms originally introduced by Rubin (1976), provided that design variables are appropriately incorporated in the analysis. Unfortunately, the modern survey research environment has had a severe negative impact on these “tried and true” methods of survey research: it has become harder and harder to contact sampled units, survey response rates continue to decline in all modes of administration (face-to-face, telephone, etc.; Brick and Williams 2013; Williams and Brick 2018), and the costs of collecting and maintaining scientific probability samples are steadily rising (Presser and McCulloch 2011). These problems raise a significant question: to what extent can samples be treated like probability samples when only a small fraction of the original sample has responded, and the response mechanism may in fact not be ignorable?

Because of the problems and costs associated with classical probability samples, researchers in the health sciences and other fields are turning to the “big data” generated from nonprobability samples of population elements (Eysenbach and Wyatt 2002; Braithwaite, Emery, de Lusignan, and Sutton 2003; Bowen, Bradford, and Powers 2007; Miller, Johnston, Dunn, Fry, and Degenhardt 2010; Brooks-Pollock, Tilston, Edmunds, and Eames 2011; Heiervang and Goodman 2011; Shlomo and Goldstein 2015; Wang, Rothschild, Goel, and Gelman 2015). These “infodemiology” data might be scraped from social media platforms such as Twitter (Chew and Eysenbach 2010; McNeil, Brna, and Gordon 2012; Bosley, Zhao, Hill, Shofer, Asch, et al. 2013; Myslín, Zhu, Chapman, and Conway 2013; Thackeray, Burton, Giraud-Carrier, Rollins, Draper 2013; Thackeray, Neiger, Burton, Thackeray 2013; Zhang, Campo, Janz, Eckler, Yang, et al. 2013; Aslam, Tsou, Spitzberg, An, Gawron, et al. 2014; Gabarron, Serrano, Wynn, and Lau 2014; Harris, Moreland-Russell, Choucair, Mansour, Staub, et al. 2014; Lee, DeCamp, Dredze, Chisolm, and Berger 2014; Mishori, Singh, Levy, and Newport 2014; Nagar, Yuan, Freifeld, Santillana, Nojima, et al. 2014; Nascimento, DosSantos, Danciu, DeBoer, van Holsbeeck, et al. 2014; O’Connor, Jackson, Goldsmith, and Skirton 2014; Reavley and Pilkington 2014; Nwosu, Debattista, Rooney, and Mason 2015; McCormick, Lee, Cesare, Shojaie, and Spiro 2017) or collected from commercial databases and online searches (to name a few potential sources; Shlomo and Goldstein 2015; DiGrazia 2017). Online surveys are other common sources of “big data” (Eysenbach and Wyatt 2002; Braithwaite et al. 2003; Evans, Wiggins, Mercer, Bolding, and Elford 2007; Brooks-Pollock et al. 2011; Heiervang and Goodman 2011), and annual academic conferences on survey research are currently dedicating entire sessions to research on online surveys of nonprobability samples (e.g., a session at the 2015 Annual Conference of the European Survey Research Association titled “Representativeness of Surveys Using Internet-Based Data Collection”).

Researchers have started to use these data sources and tools to collect information about underlying populations (Koh and Ross 2006; Evans et al. 2007; Myslín et al. 2013; Zhang et al. 2013; Nascimento et al. 2014), given that these data are inexpensive, and a researcher can easily collect large quantities of information from existing data sources or online data collection. However, these are ultimately nonprobability samples, and classical design-based methods of inference have at best questionable validity when applied to data from these samples. The protection of ignorable selection conveyed by probability sampling no longer applies; nonprobability samples may lead to estimates that are substantially biased, depending on the features of the population elements that self-select into the sample (Pasek and Krosnick 2011; Yeager, Krosnick, Chang, Javitz, Levendusky, et al. 2011).

Rubin (1976) originally described the key theoretical notion of the ignorability of a missing data mechanism. The key aspect of nonignorability is that the probability of missingness does depend on missing data, even after conditioning on observed data. This definition can also be applied to sample selection (Rubin 1978; Little 2003). Probability sampling ensures that the sample selection mechanism is ignorable; but ignorability of nonprobability samples is a strong assumption that is often invalid. Inferences based on nonignorable samples paint a potentially biased picture of the target population, so survey researchers need theoretically sound measures of how far nonprobability selection mechanisms deviate from ignorability. A 2013 task force on nonprobability sampling from the American Association for Public Opinion Research (AAPOR) called for more research into appropriate models for data collected from nonprobability samples (Baker, Brick, Bates, Battaglia, Couper, et al. 2013). More recently, Pasek (2016) proposed general approaches using existing methods for empirically assessing whether a given nonprobability sample will mirror a probability sample (i.e., is the nonprobability sample selection ignorable?). We build on this recent work by using Rubin’s framework to develop a principled, easy-to-use index of nonignorable selection bias and methods of adjusting population inferences for this bias.

Our proposed index is based on work by Andridge and Little (2009, 2011), who developed proxy pattern-mixture models (PMMs) for nonignorable nonresponse in surveys. These authors used a model-based approach to develop adjusted estimators of means when nonresponse is potentially nonignorable and proposed sensitivity analysis to examine the sensitivity of inferences to the extent that survey nonresponse is nonignorable. West and Little (2013) adapted this approach in evaluating the ability of PMMs to repair the nonresponse bias in survey estimates when missingness depends on the true value of an unobserved auxiliary variable U, but a variable Z is fully observed and serves as a noisy proxy for U. West, Wagner, Gu, and Hubbard (2015) also discussed this approach in the context of “big” data sets obtained from commercial vendors. In this article, we adapt PMMs to the selection bias problem in nonprobability samples, where the missing data problem arises from the fact that not everyone in a population of interest self-selects into a given nonprobability sample. These methods provide a bias correction for estimates of survey means as a function of a parameter measuring the degree of deviation from ignorability; see (9) below.

One widely considered alternative measure of survey representativeness in surveys subject to nonresponse is the “R-indicator” (Schouten, Cobben, and Bethlehem 2009; Schouten, Bethlehem, Beullens, Kleven, Loosveldt, et al. 2012), which measures the variability in the probability of responding to a survey as a function of auxiliary covariates available for an entire sample. Low variability in response propensities as a function of the auxiliary covariates suggests more balance (in terms of the covariates used) in the final set of respondents. Särndal and Lundström (Särndal and Lundström 2010; Särndal 2011) proposed variants of the R-indicator, including the coefficient of variation of nonresponse adjustment factors applied to existing sampling weights based on a calibration adjustment. In this case, if there is greater variability in the adjustments, there is a higher risk of selection bias due to nonresponse. While these indicators have attractive properties and can be applied to the problems of sample selection as well as nonresponse, they require a well-specified model for selection, and most importantly, they are agnostic with regard to specific survey variables of interest, failing to reflect the fact that selection bias depends on the strength of the relationship of selection with the survey variable.

Another major limitation of measures using the R-indicator is that their variability depends on response across values of the available auxiliary variables and therefore does not reflect nonignorable selection. The measure H₁ in Särndal and Lundström (2010), unlike the R-indicator, is tailored to each survey variable Y and, like our proposed measure, is based on a regression of each survey variable Y on the auxiliary variables. However, unlike our approach, it assumes that the regression equation estimated on the selected cases applies to the nonselected cases and, as such, assumes that the selection mechanism is ignorable. This measure also relies on survey weights accounting for unequal probabilities of selection and nonresponse adjustment, which is not the context considered for this study. For these reasons, we did not evaluate this measure in this study.

In simulation experiments, Nishimura et al. found that the R-indicator was not an effective indicator of nonresponse bias when the missing data mechanism was nonignorable (Nishimura, Wagner, and Elliott 2016). These authors did find that when the estimated fraction of missing information (or FMI; Wagner 2010), which is an outcome-specific measure that is a byproduct of a model-based multiple imputation analysis, is greater than the nonresponse rate associated with a given estimate, this may indicate potential nonignorable nonresponse bias (Nishimura et al. 2016). Their results suggested that the FMI may be worthy of additional consideration but that additional indicators of potential selection bias are still needed (especially for nonignorable mechanisms). Our proposed indices fill this need since they focus on nonignorable selection bias and are based on models for the selection mechanism and the survey variable(s) of interest and as such reflect differential effects of selection for different substantive variables.

The remainder of the article is organized as follows: In section 2, we review Rubin’s (1976) framework for ignorable and nonignorable nonresponse, relating it to sample selection and probability sampling. In section 3, we present our proposed index for measuring departures from ignorable selection for a continuous survey variable and discuss associated sensitivity analyses to assess the impact of deviations from ignorable selection. In section 4, we apply our index and other alternatives (like the FMI) to real data from the National Survey of Family Growth (NSFG), treating the full NSFG sample as a hypothetical population and smartphone users in the NSFG as a nonprobability sample. We conclude in section 5 with a summary of our proposed approach, and we outline possible future extensions to non-normal survey variables and estimands other than means.

2. RUBIN’S MISSING DATA FRAMEWORK APPLIED TO SAMPLE SELECTION

In a landmark article for the modeling of data with missing values, Rubin (1976) defined joint models for the data and the missingness mechanism and defined sufficient conditions under which the missingness mechanism can be ignored for likelihood and frequentist inference. This framework is applied to sample selection in Rubin (1978), the first chapter of Rubin (1987), and Little (2003), with the indicator for response being replaced by the indicator for selection into the sample.

We define the following notation, with vectors or matrices of values of variables in boldface:

$$\mathbf{Y}=(y_1,\mathrm{\dots },y_N),\hspace{0.17em}{y}_i\text{=value of }\mathrm{a}\text{ particular survey variable }Y\text{ for population unit }i,i=1,\mathrm{\dots },N$$

 

$$\mathbf{Z}=(Z_1,\mathrm{\dots },Z_n)\text{=vector or matrix of fully}-\text{observed auxiliary and}/\text{or design variables }Z$$

 

$$Q=Q(\mathbf{Y},\mathbf{Z})\text{=finite population quantity}$$

 

$$\mathbf{S}=(S_1,\mathrm{\dots },S_N)\text{ =vector of sample inclusion indicators},\text{ with }{S}_i=\{\begin{array}{c}1,y_i\text{ sampled }\\ 0,\text{ otherwise }\end{array}$$

 

$$\begin{array}{c}\mathbf{Y}=({\mathbf{Y}}_{\text{inc}},\hspace{0.17em}{\mathbf{Y}}_{\text{exc}}),\hspace{0.17em}{\mathbf{Y}}_{\text{inc}}=\left\{y_i\right\}\text{ for units }i\text{ included in the sample},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{Y}}_{\text{exc}}\text{=}\left\{y_i\right\}\text{ for units }i\text{ not included in the sample}\end{array}$$

We initially adopt a model-based (more specifically, Bayesian) framework and assume a model for the joint distribution of the survey variables Y and the sample inclusion indicator S. We assume a selection model, where this joint distribution is factored into the marginal distribution of Y and the conditional distribution of S given Y, that is,

$$f_{Y,S}(\mathbf{Y},\mathbf{S}|\mathbf{Z},\theta ,\phi )=f_Y(\mathbf{Y}|\mathbf{Z},\theta )f_{S|Y}(\mathbf{S}|\mathbf{Y},\mathbf{Z},\phi ).$$ (1)

In (1), $f_Y(\mathbf{Y}|\mathbf{Z},\theta )$ is the density for Y given Z indexed by unknown parameters $\theta$, and $f_{S|Y}(\mathbf{S}|\mathbf{Y},\mathbf{Z},\phi )$ is the density for S, given Z and Y, indexed by unknown parameters $\phi$. The full likelihood based on the joint model for Y and S is then

$$L(\theta ,\phi |\mathbf{Z},{\mathbf{Y}}_{\text{inc}},\mathbf{S})\propto f_{Y,S}({\mathbf{Y}}_{\text{inc}},\mathbf{S}|\mathbf{Z},\theta ,\phi )=\int f_Y(\mathbf{Y}|\mathbf{Z},\theta )f_{S|Y}(\mathbf{S}|\mathbf{Y},\mathbf{Z},\phi )d{\mathbf{Y}}_{\text{exc}}.$$ (2)

The corresponding posterior distributions for $\theta ,\phi$ and ${\mathbf{Y}}_{\text{exc}}$, given the full likelihood in (2), are then

$$\begin{array}{c}p(\theta ,\phi |\mathbf{Z},\mathbf{S},{\mathbf{Y}}_{\text{inc}})\propto p(\theta ,\phi |\mathbf{Z})L(\theta |\mathbf{Z},\mathbf{S},{\mathbf{Y}}_{\text{inc}})\\ p({\mathbf{Y}}_{\text{exc}}|\mathbf{Z},\mathbf{S},{\mathbf{Y}}_{\text{inc}})\propto \int p({\mathbf{Y}}_{\text{exc}}|\mathbf{Z},\mathbf{S},{\mathbf{Y}}_{\text{inc}},\theta ,\phi )p(\theta ,\phi |\mathbf{Z},\mathbf{S},{\mathbf{Y}}_{\text{inc}})d\theta d\phi ,\end{array}$$ (3)

where $p(\theta ,\phi |\mathbf{Z})$ is a prior distribution for the parameters. In many models, $p({\mathbf{Y}}_{\text{exc}}|\mathbf{Z},\mathbf{S},{\mathbf{Y}}_{\text{inc}},\theta ,\phi )=p({\mathbf{Y}}_{\text{exc}}|\mathbf{Z},\mathbf{S},\theta ,\phi )$, so the posterior distribution of the nonsampled data depends on S and ${\mathbf{Y}}_{\text{inc}}$ only through the parameters.

The specification of the model for the inclusion indicators S is difficult because the mechanisms leading to inclusion are often not well understood. The likelihood ignoring the selection mechanism is based on a model for Y given Z and is

$$L_{\text{ign}}(\theta |{\mathbf{Y}}_{\text{inc}},\mathbf{Z})\propto p_Y({\mathbf{Y}}_{\text{inc}}|\mathbf{Z},\theta )=\int p_Y(\mathbf{Y}|\mathbf{Z},\theta )d{\mathbf{Y}}_{\text{exc}},$$ (4)

which does not require a model for S. The corresponding posterior distributions for $\theta$ and ${\mathbf{Y}}_{\text{exc}}$, given the likelihood in (4), are then

$$\begin{array}{c}p(\theta |{\mathbf{Y}}_{\text{inc}},\mathbf{Z})\propto p(\theta |\mathbf{Z})L_{\text{ign}}(\theta |{\mathbf{Y}}_{\text{inc}},\mathbf{Z})\\ p({\mathbf{Y}}_{\text{exc}}|{\mathbf{Y}}_{\text{inc}},\mathbf{Z})\propto \int p({\mathbf{Y}}_{\text{exc}}|{\mathbf{Y}}_{\text{inc}},\mathbf{Z},\theta )p(\theta |{\mathbf{Y}}_{\text{inc}},\mathbf{Z})d\theta .\end{array}$$ (5)

When the full posterior distributions (3) reduce to these simpler posterior distributions (5), the selection mechanism is called ignorable for Bayesian inference about $\theta$ and ${\mathbf{Y}}_{\text{exc}}$.

Two general and simple sufficient conditions for ignoring the data collection mechanism are

$$\text{Selection at Random }(\text{SAR}):f_{S|Y}(\mathbf{S}|\mathbf{Y},\mathbf{Z},\phi )=f_{S|Y}(\mathbf{S}|{\mathbf{Y}}_{\text{inc}},\mathbf{Z},\phi )\text{ for all }{\mathbf{Y}}_{\text{exc}}.$$

$$\text{Bayesian Distinctness: }p(\theta ,\phi |\mathbf{Z})=p(\theta |\mathbf{Z})p(\phi |\mathbf{Z}).$$

The parameters $\phi$ that control selection into the sample are typically assumed to be unrelated to the parameters $\theta$ of the model for Y, so it is reasonable to assign $\theta$ and $\phi$ independent prior distributions, as Bayesian Distinctness implies.

It is easy to show that these conditions together imply that

$$p(\theta ,{\mathbf{Y}}_{\text{exc}}|{\mathbf{Y}}_{\text{inc}},\mathbf{Z})=p(\theta ,{\mathbf{Y}}_{\text{exc}}|{\mathbf{Y}}_{\text{inc}},\mathbf{Z},\mathbf{S}),$$

so the model for the data collection mechanism does not affect inferences about the parameter $\theta$ or the finite population quantities Q.

A special form of SAR is probability sampling, where the probability of selection is known and does not depend on the survey outcomes:

$$\text{Probability Sampling}:\hspace{0.17em}{f}_{S|Y}(\mathbf{S}|\mathbf{Y},\mathbf{Z},\phi )=f_{S|Y}(\mathbf{S}|\mathbf{Z})\text{ for all }{\mathbf{Y}}_{\text{exc}}.$$ (6)

Note that the right side of (6) does not include an unknown parameter $\phi$, since the selection mechanism in probability sampling is known and under the control of the sampler. Probability sampling is stronger than SAR in three important respects: first, it is automatically valid (in terms of guaranteeing ignorability), and not an assumption, if probability sampling is used to select the sample and there is complete response; second, it implies that, conditional on Z, inclusion is independent of Y and also any other unobserved variables that might be included in a model, such as latent variables in a factor analysis; third, probability sampling implies that selection is independent of the observed values of Y, ${\mathbf{Y}}_{\text{inc}}$, whereas SAR only requires independence of S and ${\mathbf{Y}}_{\text{exc}}$ after conditioning on ${\mathbf{Y}}_{\text{inc}}$ and Z, which is a weaker condition. Also, ignorability is specific to the particular survey variable Y, unlike probability sampling, which guarantees ignorability for any variable, whether or not observed.

These facts imply that probability sampling is highly desirable. However, as indicated in the Introduction, it is an ideal that is rarely attained. The weaker SAR condition is more relevant to nonrandom selection mechanisms and is the basis for our adjusted indices of nonignorable selection, which we describe in the next section.

3. AN INDEX OF SELECTION BIAS FOR THE MEAN OF A CONTINUOUS VARIABLE

We assume that the nonprobability sample has data $\mathbf{D}=\{y_i,z_i,i=1,\mathrm{\dots },n\}$, where i is the unit of analysis, the sample is of size n, $z_i$ is a vector of auxiliary variables for which summary statistics are available for the population (from administrative data or some other external source, denoted by A), and $y_i$ is a continuous variable of interest. In general, subject matter considerations should be employed to “design” the best vector of auxiliary variables given the variables of primary interest (Särndal and Lundström 2010). To be useful, this vector should be predictive of the variables of interest, and summary information for these variables needs to be available at the population level (from A). In the absence of good auxiliary variables in a given nonprobability sample, one could use data fusion techniques to link auxiliary variables with these required properties from another independent sample (Kamakura and Wedel 1997; Saporta 2002; Van Der Puttan, Kok, and Gupta 2002; ZuWallack, Dayton, Freedner-Maguire, Karriker-Jaffe, and Greenfield 2015).

We consider first the development of an index of bias for the mean of a continuous survey variable Y. First, we regress Y on the auxiliary variables Z, using the data in the nonprobability sample. Let X be the best predictor of Y from a multiple regression of Y on all the auxiliary variables Z. In particular, X could be the linear predictor of Y based on the additive linear regression of Y on Z. X is scaled as discussed below (7). We assume that one is able to compute asymptotically unbiased summary measures of X at the population level from A, regardless of its form. As is the case with all model-based methods, the use of X as the “best” predictor of Y requires careful diagnostic assessment of the regression of Y on Z to assess the model fit and make sure that there is not strong evidence of model misspecification. We rescale X to

$$X^{*}=X\sqrt{{\sigma }_{\mathit{YY}}^{(1)}/{\sigma }_{\mathit{XX}}^{(1)}},$$ (7)

where ${\sigma }_{\mathit{YY}}^{(1)}\text{ and }{\sigma }_{\mathit{XX}}^{(1)}$ are respectively the variances of Y and X for the selected cases, S = 1; then $X^{*}$ and Y have the same variance given S = 1. We call $X^{*}$ the auxiliary proxy for Y.

Our proposed index is based on maximum likelihood (ML) estimates for a normal proxy pattern-mixture model (PMM) (Little 1994; Andridge and Little 2011) relating Y and X. Suppose that S = 1 for units in the sample, S = 0 for units not in the sample, and for j = 0 or 1,

$$\begin{array}{c}(X,Y|S=j)\sim N_2\left(\left({\mu }_X^{(j)},{\mu }_Y^{(j)}\right),\left(\begin{array}{cc}{\sigma }_{\mathit{XX}}^{(j)}& {\sigma }_{\mathit{XY}}^{(j)}\\ {\sigma }_{\mathit{XY}}^{(j)}& {\sigma }_{\mathit{YY}}^{(j)}\end{array}\right)\right),\\ \mathrm{Pr}(S=1|X,Y)=g\left(V\right),\text{ where }V=(1-\phi )X^{*}+\phi Y,\end{array}$$ (8)

where N₂() is a bivariate normal distribution, $\phi$ is unknown scalar parameter, g is an unknown function, and $X^{*}$ is the rescaled best predictor of Y, as in (7). Here, “nonselection” (S = 0) corresponds to “missing” (M = 1) in the nonresponse setting of Andridge and Little (2011), and that article uses the alternative parameterization $\lambda =\phi /(1-\phi )$ rather than $\phi$. Since $X^{*}$ is a proxy for Y, we assume here that $0\le \phi \le 1$. The parameter $\phi$ is a measure of the “degree of nonrandom selection,” after conditioning on $X^{*}$.

One can extend the missingness mechanism in (8) to a more general form. First, write Z = (X, U), where U is the set of available auxiliary variables other than X. Without loss of generality, we can transform U to be orthogonal to X for selected cases, S = 1. Since X is the best linear predictor of Y, the mean of Y does not depend on U for S = 1. In Andridge and Little (2011), the exclusion of U from the proxy pattern-mixture model in (8) was rationalized informally. In Appendix 1, we show more formally that if, for nonselected cases S = 0, X is also the best predictor of Y, and U is orthogonal to X, then maximum likelihood (ML) or Bayes for the normal PMM (8) are also valid under a more general mechanism:

$$\mathrm{Pr}(S=1|X,Y,U)=g\left(U,V\right),\text{ where }V=(1-\phi )X^{*}+\phi Y,$$ (9)

where g is an arbitrary function of its two arguments. This more general form in (9) increases the realism of the model by allowing the selection mechanism to depend on U and V.

Following Andridge and Little (2011), the ML estimate of the population mean of Y for a given $\phi$ for the model (8) is

$${\widehat{\mu }}_Y(\phi )={\overline{y}}^{(1)}+\frac{\phi +(1-\phi )r_{\mathit{XY}}^{(1)}}{\phi r_{\mathit{XY}}^{(1)}+(1-\phi )}\sqrt{\frac{s_{\mathit{YY}}^{(1)}}{s_{\mathit{XX}}^{(1)}}}(\overline{X}-{\overline{x}}^{(1)}),$$ (10)

Where $\overline{X}$ is the mean of X in the whole population, and for units in the sample (S = 1), ${\overline{x}}^{(1)},{\overline{y}}^{(1)}$ are the means of X and Y, $s_{\mathit{XX}}^{(1)}\text{ and }{s}_{\mathit{YY}}^{(1)}$ are the variances of X and Y, and $r_{\mathit{XY}}^{(1)}$ is the correlation of X and Y. Because X is the best predictor of Y, we can define it in such a way that it has a positive correlation with Y; consequently, we restrict $r_{\mathit{XY}}^{(1)}$ to be greater than 0. We note that the term $\sqrt{s_{\mathit{YY}}^{(1)}/s_{\mathit{XX}}^{(1)}}$ arises from the rescaling of the proxy X to have the same variance as Y in the sample. A useful feature of ML estimation for the model defined in (8) is that the ML estimates are valid for all functions g, so a specific form for g does not need to be specified; see Andridge and Little (2011) for more discussion of this point.

It follows from (10) that a measure of unadjusted bias (MUB) of the sample mean ${\overline{y}}^{(1)}$ is

$$\text{MUB}(\phi )={\overline{y}}^{(1)}-{\widehat{\mu }}_Y(\phi )=\frac{\phi +(1-\phi )r_{\mathit{XY}}^{(1)}}{\phi r_{\mathit{XY}}^{(1)}+(1-\phi )}\sqrt{\frac{s_{\mathit{YY}}^{(1)}}{s_{\mathit{XX}}^{(1)}}}({\overline{x}}^{(1)}-\overline{X}).$$ (11)

The bias measure in (11) is dependent on the scale of Y and does not readily allow comparisons of the size of bias between Y variables. Scaling the measure to increase comparability is useful. For positive variables, one approach is to express MUB as a fraction of the mean. A more broadly useful approach is to standardize the bias by dividing $\text{MUB}(\phi )$ by the standard deviation of Y in the sample, $\sqrt{s_{\mathit{YY}}^{(1)}}$. This leads to a standardized measure of unadjusted bias (SMUB):

$$\text{SMUB}(\phi )=\frac{\phi +(1-\phi )r_{\mathit{XY}}^{(1)}}{\phi r_{\mathit{XY}}^{(1)}+\mathrm{(1}-\mathrm{\phi )}}\frac{({\overline{x}}^{(1)}-\overline{X})}{\sqrt{s_{\mathit{XX}}^{(1)}}}.$$ (12)

To define a single index of selection bias, we need to choose a value of the unknown $\phi$. As seen in (8), when $\phi =0$, selection depends on X and Y only through X, and since X is fully observed, the data are SAR. At the other extreme, when $\phi =1$, selection depends on X and Y only through the survey variable Y. In the absence of knowledge about the value of $\phi$, we suggest defining the index at $\phi =0.5$, which is an intermediate value of $\phi$ that corresponds to selection depending on $X^{*}$ + Y. This leads to a very simple standardized measure:

$$\text{SMUB}(0.5)=\frac{({\overline{x}}^{(1)}-\overline{X})}{\sqrt{s_{\mathit{XX}}^{(1)}}}.$$ (13)

To reflect sensitivity to the choice of $\phi$, a simple approach is to compute the interval (SMUB[0], SMUB[1]), where

$$\text{SMUB}(0)=r_{\mathit{XY}}^{(1)}\frac{({\overline{x}}^{(1)}-\overline{X})}{\sqrt{s_{\mathit{XX}}^{(1)}}}\hspace{0.17em}\text{and}\hspace{0.17em}\text{SMUB}(1)=\frac{1}{r_{\mathit{XY}}^{(1)}}\frac{({\overline{x}}^{(1)}-\overline{X})}{\sqrt{s_{\mathit{XX}}^{(1)}}},$$ (14)

from substituting $\phi =0\text{ and }\phi =1$ in (12). All three measures can be easily computed using the R function nisb(), which is available in the supplementary materials online or via the GitHub repository located at github.com/bradytwest/IndicesOfNISB.

We make nine remarks regarding the measures in (13) and (14). First, we note that SMUB(0), SMUB(0.5), and SMUB(1) do not require the presence of microdata for the population elements not included in the nonprobability sample. Part of the appeal of these indices is that they only require knowledge of the aggregate population mean for X. This in turn requires knowledge of the population means of the auxiliary variables Z.

Second, the three bias measures SMUB(0), SMUB(0.5), and SMUB(1) correspond to the sensitivity analysis for nonresponse proposed by Andridge and Little (2011).

Third, the expression

$$\text{SMAB}(\phi )=\text{SMUB}\left(\phi \right)-\text{ SMUB}\left(0\right)=\frac{\phi (1-r_{\mathit{XY}}^{(1)2})}{\phi r_{\mathit{XY}}^{(1)}+\mathrm{(1}-\mathrm{\phi )}}\frac{({\overline{x}}^{(1)}-\overline{X})}{\sqrt{s_{\mathit{XX}}^{(1)}}}$$ (15)

measures the difference in the mean of Y when $\phi \ne 0$ from the adjusted mean obtained when $\phi =0$ and is thus a standardized measure of adjusted bias (SMAB). That is, it measures the potential bias of the adjusted mean of Y that accounts for the known auxiliary variables and is caused by deviations from SAR. Such a measure is clearly desirable, but we caution that it is strongly dependent on the assumptions underlying the model (8); without some such model assumptions, there is no way of predicting the bias due to deviations from SAR. As per (15), SMUB($\phi$) can be rewritten as SMUB(0) + SMAB($\phi$), which means that SMAB captures the portion of the overall bias in an unadjusted estimate that exists after adjustment for the known auxiliary variables (given a choice of $\phi$), assuming that selection is only a function of X (or SAR). In this sense, the ability of SMAB to indicate this “residual” selection bias due to deviations from SAR strongly depends on the auxiliary variables used to make the initial adjustment. This result shows how our general approach is less restrictive than existing measures that assume SAR and essentially set $\phi$ to 0, including the R-indicator or the measure H₁ in Särndal and Lundström (2010). Therefore, SMUB($\phi$) serves as a more robust overall indicator of the selection bias in an unadjusted estimate computed from a given nonprobability sample and should be used to identify variables that would likely benefit from adjustment procedures.

Fourth, SMUB(1) is unstable when $r_{\mathit{XY}}^{(1)}$ is close to zero; that is, the proxy variable X is not a good predictor of Y. The bias in such cases cannot be reliably estimated from the sample.

Fifth, intuitively, the measures in (13)–(14) capture relevant features of the sample selection problem: $r_{\mathit{XY}}^{(1)}$ measures the strength of the best proxy as a predictor of Y (larger being better), and $\left({\overline{x}}^{(1)}-\overline{X}\right)$ measures how much the sample deviates from the population on the mean of X, which is the best proxy for Y (smaller being better). Also,

$${\overline{x}}^{(1)}-\overline{X}=(1-f)({\overline{x}}^{(1)}-{\overline{x}}^{(0)}),$$

where ${\overline{x}}^{(0)}$ is the mean of X for the nonselected part of the population and f is the fraction of the population sampled. Our measures, therefore, also reflect the fraction f of the population included in the sample, with a higher f leading to a smaller value of the measure, other factors being equal. A nonprobability sample would be considered “good” in a loose sense if X and Y are strongly correlated and ${\overline{x}}^{(1)}$ is close to $\overline{X}$, meaning that the sample is “representative” on a variable X that is a good proxy for Y. A nonprobability sample is “bad” if X and Y are weakly correlated, and ${\overline{x}}^{(1)}$ is far from $\overline{X}$, meaning that the sample is not representative with respect to X, and the ability to adjust for the bias is weak. There are intermediate cases, but in short, good samples will have lower absolute values on these indices, and bad samples will have higher absolute values on these indices.

Sixth, the central measure SMUB(0.5) is closely related to the Bias Effect Size proposed by Biemer and Peytchev (2011), when applied to the best predictor of the survey variable Y. The difference is that their numerator is the difference in the means of X for selected and nonselected units, whereas the numerator in (15) is this difference multiplied by (1- f) and, as such, incorporates the impact of the nonselection rate (see the fifth point mentioned previously). Our indices have a more formal justification in terms of bias under the normal pattern-mixture model, and they are defined for choices of $\phi$ other than 0.5.

Seventh, the strengths of $\text{SMUB}(\phi )$ are that it is relatively simple, and unlike previous proposals, it does not assume SAR. However, there is no perfect measure, and our measure has limitations. It is founded on the normal model in (8) and in particular on the assumption that selection depends on $X^{*}$ and Y only through the linear combination $(1-\phi )X^{*}+\phi Y,\text{ for }0\le \phi \le 1$. The bivariate normality assumption for the variables of interest leads to the straightforward result in (10) and provides a clear theoretical basis for development and evaluation of the indices proposed here. Because $\text{SMUB}(\phi )$ is founded on a normal model, it is less suitable for nonnormal outcomes. Extensions of the pattern-mixture model to nonnormal outcomes are possible (Andridge and Little 2009, 2018), but resulting measures are less straightforward, and our application later on suggests that $\text{SMUB}(\phi )$ still has value for nonnormal variables. Negative values of $\phi$ are not considered, although they are technically possible, and $\text{SMUB}(\phi )$ is close to zero when the sample and population means of X are close, even though selection bias is clearly still possible in that situation. In particular, the auxiliary variables cannot include variables used for stratification in sample selection, since these have the same means in the sample and population by design.

Eighth, if the sample with S = 1 is the responding component of a probability sample of the population subject to frame errors and nonresponse, then the component of the model for nonselected cases, S = 0, should more realistically be confined to the subpopulation of nonrespondents and individuals outside the sampling frame. It can be shown, however, that the resulting ML estimate of the bias for that model is similar to the estimate from the model (7), at least when the sample design is with equal probability.

Ninth, a refinement of our measures is to incorporate measures of sampling uncertainty. This is possible if we have the sample mean and variance of X for the nonsampled population, which in turn requires the sample mean and covariance matrix of Z in the nonsampled population. If only the means of Z are available, as would often be the case, we need to assume that the population covariance matrix of Z is the same for sampled and nonsampled units, allowing this matrix to be estimated from the sampled cases. As in Andridge and Little (2011), one approach to incorporating parameter uncertainty is to assign the parameters of the pattern-mixture model (8) a prior distribution and compute the posterior distribution of the bias of ${\overline{y}}^{(1)}$ and, hence, of the SMUB. The interval $[\text{SMUB}(0),\hspace{0.17em}\text{ SMUB}(1)]$ can then be replaced by a credible interval from the posterior distribution of SMUB. If desired, a formal test of the null hypothesis of no selection bias is obtained by checking whether this interval includes zero. Appendix 2 outlines how to compute draws from the posterior distribution of SMUB when $\phi$ is assigned a beta prior distribution,

$$p(\phi |\alpha ,\beta )={\phi }^{\alpha -1}{(1-\phi )}^{\beta -1}/B(\alpha ,\beta ),$$

where $B(\alpha ,\beta )$ is the incomplete beta function, and other parameters in the model (8) are assigned relatively noninformative Jeffreys’ prior distributions. The choice $\alpha =\beta =1$ yields a uniform prior distribution for $\phi$, which reflects limited knowledge about this parameter. We have developed an R function, nisb_bayes(), that implements this Bayesian approach. This function can also be found in the supplementary materials online or via the GitHub repository located at github.com/bradytwest/IndicesOfNISB.

4. APPLICATION: SMARTPHONE USERS IN THE NSFG

To illustrate the utility of our proposed index in practice, we applied the index to real data from the NSFG. The NSFG is an ongoing national probability survey of women and men age 15–49, using a continuous cross-sectional sample design. We analyzed sixteen quarters (four years) of NSFG data, collected from September 2012 to August 2016. During this time period, two questions (on internet access and smartphone ownership) were added to the NSFG. Specifically, the NSFG recorded an indicator of whether the randomly selected individual responding to the survey in a sample household currently owned a smartphone (Couper, Gremel, Axinn, Guyer, Wagner, et al. 2018). For purposes of this illustration, we treated the full set of NSFG respondents in this data set as a hypothetical “population,” enabling the calculation of “true” values of selected population parameters (means and proportions) describing the distributions of key NSFG variables. We analyzed males and females separately and considered smartphone (SPH) users as a nonprobability sample arising from the larger NSFG “population.” We note that the selection fractions for this hypothetical illustration were quite different from zero; the typical selection fraction for most nonprobability samples selected from large populations would be a number close to zero. For variables measured on males, the selection fraction was 0.788 (6,942 smartphone users out of 8,809 males), and for variables measured on females, the selection fraction was 0.817 (8,981 smartphone users out of 10,991 females).

For each of several NSFG variables important to data users, we then identified all males or females in the NSFG “population” (defined by both SPH and non-SPH cases) with complete data on both the variable of interest and several auxiliary variables. We selected auxiliary variables Z that 1) may be available in aggregate (at the population level) or for each unit in a given population in other nonprobability surveys and 2) could be used to predict each variable of interest in the NSFG. These auxiliary variables included age, race/ethnicity, marital status, education, household income, region of the United States (based on definitions from the US Census Bureau), current employment status, and presence of children under the age of 16 in the household. Specifically, we computed our proposed index of selection bias for the following survey variables Y, which we again assumed to be measured for the SPH sample only: lifetime parity, or number of live births (females only); age at first sex (males and females); number of sexual partners in the past year (first analyzed “as is” for both males and females and then top-coded at seven for females) and number of sexual partners in the lifetime (males and females, again both “as-is” and top-coded at seven); and number of months worked in the past year (males and females).

For each of these survey variables (and separately for males and females), we initially regressed the variable on all of the auxiliary variables Z described previously (using the SPH respondents only), and we then used the estimated coefficients to compute the linear predictor X for a given survey variable Y (for both the SPH respondents only and all cases in the overall NSFG “population”). For purposes of this illustration, we also treated recoded binary indicators representing the auxiliary variables as additional survey variables of interest (Y), assumed to be measured on SPH respondents only. In these analyses, we only regressed the binary indicators on all other auxiliary variables (i.e., excluding the auxiliary variable used to form the binary indicator from the set of predictors) when computing the linear predictor X because the previously described survey variables Y (e.g., number of sexual partners in the lifetime) generally would not be available as auxiliary variables for a full population. This allowed for multiple illustrations of the computation of our indices and also allowed us to assess the ability of our index (and its proposed “interval”) to reflect actual bias in a parameter estimate computed based on a nonprobability sample when the variable of interest does not follow a normal distribution.

Because the means of the Y variables were also available for the entire NSFG “population,” we were able to assess how well our indices predicted the actual bias in the estimates based on the SPH sample. For evaluation purposes, we computed the standardized true estimated bias (STEB), defined as the difference between the SPH estimate and the true population parameter, scaled by the standard deviation of the population measures. These bias measures were used as benchmarks for our proposed index. Measures based on the R-indicator would be of limited use here, since they do not vary with the survey variable. An alternative variable-specific measure of selection bias is the fraction of missing information (FMI), and we also assess how well this measure predicted STEB, compared with our proposed index. The FMI is a function of the multiple R-squared of the regression of Y on Z, which is one of the elements that affects our proposed index, but it does not reflect deviations from ignorable sample selection.

4.1 Results

Table 1 presents, for each of the survey means of interest (for males and females), the computed values of the proposed SMUB(0.5) index, the corresponding (SMUB[0], SMUB[1]) interval, and the 95 percent Bayesian credible interval for SMUB based on a uniform prior distribution for $\phi$. We also present values of $r_{\mathit{XY}}^{(1)}$ based on the SPH sample and the STEB measures for each mean. The estimates in table 1 are displayed in descending order by the estimates of $r_{\mathit{XY}}^{(1)}$ based on the SPH sample. We also display scatter plots of SMUB(0), SMUB(0.5), SMUB(1), and FMI against the STEB in figures 1–4, together with Pearson correlations. The dots in the scatter plots represent the indices of all the survey variables of interest and the corresponding values of the benchmarks. We fitted ordinary least squares regression lines to the data in these plots, which are shown in red, and included 45-degree lines (y = x), which are dashed and would represent perfect correspondence of the index values with the STEB measures. We also plot the indices against the benchmarks restricting to those survey variables where the best predictor has some predictive power, defined as $r_{\mathit{XY}}^{(1)}$ > 0.4 (see the shaded points and black fitted lines in figure 1).

Table 1.

Computed Values of the SMUB(0.5) Index, the Proposed (SMUB[0], SMUB[1]) Intervals, and 95 Percent Bayesian Credible Intervals for the SMUB(0) and SMUB Indices (the Latter Assuming a Uniform Prior for $\phi$) for Selected Survey Means Based on NSFG Measures Collected on the SPH Sample, in Addition to Measures of Standardized True Estimated Bias (STEB) for Each Estimated Mean^a

NSFG Variable Label	Gender	$r_{\mathit{XY}}^{(1)}$	STEB	SMUB(0)	SMUB(0.5)	SMUB(1)	Proposed Interval Cover STEB?	95% Credible Interval for SMUB(0)	Interval Cover STEB?	95% Credible Interval for SMUBb	Interval Cover STEB?
# of months worked last year	F	0.791	69	55	70	88	Y	(48, 62)	N	(53, 91)	Y
# of months worked last year	M	0.785	90	73	93	118	Y	(64, 83)	N	(70, 122)	Y
Number of live births	F	0.705	−43	−33	−47	−66	Y	(−39, −26)	N	(−69, −31)	Y
Never been married (binary)	M	0.646	−24	−17	−27	−42	Y	(−25, −9)	Y	(−48, −12)	Y
Never been married (binary)	F	0.590	−3	−3	−5	−8	Y	(−9, 4)	Y	(−16, 5)	Y
Age = 30–44 (binary)	M	0.581	−4	32	55	94	N	(24, 39)	N	(30, 97)	N
Lifetime sex partners (top-coded)	M	0.543	36	14	26	48	Y	(6, 23)	N	(9, 56)	Y
Age = 30–44 (binary)	F	0.532	−15	17	31	59	N	(11, 22)	N	(15, 61)	N
Currently employed (binary)	M	0.532	86	37	69	130	Y	(29, 45)	N	(36, 131)	Y
Lifetime sex partners (top-coded)	F	0.530	19	2	4	7	N	(−4, 8)	N	(−7, 17)	N
Children present in HU (binary)	M	0.476	−12	−5	−10	−20	Y	(−12, 3)	Y	(−32, 3)	Y
Currently employed (binary)	F	0.406	63	26	64	156	Y	(20, 31)	N	(26, 152)	Y
Age at first sex	M	0.375	22	32	85	226	N	(23, 40)	N	(31, 218)	N
Children present in HU (binary)	F	0.371	−19	−21	−56	−152	N	(−26, −15)	Y	(−146, −21)	N
“Other” race (binary)	F	0.365	17	23	63	172	N	(17, 28)	Y	(23, 166)	N
Age at first sex	F	0.363	10	19	52	143	N	(12, 24)	N	(18, 138)	N
“Other” race (binary)	M	0.329	12	30	91	276	N	(22, 37)	N	(31, 261)	N
# of sex partners in last year	M	0.298	27	8	28	95	Y	(0, 16)	N	(5, 101)	Y
Education: “Some coll.” (binary)	M	0.267	50	10	38	143	Y	(3, 18)	N	(9, 139)	Y
Life sex partners	F	0.258	−1	−2	−9	−34	N	(−7, 4)	Y	(−49, 6)	Y
Education: “Some coll.” (binary)	F	0.251	29	3	12	47	Y	(−3, 8)	N	(−1, 55)	Y
Life sex partners	M	0.242	9	−1	−2	−9	N	(−8, 7)	N	(−44, 34)	Y
Region = “south” (binary)	F	0.230	14	−7	−30	−130	N	(−13, −1)	N	(−124, −6)	N
Region = “south” (binary)	M	0.215	26	−3	−13	−62	N	(−10, 6)	N	(−84, 10)	N
# of sex partners in last year, top-coded	F	0.213	16	2	8	37	Y	(−5, 8)	N	(−11, 56)	Y
Income: $20K–$59, 999 (binary)	M	0.207	10	−6	−30	−146	N	(−13, 2)	N	(−148, −4)	N
# of sex partners in last year	F	0.175	−5	2	11	64	N	(−5, 8)	Y	(−8, 83)	Y
Income: $20K–$59, 999 (binary)	F	0.134	11	1	9	70	Y	(−5, 7)	N	(-15, 95)	Y

^aValues of STEB, SMUB(0), SMUB(0.5), and SMUB(1) have been multiplied by 1,000 in the table.

^bComputed using a Uniform(0,1) prior distribution for $\varphi$.

Figure 1.

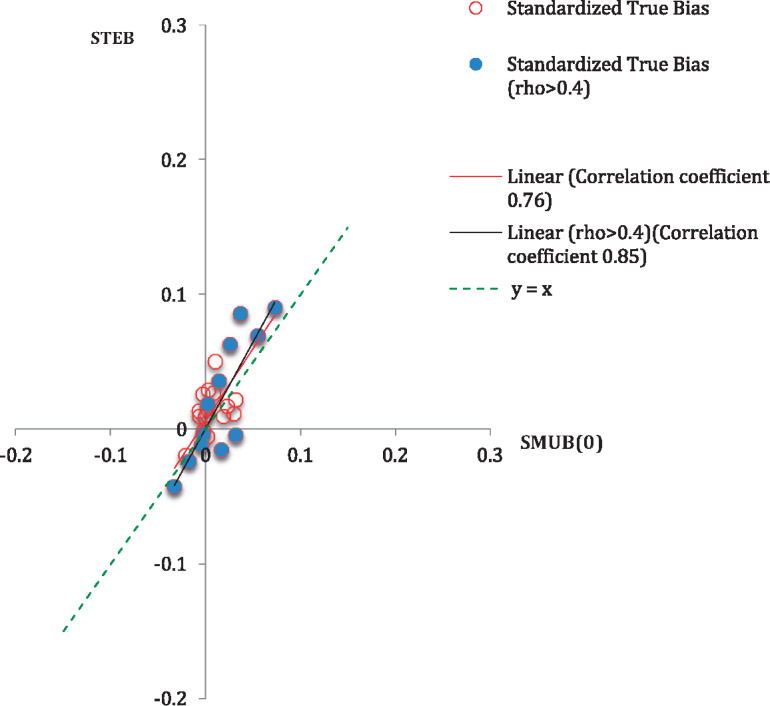
Scatterplot of STEB Against SMUB(0), Including Measures of Linear Association. note: rho =$r_{\mathit{XY}}^{(1)}$.

Figure 2.

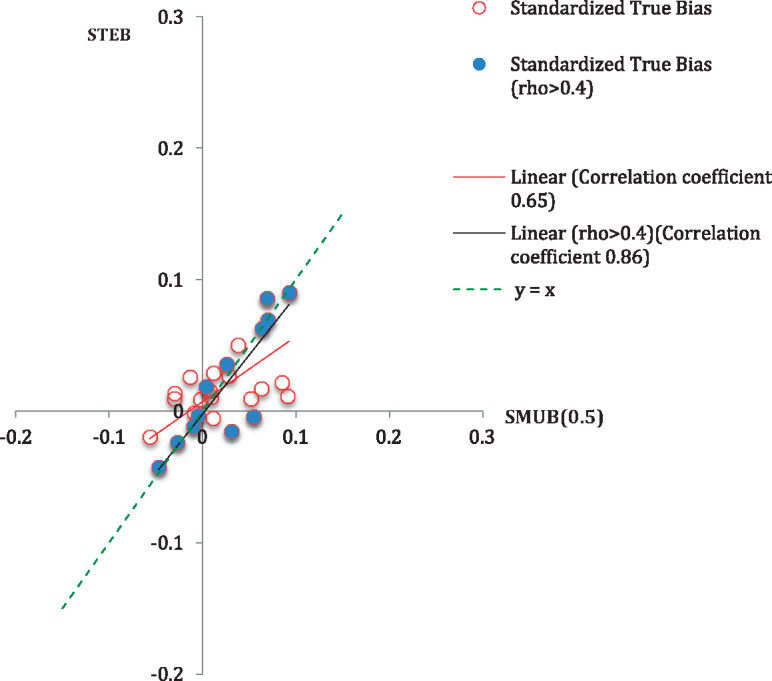
Scatterplot of STEB Against SMUB(0.5), Including Measures of Linear Association. note: rho =$r_{\mathit{XY}}^{(1)}$.

Figure 3.

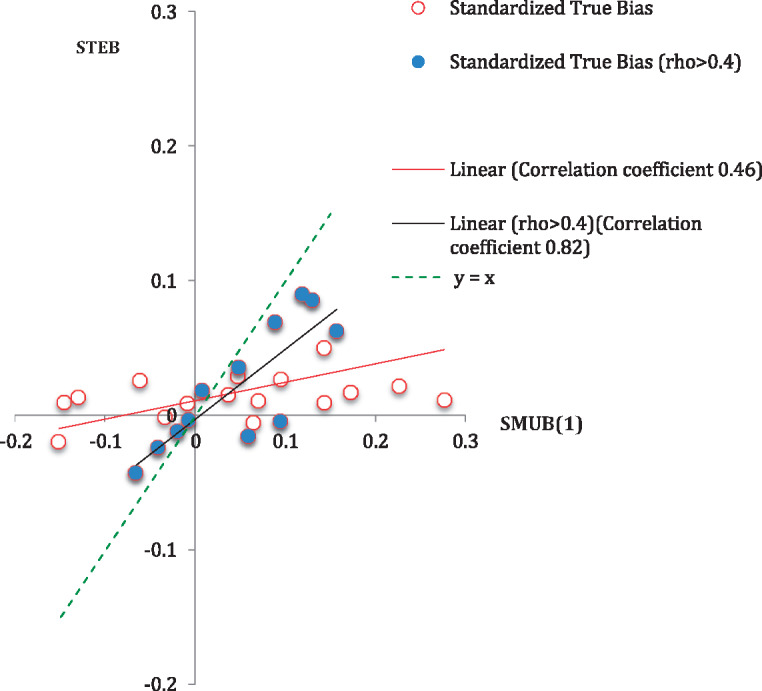
Scatterplot of STEB Against SMUB(1), Including Measures of Linear Association. note: rho =$r_{\mathit{XY}}^{(1)}$.

We make the following observations from table 1 and figures 1–4. First, for survey variables with estimates of $r_{\mathit{XY}}^{(1)}$ greater than 0.4, our index does quite well. All three SMUB indices had strong linear associations with the STEB that we use as the benchmark. The particularly strong performance of SMUB(0) in this illustration when $r_{\mathit{XY}}^{(1)}$ is greater than 0.4 likely reflects a selection mechanism for SPH respondents that is close to ignorable (i.e., SAR), but our compromise choice, SMUB(0.5), also does well. The correlations of SMUB with the STEB were much stronger than those found for the FMI (figure 4). Nine of the twelve intervals (SMUB[0], SMUB[1]) and nine of the twelve Bayesian credible intervals covered the STEB.

Figure 4.

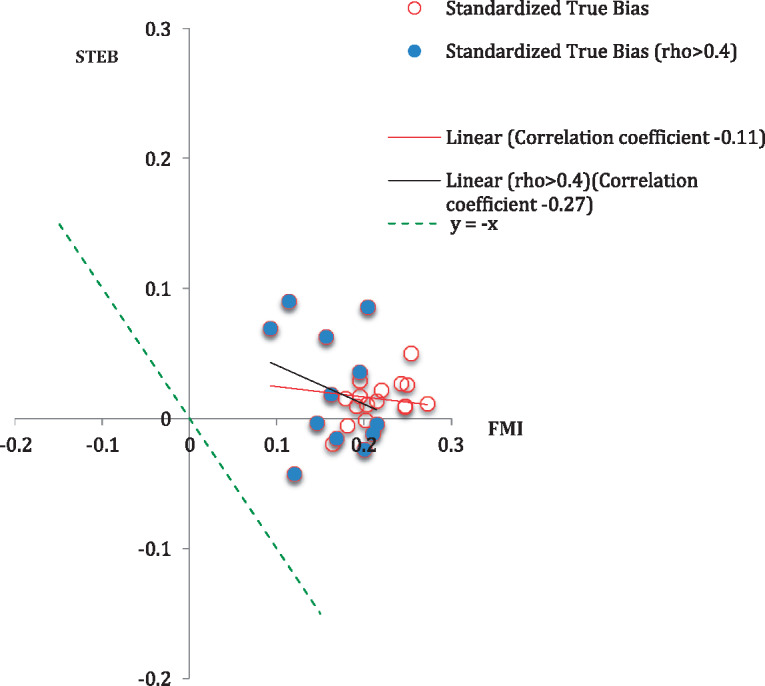
Scatterplot of STEB Against FMI, Including Measures of Linear Association. note: rho =$r_{\mathit{XY}}^{(1)}$.

Second, for survey variables with correlations less than 0.4, the index tends to deviate more from STEB in these cases, and only five of the sixteen intervals (SMUB[0], SMUB[1]) and eight of the sixteen Bayesian intervals covered the STEB. We note that when the correlation is low, the Bayesian credible intervals are considerably wider than the intervals (SMUB[0], SMUB[1]) that ignore sampling variability and thus are more likely to include the STEB. Whether 0.4 is a useful cutoff in general requires more study in other applications.

Third, the Bayesian intervals for SMUB(0), which correspond to the SAR case, performed poorly relative to the more general Bayesian intervals for SMUB that incorporated random draws of $\phi$ from a Uniform(0, 1) distribution. Only seven of the twenty-eight Bayesian intervals for SMUB(0) covered the STEB, despite the relatively high correlation of SMUB(0) with STEB noted previously. The Bayesian intervals based on a prior distribution for $\phi$ are wider and have much better coverage of the STEB, particularly when X and Y have a strong correlation. This suggests that making some allowance for uncertainty in $\phi$, either by assigning $\phi$ a prior distribution or by a sensitivity analysis for different values of $\phi$, is better than approaches that assume SAR (i.e., $\phi$ = 0).

For further insight on this performance, we note that our index does well when the estimated bias SMUB(0) (which adjusts for the auxiliary variables) has the same sign as the STEB and is smaller than the STEB in absolute value. In such cases, fourteen of the sixteen intervals (SMUB[0], SMUB[1]) cover the STEB. In other cases, SMUB(0) and SMUB(1) fails to cover the STEB since the interval extends in the wrong direction. We expect that adjustment of the sample mean based on strong auxiliary predictors tends to reduce bias, and this is the setting in which our approach does well. However, adjustment for auxiliary predictors that are poor predictors of the outcome often does not reduce the bias, and in these cases, our indices are less effective.

We note that two of the three intervals for correlations greater than 0.4 that do not cover the STEB are for binary age indicators, perhaps reflecting the fact that binary outcomes violate the normality assumption of the underlying PMM in (8).

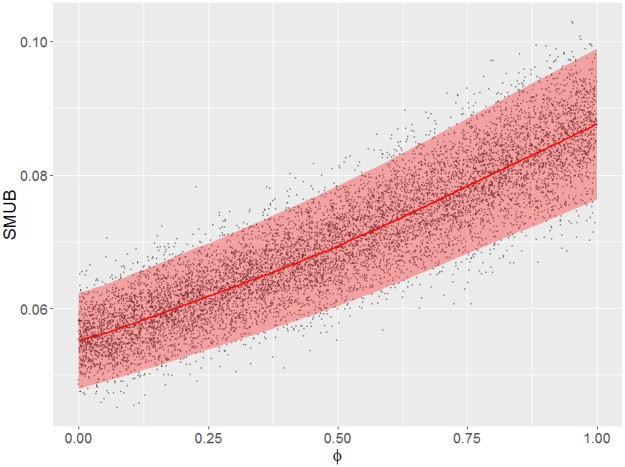
We also present an illustration of our proposed Bayesian approach, assuming that one is able to compute sufficient statistics for the Z variables for cases not included in the nonprobability sample (as was the case in our NSFG example). After executing the nisb_bayes() code described in the online supplementary materials, a plot similar to figure 5 will be generated automatically, presenting draws of SMUB as a function of draws of the $\phi$ parameter, predictions of SMUB as a function of the $\phi$ parameter, and 95 percent credible intervals for these predictions. From the first row of table 1 (the mean number of months worked in the past twelve months for females), the STEB associated with selection into the SPH sample was 0.069 (multiplied by 1,000 in the table), the 95 percent credible interval for SMUB based on the resulting posterior draws of SMUB was (0.053, 0.091), and the median of the posterior draws was 0.069. Figure 5 indicates that a choice of 0.5 for the $\phi$ parameter does a good job of reflecting the STEB for this particular mean and that our proposed interval clearly covers the STEB, allowing for uncertainty in the value of the $\phi$ parameter.

Figure 5.

Scatterplot of Drawn Values of SMUB Versus Drawn Values of the $\phi$ Parameter for the Mean of Number of Months Worked in the Past Twelve Months (Females), Following Our Proposed Bayesian Approach in the Presence of Sufficient Statistics on Z for Nonsampled Cases.

Finally, we evaluate the performance of the proposed SMAB index in table 2. The standardized adjusted bias (SAB) is computed as the difference between the adjusted mean and the true mean, divided by the standard deviation of the true values for the “population.” Correlations of the SMAB(0.5) and SMAB(1) values with SAB were poor (−0.057 and −0.110) and improved substantially for cases with $r_{\mathit{XY}}^{(1)}$ > 0.4 (0.462 and 0.484, respectively). This result underscores our earlier remark about the importance of the underlying model used for the initial adjustment when using the SMAB index to indicate selection bias in adjusted estimates; the index will perform poorly when the initial adjustments assuming SAR are poor. The overall coverage of the SAB values by the Bayesian intervals for SMAB is identical to the coverage of the STEB values by the Bayesian intervals for SMUB in table 1. This suggests that the SMAB index can still do reasonably well at capturing the SAB when allowing for sampling variance in the input estimates.

Table 2.

Computed Values of the SMAB(0.5) and SMAB(1) Indices and 95 Percent Bayesian Credible Intervals for the SMAB Index, Along with Measures of Standardized Adjusted Bias (SAB) for Each Mean Estimated from the NSFG Data^a

NSFG Variable Label	Gender	$r_{\mathit{XY}}^{(1)}$	SABb	SMAB (0.5)	SMAB (1)	95% Credible Interval for SMABc	Credible Interval Cover SAB?
# of months worked last year	F	0.791	15	15	33	(1, 33)	Y
# of months worked last year	M	0.785	20	20	45	(1, 45)	Y
Number of live births	F	0.705	−10	−14	−33	(−33, 0)	Y
Never been married (binary)	M	0.646	−6	−10	−24	(−26, 0)	Y
Never been married (binary)	F	0.590	−1	−2	−5	(−9, 2)	Y
Age = 30–44 (binary)	M	0.581	−35	23	62	(1, 62)	N
Life sex partners (top-coded)	M	0.543	22	12	34	(0, 38)	Y
Age = 30–44 (binary)	F	0.532	−32	15	42	(1, 43)	N
Currently employed (binary)	M	0.532	51	32	93	(1, 91)	Y
Life sex partners (top-coded)	F	0.530	17	2	5	(−4, 11)	N
Children present in HU (binary)	M	0.476	−6	−5	−16	(−23, 2)	Y
Currently employed (binary)	F	0.406	38	38	131	(1, 125)	Y
Age at first sex	M	0.375	−9	53	194	(2, 185)	N
Children present in HU (binary)	F	0.371	2	−35	−13	(−125, −1)	N
“Other” race (binary)	F	0.365	−5	40	149	(1, 142)	N
Age at first sex	F	0.363	−9	33	124	(1, 118)	N
“Other” race (binary)	M	0.329	−17	61	246	(2, 230)	N
# of sex partners in last year	M	0.298	19	20	86	(1, 91)	Y
Education: “Some coll.” (binary)	M	0.267	40	28	133	(1, 127)	Y
Life sex partners	F	0.258	1	−6	−32	(−45, 4)	Y
Education: “Some coll.” (binary)	F	0.251	26	9	44	(0, 50)	Y
Life sex partners	M	0.242	10	−2	−8	(−40, 31)	Y
Region = “south” (binary)	F	0.230	20	−23	−123	(−117, −1)	N
Region = “south” (binary)	M	0.215	29	−10	−59	(−79, 8)	N
# of sex partners in last year, top-coded	F	0.213	14	6	35	(−10, 53)	Y
Income: $20K–$59, 999 (binary)	M	0.207	17	−24	−139	(−141, −1)	N
# of sex partners in last year	F	0.175	−6	9	62	(−8, 80)	Y
Income: $20K–$59, 999 (binary)	F	0.134	10	8	69	(−14, 92)	Y

^aValues of SAB, SMAB(0.5) and SMAB(1) have been multiplied by 1,000 in the table.

^bWe first computed adjusted estimates of the means (assuming SAR) by (i) imputing the values of each variable of interest 100 times for each nonselected case, using the aforementioned auxiliary variables as covariates, and then (ii) applying Rubin’s combining rules to form a point estimate of the adjusted mean. Next, we computed the standardized adjusted bias (SAB) as the difference between the adjusted mean and the true mean, divided by the standard deviation of the true values for the “population.” Finally, we computed SMAB(0.5), SMAB(1), and a 95% Bayesian credible interval for SMAB (assuming a uniform prior for $\phi$); SMAB(0) is by definition zero.

^cComputed using a Uniform(0,1) prior distribution for $\phi$.

5. SUMMARY AND FUTURE WORK

We have proposed a variable-specific index of nonignorable selection bias for nonprobability samples, namely the standardized measure of unadjusted bias (SMUB). This model-based and variable-specific index is easy to compute and allows for case-level or aggregate information for an entire population. The index is based on comparisons between the sample and population distributions of auxiliary variables that have not been matched in the estimation, neither by stratification or weighting. The proposed index is therefore suitable for nonprobability samples, which seldom rely on stratified sampling and do not permit the computation of weights based on known probabilities of selection. Although the nonprobability sampling literature has proposed weighted estimators based on pseudo-randomization approaches (Elliott and Valliant 2017), these weights are generally global in nature and not variable-specific, meaning that any bias correction engendered by these weights will not be tailored for individual variables. We have also described a Bayesian approach for describing uncertainty in the index, given case-level information for an entire population (or at least aggregate information for population members that are not selected for a nonprobability sample). All methods have been implemented in R, and these functions are available in the online supplementary materials.

Using real data from the NSFG, we have shown that the index is a good indicator of the actual bias in estimates based on nonprobability samples when the administrative proxy X is somewhat predictive of the survey variable of interest Y, as measured in our application by a correlation greater than 0.4. In situations where this correlation is weak, we suggest that any approach based on information in the auxiliary variables is likely to be ineffective because these variables do not provide much pertinent information for that survey variable. We emphasize that our proposed indices of selection bias are variable-specific, and the NSFG illustration suggests that intervals based on SMUB can provide a good sense of variables that may be particularly prone to selection bias. Depending on the magnitude of the X-Y correlations and how far away the intervals are from zero, our indices allow us to identify variables for which descriptive estimates should be interpreted with caution because of the risk of potential selection bias.

The proposed index is based on a normal pattern-mixture model (see [8]), and its performance is dependent on the extent to which this model is realistic. In particular, it is best suited to normal survey variables, although our illustration shows that it can still be useful qualitatively for nonnormal variables. Andridge and Little (2009, 2018) develop proxy PMMs for nonignorable nonresponse in binary survey variables, providing similar indices of nonignorable selection bias for estimated proportions. Work in progress includes simulation assessments of this method, and the development of indices of selection bias for regression coefficients.

In forming our Bayesian credible intervals for the proposed index, we used uniform priors for the parameter capturing dependence of sample selection on X and Y; we feel that this is a reasonable choice in the absence of any information about this parameter, but alternative priors may improve the overall performance of these intervals in terms of coverage of the true bias. Finally, since our setting is situations where the sample is not collected by probability sampling and summary auxiliary data are available for the population, complex design elements available for the sample, like sampling weights, are not generally relevant. The situation where the auxiliary data X are available for a probability sample rather than the population—and thus are subject to sampling error—will also be addressed in future work.

SUPPLEMENTARY MATERIALS

Supplementary materials are available online at academic.oup.com/jssam.

Appendix 1: Refining the Proxy Pattern-Mixture Model of Andridge and Little (2011)

As in section 3, write S = selection indicator; Y = survey variable, measured only when S = 1; and Z = auxiliary variables, measured for S = 0 and 1.

Assume $E(Y|Z,S=1)={\beta }_{y0\cdot z}^{(1)}+{\beta }_{\mathit{yz}\cdot z}^{(1)}Z, \hspace{0.17em}\text{so} X= ({\beta }_{\mathit{yz}\cdot z}^{(1)}Z)=$ best predictor of Y for respondents. Let $X^{*}=X\sqrt{{\sigma }_{\mathit{yy}}^{(1)}/{\sigma }_{\mathit{xx}}^{(1)}}=$ auxiliary proxy for Y, or X scaled to have the same variance as Y given S = 1. Write Z = (X, U), U = auxiliary variables orthogonal to X, so ${\beta }_{\mathit{xu}\cdot u}^{(1)}=0.$

Assume that for nonselected cases S = 0, X is also the best predictor of Y, and U is also orthogonal to X. Then we show that ML or Bayes for the normal PMM in (8) is also ML or Bayes under the more general bivariate normal pattern-mixture model that conditions on U:

$$\begin{array}{c}\left(\left(\begin{array}{c}X\\ Y\end{array}\right)|U,S=s\right)\sim N\left(\left(\begin{array}{c}{\beta }_{x0\cdot u}^{(s)}+{\beta }_{\mathit{xu}\cdot u}^{(s)}U\\ {\beta }_{y0\cdot u}^{(s)}+{\beta }_{\mathit{yu}\cdot u}^{(s)}U\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\mathit{xx}\cdot u}^{(s)}& {\sigma }_{\mathit{xy}\cdot u}^{(s)}\\ {\sigma }_{\mathit{xy}\cdot u}^{(s)}& {\sigma }_{\mathit{yy}\cdot u}^{(s)}\end{array}\right)\right)\left(\text{*}\right)\\ \mathrm{Pr}(S=1|X,Y,U)=g\left(U,V\right),\text{ where }V=(1-\phi )X^{*}+\phi Y,\end{array}$$

where g is an arbitrary function of its two arguments.

Assume that:

1. $E(Y|Z,S=0)={\beta }_{y0\cdot z}^{(0)}+{\beta }_{\mathit{yz}\cdot z}^{(0)}Z,$ where ${\beta }_{\mathit{yz}\cdot z}^{(0)}=\lambda {\beta }_{\mathit{yz}\cdot z}^{(1)};$ that is, $X\hspace{0.5em}=({\beta }_{\mathit{yz}\cdot z}^{(1)}Z)$ is the best predictor of Y for nonsampled as well as sampled units; and

2. U is orthogonal to X for nonsampled units, so ${\beta }_{\mathit{xu}\cdot u}^{(s)}=0 \mathrm{for} s=0,1.$

Then, $0={\beta }_{\mathit{yu}\cdot \mathit{xu}}^{(r)}={\beta }_{\mathit{yu}\cdot u}^{(r)}-\frac{{\sigma }_{\mathit{xy}\cdot u}^{(s)}{\beta }_{\mathit{xu}\cdot u}^{(s)}}{{\sigma }_{\mathit{xx}\cdot u}^{(s)}}={\beta }_{\mathit{yu}\cdot u}^{(r)}$ for r = 0, 1, so (*) reduces to

$$\left(\left(\begin{array}{c}X\\ Y\end{array}\right)|U,S\right)\sim N\left(\left(\begin{array}{c}{\beta }_{x0\cdot u}^{(s)}\\ {\beta }_{y0\cdot u}^{(s)}\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\mathit{xx}\cdot u}^{(s)}& {\sigma }_{\mathit{xy}\cdot u}^{(s)}\\ {\sigma }_{\mathit{xy}\cdot u}^{(s)}& {\sigma }_{\mathit{yy}\cdot u}^{(s)}\end{array}\right)\right).$$ (**)

Since (X, Y) do not depend on U given S, we can simplify the notation by dropping the subscript u in the parameters, replacing (**) by $\left(\left(\begin{array}{c}X\\ Y\end{array}\right)|U,S\right)\sim N\left(\left(\begin{array}{c}{\mu }_x^{(r)}\\ {\mu }_y^{(r)}\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\mathit{xx}}^{(r)}& {\sigma }_{\mathit{xy}}^{(r)}\\ {\sigma }_{\mathit{xy}}^{(r)}& {\sigma }_{\mathit{yy}}^{(r)}\end{array}\right)\right),$ which is the model of Eq. (8). So ML or Bayes under this model is the same as ML or Bayes under (*).

Appendix 2: Simulating the posterior distribution of the population mean of Y

A. Expressions for the posterior mean and variance of the population mean of Y, assuming that the best predictor X is known:

Pattern-mixture model: Transform Y to $V=\phi Y+(1-\phi )X^{*},X^{*}\text{=}X\sqrt{{\sigma }_{\mathit{yy}}^{(1)}/{\sigma }_{\mathit{xx}}^{(1)}}$, assuming $\phi >0$  

$$\text{Model}:\left(\left(\begin{array}{c}X\\ V\end{array}\right)|\theta ,s=j\right)\sim N\left[\left(\begin{array}{c}{\mu }_x^{(j)}\\ {\mu }_v^{(j)}\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\mathit{xx}}^{(j)}& {\sigma }_{\mathit{xv}}^{(j)}\\ {\sigma }_{\mathit{xv}}^{(j)}& {\sigma }_{\mathit{vv}}^{(j)}\end{array}\right)\right],$$

where s = 1 for sampled cases, 0 for non-sampled cases, $\theta$ = set of all parameters

$$\mathrm{Pr}(s=1|x,v)=g(v)(\text{***})$$

By properties of the normal distribution, the slope, intercept, and residual variance of the regression of X on V given s = j are:

$${\beta }_{\mathit{xv}·v}^{(j)}={\sigma }_{\mathit{xv}}^{(j)}/{\sigma }_{\mathit{vv}}^{(j)},{\beta }_{x0·v}^{(j)}={\mu }_x^{(j)}-{\beta }_{\mathit{xv}·v}^{(j)}{\mu }_v^{(j)},{\sigma }_{\mathit{xx}·v}^{(j)}={\sigma }_{\mathit{xx}·v}^{(j)}-{\beta }_{\mathit{xv}·v}^{(j)2}{\sigma }_{\mathit{vv}}^{(j)}.$$

Then (***) implies that S and X are conditionally independent given V, and hence

$${\beta }_{\mathit{xv}·v}^{(0)}={\beta }_{\mathit{xv}·v}^{(1)},{\beta }_{x0·v}^{(0)}={\beta }_{x0·v}^{(1)},{\sigma }_{\mathit{xx}·v}^{(0)}={\sigma }_{\mathit{xx}·v}^{(1)}.$$

These constraints just identify the model, and imply that:

$$\begin{array}{c}{\mu }_v^{(0)}={\mu }_v^{(1)}+\frac{{\mu }_x^{(0)}-{\mu }_x^{(1)}}{{\beta }_{\mathit{xv}·v}^{(1)}},{\sigma }_{\mathit{vv}}^{(0)}={\sigma }_{\mathit{vv}}^{(1)}+\frac{{\sigma }_{\mathit{xx}}^{(0)}-{\sigma }_{\mathit{xx}}^{(1)}}{{\left[{\beta }_{\mathit{xv}·v}^{(1)}\right]}^2},{\sigma }_{\mathit{xv}}^{(0)}={\sigma }_{\mathit{xv}}^{(1)}+\frac{{\sigma }_{\mathit{xx}}^{(0)}-{\sigma }_{\mathit{xx}}^{(1)}}{{\beta }_{\mathit{xv}·v}^{(1)}}\\ {\beta }_{\mathit{vx}·x}^{(0)}={\sigma }_{\mathit{xv}}^{(0)}/{\sigma }_{\mathit{xx}}^{(0)},{\beta }_{v0·x}^{(0)}={\mu }_v^{(0)}-{\beta }_{\mathit{vx}·x}^{(0)}{\mu }_x^{(0)}.\end{array}$$

For non-sampled values v_i of V, and their average ${\overline{v}}^{(0)}$:

$$\begin{array}{c}E(v_i|x_i,s_i=0,\theta )={\beta }_{v0·x}^{(0)}+{\beta }_{\mathit{vx}·x}^{(0)}{x}_i\\ E({\overline{v}}^{(0)}|\text{data},\theta )={\beta }_{v0·x}^{(0)}+{\beta }_{\mathit{vx}·x}^{(0)}{\overline{x}}^{(0)},\text{Var}({\overline{v}}^{(0)}|\text{data},\theta )={\sigma }_{\mathit{vv}·x}^{(0)}/n^{(0)}\end{array}$$

where n⁽⁰⁾ and ${\overline{x}}^{(0)}$ are respectively the number and the mean of X for non-selected cases.

Hence posterior mean and variance of ${\overline{v}}^{(0)}$ are:

$$\begin{array}{c}E({\overline{v}}^{(0)}|\text{data})=E({\beta }_{v0·x}^{(0)}+{\beta }_{\mathit{vx}·x}^{(0)}{\overline{x}}^{(0)}\left|\text{data}\right)\\ \text{Var}({\overline{v}}^{(0)}|\text{data})=\text{Var}({\beta }_{v0·x}^{(0)}+{\beta }_{\mathit{vx}·x}^{(0)}{\overline{x}}^{(0)}\left|\text{data}\right)+E\left({\sigma }_{\mathit{vv}·x}^{(0)}\right|\text{data})/n^{(0)}\end{array}$$

The corresponding posterior mean and variance of the overall mean v are:

$$\begin{array}{c}E(\overline{v}|\text{data})=f{\overline{v}}_S+(1-f)E({\beta }_{v0·x}^{(0)}+{\beta }_{\mathit{vx}·x}^{(0)}{\overline{x}}^{(0)}\left|\text{data}\right)\\ \text{Var}(\overline{v}|\text{data})={(1-f)}^2\text{Var}({\overline{v}}^{(0)}\left|\text{data}\right)\end{array}$$

where n⁽¹⁾ is the number of selected cases, and $f=n^{(1)}/\left(n^{(0)}+n^{(1)}\right)$ is the sampling fraction (assumed to be very close to zero in most cases).

B. Simulating draws of the mean of Y and SMUB from their posterior distributions.

Draw $({\beta }_{y0·z}^{(d)},{\beta }_{\mathit{yz}·z}^{(d)})$ from posterior distribution of regression of Y on Z given sample data

Define $X^{(d)}={\beta }_{y0·z}^{(d)}\text{+}{\beta }_{\mathit{yz}·z}^{(d)}Z$

Draw ${\phi }^{(d)}$ from prior distribution of $\phi$

Replace $X,\phi$ in above by X^(d), ${\phi }^{(d)}$

${\overline{x}}_S^{(d)},{\overline{x}}_N^{(d)}$ = sample means of X^(d) for selected and non-selected cases

S ^(d) = sample covariance matrix of (X^(d), Y) for selected cases

$s_{\mathit{xxN}}^{(0)(d)}$ = sample variance of X^(d) for non-selected cases

Draw $\left(\begin{array}{cc}{\sigma }_{\mathit{xx}}^{(1)(d)}& {\sigma }_{\mathit{xy}}^{(1)(d)}\\ {\sigma }_{\mathit{xy}}^{(1)(d)}& {\sigma }_{\mathit{yy}}^{(1)(d)}\end{array}\right)~\text{IW}\left[S^{(d)},n-1\right]$, IW = inverse Wishart

$$\left(\begin{array}{c}{\mu }_x^{(1)(d)}\\ {\mu }_y^{(1)}\end{array}\right)~N\left(\left(\begin{array}{c}{\overline{x}}_S^{(d)}\\ {\overline{y}}_S\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\mathit{xx}}^{(1)(d)}& {\sigma }_{\mathit{xy}}^{(1)(d)}\\ {\sigma }_{\mathit{xy}}^{(1)(d)}& {\sigma }_{\mathit{yy}}^{(1)(d)}\end{array}\right)/n\right)$$

 

$$\begin{array}{c}(1/{\sigma }_{\mathit{xx}}^{(0)(d)}\text{=}{\chi }_{N-n-1}^2/((N-n-1)s_{\mathit{xxN}}^{(0)(d)})\\ {\mu }_x^{(0)(d)}\sim N\left({\overline{x}}_N^{(d)},{\sigma }_{\mathit{xx}}^{(0)(d)}/(N-n)\right)\\ {\rho }_{\mathit{xy}}^{(1)(d)}={\sigma }_{\mathit{xy}}^{(1)(d)}/\sqrt{{\sigma }_{\mathit{xx}}^{(1)(d)}{\sigma }_{\mathit{yy}}^{(1)(d)}},\\ {\mu }_y^{(0)(d)}={\mu }_y^{(1)(d)}+\frac{{\phi }^{(d)}+(1-{\phi }^{(d)}){\rho }_{\mathit{xy}}^{(1)(d)}}{(1-{\phi }^{(d)})+{\phi }^{(d)}{\rho }_{\mathit{xy}}^{(1)(d)}}\sqrt{\frac{{\sigma }_{\mathit{yy}}^{(1)(d)}}{{\sigma }_{\mathit{xx}}^{(1)(d)}}}\left({\mu }_x^{(0)(d)}-{\mu }_x^{(1)(d)}\right),\\ {\sigma }_{\mathit{yy}}^{(0)(d)}={\sigma }_{\mathit{yy}}^{(1)(d)}+{\left(\frac{{\phi }^{(d)}+(1-{\phi }^{(d)}){\rho }_{\mathit{xy}}^{(1)(d)}}{(1-{\phi }^{(d)})+{\phi }^{(d)}{\rho }_{\mathit{xy}}^{(1)(d)}}\right)}^2\left(\frac{{\sigma }_{\mathit{yy}}^{(1)(d)}}{{\sigma }_{\mathit{xx}}^{(1)(d)}}\right)\left({\sigma }_{\mathit{xx}}^{(0)(d)}-{\sigma }_{\mathit{xx}}^{(1)(d)}\right),\\ {\sigma }_{\mathit{xy}}^{(0)(d)}={\sigma }_{\mathit{xy}}^{(1)(d)}+\frac{{\phi }^{(d)}+(1-{\phi }^{(d)}){\rho }_{\mathit{xy}}^{(1)(d)}}{(1-{\phi }^{(d)})+{\phi }^{(d)}{\rho }_{\mathit{xy}}^{(1)(d)}}\sqrt{\frac{{\sigma }_{\mathit{yy}}^{(1)(d)}}{{\sigma }_{\mathit{xx}}^{(1)(d)}}}\left({\sigma }_{\mathit{xx}}^{(0)(d)}-{\sigma }_{\mathit{xx}}^{(1)(d)}\right)\\ {\beta }_{\mathit{yx}·x}^{(0)(d)}={\sigma }_{\mathit{xy}}^{(0)(d)}/{\sigma }_{\mathit{xx}}^{(0)(d)},{\beta }_{y0·x}^{(0)(d)}={\mu }_y^{(0)(d)}-{\beta }_{\mathit{yx}·x}^{(0)(d)}{\mu }_x^{(0)(d)}\end{array}$$

Positive definite covariance matrix check:

If ${\sigma }_{\mathit{yy}·x}^{(0)(d)}={\sigma }_{\mathit{yy}}^{(0)(d)}-{\left({\beta }_{\mathit{yx}·x}^{(0)(d)}\right)}^2\left({\sigma }_{\mathit{xx}}^{(0)(d)}\right)\le 0$ then discard and redraw.

$${\overline{Y}}^{(d)}=(n/N){\overline{y}}_S^{(d)}+(1-n/N)({\beta }_{y0·x}^{(0)(d)}+{\beta }_{\mathit{yx}·x}^{(0)(d)}{\overline{x}}_N^{(d)})$$

 

$$\mathit{SMU}{B}^{(d)}=\left({\overline{y}}^{(1)}-{\overline{Y}}^{(d)}\right)/\sqrt{{\sigma }_{\mathit{yy}}^{(1)(d)}}$$

Repeat for d = 1,…D to simulate posterior distribution of ${\overline{Y}}^{(d)}$ and SMUB^(d), hence estimate posterior mean and variance as sample mean and variance of draws.

 

Financial support for this study was provided by a grant from the National Institutes for Health (1R21HD090366-01A1). The authors do not have any conflicts of interest involving the research reported here. The National Survey of Family Growth (NSFG) is conducted by the Centers for Disease Control and Prevention's (CDC’s) National Center for Health Statistics (NCHS), under contract #200-2010-33976 with University of Michigan’s Institute for Social Research with funding from several agencies of the U.S. Department of Health and Human Services, including CDC/NCHS, the National Institute of Child Health and Human Development (NICHD), the Office of Population Affairs (OPA), and others listed on the NSFG webpage (see http://www.cdc.gov/nchs/nsfg/). The views expressed here do not represent those of NCHS nor the other funding agencies.