The PATH Statement Explanation and Elaboration Document

Abstract

The PATH (Predictive Approaches to Treatment effect Heterogeneity) Statement was developed to promote the conduct of, and provide guidance for, predictive analyses of heterogeneous treatment effects (HTE) in clinical trials. The goal of predictive HTE analysis is to provide patient-centered estimates of outcome risks with versus without the intervention, taking into account all relevant patient attributes simultaneously, to support more personalized clinical decision making than can be made based only on an overall average treatment effect. We distinguished two categories of predictive HTE approaches (a “risk modeling” and an “effect modeling” approach) and developed four sets of guidance statements: 1) criteria to determine when risk modeling approaches are likely to identify clinically meaningful HTE; 2) methodological aspects of risk modeling methods; 3) considerations for translation to clinical practice; and 4) considerations and caveats in the use of effect modeling approaches. We also discuss limitations of these methods and enumerate research priorities for advancing methods designed to generate more personalized evidence. This explanation and elaboration document describes the intent and rationale of each recommendation; and discusses related analytic considerations, caveats, and reservations.

Introduction

In medical care, treatment decisions made by clinicians and patients are generally based implicitly or explicitly on predictions of comparative outcome risks under alternative treatment conditions. Randomized controlled trials (RCTs), widely accepted as the gold standard for determining causal effects, have provided the primary evidence for these predictions. However, there has been mounting recognition within Evidence-Based Medicine (EBM) of the limitations of RCTs as tools to guide clinical decision making at the individual patient level.^1–4 Although historically the overall summary result from randomized trials (“average treatment effect”) has been the cornerstone of evidence-based clinical decisions, there is growing interest in understanding how a treatment’s effect can vary across patients—a concept described as heterogeneity of treatment effect (HTE).^5–11

There is a large literature on the limitations of conventional “one-variable-at-a-time” subgroup analyses, which serially divide the trial population into groups (e.g., male versus female; old versus young) and examine the contrast in the treatment effect across these groups.^12–22 The limitations include the risks of false negative and false positive results—due to low power for statistical interactions, weak prior theory on potential effect modifiers and multiplicity.^4;10;23–25 These analyses also are incongruent with the way clinical decision making occurs at the level of the individual patient, since patients have multiple attributes simultaneously that can affect the trade-offs between benefits and harms of the intervention. Individual patients therefore may belong to multiple different subgroups, each potentially yielding different treatment effect estimates.^4;10

The Predictive Approaches to Treatment effect Heterogeneity (PATH) Statement offers guidance relevant for “predictive” approaches to HTE analysis²⁶ that are designed to address some of the limitations mentioned above. The goal of predictive HTE analysis is to provide individualized predictions of treatment effect, specifically defined by the difference between expected potential outcome(s) of interest with one intervention versus an alternative.^4;8 We refer to this as the “individualized treatment effect” and avoid the term “individual treatment effects,” since this latter term confusingly suggests that treatment effects can be estimated at the person-level; such effects are inherently unobservable in parallel arms clinical trials.^10;27 Individualized treatment effects have also been termed “conditional average treatment effects” ²⁸—denoting that they are the averaged treatment effect in a subpopulation (i.e. conditioned on a set of covariates). However, for prediction, we are specifically interested in identifying the best conditional average treatment effect given all available patient characteristics, where ‘best’ is defined as that which best discriminates between future patients who do and do not benefit from a treatment to optimize individual patient decision making. By accounting for multiple variables simultaneously, predictive HTE analysis is foundational to the concept of personalization in EBM.⁴

Distinct approaches to PATH

The PATH Statement outlines a set of principles, criteria, and key considerations for predictive approaches to HTE in RCTs to provide patient-centered evidence in support of decision making. The focus of the PATH Statement guidance is on identifying “clinically important HTE,”^4;7;10 or variation in the risk difference across patient subgroups sufficient to span important decision thresholds, which reflect treatment-related harms and burdens. The PATH Statement²⁶ offers guidance on two distinct approaches to predictive HTE analysis.⁴ With a “risk modeling” approach, first, a multivariable model that predicts the risk of an outcome (usually the primary study outcome) is identified from external sources (an “external model”) or developed directly on the trial population without a term for treatment assignment (an “internal model”). This prediction model is then applied to disaggregate patients within trials to examine risk-based variation in treatment effects. In a second, “effect modeling,” approach, a model is developed on RCT data with inclusion of a treatment assignment variable, and potential inclusion of treatment interaction terms. These more flexible effect modeling approaches have the potential to improve discrimination of patients who do and do not benefit but are especially vulnerable to overfitting and to false discovery of promising subgroup effects (or require very large databases well powered for the detection of interaction effects)²⁹. Both approaches can be used to predict individualized treatment effects, i.e., the difference in expected outcome risks under two alternative treatments, conditional on multiple important clinical variables. A fuller introduction to risk and effect modeling is presented in prior literature.⁴

In this PATH Statement Elaboration and Explanation, we expand on the intent and motivation (and reservations) regarding the PATH statements, criteria, and considerations and caveats. Recommendations are explained in more detail and accompanied by clinical applications of selected methods and supporting methodological evidence where relevant. A glossary of terms relevant to these methods is also provided in an Appendix.

Clarification of Terms and PATH Statement Scope

The term heterogeneous treatment effects (HTE) has been used in the literature in different ways. In this paper, we define the term HTE as non-random variation of treatment effects across levels of a covariate (i.e., a patient attribute or a score comprised of multiple attributes), as measured on a selected scale, against a clinical outcome. It corresponds to the epidemiological concept of effect measure modification, but applies specifically to treatment effects. HTE is identified in clinical trials by contrasting treatment effects on a chosen scale between subgroups and testing for statistical interactions. Importantly, HTE, effect measure modification, and statistical interaction are all ‘scale-dependent’ concepts—that is, their presence or absence depends on what scale one selects to measure treatment effect.³⁰ The scale dependence of HTE is illustrated in Figure 1, which contrast three different analyses (the first showing HTE only on the absolute scale, the second only on the relative scale, and the third on both). To underscore the scale dependence of HTE, we also show the results of a risk modeling analysis of the Diabetes Prevention Program (DPP) Trial, which tested lifestyle modification and Metformin against usual care for prevention of diabetes (Figure 2). While only one of the tested therapies shows statistically significant HTE on the relative (hazard ratio) scale, both therapies had substantial HTE on the clinically important absolute scale. The Appendix Glossary contains definitions of key terms described here and elsewhere in the PATH Statement and E&E document.

Figure 1. The Scale Dependence of Heterogeneity of Treatment Effect (HTE).

The above plots depict the scale dependence of effect heterogeneity. All 3 scenarios are drawn from hypothetical trials with the same overall results (outcome rates 8.8% versus 6.6% in the control (open circles) versus treatment (closed circles) groups) and depict outcomes in low risk (75% of patients, Q1–3) and high risk (25% of patients, Q4) groups (where control event rates are 5% versus 20%, respectively). Plots in the left, middle and right column display outcome risks, relative effects and absolute effects, respectively. In the first row, effect heterogeneity is absent on the relative scale, but present on the absolute scale. In the second row, effect heterogeneity is present on the relative scale but absent on the absolute scale. In third row, effect heterogeneity is present on both the relative and the absolute scale. Most typically, the statistical significance of HTE is tested on the relative scale (middle column), since regression analyses are often performed on these scales. Provided sufficient statistical power, analyses 2 and 3 would show statistically significant HTE. However, regardless of the scale of the analysis, the clinical importance of HTE should generally be evaluated on the absolute scale. When absolute effects span a decisionally-important threshold, which depends on the treatment burden (e.g. harms and costs), HTE is said to be clinically important. In this example, for illustratrive purposes we have arbitrarily set a decisionally relevant threshold at a 1 percentage point reduction in outcome risk. Here, while there is HTE on the absolute scale in both analyses 1 and 3, clinically-important heterogeneity is present only in the third analysis, where the treatment that is beneficial on average may not be worth the treatment burden for many (indeed most) patients. Note, the presence of statistically significant interaction (on the relative scale) does not imply clinically important HTE, and that the absence of a statistically significant interaction does not imply the absence of clinically important HTE. It is also important to note that testing heterogeneity on the relative scale does not test a specific causal hypothesis regarding effect modification (regardless of the subgrouping variable), but merely tests the hypothesis that relative effects are the same in one group versus another group. Establishing causal interaction effects are not necessary to improve the targeting of therapy. We also note that this diagram makes the simplifying assumption of uniform treatment burdens across all levels of risk.In practice adverse events may vary across risk groups, and the threshold is also sensitive to patient values and preferences.

Figure 2. Effects of Lifestyle Modification and Metormin versus Usual Care in Patients with Prediabetes at Different Risks of Developing Diabetes⁷¹.

Figure 2 presents HTE analysis of the Diabetes Prevention Program (DPP) Trial as a function of baseline risk⁷¹. Event rates (top graph), hazard ratios (middle graph) and absolute effects (lower graph) are shown. Both lifestyle modification (left panel) and metformin (right panel) are compared to usual care as a function of baseline risk. For lifestyle modification, a consistent 58% reduction in the hazard of developing diabetes over three years was found across all levels of risk. This consistent relative effect yields HTE on the absolute scale of potential clinical importance. In contrast, the effects of metformin are heterogeneous on the both the hazard ratio scale and on the absolute scale. Penalized splines were used to model the relationship between the linear predictor of risk and the time to event outcome. Vertical lines denote 95% confidence intervals and p-values are based on the null hypothesis of no effect modification tested using the linear predictor of risk in a Cox model. The dashed lines show the average effects in the trial. Prediction of incient diabetes with an external model derived from the Framingham cohort yielded a similar pattern¹²³.

HTE analysis for causal interaction versus for prediction and decision making

We also note that HTE (and statistical interactions) are used to make two very different kinds of inferences: 1) causal inferences (e.g. regarding causal/biological interaction) and 2) inferences for clinical decision making. Although the importance of statistical interactions is often stressed for HTE analysis, we note that these inferences are only weakly related to the presence of “statistically significant HTE.” Statistical interactions should not be confused with causal interactions and statistically significant HTE should also not be conflated with clinically-important HTE. These issues are described briefly below.

In regression models examining HTE, causal inferences depend on interpretation of model inputs (i.e. model covariates). The PATH guidance does not address causal interpretations of HTE. These analyses are important for identifying biomarkers that might biologically interact with therapy. Interaction on a multiplicative (relative) scale is taken by many as being stronger evidence in support of a causal interaction than interaction on an absolute scale (although this is by no means a universal view).^31–37 Nevertheless, we note that treatment-by-covariate interactions (on any scale) are generally descriptive measures of association (when the covariate is not randomly assigned, as in a factorial trial), since an interacting covariate may be acting as a proxy for many measured and unmeasured variables. To attribute a change in the treatment effect to the covariate, one would need to control for all differences in these other variables (i.e. observed and unobserved confounders) across levels of the subgrouping factor. In any event, demonstrating causal interaction is not necessary for “predictive” HTE analyses that seek to target therapies to those who most benefit (see immediately below).

In regression models examining HTE, inferences for clinical decision making depend on interpretation of model outputs. Because these analyses depend on model outputs, they have been referred to as “predictive” HTE analyses.^4;8 The PATH guidance is limited to predictive approaches to HTE. The goal of predictive HTE analysis is to develop models that can be used to predict which of two or more treatments will be better for a particular individual, taking into account multiple relevant variables.^4;8 Clinically-important HTE occurs when variation in the risk difference across patient subgroups spans a decisionally-important threshold, which depends on treatment burden (including treatment-related harms and costs). It is generally assessed on the absolute scale, regardless of the scale of the analysis. The scale dependence of effect heterogeneity is also illustrated in Figure 1. We also note that controlling for confounding factors (i.e. those factors that differ between levels of the subgrouping variable) is not necessary for prediction.^32;38

A new term, “risk magnification,” has recently been coined to describe a method of identifying high risk-high benefit patients. ^39;40 This approach depends on the observation that relative effects (and in particular those on the odds ratio scale) are often more stable than absolute effects.^41–43 Risk magnification is distinct from the risk modeling approach described here, since it may be applied without any data based on the assumption of a contant relative treatment effect. Indeed, the use of the Pooled Cohort Equation⁴⁴ (also known as the Atherosclerotic Cardiovascular Disease [ASCVD] Risk Estimator) to target statin therapy to patients at high risk of developing coronary heart disease might be described as an application of “risk magnification.” Because many (observed and unobserved) patient attributes change across different risk levels, and because the causes of the outcomes may also change, the assumption of a consistent treatment effect across all levels of risk is a strong assumption that should ideally be examined using randomized data. Additionally, the rate of adverse events may also differ across levels of baseline risk (see Box B, Recommendation 9). Examining randomized data stratified by a risk model also permits these other (non-primary) outcomes to be examined across levels of risk.

PATH Statement Criteria for When Risk Modeling is Likely to be of Value (Box 1)

The below criteria identify the data, modeling, and clinical decisional features common to scenarios in which the application of predictive HTE analyses to treatment comparisons is likely to be relevant for individualized clinical decision-making. The motivation and reservations regarding these criteria (and excluded ones) are elaborated.

• 1When there is a well-established overall treatment effect. Subgroup results (including risk-based subgroup results) from overall null trials should be interpreted cautiously.

  When clinical trials are null, there may be a temptation to find subgroups of patients in whom the treatment might work. However, clinically important subgroup effects discovered through a risk modeling approach are likely to be rare when treatment efficacy has not been established. For example, among 18 null trials in a recent study, risk modeling did not yield clinically informative results on any.⁴⁵ More “aggressive” effect modeling approaches (i.e., those reliant on including treatment-by-covariate interaction terms within a prediction model) may identify groups of patients that appear to benefit, but such approaches also are likely to yield spurious false positive results.^28;46 Groups may be suggested by pure chance, aggravated by multiple testing, even when treatments have no effects whatsoever.²⁹ Thus, predictive HTE analyses are more appropriately conducted on interventions for which an overall effect has been established. Despite a tendency to focus on any positive subgroup in an otherwise null trial, in the absence of strong, a priori clinical justification, predictive HTE analyses on null trials are unlikely to lead to reliable clinical evidence.

  Possible exceptions to this general rule are interventions with known treatment-related harms that mediate primary outcomes in the treatment arm that might nullify an overall effect. For example, ACE inhibitors both cause and prevent renal insufficiency; thrombolytics both cause (via hemorrhage) and prevent (via reperfusion) functional disability in patients presenting with acute stroke;⁴⁷ carotid surgery can both cause and prevent ischemic stroke in patients with carotid stenosis;⁴⁸ and antiarrhythmic agents both cause and prevent serious cardiac arrhythmias.^49;50 In these circumstances, even when trials are null overall for the average treatment effect, risk models may be helpful in disaggregating patients who benefit from those who are harmed, either through application of an outcome risk model or a model identifying those patients at high risk for treatment-related harm (i.e., for “treatment deselection”).^47;51;52 Such an approach is possible particularly when the predictors of outcome risk are poorly (or negatively) correlated with predictors of the risk of treatment-related harm. For example, excluding patients at high risk for thrombolytic-related intracranial hemorrhage in stroke (e.g. younger age, lower blood pressure), may uncover benefit in patients at lower risk (ref).⁴⁷

• 2When the benefits and harms/burdens of a given intervention are finely balanced (i.e. of similar magnitude on average), increasing the sensitivity of the treatment decision to risk prediction.

  Risk models are more likely to be useful when they support a particular “risk-sensitive” decision. This criterion corresponds to the observation that a prediction model or decision rule has maximum expected utility when the decision threshold is at or near the mean population risk.^53;54 The threshold depends on the clinical context and involves weighing the expected benefits against the expected harms or costs of a decision. This assessment may be done with formal decision analysis, but more often it is done informally.

  That the value of a risk model is higher for decisions where the threshold is near the population mean can be intuitively understood by considering that the value depends on the proportion of patients for whom the optimal treatment switches from the treatment that is better on average to the alternative given their model-estimated risk, and the benefits that accrue to those switching.^55–57 Beyond measuring model accuracy, various methods have been proposed as a means to evaluate the potential impact that model use might have on a particular decision, including risk stratification tables,⁵⁸ relative utility curves,⁵⁹ predictiveness curves,⁶⁰ and decision curves.⁵⁶

  This discussion with respect to risk prediction also fully applies to benefit prediction. When the overall average benefit in a trial is balanced by the average treatment-related harms and costs (i.e. when net benefit is near zero), any additional prognostic/predictive information is likely to be especially useful for determining the better therapy for a particular patient.

  The relative utility of risk prediction when average risk is near versus far from a threshold is described schematically in Figure 3, which depicts the distribution of expected benefits when a risk model with a C statistic of 0.75 is applied to a population with an average risk of 25%. We consider two different treatment conditions: 1) a treatment with a moderate average treatment effect (a 15% relative risk reduction; 3.8% risk difference) and a slightly favorable average benefit-harm trade-off (compared to a minimally clinically important difference of 3%), and 2) a treatment with a large treatment effect (a 50% relative risk reduction; 12.5% risk difference) and a clearly favorable average benefit-harm tradeoff. All else being equal, the net benefit of risk modeling would be greater when the harm-benefit trade-offs are more finely balanced since risk-stratification would reveal many patients (almost half the trial population in the first schematic example) whose risk-specific optimal treatment differs from the treatment that is best on average. Preliminary evidence from careful simulations or even simple algebraic calculations (see Figure 4A) using plausible assumptions may be important in motivating research and should generally be included in research proposals and protocols.

  We acknowledge that the presentation of a single threshold is a simplification, since the threshold is sensitive to patient values and preferences, and because treatment harms and burdens are likely to vary across risk groups. For example, the CHADS Score (and its variants) are used to target anticoagulation to patients with non-valvular atrial fibrillation, but it is also known that higher-CHADS Score patients are also at higher risk for anticoagulation-related hemorrhage.⁶¹ Given the potential (positive or negative) correlation between the benefits and harms, we recommend that harms should be reported in each risk stratum to support strata-specific evaluation of benefit-harm trade-offs (Box B, recommendation 9).

• 3When treatments are associated with a non-trivial amount of serious harm or burden, increasing the importance of careful patient selection.

  This criterion is related to the previous two in that HTE will be most important to decision making in the presence of a qualitative interaction, meaning that some patients benefit while others are harmed. Qualitative interactions, by definition, do not arise where treatments are totally innocuous. In the presence of a small amount of treatment-related harm, the harm may be quantitatively negligible among high risk patients, but sufficient to erode much (or all) of the benefit in low risk patients (Figure 4). The importance of risk modeling for HTE in treatments with treatment-related harm has been demonstrated in simulation studies^46;62 and observed empirically for carotid endarterectomy,⁴⁸ stroke prevention in non-valvular atrial fibrillation,^63;64 and medical or mechanical reperfusion in ST-elevation myocardial infarction.^65–67 Treatment-related harm may be reflected in the primary outcome, or may be ascertained as a separate outcome (e.g., acute kidney injury, major hemorrhage,^51;68 serious bone fractures).^52;69 Risk modeling may also be appropriate for particularly burdensome interventions (e.g., major lifestyle commitments,^70;71 treatment-related costs).^72;73

• 4When several large, randomized, well-conducted clinical trials of contemporary interventions are available and appropriate for pooling in individual patient meta-analysis

  Clinical trials are typically powered to detect an overall average treatment effect in a population, not estimate effects in relevant subgroups. Very large databases are required for effect modeling, in which multiple individual covariate-by-treatment interactions are considered. The sample size required to detect a subgroup effect is four-fold higher than for a main effect even under favorable conditions (e.g., well-balanced subgroups, overall effect and subgroup effect similar in size), but will generally be much higher than that.^23;24 While a risk modeling approach does not depend on the discovery of statistically significant covariate-by-treatment interaction terms, greater statistical power improves the precision of effect estimation across risk strata, thus improving the ability to estimate benefit- harm trade-offs across strata. We also emphasize the need for contemporary trials, as they are more likely to be relevant for contemporary clinical care. In addition, while such analyses have not been consistently successful in the discovery of reliable treatment effect interactions,⁷⁴ combining data is likely to lead to substantial increases in risk heterogeneity in the study population (see Criterion 5), increasing the likelihood of uncovering clinically important HTE (i.e. on the risk difference scale).^75;76

• 5When substantial, identifiable heterogeneity of risk in the trial population is anticipated

  Risk heterogeneity is dependent on the presence of significant factors to predict outcome risk and differences in the distribution of these factors across the population (i.e. a non-homogeneous population). In the absence of factors that can predict outcome risk, there is no risk heterogeneity. Conversely, risk heterogeneity is highest in the presence of good discrimination (i.e., a high C-statistic). Indeed, risk heterogeneity in a given population is a model-dependent property.⁷⁷ Figure 5 shows the empirical relation between the C-statistic and the extreme quartile risk ratio (EQRR, the ratio of outcome rate in the highest risk quartile to the rate in the lowest risk quartile⁷⁸) across 32 publically available trials.⁴⁵ Because there is an abundance of clinical prediction models,^7;79;80 the predictability of trial outcomes can generally be evaluated, at least informally, from the literature. Trials with broad inclusion criteria, and thus a broad case mix, are more likely to show greater risk-heterogeneity compared to trials with more narrowly restrictive enrollment criteria. Nevertheless, there seems to be substantial risk heterogeneity even in classic efficacy trials.^45;66-68;71 Because individual patient meta-analyses (i.e., combining trials) have even higher patient-level risk heterogeneity, they are an ideal substrate for these analyses.^75;76

• 6When there is strong preliminary evidence that a prediction model is clinically useful for treatment selection, or when there are models in current use for treatment selection

  The vast majority of prediction models developed are not applied in clinical practice.⁷⁹ Some fields produce massive numbers of new prediction models without clear purpose except as publishable analytic exercises. Conversely, the development of new models should start from some clinical need. Thoughtful selection of a “risk-sensitive” decision is one of the most crucial steps in developing a useful clinical prediction model.⁸¹ The use of a prediction model in clinical practice may be an implicit marker of such a risk-sensitive decision for which clinicians sense that the balance of the benefits and burdens of a treatment decision vary across the population in a clinically meaningful way. For example, the widespread use of the CHADS score^63;64 (and its variations⁸²), the ASCVD score,⁴⁴ and chest pain tools^83;84 may be considered a marker of the risk-sensitivity of these decisions. Similarly, the widespread use of certain diagnostic prediction models in emergency departments to rule out rare but serious conditions (e.g. cervical spine fracture,⁸⁵ intracranial hemorrhage,⁸⁶ or pulmonary embolism⁸⁷) in low risk patients to reduce the harms/burdens of further diagnostic testing is a marker for the risk-sensitivity of this class of decisions. Such consensually-established, implicitly-revealed risk-sensitive decisions remain relatively uncommon. Moreover, randomized data are relatively scarce and risks may change meaningfully over time. Hence, opportunities to re-examine the risk-specific benefits (or validate predictions of benefit) in new trial data are highly valuable.

• 7When the clinical variables in the proposed model are routinely available in clinical care.

  The advantages of easily and reliably obtainable clinical characteristics as predictors should be obvious. Nevertheless, there are many examples in the literature of models including variables not ordinarily obtained in clinical care. For example, waist-to-hip ratio is a very strong predictor of diabetes and of cardiovascular risk,^88;89 but it is rarely ascertained in routine clinical care. Prostate volume is an important predictor of prostate cancer risk, but can only be obtained by an invasive test and is therefore of quesitonnable value for use in models.⁸⁴ By raising the burden of variable ascertainment, the probability that a prediction model will be used—compared to selecting the best treatment on average—is lowered. Again, because of the abundance of published risk models, it is usually possible to ascertain from the literature well established risk predictors prior to the analysis of trial data, even when internal risk models will be used to stratify the trial.

Figure 3: The Value of a Risk Modeling Approach is Likely to be Greater when the Average Treatment Effect in a Trial (Treatment A) is Near a Decision Threshold.

Figure 3 depicts the anticipated influence of a risk modeling approach in two trials testing different treatments in the same population, one of a treatment (A) with a slightly favorable benefit-harm trade-off, and the other of a treatment with an extremely favorable benefit-harm trade-off (treatment B). Under both conditions, the control event rate is 25% and the minimal clinically significant difference (MCSD, i.e., the absolute benefit that would justify the experimental therapy) is 3 percentage points. (For simplicity, we display a single MCSD, with grey shading corresponding to portions of the population that should not be treated, but this value varies according to individual patient values and preferences.) A risk modeling approach would be of substantially greater value for the trial of therapy A, with the slightly favorable trade-off (with a relative risk reduction [RRR] of 0.15; absolute risk difference = 3.75%, just above the MCSD), compared to the trial of the therapy B with the extremely favorable trade-off (RRR of 0.5; risk difference = 12.5%, substantially above the MCSD). The distributions show the anticipated risk differences that emerge with a constant RRR when the same moderately-predictive risk prediction model (i.e., with a c-statistic = ~0.70) is applied to the population. In the slightly favorable treatment condition (A), harms outweigh benefits in almost half the trial population (43%), despite overall results showing benefit on average. In the extremely favorable treatment condition (B), treatment remains worthwhile in virtually the entire population (97%). Thus, applying the risk modeling approach is very valuable in the low benefit condition, as it reclassifies many patients as treatment-unfavorable who would otherwise have been treated based on the overall result.

Figure 4. Schematized and Actual Risk-based Heterogeneous Treatment Effects.

This figure schematically depicts outcome risks for a trial testing a hypothetical intervention with an odds ratio of 0.75 but with an absolute treatment-related harm of 1% (shown in the top panel). Observed odds ratios (middle panel) and risk differences (bottom panel) are shown. Overall trial results are dependent on the average risk of the enrolled trial population. When the average risk is ~7% (as above), a well-powered study would detect a positive overall treatment benefit (shown by the horizontal dashed line in the middle and bottom panels). However, a prediction model with a C-statistic of 0.75 generates the risk distribution at the top of the figure. A treatment-by-risk interaction emerges (middle panel). Whether or not this interaction is statistically significant, examination of treatment effects on the absolute risk difference scale (bottom panel) reveals harm in the low risk group and very substantial benefit in the high risk group, both of which are obscured by the overall summary results. Conventional one-variable-at-a-time subgroup analyses are typically inadequate to disaggregate patients into groups that are sufficiently heterogeneous for risk such that benefit-harm trade-offs can misleadingly appear to be consistent across the trial population. Baseline risk is logit normal distributed with mu=−3 and sigma=1 (the log odds are normally distributed). Figure adapted from Kent DM et al. JAMA 2007.³

The RITA-3 trial (N=1810) tested early intervention versus conservative management of non-ST-elevation acute coronary syndrome. Results for the outcome of death or non-fatal myocardial infarction at 5 years are shown above, stratified into equal-sized risk quarters using an internally-derived risk model; the highest risk quarter is sub-stratified in halves (groups 4a and 4b). Event rates with 95% confidence intervals (top panel), odds ratios (middle panel), and risk difference (bottom panel) are displayed. The risk model is comprised of the following easily obtainable clinical characteristics: age, sex, diabetes, prior MI, smoking status, heart rate, ST depression, angina severity, left bundle branch block, and treatment strategy. As in the schematic diagram to the left, the average treatment effect seen in the summary results (horizontal dashed line in middle and bottom panels) closely reflect the effect in patients in risk quarter 3, while fully half of patients (q1 and q2) receive no treatment benefit from early intervention. Absolute benefit (bottom panel) in the primary outcome was very pronounced in the eighth of patients at highest risk (4b). A statistically significant risk-by-treatment interaction* can be seen when results are expressed in the odds ratio scale (middle panel). Such a pattern can emerge if early intervention is associated with some procedure-related risks that are evenly distributed over all risk groups, eroding benefit in low risk but not high risk patients, as illustrated schematically in Figure 4A.

*The interaction p value is from a likelihood ratio test for adding an interaction between the linear predictor of risk and treatment assignment (one degree of freedom).

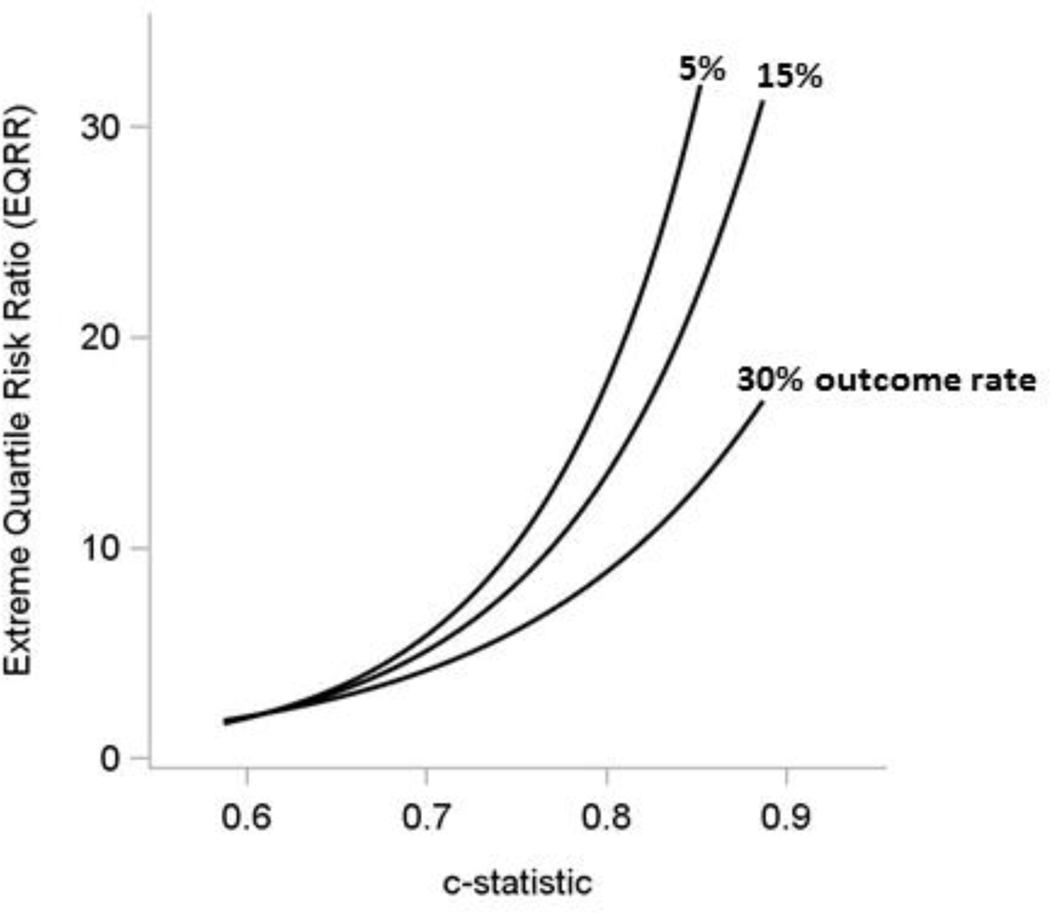
Figure 5: Risk heterogeneity increases with higher discrimination – Extreme Quartile Risk Ratio Increases With Increasing C-Statistic, Especially at Low Outcome Rates.

The curves above depict the relationship between the c-statistic and extreme quartile risk ratio (EQRR) – that is, the risk in the highest quartile compared to the risk in the lowest quartile – for different outcome rates across 32 trials.⁴⁵ Unsurprisingly, the degree of risk heterogeneity (as represented by the EQRR) is strongly related to the discriminatory power of the prediction model. The relationship is strongest when the overall outcome rates are low. The c-statistic and EQRR both reflect how well the risk factors predict the outcome in a given population. For reference, in a trial with an outcome rate of 15%, a predictive model with a c-statistic of 0.80 is anticipated to yield an outcome rate that is 13-fold higher in the high risk quartile compared to the low risk quartile. When the outcome rate is lower (5%), this ratio is expected to be greater than 20-fold for a model with similar discrimination. Patient groups with such different outcome risks are unlikely to have similar benefit-harm trade-offs for most therapies, even thought they may be included in the same trial.

Explication of Excluded Criteria

The PATH Technical Expert Panel (TEP) failed to reach consensus (as defined by a mean agreement score of less than 3) on two additional criteria to identify when a risk modeling approach is likely to be of value to analyze RCT results. The standard deviation of the agreement scores were also relatively high (SD>1) for these criteria, reflecting the conflicting positions held by panelists. These excluded criteria are described below.

When the outcome rate is lower

A low outcome rate is associated with a more asymmetric distribution of estimated absolute benefit (on the probability scale) across individuals in a trial (Figure 5). For example, when the outcome rate is 6% overall and the C-statistic is 0.80, the average outcome rate in the lowest risk quartile of patients is anticipated to be approximately 1%.⁴⁵ While benefit is limited by a floor effect—it is impossible to lower outcome risk to less than zero—treatment-related harms can still be substantial. The high risk group (e.g. the highest risk quartile) in these low outcome trials frequently has outcome rates more than tenfold the rates found in the low risk group, and may account for most of the benefit in the trial (see Figure 4B). These skewed distributions follow from the logistic regression scale (log odds) and Cox regression scale (log hazard⁴⁵). This makes the average risk (and treatment benefit) misleading even for typical patients enrolled in the trial.^45;90 Nevertheless, there was disagreement among the expert panelists that a low outcome rate was a useful criterion to identify worthwhile target trials for risk modeling. Outcome rate is estimated from empirical data with unavoidable uncertainty and unknown generalizability in other populations, which may have higher outcome rates.

When the two treatments are clinically very different (e.g., medicine versus surgery)

Several treatment selection models have been successfully developed on RCT data comparing treatments that have substantially different mechanisms of action. For example, well known prediction models have been developed on randomized data to disaggregate treatment-favorable from treatment-unfavorable patients for carotid endarterectomy versus medical therapy for patients with symptomatic carotid stenosis⁴⁸ or percutaneous coronary intervention (PCI) compared to coronary artery bypass grafting (CABG) for patients with non-acute coronary artery disease.⁹¹ Nevertheless, the TEP disagreed on whether this criterion was a reliable marker of worthwhile opportunities for risk modeling. Indeed, when interventions in alternative trial arms differ substantially, one might anticipate that individual variables may interact with treatment, making an effect modeling approach more advantageous than a risk modeling approach. Indeed, the SYNTAX Score II Model for CABG versus PCI.⁹¹

Justification of Guidance on Risk Modeling Strategies to Identify HTE (Box B)

The below criteria describe the best methodological practices in the conduct of risk modeling approaches to identify HTE. The motivation regarding these statements are elaborated, including reservations and considerations and caveats.

• 8Reporting RCT results stratified by a risk model is encouraged when overall trial results are positive to better understand the distribution of effects across the trial population.

  When outcome risk is described using a multivariable model, the control event rate will vary substantially across risk strata of a RCT. It is not uncommon for the control event rate to vary between 5- and even 20-fold across risk strata in trial populations.^45;92 The control event rate is a mathematical determinant of the treatment effect, regardless of what scale is used to measure treatment effect (Table 1). Because typical treatment effect metrics are different (non-linearly related) contrasts of the same two quantities (control and treatment event rates), when the control event rate changes across subgroups, the treatment effect can remain constant on (at most) one scale. In particular, large changes in the control event rate almost always lead to substantial changes in the most clinically relevant scale of effect measure, the absolute risk difference.^4;93 Thus, the widespread assumption that harm-benefit trade-offs are usually similar for patients meeting trial enrollment criteria is demonstrably false and potentially harmfully misleading.⁴ Indeed, the assumption of a constant relative treatment effect across groups of patients that vary dramatically in their control event rate—especially in the presence of treatment related harm— needs to be carefully examined. Presenting overall trial results without showing how the treatment effect varies across risk strata—and particularly whether changes in the risk difference are clinically important across risk strata—may be considered a form of under-reporting of trial results.⁶

• 9Predictive approaches to HTE require close integration of clinical and statistical reasoning and expertise.

  The optimum treatment selection model will generally be grossly underdetermined by the available data, particularly from a single RCT and when multiple potentially important risk markers are considered. Thus, it is generally not possible to use totally agnostic, data-driven approaches alone for variable and model selection when analyzing clinical trials for HTE. Prediction of treatment effect at the individual patient level may be very sensitive to arbitrarily-determined model-building choices that define the reference class (i.e. subgrouping) scheme.^94;95 While in theory, these issues asymptotically diminish as databases become infinitely large, clinical reasoning remains critical to the process of variable selection and model specification in the identification of a clinically-plausible, clinically useful and clinically useable model from the limited data sources generally available. Similarly, given the specialized expertise needed for prediction modeling, clinical investigators should generally not proceed without experienced statistical collaborators. Thus, realizing the goal of predictive HTE analysis requires close partnership between clinical and methodological experts.

Table 1:

Treatment Effect is Mathematically Dependent on the Control Event Rate

Measure	Definition
Absolute Risk Difference	CER-TER
Relative Risk Reduction	$\text{1-}\frac{\text{TER}}{\mathbf{\text{CER}}}$
Odds Ratio	$\frac{\text{TER/}\left(\text{1-TER}\right)}{\mathbf{\text{CER/(1-CER)}}}$

CER=control event rate

TER=treatment event rate

Identify or Develop a Model

• 10When available, apply a high-quality, externally-developed, compatible risk model to stratify trial results.

  For major clinical trials (those that assess a treatment’s effect on mortality, major morbidity or other key clinical outcomes), it is often possible to perform risk-based analysis of HTE using an externally developed tool. Prediction models are available to predict overall risk for most major conditions and their complications.⁷ Nevertheless, differences in populations or variable definitions may render published models incompatible with completed RCTs. Investigators may also choose to develop a new model using data from a related observational study or clinical trial. An external model is more relevant if the eligibility criteria for the derivation cohort align with, or are even broader than, those in the target trial. Ideally, predictor and outcome variable definitions should be similar to those available in the RCT. An externally-derived model enables translation into practice, especially when well-validated and clinically-accepted models compatible with the RCT are available.

• 114. When a high-quality, externally-developed model is unavailable, consider developing a model using the entire trial population to stratify trial results; avoid modeling on the control arm only.

  When such models are not available, internally derived (or endogenous) models may be employed. Guidance on good prediction modeling practice should be followed, e.g., a large number of events per independent variable, and pre-specified, a priori, selection of risk variables based on prior literature.^96;97 Models derived directly on RCT data may provide internally valid treatment effect estimates within risk strata. One approach is to develop the model ignoring treatment assignment.⁹⁸ The risk model defines the reference class or subgrouping scheme;⁴ a second step then estimates treatment effects across risk strata. Separating the variable selection and model specification process from treatment effect estimation minimizes some of the biases (such as so-called “testimation bias”⁹⁶) that complicate effect modeling. Alternatively, some have recommended that only the control arm be used to model risk⁹⁹ as ostensibly the best estimate of the control event rate. However, modeling on the control arm only can potentially induce differential model fit on the two trial arms, biasing treatment effect estimates across risk strata, and generally exaggerating HTE;^46;98;100 various cross-validation techniques have been proposed to address this bias even when modeling on only the control arm.¹⁰¹ Concerns about differential fit between arms from endogenously derived models may also apply when randomization is unbalanced (e.g., 1:2 or 1:3 randomization) or when treatment effects are very large, such that the number of events in the control arm is much larger than in the treatment arm. When imbalance in events is caused by very large treatment effects, risk-based HTE may be less clinically relevant (see Figure 3). Potential approaches to modeling on trials with imbalanced randomization and/or strong treatment effects should be evaluated in future research (Table 2).

• 125. When developing new risk models or updating externally-developed risk models, follow guidance for best practice for prediction model development.

  While not the focus of the PATH Statement, there is existing guidance to support development of new risk models, or the updating of externally-developed models.^{96;97;102;102} In particular, the TRIPOD Explanation and Elaboration document¹⁰² offers detailed, referenced guidance on how to design, conduct, and analyze prediction model studies – with published exemplars – with a view to limiting risk of bias and maximizing the clinical usefulness of the model. We emphasize that TRIPOD indicates that continuous predictors should ideally be kept as continuous (and examined for linear or nonlinear relations with the outcome). This best practice of modeling continuous variables continuously, or modeling risk continuously, does not necessarily proscribe the common practice of displaying clinical trial data to readers in subgroups which is part of the guidance below. The TRIPOD Explanation and Elaboration document¹⁰² also provides a good discussion of the considerations for handling missingness for clinical prediction models, which are relevant here. When important risk factors are missing on some patients, analyses should apply techniques, including multiple imputation when appropriate, to avoid exclusion of randomized patients. Alternative approaches for subgroup identification in the presence of missing variables should be investigated in future research (see Table 4: A Meta-Research Agenda for Predictive Approaches to Treatment Effect Heterogeneity). The PROGRESS series of papers^103–106 and several textbooks also offer guidance on the optimal development of clinical prediction models.^96;97

  Since adequate power for HTE analysis might best be achieved by combining multiple randomized trials, prediction modeling guidance should be complemented in these cases by guidance for best practice for individual patient meta-analysis (IPDMA).¹⁰⁷ In particular, it is recommended to include study-specific intercepts to account for unexplained risk heterogeneity.^108;109 Similarly, study-specific effects should be accounted for in analyzing treatment effects. Alternative meta-analytic approaches are discussed in the literature and are beyond the scope of this guidance.^110;111

Table 2:

Hypothetical Example Presentation of the Effects of Model-based Decision Making

Strategy	Number of Patients Treated	Number of Events	Decrease in Event Rate
Treat no patient	0	250	--
Treat all patients	1000	200	50
Treat only those with a predicted benefit >5%	400	215	35

Table 4.

A Meta-Research Agenda for Predictive Approaches to Treatment Effect Heterogeneity More research is needed to:

High Priority Research Needs
Better understand the value of HTE methods through empirical analyses across a wider range of clinical domains.
Determine optimal approaches to penalization/regularization in effect modeling to mitigate the risks of overfitting; or other methods that permit the exploration of plausible hypotheses of effect modification on the relative scale while strongly protecting against false positive findings.
Determine optimal methods to simultaneously predict multiple risk dimensions (e.g. risk of the primary outcome versus risk of treatment-related harm) and/or optimal approaches to combine models predicting these outcome risks for improved benefit-harm discrimination.
Determine the optimal measures to evaluate models intended to predict treatment benefit.
Identify heuristics or general principles to judge the adequacy of sample sizes for predictive analytic approaches to HTE, particularly for treatment effect modeling.
Determine optimal methods to validate, recalibrate, and/or update models predicting treatment effect in the absence of new randomized trials.
Other Research Needs
Determine optimal methods to combine predictive HTE analyses with methods that permit the estimation of direct treatment effects or adherence-adjusted effects in the presence of drop out, loss to follow up, poor adherence and treatment switching.
Identify the appropriate clinical contexts for which modeling multiple dimensions of risks (e.g., risk of the primary outcome; risk of treatment-related harm; risk of an important competing outcome) is important and feasible for adequate disaggregation of benefit-harm trade-offs.
Determine methods to analyze trials with multiple important outcomes, or outcomes where differences in treatment effect may be related to the choice of follow-up time.
Better understand the impact of different missingness mechanisms and develop principled methods for dealing with missing data in the context of subgroup identification.
Determine methods to permit models predicting treatment effect to cope with missing data in clinical practice.
Determine optimal methods for modeling the functional form of the risk-by-treatment interaction to translate risk stratified results from trials into continuous treatment effect predictions for clinical application.
Address concerns about differential fit between arms from endogenously derived risk models when randomization is unbalanced (e.g., 1:2 or 1:3 randomization).
Determine optimal methods to achieve balance in covariates across subgroups in observational databases.
Determine whether novel methods, including machine learning techniques, have distinct advantages over traditional statistical approaches for predicting treatment benefit.
Examine how to best extend these approaches to other trial designs (e.g. longitudinal studies, dynamic treatment regimens)

Apply the Model and Report Results

• 13Report metrics for model performance for outcome risk prediction on the RCT, including measures of discrimination and calibration (when appropriate).
• 14Report distribution of predicted risk (or the risk score) in each arm of the trial, and in the overall study population.
• 15Report outcome rates and both relative and absolute risk reduction across risk strata.
• 16When there are important treatment-related harms, these harms should be reported in each risk strata to support strata-specific evaluation of benefit-harm trade-offs.

Consistent with the TRIPOD Statement, measures of discrimination and calibration should be presented whether an externally or internally derived model is applied (Box B, Recommendation 6). However, one should not confuse these conventional measures of model performance with discrimination and calibration of predicted benefit (see Special Considerations for Evaluating Models that Predict Benefit). We also note that point scores, such as TIMI,¹¹² CHADS-VASC⁸² or ABCD2,¹¹³ may be useful for trial risk stratification but do not yield predictions for calibration.

Although its importance was highlighted two decades ago,⁹² reporting the distribution of baseline risk is rarely done (Box B, Recommendation 7). It is thus generally impossible to assess the degree of baseline risk heterogeneity in most published clinical trials. Risk reporting should allow readers to assess the full distribution of risk in the study population, either graphically or by including information on the mean, standard deviation, median, and interquantile ranges. The precise approach for presentation is not important, as long as it allows the reader to understand the distribution of predicted baseline risk (or the risk score of a risk index) in the study population. The “Table 1” of a clinical trial report (which conventionally includes patient attributes for participants in each study arm) should also include the population mean and median predicted baseline risk (or risk score) with measures of variability, and additional information on the population distribution of risk if there is substantial skewness (such as quartiles/percentiles, a histogram, or a box plot). ​If the study includes a largely homogeneous population with regard to overall risk, the reader will know that generalizing the study results to populations with substantially different risk would be speculative. If there is substantial heterogeneity in the study population, then reviewers will know that conducting a risk-stratified analysis is particularly important.

We recommend grouping patients using quantiles (e.g. quartiles) for reporting purposes and displaying and estimating treatment effects separately (e.g. dividing patients into equal-sized quarters) in these groups, as an initial step (Box B, Recommendation 8). Reporting treatment effect across strata is important because it illustrates how the absolute risk difference varies across the study population, whether or not the relative effect is constant (see Figure 4B for an example). Additionally, it permits the assumption of a constant relative effect across risk strata to be evaluated (see Box B, Recommendation 10, explanation below). As an alternate presentation, treatment effects may also be displayed by continuous risk, as seen in Figure 2, rather than by quantiles (which are sample-dependent). As discussed above, examining variation in the relative treatment effects may be particularly important when there is even a small amount of treatment-related harm.^3;62 In the case of time-to-event analysis, treatment effects should be analyzed and reported by cumulative incidence curves. Relative treatment effect estimates can be summarized by hazard ratios over a clinically meaningful time horizon (or several meaningful time horizons). Absolute treatment effect estimates can be summarized by cumulative incidences at a clinically meaningful time point (or several meaningful time points). In reporting risk-stratified results, readers should be provided with the information needed to easily determine the amount of variation in risk difference/number needed to treat (NNT) and relative effects. These stratum-specific results can provide a rough guide for clinical interpretation, which can be further refined for clinical implementation by continuous modeling (see Box C, Recommendation 3).

From a decision analytic perspective, the clinical value of a prediction model is determined by its ability to distribute patients by their absolute treatment effect across an important decision threshold. This threshold depends on the burdens of treatment, which depend on treatment harms and costs and patient values and preferences. However, even apart from patient values and preferences (which are inherently patient-specific), treatment burden may differ substantially across patient subgroups. Because patients in different risk strata vary in many clinically important characteristics, one cannot assume that subgroups stratified by their risk of the primary outcome have similar rates of treatment-related harms. For example, patients with atrial fibrillation who have higher CHADS scores (indicating higher stroke risk and greater potential benefit from anticoagulation) also have substantially higher risks of bleeding.⁶⁹ Stroke patients with a higher risk of stroke recurrence, according to a recurrence risk score, have potentially greater benefit from pioglitazone, but also have a higher risk of pioglitazone-related bone fracture.⁶¹ Because of the potential correlation between these two different risk dimensions (i.e., between the risk of the primary outcome and the risk of treatment-related harm), event rates for these harms should be presented at a congruent level of disaggregation as the primary outcome in order for readers to determine within risk-strata benefit-harm trade-offs (Box B, Recommendation 9).

Risk modeling is potentially most useful when predictors of the risk of the primary outcome and the benefits of therapy are poorly (or negatively) correlated with the risks of treatment-related harm. This will maximize heterogeneity in the benefit-harm trade-offs across risk strata, increasing the decisional value of the risk model. While several investigators have sought to arithmetically combine separate prediction models predicting outcome risk and treatment-related harm to stratify trial results by the benefit-harm trade-off,^48;65;68 this approach can be exquisitely sensitive to miscalibration of the two models (which may compound miscalibration of the harm-benefit trade-offs). The best approach to model benefits and harms simultaneously is beyond the scope of these recommendations and is an important topic for future research.

• 17To test the consistency of the relative treatment effect across prognostic risk, a continuous measure of risk (e.g., the logit of risk) may be used in an interaction term with treatment group indicator

  While it has generally been stressed that testing for a statistical interaction between subgroups is recommended to determine HTE, when the outcome rates vary substantially across strata, one may assume that the risk difference also varies (Table 1; Figure 4). Thus, even though the absolute scale is the most relevant clinically, null hypothesis testing for HTE across risk strata on the risk difference scale is generally not useful, as a non-signficant result is far more likely to reflect low power rather than true consistency of effects on the risk difference scale. Statistically testing a risk-by-treatment interaction on the relative scale (e.g., whether the linear predictor of risk interacts with treatment) provides information on whether a constant relative treatment effect may be a reasonable approximation with which to estimate a risk-specific (“individualized”) treatment effect. Yet the presence or absence of a statistically significant result should not be conflated with the clinical significance of HTE (which should always be evaluated on the risk difference scale). In conducting a risk-by-treatment interaction test, using a continuous measure of risk (e.g., the logit of risk) typically provides superior power compared to testing for effect differences across distinct risk groups (see middle panel Figure 4B).¹¹⁴ Nevertheless, a visual (non-parametric) exploration of how the relative effect varies across values of outcome risk may ensure the appropriateness of linear effect modification. Testing for a non-linear interaction between risk and treatment (e.g., using the logit of risk in a quadratic term, or with another flexible non-linear shape^115;116) may also be useful. However, it should be recognized that such an interaction test may be poorly powered to detect deviations from linearity, particularly when only a single trial with a limited number of events is the substrate for modeling. Moreover, once it is established that there is an overall treatment effect, determining the risk-specific treatment effect should be considered an estimation problem (rather than a hypothesis testing problem). Standard errors across levels of risk can be estimated through a proportional interactions model.^117;118 Flexibly modeling the treatment effect across risk strata, or simply reporting the effects across subgroups defined by quantiles (e.g., quartiles) provides useful information regardless of the p-value of the interaction terms testing effect modification on the relative scale. Most importantly, the presence or absence of a statistically significant treatment interaction term should not be conflated with the presence or absence of clinically important HTE (see below).

Justification of Caveats and Considerations Before Moving to Clinical Practice (Box C)

The below considerations relate to the translation of findings from predictive approaches to HTE analyses into clinical practice. Clinical translation of these analyses is a complex topic including many issues, and a detailed discussion of these challenges is beyond the scope of this project, where we focus on analysis and reporting of RCT findings. However, below are some priority analytical considerations for facilitating model translation into clinical practice.

1. Clinical interpretation of HTE should stress differences in the absolute treatment effects across risk groups: the statistical significance of effect modification on the relative scale should not be conflated with the clinical significance of absolute treatment effect estimates.

   As discussed, it is generally agreed that the most important scale for clinical interpretation is the absolute risk difference scale (or its reciprocal, the number needed to treat). The clinical significance of HTE should generally be discussed with reference to the absolute scale, while a relative scale (e.g., odds ratio or hazard ratio) is typically appropriate for null hypothesis testing in HTE analyses. Investigators should consider reporting results in ways that facilitate clinical interpretation of how treatment decisions might be changed with use of the risk model (e.g., number of patients treated or the number of events avoided with versus without model use) and should consider decision analytic approaches for evaluation.^55;119 Table 2 illustrates how results can be presented in a simple way that facilitates understanding of the clinical relevance of risk-modeling. Presentation of important treatment-related harms should also permit within-strata evaluation of absolute effects.

2. External validation and calibration of risk prediction is important for translation of risk-specific treatment effects into clinical practice.

   Although internally-derived (or endogenous) prognostic models can provide reliable internally valid estimates of treatment effects within trial risk strata, implementation of an externally valid prognostic model is necessary for translation into practice.¹⁰⁵ Finding clinically important HTE across risk strata within a trial with an endogenous model provides an important impetus for developing and implementing an externally valid prognostic model. It should be noted that external validity is a general concern for RCT results and their subgroup analyses, not one confined to results subgrouped using prediction models.¹²⁰

3. Clinical implementation may be supported by translating multivariable risk-based subgroup analysis into models yielding continuous treatment effect predictions to avoid artefactual discontinuities in estimation at the quantile boundary of an outcome risk group.

   In presenting HTE analyses of clinical trial results, it is customary to categorize patients into subgroups. Here, we have recommended presenting results in risk strata. Nevertheless, dividing patients into discrete groups based on values of a continuous measure has some disadvantages.¹²¹ Categorization into risk groups suggests that risk and treatment effects are homogeneous within groups, and leads to a potentially misleading “step function” in either risk or in treatment effect estimation. With such an approach, for example, a very small change in risk at the boundary of a group defined by a quantile can lead to a very large change in the anticipated benefit. Additionally, quantiles have specific disadvantages in that they are sample-driven cut points, leading to difficulties in comparing results across studies,¹²² and also potentially obscuring problems with model calibration. For example, using an internally developed risk model and the Framingham model to stratify patients in the Diabetes Prevention Program (DPP) Trial appeared to yield near-identical results.^71;123 However, if the trial population was divided into groups of patients based on predicted risk thresholds (as they would in clinical practice), risk groups defined by the Framingham model would have revealed that the Framingham model was poorly calibrated to the DPP Trial population. Thus, while trial results displayed by risk strata are frequently sufficient to evaluate the clinical importance of risk-based HTE, clinical implementation may be supported by translating multivariable risk-based subgroup analysis into models yielding continuous predictions of outcome risks with and without therapy (see Legend Figure 1).

Treatment Effect Modeling to Identify HTE (Box D)

Conventional one-variable-at-a-time subgroup analysis are known to have low credibility due to noisy data (very low power for interactions) weak theory (little prior knowledge about effect modification) and multiplicity⁴. Including relative effect modifiers as interaction terms within a prediction model engenders the same concerns.

While relative effect modifiers are difficult to reliably identify, they are highly influential on individual patient predictions of benefit¹²⁰. Including spurious false positive interaction terms in models that predict treatment benefit can mis-target therapies; excluding true interaction terms limits the usefulness of prediction by substantially lowering discrimination of patients who benefit from those who don’t²⁹. Whether or not to include a treatment effect interaction term in a prediction model is a fraught and consequential decision; the PATH TEP accordingly recommends a cautious approach. We restrict our recommendations to the unusual situation where highly credible effect modifiers have been identified, and otherwise offer caveats and considerations for more data driven approaches.

1. When highly credible relative effect modifiers have been identified, they should be incorporated into prediction models using multiplicative treatment-by-covariate interaction terms.

   • ACredibility should be evaluated using rigorous multidimensional criteria (such as described by the ICEMAN tool) and should not rely solely on statistical criteria (such as p-value thresholds).

     There have been important efforts to establish criteria that might identify highly credible subgroup analyses.^9;19;124 A newly proposed tool (Instrument for assessing the Credibility of Effect Modification ANalyses, (ICEMAN)¹²⁴) is based on 5 criteria to evaluate credibility of effect modification: Four of these criteria are related to pre-specification and markers of the “prior probability” or plausibility of effect modification: 1) presence of prior evidence; 2) prespecification of a few primary subgroup analyses; 3) prespecification of the anticipated directionality of effect modification; 4) full specification of cut points when thresholds are used for continuous variables. The fifth criterion (a low p-value) is a measure of the statistical strength of the interaction effect in the data being analyzed. The PATH group endorses the rigorous and multidimensional approach recommended in ICEMAN to identify highly credible interaction terms. Examples of highly credible effect modifiers include symptom onset to treatment time for thrombolytic therapy in acute myocardial infarction or acute ischemic stroke^125;126, and urinary protein excretion as a modifier of the effect of ACE inhibition on the progression of chronic kidney disease^75;127.

     In the analysis of trial data, identification of credible interaction terms can be facilitated by explicitly distinguishing those subgroup analyses that are intended to be confirmatory analyses (hypothesis testing analyses, well-motivated by prior evidence and intended to produce clinically actionable results), from secondary (exploratory) subgroup analyses (performed to inform future research).^7;8 Because in any given clinical trial, there is typically limited prior information regarding effect modification, subgroup analyses will frequently be exclusively exploratory, and therefore not yield any covariate-by-treatment interaction effects appropriate for inclusion in prediction models intended for informing clinical care.

     Prespecification of primary subgroups should include explicit definitions and categories of the subgroup variables, including cut-off thresholds for continuous or ordinal variables where these are used, and the anticipated direction of the effect modification. By conducting primary subgroup analysis that are few in number, fully pre-specified, hypothesis-driven and statistically robust (i.e. based on multiplicative interactions), subgroups can produce evidence regarding factors that influence the benefit of treatment that might then be carried forward into models to yield clinically actionable predictions.

     Although only primary (confirmatory) subgroup analyses are relevant for clinical decisions and the predictive HTE analyses we address here, we acknowledge the importance of secondary subgroup analyses to explore more uncertain or unexpected relationships between individual patient attributes and treatment effects; such analyses are appropriate for hypotheses generation, which can then be tested (and usually disproved^{23;25;128;129} in future studies.

     We note that because p-values (or other statistical criteria) in general are influential in how subgroup analyses are interpreted (and are included in ICEMAN criteria) and because interaction effects are poorly estimated in trials of conventional size (even when these are pooled), treatment interaction terms selected for inclusion are likely to overestimate the true interaction effects (i.e. from overfitting).^4;29;130 Therefore, even when only highly credible interaction terms are included, we recommend model building procedures that take into account model complexity (i.e. approaches using regularization/penalization) whenever interactions are included (see Box D, Recommendation #3).

Caveats and Considerations for Data Driven Effect Modeling

Emerging ‘data driven’ methods proposed to develop effect models on trial data when there is little prior information on effect modifiers are a promising area of research²⁸, but were felt by the TEP to be at too formative a stage to offer recommendations. A systematic scoping review¹³¹ was conducted in an effort to characterize this rapidly evolving literature, and revealed future research opportunities. Table 3 summarizes at a high level the key features of the differing approaches. In addition to risk and effect modeling, the scoping review identified methods collectively described as optimal treatment rules that use combinations of relative effect modifiers to classify patients into treatment favorable and treatment unfavorable categories—i.e. based only on the sign of the effect. Because these are classification, rather than prediction methods, we do not discuss these in our guidance, but direct interested readers to the literature on these approaches^132–142. A key feature of many of the procedures for predictive analyses (and particularly effect modeling) is that they separate the variable selection procedure in building a model that defines subgroups (or reference class scheme) from the estimation of treatment effects, thereby avoiding testimation bias.^96;143;144 Alternatively, various methods of penalization/regularization to reduce the likelihood of overfitting have been proposed and tested.¹⁴⁵ Although the PATH TEP did not articulate a full set of methodological best practices for treatment effect modeling given more limited practical experience (as compared to risk modeling), we offer caveats and considerations for this type of predictive HTE analysis (and their justifications) below.

Table 3.

Methodological Literature on the Conduct of Regression Modeling Approaches to Treatment Effect Heterogeneity Analysis

Approach	Description
Risk-modeling approaches7;45;62;98;117;118;120;183–186	Using a multivariable risk model developed blinded to treatment effect, analyze the relationship between baseline risk and treatment effect on the relative and on the absolute scale. While treatment effect modification on the relative scale across different levels of baseline risk is considered, treatment effect modification on the relative scale for individual risk factors is not.
Treatment effect modeling approaches120;143-145;151;186–193 Subgroup identification (2-step process)143;144;187 Individualized treatment effects (1-step process)120;145;186;188–190	Use both the main effects of risk factors and interaction effects with treatment assignment (on the relative scale) to estimate more individualized treatment effects. They can be used either for defining patient subgroups with similar expected treatment effects or for predicting individualized treatment effects on the absolute scale for future patients.
Optimal treatment regimens132–142	Classify patients into those who benefit from treatment (positive individualized treatment effect) and those who do not (negative individualized treatment effect), through the identification of modifiers of treatment effects on the relative scale.

• 2Avoid one-variable-at-a-time null hypothesis testing or stepwise selection (e.g., backward selection, forward selection) strategies to select single relative effect modifiers

  One-variable-at-a-time null hypothesis testing will preferentially select effects that are over-estimated within the sample database (i.e., Type I error and testimation bias). Including treatment interaction terms in models predicting benefit generally requires reliable prior information regarding relative effect modifiers. Interaction terms for well-established treatment effect modifiers should be included in the prediction model, regardless of the statistical significance of the interaction (see Box D, Recommendation 1). When multiple relative effect modifiers are hypothesized to be of potential importance in determining treatment effects, the value of including these interactions may be assessed simultaneously by a single overall test, limiting the opportunity for Type I error and testimation bias.¹⁰² To increase the power of this test, the number of treatment effect interactions included should be limited.¹⁰² Investigators should use clinical considerations and should also consider examining associations between candidate effect modifiers to reduce the number of interactions assessed within the overall test. A null result on the overall test for interaction suggests that an effect modeling approach (i.e., including interaction terms) will not add substantially to a risk modeling approach.

• 33. Avoid the use of regression methods that do not take into account model complexity when estimating coefficients (e.g. ‘conventional’ unpenalized maximum-likelihood regression) when one or more treatment by covariate interaction terms are included in a treatment effect model.

  Although there is no consensus on the optimal approach for including relative effect modifiers in a risk prediction model (“effect model”), conventional regression techniques should be anticipated to result in overfitting. Penalized estimation (e.g. LASSO; penalized/ridge; elastic net regularization regression; Bayesian penalization, as well as other non-regression based methods discussed above) at least partially addresses the tendency to overfit benefit predictions. The optimal approach to penalization for effect modeling is a subject of current research, but avoiding overfitting for benefit prediction is much more difficult than avoiding overfitting for outcome prediction (Figure 6). Alternatively, 2-stage methods relying on different datasets (or subsets) for variable and model selection for determining the subgrouping (i.e. reference class) scheme and for treatment effect estimation can also avoid/mitigate ‘testimation’ bias.

• 44. Avoid evaluating models that predict treatment benefit using only conventional metrics for outcome prediction (e.g. based on discrimination and calibration of outcome risk prediction).

  The performance of models intended to predict benefit should be evaluated for the prediction of benefit (i.e., predicted versus observed outcome rates across subgroups defined by quantiles of predicted benefit occurring with versus without treatment), not for their ability to predict outcome risk. Calibration for outcome risk can be seriously misleading when evaluating models that purport to predict treatment benefit (Figure 6). The discrepancy arises because benefit miscalibration compounds the error in the risk estimation in the control and treatment groups and magnifies this error (i.e., the scale of the risk difference is typically much smaller than that of outcome rate). Evaluation methods that pertain to models intended for treatment selection or to predict benefit are discussed further in the section immediately below.

Figure 6: Evaluating Model Performance: A Comparison of Conventional Outcome Risk Calibration versus Treatment Effect (Benefit) Calibration.

These data represent box plots of predicted and observed event rates by quartiles of predicted risk in the control and treatment arm of a hypothetical RCT (500 simulations; panel A). These rates appear to demonstrate appropriate model calibration. However, examining the same data for predicted and observed benefit (differences in event rates) by quarters of predicted benefit (panel B) reveals very poor model calibration at the extreme quarters. This poor calibration occurs because miscalibration for the risk difference includes error from both the control and treatment arm, and because the scale of the risk difference is much smaller than that for the outcome risk. These data was generated from a simulation of a prediction model that included 12 treatment effect interactions, 6 of which represented true interactions. The boxes represent, in line with Tukey’s definition, the 25% quantile to the 75% quantile (with the median shown). The lower and upper whiskers include the most extreme observations within the range of 1.5 times the interquartile range, from the 25% and 75% quantiles, respectively.

Special Considerations for Evaluating Models that Predict Benefit

The statistical performance of prediction models is typically decomposed into measures of calibration (“Do x of 100 patients with a predicted risk of x% actually have the outcome?”) and discrimination (“What is the probability that patients with the outcome have a higher predicted risk than those without the outcome?”). Evaluating a prediction model intended to predict treatment effect using these usual metrics related to outcome risk prediction (e.g., C-statistic) fails to provide information on how well the model performs for predicting benefit and informing treatment decisions. Efforts to develop measures to assess model accuracy for predicting benefit (in particular, evaluating measures of discrimination for benefit) are hampered by the fundamental problem of causal inference for the individual. That is, individual patient treatment effects are inherently unobservable, as only one of the possible outcomes is observed for each patient (the actual outcome they experienced under randomization).¹⁴⁶

For example, for “predictive” biomarkers (i.e., factors that can aid in treatment selection), it has been suggested to evaluate performance by the sensitivity and the specificity of the biomarker for benefit rather than risk, i.e., the probability that the biomarker is positive for patients that benefit from treatment, and the probability that the biomarker is negative for patients that do not benefit from treatment, respectively.¹⁴⁷ However, it has been shown that one can estimate these quantities only under strong unverifiable assumptions about the joint distribution of observed and unobserved outcomes so that each patient can be assigned to a treatment response (bad outcome without treatment, good outcome with treatment, [1,0]), neutral (good or bad outcome regardless of treatment [0,0 or 1,1]) and harm (good outcome without treatment, bad outcome with treatment [0,1])).¹⁴⁸ For example, one proposed method assumes that no subjects are harmed by treatment;¹⁴⁹ others that, conditional on a set of covariates, the potential outcomes with and without treatment are independent.^150;151 Without such assumptions, we can only focus on a model’s ability to predict outcome risk in one arm of a trial or the other, rather than the difference in outcome across arms.^148;152

However, for treatment decision making purposes, we are more interested in optimizing the ability to predict the difference in outcome risk under two treatment conditions. Due to the fact that counterfactual outcomes are unobservable at the individual patient level, evaluating benefit prediction requires some form of stratification of patients into groups with similar predicted benefit. The smallest possible strata are pairs of matched patients. Recently, the C-statistic, commonly used to measure discrimination in outcome risk models, has been adapted to evaluate treatment effect prediction.¹⁵¹ To do so, two patients discordant on treatment assignment are matched according to their predicted benefit (i.e., the absolute difference in their outcome risk with and without therapy). These matched pairs of patients with a similar “propensity for benefit” can then be classified into the three benefit categories according to their “observed benefit” based on a comparison of outcomes in the control and treated patients: 1) benefit (1,0); 2) neutral (1,1 or 0,0); or 3) harm (0,1); the C-statistic assesses how well the model discriminates pairs of patients based on this trinary “outcome.” Again, the definition of “observed benefit” assumes that the potential outcomes with the two therapies are independent within each patient. Since the potential outcomes within each patient are presumably dependent to some (unknowable) degree, the “observed benefit” contains more randomness than the actual (unobservable) individual patient treatment benefit. This leads to conservative estimates of the C-statistic.

Ultimately, the usefulness of a model depends not just on its ability to provide accurate predictions of within-strata treatment effect, but on its ability to improve decisions. Of course, the ultimate test of a predictive approach is to compare decisions (or outcomes) in settings using such individualized predictions to usual care in an experiment.¹⁵³ Lamentably, this is seldom done; well-controlled trials of predictive tools are rare and more are needed. However even in the absence of a randomized trial, methods have been developed to assess the potential impact of models on clinical decision-making. Evaluating clinical usefulness depends on model performance relative to a specific decision threshold—i.e., the absolute risk difference that perfectly balances the burdens, harms, and costs of therapy. Decision curve analysis,⁵⁶ has been proposed to evaluate the clinical usefulness of prediction models on decision making. Decision curve analysis examines the Net Benefit across multiple decision thresholds, where each threshold is used to simultaneously determine allocation to a particular treatment strategy and also to mathematically derive an utility weight of benefits versus harms. The approach has also been adapted to evaluate the potential impact of prediction of treatment benefit on decision making compared with the default best overall strategy (i.e., treat all or treat none).¹¹⁹

While it is impossible to identify the correct treatment for any given individual (since individual treatment effects are unidentifiable in the absence of repeated N of 1 trials^27;154), all these methods evaluate whether a particular prediction-decision strategy optimizes benefits for a population,⁵⁵ since population-wide benefits are optimized when treatments are optimized for each individual.

Limitations of the PATH Statement

We note several limitations of the PATH Statement. The guidance here is intended only for binary or time to event models, which account for the vast majority of large phase 3 clinical trials.^155–158 Much of the guidance would nevertheless pertain also to continuous outcomes. The complexities of HTE analyses for increasingly common longitudinal data involving interaction with time are not discussed. Further, we focus on treatments where a decision is made at a particular point in time (corresponding to the trial baseline) rather than dynamic treatment regimens where treatment decisions may be continually revisited. We also focus on subgroup identification and treatment effect estimation rather than on HTE analyses to inform trial design. The Statement also does not provide advice about performing n-of-1—or multi-person n-of-1—trials, which some consider the only means of estimating “person-level” treatment effects. While we anticipate that observational studies will play an increasingly important role in studying both treatment effects and HTE, the PATH Statement does not address HTE in observational studies (except to stress that methods of debiasing treatment comparisons to support HTE are a research priority). Although each of the above approaches are consistent with the broad goal of evidence personalization, the methods are sufficiently distinct so as to be beyond the scope of this Statement. Notwithstanding the above limitations, we emphasize that the PATH Statement applies to the comparison of treatments as well as the comparison of treatment to no treatment.

An additional limitation of the PATH Statement is that it does not address the topic of the best estimand for predictive HTE analyses and how to best cope with post-randomization events, including drop out, non-adherence, treatment switching and loss to follow up. These issues have received considerable attention in the methodological and regulatory literature, particularly since The National Research Council (NRC) Expert Panel Report on Prevention and Treatment of Missing Data in Clinical Trials^159;160 highlighted the need for clearly defining objectives and estimands and the subsequent ICH E9(R1) draft addendum¹⁶¹. We direct readers to recent literature on this topic^162–164. In general, the primary analysis of most trials is often an intent to treat (ITT) analysis. However, other contrasts are also of clinical import and interest. In particular, the direct causal effect of treatment (i.e. the effect if a patient adheres to their treatment, estimated with a per protocol (PP) or adherence-adjusted analysis^165–169) is often considered the most appropriate estimand for shared decision making in the individual patient. However, as with observational studies, estimating the direct treatment effect can only be done with methods based on unverifiable assumptions; mis-specifying a model predicting non-adherence (or using an instrumental variable approach when causes of non-adherence or drop outs are complex) can lead to biased estimates of treatment effects. An ITT analysis is general felt to yield an unbiased estimate of the treatment policy, though this may be less appropriate for shared decision making. More research is needed regarding optimal approaches to combine predictive HTE approaches with approaches that estimate direct treatment or adherence-adjusted effects.

Discussion

The PATH Statement is comprised of four sets of guidance on the conduct of predictive HTE analyses. The purpose of the Explanation and Elaboration document is to explain the rationale and support for these guidance statements, and to detail caveats or reservations where applicable.

The goal of predictive HTE analysis is prediction of treatment effect to support decision making in each patient.^8;170 Developers of the PATH Statement recognize the inherent difficulties and fundamental limitations of using group data to estimate treatment effects in individuals, and enumerated some of these challenges.²⁶ As more deeply explored in this Explanation and Elaboration document, there remain substantial barriers to fully understand the potential of the predictive HTE approaches to usher in a new era of Personalized EBM.¹⁷¹ Table 4 outlines some outstanding research questions related to methodological issues raised in the development of the PATH Statement. Stronger methodological and evidentiary standards will need to be established to assure that incorporating these methods do not cause more harm than benefit. We also need research to better integrate clinical prediction into practice,¹⁷² to understand how to individualize clinical practice guidelines, to establish or extend reporting guidelines,¹⁷³ to establish new models of data ownership to facilitate individual level meta-analyses,¹⁷⁴ and to re-engineer the clinical research infrastructure to support substantially larger clinically-integrated trials sufficiently powered to determine HTE (and/or to develop our ability to predict when observational data are likely to be sufficiently de-biased for reliable HTE determination).¹⁷⁵ Many recent and ongoing organizational and technical advances should help towards this evolution.^{174;176–178}

As the PATH Statement focused on prediction in randomized trials, we did not explore the use of observational data – and when they may be sufficiently de-biased for reliably identifying HTE.^10;179;180 In addition, there is an evolving set of tools for data-driven approaches to predicting patient benefit, including machine learning techniques.^28;181;182 The PATH Statement should thus be understood as a formative first step (along a much longer path) towards the goal of personalized predictions of treatment benefit using the best available evidence.