BnpC: Bayesian non-parametric clustering of single-cell mutation profiles

Abstract

Motivation

The high resolution of single-cell DNA sequencing (scDNA-seq) offers great potential to resolve intratumor heterogeneity (ITH) by distinguishing clonal populations based on their mutation profiles. However, the increasing size of scDNA-seq datasets and technical limitations, such as high error rates and a large proportion of missing values, complicate this task and limit the applicability of existing methods.

Results

Here, we introduce BnpC, a novel non-parametric method to cluster individual cells into clones and infer their genotypes based on their noisy mutation profiles. We benchmarked our method comprehensively against state-of-the-art methods on simulated data using various data sizes, and applied it to three cancer scDNA-seq datasets. On simulated data, BnpC compared favorably against current methods in terms of accuracy, runtime and scalability. Its inferred genotypes were the most accurate, especially on highly heterogeneous data, and it was the only method able to run and produce results on datasets with 5000 cells. On tumor scDNA-seq data, BnpC was able to identify clonal populations missed by the original cluster analysis but supported by Supplementary Experimental Data. With ever growing scDNA-seq datasets, scalable and accurate methods such as BnpC will become increasingly relevant, not only to resolve ITH but also as a preprocessing step to reduce data size.

Availability and implementation

BnpC is freely available under MIT license at https://github.com/cbg-ethz/BnpC.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Cancer is an evolutionary process characterized by the accumulation of mutations that drive tumor initiation, progression and treatment resistance (Weinberg, 2014). The interplay between variation and selection ultimately leads to multiple coexisting cell populations (clones) that differ in their genotypes (Davis et al., 2017; Turajlic et al., 2018). This genomic heterogeneity, also known as intratumor heterogeneity (ITH), poses major challenges for cancer treatment as parts of the tumor may already be therapy-resistant (Burrell et al., 2013; Gillies et al., 2012). Therefore, it is beneficial to identify the clonal composition of the tumor and to adapt the treatment accordingly. Recent advances in the field of single-cell DNA sequencing (scDNA-seq) have led to new insights into cancer evolution and ITH. Examples include the detection of rare subclones in breast cancer patients (Wang et al., 2014), the identification of novel treatment resistance clones in glioblastomas (Francis et al., 2014) and major advancements in the reconstruction of cancer evolution (Schwartz and Schäffer, 2017). Compared to bulk sequencing, scDNA-seq offers the possibility to directly access clonal genotypes at the cellular level and to more easily detect branching in clonal evolution. However, scDNA-seq data tends to be very noisy. Experimental procedures, such as DNA amplification, but also analytic ones like alignment and mutation calling introduce a large fraction of errors in the data as well as missing values (Estévez-Gómez et al., 2018). Errors can be either missed true mutations, namely false negatives (FN), or mutations not present in a cell but falsely reported, namely false positives (FP). Characteristic of scDNA-seq data are high FN rates, arising from the technical failure to measure both alleles at a mutated locus, and a large fraction of missing values, resulting from non-uniform coverage and drop-outs. Generic clustering algorithms, such as partitioning or density-based methods, do not account for scDNA-seq characteristics and are therefore unsuitable for this type of data. Hence, various methods were recently introduced tailored to single-cell mutation profiles, i.e. the absence or presence of called mutations in each cell. These approaches differ in their main objective, model choice and inference scheme. The majority of them focuses on resolving the phylogenetic relationship among cells and in doing so can also provide clusters and genotypes (Ciccolella et al., 2018; El-Kebir, 2018; Jahn et al., 2016; Malikic et al., 2019; Zafar et al., 2017). Currently, the only method focusing entirely on clustering and genotyping is SCG (Roth et al., 2016), which uses a parametric model and applies mean field variational inference to learn genotypes and the clonal composition. Alternatively, the centroid-basted clustering approach celluloid (Ciccolella et al., 2019) adapts k-modes with a novel dissimilarity for scDNA-seq data but does not provide any genotyping. The probabilistic frameworks BitPhylogeny (Yuan et al., 2015) and SiCloneFit (Zafar et al., 2019), and the nested effects model OncoNEM (Ross and Markowetz, 2016) jointly cluster cells into clones and infer their phylogenetic relations. Despite these successes, the growing size of scDNA-seq datasets challenges the scalability of these methods, compromising their accuracy and efficiency. Especially the inference of phylogenetic relations is a computational expensive task that scales poorly with data size due to difficulties in the tree search. Here, we introduce BnpC, a fully Bayesian method to analyze large-scale scDNA-seq datasets and to accurately determine the clonal composition and genotypes, handling noisy data and an unknown number of clones non-parametrically. We benchmark our approach against state-of-the-art methods on simulated data using various data sizes and demonstrate that BnpC outperforms current methods in terms of accuracy, runtime and scalability. We also reanalyze published scDNA-seq data, and with our method not only manage to recapitulate the original results, but we also resolve populations that in the original publications were detected only with additional data or after manual preprocessing steps.

2 Materials and methods

2.1 Model

BnpC takes as input a binary matrix with missing values $\mathit{X}=(x_{ij})\in {\{0,1,-\}}^{N\times M}\hspace{0.17em}\text{of}\hspace{0.17em}N$ cells and M mutations, where 0 indicates the absence of a mutation, 1 its presence, and – a missing value (Fig. 1A). We assume that the N cells were sampled from an unknown number K of clones, each with a distinct mutation profile ${\mathit{\theta }}_k\in {[0,1]}^M$, coming from a prior distribution $G_0$. The probabilities of observing a FP or FN in the cell data are given by the parameters α and β, respectively, with prior distributions, as stated in Figure 1B. The assignment of cells to clones is represented by a vector c, where $c_i=k$ is the assignment of cell i to clone k. To model the cell assignments c, we use a Chinese Restaurant Process (CRP) (Pitman, 1995). The CRP is a probability distribution over partitions of the natural numbers, which in our model are cell assignments. Because each partition is a possible way of clustering cells, the CRP serves as a prior distribution for grouping cells into clones. The concentration parameter ${\alpha }_0$ of the CRP determines the probability of assigning a cell to a novel clone.

Fig. 1.

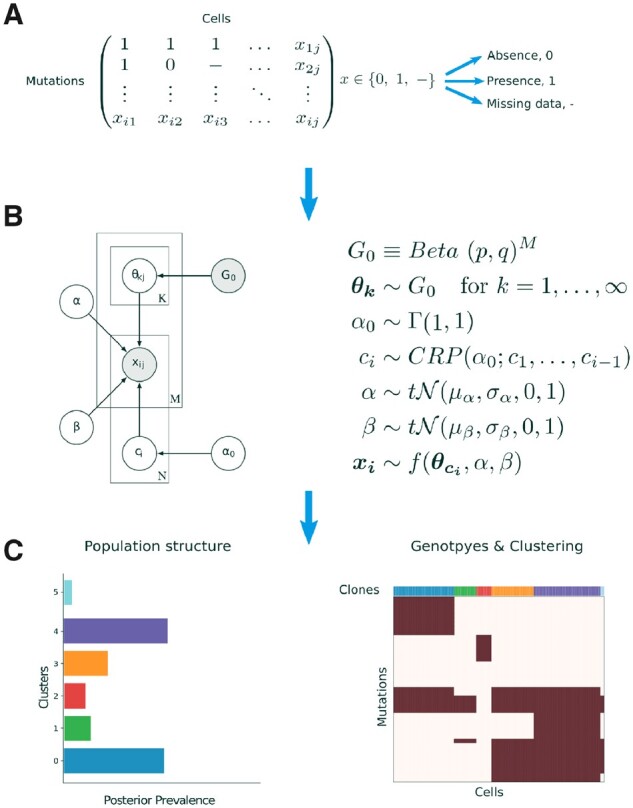
BnpC model overview. (A) The model’s input is a binary mutation matrix, where each row represents a mutation and each column represents a single cell. Possible values are 0, indicating the absence of a mutation, 1, indicating the presence of a mutation and missing values. (B) BnpC’s probabilistic graphical model. The binary input data X, consisting of N cells and M clones, contains a fraction of FP and FN entries, indicated by α and β respectively. G₀ is a base distribution over the genotypes $\theta$ of an infinite number of clones. c is the assignment of cells to the clones, sampled from a CRP with concentration parameter ${\alpha }_0$, and $f(·)$ is the model’s likelihood. Shaded nodes represent observed or fixed values, while the values of unshaded nodes are learned using MCMC. (C) BnpC predicts clonal composition, corresponding genotypes and the population structure

With the parameters described above, we can formulate the likelihood of BnpC as

$$\begin{array}{c}P(\mathit{X}|\mathit{\theta },\mathit{c},\alpha ,\beta )=\prod _{i=1}^N\prod _{j=1}^M{\theta }_{ci,j}\left[{(1-\beta )}^{x_{i,j}}·{\beta }^{1-x_{i,j}}\right]+\\ (1-{\theta }_{c_i,j})[{(1-\alpha )}^{1-x_{i,j}}·{\alpha }^{x_{i,j}}]\end{array}$$ (1)

where the first term accounts for the presence of a mutation in a clone and the observation of a true positive or FN, and the second term accounts for the absence of a mutation in a clone and the observation of a true negative or a FP. Missing values are skipped.

The full posterior distribution over the latent variables factorizes as

$$\begin{array}{cc}P(\mathit{\theta },\mathit{c},\alpha ,\beta ,{\alpha }_0|\mathit{X})\propto \hspace{0.17em}\hfill & \mathit{P}(\mathit{X}|\mathit{\theta },\mathit{c},\alpha ,\beta )\mathit{P}(\mathit{\theta }|{\mathit{G}}_0)\mathit{P}(\mathit{c}|{\alpha }_0)\hfill \\ \hfill & \mathit{P}({\alpha }_0)\mathit{P}(\alpha )\mathit{P}(\beta )\hfill \end{array}$$ (2)

2.2 Inference

As the posterior distribution in Equation (2) is not analytically tractable, we use a Markov chain Monte Carlo (MCMC) sampling scheme, in particular, a generalized Gibbs sampler, to obtain samples from the posterior distribution. Cluster parameters and error rates are updated via Metropolis–Hastings moves; the concentration parameter ${\alpha }_0$ is learned as described in the study by Escobar and West (1995); cell assignments are updated with Gibbs sampling and a modified non-conjugate split-merge move (Jain and Neal, 2007; Neal, 2000).

We modified the split-merge move introduced by Jain and Neal (2004) to increase the probability of merging small clones. We first choose which move to perform. For a split move, two cells are drawn from a clone selected proportionally to its size; for a merge move, two cells are drawn from different clones, themselves selected in a manner inversely proportional to their size. This increases the probability of merging spurious clones. To account for these changes, the proposals’ ratio in Metropolis–Hastings update is modified as follows. For a split move, we introduce the ratio

$$\frac{\widetilde{K_i}\widetilde{K_j}}{{(\sum _l\widetilde{K_l})}^2}{\left(\frac{\left|K_k^{\text{split}}\right|}{N}\left(\begin{array}{c}\left|K_k^{\text{split}}\right|\\ 2^{-1}\end{array}\right)\right)}^{-1}$$ (3)

where l is an index over all occupied clusters. The second term describes the probability of sampling clone $K_k^{\text{split}}$ according to its size $\left|K_k^{\text{split}}\right|$, and choosing two cells I and j from it ($c_i=c_j=k$). After the split, let $K_i\hspace{0.17em}\text{and} K_j$ denote the two different clones to which i and j belong. Let $\widetilde{K_i}={\left(\frac{\left|K_i\right|}{N}\right)}^{-1}$ represents the inverse clone size of the clone with cell i The first term in Equation (3) denotes the probability of choosing the clone with cells i and j to reverse the split move.

Similarly, for a merge move, we extend the Metropolis–Hastings ratio with the following factor:

$$\frac{1}{N(|K_k^{\text{merge}}|-1)}{\left(\frac{\widetilde{K_i}\widetilde{K_j}}{{(\sum _l\widetilde{K_l})}^2}\frac{1}{\left|K_i\right|\left|K_j\right|}\right)}^{-1}$$ (4)

Here, the second term accounts for choosing two distinct clones in a manner inversely proportional to their size, and then two cells i and j uniformly from each clone. The first term undoes the merge move by selecting the merged clone $K_k^{\text{merge}}$ according to its size, and selecting cells i and j from it.

To assess convergence, we implemented an updated version of the Gelman–Rubin diagnostic (Vats and Knudson, 2018) and compared posterior means of scalar quantities from multiple chains with random starting positions (Supplementary Fig. S11). BnpC can be run for a given number of MCMC iterations, with a given time limit, or until the convergence diagnostics drop below a given threshold.

2.3 Estimators

Downstream analyses and interpretation generally require a single set of clusters and genotypes for all cells, and thus the posterior samples obtained by our model need to be summarized. To provide an estimate of the inferred clones, we used the MPEAR criterion (Fritsch and Ickstadt, 2009). The genotypes were subsequently inferred independently for each clone from a selected subset of posterior samples. For each clone, we selected posterior samples based on two criteria: (i) all cells assigned to the clone are clustered together; (ii) no other cell is clustered with these cells. If no sample fulfills both criteria, we selected samples that satisfy only the first criterion. The final genotype is the rounded mean over the cluster parameters from the selected posterior samples. While biased, this estimator performed well in practice. We evaluated our estimator against the maximum likelihood (ML) and maximum a posteriori (MAP) point estimators, which were outperformed in all cases (Supplementary Figs S14 and S15). All of these estimators are implemented in BnpC and are available to the user.

3 Results

3.1 Benchmarking on simulated data

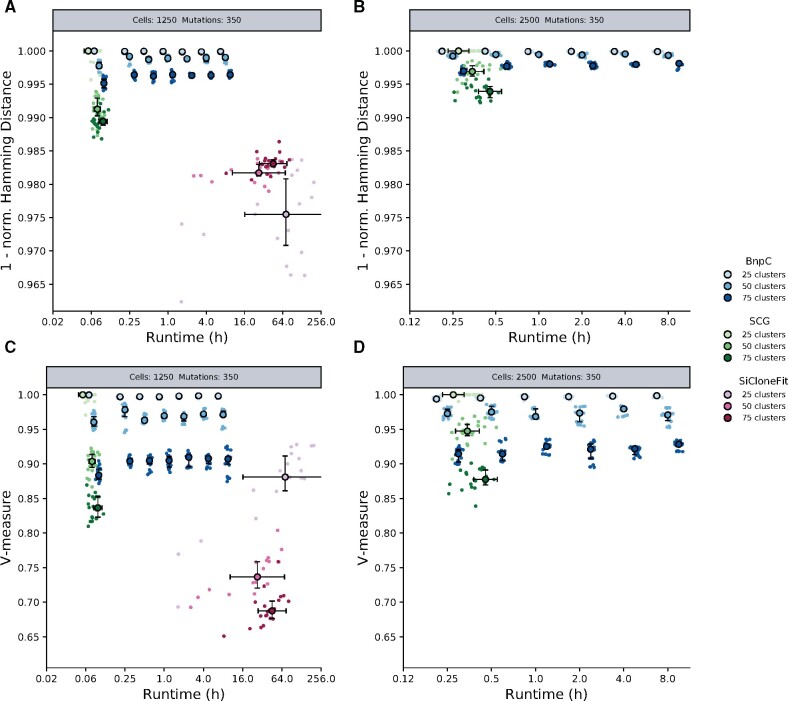
We generated 180 datasets varying the numbers of cells (1250, 2500, 5000, 10 000), mutations (200, 350, 500) and clones (25, 50, 75) to assess BnpCs scalability, run time and performance. Each combination was simulated five times with fixed FN, FP and missing value rates at 0.3, 0.001 and 0.2, respectively. The underlying phylogeny was also fixed (minimal trunk size of 0.1 and mutation rate of 0.25). A description of the simulation process is provided in Supplementary Material (Supplementary Section S1). All algorithms were run four times per dataset with different seeds. Clustering accuracy was evaluated using the V-Measure (Rosenberg and Hirschberg, 2007), where high values correlate with more accurate clusterings. Genotyping accuracy was measured as one minus the Hamming distance between the predicted cellular genotypes and the true ones, normalized by the maximum value it can achieve, that is the product of the number of cells and the number of mutations. Higher values denote more accurate genotypes. We also evaluated sensitivity, specificity and the $F_1$ score, and note that, the normalized Hamming distance is the only metric treating FP and FN equally (Supplementary Fig. S10).

We benchmarked BnpC against SCG (Roth et al., 2016) and SiCloneFit (Zafar et al., 2019). Celluloid clustering with the silhouette method for clone number determination was excluded as it does not provide genotypes and performed poorly on small datasets (Supplementary Figs S8, S9). Methods aiming to resolve phylogenetic relations were excluded as they only provide genotypes directly, while the inference of clones from phylogenetic trees is a non-trivial task. We also excluded BitPhylogeny and OncoNEM, which jointly infer clones and their phylogenetic relations, as both were previously shown to produce less accurate results than SCG and SiCloneFit (Roth et al., 2016; Zafar et al., 2019). BnpC was run for 0.08, 0.25, 0.5, 1, 2, 4 and 8 h. SCG was run with a maximum number of iterations set to ${10}^9$, so as to ensure convergence for every run. The number of clusters was set to a fourth of the number of cells. We were only able to run SiCloneFit for 10 steps on the dataset with the smallest number of cells, as its runtime there already exceeded 48 h (Fig. 2). Therefore, we excluded SiCloneFit from the benchmarks on larger datasets. The algorithms and running parameters are described in greater detail in Supplementary Section S2. Algorithms were run on a high-performance computing cluster, each algorithm ran on a single core with a maximum of 64 GiB memory and 2.4 GHz CPU.

Fig. 2.

Performance of BnpC, SCG and SiCloneFit on synthetic data. (A, B) Genotyping accuracy measured by 1 - Hamming distance/(#cells. #mutations). (C, D) Clustering accuracy measured by the V-Measure. Simulated datasets contained 350 mutations and (A, C) 1250 cells or (B, D) 2500 cells, clustered into 25, 50 or 75 distinct clones. For all datasets, the FN rate was fixed at 30%, the FP rate at 0.1% and the missing value fraction at 20%. Each cell and clone number combination was simulated five times; algorithms were run four times on every simulated dataset

On datasets with 1250 cells (Fig. 2A, C), when the number of clones was 50 or 75, BnpC performed best. For 25 clones, its performance was on par with SCG. As expected, SCG ran fastest, but BnpC’s results showed the least variance and did not substantially improve after 15 min, indicating quick convergence. SiCloneFit’s performance was poorest, and its average runtime was usually $\ge$48 h. Therefore, we excluded it from larger benchmarks. We observed a similar trend on the datasets with 2500 cell (Fig. 2B, D). Interestingly, BnpC was able to obtain accurate results more quickly than SCG. On datasets with 5000 and 10 000 cells, we were unable to run SCG with our parameters and on our hardware due to lack of convergence or insufficient computer memory. BnpC’s prediction accuracy did not improve after 1 h on 5000 cells and after 2 h on 10 000 cells and was $\ge$0.995 for genotyping and $\ge$0.89 for clustering (Supplementary Fig. S2).

Varying the number of clusters, which represents data heterogeneity and hence complexity, revealed that the clustering accuracy of all algorithms decreased as complexity increased. The same was observed for the genotyping performance of BnpC and SCG, but not of SiCloneFit, a result probably explained by the phylogenetic constraints of its model. In general, BnpC’s performance was more robust to complex data, leading to the most precise predictions in datasets with more than 25 clusters.

To further investigate the effect of data heterogeneity on the accuracy of the results, we considered the inference of the number of clusters (Supplementary Fig. S7). On the least complex dataset (25 clusters), BnpC tended to overestimate the number of clusters, SiCloneFit underestimated it, while SCG reported the correct number in most cases, thus explaining its higher clustering accuracy. On more heterogeneous datasets (50 and 75 clusters), SCG and SiCloneFit consistently underestimated the number of clusters, while BnpC’s predictions were closer to the correct value.

Interestingly, only BnpC’s accuracy increased with the number of mutations (Supplementary Figs S3, S4, S5, S6). The decrease in SiCloneFit’s performance could result from the increase in data size and, therefore, an initialization farther away from regions of high posterior probability. In our simulations, SCG appeared unable to handle highly complex data. In all runs, it underestimated the number of clusters, regardless of the number of mutations supporting them. This can explain SCG’s decrease in accuracy as the number of mutations increases.

Fig. 3.

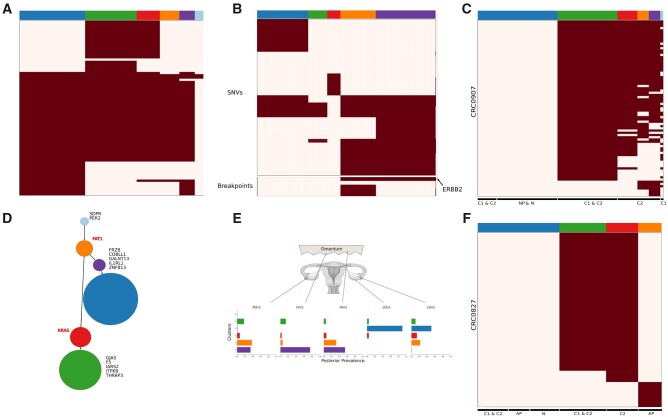
Analysis of real datasets by BnpC. (A, D) Patient 4 of the Gawad dataset. (A) Clones and genotypes inferred by BnpC. (D) Resulting minimum spanning tree from the clonal genotypes as obtained in Gawad et al. Gene labels in the tree determine either mutations leading to a new clone (black) or known ALL driver genes (red). Node size corresponds with the clonal size. (B, E) Patient 9 of the McPherson dataset. (B) Clones and genotypes inferred by BnpC. (E) Estimated prevalence of clones across samples from the posterior distribution estimated by the model. (C, F) Analysis for patients. CRC0827 (C) and CRC0907 (F) of the Wu dataset. Heatmaps depict absence (white) or presence (red) of mutations for every mutation (row) in every cell (column)

Additionally, we tested the effects of varying error and missing value rates on two smaller datasets, one with 100 mutations, 100 cells and 5 clones and one with 50 mutations, 200 cells and 10 clones (Supplementary Figs S8, S9). On the smaller dataset, all algorithms were able to identify the correct clusters and infer genotypes with $\ge$0.995 accuracy. On the dataset with 10 clones, the performance of all algorithms degraded as the error rates increased. Regardless of the error rate, BnpC was best at clustering, and obtained at least as accurate genotypes as the other methods.

We observed the same trends regardless of the simulated evolutionary history. Unsurprisingly, the simulation of different evolutionary histories showed that frequent and early branching events, resulting in clones with highly diverse mutation profiles, led to a higher clustering accuracy for all methods when compared to a linear evolution with late branching events (Supplementary Fig. S1).

To evaluate the scalability of BnpC, we investigated the runtime per MCMC step according to the data size (Supplementary Fig. S12). On the benchmarking datasets, BnpCs runtime increased linearly with data size, independently of the number of clones in the data.

3.2 BnpC performance on tumor scDNA-seq

We analyzed the sequencing data of five patients with childhood leukemia (Gawad et al., 2014), one high-grade serous ovarian cancer (HGSOC) patient (McPherson et al., 2016) and two colorectal cancer (CRC) patients (Wu et al., 2017).

3.2.1 Acute lymphoblastic leukemia

We reanalyzed scDNA-seq data of five Acute Lymphoblastic Leukemia (ALL) patients (Gawad et al., 2014). The data contain between 16 and 105 mutations and between 96 and 143 cells per patient. Gawad et al. used a combination of a multivariate Bernoulli model and the Jaccard distance to predict the clonal composition and to infer genotypes. Inferred genotypes and clones by Gawad et al. as well as the ones inferred by BnpC are displayed in Supplementary Figure S13. Genotypes and clones predicted by BnpC are largely in accordance with those previously determined. BnpC predicted some additional clones of small size.

BnpC predictions were of partly higher resolution. Specifically for patient 4, BnpC was able to detect an additional clone (orange) differing from the closest clone by five mutations (Fig. 3A). The identification of this particular clone results in a different and more accurate evolutionary pattern, as a common ancestor for the two tumor branches is obtained (Fig. 3D). Gawad et al. confirmed the existence of this additional clone in their subsequent analysis by incorporating copy number data. These findings show that our approach is sensitive to small clones and able to recover biological meaningful results.

3.2.2 High-grade serous ovarian cancer

The HGSOC data of patient 9 from the McPherson dataset (McPherson et al., 2016) were obtained by whole-genome sequencing of five samples taken from three tumor sites: left ovary, right ovary and omentum. The data consist of 420 cells, 43 SNVs and five breakpoints. We compared our predictions to the results obtained by Roth et al. using SCG. Their initial clustering analysis identified a normal population and eight tumor clones, of which they filtered out three clones due to a high fraction of missing values in the corresponding cells (mean $\ge$20% SNV events missing per cell).

BnpC was able to produce the same findings as SCG (Roth et al., 2016) without applying any additional filtering step (Fig. 3B, E). By excluding the three clusters, 28 cells which represent 7% of the patient data were discarded.

The clonal prevalence shows differences between the two samples coming from the left ovary (LOv) (Fig. 3E). Populations within one of the two samples (LOv2) contain the amplification in ERBB2, while the other (LOv1) does not. These populations harboring the amplification correspond to clones 0 (purple) and 1 (orange). Knowing that the primary site of the tumor was in the left ovary and that all other clones carry this amplification, our findings are in accordance with Roth et al.

3.2.3 Colorectal cancer

Patients CRC0827 and CRC0907 from Wu et al. (2017) were collected by single-cell Whole Exome Sequencing on CRC tissue samples (C1 and C2) and matched normal tissue (N). Additional samples from normal polyp (NP, CRC0907) and adenomatous polyp tissue (AP, CRC0827) were sequenced for the analysis. While BnpC recapitulated the results for patient CRC0827 (Fig. 3F), we identified additional clones in patient CRC0907 (Fig. 3C). These new clones suggest additional steps in the clonal evolution of the tumor. For patient CRC0907, Wu et al. identified two tumor clones harboring somatic mutations. They subsequently analyzed a subset of functionally related mutations to CRC development and separated them into unique clonal (detected by bulk sequencing) and unique subclonal (not detected).

Both, the original study and BnpC, identified a large clone with unique clonal mutations accumulated (green clone). BnpC, however, predicted greater heterogeneity in tissue C2, consisting of three clones (red, orange and purple clones). Based on the mutation patterns, it is difficult to identify an evolutionary order. In the original study, clusters were identified by hierarchical clustering and not experimentally validated, hence, we cannot validate the additional clusters indicated by BnpC. However, the two results are consistent and vary only in resolution.

4 Discussion

The identification of the heterogeneous tumor composition and the clonal genotypes is potentially advantageous for cancer treatment. ScDNA-seq provides the opportunity to resolve ITH in greater detail and to detect rare clones, despite experimental protocols still producing a high fraction of FN and missing events. We have introduced a novel non-parametric probabilistic method BnpC, especially designed for accurate and scalable clustering and genotyping of heterogeneous large-scale scDNA-seq data. Our method implements a modification of a non-conjugate split–merge move and uses a novel genotype estimator.

We compared our method with the state-of-the-art methods SCG and SiCloneFit on simulated and biological data. On small datasets, all methods performed equally well. On larger datasets, BnpC was best at recovering genotypes and clusters, except for datasets with low heterogeneity, where SCG inferred clusters more accurately. As sequencing experiments increase, the number of single cells that can be measured in parallel, one’s ability to detect small subpopulations will increase too. In our tests, BnpC was the only method capable of resolving highly heterogeneous data. Additionally, in our hands, BnpC was the only method that could be applied to datasets with more than 2500 cells in a reasonable time.

On biological data, our method not only recapitulated previous findings for three different datasets but also identified additional clones not detected in the original analysis but confirmed by additional data in patient 4 from Gawad et al. These findings highlight that more accurate analytic methods can identify signal and lead to biological conclusions, which can otherwise only be drawn from additional experimental data. Additionally, we demonstrated that BnpC is able to recapitulate previous results for patient 9 from McPherson et al. without the manual preprocessing step conducted in the original analysis. This is of special interest, for example, for an automated analysis pipeline, where one tries to minimize manual intervention without losing accuracy.

A limitation of the BnpC model is the absence of a phylogenetic structure on cells. The information given by the mutation order could be used to correct errors in the data or to infer missing values. It is possible that this is why SiCloneFit is more robust to noise in the data on small datasets. However, approaches that use a tree structure are computationally expensive and scale poorly with data size, as seen in the benchmarking. The trade-off between accuracy, runtime and possible optimizations needs to be investigated further. A feature currently missing from BnpC is the handling of doublets, two single cells pooled and measured together during sequencing. Currently, doublets may be reported as separate clones. Identifying and handling them explicitly as doublets could improve clustering and genotyping through the removal of spurious clones.

In summary, our model produces robust inferences of clonal composition and genotype for large single-cell datasets in a reasonable computational time. Besides their relevance for personalized treatment, the inferred clusters and genotypes can be used to reduce data size significantly, thereby facilitating downstream analyses. A potential application of BnpC on large-scale datasets could be, therefore, as a preprocessing step for the inference of phylogenetic trees. Additionally, not assuming a tree-structure makes our method applicable to other fields. For example, our method could be used for the analysis of methylation profiles or the analysis of microbiome data, where the input matrix may indicate the presence or absence of species in samples. As scDNA-seq data size continues to grow due to technological improvements and falling costs, so will the chance of sampling novel subpopulations, leading to more complex and heterogeneous datasets. Scalable and accurate inference, as provided by BnpC, will thus be increasingly relevant.