A Model-Driven Quantitative Analysis of Retrotransposon Distributions in the Human Genome

Abstract

Retrotransposons, DNA sequences capable of creating copies of themselves, compose about half of the human genome and played a central role in the evolution of mammals. Their current position in the host genome is the result of the retrotranscription process and of the following host genome evolution. We apply a model from statistical physics to show that the genomic distribution of the two most populated classes of retrotransposons in human deviates from random placement, and that this deviation increases with time. The time dependence suggests a major role of the host genome dynamics in shaping the current retrotransposon distributions. Focusing on a neutral scenario, we show that a simple model based on random placement followed by genome expansion and sequence duplications can reproduce the empirical retrotransposon distributions, even though more complex and possibly selective mechanisms can have contributed. Besides the inherent interest in understanding the origin of current retrotransposon distributions, this work sets a general analytical framework to analyze quantitatively the effects of genome evolutionary dynamics on the distribution of genomic elements.

Significance

Using methods from statistical physics we try to understand why transposable elements are in certain positions in the genome. First, we show that they are not placed at random and this is more evident for older transposons. We explored different simple models of genome evolution that could reproduce this result. For example, random placement followed by subsequent sequence duplications could explain the empirical positions. More generally, this work sets a mathematical framework to evaluate the effect of genome dynamics on the distribution of small genomic elements, such as transposons.

Introduction

Transposable elements (TEs or transposons) are sequences of DNA able to move within a host genome. Transposons are a crucial force driving genome evolution, they are found in all the organisms, with very few exceptions, and compose nearly half of the human genome (Lander 2001; Feschotte and Pritham 2007; Cordaux and Batzer 2009; Huang et al. 2012).

A large number of TEs in human belongs to the class of retrotransposable elements (REs) or retrotransposons, which proliferates through a “copy-and-paste” mechanism. Indeed, they are first transcribed into RNA intermediates, and then reverse transcribed into the host genome at a new position (Feschotte and Pritham 2007; Cordaux and Batzer 2009; Roy-Engel 2012). The two most abundant RE classes in human are Short Interspersed Nuclear Elements and Long Interspersed Nuclear Elements whose main representative members are Alu and L1 families, respectively (Deininger and Batzer 2002; Cordaux and Batzer 2009). These two families globally consist of $\approx 2$ millions elements and together account for nearly 30% of our genome (Lander 2001; Konkel and Batzer 2010). Both Alus and L1s can then be divided into subfamilies depending on the nucleotide sequence of the active TE driving the subfamily expansion (Cordaux and Batzer 2009; Roy-Engel 2012). Throughout the paper, the term family refers to Alu and L1, while the term subfamily refers to these subgroups.

The proliferation dynamics of these subfamilies has a relatively short timescale. In fact, after a rapid burst of amplifications and insertions, during which every new element becomes a potential source of retrotranspositions, the subfamily turns silent or inactive (Deininger and Batzer 2002; Wagstaff et al. 2013). Further rounds of transcription and insertion of the REs are typically prevented by the accumulation of sequence mutations, rearrangements, truncations or specific methylations able to inactivate the process (Deininger and Batzer 2002; Cordaux and Batzer 2009; Huang et al. 2012; Wagstaff et al. 2013). Thus, the REs that can be identified in the current genomes are generally a fossil track of the history of subsequent birth-extinction cycles of different mobile sequences, with few subfamilies still currently expanding in the human genome, such as the L1H subfamily (Ewing and Kazazian 2010; Huang et al. 2012).

Therefore, the genomic distributions of RE subfamilies reflect possible specific preferences or biases of the insertion mechanism during the subfamily active period, but carry also information about the most relevant evolutionary forces driving the rearrangement of the host genome after the subfamily expansion. For example, evolutionary moves such as genome expansion or duplications of DNA segments should alter the RE distributions in specific ways.

This work addresses the evolutionary mechanisms that have shaped the current distributions of genomic distances between REs of different subfamilies, focusing on members of the abundant Alu and L1 families as relevant examples. Despite the well-recognized importance of retrotransposons in the evolution of genomes, several aspects of their proliferation dynamics are still obscure. The RE position on the genome is arguably the simplest observable that contains information about this dynamics, and nonetheless has still to be fully characterized and explained.

We will show, using analytical arguments and data analysis, that these empirical distributions can be explained as a result of a process of insertion in random genomic positions, followed by sequence duplications and expansion of the host genome. A model based on these mechanisms can not only explain empirical RE distributions but it also naturally leads to predictions (e.g., on the role of RE density) that were confirmed by data analysis.

Besides the interest that the still partial understanding of the REs dynamics and its interactions with the host genome has in itself (Kazazian 2004; Konkel and Batzer 2010; Levin and Moran 2011; Jeck et al. 2013), the theoretical framework developed in this paper is general and can be easily extended to the study of spatial distributions of other functional genomic elements along the genome.

Results

Retrotransposons Are Not Randomly Distributed along the Genome

The first question we address in this section is how far the empirical RE distributions are from the simplest assumption of random genomic placement. An eventual deviation from random placement can be due to biases in the insertion process itself due to specific sequence preferences for insertion, as well as subsequent neutral processes of the genome such as rearrangements and duplications or selective processes such as specific deletions of detrimental insertions. The presence of biases in the insertion mechanism is still debated. While there is convincing evidence that the insertion process of REs actually occurs at random positions along the genome (Ovchinnikov et al. 2001; Cordaux and Batzer 2009; Ewing and Kazazian 2010), specific sequence preferences for the insertion sites have also been reported (Graham and Boissinot 2006). However, several works highlighted nonrandom properties of the current RE positioning that could in principle be ascribed to subsequent genomic processes. For example, there is a density enrichment of specific subfamilies in genomic regions with high or low GC content (Lander 2001; Pavlíček et al. 2001; Medstrand et al. 2002; Hackenberg et al. 2005), and a signal of formation of clusters of REs (Jurka et al. 2004). A recent comparison between the distribution of newly inserted L1s and pre-existing elements also suggests a predominant role for postintegrative processes (Sultana et al. 2019). On a global scale, the distributions of distances between REs of different families has been observed to deviate from random positioning by visually comparing the empirical distributions with randomly generated surrogate data sets of RE positions (Sellis et al. 2007).

A mathematical model for random placement would allow us to place the above observations in a well-defined quantitative setting and to actually measure possible deviations from a random placement assumption. This model can be easily formulated by realizing an analogy between the positioning of relatively small genomic elements and a well-studied process in statistical physics, the stick-breaking (SB) process. The SB process was originally formulated as a model of the stochastic fragmentation of a polymer chain (Montroll and Simha 1940; Ziff and McGrady 1985; Massip and Arndt 2013; Arndt 2019) and it is described in the Materials and Methods section. The SB provides an analytical expression for the expected distribution of fragment lengths that only depends on the length of the polymer L and the number of breaks B (see eq. 1 in the Materials and Methods section). The analogy with the RE insertion process is based on the observation that the REs can be safely considered point-like, since their length is extremely small with respect to the genome itself (Lander 2001; Kazazian 2004), and thus are equivalent to the point breaks in the SB formulation. In fact, the average RE sequence length is around 300 bp for the Alu class and 1 kbp for the L1 elements (see supplementary fig. S1, Supplementary Material online), which are negligible with respect to the genome length in human (around 3.2 Gbp). Therefore, the distribution of distances between REs should be precisely equivalent to the length distribution of fragments defined by the SB process, if the REs are randomly positioned.

The two parameters B and L that define the random positioning distribution for REs simply correspond to the number of retrotransposons of a specific subfamily and to the genome length considered. The Materials and Methods section reports in detail our estimation of these two parameters.

Figure 1 and supplementary figures S2 and S3, Supplementary Material online show the comparison between the SB parameter-free predictions and some illustrative examples of empirical inter-RE distance distributions. The statistical significance of the deviations between the SB prediction and the empirical distributions can be assessed with a Kolmogorov–Smirnov test. The results of this test are reported in supplementary table 1, Supplementary Material online for Alus, and confirm that the vast majority of RE subfamilies are not placed in random positions. The empirical deviations from a SB are due to an enrichment of both short and long distances, suggesting that the mechanisms that shaped current RE distance distributions must have both increased the “clustering” of retrotransposons and correspondingly fostered the presence of very distant elements. The same trend is observed if the inter-RE distributions are analyzed on single chromosomes rather than on the whole genome (supplementary fig. S2, Supplementary Material online). Even if the deviation from random placement makes the empirical distribution more “long-tailed” with respect to the null expectation, there is no clear evidence of a power-law behaviour of these distributions as was previously suggested (Sellis et al. 2007).

Fig. 1.

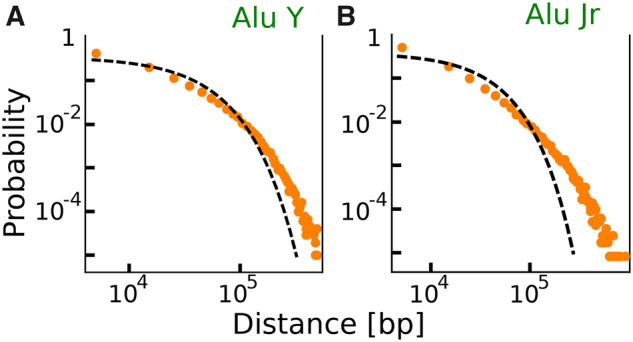
The genomic distribution of REs shows deviations from random placement. Figure shows the empirical inter-REs distance distribution (symbols) of two different Alu subfamilies in the human genome. Specifically, (A) and (B) refer to genomic distribution of Alu Jr and Alu Y subfamilies. The dashed black line represents the parameter-free analytical expectation given by the null model based on a random-placement hypothesis (eq. 1 in the Materials and Methods section). The parameter values are set by the number of RE elements B and the sequence length L, as discussed in the Materials and Methods section. The empirical values for the different subfamilies are reported in supplementary tables 1 and 2, Supplementary Material online. For the two depicted illustrative examples $B\simeq {10}^5$ and $L\simeq 2.8 {10}^9$. More examples supporting similar deviations from random placement can be found in supplementary figures S2 and S3, Supplementary Material online.

Several previous analysis reported that different families can have specific preferences for genomic regions with different GC content at the level of initial insertions or because of subsequent sequence-specific selection of RE elements (Lander 2001; Pavlíček et al. 2001; Medstrand et al. 2002; Jurka et al. 2004; Hackenberg et al. 2005). For example, both Alus and L1s have been reported to have an insertion preference for AT-rich regions (Lander 2001; Pavlíček et al. 2001), even though current distributions can show an opposite bias: high density of Alus in GC-rich regions, and vice versa a high density of L1s in GC-poor regions (Pavlíček et al. 2001). To test if the deviations from random positioning we observe are simply associated with the GC content, we divided the genome in GC rich and GC poor regions, and analyze the inter-RE distance distributions limited to these regions for different subfamilies. The details of this procedure are reported in the supplementary material. Even though the density of REs is indeed dependent on the GC content, the deviations of the inter-RE distance distributions from the random expectation do not differ in genomic regions with different GC content (supplementary fig. S4, Supplementary Material online). The deviation from random is still statistically significant if evaluated on GC rich or GC poor regions for essentially all Alu subfamilies we tested (supplementary table 3, Supplementary Material online). Moreover deviation from random evaluated on single chromosomes is comparable with the one estimated on the whole genome, and it is not trivially determined by the chromosome GC content (supplementary fig. S5, Supplementary Material online). Therefore, the general trend reported in figure 1 is robust, suggesting that it cannot be simply explained by a random-positioning process with different insertion probabilities depending on the GC content.

The Age of a Retrotransposon Subfamily Is Correlated with Its Deviation from Random Placement on the Genome

The deviations from random positioning described in the previous section can be dominated by biases in the insertion process or by subsequent genome evolutionary mechanisms. In the latter case, the deviations from random placement should be time dependent. In fact, the inter-RE distributions of young or currently active subfamilies would be mainly determined by the choice of retrotranscription sites, while the positioning of old subfamilies would be dominated by subsequent genomic processes. To test this, we introduce a measure that quantifies the deviations of empirical inter-RE distance distributions from the corresponding distributions predicted by the SB process. This measure is analogous to the Cramér-von Mises criterion (Cramér 1928), and it is based on the area between the two cumulative distributions (empirical and theoretical), normalized by the RE density (eq. 2, see Materials and Methods section). The normalization is necessary to safely compare deviations for RE subfamilies that have different global densities.

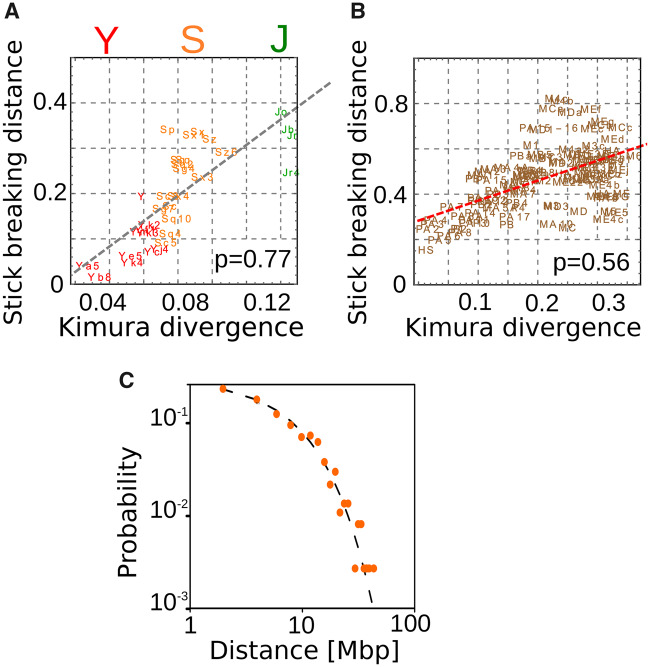
Figure 2A and B shows that this distance from random positioning is well correlated with the age of the RE subfamilies both for Alus (Pearson correlation P = 0.77) and for L1s (P  = 0.56). The age of a subfamily can be estimated by evaluating the number of mutations between the RE sequences and a reference consensus sequence (Kimura 1980). The consensus sequences for each subfamily come from Repbase (Bao et al. 2015) and the Kimura divergences are automatically inferred by RepeatMasker (Smit et al. 2015). While figure 2 reports the Kimura divergence as the estimate of the subfamily age, the trend is conserved if other estimates, such as the Jukes–Cantor divergence, are used.

Fig. 2.

The deviation from random placement increases with the RE subfamily age. The deviations (estimated with eq. 2) between the empirical inter-RE distance distributions and the corresponding expectation for random placement are shown as a function of the age of retrotransposon subfamilies for Alus (A) and L1 (B). The correlation is supported by the correlation coefficients reported in the figures while the dashed lines are linear fits. The age of different subfamilies is estimated by the Kimura divergence corrected for CpG hypermutability (more detail in the supplementary material). Panel C shows that very recently inserted retrotransposons are distributed along the genome in perfect agreement with the model based on random insertion. Specifically, we considered 367 L1 elements detected in a sample of 25 individual human genomes [data from (Ewing and Kazazian 2010)] and not included in the reference genome.

The fact that recent subfamilies are better described by the null model supports the hypothesis that retrotransposition sites are close to random, in agreement with previous observations (Ovchinnikov et al. 2001; Jurka et al. 2004; Beck et al. 2010; Costantini et al. 2012). The Kolmogorov–Smirnov test reported in supplementary table 1, Supplementary Material online quantitatively confirms this result since the few subfamilies for which the P value is not highly significant (i.e., AluYb8 and AluYk4) are relatively recent. As a further test, we analyzed the inter-RE distances for 367 L1H elements detected in a sample of 25 individual human genomes (data from (Ewing and Kazazian 2010)). These insertions are not fixed in the human population since they are not present in the reference genome. Therefore, we can confidently assume that this set of L1s is originated by very recent retrotransposition events, and thus genomic rearrangements did not have the time to reshape the RE positions. Figure 2C shows that indeed their relative distances are perfectly compatible with the random expectation.

We tested that the trend is consistent if GC-rich or GC-poor genomic regions are considered separately (supplementary fig. S6, Supplementary Material online). The regions with different GC content can also be reshaped by genomic rearrangements over long evolutionary time scales (Figuet et al. 2015). However, the current GC content still significantly correlate with the density of REs even for old subfamilies (supplementary fig. S5, Supplementary Material online). This could suggest that at this large scale of observation the GC content was not dramatically changed. However, we cannot exclude that the complex remixing pattern of the GC isochores (Romiguier et al. 2010) played a role in shaping the distributions of REs.

Genome Expansion and Sequence Mutations Cannot Explain Current Retrotransposon Position Distributions

The previous section strongly supports a scenario in which random insertion of REs has been followed by rearrangements of the host genome that reshaped their positions. Now, the question is which specific genomic events may explain the features of current RE distributions. A previous analysis suggested that genome expansion due to random insertions of new genomic elements coupled with progressive elimination of REs (e.g., by mutation-induced “degradation” of their sequences) could explain current spatial RE distributions (Sellis et al. 2007). However, this section will show that a model based on these two simple mechanisms, called insertion-elimination model (IE) by the authors (Sellis et al. 2007), cannot actually fully explain the empirical RE distributions.

First, most of the insertions driving genome expansion are actually due to TEs themselves. As we discussed previously, the length of these elements is less than $\sim 1$ kbp (supplementary fig. S1, Supplementary Material online), thus typically much shorter than the inter-RE distances. If we consider a genome expansion driven by the insertion of small elements, we can show analytically that the shape of the RE inter-distance distribution does not change. The only effect of genome expansion is to rescale all distances by the same factor as they simply expand with the same rate of the genome itself. The analytical proof of this intuitive behavior is reported in the Materials and Methods section. The master equation in equation (3) is a good approximation of the process for insertion lengths $\lambda \lesssim L/B$ and the solution of this equation is still the solution of a SB process but on a longer support (eq. 4).

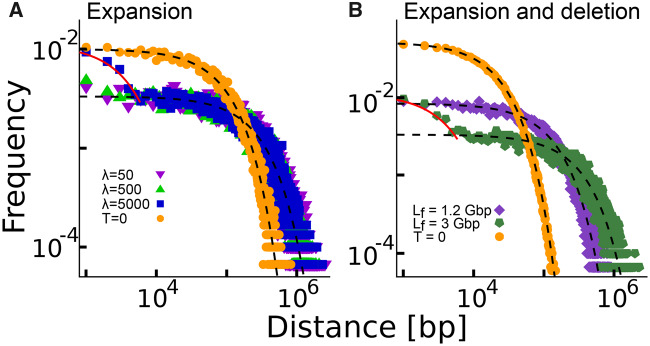
In presence of a large number of inserted sequences that are longer than existing inter-RE distances we can observe a deviation from a random distribution (fig. 3 and the Materials and Methods section). In this case, the “preferential-attachment” mechanism suggested by Sellis et al. (2007) can take place. Distances shorter than insertion length λ cannot be created by expansion and they are progressively less likely to be hit by a new insertion since the insertion probability is proportional to the segment length. The overall effect is that the final distribution is an overlap of two distributions corresponding to two different rates of expansion. Simulations suggest that this effect becomes relevant only after an extremely high number of insertion events (e.g., at least doubling the initial genome size) as reported in figure 3. This large number of insertions of very long sequences sounds very unlikely as an explanation of the empirical deviations from random placement of REs. As a further test we simulated, for a couple of illustrative RE subfamilies, a realistic genome expansion by considering the insertion of other REs from younger subfamilies and sequence duplications (not involving the REs under analysis) directly estimated from the human genome sequence (supplementary fig. S7, Supplementary Material online). Also in this case, the empirical deviations from random placement cannot be explained by the model.

Fig. 3.

Genome expansion and loss of REs cannot affect the shape of the inter-RE distribution. (A) The simulated distribution of distances between $B_0={10}^4$ points randomly placed on a segment of length $L_0={10}^9$ (dots, T = 0) and the effect of an expansion process due to insertions of segments of different lengths λ (different symbols as in legend). The final genome size is $L_f=3·{10}^9$ for all the distributions. (B) We added in the simulations the random elimination of “break” points. The initial distribution of distances (dots, T = 0) is given by $B_0=5·{10}^4$ points randomly placed on a segment of length $L_0={10}^9$. After genome expansion (with λ  =  5000) and RE random elimination at different rates (different symbols as in legend), we report the inter-RE distance distributions when the final number of REs has reached $B_f={10}^4$. Black dashed lines correspond to the SB distribution with the correct number of REs B and genome size L as in equation (4). Continuous lines represent the solution for $x<\lambda$ in equation (5). Only for large genome expansion driven by large insertions a small deviation from random placement can be observed.

The addition of elimination of REs in the process does not change the results. Intuitively, random elimination of breaks (e.g., due to mutations) simply decreases the parameter B₀ in the SB process without affecting the shape of the distribution. Therefore, the combination of genome expansion and RE elimination would still lead to a distribution equivalent to the one obtained by considering genome expansion alone. We tested this result with numerical simulations (fig. 3B).

A Simple Neutral Model Including Genomic Duplications Can Explain the Observed Distributions of Retrotransposons

A main evolutionary force of genome evolution that we have not considered so far is sequence duplication. Segmental duplication is a major source of genomic rearrangements and it is quite common across the whole phylogenetic tree (Bailey and Eichler 2006; Gao and Miller 2011) and can eventually contain REs. If the duplicated segment does not contain any of the REs under study, we are back to the model of the previous section. In fact, no additional “break” is added, and the net effect of the duplication is just a sequence insertion in a given position that expands a certain inter-RE distance. However, if the duplicated segment does contain some REs, the relative distances between the duplicated REs will add to the distance distribution. This can be modeled by assuming that duplications effectively represent a source of new REs and thus of new distances, as detailed more formally in the Materials and Methods section. This source term essentially captures the probability of adding an inter-RE distance of given length as a result of a duplication event, thus in general could depend in a nontrivial way on the sizes of duplicated segments. This phenomenological description greatly simplifies the model and it is amenable of analytic calculations. However, we also performed explicit simulations of the process of segmental duplication with different lengths of the duplicated segments to test that our simplified model correctly capture the emergent dynamics and to directly observe the functional form of the source terms (supplementary fig. S13, Supplementary Material online). The resulting effective functional forms can be intuitively understood with the following simple arguments.

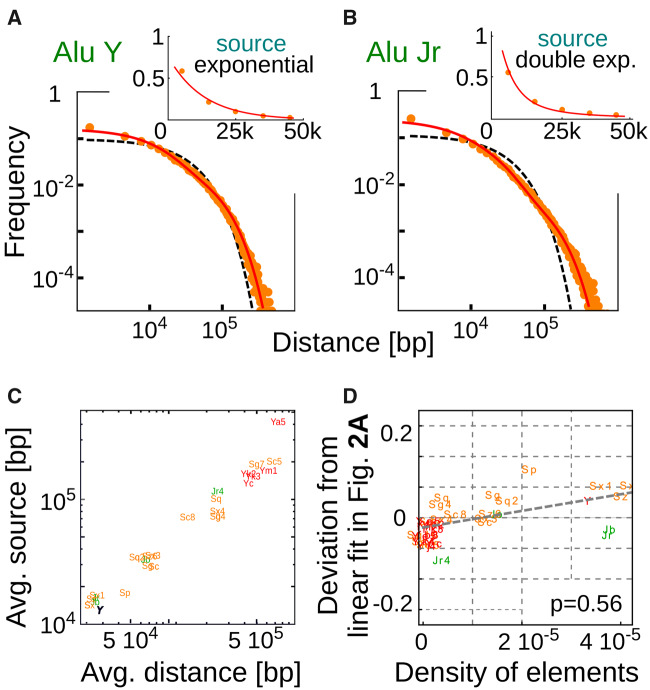
If the REs are initially inserted at random on the genome, the distribution of the REs on a sequence that is duplicated is expected to be still a random distribution described by the SB process (eq. 4) but on a support of size given by the length of the duplicated region. Therefore, a duplication event adds to the initial random distribution another random distribution but defined on a segment of much smaller length. This means that the probability of adding an inter-RE distance of length x by a duplication event is well approximated by an exponentially decreasing function of x (eq. 1). Therefore, as long as the process has not yet significantly changed the initial RE distribution, the source term should be well described by an exponential function. This intuitive argument is well supported by explicit simulations of the duplication process (supplementary fig. S13, Supplementary Material online). The analytical solution of our model with this specific source term (reported in the Materials and Methods section eq. 9) can fit very well the empirical distributions of relatively young subfamilies. An illustrative example is reported in figure 4A. However, if the dynamics had a sufficiently long time to alter the initial random distribution through duplications, the inter-RE distances that are added by a duplication event will not be well described by an exponential function anymore. After several duplication events, a duplicated segment will contain inter-RE distances following a distribution that already has an increased number of relatively short distances, thus generating a positive feedback that drives an effective strong clustering of REs. As a consequence, the source term should be better described by a decay faster than exponential. Again, this effect can be observed in long simulations of the duplication dynamics (supplementary fig. S13, Supplementary Material online) and can explain the observed position distributions for older subfamilies. In fact, the model with a faster-than-exponential functional form for the source term is able to fit much better these distributions as figure 4B shows for one illustrative example using a double exponential.

Fig. 4.

(A) model including local duplications and genome expansion reproduces the empirical distances between REs. (A) and (B) The inter-Alu distance distributions (dots) for two subfamilies of different age. The best fit with a superposition of a SB solution and a source term capturing the effect of duplications (eq. 9) is plotted as a continuous line. The expectation for random positioning (eq. 1) is also reported as dashed black line for reference. The insets show that the estimated source terms (dots, see Materials and Methods section) can be well approximated by an exponential function for the relatively young AluY subfamily (A) and by a double exponential function for the older AluJr subfamily (B). Panel C reports the correlation between the average length of the added distances by the duplication process (average of the source term in eq. 11) and the average distance between REs of the different subfamilies. (D) The deviation from random positioning is dependent on the subfamily density and on the subfamily age. In fact, the deviation from the linear dependence on age reported in figure 2A can be, at least partially, explained by the differences in subfamily densities.

In any case, duplications are expected to generate an excess of short distances (or more clustering) with respect to random placement. Therefore, the right tail of the inter-RE distance distribution should not be significantly affected by the duplication process. This observation allows us to devise a simple method for estimating the source term directly from data. The hypothesis is that the right part of the distribution should be well described by random placement of a number of REs B₀ smaller than the one currently observed B. This corresponds to the initial distribution of the REs of the subfamily we are studying. The subsequent duplications are expected to increase the number of REs (from B₀ to the observed value B) and only change significantly the left part of the distribution. Therefore, we can assume that current distributions are a superposition of a SB process which dominates for large distances and of a term defined by the source that defines the short-distance part of the distribution (supplementary fig. S8, Supplementary Material online). As explained more formally in the Materials and Methods section, under this assumptions we can directly estimate the source term and the initial number of REs B₀ with a simple fitting procedure. The results of this direct estimate of the source terms confirm the above considerations and are in line with the results of simulations of the process: an exponential source term is enough to explain the distance distributions of most subfamilies while for the older Alu subfamilies a steeper function, such as a double exponential, better explains the data (supplementary fig. S9, Supplementary Material online).

Moreover, the fraction of duplicated REs $(B-B_0)/B$ is correlated with the age of the RE subfamily as expected in a scenario of subsequent duplications after a random retrotranscription process (supplementary fig. S10, Supplementary Material online). The estimated percentage of REs that were duplicated can be as high as ∼85% for the older Alu J subfamilies, while for the youngest Alu Ya5 is approximately the 8% (supplementary table 1 and fig. S10, Supplementary Material online). It is important to notice that the fitting procedure assumes that the distribution tail is a perfectly conserved SB distribution. Any possible deviation from this behavior will limit the part of the distribution that is fitted by the SB distribution and will increase the estimate of the number of duplicated sequences. Therefore, the estimated fractions of duplicated REs should be taken as indicative upper bounds, proportional to the actual fraction of duplicated REs. The main goal of the procedure is to extract the empirical form of the source terms and the relative importance of duplications for subfamilies of different age.

A natural consequence of the considerations above is an expected correlation between the average inter-RE distance added by a duplication event (i.e., the average of the source term) and the density of a subfamily. In fact, a duplicated segment simply contains a smaller part of the RE distribution of a given subfamily that is well approximated by a SB at the beginning. The more elements are present, the shorter is their typical distance and thus the shorter will also be the typical RE distances duplicated in the evolutionary process. Figure 4C shows that this prediction is confirmed by empirical data. The average inter-RE distance is well correlated with the average distances added by the source term.

A more subtle prediction of our model concerns the role of RE density. We have shown that the deviation from random placement is correlated with the time elapsed from the birth of a subfamily. However, if this deviation is mainly driven by duplications, subfamilies of similar age but with different densities on the genome should display different degrees of deviations. A random duplication event is likely to include a number REs of a subfamily that depends on their density on the genome. Therefore, the variability that can be observed in figure 2A and B should be explained by a variability in subfamilies densities. We tested this prediction by measuring the deviation from the linear fit in figure 2 as a function of RE density for the different subfamilies. The results are reported in figure 4D and confirms the presence of a correlation. In other words, the deviation from random placement depends on the age of a subfamily but also on its density on the genome, further supporting the hypothesis that random duplications were a main evolutionary force in shaping current inter-RE distance distributions.

To provide further and model-free evidence that several REs have been indeed duplicated, we analyzed their flanking regions. Flanking regions of a significant fraction of REs should align better than expected by chance if the corresponding REs have actually been duplicated. Supplementary figure S8, Supplementary Material online shows that this is indeed the case. The scores for the alignment of flanking regions of 50 and 120 bp of REs belonging to different Alu subfamilies are compared with the scores obtained using random sequences of the same length or the flanking regions in the reverse orientation with respect the Alu orientation (to avoid potential biases due to local sequence composition). The two “null models” actually give very similar results. For young families, the fraction of putatively duplicated transposons is also well correlated with the subfamily age as expected from our description (fig. S8D  Supplementary Material online). However, the time dependence is not detectable for older families, and generally the fractions of duplicated elements estimated from the flanking regions are smaller than the ones estimated with our model-based fitting procedure. Different technical reasons could be at the basis of this discrepancy (detailed discussion in the supplementary material). Basically, RepeatMasker is a powerful tool capable to identify Alus even when they are highly divergent from consensus sequence, thus it is possible that even if the transposons can still be identified, their flanking regions cannot be well aligned anymore due to mutation accumulation. This effect will be more dramatic for old families. Moreover, as previously discussed, our model-based fitting procedure is prone to an overestimation of the fraction of duplicated transposons. Finally, we cannot exclude that selective forces also played a role in the clustering of TEs, and this could also explain the overestimation of the number of duplicated transposons when a model essentially based on a purely neutral scenario is used. We focused on a neutral scenario and showed that a simple model including duplications has the correct ingredients to explain several empirical observations, but selection could have played an additional role (see the Discussion section).

Discussion

REs, and in particular L1s and Alus, compose a large fraction of the human genome and their role in genome evolution has been increasingly recognized (Babcock et al. 2003; Bailey and Eichler 2006; Bourque 2009; Ade et al. 2013). TEs impact the genome in a variety of ways since they can promote structural rearrangements, contain regulatory elements, harbor transcription and splicing sites, and are involved in the production of noncoding RNAs (Kazazian 2004; Konkel and Batzer 2010; Oliver and Greene 2011; Testori et al. 2012; Jeck et al. 2013; Chuong et al. 2017). A large number of genetic diseases and cancers have been linked to mobile elements (Kazazian et al. 1988; Hassoun et al. 1994; Kobayashi et al. 1998; Roy-Engel 2012), although the causal relation is still unclear (Lin et al. 1988; Solyom et al. 2012; Chénais 2013; Tubio et al. 2014). Despite their importance, a clear understanding of their dynamics in the genome is still elusive.

This work focuses on the position distribution of retrotransposons at the genome scale, and on the role of the host genome dynamics in shaping their relative genomic distances. To this aim, we introduced a formal analogy between the retrotransposition process and the well-studied process in statistical physics of random insertion of breaks in a polymer chain (Barrow 1981; Ziff and McGrady 1985; Cheng and Redner 1990; Massip and Arndt 2013). Leveraging on this analogy, we could rephrase in a quantitative setting several longstanding questions. First, we provided evidence that current positions of most RE subfamilies are not randomly distributed along the genome. While previous studies made this observation (Sellis et al. 2007), we could assessed it quantitatively and, more importantly, define a natural measure of the extent of the deviation from random placement of empirical distributions. This measure indicated that the degree of nonrandomness of RE positions is strongly correlated with the age of the subfamily in analysis. More specifically, the position of REs of very recent or still active subfamilies is well described by random placement, while this description becomes progressively less accurate as the age of the subfamily increases. REs tend to become more clustered over time than expected from the random model.

The analysis of recent or active subfamilies further confirms that retrotranscription occurs approximately at random sites in the genome (at least at this large observation scale), giving a quantitative support to previous empirical observations (Ovchinnikov et al. 2001; Cordaux and Batzer 2009; Ewing and Kazazian 2010). Note that “local constraints” for fixation of retrotransposition events could be present and induce specific biases in the insertion sites. For example, sequence preferences linked to GC content were suggested for L1s (Graham and Boissinot 2006). In this regard, we analyzed in detail the role of GC content to show that the phenomenology of RE progressive clustering here described do not change qualitatively in regions with different GC content. Analogously, insertions in coding genes or in regulatory regions can be detrimental, and thus under strong negative selection. For example, the proximity with genes seems to bias the probability of observing different RE families (Medstrand et al. 2002). While at a local scale these constraints can be relevant, our analysis suggests that they do not play a major role in the RE positioning at the genomic or at the chromosomal level. Indeed, only a small fraction of our genome is actually coding, and a recent estimate based on mutational load considerations of the functional fraction of our genome leads to a conservative upper bound of 25% (Graur 2017). As previously suggested, most transposon insertions seem indeed to be neutral or only mildly deleterious and thus simply subjected to genetic drift (Arkhipova 2018).

Several recent works provide evidence of an interplay between the retrotransposition mechanism and the cell-cycle dynamics (Mita et al. 2018; Flasch et al. 2019; Sultana et al. 2019). As a consequence, at the genomic level the integration of L1 elements seems to be influenced by the replication timing of the target sequences. While our analysis suggests that generally recent insertions are compatible with a random model, chromosome-specific biases in the origin positioning could generate specific biases in L1 integration sites that could explain the large variability of position distributions across chromosomes we observe (supplementary fig. S4  Supplementary Material online). Our analytical framework would actually be well suited for a quantitative study of the position distribution of replication origins.

However, the inter-RE distance distribution for most subfamilies is far from random. As the time dependence of this nonrandomness suggests, the progressive evolution of the host genome must have reshaped the RE positioning in a specific way. While the genome evolves and rearrange, the RE already present will be passively moved and repositioned in the genome. Thus, we tried to pinpoint the possible evolutionary mechanisms responsible for the specific nonrandom features of current RE distributions by testing different simple evolutionary models. We first analyzed a model based on genome expansion and RE elimination that was previously proposed as a candidate to explain RE positions (Sellis et al. 2007). However, analytical calculations and extensive simulations showed that these mechanisms are not sufficient to quantitatively explain the empirical distributions. Therefore, we added genomic duplications in the model, and the resulting effect on the distribution of inter-RE distance was precisely the one empirically observed: a time-dependent increase in the REs at short distances that could well match the data relative to different subfamilies. Several tests of the model, such as the effect of RE density on the typical distance between duplicated REs or on the deviation from random position, further confirmed that genomic duplications and genome expansion are in principle sufficient ingredients to reproduce current retrotransposon positions in human.

A major role for genomic duplication in molding current genomes has been widely recognized since the pioneering work of Ohno (1970). Therefore, it should not be surprising that RE distributions could have been influenced by duplications. While this paper shows that a simple neutral model based on duplications can reproduce several features of RE distributions, we cannot exclude the presence of more complex, and possibly selective, evolutionary mechanisms. The rough estimates that our method provides for the fraction of duplicated REs range from few percent for recent families, to more than half for older ones. The fact that such a large fraction of old TEs is likely to come from duplications rather than direct retrotransposition is puzzling. This is probably due to an overestimation of our method of inference when the distributions are far from random, and indeed the estimates based on the alignment of flanking regions are smaller. It should be also noted that duplications due to nonallelic homologous recombination, such as large segmental duplications (Bailey et al. 2002; Bailey and Eichler 2006), can be promoted by the presence of repeated sequences such as transposons. For example, Alus are often found at the border of a particular class of segmental duplications called tandem duplication (Bailey and Eichler 2006; Colnaghi et al. 2011). Therefore, the presence of retrotransposons can enhance the duplication probability. This interplay would establish a positive feedback between duplication and retrotransposon density that may indeed drive the inter-RE distance distribution toward the “clustering” we observe, and could partially explain the large fraction of duplicated RE we estimate for old subfamilies.

In this paper, we focused on an essentially neutral scenario where transposons are mainly subjected to genetic drift (Arkhipova 2018). However, the realistic situation can be much more complex. Insertions can be neutral but also deleterious and, in few cases, beneficial and involved in genome adaptation (Barrn et al. 2014). In presence of selection forces that do not have location asymmetries, the picture would not drastically change since elimination of REs in random positions could not drive the clustering effect we observe. However, purifying selection can easily be region-specific. For example, transposons inserted in euchromatic regions could be transcribed and/or translated with a cost for the host organism or could be involved in deleterious ectopic recombination events. The presence of regions with different recombination rates have been shown theoretically (Dolgin and Charlesworth 2008) and empirically (Campos-Sánchez et al. 2016) to play a role in the fixation of transposons. Analogously, methylation, histon placement and regions with different DNA conformations have specific position patterns and influence the fitness of a transposon insertion (Campos-Sánchez et al. 2016). All these factors can be relevant in shaping the position distribution of REs and thus can concur in explaining the empirical observations we reported. Building a quantitative model that encompasses all these possible factors and disentangles the relative contribution of neutral and alternative selection-based explanations is a nontrivial task. One qualitative argument might slightly favor the neutral scenario based on duplications as the main driver of RE positions at a large observation scale. The argument is based on the time dependence that we observe. Many of the subfamilies analyzed have been in the genome for a rather large amount of time. Rough estimate indicates that we are looking at families that can be tens to hundreds million years old. Thus, one could hypothesized that selection could have removed all the (even slightly) deleterious insertions in this time scale, thus eliminating also the time-dependence of the deviation for random placement that can instead be clearly observed even for old families. A simple model based on the continuous process of segmental duplications instead naturally leads to a time dependence without any fine-tuning of the parameters.

Finally, the analytical framework developed here thanks to the analogy with the SB process can be a powerful tool. In fact, it gives analytic and parameter-free predictions for random positioning of small genomic elements that can be directly compared with the empirical ones. In the same framework, we introduced a measure of nonrandomness and developed simple but tractable evolutionary models that can be used to quantify and disentangle the different evolutionary contributions to the positioning of the genomic elements. Given its generality, this approach can be naturally extended to the study of other elements such as, for example, small regulatory sequences or single nucleotide polymorphisms.

Materials and Methods

Genomic Data

The human genome sequence (Homo sapiens assembly GRCh38/hg38) was downloaded from UCSC database (Kent et al. 2002). We considered only sequences referred to chromosomes 1-22, X, Y. The number and genomic positions of TEs in hg38 were downloaded from RepeatMasker official website (Smit et al. 2015) ($\text{RepeatMasker open}-\mathrm{4.0.5}$—Repeat Library 20140131). The analysis was performed on Alu and L1 subfamilies with more than 1,000 elements, to guarantee sufficient statistics. We included in the analysis a total of 32 Alu subfamilies and 107 L1 subfamilies. The number RE elements and their genomic density are reported for all Alu subfamilies in supplementary tables 1 and 2, Supplementary Material online for L1s. We verified that the typical size of Alu elements is around 300 bp, while of L1s is less than 1 kbp (see supplementary fig. S1, Supplementary Material online) (Lander 2001; Kazazian 2004). Several L1 elements detected by RepeatMasker are smaller than 1 kbp, and thus much smaller than the typical active version of L1 sequences which is around 6 kbp. This result is however in agreement with an empirical evidence pointing out that L1 elements in the human genome are not typically full length but rather truncated (Penzkofer et al. 2017). The full length version of L1 is however represented in the analyzed sequences as shown in supplementary figure S1, Supplementary Material online.

The distance between successive REs of each subfamily was calculated as the difference between the start genomic coordinate of an element and the stop coordinate of the previous one. We verified that an alternative definition of the inter-REs distance using half-length coordinate of REs does not alter our conclusions, as it was expected given that our analysis is based on large scale observations.

The distances between the start (end) of each chromosome and the first (last) RE of the considered subfamily have been excluded. Distances falling in centromeric and pericentromeric regions were also neglected since these regions are usually highly repetitive, rich in copy number variations and difficult to sequence properly. As a consequence, they contain few extremely long inter-RE distances that show in the distributions as outliers of the order of few Mbp.

At the end of this filtering process less than 50 inter-RE distances have been discarded for each subfamily and the effective human genome length has been reduced to about 2.8 Gbp, depending on the subfamily. Moreover, also REs inserted in the middle of pre-existing elements of the same subfamily were discarded from the analysis to avoid an excess of zeros in the distance distribution. This procedure is necessary to ensure the validity of our assumption of point-like REs and affects only about 3% of L1 elements while is completely negligible (i.e., $<0.01\%$) for the Alu family.

Stick-Breaking Process as a Null Model for Random Positioning of Small Genomic Elements

We consider a set of B genomic elements whose length is small enough relatively to the genome or chromosome size L of interest. In this case, we can introduce a formal analogy with the SB process or the fragmentation process well studied in statistical physics (Montroll and Simha 1940; Ziff and McGrady 1985; Cheng and Redner 1990; Gherardi et al. 2016). This process considers point-like fractures randomly positioned on a stick or polymer of fixed length. The length distribution of the fragments after B breaks are positioned can be analyzed analytically. To make the analogy exact, the genomic elements of interest have to be well approximated by point-like elements, as it is the case for REs given their short length with respect to the genome or to chromosomes (Lander 2001; Kazazian 2004).

The analytical solution of the SB process can be used to test if the genomic elements of interest are indeed randomly placed along a genomic sequence. According to Ziff and McGrady (1985) and Arndt (2019), the expected number of inter-break distances equal to x after the random placement of B breaks on a support of length L is

$$\left\{\begin{array}{l}\begin{array}{cc}\text{SB}(x;B,L)=\left[2\frac{B}{L}+{\left(\frac{B}{L}\right)}^2(L-x)\right]& {\mathrm{e}}^{-\frac{B}{L}x} \text{for}0<\mathrm{x}<\mathrm{L}\end{array}\\ \begin{array}{cc}\text{SB}(x;B,L)={\mathrm{e}}^{-B}& \text{for}x=L\end{array}\end{array}\right.$$ (1)

The probability distribution $p_{\text{SB}}(x;B,L)$ is simply obtained by normalizing $\text{SB}(x;B,L)$ with the total number of distances B + 1. An alternative parametrization of the process has been recently proposed (Arndt 2019), but for large values of B (as it is the case here) the two descriptions are essentially equivalent. This is clearly shown in figure S14, Supplementary Material online. Therefore, we can safely use the description in equation 1 that will make the subsequent calculations easier without loss of generality.

The position distribution of a subfamily with B elements can be compared with the SB prediction using B as the number of breaks and L as the length of the sequence on which the distribution is evaluated (e.g., the whole genome or a single chromosome). To make the RE point-like as in the model, we actually used as L the sequence length minus the sum of the lengths of the REs in analysis. However, the results are not particularly sensitive to this choice since the length of REs is relatively small with respect to the genome or chromosome lengths. The parameter values estimated for the different subfamilies are reported in supplementary tables 1–3, Supplementary Material online.

A Measure of Deviation from Random Placement

We developed a measure of the deviation of an empirical distribution of inter-element distances from the parameter-free distribution expected for random placement and described by equation 1. This measure is proportional to the area between the empirical and null model distributions, in analogy with the Cramér-von Mises criterion (Cramér 1928). More specifically, it is the integral between the two cumulative distributions. However, since the mean and standard deviation of a SB depend on the density of elements ($\sigma \sim B/L$ for large B), we normalized this integral by the density of each subfamily to make the deviations comparable for sets with a different number of elements. As discussed in more detail in the supplementary material, distributions relative to random placement for different values of B and L collapse to a single functional form thanks to the normalization. Thus, the distance from the expected SB in equation 1 for a given subfamily i can be defined as

$$D_i=\underset{0}{\overset{L_i}{\int }}\frac{B_i}{L_i}|F_i(x)-F_0(x;B_i,L_i)|dx,$$ (2)

where F_i and F₀ are the empirical and theoretical cumulative distributions. The normalization factor $B_i/L_i$ is the density of subfamily i and allows the comparison of D_i for subfamilies of different abundances.

The measure here introduced is also analogous to the distance between cumulative distributions on which the Kolmogorov–Smirnov test is based. The high correlation between the two measures is reported in figure S11, Supplementary Material online.

The Insertion-Elimination Model

This section formalizes a model describing the dynamics of distances between a set of point-like elements (REs in our case) on a genome under the hypothesis that the two main evolutionary forces are genome expansion due to insertion of other genomic elements, and random deletions of the point-like elements under consideration, which effectively leads to the “fusion” of two existing distances. The simplest assumption is that the probability of insertion of new sequences is uniform over the whole genome and that all elements have the same probability of being deleted. These are precisely the assumptions considered in Sellis et al. (2007). In this case, the probability that a new insertion event expands the distance x between two existing REs is proportional to x. If we introduce a typical length scale λ of the inserted sequences and the rate γ at which on average an insertion happens, we can describe the process as

$$\frac{\partial p(x,t)}{\partial t}=-\gamma \frac{x}{L(t)}p(x,t)+\gamma \frac{x-\lambda }{L(t)}p(x-\lambda ,t).$$ (3)

The equation (3) describes the time evolution of the distribution p(x, t) of distances of length x while the support L(t) is expanding. It assumes that the probability of inserting a sequence of length λ into an existing inter-element distance of length x is simply proportional to its length (i.e., to $x/L(t)$), and that there is a constant rate γ of new insertions. As described in the supplementary material, equation 3 can be solved in the continuous limit that is valid as long as the distances are long enough as it is always the case for REs. The solution is simply $p(x,t)=p(x(0),0){\mathrm{e}}^{\gamma \lambda {\int }_0^t\left(dt\prime /L(t\prime )\right)}$, where $p(x(0),0)$ is the distance distribution before the dynamics starts.

The initial condition is given by the SB process with B₀ breaks described in the previous section since we are assuming an initial random placement. In other words, $p(x(0),0)=p_{\text{SB}}(x(0);B_0,L(0))$ from equation 1. As shown in more detail in the supplementary material, the factor multiplying the SB initial condition in the solution is just a rescaling of the support. In fact, the evolved inter-RE distances at time t is simply described by

$$p(x,t)=p_{\text{SB}}(x;B_0,L(t)),$$ (4)

where $L(t)=L(0)+\gamma \lambda t$. In conclusion, the shape and the functional form of the initial SB distribution are not modified by the expansion dynamics, and the distribution can be still described by a SB on an expanded genome L(t). The model can be generalized by assuming that there is a distribution $\rho (\lambda )$ of the lengths of insertions, but the result does not change qualitatively. Analogously, deletions of genomic segments can be considered, but also in this case the distribution would not change its shape as long as the deletions are randomly placed.

So far we implicitly assumed that the inserted sequences have a length λ smaller than existing inter-RE distances. If this is not always the case (i.e., if there are $x_0<\lambda$), the last term in equation 3 is not relevant for these short distances, and the solution has an additional term of the form

$$p(x,t)=p_{\text{SB}}(x;B_0,L(0\left)\right){\left(\frac{L\left(0\right)}{L\left(t\right)}\right)}^{x/\lambda }.$$ (5)

Therefore, the complete solution has two terms: for short distances ($x<\lambda$) there is an exponential behavior that deviates from the SB distribution, while for long distances the process is described by an expanded SB. This behavior is confirmed by simulations as explained in detail in the Results section. The introduction of RE elimination, for example due to sequence mutations, would not alter the picture above. In fact, if we take the solution of the SB process with B breaks in equation 1 and we randomly eliminate a certain number n of breaks, the resulting distribution would still be a solution of a SB process with B – n breaks. This intuitive result is confirmed by numerical simulations in figure 3.

A Model Including Genomic Duplications

The model presented in the previous section can be effectively extended to take into account the result of genomic duplications. The extension is based on the observation that a duplication event that also duplicates some of REs of interest adds to the distance distribution precisely the distances between the duplicated elements. Specifically, the distribution p(x, t) of inter-RE distances will have some new distances of a certain length x that depends on the relative position of the REs that have been duplicated. This effect can be phenomenologically captured in the model by assuming that there is an external source of new distances described by a term q(x). This term represents the probability of adding a distance of size x as a result of a duplication event and its form should depend on the existing distance distribution at the moment the duplication occurs. We can also introduce a parameter μ for the rate of duplications.

Therefore, a model that includes both genome expansion and duplication of genome portions can be formalized by the equation

$$\begin{array}{cc}\frac{\partial p(x,t)}{\partial t}& =-\gamma \frac{x}{L\left(t\right)}p(x,t)+\gamma \frac{x-\lambda }{L\left(t\right)}p(x-\lambda ,t)+\mu q\left(x\right)\approx \\ & \approx -\frac{\gamma \lambda }{L\left(t\right)}\frac{\partial }{\partial x}\left(xp(x,t))+\mu q(x\right),\end{array}$$ (6)

which simply extends equation 3 by adding the source term $\mu q(x)$. In the continuous limit, the method of characteristic leads to the following system of equations

$$\left\{\begin{array}{l}\begin{array}{c}\frac{dx}{dt}=\gamma \frac{\lambda }{L\left(t\right)}x\\ \frac{1}{x}\frac{d\left(xp(x,t)\right)}{dt}=\mu q\left(x\right)\end{array}\\ \end{array}\right.$$ (7)

Rewriting equation (7) and assuming a linear increase in the genome size $L(t)=L(0)+\phi t$ (where $\phi$ is the combined growth of the genome given by expansion and insertions) we can derive

$$\begin{array}{c}x\left(t\right)=x\left(0\right){\left(\frac{L\left(t\right)}{L\left(0\right)}\right)}^{\gamma \lambda /\phi }\to f\left(t\right)=\frac{x\left(t\right)}{x\left(0\right)}={\left(\frac{L\left(t\right)}{L\left(0\right)}\right)}^{\gamma \lambda /\phi }\end{array},$$ (8)

 

$$p(x,t)=\frac{1}{f\left(t\right)}p\left(\frac{x\left(t\right)}{f\left(t\right)},0\right)+\frac{\mu }{f\left(t\right)}{\int }_0^{t}q\left(x\right(t`\left)\right)f(t`)dt`.$$ (9)

The solution (9) is composed of two terms: the first one describes the expansion of the original SB while the second represent the source expansion over time. f(t) is a monotonic and increasing function of time, as defined in (8), that weights the initial condition relative to the source at a specified time t. It is obtained from the first equation in (7). Note that $\gamma \lambda /\phi <1$, since $\phi$ includes both expansion (γ) and source (μ). By substituting $p_{\text{SB}}(x;B_0,L(0))$ as initial condition for the first term on the right in equation 9, we still find a SB

$$\begin{array}{c}p\left(x\right(0),0)=\frac{1}{f\left(t\right)}{p}_{\text{SB}}\left(x\right(0)=\frac{x\left(t\right)}{f\left(t\right)},B_0,L(0\left)\right)=\\ =\left(2\frac{B_0}{L_{\mathrm{E}}\left(t\right)}+{\left(\frac{B_0}{L_{\mathrm{E}}\left(t\right)}\right)}^2\left(L_{\mathrm{E}}\left(t\right)-x\left(t\right)\right)\right)\frac{{\mathrm{e}}^{-B_{0}x\left(t\right)/L_{\mathrm{E}}\left(t\right)}}{B_0+1}.\end{array}$$ (10)

The expanded genome is now $L_{\mathrm{E}}(t)=L(0)f(t)$, since the whole genome L(t) contains also the contribution of the (expanded) source. In the limit $\phi \to \gamma \lambda$ we recover the result of the former section. To fully solve the expansion-insertion model we have to choose an explicit form for the source function q(x). While its precise functional form is in principle unknown, several considerations (see Results section), point to a fast decreasing function of x (such as an exponential decay).

Direct Estimate of the Effect of Duplications on inter-RE Distances

If the source term q(x) is a fastly decreasing function of x, such as an exponential decay, the probability of adding long distances to the inter-break distribution is extremely small. Therefore, the presence of a source term in our dynamical model is not expected to alter significantly the shape of the right tail of the initial inter-break distribution. In our case, the initial distribution is supposed to be the SB solution in equation (1). Moreover, we have previously shown that the expansion of the support by random sequence insertion cannot change the functional form of the initial random distribution, equations (9) and (10). Relying on these considerations, the right-tail of the inter-RE distribution should be well approximated by random placement of a smaller number of elements with the correct normalization and length of the support, respectively B₀ and $L_{\mathrm{E}}(t)$ in equation (10). More formally, normalizing equation (9) by the total number of breaks and taking into account the relation in equation (10), the current distribution can decompose as follow

$$p(x,B,L)=\theta p_{\text{SB}}(x;B_0,L_E)+(1-\theta )\stackrel{\sim }{q(x)},$$ (11)

where θ is the fraction of RE distances that are still distributed according to the initial SB solution. The effective source $\stackrel{\sim }{q(x)}$ is proportional to the source q(x) weighted over the time with f(t), that is, the initial source expanded and averaged over f(t).

Within the assumption that the source q(x) of new segments only affects the short scale distances, we can assume that the long-distance tail of the distribution of B breaks on a genome L can be well explained by a SB solution with a smaller initial number of breaks B₀, while the short-distance region of the distribution is a superposition of this SB process with the contribution of duplications captured by the fastly decaying source term $\stackrel{\sim }{q}(x)$. This also implies the existence of a minimum distance x_min, above which the effect of the external source is negligible (supplementary fig. S9, Supplementary Material online). In other words, for $x>x_{\text{min}}$ the observed distances should be well fitted by a SB solution with an initial number of breaks B₀ (smaller than the empirical subfamily size), while for $x<x_{\text{min}}$ we have a superposition of the SB solution and of the source term $\stackrel{\sim }{q(x)}$. Following the same idea from Clauset et al. (2009), we identify x_min, B and L for each subfamily using a maximum likelihood approach to find the best possible fit of equation (11). With this approach we can directly estimate both the initial number of breaks B₀, and the fraction of duplicated REs $1-\theta$. Finally, the source term $\stackrel{\sim }{q(x)}$ can be deduced as the difference between the empirical distribution and the best estimate of $p_{\text{SB}}(x;B_0,L_{\mathrm{E}})$.

The procedure has been applied to all Alu subfamilies. The estimated thresholds x_min are of the order of 10⁵ bp. The resulting source terms $\stackrel{\sim }{q(x)}$ can be generally well fitted by an exponentially decreasing function (supplementary fig. S10, Supplementary Material online) and their averages correlate with the density B/L of the subfamily as discussed in the Results section and shown in detail in the supplementary material. For the older Alu subfamilies, $\stackrel{\sim }{q(x)}$ can be better approximated with a steeper function (fig. 4B, where a double exponential has been used).

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.