Density Functional Theory for Molecule–Metal Surface Reactions: When Does the Generalized Gradient Approximation Get It Right, and What to Do If It Does Not

Abstract

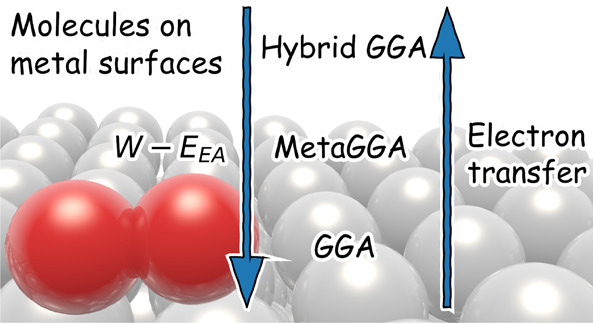
While density functional theory (DFT) is perhaps the most used electronic structure theory in chemistry, many of its practical aspects remain poorly understood. For instance, DFT at the generalized gradient approximation (GGA) tends to fail miserably at describing gas-phase reaction barriers, while it performs surprisingly well for many molecule–metal surface reactions. GGA-DFT also fails for many systems in the latter category, and up to now it has not been clear when one may expect it to work. We show that GGA-DFT tends to work if the difference between the work function of the metal and the molecule’s electron affinity is greater than ∼7 eV and to fail if this difference is smaller, with sticking of O₂ on Al(111) being a spectacular example. Using dynamics calculations we show that, for this system, the DFT problem may be solved as done for gas-phase reactions, i.e., by resorting to hybrid functionals, but using screening at long-range to obtain a correct description of the metal. Our results suggest the GGA error in the O₂ + Al(111) barrier height to be functional driven. Our results also suggest the possibility to compute potential energy surfaces for the difficult-to-treat systems with computationally cheap nonself-consistent calculations in which a hybrid functional is applied to a GGA density.

Kohn–Sham DFT has become very popular and is now being used in more than 30 000 papers per year. Nevertheless, much of the theory remains not yet well understood, even concerning much of its practical aspects. One surprising practical aspect is that density functionals (DFs) at the generalized gradient approximation (GGA) are quite accurate for barriers for dissociative chemisorption (DC) reactions on metal surfaces. In contrast, semilocal functionals tend to systematically underestimate reaction barrier heights of gas-phase reactions,^1,2 and it has been assumed that this overestimation should carry over to surface reactions in general.³ Nonetheless, a semiempirical version of DFT, the specific reaction parameter (SRP) approach to DFT, has achieved chemically accurate descriptions of sticking in many molecule–metal surface systems by using functionals in which the exchange part is a weighted average of GGA exchange functionals.⁴⁻¹² Here, often (the exchange part of) the PBE¹³ (or PW91¹⁴) and the RPBE¹⁵ DFs are used, with PBE and PW91 yielding too low, and RPBE too high barriers.^4,6 Dynamics studies using nonempirical GGA DFs have semiquantitatively described many experiments on DC on metals.¹⁶⁻²⁰ Perhaps even more surprisingly, a recent comparison of DFT results for a database of molecule–metal surface reactions based on experiments and SRP-DFT (SBH10) suggested a better performance for a GGA-exchange-based DF (i.e., BEEF-vdW²¹) than for the meta-GGA and screened hybrid representative examples that were tested.²²

In spite of the above, also many molecule–metal surface systems exist for which SRP-DFs based on GGA exchange DFs do not work because even the most repulsive GGA exchange DFs still obeying the uniform electron gas limit (such as RPBE, a nonempirical functional which describes adsorption on metals with quite high accuracy, but already performs rather poorly at describing solid state properties^21,23) are too reactive compared to experiment, even when simulating the effect of energy dissipation to electron–hole pairs and surface phonons.²⁴⁻²⁹ As a result, the barrier height cannot be “tweaked” to a good value by mixing exchange DFs yielding too high barriers (such as RPBE) and too low barriers (as often the case with PBE or PW91). That is a pity, as a DC transition state (TS) on a metal surface is often the rate-controlling state in industrially important heterogeneously catalyzed processes³⁰⁻³² like ammonia production³³ and steam reforming.³⁴ A further problem is that it is not clear which property of the system determines whether GGA-DFT may yield a reliable barrier height. Reasons to explain the GGA-DFT failure for individual systems have, however, been cited, with an often cited reason being that electron transfer occurs from the metal surface to the molecule.^35,36

In this connection, often reference is made to the following explanation for why GGA-DFT fails at describing gas-phase reactions: the GGA’s tendency to underestimate gas-phase barrier heights is caused by the electrons delocalizing over additional atoms at the TS, artificially lowering the GGA energy of the TS relative to that of the reactants.^2,37,38 The delocalization error finds its origin in what has been called “the lack of derivative discontinuities of semi-local functionals” or alternatively the violation of the Perdew–Parr–Levy–Balduz condition³⁹ by these functionals. According to Yang and co-workers⁴⁰ the delocalization error is similar but not equal to the self-interaction error (SIE),⁴¹ which is also often invoked to explain the underestimation of gas-phase reaction barrier heights. However, the above does not yet explain why GGA-DFT does work for many molecule–metal surface reactions. Also, a property of the system on the basis of which one could straightforwardly predict whether GGA-DFT should, at least in principle, work is still missing. Fortunately, the “charge transfer” explanation does suggest such a criterion, as we will now show.

Here, we will show that a single property of molecule–metal surface systems exists on the basis of which one can decide whether it should be possible to find a GGA functional with which one can describe the barrier to dissociative chemisorption with chemical accuracy. This allows one to define a single corresponding criterion stating whether GGA functionals should be able to deliver chemical accuracy for the corresponding “easy-to-handle” reactions. We also show that the solution applicable to the problem that gas-phase reaction barriers are not well-described with GGA functionals (i.e., resorting to hybrid functionals) also works for a prominent example of “difficult” surface reactions, i.e., that of O₂ + Al(111). Our findings suggest the possibility of extending SRP-DFT to the full range of dissociative chemisorption reactions on metals. Such an extension should enable the development of databases for such reactions⁴² without bias to specific rungs of functionals, similar to databases that already exist for gas-phase reactions.^1,2

Obviously, one would expect the tendency of a system to display charge transfer to correlate with the difference (W – E_ea) between the work function W of the metal and the electron affinity E_ea of the molecule. Systematic evidence is collected in Figure 1, where we show how the ability to accurately describe the measured reactivity of molecule–metal surface systems with DFs containing GGA exchange correlates with W – E_ea. Figure 1 shows that it has been possible to achieve chemical accuracy in descriptions of sticking experiments with GGA-exchange-based SRP-DFs^4,5,7−9 (in blue) and candidate SRP-DFs^6,10−12 (in green) if W – E_ea exceeds 7 eV. (Candidate SRP-DFs describe a sticking experiment on a specific system with chemical accuracy, but their validity has not (yet) been confirmed through comparison with another experiment on the same system.) However, for systems with W – E_ea < 7 eV DFs with repulsive RPBE exchange either overestimate sticking notoriously^{24,25,28,43−45} (red), or they show a suspect performance^26,27,29,46 (orange). In Figure 1 we also observe a trend that when the difference between W and E_ea decreases, so that one might also expect the amount of electron transfer to increase, the SRP or GGA DF needs to be made increasingly repulsive to describe the system’s reactivity with chemical accuracy. For example, CH₄ + Ni(111)⁴⁷ and Pt(111)⁴⁸ are quite well-described with the attractive PBE functional,¹³ and this is also true for H₂ + Pt(111)⁴⁹ (here the PW91¹⁴ functional was used, which may be considered the predecessor to PBE, which was designed to replace it¹³) and Ru(0001)⁶. On the other hand, the SRP DF for H₂ + Cu(111)⁴ and Cu(100)⁵ needs to contain about 50% RPBE exchange, and a good description of N₂ + Ru(0001) was recently obtained with the RPBE DF.¹⁰

Figure 1.

Correlation between the difference of the work function of the metal surface and the electron affinity of the molecule (eV) with the ability of GGA exchange-based DFs to accurately describe barrier heights to DC in the systems described. Red, orange, green, and blue indicate whether efforts to develop an SRP DF based on GGA exchange for a molecule–metal surface reaction have failed, proven difficult, yielded a candidate SRP DF, or yielded an SRP DF, respectively. The values of the work functions (Table S1) and electron affinities (Table S2) are obtained as described in Section S1.5 of the Supporting Information.

A caveat with the above comparison between dynamics based on DFT and experiment is that the difference (W – E_ea) has also been correlated with the extent to which (reactive) scattering in a system may be affected by energy dissipation through electron–hole pair excitation.⁵⁰ Here, the reasoning used could be that (electronically adiabatic) dynamics simulations using repulsive RPBE exchange might overestimate the DC probability because the dissipation of the molecule’s incident kinetic energy to electron–hole pairs is not modeled. However, in this type of analysis evidence for strongly nonadiabatic molecule–metal surface scattering comes mostly from experiments on vibrationally inelastic scattering^51,52 and scattering of H atoms from metal surfaces,⁵³ whereas dynamics calculations only suggested small effects of electron–hole pair excitation in some of the hard to model systems in Figure 1, i.e., D₂O + Ni(111)⁵⁴ and HCl + Au(111).²⁸ More definite evidence that electronically nonadiabatic effects are most likely not the explanation for the trend observed in Figure 1 comes from a direct comparison between barrier heights obtained with first-principles and RPBE calculations. Barrier heights obtained with diffusion Monte Carlo (DMC)⁵⁵ and DFT using the RPBE and PBE DFs are compared for three H₂ + metal surface systems in Table 1. For H₂ + Cu(111)⁵⁶ and Al(110)¹¹² GGA DFT is able to reproduce the DMC barrier height, and W – E_ea > 7 eV. In contrast, the RPBE DF underestimates the DMC barrier height for H₂ + Mg(0001)⁵⁷ (W – E_ea < 7 eV). Note that for H₂ + Cu(111) DMC was shown⁵⁶ to be able to reproduce the best estimate of the barrier height to within 6.7 ± 4.2 kJ/mol. Below we will attempt an explanation of the success of exchange-correlation functionals containing semilocal exchange at describing reaction barrier heights for molecule–metal surface systems with W – E_ea > 7 eV and of their failure for systems with W – E_ea < 7 eV. However, first we will investigate whether and how the problem can be fixed for one of the “difficult” systems described above.

Table 1. Barrier Heights (kJ/mol) Computed with DMC Compared with Values Calculated with the RPBE and PBE (or PW91^‡) DFs of DFT for Three Different H₂ + Metal Surface Systems^a.

molecule–metal surface	EbQMC	EbRPBE	EbPBE	W – Eea
H2 + Cu(111)	54.4 ± 4.256	79.14	46.9‡4	8.06
H2 + Al(110)	105.0 ± 0.8	100.4	79.9	7.39
H2 + Mg(0001)	113.8 ± 2.957	103.357	84.957	6.92b, 6.82c

^aAlso shown are the differences W – E_ea (eV) between the work function of the metal and the electron affinity of H₂ as computed at the semi-empirical composite G4 level of theory.⁵⁸

^bCalculated for Mg(0001) with PBE-DFT.⁵⁹

^cMeasured for a thin layer of Mg.⁶⁰

The standard way of dealing with errors in barriers for gas-phase reactions is to ascend the DFT ladder to higher functionals, i.e., to use meta-GGA or hybrid DFs. We will now show that this route can also be successful when dealing with molecule–metal surface reactions. One clear example where DFT tends to overestimate the reactivity is for useful benchmark systems⁴² of activated dissociation of O₂ on metal surfaces^24,26 (see also the Supporting Information), with O₂ + Al(111) being an infamous example.²⁴ Molecular dynamics (MD) simulations employing GGA DFs predict a nonactivated reaction,^24,43 whereas experiments show that the reaction is activated^61,63 (see Figure 2a). To date, of the MD simulations that use a GGA DF (or a semiempirical potential energy surface (PES) based on a GGA DF),^24,43,64 only calculations that treat the O₂–metal system nonadiabatically have been shown to yield sticking probabilities in semiquantitative agreement with experiment. On the other hand, electronically adiabatic simulations that use embedded correlated wave function (ECW) theory for the PES have also yielded quite good agreement with experiment⁶² (see Figure 2a). The latter results led Carter and co-workers to suggest that modeling electronically nonadiabatic effects should not be necessary for O₂ + Al(111).³⁶ Specifically, electronic structure calculations based not only on ECW theory but also on hybrid DFT yield adiabatic barriers,^36,65−70 suggesting that an electronically adiabatic approach could well be valid, but that the way the electronic structure is treated is crucial. However, drawbacks of the ECW method are that it is expensive to use and that it is hard to converge the molecule–surface interaction energy with respect to the size of the embedded cluster.³⁶ Consequently, Yin et al.⁶² had to base their PES on a limited amount of points, which forced them to adopt a fitting method that is of only medium accuracy (i.e., a flexible periodic London–Eyring–Polanyi–Sato (FPLEPS) function⁷¹) to represent their ECW data. Additionally, it is not so clear how the ECW method could be used in an SRP approach, whereas this is rather obvious for DFT.

Figure 2.

(a) Sticking probability of O₂ on Al(111) as a function of translational energy for normal incidence. The green line indicates results obtained with the (R)PBE DF,^24,43 whereas the blue and red circles indicate QCT results obtained here with the MS-RPBEl and HSE03-1/3X DFs, respectively. The black diamonds and orange squares indicate experimental results⁶¹ and QCT results obtained with an ECW PES,⁶² respectively. (b) Sticking probability of O₂ (ν = 0, J = 2, K = 1) on Al(111) for the helicopter (red downward pointing triangle), random (black circle), and perpendicular (blue upward pointing triangle) orientations. The solid and open symbols indicate the computed (HSE03-1/3X) and experimental⁶³ results, respectively. The lines merely guide the eye.

We have investigated the dissociative chemisorption of O₂ on a static Al(111) surface with the quasi-classical trajectory (QCT)⁷² method using PESs based on DFs that go beyond the standard GGA. Like Carter and co-workers, we make the static surface approximation and the Born–Oppenheimer approximation, thereby neglecting nonadiabatic effects related to the spin- and charge-states of O₂ and to electron–hole pair excitation. For our calculations, we have developed 6D PESs with the meta-GGA MS-RPBEl DF⁷³ and the screened hybrid HSE03-1/3X DF.^74,75 The MS-RPBEl DF⁷³ is able to describe both covalent and metallic interactions accurately by relying on a switching function dependent on the kinetic energy density.⁷⁶ With this DF the SIE is reduced by ensuring that the exact energy of the free hydrogen atom is reproduced. For the metallic density regime the low-order gradient expansion of the exchange energy of the homogeneous electron gas is reproduced, which ensures a good description of the metal. The HSE03-1/3X DF is based on the HSE03 DF,^74,75 with the only difference being the maximum fraction of exact exchange α, which may be viewed as a semiempirical parameter. Specifically, we use α = 1/3 instead of α = 1/4, because Cortona and co-workers^77,78 have shown that increasing α to 1/3 is also valid according to the standard DFT adiabatic connection,⁷⁷ and that the increase from 1/4 as in PBE0 to 1/3 improves the description of gas-phase reaction barriers.⁷⁸ More generally, it is known that hybrid functionals with high fractions of exact exchange tend to perform better at describing reaction barrier heights.² Importantly, the HSE03 DF uses screened exact exchange so that a correct description of the long-range Coulomb interaction is recovered for the metal, and screened hybrid DFT is an order of magnitude cheaper than global hybrid DFT for metals.⁷⁹⁻⁸⁴ Both PESs have been constructed by interpolating the DFT data with the corrugation reducing procedure (CRP),^85,86 of which we summarize the computational details in Sections S1.2 and S1.3. Two-dimensional cuts through the computed PESs are shown for the minimum barrier geometry found in Figures S1 and S2. For the MD, the QCT method^72,87 is employed, which is also summarized in Section S1.4. The sticking probabilities are computed as described in the Supporting Information of ref (62).

Table 2 compares several barrier heights and locations (i.e., the distance to the surface 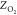) obtained with ECW theory,⁶² the MS-RPBEl DF, and the HSE03-1/3X DF. The DFs yield similar trends as ECW theory, except for the geometries with parallel orientations at the fcc site. Generally, both the barrier heights and the anisotropy are lower with the DFs than with ECW theory, and the discrepancies between MS-RPBEl and ECW theory are greater than between HSE03-1/3X and ECW theory. More specifically, among the barrier heights listed the minimum barriers are 3.4, 11.4, and 18 kJ/mol for the meta-GGA DF, the hybrid GGA DF, and ECW theory, respectively. Furthermore, the difference between the smallest and largest barrier heights listed, which measures how the barrier height varies with impact site (energetic corrugation) and molecular orientation (anisotropy) increases in the same order as 10.9, 17.1, and 46 kJ/mol, respectively. Qualitative predictions regarding the dependence of the sticking (or dissociative chemisorption) probability (S₀) on incidence energy (E_i) can then be made with the hole model.⁸⁸ This model holds that S₀(E_i) is proportional to the fraction of impact sites and orientations for which E_i exceeds the barrier height. The hole model then predicts that the meta-GGA DF yields the lowest energy threshold in the S₀ curve, while the highest threshold should be found for the ECW results, with the HSE03-1/3X threshold being intermediate. Additionally, based on the barrier height variation the model predicts the steepest S₀ curve for the meta-GGA DF and the slowest rising curve for the ECW method.

Table 2. Barrier Location (Z_O2, Å) and Height (E_b, kJ/mol) of O₂ on Al(111) Obtained from Raw ECW Data⁶² and the MS-RPBEl and HSE03-1/3X CRP PESs Generated in This Work^a.

		ZO2 (Å)			Eb (kJ/mol)
site	orientation	ECW	MS-RPBEl	HSE03-1/3X	ECW	MS-RPBEl	HSE03–1/3X
fcc	//1	1.9	3.0	2.6	60	3.7 (3.7)	12.3 (12.9)
	//2	2.2	3.0	2.7	43	3.4 (2.0)	11.4 (10.7)
	//3	2.4	3.0	2.6	18	3.7 (1.0)	12.3 (10.0)
	⊥	1.9	3.0	2.8	41	8.8 (7.4)	26.9 (26.7)
top	//	2.6	2.8	2.6	64	9.3 (7.8)	22.2 (21.3)
	⊥	2.8	3.1	2.8	64	12.0 (10.6)	26.8 (26.8)
bridge	//	2.4	2.7	2.5	54	14.3 (12.9)	29.4 (28.8)
	⊥	2.7	3.2	2.9	43	7.3 (5.9)	19.4 (15.7)

^aThe nomenclature of the different orientations is taken from ref (62). The zero-point energy corrected barriers are provided in the brackets.

The computed S₀(E_i) curves shown in Figure 2a display the behavior predicted by the hole model on the basis of the barrier heights shown in Table 2. We focus on the overall sticking of O₂ on Al(111) even though this includes contributions from both dissociative chemisorption and abstraction.⁸⁹ The MS-RPBEl DF yields a qualitative improvement over the (R)PBE GGA DF by describing the reaction as activated, but with its low-energy threshold and steep rise with E_i it still overestimates the reactivity considerably. The HSE03-1/3X DF yields considerably better agreement with experiment. The comparison suggests that the minimum barrier height is well-described with the HSE03-1/3X DF, although the slope of the sticking curve is still too steep. In line with the above the latter observation suggests that the anisotropy of the barrier height in θ and ϕ is underestimated and that the energetic corrugation of the barrier height may be too low. The too low anisotropy of the HSE03-1/3X PES also explains why the rotational alignment dependence of the sticking probability is underestimated, even though the calculations qualitatively reproduce the dependence found experimentally (see Figure 2b and Section S2.5 for further discussion). ECW theory yields the best overall agreement with experiment, especially regarding the slope. However, the reaction threshold appears to be better described with the tested hybrid functional, suggesting that the HSE03-1/3X minimum barrier height is more accurate than the ECW value. We also note that the ECW results are based on an approximately fitted FPLEPS PES whereas our dynamics results are based on PESs accurately interpolating the DFT data with the CRP. Furthermore, the agreement of the ECW results with experiment at low incidence energies may have been improved artificially by simulating the reaction of nonrotating O₂ instead of using the appropriate rotational distribution⁶² (see Figure S4 and Section S2.4).

The above conclusions are valid provided that the sticking is not much affected by electron–hole pair (ehp) excitation and surface atom motion, the effects of which could lower the energy threshold and the steepness of S₀(E_i). We believe these possible effects to be unimportant for the following reasons: First, experimental results indicate that the surface temperature does not influence S₀.⁶¹ Second, according to the local density friction approximation, the probability to excite ehps will be high only if the dynamics sample high electron densities. However, for O₂ + Al(111), the barrier is early (far away from the surface), so that the electron density sampled by O₂ before it encounters a barrier is low. Third, the location of the barrier far from the surface also suggests small electronic and mechanical couplings^90,91 with surface atom motion, i.e., the barrier height and location should not vary much with the motion of the nearest surface atom. According to the lattice relaxation sudden model,^90,91 surface atom motion should then not much affect S₀.

We suggest that the reasonably good description of the minimum barrier obtained with the HSE03-1/3X DF is due to the reduction of the delocalization error (or the SIE) as a fraction of exact exchange energy is included.^38,92−95 Furthermore, the HSE03-1/3X DF also qualitatively reproduces experimental alignment and incidence angle-dependent sticking probabilities (see Sections S2.5 and S2.6, respectively). We conclude that the HSE03-1/3X DF already gives a reasonable description of the reaction of O₂ on Al(111), suggesting that an accurate SRP-DF for this system can be developed on the basis of screened hybrid DFs. As further discussed in Section S3.2, we expect that a functional better describing the sticking in O₂ + Al(111) would contain a correlation function approximately describing the van der Waals dispersion interaction,⁹⁶⁻⁹⁸ while α should then probably be increased in the hybrid functional.

We now come to a tentative explanation of why semilocal DFT may be quite accurate for barriers to dissociative chemisorption on metals if (W – E_ea) > 7 eV. One of us along with others has recently suggested⁷ a possible reason for this success in terms of the delocalization error of Yang and co-workers.^37,38,40 The explanation is necessarily of a hand waving nature, as delocalization errors, like self-interaction errors,^94,99 are usually hard to quantify for most systems of practical interest. The explanation takes its cue from the explanation of the GGA’s tendency to underestimate gas-phase barrier heights given in the introductory paragraphs of our Letter. The explanation of the GGA’s success in describing molecule–metal surface reactions that may be applied if (W – E_ea) > 7 eV runs as follows: The electrons coming from the molecule to form new bonds are too delocalized at the TS, and this leads to a delocalization error;⁴⁰ but the electrons coming from the metal were already quite delocalized in the metal, and they become more localized at the TS, leading to a localization error. If electron transfer does not occur too easily (i.e., W – E_ea > 7 eV), then apparently a cancellation of errors occurs, allowing one to tweak the barrier by mixing GGA-exchange-based DFs. Presumably, the cancellation effect disappears once (W – E_ea) < 7 eV and the electrons coming from the metal start to spill over to the molecule because of charge transfer. The diffuse charge distribution on the negatively charged molecule upsets the balance leading to too much electron delocalization and therefore an underestimation of the TS energy. The explanation finds quantitative support in the high Bader charges found on the molecules in the TSs of the difficult systems (see Table S8 and Section S2.3).

A remaining question concerns the origin of the delocalization error that plagues the accuracy of GGA barrier heights for systems with (W – E_ea) < 7 eV, which we address here for O₂ + Al(111). There are two possibilities. First, it is possible that the change from reactants to the TS (at which the true electron density will usually be more delocalized) by itself drives the underestimation of the barrier height, i.e., that the error in the barrier height is functional driven.^100,101 Second, the error may also come about, or be further increased, because semilocal functionals yield self-consistent electron densities at the TS that differ from the true densities to the extent that density driven errors, which may result from over-delocalization, result.^100,101 The question is relevant: even for stretched H₂⁺ , which is a prototypical case for delocalization error,³⁸ the error of GGAs is still predominantly functional-driven.¹⁰² In other words, the self-consistent results are not much improved when GGAs are evaluated on the exact density of stretched H₂⁺.¹⁰²

To estimate the RPBE’s density-driven error (DDE) for the barrier height of O₂ + Al(111), we evaluate RPBE on the presumably more accurate HSE03-1/3X DF electron density, i.e., RPBE@HSE03-1/3X. Interestingly, this yields almost the same barrier height as the self-consistent RPBE (see Figure 3). This shows, at least for the early barrier system investigated here, that the error of RPBE is functional-driven and not density-driven. At the same time, to a good approximation, the HSE03-1/3X@RPBE energy equals the HSE03-1/3X energy in the entrance and barrier region of the O₂ + Al(111) PES (see Figure 3 and Table S6). Our results therefore show that the RPBE error in the barrier height is not due to “spuriously easy charge transfer” as suggested in ref (36) because this should be reflected in the RPBE density to which the HSE03-1/3X is applied in HSE03-1/3X@RPBE. Our result that HSE03-1/3X@RPBE yields similar energies as HSE03-1/3X in the entrance and barrier regions of the O₂ + Al(111) PES suggests that the HSE03-1/3X@RPBE approach might accurately describe the sticking probability for this and other DC on metal systems. This is a potentially useful finding because using the HSE03-1/3X@RPBE approach to compute energies is roughly an order of magnitude less expensive than using the HSE03-1/3X DF,¹⁰³ with obvious implications for dynamics studies based on hybrid density functionals. While the DDE has a small contribution to the total RPBE error around the TS, its DDE becomes large when the molecule gets closer to the surface (see Figure 3 and Section S2.2). This finding is consistent with the results of Perdew and co-workers for molecular adsorption of CO on Pt(111), who also find that the DDE of semilocal DFT is large when the molecule is close to the surface.¹⁰⁴

Figure 3.

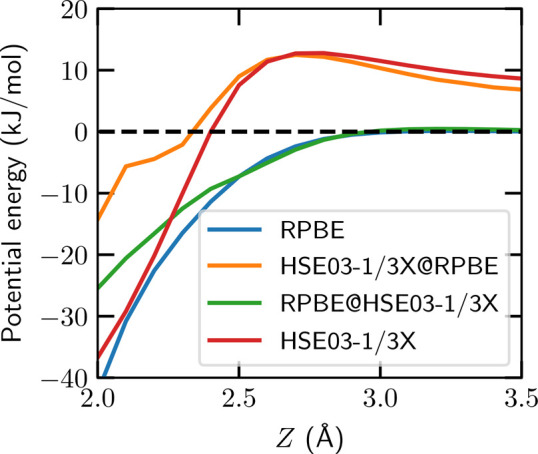
Potential energy of O₂ + Al(111) as a function of for r = 1.25 Å and the fcc //3 configuration computed self-consistently and nonself-consistently with the RPBE and HSE03-1/3X functionals applied to self-consistent RPBE and HSE03-1/3X electron densities.

In conclusion, comparison of experiment and DFT-based theory, and of DMC and RPBE DFT calculations for sticking of molecules on metal surfaces suggests that GGA-DFT starts to fail for molecule–metal surface reaction barriers when W – E_ea < 7 eV. Our results obtained for O₂ + Al(111) with the MS-RPBEl DF suggest that meta-GGA DFs of the “made simple (MS)” kind can slightly remedy the SIE problem, but not sufficiently for this system. Screened hybrid DFs like HSE03-1/3X, and its much cheaper HSE03-1/3X@RPBE alternative, offer a considerably improved description of O₂ + Al(111) in that they yield sticking probabilities in semiquantitative agreement with experiment, thus offering more promise, as also implied by single-point calculations performed at reaction barrier geometries of two other difficult systems (see Table S7 and Section S2.2). The HSE03-1/3X DF gives a good description of the reaction threshold but still overestimates the slope of the sticking probability curve for O₂ + Al(111). Our results suggest that SRP-DFs can be built on the basis of screened hybrid exchange DFs for DC systems in which (W – E_ea) < 7 eV, i.e., when electron transfer is facile. Such calculations have the potential to widen the scope of existing databases (now only SBH10²²) of barriers for molecule–metal-surface systems. Indeed, it is likely that the choice of systems in this database (SBH10 contains only H₂–metal, CH₄–metal, and N₂–metal systems that are all in the green-blue part of the spectrum made up by Figure 1) has led to systematic bias: The inadvertent choice of systems for which GGA-based exchange works well may actually be responsible for the outcome²² that the GGA-exchange-based DF performed better than the also tested meta-GGA and hybrid functionals. Even more importantly, the calculations referred to might also increase the range of heterogeneously catalyzed processes that may be simulated reliably based on accurate DFT calculations on the constituent elementary molecule–metal surface reactions.

Computational Methods

For the MS-RPBEl (HSE03-1/3X) DF a 2 × 2 Al supercell with 4 layers and 15 (10) Å vacuum distance is used. Furthermore, a plane wave kinetic energy cutoff of 600 (400) eV and an 8 × 8 × 1 Γ-centered k-point grid are used. All DFT calculations are performed with the Vienna Ab-initio Simulation Package (VASP version 5.4.4),^105−109 with a user modification to allow the use of the MS-RPBEl DF, using spin polarization when necessary. The core electrons have been represented with the projector augmented wave (PAW) method.^109,110 In order to speed up convergence, first-order Methfessel–Paxton smearing¹¹¹ with a width parameter of 0.2 eV has been employed. Additional information is provided in the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c02452.

• Description of the DFs used (Section S1.1), the DFT calculations (Section S1.2), how the CRP is applied (Section S1.3), the QCT calculations (Section S1.4), and how work function and electron affinity values are obtained (Section S1.5); discussion of several static DFT calculations (Section S2.1), nonself-consistent DFT calculations (Section S2.2), the correlation between (W – E_ea) and charge transfer at the TS (Section S2.3), the dependence of S₀ on the molecular beam conditions (Section S2.4), the alignment of O₂ relative to the surface (Section S2.5), and incidence angle (Section S2.6), on O₂ + metal systems as benchmarks (Section S3.1), and the development of an SRP functional for O₂ + Al(111) (Section S3.2); elbow plot of the MS-RPBEl and HSE03-1/3X PESs at its minimum barrier geometry (Figures S1 and S2, respectively); total magnetic moment of the fcc //3 reaction coordinate (Figure S3); S₀ computed for (ν = 0, J = 0) and for T_vib = 300 K, T_rot = 9 K (Figure S4), and for its dependence on the angle of incidence (Figure S5); work function and electron affinity values (Tables S1 and S2, respectively); effect of varying the screening length parameter and exact exchange fraction (Table S3); vibrational energies (Tables S4 and S5); HSE03-1/3X@RPBE(-vdW-DF1) barrier heights (Tables S6 and S7); excess charge at the TS for several molecule–metal surface systems (Table S8) (PDF)

• Software to obtain energies and forces from the MS-RPBEl and HSE03-1/3X PESs developed here (ZIP)

The authors declare no competing financial interest.