Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Nov 23;11(24):10306–10314. doi: 10.1021/acs.jpclett.0c03123

Static Disorder in Excitation Energies of the Fenna–Matthews–Olson Protein: Structure-Based Theory Meets Experiment

Marten L Chaillet †, Florian Lengauer ‡, Julian Adolphs §, Frank Müh ‡, Alexander S Fokas ∥, Daniel J Cole ⊥, Alex W Chin ∇, Thomas Renger ‡,*
PMCID: PMC7751012  PMID: 33227205

Abstract

graphic file with name jz0c03123_0006.jpg

Inhomogeneous broadening of optical lines of the Fenna–Matthews–Olson (FMO) light-harvesting protein is investigated by combining a Monte Carlo sampling of low-energy conformational substates of the protein with a quantum chemical/electrostatic calculation of local transition energies (site energies) of the pigments. The good agreement between the optical spectra calculated for the inhomogeneous ensemble and the experimental data demonstrates that electrostatics is the dominant contributor to static disorder in site energies. Rotamers of polar amino acid side chains are found to cause bimodal distribution functions of site energy shifts, which can be probed by hole burning and single-molecule spectroscopy. When summing over the large number of contributions, the resulting distribution functions of the site energies become Gaussians, and the correlations in site energy fluctuations at different sites practically average to zero. These results demonstrate that static disorder in the FMO protein is in the realm of the central limit theorem of statistics.

The conformational motion of proteins spans many orders of magnitude in time, ranging from femtosecond vibrations of individual atoms and molecular groups via the nanosecond regime of the concerted motion of structural elements such as groups of residues toward the microsecond and longer time scales of large-scale conformational transitions of whole protein domains. This multiscale flexibility allows the protein to perform such complex functions as light-driven catalysis. In photosynthesis, sunlight is absorbed by light-harvesting antennae and transferred to a reaction center, where the light energy is converted to the free energy of chemical compounds. The Fenna–Matthews–Olson (FMO) protein is a trimeric pigment–protein complex (PPC) (Figure S1) that connects an outer antenna system (chlorosome) with the reaction center complex in green sulfur bacteria. Every monomer binds 8 BChl a pigments (Figure 1). Two-dimensional electronic spectroscopy was developed and applied to resolve details of the energy transfer in the FMO protein1,2 and in whole cells3 of green sulfur bacteria. Small-amplitude long-lived coherent oscillations found in these 2D spectra4−8 gave birth to the field of quantum biology.9,10 A full appreciation of the spectroscopic data requires structure-based simulations, which are, however, difficult because of the complexity of this system. Multiscale methods11,12 are needed in order to obtain a realistic picture of the light-harvesting dynamics. The workhorse in such a description has been a Frenkel exciton Hamiltonian H = Hex + Hex–vib + Hvib expanded in the basis of localized excited states |m⟩ of the PPC. In the latter state, pigment m is excited and all other pigments are in their electronic ground state. The exciton part of this Hamiltonian reads

graphic file with name jz0c03123_m001.jpg 1

where Em(c) and Vmn(c) are the local transition energy, termed site energy, of pigment m and the excitonic coupling between pigments m and n, respectively. Both quantities depend on the conformation c of the PPC, which changes slowly compared to the excited-state lifetime (fs to ns) of the pigments. Any fast conformational motion that modulates the excitonic couplings and transition energies is contained in the exciton–vibrational coupling Hamiltonian Hex–vib, and the nuclear motion is described by Hvib. (Explicit expressions for these Hamiltonians are given in the Supporting Information (SI)).

Figure 1.

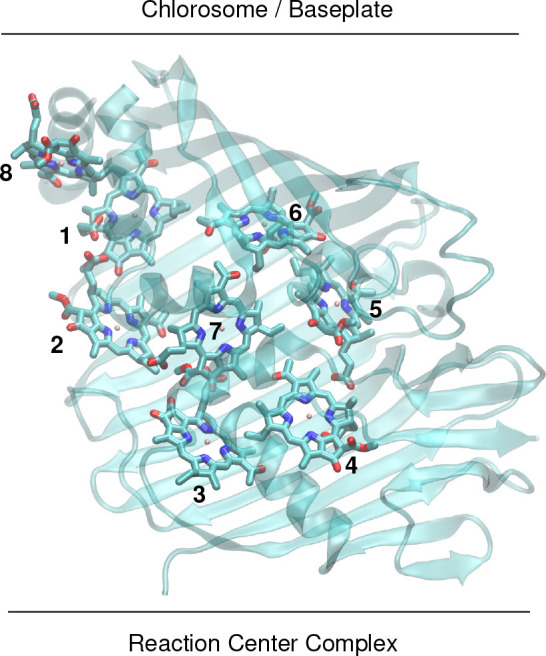
Figure 1

Open in a new tab

Monomeric subunit of the trimeric FMO protein from P. aestuarii, which connects the outer antenna system (chlorosome) with the reaction center complex in an orientation as indicated in this figure. The protein part is shown in transparent ribbon style, and the pigments are numbered as in PDB file 3EOJ.13 The phytyl tails of the pigments were truncated for better visibility. The complete structure of the FMO trimer is shown in Figure S1. Graphics were prepared with VMD.14

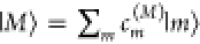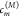In linear spectroscopy, to good approximation, the eigenstates Inline graphic of Hex are excited, where the eigenenergies EM correspond to the transition energies seen in the spectra. The coefficients Inline graphic of the eigenstates are obtained from the respective eigenvectors of the exciton matrix Hex. These coefficients together with the local transition dipole moments dm determine the amplitudes of the optical lines seen in the absorption spectrum, which is obtained as

graphic file with name jz0c03123_m004.jpg 2

where the transition dipole moment dM of exciton state |M⟩ reads 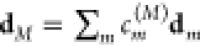Inline graphic. The line shape function DM(ω), obtained by taking into account the exciton–vibrational coupling, contains homogeneous line broadening caused by the excitation of vibrational side bands and exciton relaxation (More details, including circular and linear dichroism spectra, are given below and in the SI.) The inhomogeneous line shape, finally, is obtained by performing an average over static disorder in site energies and excitonic couplings, denoted as ⟨···⟩c.

The determination of (mean) site energies Em and excitonic couplings Vmn of the FMO protein has been a problem for many decades.15 Major progress concerning the site energies was obtained by Aartsma and co-workers,16 who recognized that using a smaller effective dipole strength of the pigments in the calculation of excitonic couplings allows one to find site energies that fit linear absorption, linear dichroism, and circular dichroism spectra. The low effective dipole strength was explained by quantum chemical/electrostatic calculations.17 It was recognized that there is a gradient in local transition energies toward BChls 3 and 4, which are located on one side of the FMO protein. On the basis of energy-transfer calculations, it was concluded that efficient light-harvesting requires BChls 3 and 4 to be the linker pigments between the FMO protein and the reaction center complex.17 This prediction was confirmed experimentally by Blankenship and co-workers using chemical labeling of solvent-exposed groups and mass spectrometry.18

Attempts to formulate a structure-based explanation of the site energy values were reported using various multiscale approaches.19−26 Some of these methods aim at a fully ab initio description without using any adjustable parameters.22−26 In other simplified approaches, the intermolecular electrostatic pigment–protein coupling is evaluated,11,19−21 and the obtained site energies are typically adjusted within a ±60 cm–1 window from a fit of the optical spectra. It was recognized that the energy sink at BChl 3 is caused by the electrical field of the backbone of two α-helices and by a hydrogen bonding network involving a hydrogen bond between a tyrosine and the keto group of BChl 3.19 In recent years, the latter prediction has been verified in a site-directed mutation study, where this Tyr was replaced by Phe.27

The fluctuations of site energies of the BChl pigments of the FMO protein have been characterized theoretically by quantum mechanics/molecular mechanics (QM/MM) approaches.24,28−33 The main focus has been on the fast fluctuations that are described by the spectral density of the exciton–vibrational coupling. The latter is related to the autocorrelation function of the site energy fluctuations, which has been calculated by combining classical molecular dynamics (MD) simulations of the complex with QM calculations of optical transition energies of the pigments.28,30 In such combinations, one has to be careful about the fact that the potential energy surfaces of the pigments are different in classical and quantum descriptions. Different strategies exist to avoid this geometry mismatch problem,24,29,31−38 which artificially enhances the intrapigment contributions to the variation of site energies. One can find a suitable interpolation between the MM and the QM potential energy surfaces of the pigments,24,32,33,36 calculate the intermolecular and the intrapigment contributions to the site energy modulations separately,29,31,34 taking special care of the intrapigment part, or neglect the latter.39−41 The intermolecular contribution to the variation in site energies was calculated by combining the electrostatic charge density coupling (CDC) method,20 which will be explained in more detail below, with classical MD29,31,34 or normal mode39 calculations. Alternatively, it was obtained in QM/MM simulations by subtracting from the full site energy variations the intrapigment contributions, obtained by switching off the environment in the calculation of site energies.34,40,41 The intrapigment contribution to the site energy variation was obtained by using a quantum mechanical normal-mode analysis (NMA) either on the isolated geometry optimized pigment34 or on a QM-optimized potential energy surface of the pigment along the classical MD trajectories.29,31 Alternatively, the geometry mismatch problem has been tackled by quantum chemical calculations of the intrapigment potential energy surfaces using density functional theory (DFT),37 tight-binding DFT,38 or semiempirical35 methods and treating only the protein environment with classical force fields. However, such approaches are numerically very costly.

The focus of the present work is on site energy variations that are much slower than excited-state lifetimes (fs to ns) and give rise to static disorder causing an inhomogeneous broadening of optical lines. The underlying slow diffusive conformational motion of the protein is anharmonic and therefore cannot be captured with an NMA. MD simulations in principle are able to describe such conformational transitions, but long simulation times are required and very likely local free-energy barriers prevent a complete sampling of the phase space. Nevertheless, by time-averaging site energies in QM/MM calculations, the first results on static site energy distribution functions were obtained.33,40,41 The most detailed investigation of static disorder was reported by Rhee and co-workers,33 who performed 100 ns QM/MM simulations of a monomeric subunit of the FMO protein using their interpolation scheme that avoids the geometry mismatch problem described above. By varying the window size for time averaging of the site energy fluctuations, they were able to visualize different fluctuation regimes. In the regime of slow fluctuations (window size of 1 ns), they inferred a standard deviation of the time-windowed averages in the 20–50 cm–1 range corresponding to a full width at half-maximum (fwhm) of 50–120 cm–1, which is in the right range when compared with estimates of inhomogeneous distribution functions of site energies from the fit of optical spectra.16,17,19,21,42

An alternative and numerically efficient way to sample low-energy conformations of proteins is given by Monte Carlo (MC) simulations, such as the framework-rigidity-optimized dynamic algorithm (FRODA).43 This technique has been applied by some of us to the monomeric subunit of the FMO protein and to whole FMO trimers.44,45 FRODA was combined with the point dipole approximation (PDA) to investigate static disorder in excitonic couplings44 and with linear scaling density functional theory (DFT) to study the correlation in site energy fluctuations between the two low-energy pigments, BChl 3 and 4.45 Because of the numerical costs of the linear scaling DFT calculations, which also included part of the environment (all atoms within a 15 Å cutoff radius of the pigment of interest), it was possible to investigate only a few different conformers of the FMO protein, generated from the first principal component of the MC trajectories. For these nine conformations, an interesting correlation in site energies was found.45 By restricting the DFT calculations to the first principal component, only the large-scale motion of the protein was captured and the geometry mismatch problem, described above, could be avoided since the pigment conformations were not affected. Correlations in dynamic site energy fluctuations have been investigated with MD simulations47 and normal-mode analysis (NMA).39 Whereas the MD simulations did not find any correlations, in the NMA they appeared at very low vibrational frequencies. We will investigate whether these correlations also prevail on the much longer time scales relevant to static disorder.

In the present work, we combine the FRODA MC technique for the sampling of low-energy conformational substates of the FMO protein with the efficient and robust electrostatic CDC method20 for the calculation of site energy shifts. Since only intermolecular Coulomb couplings are calculated and the intrapigment contributions to the static site energy shifts are neglected, the geometry mismatch problem is avoided. In this way, it is possible to study a large number of different conformations, reinvestigate the presence of correlations in static disorder, and provide a fully structure-based simulation of the inhomogeneous spectroscopic properties of the FMO protein.

The present simulations of static disorder in site energies and excitonic couplings are based on conformational substates of the FMO protein that were obtained in earlier work using a combination of the FIRST (floppy inclusions and rigid substructure topography) and the FRODA (framework-rigidity-optimized dynamic algorithm) algorithms.43 On the basis of the geometry-optimized holo form of the crystal structure of FMO trimers of Prosthecochloris aestuarii,13 FIRST was used to identify flexible and rigid regions of the complex by taking into account covalent as well as noncovalent interactions. The “hard” degrees of freedom, containing the variation of covalent bond lengths and angles, as well as certain dihedral angles (e.g., for rotation around peptide bonds) define rigid clusters. The flexibility of the macromolecule is determined by rotation around single bonds connecting the rigid clusters. Hydrogen bonds and hydrophobic contacts were also considered in the definition of these clusters. A hydrogen bond energy cutoff value Ecut of −4.6 kcal/mol was applied, and all hydrogen bonds with a larger binding energy were kept intact during the subsequent MC generation of conformational substates with FRODA. Several (713) hydrogen bonds were identified in this way. In addition, 236 hydrophobic constraints were taken into account by not allowing atoms of two hydrophobic groups in van der Waals contact to separate by more than the sum of their van der Waals radii plus 0.5 Å in the course of the conformational sampling. Once the rigid clusters have been defined with FIRST using the graph-theoretical pebble game algorithm,48 FRODA is used for an efficient MC sampling of the remaining flexibility of the macromolecule. In an MC step, every atom is displaced in a random direction by a magnitude of 0.1 Å, and ghost templates, containing the internal structure of the rigid clusters, are moved such as to minimize the distances between the new atom positions and the corresponding points on the ghost templates. In an iterative procedure, atom positions and ghost templates are moved further until the atom positions fulfill the original constraints; that is, all atoms are close to the corresponding positions on the ghost templates. In comparison to the original structure, the rigid clusters have moved without internal distortion, just by geometric means without using any potential energy function. Hence, FRODA is not restricted to harmonic motion around some minimum of the potential energy surface. By repeating this procedure, a whole ensemble of conformational substates is obtained. The applied constraints allow for an efficient sampling of conformational states (scaling linearly with the number of atoms43) and restrict the conformations to those of the lowest energies connected by diffusive protein motion. The energy differences between the states are assumed to be so small that all states have the same statistical weight, independent of temperature. The downside of this simple approach lies in the neglect of long-range electrostatic and solvation effects which would alter the statistical weights of the states and could shift the borders between flexible and rigid regions. Despite and because of these simplifications, FIRST/FRODA has proven to provide realistic conformational ensembles of proteins, as judged by comparison of atomic mobilities with experimental NMR43 and molecular dynamics simulation data.49 In the present work, we provide further evidence by monitoring the static disorder in local transition energies of protein-bound pigments and by comparing with experimental optical spectra of the inhomogeneous ensemble. A more detailed description of the FIRST/FRODA method and its application to the FMO protein can be found in earlier work.43,44,48

Using the FIRST/FRODA method described above, 5200 conformations of the trimeric FMO protein were generated.44 Local transition energies (site energies) of the 24 BChl a pigments are calculated with the charge density coupling (CDC) method for each of these conformations.20 The site energy of pigment m is obtained as

graphic file with name jz0c03123_m006.jpg 3

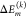where Inline graphic is the contribution of building block k of the PPC. It contains the difference in charge density coupling of the electronic ground state of this building block with the first excited and ground state of pigment m, reading

graphic file with name jz0c03123_m008.jpg 4

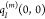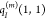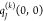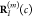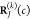Since the charge densities of the ground and excited states of pigment m and that of the ground state of the environment are approximated by atomic partial charges Inline graphic, Inline graphic, and Inline graphic, respectively, it is very simple to take into account a variation of the respective atomic positions Inline graphic and Inline graphic with respect to different conformations c of the complex. Parameters E0 and ϵeff are inferred from the center and the overall width, respectively, of the experimental optical spectra. In this way, uncertainties in the quantum chemical method and additional terms in the pigment–protein coupling (e.g., dispersive interactions) are implicitly taken into account. For the present system, we find optimal values of E0 = 12 560 cm–1 and ϵeff = 3.6. These values give a good correlation between the mean site energies calculated with FRODA/CDC and the reference values from the literature (Figure S2). The ground-state partial charges of the protein were taken from the CHARMM22 force field,50 assuming a standard protonation pattern of the titratable residues. The atomic partial charges of the pigments were obtained in earlier work46 from a fit of the ab initio electrostatic potential of the ground and excited states of geometry-optimized BChl a, computed with time-dependent DFT and the B3LYP exchange-correlation functional. The numerical values of the atomic partial charges of BChl a are given in Table S2. The statistical analysis of the site energies was done with Octave.51 Please note that the present approach takes advantage of the stiffness of the closed-ring structure of the BChl a pigments, assuming that the intrapigment contribution to static disorder in transition energies can be neglected. In the case of open-ring chromophores such as bilins,37 such a simple description, most likely, would not be appropriate. Instead, one would have to take into account an intrinsic site energy shift that could be calculated only quantum chemically, and a new set of partial charges would have to be calculated for every conformation of the chromophore in order to describe the electrostatic interaction with the environment.

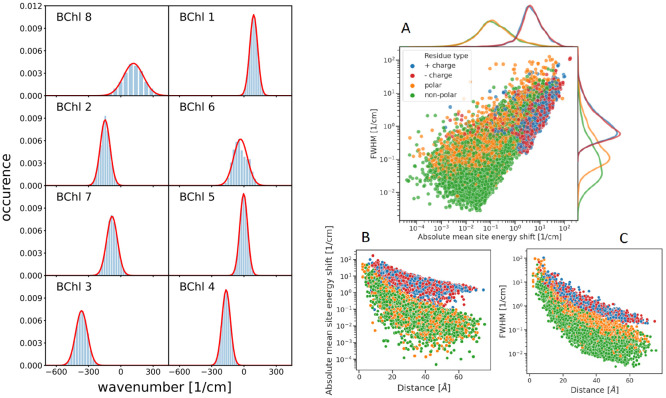
The distribution of site energy shifts of the 8 BChl pigments of one monomeric subunit of the FMO protein, obtained by applying the CDC method to 5200 different conformations of the PPC, computed with FRODA,45 is shown in the left half of Figure 2. These distribution functions can be well described by Gaussian functions of different widths (red lines), varying between 86 cm–1 for BChl 5 and 220 cm–1 for BChl 8 (Table S1). The large width of the latter reflects the large conformational flexibility of BChl 8, which is bound at the surface of the FMO protein, whereas all other BChls are packed closely inside a protein bag of mostly β-sheet secondary structures (Figure 1). The inhomogeneous widths are in the same range as those suggested from the fit of optical spectra16,17,19,21,42 and those based on QM/MM simulations with interpolated potential energy surfaces of the pigments.33 Note, however, that in these approaches the estimation was more indirect since the effect of dynamic disorder had to be evaluated as well.

Figure 2.

Figure 2

Open in a new tab

(Left) Distribution of site energy shifts ΔEm(c) = Σk ΔEm(k)(c) (eqs 3 and 4) of the eight pigments BChl m (m = 1,..., 8) in one monomeric subunit of the FMO protein, obtained by combining the FRODA MC sampling of protein conformations and the CDC method for the calculation of site energy shifts. The red lines are Gaussian functions fitted to the histograms using the parameters in Table S1. (Right) Analysis of site energy shifts ΔEm(c) (eq 4) caused by single amino acid residues k of different types (blue, positively charged; red, negatively charged; orange, polar; green, nonpolar). Panel A contains the correlation between the full width at half-maximum (fwhm) of the distribution function of ΔEm(k)(c) and the absolute mean site energy shift |⟨ΔEm(c)⟩|. The curves on top and on the right side give the respective distribution functions for the various types of amino acids. Panels B and C contain the dependence of the fwhm and the |⟨ΔEm(k)(c)⟩|, respectively, on the distance between amino acid k and pigment m.

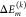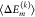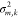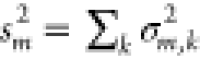The Gaussian functional form of the distribution functions suggests that the FMO protein obeys the central limit theorem. The latter states that a sum (eq 3) of independent random variables Inline graphic (eq 4), which may have different individual distribution functions characterized by a mean value Inline graphic and variance Inline graphic, will be distributed by a Gaussian function of variance Inline graphic centered at 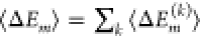Inline graphic. This result holds only if none of the random variables 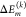Inline graphic in the sum over k (eq 3) are too dominant. A quantitative measure of this condition was provided by Ljapunov and Lindeberg.52,53

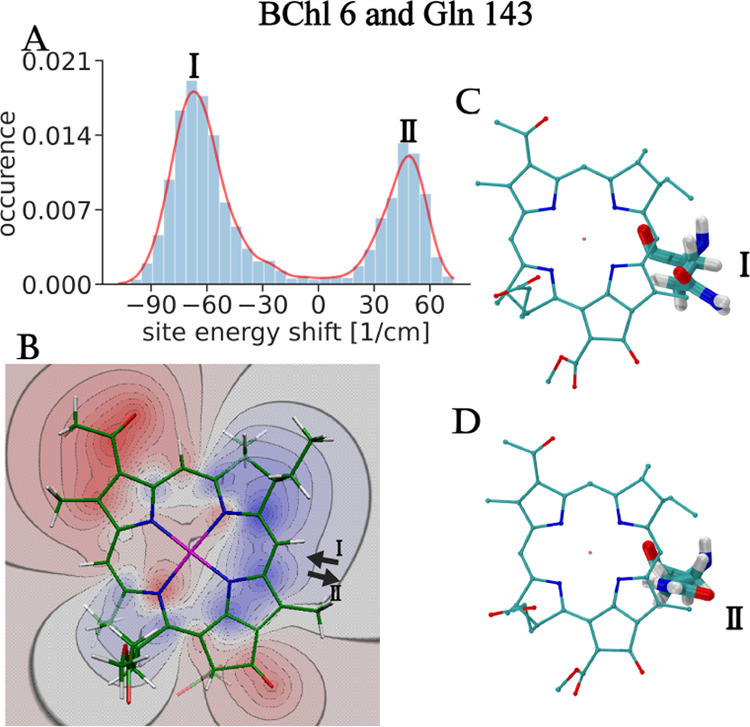
In the case of the FMO protein, there are many individual contributions 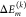Inline graphic from different amino acid residues k to the mean value ⟨ΔEm⟩ and the variance sm2 of the site energy shift of pigments m (Figure 2, right half). Interactions of the pigments with charged amino acid residues give large individual contributions (panel A) and exhibit the weakest distance dependence (panels B and C) as expected. Interestingly, the polar and nonpolar amino acid residues give very similar site energy shifts on average (top orange and green curves in panel A), whereas the contribution of the former to the width of the distribution function is significantly larger than that of the latter (right orange and green curves in panel A). This behavior is explained by the fact that polar side chains often exhibit different rotamers, which give rise to opposite site energy shifts that cancel on average, but widen the distribution function.

An example is given in Figure 3, where the contribution of Gln 143 to the site energy shift of BChl 6 is analyzed. Because of rotamers I and II (Figure 3, panels C and D, respectively), in which the polar amide group is oriented in opposite directions, a bimodal distribution function of the site energy shift results (Figure 3A) with maxima I and II at roughly −70 and +50 cm–1. In conformation I, the negative end of the amide dipole of Gln 143 points toward the region of a positive (excited state minus ground state) difference potential of BChl 6, whereas in conformation II it is the positive end (Figure 3B) causing red and blue shifts of the site energy, respectively.

Figure 3.

Figure 3

Open in a new tab

Site energy shift of BChl 6 caused by protein residue Gln 143. In panel A, the distribution function of this site energy shift is shown. The red line on top of the histograms was added to guide the eye. Representative conformations of Gln 143 giving rise to the two peaks I and II of the distribution function are given in panels C and D, respectively. Panel B contains the difference electrostatic potential between the excited and ground states of BChl a obtained with TD-DFT calculations using the B3LYP XC functional. Red (blue) regions correspond to a negative (positive) difference potential. Black arrows I and II represent the dipole moment of the amide side chain of Gln 143 in conformations I and II of this residue shown in panels C and D, respectively.

For charged amino acids, such a switch in the sign of the site energy shift for different rotamers is not observed since the displacement of the charge is too small to enter regions of different sign in the difference potential of the pigments. A typical example is shown in Figure 4. The distribution function of the site energy shift of BChl 8 caused by the negatively charged Asp 160 has a maximum at 140 cm–1 and a shoulder at 220 cm–1 (Figure 4A). In underlying conformations I and II, respectively, the negative charge is located in the negative region of the difference potential of BChl 8 (Figure 4B), explaining the blue shift of the site energy. The larger blue shift in conformation II is explained by the smaller distance between the charge and the pigment.

Figure 4.

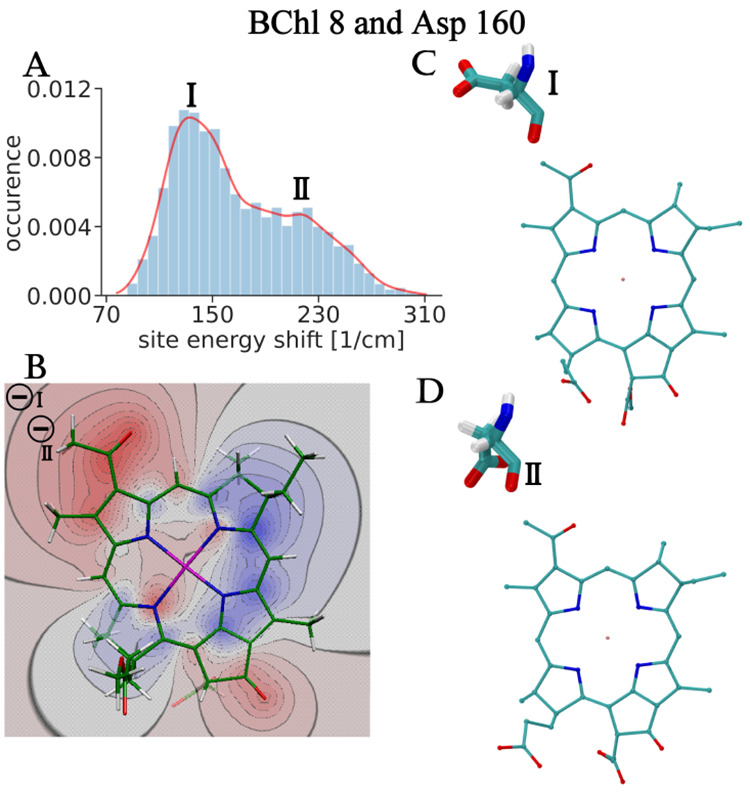
Figure 4

Open in a new tab

The same as in Figure 3 but for BChl 8 and negatively charged Asp 160. The two negative signs in the upper left corner of panel B illustrate the relative positions of the negative charge of Asp 160 in the two conformations.

It can be expected that the present calculations will help to pave the way for a microscopic understanding of single-molecule and hole-burning spectra of PPCs, where the conformational transitions are detected as jumps in optical lines and antiholes, respectively.54−58 The bimodal distribution function in Figure 3 provides a first microscopic representation of the empirical bistable conformational substates usually assumed in the interpretation of these experiments.54−56 In hole-burning experiments, the excess energy deposited in the pigment–protein complex by repeated nearly monochromatic optical excitation (burning) of a pigment drives conformational transitions of the local protein environment. According to the present calculations, a candidate for this conformational transition is the rotation of polar side groups of amino acid residues in the close neighborhood of the pigment, which leads to a change in its transition energy (Figure 3). The hole-burning signal is defined as the difference between the postburn and the preburn absorption spectrum. Hence, a negative (hole)/positive (antihole) difference signal is detected at the pre/postburn transition energy of the pigment. Note that the interpretation of such experiments is often complicated by the delocalization of excited states, which can, however, be taken into account.57,58

The maxima of the site energy shift distribution functions in Figure 2 (left half) representing the mean site energy shifts of the pigments reveal the site energy funnel discovered earlier.17,19−21 The pigments that are closer to the reaction center (BChls 3 and 4) are red-shifted with respect to those that are located at the interface of the baseplate (BChls 8 and 1), which connects the FMO protein with the outer chlorosome antenna (Figure 1). Indeed, there is an excellent correlation between the mean site energies, obtained here with FRODA/CDC, and the reference values from the literature (upper part of Figure S2), obtained from CDC calculations and a refinement fit of optical spectra.21 A notable exception is the mean site energy of BChl 1, which is about 200 cm–1 larger than the reference value.

A much weaker correlation is obtained between the present FRODA/CDC average site energies and ab initio values from the literature22,24,26 (lower part of Figure S2), illustrating the challenges that a full ab initio calculation is facing. The most encouraging results are obtained with a QM/MM method that uses a Shepard interpolation correction for the potential energy surfaces of the pigments.24

For the calculation of optical spectra, a line shape theory that is based on time-local density matrix theory is used. In this theory, the diagonal elements of the exciton-vibrational coupling in the exciton basis are treated nonperturbatively and a Markov and secular approximation is used for the off-diagonal elements. The details of this theory are given in earlier work59 and in the SI. Because BChl 8 is bound at the surface of the FMO protein, it is easily lost in the preparation of the complex. We have assumed an occupation of 35% of the eighth site in the calculation of the spectra, as has been estimated from the crystal structure.13 Note, however, that this number is highly uncertain since it depends on the details of the sample preparation. So far, no systematic study is available on this subject. Fortunately, BChl 8 affects only the blue side of the spectrum in P. aestuarii.21 Excitonic couplings are obtained first in a point-dipole approximation for the crystal structure using an effective dipole strength of 30 D2.17

The resulting low-temperature (4 K) linear absorption, circular dichroism, and linear dichroism spectra of a monomeric subunit of the FMO protein are compared in Figure 5 with experimental data,42 revealing good agreement. Qualitative disagreement is obtained only in the blue wing of the spectrum and can be traced back to the site energy of BChl 1. A difference between BChl 1 and the remaining pigments is that the crystal structure suggests the formation of a hydrogen bond between the 3-acetyl group of this pigment and a nearby water molecule, which is broken in the FRODA conformations (Figure S3). Earlier electrostatic calculations suggest that this hydrogen bond red shifts the site energy of BChl 1 by 120 cm–1 (SI, Table 4 in ref (19)), which would improve the agreement between the calculated and experimental spectra in Figure 5. Because of the uncertainty in the treatment of hydrogen bond networks involving water molecules, we have omitted all water molecules in the calculation of the site energy shifts. Including them leads to slightly worse agreement with the experimental spectra (Figure S4) but has no qualitative influence.

Figure 5.

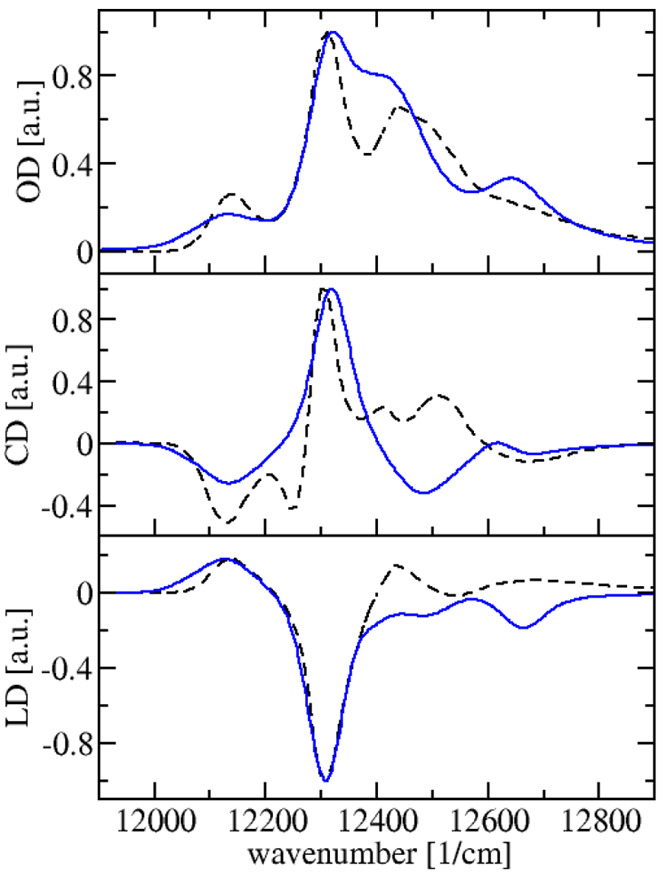
Figure 5

Open in a new tab

Calculations (blue solid lines) of low-temperature (4 K) absorbance (top part), circular dichroism (middle part), and linear dichroism (lower part) spectra of the FMO protein are compared with experimental data42 (black dashed lines).

In two other cases, BChls 2 and 3, there are some deviations in the site energies between the monomeric subunits of the FMO protein (Figure S2), which can be traced back to hydrogen bonds of the 3-acetyl groups of BChls 2 and 3 with Ser 72 and Tyr 15, respectively. Whereas these hydrogen bonds are permanently formed in one monomer, they have a high probability of being broken in the other two monomers (Figures S5 and S7). The resulting distribution functions of the site energy shift caused by the respective amino acid residue clearly demonstrate that there is a distinct red shift of the site energy by the hydrogen bond (Figures S6 and S8). It seems that the standard cutoff value for fixing hydrogen bonds in FRODA is in between those found in the three monomeric subunits for these two BChls, after the original C3-symmetric crystal structure has been geometry-optimized. The spectra of the monomer with the intact hydrogen bond agree better with the experimental data than do those calculated for the other two monomers (Figure S9). In the case of Tyr 15, there is independent evidence of the presence of the hydrogen bond in the inhomogeneous ensemble from the mutagenesis studies27 discussed above. The above examples show the limitations of the present FIRST/FRODA approach. A refinement of the MC moves by using a potential energy function that includes electrostatic interactions could help to treat these hydrogen bonds in a more realistic way.

In the next step, we have investigated static disorder in the interpigment excitonic couplings. It is well known that the point-dipole approximation (PDA) holds for the pigment positions in the crystal structure.17,60 In order to take into account possible deviations from the PDA in our inhomogeneous ensemble, we have applied the transition charge from electrostatic potential (TrEsp) method,20 as described in the SI. Gaussian distribution functions are obtained for the couplings with mean values that, for most couplings, agree well with those obtained in PDA for the crystal structure (Table S4). The fwhm’s of the resulting distribution functions of the large couplings are within around 30% of the average coupling values. For some pigment pairs with small interpigment distances and small excitonic couplings (e.g., 3–7 and 5–7), the fwhm of the distribution function is larger by a factor of up to 3 than the average coupling. Obviously, in these cases the mutual orientation of transition dipoles is unfavorable for strong coupling, but the coupling is more sensitive to conformational changes. The present results are very similar to those obtained earlier using the PDA in combination with FIRST and FRODA44 (Table S4, monomer 1), demonstrating that the PDA is valid for the conformational substates of the present system. In agreement with earlier work,44 we find that the variations in excitonic couplings are so small that their effect on the inhomogeneous broadening of optical spectra is negligible (Figure S9).

Finally, we have investigated the correlation in site energy variations between different BChls. The Pearson correlation coefficient is close to zero for all pigment pairs in all three monomeric subunits of the FMO protein (Figure S10). By restricting the protein part in the site energy calculations to specific structural elements, correlations and anticorrelations appear. For example, the conformational changes in the backbone of one α-helix are found to cause an anticorrelated variation of the site energies of BChls 3 and 4 (Figure S11). However, because of the large number of contributions to the site energy disorder, this correlation is washed out if the whole protein is taken into account. In our earlier work, it has been hypothesized that correlated static disorder may lead to more efficient energy transfer since the energy gaps between exciton states are kept small enough that efficient energy dissipation can occur44,45 and that this correlation could be responsible for long-lived interexciton coherences39 found in 2D electronic spectroscopy. The present finding (Figure S10) excludes these hypotheses. It is the contribution of intramolecular and intermolecular vibrations to the spectral density, used for the description of dynamic disorder, that allows the protein to dissipate smaller and larger portions of an exciton’s excess energy throughout the full inhomogeneous width of the Qy absorption spectrum.17,39 The large number of degrees of freedom makes the PPC flexible enough for broad band dissipation without the need to restrict the energy gaps between exciton states.

The earlier study45 was restricted by the number of conformations and the protein volume that could be included in the QC calculation, and the focus was put on the very low frequency conformational motion extracted from the first principal component of the MC trajectories. In the present study, all of these restrictions are lifted and the many contributions to the site energy correlations essentially average out. The fact that the line widths of the different exciton transitions agree qualitatively with the experimental line widths (Figure 5) suggests that static disorder is well represented by the present FRODA trajectories without restricting these trajectories to certain principal components. In addition, this result shows that the intrapigment contributions to the site energy shifts, which are not taken into account in CDC calculations, most likely are more relevant for dynamic disorder (fast time scales) as expected.

Concerning the long-lived coherences found in 2D spectroscopy,4−8 there is accumulating evidence that the origin is of a vibrational rather than an excitonic nature.6−8,61,62 The most direct evidence was obtained in low-temperature 2D experiments on mutants by the Scholes and Blankenship groups.6 In one of their experiments, they genetically exchanged the tyrosine, which forms a hydrogen bond to the 3-acetyl group of BChl 3. As discussed above, this mutation shifts the site energy of BChl 3 to the blue to an extent that the low-energy absorption band (dominated by BChl 3) disappears.19,27 Nevertheless, no change in the frequency of coherent oscillations, which originally had been assigned to interexciton coherences between the lowest two exciton states,4,5 was observed.6 Recently, the Blankenship and Harel groups8 detected a 60 fs decay of an interexciton coherence at physiological temperatures, which they identified as the one between exciton states 2 and 7. This decay time is in full agreement with recent theoretical estimates that assume uncorrelated static disorder in site energies.10 The justification for this assumption is provided here.

Acknowledgments

Support by the Austrian Science Fund (FWF) through grant P 33155-NBL (T.R.) is gratefully acknowledged. The atomic coordinates of the 5200 different conformational substates of the FMO protein analyzed here can be obtained from the zenodo public repository via the following link: https://doi.org/10.5281/zenodo.4267945.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c03123.

  • Hamiltonian of exciton-vibrational coupling, line-shape function of optical spectra, calculation of static disorder in excitonic couplings, structure of FMO trimer, correlation between mean site energies and reference values from the literature, analysis of the hydrogen bond between BChl 1 and a water molecule, effect of water molecules on the optical spectra of the three monomeric subunits of the FMO protein, analysis of the hydrogen bond between BChl 2 and Ser 72 and the resulting site energy shift, analysis of the hydrogen bond between BChl 3 and Tyr 15 and the resulting site energy shift, effect of static disorder in excitonic couplings on the optical spectra, analysis of correlations in site energy fluctuations including the effects caused by the backbones of two α helices, parameters of the Gaussian distribution functions in Figure 2, atomic partial charges of the ground and excited states of BChl a, atomic transition charges of BChl a, and excitonic couplings including a characterization of static disorder (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz0c03123_si_001.pdf (13.2MB, pdf)

References

  1. Brixner T.; Stenger J.; Vaswani H. M.; Cho M.; Blankenship R. E.; Fleming G. R. Two-dimensional spectroscopy of electronic couplings in photosynthesis. Nature 2005, 434, 625–628. 10.1038/nature03429. [DOI] [PubMed] [Google Scholar]
  2. Thyrhaug E.; Zidek K.; Dostal J.; Bina D.; Zigmantas D. Exciton Structure and Energy Transfer in the Fenna-Matthews-Olson Complex. J. Phys. Chem. Lett. 2016, 7, 1653–1660. 10.1021/acs.jpclett.6b00534. [DOI] [PubMed] [Google Scholar]
  3. Dostal J.; Psencik J.; Zigmantas D. In situ mapping of the energy flow through the entire photosynthetic apparatus. Nat. Chem. 2016, 8, 705–710. 10.1038/nchem.2525. [DOI] [PubMed] [Google Scholar]
  4. Engel G. S.; Calhoun T. R.; Read E. L.; Ahn T.-K.; Mancal T.; Cheng Y.-C.; Blankenship R. E.; Fleming G. R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. 10.1038/nature05678. [DOI] [PubMed] [Google Scholar]
  5. Panitchayangkoon G.; Hayes D.; Fransted K. A.; Caram J. R.; Wen J.; Blankenship R. E.; Engel G. S. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 12766–12770. 10.1073/pnas.1005484107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Maiuri M.; Ostroumov E. E.; Saer R. G.; Blankenship R. E.; Scholes G. D. Coherent wavepackets in the Fenna-Matthews-Olson complex are robust to excitonic-structure perturbations caused by mutagenesis. Nat. Chem. 2018, 10, 177–183. 10.1038/nchem.2910. [DOI] [PubMed] [Google Scholar]
  7. Thyrhaug E.; Tempelaar R.; Alcocer M. J.; Zidek K.; Bina D.; Knoester J.; Jansen T. L. C.; Zigmantas D. Identification and characterization of diverse coherences in the Fenna-Matthews-Olson complex. Nat. Chem. 2018, 10, 780–786. 10.1038/s41557-018-0060-5. [DOI] [PubMed] [Google Scholar]
  8. Irgen-Gioro S.; Gururangan K.; Saer R. G.; Blankenship R. E.; Harel E. Electronic coherence lifetimes of the Fenna-Matthews-Olson complex and light harvesting complex II. Chem. Sci. 2019, 10, 10503–10509. 10.1039/C9SC03501J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fleming G. R.; Scholes G. D.; Cheng Y. C. Quantum effects in biology. Procedia Chem. 2011, 3, 38–57. 10.1016/j.proche.2011.08.011. [DOI] [Google Scholar]
  10. Cao J.; Cogdell R. J.; Coker D. F.; Duan H.-G.; Hauer J.; Kleinekathöfer U.; Jansen T. L. C.; Mancal T.; Miller R. J. D.; Ogilvie J. P.; et al. Quantum Biology Revisited. Science Advances 2020, 6, eaaz4888 10.1126/sciadv.aaz4888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Renger T.; Müh F. Understanding photosynthetic light-harvesting: a bottom up theoretical approach. Phys. Chem. Chem. Phys. 2013, 15, 3348–3371. 10.1039/C3CP43439G. [DOI] [PubMed] [Google Scholar]
  12. Mennucci B.; Corni S. Multiscale modelling of photoinduced processes in composite systems. Nat. Rev. Chem. 2019, 3, 315–330. 10.1038/s41570-019-0092-4. [DOI] [Google Scholar]
  13. Tronrud D. E.; Wen J.; Gay L.; Blankenship R. E. The structural basis for the difference in absorbance spectra for the FMO antenna protein from various green sulfur bacteria. Photosynth. Res. 2009, 100, 79–87. 10.1007/s11120-009-9430-6. [DOI] [PubMed] [Google Scholar]
  14. Humphrey W.; Dalke A.; Schulten K. VMD-Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  15. Milder M. T. W.; Brüggemann B.; van Grondelle R.; Herek J. L. Revisiting the optical properties of the FMO protein. Photosynth. Res. 2010, 104, 257–274. 10.1007/s11120-010-9540-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Louwe R. J. W.; Vrieze J.; Hoff A. J.; Aartsma T. J. Toward an integral interpretation of the optical steady-state spectra of the FMO-complex of Prosthecochloris aestuarii. 2. Exciton simulations. J. Phys. Chem. B 1997, 101, 11280–11287. 10.1021/jp9722162. [DOI] [Google Scholar]
  17. Adolphs J.; Renger T. How proteins trigger excitation energy transfer in the FMO complex of green sulfur bacteria. Biophys. J. 2006, 91, 2778–2797. 10.1529/biophysj.105.079483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wen J.; Zhang H.; Gross M. L.; Blankenship R. E. Membrane orientation of the FMO antenna protein from Chlorobaculum tepidum as determined by mass spectrometry-based footprinting. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 6134–6139. 10.1073/pnas.0901691106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Müh F.; Madjet M. E.; Adolphs J.; Abdurahman A.; Rabenstein B.; Ishikita H.; Knapp E. W.; Renger T. α-helices direct excitation energy flow in the Fenna-Matthews-Olson protein. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 16862–16867. 10.1073/pnas.0708222104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Adolphs J.; Müh F.; Madjet M. E.; Renger T. Calculation of pigment transition energies in the FMO protein: From simplicity to complexity and back (erratum: https://doi.org/10.1007/s11120–007–9276–8). Photosynth. Res. 2008, 95, 197–209. 10.1007/s11120-007-9248-z. [DOI] [PubMed] [Google Scholar]
  21. Schmidt am Busch M.; Müh F.; Madjet M. E.; Renger T. The Eighth Bacteriochlorophyll Completes the Excitation Energy Funnel in the FMO Protein. J. Phys. Chem. Lett. 2011, 2, 93–98. 10.1021/jz101541b. [DOI] [PubMed] [Google Scholar]
  22. Jurinovich S.; Curutchet C.; Mennucci B. The Fenna-Matthews-Olson Protein Revisited: A Fully Polarizable (TD)DFT/MM Description. ChemPhysChem 2014, 15, 3194–3204. 10.1002/cphc.201402244. [DOI] [PubMed] [Google Scholar]
  23. Goez A.; Jacob C. R.; Neugebauer J. Modeling environment effects on pigment site energies: Frozen density embedding with fully quantum-chemical protein densities. Comp. Theor. Chem. 2014, 1040. [Google Scholar]
  24. Saito S.; Higashi M.; Fleming G. R. Site-Dependent Fluctuations Optimize Electronic Energy Transfer in the Fenna-Matthews-Olson Protein. J. Phys. Chem. B 2019, 123, 9762–9772. 10.1021/acs.jpcb.9b07456. [DOI] [PubMed] [Google Scholar]
  25. Kaliakin D. S.; Nakata H.; Kim Y.; Chen Q.; Fedorov D. G.; Slipchenko L. V. FMOxFMO: Elucidating Excitonic Interactions in the Fenna-Matthews-Olson Complex with the Fragment Molecular Orbital Method. J. Chem. Theory Comput. 2020, 16, 1175–1187. 10.1021/acs.jctc.9b00621. [DOI] [PubMed] [Google Scholar]
  26. Kim Y.; Morozov D.; Stadnytski S.; Savikhin V.; Slipchenko L. V. Predictive First-Principles Modeling of a Photosynthetic Antenna Protein: The Fenna-Matthews-Olson Complex. J. Phys. Chem. Lett. 2020, 11, 1636–1643. 10.1021/acs.jpclett.9b03486. [DOI] [PubMed] [Google Scholar]
  27. Saer R. G.; Stadnytskyi V.; Magdaong N. C.; Goodson C.; Savikhin S.; Blankenship R. E. Probing the excitonic landscape of the Chlorobaculum tepidum Fenna-Matthews-Olson (FMO) complex: a mutagenesis approach. Biochim. Biophys. Acta, Bioenerg. 2017, 1858, 288–296. 10.1016/j.bbabio.2017.01.011. [DOI] [PubMed] [Google Scholar]
  28. Olbrich C.; Strümpfer J.; Schulten K.; Kleinekathöfer U. Theory and simulation of the environmental effects on FMO electronic transitions. J. Phys. Chem. Lett. 2011, 2, 1771–1776. 10.1021/jz2007676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Rivera E.; Montemayor D.; Masia M.; Coker D. F. Influence of site-dependent pigment–protein interactions on excitation energy transfer in photosynthetic light harvesting. J. Phys. Chem. B 2013, 117, 5510–5521. 10.1021/jp4011586. [DOI] [PubMed] [Google Scholar]
  30. Chandrasekaran S.; Aghtar M.; Valleau S.; Aspuru-Guzik A.; Kleinekathofer U. Influence of Force Fields and Quantum Chemistry Approach on Spectral Densities of BChl a in Solution and in FMO Proteins. J. Phys. Chem. B 2015, 119, 9995–10004. 10.1021/acs.jpcb.5b03654. [DOI] [PubMed] [Google Scholar]
  31. Lee M. K.; Coker D. F. Modeling Electronic-Nuclear Interactions for Excitation Energy Transfer Processes in Light-Harvesting Complexes. J. Phys. Chem. Lett. 2016, 7, 3171–3178. 10.1021/acs.jpclett.6b01440. [DOI] [PubMed] [Google Scholar]
  32. Kim C. W.; Rhee Y. M. Constructing an Interpolated Potential Energy Surface of a Large Molecule: A Case Study with Bacteriochlorophyll a Model in the Fenna-Matthews-Olson Complex. J. Chem. Theory Comput. 2016, 12, 5235–5246. 10.1021/acs.jctc.6b00647. [DOI] [PubMed] [Google Scholar]
  33. Kim C. W.; Choi B.; Rhee Y. M. Excited state energy fluctuations in the Fenna-Matthews-Olson complex from molecular dynamics simulations with interpolated chromophore potentials. Phys. Chem. Chem. Phys. 2018, 20, 3310–3319. 10.1039/C7CP06303B. [DOI] [PubMed] [Google Scholar]
  34. Jing Y.; Zheng R.; Li H.-X.; Shi Q. Theoretical Study of the Electronic-Vibrational Coupling in the Qy States of the Photosynthetic Reaction Center in Purple Bacteria. J. Phys. Chem. B 2012, 116, 1164–1171. 10.1021/jp209575q. [DOI] [PubMed] [Google Scholar]
  35. Rosnik A. M.; Curutchet C. Theoretical Characterization of the Spectral Density of the Water- Soluble Chlorophyll-Binding Protein from Combined Quantum Mechanics/Molecular Mechanics Molecular Dynamics Simulations. J. Chem. Theory Comput. 2015, 11, 5826–5837. 10.1021/acs.jctc.5b00891. [DOI] [PubMed] [Google Scholar]
  36. Higashi M.; Saito S. Quantitative Evaluation of Site Energies and Their Fluctuations of Pigments in the Fenna-Matthews-Olson Complex with an Efficient Method for Generating a Potential Energy Surface. J. Chem. Theory Comput. 2016, 12, 4128–4137. 10.1021/acs.jctc.6b00516. [DOI] [PubMed] [Google Scholar]
  37. Blau S. M.; Benneth D. I. G.; Kreisbeck C.; Aspuru-Guzik A. Local protein solvation drives direct down-conversion in phycobiliprotein PC645 via incoherent vibronic transport. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, E3342–E3350. 10.1073/pnas.1800370115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Maity S.; Bold B. M.; Prajapati J. D.; Sokolov M.; Kubar T.; Elstner M.; Kleinekathöfer U. DFTB/MM Molecular Dynamics Simulations of the FMO Light- Harvesting Complex. J. Phys. Chem. Lett. 2020, 11, 8660–8667. 10.1021/acs.jpclett.0c02526. [DOI] [PubMed] [Google Scholar]
  39. Renger T.; Klinger A.; Steinecker F.; Schmidt am Busch M.; Numata J.; Müh F. Normal Mode Analysis of the Spectral Density of the Fenna-Matthews-Olson Light-Harvesting Protein: How the Protein Dissipates the Excess Energy of Excitons. J. Phys. Chem. B 2012, 116, 14565–14580. 10.1021/jp3094935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Cupellini L.; Caprasecca S.; Guido C. A.; Muh F.; Renger T.; Mennucci B. Coupling to Charge Transfer States is the Key to Modulate the Optical Bands for Efficient Light Harvesting in Purple Bacteria. J. Phys. Chem. Lett. 2018, 9, 6892–6899. 10.1021/acs.jpclett.8b03233. [DOI] [PubMed] [Google Scholar]
  41. Slama V.; Cupellini L.; Mennucci B. Exciton properties and optical spectra of light harvesting complex II from a fully atomistic description. Phys. Chem. Chem. Phys. 2020, 22, 16783–16795. 10.1039/D0CP02492A. [DOI] [PubMed] [Google Scholar]
  42. Wendling M.; Przyjalgowski M. A.; Gülen D.; Vulto S. I. E.; Aartsma T. J.; van Grondelle R.; van Amerongen H. The quantitative relationship between structure and polarized spectroscopy in the FMO complex of Prosthecochloris aestuarii: refining experiments and simulations. Photosynth. Res. 2002, 71, 99–123. 10.1023/A:1014947732165. [DOI] [PubMed] [Google Scholar]
  43. Wells S.; Menor S.; Hespenheide B.; Thorpe M. F. Constrained geometric simulation of diffusive motion in proteins. Phys. Biol. 2005, 2, S127–S136. 10.1088/1478-3975/2/4/S07. [DOI] [PubMed] [Google Scholar]
  44. Fokas A. S.; Cole D. J.; Chin A. W. Constrained geometric dynamics of the Fenna-Matthews-Olson complex: the role of correlated motion in reducing uncertainty in excitation energy transfer. Photosynth. Res. 2014, 122, 275–292. 10.1007/s11120-014-0027-3. [DOI] [PubMed] [Google Scholar]
  45. Fokas A. S.; Cole D. J.; Hine N. D. M.; Wells S. A.; Payne M. C.; Chin A. W. Evidence of Correlated Static Disorder in the Fenna-Matthews-Olson Complex. J. Phys. Chem. Lett. 2017, 8, 2350–2356. 10.1021/acs.jpclett.7b00669. [DOI] [PubMed] [Google Scholar]
  46. Madjet M. E.; Abdurahman A.; Renger T. Intermolecular Coulomb couplings from ab initio electrostatic potentials: application to optical transitions of strongly coupled pigments in photosynthetic antennae and reaction centers. J. Phys. Chem. B 2006, 110, 17268–17281. 10.1021/jp0615398. [DOI] [PubMed] [Google Scholar]
  47. Olbrich C.; Strümpfer J.; Schulten K.; Kleinekathöfer U. Quest for Spatially Correlated Fluctuations in the FMO Light-Harvesting Complex. J. Phys. Chem. B 2011, 115, 758–764. 10.1021/jp1099514. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Jacobs D. J.; Rader A. J.; Kuhn L. A.; Thorpe M. F. Protein Felexibility Predictions Using Graph Theory. Proteins: Struct., Funct., Genet. 2001, 44, 150–165. 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
  49. Fulle S.; Christ N. A.; Kestner E.; Gohlke H. HIV-1 TAR RNA Spontaneously Undergoes Relevant Apo-to-Holo Conformational Transitions in Molecular Dynamics and Constrained Geometrical Simulations. J. Chem. Inf. Model. 2010, 50, 1489–1501. 10.1021/ci100101w. [DOI] [PubMed] [Google Scholar]
  50. MacKerell A. D. Jr.; Bashford D.; Bellott M.; Dunbrack R. L. Jr.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  51. Eaton J. W.; Bateman D.; Hauberg S.; Wehbring R.. GNU Octave Version 5.1.0 Manual: A High-Level Interactive Language for Numerical Computations; 2019. [Google Scholar]
  52. Lindeberg J. W. Eine neue Herleitung des Exponentialgesetzes in der Wahrscheinlichkeitsrechnung (in German). Math. Z. 1922, 15, 211–225. 10.1007/BF01494395. [DOI] [Google Scholar]
  53. Cam L. L. The Central Limit Theorem around 1935. Statistical Science 1986, 1, 78–91. 10.1214/ss/1177013818. [DOI] [Google Scholar]
  54. Jankowiak R.; Hayes J. M.; Small G. J. Spectral Hole-Burning Spectroscopy in Amorphous Molecular Solids and Proteins. Chem. Rev. 1993, 93, 1471–1502. 10.1021/cr00020a005. [DOI] [Google Scholar]
  55. Purchase R.; Völker S. Spectral hole burning: examples from photosynthesis. Photosynth. Res. 2009, 101, 245–266. 10.1007/s11120-009-9484-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Jankowiak R.; Reppert M.; Zazubovich V.; Pieper J.; Reinot T. Site Selective and Single Complex Laser-Based Spectroscopies: A Window on Excited State Electronic Structure, Excitation Energy Transfer and Electron-Phonon Coupling of Selected Photosynthetic Complexes. Chem. Rev. 2011, 111, 4546–4598. 10.1021/cr100234j. [DOI] [PubMed] [Google Scholar]
  57. Reppert M. Modeling of Resonant Hole-Burning Spectra in Excitonically Coupled Systems: The Effects of Energy-Transfer Broadening. J. Phys. Chem. Lett. 2011, 2, 2716–2721. 10.1021/jz2012353. [DOI] [Google Scholar]
  58. Adolphs J.; Berrer M.; Renger T. Hole-Burning Spectroscopy on Excitonically Coupled Pigments in Proteins: Theory Meets Experiment. J. Am. Chem. Soc. 2016, 138, 2993–3001. 10.1021/jacs.5b08246. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Renger T.; Marcus R. A. On the relation of protein dynamics and exciton relaxation in pigment-protein complexes: an estimation of the spectral density and a theory for the calculation of optical spectra. J. Chem. Phys. 2002, 116, 9997–10019. 10.1063/1.1470200. [DOI] [Google Scholar]
  60. Renger T. Theory of excitation energy transfer: from structure to function. Photosynth. Res. 2009, 102, 471–485. 10.1007/s11120-009-9472-9. [DOI] [PubMed] [Google Scholar]
  61. Tiwari V.; Peters W. K.; Jonas D. M. Electronic resonance with anticorrelated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 1203–1208. 10.1073/pnas.1211157110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Duan H.-G.; Prokhorenko V. I.; Cogdell R. J.; Ashraf K.; Stevens A. L.; Thorwart M.; Miller R. J. D. Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 8493–8498. 10.1073/pnas.1702261114. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c03123_si_001.pdf (13.2MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES