Seed size, number and strategies in annual plants: a comparative functional analysis and synthesis

John G Hodgson; Gabriel Montserrat Marti; Bozena Šerá; Glynis Jones; Amy Bogaard; Mike Charles; Xavier Font; Mohammed Ater; Abdelkader Taleb; Bianca A Santini; Younes Hmimsa; Carol Palmer; Peter J Wilson; Stuart R Band; Amy Styring; Charlotte Diffey; Laura Green; Erika Nitsch; Elizabeth Stroud; Gemma Warham

doi:10.1093/aob/mcaa151

. 2020 Aug 19;126(7):1109–1128. doi: 10.1093/aob/mcaa151

Seed size, number and strategies in annual plants: a comparative functional analysis and synthesis

John G Hodgson ^1,^2,^✉, Gabriel Montserrat Marti ³, Bozena Šerá ⁴, Glynis Jones ², Amy Bogaard ⁵, Mike Charles ⁵, Xavier Font ⁶, Mohammed Ater ⁷, Abdelkader Taleb ⁸, Bianca A Santini ^9,¹⁰, Younes Hmimsa ⁷, Carol Palmer ², Peter J Wilson ¹, Stuart R Band ¹, Amy Styring ⁵, Charlotte Diffey ⁵, Laura Green ⁵, Erika Nitsch ⁵, Elizabeth Stroud ⁵, Gemma Warham ²

PMCID: PMC7751024 PMID: 32812638

Abstract

Background and Aims

Plants depend fundamentally on establishment from seed. However, protocols in trait-based ecology currently estimate seed size but not seed number. This can be rectified. For annuals, seed number should simply be a positive function of vegetative biomass and a negative function of seed size.

Methods

Using published values of comparative seed number as the ‘gold standard’ and a large functional database, comparative seed yield and number per plant and per m² were predicted by multiple regression. Subsequently, ecological variation in each was explored for English and Spanish habitats, newly calculated C-S-R strategies and changed abundance in the British flora.

Key Results

As predicted, comparative seed mass yield per plant was consistently a positive function of plant size and competitive ability, and largely independent of seed size. Regressions estimating comparative seed number included, additionally, seed size as a negative function. Relationships differed numerically between regions, habitats and C-S-R strategies. Moreover, some species differed in life history over their geographical range. Comparative seed yield per m² was positively correlated with FAO crop yield, and increasing British annuals produced numerous seeds. Nevertheless, predicted values must be viewed as comparative rather than absolute: they varied according to the ‘gold standard’ predictor used. Moreover, regressions estimating comparative seed yield per m² achieved low precision.

Conclusions

For the first time, estimates of comparative seed yield and number for >800 annuals and their predictor equations have been produced and the ecological importance of these regenerative traits has been illustrated. ‘Regenerative trait-based ecology’ remains in its infancy, with work needed on determinate vs. indeterminate flowering (‘bet-hedging’), C-S-R methodologies, phylogeny, comparative seed yield per m² and changing life history. Nevertheless, this has been a positive start and readers are invited to use estimates for >800 annuals, in the Supplementary data, to help advance ‘regenerative trait-based ecology’ to the next level.

Keywords: Allometry, bet-hedging, canopy structure, conservation status, C-S-R strategy, functional traits, inflorescence structure, life history, phylogeny, plant size, regenerative strategy, seed–phytomer–leaf (SPL) theory, trade-offs

INTRODUCTION

Although plants produce an abundance of seed, a plethora of risk factors impact upon subsequent seed dispersal and the development of new plants (Fenner and Thompson, 2005). In consequence, the exact ecological circumstances and location of establishment events are difficult to predict and, even as late as 1994, Chambers and MacMahon were complaining ‘we do not have a balance sheet, in space or time, that permits us to account the seeds that a plant produces’ (Chambers and MacMahon, 1994). Despite impressive subsequent progress (e.g. Aarssen and Jordan, 2001; Forget et al., 2005; Westerman et al., 2008; Dalling et al., 2011; Germain et al., 2013; Crawley, 2014; Lustenhouwer et al., 2017), the subject has been constrained by a shortage of data, the difficulty in generating general ecological rules and an insufficient integration between the subject area and other established disciplines within plant ecology (Larios et al., 2017; Moles, 2018).

The world’s flora is characterized by mass extinction and colonization events, with the trajectory of change strongly influenced by the ability or failure of species to regenerate from seed (Walck et al., 2011; Pimm et al., 2014). Relevantly, Barton and Hanley (2013) and Parmesan and Hanley (2015) strongly argue that it is the primary ‘life and death’ factors relating to establishment from seed that fundamentally determine presence or absence. Nevertheless, the scientific literature focuses primarily upon the secondary selective forces operating, post-establishment, on vegetative plant performance. Regeneration remains largely neglected within trait-based ecology (Larson and Funk, 2016) and is poorly understood in weed science (Norris, 2007). The tools at our disposal to model ecological scenarios relating to climate change and the global destruction of habitats are fundamentally flawed. Accordingly, here, we will attempt to partially redress this imbalance between features of regeneration and those of the established vegetative plant.

Many complex ecological relationships can be understood using trait-based ecology (Kattge et al., 2011), and we predict that the relationships between seed risk factors and plant establishment can be similarly integrated into a generalized theory using readily measured plant functional traits. Nevertheless, at this early stage in synthesis, we will confine our efforts to one of the fundamentals: primary seed production. We will attempt to quantify the number and size of seeds produced by plants and to place findings in an ecological context. Moreover, for simplicity, we will restrict our attention to annuals. Perennials with vegetative organs of reproduction and/or perennation that might act as an additional sink for resources will be excluded.

Encouragingly, there are ecological foundations already established upon which to commence this building process.

Relationship 1: seed size vs. seed number

This is described first not because it is necessarily the most important but because it has been the most widely studied. For a given allocation of resources, a species may produce either many small seeds or fewer larger ones (Shipley and Dion, 1992; Aarssen and Jordan, 2001; Moles, 2018). The optimal strategy for the ‘colonization–competition’ trade-off between few large seeds with potentially higher seedling survivorship and many small widely dispersed seeds depends upon ecological circumstance (Grime, 2001; Westoby et al., 2002; Moles and Westoby, 2006). Unfortunately, plants are phenotypically plastic and their size and age structure may vary between populations. As a result, the relationship between seed size and number continues to be difficult to quantify in all but the most general terms.

Relationship 2: resource allocation to seed – the key trait?

Seed production may be viewed simultaneously as the product of the vegetative and the regenerative strategies of the plant. First, resource allocation to seed is a key regenerative process, with seed allocation essentially defined as seed mass × seed number (Smith and Fretwell, 1974; Paul-Victor and Turnbull, 2009). It identifies the total resources available to the ‘colonization–competition’ trade-off between few large seeds with potentially higher seedling survivorship and many small widely dispersed seeds (Westoby et al., 2002; Moles and Westoby, 2006). Secondly, seed production is fuelled by the vegetative plant, and, particularly for annuals, where resources are not diverted into long-lived vegetative structures, seed yield is likely to be quantitatively defined by size-related vegetative traits. Consistent with this, fecundity has been found to be positively correlated with vegetative biomass in monocarpic species both between and within species (Sugiyama and Bazzaz, 1998; Aarssen and Jordan, 2001; Chambers and Aarssen, 2009; Lutman et al., 2011).

A general model incorporating relationships 1 and 2

Relationships between seed number and plant size have already been experimentally defined by Shipley and Dion (1992), for the rametes of 57 species, ranging from annuals to polycarpic herbaceous perennials [eqn (1a)] and by Aarssen and Jordan (2001), for the whole vegetative shoots of 15 monocarpic species [eqn (1b)]

\begin{array}{l} \begin{array}{l} P r e d i c t e d s e e d s p e r p l a n t = & 1 . 4 (v e g e t a t i v e m a s s r a m e t)^{0. 93} \\ \times {(i n d i v i d u a l s e e d m a s s)}^{0. 78} \end{array} \end{array}

(1a)

\begin{array}{l} \begin{array}{l} P r e d i c t e d s e e d s p e r p l a n t = & 2 . 8 (v e g e t a t i v e m a s s s h o o t)^{0. 91} \\ \times {(i n d i v i d u a l s e e d m a s s)}^{0. 83} \end{array} \end{array}

(1b)

These equations for species, with, additionally, the identification of similar relationships within species (Mohler and Callaway, 1995; Gallart et al., 2010), provide a conceptual as well as, potentially, an arithmetic basis for routinely quantifying seed yield per plant in terms of relationship 1, the negative correlation between seed size vs. seed number, and relationship 2, the positive correlation between vegetative and seed biomass.

Relationship 3: an ecological perspective – seed yield and C-S-R strategy theory

Since it is primarily a function of vegetative mass [relationship 2, eqns (1a and 1b)], seed yield in annual plants is, by definition, regulated by the same fundamental rules that determine the success or failure of vegetative growth. Thus, arguably, it is in part defined by C-S-R strategy theory (Grime 1974, 2001), perhaps the most all-embracing set of ecological rules relating vegetative plant performance to environmental factors (Pierce et al., 2017). In C-S-R strategy theory, it is argued that two groups of external environmental factors vitally affect plant performance. The first, stress, includes factors that place prior restrictions on plant production. The most important of these are mineral nutrients, equivalent to the worldwide leaf economics spectrum of Wright et al. (2004). The converse, eutrophication, releases plants from nutrient stress. Other stresses include sub-optimal temperatures and shortages of light and water. The second group of environmental factors, disturbance, results in the destruction of already produced plant biomass. The group includes impacts of land use such as grazing, trampling, mowing and ploughing, and extreme climatic events including drought, fire, frost, soil erosion and wind damage. In the third extreme scenario, where stress and disturbance are both low, the distribution of species is determined by competition. Importantly, the abandonment or relaxation of land use intensity, dereliction, is associated with increased competition following a release from disturbance under conditions of low stress. C-S-R strategy theory has been routinely measured using functional traits (Hodgson et al., 1999; Pierce et al., 2013, 2017; Novakovskiy et al., 2016). Its inclusion here relates to (1) a methodological relevance, quantifying seed production, and (2) a practical relevance, linking ‘regenerative functional ecology’ to theoretically key ecosystem processes and to important impacts of changing land use and climate on vegetation composition.

From precision to generality – methodological constraints

As part of an ongoing debate, Shipley et al. (2016) and Brodribb (2017) have questioned various theoretical fundamentals of trait-based plant ecology. In particular, in a provocative opinion piece entitled ‘Progressing from “functional” to “mechanistic” traits’, Brodribb (2017) argues ‘by “mechanistic traits”, I mean traits whose function can be clearly physiologically defined, as opposed to the more abstract “functional” traits, such as leaf mass per area (LMA), that have been used to great effect in explaining plant economics over the last 15 years (Wright et al., 2004)’. While we share Brodribb’s misgivings about the use of LMA as a ‘flagship’ trait (Hodgson et al., 2011), we dispute the implication that ‘functional’ traits are of lesser value. Importantly, ‘mechanistic’ studies generate precision, leading to an exact definition of key mechanisms. However, most involve time-consuming experimental/physiological measurements. As a result, global datasets of ‘mechanistic’ traits remain small, and difficult to integrate with other ‘mechanistic’ fields of study. They do not describe ‘the big picture’. They neither demonstrate the universality of mechanisms within whole floras nor directly identify how mechanisms complement, and integrate with, other specializations.

This is where trait-based ecology offers synergy. True, as Brodribb points out, ‘functional’ traits are imprecise, both in measurement and in potential interpretation. Equally, with the current lack of easily measured biochemical traits, the whole subject area is strongly and unhealthily skewed towards morphology. Nevertheless, imprecise but easily measured ‘functional’ traits can be validated against a ‘gold standard’ derived from ‘mechanistic’ or related studies, and large datasets can be generated with each species characterized with respect to many contrasted ecological dimensions. Subsequently, functional links between traits can be identified and floras functionally characterized. Trait-based ecology can add generality, and often greater utility, to studies of ecological mechanisms. We believe that a balance between the two complementary methodologies can provide a powerful, and optimal, mix of precision and generality.

Unfortunately, in practice, ‘mechanistic’ and ‘functional’ studies are not always easy to integrate and, regrettably, neither Shipley and Dion (1992) nor Aarssen and Jordan (2001), the sources of eqns (1a) and (1b), respectively, can be used as ‘gold standards’ in our functional studies. Each falls broadly into the mechanistic category of Brodribb (2017) with time-consuming measurements and relatively small datasets (only 15 species in each are usable by us). However, in this instance, progress is equally hampered by ‘functional’ problems. The only relevant ‘functional’ traits in regular use identify plant height, leaf size and leaf construction costs. They provide an incomplete basis for estimating vegetative biomass.

Objectives

Despite the problems outlined above, our primary objective remains to generate ‘best estimates’ of seed yield for annual plant species and to present these values in an ecological context. Also, we are not totally data deficient. Medium-sized datasets for seed number per plant do exist for both the UK (Salisbury, 1942) and the USA (Stevens, 1932, 1957), albeit without additional measurements of biomass. Furthermore, seed number per m² values are available for Bohemia (Šerá and Šerý, 2004). Assuming that standardized protocols were in place (i.e. seed number was measured using ‘representatively sized’ individuals for each species), such values may be provisionally treated as best estimates, or a ‘comparative gold standard’ definition of regenerative potential. Equally, while it is not customary to directly measure biomass in trait-based ecology, the various components of biomass and performance routinely assessed may be augmented by other size-related traits. From these combined sources, eqns (1a) and (1b) may be recast as:

\begin{array}{l} \begin{array}{l} P r e d i c t e d s e e d s p e r p l a n t ≅ & f_{1} (p l a n t s i z e) \times f_{2} (l e a f s i z e) \\ \times f_{3} (l e a f c o n s t r u c t i o n c o s t s) \\ / f_{4} (m a s s o f a n i n d i v i d u a l s e e d) \end{array} \end{array}

(1c)

which may be in turn recast as

\begin{array}{l} \begin{array}{l} P r e d i c t e d s e e d m a s s p e r p l a n t = & p r e d i c t e d s e e d s p e r p l a n t \\ \times m a s s o f a n i n d i v i d u a l s e e d \\ ≅ f_{1} (p l a n t s i z e) \times f_{2} (l e a f s i z e) \\ \times f_{3} (l e a f c o n s t r u c t i o n c o s t s) / f_{4} \end{array} \end{array}

(1d)

where the functional terms, f₁, f₂ and f₃, relate to different components of vegetative biomass production and with f₁–f₄ all awaiting an exact arithmetic definition.

Accordingly, first, using an unpublished database with functional traits for >800 annual species from Europe, North Africa and the Middle East and published datasets for seed yield, we will attempt to validate and arithmetically define eqns (1c) and (1d). We will generate multiple regression equations that predict both ‘reproductive allocation’ (seed mass × seed number) and seed number (‘fecundity’). Secondly, we will explore how the resultant predictions of ‘reproductive allocation’ and the relationship between seed size and predicted seed number pattern in the field by reference to extensive vegetation surveys from Spain and the UK. Here, we consider it essential to analyse seed yield and number in relation to ruderality and C-S-R strategy theory (Grime, 2001). Unfortunately, as noted in Hodgson et al. (2017), the calculation of the R (ruderal) axis is in need of a radical revision and this field analysis will utilize a new revised C-S-R classification designed specifically for annuals. Thirdly, we will consider commonness and rarity, and show that seed number effects a better separation of increasing and decreased species in the UK flora than seed size. Fourthly, the problems and prospects of using a functional approach to ‘reproductive functional ecology’ will be discussed. Finally, our predictions of seed size and number for in excess of 800 annuals will be appended online to encourage further studies.

A methodological caveat

Some key plant attributes are difficult to measure in an ecologically relevant way. Vegetative biomass and seed yield achieved in the field are both very variable (Venable and Brown, 1988; Clauss and Aarssen 1994; Aarssen and Jordan, 2001; Lutman et al., 2011; Shriver, 2016). For example, Amaranthus retroflexus routinely produces 200–500 seeds per (small) plant in one habitat but approx. 100 000 seeds per (much larger) plant in another (Mohler and Callaway, 1995). Annual species are able to set seed even when small and stunted (Grime, 2001; Chambers and Aarssen, 2009; Tracey et al., 2016) with, importantly, increased competitive success (i.e. increased vegetative biomass production) likely to provide a ‘reproductive economy advantage’ even for small plants (Aarssen et al., 2006; Aarssen, 2008, 2015).

This innate plasticity, itself an important ecological attribute, makes the quantification and interpretation of growth-related processes difficult. Nevertheless, growth remains too important to ignore. One experimental option has been to standardize conditions and to make precise measurements of vegetative growth (Grime and Hunt, 1975). However, this approach is extremely time-consuming, and the difficulties in exactly replicating growth conditions at other research establishments has further restricted the pool of species for which we have comparative values. In consequence, ecologists have been more reliant upon less precise but easily measured surrogate traits generated within trait-based plant ecology (Pérez-Harguindeguy et al., 2012). Using the theory and methodologies associated with the worldwide leaf economics spectrum (Wright et al., 2004), potential growth rate has been routinely assessed indirectly, in comparative rather than in absolute quantitative terms, from specific leaf area (SLA) and leaf dry matter content (LDMC), and these comparative values have been subsequently used in ecological interpretation. Of necessity, our assessment of the equally variable, growth-related process, seed yield, will be similarly indirect and comparative. We hope that it will prove equally successful and that ‘comparative regeneration’ will stand with comparative estimates of the worldwide leaf economics spectrum of Wright et al. (2004) at the productive heart of trait-based plant ecology.

MATERIALS AND METHODS

Field data and study sites

As described in Hodgson et al. (2017), a field context was provided by vegetation surveys of Central England (Grime et al., 2007) and relevés from Tortosa, Catalonia, North-east Spain (Royo Pla, 2006) and Zaragoza, Aragon, North central Spain (Braun Blanquet and de Bolós, 1953). Spanish data were abstracted from the SIVIM database (Font et al., 2012). Intensity of land use was generally low in Zaragoza (the survey pre-dates arable intensification) but in Tortosa and England it was high except in areas difficult to cultivate. England → Tortosa → Zaragoza constituted a gradient from a cool wet (‘Atlantic’) to a ‘Mediterranean’ semi-arid climate (Hodgson et al., 2017) with, in Zaragoza, the irregular incidence of autumn–spring rainfall and with the frequent regenerative failure of annuals. Indeed, climatic conditions and floristic composition are so variable in the Zaragoza region that a full complement of annual species is only present in many plant communities approximately every 6 years (G. Montserrat Marti, field observations).

Using the habitat classification of Grime et al. (2007) for English data and of Rivas-Martínez et al. (2002) for Spanish data, the above vegetation surveys were used to assess the primary habitat with which each study species was associated in each region. In addition, monocarpic species, and ephemeroids with a vernal phenology, are good indicators of high levels of temporal and/or spatial disturbance. Accordingly, as in Hodgson et al. (1999), mean ‘Annual Index’ value (AnnIndex, (cover_annuals + cover_ephemeroids)/cover_{all_species}) was also calculated for each species from vegetation survey data. As described in the ‘Phylogeny’ section below, mean leaf dry matter content values were also calculated for each vegetation sample.

The Online Atlas of the British and Irish flora (Botanical Society of Britain and Ireland and the Biological Records Centre, 2018) separated species that had increased from those that had decreased in the UK. From these data, Status index (number of species_increasing – number of species_decreasing)/(number of species_increasing + number of species_decreasing) was calculated for vegetation samples. A value of +1 identified vegetation where all species had increased and one of –1 vegetation where all had decreased.

Nomenclature follows The Plant List (2013).

The trait dataset

Trait data were derived from a large functional dataset currently being prepared for publication. Most came from ‘in-house’ measurements but many other data sources were consulted including the FIFTH database (Cerabolini et al., 2010), Flora Iberica (Aedo et al., 1980 onwards), Flora Europaea (Tutin et al., 1964–1980), Hungarian seed bank data (Csontos et al., 2003, 2007; Török et al., 2013), LEDA Traitbase (Kleyer et al., 2008) and SID (Royal Botanic Gardens Kew, 2015). Hemiparasites, which derive nutritional benefit for seed production from their host, and succulents, for which LDMC does not adequately define growth and soil fertility (Vendramini et al., 2002) were excluded from the analyses. Although the study focuses upon annuals, the functional traits of perennial species with which these annuals were growing were also briefly investigated.

The key traits

The traits used to test eqns (1c) and (1d), and their abbreviations, are listed in Table 1. Leaf nitrogen (LeafN, mg g^–1) and leaf silica [LeafSi (percentage dry mass)] were also considered, with in-house measurements augmented mainly by Han et al. (2005), Hodson et al. (2005) and Stock et al. (2012). Additionally, in relation to flowering phenology, month of commencement (FlStart, negatively correlated with the R axis in C-S-R strategy theory; Hodgson et al., 1999) and duration (FlDuration, positively correlated) were abstracted from Clapham et al. (1987). These data relate to the UK, with the scaling-up of flowering phenology to include all study areas not yet feasible.

Table 1.

The functional traits potentially contributing to the expression of comparative number of seeds per plant in eqns (1c) and (1d)

Trait	Abbreviation	Units	Comments
(1) Plant size, potentially contributing positively to the f₁ term
Canopy height⁺	HtCan	log₂ mm	1 ≤ 20 mm; 2 = 21–40 mm …… 10 ≥ 5 m.
Canopy diameter⁺	DiamCan	log₂ mm	1 ≤ 20 mm; 2 = 21–40 mm …… 10 ≥ 5 m.
Canopy size⁺	SizeCan	log₂ mm³	Height × radius² {= HtCan + [2 × (DiamCan – 1)]}
Canopy shape⁺	ShapeCan		Height/diameter [= HtCan – DiamCan]
Plant height⁺	HtPl	log₂ mm	1 ≤ 20 mm; 2 = 21 – 40 mm …… 10 ≥ 5 m.
Plant diameter⁺	DiamPl	log₂ mm	1 ≤ 20 mm; 2 = 21 – 40 mm …… 10 ≥ 5 m.
Plant size⁺	SizePl	log₂ mm³	Height × radius² {= HtPl + [2 × (DiamPl – 1)]}
Plant shape⁺	ShapePl		Height/diameter [= HtPl – DiamPl]
(2) Leaf size, potentially contributing positively to the f₂ term
Leaf area⁺	LA_morph	mm² (log₁₀)	The conventional ‘morphological’ unit
Leaf area per node⁺	LA_devel	mm² (log₁₀)	LA_morph × number of leaves per node; quantifies incremental growth more exactly than LA_morph
Leaf width⁺	LA_funct	log₂ mm	0 ≤ 0.5 mm; 1 = 0.51–1.0 mm, …… 9 ≥ 128; A ‘competitive’ attribute that patterns with thickness of the boundary layer and efficiency of vascular transport within the lamina
Leaf mass⁺	LM_morph	mg (log₁₀)	Converted from LA_morph using mean SLA values
Leaf mass per node⁺	LM_devel	mg (log₁₀)	Converted from LA_devel using mean SLA values
(3) Leaf construction costs, potentially contributing negatively to the f₃ term
Leaf dry matter content^–	LDMC	% (square root)	100 × dry mass of leaf/saturated mass of leaf; correlates positively with soil fertility and growth rate
Leaf thickness^?	Lthick	mm² (log₁₀)	Negatively correlated with irradiance and positively with succulence
Specific leaf area⁺	SLA	mm² per mg (log₁₀)	Positively correlated with fertility and negatively with irradiance
(4) Mass of an individual seed contributing negatively as the f₄ term
Seed mass of germinule^–	SeedM	mg (log₁₀)	Seed after investing structures that aid dispersal removed

Open in a new tab

Reasons for their use are more fully described in Hodgson et al. (2017), and transformations of continuous trait variables prior to statistical analysis are identified in parentheses within ‘Units’.

The suffices ⁺, ^– and ^? identify traits predicted to be expressed, respectively, positively, negatively and uncertainly in eqns (1c) and (1d).

Sources of comparative seed yield data

The Canadian datasets of Shipley and Dion (1992) and Aarssen and Jordan (2001), from which eqns (1a) and (1b) were calculated, both contained too few usable species to be directly utilized in our analyses. Thus, linked seed number/vegetative biomass data were unavailable to this study. Instead, comparative values of seed number per plant (SeedNo_Pl) without vegetative biomass quantification were abstracted from Stevens (1932, 1957) for the USA and from Salisbury (1942) for the UK. Additionally, comparative data on maximum seed number per m² (SeedNo_m2; seed yield where vegetative cover of the subject species was 100 %) were derived from Šerá and Šerý (2004) for plants growing wild in Bohemia. Unfortunately, these three datasets are not expected to be exactly numerically equivalent: they originated from areas with contrasted climates and land use. Also FAO (2018) provided agricultural yield data for seed crops with ‘maximum crop yield’ (SeedM_ha) expressed as hg ha^–1, calculated arbitrarily as the 90th percentile of seed yield values since 2000 for all countries where the crop was grown.

In both Shipley and Dion (1992) and Aarssen and Jordan (2001), the statistically strongest relationship was between the vegetative and the seed mass of the plant (SeedM_Pl). Accordingly, prior to regression analysis, we converted our ‘gold standard’ values for comparative seed number (SeedNo_PlUSA and SeedNo_PlUK) to seed mass per plant (SeedM_PlUSA and SeedM_PlUK) by multiplying SeedNo_Pl by SeedM. Subsequently, to identify how this comparative estimate of seed yield was partitioned – a few large seeds or many small ones – predicted values of seed mass per plant were transformed back to seed number by dividing SeedM_Pl by SeedM.

C-S-R strategy

Initially, relationships were explored with principal component analysis (PCA) using, for simplicity, only four functional traits. Two, LA_funct, a key component of the dominance index, and LM_devel, which defines the size of each modular unit of growth (Hodgson et al., 2017), both contribute positively to competitive exclusion, and are negatively correlated with the ruderal (R) and stress (S) axes. Of the others, one, Size_Can, is an integral of qualitative and quantitative aspects of the growth period whilst the other, LDMC, is inversely related to growth rate and soil fertility and positively correlated with the S axis. Regrettably, since, as described above, the dataset for FlStart and FlDuration included only UK species, we were unable to include direct predictors for the R axis.

Subsequently, three ‘gold standard’ predictors were chosen to validate/interpret the PCA analysis. Competition may be defined as ‘the attempt by neighbours to capture the same unit of resource’ (Grime et al., 2007). Moreover, the sequestering of resources into seeds is crucial for the survival of annual species into another generation. Thus, on theoretical grounds, published values of SeedM_Pl, which defines the mass of seed produced by each plant, should objectively predict the C axis. Importantly, this first relationship has also been validated in practice (Pierce et al., 2014). For 371 annual and perennial species of the Italian flora, ‘total mass of seeds’ (i.e. SeedM_Pl) was significantly positively correlated both with the degree of C selection derived from the trade-off between vegetative traits, and with single size-related traits such as canopy height. Secondly, LeafN, a key element of the worldwide leaf economics spectrum (Wright et al., 2004), correlates inversely with the S axis (Pierce et al., 2014). Thirdly, as in Hodgson et al., 1999, AnnIndex was utilized as the ‘gold standard’ for the R dimension. Subsequently, the relationships between the three ‘gold standard’ predictors and PCA axes 1 and 2 were identified by multiple regression and ‘contour lines’ for each ‘gold standard’ predictor added to the PCA ordination diagram. The positions of C-S-R strategy types were then tentatively located by reference to these contours, and to ecological theory (Grime, 2001). Previous C-S-R classifications have additionally included a full range of perennial life histories. Therefore, to avoid confusion, our new designations are preceded by the prefix Ann_ with annual species with ‘competitive tendencies’ (CR in Grime’s classification) identified as Ann_C, those with ‘stress-tolerant tendencies’ (SR) as Ann_S and those with ‘ruderal tendencies’ (R) as Ann_R.

Phylogeny

SeedM is an ecologically important trait that is conservatively expressed within major taxa, both within our flora (Hodgson and Mackey, 1986) and elsewhere (Westoby et al., 1992; Moles et al., 2005). Its expression and that of other important functional traits within our dataset is potentially constrained by two contrasted evolutionary processes. First, and more anciently, some functions will be in part pre-defined by structures or processes that have originated from the integration of a whole suite of mechanistic features over evolutionary time. These functions, and attendant mechanistic features, have subsequently been retained simply because they are too developmentally complex to be readily modified (Stebbins, 1974; Hodgson and Mackey, 1986). Secondly, and more recently, adaptive radiation of taxa, often involving hybridization and polyploidy (Ehrendorfer, 1980; Stebbins, 1985), provides an evolutionary mechanism enabling floras to rapidly adapt to altered ecological conditions. During episodes of climate change and the development and intensification of agriculture that has characterized the shared recent evolutionary history of our studied floras from the Pleistocene onwards, adaptive radiation of this type will have impacted upon the composition of our studied flora (West, 1969; Valentine, 1970; Hodgson, 1987).

These two contrasted evolutionary mechanisms will pattern differently with respect to phylogeny. Developmental constraints associated with complex structures are likely to result in conservatism in trait expression at deep ancestral levels of phylogeny. Such conservatism should be similarly evident in floras with contrasted recent evolutionary histories. Superimposed upon this, recent adaptive radiation will cause functional characteristics to be conservatively expressed at the uppermost branches of the phylogenetic tree. This ‘conservatism’ is simply a consequence of a shared recent evolutionary origin, not of trait immutability. Such phylogenetically correlated similarities in trait expression are unlikely to be replicated in floras with contrasted recent evolutionary histories.

To explore these potential evolutionary dimensions, the expression of functional traits is compared between major families, tribes and sub-tribes. Additionally, for the C-S-R analysis, we provide an ecological–phylogenetic comparison for LDMC, a key element of the Ann_S axis. Mean LDMC of associated annual species, weighted by abundance, was calculated for different taxonomic sub-sets of annual species from both UK and Spanish field survey data.

Other analyses

Prior to statistical analysis, LDMC was square root transformed and the remaining continuous trait variables log₁₀ transformed. Two other transformations were applied less universally. First, to provide estimates relevant to ecosystem properties, trait data weighted by abundance (rooted frequency/domin scale) were used to generate ‘functional averages’ for vegetation samples. Secondly, since seed number is potentially a function of plant size and strategy, trends are difficult to interpret where a wide range of plant sizes and/or strategies are present. To partially offset this problem, species were assigned to Ann_C-S-R strategy groupings and, within each grouping, species were ranked so that the lowest rank had a value of –1 (extremely small numbers of seeds produced) and the highest a value of +1 (numerous seeds produced). Subsequently, values of this non-parametric ranked seed number (RSN) were combined to provide a more size-independent comparative estimate of seed number.

Except for measured seed mass against predicted comparative seed number, where the ordinary mean squares method was preferred, linear regressions all relate to the Type II of Warton et al. (2006). Other statistical tests were performed with SPSS for Windows™ (Version 16.0). Correlation, χ ², multiple regression, Mann–Whitney U-tests and one- and two-way analysis of variance (ANOVA) were used to explore relationships within the dataset.

RESULTS

Range of values for plant traits

The range of values for each measured trait within our core dataset of 886 annuals is presented in Supplementary data Table S1. There was a >8-, 250-, 1000- and 10 000-fold variation in untransformed variables relating to leaf structure, plant size, both leaf size and seed mass, and comparative number, respectively. However, in contrast to the wide ecological spectrum of species within our own dataset, the published datasets defining comparative seed yield and leaf nitrogen were from a much narrower sub-set of species and there were significant differences in trait ranges between each (Table 2).

Table 2.

Species in ‘golden standard’ datasets measuring seed production

	All annuals (n = 886)	One-way ANOVA (F value)	USA (n = 56)	UK (n = 51)	Bohemia (n = 123)	FAO crops (n = 20)	Leaf N (n = 58)
(A) Log₁₀SeedM (mg)	–0.04 ± 0.88	30.8***	0.00 ± 0.73^b	–0.73 ± 0.76^a	–0.15 ± 0.72^b	1.47 ± 0.77^c	0.12 ± 0.83^b
(B) Plant size and shape
Ht_Can (log₂ scale)	4.38 ± 1.44	12.1***	5.63 ± 1.04^b	4.33 ± 1.53^a	5.23 ± 1.34^b	6.75 ± 0.91^c	5.44 ± 1.53^b
Ht_Pl (log₂)	5.22 ± 1.54	10.1***	6.59 ± 1.09^b	5.37 ± 1.44^a	6.14 ± 1.34^b	7.40 ± 0.91^c	6.39 ± 1.40^b
Diam_Can (log₂)	4.90 ± 1.32	4.6***	5.59 ± 1.16^b	4.68 ± 1.43^a	5.47 ± 1.05^b	5.80 ± 1.06^b	5.75 ± 1.35^b
Diam_Pl (log₂)	5.30 ± 1.20	6.0***	6.16 ± 1.06^b	5.10 ± 1.33^a	5.93 ± 0.93^b	6.10 ± 0.79^b	6.18 ± 1.11^b
Size_Can (log₂)	12.20 ± 3.55	8.3***	14.52 ± 3.63^b	12.04 ± 3.62^a	14.21 ± 2.87^b	16.35 ± 2.76^c	15.00 ± 3.72^bc
Size_Pl (log₂)	13.84 ± 3.32	11.1***	15.45 ± 4.52^b	13.16 ± 3.69^a	16.03 ± 2.65^b	17.60 ± 2.30^c	16.80 ± 2.94^bc
Shape_Can (log₂)	–0.51 ± 1.39	4.9***	0.04 ± 1.13^a	–0.36 ± 1.22^a	–0.19 ± 1.19^a	0.95 ± 0.89^b	–0.25 ± 1.35^a
Shape_Pl (log₂)	–0.07 ± 1.54	3.1**	0.43 ± 1.20^a	0.26 ± 1.47^a	0.25 ± 1.20^a	1.30 ± 0.73^b	0.25 ± 1.50^a
(C) Leaf size
Log₁₀LA_morph (mm²)	2.66 ± 0.75	6.8***	3.22 ± 0.60^b	2.60 ± 0.91^a	2.94 ± 0.64^ab	3.61 ± 0.54^c	3.05 ± 0.68^ab
Log₁₀LA_devel (mm²)	2.74 ± 0.72	5.6***	3.27 ± 0.60^b	2.84 ± 0.89^a	3.02 ± 0.64^ab	3.62 ± 0.55^c	3.15 ± 0.65^ab
LA_funct (log₂)	3.93 ± 1.72	11.6***	6.55 ± 1.14^c	4.49 ± 1.69^a	4.94 ± 1.91^ab	5.60 ± 1.35^b	5.26 ± 1.86^ab
Log₁₀LM_morph (mg)	1.30 ± 0.75	7.7***	1.81 ± 0.64^b	1.30 ± 0.95^a	1.52 ± 0.66^ab	2.24 ± 0.57^c	1.67 ± 0.71^ab
Log₁₀LM_devel (mg)	1.37 ± 0.72	6.8***	1.86 ± 0.64^b	1.41 ± 0.91^a	1.59 ± 0.64^ab	2.25 ± 0.59^c	1.75 ± 0.67^ab
(D) Leaf structure
√LDMC (%)	4.15 ± 0.65	4.7**	4.07 ± 0.49^a	3.88 ± 0.53^a	4.06 ± 0.49^a	4.42 ± 0.58^b	4.14 ± 0.53^a
Log₁₀SLA (mm² per mg)	1.39 ± 0.15	4.4**	1.40 ± 0.11^ab	1.43 ± 0.13^b	1.44 ± 0.10^b	1.37 ± 0.10^a	1.40 ± 0.12^ab
Log₁₀LThick (mm)	-0.68 ± 0.22	2.4^†	–0.64 ± 0.18^a	–0.63 ± 0.18^a	–0.72 ± 0.17^a	–0.72 ± 0.17^a	–0.70 ± 0.21^a
(E) Phenology
Month of first flowering	5.8 ± 1.1	2.9*	6.2 ± 1.3^a	5.5 ± 1.1^b	5.8 ± 1.2^ab		6.1 ± 1.3^a
Summer annual (%)	21		45^a	27^b	31^b		43^a

Open in a new tab

Stevens, 1932, 1957 (USA); Salisbury, 1942 (UK); Šerá and Šerý, 2004 (Bohemia), FAO, 2018 (crops); and leaf nitrogen (composite database) show significant differences in trait expression

Values are the average ± s.d. For comparison, values for all species in the database were included in italics. For summer annuals, statistical comparisons involved χ ² using 2 × 2 contingency tables.

Here, and in the remaining tables and figures, ***, **, * and ^† indicate P < 0.001, <0.01, <0.05, and <0.10, and groupings with the same superscript are not statistically significantly different at P < 0.05.

Predicting comparative seed yield per plant: a test of eqns (1c) and (1d)

Both SeedM_Pl and SeedNo_Pl were identified as a positive product of plant size, leaf/phytomer size and SeedM for both USA and UK datasets (Table 3A). Thus, appart from the exclusion of traits relating to leaf construction cost, f₃, the results conform to the expectations of eqns (1a–d). Furthermore, consistent with the results of Shipley and Dion (1992) and Aarssen and Jordan (2001), SeedM, a key determinant of SeedNo_Pl, had relatively little impact on the expression of SeedM_Pl. Its exclusion from the regression gave a reduction of only 0.04 and 0.02, respectively, in the value of r² (Table 3Ai). However, as expected (see ‘A methodological caveat’, above), the two regional estimates lacked an exact numerical correspondence [eqn (2)]. Predicted values derived using the USA regression (Table 3Aia) were considerably higher than those for the UK (Table 3Aib).

Table 3.

Functional traits identifying (I) plant size (f₁), (II) leaf size (f₂) and (IV) seed mass traits (f₄), but not (III) leaf construction costs (f₃), contribute in multiple regressions to the expression of (i) comparative seed mass and (ii) comparative seed number per plant

				(I) Plant size (f₁)				(II) Leaf size (f₂)			(IV) Seed size (f₄)
Predicted trait	r ²	P	SeedM _Pl	SizeCan	ShapeCan	SizePl	ShapePl	LA_devel	LA_funct	LM_morph	SeedM	Constant
Ai SeedM_Pl
a USA (+ SeedM)	0.52	***		0.076¹				–1.147³		1.460²	0.229⁴	3.721
(– SeedM)	0.48	***		0.095¹				–1.044³		1.445²		3.143
b UK (+ SeedM)	0.77	***				0.145¹			0.118³		0.272²	0.145
(– SeedM)	0.75	***				0.176¹			0.141²			–0.522
ii SeedNo_Pl
a USA	0.55	***				0.088⁴		–1.124³		1.346²	–0.739¹	3.498
b UK	0.58	***				0.145¹			0.124³		–0.737²	0.147
Bi SeedM_m2
a USA	0.25	***	0.638 ¹	0.110³	0.248⁵	– 0.115²	– 0.326⁴					2.901
b UK	0.22	***	0.623 ¹	0.284³	0.160⁵	– 0.192²	– 0.360⁴					3.642
ii SeedNo_m2	0.13	***									– 0.352¹	4.959

Open in a new tab

(A) includes regressions predicting comparative yield per plant from Stevens (1932, 1957) for the USA (n = 56); and from Salisbury (1942) for the UK (n = 51).

In (B) comparative yield per m² relates to Bohemia (Šerá and Šerý, 2004; n = 123). Only traits accepted into regressions (4 3, 0 and 1, respectively, of types I, II, III and IV) are included here, with the numerical suffix after each coefficient identifying the order of acceptance into the regression. A full list of traits is included in Table 1

\begin{array}{l} l o g_{10} S e e d M_{P l U S A p r e d i c t e d} = 0. 936 l o g_{10} S e e d M_{P l U K p r e d i c t e d} + 0. 835 \end{array}

95% confidence intervals: slope 0.90–0.97, constant 0.74–0.93; r² = 0.72***, n = 868; mean values ± s.d.: SeedM_{PlUSApredicted} 3.43 ± 0.73, SeedM_{PlUKpredicted} 2.78 ± 0.71; paired t = 50.1***, r² = 0.72***, n = 868: similar results relating to SeedNo_Plpredicted not shown. (2)

Predicting comparative seed yield per m²

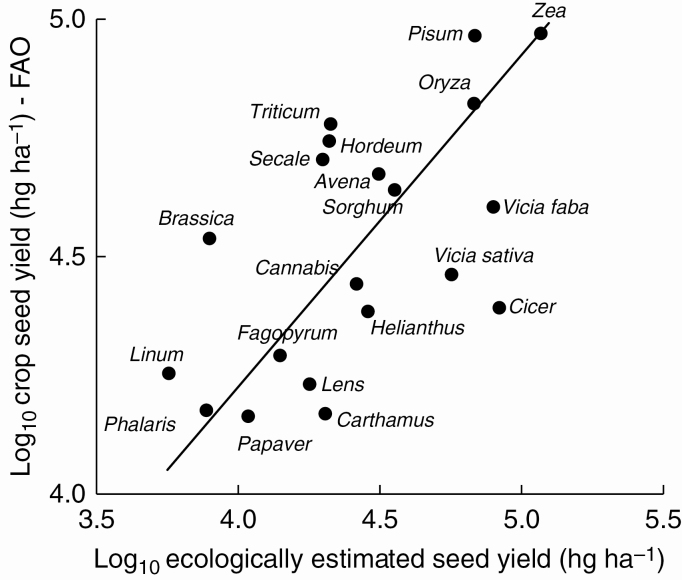
SeedM_m2 was a function of SeedM_Plpredicted, and traits defining canopy and plant size (Table 3Bi). However, values of r² (0.22–0.25) were low. Moreover, irrespective of the estimate of SeedM_Pl used, only SeedM contributed to the expression of SeedNo_m2 (Table 3Bii). Nevertheless, estimates of SeedM_m2, from Table 3Bi, predicted FAO-derived crop seed yield values (Fig. 1).

Fig. 1. — Comparative seed yield, estimated from Table 3Aiia, predicts FAO-derived crop seed yield values for annual crops. Values for the x-axis are converted to hg ha^–2. Log₁₀SeedM_ha = 0.699log₁₀ SeedM_m2USApred + 1.429 (95 % confidence intervals; slope: 0.48–1.02; constant: 0.22–2.64; r² = 0.38**, n = 20). [For UK data, Table 3Aiib: log₁₀SeedM_ha = 0.766log₁₀SeedM_m2UKpred + 1.211 (95 % confidence intervals; slope: 0.52–1.13; constant: –0.12– 2.54; r² = 0.35**, n = 20).] Abbreviations for crops: *Avena* spp. (mainly *Avena sativa*, oats), *Brassica napus* var. oleifera (rapeseed), *Cannabis sativa* (hempseed), *Carthamus tinctorius* (safflower seed), *Cicer arietinum* (chick peas, chickpea, Bengal gram, garbanzos), *Fagopyrum esculentum* (buckwheat), *Helianthus annuus* (sunflower seed), *Hordeum* spp. [two-row barley (*H. disticum*), six-row barley (*H. hexasticum*), four-row barley (*H. vulgare*); barley], *Lens esculenta* (*Ervum lens*, lentils), *Linum usitatissimum* (linseed), *Oryza* spp. (mainly *O. sativa*, paddy rice), *Papaver somniferum* (poppy seed), *Phalaris canariensis* (canary seed), *Pisum sativum* [garden pea plus field pea (*P. arvense*); dry peas], *Secale cereale* (rye), *Sorghum* spp. [*Sorghum*, guinea corn (*S. guineense*), common, milo, feterita, kaffir corn (*S. vulgare*); durra, jowar, kaoliang (*S. dura*)], *Triticum* spp. [common (*T. aestivum*) durum (*T. durum*) spelt (*T. spelta*) wheat], *Vicia faba* (broad beans, horse beans, dry), *Vicia sativa* (vetches, spring/common vetch), *Zea mays* (maize, corn, Indian corn, mealies).

Ann_C-S-R, providing an ecological context

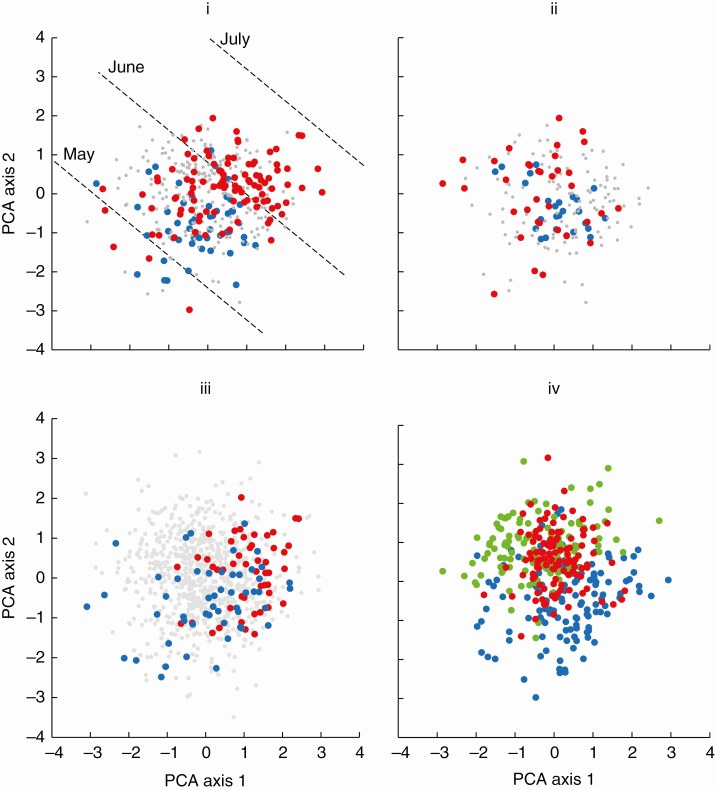
The PCA axis 1 of the ordination explained 54 % of the variance and identified size, and the Ann_C axis (Fig. 2). PCA axis 2 (24 %) scaled positively with LDMC and Size_Can (i.e. negatively with ruderality). The multiple regression equations defining these axes were as follows:

\begin{array}{l} \begin{array}{l} P C A 1 = & 0. 570 l o g_{10} L M_{d e v e l} - 0. 288 \sqrt L D M C \\ + 0. 10 4 S i z e_{C a n} - 0. 218 L A_{f u n c t} - 1.844 \end{array} \end{array}

(3)

\begin{array}{l} \begin{array}{l} P C A 2 = & 0. 199 l o g_{10} L M_{d e v e l} + 1.482 \sqrt L D M C \\ + 0. 118 S i z e_{C a n} 0.0 42 L A_{f u n c t} 7.807 \end{array} \end{array}

(4)

In addition, ‘gold standard’ variables patterned variously with the PCA axes [eqns (5)–(7)].

\begin{array}{l} l o g_{10} S e e d M_{P l U S A} = & 0. 538 P C A 1 + 0. 176 P C A 2 + 3 . 195 \\ (r^{2} = 0. 38 * * *, n = 55) \end{array}

(5a)

\begin{array}{l} l o g_{10} S e e d M_{P l U K} = & 0. 60 6 P C A 1 + 0. 189 P C A 2 + 2.567 \\ (r^{2} = 0. 73 * * *, n = 51) \end{array}

(5b)

\begin{array}{l} l o g_{10} L e a f N = & 0.0 64 P C A 1 - 0.0 65 P C A 2 + 1.380 \\ (r^{2} = 0. 14 *, n = 55) \end{array}

(6)

\begin{array}{l} A n n I n d e x_{U K} = & - 0.0 44 P C A 2 + 0. 522 \\ (r^{2} = 0.0 6 * *, n = 178) \end{array}

(7a)

\begin{array}{l} A n n I n d e x_{S I M I V} = & - 0.0 14 P C A 2 + 0. 670 \\ (r^{2} = 0.0 1 *, n = 734) \end{array}

(7b)

(AnnIndexUK vs AnnIndexsimiv t = 7.7***; r2 = 0.65***; mean difference 0.09 ± 0.16, n = 171)

SeedM_PlUSA and, even more strongly, SeedM_PlUK define the putative Ann_C axis with a relatively high r² [eqn (5)]. However, values of r² were much lower for the ‘gold standard’ variables expected to define the Ann_S and Ann_R axes [eqns (6) and (7)]. Furthermore, in our ‘annuals-only’ analysis, FlStart and FlDuration, the ‘key ruderal traits’ in Hodgson et al. (1999), failed to pattern strongly with the Ann_R axis. FlDuration was more centrally positioned within the Ann_CSR region and FlStart was, broadly, positively correlated with the Ann_C axis (Fig. 3 i, ii). Instead, the key diagnostic specialization identifying Ann_R strategists appeared to be miniaturization. Ann_R strategists were small, with both precocious flowering and precocious seed set (e.g. Bellis annua and Limosella aquatica). Moreover, many species previously identified as R strategists in Hodgson et al. (1999) and Grime et al. (2007) were classified here as of intermediate strategy (e.g. Poa annua, Ann_CSR, $≅$ R-CSR in Grime’s classification; Senecio vulgaris, Ann_CR, $≅$ R-CR). Less controversially, typical Ann_C strategists ( $≅$ CR) included robust weeds (e.g. Xanthium strumarium) and crops (e.g. Zea mays) and Ann_S strategists ( $≅$ SR) consisted of a small group of slower-growing, later-maturing annuals (e.g. Crucianella patula and Minuartia campestris); Fig. 2. In the absence of a reliable ‘gold standard’ measurement to define the Ann_R axis, our allocation to Ann_C-S-R strategies in Fig. 2 remains provisional.

Fig. 3. — Comparing traits and datasets. (i) Flowering start time (from Clapham *et al.*, 1987): April or earlier (blue dots), May to June (grey dots), July onwards (red dots). FlStart = 0.256PCA1 + 0.311PCA2 + 5.750 (r² = 0.13***, n = 412). (ii) Flowering period in the UK: 1–2 months (red dots), 3–5 months (grey dots), >5 months (blue dots). Log₁₀FlDuration = 0.027PCA1 – 0.025PCA2 + 0.489 (r² = 0.03***, n = 372). (iii) ‘Gold standard’ datasets for SeedNo_Pl PCA axis 1 (mean values ± s.d.): UK (blue dots) 0.13 ± 1.12; USA (red dots) 1.05 ± 0.71; t = 5.0***; PCA axis 2: UK –0.55 ± 0.91, USA 0.10 ± 0.87; t = 3.7***. (iv) Major families PCA axis 1: Asteraceae (blue dots) 0.30 ± 1.02^b, n = 134; Fabaceae (red dots) 0.05 ± 0.94^b, n = 119; Poaceae (green dots) –0.37 ± 0.95^a, n = 125; ANOVA F_{2, 377} = 18.5***. PCA axis 2: Asteraceae 0.48 ± 0.94^a; Fabaceae 0.57 ± 0.74^b; Poaceae 0.90 ± 0.71^c; ANOVA F_{2, 377} = 103.6***.

The PCA ordination further illustrated a lack of ecological equivalence between the two ‘gold standard’ datasets defining SeedM_Pl. Consistent with results in Table 2, the species in Salisbury’s UK dataset exhibited a wider spread of values for PCA axes 1 and 2 than those from the USA (Fig. 3 iii).

Reproductive strategy patterns with Ann_C-S-R

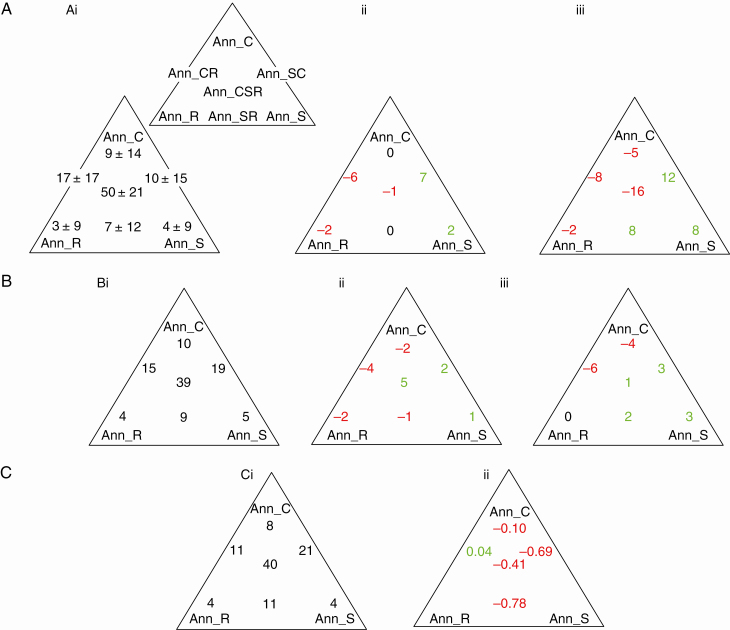
As with measured data (Fig. 2), predicted values for comparative seed yield patterned with the Ann_CSR ordination (Fig. 4A). Comparative seed mass yield, both per plant and per m², were highest for Ann_C strategists and lowest for Ann_S, Ann_R and Ann_SR, with intermediate strategies occupying an intermediate position (Fig. 4 AI, II). Similarly, SeedM could be ordered Ann_R < Ann_S < Ann_C (Fig. 4 AIII). Ann_C strategists were also characterized by high SeedNo_Pl (Fig. 4 AIVi), while the estimate of SeedNo_m2 patterned least strongly with strategy (Fig. 4 AIVii).

Despite the above tendency for comparative seed yield to pattern with strategy, there was still a wide range of values within each strategy class. Thus, Ann_C strategists included both the highly fecund small-seeded Sisymbrium loeselii [SeedM 0.09 mg, SeedNo_Pl 31894 (estimated), 37200 (measured)] and the few but large-seeded Vicia narbonensis (136 mg, 60). Similarly, Ann_R strategists included both Limosella aquatica [0.015 mg, 986 (estimated), 4236 (measured)] and Montia fontana subsp. chondrosperma (0.26 mg, 47) and Ann_S strategists both Catapodium rigidum (0.22 mg, 420) and Brachypodium distachyon (3.52 mg, 99). As a result, and associated with this wide range of values, there was also a strong negative correlation between SeedM and predicted SeedNo per plant within each strategy grouping (Fig. 4B). Regression equations for these relationships shared a common slope but differed significantly in intercept value. Small and/or slow-growing species (Ann_R and Ann_S strategists) had low intercept values and large plants (e.g. Ann_C strategists) had high values (Fig. 4B).

Taxonomic variation in trait expression

All functional traits were to some extent conservatively expressed with respect to phylogeny. Statistically significant differences in trait expression were detected between (a) major families, (b) tribes within families and (c) sub-tribes within tribes and, as a consequence, our predictions of comparative seed yield and the PCA axes defining the Ann_CSR similarly patterned with taxonomy (Supplementary data Table S2; Fig. 3iv). Despite these phylogenetically related differences in trait expression, for LDMC, a key element of the worldwide leaf economics spectrum (Wright et al., 2004), mean values for associated annual vegetation were similar for Asteraceae, Fabaceae and Poaceae, the three best represented families in the dataset (Supplementary data Table S3). Moreover, the high values of LDMC in Poaceae did not appear attributable simply to silicon accumulation, which adds leaf mass to Poaceae at little metabolic cost (Raven, 1983; Hodson et al., 2005; Katz, 2019). We calculate, from published values, that silica content accounts for only approx 1.8 % of leaf dry mass for annual grasses. Excluding silica content reduces the mean LDMC of annual Poaceae only slightly from 22.1 to 21.7 %. This is still much higher than the mean of 16.2 % LDMC characteristic of other annuals. Equally, ‘Si-corrected’ values for LDMC and LM_devel had a negligible impact when the PCA ordination was repeated (data not shown).

Comparing traits of annuals in different floras

Mean SeedM of the annual vegetation and of the annual flora of each region was ordered Central England < North-east Spain < North central Spain, with SeedNo_Pl and RSN showing the converse relationship (Table 4A). The three regions also patterned in relation to strategy (Fig. 5A, B) with Central England (Ann_C, Ann_CR and Ann_R well represented) < North-east Spain < North central Spain (Ann_S, Ann_SR and Ann_SC). Equally, within regions, SeedM, SeedNo and RSN varied with respect to both habitat (Table 4B) and Ann_C-S-R strategy (data not shown). Nevertheless, two-way ANOVAs identified strategy as the more consistently important determinant of seed size and comparative number than habitat within all three regions (Table 5). However, when RSN replaced SeedNo_Pl, habitat and interaction terms showed generally greater statistical significance and strategy exhibited lesser significance (data not shown).

Table 4.

The seed size, comparative number and RSN (± s.d.) of annuals differs between (A) regions, (B) habitats and (C) UK status relative to (i) vegetation samples and (ii) species

	n	Log₁₀seed mass	Log₁₀seed number	RSN
(A) Regions
(i) Vegetation samples with ≥ 5 annual species
Central England	1500	–0.38 ± 0.33^a	3.21 ± 0.23^c	0.40 ± 0.17^c
North-east Spain	465	–0.23 ± 0.34^b	3.04 ± 0.33^b	0.25 ± 0.25^b
North central Spain	275	–0.15 ± 0.40^c	2.79 ± 0.31^a	0.06 ± 0.25^a
One-way ANOVA (F)		74.8***	323.2***	376.0***
(ii) Species
Central England	200	–0.29 ± 0.71^a	3.10 ± 0.55^b	0.26 ± 0.49^b
North-east Spain	323	–0.07 ± 0.83^b	2.90 ± 0.66^a	0.10 ± 0.57^a
North central Spain	284	–0.03 ± 0.82^b	2.78 ± 0.67^a	0.02 ± 0.59^a
One-way ANOVA (F)		7.0***	13.9***	11.0***
(B) Habitats
(i) Vegetation samples
(a) Central England
Wetland	57	–0.60 ± 0.32^a	3.52 ± 0.17^d	0.58 ± 0.13^b
Rocky	136	–0.65 ± 0.31^a	3.03 ± 0.16^a	0.36 ± 0.14^a
Pasture	30	–0.48 ± 0.41^ab	3.07 ± 0.17^ab	0.30 ± 0.15^a
Arable	391	–0.17 ± 0.29^c	3.20 ± 0.19^bc	0.33 ± 0.15^a
Spoil	371	–0.47 ± 0.28^ab	3.32 ± 0.20^c	0.50 ± 0.13^b
Wasteland	499	–0.38 ± 0.29^b	3.17 ± 0.25^ab	0.38 ± 0.17^a
Woodland	8	–0.05 ± 0.29^c	3.15 ± 0.18^ab	0.31 ± 0.21^a
One-way ANOVA (F)		66.0***	60.8***	58.3***
(b) North-east Spain
Wetland	23	–0.58 ± 0.38^a	3.37 ± 0.23^b	0.52 ± 0.17^c
Artificial	323	–0.21 ± 0.32^bc	3.10 ± 0.31^ab	0.28 ± 0.23^b
Grassland	80	–0.19 ± 0.32^bc	2.77 ± 0.27^a	0.08 ± 0.24^a
Maritime/saline	16	–0.42 ± 0.37^ab	2.97 ± 0.30^ab	0.34 ± 0.24^b
Open habitats	16	–0.14 ± 0.38^c	2.85 ± 0.32^a	0.07 ± 0.24^a
Dwarf shrub	[2	–0.18 ± 0.37	2.77 ± 0.44	0.03 ± 0.38]
Woodland	[5	–0.07 ± 0.29	3.08 ± 0.15	0.34 ± 0.11]
One-way ANOVA (F)		8.2***	28.3***	23.2***
(c) North central Spain
Wetland	[2	–0.74 ± 0.05	3.16 ± 0.24	0.48 ± 0.14]
Artificial	121	0.09 ± 0.29^c	2.92 ± 0.28^c	0.12 ± 0.23^b
Grassland	94	–0.21 ± 0.22^b	2.66 ± 0.32^abc	-0.01 ± 0.25^ab
Maritime/saline	25	–0.98 ± 0.23^a	2.90 ± 0.18^bc	0.17 ± 0.15^b
Open habitats	12	–0.29 ± 0.24^b	2.62 ± 0.18^a	0.01 ± 0.19^ab
Dwarf shrub	13	–0.15 ± 0.30^bc	2.43 ± 0.20^a	-0.19 ± 0.17^a
Woodland	8	–0.15 ± 0.35^bc	2.65 ± 0.19^ab	0.09 ± 0.22^b
One-way ANOVA (F)		72.6***	16.4***	7.6***
(ii) Species
(a) Central England
Wetland	19	–0.59 ± 0.74^a	3.09 ± 0.56	0.49 ± 0.39^ab
Rocky	25	–0.54 ± 0.73^ab	3.34 ± 0.38^bc	0.15 ± 0.46^a
Pasture	[4	0.22 ± 0.45	2.80 ± 0.38	0.23 ± 0.15]
Arable	77	–0.09 ± 0.61^ab	2.65 ± 0.21^a	0.18 ± 0.49^a
Spoil	32	–0.64 ± 0.69^a	3.08 ± 0.54^abc	0.63 ± 0.28^b
Wasteland	40	–0.21 ± 0.75^ab	3.49 ± 0.52^c	0.09 ± 0.54^a
Woodland	7	–0.10 ± 0.42^ab	2.90 ± 0.61^abc	0.11 ± 0.48^a
One-way ANOVA (F)		4.7***	7.2***	6.9***
(b) North-east Spain
Wetland	38	–0.08 ± 0.84^ab	3.35 ± 0.54^b	0.46 ± 0.46^b
Artificial	123	–0.52 ± 0.90^a	2.93 ± 0.66^ab	0.08 ± 0.58^ab
Grassland	57	0.01 ± 0.81^ab	2.61 ± 0.57^a	–0.06 ± 0.55^a
Maritime/saline	27	–0.02 ± 0.91^ab	2.96 ± 0.58^ab	0.20 ± 0.56^ab
Open habitats	42	–0.13 ± 0.76^ab	2.80 ± 0.69^a	0.03 ± 0.64^a
Dwarf shrub	28	–0.06 ± 0.84^ab	2.75 ± 0.74^a	–0.02 ± 0.63^a
Woodland	17	–0.15 ± 0.71^ab	3.01 ± 0.47^ab	0.21 ± 0.44^ab
One-way ANOVA (F)		5.7***	5.9***	3.8**
(c) North central Spain
Wetland	0
Artificial	113	0.27 ± 0.76^c	2.85 ± 0.74	–0.01 ± 0.62
Grassland	74	–0.29 ± 0.83^ab	2.69 ± 0.67	–0.01 ± 0.59
Maritime/saline	18	–0.68 ± 0.87^a	2.91 ± 0.69	0.20 ± 0.60
Open habitats	27	–0.27 ± 0.68a^b	2.73 ± 0.54	0.06 ± 0.52
Dwarf shrub	33	–0.09 ± 0.68^bc	2.53 ± 0.64	–0.14 ± 0.14
Woodland	28	–0.01 ± 0.81^bc	2.93 ± 0.58	0.21 ± 0.51
One-way ANOVA (F)		8.2***	1.8 n.s.	1.4 n.s.
(C) UK status
(i) Vegetation samples
Decreased	418	–0.33 ± 0.38^b	3.14 ± 0.21^a	0.34 ± 0.16^a
Increased	450	–0.40 ± 0.30^a	3.29 ± 0.23^b	0.46 ± 0.17^a
t-test		3.0**	10.0***	11.8***
(ii) Species
Decreased	172	–0.22 ± 0.79	2.87 ± 0.54^a	0.09 ± 0.51^a
Increased	71	–0.27 ± 0.70	3.17 ± 0.60^b	0.26 ± 0.50^b
t-test		0.5 n.s.	3.8***	2.4*

Open in a new tab

In (i), vegetation samples were categorized as ‘decreased’ if status index < –0.5 and ‘increased’ if status index > +0.5.

n.s., not significant.

Fig. 5. — Both with respect to (A) vegetation samples with ≥ 5 annual species and (B) the species complement, our three study areas differed in their representation of Ann_CSR strategy types, and in (C) changed abundance within UK also patterns with strategy. In Ai (± s.d.), Bi and Ci, values relate to Central England and are percentages. In the remainder of A and B, values identify regional differences between Central England and (ii) North-east and (iii) North central Spain, respectively. Green identifies values higher and red lower than Central England. In (A), coloured values indicate statistically significant differences (P < 0.05 using the Mann–Whitney U-test). In Cii, values relate to status index and are not calculated for strategies where n < 10.

Table 5.

Two-way ANOVAs identify strategy as more consistently important than habitat as a determinant of seed size and comparative number both for vegetation samples (veg) and for species (spp)

		n	Habitat			Strategy			Habitat × Strategy
			d.f.	F	P	d.f.	F	P	d.f.	F	P
(A) SeedM_Pl
Central England	veg	836	5	6.8	***	4	46.7	*******	11	1.4	n.s.
	spp	182	5	2.7	***	5	12.2	*******	18	1.2	n.s.
North-east Spain	veg	454	4	3.5	**	4	9.5	*******	9	1.5	n.s.
	spp	331	6	1.4	n.s.	7	9.8	*******	33	1.1	n.s.
North central Spain	veg	264	4	10.5	*******	4	2.9	*	7	0.6	n.s.
	spp	292	5	1.5	n.s.	7	6.7	*******	28	0.9	n.s.
(B) SeedNo_Pl
Central England	veg	836	5	10.4	***	4	33.2	*******	11	4.5	n.s.
	spp	182	5	5.0	***	5	6.1	*******	18	1.1	n.s.
North-east Spain	veg	454	4	4.4	**	4	6.1	*******	9	1.0	n.s.
	spp	331	6	2.2	*	7	6.9	*******	33	1.0	n.s.
North central Spain	veg	264	4	3.8	**	4	0.6	n.s.	7	1.9	^†
	spp	292	5	1.9	^†	7	4.9	*******	28	0.5	n.s.

Open in a new tab

High values for variance ratio (F), together with associated degrees of freedom (d.f.) and P, are in bold.

n.s., not significant.

A further feature of the dataset and field observations was that some species varied ecologically between study areas. Habitat range, and even life history, differed markedly between Spain and the UK for some species (Table 6).

Table 6.

Examples of less common species whose populations were found to differ between the UK and Spain in (A) ecological range or (B) life history

Species	UK	Spain
(A)Habitat range
Galeopsis angustifolia, Ononis reclinata, Thlaspi perfoliatum	Uncommon – very rare in UK. Now primarily confined to rocky sites with habitat continuity	Wide range of habitats including crop and/or fallow fields
Galeopsis segetum	Former arable weed, now extinct	Former arable weed, now largely restricted to open shaded sites with habitat continuity
(B)Life history
Clinopodium acinos	Much reduced as an annual arable weed; increasingly a woody perennial of rocky sites with habitat continuity	Occupies a range of habitats but still characteristically an arable weed
Gaudinia fragilis	Primarily a tufted perennial of unimproved grassland	Typically an annual of disturbed habitats. (Seen in arable habitats in north Morocco.)

Open in a new tab

Based upon field observations augmented by published records.

Inter-relationships between the annual and perennial components of vegetation

Functional traits of annuals patterned with those of co-occurring perennials. SeedM_annual was correlated positively with both SeedM_peren and DomI within each region (Table 7). Similarly, albeit less consistently, SeedNo_annual and RSN were negatively correlated with SeedM_peren and positively with DomI (Table 7), with broadly similar patterns observed within individual habitats (Supplementary data Table S4). In contrast, since large seeds occurred at both extremes of fertility (Fig. 4B), no clear and consistent trends were detected between annual seed traits and LDMC_peren. Instead, positive and negative correlations were variously recorded according to ecological circumstance (Table 7; Supplementary data Table S4).

Table 7.

Seed traits of annuals correlate with the functional traits of coexisting perennials weighted by abundance

	SeedM_peren	LDMC_peren	DomI
(A) SeedM_annual
Central England (1474)	0.269***	0.043⁺	0.256***
North-east Spain (427)	0.225***	0.086⁺	0.175***
North central Spain (255)	0.158*	–0.326***	0.293***
(B) SeedNo_annual
Central England	–0.048⁺	–0.101***	0.219***
North-east Spain	–0.074	–0.061	0.141**
North central Spain	–0.297***	–0.305***	0.040
(C) RSN
Central England	–0.095***	–0.048⁺	0.075**
North-east Spain	–0.099*	–0.103*	0.094⁺
North central Spain	–0.365***	–0.099	–0.067

Open in a new tab

Values relate to Pearson r coefficients with number of relevés in parentheses.

The changed dynamics of Ann_C-S-R strategies and seed size vs. number in the British flora

Whether species have recently increased or decreased in abundance appears to depend strongly upon both habitat and Ann_C-S-R strategies. Increased species were particularly associated with urban landscapes and with wasteland and spoil habitats (Supplementary data Table S5). They also formed a slight majority within the Ann_CR strategy and were well represented in Ann_C (Fig. 5C). In contrast, declined species were characteristic of pastural (upland) landscapes and wetland and arable habitats and with more ‘stressed’ strategies (Fig. 5C; Supplementary data Table S5). However, there are additional reproductive differences. Increased species consistently produce greater SeedNo_Pl, a relationship that appears largely independent of SeedM and plant size (Tables 2C and 5).

The appended database

Our predictions of comparative seed number are inevitably rather imprecise and, for some species (e.g. Minuartia hamata, where only three seeds per plant are predicted), values may be wrong by several orders of magnitude. Accordingly, to encourage further work, data relating to SeedM, SeedM_Pl, SeedM_m2, SeedNo_Pl and SeedNo_m2 coupled with values for the PCA axes used to define Ann_CSR strategies are included in Supplementary data Table S6 for 842 annual taxa.

DISCUSSION

Theoretically expected traits predict SeedM_Pl and SeedNo_Pl

The regression equations predicting SeedM_Pl (Table 3) conformed to theoretical expectations. They were consistent with relationships between size, flowering and yield observed by Gross (1981), Gross and Werner (1983), Shipley and Dion (1992) and Aarssen and Jordan (2001). Thus, for the UK with an r² of 0.75, SeedM_Pl was essentially a positive function of plant size (Size_Pl) and performance (LA_funct, a key component of competitive ability; Keddy et al., 2002; Hodgson et al., 2017) with SeedM having only a marginal impact (compare equations + and – SeedM in Table 3). The equation for the USA dataset included functionally similar, but not identical, terms (Table 3). Expectedly, since the two datasets came from different regions, and a contrasted set of growing conditions (see ‘A methodological caveat’, above), our two SeedNo_Pl datasets for the UK (Salisbury, 1942; from the less productive British landscapes prior to agricultural intensification) and for the USA (Stevens, 1932, 1957; robust agricultural weeds collected from intensively productive arable landscapes) did not provide identical predictions [eqn (2)]. Nevertheless, the two sets of predicted values were strongly correlated, with an r² of 0.72, with a slope close to 1:1 [eqn (2)]. Our estimates appear appropriate for ranking relatively well-grown examples of species in terms of seed yield. SeedM_Pl can now be viewed as a readily, albeit crudely, estimated comparative trait defined by vegetative attributes and suitable for use in ‘broad-brush’ ecological comparisons. As a result, SeedNo_Pl can also be assessed in comparative although, again, not in exact, quantitative terms and, encouragingly, our predicted values of SeedNo_Pl appear to have functional relevance to species distribution and floristic change (Figs 1, 4 and 5; Tables 3, 4, 7 and 8).

Table 8.

Decreasing annual species in the UK produce significantly fewer seeds, but not significantly larger ones, than species with a stable or increasing distribution

	Mean log₁₀SeedM ± s.d.					Mean log₁₀SeedNo_Pl ± s.d.
	Decreased		Stable/increased		t	Decreased	Stable/increased	T
All	172	–0.22 ± 0.79	165	–0.31 ± 0.72	1.2 n.s.	2.87 ± 0.54	3.08 ± 0.60	3.5***
Ann_C	11	0.47 ± 0.33	15	0.20 ± 0.68	1.3 n.s.	3.22 ± 0.35	3.71 ± 0.47	2.9**
Ann_CR/SC	55	0.19 ± 0.66	53	0.09 ± 0.53	0.9 n.s.	2.83 ± 0.57	3.07 ± 0.68	2.0*
Ann_CSR	69	–0.19 ± 0.63	66	–0.48 ± 0.66	2.6**	2.89 ± 0.52	3.12 ± 0.47	2.7**
Ann_S/SR/R	35	–1.06 ± 0.62	28	–0.94 ± 0.61	0.8 n.s.	2.70 ± 0.47	2.72 ± 0.43	0.2 n.s.

Open in a new tab

Number of species are given in parentheses and, because of a shortage of data, strategies with similar regression equations in Fig. 4B are combined. [For comparison: RSN_Decreased 0.09 ± 0.51; RSN_{Stable/increased} 0.25 ± 0.49; t = 3.0**.]

n.s., not significant.

The next steps in ‘regenerative trait-based ecology?’

Reshaping general approaches

Intensive land use and climate change are reshaping our floras (Hodgson, 1986a; Pyke, 2003; Cirujeda et al., 2011; Pimm et al., 2014). An important element in understanding and moderating these effects is the ability to predict which species are capable of establishing, and which are not. To date, for methodological reasons, the only regenerative trait in regular use is SeedM and, as a result, trait-based ecology is failing to deliver. Like all branches of science, functional trait ecology is dependent for its effectiveness upon the creation of general rules. Initially, these tend to have been generated through major analyses of functional trait data abstracted from a geographically diverse range of data sources (e.g. Wright et al., 2004). Subsequently, generality can be improved by further increasing the geographical range over which a ‘traditional’ trait is measured. Unfortunately, this important validation process appears to have taken place almost to the exclusion of more exploratory studies into new ecological processes and traits. As a result, there remain many gaps and ‘half-truths’ within trait-based ecology (Shipley et al., 2016; Hodgson et al., 2017; Moles, 2018).

Less mainstream, but still ‘big science’, is an ‘eco-taxonomic’ approach pioneered in Central Europe. The initial stage provides a description and classification of vegetation. Subsequently, key ecological factors are identified and, from a working ecological knowledge of the flora under study, ‘ecological values’ for species within the flora have been generated on an industrial scale. Importantly, the approach focuses upon all factors considered ecologically important, not just those that are most easily measured. An historical illustration of its power and utility is provided by Ellenberg et al. (1992) and their phytosociologically related habitat preference classes, ‘Ellenberg numbers’. We believe that the reliance upon a classification based solely upon where plants grow (‘Ellenberg numbers’) rather than how plants function (trait-based ecology) is outdated. Nevertheless, Ellenberg attempted to include all key ecosystem processes in his scheme. Thus, arguably, in scope and scale, he remains ahead of much of trait-based ecology.

We suggest that the way forward is not directly through global analyses. Instead, like Ellenberg, studies in trait-based ecology should initially operate at a more local level where strong links can be maintained between measured traits and both vegetation descriptions and the observable ecosystem processes shaping the flora (e.g. LEDA Traitbase, Kleyer et al., 2008; FIFTH database, Cerabolini et al., 2010). At this more parochial but focused scale, additional important ecosystem processes can be explored more readily and new traits added to analyses. Positive outcomes will encourage ‘replicate’ studies in other regions and ultimately global analyses, allowing trait-based plant ecology to grow and diversify.

The regional approach may also cast light on the currently intractable relationships between present-day ecosystem processes and past evolutionary events in trait expression. In this study, all functional traits and, in consequence, all predictions of reproductive allocation and strategy were conservatively expressed within families, tribes and sub-tribes (Supplementary data Tables S2–S4; Fig. 3iv). This apparent link between functional traits and phylogeny is not unexpected: take SeedM, a key element in comparative seed yield relationships whose expression appears to have been constrained throughout the evolution of the angiosperms (Westoby et al., 1992; Moles et al., 2005). Seed size may be subject to deep-seated evolutionary constraints associated with developmentally complex structures and processes that are difficult to modify (Hodgson and Mackey, 1986). This has inevitable developmental impacts on plant size, particularly those with a short life span. Consistent with seed–phytomer–leaf strategy theory, all elements of vegetative plant size correlate positively with seed size (Hodgson et al., 2017), and, since it is a function of vegetative size [eqn (1); Table 3], so too will comparative seed yield. In addition, phylogeny is linked locally to commonness, rarity and plant strategy, and both commonness and plant strategy are strongly correlated with polyploidy (Hodgson, 1986b, c, 1987). Such phylogenetic correlates were not identified in other regions (Edwards and Westoby, 2000). Nevertheless, phylogenetic niche conservatism is very much a feature of the flora of Central Europe (Prinzing et al. (2001). We suspect that, unlike the evolutionary factors constraining the expression of SeedM, some correlations (e.g. those relating to Ann_CSR) stem, at least in part, from the shared recent evolutionary history of our study areas, from the Pleistocene onwards (West, 1969), and an adaptive radiation of the flora from a common pool of founder species.

Broad replicate studies of comparative seed yield and its predictor traits are required in other regions to further explore the relationships identified in this study. These should include new ‘gold standard’ datasets that include measurements of both seed yield and vegetative biomass. Moreover, the choice of species should be such that separate predictor equations estimating SeedM_Pl can be generated for a contrasted range of phylogenetic groupings. Such work is important to confirm the generality of and refine the ‘comparative precision’ of the seed yield relationships identified here.

Adding new traits

The Ann_R axis remains difficult to quantify (Hodgson et al., 1999; Pérez-Harguindeguy et al., 2012; Pierce et al., 2017) with, for annual species, the current ‘gold standard’ ruderal variables, FlStart and FlDuration, ‘not fit for purpose’. First, FlStart does not consistently predict flowering precocity. Although most flower early, some equally precocious UK ruderals grow on mud exposed by summer drought and necessarily commence flowering in autumn (e.g. Elatine). Secondly, a long FlDuration may be associated with two very different strategies. A single individual may flower for a long time (e.g. Veronica persica, which may commence flowering from the second- or third-formed phytomer with additional flowers produced at each successive phytomer until both vegetative and reproductive growth ceases). Equally, individuals may be short lived but produce several generations of plants within a single growing season (e.g. Senecio vulgaris). We suggest that, in accordance with seed–phytomer–leaf theory (Hodgson et al., 2017), phytomer miniaturization and a reduction in the number of juvenile phytomers, which both promote early maturity, could replace FlStart as an estimate of precocity. Equally, identifying the phytomer number at which flowering begins and ends may provide a developmentally appropriate trait to replace FlDuration.

Consolidating regenerative theory

The Ann_R axis is defined by the intensity, frequency and predictability of disturbance events. Disturbance may be seasonally unpredictable, variously weak and strong in different years (e.g. drought on very shallow soils or in regions where rainfall varies greatly from year to year, grazing, patchy shade, trampling and weeding). Alternatively, it may be late, severe but seasonally predictable (e.g. crop harvesting, ploughing, shade caused by leafing-out of forest trees and summer drought on deeper soils and in regions with predictable rainfall). Shemesh and Novoplansky (2013) argue persuasively that important functional trade-offs relate to the probability and severity of risks associated with these two scenarios. Species whose habitats or microsites are prone to less intense or intermittent disturbance are predicted to exhibit deterministic bet-hedging (sensuCohen, 1966). They flower at an early developmental stage. This ‘risk-averse’ pattern of growth mitigates in favour of ‘minimum fitness’ (i.e. the production of some seed even in unfavourable years). Moreover, if there is no early catastrophic disturbance event, modular increments of vegetative growth, flowering and seed set continue. However, as a result of the continuing partial sequestration of resources into seed production, growth rates inevitably remain relatively low. Alternatively, where the opportunity for growth is usually prolonged, the more productive strategy is a long period of purely vegetative growth before flowering. Annuals adapted to this latter scenario are potentially larger and have more structurally complex branch units. They are, therefore, less ruderal, and, important for estimating comparative seed yield, they may be expected to produce more seed mass relative to their vegetative size. Our attempts to factor these relationships into predictions of comparative seed mass yield may benefit from links to plant morphology and physiology (Prusinkiewicz et al., 2007).

Comparative seed yield per m²

Regressions predicting SeedM_m2 from SeedM_Pl have a low r² (Table 3) and much lower predictive power. SeedM_m2 is measured under field conditions where the target species has close to 100 % cover. For most annual species, this is an unusual circumstance with populations likely to exhibit a range of plant sizes. Our estimates of SeedM_Pl were derived using traits relating to large ‘well-grown’ plants. As a result, the relationship between plant size and yield per plant may not be wholly appropriate for scaling up to 1 m². Nevertheless, estimates of SeedM_m2 will be important for extending predictions to comparative seed yield in perennial species. Also, numerous values are already available (Šerá and Šerý, 2004). SeedNo_m2 remains a potentially crucial attribute albeit one in need of further study.

SeedNoPl, a valuable new regenerative dimension to trait-based studies of floristic change

In our most intensively studied region, Central England, eutrophication and disturbance in managed habitats and abandonment of marginal ones have fundamentally altered the nature of the landscape, and the flora. Many tall species and those of fertile soils have increased, particularly those with small seeds (Table 8; Hodgson, 1986a; Hodkinson and Thompson 1997). In contrast, low-growing species of infertile soils have generally decreased and many are now restricted to small isolated fragments of habitat (Hodgson, 1986a; Preston et al., 2002; Hodgson et al., 2014).

Encouragingly, regeneration from seed adds an additional dimension to this well-established story. High SeedNo_Pl is consistently a better predictor of increased abundance than low SeedM (Table 8). This relationship has important implications. Because key evolutionary processes impact upon survival and trait expression at the level of the population (Harper, 1967; Moles, 2018), populations of the same species may come to differ in both habitat and life history across their geographical range (Table 6). In particular, the ‘colonization–competition’ trade-off between few large seeds with potentially higher seedling survivorship and many small widely dispersed seeds (Westoby et al., 2002; Moles and Westoby, 2006) routinely operates at the population level. Populations of annuals from warm favourable climates tended to have smaller seeds than those from cool less favourable ones (McWilliams et al., 1968; Montesinos-Navarro et al., 2011; Burcu et al., 2017). On the basis of data from our study area, we predict that there is likely to be selection for larger seeds and potentially increased seedling survivorship in populations of rare species confined to small isolated patches of habitat (Fig. 6). In contrast, the production of a larger number of smaller widely dispersed seeds may facilitate the spread of increasing species. In extremis, since SeedM_Pl is a positive function of vegetative performance both theoretically [eqns (1a)–(1d)] and practically (Table 3), poor growth may consistently result in the occurrence of non-viable combinations of seed size and number. In this context, we provide regional examples of formerly annual species that now tend to behave as perennials, less dependent upon regeneration by seed (Table 6). As illustrated here (Fig. 6), the comparative regenerative traits devised in this study complement the established set of vegetative traits routinely used in trait-based plant ecology and enhance their diagnostic capabilities.

Conclusions

With many seeds produced but few surviving, establishment from seed is a crucial but poorly understood ‘extreme event’ regulating species distribution. To date, within functional trait plant ecology, this process has only been studied in the context of seed size. Now, following this investigation, we have, additionally, comparative estimates for seed number including provisional values for >800 annuals, appended as Supplementary data Table S6. Although, as emphasized in the Discussion, many methodological problems remain, for the first time, in addition to SeedM, we are in a position to routinely include comparative estimates of SeedNo_Pl. As a result, we can extend functional analyses to the fundamental ‘colonization–competition’ trade-off between few large seeds with potentially higher seedling survivorship and many small widely dispersed seeds (Westoby et al., 2002; Moles and Westoby, 2006). Also, our analyses within the European flora illustrate the value of routinely including this additional regenerative element in trait-based plant ecology (Figs 1, 4 and 5; Tables 3, 4, 7 and 8).

Regenerative strategies will never conform to the linear elegance of the leaf economics spectrum of Wright et al. (2004). They are regulated by a complex network of factors sensuMessier et al. (2017), and some, such as seed dispersal, we have yet to study. The challenge is to sufficiently distil down these dimensions of complexity so that we can emulate C-S-R strategy theory (Grime 1974, 2001) and provide a simple theoretically and practically useful multidimensional diagnostic system. Trait-based ecology is some way from this synthesis but we are making significant progress. Importantly, our new regenerative dimension to trait-based plant ecology is already addressing key but poorly understood ecological processes, the establishment of ‘winners’ by seed, and the associated extinction of ‘losers’, during episodes of vegetation change (Fig. 6). We invite others to explore the potential of the appended database, to improve the methodology and to take ‘regenerative functional plant ecology’ to the next level.

Fig. 6. — Some predicted changes in trait expression by annuals in response to changing land use in the UK. Fertile relict habitats include meadows, pastures, wetland and woodland, and are very vulnerable to changes in land use. Rocky/sandy habitats are less vulnerable since change is potentially buffered to some degree by a combination of lower soil fertility and summer drought. Predictions were based upon descriptions of the status of the flora (Hodgson, 1986a; Hodkinson and Thompson, 1997; Preston *et al.*, 2002; Cheffings and Farrell, 2005, Hodgson *et al.*, 2014; Botanical Society of Britain and Ireland and the Biological Records Centre, 2018), the ‘colonization–competition’ trade-off between few large seeds with potentially higher seedling survivorship and many small widely dispersed seeds (Westoby *et al.*, 2002; Moles and Westoby, 2006) and field observations (Table 6). Arrows identify predicted direction of change. {*A supplementary Spanish dimension*. Consistent with Fig. 5, the relative abundance of relict (fertile) vs. sandy/rocky habitats and their importance for annuals was considered to be: Central England > North-east > North central Spain. Putative differences in the Spanish status of species was identified by the following suffices – habitat range: ^asimilar, ^bwider habitat range, ^carable still an important habitat; ^dlife history different, Spanish populations typically annual. A number of potential impacts relating to the Mediterranean climate are not included [e.g. arid: dry years (large seeds) vs. wet years (small) (Venable and Brown, 1988; Pake and Venable, 1996; Metz *et al*., 2010; Shriver, 2016); cool less favourable (large) vs. warm favourable (small) (McWilliams *et al.*, 1968; Montesinos-Navarro *et al.*, 2011; Burcu *et al.*, 2017)].}

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Table S1: range of trait values. Table S2: comparing traits between families, tribes and sub-tribes. Table S3: comparing LDMC between families and regions. Table S4: comparing traits of annuals with those of co-occurring perennials. Table S5: comparing mean status index in different regions and habitats in central England. Table S6: functional estimates and measures of seed traits for >800 annuals.

mcaa151_suppl_Supplementary_Table_S1_S5

Click here for additional data file.^{(46.9KB, docx)}

mcaa151_suppl_Supplementary_Table_S6

Click here for additional data file.^{(199.1KB, docx)}

ACKNOWLEDGEMENTS

We thank Philip Grime and other former colleagues for access to unpublished datasets from the Unit of Comparative Plant Ecology, past members of the Department of Archaeology, Sheffield and Instituto Pirenaico de Ecología, Zaragoza for their important early contributions to the database, and Grup de Recerca Científica, Terres de l’Ebre and the Unita di Analisi e Gestione Biocenosi, Varese for their scientific guidance and hospitality during our many early trips to Catalonia and Lombardy. We are grateful to Simon Pierce, Mick Hanley and three anonymous reviewers for their constructive criticism of previous versions of the paper, and the analyses of floristic change in the UK would not have been possible without access to the data holdings and the interpretative information on the Botanical Society of the British Isles website (Botanical Society of Britain and Ireland and the Biological Records Centre, 2018), which is in the public domain.

J.G.H. participated in vegetation surveys, plant collection and the subsequent measurement of traits, curated the databases, carried out the analyses and wrote the various drafts of the paper. G.M.M.* provided independently collected functional data from Spain and participated in/led a number of collecting/measuring trips. Ferran Royo Pla provided field survey data and participated in/led some collecting/measuring trips. B. Šerá* provided the dataset on seed yield m^–2. G.J.*, A.B.* and M.C.* are key archaeobotanical contributors since the 1990s involved routinely in plant collecting and measurement. X.F.* provided Spanish field survey data. M.A.*, Y.H. and A.T. organized and supervised several collecting trips to Morocco. B. Santini* provided independently collected trait data. C.P*, P.J.W and S.R.B were historically major collectors of, as yet, unpublished functional data. C.P. additionally had a major early role in the production of the archaeobotanist’s version of the database. The archaeobotanists, A.S., C.D., L.G., E.N., E.S. and G.W. were involved in functional trait measurement on key recent field trips. Minor (and historically less recent) participants: Bruno Cerabolini organizing collecting trips in 2003–4 (and published the FIFTH database, already acknowledged in the paper), Alyson Hynd (unpublished trait data, 1996: little on annuals), Angel Romo-Dıėz and Lluis de Torres Espuny organizing collecting trips in 2004 and 2003, 2004 and 2006, respectively. [UCPE input acknowledged generally within the paper.] *Paper sent directly to senior ecologists and archaeobotanists for comment.

Dedicated to Ferran Royo Pla 1969–2016: leader of Grup de Recerca Terres de l’Ebre, Catalonia, and friend.

FUNDING

A considerable quantity of the data used in this project was collected during projects funded by NERC (UK), Comisión Interministerial de Ciencia y Tecnología (Spain) and the European Research Council (AGRICURB project; Grant agreement ID: 312785).

LITERATURE CITED

Aarssen LW. 2008. Death without sex – the ‘problem of the small’ and selection for reproductive economy in flowering plants. Evolutionary Ecology 22: 279–298. [Google Scholar]
Aarssen LW. 2015. Body size and fitness in plants: revisiting the selection consequences of competition. Perspectives in Plant Ecology Evolution and Systematics 17: 236–242. [Google Scholar]
Aarssen LW, Jordan CY. 2001. Between-species patterns of covariation in plant size, seed size and fecundity in monocarpic herbs. Ecoscience 8: 471–477. [Google Scholar]
Aarssen LW, Schamp BS, Pither J. 2006. Why are there so many small plants? Implications for species coexistence. Journal of Ecology 94: 569–580. [Google Scholar]
Aedo C, et al. 1980. onwards. Flora Iberica: plantas vasculares de la Península Ibérica e Islas Baleares. Madrid: Consejo Superior de Investigaciones Científicas. [Google Scholar]
Barton KE, Hanley ME. 2013. Seedling–herbivore interactions: insights into plant defence and regeneration patterns. Annals of Botany 112: 643–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
Botanical Society of Britain and Ireland and the Biological Records Centre 2018. Online atlas of the British and Irish flora http://www.brc.ac.uk/plantatlas (3 August 2018).
Braun Blanquet J, de Bolós O. 1953. La comunidades vegetales de la Depresion del Ebro y su dinamismo. Anales de la Estación Experimental de Aula Dei 5: 1–266. [Google Scholar]
Brodribb TJ. 2017. Progressing from ‘functional’ to mechanistic traits. New Phytologist 215: 9–11. [DOI] [PubMed] [Google Scholar]
Burcu YE, Sadik E, Cagatay T. 2017. Inter-population variability in seed dormancy, seed mass and germination in Helianthemum salicifolium (Cistaceae), a hard-seeded annual herb. Folia Geobotanica 52: 253–263. [Google Scholar]
Cerabolini BEL, Brusa G, Ceriani RM, de Andreis R, Luzzaro A, Pierce S. 2010. Can CSR classification be generally applied outside Britain? Plant Ecology 210: 253–261. [Google Scholar]
Chambers J, Aarssen LW. 2009. Offspring for the next generation: most are produced by small plants within herbaceous populations. Evolutionary Ecology 23: 737–751. [Google Scholar]
Chambers JC, MacMahon JA. 1994. A day in the life of a seed: movements and fates of seeds and their implications for natural and managed systems. Annual Review of Ecology and Systematics 25: 263–292. [Google Scholar]
Cheffings C, Farrell L, eds.2005. The vascular plant red data list for Great Britain. Peterborough, UK: Joint Nature Conservation Committee. [Google Scholar]
Cirujeda A, Aibar J, Zaragoza C. 2011. Remarkable changes of weed species in Spanish cereal fields from 1976 to 2007. Agronomy for Sustainable Development 31: 675–688. [Google Scholar]
Clapham AR, Tutin TG, Moore DM. 1987. Flora of the British Isles. Cambridge: Cambridge University Press. [Google Scholar]
Clauss MJ, Aarssen LW. 1994. Phenotypic plasticity of size–fecundity relationships in Arabidopsis thaliana. Journal of Ecology 82: 447–455. [Google Scholar]
Cohen D. 1966. Optimizing reproduction in a randomly varying environment. Journal of Theoretical Biology 12: 119–129. [DOI] [PubMed] [Google Scholar]
Crawley MJ. 2014. Seed predators and plant population dynamics. In: Gallagher RS. ed. Seeds: the ecology of regeneration in plant communities. New York: CABI Publishing, 94–110. [Google Scholar]
Csontos P, Tamás J, Balogh L. 2003. Thousand seed weight records of species from the flora of Hungary, I. Monocotyledonopsida. Studia Botanica Hungarica 34: 121–126. [Google Scholar]
Csontos P, Tamás J, Balogh L. 2007. Thousand seed weight records of species from the flora of Hungary, II. Dicotyledonopsida. Studia Botanica Hungarica 38: 179–189. [Google Scholar]
Dalling JW, Davis AS, Schutte BJ, Arnold E. 2011. Seed survival in soil: interacting effects of predation, dormancy and the soil microbial community. Journal of Ecology 99: 89–95. [Google Scholar]
Edwards W, Westoby M. 2000. Families with highest proportions of rare species are not consistent between floras. Journal of Biogeography 27: 733–740. [Google Scholar]
Ehrendorfer F. 1980. Polyploidy and distribution. In: Lewis WH, ed. Polyploidy: biological relevance. New York: Plenum Press, 45–60. [Google Scholar]
Ellenberg H, Weber HE, Dull R. 1992. Zeigwerte von Pflanzen in Mitteleuropa. (2nd ed.). Scripta Geobotanica 18: 1–258. [Google Scholar]
Fenner M, Thompson K. 2005. The ecology of seeds. Cambridge: Cambridge University Press. [Google Scholar]
Font X, Pérez-García N, Biurrun I, et al. 2012. The Iberian and Macaronesian Vegetation Information System (SIVIM, www.sivim.info), five years of online vegetation’s data publishing. Plant Sociology 49: 89–95. [Google Scholar]
FAO 2018. FAOSTAT: food and agriculture data http://www.fao.org/faostat/en/#data (23 January 2018).
Forget P-M, Lambert JE, Hulme PE, Vander Wall SB, eds.2005. Seed fate: predation, dispersal, and seedling establishment. Wallingford, UK: CABI Publishing. [Google Scholar]
Gallart M, Mas MT, Verdu AMC. 2010. Demography of Digitaria sanguinalis: effect of the emergence time on survival, reproduction, and biomass. Weed Biology and Management 10: 132–140. [Google Scholar]
Germain RM, Johnson L, Schneider S, Cottenie K, Gillis EA, MacDougall AS. 2013. Spatial variability in plant predation determines the strength of stochastic community assembly. The American Naturalist 182: 169–179. [DOI] [PubMed] [Google Scholar]
Grime JP. 1974. Vegetation classification by reference to strategies. Nature 250: 26–31. [Google Scholar]
Grime JP. 2001. Plant strategies, vegetation processes, and ecosystem properties, 2nd edn. Chichester: Wiley. [Google Scholar]
Grime JP, Hunt R. 1975. Relative growth-rate: its range and adaptive significance in a local flora. Journal of Ecology 63: 393–422. [Google Scholar]
Grime JP, Hodgson JG, Hunt R. 2007. Comparative plant ecology, 2nd edn. Dalbeattie, UK: Castlepoint Press. [Google Scholar]
Gross KL. 1981. Predictions of fate from rosette size in four ‘biennial’ plant species: Verbascum thapsus, Oenothera biennis, Daucus carota, and Tragopogon dubius. Oecologia 48: 209–213. [DOI] [PubMed] [Google Scholar]
Gross RS, Werner PA. 1983. Probabilities of survival and reproduction relative to rosette size in the Common Burdock (Arctium minus: Compositae). The American Midland Naturalist 109: 184–193. [Google Scholar]
Han W, Fang J, Guo D, Zhang Y. 2005. Leaf nitrogen and phosphorus stoichiometry across 753 terrestrial plant species in China. New Phytologist 168: 377–385. [DOI] [PubMed] [Google Scholar]
Harper JL. 1967. A Darwinian approach to plant ecology. Journal of Ecology 55: 247–270. [Google Scholar]
Hodgson JG. 1986a Commonness and rarity in plants with special reference to the Sheffield Flora. II. The relative importance of climate, soils and land use. Biological Conservation 36: 253–274. [Google Scholar]
Hodgson JG. 1986b Commonness and rarity in plants with special reference to the Sheffield Flora. Part III. Taxonomic and evolutionary aspects. Biological Conservation 36: 275–296. [Google Scholar]
Hodgson JG. 1986c Commonness and rarity in plants with special reference to the Sheffield Flora. Part IV. A European context with particular reference to endemism. Biological Conservation 36: 297–314. [Google Scholar]
Hodgson JG. 1987. Why do so few plant species exploit productive habitats? An investigation into cytology, plant strategies and abundance within a local flora. Functional Ecology 1: 243–250. [Google Scholar]
Hodgson JG, Mackey JML. 1986. The ecological specialization of dicotyledonous families within a local flora: some factors constraining optimization of seed size and their possible evolutionary significance. New Phytologist 104: 497–515. [Google Scholar]
Hodgson JG, Wilson PJ, Hunt R, Grime JP. 1999. Allocating CSR plant functional types: a soft approach to a hard problem. Oikos 85: 282–294. [Google Scholar]
Hodgson JG, Montserrat-Martí G, Charles M, et al. 2011. Is leaf dry matter content a better predictor of soil fertility than specific leaf area? Annals of Botany 108: 1337–1345. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hodgson JG, Tallowin J, Dennis RLH, et al. 2014. Changing leaf nitrogen and canopy height quantify processes leading to plant and butterfly diversity loss in agricultural landscapes. Functional Ecology 28: 1284–1291. [Google Scholar]
Hodgson JG, Santini BA, Montserrat Marti G, et al. 2017. Trade-offs between seed and leaf size (seed–phytomer–leaf theory): functional glue linking regenerative with life history strategies … and taxonomy with ecology? Annals of Botany 120: 633–652. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hodkinson DJ, Thompson K. 1997. Plant dispersal: the role of man. Journal of Applied Ecology 34: 1484–1496. [Google Scholar]
Hodson MJ, White PJ, Mead A, Broadley MR. 2005. Phylogenetic variation in the silicon composition of plants. Annals of Botany 96: 1027–1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kattge J, Díaz S, Lavorel S, et al. 2011. TRY – a global database of plant traits. Global Change Biology 17: 2905–2935. [Google Scholar]
Katz O. 2019. Plant silicon content is a functional trait: implications in a changing world. Flora 254: 88–94. [Google Scholar]
Keddy P, Nielsen K, Weiher E, Lawson R. 2002. Relative competitive performance of 63 species of terrestrial herbaceous plants. Journal of Vegetation Science 13: 5–16 [Google Scholar]
Kleyer M, Bekker RM, Knevel IC, et al. 2008. The LEDA Traitbase: a database of life-history traits of the Northwest European flora. Journal of Ecology 96: 1266–1274. [Google Scholar]
Larios L, Pearson DE, Maron JL. 2017. Incorporating the effects of generalist seed predators into plant community theory. Functional Ecology 31: 1856–1867. [Google Scholar]
Larson JE, Funk JL. 2016. Regeneration: an overlooked aspect of trait-based plant community assembly models. Journal of Ecology 104: 1284–1298. [Google Scholar]
Lustenhouwer N, Moran EV, Levine JM. 2017. Trait correlations equalize spread velocity across plant life histories. Global Ecology and Biogeography 26: 1398–1407. [Google Scholar]
Lutman PJW, Wright KJ, Berry K, Freeman SE, Tatnell L. 2011. Estimation of seed production by Myosotis arvensis, Veronica hederifolia, Veronica persica and Viola arvensis under different competitive conditions. Weed Research 51: 499–507. [Google Scholar]
McWilliams EL, Landers RQ, Mahlstede JP. 1968. Variation in seed weight and germination in populations of Amaranthus retroflexus L. Ecology 49: 290–296. [Google Scholar]
Messier J, Lechowicz MJ, McGill BJ, Violle C, Enquist BJ. 2017. Interspecific integration of trait dimensions at local scales: the plant phenotype as an integrated network. Journal of Ecology 105: 1775–1790. [Google Scholar]
Mohler CL, Callaway BM. 1995. Effects of tillage and mulch on weed seed production and seed banks in sweet corn. Journal of Applied Ecology 32: 627–639. [Google Scholar]
Moles AT. 2018. Being John Harper: using evolutionary ideas to improve understanding of global patterns in plant traits. Journal of Ecology 106: 1–18. [Google Scholar]
Moles AT, Westoby M. 2006. Seed size and plant strategy across the whole life cycle. Oikos 113: 91–105. [Google Scholar]
Moles AT, Ackerly DD, Webb CO, Tweddle JC, Dickie JB, Westoby M. 2005. A brief history of seed size. Science 307: 576–580. [DOI] [PubMed] [Google Scholar]
Montesinos-Navarro A, Wig J, Pico FX, Tonsor SJ. 2011. Arabidopsis thaliana populations show clinal variation in a climatic gradient associated with altitude. New Phytologist 189: 282–294. [DOI] [PubMed] [Google Scholar]
Norris RF. 2007. Weed fecundity: current status and future needs. Crop Protection 26:182–188. [Google Scholar]
Novakovskiy AB, Maslova SP, Dalke IV, Dubrovskiy YA. 2016. Patterns of allocation CSR plant functional types in Northern Europe. International Journal of Ecology 2016: Article ID 1323614. [Google Scholar]
Pake CE, Venable DL. 1996. Seed banks in desert annuals: implications for persistence and coexistence in variable environments. Ecology 77: 1427–1435. [Google Scholar]
Parmesan C, Hanley ME. 2015. Plants and climate change: complexities and surprises. Annals of Botany 116: 849–864. [DOI] [PMC free article] [PubMed] [Google Scholar]
Paul-Victor C, Turnbull LA. 2009. The effect of growth conditions on the seed size/number trade-off. PLoS One 4: e6917. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pérez-Harguindeguy N, Díaz S, Garnier E, et al. 2012. New handbook for standardised measurement of plant functional traits worldwide. Australian Journal of Botany 61: 167–234. [Google Scholar]
Pierce S, Brusa G, Vagge I, Cerabolini BEL. 2013. Allocating CSR plant functional types: the use of leaf economics and size traits to classify woody and herbaceous vascular plants. Functional Ecology 27: 1002–1010. [Google Scholar]
Pierce S, Bottinelli A, Bassani I, Ceriani RM, Cerabolini BEL. 2014. How well do seed production traits correlate with leaf traits, whole plant traits and plant ecological strategies? Plant Ecology 215: 1351–1359. [Google Scholar]
Pierce S, Negreiros D, Cerabolini BEL, et al. 2017. A global method for calculating plant CSR ecological strategies applied across biomes world-wide. Functional Ecology 31: 444–457. [Google Scholar]
Pimm SL, Jenkins CN, Abell R, et al. 2014. The biodiversity of species and their rates of extinction, distribution, and protection. Science 344: 1246752. [DOI] [PubMed] [Google Scholar]
Preston CD, Telfer MG, Arnold HR et al. 2002. The changing flora of the UK. London: DEFRA. [Google Scholar]
Prinzing A, Durka W, Klotz S, Brandl R. 2001. The niche of higher plants: evidence for phylogenetic conservatism. Proceedings of the Royal Society B: Biological Sciences 268: 2383–2389. [DOI] [PMC free article] [PubMed] [Google Scholar]
Prusinkiewicz P, Erasmus Y, Lane B, Harder LD, Coen E. 2007. Evolution and development of inflorescence architectures. Science 316: 1452–1456. [DOI] [PubMed] [Google Scholar]
Pyke S. 2003. Catálogo Florístico de las plantas vasculares de Zaragoza. Zaragoza, Spain: Consejo de Protección de la Naturaleza de Aragón. [Google Scholar]
Raven JA. 1983. The transport and function of silicon in plants. Biological Reviews of the Cambridge Philosophical Society 58: 179–207. [Google Scholar]
Rivas-Martínez S, Díaz TE, Fernández-González F, et al. 2002. Vascular plant communities of Spain and Portugal. Addenda to the Syntaxonomical checklist of 2001. Itinera Geobotanica 15: 5–922. [Google Scholar]
Royal Botanic Gardens Kew 2015. Seed Information Database (SID). Version 7.1 http://data.kew.org/sid/ (September 2015).
Royo Pla F. 2006. Flora i vegetació de les planes i serres litorals compreses entre el riu Ebro i la serra d’Irta. Barcelona: Universidad de Barcelona. [Google Scholar]
Salisbury EJ. 1942. The reproductive capacity of plants. London: Bell and Sons. [Google Scholar]
Šerá B, Šerý M. 2004. Relation between number and weight of diaspores and reproductive strategies of herbacaeous plants. Folia Geobotanica 39: 27–42. [Google Scholar]
Shemesh H, Novoplansky A. 2013. Branching the risks: architectural plasticity and bet-hedging in Mediterranean annuals. Plant Biology (Stuttgart, Germany) 15: 1001–1012. [DOI] [PubMed] [Google Scholar]
Shipley B, Dion J. 1992. The allometry of seed production in herbaceous angiosperms. American Naturalist 139: 467–483. [Google Scholar]
Shipley B, De Bello F, Cornelissen JH, Laliberté E, Laughlin DC, Reich PB. 2016. Reinforcing loose foundation stones in trait-based plant ecology. Oecologia 180: 923–931. [DOI] [PubMed] [Google Scholar]
Shriver RK. 2016. Quantifying how short-term environmental variation leads to long-term demographic responses to climate change. Journal of Ecology 104: 65–78. [Google Scholar]
Smith CC, Fretwell SD. 1974. The optimal balance between size and number of offspring. The American Naturalist 108: 499–506. [Google Scholar]
Stebbins GL. 1974. Flowering plants: evolution above the species level. Cambridge, MA: Belknap Press. [Google Scholar]
Stebbins GL. 1985. Polyploidy, hybridization, and the invasion of new habitats. Annals of Missouri Botanical Garden 72: 824–832. [Google Scholar]
Stevens OA. 1932. The number and weight of seeds produced by weeds. American Journal of Botany 19: 784–794. [Google Scholar]
Stevens OA. 1957. Weights of seeds and numbers per plant. Weeds 5: 46–55. [Google Scholar]
Stock WD, Verboom GA. 2012. Phylogenetic ecology of foliar N and P concentrations and N:P ratios across Mediterranean-type ecosystems. Global Ecology and Biogeography 21: 1147–1156. [Google Scholar]
Sugiyama S, Bazzaz FA. 1998. Size dependence of reproductive allocation: the influence of resource availability, competition and genetic identity. Functional Ecology 12: 280–288. [Google Scholar]
The Plant List 2013. Version 1.1. Published on the Internet; http://www.theplantlist.org/ (23 January 2018).
Török P, Miglécz T, Valkó O, et al. 2013. New thousand-seed weight records of the Pannonian flora and their application in analysing social behaviour types. Acta Botanica Hungarica 55: 429–472. [Google Scholar]
Tracey AJ, Stephens KA, Schamp BS, Aarssen LW. 2016. What does body size mean, from the ‘plant’s eye view’? Ecology and Evolution 6: 7344–7351. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tutin TG, Heywood VH, Burges NA, et al. 1964–1980. Flora Europaea, Vols 1–5 Cambridge: Cambridge University Press. [Google Scholar]
Valentine DH. 1970. Evolution at zones of vegetational transition. Feddes Repertorium 81: 33–39. [Google Scholar]
Venable DL, Brown JS. 1988. The selective interactions of dispersal, dormancy, and seed size as adaptations for reducing risk in variable environments. The American Naturalist 131: 360–384. [Google Scholar]
Vendramini F, Diaz S, Gurvich DE, et al. 2002. Leaf traits as indicators of resource-use strategy in floras with succulent species. New Phytologist 154: 147–157. [Google Scholar]
Walck JL, Hidayati SN, Dixon K, Thompson K, Poschlod P. 2011. Climate change and plant regeneration from seed. Global Change Biology 17: 2145–2161. [Google Scholar]
Warton DI, Wright IJ, Falster DS, Westoby M. 2006. Bivariate line-fitting methods for allometry. Biological Reviews of the Cambridge Philosophical Society 81: 259–291. [DOI] [PubMed] [Google Scholar]
West RG. 1969. Pleistocene geology and biology. London: Longmans. [Google Scholar]
Westerman PR, Borza JK, Andjelkovic J, Liebman M, Danielson B. 2008. Density-dependent predation of weed seeds in maize fields. Journal of Applied Ecology 45: 1612–1620. [Google Scholar]
Westoby M, Jurado E, Leishman M. 1992. Comparative evolutionary ecology of seed size. Trends in Ecology & Evolution 7: 368–372. [DOI] [PubMed] [Google Scholar]
Westoby M, Falster DS, Moles AT, Vesk PA, Wright IJ. 2002. Plant ecology strategies: some leading dimensions of variation between species. Annual Review of Ecology and Systematics 33: 125–159. [Google Scholar]
Wright IJ, Reich PB, Westoby M, et al. 2004. The worldwide leaf economics spectrum. Nature 428: 821–827. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

mcaa151_suppl_Supplementary_Table_S1_S5

Click here for additional data file.^{(46.9KB, docx)}

mcaa151_suppl_Supplementary_Table_S6

Click here for additional data file.^{(199.1KB, docx)}

[CIT0001] Aarssen LW. 2008. Death without sex – the ‘problem of the small’ and selection for reproductive economy in flowering plants. Evolutionary Ecology 22: 279–298. [Google Scholar]

[CIT0002] Aarssen LW. 2015. Body size and fitness in plants: revisiting the selection consequences of competition. Perspectives in Plant Ecology Evolution and Systematics 17: 236–242. [Google Scholar]

[CIT0003] Aarssen LW, Jordan CY. 2001. Between-species patterns of covariation in plant size, seed size and fecundity in monocarpic herbs. Ecoscience 8: 471–477. [Google Scholar]

[CIT0004] Aarssen LW, Schamp BS, Pither J. 2006. Why are there so many small plants? Implications for species coexistence. Journal of Ecology 94: 569–580. [Google Scholar]

[CIT0005] Aedo C, et al. 1980. onwards. Flora Iberica: plantas vasculares de la Península Ibérica e Islas Baleares. Madrid: Consejo Superior de Investigaciones Científicas. [Google Scholar]

[CIT0006] Barton KE, Hanley ME. 2013. Seedling–herbivore interactions: insights into plant defence and regeneration patterns. Annals of Botany 112: 643–650. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0007] Botanical Society of Britain and Ireland and the Biological Records Centre 2018. Online atlas of the British and Irish flora http://www.brc.ac.uk/plantatlas (3 August 2018).

[CIT0008] Braun Blanquet J, de Bolós O. 1953. La comunidades vegetales de la Depresion del Ebro y su dinamismo. Anales de la Estación Experimental de Aula Dei 5: 1–266. [Google Scholar]

[CIT0009] Brodribb TJ. 2017. Progressing from ‘functional’ to mechanistic traits. New Phytologist 215: 9–11. [DOI] [PubMed] [Google Scholar]

[CIT0010] Burcu YE, Sadik E, Cagatay T. 2017. Inter-population variability in seed dormancy, seed mass and germination in Helianthemum salicifolium (Cistaceae), a hard-seeded annual herb. Folia Geobotanica 52: 253–263. [Google Scholar]

[CIT0011] Cerabolini BEL, Brusa G, Ceriani RM, de Andreis R, Luzzaro A, Pierce S. 2010. Can CSR classification be generally applied outside Britain? Plant Ecology 210: 253–261. [Google Scholar]

[CIT0012] Chambers J, Aarssen LW. 2009. Offspring for the next generation: most are produced by small plants within herbaceous populations. Evolutionary Ecology 23: 737–751. [Google Scholar]

[CIT0013] Chambers JC, MacMahon JA. 1994. A day in the life of a seed: movements and fates of seeds and their implications for natural and managed systems. Annual Review of Ecology and Systematics 25: 263–292. [Google Scholar]

[CIT0014] Cheffings C, Farrell L, eds.2005. The vascular plant red data list for Great Britain. Peterborough, UK: Joint Nature Conservation Committee. [Google Scholar]

[CIT0015] Cirujeda A, Aibar J, Zaragoza C. 2011. Remarkable changes of weed species in Spanish cereal fields from 1976 to 2007. Agronomy for Sustainable Development 31: 675–688. [Google Scholar]

[CIT0016] Clapham AR, Tutin TG, Moore DM. 1987. Flora of the British Isles. Cambridge: Cambridge University Press. [Google Scholar]

[CIT0017] Clauss MJ, Aarssen LW. 1994. Phenotypic plasticity of size–fecundity relationships in Arabidopsis thaliana. Journal of Ecology 82: 447–455. [Google Scholar]

[CIT0018] Cohen D. 1966. Optimizing reproduction in a randomly varying environment. Journal of Theoretical Biology 12: 119–129. [DOI] [PubMed] [Google Scholar]

[CIT0019] Crawley MJ. 2014. Seed predators and plant population dynamics. In: Gallagher RS. ed. Seeds: the ecology of regeneration in plant communities. New York: CABI Publishing, 94–110. [Google Scholar]

[CIT0020] Csontos P, Tamás J, Balogh L. 2003. Thousand seed weight records of species from the flora of Hungary, I. Monocotyledonopsida. Studia Botanica Hungarica 34: 121–126. [Google Scholar]

[CIT0021] Csontos P, Tamás J, Balogh L. 2007. Thousand seed weight records of species from the flora of Hungary, II. Dicotyledonopsida. Studia Botanica Hungarica 38: 179–189. [Google Scholar]

[CIT0022] Dalling JW, Davis AS, Schutte BJ, Arnold E. 2011. Seed survival in soil: interacting effects of predation, dormancy and the soil microbial community. Journal of Ecology 99: 89–95. [Google Scholar]

[CIT0023] Edwards W, Westoby M. 2000. Families with highest proportions of rare species are not consistent between floras. Journal of Biogeography 27: 733–740. [Google Scholar]

[CIT0024] Ehrendorfer F. 1980. Polyploidy and distribution. In: Lewis WH, ed. Polyploidy: biological relevance. New York: Plenum Press, 45–60. [Google Scholar]

[CIT0025] Ellenberg H, Weber HE, Dull R. 1992. Zeigwerte von Pflanzen in Mitteleuropa. (2nd ed.). Scripta Geobotanica 18: 1–258. [Google Scholar]

[CIT0026] Fenner M, Thompson K. 2005. The ecology of seeds. Cambridge: Cambridge University Press. [Google Scholar]

[CIT0027] Font X, Pérez-García N, Biurrun I, et al. 2012. The Iberian and Macaronesian Vegetation Information System (SIVIM, www.sivim.info), five years of online vegetation’s data publishing. Plant Sociology 49: 89–95. [Google Scholar]

[CIT0028] FAO 2018. FAOSTAT: food and agriculture data http://www.fao.org/faostat/en/#data (23 January 2018).

[CIT0029] Forget P-M, Lambert JE, Hulme PE, Vander Wall SB, eds.2005. Seed fate: predation, dispersal, and seedling establishment. Wallingford, UK: CABI Publishing. [Google Scholar]

[CIT0030] Gallart M, Mas MT, Verdu AMC. 2010. Demography of Digitaria sanguinalis: effect of the emergence time on survival, reproduction, and biomass. Weed Biology and Management 10: 132–140. [Google Scholar]

[CIT0031] Germain RM, Johnson L, Schneider S, Cottenie K, Gillis EA, MacDougall AS. 2013. Spatial variability in plant predation determines the strength of stochastic community assembly. The American Naturalist 182: 169–179. [DOI] [PubMed] [Google Scholar]

[CIT0032] Grime JP. 1974. Vegetation classification by reference to strategies. Nature 250: 26–31. [Google Scholar]

[CIT0033] Grime JP. 2001. Plant strategies, vegetation processes, and ecosystem properties, 2nd edn. Chichester: Wiley. [Google Scholar]

[CIT0034] Grime JP, Hunt R. 1975. Relative growth-rate: its range and adaptive significance in a local flora. Journal of Ecology 63: 393–422. [Google Scholar]

[CIT0035] Grime JP, Hodgson JG, Hunt R. 2007. Comparative plant ecology, 2nd edn. Dalbeattie, UK: Castlepoint Press. [Google Scholar]

[CIT0036] Gross KL. 1981. Predictions of fate from rosette size in four ‘biennial’ plant species: Verbascum thapsus, Oenothera biennis, Daucus carota, and Tragopogon dubius. Oecologia 48: 209–213. [DOI] [PubMed] [Google Scholar]

[CIT0037] Gross RS, Werner PA. 1983. Probabilities of survival and reproduction relative to rosette size in the Common Burdock (Arctium minus: Compositae). The American Midland Naturalist 109: 184–193. [Google Scholar]

[CIT0038] Han W, Fang J, Guo D, Zhang Y. 2005. Leaf nitrogen and phosphorus stoichiometry across 753 terrestrial plant species in China. New Phytologist 168: 377–385. [DOI] [PubMed] [Google Scholar]

[CIT0039] Harper JL. 1967. A Darwinian approach to plant ecology. Journal of Ecology 55: 247–270. [Google Scholar]

[CIT0040] Hodgson JG. 1986a Commonness and rarity in plants with special reference to the Sheffield Flora. II. The relative importance of climate, soils and land use. Biological Conservation 36: 253–274. [Google Scholar]

[CIT0041] Hodgson JG. 1986b Commonness and rarity in plants with special reference to the Sheffield Flora. Part III. Taxonomic and evolutionary aspects. Biological Conservation 36: 275–296. [Google Scholar]

[CIT0042] Hodgson JG. 1986c Commonness and rarity in plants with special reference to the Sheffield Flora. Part IV. A European context with particular reference to endemism. Biological Conservation 36: 297–314. [Google Scholar]

[CIT0043] Hodgson JG. 1987. Why do so few plant species exploit productive habitats? An investigation into cytology, plant strategies and abundance within a local flora. Functional Ecology 1: 243–250. [Google Scholar]

[CIT0044] Hodgson JG, Mackey JML. 1986. The ecological specialization of dicotyledonous families within a local flora: some factors constraining optimization of seed size and their possible evolutionary significance. New Phytologist 104: 497–515. [Google Scholar]

[CIT0045] Hodgson JG, Wilson PJ, Hunt R, Grime JP. 1999. Allocating CSR plant functional types: a soft approach to a hard problem. Oikos 85: 282–294. [Google Scholar]

[CIT0046] Hodgson JG, Montserrat-Martí G, Charles M, et al. 2011. Is leaf dry matter content a better predictor of soil fertility than specific leaf area? Annals of Botany 108: 1337–1345. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0047] Hodgson JG, Tallowin J, Dennis RLH, et al. 2014. Changing leaf nitrogen and canopy height quantify processes leading to plant and butterfly diversity loss in agricultural landscapes. Functional Ecology 28: 1284–1291. [Google Scholar]

[CIT0048] Hodgson JG, Santini BA, Montserrat Marti G, et al. 2017. Trade-offs between seed and leaf size (seed–phytomer–leaf theory): functional glue linking regenerative with life history strategies … and taxonomy with ecology? Annals of Botany 120: 633–652. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0049] Hodkinson DJ, Thompson K. 1997. Plant dispersal: the role of man. Journal of Applied Ecology 34: 1484–1496. [Google Scholar]

[CIT0050] Hodson MJ, White PJ, Mead A, Broadley MR. 2005. Phylogenetic variation in the silicon composition of plants. Annals of Botany 96: 1027–1046. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0051] Kattge J, Díaz S, Lavorel S, et al. 2011. TRY – a global database of plant traits. Global Change Biology 17: 2905–2935. [Google Scholar]

[CIT0052] Katz O. 2019. Plant silicon content is a functional trait: implications in a changing world. Flora 254: 88–94. [Google Scholar]

[CIT0053] Keddy P, Nielsen K, Weiher E, Lawson R. 2002. Relative competitive performance of 63 species of terrestrial herbaceous plants. Journal of Vegetation Science 13: 5–16 [Google Scholar]

[CIT0054] Kleyer M, Bekker RM, Knevel IC, et al. 2008. The LEDA Traitbase: a database of life-history traits of the Northwest European flora. Journal of Ecology 96: 1266–1274. [Google Scholar]

[CIT0055] Larios L, Pearson DE, Maron JL. 2017. Incorporating the effects of generalist seed predators into plant community theory. Functional Ecology 31: 1856–1867. [Google Scholar]

[CIT0056] Larson JE, Funk JL. 2016. Regeneration: an overlooked aspect of trait-based plant community assembly models. Journal of Ecology 104: 1284–1298. [Google Scholar]

[CIT0057] Lustenhouwer N, Moran EV, Levine JM. 2017. Trait correlations equalize spread velocity across plant life histories. Global Ecology and Biogeography 26: 1398–1407. [Google Scholar]

[CIT0058] Lutman PJW, Wright KJ, Berry K, Freeman SE, Tatnell L. 2011. Estimation of seed production by Myosotis arvensis, Veronica hederifolia, Veronica persica and Viola arvensis under different competitive conditions. Weed Research 51: 499–507. [Google Scholar]

[CIT0059] McWilliams EL, Landers RQ, Mahlstede JP. 1968. Variation in seed weight and germination in populations of Amaranthus retroflexus L. Ecology 49: 290–296. [Google Scholar]

[CIT0060] Messier J, Lechowicz MJ, McGill BJ, Violle C, Enquist BJ. 2017. Interspecific integration of trait dimensions at local scales: the plant phenotype as an integrated network. Journal of Ecology 105: 1775–1790. [Google Scholar]

[CIT0061] Mohler CL, Callaway BM. 1995. Effects of tillage and mulch on weed seed production and seed banks in sweet corn. Journal of Applied Ecology 32: 627–639. [Google Scholar]

[CIT0062] Moles AT. 2018. Being John Harper: using evolutionary ideas to improve understanding of global patterns in plant traits. Journal of Ecology 106: 1–18. [Google Scholar]

[CIT0063] Moles AT, Westoby M. 2006. Seed size and plant strategy across the whole life cycle. Oikos 113: 91–105. [Google Scholar]

[CIT0064] Moles AT, Ackerly DD, Webb CO, Tweddle JC, Dickie JB, Westoby M. 2005. A brief history of seed size. Science 307: 576–580. [DOI] [PubMed] [Google Scholar]

[CIT0065] Montesinos-Navarro A, Wig J, Pico FX, Tonsor SJ. 2011. Arabidopsis thaliana populations show clinal variation in a climatic gradient associated with altitude. New Phytologist 189: 282–294. [DOI] [PubMed] [Google Scholar]

[CIT0066] Norris RF. 2007. Weed fecundity: current status and future needs. Crop Protection 26:182–188. [Google Scholar]

[CIT0067] Novakovskiy AB, Maslova SP, Dalke IV, Dubrovskiy YA. 2016. Patterns of allocation CSR plant functional types in Northern Europe. International Journal of Ecology 2016: Article ID 1323614. [Google Scholar]

[CIT0068] Pake CE, Venable DL. 1996. Seed banks in desert annuals: implications for persistence and coexistence in variable environments. Ecology 77: 1427–1435. [Google Scholar]

[CIT0069] Parmesan C, Hanley ME. 2015. Plants and climate change: complexities and surprises. Annals of Botany 116: 849–864. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0070] Paul-Victor C, Turnbull LA. 2009. The effect of growth conditions on the seed size/number trade-off. PLoS One 4: e6917. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0071] Pérez-Harguindeguy N, Díaz S, Garnier E, et al. 2012. New handbook for standardised measurement of plant functional traits worldwide. Australian Journal of Botany 61: 167–234. [Google Scholar]

[CIT0072] Pierce S, Brusa G, Vagge I, Cerabolini BEL. 2013. Allocating CSR plant functional types: the use of leaf economics and size traits to classify woody and herbaceous vascular plants. Functional Ecology 27: 1002–1010. [Google Scholar]

[CIT0073] Pierce S, Bottinelli A, Bassani I, Ceriani RM, Cerabolini BEL. 2014. How well do seed production traits correlate with leaf traits, whole plant traits and plant ecological strategies? Plant Ecology 215: 1351–1359. [Google Scholar]

[CIT0074] Pierce S, Negreiros D, Cerabolini BEL, et al. 2017. A global method for calculating plant CSR ecological strategies applied across biomes world-wide. Functional Ecology 31: 444–457. [Google Scholar]

[CIT0075] Pimm SL, Jenkins CN, Abell R, et al. 2014. The biodiversity of species and their rates of extinction, distribution, and protection. Science 344: 1246752. [DOI] [PubMed] [Google Scholar]

[CIT0076] Preston CD, Telfer MG, Arnold HR et al. 2002. The changing flora of the UK. London: DEFRA. [Google Scholar]

[CIT0077] Prinzing A, Durka W, Klotz S, Brandl R. 2001. The niche of higher plants: evidence for phylogenetic conservatism. Proceedings of the Royal Society B: Biological Sciences 268: 2383–2389. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0078] Prusinkiewicz P, Erasmus Y, Lane B, Harder LD, Coen E. 2007. Evolution and development of inflorescence architectures. Science 316: 1452–1456. [DOI] [PubMed] [Google Scholar]

[CIT0079] Pyke S. 2003. Catálogo Florístico de las plantas vasculares de Zaragoza. Zaragoza, Spain: Consejo de Protección de la Naturaleza de Aragón. [Google Scholar]

[CIT0080] Raven JA. 1983. The transport and function of silicon in plants. Biological Reviews of the Cambridge Philosophical Society 58: 179–207. [Google Scholar]

[CIT0081] Rivas-Martínez S, Díaz TE, Fernández-González F, et al. 2002. Vascular plant communities of Spain and Portugal. Addenda to the Syntaxonomical checklist of 2001. Itinera Geobotanica 15: 5–922. [Google Scholar]

[CIT0082] Royal Botanic Gardens Kew 2015. Seed Information Database (SID). Version 7.1 http://data.kew.org/sid/ (September 2015).

[CIT0083] Royo Pla F. 2006. Flora i vegetació de les planes i serres litorals compreses entre el riu Ebro i la serra d’Irta. Barcelona: Universidad de Barcelona. [Google Scholar]

[CIT0084] Salisbury EJ. 1942. The reproductive capacity of plants. London: Bell and Sons. [Google Scholar]

[CIT0085] Šerá B, Šerý M. 2004. Relation between number and weight of diaspores and reproductive strategies of herbacaeous plants. Folia Geobotanica 39: 27–42. [Google Scholar]

[CIT0086] Shemesh H, Novoplansky A. 2013. Branching the risks: architectural plasticity and bet-hedging in Mediterranean annuals. Plant Biology (Stuttgart, Germany) 15: 1001–1012. [DOI] [PubMed] [Google Scholar]

[CIT0087] Shipley B, Dion J. 1992. The allometry of seed production in herbaceous angiosperms. American Naturalist 139: 467–483. [Google Scholar]

[CIT0088] Shipley B, De Bello F, Cornelissen JH, Laliberté E, Laughlin DC, Reich PB. 2016. Reinforcing loose foundation stones in trait-based plant ecology. Oecologia 180: 923–931. [DOI] [PubMed] [Google Scholar]

[CIT0089] Shriver RK. 2016. Quantifying how short-term environmental variation leads to long-term demographic responses to climate change. Journal of Ecology 104: 65–78. [Google Scholar]

[CIT0090] Smith CC, Fretwell SD. 1974. The optimal balance between size and number of offspring. The American Naturalist 108: 499–506. [Google Scholar]

[CIT0091] Stebbins GL. 1974. Flowering plants: evolution above the species level. Cambridge, MA: Belknap Press. [Google Scholar]

[CIT0092] Stebbins GL. 1985. Polyploidy, hybridization, and the invasion of new habitats. Annals of Missouri Botanical Garden 72: 824–832. [Google Scholar]

[CIT0093] Stevens OA. 1932. The number and weight of seeds produced by weeds. American Journal of Botany 19: 784–794. [Google Scholar]

[CIT0094] Stevens OA. 1957. Weights of seeds and numbers per plant. Weeds 5: 46–55. [Google Scholar]

[CIT0095] Stock WD, Verboom GA. 2012. Phylogenetic ecology of foliar N and P concentrations and N:P ratios across Mediterranean-type ecosystems. Global Ecology and Biogeography 21: 1147–1156. [Google Scholar]

[CIT0096] Sugiyama S, Bazzaz FA. 1998. Size dependence of reproductive allocation: the influence of resource availability, competition and genetic identity. Functional Ecology 12: 280–288. [Google Scholar]

[CIT0097] The Plant List 2013. Version 1.1. Published on the Internet; http://www.theplantlist.org/ (23 January 2018).

[CIT0098] Török P, Miglécz T, Valkó O, et al. 2013. New thousand-seed weight records of the Pannonian flora and their application in analysing social behaviour types. Acta Botanica Hungarica 55: 429–472. [Google Scholar]

[CIT0099] Tracey AJ, Stephens KA, Schamp BS, Aarssen LW. 2016. What does body size mean, from the ‘plant’s eye view’? Ecology and Evolution 6: 7344–7351. [DOI] [PMC free article] [PubMed] [Google Scholar]

[CIT0100] Tutin TG, Heywood VH, Burges NA, et al. 1964–1980. Flora Europaea, Vols 1–5 Cambridge: Cambridge University Press. [Google Scholar]

[CIT0101] Valentine DH. 1970. Evolution at zones of vegetational transition. Feddes Repertorium 81: 33–39. [Google Scholar]

[CIT0102] Venable DL, Brown JS. 1988. The selective interactions of dispersal, dormancy, and seed size as adaptations for reducing risk in variable environments. The American Naturalist 131: 360–384. [Google Scholar]

[CIT0103] Vendramini F, Diaz S, Gurvich DE, et al. 2002. Leaf traits as indicators of resource-use strategy in floras with succulent species. New Phytologist 154: 147–157. [Google Scholar]

[CIT0104] Walck JL, Hidayati SN, Dixon K, Thompson K, Poschlod P. 2011. Climate change and plant regeneration from seed. Global Change Biology 17: 2145–2161. [Google Scholar]

[CIT0105] Warton DI, Wright IJ, Falster DS, Westoby M. 2006. Bivariate line-fitting methods for allometry. Biological Reviews of the Cambridge Philosophical Society 81: 259–291. [DOI] [PubMed] [Google Scholar]

[CIT0106] West RG. 1969. Pleistocene geology and biology. London: Longmans. [Google Scholar]

[CIT0107] Westerman PR, Borza JK, Andjelkovic J, Liebman M, Danielson B. 2008. Density-dependent predation of weed seeds in maize fields. Journal of Applied Ecology 45: 1612–1620. [Google Scholar]

[CIT0108] Westoby M, Jurado E, Leishman M. 1992. Comparative evolutionary ecology of seed size. Trends in Ecology & Evolution 7: 368–372. [DOI] [PubMed] [Google Scholar]

[CIT0109] Westoby M, Falster DS, Moles AT, Vesk PA, Wright IJ. 2002. Plant ecology strategies: some leading dimensions of variation between species. Annual Review of Ecology and Systematics 33: 125–159. [Google Scholar]

[CIT0110] Wright IJ, Reich PB, Westoby M, et al. 2004. The worldwide leaf economics spectrum. Nature 428: 821–827. [DOI] [PubMed] [Google Scholar]

PERMALINK

Seed size, number and strategies in annual plants: a comparative functional analysis and synthesis

John G Hodgson

Gabriel Montserrat Marti

Bozena Šerá

Glynis Jones

Amy Bogaard

Mike Charles

Xavier Font

Mohammed Ater

Abdelkader Taleb

Bianca A Santini

Younes Hmimsa

Carol Palmer

Peter J Wilson

Stuart R Band

Amy Styring

Charlotte Diffey

Laura Green

Erika Nitsch

Elizabeth Stroud

Gemma Warham

Abstract

Background and Aims

Methods

Key Results

Conclusions

INTRODUCTION

Relationship 1: seed size vs. seed number

Relationship 2: resource allocation to seed – the key trait?

A general model incorporating relationships 1 and 2

Relationship 3: an ecological perspective – seed yield and C-S-R strategy theory

From precision to generality – methodological constraints

Objectives

A methodological caveat

MATERIALS AND METHODS

Field data and study sites

The trait dataset

The key traits

Table 1.

Sources of comparative seed yield data

C-S-R strategy

Phylogeny

Other analyses

RESULTS

Range of values for plant traits

Table 2.

Predicting comparative seed yield per plant: a test of eqns (1c) and (1d)

Table 3.

Predicting comparative seed yield per m2

Fig. 1.

Ann_C-S-R, providing an ecological context

Fig. 2.

Fig. 3.

Reproductive strategy patterns with Ann_C-S-R

Fig. 4.

Taxonomic variation in trait expression

Comparing traits of annuals in different floras

Table 4.

Fig. 5.

Table 5.

Table 6.

Inter-relationships between the annual and perennial components of vegetation

Table 7.

The changed dynamics of Ann_C-S-R strategies and seed size vs. number in the British flora

The appended database

DISCUSSION

Theoretically expected traits predict SeedMPl and SeedNoPl

Table 8.

The next steps in ‘regenerative trait-based ecology?’

Reshaping general approaches

Adding new traits

Consolidating regenerative theory

Comparative seed yield per m2

SeedNoPl, a valuable new regenerative dimension to trait-based studies of floristic change

Conclusions

Fig. 6.

SUPPLEMENTARY DATA

ACKNOWLEDGEMENTS

FUNDING

Predicting comparative seed yield per m²

Theoretically expected traits predict SeedM_Pl and SeedNo_Pl

Comparative seed yield per m²