Genetic association among feeding behavior, feed efficiency, and growth traits in growing indicine cattle

Abstract

This study aimed to estimate genetic parameters, including genomic data, for feeding behavior, feed efficiency, and growth traits in Nellore cattle. The following feeding behavior traits were studied (861 animals with records): time spent at the feed bunk (TF), duration of one feeding event (FD), frequency of visits to the bunk (FF), feeding rate (FR), and dry matter intake (DMI) per visit (DMIv). The feed efficiency traits (1,543 animals with records) included residual feed intake (RFI), residual weight gain (RWG), and feed conversion (FC). The growth traits studied were average daily gain (ADG, n = 1,543 animals) and selection (postweaning) weight (WSel, n = 9,549 animals). The (co)variance components were estimated by the maximum restricted likelihood method, fitting animal models that did (single-step genomic best linear unbiased prediction) or did not include (best linear unbiased prediction) genomic information in two-trait analyses. The direct responses to selection were calculated for the feed efficiency traits, ADG, and WSel, as well as the correlated responses in feed efficiency and growth by direct selection for shorter TF. The estimated heritabilities were 0.51 ± 0.06, 0.35 ± 0.06, 0.27 ± 0.07, 0.34 ± 0.06, and 0.33 ± 0.06 for TF, FD, FF, FR, and DMIv, respectively. In general, TF and FD showed positive genetic correlations with all feed efficiency traits (RFI, RWG, and FC), ADG, DMI, and WSel. Additionally, TF showed high and positive genetic and phenotypic correlations with RFI (0.71 ± 0.10 and 0.46 ± 0.02, respectively) and DMI (0.56 ± 0.09 and 0.48 ± 0.03), and medium to weak genetic correlations with growth (0.32 ± 0.11 with ADG and 0.14 ± 0.09 with WSel). The results suggest that TF is a strong indicator trait of feed efficiency, which exhibits high heritability and a weak positive genetic correlation with growth. In a context of a selection index, the inclusion of TF to select animals for shorter TF may accelerate the genetic gain in feed efficiency by reducing RFI but with zero or slightly negative genetic gain in growth traits.

Introduction

The feeding behavior of ruminants is characterized by the uneven distribution of a succession of discrete periods of activity (Penning et al., 1991), which is determined by the integration of central and peripheral signals from brain feeding centers (Allen, 2014), including signals that stimulate and increase hunger and inhibitory signals that increase satiety (Steinert et al., 2013). Records of feeding behavior are based on feeding events or visits to the feed bunk, which are separated by intervals of varying duration (Mendes et al., 2011). Voluntary feed intake is also the result of the diet characteristics such as composition and quality (Fitzsimons et al., 2017). In general, there are a number of feeding behavior traits that are typically studied, including the frequency and duration of visits to the feed bunk, frequency and duration of feeding, average duration and size of the meals, and feeding rate (FR; Green et al., 2013).

Considering the phenotypic differences in dry matter intake (DMI) between most and least efficient animals of beef cattle herds (Kelly et al., 2010; Fitzsimons et al., 2013) and the energy costs associated with feeding (Montanholi et al., 2009), feeding behavior probably makes an important contribution to the variation in the feed efficiency of beef cattle. In addition, the animal’s feeding behavior is generally consistent and repeatable and can be used to predict the differences in the performance and feed efficiency during its useful life (Kelly et al., 2010). Evidence indicates that feeding behavior traits could be included in breeding programs as indicators of economically important traits (Robinson and Oddy, 2004; Nkrumah et al., 2007). The medium to high heritability of these traits (Nkrumah et al., 2007; Durunna et al., 2011; Chen et al., 2014), in addition to their generally favorable genetic correlation with growth and feed efficiency traits (Chen et al., 2014), can assist the selection of beef cattle for growth and feed efficiency.

However, there is a paucity of quantitative genetic studies including feeding behavior traits and other traits of economic importance in beef cattle, and studies involving Bos indicus are even rarer. The aim of this study was to estimate genetic parameters, including genomic data, for feeding behavior, feed efficiency, and growth traits in Nellore (B. indicus) cattle.

Materials and Methods

All management procedures followed animal welfare guidelines and were conducted in accordance with State Law No. 11.977 of the State of São Paulo, Brazil.

Animals

The data used in the study were from animals belonging to the three selection lines of Nellore cattle of the Institute of Animal Science (IZ), Sertãozinho, SP, Brazil (Coutinho et al., 2015; Ceacero et al., 2016; Cardoso et al., 2018). The database of selection weight (WSel, postweaning weight adjusted to 378 d of age for males in feedlot performance tests and postweaning weight adjusted to 550 d of age for females on pasture) consisted of 9,549 animals (4,781 males and 4,768 females), born between 1978 and 2018 to 383 sires and 2,510 dams. Of these, 1,644 animals were from the control line (animals selected for average postweaning weight), 3,210 and 4,114 animals were from the selection lines selected for higher postweaning weight and for higher postweaning weight plus lower residual feed intake (RFI), respectively, and 581 animals were from the founder herd.

Feeding behavior, feed intake, and growth data

The animals were kept in individual pens (n = 679) or in two collective paddocks equipped with the GrowSafe (Airdrie, Alberta, Canada) (n = 719) or Intergado (Contagem, Minas Gerais, Brazil) (n = 145) electronic monitoring system, with ad libitum access to diet and water. The diet offered twice a day (0800 and 1500 hours) consisted of corn silage, Brachiaria hay, soybean meal, ground corn, and mineral salt + urea, with 67% total digestible nutrients and 13% crude protein at a forage:concentrate ratio of 65:35. The diet was formulated for an average daily gain (ADG) of 1.1 kg per day.

Feed intake was obtained in 30 feed efficiency tests after weaning (287 ± 38 d of age at the beginning of the test) with a minimum of 21 d of adaptation to the diet and facilities and 73 ± 11 test days. Weights were recorded at a maximum interval of 28 d. The feeding behavior data were obtained only in males kept in collective pens equipped with electronic troughs in 10 feed efficiency tests. The electronic trough systems were configured to scan the electronic identification tags of animals that enter the trough every 1.0 to 6.3 s. The start of a feeding event is defined when the tag of an animal is identified by the system. The feeding event ends when the time between the last two readings of the same tag is longer than 300 s, when the same animal is detected in another trough, or when a new tag is detected in the same trough (Mendes et al., 2011). Feeding events with a feed intake of 0 kg were discarded (Chen et al., 2014). The following feeding behavior traits were analyzed: time spent at the feed bunk (TF, average daily time the animal spent at the feed bunk during the test period, min per day), duration of one feeding event (FD, average difference between the final and initial time of each feeding event, min per visit), frequency of visits to the feed bunk (FF, average sum of feeding events of the animal per day, number per day), FR (average ratio between DMI and TF, kg/h), and DMI per visit (DMIv, average DMI during each feeding event, kg per visit).

The DMI was obtained as the average of all valid days of intake, pre-multiplied by the dry matter content of each week. The ADG was estimated as the linear regression coefficient of weights as a function of days on test $(\mathrm{D}\mathrm{O}\mathrm{T})):{\mathrm{y}}_i=\mathrm{\alpha }+\mathrm{\beta }\times \mathrm{D}\mathrm{O}{\mathrm{T}}_{\mathrm{i}}+{\mathrm{e}}_{\mathrm{i}}$, where $\mathrm{y}\mathrm{i}$ is the animal’s weight in the ith observation; $\mathrm{\alpha }$ is the intercept corresponding to the initial weight; $\mathrm{\beta }$ is the linear regression coefficient corresponding to ADG; and ${\mathrm{e}}_{\mathrm{i}}$ is the random error. The mid-test metabolic weight (BW^0.75) was estimated as: $[\alpha +(0.5\mathrm{D}\mathrm{O}\mathrm{T}\times \mathrm{A}\mathrm{D}\mathrm{G})$]. RFI was estimated as the residual of the linear regression equation of DMI on ADG and BW^0.75, and residual weight gain (RWG) as the residual of the regression equation of ADG on DMI and BW^0.75 (Koch et al., 1963) in each test group. Feed conversion (FC) was obtained as the ratio between DMI and ADG.

The WSel of males (W378) and females (W550) was assumed to be a single trait as suggested by Ceacero et al. (2016). The pedigree file included 11,405 animals.

Genotype data

A total of 1,561 animals were genotyped, 773 with the Illumina BovineHD BeadChip (770k, Illumina Inc., San Diego, CA, USA) and 788 with GeneSeek Genomic Profiler HDi 75K (GeneSeek Inc., Lincoln, NE, USA). The genotyped animals included 226 animals that belong to the control line, 385 and 948 animals that belong to each of the selection lines, and 2 founder animals. Most of the animals with records of ingestive behavior and feed efficiency had genomic information.

The genotype of animals genotyped with the lower density panel (75k) was imputed to the high definition (HD) panel using the FImpute v.3 software (Sargolzaei et al., 2014). An imputed dataset containing approximately 6,862 animals with HD genotypes was used. Quality control of the genomic data was performed, maintaining only autosomal single nucleotide polymorphisms (SNPs) with a minor allele frequency (MAF) > 0.02, P-value for Hardy–Weinberg equilibrium > 10^–5, a call rate > 92% for SNPs, and a call rate > 85% for the samples.

Quantitative genetic analysis

Animals with records for the traits studied outside the interval of ±3.5 standard deviations of the mean of the test group (year of birth × facility) or contemporary group (year of birth × selection line × sex) were removed from the database. The analysis model for the feeding behavior traits (TF, FD, FF, FR, and DMIv), feed efficiency traits (RFI, RWG, and FC), ADG, and DMI included random direct additive genetic effects, the fixed effects of test group and month of birth, linear and quadratic effects of cow age, and linear effect of animal age at the beginning of the test. For WSel, the model included random direct additive genetic effects, the fixed effects of contemporary group and month of birth, linear and quadratic effects of cow age, and linear effect of animal age at weight recording.

The (co)variance components were estimated by the maximum restricted likelihood method in two-trait ssGBLUP analysis using the BLUPF90 family of programs (Misztal et al., 2009). The heritabilities reported in the present study were estimated in two-trait analysis with WSel. The general model used can be written in matrix form as: $\mathbf{y}=\mathbf{X}\mathit{\beta }+\mathbf{Z}\mathit{\alpha }+\mathbf{e}$, where $\mathbf{y}$ is the vector of the traits observed; $\mathit{\beta }$ is the vector of fixed effects; $\mathit{\alpha }$ is the vector of direct additive genetic effects; $\mathbf{e}$ is the vector of residual effects; and $\mathbf{X}$ and $\mathbf{Z}$ are incidence matrices. In the present study, it was assumed that $\mathrm{E}\left[\mathbf{y}\right]=\mathbf{X}\mathbf{b}$, var ($\alpha$) = A  $\otimes$  Sa or var ($\alpha$) = H  $\otimes$  Sh, and var (e) = I  $\otimes$  Se, where Sa is the additive genetic (co)variance matrix; Sh is the additive genetic covariance matrix (A) combined with the genomic matrix (G); S is the residual (co)variance matrix; A is the additive genetic relationship matrix; H is the additive genetic relationship matrix based on genotype data; I is an identity matrix; and $\otimes$ is the direct product between matrices.

According to Aguilar et al. (2010), the inverse of H (H^-1) can be obtained as follows:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{H}}^{-1}={\mathbf{A}}^{-1}+\left[\begin{array}{cc}0& {\displaystyle 0}\\ 0& {\displaystyle {\mathbf{G}}^{-1}-{\mathbf{A}}_{22}^{-1}}\end{array}\right]}\end{array}}$$

where ${\mathbf{A}}^{-1}$ is the inverse of the pedigree-based relationship matrix; ${\mathbf{G}}^{-1}$ is the inverse of the genomic relationship matrix; and ${\mathbf{A}}_{22}^{-1}$ is the inverse of the pedigree-based relationship matrix for genotyped animals. According to VanRaden (2008), matrix G can be written as follows:

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{G}=\left[(\mathbf{M}-\mathbf{P}){(\mathbf{M}-\mathbf{P})}^{\prime }\right]/\left[2{\displaystyle \underset{\mathrm{j}=1}{{\displaystyle \sum ^{\mathrm{m}}}}}{\mathrm{p}}_{\mathrm{j}}(1-{\mathrm{p}}_{\mathrm{j}})\right]}\end{array}}$$

where $\mathbf{M}$ is an allele-sharing matrix with m columns (m = total number of markers) and n lines (n = total number of genotyped animals), and P is a matrix that contains the frequency of the second allele (${\mathrm{p}}_{\mathrm{j}}$), expressed as 2${\mathrm{p}}_{\mathrm{j}}$. $\mathrm{M}\mathrm{i}\mathrm{j}$ is 0 if animal i genotyped for SNP and j is homozygous for the first allele, 1 if heterozygous, and 2 if the genotype is homozygous for the second allele. Two-trait BLUP analysis was also performed using the BLUPF90 family of programs (Misztal et al., 2009) to visualize the differences in the estimates and SEs of the genetic parameters obtained with and without the inclusion of genomic information. SE for genetic parameters was calculated by repeated sampling of parameters estimates from their asymptotic multivariate normal distribution, as presented by Houle and Meyer (2015). Significant differences between BLUP and ssGBLUP genetic parameters estimates were determined using SE on a Z-test (95% confidence interval).

Direct and correlated response to selection

Direct responses to selection aimed at increasing feed efficiency (lower RFI, higher RWG, lower FC), as well as increasing ADG and WSel, were estimated using the following equation (Falconer and Mackay, 1996):

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{\Delta }{\mathrm{G}}_{\mathrm{y}}=\frac{{\mathrm{r}}_{\mathrm{T}\mathrm{I}\mathrm{y}}{\mathrm{i}}_{\mathrm{y}}{\mathrm{\sigma }}_{\alpha \mathrm{y}}}{\mathrm{G}\mathrm{I}}}\end{array}}$$

where$\mathrm{\Delta }{\mathrm{G}}_{\mathrm{y}}$ is the genetic gain per year in trait y; ${\mathrm{r}}_{\mathrm{T}\mathrm{I}\mathrm{y}}$is the accuracy of genetic prediction of y (square root of heritability in the case of selection based on the animal’s own performance); ${\mathrm{i}}_{\mathrm{y}}$is the intensity of selection; ${\mathrm{\sigma }}_{\alpha \mathrm{y}}$is the genetic variation (standard deviation of additive genetic effect) of trait y; and GI is the generation interval. Correlated responses in RFI, RWG, FC, ADG, and WSel were calculated considering direct selection for shorter TF according to the following equation (Falconer and Mackay, 1996):

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{\Delta }{\mathrm{G}}_{{}^{\mathrm{y}}╱{}_{\mathrm{x}}}=\frac{{\mathrm{r}}_{\mathrm{g}\mathrm{x}\mathrm{y}}{\mathrm{r}}_{\mathrm{T}\mathrm{I}\mathrm{x}}{\mathrm{i}}_{\mathrm{x}}{\mathrm{\sigma }}_{\alpha \mathrm{y}}}{\mathrm{G}\mathrm{I}}}\end{array}}$$

where $\mathrm{\Delta }{\mathrm{G}}_{{}^{\mathrm{y}}╱{}_{\mathrm{x}}}$ is the annual genetic gain in trait y obtained by selection based on trait x; ${\mathrm{r}}_{\mathrm{g}\mathrm{x}\mathrm{y}}$ is the genetic correlation between x and y; ${\mathrm{r}}_{\mathrm{T}\mathrm{I}\mathrm{x}}$ is the accuracy of selection based on trait x; ${\mathrm{i}}_{\mathrm{x}}$ is the intensity of selection based on trait x; ${\mathrm{\sigma }}_{\alpha \mathrm{y}}$ is the standard deviation of the additive genetic effect of y; and GI is the generation interval.

The average selection intensity on the male side (1.92) was obtained from the WSel database considering the number of males of the three selection lines that were retained for breeding (7%) in relation to the candidates for selection. The selection intensity of females was assumed to be zero. The average generation interval (3.7 years for males and 6.3 years for females) was calculated as the average age of the parents at the birth of the calves.

Results

Table 1 presents the descriptive statistics of the feeding behavior, feed efficiency, and growth traits. The animals spent on average 155 min per day at the feed bunk, with a duration of 8.11 min per feeding event. The animals visited the bunk on average 29.6 times per day, with a mean intake of 3.26 kg of dry matter per hour of feeding time and 0.35 kg of dry matter per visit.

Table 1.

Descriptive statistics and data structure

Trait	Mean ± SD	Year of birth	No. of animals	No. of genotyped animals	No. of contemporary groups
TF, min/d	155 ± 42.6	2011 to 2018	861	710	12
FD, min/visit	8.11 ± 6.07	2011 to 2018	861	710	12
FF, number/d	29.6 ± 17.1	2011 to 2018	861	710	12
FR, kg/h	3.26 ± 0.99	2011 to 2018	861	710	12
DMIv, kg/visit	0.35 ± 0.20	2011 to 2018	861	710	12
RFI, kg/d	0 ± 0.612	2004 to 2018	1,543	1,293	30
RWG, kg/d	0 ± 0.121	2004 to 2018	1,543	1,293	30
FC, kg DM/kg gain	7.39 ± 1.82	2004 to 2018	1,543	1,293	30
ADG, kg/d	1.029 ± 0.248	2004 to 2018	1,543	1,293	30
DMI, kg/d	7.33 ± 1.51	2004 to 2018	1,543	1,293	30
WSel1, kg	302 ± 51.7	1978 to 2018	9,549	1,542	236

¹W378 and W550.

The heritability estimates for the five feeding behavior traits are presented in Table 2. Heritability ranged from 0.27 for FF to 0.51 for TF. The heritabilities obtained by the ssGBLUP method for the feeding behavior, feed efficiency, and growth traits were lower, but then not significantly different, than those estimated by BLUP. The same was observed for the SEs of the estimates, which were lower or similar when ssGBLUP was used. Similarly, all models including genomic data performed better in terms of likelihood. The heritability estimates for the feed efficiency traits ranged from 0.11 to 0.17. Higher estimates were obtained for the traits composing feed efficiency (ADG and DMI) and for WSel.

Table 2.

Estimates of additive genetic (σ _a) and residual (σ _e) standard deviation components and heritability for feeding behavior, feed efficiency, and growth traits including (ssGBLUP) or not (BLUP) genomic data

Trait	Method	σ a ± SE1	σ e ± SE	h2 ± SE	−2LogL2
TF, min/d	BLUP	21.5 ± 8.89	17.1 ± 7.39	0.61 ± 0.08	95,689
	ssGBLUP	19.2 ± 7.64	18.9 ± 6.35	0.51 ± 0.06	95,596
FD, min/visit	BLUP	1.45 ± 1.85	1.77 ± 0.641	0.40 ± 0.08	91,547
	ssGBLUP	1.35 ± 0.624	1.83 ± 0.557	0.35 ± 0.06	91,464
FF, number/d	BLUP	4.46 ± 2.60	7.37 ± 2.42	0.27 ± 0.09	93,822
	ssGBLUP	4.45 ± 2.38	7.37 ± 2.22	0.27 ± 0.07	93,743
FR, kg/h	BLUP	0.359 ± 0.173	0.423 ± 0.141	0.42 ± 0.09	89,146
	ssGBLUP	0.320 ± 0.141	0.448 ± 0.141	0.34 ± 0.06	89,068
DMIv, kg/visit	BLUP	0.0657 ± 0.0344	0.0922 ± 0.0313	0.34 ± 0.08	86,447
	ssGBLUP	0.0657 ± 0.0312	0.0923 ± 0.0282	0.33 ± 0.07	86,367
RFI, kg/d	BLUP	0.281 ± 0.141	0.552 ± 0.141	0.20 ± 0.05	23,797
	ssGBLUP	0.256 ± 0.123	0.559 ± 0.141	0.17 ± 0.03	23,769
RWG, kg/d	BLUP	0.045 ± 0.0264	0.113 ± 0.0264	0.14 ± 0.04	19,183
	ssGBLUP	0.042 ± 0.0223	0.113 ± 0.0225	0.13 ± 0.04	19,153
FC, kg DM/kg gain	BLUP	0.407 ± 0.245	1.04 ± 0.245	0.13 ± 0.05	25,822
	ssGBLUP	0.373 ± 0.224	1.05 ± 0.224	0.11 ± 0.04	25,797
ADG, kg/d	BLUP	0.100 ± 0.0447	0.12 ± 0.0316	0.40 ± 0.05	19,816
	ssGBLUP	0.087 ± 0.0316	0.130 ± 0.0316	0.31 ± 0.04	19,792
DMI, kg/d	BLUP	0.589 ± 0.224	0.67 ± 0.198	0.43 ± 0.05	24,791
	ssGBLUP	0.535 ± 0.198	0.705 ± 0.173	0.36 ± 0.04	24,759
WSel3, kg	BLUP	20.9 ± 5.35	22.2 ± 4.17	0.47 ± 0.02	95,689
	ssGBLUP	19.9 ± 5.13	22.7 ± 4.037	0.43 ± 0.02	95,596

¹SE is estimated according to Houle and Meyer (2015).

²−2LogL of the maximum likelihood function.

³W378 and W550.

Table 3 presents the genetic and phenotypic correlations of the five feeding behavior traits with the feed efficiency and growth traits. In general, the genetic correlations and SEs estimated with the inclusion of genomic data (ssGBLUP) were lower than those obtained without the inclusion of genomic data (BLUP); nonetheless, genetic correlations estimates were not significantly different between methods.

Table 3.

Genetic and phenotypic correlations between feeding behavior, feed efficiency, and growth traits

Traits	TF ± SE1 (BLUP)	TF ± SE (ssGBLUP)	FD ± SE (BLUP)	FD ± SE (ssGBLUP)	FF ± SE (BLUP)	FF ± SE (ssGBLUP)	FR ± SE (BLUP)	FR ± SE (ssGBLUP)	DMIv ± SE (BLUP)	DMIv ± SE (ssGBLUP)
Genetic correlation
RFI	0.79 ± 0.11	0.71 ± 0.10	0.68 ± 0.15	0.59 ± 0.14	−0.24 ± 0.24	−0.07 ± 0.20	−0.53 ± 0.18	−0.45 ± 0.17	0.42 ± 0.18	0.41 ± 0.16
RWG	0.16 ± 0.20	0.08 ± 0.17	0.00 ± 0.23	−0.08 ± 0.19	−0.11 ± 0.35	0.02 ± 0.24	0.39 ± 0.31	0.38 ± 0.22	0.30 ± 0.31	0.15 ± 0.24
FC	0.03 ± 0.27	0.12 ± 0.19	0.12 ± 0.25	0.20 ± 0.21	0.34 ± 0.34	0.13 ± 0.27	−0.34 ± 0.30	−0.41 ± 0.26	−0.12 ± 0.28	0.01 ± 0.45
ADG	0.32 ± 0.11	0.32 ± 0.11	0.30 ± 0.14	0.22 ± 0.13	−0.21 ± 0.20	−0.15 ± 0.16	0.14 ± 0.15	0.19 ± 0.13	0.62 ± 0.12	0.39 ± 0.14
DMI	0.56 ± 0.09	0.54 ± 0.08	0.56 ± 0.11	0.49 ± 0.11	−0.23 ± 0.18	−0.21 ± 0.15	−0.06 ± 0.13	0.01 ± 0.12	0.49 ± 0.15	0.56 ± 0.11
WSel2	0.11 ± 0.09	0.14 ± 0.09	0.30 ± 0.12	0.29 ± 0.10	−0.33 ± 0.16	−0.33 ± 0.14	0.26 ± 0.11	0.25 ± 0.10	0.50 ± 0.12	0.47 ± 0.10
Phenotypic correlation
RFI	0.46 ± 0.02		0.33 ± 0.03		0.04 ± 0.03		−0.01 ± 0.03		0.31 ± 0.03
RWG	−0.02 ± 0.03		−0.04 ± 0.03		0.01 ± 0.03		−0.03 ± 0.03		−0.07 ± 0.03
FC	0.16 ± 0.03		0.15 ± 0.03		0.04 ± 0.03		0.01 ± 0.03		0.18 ± 0.03
ADG	0.20 ± 0.03		0.15 ± 0.03		−0.04 ± 0.03		0.09 ± 0.03		0.22 ± 0.03
DMI	0.48 ± 0.03		0.39 ± 0.03		−0.03 ± 0.03		0.14 ± 0.03		0.50 ± 0.02
WSel2	0.13 ± 0.03		0.17 ± 0.03		−0.11 ± 0.03		0.21 ± 0.03		0.30 ± 0.03

¹SE is estimated according to Houle and Meyer (2015).

²W378 and W550.

All feeding behavior traits exhibited some degree of genetic correlation with the feed efficiency traits. The highest genetic correlation was observed between TF and RFI (0.71 ± 0.10). In general, TF and FD showed positive genetic correlations with all feed efficiency traits and with ADG, DMI, and WSel. The FF was the only feeding behavior trait that showed a negative genetic correlation with WSel. Strong positive genetic correlations were observed for TF, FD, and DMIv with RFI and DMI.

With respect to phenotypic correlations, TF and FD were positively correlated with the feed efficiency and growth traits, except for RWG whose correlations were close to 0. The FF was not phenotypically correlated to the feed efficiency traits, ADG and DMI but was negatively correlated with WSel. The same trend was observed for FR, which was not phenotypically correlated to the feed efficiency traits and ADG but was positively weakly correlated with DMI (0.14) and WSel (0.21). A positive phenotypic correlation was observed between DMIv and the feed efficiency traits, ADG and DMI, but this trait was not phenotypically correlated to RWG.

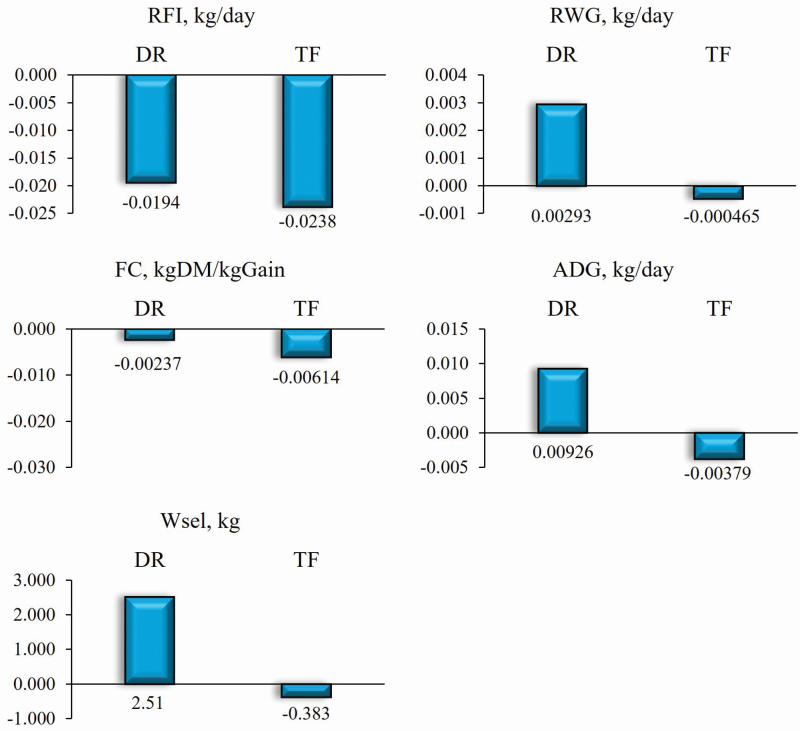
Figure 1 shows the direct response estimates considering the selection of 7% of males based on the animal’s own performance for each feed efficiency (lower RFI, higher RWG, and lower FC) and growth trait (higher ADG and higher WSel). This figure also illustrates the correlated responses in these traits to direct selection for shorter TF also based on the animal’s own performance. According to these results, direct selection for the feeding behavior trait will result in correlated responses in the feed efficiency and growth traits.

Figure 1.

Estimates of the annual direct response (DR) to selection for lower RFI, higher RWG, lower FC, and higher ADG and WSel as well as the annual correlated responses in these traits by direct selection for less TF.

Discussion

Feeding mechanisms such as feeding behavior are strongly associated with the type of diet (Durunna et al., 2011), DMI (Cantalapiedra-Hijar et al., 2018), and possible energy expenditure (Herd et al., 2019). In the present study, the feeding behavior of the animals was evaluated during the postweaning growth phase (285±36 d of age at the beginning of the test) with the animals being fed a grower diet consisting of 65% roughage. The animals spent 155 ± 42.6 min per day at the feed bunk, with a meal duration of 8.11 ± 6.07 min per visit, and visited the bunk 29.6 ± 17.1 times per day. Montanholi et al. (2010), evaluating the feeding behavior of Bos taurus at electronic troughs fed a high-roughage diet, reported a very similar TF (155.39 ± 23.36 min per day); however, the animals exhibited a longer meal duration (15.06 ± 2.42 min) and a smaller number of daily meals (9.21 ± 1.21 meals). Nkrumah et al. (2007) and Chen et al. (2014), also studying B. taurus at electronic troughs but fed a high-grain diet, found a shorter TF (66.09 ± 18.61 and 68.8 ± 11.1 min per day) and similar FF (29.62 ± 10.19 and 26.5 ± 7.3 times per day) compared with the present study. Kenny et al. (2018) conducted a meta-analysis of nine published studies on growing beef cattle receiving high-concentrate diets and showed an average daily feeding duration of 93 min. This result confirms that animals receiving high-concentrate diets spend less time feeding. Data regarding the feeding behavior of B. indicus are scarce. Pereira et al. (2016) and Aldrighi et al. (2019) evaluated the feeding behavior of B. indicus fed high-grain and high-roughage diets, respectively, using focal sampling at intervals of 5 min over a 24-h period and reported a TF of 230.49 and 240 min per day, respectively, values much higher than those recorded in the present study.

Heritability of feeding behavior traits

In the present study, the magnitude of the heritability estimates for the feeding behavior traits obtained by BLUP was slightly higher but not significantly different than that obtained by ssGBLUP, except for the heritability for FF which was the same (0.27). As expected, the estimates obtained by ssGBLUP were always associated with lower SEs. Comparing the estimates of variance components across different relationship matrices models within the same data set, Legarra et al. (2016) and Aldridge et al. (2020) showed not only slightly higher heritabilities estimates when using pedigree-based relationships but also higher minus twice the loglikelihood (worst goodness of fit) than genomic relationships models. Differently, Onogi et al. (2014) and Gordo et al. (2016) obtained higher heritability estimates by ssGBLUP compared with the BLUP method for carcass traits in Black Japanese and Nellore animals. In the study of Gordo et al. (2016), part of the animals evaluated was offspring of unknown parents, and the inclusion of genomic data thus allowed to capture a higher proportion of the additive genetic variance. In contrast to the animals evaluated by Gordo et al. (2016), the animals studied here are from three selection lines established in 1980, two of them closed to outside genetic material for four decades and one closed for three decades (Cardoso et al., 2018). These lines were maintained with 60, 120, and 180 dams and with the use of 7% of males as sires; consequently, matrix A is dense within selection lines and sparse between them, with low genetic variability within and high variability between lines. The combination of matrix A and matrix H may have contributed to the better identification of genetic similarities and differences within and between animals of the same selection line, reducing genetic variability and the heritability estimates. In the context of comparing estimates among methods, de los Campos et al. (2015) showed that the genomic heritability (using marker-based regressions) and the trait heritability parameters are equal only when all causal variants are typed.

The heritabilities estimated for the feeding behavior traits are of medium to high magnitude. Among the five traits evaluated, the highest heritability was obtained for TF, indicating that this trait is the most controlled by additive genetic effects and the least influenced by the environment and/or less measurement errors. This result is consistent with the findings of Chen et al. (2014) for Charolais cattle (B. taurus), who reported a heritability for TF of 0.49 ± 0.12. However, the same authors studying Angus animals and Nkrumah et al. (2007) and Durunna et al. (2011) investigating crossbred animals found heritability estimates of lower magnitude for TF (0.27 ± 0.09, 0.28 ± 0.12, and 0.25 ± 0.16, respectively).

On the other hand, the feeding behavior trait showing the lowest heritability was FF, indicating a greater influence of the environment and/or more measurement errors. Robinson and Oddy (2004), Nkrumah et al. (2007), Durunna et al. (2011), and Chen et al. (2014) described higher heritability estimates for this trait (0.44 ± 0.07, 0.38 ± 0.13, 0.56 ± 0.19, and 0.43 ± 0.11, respectively). In contrast to the feeding behavior traits, the heritabilities for the feed efficiency traits were of low magnitude. This finding is consistent with a meta-analysis comprising 39 heritability estimates for RFI that mainly included studies on B. taurus or composites (pooled heritability for RFI of 0.255 ± 0.008; Del Claro et al., 2012) and with previous studies involving the same Nellore selection lines (Grion et al., 2014;  Ceacero et al., 2016). For ADG, DMI, and WSel, the heritabilities ranged from medium to high and are consistent with the estimates obtained in a meta-analysis (pooled heritability for ADG and DMI of 0.31 ± 0.014 and 0.40 ± 0.012; Berry and Crowley, 2013).

Genetic and phenotypic correlations between feeding behavior, feed efficiency, and growth traits

Some of the genetic correlations estimated in the present study exhibited a high SE, especially those involving two traits of lower heritability such as FF with feed efficiency (RFI, RWG, and FC). In general, the genetic correlations estimated using matrix H (ssGBLUP) were associated with a lower SE than those estimated using matrix A (BLUP). The difference in the SE of the heritabilities and/or genetic correlations between the two methods shows that genomic data provide additional information for the estimation of breeding values, capturing variation in Mendelian sampling and resulting in more accurate variance components estimates than those obtained when only matrix A is used (Mehrban et al., 2019). In addition, the genetic correlations obtained by ssGBLUP had a lower magnitude although not significantly different than those obtained by BLUP. This finding may suggest that matrix H corrected deviations from the relationship in relation to the average relationship (matrix A), weakening the correlations between genetic effects of the two traits.

The genetic correlations between the feeding behavior and feed efficiency traits were consistent in showing a strongly (in the case of RFI) or weakly (in the case of FC) unfavorable correlation of TF, FD, and DMIv with feed efficiency, that is, animals that spend more time at the feed bunk with a longer FD and higher DMIv have the lowest feed efficiency, that is, animals with positive expected breeding value (EBV) for RFI and FC. In general, the genetic correlations estimated in the present study between the feeding behavior and feed efficiency traits had a higher magnitude but the same direction as those reported in other studies. Chen et al. (2014) reported genetic correlations of 0.44 ± 0.19 and 0.29 ± 0.17 and Robinson and Oddy (2004) and Nkrumah et al. (2007) of 0.35 ± 0.17 and 0.57 ± 0.28, respectively, between TF and RFI, suggesting that the selection of more efficient animals (lower RFI) also tends to select animals that spend less time at the feed bunk. These genetic relationships may indicate that more efficient animals (negative EBV for RFI and FC) behave as less gluttonous animals or have less appetite. According to Lines et al. (2018), selection for divergence in RFI has led to cattle that differ in feed intake, with negligible differences in postweaning weight and ADG, and differences in RFI can be attributed to appetite (energy demand).

The strong and negative genetic correlations between FR and RFI (and also between FR and FC despite the high SE of the latter) also show that genetically more efficient animals (lower EBV for RFI and FC) tend to have a higher FR, suggesting that these animals eat faster and consume a larger amount of feed per unit of time. Interestingly, these results are consistent with reports on the effect of selection for feed efficiency in pigs. Feed efficiency may be affected by feed intake behavior. Differences between lines of Yorkshire pigs show that feeding behavior may be a determinant of the feed efficiency of an animal. Low-RFI pigs ate faster and less per day and spent less time eating per day than the nonselected animals, even after adjusting for differences in feed intake. Feed efficiency may be affected by feed intake behavior because selection for decreased RFI has resulted in pigs that spend less time eating and eat faster (Young et al., 2011).

Positive moderate to high genetic correlations of the feeding behavior traits with ADG and DMI were also described in other studies on B. taurus (Nkrumah et al., 2007; Chen et al., 2014) and confirm that, in cattle, these traits are linked to pathways that regulate hunger and satiety (Nkrumah et al., 2007). The positive correlations of feeding behavior traits with ADG, DMI, and WSel show that animals with higher EBV for TF, FD, and DMIv have higher EBV for feed intake and weight gain and may be heavier at selection.

The average EBV of the sample of animals from the three Nellore selection lines with records of the five feeding behavior traits (born from 2011 to 2018) shows that the selection for postweaning weight performed for four decades (Coutinho et al., 2015; Ceacero et al., 2016; Cardoso et al., 2018) has resulted in animals with higher EBV for WSel (14.5, 69.3, and 72.2 kg for the control and for the two selection lines, respectively). However, these animals also exhibit higher EBV for TF (−12.1, 7.99, and 10.4 min per day for the control and for the two selection lines, respectively), FD (−0.352, 1.15, and 1.32 min per visit), DMIv (−0.003, 0.112, and 0.099 kg), ADG (−0.224, 0.070, and 0.041 kg per day), and DMI (−1.42, 0.366, and 0.176 kg per day)). These results suggest that selection for weight can lead to animals with greater appetite.

The phenotypic correlations between traits were generally of low magnitude, except for the correlations of TF, FD, and DMIv with RFI and DMI, which were positive and strong. There was no evidence of a phenotypic correlation of FF or FR with feed efficiency. Kenny et al. (2018) conducted a meta-analysis of nine published studies on growing beef cattle receiving high-concentrate diets and also found that high-RFI cattle spent more time eating (10.3 min longer, or 0.12 more) than their low-RFI contemporaries. In contrast to the findings of the present study, the 0.17 proportionately higher DMI of the high-RFI animals in that analysis implies that they also had a faster eating rate than the low-RFI animals (Cantalapiedra-Hijar et al., 2018).

Direct and correlated responses to selection

Unfavorable genetic correlations between traits make it hard to deliver a breeding goal, and this may well be one of the most important limitations to all breeding programs (Knap, 2020). Therefore, even if a given selection scheme aims to improve only one trait, the genetic correlations show that selection for feeding behavior traits will affect the expression of feed efficiency and growth, and vice versa, with consequent favorable or unfavorable correlated responses. For a better understanding of the correlated responses, it is important to know the desired direction of selection, that is, if the favorable direction is an increase or decrease in the average of the trait. For RFI, which is DMI phenotypically corrected for weight gain and metabolic weight, and FC, which is the amount of feed necessary for each kilogram of gain, a decrease is desirable. For the other feed efficiency trait (RWG, which is weight gain phenotypically corrected for DMI and metabolic weight) and for ADG and WSel, an increase in the average is desirable.

Direct selection for shorter TF will provide annual genetic gains in RFI of −0.0238 kg per day, that is, a reduction in the EBV of animals for DMI of −0.0238 kg per day without theoretically altering the weight gain of the animals. On the other hand, in the case of direct selection for lower RFI, a reduction of −0.0194 kg per day is expected and the efficiency of indirect selection, in this case, is 122% of direct selection. However, selection for shorter TF will result in a zero or slightly negative genetic gain for RWG, ADG, and WSel. Correlated responses superior to direct responses are due to strong genetic correlations between traits and to the greater accuracy of EBV prediction (considering selection based on the animal’s own performance, accuracy is the root square of heritability) for the indicator trait used for indirect selection. Although selection based on the phenotypic value of a feeding behavior trait, which can be recorded concomitantly with feed efficiency traits, is a very simplistic scenario, this result shows that TF should be included in the selection index to accelerate the genetic gain of animals for increased feed efficiency. In addition, selection based on a trait of low heritability such as RFI has a high probability of co-selecting relatives and leads to an increase in inbreeding. In this respect, the inclusion of TF in the selection for increased feed efficiency will certainly minimize the increase in inbreeding because of its high heritability.

In conclusion, the feeding behavior traits of growing Nellore cattle exhibit sufficient genetic variability to respond to direct selection, and the magnitude of their heritability estimates is higher than that of feed efficiency and growth traits. The TF seems to be a strong indicator trait of feed efficiency, which has a high heritability and high and positive genetic correlation with RFI and lower genetic correlations with growth.

Glossary

Abbreviations

ADG

average daily gain

BW^0.75

mid-test metabolic weight

DMI

dry matter intake

DMIv

dry matter intake per visit

FC

feed conversion

FD

duration of one feeding event

FF

frequency of visits to the feed bunk

FR

feeding rate

MAF

minor allele frequency

RFI

residual feed intake

RWG

residual weight gain

TF

time spent at the feed bunk

WSel

weight at selection

Conflict of interest statement

The authors declare that there is no conflict of interest regarding the publication of this research article.