Abstract
Human induced pluripotent stem cell (iPSC)-derived cardiomyocytes are an established model for testing potential chemical hazards. Interindividual variability in toxicodynamic sensitivity has also been demonstrated in vitro; however, quantitative characterization of the population-wide variability has not been fully explored. We sought to develop a method to address this gap by combining a population-based iPSC-derived cardiomyocyte model with Bayesian concentration-response modeling. A total of 136 compounds, including 54 pharmaceuticals and 82 environmental chemicals, were tested in iPSC-derived cardiomyocytes from 43 nondiseased humans. Hierarchical Bayesian population concentration-response modeling was conducted for 5 phenotypes reflecting cardiomyocyte function or viability. Toxicodynamic variability was quantified through the derivation of chemical- and phenotype-specific variability factors. Toxicokinetic modeling was used for probabilistic in vitro-to-in vivo extrapolation to derive population-wide margins of safety for pharmaceuticals and margins of exposure for environmental chemicals. Pharmaceuticals were found to be active across all phenotypes. Over half of tested environmental chemicals showed activity in at least one phenotype, most commonly positive chronotropy. Toxicodynamic variability factor estimates for the functional phenotypes were greater than those for cell viability, usually exceeding the generally assumed default of approximately 3. Population variability-based margins of safety for pharmaceuticals were correctly predicted to be relatively narrow, including some below 10; however, margins of exposure for environmental chemicals, based on population exposure estimates, generally exceeded 1000, suggesting they pose little risk at current general population exposures even to sensitive subpopulations. Overall, this study demonstrates how a high-throughput, human population-based, in vitro-in silico model can be used to characterize toxicodynamic population variability in cardiotoxic risk.
Keywords: toxicodynamic, population variability, drug, environmental chemical, in vitro
Current risk assessments address population variation in susceptibility by the use of a default uncertainty factor (UF) of 10 for human variability. This factor is divided equally into toxicokinetic (TK) and toxicodynamic (TD) variability components, each having a value of 101/2 (Laverty et al., 2011; Meek et al., 2002; WHO/IPCS, 2005). Although there is a long history of population TK modeling driven by the needs of drug development (Andersen and Dennison, 2002; Sun et al., 1999), only in recent years has there been an increased effort to develop population-based models that may provide valuable estimates of diversity in TD responses to chemicals (Abdo et al., 2015; Burnett et al., 2019; Grimm et al., 2018). Specifically, several approaches aim to quantify population variability in the form of a toxicodynamic variability factor (TDVF), defined as the ratio between the effective concentration (EC) for the median individual and that for a sensitive individual, such as the 5th or 1st percentile of the population (Chiu et al., 2017). The resulting TDVF values can then be used as a chemical-specific adjustment factor to derive risk-based estimates for that compound through the replacement of the default UF (WHO/IPCS, 2005).
An emerging in vitro model for testing both hazard and risk for cardiotoxicity in a population is human induced pluripotent stem cell (iPSC)-derived cardiomyocytes (Burridge et al., 2016; Karakikes et al., 2015; Sharma et al., 2018). A number of studies have used patient-derived iPSC cardiomyocytes to replicate congenital cardiac abnormalities and interindividual variability in drug toxicity (Kilpinen et al., 2017; Magdy et al., 2018). Grimm et al. (2018) established that a compendium of iPSC-derived cardiomyocytes from nondiseased individuals can reliably reproduce both baseline and chemical-induced interindividual variability; this study found that observed variability was primarily driven by intrinsic factors specific to each donor, rather than experimental factors. Burnett et al. (2019) recently showed how this model can be used as a screening tool for hazard assessment of environmental chemicals and drugs, examining the population variability with iPSC cardiomyocytes from 43 nondiseased donors. By combining this in vitro model with in silico Bayesian concentration-response modeling, we have previously shown that accurate prediction of in vivo concentration-QTc relationships for 13 pharmaceuticals can be achieved (Blanchette et al., 2019). Furthermore, we demonstrated how this approach could serve as an alternative to the human Thorough QT/QTc test (Blanchette et al., 2019; E14 Implementation Working Group, 2015).
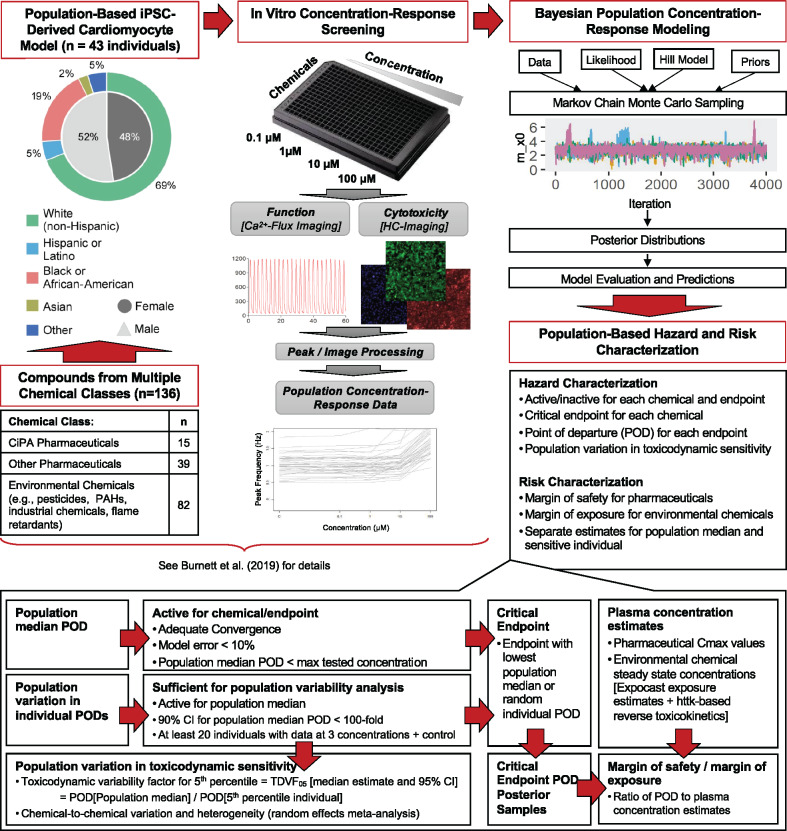
Here, we sought to conduct a quantitative evaluation of the population-wide TD variability in potential cardiotoxicity hazards for a wide array of pharmaceuticals and environmental chemicals (Figure 1). Specifically, we apply the Bayesian concentration-response (C-R) modeling approach from Blanchette et al. (2019) to a recently published dataset from a large population of iPSC cardiomyocytes derived from 43 individuals that were treated with 136 compounds (Burnett et al., 2019). In addition to deriving statistically rigorous estimates of bioactivity and potency, Bayesian population modeling enables quantification of TD variability through the derivation of chemical- and endpoint-specific TDVF. In addition, we demonstrate how probabilistic in vitro-to-in vivo extrapolation (IVIVE) can be used to derive margins of safety (MOS) for pharmaceuticals and margins of exposure (MOE) for environmental chemicals, while accounting for population variability (Figure 1).
Figure 1.
Workflow for data collection, Bayesian modeling, and hazard and risk characterization.
MATERIALS AND METHODS
In vitro Experimental Data
The chemicals, iPSC-derived cardiomyocyte lines, Ca2+ flux assay, and high-content imaging assays were previously described in Burnett et al. (2019). Briefly, a panel of 136 test chemicals (Supplementary Table 1), including compounds identified as part of the Comprehensive In Vitro Pro-Arrhythmia Assay (CiPA) initiative, was provided by the U.S. Environmental Protection Agency, National Center for Computational Toxicology (Research Triangle Park, North Carolina). Deidentified iPSC-derived cardiomyocytes from 43 donors with no known cardiovascular disease or familial history of cardiovascular disease were obtained from Fujifilm Cellular Dynamics (Madison, Wisconsin). The methods for in vitro testing of cardiomyocytes were previously reported (Burnett et al., 2019). The donor population (Supplementary Table 2) was representative of the U.S. population, consisting of 52% male and 48% female donors representing White (69%), Hispanic or Latino (5%), African-American (24%), and Asian (2%) ancestry (Burnett et al., 2019) as identified using the Infinium 147 Global Screening Array-24 v2.0 Kit (Cat. No. 20024444, Illumina, San Diego, California). Catalog numbers and demographic information for the donors was previously reported (Burnett et al., 2019). The iPSC cardiomyocytes were treated with chemicals, and analyzed with both a Ca2+ flux assay and high content imaging to evaluate both functional performance and viability following a 90-min treatment. Ca2+ flux data were imported in RStudio (version 1.2.1335, R version 3.6.0) and analyzed with a peak processing algorithm previously described (Blanchette et al., 2019). High-content cell imaging was performed using an established protocol in the ImageXpress Micro Confocal Cellular Imaging System (Molecular 183 Devices) as described previously (Burnett et al., 2019; Grimm et al., 2015, 2018; Sirenko et al., 2017). Image processing and quantification were performed using the multi192 wavelength cell scoring module in the instrument-specific MetaXpress software package. All experiments included testing in C-R format, with both positive and negative intraplate controls (Burnett et al., 2019).
Statistical Analysis: Bayesian Population Concentration-response Modeling of In Vitro Data
Data on total cell count (cytotoxicity), peak frequency, and decay-rise ratio (defined as the ratio of the time from peak maximum to baseline and the time from baseline to peak maximum) were used in these analyses (Blanchette et al., 2019; Burnett et al., 2019; Grimm et al., 2018; Sirenko et al., 2017). A total of 5 phenotypes (Table 1) were used to derive points of departure (PODs) as follows. Positive and negative chronotropy were defined as a 5% increase or decrease relative to controls in peak frequency, with PODs represented by the EC at the 5% change. Asystole was defined as a 95% decrease in peak frequency, and its POD represented by the EC95. The POD for delayed action potential leading to QT prolongation was represented by the EC05 for the decay-rise ratio, which was demonstrated in Blanchette et al. (2019) to be an accurate in vitro surrogate for in vivo QTc increases. Cytotoxicity is represented by the EC10 for Total Cells (cytotoxicity), indicating a decrease in 10% in viability from its control value, consistent with previously published methods (Abdo et al., 2015; Chiu et al., 2017).
Table 1.
Phenotypes Examined in This Study, Their Abbreviation, the In Vivo Equivalent, and Description of Data Preprocessing Conducted, If Any
| In Vivo Phenotype | In Vitro Endpoint | Positive Control | Data Preprocessing |
|---|---|---|---|
| Cytotoxicity | 10% decrease in total cells |
|
None |
| QT prolongation | 5% increase in decay/rise ratio |
|
Data with amplitude = 0 dropped; concentrations above notch dropped |
| Positive [+] chronotrope | 5% increase in peak frequency |
|
Data with amplitude = 0 dropped |
| Negative [−] chronotrope | 5% decrease in peak frequency |
|
Data with amplitude = 0 dropped |
| Asystole | 95% decrease in peak frequency |
|
None |
For C-R modeling, additional preprocessing was performed depending on the phenotype. For the positive chronotropy, negative chronotropy, and QT prolongation phenotypes, any concentrations with no beating cells were omitted to avoid confounding or nonmonotonicity caused by asystole or cytotoxicity. In addition, for QT prolongation, any concentrations above the development of a “notch” phenotype were also removed, as described by Blanchette et al. (2019). This is done because “notch” formation always occurs at concentrations above the EC05 for decay-rise ratio, and because responses often become nonmonotonic (eg, decrease in amplitude and decay-rise ratio and increase in peak frequency) or irregular. For asystole and cytotoxicity, no preprocessing was performed.
Population concentration-response modeling was conducted in an R (version 3.5.0) module on the Texas A&M High Performance Research Computing Core. For each compound, concentration-response data for all phenotypes was fit using hierarchical Bayesian random-effects Hill models as described in Chiu et al. (2017). An “upward” Hill model, was used for positive chronotropy and QT prolongation, and reparametrized as follows at the donor level:
| (1) |
The variable y is the calculated response, y0 is the baseline value, x is the nominal treatment concentration, x0 is the concentration at half the maximal response, Emax is the maximal fractional change from baseline, n is the Hill coefficient, and ε is the residual error. All model parameters are held to be strictly positive and as such were natural-log transformed for analysis. A “downward” version of this model was used for negative chronotropy. Parameterization was changed as follows:
| (2) |
To avoid pathological parameter values and improve convergence, the model hyperparameter natural log-transformed population mean of Emax (m_Emax) was restricted to be > −3, and that for the natural log-transformed hill parameter (m_n) was restricted within the range between −2 and 2. Finally, for asystole and cytotoxicity, a further simplified “zero” version of the model was used that does not include Emax, under the assumption that responses will eventually to go to zero. Here, the model was parameterized as follows using the same restrictions to m_n as the “downward” model:
| (3) |
For all models, the natural log-transformed parameters were assumed to have normal random effects; ie, that individuals in the population were distributed normally given population mean and standard deviation hyperparameters. Prior distributions for hyperparameters were normal for population means and half-normal for population standard deviations. The error ε was assumed to follow a scaled Student’s t distribution with scale parameter σ, where (ε/σ) has a standard Student’s t distribution, with ν = five degrees of freedom, to be robust for outliers (Chiu et al., 2017).
Posterior distribution sampling was conducted using the Markov chain Monte Carlo algorithm through R (version 3.5.0) interfaced with the STAN software package (version 2.17.3) on the Texas A&M Univeristy High Performance Research Computing Core. Simulations consisted of 4 chains of 8000–36 000 iterations each, the first half of which being warm-up iterations that were subsequently discarded. Depending on what was required for convergence, chemicals and endpoints varied in the number of iterations used (Supplementary Table 3). For the “upward” and “downward” models, the tuning parameters adapt_delta (step size) and max_treedepth (number of steps taken in the random walk) were increased from their default values of 0.8 and 10 to 0.99 and 15, respectively to improve the efficiency of the modeling and prevent the occurrence of divergent transitions. For each parameter, both interchain and intrachain variability was assessed to determine convergence, with the potential scale reduction factor ≤ 1.2 considered converged (Gelman and Rubin, 1992). If convergence was not reached for a given chemical and endpoint, the iterations of the simulation were increased up to 36 000 per chain. Should convergence still not be reached for a given chemical and endpoint, it was not used in subsequent data analysis. A total of 1,000 posterior samples (4 chains, 250 random samples/chain) were saved for further analysis.
Hazard Characterization
Phenotype- and chemical-specific activity calls
All subsequent data processing and analysis were conducted in R (3.6.0). For each compound-endpoint combination, the results were evaluated using the following criteria: (1) convergence was reached as indicated by ≤1.2; (2) model scale parameter for the error (σ) across the 4 chains was less than or equal to 0.1, indicating less than about 10% typical error in concentration-response fit; and (3) the median estimate for the median individual POD was below the top concentration tested, so that the POD is not extrapolated beyond the range of the data. Compounds that fulfilled the criteria for convergence, C-R fit, and POD < top tested concentration were considered “active” in terms of their cardiotoxicity hazard at the population median level for that endpoint. Inactivity, then, may reflect either inadequate convergence, inadequate concentration-response fits, or inadequate potency (POD above the tested concentration range).
To be considered sufficient for population variability analysis, compounds had to satisfy the following criteria in addition to the aforementioned criteria for activity: (1) dose-response data after any preprocessing were available for at least 20 individuals for at least 3 concentrations above the control, so there were sufficient individuals with adequate data to estimate population variability; and (2) the quotient of the 95th and 5th percentile estimates for the median individual POD was under 100, so that chemicals/endpoints for which concentration-response fits had more than two orders of magnitude uncertainty are dropped.
Compounds therefore can be considered active but insufficient for population variability analysis. Due to these criteria, 2 endpoints, positive chronotropy and cytotoxicity, have 2 positive controls for their effects. Although both isoproterenol and tetraoctyl ammonium bromide were used as positive controls in previous studies (Grimm et al., 2018; Sirenko et al., 2017) for these phenotypes, these compounds had maximal effects at the lowest tested concentration above controls (isoproterenol) or were not tested in C-R (tetraoctyl ammonium bromide). Thus, these compounds were found to be insufficient for population variability analysis, as isoproterenol had a high levels of median individual POD uncertainty and tetraoctyl ammonium bromide had a lack of dose response data. Therefore, nifedipine (positive chronotropy) and terfenadine (cytotoxicity) were also used as positive controls due to both having well-established activity for these phenotypes and being testing in C-R (O'Brien, 2014; Sato et al. 2001; Snider and Veverka, 2008; Woosley et al., 1993).
Chemical-specific critical phenotype determination
For each compound that was active for at least one endpoint, a critical phenotype (PCrit) was determined as follows. For each iteration out of the 1000 samples saved for analysis, a POD based on the population median and a POD estimate derived from a simulated “random” individual (ie, using simulated Z-scores to account for interindividual variability) were taken, and the lowest POD across all active phenotypes is considered the PCrit for that iteration. This process was repeated for each of the iterations and the phenotype most commonly found to be the most sensitive was determined to be the chemical-specific PCrit.
Population variation in TD sensitivity
If a compound was found to be sufficient for population variability analysis for a given phenotype, population variability in the POD was estimated. Specifically, for each phenotype, the toxicodynamic variability factor at 5% (TDVF05) as defined as the ratio of the POD for the median individual to the POD for the most sensitive 5th percentile individual. For instance, for cytotoxicity, the POD we use at the individual level is the EC10 corresponding to a 10% response (Table 1). If we denote as the EC10 for the median individual, and as the EC10 for the 5th percentile individual, then the TDVF05 = /. The generally accepted default fixed UF for TD variability was considered to be 101/2, or half an order of magnitude, corresponding to TDVF = 3.16 (WHO/IPCS, 2005). Uncertainty in the POD estimates was also incorporated, so the TDVF05 included a central tendency (median) estimate and 95% CI, and was derived for all compounds that were found to be sufficient for population variability analysis.
To estimate the chemical-to-chemical heterogeneity in TDVF05 values for a given endpoint, a random-effects meta-analysis approach was employed for all compounds sufficient for population variability analysis for a given endpoint and implemented using the R metafor package version 2.1 (Viechtbauer, 2010). Although a Bayesian method was considered for use to estimate chemical-to-chemical heterogeneity, a traditional frequentist method was ultimately selected due to the availability and general familiarity with standard meta-analysis methods, especially methods to test for and estimate heterogeneity. In addition, whereas it is possible, in principle, to combine all the concentration-response analyses across all chemicals in a single hierarchical analysis, we decided against this approach because of the computational burden as well as additional complexity in communicating the results. First, TDVF05 values were converted to the natural log σH under the assumption of a log-normal distribution for human population variability: TDVF05=exp(Z0.95×σH) where Z0.95=1.645, the Z-score for the 95th percentile. Log σH is related to another metric for population variability, the geometric standard deviation for human variability GSDH=exp(σH). The additional log transformation for σH was motivated by the observation by WHO/IPCS that log σH is approximately normally distributed across chemicals, as well as the fact that the posterior uncertainty distributions for log σH are approximately symmetric. For each endpoint, the log σH values were combined using standard random effects meta-analysis, and chemical-specific best linear unbiased predictions (random effects shrunken estimates) were derived. We then converted log σH back to TDVF05, and compared the results from 2 previous studies of TD variability: (1) Chiu et al. (2017), which reanalyzed data from Abdo et al. (2015) on in vitro cytotoxicity screening of lymphoblastoid cells derived from > 1000 individuals tested with 179 chemicals; and (2) WHO/IPCS (2018), which reanalyzed data from Hattis and Lynch (2006) on human in vivo TD variability of 22 chemicals, some evaluated for multiple endpoints. Because these previous studies derived TDVF01 values, they were converted to TDVF05 values with the conversion formula TDVF05 = where z01 and z05 are Z-scores for the 1% and 5% individuals equaling about −2.32 and −1.64 respectively.
Risk Characterization Using a Probabilistic IVIVE Analysis
Pharmaceuticals
For pharmaceuticals with at least one active phenotype and available human pharmacokinetic data, potential risk was characterized by comparing sampled in vitro PCrit POD values across 1000 iterations with Cmax values similarly sampled from a pool of values sourced from the PharmaPendium database (with replacement and excluding outliers), to derive a MOS. The MOS is a risk indicator of the degree of possible overlap between maximum blood concentrations of a drug when administered as intended and the estimated PCrit POD. The risk characterization was carried out in a probabilistic context which allows for a capture of uncertainty and variability in both exposure and TD. Thus, POD values and in vivo blood concentrations were sampled from statistical distributions. For each pharmaceutical and in vitro phenotype, separate distributions were sampled for the population median POD and a “random” individual POD (generated by randomly sampling the population medians and variances as well as generating random Z-scores for each parameter). From each type of POD, 2 MOS calculations were made: the MOS for a median individual, estimated by dividing the 5th percentile POD from the population median distribution by the 95th percentile blood concentration; and the MOS for a sensitive individual, calculated by dividing the 5th percentile POD from the random individual distribution by the 95th percentile blood concentration. Should a compound be included in the IVIVE analysis and have an PCrit that was not sufficient for population variability analysis, only the population median distribution was produced and only the median individual MOS was calculated.
Environmental chemicals
For environmental compounds, the same probabilistic method as detailed for the pharmaceuticals was used in deriving the two types of PODs and an equivalent measurement of risk, the MOE. However, the derivation of the in vivo blood concentration used for the environmental chemicals was conducted differently. Exposure predictions were sourced from Expocast through the EPA CompTox database and from the values published by Ring et al. (2019). Oral exposure estimates were then sampled from a lognormal distribution fit to these exposure estimates. Each exposure sample was then converted to a steady-state plasma concentration (Css) using the httk package (Pearce et al., 2017) (version 1.9.2) in R, using the sampled exposure value and the population median value outputted by the calc_mc_css function, executed with a chemical-specific physiologically based toxicokinetic model. In preliminary tests, we found that using Monte Carlo samples for the TK conversion to Css outputs resulted in only small differences (due to the much larger uncertainty in exposure estimates), so population median values for TK conversion to Css were used to simplify the analysis. Both the MOE for a median individual and the MOE for a sensitive individual were then calculated using the same approach as the MOSs for pharmaceuticals.
RESULTS
Bayesian Population Concentration-response Modeling
Population C-R modeling was conducted on 136 test compounds and 5 phenotypes: positive chronotropy, negative chronotropy, QT prolongation, asystole, and cytotoxicity (Figure 2). With sufficient number of Markov Chain Monte Carlo samples, most models for all compounds and phenotypes adequately converged except for 2 compounds for positive chronotropy, one compound for QT prolongation, seven compounds for asystole, and one compound for cytotoxicity (see Supplementary Table 3). The C-R data for each compound, phenotype, and individual are provided in supplemental materials (Supplementary Figs. 1 and 2). Across the five phenotypes, most compounds converged at 8000 or 16 000 iterations, only 7 compounds required more. Model fits across all compounds, regardless of whether they were found to be active or not, were largely adequate. Median estimates of the model scale parameter σ across all compounds were 0.056, 0.057, 0.052, 0.064, and 0.076 for positive chronotropy, negative chronotropy, QT prolongation, asystole, and cytotoxicity, respectively.
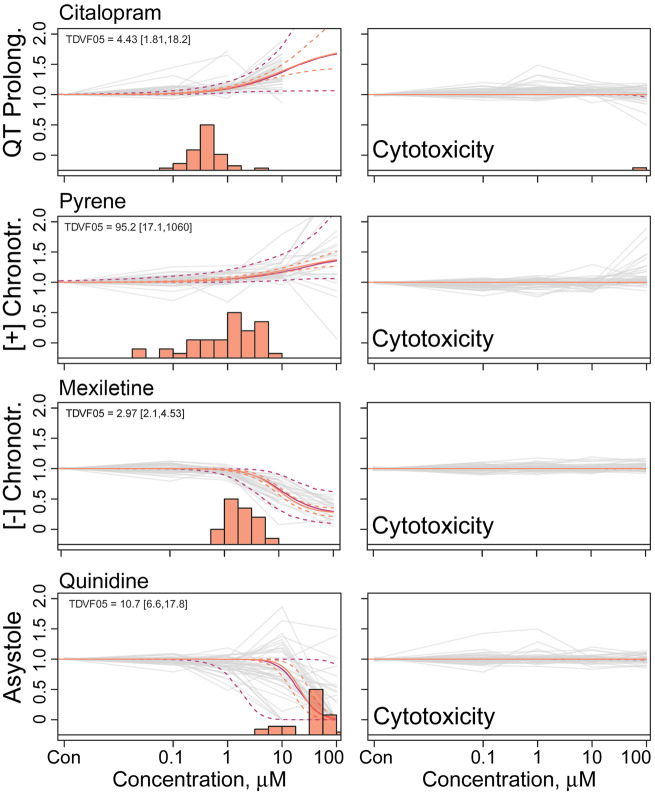
Figure 2.
Population concentration response modeling of representative compounds for each phenotype. All compounds shown are considered active for their respective functional endpoint. Orange and purple solid and dotted lines reflect the median estimate and 90% CI of the population median and the “random” individual, respectively. In vitro data for each donor is shown as a gray line. Histogram of median estimates for the 43 individuals’ point of departure is shown at the bottom of each plot. Each representative compound’s cytotoxicity concentration-response (C-R) is shown to the right of its C-R for one of the four other phenotypes.
Hazard Characterization
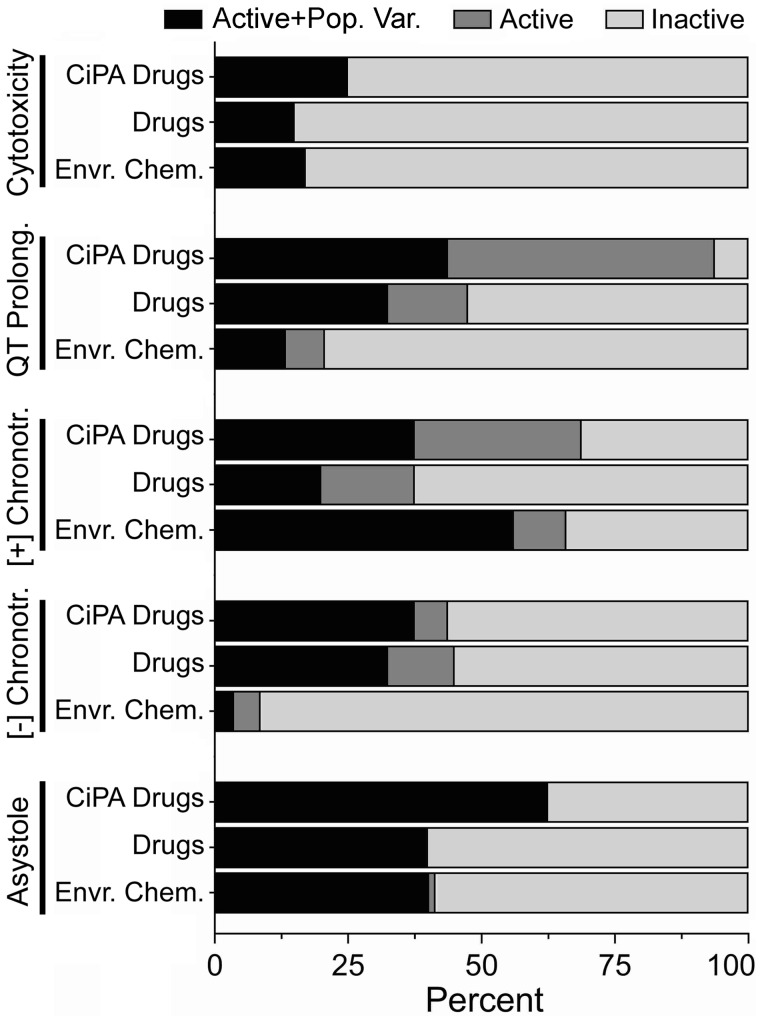
The results of the hazard characterization step of the analysis are summarized in Figure 3. Overall, the smallest degree of activity across all compound classes was observed for the cytotoxicity phenotype, with less than 25% of compounds active regardless of chemical class. The QT prolongation phenotype had the greatest percentage of CiPA drugs being both active and sufficient for population variability analysis. The negative chronotropy phenotype mostly had activity with drugs (both CiPA and non-CiPA), with little representation from the environmental chemicals. This is in contrast with the positive chronotropy phenotype, which was dominated by environmental chemicals, followed by CiPA drugs and then non-CiPA drugs. The asystole phenotype had broad activity across all compound classes, with a minimum of 40% of compounds in each class being active and sufficient for population variability analysis. Detailed hazard characterization results for each compound and phenotype are shown in Supplementary Table 4.
Figure 3.
Cardiotoxicity hazard characterization. Percentage of compounds for each phenotype that were found to be active and sufficient for population variability analysis (“Active+Pop. Var.”), active but insufficient for population variability analysis (“Active”), and inactive and insufficient for population variability analysis (“Inactive”), differentiated by color intensity and separated by class.
Figure 4 shows, for each chemical class, the distribution of PCrit designations as defined by the effect with the lowest POD, across the 1000 iterations of the sampling analysis. Although a PCrit was determined at both the population level and the individual level, the designations were identical for all chemicals in the analysis. Cytotoxicity was found to the PCrit for one compound—the pesticide captan. Similarly, the second viability phenotype, asystole, was identified as PCrit for only 4 compounds, the industrial chemical 3,4-dichlorophenyl isocyanate, the food additives 4-hexylresorcinol and propyl gallate; and the flame retardant 3,3′,5,5′-tetrabromobisphenol A. The CiPA drugs were most likely to elicit QT prolongation as their critical effect, with positive chronotropy also having a significant representation among this class of test compounds. Non-CiPA drugs had a relatively even distribution of PCrit designations, with 25%, 30%, and 20% of compounds in this class having an PCrit of QT prolongation, positive chronotropy, or negative chronotropy, respectively. Treatment with environmental chemicals most often resulted in positive chronotropy as the PCrit, both overall, as well as across subclasses (with the exception of the metals).
Figure 4.
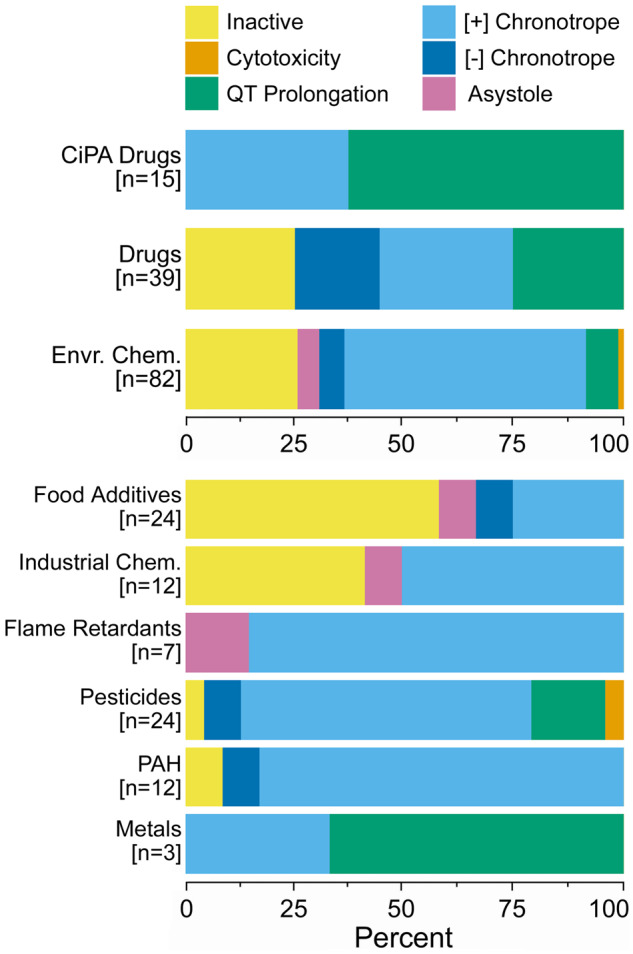
Critical phenotype calls. Critical (most sensitive) phenotype occurrence (percentage out of the number of compounds in the class) from population median-derived points of departure, colored by endpoint and separated into compound class. The environmental chemicals are also further broken down into subclasses.
To further characterize chemical-to-chemical heterogeneity in TDVF05, a random effects meta-analysis approach was employed. First, TDVF05 values were converted to log σH values so that the confidence intervals are more symmetric and because prior analysis have suggested that the chemical-to-chemical heterogeneity in log σH can be approximated by a normal distribution (Hattis and Lynch, 2006; WHO/IPCS, 2018). A standard random effect analysis was conducted for each of the five phenotypes, with a subgrouping analysis in each chemical class. The results of this analysis included both the pooled estimate of the log σH (and hence the TDVF05) for each phenotype (and chemical class, with subgrouping, Supplementary Figure 4), the standard deviation of the random effects reflecting heterogeneity, represented by τ, and best linear unbiased predictions for phenotype- and chemical-specific estimations of variability. Heterogeneity was also calculated for each chemical class subgroup. An additional multivariate mixed effects analysis was conducted to determine whether the chemical classes vary significantly from one another in their random effects (ie, their population variability, Supplementary Figure 3).
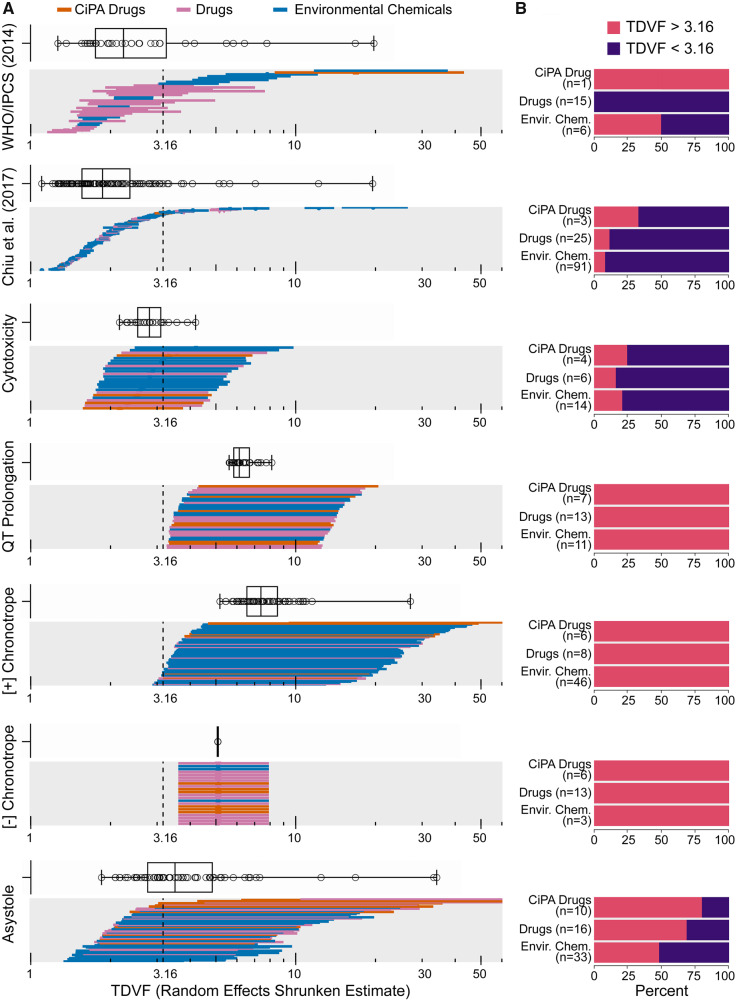
The meta-analysis results for log σH for each phenotype can be converted back to TDVF05 values and their random effects shrunken estimates can be compared with both the default human toxicodynamic UF (UFH, TD) value of 3.16, as well as to previous studies of TD variability, as shown in Figure 5. Figure 5A shows the distribution of the random effects shrunken TDVF05 estimates (median estimate and 95% CI) for each phenotype, with the distribution of the median estimates shown as the boxplot above each panel. These were compared with the shrunken TDVF05 estimates from 2 previous studies using different population variability models: in vitro cytotoxicity population variability estimates from Chiu et al. (2017) using data from Abdo et al. (2015) in > 1000 individual lymphoblastoid cell lines, and human in vivo population variability from Hattis and Lynch (2006) as analyzed by WHO/IPCS (2018).
Figure 5.
Distribution of random effects derived shrunken TDVF05 estimates. A, Shrunken median estimate and 95% CI TDVF05 values separated by phenotype or study and color coded by chemical class. The vertical dotted line reflects the default uncertainty factor (UFH, TD = 3.16). The distribution of shrunken median estimate TDVF05 values is illustrated as the boxplot above each endpoint panel. B, Barplots showing the percentage of compounds by class whose shrunken median estimate TDVF05 value exceeds or falls below the default UFH, TD. Number of compounds reported in each class is the number of unique compounds, not accounting for multiple compound/endpoint combinations.
The functional phenotypes (QT prolongation and positive or negative chronotropy) tended to be more variable than the other phenotypes and comparison studies, reflected in their distributions being shifted to the right of default TDVF05 = 3.16, with all median estimates and almost all confidence intervals for the shrunken TDVF05s exceeding this value. In the case of positive chronotropy, a substantial percentage of test chemicals exceeded a TDVF05 value of 10. This contrasts with the cytotoxicity phenotype, where most compounds regardless of class have shrunken median estimate TDVF05 values under the default UFH,.TD. The asystole phenotype had more compounds that exceed the default UFH, TD than the other viability phenotype, but less than the functional phenotypes. Asystole also had the highest measure of heterogeneity (τ2) of the 5 evaluated phenotypes, with a value comparable with the values calculated from Chiu et al. (2017) and WHO/IPCS (2018). The cytotoxicity phenotype TDVF05 measurements are most similar to that of the TDVF estimates derived from Chiu et al. (2017), which are also based on cytotoxicity measurements, albeit in a different human in vitro model. The negative chronotropy phenotype has a heterogeneity value of 0, resulting in all shrunken TDVF05 estimates to be the same, but still exceeding the default value. The overall tendency of functional phenotypes to have more inherent variability in response is shown in Figure 5B. It is evident that the fraction of compounds where the random effects shrunken median estimate TDVF05 value was greater than the default value was considerably higher for the functional endpoints than for cytotoxicity. With respect to class-specificity, we did not find a statistically significant effect of chemical class on the degree of variability within any phenotype with the exception of CiPA drugs for the positive chronotropy phenotype (Supplementary Figure 4).
Risk Characterization
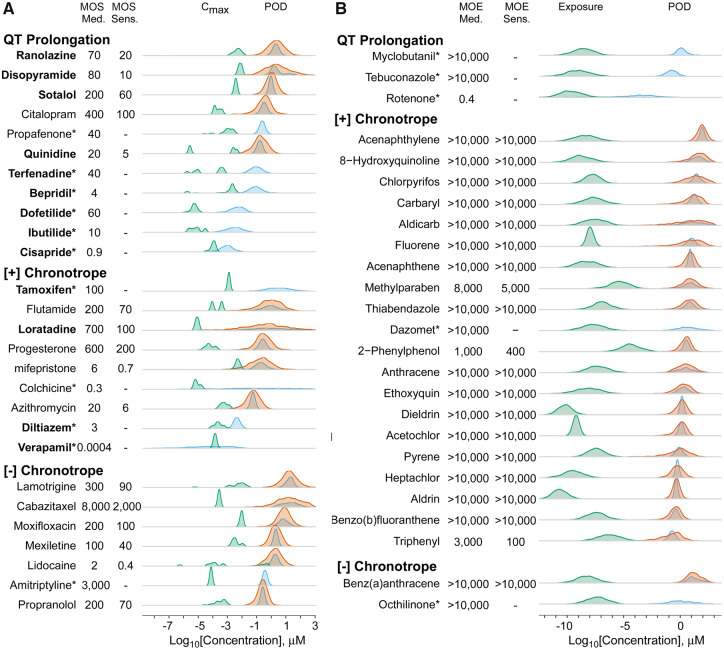
Figure 6A compares the uncertainty distributions of the Cmax and the POD estimate for the chemical-specific PCrit. Blood concentrations were available from PharmaPendium for 27 out of 54 pharmaceuticals, including 13 CiPA pharmaceuticals indicated by the chemical name in bold face. Median and sensitive individual (where possible) MOSs were calculated, for each compound. If a compound had a PCrit not considered sufficient for population variability estimate, only the population median POD distribution is shown, and an asterisk appended to the compound’s name. In addition, in this case, the sensitive individual MOS was not derived and was instead replaced with a dash. The overall distributions of MOSs are shown in Figure 7.
Figure 6.
Distributions of exposures (green) as compared with distributions of population based (blue) and random individual POD estimates (orange) for critical phenotypes for both drugs (A) and environmental chemicals (B) ordered from lowest to highest population median critical phenotype population point of departure (POD) and separated by phenotype. Pharmaceutical exposures are based on the Cmax values extracted from the Pharmapendium database. Environmental chemical exposure estimates are in the form of a Css value based on Expocast exposure estimates and Monte Carlo based estimation of the Css using the httk package in R. POD and exposure estimates are both log10 transformed. Median and sensitive individual margins of safety (MOS)/margins of exposure (MOE) values are derived, if possible, and shown next to each compound name. CiPA drugs are designated with a bold face chemical name. Compounds with no derived random individual distribution and sensitive individual MOS/MOE are designated with an asterisk (*).
Figure 7.
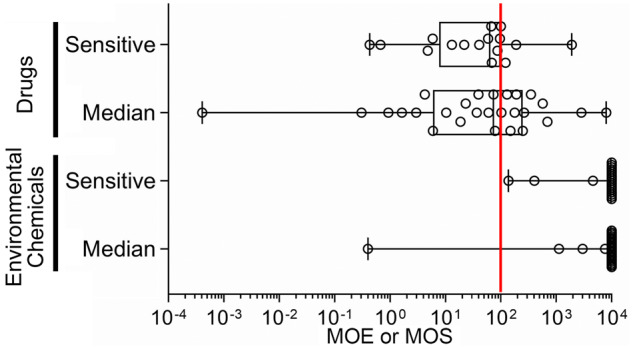
Distribution of median and sensitive individual’s margins of safety (MOS)/margins of exposure (MOE). Box and whiskers plots show the range in MOE/MOS across tested compounds. Box is interquartile range, vertical line is the median, whiskers are min-max values. All individual data are shown as circles. Red vertical line indicates a MOS or MOE of 100.
For more than half of pharmaceuticals tested, there was at least some overlap between the Cmax distributions and the POD distributions. For example, 15 compounds with median individual MOS predictions, and 11 of the 16 compounds with sensitive individual MOS predictions had values under 100. Notably, 10 of the 13 CiPA drugs had median individual MOS predictions below 100, with 9 of them being for the QT prolongation phenotype. Cisapride, colchicine, and verapamil were the compounds with the lowest MOS.
Figure 6B similarly compares the uncertainty distributions of the estimated general population exposure-derived in vivo blood concentration for environmental chemicals, this time in the form of a Css, and the chemical-specific PCrit POD estimate for both the population and individual level. Blood concentrations could be predicted for 23 out of the 83 tested environmental chemicals included in this analysis. The lowest population median MOE was 0.4 for the pesticide rotenone, whereas no other median individual MOE was less than 1000. The flame retardant triphenyl phosphate and the pesticide 2-phenylphenol had the lowest calculated sensitive individual MOEs with values of 100 and 400, respectively. The remaining compounds had sensitive individual MOE predictions of 5000 or greater. The overall distribution of the MOE values for both the median and sensitive individual are shown in the lower section of Figure 7.
Detailed comparisons of blood concentrations (Cmax or Css) and PODs for each individual phenotype are shown in Supplementary Figure 5.
DISCUSSION
In this study, we demonstrate how combining a population-based iPSC-derived cardiomyocyte in vitro model with Bayesian C-R modeling can provide a quantitative characterization of population TD variability in cardiotoxicity hazards. This approach can be applied for both pharmaceuticals and environmental chemicals. Ensuring protection of more sensitive members of the population remains a challenge in both drug safety evaluation and chemical risk assessment, with continued reliance largely on generally accepted “rules-of-thumb,” such as 10- or 100-fold safety factors, rather than empirical data. Attempts to address this challenge more broadly have been constrained by a paucity of population variability data in vivo (Zeise et al., 2013) and concerns about the in vivo relevance of population-based models using immortalized cell lines (Abdo et al., 2015; Chiu et al., 2017). Our model based on iPSC-derived differentiated cells from a population of nondiseased individuals provides a unique opportunity to bridge these gaps by utilizing functional, nonimmortalized cells in a population context. Although Burnett et al. (2019) were able to utilize this population model to examine TD variability in a frequentist context, we demonstrate in this study the benefits of using Bayesian approaches in better characterizing the degree of population variability along with its uncertainty. Specifically, hierarchical Bayesian methods allows for better characterization of uncertainty in not only in the model parameters for each individual (eg, accounting for shrinkage toward the mean), but also in the degree of variability across individuals overall (Zhao et al., 2010). This was not possible in Burnett et al. (2019), which derived individual POD values independently for each individual. Ultimately, we have demonstrated that population-based experimental data, together with population-based hierarchical Bayesian modeling, can be applied to rigorously estimate the degree of population variation in TD sensitivity for a panel of clinically relevant outcomes.
For pharmaceuticals, our model reproduced the in vivo observation that QT prolongation represents a common liability, particularly for CiPA drugs, at both the population and the individual level. For environmental chemicals, we found QT prolongation to be a less common potential liability, with positive chronotropy being the most observed potential human health hazard. However, it should be noted that many test compounds elicited multiple effects, both related to cardiomyocyte function and viability. Nonetheless, functional effects tended to be the most sensitive hazard indicators as they were observed at lower concentrations than effects on viability. This was consistent with observed effects on beat rhythmicity and action potential duration being independent of and not secondary to cytotoxicity, thus implying that cytotoxicity alone is insufficiently sensitive to identify cardiotoxic compounds. More broadly, our results show the importance of using differentiated, functional cells for drug safety and chemical toxicity screening, not only because the effects are more interpretable, but because they are likely to identify more sensitive endpoints.
The primary innovation of this work is in the development of a combined experimental-computational approach to quantify TD variability in susceptibility so as to directly inform drug and chemical safety assessments for cardiotoxicity. Specifically, our approach results in the derivation of a TD variability factor, or TDVF, that can provide compound- and endpoint-specific replacements to widely used default safety factors. Although similar approaches have been previously applied to a population-based immortalized cell line model evaluating cytotoxicity (Chiu et al., 2017; WHO/IPCS, 2018), and to functional studies in patient-derived cardiomyocytes (Magdy et al., 2018), the use of a population of differentiated human cells from nondiseased individuals provides information on functional phenotypes that have not been available previously, and is more representative of the general population variability. This is particularly important because we found that functional phenotypes not only tend to have greater levels of population variability as compared with cell viability endpoints, but also have TDVF values almost uniformly greater than the usual default assumption of 3-fold used in both pharmaceutical safety and chemical risk assessments. Other studies utilizing similar populations of iPSC-derived cardiomyocytes coupled to an in silico model have not had the pointed focus on TD variability quantification for use in risk assessment. For instance, a recent study by Kernik et al. (2019) developed a computational whole-cell model to examine cell-to-cell variability and more specifically, experimental variability within a given donor, which they posit is a strength when properly incorporated into a model (Kernik et al., 2019). This contrasts with the Bayesian framework used in this study, which disaggregates the impact of experimental variability while also providing hazard, risk, and population variability estimates. An in silico cardiotoxicity study by Passini et al. (2017) similarly did not address variability at an endpoint and chemical-specific level, instead utilizing a population of human ventricular action potential model to demonstrate the accuracy of in silico trials in predicting TdP risk. Passini et al. (2017) also diverges from this study in that we use Ca2+ data and the decay-rise ratio as the in vitro surrogate for the QT prolongation phenotype as opposed to action potential duration. However, the authors noted that the results from their study are in agreement with experimental recordings from iPSC-derived cardiomyocytes (Passini et al., 2017). This study also represents a natural extension of both Blanchette et al. (2019) and Burnett et al. (2019), providing a complete, high-throughput experimental and computational workflow to provide high throughput, population-based estimates of hazard, risk, and TD variability that can be applied in both the pharmaceutical and risk assessment arenas (Pang, 2020).
Two previous studies (Chiu et al., 2017; WHO/IPCS, 2018) that we used for comparison included drugs that overlap with the CiPA-list pharmaceuticals included in our study; therefore, direct comparisons of TDVF estimates were possible. The only overlapping compound from the WHO/IPCS (2018) study with a TD phenotype was sotalol, whose principal hazard phenotype is QT prolongation. This WHO/IPSC study utilized an EC50 for the POD and therefore their derivation of a TDVF. We recalculated a TDVF05 shrunken estimate using an EC50 for the purposes of comparison. The shrunken median estimate and 95% confidence interval TDVF05 for sotalol as derived by our study was 6.0 (2.8, 23.0) whereas the TDVF05 shrunken estimate derived from WHO/IPCS (2018) was 16.9 (11.7, 37.5). Although the shrunken estimate derived using the WHO/IPCS (2018) dataset was larger, the confidence intervals of both our study and theirs are indistinguishable. The only direct comparison between CiPA drugs from the Chiu et al. (2017) study and our study was with tamoxifen. The shrunken TDVF05 estimate derived from our data for this compound was 2.5 (1.7, 4.8), whereas the estimate derived using the Chiu et al. (2017) data set was 1.31 (1.29, 1.33). This comparison is less informative because although both are based on cytotoxicity, and it is not unexpected that different cell types may have different degrees of variability for viability. Indeed, this result may suggest that immortalized cell lines such as lymphoblastoid cells might underestimate the degree of population variation as compared with the functional cell types such as cardiomyocytes.
To place our results in a decision-making context, we further demonstrated how a MOS or MOE can be derived from these data to also incorporate population variability. As expected, many pharmaceuticals had relatively narrow MOSs, and population variability further narrowed their margins by 1.5- to 8.8-fold, as a consequence of TDVF values for these compounds often being greater than the default value of 3.16. For the environmental chemicals, only four had MOEs less than 10 000, and of these only three had sufficient data on population variability to estimate a sensitive individual MOE. Although the impact of population variability for the two pesticides was relatively small, for the flame retardant triphenyl phosphate, the sensitive individual MOE of 140 was more than 20-fold less than the population median-based MOE, indicating that estimated human exposures may be approaching levels of concern for cardiotoxicity when taking toxicodynamically sensitive individuals into account.
This study has several limitations that are important to note. First, the number of individuals (43) tested herein was relatively limited, and whereas it can be used to provide an estimate of the degree of variability in the population as a whole, it is insufficient to identify idiosyncratic individuals. Thus, the proposed model is not to replace the need for careful postmarketing surveillance or the development of personalized, precision-medicine-based approaches that use patient-specific cells (Burridge et al., 2016) to identify susceptibility to potential cardiotoxic liabilities of drug candidates. Secondly, despite the model being high-throughput in nature, the routine use of 43 different cell lines for screening a large number of compounds will be impractical and costly. There is therefore a need to better characterize the tradeoffs between the cost/time needed to test a greater number of cell lines with the model’s ability to accurately capture hazard and characterize risk. Third, because our study utilized data from Burnett et al. (2019), a number of the limitations acknowledged in that study also apply here. These include being unable to examine the potential effects of underlying disease on hazard and variability due to the use of only nondiseased donors, and the relatively small number of compounds tested compared with the total number of pharmaceuticals and chemicals in the environment.
Overall, this study demonstrates how a combined in vitro-in silico approach can help to close the ever-widening data gap of chemicals with insufficient or no data on cardiotoxicity and its population variation in susceptibility. Not only can this model be effectively utilized in characterizing cardiotoxicity hazards, but it also enables quantification of TD variability through the derivation of a TDVF that can replace default assumptions with respect to numerous cardiotoxicity phenotypes. Of particular importance is our finding that for a large number of compounds, cardiomyocyte-derived TDVFs far exceeded the default TD safety factor/UF of 3.16, suggesting that this default factor may not be sufficiently protective of sensitive members of the population. Moreover, greater variability was observed largely for functional phenotypes such as beat rate and action potential duration, rather than measures of viability such as cytotoxicity. In terms of risk characterization, we found that although a number of pharmaceuticals had relatively narrow MOS, for environmental chemicals tested current estimates of the general population exposures were not high enough to pose a concern, even for sensitive individuals. In conclusion, we have extended the utility of iPSC-derived cardiomyocyte-based in vitro model from being a primarily cardiotoxicity hazard screening tool to an approach that can be used to quantify the extent of population variability in susceptibility for drugs and environmental chemicals. This provides a critically important experimental-computational approach for ensuring that decisions in both drug development and environmental chemical risk assessment are protective of the health across the population.
SUPPLEMENTARY DATA
Supplementary data are available at Toxicological Sciences online.
Supplementary Material
ACKNOWLEDGMENTS
The authors wish to acknowledge assistance from the scientists and technicians at FujiFilm Cellular Dynamics for enabling these studies by establishing a large panel of iPSC-derived human cardiomyocytes.
FUNDING
National Institute of Environmental Health Sciences (P42 ES027704 and T32 ES026568) and a cooperative agreement with the U.S. Environmental Protection Agency (STAR RD83580201). F.A.G. was the recipient of the Society of Toxicology Colgate-Palmolive and Society of Toxicology Syngenta Fellowship Awards. The views expressed in this manuscript do not reflect those of the funding agencies. The use of specific commercial products in this work does not constitute endorsement by the authors or the funding agencies.
DECLARATION OF CONFLICTING INTERESTS
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
REFERENCES
- Abdo N., Xia M., Brown C. C., Kosyk O., Huang R., Sakamuru S., Zhou Y. H., Jack J. R., Gallins P., Xia K., et al. (2015). Population-based in vitro hazard and concentration-response assessment of chemicals: The 1000 genomes high-throughput screening study. Environ. Health Perspect. 123, 458–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen M. E., Dennison J. E. (2002). Toxicokinetic models: Where we've been and where we need to go! Human and Ecological Risk Assessment. Int. J. 8, 1375–1395. [Google Scholar]
- Blanchette A. D., Grimm F. A., Dalaijamts C., Hsieh N. H., Ferguson K., Luo Y. S., Rusyn I., Chiu W. A. (2019). Thorough QT/QTc in a dish: An in vitro human model that accurately predicts clinical concentration-QTc relationships. Clin. Pharmacol. Ther. 105, 1175–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnett S. D., Blanchette A. D., Grimm F. A., House J. S., Reif D. M., Wright F. A., Chiu W. A., Rusyn I. (2019). Population-based toxicity screening in human induced pluripotent stem cell-derived cardiomyocytes. Toxicol. Appl. Pharmacol. 381, 114711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burridge P. W., Li Y. F., Matsa E., Wu H., Ong S. G., Sharma A., Holmstrom A., Chang A. C., Coronado M. J., Ebert A. D., et al. (2016). Human induced pluripotent stem cell-derived cardiomyocytes recapitulate the predilection of breast cancer patients to doxorubicin-induced cardiotoxicity. Nat. Med. 22, 547–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiu W. A., Wright F. A., Rusyn I. (2017). A tiered, Bayesian approach to estimating of population variability for regulatory decision-making. ALTEX 34, 377–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- E14 Implementation Working Group. (2015). ICH E14 Guideline: The Clinical Evaluation of QT/QTc Interval Prolongation and Proarrhythmic Potential for Non-antiarrhythmic Drugs Questions & Answers (R3). International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use, Geneva, Switzerland. [Google Scholar]
- Gelman A., Rubin D. B. (1992). Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–472. [Google Scholar]
- Grimm F. A., Blanchette A., House J. S., Ferguson K., Hsieh N. H., Dalaijamts C., Wright A. A., Anson B., Wright F.A., Chiu W. A., et al. (2018). A human population-based organotypic in vitro model for cardiotoxicity screening. ALTEX 35, 441–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimm F. A., Iwata Y., Sirenko O., Bittner M., Rusyn I. (2015). High-content assay multiplexing for toxicity screening in induced pluripotent stem cell-derived cardiomyocytes and hepatocytes. Assay Drug Dev. Technol. 13, 529–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hattis D., Lynch M. (2006). Empirically Observed Distributions of Pharmacokinetic and Pharmacodynamic Variability in Humans—Implications for the Derivation of Single-point Component Uncertainty Factors Providing Equivalent Protection as Existing Reference Doses. In Toxicokinetics and Risk Assessment (E. V. Ohanian and J. C. Lipscomb, Eds.), pp. 69–93, CRC Press, Boca Raton. [Google Scholar]
- Karakikes I., Ameen M., Termglinchan V., Wu J. C. (2015). Human induced pluripotent stem cell-derived cardiomyocytes: Insights into molecular, cellular, and functional phenotypes. Circ Res 117, 80–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kernik D. C., Morotti S., Wu H., Garg P., Duff H. J., Kurokawa J., Jalife J., Wu J. C., Grandi E., Clancy C. E. (2019). A computational model of induced pluripotent stem‐cell derived cardiomyocytes incorporating experimental variability from multiple data sources. J. Physiol. 597, 4533–4564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilpinen H., Goncalves A., Leha A., Afzal V., Alasoo K., Ashford S., Bala S., Bensaddek D., Casale F. P., Culley O. J., et al. (2017). Common genetic variation drives molecular heterogeneity in human iPSCs. Nature 546, 370–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laverty H., Benson C., Cartwright E., Cross M., Garland C., Hammond T., Holloway C., McMahon N., Milligan J., Park B., et al. (2011). How can we improve our understanding of cardiovascular safety liabilities to develop safer medicines? Br. J. Pharmacol. 163, 675–693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magdy T., Schuldt A. J. T., Wu J. C., Bernstein D., Burridge P. W. (2018). Human induced pluripotent stem cell (hiPSC)-derived cells to assess drug cardiotoxicity: Opportunities and problems. Annu. Rev. Pharmacol. Toxicol. 58, 83–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meek M. E., Renwick A., Ohanian E., Dourson M., Lake B., Naumann B. D., Vu V. (2002). Guidelines for application of chemical-specific adjustment factors in dose/concentration-response assessment. Toxicology 181–182, 115–120. [DOI] [PubMed] [Google Scholar]
- O'Brien P. J. (2014). High-content analysis in toxicology: Screening substances for human toxicity potential, elucidating subcellular mechanisms and in vivo use as translational safety biomarkers. Basic Clin. Pharmacol. Toxicol. 115, 4–17. [DOI] [PubMed] [Google Scholar]
- Pang L. (2020). Toxicity testing in the era of induced pluripotent stem cells: A perspective regarding the use of patient-specific induced pluripotent stem cell-derived cardiomyocytes for cardiac safety evaluation. Curr. Opin. Toxicol. 23–24, 50–55. [Google Scholar]
- Passini E., Britton O. J., Lu H. R., Rohrbacher J., Hermans A. N., Gallacher D. J., Greig R. J. H., Bueno-Orovio A., Rodriguez B. (2017). Human in silico drug trials demonstrate higher accuracy than animal models in predicting clinical pro-arrhythmic cardiotoxicity. Front. Physiol. 8, 668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce R. G., Setzer R. W., Strope C. L., Wambaugh J. F., Sipes N. S. (2017). httk: R package for high-throughput toxicokinetics. J. Stat. Softw. 79, 1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ring C. L., Arnot J. A., Bennett D. H., Egeghy P. P., Fantke P., Huang L., Isaacs K. K., Jolliet O., Phillips K. A., Price P. S., et al. (2019). Consensus modeling of median chemical intake for the U.S. population based on predictions of exposure pathways. Environ. Sci. Technol. 53, 719–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato H., Arai H., Fukuda E., Tsutsumi Y., Yamamoto M., Aizawa T., Long-Tai F. L. (2001). Effects of nifedipine retard on heart rate and autonomic balance in patients with ischemic heart disease. Int. J. Clin. Pharmacol. Res. 21, 65–71. [PubMed] [Google Scholar]
- Sharma A., McKeithan W. L., Serrano R., Kitani T., Burridge P. W., Del Álamo J. C., Mercola M., Wu J. C. (2018). Use of human induced pluripotent stem cell-derived cardiomyocytes to assess drug cardiotoxicity. Nat. Protoc. 13, 3018–3041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirenko O., Grimm F. A., Ryan K. R., Iwata Y., Chiu W. A., Parham F., Wignall J. A., Anson B., Cromwell E. F., Behl M., et al. (2017). In vitro cardiotoxicity assessment of environmental chemicals using an organotypic human induced pluripotent stem cell-derived model. Toxicol. Appl. Pharmacol. 322, 60–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snider N. D., Veverka A. (2008). Long-acting nifedipine in the management of the hypertensive patient. Vasc. Health Risk Manag. 4, 1249–1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H., Fadiran E. O., Jones C. D., Lesko L., Huang S. M., Higgins K., Hu C., Machado S., Maldonado S., Williams R., et al. (1999). Population pharmacokinetics. A regulatory perspective. Clin. Pharmacokinet. 37, 41–58. [DOI] [PubMed] [Google Scholar]
- Viechtbauer W. (2010). Conducting meta-analyses in r with the metafor package. J. Stat. Softw. 36, 1–48. [Google Scholar]
- WHO/IPCS. (2005). Chemical-specific Adjustment Factors for Interspecies Differences and Human Variability: Guidance Document for Use of Data in Dose/Concentration-Response Assessment. World Health Organization, Geneva. [Google Scholar]
- WHO/IPCS (World Health Organization & International Programme on Chemical Safety). (2018). Guidance document on evaluating and expressing uncertainty in hazard characterization, 2nd ed. World Health Organization, Geneva. [Google Scholar]
- Woosley R. L., Chen Y., Freiman J. P., Gillis R. A. (1993). Mechanism of the cardiotoxic actions of terfenadine. JAMA 269, 1532–1536. [PubMed] [Google Scholar]
- Zeise L., Bois F. Y., Chiu W. A., Hattis D., Rusyn I., Guyton K. Z. (2013). Addressing human variability in next-generation human health risk assessments of environmental chemicals. Environ. Health Perspect. 121, 23–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., Lee A. H., Barnes T. (2010). On application of the empirical Bayes shrinkage in epidemiological settings. Int. J. Environ. Res. Public Health 7, 380–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.