An index framework founded on the future profit potential of female beef cattle to aid the identification of candidates for culling

Abstract

Meticulous culling decisions, coupled with careful breeding decisions, are fundamental to shifting a population distribution in the favorable direction and improving profit per cow. Nevertheless, there is a paucity of easy-to-use dynamic tools to aid in culling decisions in beef cattle. The motivation for the present study was to develop a monetary-based culling tool, here referred to as the Beef Female’s Profit Potential (BFPP), to identify females for culling. The BFPP reflects the expected lifetime profitability of an individual female in a herd for the expected remainder of her lifetime; this profit included that of the beef female herself as well as her progeny. The BFPP index framework was composed of 4 subindexes reflecting the value of an animal: (1) as a nulliparae (this was voided if the cow had already calved), (2) for the remainder of her current parity, (3) summed across each of her expected remaining parities, and (4) when she is retained within the herd and not voluntarily culled. Each subindex was comprised of different components reflecting both genetic and non-genetic effects associated with each female. Transition matrices predicting the expected longevity of each female and their expected month of calving were also utilized in calculating the expected remaining lifetime profitability of each female. The BFPP index was validated on 21,102 beef cows as well as their harvested progeny from 875 herds by stratifying the cows, within herd, into 4 strata based on their BFPP. The mean of the within-herd correlation between the BFPP and the Irish national replacement (i.e., breeding) index was, on average, 0.45 indicating the shortcomings of the breeding index as a culling tool. Cows within the top BFPP stratum had a genetic expectation of accruing almost an additional €36 profit per calving, relative to cows within the worst stratum; when validated on the cow’s own calving interval and survival performance as well as their progeny’s carcass performance, the actual phenotypic value was estimated to be an additional €32 profit per calving. A proportion of this additional profit was due to the harvested progeny of the high BFPP cows having, on average, heavier, more conformed carcasses with less fat cover relative to their poor BFPP contemporaries. This BFPP framework is a useful and easy-to-use tool to aid in producer decision making on the choice of females to voluntarily cull but also on which replacement heifers to graduate into the mature herd.

Introduction

Culling decisions in cattle are complex and multifactorial (Bascom and Young, 1998); an inefficient culling strategy will impact the overall profitability of the enterprise (Orpin and Esslemont, 2010). Despite this, the majority of research on culling decisions and implications, as well as the development of decision support tools that support culling decision-making, are almost exclusively for dairy herds (Stewart et al., 1977; Bascom and Young, 1998; Kelleher et al., 2015). Many of the factors impacting voluntary culling decisions are likely to overlap between the dairy and beef sectors such as animal age, health status, and reproductive performance. Nonetheless, not all risk factors for culling in dairy cows are pertinent to beef cows and additional risk factors unique to beef production systems also exist. Crosson et al. (2016) reported that animal performance, in the form of the value of animals sold per beef cow, is one of the main factors contributing to profitability in beef herds. Given the high heritability of carcass weight (Pabiou et al., 2009), conformation (Coyne et al., 2018) and animal value (McHugh et al., 2011) in beef cattle, the cow herself has a large impact on the value of her progeny; hence, the future predicted value of offspring will have a large bearing on whether or not a given beef cow is a candidate for culling.

An opportunity therefore exists to develop the framework for a novel decision support tool tailored specifically to the beef sector; this should incorporate chief performance metrics relevant to a beef female reflecting her (future) relative economic worth to the herd. For instance, both the ability of a beef female to produce a calf per year at the desired time of year and her probability of continuing to produce several more quality offspring are important key performance indicators. Indicators of milk production reflected in the expected relative weaning weight of her future progeny will impact her contribution to herd profit; maternal weaning weight in cattle is known to be both heritable and repeatable (McHugh et al., 2014).

The objective of the present study was to develop the framework for a decision support tool which ranks beef females based on their expected remaining lifetime profit potential. The proposed Beef Female’s Profit Potential (BFPP) index was developed to be applicable to both beef heifers and cows and therefore incorporates: (1) the animal’s potential as a heifer (if she is nulliparous), (2) the remaining profit potential of the cow (provided she has calved at least once) for the current parity (CP), (3) the projected profit potential up to a further 10 parities, and (4) the cost–benefit value of the animal if she was to be retained within the herd and not voluntarily culled, considering both the replacement cost and the value recouped from the cull carcass. The BFPP was designed to not only take cognizance of the beef female’s additive genetic merit but also her non-additive genetic and environmental effects associated with her performance; the outcome is a data-driven support mechanism for producers when making culling decisions.

Material and Methods

Model development

The beef female’s profit potential (BFPP) is intended to be an economically driven decision-support tool developed to rank beef females based on their expected remaining lifetime profit potential. The BFPP framework encompasses 4 main components of a beef female’s production life: (1) the animal’s heifer profit potential (HP) until she first calves, (2) the cow’s profit potential for the remainder of her current parity (CP), (3) the cow’s future profit potential for her remaining parities (FP) and (4) the value of the beef female if she is retained within the herd and therefore does not require replacement (RV). The BFPP was therefore calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{B}\mathrm{F}\mathrm{P}\mathrm{P}=\mathrm{H}\mathrm{P}+\mathrm{C}\mathrm{P}+\mathrm{F}\mathrm{P}+\mathrm{R}\mathrm{V}}\end{array}}$$ (1)

The BFPP represents the beef female’s own performance throughout the (expected) remainder of her lifetime comprised of not only the value she transmits directly to her progeny but also the maternal effects she has on her progeny’s performance and her value herself. Therefore, the beef female’s total merit for each trait was calculated using production values (PVs) in order to accurately reflect her total contribution to each trait; both genetic and non-genetic effects were used in the calculation of PVs. For traits pertaining to the female’s own performance, PVs were calculated using the animal’s estimated breeding value (EBV) for a given trait, her own heterosis value (unless it was a maternal trait, in which case a maternal heterosis value was used, e.g., maternal calving difficulty) and, where available, the contribution of her permanent environment to her performance (with the exception of maternal calving difficulty where a maternal permanent environment was included); these female traits were: age at first calving (AFC), maintenance (i.e., live-weight), docility, maternal weaning weight, maternal calving difficulty, calving interval (CIV), survival and cull cow carcass weight (Table 1). A 17-kg weaning weight difference existed between the average weaning weight of parity 2 and older cows relative to parity 1 cows; therefore, an age adjustment was included in the PV for maternal weaning weight so that first parity cows were not negatively biased due to the expected lighter weaning weight of their progeny.

Table 1.

Traits included within the 3 animal categories (i.e., heifer, cow, and terminal progeny) when calculating the heifer potential (HP), current Parity (CP), future parity (FP), retention value (RV), and Irish national replacement index (Rindex) components of the beef female’s profit potential (BFPP) index as well as the traits associated economic values (EV)

								PV estimation1
								Direct effect2			Maternal effect3
Animal category	Trait	HP	CP	FP	RV	RIndex	EV	BV	Het	PE	Het	PE	DFract	Age adj4
Heifer	AFC	✓				✓	-€1.61	EBV	✓
	Maintenance	✓				✓	-€1.24	EBV	✓	✓
Cow	Maintenance		✓	✓		✓	-€0.25	EBV	✓	✓
	Cow docility		✓	✓		✓	€35.06	EBV	✓	✓
	Maternal calving difficulty			✓		✓	-€2.26	EBV			✓	✓
	Maternal weaning weight			✓		✓	€2.53	EBV			✓			✓
	Cull cow weight				✓	✓	€3.15	EBV	✓
	CIV			✓		✓	-€2.30	EBV	✓	✓
	Survival			✓		✓	€4.02	EBV	✓	✓
Terminal progeny	Calf docility		✓	✓		✓	€18.40	PTA
	Feed intake		✓	✓		✓	-€0.13	PTA			✓		✓
	Direct calving difficulty			✓		✓	-€4.65	PTA
	Direct mortality			✓		✓	-€5.34	PTA			✓	✓
	Direct gestation length			✓		✓	-€2.25	PTA			✓	✓
	Carcass weight		✓	✓		✓	€3.89	PTA			✓	✓	✓
	Carcass conformation		✓	✓		✓	€18.93	PTA			✓	✓	✓
	Carcass fat		✓	✓		✓	-€10.08	PTA			✓	✓	✓

¹Effects included in the estimation of PVs.

²Direct effects included BV= breeding value where EBV = estimated breeding value and PTA = predicted transmitting ability; Het = Beef cow’s own heterosis effect, PE = Beef cow’s own permanent environmental effect.

³Maternal effects included: Het = beef cow’s maternal heterosis effect on progeny, PE = beef cow’s maternal permanent environmental effect on progeny, DFract = dam dairy fraction.

⁴Age adj = a −17 kg weaning weight EBV adjustment applied to dams who were parity 2 and older so that positive bias did not exist toward older females.

For traits pertaining to the beef female’s progeny performance, PVs were calculated using the beef female’s predicted transmitting ability (PTAs, i.e., half the EBV) for the trait of interest, her corresponding maternal heterosis value and, where available, the female’s maternal permanent environmental effect as well as the effect the beef female’s dairy breed fraction has on her progeny’s performance (as per the national genetic evaluation models discussed later); these progeny-related traits were: progeny carcass traits (i.e., weight, conformation, and fat), feed intake, docility, and calving-related traits (i.e., calving difficulty, mortality, and gestation length; Table 1). The statistical models pertaining to the calculation of a beef female’s PV for each given trait are described in Supplementary Material S1. All fixed and random effect solutions were those estimated for the national genetic evaluations as discussed later.

The economic parameters incorporated into the BFPP were obtained from the Grange Beef Model, a mathematical model used to simulate the Irish beef production system (Crosson et al., 2006). As described by Crosson et al. (2006), the model assumes that the beef enterprise is a beef spring-calving (i.e., early March) herd operating on 40 ha and maintaining a predominantly grass-based diet (i.e., grazed grass and grass silage) but extends to concentrates and maize silage, if available. Factors accounted for within the Grange Beef Model include: (1) animal and feeding activities, (2) labor, and (3) environmental considerations.

Heifer potential

The heifer potential (HP) component of the BFPP was calculated as the estimated profit potential of a beef heifer based on the expected duration until her projected first calving. If the beef female had already had at least one calf when the BFPP was generated, then the HP component of the BFPP was set to 0; otherwise, if the female is nulliparous, then the HP component was calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{H}\mathrm{P}=(\mathrm{E}{\mathrm{V}}_{\mathrm{h}\mathrm{a}\mathrm{f}\mathrm{c}}\cdot \mathrm{P}{\mathrm{V}}_{\mathrm{h}\mathrm{a}\mathrm{f}\mathrm{c}})\cdot {\left(\frac{1}{1+r}\right)}^y+\frac{y}{2}\cdot ((\mathrm{E}{\mathrm{V}}_{\mathrm{h}\mathrm{l}\mathrm{w}\mathrm{t}}\cdot \mathrm{P}{\mathrm{V}}_{\mathrm{h}\mathrm{l}\mathrm{w}\mathrm{t}})\cdot {\left(\frac{1}{1+r}\right)}^y)+\pi }\end{array}}$$ (2)

where HP is the heifer potential component. The economic values (EV) relating to heifer traits were calculated based on the time taken from birth to when the trait is expected to be expressed and included heifer age at first calving (hafc) and heifer maintenance (hlwt) (Table 1). The production values (PVs) relevant to both heifer traits (i.e., PV_hafc and PV_hlwt) are described in Table 1. A discount factor, ${(1/(1+r))}^y$, with an annual discount rate of 7% (Berry et al., 2006), accounts for the monetary depreciation of the value of a trait based on the time delay to the expression of the trait where y is the estimated number of years (i.e., y = 1 or 2) until a heifer is predicted to express the trait under consideration. For instance, if a heifer is 1 year old and is expected to express the trait in 1 years’ time, then the cost of that trait is halved. A profit differential ($\pi$) was added to the HP component to reflect the heifer’s predicted first month of calving group (MOCG) which was estimated based on her birth date plus the national average AFC for beef heifers which was 950 d (McHugh et al., 2014), and subsequently adjusted based on the heifer’s PV for AFC. The profit differential by MOCG was relative to a base female calving in March as described in Table 2.

Table 2.

Net profit margin differential, adjusted to the base month of March, for each month of calving group (MOCG), including the additional dry cow penalty cost (€)

			Additional dry cow penalty (€)1
Predicted and current MOCG			Transition state MOCG
Group	Name	Net profit differential (€/cow calving)	Jan	Feb and March	April to Aug
1	January	0	—	—	—
2	February	80	—	—	—
3	March	0	—	—	—
4	April	−120	—	—	—
5	May	−210	−399	−474	−649
6	June	−210	−349	−424	−599
7	July and August	−210	−275	−349	−524
8	September	74	−200	−275	−449
9	October to December	−116	−100	−175	−349

¹Additional dry cow penalty was applied to the transition state month of calving groups 10, 11, and 12 in the fertility transition matrix within the FP component of the BFPP Index to capture animals that re-calved 2 calendar years after their most recent calving.

Current parity

The current parity component was calculated as the estimated profit potential accruing from the remainder of the CP, given the cow’s month of calving for that parity. If the beef female for which the BFPP was being generated was nulliparous, then the CP component was set to 0. The CP component for cows that had at least 1 calving was calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{C}\mathrm{P}={\displaystyle \underset{c=1}{{\displaystyle \sum ^2}}}\mathrm{E}{\mathrm{V}}_c\cdot \mathrm{P}{\mathrm{V}}_c+((1-R)\cdot {\displaystyle \underset{t=1}{{\displaystyle \sum ^5}}}\mathrm{E}{\mathrm{V}}_t\cdot \mathrm{P}{\mathrm{V}}_t)+R\cdot \mathrm{R}\mathrm{I}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}+\pi }\end{array}}$$ (3)

where CP is the current parity component. The economic values (EV) are described in Table 1 and refer to: (1) cow traits (subscript c) represented by the traits of cow maintenance and docility, (2) traits relevant to terminal progeny destined for harvesting (subscript t) represented by the carcass traits of weight, conformation and fat as well as feed intake and calf docility. The associated production values (i.e., PV_c and PV_t) for the cow and terminal progeny traits are described in Table 1. The term R represents the proportion of females that were assumed to be retained as replacements, which was assumed to be 20%; thus, the remaining proportion of progeny (i.e., 1 − R) was assumed to be harvested. The Irish national replacement index value (Rindex) of the beef female’s progeny that will be retained within the herd as replacement heifers was expressed as a PTA, in Euros, of profit due to the additive genetic merit of the beef female. The Rindex was estimated in line with the current Irish national replacement index using PTAs directly generated from the national genetic evaluations described within, for the 17 traits listed in Table 1 and therefore were not adjusted to a base population. Similar to the HP component already described, a profit differential ($\pi$), relative to a base female calving in March, was added to the CP component which represented the cow’s most recent MOCG (Table 2).

Future Parity

The future parity (FP) component of the BFPP reflects the estimated profit potential culminated across future projected parities (up to a maximum of 10 additional parities) based on two fundamental transition matrices. Firstly, a survival transition matrix was used to estimate the beef female’s probability of surviving and completing her next full parity (i.e., i*) and surviving each potential future parity (i.e., $i$); this was the same approach as used by Kelleher et al. (2015) for dairy cows but populated in the present study with beef cow statistics estimated from the national data (described later). The survival matrix was dependent on the beef female’s current MOCG within her current or predicted parity (i.e., x; which was assumed to be parity 1 if she is a nulliparous female) as well as her percentile group for survival generated from her PV for survival (i.e., $\mathrm{P}\mathrm{G}(\mathrm{P}{\mathrm{V}}_{\mathrm{S}\mathrm{U}})$). Secondly, a fertility transition matrix was used to estimate the probability of a beef female calving in the qth MOCG in the subsequent parity ($\mathrm{M}\mathrm{O}\mathrm{C}{\mathrm{G}}_{\mathrm{n}\mathrm{e}\mathrm{x}{\mathrm{t}}_q}$), given her most recent pth MOCG (or predicted MOCG in the case of nulliparae) ($\mathrm{M}\mathrm{O}\mathrm{C}{\mathrm{G}}_p$), and her percentile group for CIV generated from her PV for CIV (i.e., $\mathrm{P}\mathrm{G}\left(\mathrm{P}{\mathrm{V}}_{\mathrm{C}\mathrm{I}\mathrm{V}}\right)$). The FP was therefore calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}& {\displaystyle \mathrm{F}\mathrm{P}=\left[{\displaystyle \underset{j=i{}^{\ast }}{{\displaystyle \sum ^{i{}^{\ast }+10}}}}\left(\begin{array}{ll}& {\displaystyle {\displaystyle \underset{i=i^{{}^{\ast }}-1}{{\displaystyle \prod ^{j-1}}}}P(\mathrm{S}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{v}\mathrm{a}{\mathrm{l}}_i|\mathrm{M}\mathrm{O}\mathrm{C}\mathrm{G},\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y},\mathrm{P}\mathrm{G}(\mathrm{P}{\mathrm{V}}_{\mathrm{S}\mathrm{U}}))}\\ & {\displaystyle \cdot {\left(\frac{1}{1+r}\right)}^{((j-i^{\ast })+1)\cdot \mathrm{c}\mathrm{i}\mathrm{v}/365}}\end{array}\right)\right]}\\ & {\displaystyle \cdot \left[\begin{array}{ll}& {\displaystyle {\displaystyle \underset{c=1}{{\displaystyle \sum ^4}}}\mathrm{E}{\mathrm{V}}_c\cdot \mathrm{P}{\mathrm{V}}_c+((1-R)\cdot {\displaystyle \underset{t=1}{{\displaystyle \sum ^8}}}\mathrm{E}{\mathrm{V}}_t\cdot \mathrm{P}{\mathrm{V}}_t)}\\ & {\displaystyle +{\displaystyle \underset{q=1}{{\displaystyle \sum ^{11}}}}P(\mathrm{M}\mathrm{O}\mathrm{C}{\mathrm{G}}_{\mathrm{n}\mathrm{e}\mathrm{x}{\mathrm{t}}_q}|\mathrm{M}\mathrm{O}\mathrm{C}{\mathrm{G}}_p,\mathrm{P}\mathrm{G}(\mathrm{P}{\mathrm{V}}_{\mathrm{C}\mathrm{I}\mathrm{V}}))\cdot \rho +R\cdot \mathrm{R}\mathrm{I}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}}\end{array}\right]}\end{array}}\end{array}}$$ (4)

where FP is the future parity component. The term ${\sum }_{j=i^{\ast }}^{i^{\ast }+10}\underset{i=i^{\ast }-1}{\prod ^{j-1}}P(\mathrm{S}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{v}\mathrm{a}{\mathrm{l}}_i|$  $\mathrm{M}\mathrm{O}\mathrm{C}\mathrm{G},\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y},\mathrm{P}\mathrm{G}(\mathrm{P}{\mathrm{V}}_{\mathrm{S}\mathrm{U}}))$ is the sum of the probabilities of the cow surviving to each of the next arbitrarily chosen 10 parities; this would equate to the expected total number of remaining parities to be achieved by the female. A discounting factor, ${(1/(1+r))}^{((j-i^{\ast })+1)\cdot civ/365}$, penalizes each counted parity for the delay between reaching parity j and the time of the next full parity plus an additional CIV (i.e., the average CIV in Ireland in 2019 of 401 d; ICBF (2019)) assumed to be the time from present until the start of the next full parity in years. The economic values (EV) are described in Table 1 and are associated with: (1) cow traits (subscript c) represented by cow maintenance and docility as well as the maternal traits of calving difficulty and maternal weaning weight, (2) traits relevant to future terminal progeny destined for harvest (subscript t) represented by the carcass traits of weight, conformation and fat as well as feed intake, calf docility, and direct calving performance traits including calving difficulty, mortality, and gestation length. The calculation of the PVs for the cow and terminal traits is described in Table 1 and Supplementary Material S1.

The term ${\sum }_{q=1}^{11}P(\mathrm{M}\mathrm{O}\mathrm{C}{\mathrm{G}}_{\mathrm{n}\mathrm{e}\mathrm{x}{\mathrm{t}}_q}|\mathrm{M}\mathrm{O}\mathrm{C}{\mathrm{G}}_p,\mathrm{P}\mathrm{G}(\mathrm{P}{\mathrm{V}}_{\mathrm{C}\mathrm{I}\mathrm{V}}))\cdot \rho$ is the summed expected profit associated with the probability of a cow calving in the next MOCG ($\mathrm{M}\mathrm{O}\mathrm{C}{\mathrm{G}}_{\mathrm{n}\mathrm{e}\mathrm{x}{\mathrm{t}}_q}$), given the beef female’s current or predicted (i.e., for a nulliparous female) MOCG (MOCG_p) and her PV for CIV percentile group ($\mathrm{P}\mathrm{G}(\mathrm{P}{\mathrm{V}}_{\mathrm{C}\mathrm{I}\mathrm{V}})$), where 𝜌 is the profit differential for each current MOCG (MOCG_p) plus an additional monetary penalty applied to MOCGs 5 to 9 (i.e., which span from May to December), inclusive, which captured the small probability of animals re-calving 2 calendar years after their last observed calving event (Table 2). This penalty was imposed to reflect the additional cost incurred from retaining a dry cow in the herd and incorporates the costs of additional feed, land, and machinery usage (Supplementary Table S1; P. Crosson, Teagasc, Meath, Ireland, personal communication). The terms R and Rindex are described previously.

Retention value

The retention value (RV_x) captures the total euro value that is saved if a beef female, who is currently in parity x, is not voluntarily culled and is therefore retained within the herd. The RV_x was calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{R}{\mathrm{V}}_x=\mathrm{R}{\mathrm{R}}_x(\mathrm{H}\mathrm{R}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}-f\left(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x\right))}\end{array}}$$ (5)

where RR_x is the remaining proportion of the production life of the beef female that would be required to be replaced if she were to be culled at the end of parity x (Table 3) and therefore accounts for the high replacement cost of voluntarily culling a younger beef female. The RR_x was calculated as

Table 3.

The proportion of animals estimated to survive their CP and therefore start their next parity (Pnext), the proportion of animals expected to survive their CP, given their chance of surviving each previous parity (Psurv) and, the proportion of an animal’s productive life required to be replaced if they were to be culled at the end of their CP (RR), as well as a beef female’s total expected number of parities (ENP) to complete, given her probability of surviving each parity

Parity1	Pnext	Psurv	RR
0	1.000	1.000	0.838
1	0.773	1.000	0.806
2	0.812	0.773	0.752
3	0.828	0.628	0.689
4	0.825	0.520	0.624
5	0.812	0.429	0.553
6	0.796	0.349	0.478
7	0.774	0.278	0.398
8	0.742	0.215	0.304
9	0.707	0.159	0.183
10	0.660	0.113	0.183
ENP		5.464

¹Parity 0 represents heifers.

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{R}{\mathrm{R}}_x=\left\{\begin{array}{cc}\frac{1+{\displaystyle \sum _{k=x+2}^{10}}{\displaystyle \prod _{j=x+2}^k}\mathrm{P}\mathrm{n}\mathrm{e}\mathrm{x}{\mathrm{t}}_j}{\mathrm{E}\mathrm{N}\mathrm{P}}& {\displaystyle \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}0\le x\le 8}\\ \\ \frac{1}{\mathrm{E}\mathrm{N}\mathrm{P}}& {\displaystyle \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}x\ge 9}\end{array}\right\}}\end{array}}$$ (6)

where it is assumed that if the beef female was not culled at the end of parity x, her probability of starting her next full parity (i.e., i*) would be one (i.e., where 1 is the guaranteed probability of starting parity i* in the numerator of Eq. 6). It is therefore assumed that a nulliparous heifer will start her first parity; however, if the heifer is voluntarily culled prior to her first parity, then RR_x equals 1. The average probability of a beef female surviving her CP, and therefore starting a subsequent parity, up to parity 10, was captured in the term Pnext_j; in the present study, the cow was not assumed to have survived if she did not have a subsequent calving within 600 d of her previous calving (taking cognizance of the date of last calving relative to the date of data extraction). The Pnext_j proportions are described in Table 3. The total expected number of parities (ENP) that a beef female was estimated to complete if not culled (Eq. 7), given her probability of surviving each parity x (Psurv_x), is described in Table 3. For a cow under consideration for culling that has already survived beyond the 9th parity limit, it was assumed that she had the same replacement requirements as if she were to be culled at the end of parity 9 (i.e., RR₉) with an expected maximum survival for only 1 additional parity. A beef female’s ENP was calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{E}\mathrm{N}\mathrm{P}={\displaystyle \underset{x=0}{{\displaystyle \sum ^{10}}}}\mathrm{P}\mathrm{s}\mathrm{u}\mathrm{r}{\mathrm{v}}_x}\end{array}}$$ (7)

where Psurv_x is the probability of surviving beyond parity x so that the next parity (i.e., i*) is started and is calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{P}\mathrm{s}\mathrm{u}\mathrm{r}{\mathrm{v}}_x=\left\{\begin{array}{cc}1& {\displaystyle \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}x=0}\\ {\displaystyle \underset{j=1}{{\displaystyle \prod ^x}}}\mathrm{P}\mathrm{n}\mathrm{e}\mathrm{x}{\mathrm{t}}_{j-1}& {\displaystyle \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}0<x\le 10}\end{array}\right\}}\end{array}}$$ (8)

where Pnext_j is as described previously in Eq. 6. It was assumed that all heifers chosen as replacements will start their first parity.

The cost of buying in a replacement heifer was captured in the term HRcost and was estimated to be €1,790 (Supplementary Table S2; P. Crosson, Teagasc, Meath, Ireland, personal communication). The estimate of the salvage value of the cull cow in parity x ($f(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x)$) was calculated from a function of average predicted cull cow carcass weight for an Irish beef cow (described later) completing parity x and combines intersecting linear and quadratic equations as follows:

$${\displaystyle \begin{array}{l}{\displaystyle f(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x)=\left\{\begin{array}{c}a+b\left(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x\right)+c\left({\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}\mathrm{t}}_x^2\right)\mathrm{i}\mathrm{f}\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x<T\\ \\ d\left(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x\right),\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right\}}\end{array}}$$ (9)

where a to d and T were estimated using the price data described in detail below; this shape is based on the pricing model adopted in Irish abattoirs. The predicted cull carcass weight ($\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x$) was calculated as

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x=\mathrm{P}{\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}\mathrm{t}}+\mathrm{L}\mathrm{S}\mathrm{M}\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x}\end{array}}$$ (10)

where $\mathrm{P}{\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}\mathrm{t}}$ is the production value for a beef female’s cull cow carcass weight. Least squares means of the cull cow carcass weight for parity x ($\mathrm{L}\mathrm{S}\mathrm{M}\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x$) was estimated from an Irish dataset of 86,949 cull cows with a linear fixed effects model fitted to cull cow carcass weight adjusting for parity, carcass fat, conformation, and EBV for cull cow weight (described in detail below); the LSMCullwt estimates for parity x are detailed in Supplementary Table S3.

Transition matrices

The probability of an animal transitioning from one state to another, over a period of time, was calculated using Markov transition matrices similar to the methodology described by Kelleher et al. (2015) for dairy cows.

Month of calving group fertility transition matrix

A 3-dimensional (i.e., a 9 × 11 × 5 matrix array) fertility transition matrix was constructed. The transition matrix dimensions were calculated as follows: firstly, animals were classified into 9 groups based on frequency into their most recent MOCG, namely: (1) January, (2) February, (3) March, (4) April, (5) May, (6) June, (7) July and August, (8) September, and (9) October to December, inclusive (Table 4); secondly, animals were partitioned into 12 transition states based on their MOCG in the next lactation and the duration of time between consecutive calvings as described in Table 4; finally, animals were stratified into 5 percentile groups of equal size based on their PV for CIV (i.e., $\mathrm{P}\mathrm{G}(\mathrm{P}{\mathrm{V}}_{\mathrm{C}\mathrm{I}\mathrm{V}})$; Eq. 4). Solely for the construction of the transition matrices, and to avoid the potential of biasing the matrices with the animal’s own records, PVs for the transition matrices were calculated using the female’s parental average EBV for CIV plus their own heterosis effect on CIV estimated from the national genetic evaluation where it exists as a fixed effect.

Table 4.

Calendar months corresponding to both the current and transition state month of calving groups (MOCG) used in the estimation of the calving interval and survival transition matrices

Calendar month	Current state MOCG	Transition state MOCG
January	1	1
February	2	2
March	3	3
April	4	4
May	5	5
June	6	6
July and August	7	7
September	8	8
October to December	9	9
January*	—	10
February and March*	—	11
April to August*	—	12

*Denotes transition state month of calving groups whereby the beef females re-calved 2 calendar years after their previous calving.

Survival transition matrix

A 3-dimensional (i.e., a 9 × 8 × 5 matrix array) survival transition matrix was constructed as follows: firstly, animals were classified into 9 groups based on their most recent MOCG (Table 4); secondly, animals were stratified based on their CP number group as 1, 2, 3, 4, 5, 6, 7, 8 to 10, inclusive; finally, animals were stratified into 5 strata of equal size based on their survival PV (i.e., PG(PV_su), Eq. 4). The survival PV used within the survival transition matrix was calculated using the animal’s parental average EBV for survival plus the beef female’s own heterosis effect on survival estimated from the national genetic evaluation where it exists as a fixed effect.

Data used in the construction of the index

Genetic and non-genetic effects, as well as the associated raw phenotypic data, were available from the Irish Cattle Breeding Federation (ICBF) national database, Bandon, Co. Cork, Ireland (http://www.icbf.com). The data used in the construction of the BFPP were calving records pertaining to the Irish national herd which were available on 3,850,256 beef females. Cows were classified as beef provided that they had ≤50 % dairy breed composition (i.e., Friesian, Holstein, and Jersey). To ensure the data analyzed were representative of the Irish national commercial beef herd, animals were removed if they were registered to a breed society or were recorded to have given birth to a calf from embryo transfer; these edits resulted in 3,377,598 cows remaining. Only animals that calved between the years 2012 and 2017, inclusive, for parities 1 to 11, inclusive, were retained. Erroneous data and calving events with CIVs (i.e., the number of days between 2 consecutive calvings) that were below 300 d or exceeded 600 d were removed and if the CIV was removed, the animal was recorded to have not survived; these edits resulted in 1,598,271 cows with 4,281,355 calving events remaining. When calculating the transition matrices, parental average EBVs were used; therefore, the beef female’s sire and dam, as well as their respective PTA for CIV and survival, were required to be known; a total of 2,218,278 records from 786,487 cows remained. Furthermore, due to the small number of animals of lactation eight or greater, animals that were in their 8th to 11th lactation, inclusive, were grouped together; therefore, the probabilities populating the survival transition matrices pertaining to lactation 8 to 11 animals were the same. Herds were also required to have a minimum of 5 calving events each year which resulted in 1,789,373 records from 689,438 animals used in the development of the CP and FP components of the BFPP index.

Further edits were applied to the dataset for the estimation of the function values within Eq. 9 and the $\mathrm{L}\mathrm{S}\mathrm{M}\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x$ (Eq. 10) within the RV component. Animals were required to have cull cow carcass phenotypes including carcass weight, conformation, and fat, as described by Englishby et al. (2016), as well as price per kilogram of carcass weight; 270,745 beef females remained. Animals were also required to have not gone through a fattening period; therefore, animals were removed if 300 d had lapsed between the cow’s last calving and when she was harvested, resulting in 86,949 beef cows remaining. Using SAS 9.4 software (SAS Institute Inc., Cary, NC), the function values embedded within Eq. 9 were estimated using a linear and nonlinear regression model in PROC NLIN. The carcass weight break-point (T; Eq. 9) was calculated as $-0.5\left(\frac{b}{c}\right)$; the upper limit euro/kg of carcass weight (d; Eq. 9) was calculated as $a+b(-0.5\left(\frac{b}{c}\right))+c{(-0.5\left(\frac{b}{c}\right))}^2$.

Index validation

The validation population was based on all beef cows that had a recorded calving event in the year 2017 within the edited dataset; the following additional edits were applied: (1) beef cows were required to have EBVs for each trait within the Irish replacement index (Rindex) available, resulting in 150,370 cows, (2) beef cows were retained if their resulting progeny from the 2017 calving were harvested, prior to data extraction, between 12 and 36 mo of age for heifers and steers and between 12 and 24 mo of age for young bulls; 124,992 beef females remained; (3) the sires of the beef cow’s progeny were required to have been known and the progeny must have resided in their final herd prior to slaughter for at least 100 d; 94,944 beef cows remained; (4) at least 3 animals must have been present in the progeny’s slaughter contemporary group, resulting in 72,059 beef cows remaining, and finally, (6) there had to be at least 15 calving events in the herd in 2017 for the beef females to be retained; this resulted in 21,102 beef cows from 875 herds remaining in the validation population as well as 21,102 of their harvested progeny (no twins were present within the validation population).

Genetic evaluations

Five suites of multitrait multibreed genetic evaluations were run to generate both random and fixed effects solutions for all traits included in the Irish national replacement index using the Mix99 software (MiX99 Development Team, 2015). The phenotypic data pertaining to the 5 genetic evaluations were truncated on the 31st December 2017 and therefore only included records pertaining to the beef females for, and prior to, the year 2017. The national fertility evaluation is a 6 × 6 multitrait evaluation. The fertility phenotypic data used in the present study consisted of 11,186,677 individual lactations with a pedigree file of 15,321,093 animals; only the fixed effect solutions and random effects pertaining to the traits AFC (days), CIV (days), and survival (SURV; %) were retained from the fertility genetic evaluation. The national calving performance evaluation is a 9 × 9 multitrait evaluation and included 19,555,773 birth records with 23,719,121 animals in the pedigree file; only the fixed effect solutions as well as random direct and maternal effects were available for the traits calving difficulty (scale 1 to 4), mortality and gestation length (days). The docility genetic evaluation is a 3 × 3 multitrait genetic evaluation; the phenotypic data used in the present study consisted of 2,761,478 individual animals with a pedigree file of 4,172,537 animals; only the fixed effect solutions and random effects pertaining to the farmer-recorded calf and cow docility traits were retained. The national beef carcass evaluation is a 24 x 24 multitrait carcass genetic evaluation including various traits relating to live-weight groups, carcass traits, and livestock auction prices; however, only the fixed and random effect solutions pertaining to the traits cow live-weight, feed intake, carcass traits (i.e., weight, conformation, and fat), and cull cow carcass weight were used in the present study; the phenotypic dataset consisted of 13,347,345 individual animal’s records and the pedigree file contained 18,918,306 animals. The national milk (i.e., maternal weaning weight) genetic evaluation is a 7 × 7 multitrait evaluation; fixed effect solutions as well as maternal and direct random effects were only retained for weaning weight; the phenotypic data used in the evaluation consisted of 8,802,215 individual animals and the pedigree file contained 13,428,159 animals.

Statistical analyses

Within each herd, Pearson correlations were used to estimate the relationship between the BFPP index itself, 3 of its subindexes (as there were no heifers in the validation population, the HP component was omitted from validation), the Irish national Replacement (Rindex), the calf (comprised of terminal traits), and cow (comprised of maternal traits) subindexes of the Rindex, and the Irish National Terminal Index. The pairwise correlations were subsequently averaged across herds. A detailed profit analysis was not possible for the herds within the present study as precise input and output data were not available. Hence, animals were stratified, within each herd, into 4 groups of equal size based on their BFPP index value and were validated based on their respective phenotypic performances. A range of descriptive statistics were estimated for each stratum as well as the mean CP, FP, and RV subindex values for each BFPP stratum. Mean calendar days of the year at calving was estimated within each BFPP stratum. Mean cow CIV within each BFPP stratum was estimated following adjustment for contemporary group of herd-year-season of calving (Berry and Evans, 2014). The log of the odds of surviving to the next lactation was estimated using logistic regression in PROC GENMOD (SAS Institute Inc., Cary, NC) as follows:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{L}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left\{P(\mathrm{S}\mathrm{u}\mathrm{r}\mathrm{v}=1|X)\right\}=\mathrm{B}\mathrm{F}\mathrm{P}\mathrm{P}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{m}+\mathrm{H}\mathrm{Y}\mathrm{S}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{v}}\end{array}}$$

where $\mathrm{L}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left\{P(\mathrm{S}\mathrm{u}\mathrm{r}\mathrm{v}=1|X)\right\}$ was the log of the odds of a positive outcome (i.e., the animals survived); BFPPstratum represented the fixed effect of the beef cow’s stratum for BFPP (i.e., 1 (top 25%) to 4 (bottom 25%), inclusive); HYScalv was the random effect of the cow’s herd-year-season contemporary group of calving. Odds ratios were calculated as the exponent of the model solutions.

Linear mixed models were used to estimate the least squares means for each progeny trait within each BFPP stratum as

$${\displaystyle \begin{array}{ll}{\displaystyle \mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{t}{\mathrm{s}}_a=}& \mathrm{B}\mathrm{F}\mathrm{P}\mathrm{P}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{m}+{\displaystyle \underset{b=1}{{\displaystyle \sum ^2}}}\mathrm{H}\mathrm{e}\mathrm{t}+\mathrm{H}\mathrm{Y}\mathrm{S}\mathrm{s}\mathrm{l}\mathrm{a}\mathrm{u}+\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}\\ & +\mathrm{A}\mathrm{g}\mathrm{e}\mathrm{S}\mathrm{l}\mathrm{a}\mathrm{u}+\mathrm{S}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{P}\mathrm{T}{\mathrm{A}}_a+\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}|\mathrm{A}\mathrm{g}\mathrm{e}\mathrm{S}\mathrm{l}\mathrm{a}\mathrm{u}\\ & +\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}|\mathrm{S}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{P}\mathrm{T}{\mathrm{A}}_a+e\end{array}}$$

$${\displaystyle \begin{array}{ll}{\displaystyle \mathrm{A}\mathrm{g}\mathrm{e}\mathrm{S}\mathrm{l}\mathrm{a}\mathrm{u}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{e}\mathrm{r}=}& \mathrm{B}\mathrm{F}\mathrm{P}\mathrm{P}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{m}+{\displaystyle \underset{b=1}{{\displaystyle \sum ^2}}}\mathrm{H}\mathrm{e}\mathrm{t}+\mathrm{H}\mathrm{Y}\mathrm{S}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{v}+\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}\\ & +\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{W}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}+\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{F}\mathrm{a}\mathrm{t}\\ & +\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}|\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{W}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}+\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}|\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{F}\mathrm{a}\mathrm{t}+e\end{array}}$$

where Carcass traits was the trait a pertaining to carcass weight (kg), conformation (EUROP scale), and fat (15-point score); AgeSlaughter was the age of the progeny when harvested (in days); BFPPstratum represented the fixed effect of the beef cow’s stratum for BFPP (i.e., 1 to 4, inclusive); Het was the heterosis coefficient which was fitted as 2 separate fixed effect heterosis coefficients to represent the progeny of the beef cows different breed crosses; HYSslau and HYScalv were the progeny of the beef cows herd-year-season contemporary group for slaughter and birth, respectively, fitted as a random effect; CarcType was the fixed effect of whether the progeny was a heifer, steer or young bull; AgeSlau was the fixed effect of the progeny’s age at slaughter in months; SirePTA_a was the progeny’s sire PTA (i.e., this was the most up-to-date PTA available on the sire from the respective national genetic evaluation) for trait a, fitted as a fixed effect; CarcType|AgeSlau was the fixed effect interaction between the progeny’s carcass type and age at slaughter; CarcType|SirePTA_a was the fixed effect interaction between the progeny’s carcass type and sire’s PTA for trait a; CarcassWeight was the fixed effect of phenotypic carcass weight (kg) of the progeny; CarcassFat was the phenotypic carcass fat score of the progeny, fitted as a fixed effect; CarcType|CarcassWeight was the fixed effect interaction between the progeny’s carcass type and phenotypic carcass weight; CarcType|CarcassFat was the fixed effect interaction between the progeny’s carcass type and phenotypic carcass fat; e was the residual.

Results

Characterization of components within the BFPP index

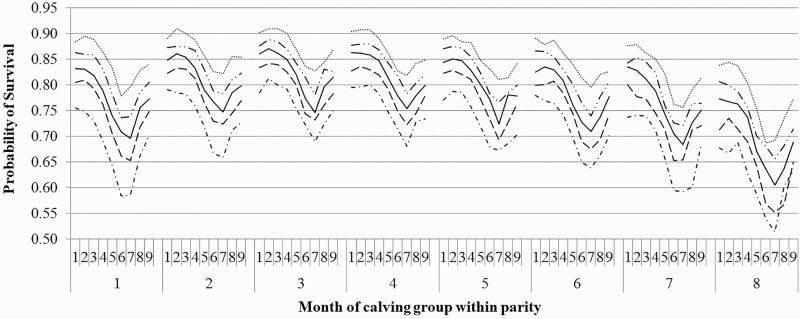
Irrespective of parity or MOCG, the probability of surviving from one parity to the next progressively improved as the percentile group for survival PV improved (Figure 1). The difference in survival between the best and worst PV percentile groups ranged from 9.65% for third parity cows calving in February to 20.95% for parity 1 cows calving in June. Cows that calved in either January or February tended to have the greatest probability of surviving to the next parity across all PV percentile groups. Irrespective of PV percentile group or MOCG, parity 2 to 6 cows, inclusive, had a greater probability of survival to the next parity than parity 1 animals. The lowest probability of surviving to the next parity was for cows that calved in July and August (Figure 1); the survival transition matrix data are in Supplementary Table S4.

Figure 1.

The probability of beef females surviving to start their subsequent parity given their current month of calving group (i.e., 1 = January, 2 = February, 3 = March, 4 = April, 5 = May, 6 = June, 7 = July and August, 8 = September, and 9 = October to December, inclusive) when stratified into 5 strata based on their parental average EBV for survival (i.e., top 20% (••••), 60% to 80% (― • •), 40% to 60 % (―), 20% to 40% (― ―), and bottom 20% (― • ―)).

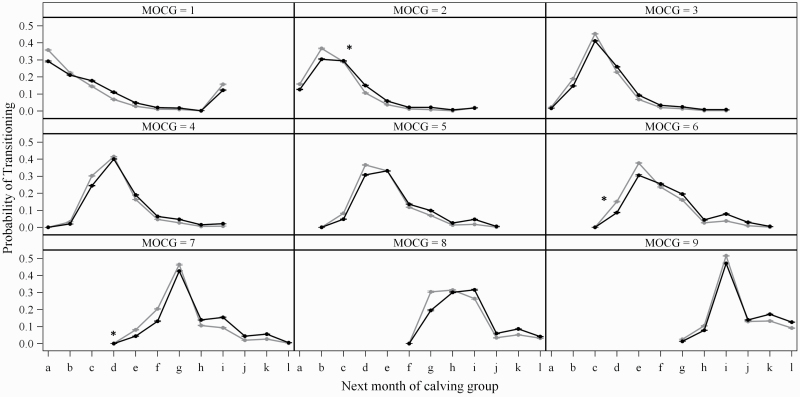
Cows that calved between January and April, inclusive, had a greater probability of re-calving in the same MOCG the following year (ranging from 0.29 in the lowest PV group for January to 0.45 in the best PV group for March) relative to transitioning into a different MOCG (Figure 2). Irrespective of the MOCG, cows in the highest PV percentile group for CIV had a greater probability of re-calving in the same MOCG relative to those in the lowest PV percentile group. Cows in the best PV stratum for CIV had a greater probability of re-calving earlier relative to cows in the worst CIV stratum (ranging from 0.03 in January and February calving cows to 0.11 for cows calving in September); whereas cows in the worst PV stratum for CIV tended to have a greater probability of re-calving later relative to cows in the best PV stratum (Figure 2). The fertility transition matrix values are available in Supplementary Table S5.

Figure 2.

The probability of beef females within the top (grey) and bottom (black) 20% strata for their parental average EBV for CIV and heterosis effect, transitioning to a next month of calving group (i.e., a, January; b, February; c, March; d, April; e, May; f, June; g, July and August; h, September; i, October to December; j, January; k, February; and l, April to August; inclusive, where groups j to l are in two calendar years’ time), given their current month of calving group (MOCG; i.e., 1, January; 2, February; 3, March; 4, April; 5, May; 6, June; 7, July and August; 8, September; and 9, October to December, inclusive); standards errors are represented in the error bars above and below the mean and * above the next month of calving group denotes where P > 0.05.

Within the RV component of the BFPP index, the beef female’s salvage value was determined by: (1) the constant value a equal to −3.309, (2) the linear coefficient of 0.037111, and (3) the quadratic coefficient −0.0000506. Thus, the cull cow carcass weight break-point value (T) was estimated to be 366.71 kg (i.e., $T=-0.5(0.037111/-0.0000506)$). The upper limit Euro per kilogram of cull cow carcass weight, d, was estimated to be €3.50 per kg (i.e., $d=a+b(T)+c\left(T^2\right)$). Therefore, the formula used in the estimation of the beef females cull cow carcass value was:

$${\displaystyle \begin{array}{l}{\displaystyle f(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x)=\left\{\begin{array}{c}-3.309+0.037111\left(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x\right)\\ +-0.0000506\left({\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}\mathrm{t}}_x^2\right)& {\displaystyle \mathrm{i}\mathrm{f}\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x<366.71\mathrm{k}\mathrm{g}}\\ 3.50\left(\mathrm{C}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{w}{\mathrm{t}}_x\right),& {\displaystyle \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}\end{array}\right\}}\end{array}}$$ (11)

Descriptive summary of the BFPP index

The mean of the within herd correlations between all the (sub-) indexes is in Table 5. Of all the 3 subindexes in the BFPP, the FP was the most strongly correlated with BFPP (r = 0.84), whereas the RV was the most weakly correlated (r = 0.49). The BFPP was moderately positively correlated with the Irish national replacement index within herd (i.e., Rindex; r = 0.45) as well as with both the calf (r = 0.29) and cow (r = 0.31) subindexes of the Rindex. The correlation between the BFPP and the Irish national terminal index was weaker at 0.27. Of the 3 subindexes of the BFPP, the FP subindex was most strongly correlated with the Rindex (r = 0.63) with correlations of 0.40 and 0.47 with the cow and calf subindexes of the Rindex, respectively. Although the correlation between the CP subindex and the Rindex was only 0.17, the correlation between the CP and the calf subindex (r = 0.28) was stronger than the correlation of 0.03 between the CP and the cow subindex. While the correlations reported are for 875 herds with at least 15 calvings, the correlations were also very similar when the dataset was limited to the 256 herds with at least 25 calvings.

Table 5.

Correlations between the beef female’s profit potential index (BFPP) and the the Current Parity (CP), Future Parity (FP) and retention value (RV) subindexes within the BFPP index, as well as the Irish national replacement index (RIndex) and the Calf (Calf RIndex) and Cow (Cow RIndex) subindexes within the RIndex and the Irish national terminal index (Terminal)

	BFPP	CP	FP	RV	RIndex	Calf RIndex	Cow RIndex	Terminal
BFPP		0.68	0.84	0.49	0.45	0.29	0.31	0.27
CP			0.55	−0.07	0.17	0.28	0.03NS	0.29
FP				0.14	0.63	0.47	0.4	0.45
RV					0.06NS	−0.15	0.14	−0.16
RIndex						0.29	0.86	0.22
Calf RIndex							−0.18	0.98
Cow RIndex								−0.24

^NSNo significant difference (P > 0.05).

Validation of the BFPP index

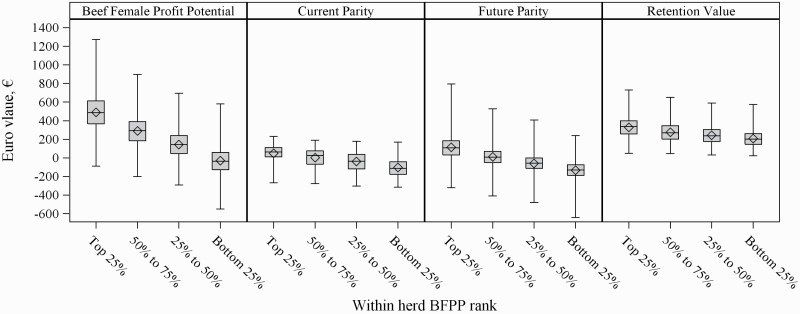
The average within-herd BFPP index and BFPP subindex values by strata are in Figure 3. The smallest mean difference between the best and worst BFPP strata was for the RV subindex (i.e., €121.64), whereas the greatest difference was for the FP subindex (i.e., €246.92). Cows within the top 25% BFPP stratum had a greater range in (sub-)index values relative to the remaining strata (Figure 3). The mean Irish national replacement index (i.e., breeding index for maternal beef traits; Rindex) and terminal index (breeding index for terminal beef traits) in each BFPP stratum is in Table 6. As the BFPP stratum improved, the Rindex and Irish national terminal index values also improved. The mean Rindex of cows in the best BFPP stratum was €32.76; therefore, the additional profit expected from each of the cow’s calvings was expected to be worth €35.69 more than cows within the worst stratum. Relative to the cows within the worst BFPP stratum, the mean Irish national terminal index value of the cows within the best stratum was almost €16 greater; thus the harvested progeny of the high BFPP beef cows were, on average, expected to be almost €16 more profitable.

Figure 3.

Average within-herd summary statistics of the BFPP index as well as the 3 BFPP subindexes, including the CP, FP, and retention value, when animals were stratified based on their BFPP value.

Table 6.

Mean Irish National Replacement and Terminal Index values for animals stratified based on their BFPP index value as well as their mean calendar day at calving, CIV, log of the odds of surviving to the next parity, and the least squares mean performance of the BFPP female’s progeny for carcass traits (i.e., weight, conformation, and fat) and age at slaughter; standard error within parenthesis

		BFPP stratum
Animal	Component	Top 25%	50% to 75%	25% to 50%	Bottom 25%
Cows traits	Replacement (€)	32.76 (0.43)	22.35 (0.41)	12.75 (0.41)	-2.93 (0.45)
	Terminal (€)	31.97 (0.40)	27.61 (0.39)	23.27 (0.39)	16.07 (0.42)
	CIV (d)	377.21 (0.55)a	372.38 (0.54)b	371.19 (0.53)b	368.88 (0.57)c
	Calendar day at calving	96.86 (1.14)a	107.44 (1.10)b	119.00 (1.07)c	135.06 (1.12)d
	Survival1 (0 to 1)	1.63 (1.52,1.72)a	1.49 (1.39,1.58)a	1.33 (1.23,1.42)a	1.00b
	Carcass weight (kg)2	398.46 (0.85)a	398.48 (0.82)a	396.61 (0.80)ab	394.29 (0.83)b
Progeny traits	Carcass conformation (EUROP scale)3	7.19 (0.02)a	7.14 (0.02)ab	7.07 (0.02)b	6.94 (0.02)c
	Carcass fat (1 to 15 scale)4	7.94 (0.02)a	7.99 (0.02)ab	8.04 (0.02)b	8.04 (0.02)b
	Age at slaughter (d)5	659.29 (1.84)a	653.72 (1.76)b	652.56 (1.73)b	650.45 (1.79)b

¹The bottom 25 % BFPP stratum was the reference stratum.

²Reference animal was a steer with 100% heterosis, slaughtered at 24 months old and sire’s carcass weight predicted transmitting ability (PTA) was 20kg.

³Reference animal was a steer with 100% heterosis, slaughtered at 24 months old and sire’s carcass conformation PTA score was 1.6 units.

⁴Reference animal was a steer with 100% heterosis, slaughtered at 24 months old and sire’s carcass fat PTA score was -0.06.

⁵Reference animal was a steer with 100% heterosis, slaughtered at 24 months old with a carcass weight of 380 kg and carcass fat score of 6.8.

Different superscripts within row indicate significant difference P < 0.05.

The mean phenotypic performance of both the beef cows and their progeny for each BFPP stratum is in Table 6. Cows within the top 25% for the BFPP had the longest CIV, 8 d, on average, longer than the bottom 25% of cows on BFPP. The top 25% BFPP cows did, however, calve, on average, 38.2 d earlier in the calendar year relative to the beef females in the bottom 25% stratum. The top 25% BFPP ranked cows were also 1.63 times more likely to survive to the next lactation than their lowest ranking contemporaries. When the progeny of the high BFPP cows were harvested, they had, on average, heavier more conformed carcasses with lower fat scores (i.e., 4.17 kg heavier, 0.25 conformation units better, and 0.10 fat score units lower, respectively) relative to the worst BFPP stratum. When adjusted to the same carcass weight, the progeny of the high BFPP cows were, however, harvested almost 8 d later than the progeny of the beef cows within the worst BFPP stratum (Table 6).

Discussion

Culling decisions have been reported to be multifarious (Bascom and Young, 1998) and can be influenced by a range of factors such as cow age (Adamczyk et al., 2017), performance relative to contemporaries (Berry et al., 2005), infertility and production (Seegers et al., 1998). Hence, actually deciding on which animal to cull given all the underlying contributing factors can become unwieldy, especially in large herds. A fundamental element to the successful deployment and adoption of any decision-support tool (DST), such as the BFPP, is providing an actual solution to a problem. Therefore, being able to collate the multifarious risk factors into a single rank per animal could be hugely beneficial in achieving more optimal culling decisions. Several tools have previously been developed to help identify animals for culling (Stewart et al., 1977; Lopez-Villalobos et al., 2010), yet to our knowledge, all are specific to the dairy sector. To date, the quality and availability of data pertaining to genetic-based beef management DSTs may have been a limiting factor in the ability to develop and implement a culling tool, such as the BFPP; therefore, the global applicability of the BFPP framework may be data resource-limited and would require data integrity systems in place which ensure sire verification.

Key drivers of the successful adoption and on-going engagement with a DST are multitudinous and include factors such as the DST’s ease-of-use, potential to improve efficiency as well as the trustworthiness of the provider (Rose et al., 2016). Therefore, incorporating components within the DSTs which are already familiar and trusted by the producer (e.g., breeding indexes) can stimulate an accelerated rate of adoption. Furthermore, being able to demonstrate the construction of the final index value by decomposing it into its individual subcomponents can facilitate a greater understanding, and thus acceptance, of the ranking tool. This was the basis of the approach adopted by Kelleher et al. (2015) in their construction of a relatively simply tool to rank dairy cows on future lifetime profitability. The motivation for the present study was to tailor, and where appropriate, modify the framework proposed by Kelleher et al. (2015) for deployment in beef females; a noteworthy addition in the present study to the tool proposed by Kelleher et al. (2015) was its expansion to also consider nulliparous females in the ranking against cows. This important addition can be beneficial in deciding whether a virgin heifer should be retained as a replacement or finished for harvesting. Similarly, the ability to compare the BFPP of a virgin heifer to that of the cows in the herd can help determine the level of voluntary culling for that herd. The end outcome is that the BFPP proposed here should be used to first and foremost identify cows for culling (and the heifers to replace them) but can also be used to identify superior females with the greatest lifetime potential within the herd. When utilized in tandem with the Irish national replacement index (Twomey et al., 2020), females who are not only genetically superior but also have a high BFPP value, and therefore a high lifetime profitability potential, can be identified and mated to suitable bulls to produce exceptional replacement females and in doing so, increase the genetic gain achievable; the end outcome being a year-on-year improvement in performance. The BFPP can also facilitate the decision-making process when trading beef females as the buyer can assess the future lifetime potential of the female. Moreover, although the research was carried out on dairy cattle, Dunne et al. (2019) reported that an animal’s performance can differ depending on the herd’s best linear unbiased estimates; therefore, there is potential for the BFPP to be tailored to each individual herd so that producers have an indication of how a female may perform specific to their own herd environment.

Framework of the culling tool

Selection indexes were first proposed in the early 1940s (Hazel and Lush, 1942) and are now ubiquitous in animal breeding globally. Ireland operates both a Terminal (Connolly et al., 2016) and Replacement (Amer et al., 2001; Twomey et al., 2020) national breeding indexes, both of which are routinely used by producers and breeders. The Irish national replacement index forms the foundations of the proposed BFPP in the present study. Inclusion of both non-additive genetic effects and non-genetic effects is a key extension for implementation of this DST. The contribution of non-additive genetic effects (Gregory et al., 1978; McHugh et al., 2019) as well as non-genetic effects (Coyne et al., 2019; Judge et al., 2019; McHugh et al., 2019) to animal performance in beef cattle has been documented elsewhere; hence, these factors will influence the decision to cull a female (as well as which heifer to retain for breeding) and thus should be considered within a decision support tool for culling and identifying profitable heifers.

The underlying principle of the BFPP was that of the simple culling index developed for dairy cows by Kelleher et al. (2015) but modified to be applicable for beef females. Consistent with the BFPP developed in the present study, Kelleher et al. (2015) considered the subindexes of the current lactation (CP in the present study), future lactations (FP in the present study), and what they called net replacement cost differential (RV in the present study). While most dairy breed females born are destined to become replacements (Kelleher et al., 2016), this is not necessarily the case in most beef enterprises with a proportion of females being grown for harvesting at, on average, 21 mo of age (Berry et al., 2020). A decision therefore needs to be made relatively early in the life of the heifer as to whether she is suitable to become a cow or would she be more profitable if harvested directly. To facilitate this decision point, the BFPP was expanded beyond that of the dairy culling index proposed by Kelleher et al. (2015) to also consider nulliparae. The end-purpose of the beef female is generally decided upon after weaning (~8 mo of age in Ireland; McHugh et al. 2014). Given that McHugh et al. (2014) also reported that the average AFC for a beef female was ~31 mo, a time delay of almost 2 yr between deciding to keep the female as a replacement and her calving for the first time would be expected to lapse. To reflect this time-delay, the HP subindex of the BFPP was developed to be adaptable to specific decision-time points, with the addition of y (i.e., the estimated number of years until a heifer is predicted to express the trait under consideration) in the HP subindex, thus ensuring that producers are provided with BFPP index values that are representative of their nulliparous females at important time-points when decisions are being made.

The transition matrices developed in the present study are instrumental in modeling the lifetime efficiency potential of the beef female and are intrinsic to the FP subindex. The fertility transition matrix was formulated to ultimately estimate the expected profit resulting from the beef female’s next parity given her probability of calving in each MOCG. In a cross-sectional analysis of the Irish national database, McHugh et al. (2014) demonstrated how 38,619 Irish cows excelling in genetic merit for CIV had indeed shorter CIVs. This observation corroborates the results from the fertility transition matrices in the present study (Figure 2 and Supplementary Table S5) where cows of superior genetic merit for CIV had the highest probability of re-calving in the same or earlier MOCG relative to the contemporaries of poorer genetic merit for CIV. This is despite the low heritability estimated for CIV in the Irish beef cow population (h² = 0.02; Berry and Evans, 2014). Although cows within the best BPFF stratum had an average phenotypic CIV of 8 d longer than the cows within the worst BFPP stratum, the top 25% BFPP females calved 38.2 d earlier in the calendar year relative to the females in the bottom 25% BFPP stratum (Table 6). Given that Irish beef production is predominantly based on spring-calving systems, and because the top 25% of beef females calved earlier in the year, these females would have been subjected to a longer voluntarily waiting period which had ramifications on their respective CIV.

Animal longevity can have a huge impact on herd profit since not only are calves from older cows more valuable (McHugh et al., 2010), owing to their superior carcass weight (Judge et al., 2019) but also because of the reduced requirement for replacement heifers who, in turn, can themselves be harvested. The robustness of the BFPP was tested across different age distributions and varying degrees of replacement rates (i.e., 10%, 20%, and 30%). When comparing across a common replacement rate, the correlation between the index values of cows at differing age distributions ranged from 0.862 to 0.977. When comparing across the same age profile, but altering the replacement rate, the correlations ranged from 0.990 to 0.999. In their analysis of 5,582 Irish beef cows from the national database, McHugh et al. (2014) reported that the logit of the probability of survival to next lactation increased linearly as PTA for survival improved again consistent with the results from the survival transition matrices in the present study; the heritability of survival in Irish beef cows is 0.02 (Berry and Evans, 2014). Relative to the lowest PV stratum for survival, cows in the top stratum for PV for survival in the present study had between 9.65 and 20.95 percentage unit greater probability of surviving to the next lactation across the different MOCG. A similar trend was detected in the validation population of the present study whereby the odds of cows within the best BFPP stratum surviving to the next lactation was 1.63 times more likely than those in the worst stratum. Nevertheless, as Irish beef production is predominantly a spring-calving-based system (Berry and Evans, 2014), animals had the highest probability of surviving if they calved within the first 3 mo of the year, regardless of their PV stratum for survival.

One of the main objectives of the present study was to develop a tool that can easily be used by producers since this is a key for successful adoption (Rose et al., 2016). This ease-of-use means that all the traits and underlying data are collapsed into a single value (i.e., the BFPP is provided from which to rank animals) and the data which populate the index are generally readily available; therefore, the marginal cost of generating the index for all beef females is low. Most of the data underlying the developed BFPP, in the form of fixed and random effects solutions, are already routinely generated in routine genetic evaluations; therefore, the solutions should be relatively easy to obtain. Moreover, the potential users of the proposed BFPP are more than likely already engaging with the Irish national replacement index and therefore trust the information generated from the genetic evaluations; having this trust in a DST is a key factor potential users consider when deciding whether or not to adopt a new DST (Rose et al., 2016). Other components determining the BFPP of an animal such as the transition matrices or the cull cow prices do not need to be regularly updated. Of course, the index itself can be modified to, for example, incorporate a dynamism for costs and prices reflective of the seasonal variability. Notwithstanding this, the objective of the present study was to develop the framework and any such modifications would be easy to implement in the future.

Breeding vs. management indexes and their applications

The BFPP is not designed to replace a maternal breeding index but instead to be complementary to such a breeding tool. The goal of most beef cow–calf producers is to shift the herd distribution of profit per cow in the favorable direction. A shift in the distribution can be achieved by breeding the females on the favorable side with genetically elite sires or by culling the females on the unfavorable side of the distribution. Fastest gain, of course, is achieved when both are applied concurrently. In fact, the mean of the within herd correlation between the BFPP and the Irish national replacement index was 0.45 (Table 5), indicating that while both indexes are profit based, animals do indeed rank differently, albeit there are some similarities. This less than unity correlation is expected, partly because the breeding index trait predictions only includes additive genetic effects, whereas the BFPP trait predictions also includes non-additive effects. Furthermore, the relative weightings on trait predictions is changed, and additional phenotypic attributes of the beef female are taken into consideration in the BFPP, such as her age, and most recent or expected month of calving. While a breeding index is generally used just prior to the start of the breeding season, the BFPP can be used at several points in the calendar year. Furthermore, breeding indexes are generally updated only a few times per year, synchronized with the relevant genetic evaluations. The BFPP, on the other hand, is developed to be dynamic and thus can be updated on the fly as new phenotypic information becomes available. This dynamic nature of the BFPP ensures that it is useful at multiple decision points during the calendar year.

Firstly, a decision can be made, using the BFPP as to whether a cow should be mated that breeding season, or just culled. When deciding what females to breed replacements from, using the BFPP in conjunction with a breeding index, ensures females with not only the greatest lifetime profit potential but also the highest maternal genetic merit can be identified; thus shifting the distribution even further in a favorable direction. When the BFPP was validated, the complementary nature of both the BFPP and the Irish national replacement index was reflected in the cow’s mean Irish national replacement index value. On average, the additional profit accruing from each cow’s calving within the best BFPP stratum was expected to be worth almost €36 greater than the cows within the worst stratum; this was considered her genetic expectation. It was possible to estimate the actual monetary value arising from the differences in phenotypic performance between the best and worst BFPP stratum by multiplying the observed phenotypic differences in performance (Table 6) by the respective economic values (Table 1). The difference in phenotypic performance of the cows in the best BFPP stratum relative to the worst for survival and CIV was estimated to be worth an additional €10.20 and the phenotypic performance of their harvested progeny for the 3 carcass traits (weight, conformation, and fat) was estimated to be worth an extra €21.92. Therefore, although not all traits were considered, it was estimated that the cows within the best BFPP stratum, on average, contributed an additional €32.31 per calving to the herd’s profitability than cows within the worst stratum. Furthermore, the harvested progeny of the cows within the best BFPP stratum had a genetic expectation of being worth almost €16 more than the progeny of the worst BFPP cows, which is very close to the phenotypic difference of €21.92 estimated.

The dynamic nature of the BFPP means that when the cow calves, the most recent calving date can be used to update both the profit from the CP but also the likelihood of calving in different months of the following year (including not calving again) and thus the FP and overall BFPP. Following the breeding season, the BFPP can again be updated once pregnancy diagnoses are recorded which generally occurs in the autumn time; if the cow is deemed not to be pregnant then she will not be calving the following calving season and should incur a large monetary penalty within the BFPP, similar to the dry cow penalty already incorporated. Similarly service dates can be used to update the likelihood of calving in different months of the year. The decision can then be made to sell the cow for fattening or fatten the cow prior to slaughtering. Although both dairy and beef cows were included, McHugh et al. (2010) documented a bimodal distribution of when Irish cows were sold in livestock auctions, which were reported to coincide with prior to and post the breeding season; thus, there is huge potential for the BFPP index to provide data-driven culling decision-support during these times.

Once the subsequent calf is born, then the BFPP of any female calves can be used to identify the females most suitable for graduation into the mature herd. Little additional information will become available on a nulliparae post birth other than through changes in her EBV either from genotyping, through changes in the EBV of her parents, or from the inclusion of her own live-weight phenotypes in the genetic evaluations. One of the advantages of the reliance of the BFPP on data is that producers who want to optimally use the BFPP to their advantage must ensure the integrity and completeness of their inputted data. These data can subsequently be used in the genetic evaluations to improve the accuracy of genetic evaluations for not only the female herself but also her relatives and contemporaries. This in turn improves the accuracy of the BFPP but also of the Irish national replacement index. Therefore, the objectives of both indexes, while different, are very complementary.

Conclusions

Voluntary culling decisions are multifactorial and can be difficult to address; therefore, the ability to collate the risk factors into a single BFPP value per animal could be hugely beneficial for users when making necessary culling decisions. The BFPP has the potential to be implemented complementary to a maternal breeding index and, when used in combination, has the potential to add substantial value to the breeding index by facilitating decisions based on heifer replacements as well as cow culling decisions. Cows that ranked highly on the BFPP index had greater odds of survival to next lactation, were more likely to calve in the same month the following year, and produced calves of superior carcass metrics. The framework is ready for deployment in Ireland but could also be considered for other industries where there is a reasonable level of sire verification and commercial cow and calf performance records captured in a centralized database system which are subsequently used in genetic evaluations.

Glossary

Abbreviations

AFC

age at first calving

BFPP

beef female’s profit potential

CIV

calving interval

CP

current parity

DST

decision-support tool

EBV

estimated breeding value

FP

future parity

HP

heifer potential

ICBF

Irish Cattle Breeding Federation

MOCG

month of calving group

PG

percentile group

PTA

predicted transmitting ability

PV

production value

Rindex

Irish national replacement index

RV

retention value

SURV

survival

Funding

This publication has emanated from research supported by a research grant from Science Foundation Ireland and the Department of Agriculture, Food and Marine on behalf of the Government of Ireland under the grant no. 16/RC/3835 (VistaMilk) as well as funding from the Irish Department of Agriculture, Food and the Marine STIMULUS research grant MultiRepro and the European Union’s Horizon 2020 research and innovation programme—679 GenTORE—under grant agreement 727213. We are also grateful for the help of Dr. Paul Crosson and Dr. Laurence Shalloo in the estimation of the economic components used within the present study.

Conflict of interest statement

The authors declare no real or perceived conflicts of interest.