Conformation and Permeability: Cyclic Hexapeptide Diastereomers

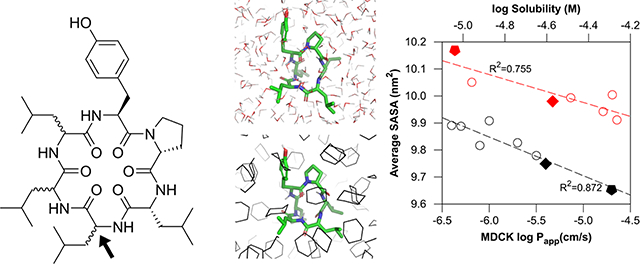
Abstract

Conformational ensembles of eight cyclic hexapeptide diastereomers in explicit cyclohexane, chloroform and water were analyzed by multicanonical molecular dynamics (McMD) simulations. Free energy landscapes (FELs) for each compound and solvent were obtained from the molecular shapes and principal component analysis at T = 300 K; detailed analysis of the conformational ensembles and flexibility of the FELs revealed that permeable compounds have different structural profiles even for a single stereoisomeric change. The average solvent accessible surface area (SASA) in cyclohexane showed excellent correlation with the cell permeability, whereas this correlation was weaker in chloroform. The average SASA in water correlated with the aqueous solubility. The average polar surface area did not correlate with cell permeability in these solvents. A possible strategy for designing permeable cyclic peptides from FELs obtained from McMD simulations is proposed.

Graphical Abstract

1. INTRODUCTION

Efficient conformational sampling of macrocycles is an emerging interest for assigning physical properties, especially for modalities in “beyond the rule-of-five (bRo5)” chemical space, such as cyclic peptides.^1–14 Conventional sampling methods have been performed in implicit solvent using molecular mechanics to predict, for example, membrane permeability.^6,7 Because cyclic peptides have many metastable states in solvents, selecting single conformations for molecular property assignment may be insufficient, requiring more powerful sampling methods. Recently, replica exchange molecular dynamics (REMD),¹⁵ metadynamics (MetaD),¹⁶ and accelerated MD (aMD)¹⁷ simulations in explicit solvent were adopted to investigate relationships between the detailed structure of cyclic peptides and their physical properties, such as cell permeability, aqueous solubility,^9,10 and structural and thermodynamic information.^11–14 Although these methods are generally used, exchange rate optimization is required for REMD simulations, and many collective variables are required for MetaD simulations. Other approaches denoted CANDLE,¹⁸ which combines molecular dynamics and quantum mechanics, BRIKARD,¹⁹ an inverse kinematics method, and EGSCyP,²⁰ a robotics based method, were used to determine cyclic peptide conformations.

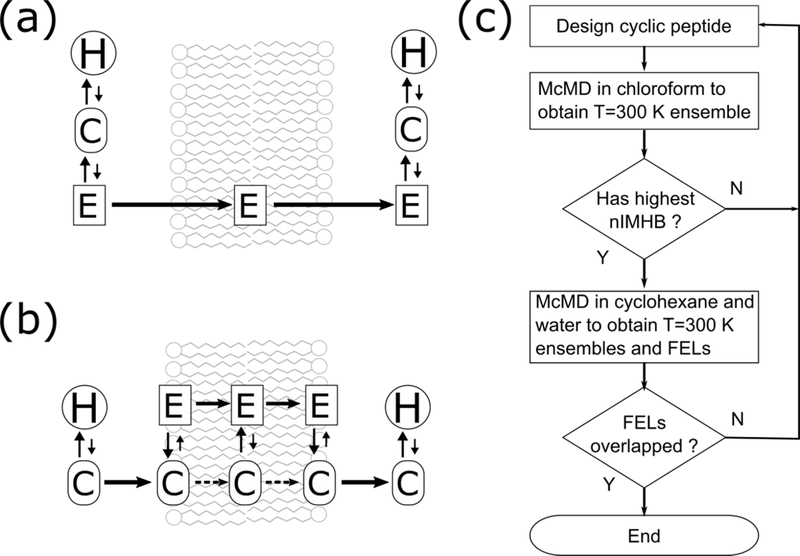
Multicanonical molecular dynamics (McMD)²¹ simulation is a powerful enhanced sampling method in which the potential energy is equally sampled between low and high temperature regions. By reweighting the entire set of sampled structures, the canonical ensemble can be obtained at any temperature provided that it is between the low and high temperature states (Figure 1). McMD simulations and their derivatives have been successfully applied to small peptides,^22–24 intrinsically disordered protein (IDP),^25,26 antibody CDR-H3 loop,²⁷ and protein-ligand docking simulations²⁸ in explicit water.

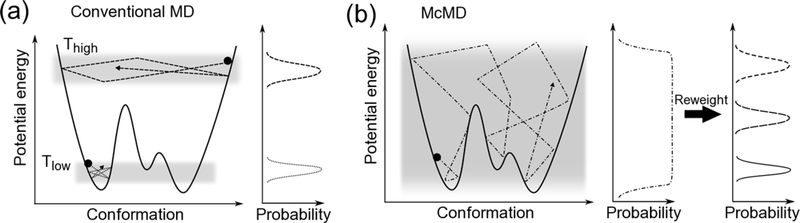
Figure 1.

Schematic view of conformational space and potential energy. Filled circles indicate initial structures. (a) Conventional MD performed at low temperature would be trapped at a local minimum and could not overcome the large potential energy barrier. High temperature MD samples a wider conformational space and overcomes large barriers; however, the structures are unrealistic. (b) McMD can equally sample a full potential energy space, easily overcome large barriers, and sample any local minima. Therefore, the staring conformation does not affect the results. After a production McMD run, canonical ensembles between low and high temperature states are easily obtained by reweighting.

It is noteworthy that solvent selection is important for conformational effects in both computation and experiments. Conventionally, conformational sampling in chloroform has been used to mimic the membrane environment in a low dielectric solvent for both implicit (ε = 4)⁷ and explicit models.^8,29 Recently, experimental hydrocarbon–water distribution coefficients, logD_hc/w, showed excellent correlation with cell permeability,³⁰ suggesting that hydrocarbons, such as cyclohexane, can be alternative solvents for mimicking membrane environments. The steep demands of conformational chameleonicity^31–33 for favorable pharmacokinetic properties in bRo5 chemical space will also require calculation of the conformations in water to determine conformationally defined aqueous solubility.

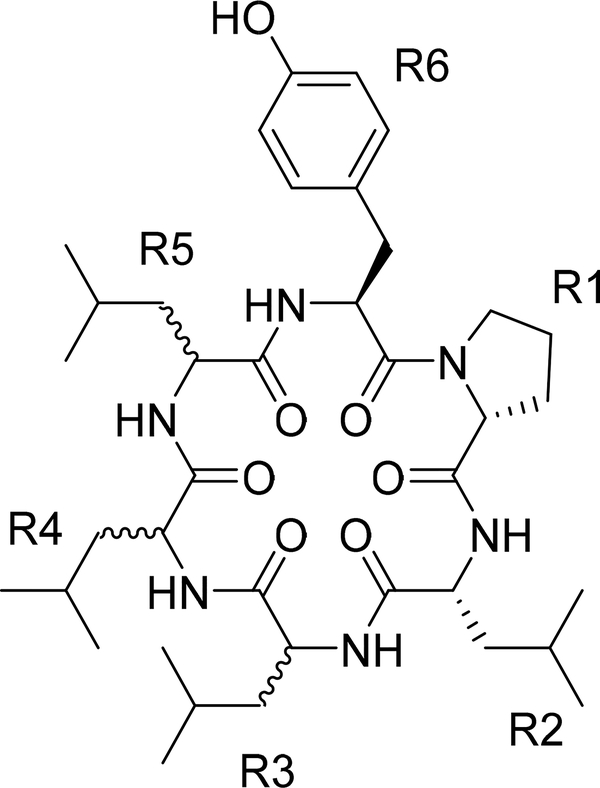
To test the hydrophobic environment, conformations of eight cyclic hexapeptide diastereomers (Figure 2 and Table 1)³⁴ were investigated in explicit cyclohexane, chloroform and water. Although the molecular properties of these cyclic peptides, such as molecular weight (MW) = 712.93, topological polar surface area (TPSA)³⁵ = 186.04, and predicted hydrophobic partition coefficient AlogP³⁶ = 3.82, were identical, the cell permeability in a low-efflux MDCK cell line³⁷ varied by over two orders of magnitude. Remarkably, these cyclic peptides have no N-methylated amino acid groups, which is considered a key feature in enhanced cell membrane permeability, as these either mask the polar amide group or stabilize the cis isomer.^38–40 We have applied McMD simulations to cyclic peptides as an effective conformational sampling method and thermodynamically stable conformations were obtained through analysis of the free energy landscape (FEL). We expected that the thermodynamically stable conformer of these cyclic hexapeptide diastereomers would have different 3D structures in the solvents to explain the differences in cell permeability. We mainly focused on the thermodynamic behavior of these compounds in bulk solvents from simulations and did not treat the atoms in the membrane explicitly (e.g., conformational changes upon binding to polar head groups of the membrane were not considered).

Figure 2.

Cyclic hexapeptide diastereomers.

Table 1.

Sequence, permeability and aqueous solubility data for each compound.

ID	R1	R2	R3	R4	R5	R6	MDCK		PAMPA	Sol.a,c
							Pappa,b	Class	Pappb
1	D-Pro	D-Leu	D-Leu	D-Leu	L-Leu	L-Tyr	0.4	low	2.27	47
2	D-Pro	D-Leu	D-Leu	D-Leu	D-Leu	L-Tyr	0.5	low	2.87	52
3	D-Pro	D-Leu	L-Leu	D-Leu	L-Leu	L-Tyr	0.8	low	1.71	--d
4	D-Pro	D-Leu	L-Leu	D-Leu	D-Leu	L-Tyr	1.9	medium	4.92	11
5	D-Pro	D-Leu	D-Leu	L-Leu	L-Leu	L-Tyr	1	medium	1.66	33
6	D-Pro	D-Leu	L-Leu	L-Leu	L-Leu	L-Tyr	2.8	medium	2.59	54
7	D-Pro	D-Leu	D-Leu	L-Leu	D-Leu	L-Tyr	4	high	7.18	27
8	D-Pro	D-Leu	L-Leu	L-Leu	D-Leu	L-Tyr	19.3	high	7.74	9.1

^aFrom Ref. 30.

^bIn units of 10⁻⁶ (cm/s).

^cAqueous Solubility pH 7.4 (μM).

^dnot determined.

Selecting the force field for cyclic peptides is another issue,^41,42 because current force fields were mainly tailored to linear peptides and proteins in water. A previous study showed that force field reparameterization may be required for cyclic peptides.⁴¹ Because our preliminary study revealed that the AMBER force field ff03⁴³ effectively reproduces the NMR or X-ray structure of known cyclic peptides, we adopted ff03 in the present research.

2. METHODS

2.1. Simulation details.

The initial conformer was built using the MOE⁴⁴ protein builder, and LowModeMD⁴⁵ implemented in MOE was used to search for the most stable conformer in vacuo. PACKMOL⁴⁶ was used to solvate the system, where the numbers of water, chloroform, and cyclohexane molecules were 2000, 400, and 300, respectively. The TIP3P water model⁴⁷ and chloroform from AmberTools17⁴⁸ were used. For cyclohexane, the atom types cD and hL from the Lipid14 force field⁴⁹ and RESP ESP charges from R.E.D. version III.52⁵⁰ were used. The AMBER ff03 force field⁴³ was used for amino acids. The topology file was created using the LEaP program and converted to GROMACS format using the ParmEd program in AmberTools17. The initially solvated system was minimized by steepest descent, following 50,000 steps of NVT calculation. The system was then equilibrated by NPT calculation at atmospheric pressure by applying the Berendsen barostat⁵¹ for 500,000 steps. A positional restraint was used for C_α atoms during equilibration. The resultant system was used as an initial structure for the following simulations.

Virtual-system-coupled Trivial Trajectory Parallelization of Multicanonical Molecular Dynamics (TTP-V-McMD)^52,53 simulations were adopted to effectively sample conformations of cyclic peptides. TTP-V-McMD is a derivative and combination of Trivial Trajectory Parallelization McMD (TTP-McMD)⁵² and Virtual-system-coupled McMD (V-McMD),⁵³ where TTP-McMD consists of several multiple independent McMD runs with same McMD parameters from different initial conformations. V-McMD consists of several virtual states with independent McMD parameters that cover different potential energies, where neighboring virtual states overlap. In this report, the term “McMD simulations” denotes “TTP-V-McMD simulations,” because TTP-V-McMD is a derivative of McMD. A total of 336 pre-TTP-V-McMD runs were initiated with random velocities for each atom at T = 300 K, then heated to T = 1525 K with 5,000 steps, followed by 495,000 steps at T = 1525 K to randomize the initial structures. To determine the potential energy zones for McMD, following pre-TTP-V-McMD runs were conducted at 14 temperatures; 1525 K, 1203 K, 1002 K, 802 K, 707 K, 633 K, 573 K, 501 K, 445 K, 400 K, 354 K, 325 K, 300 K, and 280 K. Then the virtual state zones and real potential energy zones were set as listed in Table S1 to S3. The transition probability to neighboring virtual states was set to 1.0. Because McMD parameters are not known a priori, we need some iterations to determine those parameters. For each virtual state, the McMD parameter was fitted to an eighth order polynomial curve according to the equation 24 in Ref. 53. Flat potential energy distributions between T = 1525 K and 280 K were obtained by iterating TTP-V-McMD simulations for five times in chloroform and water, or six times in cyclohexane with eight virtual states (See detail in Figure 3). The cut-off for coulombic and van der Waals interactions was 1.0 nm, and PME was used to calculate the long-range electrostatics. The NVT ensemble was used for all TTP-V-McMD simulations using the velocity rescaling method (Bussi thermostat).⁵⁴ The LINCS algorithm⁵⁵ was used to constrain the bonds with a hydrogen atom, allowing time steps of 2.0 fs. For each compound and solvent, 1.0 × 10⁷ steps × 336 runs (Total 6.72 μs) were performed as a final production run. The structure and potential energy were stored every 2 ps. The virtual state was exchanged in every 5,000 steps. Solvent atoms were removed before analysis. For cluster and property analysis, a resampling method was used to extract the canonical ensemble at T = 300 K, where structures were drawn from the simulated ensemble with relative probabilities according to their Boltzmann weights. Typically, approximately 18,000 conformers were obtained, and then 5,000 conformers were randomly selected to use for further cluster and property analysis. All 3.36 million conformers were taken into account to determine the FEL by a potential of mean force (PMF) calculation; W = −k_BT ln ρ, where k_B is the Boltzmann constant and ρ is the density of state.⁵⁶ An in-house implemented TTP-V-McMD using GROMACS⁵⁷ version 5.1.4 was used for the simulations. The density of the bulk solvents was confirmed by NPT ensemble at T = 300 K. The calculated densities for water, chloroform and cyclohexane were 0.984, 1.470, and 0.771 g/cm³, respectively, which are close to the experimental values.

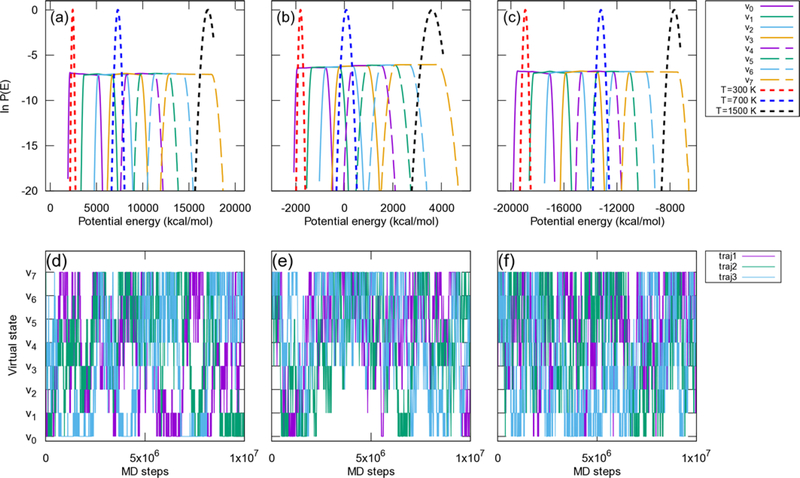
Figure 3.

Flat potential energy distribution of compound 8 for virtual states (v₀ to v₇) and reweighted canonical ensembles at T = 300, 700, and 1500 K. (a) in cyclohexane, (b) in chloroform and (c) in water. The exchange among virtual states for trajectories 1 to 3 out of 336 trajectories are shown for (d) in cyclohexane, (e) in chloroform and (f) in water. The following virtual state ranges were used: v₀ = [0.0, 0.2], v₁ = [0.1, 0.3], v₂ = [0.2, 0.4], v₃ = [0.3, 0.5], v₄ = [0.4, 0.6], v₅ = [0.5, 0.7], v₆ = [0.6, 0.8], and v₇ = [0.7, 1.0].

2.2. Clustering analysis.

TTClust⁵⁸ was used to cluster each ensemble. Backbone root mean square deviation (RMSD) was used to obtain a distance matrix. The Ward method⁵⁹ was used for hierarchical clustering. A total of 5,000 structures obtained for a T = 300 K ensemble of each compound and solvent, were divided into 1,000 structures × 5 groups to calculate the standard deviations of each cluster. Some trials were performed to determine the optimal number of clusters (i.e., N = 3 or 5). After inspecting the cluster analysis dendrograms and FELs, we set the cluster number to five for all clustering analyses to automate the TTClust script. The clusters which had same conformation were then combined to one, if exist. The pattern of backbone-backbone H-bonds was calculated by VMD⁶⁰ with a donor-acceptor atomic distance below 0.35 nm and an angle cut-off (D-H … A) below 30 degrees.

2.3. Property calculation.

Principal moments of inertia (PMI) around inertial axes, I₁, I₂ and I₃ were obtained in GROMACS using the command gmx principal. The molecular shape⁶¹ was represented by the normalized PMI ratios (I₁/I₃ and I₂/I₃) for each frame. The surface area was obtained in GROMACS using gmx sasa. The solvent accessible surface area (SASA) was defined by all the atoms of the cyclic peptide. The polar surface area (PSA) was defined by nitrogen, oxygen, and hydrogen atoms attached to either a nitrogen or an oxygen atom of amino acids. The radius of the solvent probe was set to 0.14 nm. The average SASA and PSA were calculated for each compound and solvent for 5,000 structures by simply arithmetically averaging, because these structures were already Boltzmann weighted.

A new flexibility index denoted Flex_FEL is introduced by,

$${Flex}_{FEL}=\sum _{x,y}\Delta d(x,y)\cdot A\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{W\left(x,y\right)}{k_{B}T}\right\}$$ (1)

where Δd(x, y) is the distance between the global minimum of the FEL and the coordinate (x, y), A is the unit area of the FEL, and W(x, y) is the PMF value at position (x, y). Flex_FEL is considered as the area weighted by the extent of the PMF in the FEL. Based on this definition, a rigid conformation shows a small Flex_FEL value, whereas this is larger for a flexible conformation.

The overlap between the FELs is defined by,

$${Overlap}_{s1\to s2}(z)=\sum _{x,y}A\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{W_{s2}(x,y)\cap \left(W_{s1}\right(x,y)\le z)}{k_{B}T}\right\}$$ (2)

where s1, s2, and z are solvent 1, solvent 2, and the PMF threshold, respectively. The overlap value represents the weighted area of the FEL in solvent 2, where the PMF in solvent 1 is less than threshold z.

2.4. Experimental section.

The PAMPA permeability was obtained as described in Ref. 30. Briefly, a membrane was prepared on a 96-well filter support (donor) with a 1% (w/v) solution of lecithin (soybean) in n-dodecane. Analytes were dissolved to 1 μM in pH = 7.4 phosphate-buffered saline containing 5% dimethyl sulfoxide applied to the donor well and placed on a Teflon acceptor plate prepared with the same solution without analyte. After incubation for ~16 h, the donor and acceptor plates were separated and quantified via LCMS, via extracted ions.

3. RESULTS and DISCUSSION

3.1. Sampling efficiency.

McMD simulations are usually performed with a flat potential energy region that corresponds to a temperature between 280 and 700 K for linear peptides and small proteins.^22–28 In the present study, we set the temperature between 280 and 1525 K to improve the sampling efficiency for conformationally restricted cyclic peptides in which a higher rotation free energy may be required. It was also expected that setting the highest potential energy region corresponding to T = 1525 K would be required to ensure cis/trans isomerization of proline.⁶² The resulting flat potential energy distributions and exchanges between virtual states revealed that McMD simulations sampled potential energy space adequately (Figure 3). The FELs of the backbone (ϕ,ψ) maps for each amino acid (Supporting Information Figures S1 to S3) also revealed that the simulations sampled conformational space adequately even though the relaxation time in cyclohexane is longer than in water and chloroform.

A previous study showed that trans to cis amide isomerization was observed in high temperature MD.⁶³ Since we set the flat potential energy region corresponding to the temperature between 1525 and 280 K, cis/trans isomerization was frequently observed, especially between L-Tyr6 and D-Pro1. However, reweighted ensembles at T = 300 K had minimal cis isomers for non-proline residues (e.g., PMF of the cis isomer was 3.6 kcal/mol or more where the trans isomer was 0.0 kcal/mol for compound 7 in chloroform), whereas for proline, the cis isomer was much favored (e.g., PMF of cis isomer was 2.0 kcal/mol for compound 7 in cyclohexane). We also confirmed the absence of continuous chiral inversion for each amino acid.

3.2. Intramolecular hydrogen bond (IMHB) patterns and 3D structures.

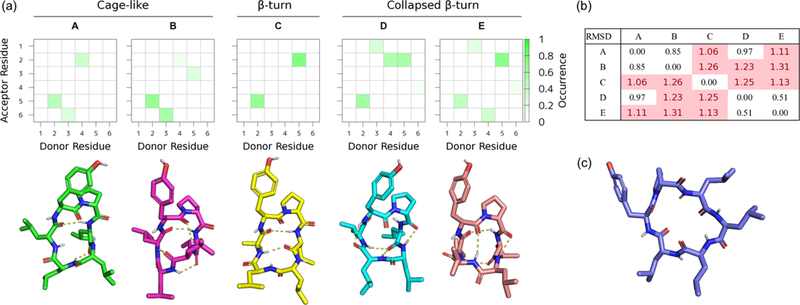
From analyzing ensembles at T = 300 K, we found five major backbone transannular H-bonding patterns, mainly in cyclohexane and chloroform (Table 2, Figure 4 and Supporting Information Figures S4 to S11). These five representative structures were extracted from the cluster analysis, namely a cage-like pattern (nIMHB (the number of IMHB) = 3 and 4 corresponding to A and B, respectively. See Table 2 and Figure 4), β-turn pattern (nIMHB = 2, corresponding to C), and collapsed β-turn pattern (nIMHB = 5, corresponding to D and E). The rest of the population remaining unclassified was mainly attributed to nIMHB = 0 or 1. Cage-like patterns exhibited one or two exposed NH amides and β-turn patterns had three exposed NH amides, whereas the collapsed β-turn had no exposed NH amides. An L-Tyr6-D-Pro1 β-turn corresponding to the matrix [2, 5] (Donor-Acceptor residue occurrence map in Figure 4) commonly appeared for five representative structures. H-bonding [4, 6] never appeared for D-Leu4 stereoisomers due to steric occlusion of Leu (over its NH) for all the obtained structures. These compounds (1 to 4) could only form collapsed β-turn pattern D in cyclohexane and chloroform. However, L-Leu4 stereoisomers (5 to 8) could form collapsed β-turn pattern E. Matrix [5, 3] also never appeared for D-Leu4 and D-Leu5 (compounds 2 and 4), suggesting that these compounds could only form cage-like pattern A. L-Leu5 stereoisomers (compounds 1, 3, 5, and 6) could form cage-like pattern B in cyclohexane and chloroform. The side chain hydroxyl group of Tyr6 rarely formed a hydrogen bond to the backbone, its occurrence being less than 0.22%.

Table 2.

Population of the patterns for each compound and solvent.

ID	Solvent	Population of the pattern (%)
		Cage-like		β-turn	Collapsed β-turn		Minor clustersb
		A	B	C	D	E
1	Cyclohexane	--a	57.4 ± 4.1	0.8 ± 1.1	28.2 ± 3.2	--a	13.6
	chloroform	--a	55.4 ± 2.0	18.9 ± 2.7	14.2 ± 1.4	--a	11.5
	water	--a	--a	49.4 ± 3.7	--a	--a	50.6
2	Cyclohexane	22.5 ± 8.3	--a	--a	65.4 ± 9.8	--a	12.1
	chloroform	56.3 ± 5.4	--a	0.6 ± 0.7	26.7 ± 3.3	--a	16.4
	water	--a	--a	45.5 ± 7.1	--a	--a	54.5
3	Cyclohexane	--a	76.5 ± 4.1	--a	5.9 ± 2.9	--a	17.5
	chloroform	--a	72.8 ± 6.9	--a	5.3 ± 3.2	--a	21.9
	water	--a	--a	10.8 ± 1.4	--a	--a	89.2
4	Cyclohexane	49.6 ± 2.6	--a	--a	21.6 ± 5.2	--a	28.7
	chloroform	79.3 ± 4.2	--a	--a	10.5 ± 3.6	--a	10.2
	water	23.2 ± 3.7	--a	45.0 ± 3.9	--a	--a	31.8
5	Cyclohexane	--a	48.1 ± 4.9	2.7 ± 3.3	--a	18.2 ± 6.2	31.0
	chloroform	--a	24.1 ± 3.5	38.7 ± 5.6	--a	--a	37.2
	water	--a	--a	44.5 ± 3.7	--a	--a	55.5
6	Cyclohexane	--a	13.1 ± 2.1	--a	--a	86.3 ± 1.8	0.5
	chloroform	--a	16.8 ± 3.8	--a	--a	79.0 ± 3.0	4.2
	water	--a	--a	--a	--a	--a	100.0
7	Cyclohexane	--a	--a	6.5 ± 2.1	--a	80.4 ± 3.8	13.1
	chloroform	--a	--a	57.2 ± 4.0	--a	24.8 ± 6.4	18.0
	water	--a	--a	37.8 ± 1.7	--a	--a	62.2
8	Cyclohexane	--a	--a	--a	--a	99.0 ± 0.5	1.0
	chloroform	--a	--a	--a	--a	90.8 ± 2.9	9.2
	water	--a	--a	25.9 ± 4.5	--a	5.6 ± 1.1	68.5

^anot classified by the pattern.

^bIncludes major clusters found in water.

Figure 4.

(a) Backbone hydrogen bond patterns and representative structures. Cage-like pattern (type A and B), β-turn pattern (type C), and collapsed β-turn pattern (types D and E). Structures 2_C1, 3_C1, 7_C1, 2_X1, and 8_C1 correspond to types A, B, C, D, and E, respectively. The subscript indicates the solvent and cluster names, where C1 is the first cluster in chloroform and X1 is the first cluster in cyclohexane. The color fade is defined by the occurrence of H-bonds obtained by the VMD H-bond plug-in for each cluster. (b) Backbone RMSD matrix between the representative structures. Highlights by red shades are larger than 1.00 Å. (c) Example of nIMHB = 0 and disk-like conformation 8 found in water.

However, the IMHB patterns in water were sparse, and hydrogen bond occupancy was lower than in cyclohexane and chloroform (Table 2 and Figures S4 to S11). This was because amide NH could form a hydrogen bond with water molecules, decreasing the occurrence of transannular H-bonding. Only compound 6 yielded no patterns in water, unlike its single stereoisomers 3, 5, and 8. Other β-turn-like patterns that were not attributed to A to E were observed in minor clusters, where hydrogen bonds were formed between Tyr6 and Leu3 (Pattern F, corresponding to hydrogen bond matrices [3,6] and [6,3]. See cluster 5 in water of 6 in Figures S9 and S14) and between Leu4 and D-Pro1 (Pattern G, matrix [4,1], cluster 1 in water of 5 in Figures S8 and S14). However, these β-turns were rarely observed in cyclohexane and chloroform, because their Pro-Tyr backbone β-turn and side-chain–side-chain interactions are effectively stabilized in these solvents.

In a previous NMR study on the exposure of amide NH obtained from Δδ/ΔT⁶⁴ in CDCl₃ (Table S10 of Supporting Information in Ref. 34), one of the amide hydrogens of compound 3 is clearly exposed to the solvent, which supports the cage-like pattern (B), whereas no amide hydrogen is exposed for compounds 7 and 8, supporting the collapsed β-turn pattern (E). Therefore, it was considered that McMD simulations with the AMBER ff03 force field appropriately sampled the diastereomeric structures.

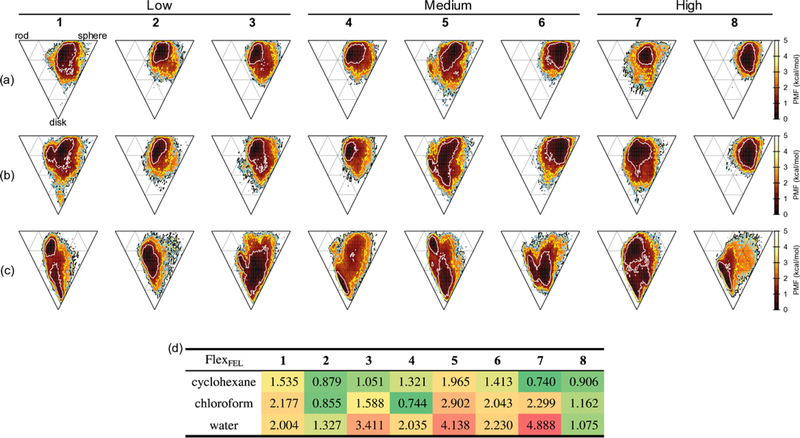
3.3. Free energy landscapes of molecular shape and principal component analysis.

The molecular shape⁶¹ was defined by the normalized principal moment of inertia and represented by 2D triangular graphs where the left top corner was rod-like, the right top corner sphere-like, and the bottom disk-like. Although these graphs were used to compare the shapes of fragments or combinatorial libraries of molecules, we applied this method to MD trajectories to represent the FEL of molecular shape (Figure 5a–c). It is noteworthy that the FEL exhibits a molecular shape distribution for cyclic peptides, rather than a single point. The FELs clearly showed that all the compounds adopt relatively rigid sphere-like conformations in cyclohexane but more flexible shapes in water. For example, compound 7 is sphere-like in cyclohexane; however, various shapes are formed in water. The FELs in chloroform were mostly the same as those in cyclohexane, except for compounds 5 and 7. We will discuss the effect of solvents in detail later. Characteristic shapes of FELs in water were disk-like to disk-rod-like, whereas these shapes never appeared in cyclohexane. Disk-like compounds 4 and 8 were flat overall. These shapes were similar to that of a cyclic peptide nanotube,^65–67 with four out of the five NH amides being almost perpendicular to the backbone circle, whereas side-chains were in-plane. (See Figure 4c).

Figure 5.

FEL of molecular shape at T = 300 K for each compound and solvent. Each vertex, top left, top right and bottom represents a rod, sphere and disk, respectively. Annotated above for the permeability class defined in Table 1. (a) is in cyclohexane, (b) in chloroform, and (c) in water. The contour lines for PMF = 1.0, 2.0, 3.0, and 4.0 kcal/mol are plotted as white, yellow, sky-blue, and black lines, respectively. (d) Flex_FEL values for each compound and solvent defined by the molecular shape plane.

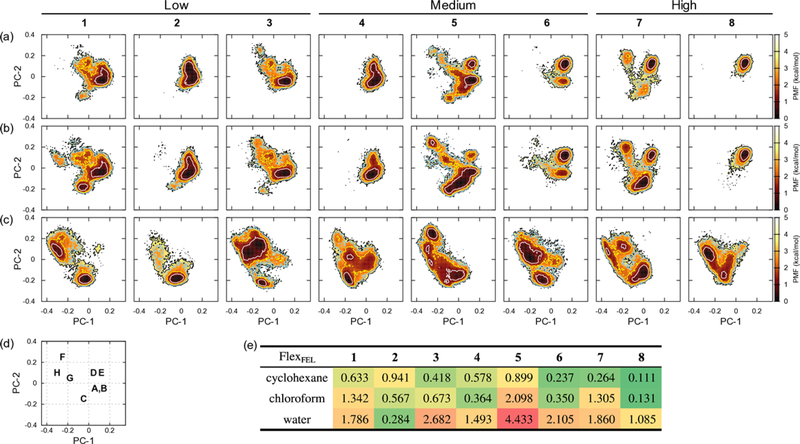
The FEL along with the principal component axes was drawn for each compound and solvent (Figures 6 and S12). The distance matrix was calculated from the distances between C_α atoms of each residue. Portions of variances are 36.7%, 28.9%, and 23.1% for the first, second, and third axes, respectively. From inspecting the coordinates and represented conformations by cluster analysis, the FELs showed the relations to the backbone H-bonding patterns describe below. A stable conformation around (PC-1, PC-2) = (0.1, ‒0.05) is a cage-like pattern (A and B in Figure 4), (PC-1, PC-2) = (‒0.05, ‒0.15) a β-turn pattern (C), (PC-1, PC-2) = (0.05, 0.1) a collapsed β-turn pattern (D), and (PC-1, PC-2) = (0.12, 0.1) another collapsed β-turn pattern (E). Relatively small free energy differences (<1 kcal/mol) were observed between cage-like and β-turn patterns (e.g., compound 5); however, large free energy differences (ca. 3 kcal/mol) were observed between β-turn and collapsed β-turn patterns (e.g., compound 7). Both conformational changes occurred by peptide-plane flips⁶⁸ of D-Leu2 and D-Leu3 for compounds 5 and 7. Other β-turn patterns that are not classified above were F (PC-1, PC-2) = (−0.25, 0.25) and G (−0.18, 0.05). A disk-like conformation was located around (PC-1, PC-2) = (−0.3, 0.1) (H in Figure 6d).

Figure 6.

FEL by PCA axis PC-1 vs. PC-2 at T = 300 K for each compound and solvent. Annotated above for the permeability class defined in Table 1. (a) is in cyclohexane, (b) in chloroform, and (c) in water. The contour lines for PMF = 1.0, 2.0, 3.0, and 4.0 kcal/mol are plotted as white, yellow, sky-blue, and black lines, respectively. (d) A representative box showing the locations of each pattern. See main text for details. (e) Flex_FEL values for each compound and solvent defined by PC-1 and PC-2 planes.

Various conformations in water were found in the FELs of both molecular shape and principal component analysis compared to those in cyclohexane and chloroform. The most structured conformation found in water was a β-turn pattern for compounds 1, 2, 5, and 7 (Table 2 and Figures S4 to S11), whose position 3 has D-Leu in common. For compound 2, the locked β-turn pattern for the FEL of molecular shape was relatively tight with only side-chains freely rotating, compared to the other compounds. (The flexibility of the compounds will be discussed later.)

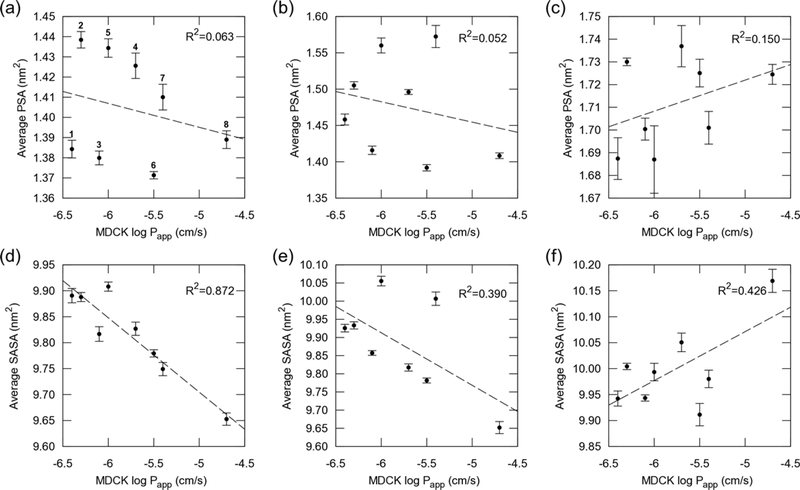
3.4. Relation between the 3D properties and cell permeability.

Cell permeability is plotted vs. the average SASA and PSA in Figure 7. The average SASA in cyclohexane showed excellent correlation with cell permeability (R² = 0.872), whereas the correlation was weaker in chloroform (R² = 0.39) and water (R² = 0.426). These results indicate that compounds with smaller SASAs in cyclohexane are more permeable, and that cyclohexane provides a better overall in silico mimic for electronic factors affecting permeability within the cell membrane. In chloroform, the average SASAs of compounds 5 and 7 were higher than the others and these were not on the line showing good correlation. This is because larger conformational changes between β-turn and cage-like patterns occurred for compound 5 and between β-turn and collapsed β-turn patterns for compound 7 (See Figure 4b for backbone RMSD differences between representative structures). It is also interesting that the compounds exhibiting high permeability, especially compounds 7 and 8, exhibited large differences in SASA in cyclohexane and water. Such large differences were also observed as a result of the changes in the FEL of molecular shape in cyclohexane and water (See Figure 5). From the FELs and Table 2, a cage-like pattern observed for compounds 1 to 5 in cyclohexane tended to be less permeable, while the collapsed β-turn pattern found for compounds 6 to 8 in cyclohexane was more permeable.

Figure 7.

Cell permeability vs. average PSA and SASA. (a) and (d) are in cyclohexane, (b) and (e) in chloroform, and (c) and (f) in water. Dashed lines are fitted for each point.

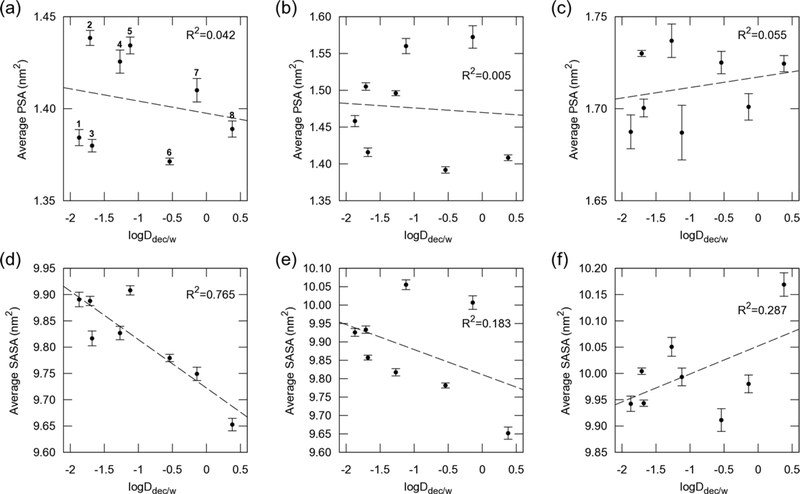
An excellent correlation between MDCK logP_app and logD_hc/w (i.e., logD_dec/w; partition coefficient with 1,9-decadiene and logD_cyc/w; partition coefficent with cyclohexane) was reported,³⁰ and we confirmed the relation between these partition coefficents and surface areas (Figures 8 and S13). As expected, the average SASA in cyclohexane correlated well with logD_dec/w (R² = 0.765) and logD_cyc/w (R² = 0.605), whereas lower correlations were found in chloroform and water.

Figure 8.

LogD_dec/w vs. average SASA and PSA. (a) and (d) are in cyclohexane, (b) and (e) in chloroform, and (c) and (f) in water. Dashed lines are fitted for each point.

The average PSA did not correlate with cell permeability and logD_dec/w in these hexapeptide diastereomers (Figure 7a–c, 8a–c, and S13a–c). The PSA is known to correlate with permeability for bRo5 compounds;^33,69,70 however, the compounds we investigated exhibited similar PSA values for each solvent. In cyclohexane, polar groups were protected by forming transannular IMHB, resulting in an average PSA of around 1.40 nm², whereas in water, polar groups were exposed to water molecules, resulting in an average PSA of around 1.72 nm². In chloroform, all compounds had larger average PSAs than in cyclohexane, especially compounds 5 and 7 again, because these compounds tended to form the β-turn pattern, with more exposed polar amide NHs, compared to in cyclohexane.

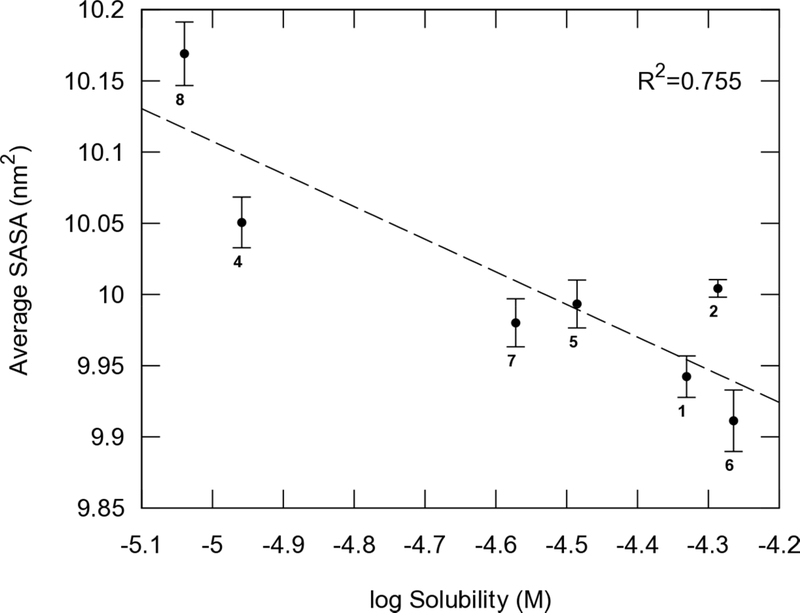
3.5. Relation between the SASA and aqueous solubility.

Although the aqueous solubility range was narrow, the average SASA in water correlates well with the aqueous solubility (R² = 0.755) (Figure 9). Compound 2 had good solubility, however, as described above, the conformation was locked to the β-turn pattern whereas three amide hydrogens are exposed to the water resulting in the average PSA being relatively high. Less soluble compounds 4 and 8 were locked around a disk-like shape in the FELs of molecular shape (Figure 5c). These compounds also had lower polarity (i.e., non-polar surface area; differences between SASA and PSA in Figure 7c and 7f), in comparison with the other compounds that can more easily access multiple other conformations with higher exposed polarity. However, this effect is less dramatic than the permeability effect.

Figure 9.

Aqueous solubility vs. average SASA in water. Dashed lines are fitted for each point.

3.6. Relation between conformation and PAMPA.

The range of PAMPA permeabilities for this series was relatively narrow compared to their cell permeabilities; the correlation between cell permeability and PAMPA was moderate (R² = 0.671). The most cell permeable compounds 7 and 8 also exhibited the highest PAMPA permeabilities. It is interesting that compounds 4 and 8, structurally identical except at position 4, had nearly the same range of PAMPA values and solubility; however, the cell permeability differed by one order of magnitude. Position 4 affects the hydrogen bonding between the amide NH of D-Leu5 and oxygen of Leu3, corresponding to the matrix [5,3] in Figure 4; that is, compound 4 formed no hydrogen bond. A possible interpretation for this observation is that compound 4 forms a mixture of the cage-like pattern (type A in Figure 4) and collapsed β-turn pattern (type D in Figure 4) in cyclohexane and chloroform (Table 2 and Figure S7). Although the thermodynamic balance of both conformers varies depending on the solvents from the FEL, the cage-like pattern is slightly preferred. This cage-like pattern has two non-hydrogen bonded amide NH groups, one of these (Tyr6) being completely exposed to solvent while the other is protected by side-chains. Conversely, compound 8 only forms a collapsed β-turn (E) in cyclohexane and chloroform, in which no amide NH groups are exposed to the solvents. The exposure of one additional hydrogen bond donor (HBD) was reported to yield a penalty from −1.6 to −1.9 units in logD_dec/w in test compounds,³⁰ and the difference between 4 and 8 was −1.65, reinforcing the observed change in the HBD count.

3.7. Flexibility and overlap of the conformation calculated from the FEL.

The Flex_FEL values are listed in Figure 5d from the molecular shape and Figure 6e from the PC-1 and PC-2 planes. The overall tendency of the values for the solvents was almost the same for Figures 5d and 6e, except for compounds 2, 6, and 8. These compounds had the same range of values among the solvents based on the molecular shape; however, compound 2 had a smaller value (i.e., rigid) and compounds 6 and 8 had a larger value (more flexible) in water based on the PC plane. It is obvious that the Flex_FEL values alone could not distinguish the detailed difference between the molecular shapes; thus, we now focus on the values obtained from the PC plane. From Figure 6e, it was observed that flexibility increased in the order of cyclohexane, chloroform, and water. Compounds 3, 4, 6, and 8 (whose position 3 has L-Leu in common) had small Flex_FEL values in cyclohexane and chloroform; however, these increased in water. Compounds 1, 5, and 7 had small values in cyclohexane but larger values in chloroform and water. The order was only reversed for compound 2. The Flex_FEL values could be rationalized by the outliers of the SASA and cell permeability plotted in Figure 7d, where compound 3 had a small value (rigid) and 5 had a large value (flexible) in cyclohexane. Figure 7e also showed that the outliers for 5 and 7 had larger Flex_FEL values, resulting in worse correlation in chloroform. The outliers for the SASA and solubility (compound 2 in Figure 9) could be attributed to the especially small Flex_FEL value in water, in which the conformation is locked to the type C pattern resulting in a large average SASA.

The overlaps_s1→s2(z) along the threshold (z) of the PMF from the PC plane were plotted in Figure S15. It is convenient to divide the threshold region by 1.0 kcal/mol. From Figure S15c and S15f, most compounds reached a plateau at z ≈ 2 kcal/mol, indicating almost identical conformations in cyclohexane and chloroform within this threshold. It is worth noting the sigmoidal profiles for compounds 5 and 7 (Figure S15f), resulting from the different stable conformations in these solvents. It is also found that the most permeable compound 8 has the sigmoidal profiles for water to cyclohexane or chloroform (Figure S15d and e). This profile may provide the insight into the possible design of the permeable compound from the overlap between the FELs.

3.8. Membrane permeation models.

Passive membrane permeation for cyclic peptides has been ascribed in part to their chameleonic properties, i.e., their ability to adopt different conformations in different environments.^31–33 A conventional model suggests that permeation occurs for the most stable conformation in the membrane when it occasionally forms in water.⁷ A congruent conformation model indicates that permeation is assisted by congruent conformations, which significantly populate in both water and the membrane.⁸ Another model proposed by Craik and co-workers suggests that the ratios of conformational polymorphism between structures were different in each state, such as aqueous, membrane head group, and membrane tail.²⁹

Considering these conformational observations in the light of the passive membrane permeation models, we speculated that the conformations of the compounds in water changed compared to those in cyclohexane via two different routes depending on the structures of compounds based on the thermodynamic properties. A conventional conformational model was supported for compound 8, where the collapsed β-turn pattern region (E in Figure 6d) overlapped well among the solvents. A possible interpretation of such a model is that the collapsed β-turn pattern could form in water and permeate the membrane while in this conformation (Figure 10a). Conversely, a more complicated permeation model was supported for compound 7, where the collapsed β-turn pattern region (E in Figure 6d) overlaps between in cyclohexane and chloroform, but not in water. A possible interpretation of the mechanism is that the β-turn pattern (C in Figure 6d) is initially formed in water, and then, possibly near the water-membrane boundary, equilibration between the β-turn and collapsed β-turn patterns occurs, and membrane permeation is achieved via the collapsed β-turn pattern, which is thermodynamically more stable in cyclohexane (Figure 10b). It was also noted that the collapsed β-turn pattern did not form in water for compound 7 (See Table 2 and Figure 6 for details). Therefore, a single stereocenter change between compounds 7 and 8 (i.e., position 3) reveals different possible conformational structural profiles related to permeability. (Further work is required to explore conformational dynamics not sampled by thermodynamic minima, e.g., Ref. 9.)

Figure 10.

Possible membrane permeation mechanisms. (a) Mechanism for compound 8. Character C, E, and H denote conformation patterns in Figure 6d. (b) Mechanism for compound 7. Note that pattern E could not form in water. (c) Flow chart of proposed strategy for designing permeable cyclic peptides.

3.9. Possible strategy for designing permeable cyclic peptides.

From the above results, a possible strategy for designing permeable cyclic peptides using McMD simulations is described in the flow chart in Figure 10c. Firstly, because the simulation timing is shorter in explicit chloroform than in cyclohexane and water, we propose running an initial simulation in explicit chloroform for designed cyclic peptides. Secondly, compounds that have the highest number of IMHBs are selected, rejecting any compounds that have exposed HBDs. Thirdly, simulation is performed in explicit cyclohexane and water for the cyclic peptides, and the FELs are compared at T = 300 K for each solvent. Fourthly, overlaps among the FELs are compared. Finally, the most overlapped compound among the solvents is selected. If no overlap occurs between solvents, the sequence is redesigned and repeated from the first step.

4. CONCLUSION

We performed the conformational analysis of eight cyclic hexapeptide diastereomers in explicit cyclohexane, chloroform, and water by McMD simulation. FELs of molecular shape and principal component axes were obtained at T = 300 K. Ensembles of each compound and solvent at T = 300 K were also obtained, and 3D properties, such as SASA and PSA, were calculated. A new flexibility index Flex_FEL was introduced. A possible strategy for designing permeable cyclic peptides is described.

A single stereoisomeric change affects the conformational patterns, resulting in permeability and solubility differences. The average SASA in cyclohexane correlated well with cell permeability, and the average SASA in water correlated with the aqueous solubility. It is surprising that only a simple arithmetic average of SASA from the ensemble at T = 300 K represents such physical properties so well. It is emphasized that no further clustering or selection of individual conformers was required for each compound, even with multiple conformations present in the ensemble. It was also found that cyclohexane is better than chloroform for hydrophobic environments based on the permeability.

Flexibility is summarized as follows from the permeation models and correlations between SASAs and experimental values: increased flexibility is good to allow conformational overlap to achieve one of the permeation models, however, it is a property over-sampled by chloroform yielding some of the lesser correlations there.

Since the MW is the same for all the compounds we examined, we did not treat the size effect explicitly. The molecular shape contains no size information, because it is calculated from normalized PMI ratios. The size effect may be required for further investigation, e.g., correction by a radius of gyration or a volume of the conformation.

Although we only calculated the cyclic hexapeptide with L- or D-amino acid, it is possible to simulate cis/trans isomerization of N-methylated amino acid by McMD simulations with current protocols. The McMD simulations have the advantage that the reaction coordinate is only the potential energy, which is independent of the system size.

ABBREVIATIONS:

MD

molecular dynamics

McMD

multicanonical molecular dynamics

FEL

free energy landscape

MDCK

Madin-Darby canine kidney

PAMPA

parallel artificial membrane permeability assay

SASA

solvent accessible surface area

PSA

polar surface area

PCA

principal component analysis

IMHB

intramolecular hydrogen bond.

logD

experimental partition coefficient at pH 7.4