High-Resolution Oscillating Steady-State fMRI using Patch-Tensor Low-Rank Reconstruction

Abstract

The goals of fMRI acquisition include high spatial and temporal resolutions with a high signal to noise ratio (SNR). Oscillating Steady-State Imaging (OSSI) is a new fMRI acquisition method that provides large oscillating signals with the potential for high SNR, but does so at the expense of spatial and temporal resolutions. The unique oscillation pattern of OSSI images makes it well suited for high-dimensional modeling. We propose a patch-tensor low-rank model to exploit the local spatial-temporal low-rankness of OSSI images. We also develop a practical sparse sampling scheme with improved sampling incoherence for OSSI. With an alternating direction method of multipliers (ADMM) based algorithm, we improve OSSI spatial and temporal resolutions with a factor of 12 acquisition acceleration and 1.3 mm isotropic spatial resolution in prospectively undersampled experiments. The proposed model yields high temporal SNR with more activation than other low-rank methods. Compared to the standard gradient echo (GRE) imaging with the same spatial-temporal resolution, 3D OSSI tensor model reconstruction demonstrates 2 times higher temporal SNR with 2 times more functional activation.

I. Introduction

FUNCTIONAL magnetic resonance imaging (fMRI) measures neural activity based on blood-oxygenation-level-dependent (BOLD) contrast and the hemodynamic correlations [1] by acquiring a time series of $T_2^{*}$-weighted brain images. BOLD signal change from fMRI images acquired with the standard gradient echo (GRE) imaging is small and can be easily buried in noise. Furthermore, as signal to noise ratio (SNR) is proportional to voxel size and functional units of the brain are on the order of 1 mm or smaller, high SNR is critical for high-resolution and high-quality fMRI. However, current methods for SNR improvements are limited: multi-coil head arrays suffer from diminished returns for deep brain structures, and high magnetic field systems are costly. This paper focuses on Oscillating Steady-State Imaging (OSSI) [2], a new fMRI acquisition method that has the potential to provide 2 times higher SNR than the standard GRE approach.

OSSI combines balanced gradients and a quadratic RF phase progression with large phase increments, and leads to a combination of high SNR of the balanced steady state and $T_2^{*}$-weighting of GRE imaging. The quadratic RF phase cycling is $\varphi (n)=\pi n^2/n_c$, where n is the RF index and n_c is the cycle length. For n_c = 1, Δϕ between RF pulses is 180°, which is balanced steady-state free precession (bSSFP). For n_c ≥ 120 with very small Δϕ, the mechanism leads to bSSFP-like contrast [3]. OSSI acquisitions use 1 < n_c < 120 that produce large and oscillating signals. Specifically, by selecting a short TR with n_c = 10, OSSI demonstrates a similar $T_2^{*}$-weighted contrast mechanism as GRE with additional $T_2^{\prime }$-weighting of about 15 ms immediately after the RF pulse. Details on how the SNR and $T_2^{*}$-sensitivity vary with n_c and other acquisition parameters can be found in [2].

The OSSI signal oscillates with a periodicity dictated by the quadratic RF phase cycling, and OSSI images have a periodic oscillation pattern that repeats every n_c images as illustrated in Figs. 1, S1 and S2. Thus, one must acquire and combine n_c as many images to get images that are free of oscillations and suitable for fMRI analysis. With standard reconstruction methods, this need would compromise temporal resolution by a factor of n_c, and the short TR requirement necessary for steady-state imaging (e.g., TR =15 ms) limits the time for traversing k-space and thus limits the single-shot spatial resolution. We aspire to improve the spatial and temporal resolutions by designing a sparse sampling scheme and an accurate reconstruction method.

Fig. 1.

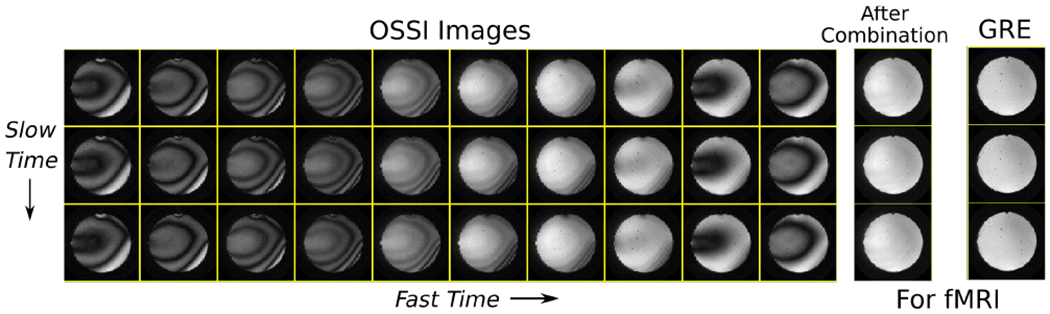
OSSI images with periodic oscillation patterns are structured along “fast time” and “slow time” dimensions. Every n_c = 10 fast time images can be 2-norm combined to generate fMRI images that are free of oscillations and have $T_2^{*}$-sensitivity comparable to standard GRE imaging.

Past works on reconstructing fMRI time series use models such as low-rank [4], low-rank and sparse [5], and low-rank plus Fourier domain sparsity [6], [7] that impose low-rankness and/or sparsity on matrices of the vectorized space dimension and time. We found them insufficient for OSSI, as the oscillations in OSSI images make them neither low-rank nor sparse along the time dimension. To simultaneously exploit redundancy in the oscillation pattern of OSSI and the repeated acquisition for fMRI time courses, we structure OSSI images to have two time dimensions and develop a patch-based tensor model.

Based on the n-rank definition [8] and tensor nuclear norm [9] for tensor competition [9], [10], global tensor low-rank or low-rank plus sparse reconstruction models have been applied to dynamic MRI via space x × space y × time [11], cardiac MRI via space × time × cardiac phases [12], and quantitative cardiovascular magnetic resonance multitasking with multiple time dimensions [13].

Instead of tensor nuclear norm, global tensor low-rank models have also been explored via Tucker decomposition or higher-order SVD (HOSVD) [8], [14] for dynamic MRI with sparse core tensors [15], high-dimensional MR imaging with sparsity constraints and tensor subspace estimated from navigator data [16], multi-dimensional dynamic phosphorus-31 magnetic resonance spectroscopy and imaging [17], and electron paramagnetic resonance oxygen imaging [18] with specialized sparse sampling strategies. Furthermore, the CANDECOMP/PARAFAC (CP) decomposition [8] was exploited for multi-contrast dynamic cardiac MRI denoising [19] and for tensor completion with designed regular sub-Nyquist sampling with applications for fMRI acceleration [20].

Previous patch-wise tensor low-rank models impose low-rank constraints on spatial submatrices of the tensor unfoldings [21], [22], select patches with both local and non-local similarities and exploit patch-tensor low-rankness using HOSVD for multi-contrast MRI reconstruction [23], or compare CP and Tucker decompositions for local and global low-rank tensor denoising [19]. Because both CP and Tucker decompositions require selection of tensor ranks, our work focuses on tensor nuclear norm minimization that avoids explicit selection of tensor ranks, and structures local patch-tensors to exploit the local and high-dimensional spatial-temporal low-rankness. We further design a sparse sampling scheme that prospectively undersamples the data with a 12-fold acceleration for 2D and a 10-fold acceleration for 3D. The proposed model provides high-resolution reconstructions with high temporal SNR (tSNR) and more functional activation than global tensor or matrix low-rank models.

Patch-tensor low-rank (patch-tensor LR) reconstruction and the sparse sampling schemes are new for fMRI, and the application to OSSI fMRI data is also new. Compared to standard GRE imaging, the proposed OSSI tensor model demonstrates a factor of 2 tSNR improvement for fMRI with 2 times larger functional activation.

The paper is organized as follows. Section II presents notations and definitions for tensors. Section III proposes the patch-tensor model and optimization algorithm. Section IV develops the incoherent undersampling and describes the experimental setup for OSSI fMRI studies. Section V demonstrates the improved functional performance using the proposed approach compared to other reconstruction and acquisition methods. Section VI discusses future directions, and Section VII concludes the paper.

II. Background and Notation

A tensor is a multidimensional array [8]. We denote tensors according to their dimensions. One-dimensional tensors or vectors are denoted by bold lowercase letters, e.g., x, and tensors of dimension two or higher are denoted by bold capital letters, e.g., X. Scalars are denoted by italic letters, e.g., x.

The inner product of two tensors $\mathbf{X},\mathbf{Y}\in {\mathbb{C}}^{I_1\times I_2\times \cdots \times I_N}$ is defined as the sum of the element-wise products [14],

$$\langle \mathbf{X},\mathbf{Y}\rangle =\sum _{i_1=1}^{I_1}\sum _{i_2=1}^{I_2}\cdots \sum _{i_N=1}^{I_N}{y}_{i_1{i}_2\cdots i_N}^{*}{x}_{i_1{i}_2\cdots i_N},$$

where * denotes the complex conjugate. Naturally, the norm of tensor X is $\Vert \mathbf{X}\Vert =\sqrt{\langle \mathbf{X},\mathbf{X}\rangle }$.

The process of reforming a tensor to matrices by reordering the vectors of the tensor is known as matricization or unfolding. Each dimension of a tensor is known as a mode, and the number of modes is known as the tensor’s order or number of dimensions. After unfolding, the tensor becomes matrices of different modes, and the number of these matrices equals the number of dimensions. Figure 2 illustrates unfolding a three-dimensional tensor to three matrices. The mode-n unfolding of tensor X is denoted by X_(n), accordingly, refolding the mode-n matrix back to X is Refold_n (X_(n)). As seen in [8] and [14], different papers may use different permutations of the vectors to get the unfoldings; the specific order is unimportant as long as it is consistent.

Fig. 2.

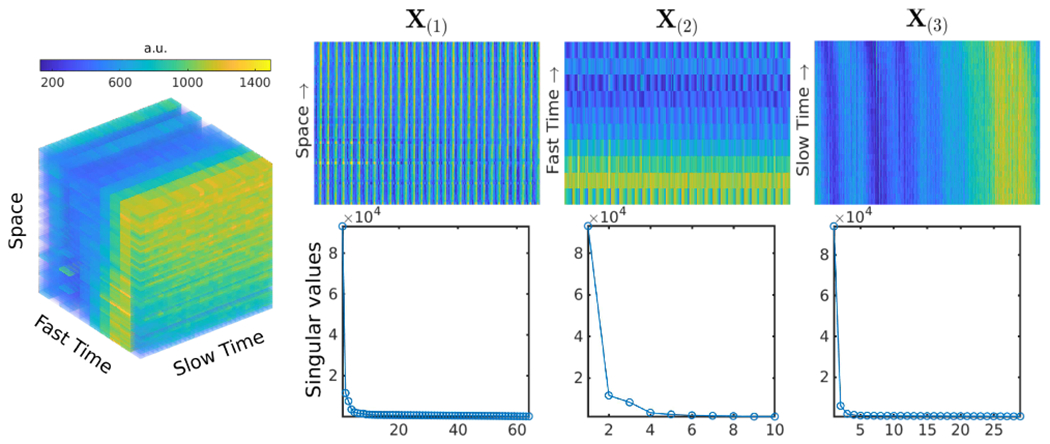
A 3D patch-tensor (left), its three matrix unfoldings of different modes (top right), and the singular values of the unfoldings demonstrating the patch-tensor low-rank (bottom right).

The n-rank of X is the column rank of X_(n) and is denoted by rank (X_(n)) = r_n. Therefore, X is a rank-(r₁, r₂, … , r_N) tensor.

III. Reconstruction Methods

This section introduces the patch-tensor LR model based reconstruction problem, the optimization algorithm, important implementation details, and other reconstruction methods for comparison.

A. Tensor Model Problem Formulation

fMRI involves acquiring a time series of images to track brain activity. In OSSI fMRI, the images periodically oscillate with every n_c time points along with the regular fMRI time course as shown in Fig. 1. Typically, we 2-norm combine every n_c consecutive and non-overlapping images to get uniform images for fMRI analysis [2]. To simultaneously exploit the redundancy in OSSI oscillatory patterns and the repetition along fMRI time series, we structure OSSI fMRI images into two time dimensions. The fast oscillation dimension is called “fast time”, and the fMRI time dimension is called “slow time”.

To improve both spatial and temporal resolutions for OSSI fMRI, and to model the reproducibility in both fast and slow time dimensions, we propose a tensor low-rank model for the undersampled reconstruction. The tensor dimensions include vectorized space, fast time = n_c, and slow time. Since the exact form of the oscillations is resonant frequency dependent and resonant frequency usually varies slowly across space, low-rankness involving the fast oscillations is a local feature (more similarities among neighboring pixels than between non-local pixels or over the whole image). Furthermore, due to the complexity of functional activity, imposing low-rankness on temporal blocks instead of the whole fMRI time series improves the modeling accuracy. Therefore, we propose a patch-tensor LR model with limited spatial and temporal extent, and impose low-rankness on all the unfoldings of the patch-tensor.

The whole fMRI time series is broken into non-overlapping time blocks. For each block, we reshape 3D (space x × space y × time t) or 4D (space x × space y × space z × time t) OSSI images into 4D (x × y × fast time n_c × slow time t_s) or 5D (x × y × z × fast time n_c × slow time t_s) tensors. We partition the 4D or 5D tensors into patches, and vectorize all the spatial dimensions to form 3D low-rank patch-tensors (vectorized space s_p × n_c × t_s). Figure 2 visualizes an in vivo 3D patch-tensor, its three unfoldings, and the corresponding singular values demonstrating the low-rankness of the unfoldings. The patch-tensor is from the center of a brain with no activation, and Fig. S5(a) plots the corresponding log-scale singular values. Figure S5(b) presents low-rank unfoldings of a different patch-tensor in an activated region.

The proposed patch-tensor LR model based reconstruction problem with non-overlapping patches is

$$\underset{\mathbf{X}}{\mathrm{arg\; min}}\sum _{m=1}^M\sum _{i=1}^3{\lambda }_i\mathbf{rank}({\mathcal{P}}_{mi}(\mathbf{X}))+\frac{1}{2}{\Vert \mathcal{A}(\mathbf{X})-\mathbf{y}\Vert }_2^2,$$ (1)

where $\mathbf{X}\in {\mathbb{C}}^{x\times y(\times z)\times t}$ is a complex OSSI fMRI time block to be reconstructed. Linear operator $\mathcal{P}(·)$ partitions and reshapes its input into M locally low-rank patch-tensors with ${\mathcal{P}}_m(\mathbf{X})\in {\mathbb{C}}^{s_p\times n_c\times t_s}$, m = 1, …, M. ${\mathcal{P}}_{\mathit{mi}}(\mathbf{X})={\mathcal{P}}_i{(\mathbf{X})}_{(i)}$ denotes the mode-i unfolding of the mth tensor patch ${\mathcal{P}}_m(\mathbf{X})$. λ_i is the regularization parameter for low-rankness of the mode-i unfolding. Linear operator $\mathcal{A}$ represents the MRI physics; it consists of coil sensitivities and the non-uniform Fourier transform (NUFFT) including undersampling. y denotes sparsely sampled k-space measurements.

We focus on the following convex relaxation of (1):

$$\underset{\mathbf{X}}{\mathrm{arg\; min}}\sum _{m=1}^M\sum _{i=1}^3{\lambda }_i{\Vert {\mathcal{P}}_{mi}(\mathbf{X})\Vert }_{*}+\frac{1}{2}{\Vert \mathcal{A}(\mathbf{X})-\mathbf{y}\Vert }_2^2.$$ (2)

This formulation encourages low-rankness of all the patch-tensor unfoldings by minimizing the sum of their singular values. Meanwhile, the data fidelity term encourages correspondence between the images and the acquired k-space samples.

B. Optimization Algorithm

The regularizers in the unconstrained cost function (2) can be handled via the alternating direction method of multipliers (ADMM) [10], [24] applied to the equivalent constrained optimization problem:

$$\underset{\mathbf{Z}}{\mathrm{arg\; min}}\underset{\left\{{\mathbf{X}}_i\right\}}{\min }\sum _{m=1}^M\sum _{i=1}^3{\lambda }_i{\Vert {\mathcal{P}}_{mi}({\mathbf{X}}_i)\Vert }_{*}+\frac{1}{2}{\Vert \mathcal{A}(\mathbf{Z})-\mathbf{y}\Vert }_2^2$$ (3)

subject to X_i = Z, i = 1, 2,3,

with ${\mathbf{X}}_i\in {\mathbb{C}}^{x\times y(\times z)\times t}$, i = 1, 2, 3 constrained to be equal to $\mathbf{Z}\in {\mathbb{C}}^{x\times y(\times z)\times t}$. The scaled form of the corresponding augmented Lagrangian is

$$\mathcal{L}(\{{\mathbf{X}}_i\},\mathbf{Z},\{{\mathbf{U}}_i\})=\sum _{m=1}^M\sum _{i=1}^3{\lambda }_i{\Vert {\mathcal{P}}_{mi}({\mathbf{X}}_i)\Vert }_{*}+\frac{1}{2}{\Vert \mathcal{A}(\mathbf{Z})-\mathbf{y}\Vert }_2^2+\frac{\rho }{2}\sum _{i=1}^3{\Vert {\mathbf{X}}_i-\mathbf{Z}+{\mathbf{U}}_i\Vert }^2-\frac{\rho }{2}\sum _{i=1}^3{\Vert {\mathbf{U}}_i\Vert }^2.$$ (4)

We update the variables {X_i}, Z and scaled dual variables {U_i} sequentially, holding the other variables fixed.

For non-overlapping patch-tensors, the update step for each patch of ${\left\{{\mathbf{X}}_i\right\}}_{i=1}^3$ is:

$${\mathcal{P}}_m({\mathbf{X}}_i^{k+1})=\underset{{\mathcal{P}}_m({\mathbf{X}}_i)}{\mathrm{arg\; min}}{\mathcal{L}}_{mi}({\mathcal{P}}_m({\mathbf{X}}_i),{\mathbf{Z}}^k,{\mathbf{U}}_i^k)$$ (5)

for m = 1, …, M and i = 1, …, 3 at iteration k + 1, where

$$\begin{array}{l}{\mathcal{L}}_{mi}={\lambda }_i{\Vert {\mathcal{P}}_{mi}({\mathbf{X}}_i)\Vert }_{*}+\frac{\rho }{2}{\Vert {\mathcal{P}}_m({\mathbf{X}}_i)-{\mathcal{P}}_m({\mathbf{Z}}^k-{\mathbf{U}}_i^k)\Vert }^2\\ ={\lambda }_i{\Vert {\mathcal{P}}_{mi}({\mathbf{X}}_i)\Vert }_{*}+\frac{\rho }{2}{\Vert {\mathcal{P}}_{mi}({\mathbf{X}}_i)-{\mathcal{P}}_{mi}({\mathbf{Z}}^k-{\mathbf{U}}_i^k)\Vert }_F^2.\end{array}$$ (6)

Because ${\mathcal{P}}_{mi}({\mathbf{X}}_i)$ and ${\mathcal{P}}_{mi}({\mathbf{Z}}^k-{\mathbf{U}}_i^k)$ are matrices, patch update ${\mathcal{P}}_{mi}\left({\mathbf{X}}_i^{k+1}\right)$ is easily obtained with a singular value soft-thresholding operator SVT(·) with threshold λ_i / ρ,

$${\mathcal{P}}_{mi}\left({\mathbf{X}}_i^{k+1}\right)=\underset{{\mathcal{P}}_{mi}({\mathbf{X}}_i)}{\mathrm{arg\; min}}{\mathcal{L}}_{mi}({\mathcal{P}}_{mi}({\mathbf{X}}_i),{\mathbf{Z}}^k,{\mathbf{U}}_i^k)={\mathrm{SVT}}_{{\lambda }_{i/\rho }}({\mathcal{P}}_{mi}({\mathbf{Z}}^k-{\mathbf{U}}_i^k)).$$ (7)

Therefore, the update for the patches of {X_i} becomes

$${\mathcal{P}}_m\left({\mathbf{X}}_i^{k+1}\right)={\mathrm{REFOLD}}_i\left({\mathcal{P}}_{\mathit{mi}}\left({\mathbf{X}}_i^{k+1}\right)\right).$$ (8)

We parallelize this step over all the unfoldings and patches.

The Z update simplifies to:

$$\begin{array}{l}{\mathbf{Z}}^{k+1}=\underset{\mathbf{Z}}{\mathrm{arg\; min}}\mathcal{L}(\{{\mathbf{X}}_i^{k+1}\},\mathbf{Z},\{{\mathbf{U}}_i^k\})\\ =\underset{\mathbf{Z}}{\mathrm{arg\; min}}(\frac{1}{2}{\Vert \mathcal{A}(\mathbf{Z})-\mathbf{y}\Vert }_2^2+\frac{\rho }{2}\sum _{i=1}^3{\Vert \mathbf{Z}-({\mathbf{X}}_i^{k+1}+{\mathbf{U}}_i^k)\Vert }^2).\end{array}$$ (9)

We use the conjugate gradient method for this least-squares minimization.

The scaled dual variables ${\left\{\mathbf{U}\right\}}_{i=1}^3$ are updated in the usual ADMM way by

$${\mathbf{U}}_i^{k+1}={\mathbf{U}}_i^k+{\mathbf{X}}_i^{k+1}-{\mathbf{Z}}^{k+1}.$$ (10)

C. Practical Considerations

1). Random Cycle Spinning:

The singular value soft-thresholding operation for non-overlapping patch-tensors leads to blocking artifacts at the boundaries of the patches. Using overlapping patches would be computationally intensive, so instead we apply random cycle spinning in every iteration as in [25], [26]. We perform a randomly chosen circular shift along each dimension of the input tensor before partitioning and reshaping, and unshift the tensor back after updating and placing the patch-tensors together. Accordingly, the actual update for the patches of each X_i is

$${\mathcal{P}}_m(\mathrm{SHIFT}({\mathbf{X}}_i^{k+1}))={\mathrm{REFOLD}}_i({\mathrm{SVT}}_{{\lambda }_{i/\rho }}({\mathcal{P}}_{mi}(\mathrm{SHIFT}({\mathbf{Z}}^k-{\mathbf{U}}_i^k)))).$$ (11)

2). Overlapping Time Blocks:

We reconstruct each fMRI time block separately to lighten the memory burden, so random cycle spinning only removes patch boundary artifacts within each block. To further reduce potential artifacts at the temporal boundaries of the blocks, we reconstruct overlapping time blocks and discard additional time points near the boundaries for all the methods. Figure S9 illustrates how the ranges and discarded portions of the time blocks are selected.

3). ADMM Implementation Details:

We scale the k-space data to have maximum magnitude of 1 before applying ADMM. With this normalization, simply setting the regularization parameters λ₁ = λ₂ = 1 works well. Because X₍₃₎ has lower rank thanX₍₁₎ and X₍₂₎ as shown in Fig. 2, we choose λ₃ = 2 to provide more weighting to the low-rankness of X₍₃₎.

For ADMM penalty parameter ρ, we investigated a range of ρ values and found ρ = 121 empirically to be a good initialization. Furthermore, for our application, using varying penalty parameter or increasing ρ after a number of inner iterations contributes to a faster convergence. After T inner iterations updating variables {X_i}, Z, and {U_i}, the following updates are performed in the outer iteration:

$$\begin{array}{l}\rho \mapsto r\rho \\ {\mathbf{U}}_i\mapsto {\mathbf{U}}_i/r.\end{array}$$ (12)

We chose rate r = 3, and rescale the scaled dual variable U_i after updating ρ. This scheme is adapted from [10], [24]. Algorithm 1 summarizes the method.

Algorithm 1.

Patch-tensor low-rank reconstruction

Input: $\mathcal{A}$, y, {λi} = [1 1 2], ρ = 121, r = 3, S = 2, T = 11
Output: OSSI images Zk+1
1:	for s = 0,…, S − 1 do
2:	for t = 0,…, T − 1 do
3:	k = s * T + t
4:	Update Zk+1 using (9)
5:	for i = 1, 2, 3 do
6:	Update ${\mathbf{X}}_i^{k+1}$ using (11)
7:	${\mathbf{U}}_i^{k+1}={\mathbf{U}}_i^k+{\mathbf{X}}_i^{k+1}-{\mathbf{Z}}^{k+1}$
8:	end for
9:	end for
10:	Update ρ and each Ui using (12)
11:	end for
12:	return Zk+1

D. Other Reconstruction Approaches

We compare the proposed reconstruction method to matrix local low-rank (MLLR) [27], global tensor low-rank (GTLR), patch-tensor low-rank plus sparse (patch-tensor L+S), and conjugate gradient SENSE [28], [29] with an edge-preserving regularizer (regularized CG-SENSE).

MLLR imposes low-rank constraints on space × time matrices by vectorizing image patches for the spatial dimension. The cost function for MLLR is the same as setting i = 1 in (2). GTLR enforces low-rankness on all the unfoldings of the tensor of size space xy × n_c × t_s without taking patches. The cost function is the same as (2) with M = 1 and without spatial partitioning. GTLR reconstructs fMRI time blocks and is global in spatial sense but not in temporal sense. It is less convenient for computation to impose low-rankness on a temporal global tensor.

The optimization problem for patch-tensor L+S is

$$\underset{L,S}{\mathrm{arg\; min}}\frac{1}{2}{\Vert \mathcal{A}(L+S)-\mathbf{y}\Vert }_2^2+\sum _{m=1}^M\sum _{i=1}^3{\lambda }_i{\Vert {\mathcal{P}}_{mi}(L)\Vert }_{*}+\mu {\Vert \Phi (S)\Vert }_1,$$

where $\mathbf{L},\mathbf{S}\in {\mathbb{C}}^{x\times y\times t}$ denote the image components to be reconstructed and Φ denotes 2D Fourier transform along both fast and slow time dimensions to enhance the Fourier domain sparsity of the sparsity component S. The low-rank component L has the same regularization as in (2), and λ_i and μ are regularization parameters.

The optimization problem for regularized CG-SENSE is

$$\underset{\mathbf{X}}{\mathrm{arg\; min}}\frac{1}{2}{\Vert \mathcal{A}(X)-\mathbf{y}\Vert }_2^2+\sum _{j=1}^J\psi ({[CX]}_j),$$

where $\mathbf{X}\in {\mathbb{C}}^{xy}$ denotes one vectorized image of the time series, $\mathbf{C}\in {\mathbb{R}}^{J\times xy}$ is the 2D spatial finite difference matrix with J = 2xy, and ψ is the Huber potential function.

We used ADMM to perform the MLLR, GTLR, and patch-tensor L+S reconstructions. The ADMM parameters for patch-tensor L+S were the same as (12) for patch-tensor LR. The CG update in the ADMM inner iterations and the regularized CG-SENSE reconstruction were implemented with the Michigan Image Reconstruction Toolbox [30].

IV. Acquisition Methods

Each oscillating state (index n) of OSSI was acquired with quadratic RF phases ϕ(n) = πn²/n_c, cycle length n_c = 10, TR = 15 ms, and flip angle = 10° for the desired SNR and $T_2^{*}$-sensitivity [2]. The short TR of 15 ms limits the readout, and n_c = 10 compromises temporal resolution. Hence, sparse sampling is important for improving OSSI spatial and temporal resolutions.

This section develops practical sparse sampling schemes with increased sampling incoherence for OSSI, and describes human fMRI studies. We collected 2D “mostly sampled” with retrospective undersampling, 2D prospectively undersampled, and 3D prospectively undersampled data. With FOV = 220 mm, slice thickness = 2.5 mm, and matrix size = 168 × 168, the spatial resolution = 1.3 × 1.3 × 2.5 mm³ for all experiments.

A. Variable-Density Spiral Sampling Trajectory

We focus on variable-density (VD) spiral trajectories that travel quickly through k-space. The sampling density of VD spirals varies at different k-space radii. By dense sampling in the center of k-space where the MR energy concentrates and sparse sampling at outer k-space, VD spirals can reduce imaging time and off-resonance blur [31], [32] compared to uniform-density (UD) spirals. We design VD spirals based on [33], [34] with uniform density and over-sampling in the k-space center, and then linearly decrease the sampling density as the spirals approach the outer part of k-space. The trajectory is parameterized by (n_i, a, b, d), where n_i = number of interleaves, a = effective FOV (in mm) at k-space center, b = effective FOV at the edge of k-space, and d denotes the number of central k-space points with uniform sampling density determined by a.

We used (n_i, a, b, d) = (9, 310, 110, 300) for the retrospective sampling pattern with spiral-out readouts. The effective FOV for n_i = 9 interleaves was a = 310 mm at the center of k-space for the first d = 300 sampling points, then decreased linearly to b = 110 mm at the edge of k-space. The readout length for each interleave was 8.3 ms. The k-space of each image can be mostly covered with all the 9 interleaves. However, due to the variable-density nature of the trajectories, the 9-interleave trajectory was still undersampled by approximately a factor of 1.5, and we refer to this sampling pattern as “mostly sampled”. We chose a = 300 mm and b = 80 mm for prospective undersampling with spiral-in readouts to increase $T_2^{*}$-sensitivity, and the readout length was 7.4 ms.

We took 1 interleave out of n_i = 9 VD spirals as the undersampled trajectory. Compared to a UD spiral with the same FOV and matrix size, the single-shot undersampled trajectory provided a factor of 12 acceleration in-plane as presented in Fig. 3 (a). We selected the VD spiral parameters for a good balance between the undersampling factor and reconstruction performance.

Fig. 3.

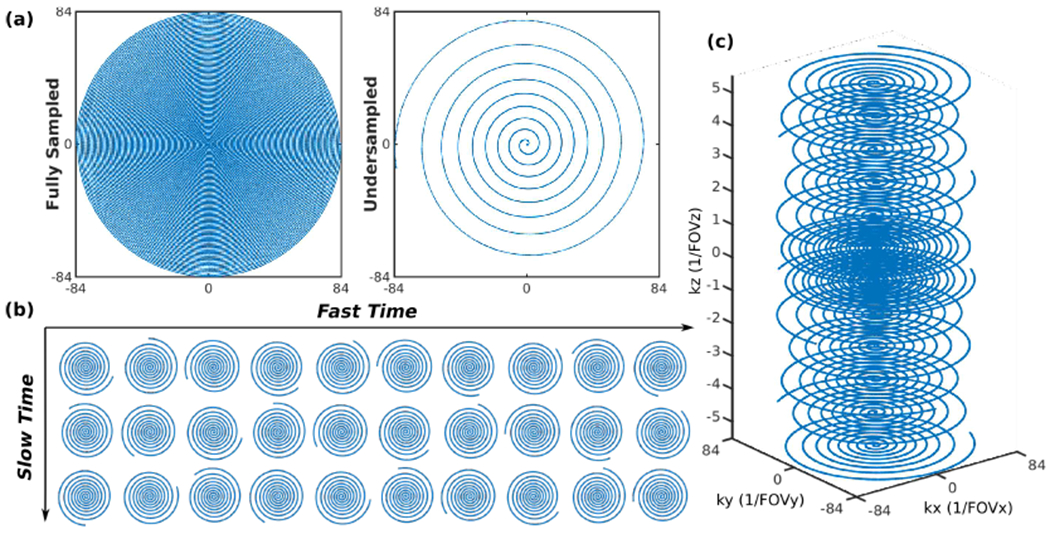
(a) Compared to the fully sampled trajectory, the designed single-shot variable-density spiral trajectory for each time frame or k_z plane enables a 12-fold acquisition acceleration. (b) Prospective 2D undersampling pattern with the incoherent rotations between fast time (the oscillation dimension) and slow time (the fMRI time dimension). (c) 3D undersampled stack-of-spirals providing a 10-fold acceleration with one spiral for the outer k_z planes, two spirals for the two central k_z planes, and golden-angle rotations between k_z planes.

B. Incoherent Sampling for Time Dimensions and 3D

The proposed spiral trajectory provides aggressive undersampling in-plane and would introduce reconstruction artifacts if used without regularization. As we are using a tensor model with two time dimensions for the undetermined reconstruction problem, we prefer the sampling pattern to be incoherently varying along the two dimensions for artifact reduction [35]. Therefore, we rotate the VD spiral using a golden-angle based approach for each temporal frame to avoid overlapping trajectories in both fast and slow time dimensions.

We define an interleave index k = 0, … , K − 1 for a time series of OSSI images with K interleaves in total. For 2D retrospective sampling with multi-shot acquisition, the rotation angle for each interleave k was

$$ga\cdot k+2\cdot ga\cdot \lfloor k/n_c/n_i\rfloor ,$$ (13)

where ga = 111.246° is the golden angle, n_c = 10 is the size of fast time dimension, n_i is the number of interleaves, and ⌊·⌋ denotes the floor function. The acquisition for the interleaves first looped through OSSI oscillation states 1 to n_c, then looped through multi-shot 1 to n_i, and after that proceeded to the next slow time point.

For 2D prospective undersampling, only 1 VD interleave was collected for each image, and the rotation angle was

$$ga\cdot k+ga\cdot \lfloor k/n_c\rfloor .$$ (14)

The index k looped through OSSI fast time oscillations for every slow time point. Figure 3 (b) presents the prospective sampling pattern. The baseline rotation was determined by the golden angle. The second terms in (13) and (14) were designed specifically to increase sampling incoherence along slow time as shown in Figs. S6 and S7 for prospective undersampling and retrospective undersampling, respectively.

For 3D prospective undersampling, we used a stack of VD spirals with 2-shot acquisition at the 2 central k_z planes and single-shot acquisition at other k_z locations as in Fig. 3 (c), providing a 10-fold acceleration compared to the fully sampled k-space. Rotations in (14) were applied, where k looped through OSSI oscillations, then k_z planes, and finally the slow time points.

Because of the increased sampling incoherence in the two time dimensions, the angular dimension of k-space can be mostly covered with sampling trajectories of 9 or 10 consecutive time frames. We used this feature and combined k-space data of every 10 slow time points to compute data-shared initialization for reconstruction, which helped decrease the number of CG iterations and computation time.

C. Human fMRI Studies

We implemented the OSSI pulse sequence and the proposed sampling scheme using GE’s standard pulse programming environment EPIC. All the data were collected on a 3T GE MR750 scanner (GE Healthcare, Waukesha, WI) with a 32-channel head coil (Nova Medical, Wilmington, MA) using the proposed retrospective and prospective undersampling schemes. Prospectively undersampled OSSI studies were further compared to standard GRE fMRI with matched spatial-temporal resolution.

The human studies were carried out under IRB approval. The fMRI task was a left vs. right reversing-checkerboard visual stimulus of 210 s with 10 s rest, 5 cycles of left or right stimulus of 20 s (20 s L/20 s R × 5 cycles).

2D OSSI used an oblique slice passing through the visual cortex. The 2D mostly sampled data were acquired with multi-shot VD spirals with number of interleaves n_i = 9, volume TR = 1.35 s (TR · n_c · n_i), and spiral-out TE = 2.7 ms. The rotation angles between interleaves and time frames were determined by (13). The number of time frames (both fast time n_c and slow time) was 1490 with 10 s discarded acquisition to ensure the steady state. The retrospectively undersampled data only contained the first VD interleave of every 9 interleaves.

The 2D prospectively undersampled data were collected with single-shot VD spirals (n_i = 1) with volume TR = 150 ms (TR · n_c) and spiral-in TE = 11.7 ms. The rotation angles of the spirals were selected by (14). The number of fast time frames was 13340 with 10 s discarded acquisition. As every n_c images were 2-norm combined for fMRI analysis, the temporal resolution for the prospectively undersampled data was 150 ms. 2D GRE fMRI images with the same spatial resolution and temporal resolution of 150 ms as OSSI were also acquired for comparison. Specifically, GRE imaging used multi-shot spiral acquisition with n_i = 3, TR = 50 ms, Ernst flip angle = 16°, and spiral-in TE = 30 ms. Each interleave was VD spiral with (n_i, a, b, d) = (3, 240, 120, 300) and readout length = 21.9 ms.

For 3D imaging, an oblique slab was selected. Prospectively undersampled OSSI was compared to GRE imaging with matched spatial resolution and matched temporal resolution of 2.1 s. The number of 3D volumes was 96 for the 200 s task. For OSSI, the number of k_z planes n_z = 12, volume TR = 2.1 s (TR · n_c · n_z), and spiral-in TE = 10.3 ms. For GRE, multi-slice TR = 700 ms with 14 slices, multi-shot acquisition with n_i = 3, spiral-in TE = 30 ms, Ernst flip angle = 16°, and same VD spiral trajectories for each slice as in 2D GRE imaging were used.

For calculation of coil sensitivity maps, we collected images with a standard spin-warp sequence at TR = 50 ms, TE = 6.3 ms, and Ernst flip angle = 16°. The 32-channel coil images were compressed to 16 virtual coils for 2D and 24 virtual coils for 3D via PCA [36], and coil sensitivity maps were calculated using ESPIRiT [37], [38]. We also created coil-combined images for extraction of the brain region using the Brain Extraction Tool [39].

D. Performance Evaluation

The reconstruction and functional performances were evaluated with normalized root-mean-square difference (NRMSD) for retrospectively undersampled data, activation maps, and tSNR maps.

The retrospectively undersampled reconstruction $\widehat{\mathbf{X}}$ was compared to X_ref reconstruction from “mostly sampled” data by regularized CG-SENSE, using the metric $\mathrm{NRMSD}=\Vert {\mathbf{X}}_{\mathrm{ref}}-\widehat{\mathbf{X}}\Vert /\Vert {\mathbf{X}}_{\mathrm{ref}}\Vert .$

Every n_c = 10 reconstructed images of OSSI were combined via 2-norm for functional analysis. The data from the first cycle (40 s) of the task were discarded to avoid the modeling error in the initial rest period. To reduce scanner drift effects, we detrended the data using the first 4 discrete cosine transform basis functions for both OSSI combined and GRE fMRI images.

The background of the activation map was the mean of reconstructed fMRI images. The activated regions were determined by correlation coefficients above a 0.45 threshold. Correlation coefficients were defined by correlating the fMRI time course for each voxel with the task-related reference waveform, and the reference waveform was given by convolving the task with the canonical hemodynamic response function [40]. The tSNR maps were generated by dividing the time course mean by the standard deviation of the time course residual (without the mean and the task) for each voxel. NMRSD within the brain (excluding the scalp and skull) from reconstructed images, number of activated voxels at the lower third of the brain (where the visual activation concentrates), and averaged tSNR within the brain were calculated for quantitative evaluations.

V. Reconstruction and Results

This section compares OSSI undersampled reconstructions using the proposed tensor model and other low-rank related approaches. 3D OSSI reconstruction is further compared to multi-slice GRE to demonstrate the SNR advantage of OSSI.

A. Regularization Parameter Adjustment

To ensure that different reconstructions have similar spatial-temporal resolutions, we compared the local impulse responses [41], [42] of the reconstruction methods. Specifically, we added an impulse perturbation $\epsilon \mathcal{A}\left({\delta }_{j,t}\right)$ to the undersampled k-space data y and reconstructed the perturbed data with different models. We selected j and t to be in the spatial and temporal center of the time block being reconstructed, respectively, and we chose ε = 1 (about 10% of the OSSI signal magnitude). Accordingly, the local impulse response is $h(j,t)=\left(\mathcal{B}\right(\epsilon \mathcal{A}\left({\delta }_{j,t}\right)+\mathbf{y})-\mathcal{B}(\mathbf{y}\left)\right)/\epsilon$, where $\mathcal{B}(·)$ denotes a reconstruction method.

Profiles of the impulse response along spatial dimension and temporal dimensions can help assess the spatial-temporal sharpness of the reconstructions for $\mathcal{B}\ne {\mathcal{A}}^{-1}$. As shown in Fig. S8, we selected regularization parameters to ensure that impulse responses of different reconstructions had similar peaks and were close to the magnitude for the regularized CG-SENSE reconstruction. Based on the ratios for the λ_i, values in (2), the final 2D reconstruction parameters were {λ_i} = [1 1 2] * 0.4 for patch-tensor LR, λ₃ = 1.6 for MLLR, {λ_i} = [1 1 2] * 4 for GTLR, {λ_i} = [1 1 2] * 0.3 and μ = 3 for patch-tensor L+S.

Furthermore, with carefully adjusted regularization parameters, reconstructing overlapping time blocks or non-overlapping time blocks for the fMRI time series led to similar results, as demonstrated by example time courses and spectra of the patch-tensor LR reconstruction in Fig. S10.

B. Retrospective and Prospective 2D Reconstructions

OSSI 2D retrospectively and prospectively undersampled data were reconstructed using the proposed method and the comparison methods. OSSI 2D mostly sampled data were reconstructed using regularized CG-SENSE. For the proposed retrospectively undersampled reconstructions, the number of time points before combination = 330 for every overlapping time block, and the patch-tensor size = 64 (8 * 8) × 10 × 33. Similarly for prospectively undersampled data, the number of time points = 420 for each overlapping time block, and the patch-tensor size = 64 (8 * 8) × 10 × 42. We used S = 2 outer iterations, T = 11 inner iterations for ADMM, and 4 iterations for the CG update of Z. The number of iterations for regularized CG-SENSE reconstruction was 19. All the OSSI reconstructions were initialized with data-shared images.

Figure 4 shows reconstructions from mostly sampled data, the proposed patch-tensor LR, MLLR, GTLR, regularized CG-SENSE, and patch-tensor L+S models. The fast time image reconstructed using the proposed approach is less noisy compared to the mostly sampled reference and other reconstructions. The oscillatory patterns and the high-resolution details of the fMRI image (after 2-norm combination of the fast time images) are also well preserved. The difference maps after combination is presented in Fig. S11.

Fig. 4.

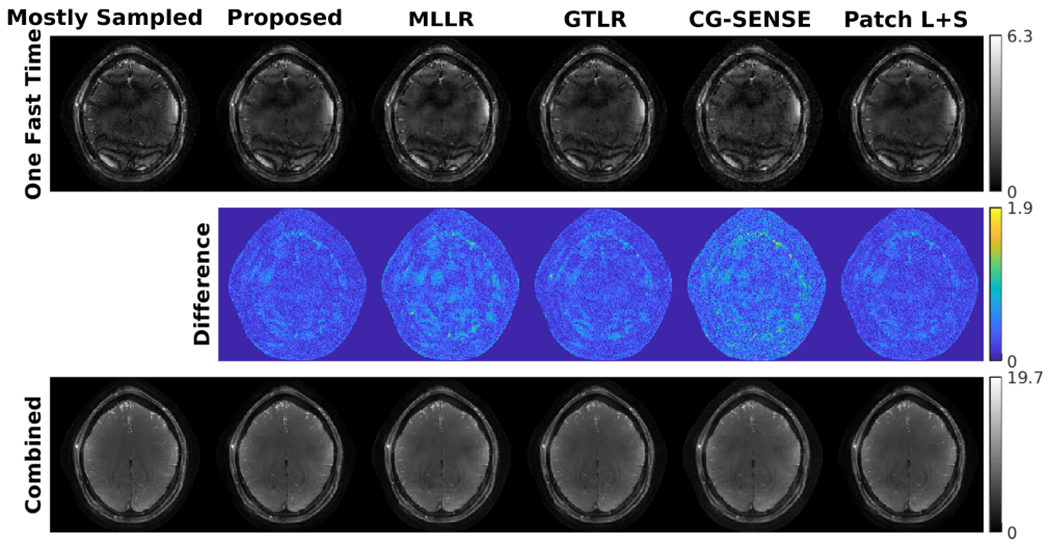
Fast time images from the retrospectively undersampled reconstructions are compared to the mostly sampled results. The proposed approach outperforms other methods with less noisy fast time images, less structure in the difference maps before combination, and high-resolution 2-norm combined images.

Figure 5 gives functional results including activation maps and tSNR maps. The proposed model enables high-resolution fMRI with larger activated regions than other undersampled reconstructions, and maintains the SNR advantage of OSSI with tSNR values that are comparable to the mostly sampled reconstruction. patch-tensor LR regularization and the patch-tensor L+S model present similar results, suggesting that L+S decomposition and Fourier sparsity along the two time dimensions were not critical given the patch-tensor modeling of the data.

Fig. 5.

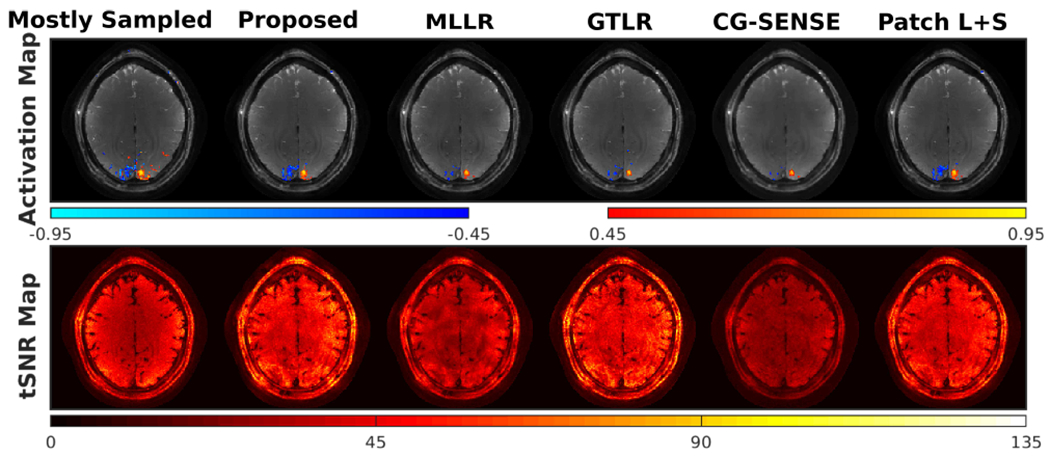
Activation maps and temporal SNR maps from retrospectively undersampled reconstructions. A contiguity (cluster-size) threshold of 2 was applied for the activated regions. The proposed model provides more functional activation than other approaches and a high temporal SNR, and shows similar results as the patch-tensor low-rank plus sparse model.

The quality of the retrospectively undersampled reconstructions was further assessed with ROC analysis. ROC curves for the activation maps of different reconstruction approaches were compared with mostly sampled activation at the lower third of the brain as ground truth. Figure S12 shows that the proposed approach leads to the largest area under the ROC curve.

Figure 6 presents prospectively undersampled reconstructions. Compared to OSSI regularized CG-SENSE reconstruction and standard GRE fMRI, the proposed approach yields more functional activity, less noisy time courses, and higher tSNR with the largely improved spatial and temporal resolutions. Other qualitative and quantitative comparisons for 2D prospectively undersampled reconstructions are in Fig. S15 and Table S1.

Fig. 6.

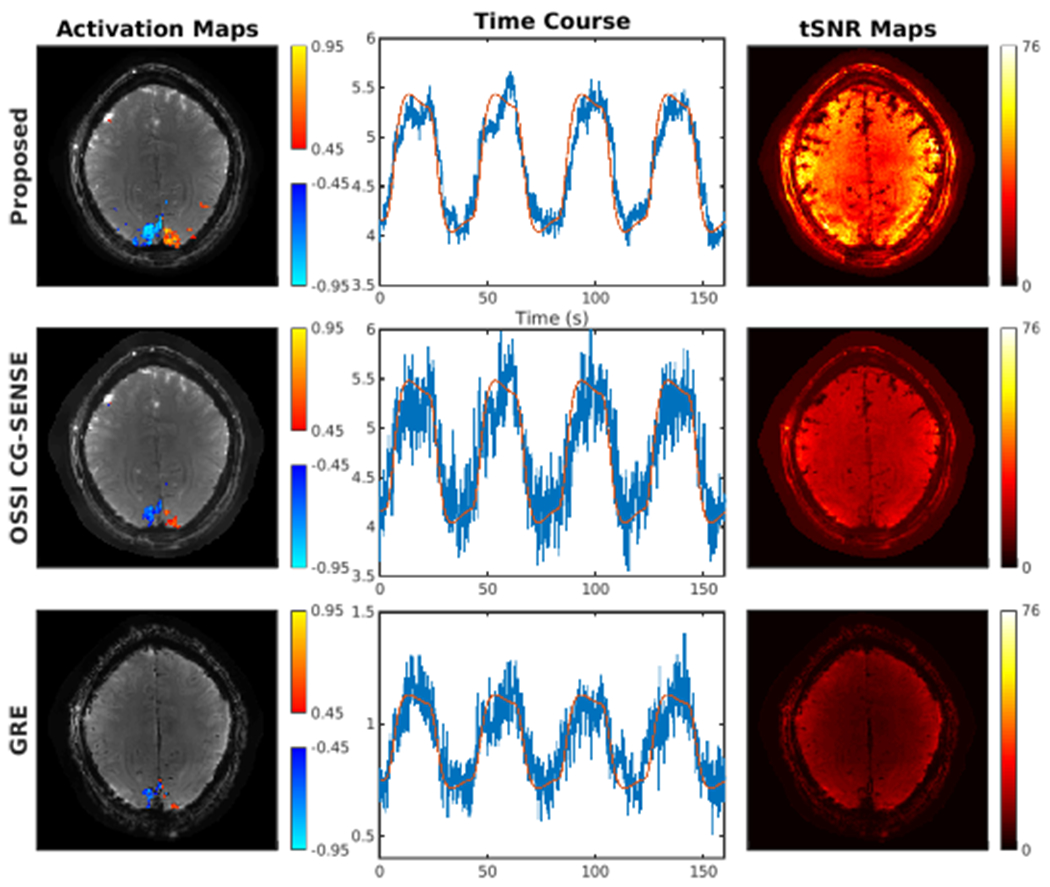
OSSI tensor model prospectively undersampled reconstruction demonstrating high-resolution and high SNR fMRI with high-resolution background and larger activated regions for the activation map, less noisy time course (red curve showing the reference waveform), and higher SNR for the temporal SNR map.

Table I summarizes quantities from different reconstructions including NRMSD for the whole dataset before and after fast time combination, number of activated voxels, and average tSNR within the brain. The proposed patch-tensor modeling outperforms other reconstruction methods with more functional activation and a high average tSNR.

TABLE I.

Quantitative comparisons of OSSI retrospectively undersampled reconstructions

	Mostly Sampled	Proposed	MLLR	GTLR	CG-SENSE	Patch L+S
NRMSD Before Comb	-	0.17	0.22	0.18	0.25	0.17
NRMSD After Comb	-	0.05	0.06	0.07	0.07	0.06
# Activated Voxels	229	168	73	68	46	153
Average tSNR	37.1	43.6	32.4	44.1	25.6	41.1

Reconstruction comparisons of a different subject are presented in Figs. S18, S19, S20, and Table S3 for retrospectively undersampled data, and Fig. S21 and Table S4 for prospectively undersampled data.

C. 3D OSSI to GRE Comparison

The 3D OSSI prospectively undersampled data were reconstructed using the proposed model with number of time points before combination = 120 for each non-overlapping time block. The patch-tensor size = 108 (6 * 6 * 3) × 10 × 12, and {λ_i} = [1 1 2]. Number of ADMM outer iterations S = 2, inner iterations T = 11, and number of CG iterations = 7 for every Z update. We used data-shared images to initialize each X_i and Z. The multi-slice GRE data were reconstructed with regularized CG-SENSE with 19 CG iterations for each slice.

Figure 7 shows the activation maps of 3D OSSI and multi-slice GRE. The proposed tensor model almost fully recovers the high-resolution structures of the OSSI images with a factor of 10 acquisition acceleration, and presents larger activated regions than multi-slice Ernst angle GRE.

Fig. 7.

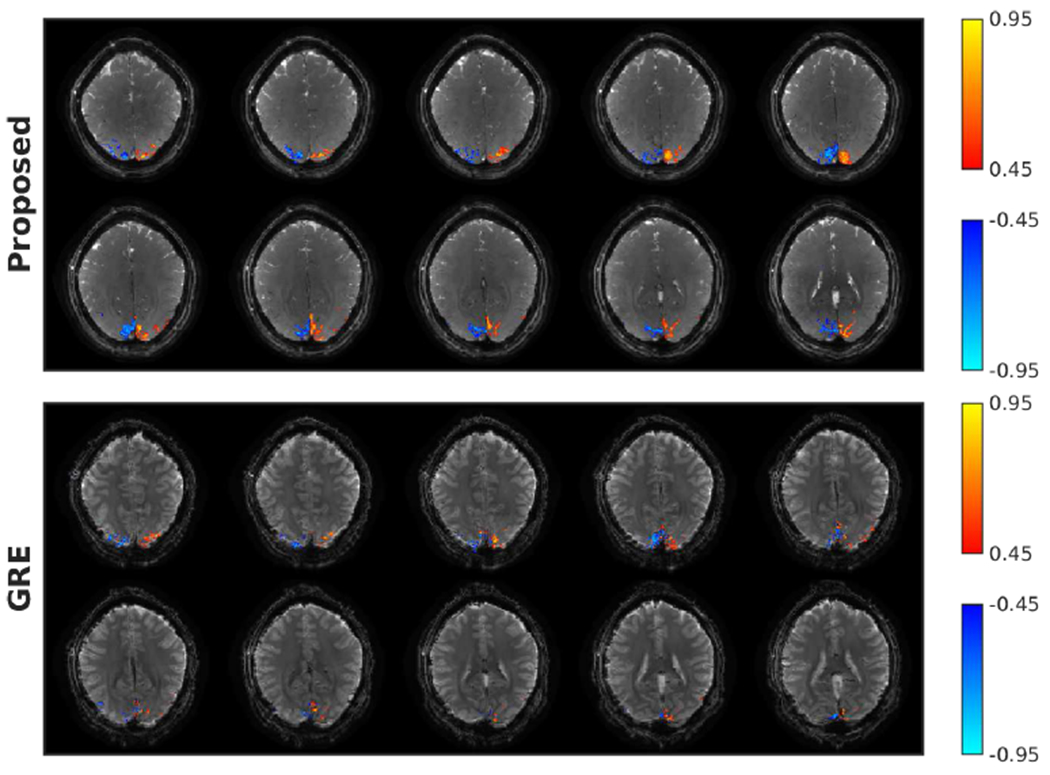
3D OSSI (prospectively undersampled) and GRE activation maps of the central 10 slices. A contiguity (cluster-size) threshold of 2 was applied for the activated regions. With matched spatial and temporal resolutions, 3D OSSI acquired and reconstructed using the proposed method presents 2 times more activated voxels compared to multi-slice Ernst angle GRE imaging at TE = 30 ms.

Figure 8 shows the 3D tSNR maps, where OSSI provides higher average tSNR than GRE. The OSSI acquisition combined with the proposed undersampling design and tensor model reconstruction enable high-resolution and high SNR fMRI.

Fig. 8.

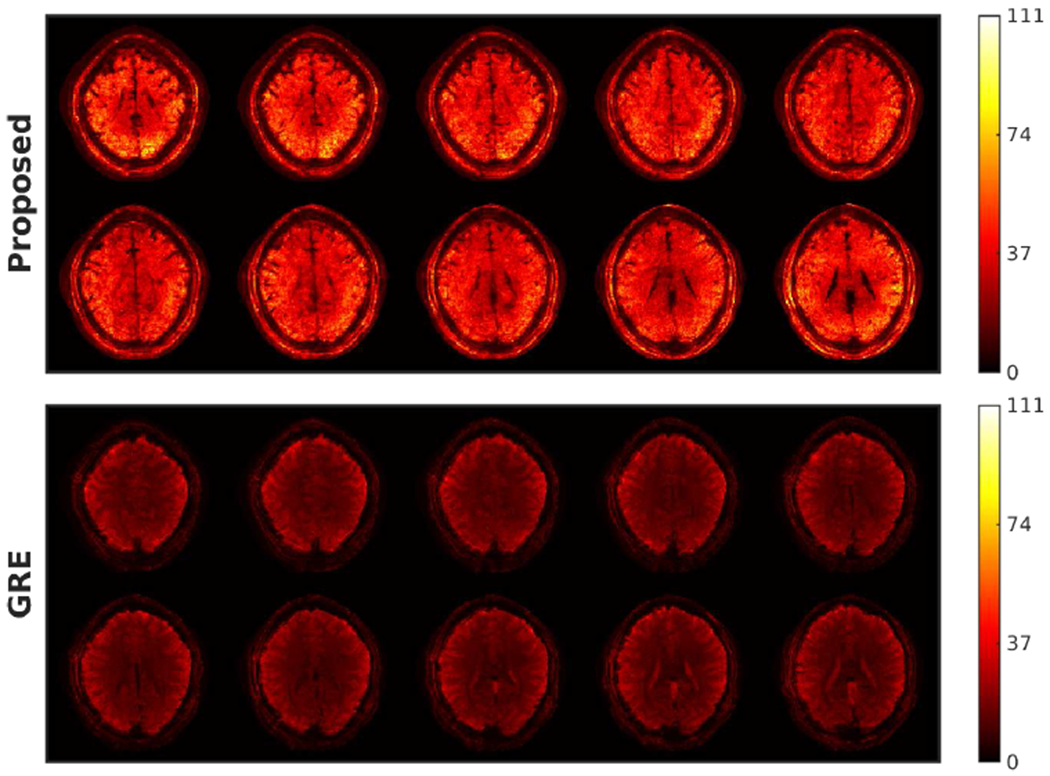
3D OSSI (prospectively undersampled) and GRE temporal SNR maps of the central 10 slices. At the same spatial-temporal resolution, 3D OSSI acquired and reconstructed using the proposed method presents at least 2 times higher temporal SNR than standard multi-slice GRE imaging.

Quantitatively as presented in Table II, the proposed 3D OSSI tensor reconstruction improves the amount of functional activity and average tSNR within the brain by a factor of 2 more than standard GRE imaging at matched spatial and temporal resolutions.

TABLE II.

Functional performances of proposed OSSI prospectively undersampled reconstruction and standard GRE imaging

	# Activated Voxels		Average tSNR
	2D	3D	2D	3D
OSSI	322	2150	32.8	34.7
GRE	83	947	9.8	15.9
Ratio	3.9	2.3	3.3	2.2

VI. Discussion

To our knowledge, the patch-tensor LR model is new for fMRI data. Reshaping and partitioning the data to patch-tensors facilitates exploiting high-dimensional structures, and considering all the unfoldings of the tensors better uses spatial-temporal low-rankness. Therefore, the model is flexible and adaptive to other high-dimensional image reconstruction problems that satisfy the patch-tensor LR constraints. Local models may be more valid than assuming low-rankness of the whole dataset.

Other reconstruction methods such as MLLR account for the locality of low-rank representations while treating the time dimension as a whole. GTLR separates the fast and slow time dimensions but enforces the low-rankness globally on the images. The proposed patch-tensor LR model combines the advantages of both methods by exploiting local low-rankness with two time dimensions, and improved the reconstruction and functional performances.

Another feature of the work is an incoherent sparse sampling scheme formed by properly rotating VD spirals along fast time and slow time. The angular dimension of the k-space can be mostly covered with different frames, and the trajectory is well accommodated with the spatial-temporal regularizers used here. Moreover, we noticed that for 3D undersampling, increasing number of interleaves in the central k_z planes greatly improves the amount of functional activation recovered and reduces false positives. The sampling pattern is practical, and the prospective undersampling is easy to implement.

We selected and vectorized patches of spatial size 8 × 8 (2D) or 6 × 6 × 3 (3D) based on the empirical reconstruction performance. The choice of spatial patch size is still an open question. At one extreme, the spatially global GTLR preserves little activation for 2D retrospectively undersampled reconstruction as presented in Fig. 5 and Table I, but performs similar to the proposed method for 2D prospective undersampling as in Fig. S15 and Table S1. In both cases, GTLR used temporal patches.

We investigated multi-scale low-rank decomposition [26] with multi-scale patch-tensors of the OSSI images to explore the idea that different parts of the data may have different density and different low-rankness; however, it provided limited performance improvement and made the reconstruction more time-consuming. We also tested a 4D patch-tensor LR model with two spatial dimensions and two temporal dimensions. The cost function is the same as (2) without vectorizing spatial dimensions in ${\mathcal{P}}_m$ . That model gave similar results as the 3D patch-tensor LR approach, making it well suited for potential applications such as GRE fMRI. The comparison results of the new models including functional maps, ROC curves, and quantitative evaluations are in Figs. S16, S17, and Table S2.

We imposed low-rankness on all the unfoldings of all the patch-tensors. However, some unfoldings of some patches are not very low-rank, especially for the second unfolding that is greatly affected by the nonlinear fast time oscillations. Therefore, nonlinear mapping approaches such as kernel methods or neural networks, that map the fast time data to a low-dimensional linear subspace [44], may further improve the model capacity, which might also help optimize combination of the OSSI fast time images instead of combing with 2-norm to yield band-free post-combined images. Because OSSI images are not very sparse in the Fourier domain, as shown in Figs. S3 and S4, the patch-tensor L+S reconstruction results in a very small sparse component seen in Fig. S14. Therefore, future work on adaptive sparsity [45] might be beneficial.

Because low-rank approaches might cause spatial-temporal smoothing that makes tSNR comparisons less compelling, we assessed and matched the amount of regularization for fast time image reconstructions based on their impulse responses. To evaluate spatial resolutions of the fMRI dynamics for different reconstructions after combination, we compared spatial autocorrelations of the different correlation maps (at the center of the brain without activation). Figure S13 demonstrates that the proposed approach has similar autocorrelation profiles as the mostly sampled reconstruction and preserves fMRI spatial resolution. We also compared ROC curves of different approaches with varying activation thresholds; these curves are invariant to the degrees of freedom for performance evaluation. The effective degrees of freedom calculation for the nonlinear reconstructions will be explored in the future as in [43].

The proposed sparse sampling uses fast VD spirals with designed rotations along the two time dimensions to increase sampling incoherence for the spatial-temporal models. However, the sampling incoherence from VD spirals is limited by the shape of the spiral, and the non-Cartesian nature requires NUFFT that needs more computation than FFT for Cartesian sampling. More importantly, designing the sampling pattern according to reconstruction models can improve the performance [46], [47], so we will further explore joint optimization of the sampling pattern and the reconstruction model.

VII. Conclusion

We proposed a novel fMRI reconstruction method based on patch-tensor low-rank for the oscillating nature of OSSI images. We also introduced an incoherent variable-density sampling pattern that is easy to implement, and retrospectively and prospectively undersampled the multi-coil data with less than 10% of the fully sampled k-space. By exploiting the inherent high-dimensional structure and local spatial-temporal low-rankness of OSSI images, the proposed model was able to recover high-resolution images and preserve functional signals compared to matrix local low-rank and tensor low-rank methods. It further enabled 3D high SNR fMRI with 2 times more functional activity and 2 times higher tSNR compared to standard GRE imaging.