Measuring Compressibility in the Optima AUC™ Analytical Ultracentrifuge

Abstract

A method is described to accurately measure the compressibility of liquids using an analytical ultracentrifuge. The method makes use of very large pressure gradients, which can be generated in the analytical ultracentrifuge at high speeds to induce a maximum compression signal. Taking advantage of the new Optima AUC, which offers 10 micron radial resolution, a novel calibration centerpiece for measuring rotor stretch, and a speed ramping procedure, even the weak compressibility of liquids like water, typically considered to be incompressible, could be detected. A model using the standard expression for the secant-average bulk modulus describing the relative compression of a liquid in the analytical ultracentrifuge is derived. The model is a function of the loading volume and the hydrostatic pressure generated in the analytical ultracentrifuge, as well as the secant-average bulk modulus. The compressibility of water and Toluene were measured and the linear secant-average bulk modulus and meniscus position were fitted. In addition to the measurement of the compressibility of liquids, applications for this method include an improved prediction of boundary conditions for multi-speed analytical ultracentrifugation experiments to better describe highly heterogeneous systems with analytical speed-ramping procedures, and the prediction of radius-dependent density variations.

Introduction:

Analytical ultracentrifugation (AUC) is a first-principle method for determining the hydrodynamic properties of macromolecules. Sedimentation velocity (SV) experiments are used to measure the partial concentration, the sedimentation coefficient, and the diffusion coefficient of each solute in a mixture. From the sedimentation and diffusion coefficients additional information can be derived, such as the frictional ratio, or anisotropy [¹], the molar mass, the partial specific volume, and the hydrodynamic radius [²]. The sedimentation and diffusion transport occurring in SV experiments is modeled by finite element solutions of the Lamm equation [^{3, 4}], using high resolution optimization approaches [1, ^{5, 6, 7, 8}]. Any error in the transport coefficients will propagate to errors in the calculations of molar mass, anisotropy and partial specific volume [⁹]. Errors in these observations result not only from measurement errors caused by the instrument [¹⁰], but also from errors in the boundary conditions used to solve the Lamm equation [^{11, 12}]. Measurement errors caused by the instrument can be mitigated by using appropriate calibration tools, and proper operation can be validated by implementing reliable reference standards [9, 10]. Boundary conditions for solutions of the Lamm equation include conservation of mass, as well as radial positions of the meniscus and the bottom of the AUC cell, and are affected by rotor stretch and imprecision in the radial position detection. In addition, the meniscus position is affected by compressibility of the solvent; as rotor speed increases, so does the hydrostatic pressure, causing an outward displacement of the meniscus position. For multi-speed experiments, each rotor speed will result in a different meniscus position, as the rotor stretches and the solution column compresses. A challenge arises from the fact that the simulation of each speed step requires precise simulation of the previous speed step in order to arrive at the appropriate concentration distribution in the AUC cell at each radial point and time point in the multi-speed experiment. This means that the boundary conditions of each speed step always differ, but must match the experimental data collected at each step. This is only possible if both the rotor stretch and the compression of the solution column are correctly considered for each speed. For a multi-speed experiment, fitting of the last speed requires accurate simulation of all previous speed steps, which can only be done if the previous speed steps are known, and their boundary conditions, acceleration rates, rotor speeds, and durations can be properly simulated. Proper consideration of these variables will increase the reproducibility and remove significant systematic errors that would otherwise be observed when fitting multi-speed experiments [11]. For quality control applications employing AUC in the biopharma environment, where Good Manufacturing Practices (GMP) must be followed, appropriate corrections for systematic errors are essential to achieve GMP validation. Previous studies have shown that errors in the modelling of sedimentation experiments that result from compressibility of aqueous solvents can lead to the underestimation of sedimentation coefficients by ~1 % at speeds below 45 000 rpm. This underestimation increases by 2 – 5 % with increasing rotor speed [¹³]. To aid in the proper calibration, a calibration centerpiece for the analytical ultracentrifuge was developed, and used to determine rotor stretching profiles in the AUC. Measurements on multiple rotors indicated that the rotor stretch from titanium AUC rotors contributes a translocation of the boundary conditions of up to 305 microns at maximum speed [9]. In this work the contributions of compressibility are considered, and a theory is developed to predict the magnitude of this effect for AUC sedimentation velocity experiments.

Theory:

Compressibility is a fluid property related to the bulk modulus, denoted by K₀, reflecting the value of the bulk modulus at ambient pressure. The bulk modulus is a measure of a material's resistance to compression, and is an inherent property of all liquid and solid materials. The bulk modulus changes as a function of pressure, which can be measured in an analytical ultracentrifuge. In response to external pressure, a liquid will compress, which leads to a change in volume. If the force varies across a solution column, the solution will develop a density gradient. In the analytical ultracentrifuge, the force changes along the radial axis as a function of column height and distance from the rotor center. The centrifugal force is given by ω²r, where r is the distance from the rotor center, and ω is the angular velocity. At 60,000 rpm, the maximum speed possible in the Optima AUC, the observed force equals 262,000 g at 6.5 cm (the cell’s center), and 290,000 g at 7.2 cm (the cell’s bottom). Hence, the observed volume change is a function of the solvent’s bulk modulus, the height of the solution column, and the rotor speed. An expression can be derived that predicts the observed volume change in an analytical ultracentrifuge cell. This volume change can then be fitted to data collected in an analytical ultracentrifuge. Typically, a fluid is considered to be incompressible because it already is in a compressed state. However, since the AUC can generate forces approaching 300,000 g when running at its highest speed, the compression of liquids, in particular those of low density, can be observed. The consideration of solvent compressibility is relevant to both organic solvents and aqueous solutions. Since hydrodynamic modelling of sedimentation velocity experiments by whole boundary methods requires precise boundary conditions, a quantitative approach that takes into account solvent compressibility is required. Experimentally, in a multi-speed experiment the shift of the meniscus position of the solution column in an AUC analytical cell can be used as a marker of this effect. The standard deviation of repeat measurements of the meniscus position at a single speed is typically less than the magnitude of the radial resolution of the Optima AUC instrument, which is 0.001 cm. In addition to the change in volume due to compressibility, the observed meniscus position also shifts due to the stretching of the rotor. In order to predict a correct meniscus position, it is therefore necessary to model both effects. As described earlier [9], the shift in the radial position due to rotor stretch can be reliably modelled by a second order polynomial (Equation 1):

$$r_s=r_0+s_1(rpm)+s_2(rpm{)}^{2}Equation$$ Equation 1

where r_s is the shift in radial position due to rotor stretch, and s_i are the first and second order stretch coefficients. The change of the volume as a function of pressure and the compressibility of the solvent can be described by a simple linear-secant modulus equation, as given in Equation 2 [14]. For most liquids, and within the pressures observed in the ultracentrifuge, a linear approximation explains the change in bulk modulus well as a function of pressure:

$$V=V_0\frac{K_{sa}-P}{K_{sa}}Equation$$ Equation 2

where V₀ is the volume at zero pressure, and V the observed volume at pressure P. K_sa is the secant-average bulk modulus of the liquid from ambient pressure to P. For the magnitudes of pressures generated in the analytical ultracentrifuge (typically less than 0.3 kbar, see Figure 1), this equation describes the compressibility of most liquids well enough using just the first order term shown here. Higher order P terms are required when pressures are significantly higher in other applications besides analytical ultracentrifugation [15]. The volume of the solution column in the sector-shaped compartment is given by:

$$V=(\frac{\theta }{360})\pi h(r_b^2-r_m^2)Equation$$ Equation 3

where h is the height, or pathlength of the centerpiece, θ is the angle of the sector (θ=2.5 degrees for a standard Beckman epon 2-channel centerpiece), r_b is the radius at the bottom of the cell, and r_m is the radius of the meniscus. Since the dimensions of the centerpiece do not change as a function of rotor speed, and the absolute position of the centerpiece merely gets shifted, it is important to note that both the bottom of the cell and the meniscus position need to be corrected for the rotor stretch, which amounts to subtracting r_s (see Equation 1), before the volume change is calculated, leading to the rotor-stretch corrected volume, V_c:

$$V_c=(\frac{\theta }{360})\pi h((r_b-r_s{)}^2-(r_m-r_s{)}^2)Equation$$ Equation 4

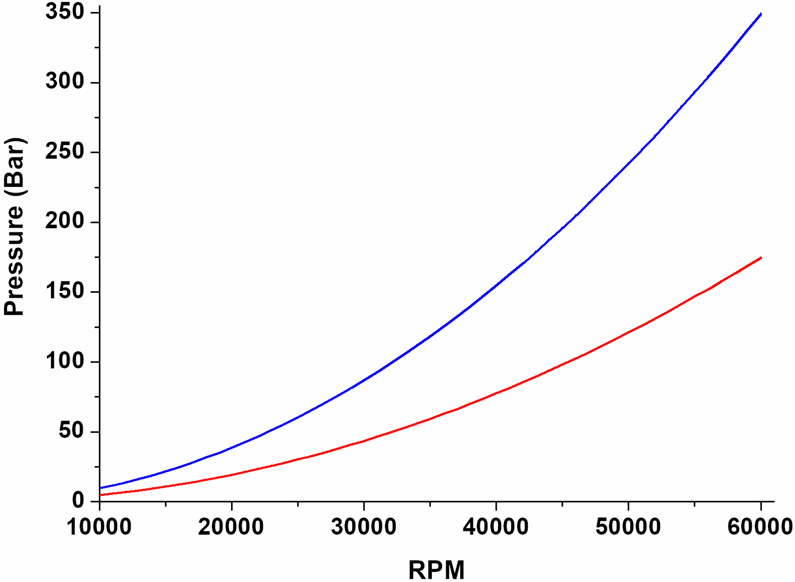
Figure 1:

Plot of the pressures in bar generated inside the analytical ultracentrifugation cell as a function of rotor speed in a water sample with a meniscus at 5.8270 cm and cell bottom at 7.1897 cm. The average pressure (red line) is obtained by integrating the pressure along the radial dimension, and maximum pressure (blue line), observed at the bottom of the cell’s solution column. Since the pressure changes as a function of radial distance as well, a different average bulk modulus will be determined for the same substance as the column height varies between experiments.

The pressure at a given radius r can be expressed by the well-known formula expressed in Equation 5 [13].

$$p(r)=\rho {\omega }^2(r^2-r_m^2)∕2$$

Where ρ is the density of the liquid. During an experiment, the volume above a radius r also compresses, changing the total volume and the meniscus r_m. This can be simulated numerically by discretizing the volume, and iteratively solving Equation 3 to determine a radius for each volume element, applying Equation 5 to determine the pressure, applying Equation 2 to determine the volume, and finally updating the meniscus from the new total volume for the next iteration. Convergence is reached when the meniscus position for the compressed solution column does not change on the next iteration (practically, within a specified tolerance). Given experimental conditions (such as rotor speeds and rotor stretch coefficients) and an initial volume V₀ and the secant-average bulk modulus K_sa, the compression can be simulated as described above and compared with experimental data. To find the best fitting compressed volume and bulk modulus, a search algorithm is used. Our current implementation utilizes a bisection method iteratively and alternatively on V₀ and K_sa to find a best fit to the experimental data. A nonlinear least squares gradient search method could also be used and may converge faster. A routine to accomplish this task will be included in UltraScan [¹⁶]. It is important to recall that the bulk modulus for a particular liquid varies as a function of pressure, and therefore it is not constant across the radial range of the solution column in the AUC (see Figure 1). Hence, only the secant-average bulk modulus can be directly observed when measuring changes of volume by monitoring the change in the meniscus position in the ultracentrifuge. This effect is noticeable when datasets with different column heights are compared (see Figure 2). Since the average pressure observed in a particular cell is also a function of the solution column length, it explains that different average bulk moduli can be observed when the loading volume varies from cell to cell.

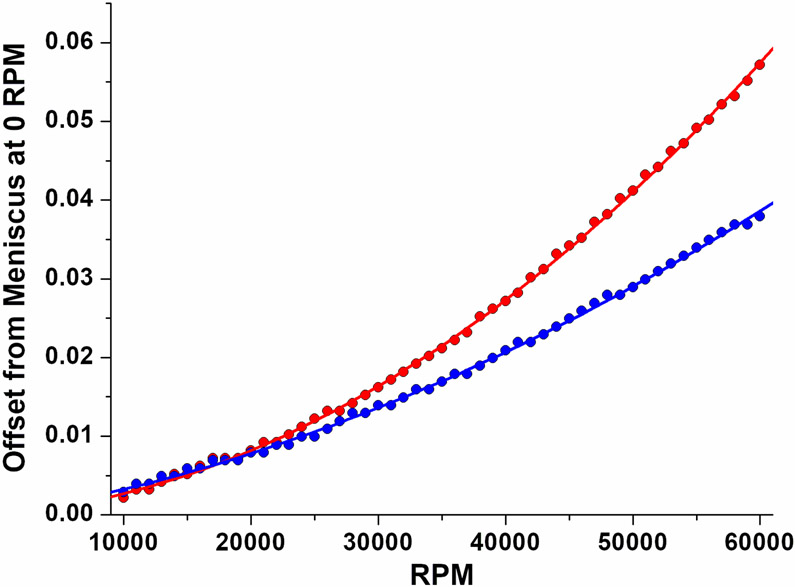
Figure 2:

Comparison of solvent compression as a function of column height. Displacements shown have had their fitted meniscus position at zero speed subtracted for easier comparison. Data shown are for Toluene with a meniscus position of 5.928 (red) and 6.052 (blue). A longer column (larger V₀) results in a steeper curvature due to higher average hydrostatic pressure (also see Figure 1), resulting in a different secant-average bulk modulus.

Materials and Methods:

All experiments were performed using the Beckman Coulter Optima AUC™ at the Canadian Center for Hydrodynamics (CCH) at the University of Lethbridge, Alberta, Canada. All measurements were performed in the AN60Ti rotor, capable of a maximum speed of 60,000 rpm. Experiments were performed in 12 mm epon charcoal centerpieces (Beckman Coulter, Indianapolis, USA), using sapphire windows. Approximately 0.46 ml of each solution was loaded into each sector, the maximum amount of volume that can be filled into a 12-mm standard double sector centerpiece, while still being able to observe a meniscus. By filling both sectors of the cell, two samples per cell can be measured. All scans were collected on a Beckman-Coulter Optima AUC using UV/visible optics, operated in intensity mode, and collecting data in the visible range at 410 nm, which maximizes the peak of the meniscus signal for both water and Toluene. Previously reported density and K₀ bulk modulus are shown in Table 1.

Table 1:

Properties of water and Toluene at 20° Celsius.

Solution	Density (g/cm3)	Bulk Modulus (K0, 1x109 N/m2)	Reference
Water	0.998234	2.17	17, 18, 19
Toluene	0.87	0.89	20

The rotor speed was started at 3,000 rpm and changed to 60,000 rpm, over 58 steps of 1,000 rpm increases. The radial scanning interval was set to 0.001 cm, the AUC's maximum resolution, taking at least 5 scans for each speed after waiting for 15 minutes to ensure rotor stretch equilibration at each speed. To test the reversibility of the observed volume change after reaching 60,000 rpm, a reverse measurement was immediately performed, where the speed was reduced in 58 increments of 1,000 rpm to 3,000 rpm. To determine the rotor stretch coefficients, a calibration centerpiece can be measured prior to or during the experiment to determine the rotor stretch coefficients (see Equation 1) as described in [9]. The rotor stretch was subtracted from the experimental data before analyzing the bulk modulus and volume of each sample (Figure 3). All experiments were performed at 20°C, and for all calculations a density of 0.998234 g/ml was assumed for pure water, and 0.87 g/ml for Toluene. The cell bottom was measured by scanning a centerpiece on a high resolution flatbed scanner (3,200 DPI), assuming a 6.5 cm center at rest, and using Euclidian geometry to measure the cell bottom position (7.1897 cm).

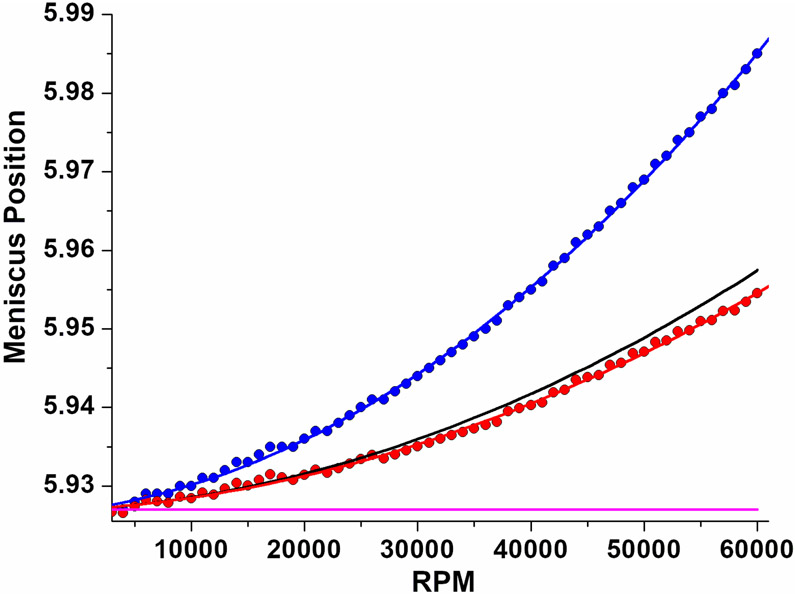
Figure 3:

Rotor stretch correction of compressibility data: All measurements (Toluene, blue) are convoluted with the rotor stretch (black line) which needs to be subtracted first to interpret the effect of compressibility to obtain a rotor stretch corrected dataset (red). For easier comparison, the rotor stretch function is offset by the meniscus position at zero RPM for this dataset (magenta line).

Results:

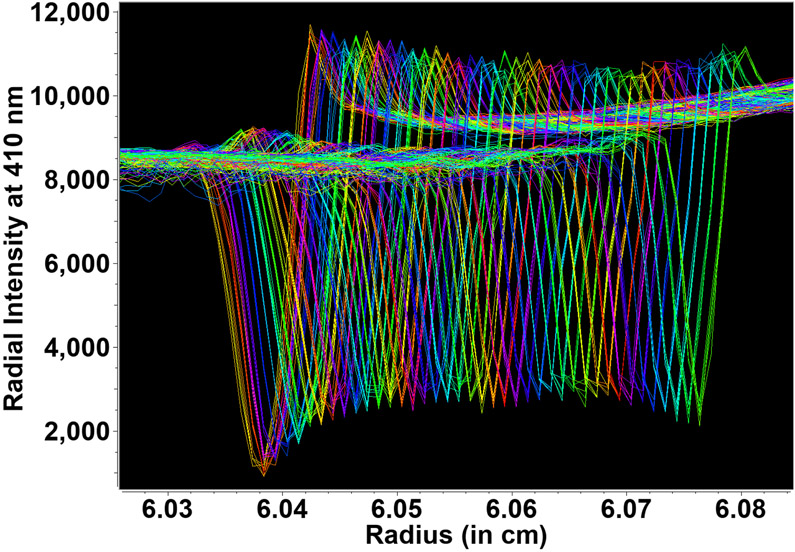
The recorded meniscus positions displayed a characteristic shift of the meniscus as a function of rotor speed, reproducibly showing the same minimum near the meniscus for scans performed at the same speed (see Figure 4). A routine was developed in UltraScan [16] which averages the minima from each scan shown in Figure 4 and reports the minimum positions at each speed. As can be seen in the zoom of the meniscus region in Figure 4, individual scans at each speed are highly reproducible in reporting the same meniscus position, an indicator for the robustness of this approach when using the Optima AUC. The older Beckman Proteomelab models have a lower resolution (0.003 cm) and are far less reproducible in their radial observations because they are not equipped with digital stepping motors, and are likely not sufficiently reliable for this approach. Our results showed that meniscus displacements below 10,000 rpm were either too small to be measured or not reproducible enough to be included in our fitted data. Hence, we included data between 10,000-60,000 rpm only in our fits. A plot of the observed speed-dependent meniscus positions for multiple samples of Toluene and water with different loading volumes are shown in Figure 5. A comparison of the forward and reverse speed direction revealed minimal, but measurable differences, leading to slightly different values of V₀ that consistently tended to be lower for the reverse direction (see Figure 6). One possible explanation could be evaporation or micro-leakage, but the effect was smaller for Toluene (0.5 μm) than for water (24.9 and 22.4 μm), even though Toluene has a higher vapor pressure (22 mm Hg for Toluene vs. 17.54 mm Hg for water), suggesting that evaporation is unlikely the cause. Furthermore, the curvature of the plot for the observed meniscus position as a function of rotor speed increased slightly, suggesting that the bulk modulus also would change. This change was consistently observed across all samples. As expected, the analysis of the rotor-stretch corrected data by the method described above provided a lower secant-average bulk modulus for both solvents (see Table 1) as a result of the expected change in the pressure when compared to the K₀ value. To emphasize the linearity of our observations, we plotted the rotor-stretch corrected data against the square of the rotor speed, resulting in linear plots. An example of the two-dimensional fit of the volume and secant-average bulk modulus for the forward and reverse speed stepping of water and Toluene is shown in Figure 7. The fitted values for the secant-average bulk modulus, the meniscus position, and the volume at zero speed for all datasets are listed in Table 2.

Figure 4:

Meniscus positions of Toluene measured in the analytical ultracentrifuge in intensity mode at rotor speeds from 10,000 rpm (orange, left) – 60,000 rpm (green, right). A shift to the right is clearly visible, with slightly increasing spacing, corresponding to the quadratic increase in rotor force and the solution compressibility.

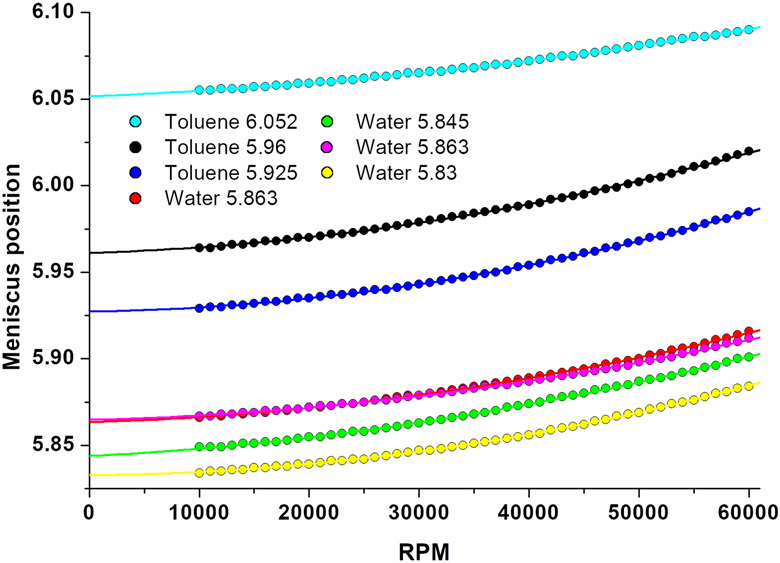
Figure 5:

Representative meniscus positions measured from the forward-speed experiments with Toluene and water samples as a function of speed from 10,000 rpm – 60,000 rpm (filled circles). The numbers in the legend indicate the meniscus positions observed at 3,000 rpm, a second order polynomial fit is shown for each data set that is extrapolated to the predicted meniscus position at zero rpm (solid lines). A slight increase in the curvature is apparent with increasing column length due to the increase in pressure (also see Figure 1 and Figure 2).

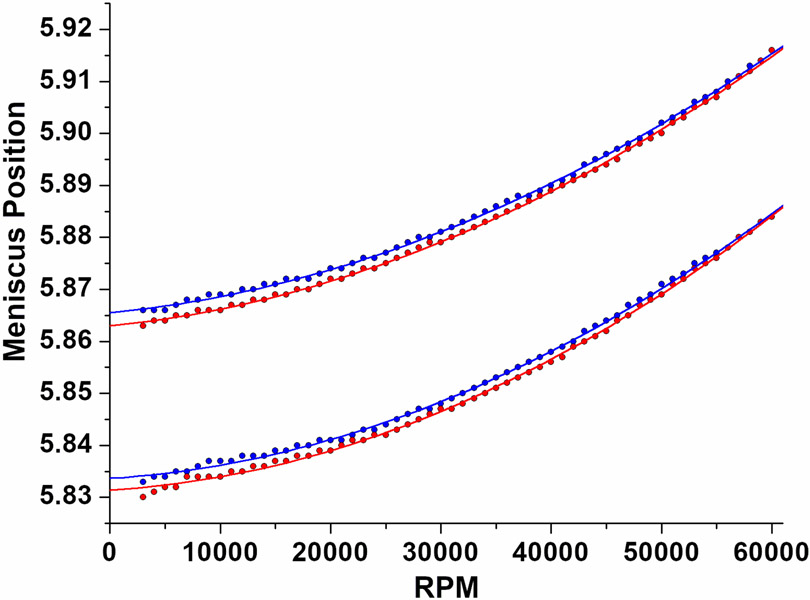
Figure 6:

Comparison of the compressibility of water between the forward (red) and reverse (blue) speed direction experiments. Consistently, a shorter solution column is observed in the reverse speed direction, leading to a slightly larger meniscus position.

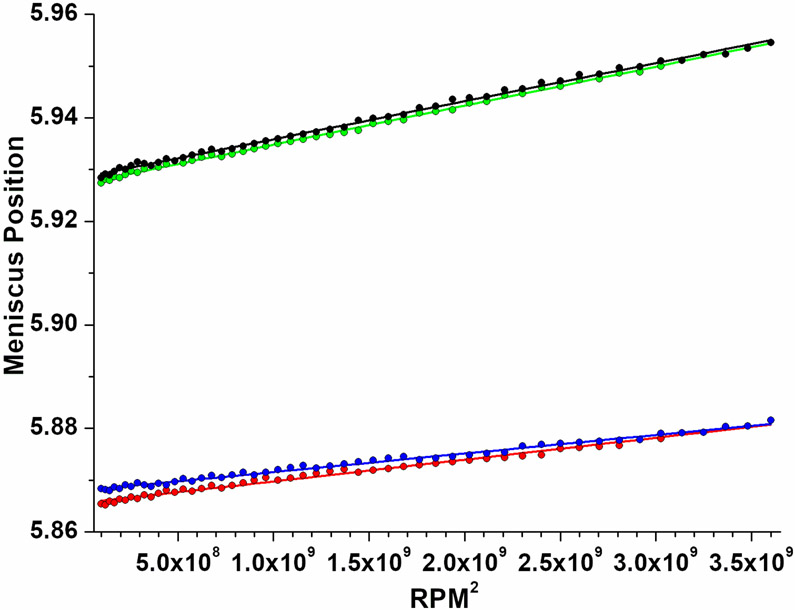
Figure 7:

Two-dimensional fits for volume and secant-average bulk modulus of Toluene (green: forward speed, black: reverse speed) and water (red: forward speed, blue: reverse speed). Rotor stretch was subtracted before the fit. When plotted against the square of the rotor speed the data exhibit linear characteristics. The slope is proportional to the bulk modulus, while the intercept at zero RPM indicates the fitted meniscus position and volume of the cell. Forward and reverse speed directions generate slight differences in fitted volume and bulk modulus as indicated by slightly different slopes and intercepts. The amount of observed change is larger for water than for Toluene (also compare Figure 6).

Table 2:

Compressibility measurements of water and Toluene at 20° Celsius for two experiments with different column lengths. Sample names refer to the position in the cell (1-4, cell 1B in the first experiment leaked), the channel (A or B), Toluene (T) or Water (W), and forward (F) or reverse (R) speed direction Sample names from experiment 2 are prefixed with (*).

Sample:	Ksa, N/m2 x 109	Bottom pressure (bar):	Volume (ml):	Meniscus (cm):	Δ Density g/cm3
1A (T, F)	0.719	278.396	0.422	5.964	0.016719
1A (T, R)	0.722	278.177	0.422	5.965	0.016625
2A (W, F)	1.26	342.343	0.453	5.866	0.013420
2A (W, R)	1.39	341.779	0.452	5.869	0.012125
2B (W, F)	1.06	346.383	0.458	5.849	0.016154
2B (W, R)	1.18	345.648	0.457	5.852	0.014422
3A (T, F)	0.735	285.661	0.434	5.929	0.016784
3A (T, R)	0.750	285.418	0.433	5.928	0.016416
3B (T, F)	2.40	259.464	0.340	6.055	0.004608
3B (T, R)	2.51	259.318	0.394	6.055	0.004386
4A (W, F)	1.66	342.188	0.453	5.867	0.010111
4A (W, R)	1.95	341.62	0.452	5.870	0.008584
4B (W, F)	1.22	349.927	0.463	5.834	0.014111
4B (W, R)	1.33	349.401	0.462	5.837	0.012962
*1A (W,F)	2.22	302.649	0.400	6.033	0.006856
*1A (W,R)	2.18	302.537	0.400	6.034	0.006976
*1B (T,F)	0.96	268.724	0.408	6.010	0.012355
*1B (T,R)	1.08	268.219	0.407	6.012	0.010921
*2A (W,F)	1.11	173.558	0.230	6.551	0.007876
*2A (W,R)	1.74	173.069	0.229	6.553	0.004986
*3A (W,F)	1.53	325.835	0.431	5.935	0.010766
*3A (W,R)	1.61	325.448	0.430	5.937	0.010206
*3B (T,F)	0.75	291.676	0.443	5.898	0.017372
*3B (T,R)	0.79	291.121	0.442	5.901	0.016245
*4A (W,F)	1.33	188.838	0.250	6.492	0.007116
*4A (W,R)	1.54	188.487	0.249	6.498	0.006146

Discussion:

We report here a novel use of the Beckman Optima analytical ultracentrifuge for the measurement of the compressibility of liquids. To quantify the compressibility, we report the measurement of the secant-average bulk modulus of liquids which can compare the compressibility of different liquids under identical conditions (same rotor speed variations, same column lengths, same temperature). The ultracentrifuge can generate sufficiently high pressures to cause liquids to compress to a degree that can be accurately measured thanks to the high radial resolution afforded by the latest generation of analytical ultracentrifugation instruments, the Beckman Optima AUC, which provides 0.001 cm radial resolution. As is shown in Figure 7, our two-dimensional fitting approach for secant-average bulk modulus and sample volume produces a linear correlation between meniscus position and the square of the rotor speed. From the results reported in Table 2 for multiple measurements with different loading volume, we observe the following trends:

1. As expected, Toluene consistently reports a lower bulk modulus than water, indicating stronger compressibility than water.

2. There is a small reduction in volume for the reverse direction visible for all samples, suggesting a consistent change in the sample. The observed change appears to be more significant for water. We did not find an explanation for this observation.

3. A longer solution column provides better signal on the compressibility, as stronger pressures are generated, causing more compression. This increase in pressure consistently leads to an increase in the secant average bulk modulus.

4. Short sample columns (meniscus position at ~6.5 cm or less) produced very little hydrostatic pressure such that compression was barely detectable (samples *2A, *2B, *4A, *4B, therefore samples *2B and *4B are not shown in Table 2). We therefore recommend to measure compressibility only in long column experiments to maximize the pressure.

5. Our model predicts the expected pressure variation across the solution column and calculates a secant average bulk modulus over the entire column, reflecting changes in the compressibility of the type of liquid under investigation, rotor speed, and the column height.

6. The outlined approach will accurately model the compression of the solution column, and provide reliable boundary conditions for the simulation of multi-speed sedimentation velocity experiments.

7. Our model reports the density variation as a function of radius, which can be used to more accurately model the solvent density corrections for s_20,W values observed at different positions in the cell. The density change between ambient conditions and 60,000 rpm at the bottom of the solution column are approximately 1.9% for Toluene and 1.3% for water.

We propose that the compressibility of solvents employed in multi-speed experiments could be characterized by measuring them with different loading volumes, using the described approach to determine their secant-average bulk modulus as a function of column height. The obtained correlation between secant-average bulk modulus and the loading volume can be fit to an interpolating function to provide K_sa for any V₀ of interest, predicting the expected meniscus offset from the theoretical meniscus at rest under ambient conditions for any speed and any loading volume. However, as mentioned above, a limitation is presented when columns are too short to generate sufficient signal. This offset must be added to the offset from the rotor stretch function to arrive at the correct meniscus position for any speed. These offset values, in turn, will provide accurate boundary conditions for fitting multi-speed sedimentation velocity experiments to finite element solutions of the Lamm equation. Furthermore, if the density increment for each radial position predicted by our model is large enough to cause a measurable difference in sedimentation speed between ambient conditions and at the bottom of the cell, finite volume modules could be used to model the local effect of increased density towards the bottom of the cell. To determine if compressibility of a particular solvent is sufficiently large to require correction of boundary conditions, in addition to correction of rotor stretch, for multi-speed experiments, a plot similar to the one shown in Figure 3 should be constructed, using data that replicates the column height of the desired experiment. Results will depend on the compressibility of the solvent, the maximum rotor speed, and the column height. If the predicted maximum meniscus displacement is less than two-fold the radial resolution of the instrument (0.001 cm for the Optima AUC absorption optics, 0.003 cm for the Proteomelab XLA), it is likely unnecessary to account for compression.