Abstract
The availability of intensive care beds during the COVID‐19 epidemic is crucial to guarantee the best possible treatment to severely affected patients. In this work we show a simple strategy for short‐term prediction of COVID‐19 intensive care unit (ICU) beds, that has proved very effective during the Italian outbreak in February to May 2020. Our approach is based on an optimal ensemble of two simple methods: a generalized linear mixed regression model, which pools information over different areas, and an area‐specific nonstationary integer autoregressive methodology. Optimal weights are estimated using a leave‐last‐out rationale. The approach has been set up and validated during the first epidemic wave in Italy. A report of its performance for predicting ICU occupancy at regional level is included.
Keywords: clustered data, COVID‐19, generalized linear mixed model, integer autoregressive, integer autoregressive model, panel data, SARS‐CoV‐2, weighted ensemble
1. INTRODUCTION
Italy has been under pressure to properly manage the recent COVID‐19 epidemic emerged from China in December 2019. Its quick spread required a global response to prepare health systems worldwide. In its present form, COVID‐19 seems to have very challenging characteristics (see, e.g., Del Sole et al., 2020; Girardi et al., 2020; Peeri et al., 2020): it is highly infectious and, despite having a benign course in the vast majority of patients, it requires hospital admission and even intensive care for a far from negligible proportion of infected.
In Italy, particularly in the two regions of Lombardia and Veneto, the COVID‐19 infection emerged in February 2020 with a basic reproductive number between 3 and 4 (Flaxman et al., 2020). At the beginning of the coronavirus outbreak, Italy was one of the countries with the lowest amount of acute care beds per person in Europe. The resources of the national health system were not designed to face a large‐scale epidemic. The national health system was equipped with a total number of approximately 5200 beds, that was substantially increased very quickly during the spread of the disease (Remuzzi & Remuzzi, 2020). This reversed a trend that started years ago, especially after financial crises, according to which resources allocated to the national health system were progressively cut.
In general, intensive care units (ICUs) are characterized by a rather low number of beds with high turnover. Most of the patients stay in intensive care only for one or few days (Diekmann, Heesterbeek, & Britton, 2013), even if some of them can stay months. However, ICU length of stay (LOS) due to COVID‐19 infection was rather long: a recent study (Grasselli et al., 2020a) involving 1591 patients admitted in ICUs in Lombardia reported a median LOS of nine days (6–13 [95% CI]). Long LOS implied a slower turnover, and increased the risk of collapse of the national ICU system. Indeed, in the absence of measures to flatten the epidemic curve, the number of ICU beds available in Italy would have achieved very quickly 100% occupation, leaving several thousand patients short of the cures needed (see also Remuzzi & Remuzzi, 2020, for a discussion).
It is now clear that measures like social distancing, use of masks, contact tracing, and a wide access to diagnostic testing coupled with isolation of positives can be very effective. Nevertheless, careful and reliable planning of resources can also aid substantially in controlling the consequences of the epidemics, and likely increase the likelihood of early diagnoses and better care. To respond to the looming threat of shortage of ICU beds, hospitals urgently need to establish and implement policies that more fairly allocate these scarce resources. If hospitals can plan in advance how many ICU beds shall be made available for the nearly following days, capacity can be increased (or decreased) to match the demand. This would avoid the ethical dilemma of severe triaging patients and not admitting those whose lives are not worth saving (White & Lo, 2020). In this work, we propose one statistical tool of this sort, which can be used to accurately forecast the ICU occupation for the next one to five days. Beds demand in intensive care depends on two factors: the number of COVID‐19 patients needing intensive care and duration of their hospitalization. Unfortunately, these data are not made available during the Italian outbreak. Public data include, anyway, daily ICU occupation by region, which we use as a proof of concept.
Existing approaches to forecast ICU occupancy are mainly based on exponential models fitted to daily numbers of occupied critical care beds out of confirmed cases (Grasselli, Pesenti, & Cecconi, 2020b; Sebastiani, Massa, & Riboli, 2020) or on SIR (susceptible, infectious, recovered) models (Giordano et al., 2020). Both approaches are subject to certain limitations in our opinion. An obvious limitation of the former approach includes ascertainment bias due to the use of counts of confirmed cases, and inappropriate modeling assumptions (including, for instance, a Gaussian assumption for log‐counts). A model of the SIR family may on the other hand be a very appropriate option. However, SIR‐based models require the possibility to precisely estimate several characteristics of the epidemics, which are still mostly unknown, and it is well known that changing even slightly the initial conditions can lead to very different results. This is even more difficult as the exposed population is only partially observed (Böhning, Rocchetti, Maruotti, & Holling, 2020; Chen, Lu, & Chang, 2020; Yue, Clapham, & Cook, 2020).
Our approach is based on optimally combining two forecasting methods. The first is based on Poisson mixed effects regression; the second one is a region‐specific time‐series model for counts, taking into account time dependence over time. The count outcome is appropriately modeled as a Poisson conditionally on observed time trends and unobserved heterogeneity including dependence, as implied by random effects or by the auto‐regressive structure of the time‐series models, and the averaged predictions give an optimal balance between pooling information over different areas (which targets a low variance prediction) and adaptation at the specific area (which targets a low bias prediction).
The rest of the paper is as follows: in the next section, we give a description of the available data. In Section 3, we describe our method for prediction of the next‐day ICU occupancy. We mention here that we have validated our method during the outbreak, by repeatedly producing ICU predictions with the current data, and waiting for the official data for the next five days. An illustration of the performance of our approach is given in Section 4. Some concluding remarks are in Section 5.
2. DATA
On January 31, 2020, the Italian Government declared the state of emergency for six months as a consequence of the health risk associated with COVID‐19 infection.
To inform citizens and make the collected data available, the Department of Civil Protection developed an interactive geographic dashboard (accessible at the addresses http://arcg.is/C1unv (desktop) and http://arcg.is/081a51 (mobile)) and built a daily updated data github‐repository (CC‐BY‐4.0 license), with a large number of variables; among them the intensive care defined as number of hospitalized patients in ICUs available at the regional level (20 Italian regions). In Figure 1, the regional time series of ICU admissions from February 24 until April 16, 2020, are reported and it appears that several sources of heterogeneity affect the data. The epidemic started at different times across regions, starting from the North of the country and evolved very differently in each region, leading to trajectories of different shapes. Population size is also very different across Italian regions (Figure 2), which are also characterized by different economic and social structures. Moreover, a further heterogeneity source relates to the ICU capacity. In Italy, the health system is regional based, so in practice there are 20 different health systems and management choices, local authorities and local policy makers play a fundamental role in the definition of health services capacities, with very few national directives.
FIGURE 1.
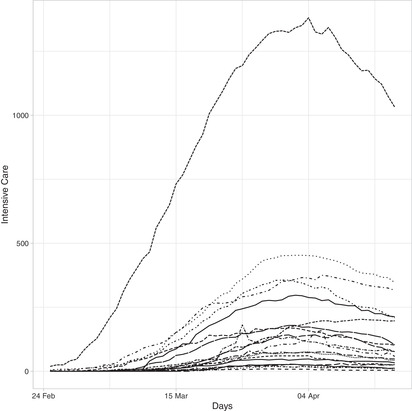
Regional time series of ICU admission from February 24, 2020, until April 16, 2020. Notice some of the regional evolutions: dashed (highest) line, Lombardia; dotted line, Piemonte; longdash‐dotted, Emilia Romagna; dash‐dotted line, Veneto
FIGURE 2.
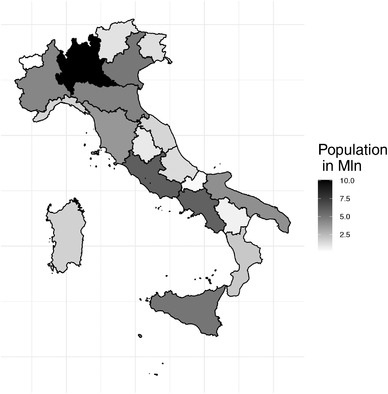
Italian regional population size. Notice the most populated region Lombardia with about 10 million inhabitants (black), followed by Lazio and Campania with 5.8 million inhabitants (dark gray), and to below one million inhabitants regions Umbria (882,015), Basilicata (562,869), Molise (305,617), and Valle D'Aosta (125,666) (white)
During the epidemic some of the northern regions went beyond the capacity of the local system. Figure 3 reports the regional rate of occupancy (occupancy over capacity1) during the epidemic. Regions are ordered geographically from North to South showing the North–South gradient of the epidemic evolution mostly affecting the northern regions. It is rather clear that the health systems of northern regions were under pressure for a longer period and this reflects the difference in the spread of the epidemic. A regional model that takes into account different sources of heterogeneity and the different timing in the spread of the epidemic is thus required.
FIGURE 3.
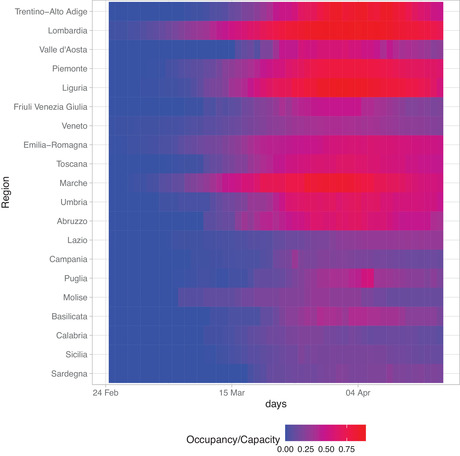
ICU rate of occupancy during the COVID‐19 epidemic in the Italian regions. Regions are ordered geographically from North to South
3. METHODS
In order to produce accurate forecasts we combined two methods, one based on joint modeling all regions through a mixed‐effects generalized linear regression model, and the other one based on separately modeling each region as a nonstationary time series of counts, which uses an integer‐valued autoregression specification, with covariates. The first approach pools information over regions, reducing variance of the final prediction; the second instead can be expected to have a lower bias due to the fact that each time series is modeled separately, hence more parameters are used. The final predictions are then averaged with weights chosen through a leave‐last‐out method. Furthermore, in order to focus more on the recent trends, we always set , that is, we use the last two weeks of data to make predictions and ignore previous measurements.
3.1. Random effects modeling of longitudinal count data
We start assuming that the observed daily ICU admissions for region at day , , are realizations of independent Poisson random variables with parameter , . The interest is in modeling as a nonlinear function of time, taking into account unobserved heterogeneity and region‐specific effects. A simple way to deal with these features is through a generalized linear mixed model (GLMM) (Breslow & Clayton, 1993) with linear predictor
| (1) |
where a canonical link has been adopted, the offset term accounts for different population exposures, represents the vector of shared fixed‐effects regression parameters, and represents the random coefficients, that is, the region‐specific intercept and slopes, with
The observed counts are assumed independent given the three‐dimensional random vector . The likelihood function is obtained integrating out the in (2)
| (2) |
Various alternative parametric specifications have been proposed for the random terms; but only in the case of log‐gamma distributed additive random effects the above integral has an analytical solution, leading to the well‐known negative binomial model. In all other cases, the integral in (2) has no analytical solution, and approximate methods should be used in order to estimate the parameters and . Here, a Laplace approximation has been used first of all to speed up computations. Adaptive Gaussian quadrature may represent a slightly more accurate option, at the expense of a higher computational burden. Indeed, an important disadvantage of this approach lies in the required computational effort, which is exponentially increasing with the dimension of the random parameter vector. Other alternatives are based on series expansion of the random effects distribution as in Gurmu and Elder (2000) or the hierarchical likelihood approach introduced by Lee, Nelder, and Pawitan (2017). Cameron and Johansson (1997) discuss an alternative approach based on series expansion of the Poisson distribution with application to both over‐ and underdispersed count data. Further possible solutions are represented by simulation methods such as Markov chain Monte Carlo methods (Chib & Winkelmann, 2001) or simulated maximum likelihood methods (Munkin & Trivedi, 1999).
Predictions are based on the posterior estimates of the random effects and the maximum‐likelihood estimate (MLE) of the fixed‐effect parameters. Predictions intervals are found through nonparametric block bootstrap using 500 replicates. Block bootstrap involves resampling regions, and once a region is included its entire time series is used for model estimation of the resampled data. This is done to preserve the dependency structure of the data.
It is worth mentioning that the specific covariance structure among the random effects has been chosen on the grounds of model selection using the Bayesian information criterion (BIC). In our data, the best covariance structure, which has been then used for all estimates and predictions, has turned out to be:
| (3) |
3.2. Region‐specific integer‐valued autoregression modeling
At the second step, we fit and obtain predictions for regional time series separately. In other words, 20 different models are fitted, as time‐series models for counts.
Let again be the daily number of ICU admissions and let denote an ()‐dimensional time‐varying covariate vector, consisting of a polynomial specification of time; notice that this vector is region specific, so different polynomial specifications can be selected for different regions. We model as a conditional Poisson distribution where the expectation at time depends on both past counts and past covariates:
| (4) |
where the coefficients and represent the effects of the expectation of the previous day and the number of ICU admissions of the previous day , respectively.
Note that the model defined by (4) belongs to the INGARCHX family (Agosto, Cavaliere, Kristensen, & Rahbek, 2016; Chen & Lee, 2016; Fokianos, Rahbek, & Tjøstheim, 2009). An alternative approach would be to examine the log‐linear INGARCH model of Fokianos (2011). However, the linear model has significant advantages in terms of interpretation, since it allows for an additive decomposition of the expectation. Under the Poisson assumption, equation (4) corresponds to a GARCH‐type model (Bollerslev, 1986) for the conditional variance of the process; hence the name INGARCH has been used frequently in the literature (though there is some debate on this terminology, see, e.g., Tjøstheim, 2012).
For each region, we compare stationary, linear, quadratic, and cubic trends (i.e., ). We select the best model specification for each one separately, according to the BIC.
Parameters in Equation (4) are estimated via conditional maximum quasi‐likelihood estimation, using the function tsglm in the tscount R package. If the Poisson assumption holds true, then we obtain an ordinary ML estimator. Prediction intervals are approximated numerically through a parametric bootstrap procedure: parameter estimates are plugged in, and several random draws are made from Poisson distributions with the resulting parameter. The approximated prediction intervals are obtained from the empirical and quantiles of the boostrap‐based predictions. See Liboschik, Fokianos, and Fried (2017) for more details.
3.3. Model averaging
Let denote the prediction obtained for the ‐th region ( for the Italian case) and time with the GLMM method, and the prediction obtained with the integer autoregressive method. The final prediction is
| (5) |
for some .
One could simply fix , but this would not lead to any optimality properties of the resulting final prediction . In order to approximate the optimal , we use a strategy that is based on estimation of an explicitely optimal weight for time , which is possible since is observed. We then set as this weight in the hope that in one day the optimal weight has not changed much. We thus first repeat model estimation excluding for ; obtaining leave‐last‐out predictions and ; and then we solve the optimization problem
The rationale is that of selecting the weight that minimizes, for each region, the absolute difference between the final prediction at time (when temporarily ignoring ), and the actually observed count at time .
It should be noticed here that for the first few days, when , we make the weight‐homogeneity assumption for all . We do so since when , the time series are too short and final weights are therefore too variable. The homogeneity assumption allows us to pool information over different regions at the weight estimation stage. For reasons of simplicity final prediction intervals are obtained as the weighted average of the limits of prediction intervals for and . It is straightforward to use Jensen's inequality to show that this conservatively guarantees the nominal level.
4. RESULTS
The reliability of our approach can be assessed by checking the next‐day performance as: (i) median absolute error over the 20 Italian regions, (ii) mean relative error over the 20 Italian regions, (iii) proportion of prediction intervals that do not contain the actually observed occupancy, (iv) proportion of observed occupancies above the upper limit of the prediction interval. For illustrative purposes, we discuss in this section predictions related to the next day, for days from March 17 to April 27.
The daily absolute error has a median of four beds, with first quartile one and third quartile eight. The daily relative error over the 20 regions has first quartile 2%, median 5%, third quartile 12%. Its mean is 9.2%. For prediction intervals, we used a nominal level of 99%. Of the 840 intervals produced, 99.4% indeed contained the observed ICU occupation. Figure 4 summarizes the main results. We report a plot of the next‐day performance for each day since March 17. It can be seen that after the first two weeks, when data available were scarce and a unique weight was used, the absolute and relative errors decreased substantially. Furthermore, coverage of the prediction intervals was always very close to 100%, with only one occasion in which one region reported an ICU occupation above the predicted upper limit. Overall, the approach is rather effective and needs just few data points to produce accurate estimates.
FIGURE 4.
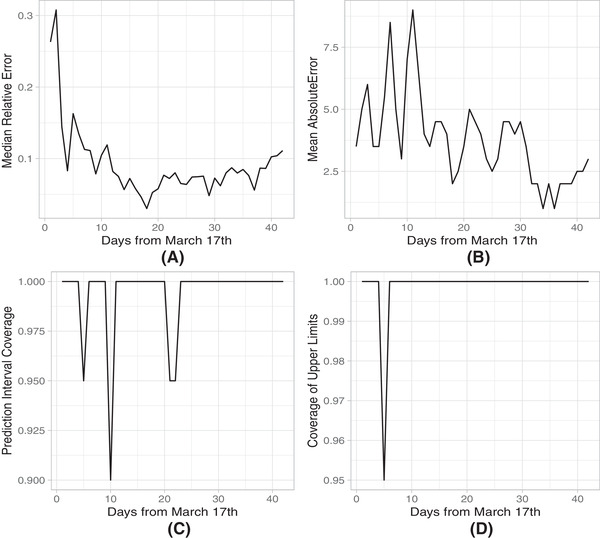
Daily median relative prediction error (a), daily mean absolute prediction error (b), daily coverage of prediction intervals (c), and daily coverage of upper limits of prediction intervals (d) for our ensemble prediction method for ICU occupation in the 20 Italian regions
Just to corroborate the results, we provide an example of the forecasts shown daily at
On April 9, we published the forecasts displayed in Table 1 on the web, along with 99% prediction intervals. In the same table, the regional systems capacities are reported. On April 10, we checked how well the ensemble approach performs. Overall, the performance of the proposal is more than satisfactory. The observed values are all into the 99% prediction intervals, whose length is reasonable and ensures a good representation of the uncertainty surrounding the forecasts. The upper bound of the prediction interval can be used as the worst possible scenario for a specific day and resources should be allocated accordingly to guarantee optimal health services. In the example only Trentino Alto Adige seems to show an alarming situation with prediction interval's upper bound coinciding with the system capacity. To be fair, the prediction interval for Puglia is rather wide. However, this is not surprising, as patients were transferred from northern regions to Puglia for a few days, and daily bursts in the time series of ICU admissions were observed.
TABLE 1.
Forecast and observed ICU beds at the regional level: April 10 together with 99% prediction intervals and regional capacity
| Regions | Observed | Forecast | Prediction interval () | Capacity |
|---|---|---|---|---|
| Abruzzo | 53 | 57 | 48–91 | 115 |
| Basilicata | 15 | 17 | 8–29 | 49 |
| Calabria | 14 | 13 | 5–23 | 107 |
| Campania | 90 | 87 | 60–107 | 586 |
| Emilia‐Romagna | 349 | 347 | 301–397 | 629 |
| Friuli Venezia Giulia | 33 | 34 | 19–48 | 127 |
| Lazio | 201 | 197 | 155–225 | 675 |
| Liguria | 151 | 142 | 111–173 | 186 |
| Lombardia | 1202 | 1202 | 1053–1305 | 1408 |
| Marche | 127 | 120 | 94–151 | 193 |
| Molise | 4 | 4 | 0–11 | 31 |
| Piemonte | 394 | 392 | 348–451 | 560 |
| Puglia | 80 | 79 | 41–159 | 289 |
| Sardegna | 26 | 24 | 13–38 | 123 |
| Sicilia | 62 | 62 | 51–94 | 392 |
| Toscana | 256 | 240 | 203–283 | 464 |
| Trentino Alto Adige | 128 | 128 | 100–157 | 157 |
| Umbria | 39 | 37 | 28–63 | 70 |
| Valle d'Aosta | 16 | 18 | 9–32 | 45 |
| Veneto | 257 | 259 | 216–299 | 938 |
In the following plot (Figure 5), we provide a focus on some regions, those whose health systems were under pressure for the longest time. The prediction intervals were slightly wide but reasonable, for instance, for Lombardia, the most severely affected region, the median length was 20% of the predicted occupancy. Median difference between upper limit of the prediction interval and total available beds in the region is 4.6% in Veneto. We also report data and estimates for Piemonte. This is because the news overlooked the situation in Piemonte, mainly focusing on Lombardia and Veneto. However, while Veneto was more effective at containing the epidemic, the health system in Piemonte was (and partially still is) under pressure, with a decay in the ICU occupancy much slower than in the other regions.
FIGURE 5.
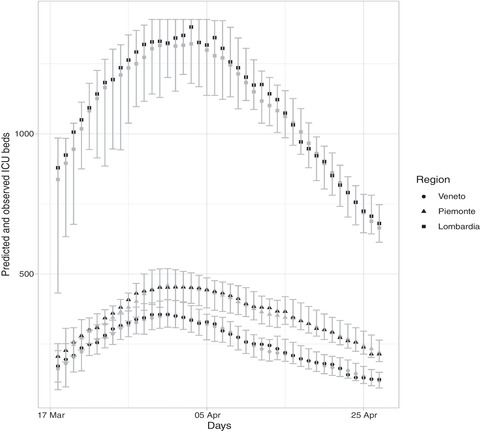
Observed (black) and predicted (gray) values with 99% prediction intervals for the three northern regions Lombardia, Piemonte, and Veneto
In Figure 6 we show the dynamic of the 99% prediction intervals during the considered time window. It is clear how the uncertainty reduces as far as the amount of available information increases. This behavior is common to all Italian regions.
FIGURE 6.
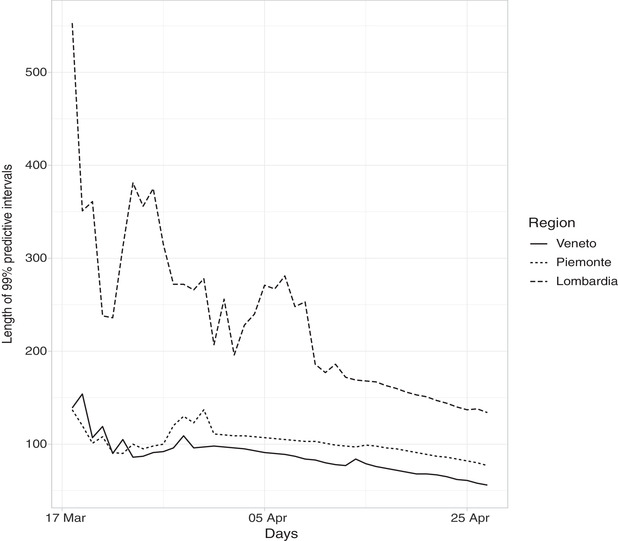
Length of daily 99% prediction intervals for the three northern regions Lombardia, Piemonte, and Veneto
5. CONCLUSIONS
We estimated the occupancy of ICU beds at the regional level in Italy during the COVID‐19 outbreak. The resulting estimates are obtained as a combination of two approaches, which address different data features, that is, heterogeneity and time‐dependence, merged via ensembling. The proposed approach is data driven, no simulated scenarios are required, and it is based on rather simple modeling assumptions. We have discussed in this paper only one‐day‐ahead predictions, but our approach can also be easily extended to three‐day and five‐day horizons.
We have here used 99% prediction intervals for a specific reason: we are actually communicating, every day, 20 prediction intervals (one for each Italian region). We thus use Bonferroni inequality to guarantee coverage for all regions for at least 95% of our days. It shall be noted that we should actually use 99.75% prediction intervals. In our implementation, we have used 99% intervals since these are more simple to interpret by practitioners, and additionally the coverage is slightly conservative due to the use of Jensen's inequality.
From the beginning of this emergency in Italy, the ICU bed capacity was identified as a major bottleneck, to be monitored to avoid the increase in the fatality rate. Accordingly, strong efforts have been dedicated to this issue from government and planners. Our approach was able to predict the demand of ICU beds since the very beginning, showing an improvement in its behavior as long as more data were available. These information and predictions were shown and freely available on a daily basis on the StatGroup‐19 Facebook page (https://www.facebook.com/StatGroup-19-100907671547894). A correct communication of the evolution of the epidemic is crucial to properly inform the general public, and avoid any unmotivated concern.
As a by‐product conclusion drawn from this analysis, we noticed that the regional health systems, though under pressure, were able to properly satisfy the demand for critical care. This might be related to the restrictions imposed by the government, which effectively reduced the spread of the COVID‐19 in regions with a low number of ICU beds.
CONFLICT OF INTEREST
The authors have declared no conflict of interest.
OPEN RESEARCH BADGES
This article has earned an Open Data badge for making publicly available the digitally‐shareable data necessary to reproduce the reported results. The data is available in the Supporting Information section.
This article has earned an open data badge “Reproducible Research” for making publicly available the code necessary to reproduce the reported results. The results reported in this article were reproduced partially due to their computational complexity.
Supporting information
Supporting Information
ACKNOWLEDGMENTS
We express deep thanks to two anonymous referees for their very valuable comments. We thank Francesco Alaimo Di Loro and Marco Mingione for a critical reading of the paper as well as developing the code for the shiny‐app, and Nicole Probst‐Hensch for valuable discussions. We also would like to express our gratitude to Rossella Migliorati and Massimo Calvi for their support to our work during the COVID‐19 epidemic. The research of Antonello Maruotti has been partially supported by the Financial Market Fund (Norwegian Research Council), project number 309218 “Statistical modelling and inference for (high‐dimensional) financial data.”
Farcomeni A, Maruotti A, Divino F, Jona‐Lasinio G, Lovison G. An ensemble approach to short‐term forecast of COVID‐19 intensive care occupancy in Italian regions. Biometrical Journal. 2021;63:503–513. 10.1002/bimj.202000189
Footnotes
Notice that in Figure 3 we use the capacity on April 16, 2020, that was augmented in the northern regions to face the COVID‐19 emergency.
REFERENCES
- Agosto, A. , Cavaliere, G. , Kristensen, D. , & Rahbek, A. (2016). Modeling corporate defaults: Poisson autoregressions with exogenous covariates (parx). Journal of Empirical Finance, 38, 640–663. [Google Scholar]
- Böhning, D. , Rocchetti, I. , Maruotti, A. , & Holling, H. (2020). Estimating the undetected infections in the Covid‐19 outbreak by harnessing capture‐recapture methods. International Journal of Infectious Diseases, 97, 197–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31, 307–327. [Google Scholar]
- Breslow, N. E. , & Clayton, D. G. (1993). Approximate inference in generalized linear mixed models. Journal of the American Statistical Association, 88, 9–25. [Google Scholar]
- Cameron, A. , & Johansson, P. (1997). Bivariate count data regression using series expansions: with applications. Journal of Applied Econometrics, 12, 203–223. [Google Scholar]
- Chen, C. W. , & Lee, S. (2016). Generalized poisson autoregressive models for time series of counts. Computational Statistics & Data Analysis, 99, 51–67. [Google Scholar]
- Chen, Y. C. , Lu, P. E. , & Chang, C. S. (2020). A time‐dependent SIR model for COVID‐19. arXiv preprint arXiv:2003.00122, 2020.
- Chib, S. , & Winkelmann, R. (2001). Markov chain Monte Carlo analysis of correlated count data. Journal of Business and Economic Statistics, 19, 428–435. [Google Scholar]
- Del Sole, F. , Farcomeni, A. , Loffredo, L. , Carnevale, R. , Menichelli, D. , Vicario, T. , … Pastori, D. (2020). Features of severe COVID‐19: A systematic review and meta‐analysis. European Journal of Clinical Investigation, 50, e13378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diekmann, O. , Heesterbeek, H. , & Britton, T. (2013). Mathematical tools for understanding infectious disease dynamics. Princeton: Princeton University Press. [Google Scholar]
- Flaxman, S. , Mishra, S. , Gandy, A. , Unwin, H. J. T. , Coupland, H. , Mellan, T. A. , … Bhatt, S. (2020). Estimating the number of infections and the impact of non‐pharmaceutical interventions on COVID‐19 in European countries: technical description update. arXiv:2004.11342v1 [stat.AP].
- Fokianos, K. (2011). Some recent progress in count time series. Statistics, 45, 49–58. [Google Scholar]
- Fokianos, K. , Rahbek, A. , & Tjøstheim, D. (2009). Poisson autoregression. Journal of the American Statistical Association, 104, 1430–1439. [Google Scholar]
- Giordano, G. , Blanchini, F. , Bruno, R. , Colaneri, P. , Di Filippo, A. , Di Matteo, A. , & Colaneri, M. (2020). Modelling the COVID‐19 epidemic and implementation of population‐wide interventions in Italy. Nature Medicine, 26, 855–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girardi Paolo, Greco Luca, Mameli Valentina, Musio Monica, Racugno Walter, Ruli Erlis, Ventura Laura (2020). Robust inference for non‐linear regression models from the Tsallis score: Application to coronavirus disease 2019 contagion in Italy. Stat, 9(1), 10.1002/sta4.309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grasselli, G. , Pesenti, A. , & Cecconi, M. (2020) Critical care utilization for the COVID‐19 outbreak in Lombardy, Italy: Early Experience and forecast during an emergency response. JAMA, 323, 1545–1546. [DOI] [PubMed] [Google Scholar]
- Grasselli, G. , Zangrillo, A. , Zanella, A. , Antonelli, M. , Cabrini, L. , Castelli, A. , … for the COVID‐19 Lombardy ICU Network (2020). Baseline characteristics and outcomes of 1591 patients infected with SARS‐CoV‐2 admitted to ICUs of the Lombardy region, Italy. JAMA, 323(16), 1574–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurmu, S. , & Elder, J. (2000). Generalized bivariate count data regression models. Economics Letters, 68, 31–36. [Google Scholar]
- Lee, Y. , Nelder, J. A. , & Pawitan, Y. (2017). Generalized Linear Models with Random Effects. Unified Analysis via H‐likelihood (2nd ed.). Boca Raton: CRC Press. [Google Scholar]
- Liboschik, T. , Fokianos, K. , & Fried, R. (2017) tscount: An R package for analysis of count time series following generalized linear models. Journal of Statistical Software, 82, 1–51. [Google Scholar]
- Munkin, M. , & Trivedi, P. (1999). Simulated maximum likelihood estimation of multivariate mixed‐Poisson regression models, with application. Econometrics Journal, 2, 29–48. [Google Scholar]
- Peeri, N. C. , Shrestha, N. , Rahman, S. , Zaki, R. , Tan, Z. , Bibi, S. , … Haque, U. (2020). The SARS, MERS and novel coronavirus (COVID‐19) epidemics, the newest and biggest global health threats: What lessons have we learned? International Journal of Epidemiology, 49, 717–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remuzzi, A. , & Remuzzi, G. (2020). COVID‐19 and Italy: What next? Lancet, 395, 1225–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebastiani, G. , Massa, M. , & Riboli, E. Covid‐19 epidemic in Italy: Evolution, projections and impact of government measures. European Journal of Epidemiology, 35, 341–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjøstheim, D. (2012). Some recent theory for autoregressive count time series. Test, 21, 413–438. [Google Scholar]
- White, D. B. , & Lo, B. (2020). A framework for rationing ventilators and critical care beds during the COVID‐19 pandemic. JAMA, 323, 1773–1774. [DOI] [PubMed] [Google Scholar]
- Yue, M. , Clapham, H. E. , & Cook, A. R. (2020). Estimating the size of a COVID‐19 epidemic from surveillance systems. Epidemiology, 31, 567–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


