Twice-FFT demodulation for signal distortion in optical fiber FP acoustic sensor

Abstract

A Twice-FFT demodulation method for signal distortion state is proposed and experimentally demonstrated in an optical fiber Fabry-Perot (FP) acoustic sensor. Here the fiber FP acoustic sensor element is build with fiber end face and combination of diaphragms which is composed of a small round aluminum foil and a polymer PET film. The hypotenuse intensity demodulation method is applied to acquire the acoustic signal in time domain assisted with a Photodetector (PD) and an oscilloscope. The first Fast Fourier transform (FFT) processing results show harmonic distortion on the frequency domain spectrum. To demodulate the acoustic frequency and amplitude information, twice-FFT processing is preformed. Experimental results reveal an accuracy up to 95.6% of acoustic signal in the frequency range 2–100 Hz. Our scheme provides a new option for signal demodulation of optical fiber acoustic sensors (OFAS).

Fiber acoustic sensor, Fabry perot interferometer, Twice-FFT algorithm, Signal distortion

1. Introduction

In the past decades, Optical fiber acoustic sensing (OFAS) technology is widely used in structural health monitoring [1], medical imaging [2], natural disaster early warning [3] and even military special weapons [4], hydrophones [5] and other fields. The application of optical fiber into the field of acoustic sensing is a new and popular research direction that combines the wide application requirements of acoustic sensing with many excellent characteristics of optical fiber (such as small size, light weight, low cost, anti-electromagnetic interference, etc.).

Recently, extensive literature reports on OFAS have emerged. They can be roughly summarized into the following three categories [6]: Fiber grating type (including Bragg fiber grating FBG [7], long period fiber grating LPG [8], etc.), Mach-Zehnder interferometer (MZI) [9] (including Sagnac [10], Michelson interferometer MI [11]), Fabry-Perot interferometer FPI [12]. Among them, the FP-type optical fiber acoustic sensor has received extensive attention due to its small size, high sensitivity, and good stability.

Different from the static signal demodulation method of physical parameters such as temperature and refractive index, the demodulation of acoustic signal finally needs to obtain a dynamic fluctuation signal. Therefore, in order to demodulate this dynamic signal accurately without distortion, researchers have proposed a series of signal demodulation methods. For example, the 3∗3 demodulation method [13], but this method needs to collect three channels of signals and perform certain operations, which increases the complexity of the system. There is also a phase-generated carrier (PGC) demodulation method [14], which can demodulate to dynamic signals without distortion, but is not suitable for application in small size FP-type sensors; In addition. The hypotenuse intensity demodulation method [15] is also widely used. It converts dynamic wavelength changes into optical power fluctuations, and then becomes a voltage signal through the PD to show intuitively, but when the disturbance exceeds a certain amplitude, the signal will appear severe distortion which is not conducive to demodulation.

To solve this problem, this paper proposes a Twice-FFT demodulation method for signal distortion in a FPI acoustic sensor. The hypotenuse intensity demodulation method is applied to demodulate the acoustic signal in the FPI sensor. In which the electrical change signal converted by the photodetector is Fourier transformed by the time domain information collected by the oscilloscope, then the acoustic signal frequency spectrum is obtained. Here harmonic distortion occurs in the spectrogram and it is difficult to determine information such as the frequency and amplitude of the acoustic signal. Then perform the twice-FFT transform on the signal spectrum, so that the main peak in the Twice-FFT spectrogram will reveal the frequency and amplitude information of the acoustic signal. This method is experimentally demonstrated in a frequency range 2–100 Hz for our lab-made FPI acoustic sensor. The demodulation accuracy of the acoustic signal in the distorted state is up to ~95.6%

2. Sensor setup and analysis

The sensor element is shown in Figure 1, the fiber end surface in a fiber external cavity FP structure designed in this paper is a reflective surface, and the other reflective surface is a combination of diaphragms which is acoustic transducer and composed of a 3-μm-thick small round aluminum foil and a ~50-μm-thick the polymer PET film. The detailed production process and parameters can refer to our previous paper [16]. The main working principle can be described as follows: When the diaphragms structure is disturbed by the acoustic signal, the diaphragms structure will vibrate to modulate the cavity length of the FP. When a stable single-wavelength laser is incident on the FP, the output power will change synchronously due to the oscillation of FSR or wavelength. The acoustic signal will be demodulated in the form of an output voltage signal. In addition, the wavelength measurement should be within the hypotenuse of half the FSR.

Figure 1.

The internal structure schematic diagram.

From the basic theory of acoustics, it can be known that for a circular membrane with a fixed perimeter, its acoustic sensitivity is determined by the maximum fine disturbance caused by a unit quantity of sound pressure change [17], namely

$$S=\frac{def}{\Delta P}=\frac{3(1-{\mu }^2)r^4}{16E{h}^3}$$ (1)

Where $r$, $h$, $\mu$ and $E$ represent the diaphragm radius, thickness, Poisson's ratio and Young's modulus, respectively. To obtain high sensitivity as well as good acoustic response, a polyethylene terephthalate (PET) film material is used in our experiment with $\mu$ = 0.39, $E$ = 2.5 GPa, $h$ = 50 μm, and $r$ = 9.6 mm, which implies sound pressure sensitivity up to 4.32 μm/Pa theoretically.

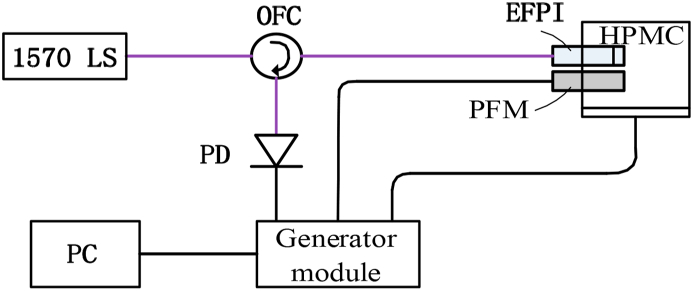
The required acoustic experiment system is shown in Figure 2. The overall sensing system can divided into two parts. The optical part includes a 1570nm DFB laser light source (long-term stability: ≤±0.02 dB), a fiber circulator and an EFPI infrasound sensor element. And the electrical part consist a photodetector (PD, New Focus 1623), generator module (B&K LAN-XI 3160) which is a complete and independent analysis and test system that combines data input and generator output, a 1/2 inch standard pressure field microphone (PFM, B&K4193) for calibration and comparison, a high pressure microphone calibrator (HPMC, B&K4221, sound range 0.01–1000 Hz, maximum sound pressure 164 dB) and PC. Here the HPMC plays a role as a sound source driving by the generator module with controllable frequency and sound pressure. The data acquisition and signal output functions of the generator module are all realized by software operation in the computer.

Figure 2.

Schematic diagram of the optical fiber FP acoustic sensing system.

In the actual experiment process, the demodulation distortion of the acoustic signal is caused by factors such as uneven acoustic diaphragm transducer, unstable acoustic excitation, or misalignment of the channel. Assuming that our optical fiber FP sensor is subject to acoustic disturbance and there is external interference at the same time, the disturbance signal can be described as the overlap of various sine waves with different frequencies and amplitudes. Which can be given as:

$$\varphi \left(t\right)=\sum _{i=1}^N{A}_i\sin ({\omega }_{i}t+{\phi }_i)$$ (2)

Here A_i, ω_i and φ_i are the amplitude, frequency and initial phase of each single sine component, N is a positive integer. Then the phase difference can be expressed as:

$$\begin{array}{l}\Delta \varphi \left(t\right)=\sum _{i=1}^N\left\{A_i\sin ({\omega }_{i}t+{\phi }_i)-A_i\sin [{\omega }_i(t-\tau )+{\phi }_i]\right\}\\ =2A\sin \left({\omega }_i\tau /2\right)\cos ({\omega }_i\tau /2+{\phi }_i)\end{array}$$ (3)

Where the time difference τ = 2L/c, L and c are the cavity length of the FP sensor and the light speed in vacuum. To acquire zero phase difference, the frequency of certain sine component would be:

$$f_{1st}={\omega }_i/2\pi =\frac{(2k-1)c}{4L}\text{,}\text{k}=1\text{,}2\text{,}\mathrm{3...}$$ (4)

Due to the large number of harmonic frequency components and the randomness of their intensity, it is difficult to accurately find the frequency of the acoustic signal. To solve this problem, we carried out a “twice-FFT” processing. What will accurately obtain the frequency interval between harmonic components:

$$f_{2\text{nd}}=\Delta f_{1st}=\frac{c}{2L}$$ (5)

Then the above mentioned problem can be solved.

3. Experimental results and discussion

As shown in Figure 3, the 7 Hz and 10 Hz acoustic disturbance signals act on the acoustic sensor, respectively. And the acquired time-domain spectra of the acoustic signal will be distorted, which are no longer the regular information of the sine or cosine changes. This will prevent us from demodulating the acoustic signal without distortion.

Figure 3.

The demodulated time-domain spectra with our acoustic sensor under acoustic disturbance at (a) 7 Hz and (b) 10 Hz.

Under normal circumstances, we perform the first FFT signal demodulation on the acoustic signal to get the frequency spectra as shown in Figure 4. It is difficult to find an obvious dominant peak on the spectra, but there are many harmonic components, which is difficult to determine at this time information such as the frequency and amplitude of the acoustic disturbance signal. But we can still find the rule from the figure, that is, the first peak and the interval frequency between the harmonic frequencies is almost the disturbance frequency value. That is useful for our further demodulating processing.

Figure 4.

The demodulated frequency-domain spectra with our acoustic sensor under acoustic disturbance at (a) 7 Hz and (b) 10 Hz.

Then we perform another FFT transformation on the frequency spectrum to obtain twice-FFT spectra as shown in Figure 5. And an obvious dominant peak (0.14397 Hz⁻¹ for 7 Hz and 0.099 Hz⁻¹ for 10 Hz) will be obtained, which reveals the frequency and amplitude information of the acoustic disturbance signal.

Figure 5.

The twice-FFT spectra with our acoustic sensor under acoustic disturbance at (a) 7 Hz and (b) 10 Hz.

In order to analyze the corresponding relationship between the sound pressure level (SPL) of the acoustic disturbance signal and the amplitude of the secondary FFT spectrum obtained by demodulation, we drew the trend curve of the them as shown in Figure 6. In which the SPL data and line represented by single FFT in black colour corresponding to the coordinates on the left, and amplitude of the twice FFT data in red colour can be seen corresponding to the coordinates on the right. Obviously, they have basically the same trend of changes in value. This implies that the twice-FFT demodulation method not only reveals the acoustic frequency, but can also demodulate the corresponding amplitude information, which proves the effectiveness of this method. What needs to be mentioned is that the trend of the single FFT and the twice FFT is not exactly the same in 20–30 Hz, which can be attributed to the fact that this frequency component is close to the audio frequency limit of the human ear and audio equipment.

Figure 6.

Data trend curve of driven acoustic SPL and the demodulated twice-FFT amplitude.

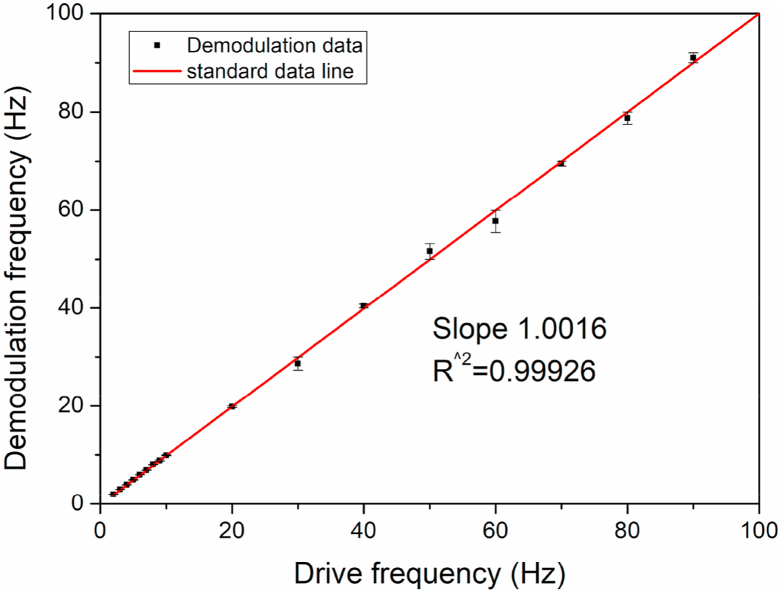
In addition, to test the accuracy of the demodulation scheme, the corresponding curve of driving frequency and demodulation frequency is drawn as shown in Figure 7. The linearity is up to 0.99926 and the maximum value for error bar is 4.4%, which means an accuracy is as high as 95.6% in the acoustic frequency range 2–100 Hz.

Figure 7.

The corresponding curve of driving frequency and demodulation frequency.

What needs to be mentioned is that based on the previous analysis, the limited frequency range can be further expanded by optimally selecting materials and structural design. What's more, if we collect more time-domain data of acoustic signals to perform the twice-FFT processing, it will be possible to further improve the accuracy of our signal demodulation. It is a work still in progress.

4. Conclusions

This paper presents and experimental demonstrated a twice-FFT demodulation method for signal distortion state in an optical fiber FP acoustic sensor. The obvious harmonic distortion on the frequency domain spectrum can be observed after the first FFT, which hinders our demodulation of the acoustic signal. Then a twice-FFT processing is preformed to demodulate the acoustic frequency and amplitude information. Experimental results reveal an accuracy up to 95.6% of acoustic signal in the frequency range 2–100 Hz. Our scheme provides an alternative way for signal demodulation of OFAS.

Declarations

Author contribution statement

Ningzhe Xing: Conceived and designed the experiments.

Shun Wang: Performed the experiments; Wrote the paper.

Shen Jin: Analyzed and interpreted the data.

Yintao Li: Contributed reagents, materials, analysis tools or data.

Funding statement

Ningzhe Xing was supported by Key Research and Development (R&D) Projects of Shanxi Province (201903D121146). Wang Shun was supported by Natural Science Foundation of Hubei Province (2018CFB395). This work was supported by Science and Technology Project of Shenzhen Power Supply Bureau Co., Ltd. (090000KK52170144).

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.