Mathematical estimation of fluid concentration in human skin during water immersion

Graphical abstract

Abstract

Introduction

The concentration of fluid and its analysis in human skin is innately a challenge due to its continuous movement and involvement in maximum life processes. The concentration of the fluid gets affected by the diffusion of fluids through the skin, which acts as the main barrier between the human body and the external environment. Therefore, it becomes imperative to study the process and impact of the diffusion of fluids through the skin. The problem becomes more interesting when the human body is immersed in water.

Objectives

The present paper studies the change in the fluid distribution of human skin during its immersion in water of different temperatures. The application part of the paper visualizes various impaired vascular function and muscle soreness by water immersion during the physiotherapy treatment.

Methods

A mathematical model based on the two-dimensional diffusion equation, along with appropriate boundary conditions, has been formulated. The maximum of the relevant parameters, such as fluid regulation, transfer coefficient, evaporation rate, etc., influencing the fluid distribution, have been incorporated. The model has been solved by variational finite element method, and numerical results have been obtained by the Crank-Nicholson scheme.

Results

The increase in fluid concentration due to treatment with cold and acute hot water immersion has been noted, and the role of water immersion in enhancing the recovery in exercise-induced muscular damage has been analyzed.

Conclusions

The paper addressed the issue of rate of water diffusion through human skin, which otherwise couldn't be drawn from the analogy of gas diffusion through the membrane due to the variation in permeabilities of the two processes. The paper has applications in water immersion therapies and other activities like monitoring swimming induced pulmonary edema, etc.

Introduction

Body fluids are liquids originating from inside as well as excreted or secreted from the bodies of living animals. They include fluids that are excreted or secreted from the body. In proportion to the total body weight of humans, a normal supply of fluid is essential because it is helpful in diagnosing various diseases through tests and the fluids are the main medium of transports for gases, nutrients, hormones, heat and waste products. The fluid concentration in the human body is continuously fluctuating due to changes in its surroundings, but generally, it remains within the bearable limits. With the remarkable advances in the methods for sample preparation, proteomics technology, and quantization, it is now possible to analyze body fluids with higher sensitivity and robust experimental design. Thus, for researchers from the field of biological sciences and hospitals, it becomes imperative to study the processes that affect the fluid concentrations directly or indirectly.

The body fluid, which is present as intracellular fluid (ICF) or extracellular fluid (ECF) in the human body, contributes almost 60 per cent of total body weight. Intracellular fluid is located inside the cells and contributes two-third to the total body fluid. Extracellular fluid, which includes lymph fluid, interstitial fluid and plasma, contributes one-third to the total body fluid and is located outside the cells, as discussed by Guyton [1]. Dehydration and excess of fluid take place mostly from extracellular fluids, as discussed by Black and Hawks [2]. The balance between fluid loss and fluid gain is very important for the normal functioning of the human body. The skin is the main tissue neutralizing the fluid imbalance in the human body due to its role in sweat regulation [3], burn injuries [4], [5], heat distribution [6] and arterial blood temperature [7]. Therefore, it looks very interesting to study the diffusion as well as the distribution of fluids through human skin during the immersion of the body in water.

A human foot immersed in water osmoses about 1–2 g of water per hour. A small quantity of this intake gets imbibed in the stratum corneum while the major portion enters the system, as observed by Buettner [8]. The mechanism of fluid transport through the various layers of skin is subject to the different life processes, as discussed by Rothman [9]. A comprehensive numerical approximation of fluid distribution with heterogeneous metabolic fluid generation in the skin and subcutaneous tissue was carried out by Khanday et al. [10]. Then again, Khanday et al. [11] improved the results in a transient state and used the finite element method to study the fluid regulation in the dermal regions of the human body during thermal stresses. Stock et al. [12] measured the intense alteration in the fluid compartments (intracellular and extracellular) during the vertical neutral and cold water immersion. Valenti et al. [13] claimed water immersion enhances aquaporin-2 excretion in normal human subjects and observed the changes in renal water handling in a healthy volunteer during six hours thermoneutral water immersion at 34–36 °C. It was concluded that immersion in water leads to a reversible increase in the aggregate urinary AQP2 excretion. Magrini et al. [14] studied that the effects of prolonged water immersion on blood pressure maturation in normotensive rats. Vienna et al. [15] claimed that their study was the first investigation of the potential protective effects of hot water immersion against ischemia–reperfusion induced vascular dysfunction in humans. The experimental study was carried out on ten healthy human subjects having no relevant illness in medical screening. Hot water immersion increases overall rectal temperature and heart rate [15]. Jiyeon et al. [16] studies the thermal effects of water on healthy adults and it was determined that the immersion could adversely affect the physiological and cognitive behaviour set up.

Thus, it is worthwhile to mention that fluid is an important component in almost all life processes and their concentration is continuously being affected by inward or outward movements of effective agents. Generally, the researchers discussed the out-ward diffusion of water through skin tissue. In this paper, we shall study how water diffuses inwards through the skin during the immersion of the human body in water. It looks very interesting because the permeability of a membrane to gases and water is not coincident, although the mechanism is similar. Therefore, this paper may be viewed as an improvement to the earlier paper by Khanday et al. [11] on fluid concentration in dermal regions of the human body. The more significant challenge is the presence of various layers of human skin, having different parametric values and physiological properties. The main barrier against the transport of fluid in inward and outward direction lies between stratum corneum and stratum spinosum is known as barrier zone and is of thickness 0.042 mm.

Materials and methods

It is well known fact that models can be better but never best, because every model is improvable and the modified one may give better result than the previous one. Due to the complex structure of domains, the models are generally simplified by some assumptions. In the present model, some negotiable assumptions are:

• •Discretized the human skin into few layers.
• •The value of parameter may be different for different regions of skin but throughout a particular region it is assumed to be constant.

We shall form a model by taking a two dimensional part of human skin with outer surface of skin as $x-\mathit{axis}$, which is in direct contact with water. The $y-\mathit{axis}$ is taken along the inward direction of skin.

For the study of fluid distribution in human skin, Khanday et al. [11] incorporated additional parameters to the modified one dimensional diffusion equation [17], [18]. Therefore, to address the fluid distribution in human skin during the immersion in water we shall use its two dimensional form as

$$\frac{\partial C}{\partial t}=\frac{\partial }{\partial x}\left(D\frac{\partial C}{\partial x}\right)+\frac{\partial }{\partial y}\left(D\frac{\partial C}{\partial y}\right)+R$$ (1)

where $C(x,y)$ is fluid concentration in the skin and R is denotes the rate of metabolic fluid generation.

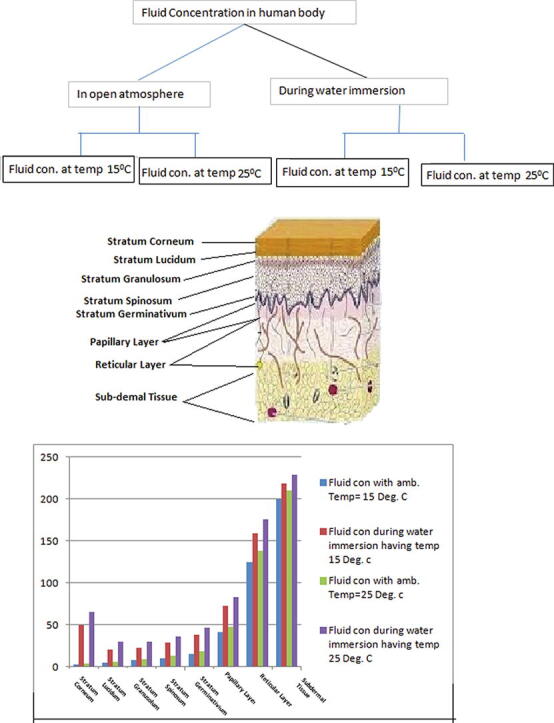
The parameters used in the model have different values in different regions of skin. Therefore, it becomes optimum to discretize the human skin into distinct layers based on the numeric values of the parameters. Depending on the similarity of physiology the different layers of human skin are taken as stratum corneum $(l_0-l_1)$, stratum lucidum $(l_1-l_2)$, stratum granulosum $(l_2-l_3)$, stratum spinosum $(l_3-l_4)$, Stratum germinativum $(l_4-l_5)$, papillary layer $(l_5-l_6)$, reticular layer $(l_6-l_7)$ and subdermal tissue $(l_7-l_8)$. In these layers, the numerical values of parameters has least variation throughout a particular region. Since we attempt to evaluate the model by variational finite element method therefore, discretizing the domain horizontally and vertically in the form of grid, where outer skin surface is taken as $x-\mathit{axis},x=0\mathrm{to}x=l$ and thickness of skin is measured along $y-\mathit{axis},y=l_0\mathrm{to}y=l_8$. Based on the anatomy of skin and following Khanday et al. [11] we have taken $l_0=0,l_1=0.5,l_2=0.07,l_3=0.10,l_4=0.15,l_5=0.20,l_6=0.35,l_7=0.60\mathrm{and}{l}_8=0.75$;. The skin and subcutaneous tissue is discritezed into 150 nodal elements with triangular shapes having 96 nodes as shown in Fig. 1, Fig. 2 along with boundary condition at skin surface as:

$${\left(D\frac{\partial C}{\partial y}\right|}_{y=0}=h(C-C_w)A+{\mathit{LET}}_a$$ (2)

where A is area of skin under consideration and is immersed in water, h is mass transfer coefficient, $T_a$ is the ambient temperature, L and E denotes the latent heat and evaporation rate respectively. $C-C_w$ is the difference of fluid concentrations of skin and water and is always negative because $C_w$ is the maximum possible concentration. Further, since the transport of fluid in tissue occurs in normal direction to skin, i.e., along direction of $y-\mathit{axis}$, the transport along $x-\mathit{axis}$ is negligible and can be taken as zero. Hence

$${\left(\frac{\partial C}{\partial x}\right|}_{x=0}=0\mathrm{and}{\left(\frac{\partial C}{\partial x}\right|}_{x=l}=0$$ (3)

Also, the concentrations of water and inner skin core remains constant; therefore the corresponding boundary conditions are

$$C(x,y_0)=C_s\mathrm{and}C(x,0)=c_w$$ (4)

where $y_0=l_8$ is the total thickness of skin from outer skin surface to inner layer of subdermal tissue.

Fig. 1.

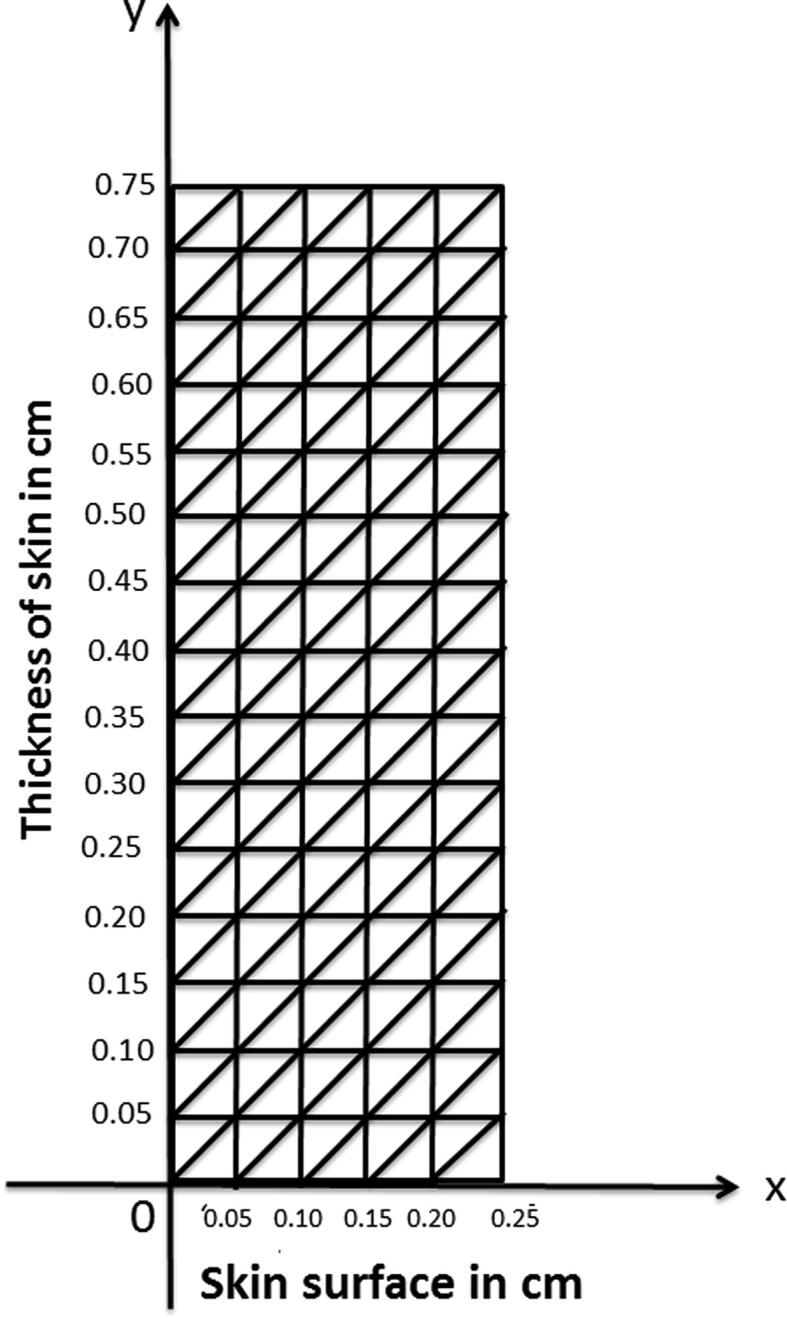
Discretization of human skin into 150 triangular elements having 96 nodes.

Fig. 2.

Triangular element.

Due to inhomogeneous and irregular geometrical structure of human skin, it will be appropriate to solve the model by finite element method as illustrated by Makrariya and Adlakha [19], and Mir Aijaz et al. [20], [21], [22], [23]. The variational integral corresponding to partial differential Eq. (1) over a region $\mathrm{\Omega }$ is

$$I={\int }_{\mathrm{\Omega }}F\left(x,y,C,C_x,C_y\right)d\mathrm{\Omega }$$ (5)

and in optimum form is equivalent to Euler–Lagrange differential equation

$$\frac{\partial F}{\partial C}-\frac{\partial }{\partial x}\left(\frac{\partial F}{\partial C_x}\right)-\frac{\partial }{\partial y}\left(\frac{\partial F}{\partial C_y}\right)=0$$ (6)

where $C_x=\frac{\partial C}{\partial x}$ and $C_y=\frac{\partial C}{\partial y}$. Based on principal of variational finite element method, boundary condition given by Eq. (2) is to be enforced in the solution, while the boundary conditions given by Eqs. (3), (4) automatically get incorporated in the model.

On comparing the Euler–Lagrange Eq. (6) with the partial differential Eq. (1) and boundary condition given by Eq. (2), the variational integral of Eq. (5) can be written as

$$\begin{array}{cc}I\hfill & =\frac{1}{2}{\iint }_A\left[D\left\{{\left(\frac{\partial C}{\partial x}\right)}^2+{\left(\frac{\partial C}{\partial y}\right)}^2\right\}-2\mathit{RC}+\frac{\partial C^2}{\partial t}\right]\mathit{dA}\hfill \\ \hfill & +\frac{1}{2}{\int }_B\left\{h{(C-C_w)}^2+2{\mathit{LET}}_a\right\}\mathit{dx}\hfill \end{array}$$ (7)

where A is the area bounded by $x=0\mathrm{to}x=l$ and $y=l_0\mathrm{to}y=l_8$, and B is the total width of outer skin surface bounded by $x=0\mathrm{to}x=l$. Finite element discretization of the domain consists of 150 elements. Therefore, from Eq. (7) we have

$$I={\displaystyle \sum _{i=1}^{150}}{I}_i,$$ (8)

where

$$\begin{array}{cc}{I}_i\hfill & =\frac{1}{2}{\iint }_{A_i}\left[D_i\left\{{\left(\frac{\partial C_i}{\partial x}\right)}^2+{\left(\frac{\partial C_i}{\partial y}\right)}^2\right\}-2R_i{C}_i+\frac{\partial C_i^2}{\partial t}\right]{\mathit{dA}}_i\hfill \\ \hfill & +\frac{1}{2}{\int }_{B_i}\left\{h{(C_i-C_w)}^2+2{\mathit{LET}}_a\right\}\text{.}\hfill \end{array}$$ (9)

Taking the two dimensional linear shape function in x and y as

$$C_i={\alpha }_{1}x+{\alpha }_{2}y+{\alpha }_3,$$ (10)

where ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ are unknown constants to be determined.

If the nodal points of a triangular element are $C_i(x_i,y_i),C_j(x_j,y_j)\mathrm{and}{C}_k(x_k,y_k)$, then from Eq. (10) we have

$$\begin{array}{cc}\hfill & {\alpha }_1=\frac{1}{2A}\left\{\left(y_i-y_k\right)C_i+\left(y_k-y_i\right)C_j+\left(y_i-y_j\right)C_k\right\}\hfill \\ \hfill & {\alpha }_2=\frac{1}{2A}\left\{\left(x_k-x_j\right)C_i+\left(x_i-x_k\right)C_j+\left(x_j-x_i\right)C_k\right\}\hfill \\ \hfill & {\alpha }_3=\frac{1}{2A}\left\{\left(x_i{y}_k-x_k{y}_i\right)C_i+\left(x_k{y}_i-x_i{y}_k\right)C_j+\left(x_i{y}_j-x_j{y}_i\right)C_k\right\}\hfill \end{array}$$

where

$$A=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill x_i\hfill & \hfill y_i\hfill \\ \hfill 1\hfill & \hfill x_j\hfill & \hfill y_j\hfill \\ \hfill 1\hfill & \hfill x_k\hfill & \hfill y_k\hfill \end{array}\right]$$

The diffusivities of the different layers of human skin varies as discussed by Khanday et al. [11], [10]. The diffusivity of stratum corneum, stratum granulosum, Stratum germinativum, papillary layer, and subdermal tissue are $D_c,D_{\mathit{gr}},D_g,D_p$ and $D_s$ respectively with their numerical values given in Table 1, while the diffusivities for stratum lucidum $D_l$, stratum spinosum $D_{\mathit{sp}}$ and reticular layer $D_r$ are given by

$$\begin{array}{c}\hfill D_l=\frac{l_2{D}_c-l_1{D}_{\mathit{gr}}}{l_2-l_1}+\frac{D_c-D_{\mathit{gr}}}{l_2-l_1}y,\\ \hfill D_{\mathit{sp}}=\frac{l_4{D}_{\mathit{gr}}-l_3{D}_g}{l_4-l_3}+\frac{D_{\mathit{gr}}-D_g}{l_4-l_3}y\end{array}$$

and

$$D_r=\frac{l_7{D}_p-l_6{D}_s}{l_7-l_6}+\frac{D_p-D_r}{l_7-l_6}y\text{.}$$

Table 1.

Numerical values of the parameters.

S. No	Parameter	Sym.	Num. Value
1	Diffusivity of st. cor.	$D_c$	$2.02\times {10}^{-3}{\text{m}}^2{\text{min}}^{-1}$
2	Diffusivity of st. luc	$D_l$	$2.023\times {10}^{-3}{\text{m}}^2{\text{min}}^{-1}$
3	Diffusivity of st. gra.	$D_{\mathit{gr}}$	$2.027\times {10}^{-3}{\text{m}}^2{\text{min}}^{-1}$
4	Diffusivity of papil.	$D_{\mathit{sp}}$	$2.029\times {10}^{-3}{\text{m}}^2{\text{min}}^{-1}$
5	Diffusivity of st. ger.	$D_g$	$2.038\times {10}^{-3}{\text{m}}^2{\text{min}}^{-1}$
6	Diffusivity of sub. derm.	$D_s$	$2.045\times {10}^{-3}{\text{m}}^2{\text{min}}^{-1}$
7	Fluid reg. of pap. lay.	$R_p$	$1.102\times {10}^{-4}l{\text{cm}}^{-3}{\text{min}}^{-1}$
8	Fluid reg. of sub. derm.	$R_s$	$2.196\times {10}^{-4}l{\text{cm}}^{-3}{\text{min}}^{-1}$
9	Mass transfer coef.	h	$3.6\times {10}^{-1}\text{m}{\text{min}}^{-1}$
10	Latent heat	L	$2.42\text{J}.{\text{g}}^{-1}$
11	Evaporation rate	E	$8.33\times {10}^{-3}\text{l}.{\text{m}}^{-2}{\text{h}}^{-1}$

The fluid regulation of the epidermis is negligible, and stratum corneum, stratum lucidum, stratum granulosum and stratum spinosum are the sections of epiderm; therefore, their fluid regulation can be taken as zero. Let $R_p$ is the fluid regulation of papillary layer whose numerical value is given in Table 1. For the fluid regulations of other layers, Khanday et al. [11], [10] used the relations

$$0,\frac{r-l_1}{l_2-l_1}{R}_p,R_p,\frac{l_4{R}_p-l_3{R}_s}{l_4-l_3}+\frac{R_s-R_p}{l_4-l_3}r\mathrm{and}2R_p\text{.}$$

The morphological configuration of dermal region and the variation in parameters like diffusivity, fluid regulation etc., of sub-domains are based on the physiological properties and inheritance of individual as discussed by Ruch and Patton [24], Keener and Sneyd [25] and Guyton [1].

For optimal value of integral values of integral I, we have

$$\begin{array}{c}\hfill \frac{\partial I_i}{\partial C_i}=0\\ \hfill \Rightarrow {\displaystyle \sum _{i=1}^{150}}\frac{\partial I_i}{\partial C_i}=0\\ \hfill \Rightarrow L\dot{C}+\mathit{MC}=N\end{array}$$ (11)

where L and M are $96\times 96$ square matrices and N is a $1\times 96$ column matrix. $C={\left[C_0,C_1\dots C_i,C_{i+1},\dots ,C_{95}\right]}^{\prime }$ is the column of nodal values and $C^{\prime }$ denotes its differential coefficients with respect to time.

Using Crank–Nicholson method for solving the system of ordinary differential equations given by Eq. (11), we have

$$L\dot{C}=-\mathit{MC}+N$$

Applying Crank–Nicholson scheme we have

$$\begin{array}{c}\hfill L\left(\frac{C^{n+1}-C^n}{\mathrm{\Delta }t}\right)=-M\frac{1}{2}\left(C^{n+1}+C^n\right)+N\\ \hfill \Rightarrow \left(L+\frac{\mathrm{\Delta }t}{2}M\right)C^{n+1}=\left(L+\frac{\mathrm{\Delta }t}{2}M\right)C^n+\mathrm{\Delta }\mathit{tN}\end{array}$$ (12)

where $\mathrm{\Delta }t$ is small time interval and

$$C^0=\left[\begin{array}{c}\hfill C_0^0\hfill \\ \hfill C_1^0\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_i^0\hfill \\ \hfill C_{i+1}^0\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_{95}^0\hfill \end{array}\right]\text{;}{C}^1=\left[\begin{array}{c}\hfill C_0^1\hfill \\ \hfill C_1^1\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_i^1\hfill \\ \hfill C_{i+1}^1\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_{95}^1\hfill \end{array}\right]\text{;}{C}^i=\left[\begin{array}{c}\hfill C_0^i\hfill \\ \hfill C_1^i\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_i^i\hfill \\ \hfill C_{i+1}^i\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_{95}^i\hfill \end{array}\right]\text{;}{C}^{i+1}=\left[\begin{array}{c}\hfill C_0^{i+1}\hfill \\ \hfill C_1^{i+1}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_i^{i+1}\hfill \\ \hfill C_{i+1}^{i+1}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill \text{.}\hfill \\ \hfill C_{95}^{i+1}\hfill \end{array}\right]$$ (13)

where $C_j^i$ denotes the concentration at the $j^{\mathit{th}}$ nodal point from skin surface and at $i^{\mathit{th}}$ time interval.

Results

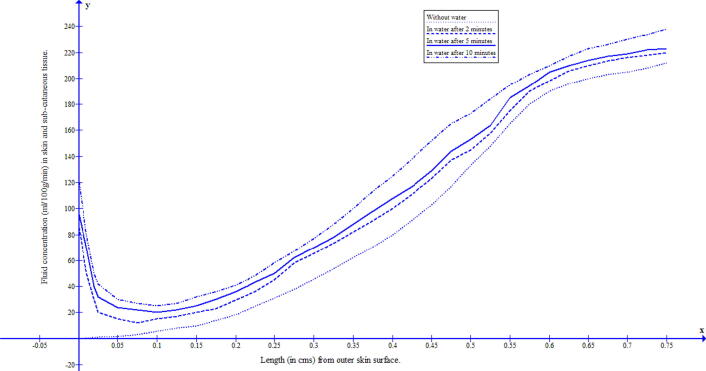
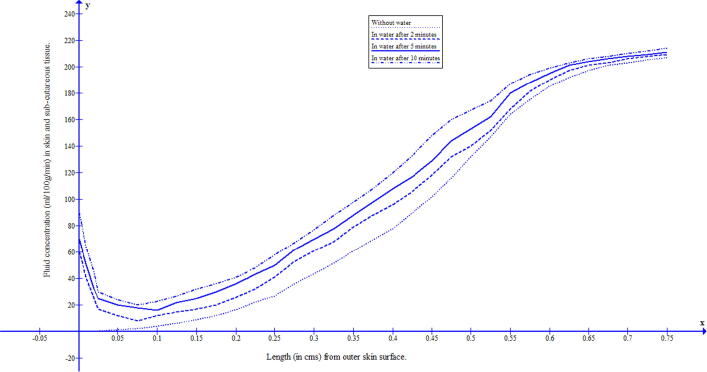
The duration of water immersion of human body prevails for 2 to 10 min. To study the behaviour of fluid concentration during this immersed in water, a mathematical model based on the two-dimensional transient diffusion equation has been formulated and solved by variational finite element method. The skin and subcutaneous tissue has been discretized into 150 triangular-shaped elements having 96 nodes, with skin surface along $x-\mathit{axis}$ and the thickness of skin along $y-\mathit{axis}$. The numerical values of the parameters have been taken from previous research papers [11], [10] and for the corresponding numerical approximations Crank–Nicholson method has been employed. The discretization of the domain gives $6\times 16=96$ nodal points and 150 nodal elements of skin as shown in Fig. 1. The fluid concentrations at 96 nodal points are given by Eq. (13). In each row parallel to $x-\mathit{axis}$ there are six nodal elements but for plotting of the graph, the common value has been taken as the average of the values of these six nodal points. The numerical values of fluid concentration in different regions of skin were obtained at $t=2$ minutes, 5 min and 10 min, and the corresponding graphs were drawn. The numerical solutions at ambient temperatures 25 °C and 15 °C were obtained and reflected in Fig. 3 and Fig. 4. It can be seen from these figures that during water immersion, the resistance for the diffusion is higher at the ambient temperature 15 °C than at 25 °C, which is due to the freedom effect of temperature on the fluid concentration and circulation of blood.

Fig. 3.

Fluid distribution in human skin and subcutaneous tissue during the immersion in water having temperature 25 °C.

Fig. 4.

Fluid distribution in human skin and subcutaneous tissue during the immersion in water having temperature 15 °C.

Discussion and conclusion

When the human body is immersed in the water, the skin gets exposed to surrounding water and a pressure difference of fluid concentrations is developed due to which water starts transporting from surrounding into the body through the skin. The water which passes through the skin into the body gets partially utilized and partially excreted with urine, sweat and other excretory means. It is a matter of common experience that the immersion in water reduces the thirst because the dearth of water is compensated (although not completely) by the water which diffuses through the skin. Even though the immersion in water is beneficial but at the same time, the hypervolemia (or fluid overload) is dangerous. Hypervolemia may cause edema, high blood pressure, heart failure, kidney problem and cirrhosis, …etc. Thus fluids need to remain within normal limits for normal functioning of the human body.

The water diffuses easily through the stratum corneum (horny layer which is dry) and the outermost layer of the epidermis (consisting of dead cells known as corneocytes). This happens only in peripheral layers of skin and then the resistance to diffusion of water increases rapidly towards inner layers of skin. It can also be seen from Fig. 3, Fig. 4 that this diffusion through the skin depends upon the temperature of the water. The raising of water temperature results in further passage of water into the skin at substantial rates. The acute hot water softens the skin thereby increasing the diffusion process and vice versa for colder water. In the present paper, to address the process of diffusion of water through human skin during water immersion, a model based on the two-dimensional diffusion equation has been formulated. To minimize the discrepancy in resultant outcome, all the relevant parameters along with appropriate boundary conditions have been incorporated in the model. The work described was performed to estimate the fluid distribution during water at a cold and acute hot temperature.

The study has specific application during the physiotherapy treatment for various impaired vascular function and muscle soreness by water immersion. By incorporating the various studies on water immersion like Aryane et al. [26], Vienna et al. [15], Herve et al. [27] and Montassar [28], the present study will be helpful in determining the range of water temperature and immersion time for optimum treatment. It is due to the sufficient fluid supply in peripherals of the human body that water immersion is beneficial in recovery from exercise-induced muscular damage (EIMD) of athletes. The water immersion therapy assists in speedy recovery provided it is used properly at appropriate areas of the body with a conducive range of temperature and time period of immersion. Following high-intensity exercise, the water immersion enhances the speed of recovery by properly managing blood lactate concentration.

The model has its physical applicability for human beings in their day to activities especially in monitoring swimming-induced pulmonary edema (SIPE) in indoor swimming pools, open water swimming and during water spot activity by young athletes.

Declaration of Competing Interest

The authors declare there is no conflict of interest.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.