Critical evaluation of the enthalpies of formation for fluorinated compounds using experimental data and high-level ab initio calculations

Abstract

The ab initio method for prediction of the enthalpies of formation for CHON-containing organic compounds proposed earlier (J. Chem. Theory Comput. 2018, 14, 5920-5932) has been extended to their fluorinated derivatives. A single experimental Δ_fH^o_m is typically available for compounds in this scope. Thus, a priori evaluation of the data quality was found to be inefficient despite all available experimental data for C₁─C₃ hydrofluorocarbons and 34 data points for medium-size organofluorine compounds being considered. The training set was derived by analyzing consistency of the experimental and predicted values and removal of outliers. Significant issues in the experimental data, including inconsistency across different laboratories, were identified and potential causes for these problems were discussed. A conservative estimate of uncertainty for the experimental Δ_fH^o_m of organofluorine compounds was proposed.

1. Introduction

Fluorinated organic compounds are an important class of chemicals used in the pharmaceutical industry, agriculture, production of polymers, refrigerants, surfactants, and oil-repellants.^1,2,3 Some of these compounds are also considered pollutants due to their toxicity, bioaccumulation, and contribution to global warming. Knowledge of their thermodynamic properties is critical for industrial applications and development of pollution prevention strategies. In this work, we focus on evaluation of their ideal-gas enthalpies of formation, a property essential to process modeling in a variety of applications.

The experimental methods used to determine enthalpies of formation for the compounds of interest include oxygen and fluorine combustion calorimetries, reaction calorimetry, primarily, with alkali metals and hydrogen, and mass spectrometry. Some enthalpies of formation were also derived from complex thermodynamic cycles involving different types of measurements.

As demonstrated below, oxygen combustion calorimetry is the most reliable and widespread method for determination of Δ_fH^o_m for the considered compounds. Two principal techniques have been used in combustion calorimetry. The most popular one involves combustion in a rotating bomb, in which a certain amount of water has been added.^4,5 To use this approach, the studied or auxiliary compound should have sufficient hydrogen content to yield aqueous HF as a main fluorine product. In the second technique, the combustion is performed in a bomb with no water added.⁶ This approach has been used for fluorocarbons. To our knowledge, presently, combustion calorimetry measurements for fluorinated compounds are only conducted at the Center of Chemical Research at the University of Porto. The number of fluorinated compounds containing, C, H, O, or N atoms, for which experimental enthalpies of formation have been determined, is well below 200.

The combustion calorimetry experiments are conducted at a high pressure of oxygen (around 3 MPa). A multi-step procedure⁴ is used to transform the experimental combustion energies into the standard-state energies of combustion at T = 298.15 K. To derive Δ_fH^o_m, the reference enthalpies of formation for water, CO₂, and HF(aq) are required. One should note that values for the suggested enthalpy of formation for the latter evolved significantly over time, and the latest recommendations are to a large extent based on the results of Johnson et al.^7,8 Consequently, the results reported in the literature need to be reevaluated with the use of updated reference values.

Another challenge of the method is that the combustion energies of organofluorine compounds are significantly lower than those of the non-fluorinated counterparts. Thus, the calorimetric results are highly sensitive to the incompletely fluorinated impurities.⁴ In many cases, the resulting values are based on the results of chemical analyses of products for HF, CO₂, HNO₃, and less frequently for CF₄ and F₂, which adds complexity to the procedure. As demonstrated below, consistency of the results for different laboratories and repeatability-based uncertainties are often worse than those for CHON compounds. All factors listed above make a reliable predictive procedure highly desirable. The existing approaches involving high-level ab initio calculations are mostly focused on small (C₁ and C₂) molecules (e.g., Refs. 9, 10).

Historically, the main contributors to the field are

• Thermodynamics Laboratory of the Bartesville Petroleum Research Center, Bureau of Mines (Bartesville, OK, U.S.A.);

• Chemical Thermodynamics Group of the National Chemical Laboratory (Teddington, U.K.)

• Thermochemistry Laboratory of the Moscow State University (Soviet Union);

• Department of Chemistry, University of Porto (Portugal);

• Institute of Organic Chemistry and Biochemistry at the University of Freiburg (Germany);

• Department of Chemistry, University of Windsor (Canada).

Some reliable values originate from the Chemistry Departments of the University of Wisconsin and the Rice University, the National Bureau of Standards (now NIST), the Argonne National Laboratory, and Thermal Research Laboratory of the Dow Chemical Company (all U.S.A). For brevity, the laboratories will be referred to by location in our discussion (e.g., the Moscow lab).

The goal of this work is to extend the ab initio method we proposed earlier^11,12 to organofluorine compounds and evaluate the reliability of the predicted and available experimental gas-phase enthalpies of formation for these compounds.

2. Calculations

We considered conformational equilibria in the studied compounds because, in our previous work, they were shown to have a significant effect even for some moderate-size molecules.¹² The model was adopted that assumed the ideal-gas equilibrium mixture of individual conformers with the entropy component of the standard Gibbs energy computed using the same rigid rotor-harmonic oscillator model as was used for the thermal correction to the enthalpy, ${\Delta }_0^{T}H$, term. Enthalpy of formation of a given compound was computed as the Gibbs-energy average for the conformer population. The generation of conformers was performed as described earlier.^13,14,15,16 An initial pool of conformer candidates was produced via systematic search using molecular mechanics based on the MMFF94 force field.¹⁷ The resulting conformer candidates were further optimized, and their vibrational spectra were computed with B3LYP/def2-TZVP-D3(BJ).^18,19,20,21 This combination is expected to provide a compromise between computational cost and accuracy for complex molecules.¹² The final set of conformers was established by eliminating duplicated structures and transition states identified from the vibrational analysis. The frequencies were scaled by 0.990 for zero-point vibrational energies (ZPVE). In the “rigid rotor – harmonic oscillator” calculations of the thermal correction Δ₀^TH, the scaling factors of 0.96 for hydrogen stretches and 0.985 for all other modes were applied. The rotational symmetry numbers needed for the entropy evaluation were obtained using the libmsym library.²² The conformer geometries for the single-point energy calculations were optimized with the density-fitted (resolution-of-identity) second-order Møller-Plesset perturbation theory (DF-MP2) with the aug-cc-pvqz basis set.^23,24 Single-point energy calculations were conducted with the 2016 version of local CCSD(T) by Kállay et al.^25,26,27 and the aug-cc-pvqz basis set. DFT calculations were performed with Gaussian 09²⁸, local CCSD(T) was carried out with MRCC (release of September 25, 2017)²⁷, and DF-MP2 was done with Psi4 v1.1.²⁹ The choice of computational tools was motivated by the performance of the methods on the hardware used.¹²

The enthalpies of formation at T = 298.15 K were evaluated as¹²:

$${\Delta }_{\mathrm{f}}{H}^{{}_{°}}=E+\text{ZPVE}+{\Delta }_0^{T}H-{\sum }_{\text{types}}{n}_i{h}_i$$ (1)

where E is the total electronic energy from the single-point calculations, ZPVE is the zero-point vibrational energy, and ${\Delta }_0^{T}H$ is the thermal correction from 0 to 298.15 K. The effective enthalpies, h_i in eq 1, for C, H, O, and N atomic types where fixed to the values determined in the previous study¹²: h(C saturated or aromatic) = −99910.32 kJ·mol⁻¹, h(C unsaturated) = −99909.44 kJ·mol⁻¹, h(H) = −1524.23 kJ·mol⁻¹, h(O) = −197138.05 kJ·mol⁻¹, and h(N) = −143612.32 kJ·mol⁻¹. Determination of the contribution h(F) is one of the goals of the present study. The h(F) values for individual compounds were determined from eq 1 using their experimental Δ_fH^o_m, and the final recommendation was derived via averaging of the individual values over the selected training set of molecules.

Reported uncertainties are the expanded uncertainties for a 0.95 level of confidence (k ≈ 2). For the experimental works, these are based on the authors’ uncertainty estimates (mainly repeatabilities) and uncertainties in the reference values.

3. Results

3.1. Experimental data

The enthalpies of formation considered in this work were derived using the original experimental data, reference enthalpies of formation presented in Table 1, and Δ_fH(HF(aq)) from Johnson et al.⁷ shifted by 0.33 kJ·mol⁻¹, as recommended by CODATA.⁸ The enthalpies of formation for hydrofluorocarbons are often determined from their enthalpies of combustion which are, in turn, based on the results of chemical analysis for CO₂ and HF. If the average values based on those two analyses differed by more than 4 kJ·mol⁻¹ and could not be explained by formation of CF₄, the enthalpy of formation was calculated from the results based on the CO₂ determination, since the latter was suggested to be more reliable.³⁰ The heat capacities of compounds required to reduce the experimental Δ_rH to T = 298.15 K were taken from NIST ThermoData Engine v.10.3 ³¹ unless specified otherwise.

Table 1.

Reference enthalpies of formation used in this work^a

Compound	ΔfHom/kJ·mol−1	Reference
CO2(g)	−393.51 ±0.13	8
H2O(l)	−285.83 ± 0.04	8
F−(aq)	−335.35 ± 0.65	8
HF(l)	−303.55 ± 0.25	7
HF(g)	−273.30 ± 0.70	8
HCl(g)	−92.31 ± 0.10	8
CF4(g)	−933.2 ± 0.8b	32
NF3	−131.5 ± 1.0	33, 34
NaF(cr)	−576.6 ± 0.7	35
KF(cr)	−569.9 ± 0.7	35
NaCl(cr)	−411.26 ± 0.12	35
propane	−104.6 ± 0.2	36

^aReported uncertainties are the expanded uncertainties for 0.95 level of confidence

^bsee discussion in the text

When fluorinated organic compounds are burnt in oxygen, CF₄ sometimes appears as a product, and larger fluorine content results in a higher yield of CF₄. Consequently, the enthalpy of formation of tetrafluoromethane is an important reference quantity affecting experimental Δ_fH^o_m for many compounds. The enthalpy of formation Δ_fH^o_m = −(933.2 ± 0.8) kJ·mol^{−1 32} was derived by Greenberg and Hubbard from the experiments on graphite combustion in fluorine. The values obtained by Domalski and Armstrong using a similar technique³⁷ and in references therein are consistent with this result. On the other hand, the enthalpy of reaction CF₄(g) + 2H₂O = CO₂(g) + 4HF(·20H₂O), Δ_rH^o_m = −(173.2 ± 1.3) kJ·mol^{−1 38,39,40}, can be derived from the results of experiments in which poly(tetrafluoroethylene) and perfluorobicyclohexyl were burnt in oxygen with some water present. This value implies Δ_fH^o_m = −(936.2 ± 2.9) kJ·mol⁻¹ for CF₄, if the reference data above are used. The difference between this value and the direct result³² is relatively large, although the corresponding error bars slightly overlap. The apparent inconsistency should be resolved by replacing the enthalpy of formation of either CF₄ or HF(aq) (or both) with more accurate value(s). In the current Active Thermochemical Tables³⁶, the statistical analysis yielded Δ_fH^o_m(HF·20H₂O) = −(321.03 ± 0.16) kJ·mol⁻¹, which is 0.86 kJ·mol⁻¹ less negative than the CODATA value. On the other hand, Ganyecz et al.⁴¹ computationally analyzed the thermochemical network for fluorinated and chlorinated methanes and ethanes using the diet-HEAT-F12 protocol⁴² and concluded that Δ_fH^o_m(CF₄) by Greenberg and Hubbard is not consistent with the ab initio results and needs further studies. Overall, the CODATA Δ_fH^o_m(HF(aq)) is supported by a larger number of experimental studies as compared to that for Δ_fH^o_m(CF₄), but it is still insufficient to make a conclusive assessment.

In this work, we used Δ_fH^o_m(CF₄) = −(933.2 ± 0.8) kJ·mol⁻¹ if CF₄ was one of the major combustion products. If a small amount of CF₄ was formed and reduction of the experimental data implied its hydrolysis, the enthalpy change Δ_rH^o_m = −(173.2 ± 1.3) kJ·mol⁻¹ was used.

Fluorinated organic compounds, for which the enthalpies of formation are available, can be tentatively divided into three groups. The first group consists of relatively large molecules typically containing more than five carbon atoms. This group has been most studied over the past decades. The second group includes small (up to three carbon atoms) hydrofluorocarbons, most of which are gases at ambient conditions. The third group consists of inorganic species such as HF or NF₃. In this work, 22 compounds (34 Δ_fH^o_m values) from group 1 (Table 2) were selected to provide reasonable variability with respect to the molecular structural features and the sources of information (i.e., the labs where the measurements were performed). Consideration of the data origins was important to avoid any bias due to a potential systematic error originating from a laboratory. The best effort was made to provide a comprehensive review of the experimental data for small hydrofluorocarbons (Table 3). The considered inorganic species included F₂, HF, OF₂, and NF₃.

Table 2.

Experimental thermochemical data at T = 298.15 K for organofluorine compounds composed of medium-size molecules^a

Compound	Formula	CASRN	Phase	ΔfHom(cond)	ΔcondgHom	Lab.b	Ref.	ΔcondgCop,m	ΔfHom,exp	ΔfHom,calc
			at T	kJ·mol−1	kJ·mol−1			J·K−1·mol−1	kJ·mol−1	kJ·mol−1
5-fluorouracil (1)	C4H3FN2O2	51-21-8	cr		132.1 ± 2.8		43	−19c
					153.6 ± 5.0		44
				−581.9 ± 1.2		A	45
				−586.8 ± 1.1	131.9 ± 1.8	A	46
				−586.8 ± 1.1	132.0 ± 1.5				−454.8 ± 1.9	−456.1
perfluoropiperidine (2)	C5F11N	836-77-1	l	−2076.2 ± 3.9	30.0 ± 0.2	B	47		−2046.2 ± 3.9	−2058.2
(trifluoroacetyl)acetone (3)	C5H5F3O2	367-57-7	l		37.2 ± 0.2		48
				−1039.4 ± 3.3		C	49
				−1034.2 ± 2.3		A	50
				−1034.9 ± 2.3					−997.7 ± 2.3	−996.6
hexafluorobenzene (4)	C6F6	392-56-3	l	−991.1 ± 4.2		D	51
				−982.7 ± 8.4		E	6
				−991.1 ± 4.2	35.6 ± 0.3d				−955.5 ± 4.2	−952.1
decafluorocyclohexene (5)	C6F10	355-75-9	l	−1966.6 ± 4.5	30.8	D	51
				−1938.0 ± 7.2	31.0	E	52
				−1966.6 ± 4.5	30.9 ± 0.1				−1935.7 ± 4.5	−1942.1
perfluoro(2-methyl-2-pentene) (6)	C6F12	1584-03-8	l	−2522.4 ± 8.8e	23.4 ± 0.4	C	53		−2499.0 ± 8.8	−2499.3
pentafluorophenol (7)	C6HF5O	771-61-9	cr	−1024.2 ± 4.5	f	D	54
					67.8 ± 0.5		55, 56g
				−1024.2 ± 4.5	67.8 ± 0.5				−956.4 ± 4.5	−954.2
4-fluoronitrobenzene (8)	C6H4FNO2	350-46-9	l	−189.6 ± 1.4	56.0 ± 0.2	A	57		−133.6 ± 1.4	−129.8
1,4-difluorobenzene (9)	C6H4F2	540-36-3	l	−342.2 ± 1.6	35.8 ± 0.2h	B	58		−306.4 ± 1.6	−302.5
2-trifluoroacetylpyrrole (10)	C6H4F3NO	2557-70-2	cr	−776.6 ± 2.8	72.8 ± 1.4	A	59	−50	−703.8 ± 3.1	−694.7
Fluorobenzene (11)	C6H5F	462-06-6	l	−150.6 ± 1.6	34.7 ± 0.1d	B	40		−115.9 ± 1.6	−112.2
4-fluoroaniline (12)	C6H6FN	371-40-4	l	−164.0 ± 1.4	54.8 ± 0.8	A	60		−109.2 ± 1.6	−103.5
5-fluoro-1,3-dimethyluracil (13)	C6H7FN2O2	3013-92-1	cr		121 ± 3		44
				−575.0 ± 1.2	96.8 ± 1.6	A	46	−30
					98.0 ± 0.9		61
					97.7 ± 0.8				−477.3 ± 1.5	−473.5
fluorocyclohexane (14)	C6H11F	372-46-3	l	−373.5 ± 2.0 i	36.9 ± 1.5	F	62	−54j	−336.7 ± 2.5	−330.4
4-fluorobenzonitrile (15)	C7H4FN	1194-02-1	cr	−53.5 ± 1.6	67.6 ± 0.5	A	63	−25	14.1 ± 1.7	24.0
4-fluorobenzoic acid (16)	C7H5FO2	456-22-4	cr	−586.7 ± 1.6		B	40
				−584.9 ± 1.4		D	51
					93.7 ± 1.7		54	−15k
				−585.2 ± 1.3		G	64
				−584.4 ± 1.4		G	64
				−585.2 ± 1.3		F	62
				−584.4 ± 1.2		A	65
					92.7 ± 1.6		66
				−584.8 ± 1.2	93.1 ± 1.1				−491.7 ± 1.6	−490.7
(trifluoromethyl)benzene (17)	C7H5F3	98-08-8	l	−635.0 ± 2.7		B	40
				−636.9 ± 2.2		B	67
				−640.6 ± 3.4		C	68
				−635.8 ± 2.3		C	49
				−636.6 ± 2.2	37.9 ± 0.9d				−598.7 ± 2.4	−596.1
4-fluoromethylbenzene (18)	C7H7F	352-32-9	l	−186.9 ± 1.3		B	58
					39.4 ± 0.1		69		−147.5 ± 1.3	−142.6
1-fluoro-4-methoxybenzene (19)	C7H7FO	459-60-9	l	−308.9 ± 1.6	48.7 ± 1.1	A	70		−260.2 ± 2.0	−260.2
5-fluoro-2-methylbenzoxazole (20)	C8H6FNO	701-16-6	l	−260.2 ± 3.8	57.2 ± 1.0	A	71		−203.0 ± 3.9	−211.3
(2,2,2-trifluoroethyl)benzene (21)	C8H7F3	21249-93-4	l	−669.0 ± 2.8	46.1 ± 0.5	F	62	l	−622.9 ± 2.8	−633.8
1,1'-(1,1,2,2-tetrafluoro-1,2-ethanediyl)bis-benzene (22)	C14H10F4	425-32-1	cr	−783.0 ± 4.6	101.9 ± 3.7	F	62	l	−681.1 ± 5.9	−691.8

^aStandard molar quantities: Δ_fH^o_m(cond), the enthalpy of combustion of a compound in the condensed state; Δ_cond^gH^o_m, the enthalpy of sublimation or vaporization; Δ_cond^gC^o_p,m, the heat capacity difference between the ideal-gas and condensed phases; Δ_fH^o_m,exp(g) and Δ_fH^o_m,calc(g), the experimental and calculated ideal-gas enthalpies of formation, respectively. All experimental enthalpies of combustion and formation are recalculated using the reference values from Table 1. Values selected for generation of the training data set are given in bold; the values not used for averaging are italicized. Reported uncertainties are the expanded uncertainties for 0.95 level of confidence

^bSource of the condensed-state enthalpy of formation: A, University of Porto; B, Bartesville Petroleum Research Center; C, Moscow State University; D, National Chemical Laboratory, Teddington; E, University of Windsor; F, University of Freiburg; G, National Bureau of Standards, Washington, DC

^cRefs. 31,72

^devaluated by NIST ThermoData Engine³¹ based on multiple sources

^ebased on CO₂ analysis

^fthe sublimation pressure data⁵⁴ include the solid-to-solid phase transition region and are not used

^gcalorimetric data by Paukov et al.⁷³ are inconsistent with the publications from the Teddington lab. The latter are used to keep consistency between different properties.

^hRefs. 31,74

ⁱassuming that the reported combustion energies refer to HF·20H₂O.

^jΔ_vapC_p estimated by NIST ThermoData Engine³¹

^kRef. 75

^lthe correction to T = 298.15 K was small compared to the uncertainty and not applied

Table 3.

Experimental thermochemical data for small hydrofluorocarbons in the ideal-gas state^a

Compound	CASRN	Ref.	Lab.b	Reaction	T / K	ΔrHom(T)	ΔfHom,expc	ΔfHom,calcc
						kJ·mol−1	kJ·mol−1	kJ·mol−1
CH2F2	75-10-5	76	A	CH2F2(g) + O2(g) = CO2(g) + 2HF(·22H2O)	298.15	−585.1 ± 0.9	−452.3 ± 1.6	−452.2
CHF3	75-46-7	76	A	CHF3(g) + 1/2O2(g) + H2O(l) = CO2(g) + 3HF(·24H2O)	298.15		−696.6 ± 3.3	−698.2
CF4	75-73-0	32	B	C(gr) + 2F2(g) = CF4(g)	298.15	−933.2 ± 0.8	−933.2 ± 0.8	−934.9
CHF2CH3	75-37-6	77	C	C2H4F2(g) + 5/2 O2(g) = 2CO2(g) + H2O(l) + 2HF(·20H2O)	298.15	−1212.6 ± 2.0	−504.0 ± 2.4	−504.5
CF3CH3	420-46-2	78, 79	C	CF3CH3 + 2O2 = 2CO2 + 3HF(·27H2O)	298.15	−1004.2 ± 2.6	−748.6 ± 3.3	−753.8
CHF2CH2F	430-66-0	80, 81, 82, 83	C,D	Multiple reactions involving CF2=CFCl	298.15		−696.0 ± 3.2	−669.5
CF3CF2H	354-33-6			See text				−1115.2
CF3CF3	76-16-4	84	E	C2F6(g) + 6K = 2C(soot) + 6KF	298.15	−2088	−1311 ± 17d
		85	F	C2F6 + 2/3NF3 = 2CF4 + 1/3N2	298.15	−434.7 ± 2.5	−1344.0 ± 3.0	−1345.5
CH2FCH2CH3	460-13-9	86	D	C3H7F(g) + H2 = C3H8(g) + HF(g)	521	−95.2 ± 1.0	−284.8 ± 1.3	−293.3
CH3CHFCH3	420-26-8	86	D	C3H7F(g) + H2 = C3H8(g) + HF(g)	521	−88.3 ± 0.7	−292.2 ± 1.1	−313.9
		87	G	CH2=CHF(g) + CH4(g) = C3H7F(g)	298.15	−112.9 ± 6.1
CH3CF2CH3	420-45-1	87	G	CH2=CF2(g) + CH4(g) = CH3CF2CH3(g)	298.15	−123.5 ± 6.1		−554.6
CF3CH2CF3	690-39-1	88,89	C	C3H2F6(g) + 2O2(g) + 2H2O(l) = 3CO2(g) + 6HF(aq)	298.15		−1406.1 ± 8.1	−1409.2
CF3CF2CF3	76-19-7	90	C	C3F8(g) + 8Na(cr) = 8NaF(cr) + 3C(amorph)	298.15	−2761.3 ± 4.9	−1783.7 ± 7.8 i	−1757.7
HFC=CH2	75-02-5	30	C	C2H3F(g) + 5/2O2(g) = 2CO2(g) + H2O(l) + HF(·40H2O)	298.15	−1256.1 ± 1.9	−138.7 +± 2.0	−143.6
F2C=CH2	75-38-7	91	A	C2H2F2(g) + 2O2(g) = 2CO2(g) + 2HF(·50H2O)	298.15	−1096.9 ± 7.0	−334.2 ± 7.1	−351.1
		92	C	C2H2F2(g) + 2O2(g) = 2CO2(g) + 2HF(·30H2O)	298.15	−1086.8 ± 8.2	−344.1 ± 8.3
F2C=CHF	359-11-5	92	C	C2HF3(g) + 3/2O2(g) = 2CO2(g) + 3HF(·30H2O)	298.15	−980.5 ± 3.9	−486.5 ± 4.3	−498.6
F2C=CF2	116-14-3	84	E	C2F4(g) + 4K = 2C(soot) + 4KF(cr)	298.15		−706 ± 8d	−673.0
		93	H	C2F4(g) + 4K = 2C(gr) + 4KF(cr)	298.15		−715 ± 11e
		94	l	C2F4(g) = C(soot) + CF4(g)	297.31	−257.0 ± 6.4	−676.2 ± 6.5e
		94	l	C2F4(g) + 2H2(g) = 2C(soot) + 4HF(l)	297.16	−555.3 ± 5.6	−658.9 ± 5.7e
		91	A	C2F4(g) + 2H2(g) = 2C(amorph) + 4HF(·18H2O)	298.15	−618.1 ± 4.5	−657.0 ± 5.4f
		91	A	C2F4(g) = C(amorph) + CF4(g)	298.15	−266.0 ± 1.6	−659.5 ± 2.0g
		95	C	C2F4(g) + 4Na = 2C(amorph) + 4NaF(cr)	298.15	−1611.3 ± 5.3	−662.1 ± 6.0h
CH2FCH=CH2, E-CH3CH=CHF, Z-CH3CH=CHF	818-92-820327-65-519184-10-2	96	J	CH2FCH=CH2 = (Z and E)-CH3CH=CHF	484.0	−22.0 ± 3.4
		97	K	CH2FCH=CH2(g) = (Z)-CH3CH=CHF(g)	658.6	−13.6 ± 0.6
		97	K	CH2FCH=CH2(g) = (E)-CH3CH=CHF(g)	658.6	−11.0 ± 0.6
		96	J	(E)-CH3CH=CHF(g) = (Z)-CH3CH=CHF(g)	470.5	−2.9 ± 0.5
		97	K	(E)-CH3CH=CHF(g) = (Z)-CH3CH=CHF(g)	658.6	−2.6 ± 0.6
CHF2CH=CH2, CH3CH=CF2	430-62-6430-63-7	97	K	CH3CH=CF2(g) = CHF2CH=CH2(g)	672.6	−10.7 ± 1.2
CF3CH=CH2	677-21-4	98	C	C3H3F3(g) + 3O2(g) = 3CO2(g) + 3HF(·xH2O), x = 13 or 45	298.15		−621.7 ± 1.4	−629.7
CF3CF=CF2	116-15-4	99,100	C,D	Multiple reactions involving CF3CFClCF2Cl			−1151.8 ± 4.4	−1150.6
		94	l	C2F4(g) = 2/3 CF3CF=CF2(g)	299	−86 ± 11

^aStandard molar quantities: Δ_rH^o_m, the enthalpy of a reaction shown; Δ_fH^o_m,exp(g) and Δ_fH^o_m,calc(g), the experimental and calculated ideal-gas enthalpies of formation, respectively. All experimental enthalpies of combustion and formation are recalculated using the reference values from Table 1. Values used in the training set are shown in bold. Reported uncertainties are the expanded uncertainties for 0.95 level of confidence

^bA, University of Wisconsin; B, Argonne National Laboratory; C, Moscow State University; D, University of Colorado at Boulder; E, Imperial Chemical Industries; F, Dow Chemical Company; G, California Institute of Technology; H, University of Göttingen; I, E. I. du Pont de Nemours & Co.; J, University of Rhode Island; K, University of Florida

^cat T = 298.15 K

^dassuming Δ_fH^o_m(soot) = 10.5 kJ·mol⁻¹

^eassuming Δ_fH^o_m(soot) = 0 kJ·mol⁻¹

^fΔ_fH^o_m(soot) = 6.2 kJ·mol⁻¹ determined experimentally

^gΔ_fH^o_m(soot) = 7.7 kJ·mol⁻¹ determined experimentally

^hΔ_fH^o_m(soot) = 16.5 kJ·mol⁻¹ determined experimentally

ⁱΔ_fH^o_m(soot) = 22.6 kJ·mol⁻¹ determined experimentally.

For all compounds from the first group (Table 2), the enthalpies of formation were derived from their energies of combustion in oxygen in a rotating bomb calorimeter. In most cases, the well-established technique of combustion in the presence of water^4,5 was used. A detailed discussion of these results is presented below.

Multiple experimental techniques, including oxygen and fluorine combustion calorimetry, reaction calorimety with alkaline metals and hydrogen, chemical equilibrium studies, and mass spectrometry were used to obtain Δ_fH^o_m for small hydrofluorocarbons.

Fluoromethanes.

Enthalpies of formation for difluoromethane and trifluoromethane were determined by Neugebauer and Margrave⁷⁶ from the results of combustion calorimetry. The recommended Δ_fH^o_m of CF₄ is based on the results of direct combustion of graphite in fluorine.³²

1,1-Difluoroethane.

The enthalpy of formation was reported by Kolesov et al.⁷⁷ The authors analyzed the CO₂ and HF content in the combustion products. The enthalpies of combustion based on these two values differed by about 13 kJ·mol⁻¹. The enthalpy of combustion accepted in this paper was calculated from the CO₂ analysis.

1,1,1-Trifluoroethane.

The enthalpy of formation was determined by Kolesov et al.⁷⁸ from the results of combustion calorimetry. Later, Kolesov and Papina⁷⁹ revised the experimental value by adding a correction for reduction to the standard state missing in the original work. Analysis of the kinetic data by Rodgers and Ford¹⁰¹ provides a similar value if Δ_fH(CH₃) and Δ_fH(CF₃) from Ref. 35 are used. However, the expanded uncertainty exceeds 10 kJ·mol⁻¹ in this case.

1,1,2-Trifluoroethane.

The enthalpy of formation was calculated from the enthalpies of chlorotrifluoroethylene hydrogenation Δ_rH^o_m(298 K) = −(271.2 ± 2.3) kJ·mol^{−1 83} and its enthalpy of formation Δ_fH^o_m(CF₂CFCl) = −(517.1 ± 2.2) kJ·mol⁻¹ found as weight-average of the results from Refs. 80,81,82.

Pentafluoroethane.

The enthalpy of formation was reported by Buckley et al.¹⁰² who studied chemical equilibria:

CF₃CF₂Br(g) + I₂(g) = CF₃CF₂I(g) + IBr(g)

Br₂(g) + C₂F₅H(g) = HBr(g) + CF₃CF₂Br(g)

The equilibrium constants for the second reaction were determined by Coomber and Whittle.¹⁰³ However, the reported Δ_fH^o_m(CF₃CF₂H) was, in turn, based on Δ_fH^o_m(CF₃CF₂I) estimated by Wu et al.¹⁰⁴ as Δ_fH^o_m(CF₃CF₂I) = ½(Δ_fH^o_m(CF₃CF₃) + Δ_fH^o_m(CF₂ICF₂I)). Thus, this compound was excluded from further data analysis.

Hexafluoroethane.

The most precise value was obtained by Sinke⁸⁵ by the reaction bomb calorimetry. The result strongly depends on reference Δ_fH^o_m of CF₄ and NF₃.

1-fluoropropane, 2-fluoropropane, 2,2-difluoropropane.

The enthalpies of formation for monofluoropropanes were obtained using the high-temperature enthalpies of hydrogenation determined in a flow calorimeter by Lacher et al.⁸⁶ Enthalpies of the formal reactions

CH₂=CHF + CH₄ = CH₃CHFCH₃

CH₂=CF₂ + CH₄ = CH₃CF₂CH₃

could be found from results of the mass-spectrometric study.⁸⁷

1,1,1,3,3,3-Hexafluoropropane.

The enthalpy of combustion and formation for this compound was reported by Kolesov.⁸⁸ The concentration of the resulting HF solution was not specified. In the review⁸⁹, the enthalpy of formation was recalculated with respect to the updated enthalpies of formation for the reference compounds.

Octafluoropropane.

Δ_fH^o_m was found⁹⁰ from the enthalpy of its reaction with sodium. Detailed analysis of the combustion products was performed.

Fluoroethylene, 1,1-difluoroethylene, trifluoroethylene.

Kolesov et al. conducted combustion calorimetry studies for these compounds.^30,92 Δ_fH^o_m of 1,1-difluoroethylene was also reported by Neugebauer and Margrave.⁹¹

Tetrafluoroethylene.

The enthalpy of formation for this compound was reported by many researchers. Neugebauer and Margrave⁹¹ and Kolesov et al.⁹⁵ measured the energy of combustion for the amorphous carbon product.

Equilibria of mono- and difluoropropenes.

We are aware of two works reporting these equilibria.^96,97 While the enthalpies of Z/E-isomerization of 1-propenes are consistent, the enthalpies of formation for 3-fluoropropene differ by 8 kJ·mol⁻¹. That cannot be explained by their temperature difference.

3,3,3-Trifluoropropene.

The enthalpy of formation for this compound was determined⁹⁸ from its enthalpy of combustion in oxygen in a bomb calorimeter. The average values of the enthalpy of combustion derived from the results of chemical analysis for HF and CO₂ differ by about 5 kJ·mol⁻¹. The enthalpy of formation was recalculated based on the amount of CO₂. The Δ_fH^o_m values obtained in experiments 1 and 3 of the original publication are over 20 kJ·mol⁻¹ too high relative to the other experiments, while the standard deviation calculated for experiments 2 and (4 to 12) is only 1.7 kJ·mol⁻¹. Thus, the enthalpy of formation was calculated using the data from experiments 2 and 4 to 12.

Hexafluoropropene.

Following Papina and Kolesov⁹⁹, the enthalpy of formation for this compound can be determined using the enthalpies of the processes

CF₂ClCFClCF₃(l) + O₂(g) + 4H₂O(l) = 3CO₂(g) + 6HF(·20H₂O) + 2HCl(·600H₂O) ΔH_m^o(298 K) = −(925.6 ± 2.0) kJ·mol^{−1 99}

CF₃CF=CF₂(g) + Cl₂(g) = CF₂ClCFClCF₃(g) Δ_rH_m^o(363 K) = −(197.3 ± 0.5) kJ·mol^{−1 100}

CF₂ClCFClCF₃(l) = CF₂ClCFClCF₃(g) Δ_l^gH_m^o(298 K) = (26.93 ± 0.03) kJ·mol^{−1 105}

The temperature dependence of Δ_rH_m^o for the chlorination reaction can be neglected.

The enthalpy of reaction

C₂F₄(g) = 2/3 CF₃CF=CF₂(g) Δ_rH_m^o(298 K) = −86 kJ·mol⁻¹

was estimated by Duus⁹⁴ using combustion experiments.

Four inorganic compounds were considered: F₂, HF, NF₃, and OF₂. The enthalpies of formation of HF and NF₃ are given in Table 1, for OF₂, Δ_fH^o_m = (24.5 ± 1.6) kJ·mol⁻¹.¹⁰⁶

3.2. Consistency of experimental data and derivation of the training set

For generation of the CHON training set¹¹, we used only those compounds for which the experimental data were available from multiple consistent sources and the resulting expanded uncertainty was under 2 kJ·mol⁻¹. If these criteria were applied to the fluorinated compounds, a training set of sufficient size could not be compiled. Thus, all available data were analyzed. The effective enthalpy of fluorine, h(F), was derived for each data point using eq 1 and the experimental Δ_fH^o_m. The resulting h(F) were used to assess the consistency among the considered data points and identification of outliers.

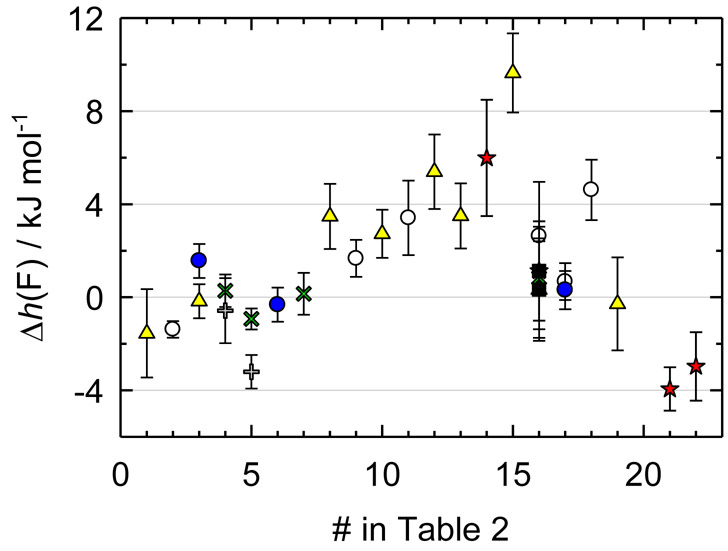
The effective enthalpies h(F) for the compounds of group 1 are compared in Figure 1. The value h(F) = −261711.5 kJ·mol⁻¹ used in the figure is a preliminary estimate based on all available experimental data. Most of the data are spread within (−4 to 6) kJ·mol⁻¹ of this estimate. One would expect h(F) values to congregate near a certain value. This consistency should be better for compounds with similar fluorine functionality (e.g., para-substituted fluorinated benzene derivatives). Considering the uncertainty of the predicted Δ_fH^o_m was (2.5 to 3.0) kJ·mol⁻¹ for CHON-containing compounds¹², variations below 1 kJ·mol⁻¹ due to computational model limitations are expected.

Figure 1.

Relative effective enthalpy, Δh(F) / (kJ·mol⁻¹) = h(F) / (kJ·mol⁻¹) + 261711.5, of a fluorine atom for the medium-size organic molecules as a function of the sequential number of a compound in Table 2: blue circles, Moscow lab; yellow triangles, Porto lab (1997-2014); green crosses, Teddington lab; gray pluses, Windsor lab; red stars, Freiburg lab; empty circles, Bartesville; black squares, Gaithersburg. The value for 5-fluoro-2-methylbenzoxazole (#20) is not shown due to a large deviation (−8.6 kJ·mol⁻¹). For 5-fluorouracil (#1) and (trifluoromethyl)benzene (#17) only the most recent values for laboratories are shown.

The results from the Moscow and Teddington labs do demonstrate reasonable consistency. On the other hand, the values from Freiburg exhibit a scatter of about ±6 kJ·mol⁻¹ around the average value for this laboratory. These data as well as those from Windsor where a less precise technique was used were excluded from the training set. Four out of six values from the Bartesville lab and five out of nine values from the Porto lab show significant positive deviation from the average. It implies that the experimental Δ_fH^o_m is more negative than the expected computed counterpart. Two reasons may be responsible for the observed behavior. First, the samples could contain incompletely fluorinated impurities. This may also explain why not all results from these laboratories are biased. Second, the reduction to the standard state could be based on obsolete reference values. The samples of 4-fluorobenzoic acid (#16) from the Bartesville lab were further studied in the Teddington lab and at the National Bureau of Standards and (1.5 to 2.3) kJ·mol⁻¹ more positive values were obtained. At the same time, the results from these and two other laboratories are consistent within ±0.5 kJ·mol⁻¹ (Table 2). The enthalpies of formation for non-fluorinated compounds from the Porto and Bartesville labs are normally consistent with the results from the other laboratories and the predicted values. Thus, it seems highly unlikely that the problem is due to the instrumental error such as incorrect calibration, etc. Further clarification of this problem clearly goes beyond the scope of this paper. All results from these two laboratories exceeding +2 kJ·mol⁻¹ deviation were excluded from the training data set. If several consistent Δ_fH^o_m were available for a compound, the weight-average was calculated with the weights determined from uncertainties of the enthalpies of combustion. The resulting values used in the training set are shown in bold in Table 2.

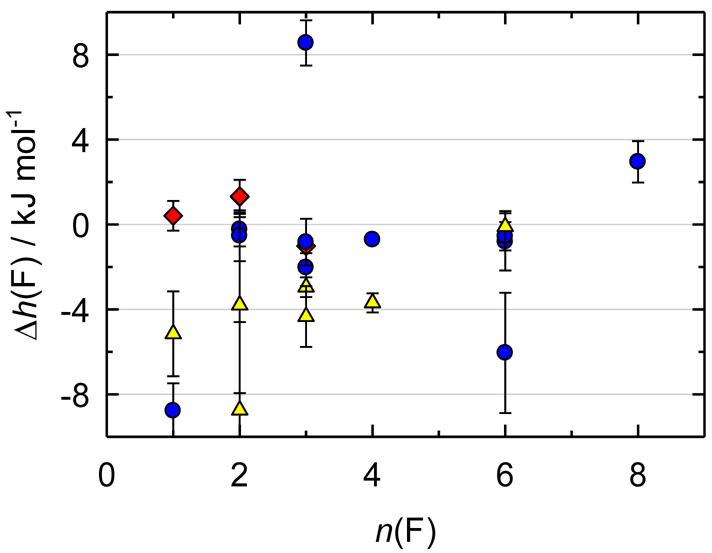
The data scatter for small fluorinated organics (Figure 2) is larger than that for the compounds of group 1, with Δh(F) generally within ±9 kJ·mol⁻¹. Seven out of twelve saturated compounds are grouped in the range −(0.2 to 2.0) kJ·mol⁻¹. Six of these values were obtained from combustion calorimetry and one from reaction calorimetry. Combustion calorimetry was used to derive only one outlying value, where a thermodynamic cycle also involved the results from a high-temperature hydrogen reaction calorimetry. Therefore, for the saturated compounds, combustion calorimetry was the most reliable technique despite all difficulties associated with quantification of the combustion process for gaseous species. Unlike the condensed-phase compounds, the exact amount of a gas introduced to the bomb is unknown and only chemical analysis of the products allows one to determine the burnt amount of the sample.

Figure 2.

Relative effective enthalpy, Δh(F) / (kJ·mol⁻¹) = h(F) / (kJ·mol⁻¹) + 261711.5, of a fluorine atom for fluoroalkanes (blue circles), fluoroalkenes (yellow triangles), and inorganic molecules (red diamonds). The value for 2-fluoropropane (−22 kJ·mol⁻¹) is not shown. For tetrafluoroethylene, the value is a weight-average of the results^91,95

Five values for the fluorinated alkenes lie close to −4 kJ·mol⁻¹. Four of these values are based on the combustion calorimetry results from the Moscow lab. Different methods were used for tetrafluoroethylene (n = 4), which is the fifth consistent compound. However, based on the high-level ab initio calculations, Δ_fH^o_m of the latter has been demonstrated to have a large error (see, for example, Ref. 9). The combination of this fact with the results in Figure 2 leads to a conclusion that the remaining four experimental values have a similar systematic error per fluorine atom. A possible explanation of this problem might be either incorrect characterization of the combustion products or incorrect reduction to the standard state. The value for perfluoropropene is consistent with those of the saturated compounds. This h(F) was derived in a different way: it is based on a thermodynamic cycle involving the results of combustion calorimetry from the Moscow lab and high-temperature chlorination calorimetry.

Based on the analysis above, we selected the consistent experimental Δ_fH^o_m of the saturated compounds and perfluoropropene for further analysis. The results for inorganic compounds are close to those of small fluorinated alkanes (Figure 2).

3.3. Effective enthalpy of the fluorine atom for ab initio calculations

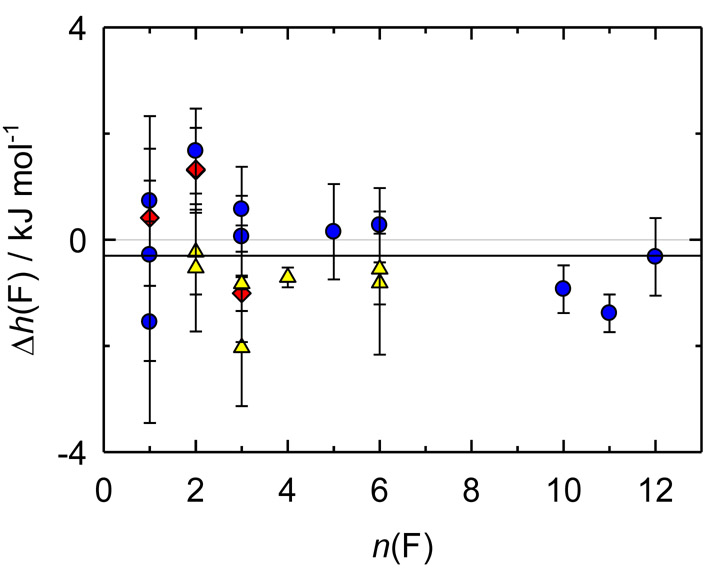
Data consistency for the training dataset is demonstrated in Figure 3. At a small number of fluorine atoms, the results for group 1 are typically higher than those for group 2. For perfluorinated compounds of group 1 except perfluorobenzene, h(F) values are close to those of group 2. The exact reason of this behavior is unknown; however, based on our limited tests, we believe that this is mainly due to the insufficient theory level for ZPVE calculations.

Figure 3.

Relative effective enthalpy, Δh(F) / (kJ·mol⁻¹) = h(F) / (kJ·mol⁻¹) + 261711.5, of a fluorine atom for group 1 (blue circles), small hydrofluorocarbons (yellow triangles), and inorganic molecules (red diamonds). The black line shows the resulting h(F) value.

The resulting h(F) = −(261711.80 ± 0.37) kJ·mol⁻¹ was found by unweighted averaging all h(F) values. The enthalpies of formation calculated with this effective enthalpy are presented in Tables 2 and 3. The uncertainty (in kJ·mol⁻¹) for compounds can be estimated as follows:

$$U({\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{{}_{°}})=\sqrt{U^2(\text{CHON})+{\left(U(h(\mathrm{F}))n(\mathrm{F})\right)}^2}$$ (2)

The first term in the right-hand side of eq 2 is a contribution associated with C, H, O, and N atoms, which can be calculated as described earlier.¹² This contribution considers uncertainty of the model as well as uncertainties of the effective enthalpies of atoms. For the considered compounds, U(CHON) is close to (2.5 to 3.0) kJ·mol⁻¹. Eq 2 does not consider uncertainties in the reference enthalpies of formation for CO₂, H₂O, HF(aq), etc. The uncertainty of h(F) could be decreased if repeated consistent measurements for some reference compounds were available, which is unlikely with current experimental infrastructure. Also, predictions could be improved through the development of efficient and reliable computational procedures for anharmonic ZPVE, which appears to be a limiting factor for the considered group of compounds.

4. Conclusion

An ab initio method for prediction of the enthalpies of formation has been extended to fluorinated compounds. Additional uncertainty associated with the presence of fluorine was estimated to be about 1 kilojoule per mole per F atom. Analysis of the experimental data with the use of the computed results revealed significant problems in the former. These included systematic errors of Δ_fH^o_m in some laboratories and a shortage of reliable Δ_fH^o_m values for fluoroalkenes. The observed agreement between the experimental and computed values was somewhat worse than for CHON compounds. If no additional information is available, 5n(F) kJ·mol⁻¹ should be considered as a conservative estimate of the expanded uncertainty for the experimental values of Δ_fH^o_m of medium-size fluorinated organic compounds. For small hydrofluorocarbons, this uncertainty should be close to 9n(F) kJ·mol⁻¹.