Collimatorless Scintigraphy for Imaging Extremely Low Activity Targeted Alpha Therapy (TAT) with Weighted Robust Least Squares (WRLS)

Abstract

A technology for imaging extremely low photon flux is an unmet need, especially in targeted alpha therapy (TAT) imaging, which requires significantly improved sensitivity to detect as many photons as possible while retaining a reasonable spatial resolution. In scintigraphy using gamma cameras, the radionuclide collimator rejects a large number of photons that are both primary photons and scattered photons, unsuitable for photon-starved imaging scenarios like imaging TAT. In this paper we develop a min-min weighted robust least squares (WRLS) algorithm to solve a general reconstruction problem with uncertainties and validate it with the extreme scenario: collimatorless scintigraphy. Ra-223, a therapeutic alpha emitting radionuclide whose decay chain includes x-ray and gamma-ray photons, is selected for an exploratory study. Full Monte Carlo simulations are performed using Geant4 to obtain realistic projection data with collimatorless scintigraphy geometry. The results show that our proposed min-min WRLS algorithm could successfully reconstruct point sources and extended sources in the collimatorless scintigraphy with a resolution close to its system resolution and figures of merit (FOM) better than the collimator-based scintigraphy for extremely low activity TAT. This approach could be expanded as a 3D algorithm, which could lead to 3D collimatorless SPECT.

1. Introduction

Targeted alpha therapy (TAT) provides a powerful technique for noninvasively and selectively killing cancer cells [1]. Because of the high linear energy transfer and short ranges of alpha particles emitted from radiopharmaceuticals, the advantages of TAT are treating cancers effectively and locally with minimal damage to neighboring healthy organs [6]. In order to have a better understanding of the in vivo biodistribution and pharmacokinetics of the radiopharmaceuticals, and to calculate and optimize the internal dose in tumors and organs at risk, quantitative and noninvasive imaging of TAT is important [5, 10]. However, the injected activity should be low because of the high cytotoxicity of alpha particles [5, 6]. Hence, the gamma-ray imaging of TAT represents a challenging problem.

Scintigraphy using gamma cameras is one of only few feasible modalities for quantitative and noninvasive imaging of TAT [10]. In a previous study, quantitative imaging of Ra-223 was performed utilizing gamma camera scintigraphy with a spatial resolution of 1.1 cm and a sensitivity of 69 cps/MBq requiring a long acquisition time [5]. In terms of imaging extremely low activity TAT, the radionuclide collimator in scintigraphy rejects a large number of photons that are both primary photons and scattered photons, making it unsuitable for any routine use in imaging TAT. For this reason, we postulated whether it is possible to image TAT via scintigraphy with a very high-sensitivity collimator (i.e., large holes) or even without a collimator. In collimatorless scintigraphy, photons coming from different directions will overlap on the detector so that the detected photons’ spatial information is mostly lost compared with collimator-based scintigraphy, resulting in degraded spatial resolution. Thus it may require a nontraditional reconstruction algorithm.

The reconstruction problem could be formulated as when the system matrix and the projection data are both uncertain. The uncertainty in the projection measurements could be resolved by some expectation maximization (EM) algorithms or weighted least squares (WLS) assuming Poisson or Gaussian statistics [3, 7, 11, 12]. The uncertainty in the system matrix is intractable and the reconstructed image quality strongly depends on the accuracy of the system matrix [3, 8, 9]. In previous well-established algorithms, including iterative reconstruction algorithms, compressed sensing and dictionary learning based reconstruction algorithms, the system matrix is regarded as a known and accurate priori [2, 3, 8, 9]. Assuming the system matrix subjects to a small variation from its theoretical value, the error propagation effect was analyzed theoretically [9], and a min-max weighted robust least squares (WRLS) algorithm was proposed to obtain stable image reconstruction by minimizing the worst case caused by the uncertainties [8]. However, those algorithms are suitable for reconstruction with small variations in the system matrix which mainly come from statistical noises or imperfect collimator performances, but unsuitable for reconstruction with large variations in the system matrix caused by undetermined or unknown spatial information. Moreover, the min-max WRLS optimization may not always guarantee an optimal reconstructed image because we want to optimize the reconstruction based on the best estimation of system matrix instead of the worst one. Currently no study has successfully resolved such an image reconstruction problem with a collimatorless geometry in scintigraphy. And the main challenge is that the system matrix is ill-conditioned and has strong uncertainties due to a loss of detected photons’ spatial information, which could not simply be approximated by the theoretical model under small perturbations.

Aiming at obtaining a robust reconstructed image with large or small uncertainties in the system matrix and the projection data, in this paper we develop a min-min WRLS algorithm. The accuracy and stability of the proposed algorithm are validated with the extreme scenario: collimatorless scintigraphy. It is an approximation imaging modality without any collimator by putting the detector as close as possible to the phantom for imaging extremely low activity TAT.

2. Materials and Methods

Full Monte Carlo simulations are performed using Geant4 with and without a collimator in scintigraphy to obtain realistic projection data containing a small number of photons from a TAT radionuclide (Ra-223) (see Fig. 1). The detector array consists of 64 by 64 CZT crystals, each with a size of 1.0 mm × 1.0 mm × 5.0 mm. The parallel-hole collimator has the same size as the CZT detector and a length of 2.5 cm. The phantom is a water tube with a diameter of 6.0 cm and a thickness of 3.0 cm, facing towards the detector system with a 1 cm gap. As an exploratory study, a small disk source of Ra-223 is embedded in the center of the phantom with a diameter of D cm and a thickness of 1.0 mm. The Livermore physics list is used in Geant4 with close to real physics processes considered (i.e. decay and scattering) and the detected energy spectrum is blurred with Gaussian noises with σ = 3 keV. The counts under the characteristic x-ray peak of Ra-223 centering at 82 keV with a width of 20% are summed up as the the projection data, which was shown in a previous study to give the best reconstruction performance [5].

Fig. 1:

Monte Carlo simulation setup with Geant4 in (a) collimatorless scintigraphy and (b) collimator-based scintigraphy. The CZT detector is shown in green and the collimator is shown in blue. Ra-223 particles are shown as the yellow dots in the center of the water phantom whose boundaries are in orange color.

The min-min WRLS algorithm combines WLS and robust optimization, by assuming the measured projection data y has independent Gaussian noises $\mathcal{N}(0,\Sigma )$ and considering possible variations in the system matrix A from its real value A_real. Instead of optimizing the worst case with respect to the uncertainty in A (min-max WRLS), the min-min WRLS is shown in Eq. 1, trying to find the best A that yields the smallest error and the closest approximation to A_real in its uncertain set $\mathcal{U}$.

$$\underset{x⪰0}{\min }\underset{A\in \mathcal{U}}{\min }{(Ax-y)}^T{\Sigma }^{-1}(Ax-y)$$ (1)

where x is the image to be reconstructed, Σ = diag(y) is the noise covariance matrix, and $\mathcal{U}$ is the convex uncertainty set of A. The shape and size of $\mathcal{U}$ is determined by real world geometries and imaging scenarios. Here $\mathcal{U}$ is defined as a weighting box-bounded uncertainty set as shown in Eq. 2, allowing each element of A to have various uncertainties Δa_ij bounded by a corresponding positive weighting factor w_ij from a weighting matrix W with the same shape as A.

$$\mathcal{U}=\left\{A\in \mathcal{F}|A=\overline{A}+\Delta A,|\Delta a_{ij}\mid \le \zeta w_{ij},i=1\dots m,j=1\dots n\right\}$$ (2)

where $\mathcal{F}=\{A\in {\mathbb{K}}_{+}^{m\times n}\mid \widehat{A}{⪯}_{{\mathbb{K}}_{+}^{m\times n}}A{⪯}_{{\mathbb{K}}_{+}^{m\times n}}1\cdot {\mathbf{1}}^T\}$ is the feasible set of A with $\widehat{A}$ being the theoretical system matrix assuming an ideal collimator performance and ${\mathbb{K}}_{+}^{m\times n}=\left\{C\in {ℝ}^{m\times n}\mid c_{ij}\ge 0,i=1\dots m,j=1\dots n\right\}$ being a proper cone, $\overline{A}$ is the mean value of A in $\mathcal{U}$, and ζ ∈ [0, 1] is a hyperparameter which could be tuned to decide how far ΔA is allowed to fluctuate along W.

Unlike the min-max WRLS, the min-min WRLS in Eq. 1 is nonconvex and intractable. It needs to be transformed to a convex problem to be solvable, which is given in Eq. 3 (see proof below). The reconstructed image is obtained by optimizing Eq. 3 with the CVXPY tool [4].

$$\begin{array}{l}\underset{x⪰0,\mu \in {ℝ}^n}{\min }{\mu }^T{\Sigma }^{-1}\mu \text{s.t.}\mu ⪰\overline{A}x-y-\zeta Wx\\ \mu ⪰-\overline{A}x+y-\zeta Wx\\ \mu ⪰0\end{array}$$ (3)

Proof.

$$\text{Eq.}1\iff \underset{x⪰0}{\min }\underset{A\in \mathcal{U}}{\min }\sum _{i=1}^m\frac{{\left(a_i^{T}x-y_i\right)}^2}{y_i}=\underset{x⪰0}{\min }\sum _{i=1}^m\frac{1}{y_i}\underset{a_i\in \mathcal{U}}{\min }{\left(a_i^{T}x-y_i\right)}^2$$

$$\begin{gathered} \because \underset{a_i\in \mathcal{U}}{\min }\left|a_i^{T}x-y_i\right|=\{\begin{array}{ll}{y}_i-{\left({\overline{a}}_i+\zeta w_i\right)}^{T}x,\hfill & \text{if}{y}_i\ge {\left({\overline{a}}_i+\zeta w_i\right)}^{T}x\hfill \\ {\left({\overline{a}}_i-\zeta w_i\right)}^{T}x-y_i,\hfill & \text{if}{y}_i\le {\left({\overline{a}}_i-\zeta w_i\right)}^{T}x\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array} \\ =\max \left\{\left|{\overline{a}}_i^{T}x-y_i\right|-\zeta w_i^{T}x,0\right\} \end{gathered}$$

$$\therefore \text{Eq.}1\iff \underset{x⪰0}{\min }\sum _{i=1}^m\frac{1}{y_i}{\left\{\max \left\{\left|{\overline{a}}_i^{T}x-y_i\right|-\zeta w_i^{T}x,0\right\}\right\}}^2\iff \text{Eq.}3$$

In terms of the collimatorless geometry, we deduce $\tilde{A}$ as an approximation of A_real by assuming the detected photons are emitted isotropically without any attenuation (see Fig. 2a). The element ${\tilde{a}}_{ij}$ in $\tilde{A}$ is expected to be proportional to the solid angle from the image pixel j to the detector pixel i, as given by Eq. 4.

$${\tilde{a}}_{ij}\propto d{\Omega }_{ij}\stackrel{r\gg p}{\simeq }\frac{p^2\cos {\theta }_{ij}}{R_{ij}^2}=\frac{p^2}{r^2}{\cos }^3{\theta }_{ij}$$ (4)

where p is the detector pixel size and r is the vertical distance from image to detector. Thus ${\tilde{a}}_{ij}$ could be approximated by cos³ θ_ij and to eliminate the dependence of ${\tilde{a}}_{ij}$ on r in scintigraphy, ${\tilde{a}}_{ij}$ is calculated as:

$${\tilde{a}}_{ij}=\frac{{\int }_{r_{\min }}^{r_{\max }}{\cos }^3{\theta }_{ij}dr}{{\int }_{r_{\min }}^{r_{\max }}dr}=\frac{1}{r_{\max }-r_{\min }}\left(\frac{r_{\max }^2+2l_{ij}^2}{\sqrt{r_{\max }^2+l_{ij}^2}}-\frac{r_{\min }^2+2l_{ij}^2}{\sqrt{r_{\min }^2+l_{ij}^2}}\right)$$ (5)

However, this $\tilde{A}$ is a weak approximation and A_real may lie in the neighborhood of $\tilde{A}$ with unknown size (see Fig. 2b). Thus, we hope to plug such $\overline{A}$ and W into Eq. 3 that the range $\overline{A}\pm W$ would be closest to A_real, where $\overline{A}=\frac{A^{\prime }+\widehat{A}}{2}$ and $W=\frac{A^{\prime }-\widehat{A}}{2}$.

Fig. 2:

(a) The solid angle estimation of the system matrix $\tilde{A}$ and (b) the uncertainty set of the collimatorless geometry. A fixed value of $\nu =\frac{1}{\max (\tilde{A}-\widehat{A})}-1$ is chosen so that $\tilde{A}+\nu (\tilde{A}-\widehat{A})$ is on the boundary of the feasible set $\mathcal{F}.\eta \in \left[\frac{\min \tilde{A}}{\min \tilde{A}-1},1\right]$ is tunable and close to zero, determining which uncertainty set is closest to A_real.

3. Results and Discussion

To validate the min-min WRLS algorithm, various sources are simulated and reconstructed in comparison with the collimator-based scintigraphy, including point sources at different positions and various concentrated disk sources with D = 1 cm and D = 2 cm. The projection data from the collimatorless scintigraphy is smoothed by a 11 × 11 Gaussian filter, denoising while retaining the same shape of projection. From both simulated projections and theoretical forward projections using $\tilde{A}$, the projection profiles of a point source and a disk source with D = 1 cm are almost the same, indicating that the point source and the disk source with D ≤ 1 cm could not be discriminated with any reconstruction algorithm (see supplementary materials Fig. S1 and Fig. S2).

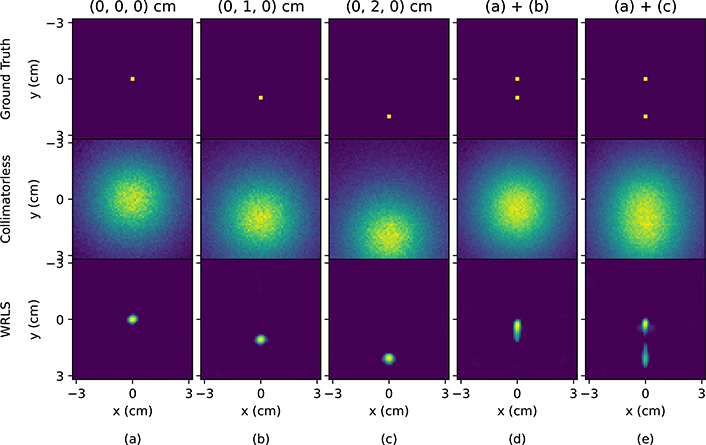
To evaluate the reconstruction performance, normalized mean square error (NMSE), peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) are compared as the figures of merit (FOMs) with and without a collimator. In the min-min WRLS algorithm, the FOMs as a function of ζ are shown in Fig. 3 when $\nu =\frac{1}{\max (\tilde{A}-\widehat{A})}-1=0.00374$ and η = −0.005 are shown to give the best reconstruction performance. In Fig. 3, the FOMs are robust with the variation of ζ within the range of 0.5 to 1.0. With ζ = 0.8 selected which yields the overall best FOMs with various sources in Fig. 3, the reconstruction results are shown in Fig. 4 to 5 and Table 1. For a single point source, the min-min WRLS could successfully reconstruct its position in Fig. 4. Two combined point sources could not be discriminated with a distance of 1 cm but become distinguishable with a distance of 2 cm. We also check that the reconstruction profiles of two point sources are about to be discriminated when they are 1.2 cm apart, giving the system spatial resolution of the collimatorless geometry to be about 1.2 cm. As discussed before, Figure 5 also shows that the disk source with D ≤ 1 cm is indistinguishable from a point source in this collimatorless geometry. For larger disk sources like D = 2 cm, it is possible to reconstruct its position with a smaller but uniform shape (see Fig. 5 and supplementary material Fig. S2), and the FOMs in Table 1 are generally better than the collimator-based scintigraphy even when the activity is extremely low. The collimator-based scintigraphy fails to reconstruct two combined large disk sources with D = 2 cm, while the reconstruction with min-min WRLS in collimatorless scintigraphy keeps higher FOMs in Table 1 and successfully resolves the positions and distances of the two sources. In Table 1, the FOMs of the collimatorless scintigraphy outperform those of the collimator-based scintigraphy when the source activity is lower than 10 nCi/ml, indicating the potential of imaging extremely low activity TAT with the collimatorless geometry.

Fig. 3:

(a) NMSE, (b) PSNR and (c) SSIM as a function of ζ to evaluate the overall performance of the min-min WRLS algorithm when setting $\nu =\frac{1}{\max (\tilde{A}-\widehat{A})}-1=0.00374$ and η = −0.005. 1e7 decayed Ra-223 particles are initialized as point sources at (0, 0, 0) cm, (0, 1, 0) cm and (0, 2, 0) cm, and disk sources with D = 1 cm and D = 2 cm at (0, 0, 0) cm.

Fig. 4:

Ground truth, projections without a collimator, and reconstruction of a single point source at (a) (0, 0, 0) cm, (b) (0, 1, 0) cm, and (c) (0, 2, 0) cm, and two point sources with a distance of (d) 1 cm and (e) 2 cm when 1e7 decayed Ra-223 particles are simulated.

Fig. 5:

Ground truth, projections with and without a collimator, and reconstruction of disk sources at (0, 0, 0) cm with (a) D = 1 cm and 30 nCi/ml (1e7 decayed Ra-223), (b) D = 1 cm and 3 nCi/ml (1e6 decayed Ra-223), (c) D = 2 cm and 7.5 nCi/ml (1e7 decayed Ra-223), (d) and (e) D = 2 cm and 0.75 nCi/ml (1e6 and 2e6 decayed Ra-223) with a corresponding measuring time of 30 min.

Table 1:

FOMs of the reconstruction in Fig. 5 with and without a collimator.

FOMs	Collimatorless					Collimator
	(a)	(b)	(c)	(d)	(e)	(a)	(b)	(c)	(d)	(e)
NMSE	0.84	0.85	0.80	0.88	0.93	0.78	0.98	0.88	0.99	0.99
PSNR	18.64	18.55	13.01	12.19	8.78	19.30	17.27	12.28	11.23	8.23
SSIM	0.93	0.93	0.77	0.80	0.62	0.70	0.74	0.38	0.72	0.44

The current min-min WRLS algorithm mainly focuses on data fidelity in reconstruction and it could be further improved by adding prior knowledge, i.e. regularization terms, on both system matrix and the image itself. Currently $\tilde{A}$ is no longer sparse and we expect it to be near-sparse when the source is much closer to the detector. By adding prior knowledge and other information to improve the algorithm, 3D collimatorless SPECT could be possible for more complex source reconstruction, and experiment will be performed in the future.

4. Conclusion

In this work we derive a min-min WRLS algorithm to solve a general reconstruction problem with either large or small uncertainties in the system matrix and the projection data. It is validated with full Monte Carlo simulations in the extreme scenario: collimatorless scintigraphy, proposed to be used for imaging extremely low activity TAT. The results show that the min-min WRLS algorithm could successfully reconstruct point sources and extended sources in the collimatorless scintigraphy with a spatial resolution close to its system resolution of 1.2 cm. The FOMs of the collimatorless scintigraphy outperform those of the collimator-based scintigraphy when the source activity is lower than 10 nCi/ml, indicating the potential of imaging extremely low activity TAT with the collimatorless geometry.