Abstract
This study aims to improve the accuracy and consistency of T1 and T2 measurements using cardiac MR Fingerprinting (cMRF) by investigating and accounting for the effects of confounding factors including slice profile, inversion and T2 preparation pulse efficiency, and B1+. The goal is to understand how measurements with different pulse sequences are affected by these factors. This can be used to determine which factors must be taken into account for accurate measurements, and which may be mitigated by the selection of an appropriate pulse sequence. Simulations were performed using a numerical cardiac phantom to assess the accuracy of over 600 cMRF sequences with different flip angles, TRs, and preparation pulses. A subset of sequences, including one with the lowest errors in T1 and T2 maps, was used in subsequent analyses. Errors due to non-ideal slice profile, preparation pulse efficiency, and B1+ were quantified in Bloch simulations. Corrections for these effects were included in the dictionary generation and demonstrated in phantom and in vivo cardiac imaging at 3T. Neglecting to model slice profile and preparation pulse efficiency led to underestimated T1 and overestimated T2 for most cMRF sequences. Sequences with smaller maximum flip angles were less affected by slice profile and B1+. Simulating all corrections in the dictionary improved the accuracy of T1 and T2 phantom measurements, regardless of acquisition pattern. More consistent myocardial T1 and T2 values were measured using different sequences after corrections. Based on these results, a pulse sequence which is minimally affected by confounding factors can be selected, and the appropriate residual corrections included for robust T1 and T2 mapping.
1. Introduction
Magnetic Resonance Fingerprinting (MRF) is a technique for simultaneously mapping multiple tissue properties [1,2]. Cardiac MRF (cMRF) has recently been proposed for quantifying myocardial T1, T2, and M0 [3]. To date, cMRF has used a FISP-based pulse sequence with time-varying flip angles, repetition times (TR), and magnetization preparation pulses to produce signal timecourses that depend on underlying relaxation times. A Bloch equation simulation is performed to generate a dictionary containing timecourses for many discrete combinations of T1 and T2. Quantitative maps are obtained by searching the dictionary for the best matching T1 and T2 value at each pixel. Because pattern matching is generally robust to incoherent aliasing artifacts, cMRF can achieve high acceleration factors, and 2D maps can be acquired in one breathhold.
One interesting feature of cMRF is that the acquisition parameters should be extremely flexible. Because measurements are matched to a dictionary of simulated timecourses, signal variations are desirable if they help to better quantify T1 or T2. Ideally, measured relaxation times should be independent of acquisition pattern or scanner. However, each sequence may be sensitive to different confounding effects, and the generation of consistent and accurate measurements may require detailed modeling of spin dynamics. Compared to MRF sequences for other applications, the cardiac-specific acquisition patterns reported use different flip angle and TR series, make extensive use of preparation pulses, and employ electrocardiogram (ECG) triggering, which introduces delay times between imaging periods in each heartbeat [3]. These differences between cardiac MRF and MRF for other applications necessitate an investigation of the effects of confounding factors on cMRF. Moreover, the desire to use cMRF to generate consistent results on a variety of MRI scanners leads to the need for sequences which yield reproducible T1 and T2 maps. Any physical effect that causes the measured timecourses to deviate from those simulated in the dictionary may produce quantitative errors. Ideally, a sequence could be designed which is less susceptible to one or more potential confounding factors; those that cannot be eliminated must be corrected by simulating the effects of error sources, a step which is important for accuracy but time-consuming.
One type of error arises when the obtained flip angles deviate from the nominal flip angles prescribed at the scanner. The original implementation of cMRF assumed an ideal slice profile. However, the actual slice profile rolls off away from the slice center and may have sidelobes, with the specific imperfections depending on radiofrequency (RF) pulse shape and duration. Furthermore, the effect of slice profile on cMRF tissue property maps may be complex since the flip angles vary throughout the scan. Slice profile corrections have been described previously for quantitative T1 and T2 mapping [4–8]. Regarding MRF, several groups have suggested modeling the slice profile in the Bloch equations when generating the dictionary [9–11]. With FISP-based MRF sequences, neglecting to model slice profile generally leads to underestimated T1 and overestimated T2 values. However, slice profile corrections have not yet been investigated with cMRF acquisition patterns, which is important since errors due to slice profile are likely sequence-dependent.
B1+ inhomogeneities cause local deviations in flip angle and are more pronounced at higher field strengths. The original cMRF sequence used small flip angles below 15° to minimize B1+-induced errors. However, this places restrictions on the flip angles which can be selected when designing an acquisition pattern, and B1+ effects in cMRF have not been systematically studied. Several approaches have been proposed for mitigating B1+ errors in other MRF applications. A separate B1+ map can be measured using the Bloch-Siegert technique in 2s per slice [9,12,13]. Then MRF images are matched to a sub-dictionary using the separately measured B1+ value at each pixel. Although the additional B1+ dimension requires a larger dictionary size and more time to create the dictionary, pattern matching is performed relatively quickly because only T1 and T2 are matched at each pixel. Alternatively, B1+ can be mapped jointly with other tissue properties directly from the MRF data. The MRF acquisition can be sensitized to B1+ by appending flip angles with alternating 90° and 0° pulses, which produces signal oscillations with frequencies proportional to the obtained flip angle [14,15]. It has also been proposed to use the first two excitations in the MRF acquisition for actual flip angle imaging [16]. In Plug-and-Play MRF, the illumination pattern of the transmit coil varies throughout the scan, and B1+ maps are estimated during pattern matching [17]. One goal of this study is to investigate the effects of B1+ inhomogeneities on cMRF to identify sequences with low sensitivity to B1+, which could potentially eliminate the need to map B1+ and reduce errors when collecting maps on different scanners.
Another potential source of error in cMRF is imperfect efficiency of the preparation pulses. Compared to other MRF acquisitions, which typically have a single inversion pulse at the beginning of the scan, cMRF relies on multiple inversions and T2 preparations to enhance the sensitivity to T1 and T2. Adiabatic pulses are used because of their robustness to B0 and B1+ [18], but they usually have long durations during which T2 relaxation occurs. For example, tissues with short T2 may experience appreciable relaxation while an inversion pulse is applied, which results in Mz > −1. Imperfect inversion efficiency is partially responsible for T1 underestimation with MOLLI and other inversion recovery-based mapping techniques [19]. One solution is to use optimized preparation pulses with shorter durations and less T2 dependence [20]. Another approach is to introduce a correction term known as an inversion factor (δ) such that [20]. However, δ must be measured empirically on each scanner, and values measured in phantoms can be different from in vivo values [21]. Thus, δ is usually measured in the myocardium in a small group of subjects and then used when processing subsequent datasets [6]. In this study the effect of precisely simulating the magnetization evolution during preparation pulses with the Bloch equations is examined.
The first aim of this work explores different cMRF acquisition patterns under ideal conditions with no confounding factors in order to assess the power of each to distinguish different combinations of T1 and T2. Simulations are presented which describe the accuracy of T1 and T2 maps collected using different schedules of flip angles, TRs, and preparation pulses. Second, the effects of error sources including non-rectangular slice profile, imperfect inversion and T2 preparation efficiency, and B1+ variations on different cMRF acquisition patterns are investigated in simulations. The goal of this second study is to understand which cMRF sequences are least affected by confounding factors, and which factors must be corrected to obtain robust T1 and T2 measurements. Third, a validation study is reported using the ISMRM/NIST system phantom [22]. It is shown that nearly all sequences produce more accurate T1 and T2 measurements after correction, while sequences with smaller maximum flip angles are more robust to slice profile and B1+ effects. Finally, the proposed corrections are tested in cardiac scans of five healthy volunteers at 3T.
2. Materials and Methods
2.1. Dictionary Correction Methods
The following sections explain how corrections for slice profile, preparation pulse efficiency, and B1+ are simulated in the dictionary.
2.1.1. Slice Profile
The MRF slice profile correction introduced in [9] was used in this study. All scans used sinc RF excitations with a duration of 0.8ms and a time bandwidth product of 2. First, the RF and slice-select gradient waveforms were simulated in the sequence programming environment at a sampling interval Δt of 10μs (Supporting Figure S-1A). Five hundred spins were simulated over three times the nominal slice thickness to account for out-of-slice excitation. Signal evolutions were generated independently for each spin, and the corrected dictionary was obtained by adding the complex-valued signals over all spins. The following events were simulated during each TR:
First, the slice-select and slice-rephasing gradients and RF pulse were segmented into bins of width Δt. Within each bin, there was rotation due to the gradients for time Δt/2, instantaneous RF excitation, and another gradient-induced rotation for time Δt/2.
At the echo time, the transverse magnetization was stored in the dictionary.
Free precession until the beginning of the spoiler gradient was simulated in one step.
The spoiler gradient was segmented into bins and simulated as in step 1.
The magnetization at the end of one TR was forwarded to the next TR.
2.1.2. Preparation Pulse Efficiency
Complete inversion may not be achieved if there is appreciable relaxation while the pulse is being applied. Thus, it may be inaccurate to model an inversion as an instantaneous 180° rotation and T2 preparations as instantaneous ±90° rotations. This study used a non-selective adiabatic hyperbolic secant inversion (11ms duration) followed by a spoiler gradient along the slice axis. The T2 preparation module consisted of a 90°x excitation, a train of 180° refocusing pulses, and a 90°−x excitation [23]. The tip-down excitation used a rectangular pulse (0.5ms duration), and the tip-up excitation was a composite 270°x[−360°x] pulse (3.5ms duration). Between the tip-up and tip-down excitations, four refocusing pulses were applied. These were implemented as composite 90°x180°y90°x rotations and were weighted in an MLEV pattern to reduce the sensitivity to B0 and B1+ inhomogeneities [24,25]. In the dictionary, the RF and gradient waveforms for the preparation pulses were simulated as was previously described for the slice profile correction (Figures S-1B and S-1C). The RF and gradient waveforms were segmented into small time steps. A separate dictionary was generated for each of 500 spins, and the corrected dictionary was obtained by adding the timecourses over all spins.
Figure S-2 demonstrates the importance of precisely modeling the magnetization evolution during the preparation pulses. Figure S-2A shows the longitudinal magnetization immediately after an adiabatic inversion for spins with T1=1400ms and several different T2 values. The inversion efficiency decreases as T2 becomes shorter. For T2=50ms, which is representative of myocardium, the inversion efficiency is only 0.93. Figure S-2B shows the longitudinal magnetization immediately after T2 preparation modules with two different T2 preparation times (TE=40ms and TE=80ms) assuming T1=1400ms. The signals generated using the simulated RF and gradient waveforms deviate more from the simple Bloch simulation (which assumes instantaneous ±90° RF rotations) as T2 becomes longer and TE becomes shorter.
2.1.3. B1+
B1+ was modeled as a coefficient that scaled the flip angle series over the entire scan. B1+ was only modeled for sinc excitations since the preparation pulses were assumed to be robust to B1+ inhomogeneities.
2.2. Numerical Simulation of cMRF Sequence Variants
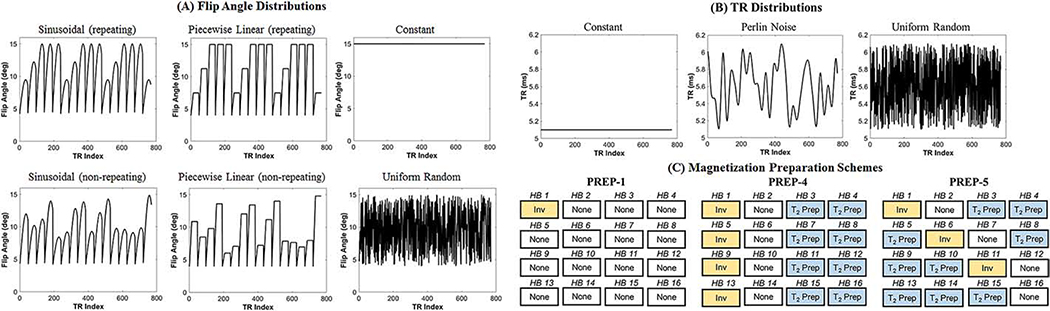
A large number of simulations was performed to heuristically determine a group of cMRF acquisition patterns that allow accurate T1 and T2 quantification. This is not a rigorous optimization, and many other sequence configurations may be feasible. These sequences were selected based on previous studies—which favor smooth flip angle variations, and constant or smooth TR variations—and the physiological constraints of cardiac motion and breath-holding [2,3,26]. Ground truth T1, T2, and M0 maps were created using the MRXCAT numerical cardiac phantom with physiological relaxation times for 3T [27]. All cMRF scans had a duration of 16 heartbeats (HB) with 48 TRs collected every heartbeat after a 600ms trigger electrocardiogram (ECG) trigger delay (see Supporting Figure S-3 for a sequence timing diagram). A constant 60bpm heart rate was assumed. Figure 1 shows several types of flip angles, TRs, and preparation schedules. A total of 648 cMRF acquisition patterns were created using every possible combination of 6 flip angle distributions, 4 maximum flip angles, 3 TR distributions, and 9 preparation schedules. The following sequence parameters were varied:
Figure 1:
Permutations of cMRF acquisition patterns tested in simulations. (A) Six classes of flip angle distributions were used. As described in the main text, for each distribution, simulations were repeated after scaling the entire flip angle series to reach maximum values of 15°, 25°, 50°, and 75°. (b) Three TR distributions were tested. (c) Three schedules of magnetization preparation pulses were investigated. As described in the main text, PREP-4 and PREP-5 schedules were simulated using inversion times and T2 preparation times that were either repeating or non-repeating.
Flip Angle distribution: Six flip angle distribution shapes were tested, ranging from no variations (i.e. constant flip angle) to high frequency oscillations. Some patterns repeated every five heartbeats while others changed throughout the scan to see if there is a benefit to using non-repeating acquisitions.
Maximum flip angle: Each flip angle distribution was scaled to reach a maximum of 15°, 25°, 50° and 75°.
TR distribution shape: Three TR distributions were tested: constant, Perlin noise (which changed gradually) [28], and uniform random (which varied rapidly). The variable TR patterns added a random time from 0–1ms to the minimum TR of 5.3ms.
Preparation pulse schedule: Nine different preparation pulse schedules were tested. The PREP-1 schedule applied an inversion with minimum TI (21ms) before the scan window of the first HB. PREP-4 consisted of an inversion (HB 1), no preparation (HB 2), and two T2 preparations (HB 3–4), and this 4-HB unit was repeated throughout the scan. PREP-5 consisted of an inversion (HB 1), no preparation (HB 2), and three T2 preparations (HB 3–5). This 5-HB unit was repeated throughout the scan. There was a total of 9 different preparation schedules since both PREP-4 and PREP-5 were simulated with repeating or non-repeating TIs and repeating or non-repeating T2 preparation times (see next two bullet points).
Inversion times: Two patterns of TIs were simulated for PREP-4 and PREP-5 schedules. The first pattern used constant minimum TIs of 21ms. The second pattern used variable TIs, which were created using logarithmically spaced values from 21–400ms and randomly permuting the order.
T2 preparation times: Two patterns of T2 preparation times were simulated for PREP-4 and PREP-5 schedules. The first pattern repeated the same TEs throughout the scan—40/80ms for PREP-4 and 30/50/80ms for PREP-5. The second pattern used non-repeating TEs, which were created using logarithmically spaced values from 25–150ms and randomly permuting the order.
For each pulse sequence, a dictionary with 4060 entries was computed with T1 [10:10:90 100:20:1000 1040:40:2000 2050:100:3000]ms and T2 [2:2:8 10:5:100 110:10:300 350:50:800]ms. Reference images were generated by inserting the appropriate timecourse from the dictionary at each pixel location using the ground truth maps. The reference images were scaled by M0 and multiplied by 8-channel simulated coil sensitivity profiles to generate multichannel data. Simulated k-space data were sampled with a variable density spiral trajectory with 0th moment compensation, 192×192 matrix, and 300mm2 FoV [29]. The spiral had 48 interleaves with 24 interleaves needed to fully sample the central 25% region of k-space. Complex Gaussian noise was added in k-space with a mean SNR of 100. Data from one spiral interleaf were gridded using the non-uniform Fast Fourier Transform (NUFFT) every TR to produce undersampled images [30]. The trajectory was rotated by the golden angle (111°) to distribute aliasing artifacts incoherently through time [31]. T1 and T2 maps were generated using a low rank MRF reconstruction as described in [32]. The normalized root mean square error (RMSE) was computed for both T1 and T2 maps over an ROI containing the heart
| (1) |
where j is the pixel index and n is the number of pixels in the ROI.
2.3. Simulation of Slice Profile, Preparation Pulse Efficiency, and B1+
Next the effects of slice profile, preparation efficiency, and B1+ were studied in simulations. A subset of acquisition patterns from the previous simulation was used, as listed in Table 1. SEQ-A is the original implementation of cMRF [3], and SEQ-B has been used in a study of cardiac T1 and T2 in normal volunteers [33]. SEQ-C had the lowest sum of T1 and T2 RMSEs in the previous simulation, and the only difference from SEQ-A is the use of a constant TR. SEQ-C through SEQ-F use sinusoidally varying flip angles that reach maxima of 15°, 25°, 50°, and 75°. SEQ-C, G, H, and I all reach a maximum of 15° but have different flip angle distribution shapes. SEQ-A through SEQ-I are ECG-triggered with a simulated 600ms trigger delay. Forty-eight TRs are acquired every heartbeat, and the scan time for each pulse sequence was fixed at 16 heartbeats, yielding 768 time points for each pulse sequence. SEQ-B through SEQ-I employ constant TRs, so the cardiac scan window is 5.3ms (TR) x 48 (TRs per heartbeat) = 254ms. SEQ-A employs variable TRs from 5.3–6.3ms, so the scan window varies between 262–291ms. SEQ-J is the original implementation of FISP-MRF and does not employ ECG triggering. It employs variable TRs (11–14ms) with a sequence length of 1000 TRs, and the scan time is fixed at 12.5s.
Table 1:
List of MRF acquisition patterns. SEQ-A through SEQ-I are ECG-triggered (i.e. cMRF sequences), while SEQ-J is the original FISP-MRF pattern and is not ECG-triggered.
| Sequence | ECG | Flip Angle Pattern | Max Flip Angle | TR Pattern | Prep Pattern | Inversion Times | T2 Prep Times |
|---|---|---|---|---|---|---|---|
| A | Yes | Sinusoidal (non-repeating) | 15° | Perlin | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| B | Yes | Piecewise linear (repeating) | 25° | Constant | PREP-5 | Repeating (all 21ms) | Repeating (30, 50, 80ms) |
| C | Yes | Sinusoidal (non-repeating) | 15° | Constant | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| D | Yes | Sinusoidal (non-repeating) | 25° | Constant | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| E | Yes | Sinusoidal (non-repeating) | 50° | Constant | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| F | Yes | Sinusoidal (non-repeating) | 75° | Constant | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| G | Yes | Piecewise linear (non-repeating) | 15° | Constant | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| H | Yes | Constant | 15° | Constant | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| I | Yes | Uniform random | 15° | Constant | PREP-4 | Non-repeating (21, 56, 400, and 150ms) | Repeating (40, 80ms) |
| J | No | Sinusoidal (non-repeating) | 75° | Perlin | PREP-1 | One inversion at beginning (21ms) | None |
Four dictionaries were simulated for each acquisition pattern that included corrections for different physical effects. Dictionary D-NONE did not contain additional corrections and was used in the original implementation of cMRF. RF excitations were modeled as instantaneous rotations by the nominal flip angles. Inversions were modeled as instantaneous 180° rotations followed by the nominal TI, and T2 preparations were modeled as a pair of 90° and −90° rotations separated by the nominal TE. Dictionary D-SP included the slice profile correction, and D-PREP included both slice profile and preparation efficiency corrections. D-B1 incorporated the previous corrections and also included B1+ as an additional dimension with values 0.5:0.05:1.5, which brought the total dictionary size to 85,260 entries.
Next, an analysis was performed to assess how T1 and T2 measurements change with each correction for different acquisition patterns. The goal was to determine which sequences were more or less susceptible to confounding factors. First, to study the errors in relaxation times when no corrections are included, a ground truth dictionary including slice profile and preparation efficiency corrections (D-PREP) was matched to a dictionary without corrections (D-NONE) for each sequence. Accuracy was assessed using the relative errors in T1 and T2. The second analysis isolated the effects of the preparation efficiency correction. A ground truth dictionary including both slice profile and preparation efficiency corrections (D-PREP) was matched to a dictionary that only included the slice profile correction (D-SP). The third analysis studied the error tolerance to B1+. A ground truth dictionary with a B1+ scaling factor of 0.7 (i.e. all flip angles reduced by 30%) was matched to a dictionary assuming an ideal B1+ of 1.0; both dictionaries included slice profile and preparation efficiency corrections. This value of B1+ is appropriate since variations up to 50% have been reported across the heart at 3T [34–36].
2.4. Phantom Validation
The ISMRM/NIST system phantom was scanned at 3T (Siemens Skyra, Erlangen, Germany) in an axial orientation with an 18-channel head coil array [22,37]. All T1 and T2 measurements were acquired from the T2 array, which has physiologically relevant ranges for T1 (between 91–2480ms) and T2 (between 6–581ms). An artificial 60bpm heart rate was simulated at the scanner. Other scan parameters included: 8mm slice thickness, 300mm2 FoV, 192×192 matrix, and 1.6×1.6mm2 in-plane resolution. Data were collected using the cMRF acquisition patterns in Table 1 with the same parameters as the previous simulations. Four cMRF dictionaries were created (D-NONE, D-SP, D-PREP, and D-B1) and maps were reconstructed using the low rank reconstruction [32]. Mean T1 and T2 values were computed within 5×5 ROIs in the phantom. Concordance correlation coefficients (CCC) were computed between reference and cMRF measurements using the following equations:
| (2) |
| (3) |
| (4) |
| (5) |
where Y1 is the reference T1 (or T2) value, Y2 is the cMRF T1 (or T2) measurement, and n=14 is the number of ROIs [38]. A linear regression was performed between reference and cMRF measurements with each dictionary type.
2.5. In Vivo Cardiac Mapping
Five healthy volunteers were enrolled in this IRB-approved, HIPAA-compliant study after obtaining written informed consent. Scans were performed during a breathhold in end-expiration in short-axis orientation at a mid-ventricular level. cMRF data acquisition and processing were performed in the same manner as the phantom study. The trigger delay was adjusted for each subject to place the scan window in mid-diastole. ECG timing information was recorded in order to generate scan-specific dictionaries that accounted for changes in heart rhythm [3]. For comparison, T1 maps were collected with 11-HB MOLLI [19], and T2 maps were acquired with a 10-HB T2-prepared FLASH sequence, which are both part of the Siemens MyoMaps software package [39]. The slice thickness, FoV, and spatial resolution were identical to the cMRF scans. ROIs were manually drawn near the intraventricular septum for computing the mean and standard deviation in T1 and T2. The T1 and T2 were first averaged for each volunteer, and the mean and standard deviation of T1 and T2 were calculated among all volunteers.
3. Results
3.1. Numerical Simulation of cMRF Sequence Variants
Table 2 summarizes results using different flip angles and preparation pulse schedules in simulated cMRF experiments. Sequences with PREP-1 preparation schedules yielded the largest errors, although the errors decreased for sequences with higher maximum flip angles. The sum of T1 and T2 RMSEs was marginally lower for PREP-4 than PREP-5 schedules. Interestingly, both constant and uniform random flip angle distributions produced the largest errors in the T1 and T2 maps, especially at higher maximum flip angles. Lower errors were obtained with sinusoidal and piecewise linear flip angles, with the former giving slightly lower errors. For sinusoidal flip angle patterns, the errors were approximately the same whether the flip angle series repeated every five HB (RMSE T1 5.6%, T2 8.4%) or were non-repeating (RMSE T1 5.4%, T2 8.5%). Supporting Table S-1 shows the effect of using different TR patterns for the sequence parameters highlighted in yellow in Table 2 (i.e. the flip angles and preparation pulses with the smallest sum of T1 and T2 RMSEs). The choice of TRs had little effect on the quantitative results, with constant TRs (RMSE T1 5.4%, T2 8.5) yielding marginally lower RMSEs than variable TRs (RMSE T1 5.5%, T2 8.5% for both Perlin and uniform random TRs). Supporting Table S-2 shows the effect of using constant vs. variable inversion and T2 preparation times for the sequence parameters highlighted in yellow in Table 2. The smallest sum of T1 and T2 RMSEs was obtained when the TI varied randomly and T2 preparation times alternated between 40 and 80ms. In summary, the sequence with the minimum RMSE (called SEQ-C in the next sections) consisted of sinusoidally varying FAs between 4–15°, constant TR (5.3ms), inversions every four HB with variable TIs, and T2 preparations every third (TE 40ms) and fourth (TE 80ms) HB. The original implementation of cMRF (called SEQ-A henceforth) used an acquisition pattern that matches the highlighted parameters except for the use of variable Perlin TRs and had RMSE T1 5.6% and T2 8.5%. The cMRF acquisition pattern used in [33] (called SEQ-B henceforth) had RMSE T1 6.3% and T2 10.3%.
Table 2.
Pivot table summarizing the simulation results using a numerical cardiac phantom with different flip angle and preparation pulse schedules. Normalized RMSE values (%) are reported as (T1 RMSE, T2 RMSE). Note that other sequence parameters were also varied, such as inversion times, T2 prep times, and TRs. Each entry in this pivot table reports RMSE values from the sequence having the smallest sum of T1 and T2 RMSEs out of all other sequences with the same flip angles and preparation pulse schedules.
| Flip Angle Pattern | Max FA 15° | Max FA 25° | Max FA 50° | Max FA 75° | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prep-1 | Prep-4 | Prep-5 | Prep-1 | Prep-4 | Prep-5 | Prep-1 | Prep-4 | Prep-5 | Prep-1 | Prep-4 | Prep-5 | |
| Sine (repeating) | 4.8, 47.5 | 5.6, 8.4 | 5.3, 9.4 | 5.2, 27.1 | 6.0, 8.2 | 5.5, 9.1 | 6.1, 14.0 | 6.7, 9.3 | 6.6, 10.3 | 7.3, 11.9 | 7.3, 10.6 | 7.7, 12.8 |
| Sine (non-repeating) | 5.0, 34.8 | 5.4, 8.5 | 5.3, 10.2 | 5.7, 18.9 | 5.9, 9.2 | 5.9, 9.6 | 6.2, 12.1 | 6.0, 9.7 | 6.3, 10.5 | 7.7, 10.4 | 6.8, 10.8 | 6.9, 11.3 |
| Piecewise linear (non-repeating) | 5.3, 27.1 | 6.1, 9.0 | 5.8, 10.6 | 5.9, 21.3 | 6.4, 8.6 | 6.1, 10.1 | 6.6, 11.5 | 6.7, 10.0 | 6.7, 11.5 | 7.9, 11.1 | 7.7, 11.2 | 8.3, 14.2 |
| Piecewise linear (repeating) | 6.0, 22.9 | 5.7, 9.2 | 5.7, 11.6 | 7.0, 18.2 | 6.5, 9.8 | 6.7, 10.1 | 7.6, 11.0 | 6.3, 10.2 | 6.2, 11.0 | 9.2, 9.7 | 7.8, 11.2 | 7.7, 11.6 |
| Constant | 11.7, 36.0 | 9.5, 15.2 | 11.7, 17.4 | 17.8, 54.0 | 13.8, 19.7 | 16.5, 28.2 | 30.7, 40.4 | 25.1, 33.4 | 27.6, 54.4 | 46.2, 39.8 | 46.8, 47.4 | 48.1, 69.4 |
| Uniform random | 10.8, 42.1 | 9.8, 15.2 | 11.1, 19.6 | 14.8, 38.5 | 12.0, 19.7 | 14.7, 26.0 | 19.9, 38.2 | 18.1, 30.7 | 20.3, 44.1 | 26.0, 42.1 | 26.0, 44.5 | 31.1, 49.0 |
3.2. Simulation of Slice Profile, Preparation Pulse Efficiency, and B1+
Supporting Figure S-4 shows examples of signal evolutions with T1=1400ms and T2=50ms, which are values representative of myocardium at 3T, for nine cMRF acquisition patterns (SEQ-A through SEQ-I) as well as the original ungated FISP-MRF acquisition (SEQ-J). Signals are plotted after corrections for slice profile, preparation pulse efficiency, and B1+ are successively included in the dictionary. Figure 2A shows the percent errors in T1 and T2 when slice profile and preparation efficiency are not modeled in the dictionary. T1 is underestimated with all sequences. T2 estimates are dependent on the flip angle series. Sequences with maximum flip angles of 25° or lower tend to underestimate T2 (SEQ-A, C, D, G, H, and I), while those with larger flip angles overestimate T2 (SEQ-E, F, and J). Table 3 shows the percent errors in T1 and T2 for spins with typical myocardial relaxation times. Compared to the cMRF acquisition patterns (SEQ-A through SEQ-I), the original FISP-MRF acquisition (SEQ-J) is more sensitive to slice profile effects, where myocardial T1 is underestimated by 11% and T2 overestimated by 62.5%. The same analysis was performed using a dictionary that corrects for slice profile but does not model inversion and T2 preparation pulse efficiency (Figure 2B). Although T1 estimates match the ground truth almost exactly, T2 is slightly overestimated by many cMRF sequences, with myocardial T2 overestimated up to 5%. Figure 2C shows the percent errors due to a 30% change in B1+ (from 1.0 to 0.7). The matched T1 is relatively robust to B1+ changes of this magnitude. However, T2 is slightly overestimated by cMRF sequences with maximum flip angles 50° or greater (SEQ-E and SEQ-F) and markedly overestimated by the original FISP-MRF sequence (SEQ-J). The errors induced by B1+ depend on the maximum flip angle in the series, which is seen by comparing the percent errors in myocardial T2 for SEQ-C (error −4.2%, max flip angle 15°), SEQ-D (error 0.0%, max flip angle 25°), SEQ-E (error 5.2%, max flip angle 50°), and SEQ-F (error 10.4%, max flip angle 75°).
Figure 2:
Contour of relative errors in T1 and T2 when different confounding effects are not modeled in the dictionary. (A) A ground truth dictionary with slice profile and preparation efficiency effects was matched to a dictionary that assumed instantaneous RF excitations (i.e. no corrections). (B) A ground truth dictionary with slice profile and preparation efficiency effects was matched to a dictionary that corrected for slice profile but assumed instantaneous inversions and T2 preparations. (C) A ground truth dictionary with B1+=0.7 (all flip angles reduced by 30%) was matched to a dictionary with B1+=1.0.
Table 3:
Relative errors in relaxation times for different acquisition patterns when T1=1400ms and T2=50ms, which are values representative of myocardial tissue at 3T. Each row refers to a physical effect or system imperfection that was modeled when generating the ground truth cMRF signal timecourses but not modeled when matching to the dictionary.
| Dictionary Corrections | cMRF Acquisition Pattern | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | ||
| Neglecting slice profile and preparation pulse efficiency; Ground truth B1+ is 100% | T1 Error (%) | −5.5 | −8.3 | −8.3 | −8.3 | −8.3 | −10.5 | −8.3 | −8.3 | −5.5 | −11.1 |
| T2 Error (%) | −4.2 | 5.2 | −4.2 | 0.0 | 10.4 | 15.6 | 0.0 | 0.0 | −6.2 | 62.5 | |
| Neglecting preparation pulse efficiency; Ground truth B1+ is 100% | T1 Error (%) | 0.0 | −2.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | −0.5 | 0.0 |
| T2 Error (%) | 5.2 | 4.5 | 5.2 | 5.2 | 0.0 | 0.0 | 5.2 | 5.2 | 6.1 | 0.0 | |
| Neglecting B1+; Ground truth B1+ is 70% | T1 Error (%) | 2.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.2 | −2.8 |
| T2 Error (%) | −4.2 | 1.0 | −4.2 | 0.0 | 5.2 | 10.4 | −3.6 | 0.0 | −4.2 | 46.9 | |
3.3. Phantom Validation
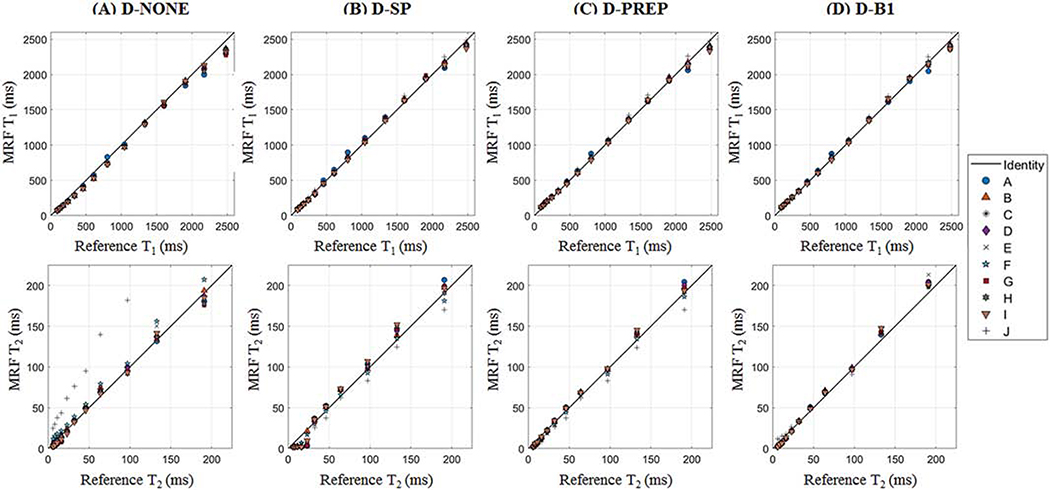
Figure 3 shows the changes in T1 and T2 in the ISMRM/NIST phantom after each correction is included in the dictionary. Although the largest T2 in the phantom is 581ms, the T2 axis is scaled from 0–225ms to visualize the ranges relevant for cardiac parameter mapping. For most acquisition patterns, T1 is slightly underestimated and T2 is overestimated when the dictionary does not include additional corrections. With slice profile correction, the T2 overestimation is less pronounced, although there are errors when T2 is very short (less than 20ms). A stronger linear agreement between cMRF and reference values is obtained when also correcting for incomplete preparation efficiency. A slightly better correlation is obtained when B1+ is matched as an additional property in the dictionary. However, the most noticeable improvement with B1+ is seen for the original FISP-MRF (SEQ-J) and not the cMRF sequences (SEQ-A through SEQ-I). Supporting Table S-3 reports the y-intercept, slope, and coefficient of determination (R2) for the best-fit lines between the reference and cMRF T1 and T2 values using different acquisition patterns and dictionary corrections.
Figure 3:
Scatterplots of reference vs cMRF T1 and T2 measurements for different acquisition patterns, labeled A-J. The dictionary was simulated using (A) no corrections (D-NONE), (B) slice profile correction only (D-SP), (C) slice profile correction and the proposed method for simulating preparation pulses (D-PREP), and (D) slice profile correction, the proposed method for simulating preparation pulses, and B1+ correction (D-B1). The identity line is displayed on each plot.
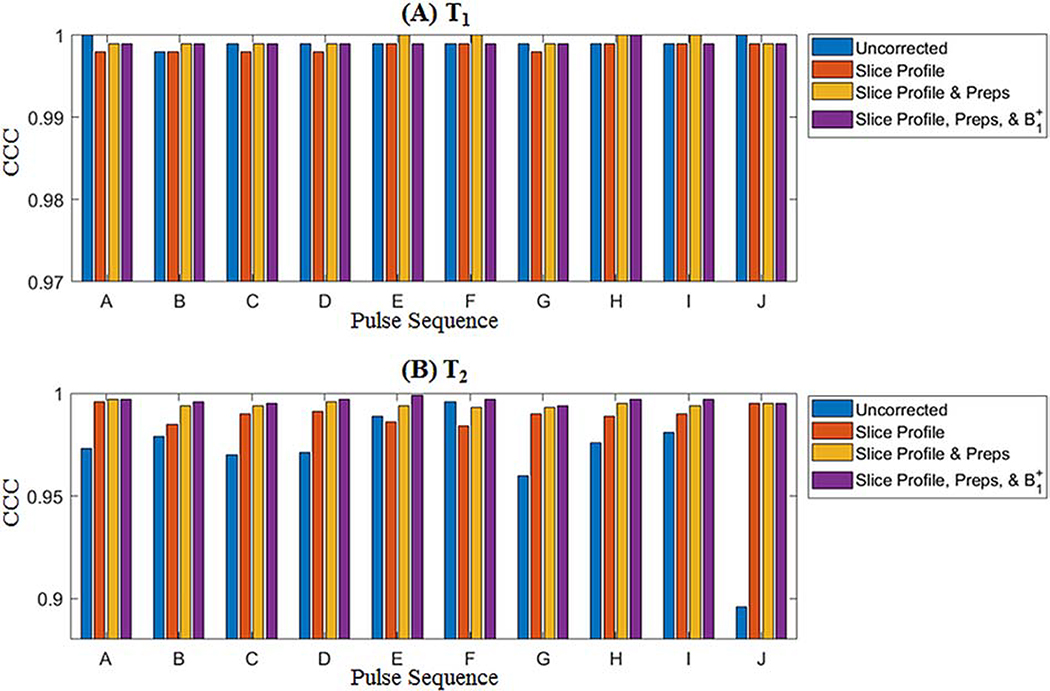
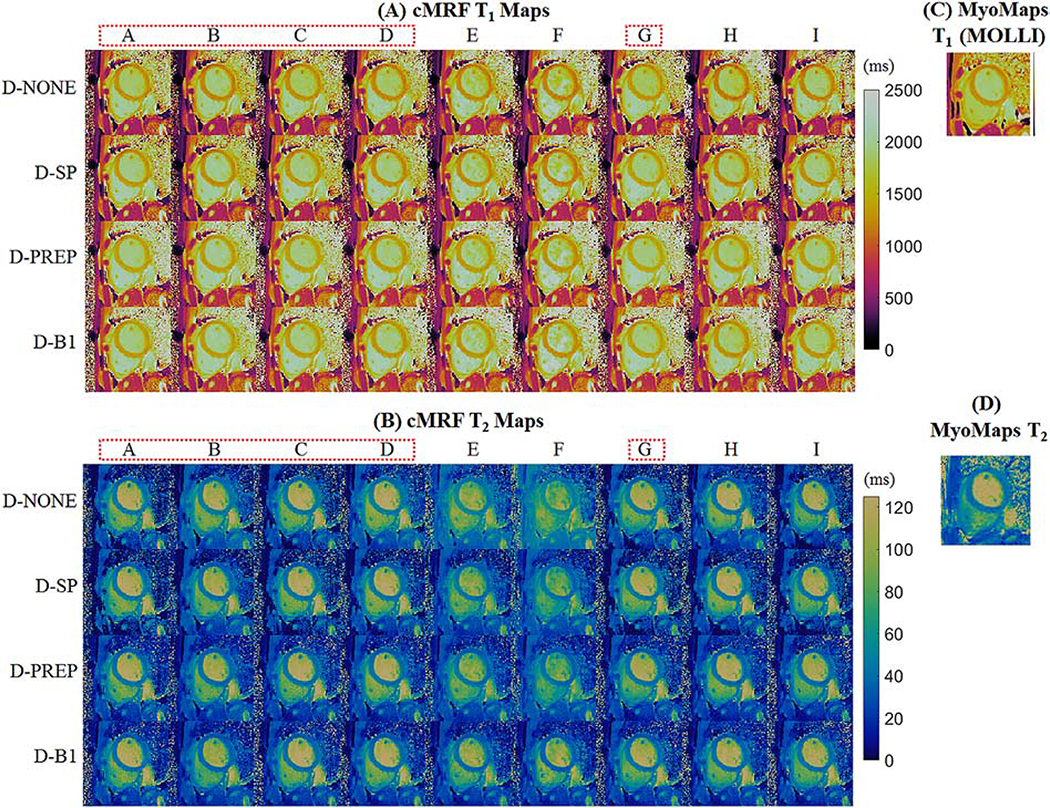
CCC values between cMRF and reference measurements are presented in Figure 4. The CCC for T1 is above 0.998 regardless of pulse sequence and correction method. For the uncorrected dictionary, T2 CCC values vary markedly for different sequences, from 0.896 for SEQ-J (the original ungated MRF FISP sequence) to 0.996 to SEQ-F. In general, the T2 CCC progressively increases as each correction is added; the mean over all sequences is 0.969 (D-NONE), 0.990 (D-SP), 0.994 (D-PREP), and 0.997 (D-B1). The consistency in measurements using different sequences also improves as each correction is added; the range in T2 CCC values over all sequences is 0.101 (D-NONE), 0.012 (D-SP), 0.004 (D-PREP), and 0.005 (D-B1). Representative T1 and T2 maps from each sequence before (D-NONE) and after each correction (D-SP, D-PREP, and D-B1) are shown in Figure 5.
Figure 4:
Concordance correlation coefficients (CCC) between cMRF and reference measurements in the ISMRM/NIST system phantom with different acquisition patterns, labeled A-J, for (A) T1 and (B) T2.
Figure 5:
cMRF T1 and T2 maps from the T2 array of the ISMRM/NIST system phantom using different acquisition patterns, labeled A-J. Maps are shown after matching to dictionaries with no additional corrections (D-NONE); slice profile correction (D-SP); slice profile and preparation pulse efficiency corrections (D-PREP); and slice profile, preparation pulse efficiency, and B1+ corrections (D-B1).
3.4. In Vivo Cardiac Mapping
Table 4 shows myocardial T1 and T2 measurements averaged over five volunteers collected with different cMRF acquisition patterns. The spread in T1 measurements decreases after all corrections are included in the dictionary (range 74ms with D-NONE vs 47ms with D-B1). The mean T1 over all sequences before corrections is 1218ms, which increases to 1260ms after slice profile correction and again to 1342ms after the preparation efficiency correction. The B1+ correction causes a slight decrease in the mean T1 to 1323ms. After all corrections, cMRF T1 values (1323 ± 47ms) are almost 100ms longer than those obtained with MOLLI (1227 ± 30ms). There is a large spread in cMRF T2 measurements before corrections (mean T2 41.2ms, range 9.4ms across acquisition patterns). In general, there is an overestimation in T2 that becomes more severe when the maximum flip angle increases. This trend can be seen by comparing the T2 values from SEQ-C (max flip angle 15°, T2 40.3 ± 3.3ms) through SEQ-F (max flip angle 75°, T2 47.3 ± 3.4ms). The slice profile correction reduces the variation in T2 among different sequences (mean T2 38.1ms, range 5.0ms). Correcting for preparation efficiency causes a slight decrease in average T2 (mean T2 36.7ms, range 4.4ms), and the B1+ correction results in little change (mean T2 37.2ms, range 4.4ms). The cMRF myocardial T2 values after correction agree well with the T2-prepared FLASH measurements (38.4 ± 3.1ms). Representative cMRF maps from one volunteer using different sequences before and after corrections are shown in Figure 6 along with conventional T1 and T2 maps. From a visual inspection, the T1 and T2 values in the myocardial wall after all corrections (D-B1) appear more consistent across different sequences. In particular, SEQ-E and SEQ-F, which employ larger flip angles, yield higher myocardial T2 values than other sequences before corrections.
Table 4:
Myocardial T1 and T2 measurements at 3T using different cMRF acquisition patterns, labeled A-I. Values are reported after matching to dictionaries with no additional corrections (D-NONE); slice profile correction (D-SP); slice profile and preparation pulse efficiency corrections (D-PREP); and slice profile, preparation pulse efficiency, and B1+ corrections (D-B1).
| SEQ | D-NONE | D-SP | D-PREP | D-B1 | ||||
|---|---|---|---|---|---|---|---|---|
| T1 (ms) | T2 (ms) | T1 (ms) | T2 (ms) | T1 (ms) | T2 (ms) | T1 (ms) | T2 (ms) | |
| A | 1255 ± 56 | 41.3 ± 3.5 | 1299 ± 52 | 40.3 ± 3.3 | 1365 ± 51 | 39.1 ± 3.3 | 1324 ± 53 | 38.9 ± 3.3 |
| B | 1207 ± 35 | 41.1 ± 3.1 | 1264 ± 40 | 37.0 ± 2.8 | 1346 ± 39 | 35.2 ± 2.5 | 1326 ± 33 | 35.2 ± 3.0 |
| C | 1242 ± 44 | 40.3 ± 3.3 | 1291 ± 51 | 39.0 ± 3.4 | 1365 ± 45 | 37.7 ± 3.3 | 1337 ± 46 | 38.5 ± 3.5 |
| D | 1221 ± 44 | 41.9 ± 3.0 | 1248 ± 42 | 38.1 ± 3.1 | 1331 ± 40 | 37.4 ± 3.0 | 1318 ± 44 | 37.6 ± 3.0 |
| E | 1186 ± 43 | 43.8 ± 3.4 | 1200 ± 37 | 35.3 ± 3.1 | 1303 ± 35 | 34.6 ± 2.7 | 1296 ± 41 | 34.6 ± 3.8 |
| F | 1194 ± 54 | 47.3± 3.4 | 1223 ± 56 | 36.5 ± 2.9 | 1309 ± 55 | 35.1 ± 2.6 | 1317 ± 55 | 36.6 ± 4.5 |
| G | 1251 ± 53 | 38.9 ± 2.7 | 1304 ± 55 | 38.1 ± 2.8 | 1375 ± 51 | 37.0 ± 2.6 | 1343 ± 53 | 37.4 ± 2.8 |
| H | 1181 ± 64 | 38.5± 2.7 | 1227 ± 56 | 39.0 ± 3.5 | 1320 ± 57 | 37.0 ± 3.0 | 1309 ± 55 | 37.2 ± 3.3 |
| I | 1227 ± 62 | 37.9± 3.1 | 1280 ± 56 | 39.5 ± 3.3 | 1361 ± 61 | 37.3 ± 2.8 | 1339 ± 59 | 39.0 ± 3.0 |
| Min | 1181 | 37.9 | 1200 | 35.5 | 1303 | 34.6 | 1296 | 34.6 |
| Max | 1255 | 47.3 | 1304 | 40.3 | 1375 | 39.1 | 1343 | 39.0 |
| Range | 74 | 9.4 | 104 | 5.0 | 72 | 4.4 | 47 | 4.4 |
| Mean | 1218 | 41.2 | 1260 | 38.1 | 1342 | 36.7 | 1323 | 37.2 |
| Stdev | 26 | 2.8 | 35 | 1.5 | 25 | 1.4 | 14 | 1.5 |
Figure 6:
Representative cMRF (A) T1 and (B) T2 maps from one volunteer at 3T. Maps are shown after matching to dictionaries with no additional corrections (D-NONE); slice profile correction (D-SP); slice profile and preparation pulse efficiency corrections (D-PREP); and slice profile, preparation pulse efficiency, and B1+ corrections (D-B1). The dotted red lines highlight those acquisition patterns which also produced acceptably low RMSEs in simulation and were robust to slice profile and B1+ effects. Conventional maps collected with (C) MOLLI and (D) T2-prepared FLASH are shown for comparison.
4. Discussion
This study examined the effects of confounding factors in cMRF T1 and T2 measurements to (1) demonstrate that different pulse sequences yield equivalent tissue property maps when appropriately corrected, (2) enable the selection of a sequence minimally affected by these confounding factors, and (3) suggest which factors should be modeled in the dictionary for accurate and reproducible results. The confounding factors examined here were slice profile imperfections, incomplete inversions and T2 preparations, and B1+ inhomogeneities. Previously, corrections for slice profile and B1+ have been proposed for MRF. However, these methods focused on brain [9,14,15] and abdominal [13] applications, and they used different sequence parameters. This work also introduced a method to correct for relaxation during inversions and T2 preparation pulses. This correction is especially important for ECG-triggered cMRF sequences that rely on preparation pulses to achieve sufficient T1 and T2 sensitivity.
One advantage of MRF is that the choice of pulse sequence is extremely flexible. Ideally, all sequences should result in the same T1 and T2 measurements as long as the signal evolutions can be differentiated and the appropriate confounding factors corrected. Correcting for such effects may make cMRF more robust across different scanners compared to conventional quantitative cardiac mapping methods, which may require rigorous tuning or calibration. Indeed, the SCMR consensus statement on parametric mapping suggests that normative values should be established on each scanner when working with MOLLI [40]. By selecting a cMRF sequence that is relatively insensitive to confounding effects and correcting the remaining error sources, it may be possible to achieve relaxation time measurements that are not vendor, software version, or hardware dependent.
The first part of this study performed a brute force comparison of different cMRF sequences to elucidate common features that enable encoding of T1 and T2 under ideal circumstances. A rigorous optimization of sequence parameters was not performed but is an active research area [26,41–44]. Simulations were performed that mimicked an actual cMRF experiment using a digital cardiac phantom with added noise, coil sensitivities, and an undersampled spiral trajectory, and sequences were compared using the RMSE in the reconstructed T1 and T2 maps. It was found that smoothly varying sinusoidal flip angle patterns yielded the lowest errors. The TR pattern had less impact on the quantitative results. For cMRF, a short constant TR may be preferred in order to minimize the scan window and reduce cardiac motion artifacts. Sequences with multiple inversion pulses and T2 preparations (e.g. PREP-4 and PREP-5) outperformed sequences with one inversion at the beginning of the scan, as is commonly done in MRF, with slightly lower RMSEs for PREP-4 sequences. cMRF has waiting periods between heartbeats where signals recover and lose some T1 and T2 weighting, and preparation pulses help to restore the T1 and T2 sensitivity.
This study also simulated the effects of several types of system imperfections on different cMRF sequence patterns. The goal of this section was to determine which confounding factors could be minimized by selecting an appropriate pulse sequence, and which must be corrected in post-processing. As seen from the simulations (Figure 2 and Table 3), a non-rectangular slice profile generally led to underestimated T1 and overestimated T2 values for most sequences. Slice profile errors were present in all acquisition patterns but were more pronounced for sequences containing larger flip angles. The slice profile correction improved both T1 and T2 in phantoms (Figures 3–4). In vivo, the mean myocardial T1 across all sequences increased from 1218ms to 1260ms and the mean T2 decreased from 41.2 to 38.1ms after slice profile correction (Table 4). The inclusion of slice profile corrections in cMRF data processing could enable the use of shorter RF pulses, which may allow a shorter scan window or breath-holding time, thereby reducing motion artifacts. Alternatively, more undersampled images could be acquired within the same scan window to improve pattern matching precision by providing additional data points.
In addition to slice profile, the effects of modeling inversion and T2-preparation pulse efficiency on the resulting T1 and T2 maps were explored for the first time. Relaxation during inversion or T2 preparation pulses generally caused T1 underestimation and T2 overestimation (Figure 2 and Table 3). Correcting for this effect improved the agreement between cMRF and reference values in the phantom (Figures 3–4). In vivo, these corrections increased myocardial T1 estimates (mean T1 over all sequences increased from 1260 to 1342ms).
Finally, errors in T1 and T2 maps due to B1+-induced variations in the flip angle series were explored. Again, the goal of this section was to identify potential sequences that minimize the effects of this source of error. B1+ effects were conspicuous for sequences containing larger flip angles of 50° or above. Correcting for B1+ improved T2 CCC values in the phantom (Figure 4) and caused slight differences in myocardial T1 and T2 in vivo (Figure 6).
It is well-reported that MOLLI produces lower myocardial T1 values than SASHA. At 3T, T1 measurements have been reported between 1050–1150ms for MOLLI [45,46] and 1487ms for SASHA [47,48]. The T1 underestimation in MOLLI is partly due to imperfect T2-dependent inversion in myocardial tissue [49], which has a short T2 below 50ms. cMRF T1 measurements before correction (1181–1255ms, Table 4) were slightly higher than literature MOLLI T1 measurements (1050–1150ms) although in agreement with MOLLI values obtained in this study (1197–1257ms). After corrections, the cMRF T1 measurements increased (1296–1343ms, Table 4), which are similar although still lower than literature SASHA T1 ranges.
Although errors due to slice profile, preparation efficiency, and B1+ can be corrected in the dictionary, it may be better to use sequences that are inherently robust against confounding effects. In particular, SEQ-A, B, C, D, and G produced accurate T1 and T2 maps in simulations (Table 2) and were least sensitive to slice profile, preparation efficiency, and B1+ (Figure 2, Table 3). In vivo maps generated from these acquisition patterns are highlighted in Figure 6. In general, these sequences contain small flip angles no greater than 25° and have multiple adiabatic inversions and T2 preparation pulses. SEQ-E and F, which employ larger flip angles, were more affected by slice profile imperfections and B1+ variations. Sequences H and I have smaller flip angles (maximum 15°) and were less sensitive to slice profile and B1+ effects. However, their flip angle patterns (constant and uniform random) may have lower T1 and T2 encoding power, which resulted in the larger T1 and T2 RMSEs in simulations. Of the sequence variants that were investigated, SEQ-C is recommended and will be employed in future studies since it produced the smallest RMSEs in simulations, gave accurate measurements in phantoms, and was robust to B1+ effects. Note that SEQ-C is identical to the original cMRF acquisition pattern (SEQ-A) except for the use of a constant TR [3].
Computation time is important to consider in cMRF because a new dictionary must be generated after each scan in order to incorporate scan-specific heart rate variations. This is different from other MRF applications that use fixed sequence timings, where it is acceptable to perform time-consuming computations upfront to create the dictionary since it can be used for subsequent scans. The dictionary without corrections (D-NONE) took approximately 12s to simulate on a standalone PC running MATLAB Mex code. The dictionary with slice profile correction (D-SP) was distributed to 8 nodes on a high-performance cluster with 12 cores per node and took 9 minutes to complete. The dictionary with slice profile and preparation efficiency corrections (D-PREP) was simulated using the same cluster configuration with a runtime of 10 minutes. The dictionary with B1+ corrections (D-B1) was distributed to 120 nodes (more nodes were used because of the larger dictionary size) and completed in roughly 20 minutes. Therefore, there is a tradeoff between accurate modeling of spin dynamics and reconstruction time, which may pose a challenge for online reconstructions. However, these problems could be addressed using optimized code, better parallelization, and GPU computing. Another way to reduce reconstruction time is to implement only the most important corrections. Thus, it may be recommended to use a sequence (like SEQ-C) that is less sensitive to B1+ and to only correct for slice profile and preparation pulse efficiency. These corrections only increase the dictionary generation time but not the dictionary size.
Moving to a 3D cMRF acquisition could obviate the need for slice profile correction since only the edges of the imaging volume would be affected by RF profile roll-off. While 3D MRF has been explored in other applications [50–52], cardiac and respiratory motion currently preclude the use of these sequences in the heart, although this is an active area of study. Whether gated or free-running, such 3D sequences will require optimization or at least an exploration of the potential error sources as performed in this study. It is anticipated that such sequences will still require correction for error sources such as relaxation during preparation pulses and B1+.
In addition, optimized RF pulses could improve the quantitative accuracy of cMRF. The hyperbolic secant inversion used in this study had a relatively long duration of 11ms. Using an inversion with a shorter duration could reduce the amount of T2 relaxation during the pulse and place less burden on the preparation efficiency correction.
This study has several limitations. First, the cMRF sequence was not optimized using an objective function, which could lead to a sequence superior in terms of its ability to distinguish relevant T1 and T2 values and its sensitivity to confounding factors. Secondly, the slice profile correction assumes there is only a single tissue type across the slice direction. Third, B1+ was only modeled for the sinc RF excitations. The adiabatic inversions and MLEV-weighted T2 preparations were assumed to be sufficiently tolerant to B1+ inhomogeneities, although the impact of B1+ on these pulses could be explored in future work. Fourth, acquisition patterns with large flip angle variations could result in nonlinearities in the RF amplifier. In this case, it may not be accurate to model B1+ as a single coefficient that scales the entire flip angle series. Fifth, errors due to heart rate variations were not considered in this study. The original cMRF publication demonstrated that modeling the subject’s actual heart rate in the dictionary minimized such errors; however, those results were only presented for SEQ-A. It is possible that the best sequence variants (in terms of accuracy and precision) may depend on heart rate, and that the impact of the dictionary corrections varies with heart rate. Finally, the combinations of T1 and T2 in the ISMRM/NIST system phantom do not exactly reflect biological tissue. For example, the T1/T2 ratios in the T2 array of the phantom range from 4.3–16.3. However, assuming a myocardial T1 of 1323ms and T2 of 37.2ms (from Table 4), the T1/T2 ratio is much higher at 35.6. Thus, the slice profile, preparation efficiency, and B1+ corrections may have different effects in the phantom and in vivo studies.
Lastly, there are many physical effects that could introduce quantitative errors that have not been considered in this study. Magnetization transfer (MT) is partially responsible for T1 underestimation in inversion-recovery based mapping sequences, such as MOLLI [53]. Spins bound to macromolecules are off-resonant and therefore not affected by the inversion pulse. When they exchange magnetization with spins in free water, an artificially shortened effective T1 is observed. cMRF acquisition patterns that employ inversion pulses would be susceptible to MT errors. MT effects are intensified at higher flip angles, which may explain some of the variation in T1 and T2 measured in vivo, such as the lower T2 seen with SEQ-E and SEQ-F (Table 4). Another possible source of error is partial volume with blood or fat in the myocardial wall, since each voxel is assumed to contain a single tissue component. For example, lower T1 measurements with both cMRF and MOLLI in the anterior wall (Figure 6) may be caused by partial volume between myocardium and fat. Partial volume effects could be mitigated by improving the spatial resolution or modeling each voxel with multiple compartments. Finally, residual cardiac or respiratory motion from the relatively long 250ms scan window and 16-heartbeat breathhold may lead to quantitative errors or blurring. Using shorter scan windows or breathholds will be investigated in future studies.
5. Conclusions
In conclusion, the effects of sources of error—namely imperfect slice profile, relaxation during inversion and T2 preparation pulses, and B1+ variations—on the accuracy of different cMRF pulse sequences were explored. Modeling these phenomena in the cMRF dictionary can improve the accuracy of and consistency between T1 and T2 values collected with different acquisition patterns. The first part of this study identified acquisition patterns that enable efficient encoding of myocardial T1 and T2. Moreover, sequences which were robust against some errors, particularly B1+ variations, were identified. These sequences may be better candidates for deployment on multiple scanners when seeking reproducible tissue property measurements. Other physical effects, including relaxation during pulses and slice profile imperfections, could not be reduced through the selection of an appropriate TR and flip angle train, and are thus important to include in the dictionary calculation. The benefit of including these corrections was demonstrated in phantom experiments, where T1 and T2 values from various cMRF pulse sequences exhibited improved accuracy and consistency after corrections. In vivo, these corrections lead to cMRF T1 values higher than those obtained with MOLLI, although lower than reported in SASHA, and cMRF T2 values which agreed with a conventional T2-prepared FLASH technique.
Supplementary Material
Funding Sources
This work was funded by the National Institutes of Health (NIH/NHLBI R01HL094557, NIH/NIDDK R01DK098503, NIH/NIBIB R01EB016728), National Science Foundation (NSF CBET 1553441), and Siemens Healthineers (Erlangen, Germany).
Declarations of Interest: This work was funded by the National Institutes of Health (NIH/NHLBI R01HL094557, NIH/NIDDK R01DK098503, NIH/NIBIB R01EB016728), National Science Foundation (NSF CBET 1553441), and Siemens Healthineers (Erlangen, Germany). The funding sources had no involvement in the study design; collection, analysis and interpretation of data; in the writing of the report; and in the decision to submit the article for publication.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, et al. Magnetic resonance fingerprinting. Nature 2013;495:187–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn Reson Med 2015;74:1621–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Hamilton JI, Jiang Y, Chen Y, Ma D, Lo WC, Griswold M, et al. MR fingerprinting for rapid quantification of myocardial T1, T2, and proton spin density. Magn Reson Med 2017;77:1446–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Tran-Gia J, Wech T, Hahn D, Bley TA, Köstler H. Consideration of slice profiles in inversion recovery Look–Locker relaxation parameter mapping. Magn Reson Imaging 2014;32:1021–30. doi: 10.1016/j.mri.2014.05.012. [DOI] [PubMed] [Google Scholar]
- [5].Cooper MA, Nguyen TD, Spincemaille P, Prince MR, Weinsaft JW, Wang Y. Flip angle profile correction for T1 and T2 quantification with look-locker inversion recovery 2D steady-state free precession imaging. Magn Reson Med 2012;000:1–7. doi: 10.1002/mrm.24151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Shao J, Rapacchi S, Nguyen K-L, Hu P. Myocardial T1 mapping at 3.0 tesla using an inversion recovery spoiled gradient echo readout and bloch equation simulation with slice profile correction (BLESSPC) T1 estimation algorithm. J Magn Reson Imaging 2016;43:414–25. doi: 10.1002/jmri.24999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Ehses P, Seiberlich N, Ma D, Breuer FA, Jakob PM, Griswold MA, et al. IR TrueFISP with a golden-ratio-based radial readout: fast quantification of T1, T2, and proton density. Magn Reson Med 2013;69:71–81. doi: 10.1002/mrm.24225. [DOI] [PubMed] [Google Scholar]
- [8].McRobbie DW, Lerski RA, Straughan K. Slice profile effects and their calibration and correction in quantitative NMR imaging. Phys Med Biol 1987;32:971–83. doi: 10.1088/0031-9155/32/8/002. [DOI] [Google Scholar]
- [9].Ma D, Coppo S, Chen Y, McGivney DF, Jiang Y, Pahwa S, et al. Slice profile and B 1 corrections in 2D magnetic resonance fingerprinting. Magn Reson Med 2017;78:1781–9. doi: 10.1002/mrm.26580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Hong T, Han D, Kim MO, Kim DH. RF slice profile effects in magnetic resonance fingerprinting. Magn Reson Imaging 2017;41:73–9. doi: 10.1016/j.mri.2017.04.001. [DOI] [PubMed] [Google Scholar]
- [11].Chiu S-C, Lin T-M, Lin J-M, Chung H-W, Ko C-W, Büchert M, et al. Effects of RF pulse profile and intra-voxel phase dispersion on MR fingerprinting with balanced SSFP readout. Magn Reson Imaging 2017;41:80–6. doi: 10.1016/j.mri.2017.04.002. [DOI] [PubMed] [Google Scholar]
- [12].Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. Magn Reson Med 2010;63:1315–22. doi: 10.1002/mrm.22357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Chen Y, Jiang Y, Pahwa S, Ma D, Lu L, Twieg MD, et al. MR Fingerprinting for Rapid Quantitative Abdominal Imaging. Radiology 2016;279:278–86. doi: 10.1148/radiol.2016152037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Buonincontri G, Sawiak SJ. MR fingerprinting with simultaneous B1 estimation. Magn Reson Med 2016;76:1127–35. doi: 10.1002/mrm.26009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Buonincontri G, Schulte R, Cosottini M, Sawiak SJ, Tosetti M. Spiral MRF at 7T with simultaneous B1 estimation. Magn Reson Med 2016:0433. doi: 10.1002/mrm.26009. [DOI] [PubMed] [Google Scholar]
- [16].Hong T, Kim M-O, Han D, Hwang D, Kim D-H. B1+ inhomogeneity compensated MRF using simultaneous AFI. Proc ISMRM 23, 2014, p. 3248. [Google Scholar]
- [17].Cloos MA, Knoll F, Zhao T, Block KT, Bruno M, Wiggins GC, et al. Multiparametric imaging with heterogeneous radiofrequency fields. Nat Commun 2016;7. doi: 10.1038/ncomms12445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Tannús A, Garwood M. Adiabatic pulses. NMR Biomed 1997;10:423–34. doi:. [DOI] [PubMed] [Google Scholar]
- [19].Messroghli DR, Radjenovic A, Kozerke S, Higgins DM, Sivananthan MU, Ridgway JP. Modified look-locker inversion recovery (MOLLI) for high-resolution T 1 mapping of the heart. Magn Reson Med 2004;52:141–6. doi: 10.1002/mrm.20110. [DOI] [PubMed] [Google Scholar]
- [20].Kellman P, Herzka DA, Hansen MS. Adiabatic inversion pulses for myocardial T1 mapping. Magn Reson Med 2014;71:1428–34. doi: 10.1002/mrm.24793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Shao J, Nguyen KL, Natsuaki Y, Spottiswoode B, Hu P. Instantaneous signal loss simulation (InSiL): An improved algorithm for myocardial T1mapping using the MOLLI sequence. J Magn Reson Imaging 2015;41:721–9. doi: 10.1002/jmri.24599. [DOI] [PubMed] [Google Scholar]
- [22].Russek SE, Boss M, Jackson EF, Jennings DL, Eveloch JL, Gunter JL, et al. C haracterization of NIST/ISMRM MRI System Phantom. Proc. 20th Annu. Meet. ISMRM, 2012, p. 2456. [Google Scholar]
- [23].Brittain JH, Hu BS, Wright GA, Meyer CH, Macovski A, Nishimura DG. Coronary angiography with magnetization-prepared T2 contrast. Magn Reson Med 1995;33:689–96. doi: 10.1002/mrm.1910330515. [DOI] [PubMed] [Google Scholar]
- [24].Jacobs JWM, Van Os JWM, Veeman WS. Broadband heteronuclear decoupling. J Magn Reson 1983;51:56–66. doi: 10.1016/0022-2364(83)90100-2. [DOI] [Google Scholar]
- [25].Shaka AJ, Rucker SP, Pines A. Iterative carr-purcell trains. J Magn Reson 1988;77:606–11. doi: 10.1016/0022-2364(88)90022-4. [DOI] [Google Scholar]
- [26].Sommer K, Amthor T, Doneva M, Koken P, Meineke J, Börnert P. Towards predicting the encoding capability of MR fingerprinting sequences. Magn Reson Imaging 2017;41:7–14. doi: 10.1016/j.mri.2017.06.015. [DOI] [PubMed] [Google Scholar]
- [27].Wissmann L, Santelli C, Segars WP, Kozerke S. MRXCAT: Realistic numerical phantoms for cardiovascular magnetic resonance. J Cardiovasc Magn Reson 2014;16:63. doi: 10.1186/s12968-014-0063-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Perlin K An image synthesizer. ACM SIGGRAPH Comput Graph 1985;19:287–96. doi: 10.1145/325165.325247. [DOI] [Google Scholar]
- [29].Hargreaves B Variable-Density Spiral Design Functions 2005. http://mrsrl.stanford.edu/~brian/vdspiral/ (accessed June 1, 2017).
- [30].Fessler J, Sutton B. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Signal Process 2003;51:560–74. [Google Scholar]
- [31].Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging 2007;26:68–76. doi: 10.1109/TMI.2006.885337. [DOI] [PubMed] [Google Scholar]
- [32].Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn Reson Med 2018;79:83–96. doi: 10.1002/mrm.26639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Pahwa S, Hamilton JI, Adedigba J, Frankel S, O’Connor G, Killinc O, et al. Simultaneous T1 and T2 mapping of the myocardium in normal volunteers using Cardiac MR Fingerprinting. Proc 25th Annu. Meet. Int Soc Magn Reson Med, 2017, p. 2726. [Google Scholar]
- [34].Edelstein WA, Glover GH, Hardy CJ, Redington RW. The intrinsic signal‐to‐noise ratio in NMR imaging. Magn Reson Med 1986;3:604–18. doi: 10.1002/mrm.1910030413. [DOI] [PubMed] [Google Scholar]
- [35].Greenman RL, Shirosky JE, Mulkern RV., Rofsky NM. Double inversion black-blood fast spin-echo imaging of the human heart: A comparison between 1.5T and 3.0T. J Magn Reson Imaging 2003;17:648–55. doi: 10.1002/jmri.10316. [DOI] [PubMed] [Google Scholar]
- [36].Saekho S, Boada FE, Noll DC, Stenger VA. Small tip angle three-dimensional tailored radiofrequency slab-select pulse for reduced B1 inhomogeneity at 3 T. Magn Reson Med 2005;53:479–84. doi: 10.1002/mrm.20358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Keenan KE, Stupic KF, Boss M, Russek SE, Chenevert TL, Prasad PV., et al. Comparison of T1 measurement using ISMRM/NIST system phantom. Proc. 24th Annu. Meet. ISMRM, Singapore, 2016, p. 3290. [Google Scholar]
- [38].Lin LI-K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989;45:255. doi: 10.2307/2532051. [DOI] [PubMed] [Google Scholar]
- [39].Siemens Medical Solutions USA. MyoMaps 2018. https://usa.healthcare.siemens.com/magnetic-resonance-imaging/options-and-upgrades/clinical-applications/myomaps (accessed February 27, 2018).
- [40].Messroghli DR, Moon JC, Ferreira VM, Grosse-Wortmann L, He T, Kellman P, et al. Clinical recommendations for cardiovascular magnetic resonance mapping of T1, T2, T2* and extracellular volume: A consensus statement by the Society for Cardiovascular Magnetic Resonance (SCMR) endorsed by the European Association for Cardiovascular Imagi. J Cardiovasc Magn Reson 2017;19:75. doi: 10.1186/s12968-017-0389-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Breithaupt M, Flassbeck S, Ladd ME. On optimizations of MRF patterns based on generalized MRI sequence schemes. Proc. 25th Annu. Meet. ISMRM, Honolulu, HI, USA, 2017, p. 936. [Google Scholar]
- [42].Hamilton JI, Wright KL, Jiang Y, Hernandez-Garcia L, Ma D, Griswold M, et al. Pulse Sequence Optimization for Improved MRF Scan Efficiency. Proc. 23rd Annu. Meet. ISMRM, Toronto, Canada, 2015, p. 3386. [Google Scholar]
- [43].Cohen O, Rosen MS. Algorithm comparison for schedule optimization in MR fingerprinting. Magn Reson Imaging 2017;41:15–21. doi: 10.1016/J.MRI.2017.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Zhao B, Haldar JP, Setsompop K, Wald LL. Towards Optimized Experiment Design for Magnetic Resonance Fingerprinting. Proc 24th Annu. Meet. Int. Soc. Magn. Reson. Med., 2016, p. 2835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Dabir D, Child N, Kalra A, Rogers T, Gebker R, Jabbour A, et al. Reference values for healthy human myocardium using a T1 mapping methodology: results from the International T1 Multicenter cardiovascular magnetic resonance study. J Cardiovasc Magn Reson 2014;16:69. doi: 10.1186/s12968-014-0069-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Piechnik SK, Ferreira VM, Dall’Armellina E, Cochlin LE, Greiser A, Neubauer S, et al. Shortened Modified Look-Locker Inversion recovery (ShMOLLI) for clinical myocardial T1-mapping at 1.5 and 3 T within a 9 heartbeat breathhold. J Cardiovasc Magn Reson 2010;12:69. doi: 10.1186/1532-429X-12-69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Chow K, Flewitt JA, Green JD, Pagano JJ, Friedrich MG, Thompson RB. Saturation recovery single-shot acquisition (SASHA) for myocardial T 1 mapping. Magn Reson Med 2014;71:2082–95. doi: 10.1002/mrm.24878. [DOI] [PubMed] [Google Scholar]
- [48].Teixeira T, Hafyane T, Stikov N, Akdeniz C, Greiser A, Friedrich MG. Comparison of different cardiovascular magnetic resonance sequences for native myocardial T1 mapping at 3T. J Cardiovasc Magn Reson 2016:1–12. doi: 10.1186/s12968-016-0286-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Kellman P, Herzka DA, Hansen MS. Adiabatic inversion pulses for myocardial T1 mapping. Magn Reson Med 2014;71:1428–34. doi: 10.1002/mrm.24793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Ma D, Jiang Y, Chen Y, McGivney D, Mehta B, Gulani V, et al. Fast 3D magnetic resonance fingerprinting for a whole-brain coverage. Magn Reson Med 2017. doi: 10.1002/mrm.26886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Liao C, Bilgic B, Manhard MK, Zhao B, Cao X, Zhong J, et al. 3D MR fingerprinting with accelerated stack-of-spirals and hybrid sliding-window and GRAPPA reconstruction. Neuroimage 2017;162:13–22. doi: 10.1016/j.neuroimage.2017.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Chen Y, Mehta B, Hamilton J, Ma D, Seiberlich N, Griswold M, et al. Free-Breathing 3D Abdominal Magnetic Resonance Fingerprinting Using Navigators. Proc. 24th Annu. Meet. ISMRM, Singapore, 2016, p. 716. [Google Scholar]
- [53].Kellman P, Hansen MS. T1-mapping in the heart: accuracy and precision. J Cardiovasc Magn Reson 2014;16:2. doi: 10.1186/1532-429X-16-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.