A constrained single-index regression for estimating interactions between a treatment and covariates

Abstract

We consider a single-index regression model, uniquely constrained to estimate interactions between a set of pretreatment covariates and a treatment variable on their effects on a response variable, in the context of analyzing data from randomized clinical trials. We represent interaction effect terms of the model through a set of treatment-specific flexible link functions on a linear combination of the covariates (a single index), subject to the constraint that the expected value given the covariates equals 0, while leaving the main effects of the covariates unspecified. We show that the proposed semiparametric estimator is consistent for the interaction term of the model, and that the efficiency of the estimator can be improved with an augmentation procedure. The proposed single-index regression provides a flexible and interpretable modeling approach to optimizing individualized treatment rules based on patients’ data measured at baseline, as illustrated by simulation examples and an application to data from a depression clinical trial.

1 |. INTRODUCTION

In precision medicine, a critical concern is to characterize individuals’ heterogeneity in treatment responses in order to enable individual-specific treatment decisions to be made (Murphy, 2003; Robins, 2004). Furthermore, estimating treatment and pretreatment covariate interactions in the setting of randomized clinical trials may provide valuable information for understanding the factors involved in heterogeneous treatment responses. In this paper, we propose a simple and flexible regression method specifically focused on estimating the interaction effects between a treatment variable and pretreatment covariates on a treatment response.

Since the seminal papers of Murphy (2003) and Robins (2004), much research has been done on development of individualized treatment rules based on pretreatment covariates. Regression-based methodologies are intended to optimize the individualized treatment rules by estimating treatment-specific mean response functions (eg, Qian and Murphy, 2011; Zhang et al., 2012; Lu et al., 2011; Petkova et al., 2019) while attempting to maintain robustness with respect to model misspecification. Machine learning approaches for developing individualized treatment rules are often framed in the context of classification problems (Zhang et al., 2012; Zhao et al., 2019); for example, the outcome weighted learning (eg, Zhao et al., 2012, 2015; Song et al., 2015) based on support vector machines, tree-based classification (eg, Laber and Zhao, 2015), and the methods of Kang et al. (2014) based on adaptive boosting, among others. Although the classification approaches are appealing in many settings, here we focus on familiar regression approaches that are frequently utilized in practice, and allow for ready interpretation.

Qian and Murphy (2011) show that the optimal individualized treatment rules (in terms of maximizing the mean treatment response) depends only on the treatment and pretreatment covariates’ interaction effects, and not on the main effects of the pretreatment covariates present in the mean response function. However, if the model inadequately represents the interaction effects, the estimated individualized treatment rule may perform poorly (Murphy, 2005; Qian and Murphy, 2011). The primary focus of this paper is to develop a semiparametric regression method for estimating the interaction effect term of the mean response function, which reduces concerns regarding misspecification of the interaction effects.

Qian and Murphy (2011) approximate the mean response function using a rich linear model with a penalized least squares criterion. However, this approach is generally not robust to misspecification of the main effect term of the model and is also restricted to a parametric regression. Also, if the main effect is responsible for a relatively large proportion of the variance in the outcome compared to the interaction effect, consistent estimation of the interaction effect is difficult. Addressing this issue, Tian et al. (2014) proposed an approach to consistently estimate the treatment-by-covariate interaction effect without having to specify the main effect. However, their approach is applicable only to the (generalized) linear model framework and only when there are exactly two treatments. In realistic situations, a linear model may be too restrictive to describe complex interactions. Zhang et al. (2012) proposed a robust approach to estimating an optimal individualized treatment rule, within a class of rules defined by a (possibly misspecified) regression model. However, their method is computationally feasible only in low-dimensional settings. Song et al. (2017) proposed a semiparametric regression model to estimate an optimal individualized treatment rule, but their approach is limited to a monotone interaction effect structure and to binary treatment conditions.

A primary contribution of this paper is in generalizing the work of Tian et al. (2014) to allow for a semi-parametrically defined interaction effect and also for more than two treatments in the context of randomized clinical trials. We do this by extending a single-index model (eg, Stoker, 1986) to allow treatment-specific nonparametric link functions (Park et al., 2020) in order to capture the treatment-by-covariates interaction effects, while allowing for an unspecified main effect of the covariates. The result is a simple and flexible regression model for the interaction effects.

2 |. CONSTRAINED SINGLE-INDEX MODELS

In the context of randomized clinical trials, we consider pretreatment covariates $X\in {ℝ}^p$ and a categorical treatment variable T ∈ {1, … , L} (with L levels) that has associated randomization probabilities (π₁, … , π_L). We let $Y^{(t)}\in ℝ(\text{t}=1,\dots ,\text{L})$ be the potential outcome if the patient received treatment T = t (t = 1, … , L); we only observe Y = Y^(T), T, and X. Throughout the paper, we assume, without loss of generality, that E[Y|T = t] = 0 (t = 1, … , L), that is, the main effect for T is centered at 0 (this is only to suppress the treatment-specific intercepts in regression models in order to simplify the exposition, and can be achieved by removing the treatment level t-specific means from Y) and that X is centered at zero.

The focus of this paper is on modeling interactions between X and T on their effects on Y. We assume Y = E[Y|X, T] + ϵ, where ϵ is a zero-mean independent noise with finite variance. Let us assume that the nested mean model associated with the interaction effects has a single-index model structure with a set of treatment t-specific link functions, for a single-index coefficient ${\alpha }_0\in {ℝ}^p$:

$$E[Y\mid X,T=t]=\underset{\text{main effect}}{\underbrace{\mu (X)}}+\underset{\text{interaction}}{\underbrace{f_t\left({\alpha }_0^{\top }X\right)}}(t=1,\dots ,L),$$ (1)

where μ(X) represents an unspecified main effect of X. In model (1), the treatment t-specific functions f_t(·) are general smooth univariate functions. To obtain an identifiable representation, without loss of generality, the treatment t-specific functions (f₁, … , f_L) in model (1) are assumed to satisfy a condition: $E\left[f_T\left({\alpha }_0^{\top }X\right)\mid X\right]={\sum }_{t=1}^L{\pi }_t{f}_t\left({\alpha }_0^{\top }X\right)=0$ (almost surely). This condition indicates that there are only L − 1 unrestricted functions f_t among the L interaction functions (f₁, … , f_L); that is, the Lth function f_L in (1) is identified by the other (L − 1) functions: $f_L\left({\alpha }_0^{\top }X\right)=-{\pi }_L^{-1}{\sum }_{t=1}^{L-1}{\pi }_t{f}_t\left({\alpha }_0^{\top }X\right)$ (almost surely).

In model (1), the single-index coefficient α₀ is identifiable only up to scale and sign due to the nonparametric nature of the link functions f_t (t = 1, … , L) and therefore, without loss of generality, we assume α₀ ∈ Θ, where

$$\Theta :=\left\{\alpha ={\left({\alpha }_1,\dots ,{\alpha }_p\right)}^{\top }\in {ℝ}^p:\Vert \alpha \Vert =1,{\alpha }_1>0\right\}.$$

The semiparametric model (1) captures the variability in X related to the treatment effects via a single index ${\alpha }_0^{\top }X\in ℝ$ and its interactions with the treatment via treatment-specific link functions (f₁, … , f_L). Interaction effects are determined by the distinct shapes of the unspecified functions (f₁, … , f_L). There are several reasons we consider a single-index ${\alpha }_0^{\top }X$ in (1) (as opposed to treatment-specific L indices). First, the common single index provides a parsimonious one-dimensional composite treatment effect modifier (defined as a linear combination of X) that allows an intuitive visualization for the interaction effect. Besides its parsimonious appeal, the single-dimensional reduction model (1) naturally and directly extends the linear model-based approach (eg, Tian et al., 2014) in the L = 2 setting. If L = 2 and we restrict the unspecified interaction function f_t(·) in model (1) to a prespecified linear form $f_t\left({\alpha }_0^{\top }X\right)=\left(t+{\pi }_1-2\right){\alpha }_0^{\top }X$, then the semiparametric model (1) reduces to the modified covariates model assumed in Tian et al. (2014) (see also Murphy, 2003; Lu et al., 2011; Shi et al., 2016, 2018; Jeng et al., 2018):

$$E[Y\mid X,T=t]=\mu (X)+{\alpha }_0^{\top }X\left(t+{\pi }_1-2\right)(t=1,2),$$ (2)

for some ${\alpha }_0\in {ℝ}^p$ which assumes a linear form for the T-by-X interaction effects.

For model (1), to estimate the interaction effect terms $f_t\left({\alpha }_0^{\top }X\right)(t=1,\dots ,L)$ in the presence of the unspecified main effect μ(X), we propose to utilize a working model:

$$E[Y\mid X,T=t]\approx g_t\left({\alpha }^{\top }X\right)(t=1,\dots ,L),$$ (3)

for α ∈ Θ, subject to the constraint:

$$E\left[g_T\left({\alpha }^{\top }X\right)|X\right]=\sum _{t=1}^L{\pi }_t{g}_t\left({\alpha }^{\top }X\right)=0$$ (4)

almost surely, for all α ∈ Θ. The constraint (4) is imposed on the treatment t-specific smooth link-functions (g₁, … , g_L) of the working model (3). Even if (3) does not generally provide a good approximation to the underlying model (1), in Section 3.3 we will show, through the consistency results (Theorem 1 and Corollary 1), that (3) is a useful model for estimating the interaction effect terms $f_t\left({\alpha }_0^{\top }X\right)(t=1,\dots ,L)$ of model (1).

In a least squares framework for model (3)

$$\begin{gathered} E\left[{\left(Y-g_T\left({\alpha }^{\top }X\right)\right)}^2/2\right] \\ \propto E\left[Y{g}_T\left({\alpha }^{\top }X\right)-g_T^2\left({\alpha }^{\top }X\right)/2\right] \\ =E\left[\left\{\mu (X)+f_T\left({\alpha }_0^{\top }X\right)\right\}{g}_T\left({\alpha }^{\top }X\right)-g_T^2\left({\alpha }^{\top }X\right)/2\right] \\ =E[E[\mu (X)g_T\left({\alpha }^{\top }X\right) \\ +f_T\left({\alpha }_0^{\top }X\right)g_T\left({\alpha }^{\top }X\right)-g_T^2\left({\alpha }^{\top }X\right)/2\mid X]], \end{gathered}$$ (5)

the condition (4) ensures that the cross-product term E[μ(X)g_T(α^⊤X)|X] vanishes to 0, and the part relevant to the estimation of the working model (3) is independent of the unspecified main effect μ(X). This independence implies that optimization of the unspecified component μ(X) and the working model (3) can be performed separately. As model (3) does not require specification of μ(X), working with (3) sidesteps issues that would arise if μ(X) were to be misspecified.

We call model (3) a constrained single-index model with multiple (ie, treatment t-specific) link functions, which is the main working model of this paper.

3 |. ESTIMATION

3.1 |. A criterion for fitting themodel

To optimize the constrained working model (3), we consider a constrained least squares criterion:

$$\begin{gathered} \underset{\alpha ,\left(g_1,\dots ,g_L\right)}{\text{minimize}}E\left[{\left(Y-g_T\left({\alpha }^{\top }X\right)\right)}^2/2\right] \\ \text{subject to\hspace{1em}}E\left[g_T\left({\alpha }^{\top }X\right)\mid X\right]=0\left(\text{almost surely}\right), \end{gathered}$$ (6)

where α ∈ Θ and each function g_t is in a suitable function space in L²(R).

Proposition 1.

For each fixed α, the minimizer (g₁, … , g_L) of the constrained minimization problem (6) satisfies

$$g_t\left({\alpha }^{\top }X\right)=E\left[Y\mid {\alpha }^{\top }X,T=t\right]-E\left[Y\mid {\alpha }^{\top }X\right](t=1,\dots ,L),$$ (7)

almost surely.

The proof of Proposition 1 is in Section A.1 of the Supporting Information. Proposition 1 suggests that solving (6) to optimize model (3) can be split into the following two iterative steps. First, for a fixed α, find the link-functions (g₁, … , g_L) from expression (7). Second, for a fixed (g₁, … , g_L), solve

$$\underset{\alpha \in \Theta }{\text{argmin}}E\left[{\left(Y-g_T\left({\alpha }^{\top }X\right)\right)}^2/2\right].$$ (8)

These two steps can be iterated until convergence to obtain a solution of (6). To obtain a sample counterpart of this population solution, we can insert sample estimates into this population algorithm, as is done in Hastie and Tibshirani (1999). We will provide the details of this estimation procedure in Section 3.2, and establish the consistency of the estimator in Section 3.3.

3.2 |. A cubic spline estimator of the model

To obtain a sample counterpart of the population solution of (6), we approximate the objective function of (6) based on sample {(Y_i, T_i, X_i), i = 1, … , n} (assumed to be independently and identically distributed across i). In particular, we use a nonparametric regression technique to approximate the solution (g₁, … , g_L) in (7) for each fixed α ∈ Θ. Although other nonparametric regression methods can also be used, in this paper we focus on a cubic B-spline (de Boor, 2001) representation of the solution (g₁, … , g_L) in (7) for each fixed α. Specifically, given each α, the functions g_t is represented by

$$g_t\left({\alpha }^{\top }X\right)=B_t{\left({\alpha }^{\top }X\right)}^{\top }{\beta }_t(t=1,\dots ,L),$$ (9)

for some vector ${\beta }_t\in {ℝ}^{d_t+4}$, where $B_t(\cdot )\in {ℝ}^{d_t+4}$ is a set of (d_t + 4) cubic B-spline basis functions (de Boor (2001)) defined on the range of the candidate single-index {(α^⊤X_i), i = 1, … , n}. We use d_t to denote the number of interior knots (placed with equal distance between neighboring knots). The number d_t depends on the treatment group sample size: $n_t={\sum }_{i=1}^n{1}_{\left(T_i=t\right)}$. Furthermore, let us represent the conditional expectation E[Y|α^⊤X] in expression (7) by E[Y|α^⊤X] = B₀(α^⊤X)^⊤β₀ for some vector ${\beta }_0\in {ℝ}^{d_0+4}$, where $B_0(\cdot )\in {ℝ}^{d_0+4}$ is a set of (d₀ + 4) cubic B-spline basis functions defined on the range of the candidate single-index {(α^⊤X_i), i = 1, … , n}. We use d₀ number of interior knots (placed with equal distance between neighboring knots), and the number d₀ depends on the sample size n.

Let $D_{\alpha }^{(t)}(t=1,\dots ,L)$ denote the treatment t-specific n × d_t design matrix, where the ith row is the 1 × d_t vector B_t(α^⊤X_i)^⊤ if T_i = t and is a row of zeros if T_i ≠ t (i = 1, … , n) (t = 1, … , L). Let $D_{\alpha }^{(0)}$ denote the n × d₀ design matrix in which the ith row is the 1 × d₀ vector B₀(α^⊤X_i)^⊤ (i = 1, … , n). Then, for each fixed α ∈ Θ, we approximate the minimizer (g₁, … , g_L) in (7) by the method of least squares (see Section A.2 of the Supporting Information for a derivation):

$$g_t(\cdot )=B_t{(\cdot )}^{\top }{\left(D_{\alpha }^{(t)\top }{D}_{\alpha }^{(t)}\right)}^{-1}{D}_{\alpha }^{(t)\top }\left(I_n-D_{\alpha }^{(0)}{\left(D_{\alpha }^{(0)\top }{D}_{\alpha }^{(0)}\right)}^{-1}{D}_{\alpha }^{(0)\top }\right)Y(t=1,\dots ,L),$$ (10)

where Y denotes the n × 1 vector of the observed responses. We define the estimator ${\widehat{\alpha }}_0$ for α₀ of model (1) by

$${\widehat{\alpha }}_0=\underset{\alpha \in \Theta }{\text{argmin }}{n}^{-1}\sum _{i=1}^n{\left(Y_i-g_{T_i}\left({\alpha }^{\top }{X}_i\right)\right)}^2/2,$$ (11)

where (g₁, … , g_L) are given in (10). Let us define the associated estimators $\left({\widehat{f}}_1,\dots ,{\widehat{f}}_L\right)$ for the treatment-specific functions (f₁, … , f_L) of model (1) by

$$\left({\widehat{f}}_1,\dots ,{\widehat{f}}_L\right)=\left(g_1,\dots ,g_L\right)\text{ given in }(10),\text{ computed at }\alpha ={\widehat{\alpha }}_0.$$ (12)

We use iteratively re-weighted least squares to solve (11), repeating the following two steps:

1. Given a current estimate α ∈ Θ, compute the functions (g₁, … , g_L) in (10).

2. Given (g₁, … , g_L), approximately solve (11), based on a linear approximation to $g_{T_i}\left({\alpha }^{\top }{X}_i\right)(i=1,\dots ,n)$ at the current estimate of α.

The iteration between the two steps continues until convergence of α ∈ Θ. We next elaborate Step 2 of this iterative procedure. For each (the kth) iterative step, the objective function in (11) is approximated based on a linear approximation of $g_{T_i}\left({\alpha }^{\top }{X}_i\right)$ at the current (the kth) iterate, say α^(k) ∈ Θ:

$$\begin{gathered} n^{-1}\sum _{i=1}^n{\left(Y_i-g_{T_i}\left({\alpha }^{\top }{X}_i\right)\right)}^2/2 \\ \approx n^{-1}\sum _{i=1}^n(Y_i-g_{T_i}\left({\alpha }^{(k)\top }{X}_i\right) \\ {-{\dot{g}}_{T_i}\left({\alpha }^{(k)\top }{X}_i\right){\left(\alpha -{\alpha }^{(k)}\right)}^{\top }{X}_i)}^2/2 \\ =n^{-1}\sum _{i=1}^n{\left(Y_i^{*(k)}-{\alpha }^{\top }{X}_i^{*(k)}\right)}^2/2, \end{gathered}$$ (13)

where the modified responses $Y_i^{*(k)}$ and the modified regressors $X_i^{*(k)}$:

$$\begin{gathered} Y_i^{*(k)}=Y_i-g_{T_i}\left({\alpha }^{(k)\top }{X}_i\right)+{\dot{g}}_{T_i}\left({\alpha }^{(k)\top }{X}_i\right){\alpha }^{(k)\top }{X}_i \\ {X}_i^{*(k)}={\dot{g}}_{T_i}\left({\alpha }^{(k)\top }{X}_i\right)X_i \end{gathered}$$ (14)

and we minimize the right-hand side of (13) over $\alpha \in {ℝ}^p$. The minimizer α^(k+1) is then scaled to satisfy α^(k+1) ∈ Θ. The algorithm terminates, when ∥(α^(k+1) − α^(k))/α^(k+1)∥ is less than a prespecified convergence tolerance.

Remark 1.

The objective function of the modified covariates model (2) (Tian et al., 2014) is

$$n^{-1}\sum _{i=1}^n{\left(Y_i-{\alpha }^{\top }{X}_i\left(T_i+{\pi }_1-2\right)\right)}^2/2,$$ (15)

in which the terms X_i(T_i + π₁ − 2) are called modified covariates. By comparing the right-hand side of (13) to (15), the modified regressors, $X_i^{*(k)}={\dot{g}}_{T_i}\left({\alpha }^{(k)\top }{X}_i\right)X_i$, take the role of the modified covariates of Tian et al. (2014) in updating α for each (the kth) iterative step. For any set of arbitrary functions (g₁, … , g_L) satisfying the constraint (4), we have E[ġ_T(α^(k)⊤X)X|X] = 0 (almost surely) for any α^(k) ∈ Θ, which is analogous to the condition: E[X(T + π₁ − 2)|X] = 0 (almost surely) satisfied by the modified covariates model (2). These conditions, satisfied by the models, make the parts relevant to the optimization of α in (13) and (15) independent of the unspecified μ(X) of the underlying models (1) and (2), respectively, as in (5). This orthogonality is attractive, as the estimation of the unspecified function μ(X) and the single-index coefficient α₀ can be performed separately, independently of each another. If we restrict the treatment t-specific functions g_t to g_t(u) := u(t + π₁ − 2), the objective function of (11) reduces to (15).

Remark 2.

As the weights ${\dot{g}}_{T_i}\left({\alpha }^{(k)\top }{X}_i\right)$ that define the modified regressors $X_i^{(k)*}$ in (14) depend on the values X_i and the shape of the link-functions $g_{T_i}$ (through the first derivatives ${\dot{g}}_{T_i}$), the iterative procedure of optimizing α that utilizes the right-hand side of (13) accounts for the nonlinear interactions captured by the flexible link-functions (g₁, … , g_L). This is in contrast to the constant weights (T_i + π₁ − 2) applied to X_i in defining the modified covariates of Tian et al. (2014).

3.3 |. Consistency and asymptotic normality of the estimator

We establish the consistency of the estimator ${\widehat{\alpha }}_0$ in (11) for α₀ and the estimators ${\widehat{f}}_t$ in (12) for f_t, where α₀ and f_t are given in model (1). The theoretical results rely on those of Wang and Yang (2009), where cubic B-splines are used to approximate the link function of their single-index model. In Wang and Yang (2009), instead of imposing the true mean function to be a function only of a single-index ${\theta }_0^{\top }X\in ℝ$, that is, $E[Y\mid X]=E\left[Y\mid {\theta }_0^{\top }X\right]$ for some single-index coefficient θ₀ ∈ Θ, the authors develop a root-n consistent cubic spline estimator of the single-index coefficient of a single-index model that is robust against deviations from the exact single-index regression relationship. Specifically, their target single-index coefficient θ₀ ∈ Θ is defined in terms of the optimal L² (single-index based) approximation to the response $Y:{\theta }_0:=\underset{\theta \in \Theta }{\text{argmin}}E\left[{\left(Y-E\left[Y\mid {\mathit{\theta }}^{\top }X\right]\right)}^2\right]$, rather than in terms of an exact single-index relationship $E[Y\mid X]=E\left[Y\mid {\theta }_0^{\top }X\right]$. In what follows, we adopt the results and assumptions of Wang and Yang (2009), and obtain uniformly consistent estimators of the conditional expectations E[Y|α^⊤X, T = t] (t = 1, … , L) and E[Y|α^⊤X] appearing on the right-hand side of (7) (uniformly over α ∈ Θ), and establish the root-n consistency of ${\widehat{\alpha }}_0$ in (11) for α₀ of model (1); cubic spline smoothing of Y(= Y^(t)) on $\left({\widehat{\alpha }}_0^{\top }X,T=t\right)$ results in uniformly consistent estimators ${\widehat{f}}_t$ in (12) for f_t (t = 1, … , L). We state our assumptions.

Assumption 1.

The response $Y_i=\mu \left(X_i\right)+f_{T_i}\left({\alpha }_0^{\top }{X}_i\right)+{ϵ}_i(i=1,\dots ,n)$, where E[ϵ_i|X_i, T_i] = 0 and $E\left[{ϵ}_i^2\mid X_i,T_i\right]={\sigma }_{T_i}^2\left(X_i\right)$, in which the standard deviation functions σ_t(·) (t = 1, … , L) are bounded below and above by positive constants, defined on a bounded domain.

Assumption 2.

The function E[(Y − f_T(α^⊤X))²] is locally convex at α = α₀.

Assumption 3.

The functions μ(·) and f_t(·) in (1) have fourth-order continuous derivatives.

Assumption 4.

The covariate X is bounded, that is, ∥X∥ ≤ c, for some c > 0. The density function of X has a fourth-order continuous derivative, and is bounded above and below by positive constants, defined on a bounded domain.

Assumption 5.

The number of interior knots d_t used in representing the function $g_{\alpha ,t}^{**}(u):=E\left[Y\mid {\alpha }^{\top }X=u,T=t\right]$ satisfies $n_t^{1/6}\ll d_t\ll n_t^{1/5}{\left(\text{log}\left(n_t\right)\right)}^{-(2/5)}(t=1,\dots ,L)$. The number of interior knots d₀ used in representing the function $g_{\alpha }^{*}(u):=E\left[Y\mid {\alpha }^{\top }X=u\right]$ satisfies n^1/6 ≪ d₀ ≪ n^1/5(log(n))^−(2/5).

Assumption 1 on the standard deviation functions σ_t(·) and Assumption 3 on the underlying regression functions are typical in the nonparametric smoothing literature; see, for instance, Hardle et al. (1993); Xia et al. (2002). Assumption 4 on the distribution of X is also assumed in Wang and Yang (2009). Assumption 5 gives the requirement for the numbers of interior knots for the cubic spline spaces in approximating the conditional expectations specified on the right-hand side of (7), and is needed to ensure the uniform convergence of the approximated criterion function in (11) to its population counterpart in (8) over α ∈ Θ. The strong consistency of ${\widehat{\alpha }}_0$ in (11) to α₀ and ${\widehat{f}}_t$ in (12) to f_t are given below.

Theorem 1.

Under Assumptions 1–5, ${\widehat{\alpha }}_0\to {\alpha }_0$, almost surely.

Corollary 1.

Under Assumptions 1–5,

$$\underset{u\in [0,1]}{\text{sup}}\left|{\widehat{f}}_t(u)-f_t(u)\right|\to 0,\mathit{\text{\hspace{1em}almost surely\hspace{1em}}}(t=1,\dots ,L).$$ (16)

In (16), without loss of generality, we take the domain of the functions ${\widehat{f}}_t$ and f_t to be [0,1], as α^⊤X (α ∈ Θ) is bounded under Assumption 4. We next consider the asymptotic normality of ${\widehat{\alpha }}_0$. In the working model (3), any vector $\alpha \in \Theta \subset {ℝ}^p$ can be expressed as: $\alpha =c(\mathit{\varphi }):={\left(1,{\mathit{\varphi }}^{\top }\right)}^{\top }/{\left(1+\Vert \mathit{\varphi }{\Vert }^2\right)}^{1/2}$, for some vector $\mathit{\varphi }={\left({\varphi }_1,\dots ,{\varphi }_{p-1}\right)}^{\top }\in {ℝ}^{p-1}$. Let J(ϕ) denote the p × (p − 1) Jacobian transformation matrix from $\mathit{\varphi }\in {ℝ}^{p-1}$ to α ∈ Θ, whose (i, j)th element is given by ∂α_i/∂ϕ_j = −α_iϕ_j/K², for (i = 1; j = 1, … , p − 1), and ∂α_i/∂ϕ_j = −α_iϕ_j/K² + 1/K, for (i = 2, … , p; j = 1, … , p − 1), where K = (1 + ∥ϕ∥²)^1/2. As the relation α = c(ϕ) is one-to-one, the parameter vector ${\mathit{\varphi }}_0\in {ℝ}^{p-1}$ corresponding to the coefficient α₀ ∈ Θ of model (1) can be specified. Let us define the (p − 1) × (p − 1) covariance matrix ${\Sigma }_0=\text{var}[\Psi \left(Y_i,T_i,X_i\mid {\mathit{\varphi }}_0\right)$, in which $\Psi \left(Y_i,T_i,X_i\mid {\mathit{\varphi }}_0\right):=J^{\top }\left({\mathit{\varphi }}_0\right)\left\{f_{T_i}\left({\alpha }_0^{\top }{X}_i\right)-Y_i\right\}{\dot{f}}_{T_i}\left({\alpha }_0^{\top }{X}_i\right)X_i$, where α₀ = c((ϕ₀). Let A₀ denote the (p − 1) × (p − 1) matrix of the first derivative of E[Ψ(Y_i, T_i, X_i|ϕ)] with respect to $\mathit{\varphi }\in {ℝ}^{p-1}$ evaluated at ϕ = ϕ₀. The asymptotic normality of the estimator ${\widehat{\alpha }}_0$ is given below.

Theorem 2.

Under Assumptions 1–5, $n^{1/2}\left({\widehat{\alpha }}_0-{\alpha }_0\right)\to \mathcal{N}\left(\mathbf{0},J_0{A}_0^{-1}{\Sigma }_0{\left(J_0{A}_0^{-1}\right)}^{\top }\right)$ in distribution, where J₀ is the Jacobian function J(ϕ) evaluated at ϕ = ϕ₀.

The proofs of Theorem 1 and 2 and Corollary 1 are in Section A.3 of the Supporting Information. Although the convergence rate of the nonparametric component ${\widehat{f}}_t$ in (12) to f_t (t = 1, … , L) is slower than root-n (see (A.11) of the Supporting Information Section A.3) under Assumption 5 on the numbers of interior knots d_t and d₀, the parametric component α₀ can be estimated at a root-n rate by letting the numbers of interior knots of the spline smoothing to increase with the sample size at an appropriate rate (Assumption 5). This indicates that the model can be estimated in two stages: estimation of α₀ by the root-n consistent ${\widehat{\alpha }}_0$; spline smoothing of Y on ${\widehat{\alpha }}_0^{\top }X$ for each T = t (t = 1, … , L) to obtain an estimator ${\widehat{f}}_t$ (as given in (12)) of f_t. Under Assumptions 1–5, Theorem 2 states that root-n rate asymptotic normality for ${\widehat{\alpha }}_0$ is achievable, and that the estimator is as efficient as if the true nonparametric functions f_t (t = 1, … , L) in model (1) were known and used as the link functions g_t (t = 1, … , L) of the working model (3). However, ${\widehat{\alpha }}_0$ is generally not the most efficient estimator (although a root-n consistent estimator). This is because ${\widehat{\alpha }}_0$ is based on a generally misspecified working model (3) that includes only the T-by-X interaction effect component and omits the main effect term. Analogous to the efficiency augmentation of Tian et al. (2014), the efficiency of the estimator can be improved by incorporating a main effect component of X to the estimation of α₀ (see Section A.4 of the Supporting Information).

3.4 |. An illustration of the consistency of ${\widehat{\alpha }}_0$

In this subsection, we illustrate the effect of the constraint (4) on the consistency of ${\widehat{\alpha }}_0$ for α₀ using a simulation experiment. For the purpose of illustration, we consider a simple case of p = 2 and L = 2. We generate {(Y_i, T_i, X_i), i = 1, … n}, where T_i takes a value in {1, 2} with equal probability, independently of $X_i={\left(X_{i,1},X_{i,2}\right)}^{\top }\in {ℝ}^2$, where X_i,1,X_i,2 ~ independent unif[−π/2, π/2]. Given T_i and X_i, we generate Y_i from model (1), that is, $Y_i=\mu \left(X_i\right)+f_{T_i}\left({\alpha }_0^{\top }{X}_i\right)+{ϵ}_i$, with additive Gaussian noise ϵ_i, where ${\sigma }_{T_i}\left(X_i\right)=0.2$ (see Assumption 1). We set n = 250. We consider two simulation settings. In setting “A,” the T-by-X interaction effect specified in model (1) is nonlinear, and it is defined by

$$\text{Setting A:}{f}_{T_i}\left({\mathit{\alpha }}_0^{\top }{X}_i\right)={(-1)}^{T_i}\left(\text{cos}\left({\mathit{\alpha }}_0^{\top }{X}_i\right)-0.5\right)(i=1,\dots ,n).$$

In setting “B,” the interaction effect is linear, as defined by

$$\text{Setting B: }{f}_{T_i}\left({\alpha }_0^{\top }{X}_i\right)={(-1)}^{T_i}{\alpha }_0^{\top }{X}_i/2.25(i=1,\dots ,n).$$

In both settings “A” and “B,” we take the main effect component in model (1) to be μ(X; δ) = δ cos(η^⊤X), where the parameter δ ∈ {1, 2, 4} regulates the contribution of the X main effect to the variance of Y. In both settings, the contribution of μ(X; δ) to the variance of Y is about 0.85, 3.5, and 14 times greater than that of the interaction effect $f_T\left({\alpha }_0^{\top }X\right)$, for δ = 1, δ = 2, and δ = 4, respectively. In both settings, ${\alpha }_0^{\top }X$ corresponds to the index of interest (as it is associated with the T-by-X interaction effects) and η^⊤X corresponds to a “nuisance” index (as it is associated only with the X main effects). We set ${\alpha }_0:={(1,1)}^{\top }/\sqrt{2}$ and $\eta :={(1,-1)}^{\top }/\sqrt{2}$. For the purpose of visualization, we parameterize vectors $\alpha \in \Theta \subseteq {ℝ}^2$ in terms of an angle θ ∈ [−π/2, π/2) such that α = (cos(θ), sin(θ))^⊤. We identify the vectors α₀ and η (in Cartesian coordinates) with the angles θ₁ = π/4 and θ₂ = −π/4 (in polar coordinates), respectively.

In this simulation example, as a function of θ ∈ [−π/2, π/2), we illustrate the squared error criterion (ie, the objective function of (11)) (reparametrized with respect to θ) of the constrained working model (3). In addition, we illustrate the squared error criterion of the unconstrained working model, which is model (3) but without enforcing the constraint (4). For comparison, we also include the modified covariates squared error criterion (15) (reparametrized with respect to θ, by setting α = γ(cos(θ), sin(θ))^⊤, in which $\gamma \in ℝ$ is “profiled out” for each value of θ under the squared error criterion).

We simulate 200 data sets and average the values of these three criterion functions for each value of θ ∈ [−π/2, π/2) (evaluated on a dense grid). Then each of the averaged criterion functions is scaled to have height 1. In Figure 2, the resulting averaged criterion functions are displayed for setting “A” on the top row, and the setting “B” on the bottom row.

FIGURE 2.

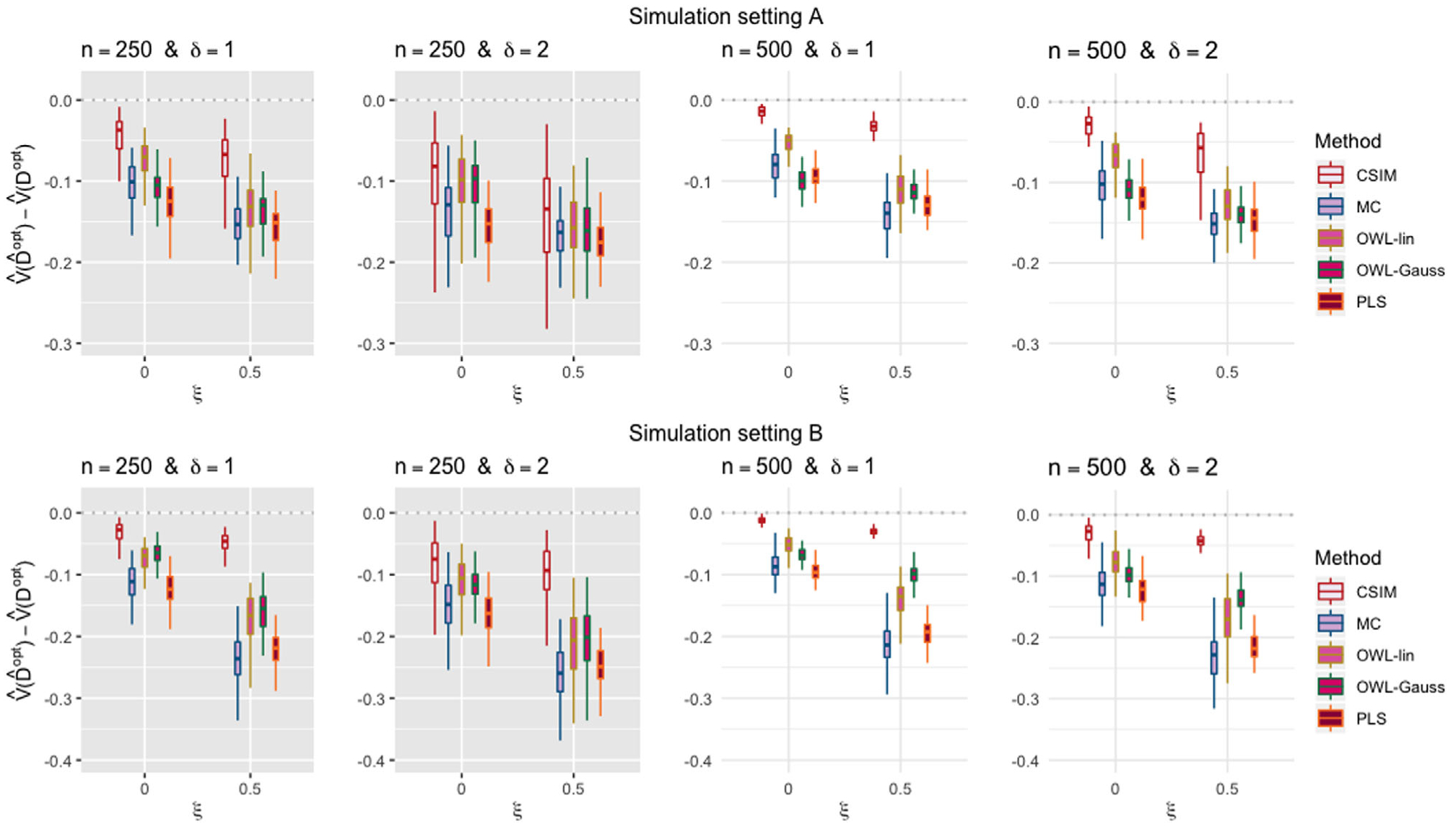
Boxplots comparing five approaches to estimating ${\mathcal{D}}^{\text{opt}}$, given each scenario indexed by ξ ∈ {0, 0.5} and δ ∈ {1, 2}, for the simulation setting “A” in the top panels and the setting “B” in the bottom panels. For each scenario, from left to right, estimation approaches for ${\mathcal{D}}^{\text{opt}}$: (1) the constrained single-index model (red); (2) the modified covariates model (green); (3) the outcome weighted learning with a linear kernel (violet); (4) the outcome weighted learning with a Gaussian kernel (purple); (5) the penalized spline least squares approach (dark purple). The case with ξ = 0 (or ξ = 0.5) corresponds to the correctly specified (or misspecified) single-index interaction model scenario; δ = 1 (or δ = 2) corresponds to the moderate (or large) main effect scenario. The dotted horizontal line represents the optimal value corresponding to ${\mathcal{D}}^{\text{opt}}$.

In Figure 1, for all three cases of δ = 1, δ = 2, and δ = 4, the constrained criterion (the red solid lines) has a “correct” global minimum at θ₁ = π/4, implying that the minimization of this constrained criterion would lead to correctly identifying the T-by-X interaction effect coefficient α₀. The unconstrained criterion (the green dotted lines) has a correct minimum at θ₁ = π/4 for the case δ = 1 (ie, when the main effect is relatively small), however, as the main effect intensity parameter δ increases (from δ = 1 to δ = 2 and to δ = 4), the unconstrained criterion function takes its global minimum at the nuisance angle θ₂ = −π/4, implying that the minimization of the unconstrained criterion would lead to an inconsistent estimate of α₀. Under the linear interaction effect (setting “B”), the constrained single-index regression criterion takes the consistent global minimum at θ₁ = π/4 for all three cases of δ = 1, δ = 2, and δ = 4. On the other hand, the unconstrained criterion has its global minimum at the nuisance angle θ₂ = −π/4, for the cases δ = 2 and δ = 4 (ie, when the main effect dominates the interaction effect).

FIGURE 1.

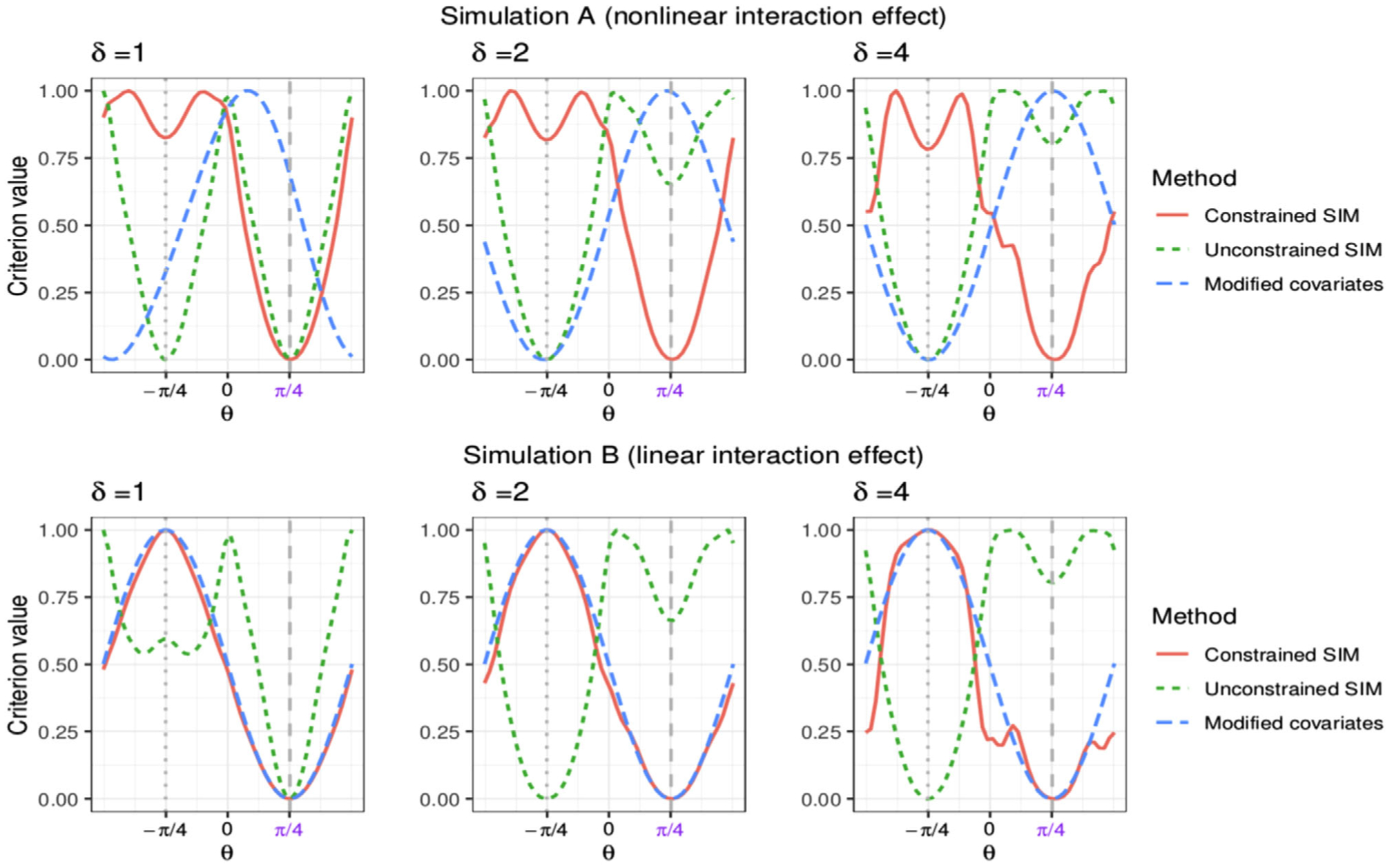
The averaged criterion functions of θ ∈ [−π/2, π/2) averaged over 200 simulated data sets. The vector α₀ corresponds to the angle θ₁ = π/4 that is indicated by the gray dashed vertical line, and the “nuisance” vector η corresponds to the angle θ₂ = −π/4 indicated by the gray dotted vertical line. The criteria and their corresponding line styles: (1) the constrained single-index criterion (the red solid curves); (2) the unconstrained single-index criterion (the green dotted curves); (3) the modified covariates criterion (the blue dashed curves).

This example has illustrated that the proposed constrained single-index regression criterion consistently takes its global minimum near the “signal” direction α₀ associated with the T-by-X interaction effect, even when the interaction effect signal is weak, unlike the case of the unconstrained criterion. In the linear interaction scenario (setting “B”), the modified covariates model (2) also produces a consistent estimate of the “signal” direction α₀ as, in this case, the modified covariates model is correctly specified and is a special case of the proposed constrained single-index model (1). However, when the interaction effect is nonlinear (scenario “A”), the modified covariates criterion does not provide relevant information for modeling the T-by-X interaction effects, as it takes its global minimum away from α₀.

4 |. SIMULATION STUDIES

In this section, we perform numerical studies to illustrate the performance of the proposed approach to optimizing individualized treatment rules, in comparison with alternative approaches including the modified covariates approach of Tian et al. (2014) and the outcome weighted learning method of Zhao et al. (2012).

We consider p = 10 with n ∈ {250, 500}. We generate covariates $X_i\in {ℝ}^p$ consisting of independent unif[−π/2, π/2] variates (a correlated covariate case is considered in Supporting Information Section B.5), and the treatment variable T_i takes a value in {1, 2} with equal probability, independently of X_i. We generate the treatment outcome $Y_i\left(=\mu \left(X_i\right)+f_{T_i}\left(X_i\right)+{ϵ}_i\right)$ from (1) the simulation setting “A”:

$$\begin{gathered} Y_i=0.8\delta \text{cos}\left({\eta }^{\top }{X}_i\right) \\ +{\left(-1\right)}^{T_i}\left\{e^{-{\left({\alpha }_0^{\top }{X}_i-0.5\right)}^2-{\left({\alpha }_1^{\top }{X}_i-0.5\right)}^2\xi }-0.5\right\}+{ϵ}_i \\ \left(i=1,\dots ,n\right), \end{gathered}$$ (17)

where the first term μ(X; δ) : = 0.8δ cos(η^⊤X) (δ = 1, 2) corresponds to the main effect of X, and the second term $f_T\left(X;\xi \right):={\left(-1\right)}^T\left\{e^{-{\left({\alpha }_0^{\top }X-0.5\right)}^2-{\left({\alpha }_1^{\top }X\right)}^2\xi }-0.5\right\}(\xi =0,0.5)$ corresponds to the T-by-X interaction effect, determined by a bell-shaped (ie, Gaussian) surface over two one-dimensional indices, ${\alpha }_0^{\top }X$ and ${\alpha }_1^{\top }X\left(if\xi \ne 0\right)$, which nonlinearly modifies the effect of the variable T on the outcome Y. We also consider (2) the simulation setting “B”:

$$\begin{gathered} Y_i=\delta \text{cos}\left({\eta }^{\top }{X}_i\right) \\ +{\left(-1\right)}^{T_i}\left\{\text{cos}\left({\left({\alpha }_0+{\alpha }_1{I}_{\left(T_i=2\right)}\xi \right)}^{\top }{X}_i-\pi /8\right)-0.5\right\}+{ϵ}_i \\ \left(i=1,\dots ,n\right), \end{gathered}$$ (18)

where the first term μ(X; δ) := δ cos(η^⊤X) (δ = 1, 2) determines the X main effect, and the second term f_T(X; ξ) : = (−1)^T{cos((α₀ + α₁I_(T=2)ξ)^⊤X_i − π/8) −0.5} (ξ = 0, 0.5) determines the T-by-X interaction effect, which is defined based on different single indices for each treatment, that is, ${\alpha }_0^{\top }X$ for T = 1 and (α₀ + α₁ξ)^⊤X for T = 2, when ξ ≠ 0.

Both models (17) and (18) are indexed by a pair (ξ, δ): the parameter ξ ∈ {0, 0.5} determines whether the T-by-X interaction effect term f_T(X; ξ) in models (17) and (18) has an intrinsic one-dimensional structure over the single index ${\alpha }_0^{\top }X\left(\xi =0\right)$ or whether it deviates from a single-index model structure (ξ = 0.5); the parameter δ ∈ {1, 2} in μ(X; δ) controls the contribution of the X main effect on the variance of Y, where δ = 1 represents a relatively moderate X main effect (contributing about the same variance as the interaction effect does) and δ = 2 a relatively large X main effect (about 4 times greater than the interaction effect), respectively. In both (17) and (18), we use additive noise ϵ_i (see Assumption 1) that follows the mean zero Gaussian distribution with standard deviation 0.5. In models (17) and (18), we set the vectors η = (−1, 1, −1, 1, −1, 1, 0, 0, 0, 0)^⊤, α₀ = (1, 0.5, 0.25, 0.125, 0, 0, 0, 0, 0, 0)^⊤, and α₁ = (1, 1, 1, 1, 1, 1, 0, 0, 0)^⊤, with each of these length p(= 10) vectors normalized to have unit norm. Without loss of generality, we assume that a larger value of Y is preferred.

For the case of a single decision time point, an individualized treatment rule, which we denote as $\mathcal{D}\left(X\right):{ℝ}^p\mapsto \left\{1,\dots ,L\right\}$, is a rule that maps an individual with (baseline) characteristics X to one of the L available treatment options. One natural measure for the effectiveness of $\mathcal{D}$ is called the value (V) of $\mathcal{D}$ (Qian and Murphy (2011)) defined as the expected mean response when everyone in the population receives treatment according to the rule $\mathcal{D}$, that is, $V\left(\mathcal{D}\right)=E\left[E\left[Y\mid X,T=\mathcal{D}\left(X\right)\right]\right]$. The optimal individualized treatment rule, which we denote as ${\mathcal{D}}^{\text{opt}}$, resulting in the largest value of V is: ${\mathcal{D}}^{\text{opt}}\left(X\right)=\text{arg}{\text{max}}_{t\in \left\{1,\dots ,L\right\}}E\left[Y\mid X,T=t\right]$. Accordingly, the estimators ${\widehat{\mathcal{D}}}^{\text{opt }}$ for ${\mathcal{D}}^{\text{opt }}$ are: ${\widehat{\mathcal{D}}}^{\text{opt}}\left(X\right)=\text{arg}{\text{max}}_{t\in \left\{1,\dots ,L\right\}}{\widehat{f}}_t\left({\widehat{\alpha }}_0^{\top }X\right)$ and ${\widehat{D}}^{\text{opt}}\left(X\right)=\text{arg}{\text{max}}_{t\in \left\{1,\dots ,L\right\}}{\widehat{\alpha }}_0^{\top }X\left(t+{\pi }_1-2\right)$, for models (1) and (2), respectively. Here, the estimators ${\widehat{\alpha }}_0$ and ${\widehat{f}}_t$ for model (1) correspond to the proposed estimators (11) and (12), and the estimator ${\widehat{\alpha }}_0$ for model (2) corresponds to the minimizer of (15).

The methods for estimating ${\mathcal{D}}^{\text{opt}}$ under comparison include:

1. The proposed method of using model (3), estimated through the procedure described in Section 3.2. We use the numbers of interior knots $d_t=\left[n_t^{1/5.5}\right]\left(t=1,2\right)$ and d₀ = [n^1/5.5], which satisfy Assumption 5. Here, [u] denotes the integer part of u.

2. The modified covariates method of Tian et al. (2014) of using model (2), estimated by minimizing (15).

3. The outcome weighted learning method (Zhao et al., 2012) based on a linear kernel, implemented in the R-package DTRlearn. To improve its efficiency, we employ the augmented outcome weighted learning approach of Liu et al. (2018). The tuning parameter κ in Zhao et al. (2012) is chosen from the grid of (0.25, 0.5, 1, 2, 4) (the default setting of DTRlearn) based on a fivefold cross-validation.

4. The same approach as in (3) but based on a Gaussian radial basis function kernel instead of a linear kernel. The inverse bandwidth parameter ${\sigma }_n^2$ in Zhao et al. (2012) is chosen from the grid of (0.01, 0.02, 0.04, … , 0.64, 1.28) and κ is chosen from the grid of (0.25, 0.5, 1, 2, 4), based on a fivefold cross-validation.

5. A penalized additive cubic spline least squares (PLS) approach. We implement this method by estimating E[Y|X, T = t] via an additive regression for each treatment separately. The implementational detail is given in Section B.4 of Supporting Information.

For each simulation run, we estimate ${\mathcal{D}}^{\text{opt}}$ from each of the five methods based on a training set (of size n), and for evaluation of these methods, we evaluate the value $V\left({\widehat{\mathcal{D}}}^{\text{opt}}\right)=E\left[E\left[Y\mid X,T={\widehat{D}}^{\text{opt}}\left(X\right)\right]\right]$ for each estimate ${\widehat{\mathcal{D}}}^{\text{opt}}$, using a Monte Carlo approximation based on a random sample of size 10³, denoted as $\widehat{V}\left({\widehat{\mathcal{D}}}^{\text{opt}}\right)$. As we know the true data-generating model in simulation studies, the optimal ${\mathcal{D}}^{\text{opt}}$ can be determined for each simulation run. Given each estimate ${\widehat{\mathcal{D}}}^{\text{opt}}$ of ${\mathcal{D}}^{\text{opt}}$, we report $\widehat{V}\left({\widehat{\mathcal{D}}}^{\text{opt}}\right)-\widehat{V}\left({\mathcal{D}}^{\text{opt}}\right)$, as the performance measure of ${\widehat{\mathcal{D}}}^{\text{opt}}$. A larger value of the measure indicates better performance.

In Figure 2, we present the boxplots, obtained from 100 simulation runs, of the normalized values $\widehat{V}\left({\widehat{\mathcal{D}}}^{\text{opt}}\right)$ (normalized by the optimal values $\widehat{V}\left({\mathcal{D}}^{\text{opt}}\right)$) of the decision rules ${\widehat{\mathcal{D}}}^{\text{opt}}$ estimated from the five approaches, for each combination of n ∈ {250, 500}, ξ ∈ {0, 0.5} (corresponding to correctly specified or misspecified single-index interaction effect models, respectively) and δ ∈ {1, 2} (corresponding to moderate or large main effects, respectively), for the simulation setting “A” in the top panels and the setting “B” in the bottom panels.

The results in Figure 2 indicate that the proposed constrained single-index model outperforms all other approaches in estimating ${\mathcal{D}}^{\text{opt}}$. With substantial nonlinearity in the interaction effect term of the models (17) and (18), the modified covariates method, which assumes a restricted linear model on the interaction term, is clearly outperformed by the proposed model that utilizes a set of flexible link functions to accommodate the nonlinear treatment effect modification. The estimated values of the outcome weighted learning with a linear kernel and a Gaussian kernel, respectively, are similar to each other, but both are outperformed by the constrained single-index regression, even when the true interaction model deviates from a single-index model (when ξ = 0.5). When n = 500 (ie, with a relatively large sample size) and ξ = 0.5 (ie, when the underlying model deviates from the exact single-index structure), the penalized additive spline approach (PLS), due to its large model space, outperforms the modified covariates method slightly; however, the approach is clearly outperformed by the proposed single-index method that is robust to the main effect model misspecification and also allows nonlinear interactions. When the X main effect dominates the T-by-X interaction effect (ie, when δ = 2), although the increased magnitude of the main effect dampens the performance of all approaches to optimizing treatment decisions, the constrained single-index regression consistently targets to model the interaction effect-related variability, and its performance is near optimal when n = 500.

5 |. APPLICATION TO DATA FROM A DEPRESSION RANDOMIZED CLINICAL TRIAL

The development of the constrained single-index model method was motivated by a randomized clinical trial comparing an antidepressant (T = 2) and placebo (T = 1) for treating major depressive disorder. The primary purpose of the study is the development of a biosignature, called a differential treatment response index, defined as a combination of multiple biomarkers that can be used for optimization of an individualized treatment rule for patients with major depressive disorder (Trivedi et al., 2016). In major depressive disorder, each patient characteristic often has at most a weak modifying effect. Therefore, the proposed single-index modeling approach that creates a differential treatment response single-index that collectively exhibits a stronger, and possibly nonlinear, interaction with the treatment is a very clinically significant endeavor.

Of the 166 subjects, 88 were randomized to placebo and 78 to drug. Pretreatment clinical characteristics X = (X₁, … , X₅)^⊤ include: X₁ = age at evaluation; X₂ = severity of depressive symptoms measured by the Hamilton rating scale at baseline; X₃ = logarithm of duration (in month) of the current major depressive episode. In addition, patients underwent neuropsychiatric testing at baseline to assess reaction time, X₄ = median choice reaction time and cognitive control, X₅ = Flanker accuracy, as these behavioral characteristics are believed to correspond to biological phenotypes related to response to antidepressants (Trivedi et al., 2016). For the purposes of regularization, all pretreatment covariates are centered and scaled to have mean 0 and unit variance. The outcome Y is the improvement in symptoms severity (assessed by the Hamilton rating scale for depression) from baseline to week 8 taken as the difference (week 0 to week 8), and thus larger values of the outcome are considered desirable.

The estimated single-index coefficients $\widehat{\alpha }={\left({\widehat{\alpha }}_1,\dots ,{\widehat{\alpha }}_5\right)}^{\top }$ of the proposed model (1) and their 95% normal approximation bootstrap confidence intervals based on 500 bootstrap replications (see Supporting Information Section B.6 for the coverage proportions of the bootstrap confidence intervals assessed by simulations) are given by ${\widehat{\alpha }}_1=0.69\left(0.31,1.06\right)$, ${\widehat{\alpha }}_2=0.23\left(-0.10,0.57\right)$, ${\widehat{\alpha }}_3=0.33\left(0.03,0.64\right)$, ${\widehat{\alpha }}_4=-0.22\left(-0.51,0.08\right)$, and ${\widehat{\alpha }}_5=-0.55\left(-0.85,-0.25\right)$, respectively. The estimated treatment t-specific functions ${\widehat{f}}_t(\cdot )\left(t=1,2\right)$ (with 95% confidence bands, given $\widehat{\alpha }$) are illustrated in the first two panels of Figure 3.

FIGURE 3.

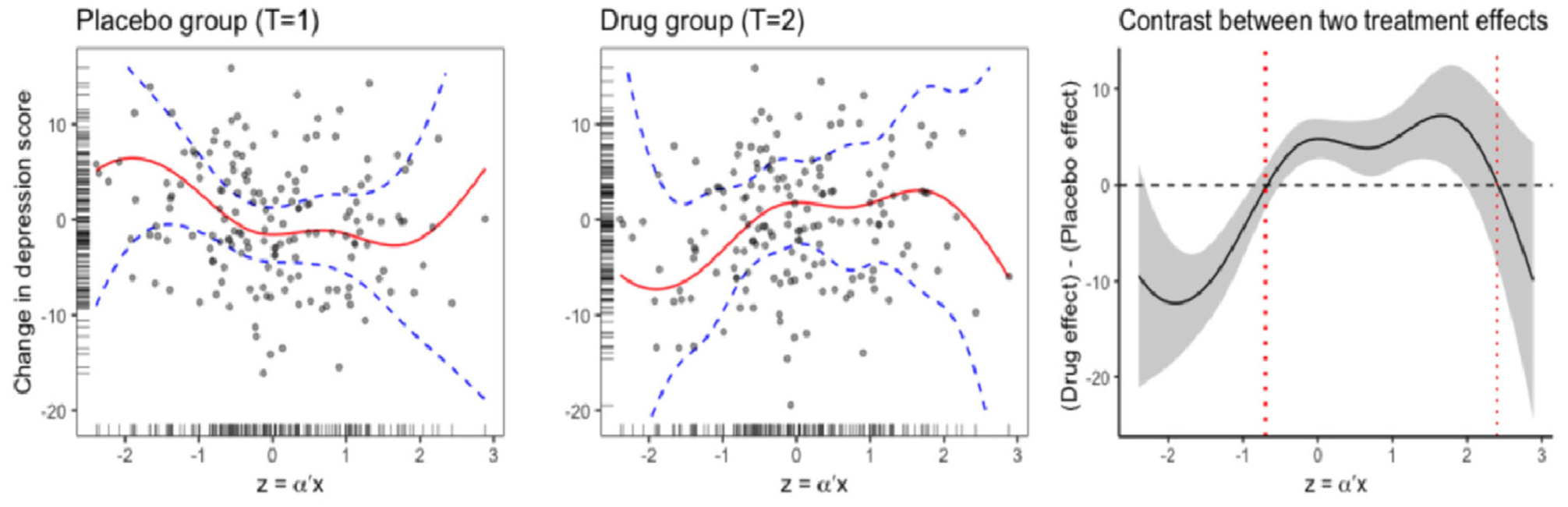
Depression randomized clinical trial: scatter plots of the outcome against the estimated single index z = α^⊤X, for the placebo group (T = 1, in the left panel) and the drug group (T = 2, in the middle panel); the estimated treatment-specific curve (with 95% confidence bands) for each group is overlaid (the red solid curve). In the right panel, the contrast between the estimated two treatment effects (drug - placebo) as a function of the estimated single-index is displayed.

The right panel of Figure 3 displays the contrast between the two estimated treatment effects (drug - placebo) versus the estimated single-index. This indicates that the superiority of the drug over placebo does not linearly increase with z = α^⊤X, but rather, it appears to plateau out with some nonlinear patterns to the right of the zero crossing point near z = −0.7, and it has another zero crossing point near z = 2.4. As implied by the contrast plot in Figure 3, an individualized treatment rule based on the single-index z = α^⊤X can be constructed by assigning patients with the index −0.7 < z < 2.4 to the active drug.

To evaluate the performance of the individualized treatment rules $\left({\widehat{\mathcal{D}}}^{\text{opt}}\right)$ estimated from five different approaches described in Section 4, we randomly split the data set at a ratio of 5 to 1 into a training set and a testing set (of size ñ), replicated 500 times, each time obtaining ${\widehat{\mathcal{D}}}^{\text{opt}}$ based on the training set and estimating the value of ${\widehat{\mathcal{D}}}^{\text{opt}}$, $V\left({\widehat{\mathcal{D}}}^{\text{opt}}\right)=E\left[E\left[Y\mid X,T={\widehat{\mathcal{D}}}^{\text{opt}}\left(X\right)\right]\right]$, by an inverse probability weighted estimator (Murphy, 2005) $\widehat{V}\left({\widehat{\mathcal{D}}}^{\text{opt}}\right)={\sum }_{i=1}^{\tilde{n}}{Y}_i{1}_{\left(T_i={\widehat{\mathcal{D}}}^{\text{opt}}\left(X_i\right)\right)}/{\sum }_{i=1}^{\tilde{n}}{1}_{\left(T_i={\widehat{\mathcal{D}}}^{\text{opt}}\left(X_i\right)\right)}$ based on the testing set (of size ñ). For the modified covariates method, we use a linear model with covariates X for efficiency augmentation. For comparison, we also include two naïve rules: treating all patients with placebo; and treating all patients with the active drug, each regardless of the individual patient’s characteristics X.

As Figure 4 shows, the proposed constrained single-index regression for estimating ${\mathcal{D}}^{\text{opt}}$ outperforms all other alternatives in terms of the average estimated values. In particular, the approach outperforms the modified covariates method and the outcome weighted learning with a linear kernel, illustrating the utility of the flexible treatment-specific link functions in approximating the nonlinear interactions. The method also outperforms the penalized additive spline least squares approach, suggesting that estimating and utilizing an optimal linear combination (a single-index α^⊤X) of biomarkers that collectively exhibits a stronger (and possibly nonlinear) interaction with the treatment is practically an appealing approach to optimizing treatment decision rules. In this example, the outcome weighted learning with a Gaussian kernel does not perform well.

FIGURE 4.

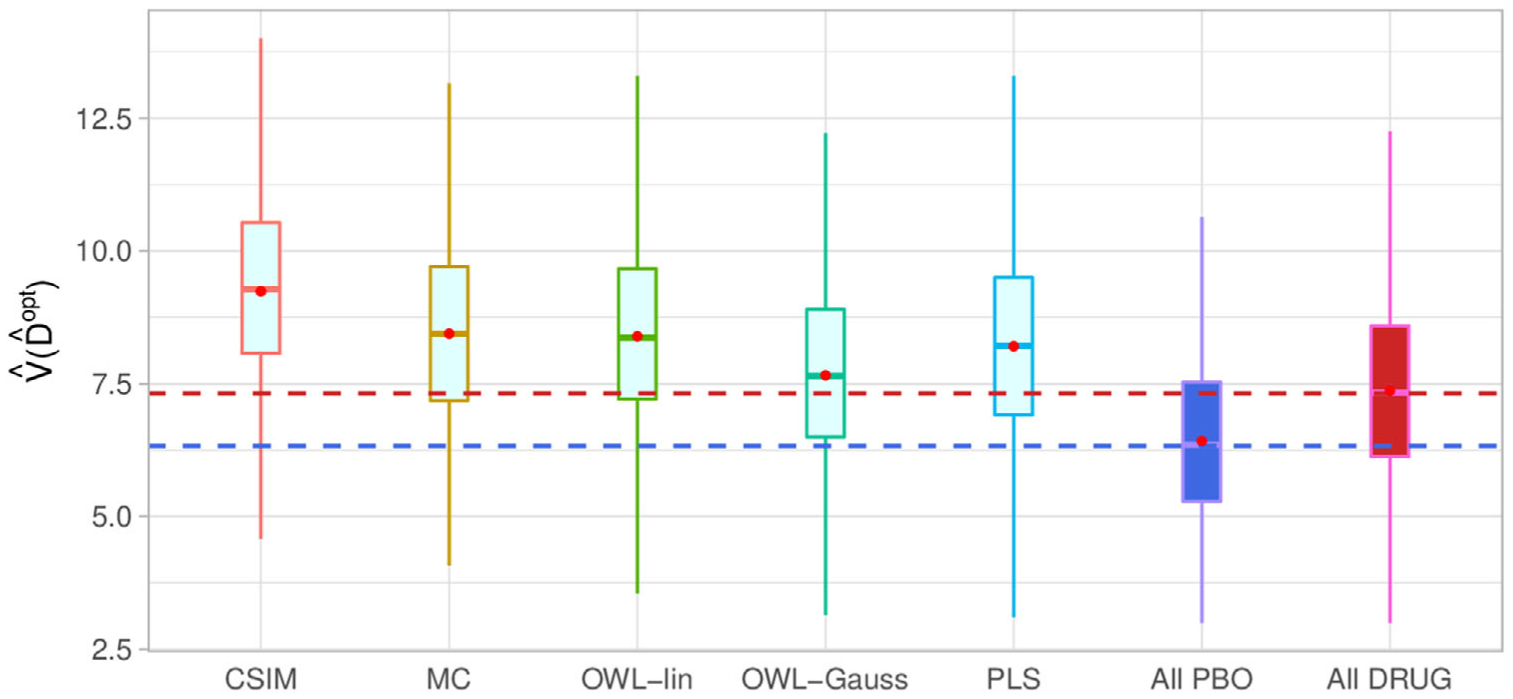
Depression randomized clinical trial: boxplots of the estimated values of the individualized treatment rules estimated from seven approaches, obtained from 500 randomly split testing sets. From left to right, estimation approaches to ${\mathcal{D}}^{\text{opt}}$: (1) the constrained single-index model; (2) the modified covariates model; (3) outcome weighted learning with a linear kernel; (4) outcome weighted learning with a Gaussian kernel; (5) the penalized spline least squares approach; (6) treating all patients with placebo; (7) treating all patients with the active drug.

The proposed single-index regression provides a visualization of the estimated single-index as shown in the panels of Figure 3, and the relative importance of each pretreatment covariate in terms of characterizing the heterogeneous treatment responses can be indicated by the coefficients (α₁, … α₅)^⊤. The practical utility of the proposed methodology is highlighted here by noting that the difference between the values of the treatment decision rule based on the new method and the values of the naïve rule that treats everyone with the drug is almost twice as large as the difference between the efficacies of the drug and placebo.

6 |. DISCUSSION

The proposed method is primarily designed to analyze data from randomized clinical trials. A limitation of the proposed method can occur when applying it to an observational study, where the covariates and treatment assignment can be correlated, in which case the estimator ${\widehat{\mathcal{D}}}^{\text{opt}}\left(X\right)=\text{arg}{\text{max}}_{t\in \left\{1,\dots ,L\right\}}{\widehat{f}}_t\left({\widehat{\alpha }}_0^{\top }X\right)$ might not yield the optimal decision rule. However, the working model (3), with the link functions (g₁, … , g_L) as defined in (7), can still be useful in fitting the T-by-X interaction effect term of model (1). If there are estimators (g₁, … , g_L), for each fixed α, that asymptotically satisfy (7), then, in the objective function (6), the part relevant to the estimation of the coefficient α₀ of model (1) is asymptotically separated from the X main effect term μ(X) of model (1), as in (5), resulting in robustness against misspecification of the X main effects in estimating the T-by-X interactions. We can utilize an iterative optimization procedure to optimize both α and (g₁, … , g_L). For each fixed α, estimators of (g₁, … , g_L) that asymptotically satisfy (7) are relatively easy to obtain. For example, we can first compute unconstrained estimators, denoted as ${\widehat{g}}_t^{**}\left({\alpha }^{\top }X\right)\left(t=1,\dots ,L\right)$, of the conditional expectations $g_t^{**}\left({\alpha }^{\top }X\right)=E\left[Y\mid {\alpha }^{\top }X,T=t\right]\left(t=1,\dots ,L\right)$, based on a one-dimensional (along the axis α^⊤X) nonparametric smoother for each treatment T = t (t = 1, … , L), and then remove the component in the fitted ${\widehat{g}}_T^{**}\left({\alpha }^{\top }X\right)$ corresponding to the main effect of α^⊤X, by fitting a one-dimensional nonparametric smoother (along the axis α^⊤X), denoted as ${\widehat{g}}^{*}\left({\alpha }^{\top }X\right)$, to the fitted ${\widehat{g}}_T^{**}\left({\alpha }^{\top }X\right)$. Then, for each fixed α, we can take ${\widehat{g}}_t\left({\alpha }^{\top }X\right)={\widehat{g}}_t^{**}\left({\alpha }^{\top }X\right)-{\widehat{g}}^{*}\left({\alpha }^{\top }X\right)(t=1,\dots ,L)$ as such estimators (g₁, … , g_L), which approximately satisfy (7). See Supporting Information Section A.6 for a justification for the robustness of this procedure against misspecification of μ(·). However, when T depends on X, the fitted T-by-X interaction effect term might result in biased causal effect estimates, as described in Supporting Information Section A.7.

In many applications, only a subset of measurements may be useful in determining an optimal treatment decision rule. Also, high-dimensional settings can lead to instabilities and issues of overfitting. Forthcoming work will introduce a regularization method that can both avoid overfitting and choose among multiple potential covariates by obtaining a sparse estimate of the single-index coefficient α₀. In this paper, the theoretical results are developed with a B-spline basis approximation, with the number of knots used as the tuning parameters. In finite samples, the choice of the number of knots can be crucial and delicate. At present an ad hoc choice of $d_t=\lfloor n_t^{1/5.5}\rfloor$ and d₀ = [n^1/55] is used for the number of knots, which is likely to be sub-optimal in practice (note that one can set $d_t=C\lfloor n_t^{1/5.5}\rfloor$ or d₀ = C[n^1/55] with an arbitrary C > 0 while still achieving the requirements in Assumption 5). In practice, a penalized spline approximation, for example, P-splines (Eilers and Marx, 1996), can be considered, which is relatively robust to the choice of the number of knots. Although in Section 3.3, Assumption 4 does not allow discrete-valued covariates, our simulation experiment (see Supporting Information Section B.2) where the covariates X include a binary variable suggests that estimation in practice is rather insensitive to departure from this assumption. Generally, multiple local optima exist in the squared error criterion in (11) (and also its population counterpart in (6) with respect to α, where g_t is defined in (7)), and in such cases the estimates can be sensitive to the choice of initialization. We assume (in Assumption 1) the local convexity of the criterion function near α = α₀, and this implies that the algorithm will converge if the initial estimate is close to α₀. Otherwise, the estimate ${\widehat{\alpha }}_0$ can be sub-optimal. One way to mitigate this problem is to consider multiple initial points for α₀ in estimation (as in Supporting Information Section B.2 and B.3). In this paper, we use a linear estimate based on the modified covariates linear model (2) (scaled to be in Θ) as an initial estimate, and the estimate ${\widehat{\alpha }}_0$, optimized to incorporate possibly nonlinear interactions, provides a significant improvement over the modified covariate initial estimate, as illustrated by the simulations in Section 4.

Future directions of this work also include an extension of the proposed regression to a multiple-index regression for modeling interactions. For example, when L = 2, model (1) can be extended to a partially linear single-index model (eg, Lian and Liang, 2016; Xia et al., 1999) by adding a modified covariate (Tian et al., 2014) linear component to the single-index interaction component. We will also investigate the incorporation of functional covariates and longitudinal outcomes.