A neural basis for categorizing sensory stimuli to enhance decision accuracy

SUMMARY

Sensory stimuli with graded intensities often lead to yes-or-no decisions on whether to respond to the stimuli. How this graded-to-binary conversion is implemented in the central nervous system (CNS) remains poorly understood. Here we show that graded encodings of noxious stimuli are categorized in a decision-associated CNS region in Drosophila larvae, and then decoded by a group of peptidergic neurons for executing binary escape decisions. GABAergic inhibition gates weak nociceptive encodings from being decoded, while escalated amplification through the recruitment of second-order neurons boosts nociceptive encodings at intermediate intensities. These two modulations increase the detection accuracy by reducing responses to negligible stimuli while enhancing responses to intense stimuli. Our findings thus unravel a circuit mechanism that underlies accurate detection of harmful stimuli.

Graphical Abstract

INTRODUCTION

While sensory stimuli are typically present in wide and graded intensity ranges, animals’ decisions on whether to respond to the stimuli are often binary. A fundamental question in neuroscience is how such graded-to-binary conversions in perceptual decision-making occur in the central nervous system (CNS) [1, 2]. While studies in vertebrates [3-6] and invertebrates [7-11] have identified important neural mechanisms underlying perceptual decision-making, the neural basis for the graded-to-binary conversion in the perceptual decision-making remains largely unknown.

Perceptual decisions are generated by emergent activities of neuronal populations in the CNS [12-16]. Consequently, assessing activity in the entire CNS is key to understanding the decision-making process. Although perceptual decision-making has primarily been studied in mammals [2], the large size of the mammalian CNS limits spatiotemporal resolution in assessing CNS-wide emergent activities. In contrast, the small size of Drosophila larval CNS, combined with recent advances in genetically encoded calcium indicators (GECIs) [17, 18], allows functional imaging of the entire larval CNS at sub-cellular and sub-second resolution [19], which makes Drosophila larvae an ideal model for assessing the CNS-wide neural activity in perceptual decision-making.

When Drosophila larvae detect noxious stimuli, they perform stereotypical escape behaviors that can be accurately quantified, including abrupt curling and nocifensive rolling [20, 21]. Moreover, recent studies have both identified neurons involved in the larval nociceptive pathway and mapped their synaptic connections, further allowing circuit analyses in this pathway (Figure S1A) [22-28]. These merits, together with powerful genetic tools available in Drosophila, make the larval nociceptive system an excellent model for multi-level studies of the neural computation in perceptual decision-making.

In this study, we performed GECI-based functional imaging of whole larval ventral nerve cord (VNC) and developed unbiased computational tools to analyze CNS-wide neural mechanisms underlying sensori-motor integration. Combining this with other approaches, including optogenetic manipulations, electrophysiological recordings, genome editing and computational modeling, we identified a “gated amplification” mechanism that underlies the graded-to-binary conversion in detecting noxious stimuli. We further provide evidence suggesting that such graded-to-binary conversion of sensory encodings boosts the accuracy of yes-or-no decisions.

RESULTS

Graded encodings of nociceptive inputs are converted to binary escape decisions

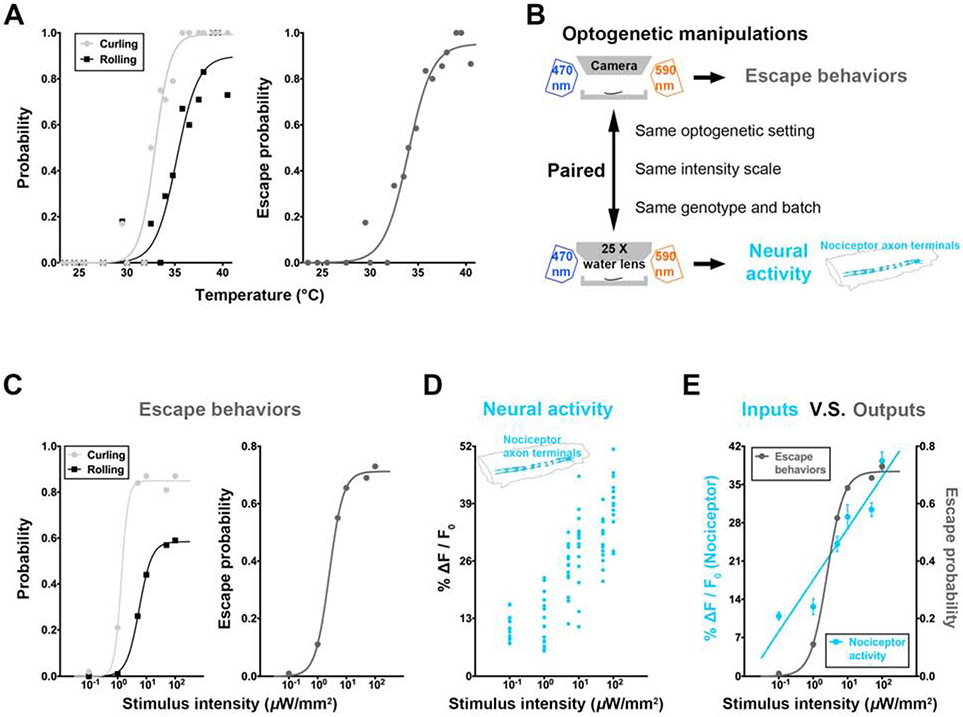
Drosophila larvae escape from noxious heat [20, 21]. The larval escape behaviors were assessed by scoring the percentage (probability) of behavioral events within 5 seconds after nociceptor stimulation (Figure 1A). The probability of larval escape behaviors in response to linearly scaled temperatures is sigmoid (Figures 1A and STAR Methods), which is a typical stimulus-response relationship in yes-or-no detection tasks [29]. To understand the neural mechanism underlying such perceptual decisions, we first assessed the relationship between the sensory encodings of noxious stimuli and escape behavioral decisions. We divided larvae that received the same optogenetic manipulation in the same batch of culture into two groups, one for calcium imaging on neural activity and the other for behavioral tests, and then assessed the neural activity and escape behaviors on the same stimulus intensity scale (Figure 1B and STAR Methods). We optogenetically stimulated larval nociceptors at various intensities and recorded both the escape behaviors and the neural activity in nociceptor axon terminals in the ventral nerve cord (VNC). Neural activities in nociceptor axon terminals were assessed by calcium imaging, also within 5 seconds after nociceptor stimulation. While the escape probability displayed a sigmoid response on the logarithmic stimulus-intensity scale, the neural activity in nociceptor axon terminals increased linearly on the same scale (Figures 1C, 1D, 1E and S1B). These results suggest a conversion of graded encodings of noxious stimuli to binary escape probability in larvae.

Figure 1. Graded noxious inputs are converted to binary escape decisions.

(A) Stimulus-response curves showing the probability (percentage of larvae) of curling and rolling (left panel) and the escape probability (right panel) under different temperatures. The escape probability is defined as the averaged probability of curling and rolling (see STAR Methods for details). Each dot represents a temperature group. N = 141 larvae (4-29 per temperature group). P < 0.0001, Extra sum-of-squares F test. Throughout this study, curve fittings (model selections) used Extra sum-of-squares F test between linear and sigmoid curves with the null hypothesis (H₀) that the curve fits a linear function (see STAR Methods for details) unless otherwise noted.

(B) A schematic showing the paired functional (calcium) imaging and behavioral tests.

(C) Larval curling and rolling (left), and escape (right) probability under different intensities of optogenetic stimulation of larval nociceptors. Each dot represents an intensity group. N = 100 larvae per intensity group.

(D) The neural activity level in the collective axon terminals of larval nociceptors under the same stimulation conditions as those in (C). The collective nociceptor axon terminals of a larva were identified by an unbiased computational method (see STAR Methods for details). Each dot represents a larva. N = 15 larvae per intensity group. The calcium traces overtime for individual larva are in Figure S1B.

(E) The stimulus-response curve of escape probability is more binary (sigmoid curve), while that of neural activity level in nociceptor axon terminals is more graded (linear curve) (P = 0.0007 for escape probability while P = 0.4237 for nociceptor activity, Extra sum-of-squares F test). Each dot represents the group mean for the nociceptor activity level or the escape probability. Throughout this study: error bars represent standard error of the mean (SEM). Data is from (C) and (D).

See also Figure S1 and Table S1.

Whole-VNC functional imaging analysis identifies a decision-associated CNS region

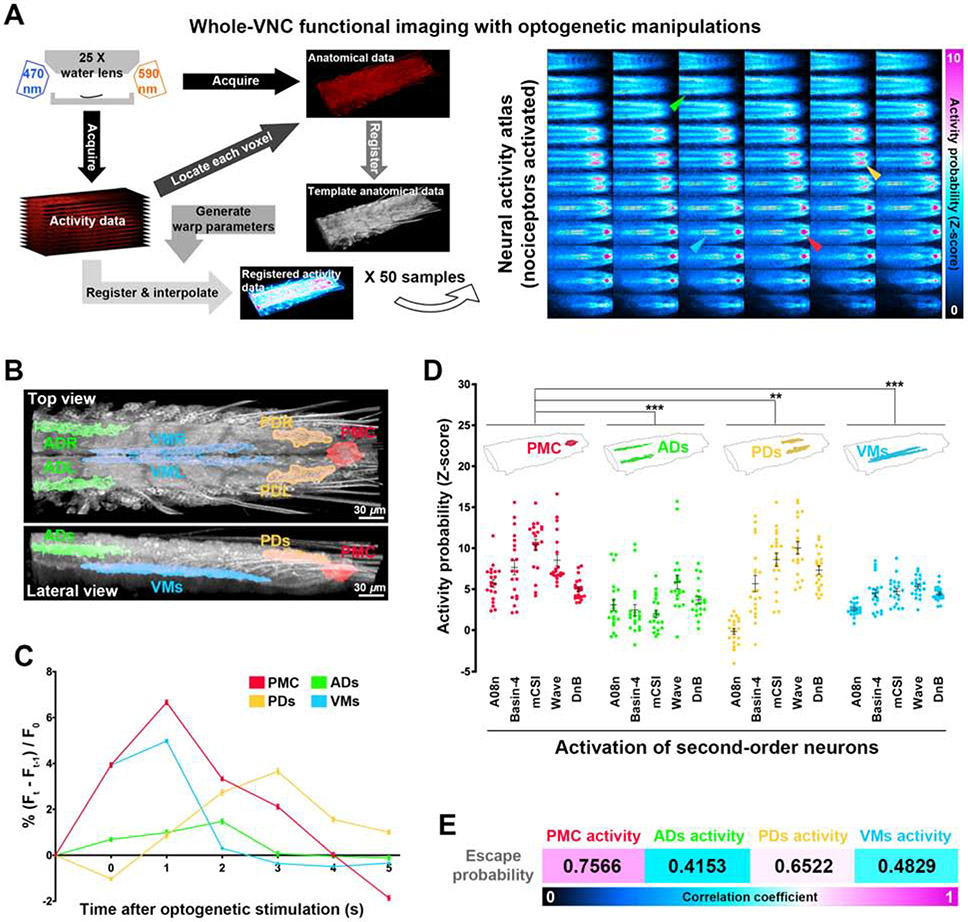
To understand how graded encodings of noxious stimuli are converted to binary escape decisions, we performed GECI-based whole-VNC functional imaging on a preparation with intact larval PNS and CNS [25] to identify the CNS regions that responded to optogenetic stimulation of nociceptors, as such regions are likely involved in processing nociceptive inputs. Larval nociceptors were activated optogentically, and neural activities in the entire VNC were recorded by calcium imaging. In order to capture the complete neural activities (including those in somas and neurites) in the VNC, we developed an unbiased machine-learning method to automatically identify CNS regions based on functional connectivity (Figure 2A and STAR Methods).

Figure 2. Whole-VNC functional imaging analysis reveals a decision-associated CNS region.

(A) The steps for identifying nociceptor-activated CNS regions. Arrows point to different nociceptor-activated CNS regions on representative z sections. N = 50 larvae. In all neural activity atlases throughout this study, red, green, yellow, and blue represent PMC, ADs, PDs, and VMs, respectively, unless otherwise noted. The anterior side of the VNC is to the left. The top-left and bottom-right panels are the dorsal-most and ventral-most z sections, respectively.

(B) The seven nociceptor-activated CNS regions.

(C) The neural activity levels in different nociceptor-activated CNS regions at each second after nociceptor stimulation (details are in Figure S2). Each dot represents the mean activity level in a CNS region. Data is from (A).

(D) Neural activity probability (indicated by Z-score) of distinct nociceptor-activated regions in each SON activation group. Each dot represents a larva. N = 20 larvae per SON activation group. Two-way ANOVA (Dunnett’s post hoc). Throughout this study, n.s.: P >= 0.05, no statistical difference; *, P < 0.05; **, P < 0.01; ***, P < 0.001.

(E) Pearson’s correlation coefficient between neural activity level of distinct nociceptor-activated CNS regions and escape probability. N = 675 larvae for neural activity and 2,294 for paired behaviors (from 20 experimental groups in this study). Details are in Figure S3.

See also Figures S1, S2 and S3, Video S1 and Table S1.

We first identified the time window for detecting nociceptor-activated CNS regions in a data-driven manner (Figure S1C and STAR Methods). To do so, we segmented the functional imaging data from a VNC into “super voxels”, which consists of neighboring voxels with similar fluorescence dynamics [30], and examined the fluorescence changes in them. Reasoning that the first peak of calcium signals after stimulation was most relevant to sensory processing, we examined the rising time for calcium signals to reach their first post-stimulation peak in all super voxels from 50 recorded VNCs and used the longest one as the time window for identifying nociceptor-activated CNS regions, which was 5 seconds after stimulation. We then defined the nociceptor-activated CNS regions based on the functional imaging data of these 50 VNCs within the 5-second time window. The response of each voxel in a functional imaging data was measured as the significance of its fluorescence intensity increase in the 5-second time window, with consideration of the noise level of the data. Inspired by a previous study [31], we registered the functional imaging data of the 50 VNCs to a template so that the shapes of these VNCs became the same. Next, the mean fluorescence response in each registered voxel was taken from the 50 registered functional imaging data, and an iterative thresholding method was used to cluster spatially connected voxels with statistically significant increase in fluorescence intensity within the abovementioned 5-second time window (Figure 2A and STAR Methods). These clusters were defined as nociceptor-activated CNS regions.

This unbiased computational approach identified seven nociceptor-activated CNS regions, which we named according to their locations in the VNC: anterior dorsal left/right (ADs), ventral medial left/right (VMs), posterior dorsal left/right (PDs), and posterior medial center (PMC) (Figures 2B and S1D, and Video S1). Among them, the PMC was uniquely located between the sensory (ventral) and motor (dorsal) neuropils [32, 33] (Figure 2B), and exhibited prolonged activity after nociceptor stimulation (Figures 2C and S2), indicating that the PMC might play a role in sensori-motor integration.

In the VNC, five types of second-order neurons (SONs) that are postsynaptic to larval nociceptors—A08n, Basin-2/4, mCSI, Wave, and DnB—have been confirmed to be involved in larval escape behaviors [22-28]. Optogenetic activation of each of these SON types resulted in distinct activation probabilities of the nociceptor-activated CNS regions, with the PMC showing the highest probability across all SONs (Figure 2D). This raises the possibility that nociceptive signals are processed through diverse SONs and converge on the PMC to generate neural encodings that represent a consensus escape decision. To test this hypothesis, we investigated the correlation between the mean activity level of each nociceptor-activated CNS region from an experimental group and the probability of escape behaviors from a group of the same genotype, batch, and stimulation and inhibition as those for neural activity analyses (Figure S3A). All the whole-VNC functional imaging data from 675 larvae (in 20 experimental groups) and their paired behavioral data from 2,294 larvae (the same 20 cohorts) in this study were analyzed. Strikingly, the level of PMC activity shows the strongest correlation with the probability of escape behaviors among all the nociceptor-activated CNS regions (Figures 2E and S3B), suggesting that the PMC activity is a neural signature representing escape decisions.

Graded nociceptive encodings become binary in the PMC and are decoded by LK neurons for executing escape decisions

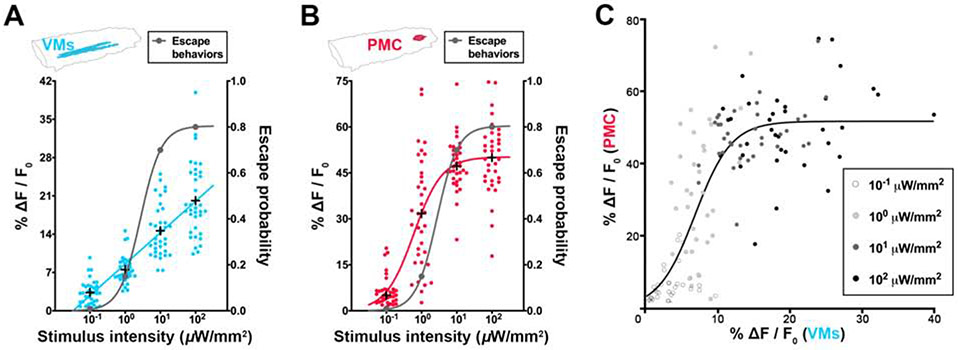
The VMs, located in the sensory neuropil, contain nociceptor axon terminals (Video S2). Similar to nociceptor activities (Figures 1D and 1E), the activity of the VMs fits into a linear stimulus-response on our stimulus-intensity scale (Figure 3A), suggesting that VM activity conveys fine-scale intensity information about noxious stimuli in a wide dynamic range. Intriguingly, PMC activity exhibited a sigmoid increase on the same stimulus- intensity scale, resembling the binary escape probability (Figure 3B). In fact, the relationship between VM activity and PMC activity from the same larvae fits a sigmoid function (Figure 3C), indicating that graded encodings of noxious stimuli in the VMs become more binary in the PMC, whose activity level represents the binary escape decision (Figures 2E and S3B).

Figure 3. Graded nociceptive encodings become more binary in the PMC.

(A-B) Stimulus-response curves for the neural activity level of VMs and PMC are plotted against the left y-axis and that for escape probability against the right y-axis. Note that while the stimulus-response curve of the VMs activity fits a linear curve (P = 0.1238, Extra sum-of-squares F test), that of PMC activity fits a sigmoid one (P < 0.0001), resembling that of escape probability (P = 0.0090). Each dot represents a larva for neural activity and an intensity group for escape probability, respectively. “+” represents the mean activity level of an intensity group. N = 35 larvae per intensity group for neural activity and 100 larvae per intensity group for escape behaviors.

(C) The relationship between neural activity level in the VMs and that in the PMC from the same larvae is sigmoid (P < 0.0001, Extra sum-of-squares F test). Each dot represents a larva. Data is from (A) and (B).

See also Video S2 and Table S1.

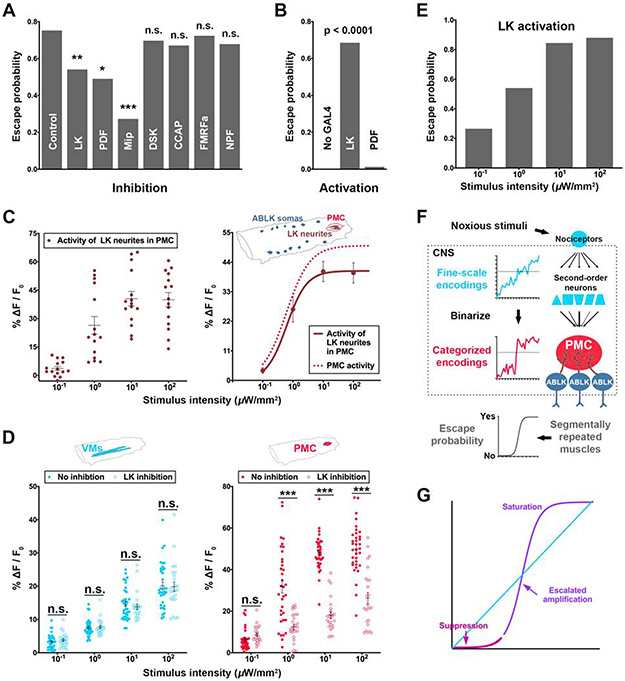
The PMC covers the neuropil of abdominal segment 9, which contains a prominent structure called “terminal plexus” (TP) [33]. Peptidergic neurons innervate TP [34, 35] and might contribute to executing the escape decisions. To test this, we optogenetically inhibited seven candidate types of peptidergic neurons with Guillardia theta anion channelrhodopsin-1 (GtACR1) [36] and examined the effects on larval escape behaviors. Inhibition of leucokinin (LK), pigment dispersing factor (PDF), or myoinhibitory peptide (Mip) neurons impaired escape behaviors (Figure 4A). The Mip-GAL4 was expressed in a large number of neurons in the VNC (Video S3) and was hence excluded from further studies due to the concern of non-specificity. Activation of LK neurons, but not PDF neurons, elicited robust escape behaviors (Figure 4B and Video S4). These results suggest that LK neurons are both required and sufficient for robust execution of escape decisions.

Figure 4. LK neurons decode the PMC activity to enable binary escape behaviors.

(A) Escape probability of larvae whose peptidergic neurons were optogenetically inhibited. N = 101, 109, 106, 108, 109, 111, 105, and 109 larvae for control, LK, PDF, Mip, DSK, CCAP, FMRFa and NPF, respectively. Chi-square test (Bonferroni post hoc).

(B) Escape probability of larvae whose LK or PDF neurons were optogenetically activated. N = 100 for No GAL4, LK and PDF, respectively. Fisher’s exact test between LK and PDF groups.

(C) The collective activity of LK neurites within the PMC in response to different intensities of nociceptor stimulation. Left: each dot represents a larva. N = 15 larvae per intensity group. Right: each dot represents the mean of an intensity group. Solid line: the activity of LK neurites within the PMC (P = 0.0018, Extra sum-of-squares F test); dotted line: the PMC activity (same as that in Figure 3B).

(D) The neural activity level in VMs and PMC upon different intensities of nociceptor stimulation when LK neurons are inhibited. Each dot represents a larva. The “no inhibition” group is from Figures 3A and 3B. N = 25 per intensity group for LK inhibition. Mann-Whitney U test.

(E) Graded activation of LK neurons results in gradually increased probability of larval escape behaviors. Each dot represents an intensity group. N = 100 per intensity group.

(F) A model of the neural network that categorizes noxious stimuli to generate binary escape decisions in Drosophila larvae.

(G) The hypothetical process of converting a linear input to a more binary output.

See also Figure S4, Videos S3 and S4, and Table S1.

There are four groups of LK neurons: ALKs (anterior), LHLKs (lateral horn), SELKs (suboesophageal), and ABLKs (abdominal ganglion) [33, 34, 37, 38]. Among them, only SELKs and ABLKs innervate TP [33, 34, 37, 38] (Video S3) and are activated by nociceptor stimulation (Figure S4A), suggesting that the nociceptive pathway only involves these two groups of LK neurons. The SELKs project axons to the TP [37, 39], which expresses the LK receptors [39]. On the other hand, the 7 pairs of segmentally repeated (A1-A7) ABLKs extend their dendrites to the TP [34, 37] (Figure S4B) and project axons to the muscles in the body wall of the equivalent segment [33, 34, 37, 38], implying that ABLKs might receive nociceptive information from the PMC and enable the escape motor programs. Indeed, activation of SONs, such as A08n and Basin-4, activates ABLK neurons (Figure S4C). Moreover, the collective activity in LK neurites within the PMC resembled the total activity of the PMC in response to nociceptor stimulation (Figure 4C). Strikingly, optogenetic inhibition of LK neurons resulted in a dramatic decrease in PMC activities (Figure 4D), further demonstrating that the collective activity of LK neurites within the PMC represents the majority of PMC activities. Furthermore, graded activation of LK neurons, which project axons to the transverse muscles [38], gradually increased the probability of larval escape behaviors (Figure 4E). These results suggest that the near-binary encoding of stimulus intensity in the PMC largely reflects the activity of LK neurons and that LK activity produces the nociceptive behavior.

Escalated amplification of nociceptive encodings by stimulus-intensity-dependent recruitment of SONs

We have thus far identified a neural network that categorizes graded encodings of noxious stimuli to generate binary escape decisions in Drosophila larvae (Figure 4F). How is the conversion of graded encodings to binary decisions achieved in this network? The transformation of a graded stimulus-response relationship to a more binary one typically involve a suppression of responses in the lower intensity range (lag phase) and an escalated amplification of responses in the mid-range intensities of stimuli (log phase), which leads to response saturation at high intensities (Figure 4G) [29]. We thus investigated the neural mechanisms that underlie these two distinct modulations.

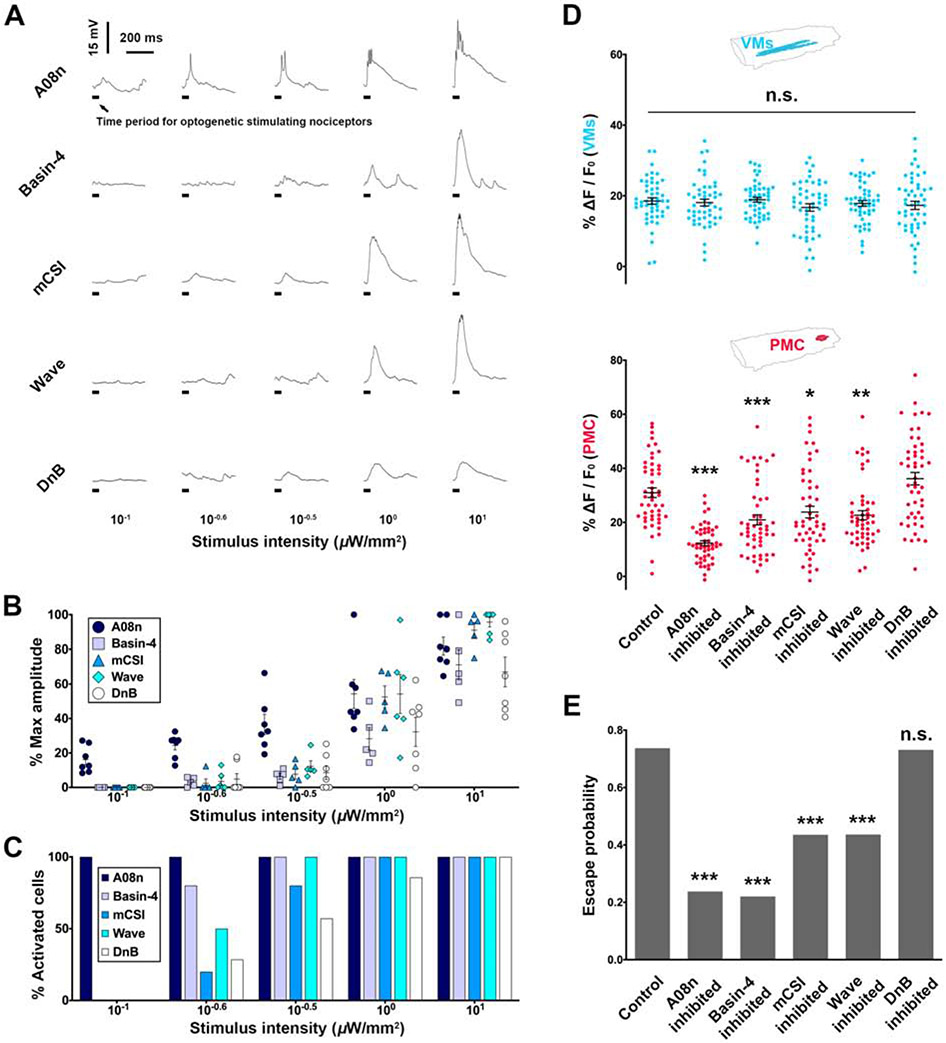
As shown above, diverse types of SONs, consisting of a number of neurons, contribute to decision-associated neural activity in the PMC (Figure 2D), raising the possibility that their collective outputs amplify the encodings of noxious stimuli. Thus, understanding how these SONs respond to noxious inputs of different intensities should be key to discovering the neural mechanism that underlies the escalated amplification phase of the sigmoid curve. Although we previously used calcium imaging as a readout for neural activity, electrophysiology is better for determining whether individual neurons are activated by a given stimulus. A previous report on other types of neurons showed similar dynamic range and linearity between membrane depolarization and calcium signals measured by jRCaMP1b [17]. Using the A08n neurons as a test case, we observed similar correlations between the average membrane depolarization and calcium signals (Figures 5A, 5B, S5A and S5B). Therefore, we used whole-cell patch clamping to determine how different types of SONs responded to various intensities of nociceptor stimulation.

Figure 5. Escalated amplification of nociceptive encodings by stimulus-intensity-dependent recruitment of SONs.

(A-C) Whole-cell patch clamping demonstrates stimulus-intensity-dependent responses of different types of SONs. N = 7, 5, 5, 6, 7 cells for A08n, Basin-4, mCSI, Wave and DnB, respectively. (A) Representative traces of SON responses to various stimulus intensities. (B) The response amplitudes of different types of SONs. Each dot represents a cell. (C) Different types of SONs exhibit different minimal intensities of nociceptor stimulations for their activations. The minimum or maximum depolarization of each cell was identified by stimulating nociceptor from low to high intensity.

(D-E) Optogenetic inhibitions of different SONs impair PMC activities and escape probability to distinct extents. Neural activity levels (D): N = 50 larvae per genotype (each dot represents a larva). The control is from Figure 2A. Escape probabilities: N = 101, 103, 102, 101, 110 and 108 larvae for control, A08n, Basin-4, mCSI, Wave and DnB, respectively. One-way ANOVA (Dunnett’s post hoc) for neural activity level and Chi-square test (Bonferroni post hoc) for escape probability.

See also Figure S5 and Table S1.

We recorded the membrane depolarization of different types of SONs upon various intensities of nociceptor stimulation. Strikingly, different SON types required different stimulus intensities for activating 100% of neurons of that type. For example, at low intensity (10⁻¹ μW/mm²), 100% of A08n neurons were activated while none of the other SONs had any response (Figures 5A, 5B, 5C and S5B). Moreover, Basin-4, Wave, mCSI, and DnB required at least 10^−0.6, 10^−0.5, 10⁰, and 10¹ μW/mm², respectively, to activate 100% of the neurons of that type. Furthermore, the intensities that elicited the minimal responses were also different for different types of SONs. As a result, the total number of activated SONs increased with the intensity of nociceptor stimulation.

The response amplitudes of individual SONs of the same type also increased with stimulus intensity (Figures 5A, 5B, and S5B), even after nearly all neurons were activated at mid-range intensities. For example, while a mid-range intensity (10⁰ μW/mm²) activated nearly 100% of neurons in all SON types, the amplitudes of individual neurons were lower than those stimulated at a high intensity (10¹ μW/mm²). This allows further amplification of the encodings of noxious stimuli until the responses saturate at high stimulus intensity. Since increases in both the activated cell number and activity level of each cell can result in a quadratic increase (i.e., escalated amplification) of the collective responses (Figure S5C), the stimulus-intensity-dependent recruitment of SONs provides a basis for the escalated amplification of graded encodings of noxious stimuli.

Supporting this notion, optogenetic inhibition of each SON type impaired the PMC activity and escape probability, though to distinct extents (Figures 5D and 5E), suggesting that all SON types are required—with different weights—for robust PMC activity. The only exception is DnB, whose inhibition by the 412-GAL4 did not affect PMC activity or escape behaviors (Figure 5D). This is possibly because the 412-GAL4 is also expressed in large numbers of GABAergic inhibitory neurons [22], whose inhibition led to hyperactivity in the VNC (Figure S5D), overriding the impairment of PMC activity. As expected, inhibition of any SON type did not change the activity of VMs (Figure 5D, upper panel), which contain nociceptor axon terminals (Video S2) and respond to nociceptor stimulations linearly (Figure 3A). These results are consistent with the notion that increasing the number of responding SONs enhances nociceptive encodings to make the log phase of the stimulus-response curve steeper.

As shown above, the collective activity of LK neurites within the PMC represents the majority of PMC activities (Figure 4D). If the stimulus-intensity-dependent recruitment of SONs leads to escalated amplification of nociceptive encodings, then inhibition of any of SONs would not only attenuate the steep slope of PMC activity, as shown in Figure 5D, but also reduce the slope of the stimulus-response curve of the LK neurites within the PMC. To test this prediction, we inhibited A08n neurons and recorded the activity in LK neurites within the PMC. The slope of stimulus-response curve of LK neurites was indeed reduced by A08n inhibition (Figure S6A).

Taken together, these results suggest that distinct types of SONs are recruited to the functional network at different intensities of nociceptor stimulation. This populationcoding network amplifies the graded encodings of noxious stimuli in an escalated manner.

GABAergic inhibition gates the encodings of weak noxious stimuli

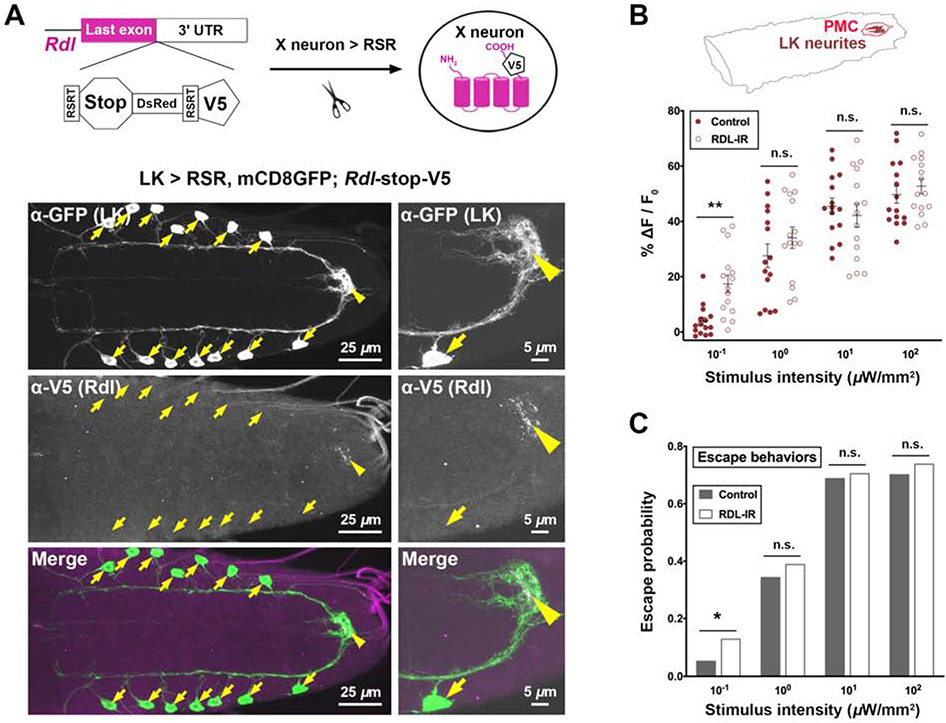
As mentioned above, the transformation of a graded stimulus-response relationship to a binary one might also involve a suppression of responses in the lower intensity range (Figure 4G). We next determined whether there existed a mechanism that suppresses the encodings of weak noxious stimuli. As in vertebrates, GABAergic synapses mediate the majority of inhibition in Drosophila, through ionotropic GABA_A receptors or metabotropic GABA_B receptors [40]. However, available reagents for studying GABA receptors in Drosophila were not suitable for determining subcellular localization of these receptors [41, 42], which is crucial for examining the presence of these receptors in neuropils, such as the PMC. We reasoned that the ionotropic GABA_A receptor Resistance to dieldrin (Rdl), which plays a major role in fast synaptic inhibition in Drosophila [43], might be involved in fast nociceptive responses. Therefore, we applied a novel technique that we developed for conditional tagging endogenous proteins in vivo [44] to generate a Rdl conditional-tag knock-in line and found that Rdl was present in the PMC (Figure S6B). We further found that Rdl was expressed in LK neurites within the PMC (Figure 6A), raising the possibility of GABAergic inhibition of LK neurons. We tested this by examining the effects of LK-neuron-specific knockdown of Rdl on PMC responses to nociceptor stimulation. Knocking down Rdl in LK neurons increased the activity levels of LK neurites within the PMC (Figure 6B) and the probability of escape behaviors (Figure 6C) only at low intensity of nociceptor stimulation (10⁻¹ μW/mm²). These results suggest that GABA_A-receptor-mediated inhibition gates the encodings of weak noxious stimuli to block them from activating ABLK neurons for motor outputs. The effect of GABAergic gating is insignificant at intermediate levels of noxious stimuli, possibly because it is overcome by the escalated amplification of decision-associated activity in the PMC (Figure 5).

Figure 6. Rdl-mediated inhibition gates encodings of weak noxious stimuli.

(A) Confocal imaging showing endogenous Rdl (tagged by V5) expression pattern in LK neurons (labeled by GFP). The schematic drawing shows the design of the Rdl-stop-V5 knock-in flies and its use for labeling endogenous Rdl in specific neuron types. Arrows and arrowheads point at LK somas and their neurites within the PMC region, respectively.

(B-C) RNAi-mediated knockdown of Rdl (Rdl-IR) in LK neurons increased the activity levels of LK neurites within the PMC (B) and the probability of escape behaviors (C) only at low intensity of nociceptor stimulation (10⁻¹ μW/mm²) but not at higher intensities. (B) Each dot represents a larva. N = 15 per genotype for each intensity group. Mann-Whitney U test. (C) N = 100 per genotype for each intensity group. Fisher’s exact test.

See also Figure S6 and Table S1.

Taken together, our results suggest that two distinct modulations operate together to convert graded sensory encodings into binary behavioral decisions. The recruitment of SONs amplifies the intermediate levels of nociceptive encodings to strengthen them, while GABAergic inhibition suppresses the weak levels of encodings to prevent them from being decoded for behavioral outputs.

Binarizing sensory encodings to enhance detection accuracy

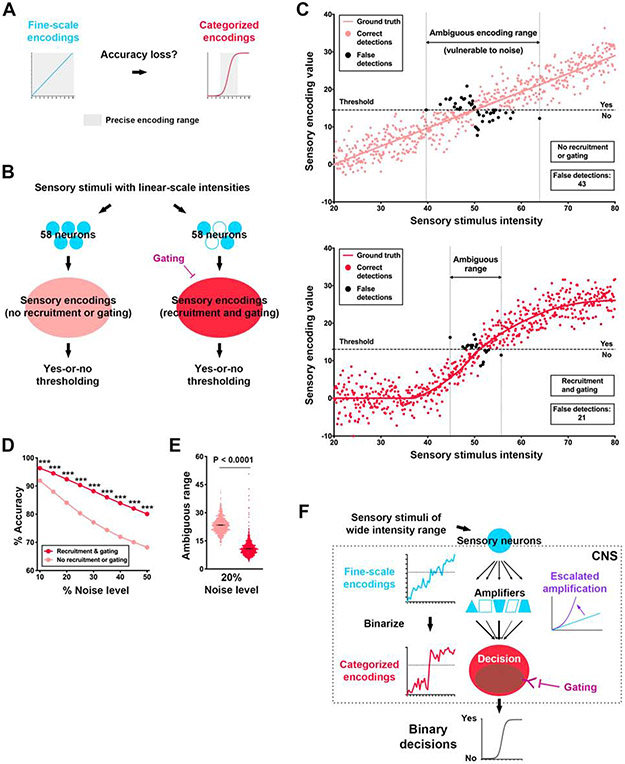
Graded encoding of sensory stimuli conveys fine-scale intensity information about the stimuli in a wide dynamic range. While the conversion of fine-scaled intensities into binary categories would conceivably enhance the certainty of yes-or-no decisions, would it impair detection accuracy (Figure 7A)? We addressed this by computationally simulating signal detection accuracy in networks with or without the graded-to-binary conversion achieved through the gated amplification mechanism discovered in this study (Figure 7B and STAR Methods). The detection of a stimulus was defined as a sensory encoding value above the yes-or-no threshold (i.e., half of the maximum ground-truth value) (Figure S6C). The ground truth of each simulated encoding value is the one without any noise. A correct detection (true yes or true no) was defined as a simulated value (with noise) that was consistent with its ground truth in being above or below the decision threshold (Figure S6C). Accordingly, the accuracy was defined as the ratio of correct detections to total ones, which was based on the signal detection theory (SDT) [1] (Figure S6C). As expected, the gated amplification converted the linear encodings of stimulus intensities into a sigmoid curve (Figure 7C). To our surprise, the graded-to-binary conversion did not impair, but increased, the detection accuracy throughout a range of noise levels from 10% to 50% (Figure 7D), suggesting that graded-to-binary conversion of sensory encodings through the gated amplification mechanism boosts the accuracy of yes-or-no decisions in noisy systems. This happens because the binary conversion of graded sensory encodings narrows the ambiguous encoding range of the stimulus intensity (Figures 7C and 7E), which is the range vulnerable to the impact of noise.

Figure 7. Graded-to-binary conversion of sensory encodings improves the accuracy in yes-or-no detections.

(A) Graded encodings convey fine-scale intensity information while binary encodings narrow the fine-scale (precise) encoding range.

(B) Diagram of the computational modeling of yes-or-no detection networks without (left) and with (right) the gated amplification mechanism (stimulus-dependent-recruitment of 58 neurons and the gating, see STAR Methods for details).

(C) Plots that show the sensory encoding values in yes-or-no detection tasks of a randomly selected, simulated larva at the noise level of 20%. Upper panel: simulations without the gated amplification mechanism; lower panel: simulations with the gate amplification mechanism. A noise level of 20% is defined as the standard deviation of the sensory encoding value that is 20% of the saturated encoding value. Each simulated larva performed 1,000 detections in response to 1,000 sensory stimulus intensities ranging from 0 to 100. Each detection generated a sensory encoding value, which is represented in the plots by a dot (- shown are those generated by the stimulus intensities between 20 and 80).

(D) The detection accuracies of the two networks at various noise levels. Each dot represents the detection accuracy at the indicated noise level. The detection accuracy at a noise level is calculated based on the detections from 1,000 simulated larvae responding to stimulus intensities ranging from 20 to 80. Fisher’s exact test.

(E) The ambiguous range of sensory encodings of the two networks at the noise level of 20%. Each dot represents the ambiguous range of a simulated larva. Unpaired t-test. The ambiguous encoding range is defined as the stimulus intensity range in which false detections appear, as shown in (C). Lines represent the means of ambiguous range.

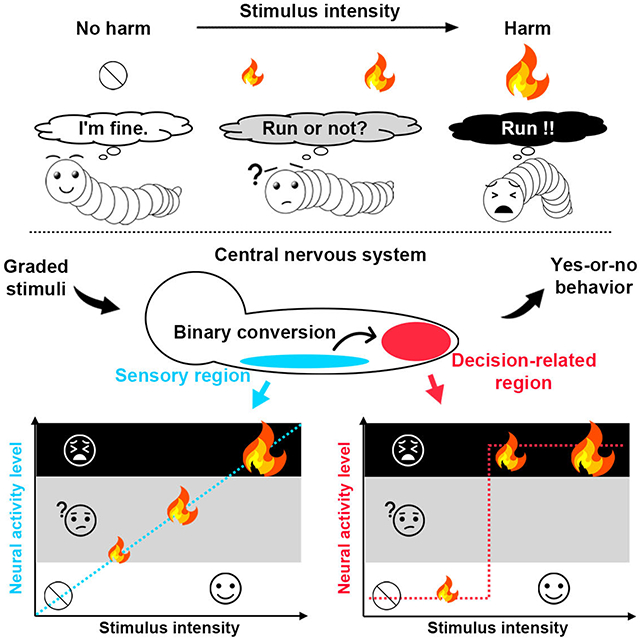
(F) Gating of weak encodings by GABAergic inhibition and escalated amplification of stronger encodings by SON recruitment make graded nociceptive encodings more binary so that noxious stimuli are categorized for enhanced detection accuracy.

See also Figure S6.

DISCUSSION

In this study, we identify a neural network that categorizes noxious stimuli of graded intensities to generate binary escape decisions in Drosophila larvae (Figure 4F), and unravel a gated amplification mechanism that underlies such binary categorization (Figure 7F). In responding to the noxious stimuli, while failure in prompt responses may cause harm, excessive escape responses to negligible stimuli would lead to the loss of resources for survival [45]. The gated amplification mechanism could reduce the responses to negligible stimuli while enhancing the responses to intense stimuli. In this way, the accuracy in deciding whether to escape from the stimuli is enhanced.

Graded-to-binary conversion of sensory encodings makes signals less vulnerable to noise

Information processing in the nervous system is affected by noise, which may be embedded in external sensory stimuli (e.g., sensory noise) or generated within the nervous system (e.g., electric noise) [46]. A recent study in C. elegans shows that activation mediated by electrical synapses and disinhibition mediated by glutamatergic chemical synapses form an AND logic gate to integrate the presentation of salience of attractive odors [11]. The AND-gate computation in worm AIA interneurons requires multiple sensory neurons to report the presence of attractive odors and, consequently, filters out the noise embedded in the sensory stimuli. Another study in the olfactory system of adult Drosophila, reported a mechanism to address the noise that is produced within the nervous system. A three-layered feedforward network averages the noise to enhance peak detection accuracy and then uses coincidence detection to distinguish real signals arrived synchronously from noise caused by spontaneous neural activities [9]. In the nervous system, the noise can be produced at each stage of the sensori-motor transformation [46]. Compared with the two mechanisms mentioned above, which filter out the existing noise, the graded-to-binary conversion through the gated amplification mechanism reported here makes the converted signals less vulnerable to the noise produced at later stages of sensori-motor transformation. This is because after the graded signals become binary, the signals are more separated (either suppressed or amplified) according to stimulus intensities and, consequently, the same level of noise is less likely to cause the binary signals to falsely pass the decision threshold than the graded ones (Figure S6D). As a result, the ambiguous encoding range of the stimulus intensity is narrowed and the frequency of false decisions is reduced, as demonstrated by computational modeling (Figure 7).

Dissociating time and accuracy in perceptual decisions by population coding

Thresholding of gradually accumulated sensory evidence has been considered to be fundamental for generating yes-or-no decisions [1, 2]. For example, a recent study in mammals has shown that visual evidence of danger can be gradually accumulated by recurrent circuits to overcome the threshold for escape behaviors [3]. Such a mechanism takes time to build up decision-associated activities for decisions with higher accuracy [16], which leads to the well-known speed-accuracy trade-off in perceptual decision-making [1, 2, 5, 47]. However, our findings add a new dimension to the processing of sensory evidence for perceptual decision-making: different from recurrent networks, the recruitment of a number of SONs can instantaneously boost the decision-associated activity to reach the decision threshold, which ensures the decision speed. Since the gated amplification mechanism reported here also ensures the detection accuracy, such mechanism might bypass the speed-accuracy trade-off in sensory signal detection.

An electron microscopy connectome study reported 13 types of SONs in Drosophila larval nociceptive system [27], each of which has distinct connectivity and functions. For example, Basin-4, DnB, and Wave neurons also receive mechanosensory inputs [22, 24, 28], while A08n does not [25]. Moreover, Wave neurons detect stimulus positions on larval body walls [24]. Furthermore, serotonergic modulation acts on this network during development to adjust the nociceptive responses [25], providing a mechanism for larvae to adjust the escape threshold according to their developmental environment. However, since at least 5 types of SONs are both required and sufficient for larval escape behaviors [22-28], it remains a mystery why there exist so many seemingly redundant neurons at the same level in the network [48]. The nociceptive system is a dedicated protective system that responds to potential tissuedamaging insults, so both speed and accuracy of the perceptual decision-making process are important. This is probably why the nociceptive system uses an amplification network formed by a large number of SONs to dissociate time from accuracy in the perceptual decision-making process and avoid the trade-off between decision speed and accuracy.

The terminal plexus is a hub for sensori-motor integration

In this study, we developed novel unbiased computational toolsets for automatically analyzing the functional connectivity of all neural structures, including both somas and neurites in larval VNC. Using these toolsets, we identified a decision-associated CNS region, the PMC, which covers the neuropil structure TP [33]. TP is concentrated with large amounts of neurites, especially those of peptidergic neurons [34, 35]. Although this anatomical structure was identified previously, its function is unknown. Our finding of its important function in sensori-motor transformation suggests that this region is possibly a hub for information exchange and integration. The detailed anatomical and functional connectivity of TP could be a fascinating direction for future studies.

In summary, we postulate a neural basis for converting graded sensory inputs to yes-or-no behavioral decisions. A previous study showed that neurons in the rat posterior parietal cortex encode a graded value of accumulating evidence while those in prefrontal cortex have a more categorical encoding that indicates the decisions [4]. Thus, the categorization of sensory evidence by making graded encodings binary in perceptual decision-making is likely an evolutionarily conserved process. In this study, we took advantage of the powerful genetic model Drosophila to unravel how such computation might be implemented at the cellular and molecular level. Finally, since whole-CNS functional imaging analysis is a key approach to decipher neural basis for sensori-motor integration and perceptual decision-making [15], we anticipate that the computational tools developed in our study will facilitate investigations in these fields.

STAR METHORDS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Bing Ye (bingye@umich.edu).

Materials Availability

The Drosophila lines generated in this study will be deposited to the Bloomington Drosophila Stock Center. DNA constructs will be deposited to Addgene. Before they are available from the public depositories, they are available from the Lead Contact upon request.

Data and Code Availability

The datasets generated and analyzed in the current study are available from the corresponding authors on reasonable request. All custom codes used in the current study will be deposited and can be accessed in GitHub.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Both male and female foraging 3^rd-instar larvae were used. All experiments were done on age- and size-matched larvae. The fly stocks used in this study are in KEY RESOURCES TABLE.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
chicken anti-GFP	Aves Laboratories	RRID: AB_2307313
rabbit anti-RFP	Rockland	RRID: AB_2209751
mouse anti-V5	Invitrogen	RRID: AB_2556564
anti-mouse Alexa Fluor 488	Jackson ImmunoResearch	RRID: AB_2340846
anti-chicken Alexa Fluor 488	Jackson ImmunoResearch	RRID: AB_2340375
anti-mouse Alexa Fluor 647	Jackson ImmunoResearch	RRID: AB_2338902
anti-rabbit Rhodamine RX	Jackson ImmunoResearch	RRID: AB_2340613
Experimental Models: Organisms/Strains
Drosophila: UAS-GtACR1-YFP	Gift from Adam Claridge-Chang	[36]
Drosophila: GMR94B10-GAL4	Gift from Kazuo Emoto	[23]
Drosophila: A08n-splitGAL4	Gift from Peter Soba	[26]
Drosophila: MB120B-splitGAL4	Gift from Akinao Nose	[24]
Drosophila: LexAop2-GtACR1-YFP	Gift from Adam Claridge-Chang	[36]
Drosophila: Canton S	Gift from Orie Shafer	N/A
Drosophila: ppk-ChR2.XXL	This study	N/A
Drosophila: Rdl-stop-V5	This study	N/A
Drosophila: nsyb-LexA	Bloomington	52247
Drosophila: LexAop2-jRCaMP1b	Bloomington	64428
Drosophila: UAS-jRCaMP1b	Bloomington	63793
Drosophila: GMR82E12-GAL4	Bloomington	40153
Drosophila: 412-Gal4	Bloomington	63300
Drosophila: GMR57F07-GAL4	Bloomington	46389
Drosophila: UAS-CD4-tdGFP	Bloomington	35836
Drosophila: UAS-mCD8-GFP	Bloomington	32185, 32186
Drosophila: UAS-mCherry	Bloomington	52267
Drosophila: UAS-DenMark	Bloomington	33061
Drosophila: UAS-CsChrimson.mVenus	Bloomington	55136
Drosophila: UAS-ChR2.XXL	Bloomington	58374
Drosophila: TrpA1-QF	Bloomington	36345
Drosophila: QUAS-ChR2T159C-HA	Bloomington	52260
Drosophila: GMR61H09-GAL4	Bloomington	49598
Drosophila: PDF-GAL4	Bloomington	6899
Drosophila: CCAP-GAL4	Bloomington	25685
Drosophila: Mip-GAL4	Bloomington	51983
Drosophila: DSK-GAL4	Bloomington	51981
Drosophila: NPF-GAL4	Bloomington	25682
Drosophila: LK-GAL4	Bloomington	51992, 51993
Drosophila: UAS-RSR	Bloomington	55795
Drosophila: phiC31-attP-9AVK00019	Bloomington	24866
Drosophila: Cas9-GFP+	Bloomington	55821
Drosophila: Rdl RNAi	Bloomington	52903
Drosophila: ppk-LexA	[60]	[60]
Drosophila: ppk-GAL4	[61]	[61]
Software and Algorithms
Prism 7	Graphpad	N/A
ImageJ 1.52g (Fiji)	NIH	N/A
Vaa3D v3.544	NIH	N/A
Matlab 2017a	MathWorks	N/A
RStudio v1.1.456 with R v3.4.0.	RStudio, Inc.	N/A
Leica Application Suite Advanced Fluorescence	Leica Microsystems	N/A
Optical Power Monitor v1.1	Thorlabs	N/A
ARDUINO 1.8.7	Arduino	N/A

METHOD DETAILS

Generation of ppk-ChR2.XXL transgenic flies

To make genetic manipulations easy, we generated the ppk-ChR2.XXL transgenic line, in which the nociceptor-specific ppk promoter directly drives (independent from binary systems such as GAL4/UAS) the expression of ChR2.XXL, a variant of Channelrhodopsin-2 (ChR2) [49]. ChR2.XXL cDNA was amplified from UAS-ChR2.XXL transgenic flies (BL# 58374) by PCR. The 1 kb ppk promoter was amplified by PCR and inserted into pJFRC81-10XUAS-IVS-Syn21-GFP-p10 [50] (Addgene# 36432), replacing the 10XUAS enhancer by In-Fusion® HD cloning (Takara Bio USA). The resulting construct, pJFRC81-ppk-IVS-Syn21-GFP-p10, was linearized by PCR and fused with ChR2.XXL cDNA by In-Fusion® HD cloning. The final construct, pJFRC81-ppk-IVS-Syn21-ChR2.XXL-p10, was then microinjected (200 ng/μl) into the embryos of phiC31-attP-9AVK00019 (BL# 24866) flies for transgenesis.

Generation of Rdl-stop-V5 knock-in flies

To reveal the endogenous expression pattern and study the function of Rdl in cell-type specific manner, we used CRISPR-Cas9 mediated genome editing to generate Rdl-stop-V5 knock-in fly line. The knock-in sequence was designed to insert right before the Rdl stop codon, and contains the isoTarget cassette (manuscript submitted) followed by the V5 epitope tag, which allows cell-type specifically tagging of endogenous Rdl with any GAL4 driver expressing R-recombinase (UAS-RSR). pBluescript SK + vector was linearized by EcoRV (New England Biolabs® Inc.) and fused with Rdl homologue sequences and abovementioned knock-in sequence by In-Fusion® HD cloning (Takara Bio USA), to generate donor construct. pCFD3-dU63gRNA [51] was used to generate gRNA construct. The donor construct (750 ng/μl) and gRNA construct (250 ng/μl) were microinjected into Cas9-GFP+ (BL#55821) fly embryos for generating knock-in flies. Rdl-stop-V5 flies are homozygous lethal, which resembles the phenotype of Rdl mutants, suggesting that dysfunction of C-terminus could disrupt Rdl function. Furthermore, the Rdl-stop-V5 flies became homozygous viable when RSR was panneuronally expressed (nsyb-GAL4 / UAS-RSR) to excise the isoTarget cassette, which points out a potential way for cell-type specifically knock-out of Rdl (by GAL80 that suppresses GAL4 activity).

Optogenetic manipulations of neuronal activity

Optogenetic stimulation of nociceptors was achieved with either ppk-ChR2.XXL or TrpA1-QF > QUAS-ChR2^T159C transgenes. To stimulate ppk-ChR2.XXL larvae, 8 μW/mm² blue light (470 nm) was applied for 250 msec. In experiments requiring precise control of the stimulus intensity and duration for testing the effects of various intensities, we used TrpA1-QF > QUAS-ChR2^T159C, which is a ChR2 variant with higher temporal kinetics and lower sensitivity than ChR2.XXL, to stimulate larval nociceptors. In experiments involving ChR2^T159C, blue light was applied at various intensities for 2.5 sec. To optogenetically stimulate CNS neurons, 15 μW/mm² 470-nm blue light (250 msec) was applied to ChR2.XXL-expressing larvae, 50 μW/mm² 488-nm in-build confocal blue laser (2.5 sec, during calcium imaging) was applied to ChR2^T159C-expressing larvae, and various intensities of 617-nm red light (2.5 sec) was applied to CsChrimson-expressing larvae, respectively. Wave neurons expressing ChR2.XXL were stimulated for 5 sec, which was required for inducing nocicefensive rolling.

GtACR1 can be activated by light with wavelength from 470 nm to 617 nm [36]. Therefore, the blue light (470 nm) used for activating ChR2s can effectively activate GtACR1. To maximize the inhibition effects and resemble the experimental conditions in calcium imaging with a 594 nm-laser, the GtACR1-mediated optogenetic inhibition was done with additional 5 sec of amber light (590 nm) when combining stimulation and inhibition. The amber light started at 20 msec before blue-light-induced optogenetic stimulation to maximize inhibition. All LEDs used were from LUXEON StarLED.

Embryos were collected on standard cornmeal containing all-trans-retinal (ATR) (A.G. Scientific). We noted that if the ATR concentration was too high, the 594 nm laser used to excite jRCaMP1b sometimes activated ChR2.XXL. We thus tested different concentrations of ATR for each GAL4 driver used to stimulate neurons with ChR2.XXL in pilot experiments, thus determining the ATR concentrations that do not lead to activation of neurons by 594 nm laser that is used to excite jRCaMP1b calcium indicator in functional imaging. We used 500 μM of ATR throughout this study, with the exception of using 10 μM for activation of LK neurons, 0.5 μM for Basin-4 or mCSI neurons, 1 μM for A08n or DnB neurons, and 50 μM for Wave neuron activation, as these concentrations of ATR do not lead to the activation of these neurons by 594 nm laser.

Functional imaging of whole-VNC and subsets of neurons

Embryos were collected for 12 hr at 25°C on standard cornmeal containing ATR (see Optogenetic manipulations). Live functional imaging of calcium signals was done using a Leica SP5 confocal system equipped with a resonant scanner that scans at 8000 Hz, an acousto-optical beam splitter, and an HC Fluotar L 25x/0.95 W VISIR immersion objective (Leica). A 594-nm laser was used to excite the calcium indicator jRCaMP1b; a 488-nm laser was used to excite GFP or YFP. The newly developed jRCaMP1b was chosen for calcium imaging because, among all the red calcium indicators that are compatible with optogenetics, jRCaMP1b has the widest dynamic range and performs the best in detecting graded calcium signals [17]. Larvae were dissected and imaged in a modified hemolymph-like 3 (HL3) saline, as previously described [25] (80 mM NaCl, 5 mM KCl, 0.75 mM CaCl₂, 20 mM MgCl₂, 5 mM trehalose, 115 mM sucrose, 5 mM HEPES, and 10 mM glutamate, pH 7.2, filtered by Corning filter system). Muscle movement and proprioceptive feedback were blocked by glutamate in this preparation. During dissection, a larva was restrained by inserting two insect pins, one into the tail and one into the head; it was then cut along the dorsal midline. Proventriculi, salivary glands, and fat bodies around VNC were carefully removed to expose the VNC while keeping each larva as intact as possible. For all experiments involving ChR2s, larvae were dissected in dim red light to avoid any activation of ChR2s before the intended stimulations.

In pilot experiments, we recorded neural activity of the entire larval CNS. However, we noticed that the majority of neural activity that was elicited by optogenetic stimulation of larval nociceptors occurred in the larval VNC (data not shown). Therefore, we decided to focus on recording neural activity in larval VNC to maximize the spatiotemporal resolutions of functional imaging. We took a data-driven approach to determine the voxel size and acquisition speed for calcium imaging of the entire VNC, which dictates the spatial and temporal resolutions of recordings. For each functional imaging sample, we collected two volumetric data sets. One was activity data (with jRCaMP1b); the other was anatomical data (with basal fluorescence of jRCaMP1b), as in a previous study [31]. The sampling rate for activity data was determined by Nyquist criterion [52], so that each neuron cell body was scanned by at least two z-steps. The theoretical distance between two z-steps (z’) would be half the diameter of a neuron cell body (D), as shown in equation 1. However, because optical focal planes in confocal microscopy have thickness (T) and any signal within the thickness of the optical focal plane can be detected, the actual distance between two z steps (z) is that shown in equation 2. The average diameter of a neuron cell body in 3rd instar larvae is 5.91 ± 3.58 μm [19], so the smaller ones are about ∅ 1.4 μm. The thickness of the optical focal plane in our settings is 3.8 μm when pinhole is set as 3 AU. Thus, the Nyquist z-step size for larval CNS neurons is about 5.2 μm, which divides the VNC into about 13 steps along the z-axis. Therefore, to acquire calcium signals, we applied unidirectional scan at a resolution of 0.71 (x) x 0.71 (y) x 5.2 (z) μm. Each pixel was scanned 3 times with line-averaging to increase signal-to-noise ratio. This spatial resolution allows the acquisition speed to be 1 VNC per second (1 Hz), which is compatible with jRCaMP1b indicator [17]. In anatomical data collection, entire VNCs were imaged using unidirectional scan at a resolution of 0.71 (x) x 0.71 (y) x 1.0 (z) μm. Each pixel was scanned 16 times with line-averaging to increase signal-to-noise ratio.

$${\mathsf{z}}^{{}_{{}_{’}}}=1∕2\mathsf{D}$$ (1)

$$\mathsf{z}=1∕2\mathsf{T}+1∕2\mathsf{T}+{\mathsf{z}}^{{}_{{}_{’}}}$$ (2)

VNCs that were accidentally touched by dissection tools during dissection were excluded before live imaging recordings. All imaging data were included in the analysis.

Identifying nociceptor-activated CNS regions

For whole-VNC functional imaging, the GECI jRCaMP1b was expressed in all neurons with the nsyb-GAL4 driver. For optogenetic stimulation of nociceptors, ChR2.XXL was expressed in nociceptors with by the ppk- promoter/enhancer. We recorded the VNCs from 50 larvae to identify nociceptor-activated CNS regions.

Alignment:

First, the activity data for each larval VNC was aligned to the anatomical data of the same VNC, using the B-Spline registration algorithm [53] to identify the corresponding positions of voxels of activity data in its anatomical data. Second, the anatomical data was aligned to a template VNC, producing warping parameters that could be used in the next step. The template VNC was the real sample that was closest to the average length and thickness of all the collected VNCs. Third, we warped the activity data to the template VNC, using the voxel correspondence from the first step and warping parameters from the second step, then linearly interpolating the missing values. This method aligned activity data to the same structural template, making it feasible to statistically analyze activity data among different larvae.

Time window for identifying nociceptor-activated CNS regions:

To define a time window for identifying CNS regions activated by optogenetic stimulation of nociceptors in a data-driven manner, we segmented the data into “super voxels” that contain neighboring voxels with similar fluorescence dynamics [30], and examined the fluorescent changes in all the super voxels. We reasoned that the first calcium signal after stimulation was most relevant to sensory processing and determined the longest rising time of the first calcium signals post-stimulation in all super voxels as the time window for identifying nociceptor-activated CNS regions, which was 5 sec after stimulation.

Discovery of CNS regions that respond to nociceptor-stimulation:

Active CNS regions were identified as a set of spatially connected voxels with co-activated calcium signals. To avoid bias, we first built an average neural activity atlas from a set of 50 samples, and then selected the regions that showed statistically significant responses. There are two essential steps in building this average neural activity atlas. One is building the neural activity atlas for a single sample from its activity data; the other is aligning all neural activity atlases of all samples to calculate the average atlas.

We used Z-score, which quantifies the probability that a fluorescence change is due to real calcium signal rather than noise, to measure the fluorescence response of a voxel. We first applied noise stabilization to the activity data and made the noise Gaussian distributed [54]. The noise on the original data is modeled as a Poisson- Gaussian distribution; after stabilization, the noise becomes Gaussian distributed with a mean of 0. We then estimated the standard deviation of the Gaussian distribution (σn), which is also the signal’s noise level in each single voxel. Next, based on order statistics [55], we estimated the mean (μ_m) and standard deviation (σ_m) of the maximum fluorescence value within the 5 sec time window. After that, for any voxel, denoting its maximum fluorescence value (f_max) and its fluorescence level before optogenetic stimulation (f_t-1), we obtained the Z-score of such fluorescence increase under the null hypothesis that this increase is caused only by noise:

$$\mathrm{Z}=\frac{{\mathrm{f}}_{\max }-{\mathrm{f}}_{\mathrm{t}-1}-{\mu }_{\mathrm{m}}}{\sqrt{{\sigma }_{\mathrm{m}}^2+{\sigma }_{\mathrm{n}}^2}}$$ (3)

The larger the Z-score is, the more likely the fluorescence change at that voxel is caused by a real calcium signal that corresponds to neural activity. In this way, the fluorescence change in the activity data is transferred into a neural activity atlas and becomes comparable across voxels and samples. Alignment among neural activity atlases is described in the Alignment section. After aligning all neural activity atlases, we averaged them across the 50 samples to obtain the average neural activity atlases. The averaging enhanced the signal-to-noise ratio, making nociceptor-activated CNS regions obvious. An iterative thresholding method was then used to define these CNS regions [56].

Identifying neural structures of subsets of neurons

To identify the neural structures (somas or neurites) of nociceptors or LK neurons in calcium imaging, the iterative thresholding method was applied for automated segmentation [56]. The 3-dimensional (3-D) neural structures were segmented based on the basal fluorescence of jRCaMP1b. We then proofread every sample to exclude false positives.

Analysis of neural activity in functional imaging

As mentioned in “Identification of nociceptor-activated CNS regions in whole-VNC functional imaging data”, the neural activity probability was quantified by Z-score, whereas the neural activity level was quantified by ΔF / F₀, where ΔF = F_max - F₀. Note that F here was used to indicate the average florescence levels of a CNS region or neural structure, which is different from f for a single voxel in equation 3. Since spontaneous activity frequently occurs even without stimulation, directly calculating the baseline fluorescence (F₀) using the mean of pre-stimulation period is prone to bias. We thus developed a data-driven method to define the baseline in an unbiased manner. This method aimed to find a time period with most stable fluorescence level (the most likely time period of the resting state of neurons) and defined the mean fluorescence level of all voxels in a certain CNS region or neural structure during this time period as the F₀ in this CNS region or neural structure. Details are in equation 4. F(t) is the fluorescence level at time t. The mean of F(t) was calculated over a sliding time window of length δ centered at t. V(t) is the variance for the same sliding time window. The maximum fluorescence level (F_max) was defined as mean fluorescence level of all voxels in in the CNS region or neural structure within 5 sec post stimulation onset.

$$\begin{gathered} F_0=\overline{F(t_0)}, \\ {t}_0=argmi{n}_{\mathrm{x}}(\overline{F(x)}-F_{min})\ast V(x), \\ \overline{F(x)}=\frac{1}{\delta }{\int }_{x-\frac{\delta }{2}}^{x+\frac{\delta }{2}}F(\tau )d\tau , \\ V(x)={\int }_{x-\frac{\delta }{2}}^{x+\frac{\delta }{2}}(F(\tau )-\overline{F(x)}{)}^{2}d\tau , \\ {F}_{min}=min(F(x)), \\ x\in [0,T] \end{gathered}$$ (4)

Behavioral tests paired with functional imaging

Since it is currently infeasible to perform functional imaging of larval VNC in behaving larvae (e.g. nocifensive rolling), we correlated neural activity in calcium imaging and escape behaviors by strictly pairing experimental conditions in the two types of experiments. Larvae from the same batches of culture were used in the two types of experiments so that their genotypes and developmental conditions (e.g. ATR consumption) were the same. Optogenetic stimulation and inhibition conditions were the same in both types of experiments. For each behavioral trial, we placed 20-25 larvae on a ∅ 35-mm plate covered with 1 mL water. Separate trials were done on different days for each genotype. For demonstration videos, single larvae were placed on plates. A complete larval escape behavior includes three types: curling, rolling and crawling. Since the crawling upon nociceptor stimulation sometimes was indistinguishable from crawling without nociceptor stimulation, for the sake of accuracy in manual quantification in this study, we only focused on curling and rolling, which have clear-cut criteria for quantification. Since larvae often exhibited only one or two types of escape behaviors under low intensity of nociceptor stimulation, in order to quantify larval escape behaviors in an unbiased manner, the escape probability was defined as the mean of curling and rolling probabilities. Curling was counted when a larva performed “C-shape” curling behavior and rolling was counted when a larva rolled its body along the rostrocaudal axis over 360. All behaviors were counted within the 5 sec after optogenetic stimulation (the time window for identifying nociceptor-activated CNS regions in functional imaging experiments). For noxious heat stimulation experiments, single larvae were placed on a heat plate for each trial after the heat plate reached desired temperature.

All behavioral tests were done in a double-blinded manner, as previously described [25]. Animals that were out of field of view during recordings were excluded from behavioral analysis. All data after behavioral analysis were included in the statistical analysis.

Immunostaining

Third instar larvae were dissected and stained as described previously [25]. The primary antibodies used were: chicken anti-GFP (1:2500), rabbit anti-RFP (1:5000) and mouse anti-V5 (1:100). Secondary antibodies used were: anti-mouse Alexa Fluor 488 (1:250), anti-chicken Alexa Fluor 488 (1:500), anti-mouse Alexa Fluor 647 (1:250) and anti-rabbit Rhodamine RX (1:250).

Electrophysiological recordings

Third instar larvae were dissected as previously described [25]. Dissection and electrophysiology recordings were performed in recording bath solution (103 mM NaCl, 3 mM KCl, 8 mM Trehalose, 26 mM NaHCO₃, 5 mM TES, 1 mM NaH₂PO₄, 1.5 mM CaCl₂, 4 mM MgCl₂, 10 mM glucose and 1 mM Na-L-glutamate, pH=7.3; the osmolarity was adjusted to 270-275 mOsm). During electrophysiology recordings, larvae were continuously perfused with oxygenated bath solution (~1 mL/min). Second-order neurons (SONs) (A08n, Basin-4, mCSI, Wave, and DnB) expressing mCherry were exposed by sliding the lateral side of VNC with a fine glass needle. Whole-cell patch-clamp recordings of SONs were performed at room temperature (23-25°C). Recording electrodes were made by borosilicate glass pipettes (Sutter, Novato, CA) and filled with the intracellular solution (140 mM K-Gluconate, 10 mM HEPES, 4 mM MgATP, 0.5 mM Na₃GTP, 1 mM Na₄EGTA and 1 mM KCl, pH=7.2; the osmolarity was adjusted to ~265 mOsm). The resistance in pipettes was 4-6 MΩ. Signals were acquired with a Digidata 1550B digitizer and MultiClamp 700B amplifier (Molecular Devices, Sunnyvale, CA). Current-clamp recordings were filtered at 3 kHz and digitized at 10 kHz.

The responses of SONs, which were elicited by optogenetic stimulation of nociceptors (TrpA1-QF > QUAS-ChR2^T159C, 50 msec), were recorded under the current-clamp mode. At each stimulation intensity, the responses of SONs were recorded at least 3 times and averaged to obtain the mean amplitude. For each recording, the optogenetic stimulation was performed from low intensity to high intensity in order to identify the minimum and maximum responses. The interval between each stimulation is at least 20 sec.

Computational modeling

Simulations were performed based on signal detection theory [1, 57] to test the effect of graded-to-binary conversion of sensory encodings (through gated amplification mechanism) on the yes-or-no decisions. We simulated two networks, with or without gated amplification mechanism. In each network, 58 neurons (to simulate the 5 types of SONs: 2 A08n, 14 Basin-4, 14 mCSI, 14 Wave, and 14 DnB) encoded linearly intensified sensory stimuli (inputs), each of which was controlled by the predefined activation function (rectified linear unit, ReLU) [58, 59]. To minimize assumptions, the sensory encoding value of each network in each simulation was defined as the summation of the outputs from all 58 SONs and the dynamic ranges of activation for SONs in each network were same. The ground truth for each simulation is the sensory encoding value without any noise in the system. In each simulation, the noise was added before and after the summation (to model the PMC region) of all SON outputs. Various levels of noise were simulated for each network, and the statistical comparison of accuracy between the two networks were always paired and performed under the same noise level. The yes-or-no decision threshold was defined as 50% of the maximum encoding value in ground truths. In each simulation, a detection was reached when the encoding value was above the decision threshold. If a simulated encoding value and its ground truth were consistent in above or below the decision threshold, it was defined as a correct detection (true yes or true no), otherwise as a false one (false yes or false no). In the network with gated amplification mechanism, 58 SONs had different activation thresholds so that the SONs could be gradually recruited with increasing input intensities. To model the GABAergic gating, an inhibition effect (20% of maximum encoding value in ground truths) was added after the summation of SON outputs. In the network without gated amplification mechanism, 58 SONs had the same activation threshold so that they were activated altogether at the same input intensity. Moreover, no inhibition was added after SON outputs. Apart from these two differences that constitute the gated amplification mechanism, all parameters and simulation conditions were the same between the two networks. We repeated each simulation experiment 1,000 times to simulate 1,000 larval detections at each noise level for each network and repeated this process at various noise levels. The same 1,000 stimulus intensities were used in each experiment.

QUANTIFICATION AND STATISTICAL ANALYSIS

Sample numbers were determined by pilot experiments with power analysis. Normality of data distribution was assessed by D'Agostino & Pearson omnibus normality test and accordingly parametric or non-parametric tests were used. Small data set with sample number (N) less than 20 was assessed by non-parametric tests. To assess whether an X-Y relationship (e.g., stimulus-response curves for either neural activity or escape probability, or the relationships between the neural activity of two CNS regions) were binary or not, extra-sum-of-squares F test was used for model selections (curve fittings). Sigmoid models were compared with linear ones in these tests since sigmoid ones are commonly used for binary classifications (or yes-or-no detection tasks) and are more binary than linear ones.

Supplementary Material

3

Video S1. Nociceptor-activated CNS regions in larval VNC, related to Figure 2.

4

Video S2. The VMs contain nociceptor axon terminals, related to Figures 2 and Figure 3.

5

Video S3. Peptidergic neurons that innervate the PMC, related to Figure 4.

6

Video S4. Activation of LK neurons elicits larval escape behaviors, related to Figure 4.