Modeling of dynamical systems through deep learning

Abstract

This review presents a modern perspective on dynamical systems in the context of current goals and open challenges. In particular, our review focuses on the key challenges of discovering dynamics from data and finding data-driven representations that make nonlinear systems amenable to linear analysis. We explore various challenges in modern dynamical systems, along with emerging techniques in data science and machine learning to tackle them. The two chief challenges are (1) nonlinear dynamics and (2) unknown or partially known dynamics. Machine learning is providing new and powerful techniques for both challenges. Dimensionality reduction methods are used for projecting dynamical methods in reduced form, and these methods perform computational efficiency on real-world data. Data-driven models drive to discover the governing equations and give laws of physics. The identification of dynamical systems through deep learning techniques succeeds in inferring physical systems. Machine learning provides advanced new and powerful algorithms for nonlinear dynamics. Advanced deep learning methods like autoencoders, recurrent neural networks, convolutional neural networks, and reinforcement learning are used in modeling of dynamical systems.

Introduction

Dynamical systems provide a mathematical framework to describe the real-world problems, modeling the rich interactions among quantities that change in time. Formally, dynamical systems concern the analysis, prediction, and understanding of the behavior of systems of differential equations or iterative mappings that describe the evolution of the state of a system. Data-driven models are an emerging field of simulating and discovering dynamical systems purely from data using techniques of machine learning and data science. We have an explosion of data in climate science, neuroscience, disease modeling, and fluid dynamics. The amount of data getting from experiments, simulations, and historical records is growing at an incredible pace. Simultaneously, the algorithms in machine learning, data science, and statistics optimization techniques are getting much better. Therefore we can discover dynamical systems and characterize them purely from data. In the past, dynamical systems were essentially written down by physical laws and derived the equations from first principles using physics. But, today the systems that we want to understand like the brain, climate, or financial market. There are no first principles physics that we can write down in an easy to understand simulate and control framework. Therefore, we are trying to build data-driven techniques more powerful for these emerging classes of problems.

Neural networks and deep learning are becoming extremely powerful techniques to learn these dynamics from data. Genetic algorithms and genetic programming have been used very effectively for discovering dynamic systems from data. The high-level overview of these dynamical systems from data can cope with nonlinearity, high-dimensional chaos. Lu proposed a linear multistep (LM) scheme to bridge the deep learning methods (Lu et al. 2018) with ordinary differential equations. LM scheme is an effective architecture that can be applied to ResNet like neural networks. The LM scheme on ResNet achieved higher accuracy than ResNet on both ImageNet and CIFAR. Rudy presented a data-driven model of dynamical systems through DNN (Rudy et al. 2019a, b). This model estimates the signal-noise at every observation. This algorithm is responsible for measuring errors and unknown dynamics. The authors demonstrated the ability of this data-driven model and issues with DNNs for dynamical systems. Harman put forward a reduced model of dynamics via neural networks (Hartman and Mestha 2017). This model has the benefit of projecting dynamical systems onto a nonlinear space. This method is applied to extract nonlinear features through DNNs.

Zhang proposed pre-classified reservoir computing techniques (Zhang et al. 2021) to analyze the fault of 3D printers. This method reduces the interclass separation by summing information labels of similar conditions. Because of the reservoir computing model and pre-classification strategy, the presented method achieves the maximum accuracy in the fault analysis of three-dimensional printers. Ibanez analyze the ability of data-driven approaches to predict the reactive extrusion in complex processes (Ibañez et al. 2020). This work is carried out based on thermo-set chase mixing steps with the polypropylene phase. The goal of this paper is to characterize the suitable processing conditions regarding the mechanical property improvements of new polypropylene materials with the help of reactive extrusion. Watson examined call detailed records from mobile networks (Watson et al. 2020) to characterize and identify the spatial-temporal multi-scales patterns in person mobility using spectral graph wavelets. This unsupervised method allows the dimensional reduction of the data to find mobility patterns and changes in humans. The mobility patterns in humans afforded by spectral graph wavelets used in urban planning and hazard risk management. Figure 1 visualizes the future direction of applied mathematics towards deep learning techniques.

Fig. 1.

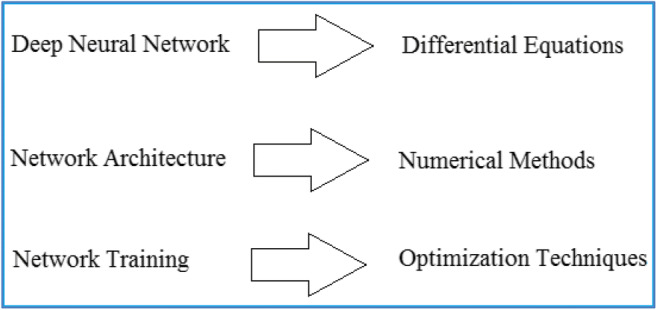
Mathematics future on deep neural networks

Dimensionality reduction methods

Singular value decomposition algorithms can be efficiently applied for data processing, high-dimensional statistics, and reduced-order modeling. SVD can be used to efficiently represent human faces, in the so-called eigenfaces. Principal component analysis (PCA) is a workhorse algorithm in statistics, where dominant correlation patterns are extracted from high-dimensional data. San projected a feed-forward ANN for nonlinear reduced-order models (San and Maulik 2018). This research mainly focuses on the selection of basis functions with the help of orthogonal decomposition and Fourier basis. This model works better compared to Galerkin projection. Lee proposed a new method for projecting complex dynamical systems using deep learning (Lee and Carlberg 2020). This method follows a practical approach based on convolutional autoencoders. Erichson introduced a spare PCA algorithm via variable projection (Erichson et al. 2020). The algorithm allows for robust sparse PCA instead of corrupted input data and performs computational efficiency on real-world data. Erichson also put forward a new CANDECOMP/PARAFAC dimensionality reduction (Benjamin Erichson et al. 2020) for multidimensional data. This research talks about approximation errors via oversampling. The challenges posed to big data by extracting important features from multidimensional data. Suarez developed an open-source pyDML (Juan Luis Suarez et al. 2020) that has a library of distance metric learning algorithms. The pyDML is used to improve nearest neighbor algorithms and dimensional reduction. This library provides parameter tuning and visualization of classifiers. Baek presented a multi-choice wavelet threshold algorithm (Baek et al. 2020) based on perception, decision, and cognition. The wavelet threshold SVMs (Rajendra et al. 2018) and information complexity are incorporated to assess learning models. The authors used to evaluate the available data-sets to illustrate the planned method and the results are compared with recent methods. Wei aim to solve the noise of internet information (Wei et al. 2020) and compares web pages in natural language processing (NLP). Web-page visualization has been implemented based on PCA. The result shows that ML processing NLP algorithm has better performance in prediction and classification accuracy. See Fig. 2 for various dimensionality reduction methods used in the literature.

Fig. 2.

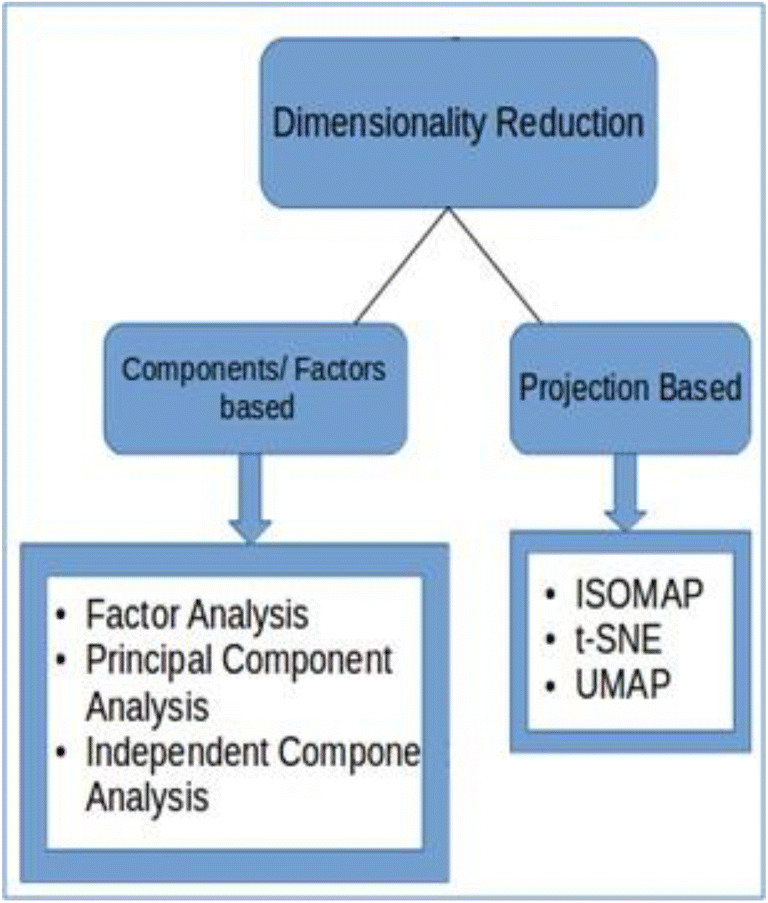
Dimensionality reduction methods

Dynamic mode decomposition

The dynamic mode decomposition (DMD) is a new framework to extract features from high-dimensional data. The DMD is applied to complex systems in fluid dynamics, disease modeling, neuroscience, plasma physics, robotics, and video modeling. Erichson introduced a compression DMD model for modeling of background (Erichson et al. 2019a). The compressed DMD algorithm is scaled with matrix rank instead of the actual matrix. The result of DMD algorithm proves that the background quantified by a recall, precision which helps the algorithm’s computational performance. Erichson also presented a randomized DMD algorithm (Erichson et al. 2019b) for computing low-rank matrices and eigenvalues. The algorithm takes about the modular probability framework. This approach provides features to extract from big data with the intrinsic rank of a matrix. Bai used DMD for compressive system identification via the Koopman operator (Bai et al. 2020). This operator is introduced in 1931 but has experienced renewed interest recently because of the increasing availability of measurement data and advanced regression algorithms. This research allows us to identify order-reduced models from limited data. The results demonstrate the extraction of the main features that are well characterized. Kaptanoglu developed a reduced-order model of characterizing magnetized plasmas with DMD (Kaptanoglu et al. 2020). The magnetic features of simulation and experimental data-sets are analyzed. This algorithm provides new insights into the plasma structure. Fujii proposed a new algorithm via multitask learning that incorporated information of labels into supervised DMD (Fujii and Kawahara 2019). The authors researched the empirical performance by utilizing synthetic datasets and validated their algorithm that can extract the label-specific structures. The supervised DMD method shows enhanced accuracy compared to conventional DMD methods. Vigneswaran presented a method to extract the features using DMD (Rahul-Vigneswaran et al. 2019). ImageNet data samples are used to perform experiments. The extracted features using DMD with a random kitchen walk approach performs better results. Brunton explored finite-dimensional linear representation by restricting the Koopman operator and investigated the choice of observable functions (Brunton et al. 2016a). Finally, the authors demonstrated the advantages of nonlinear observable subspaces via Koopman operator. Yu proposed a low-rank DMD model for the prediction of traffic flow (Yu et al. 2020). The low-rank DMD predicts the traffic flow via the state transmission matrix. The result shows that the low-rank DMD performs better on modern methods. Takeishix proposed a data-driven approach via “learning Koopman invariant subspaces” principle from observed data (Takeishix et al. 2017). The authors introduced ANN to evaluate the data-driven DMD performance using nonlinear dynamical systems and estimated a set of parametric functions. See Fig. 3 for the accuracy of various dynamic mode decomposition methods versus their training frequencies.

Fig. 3.

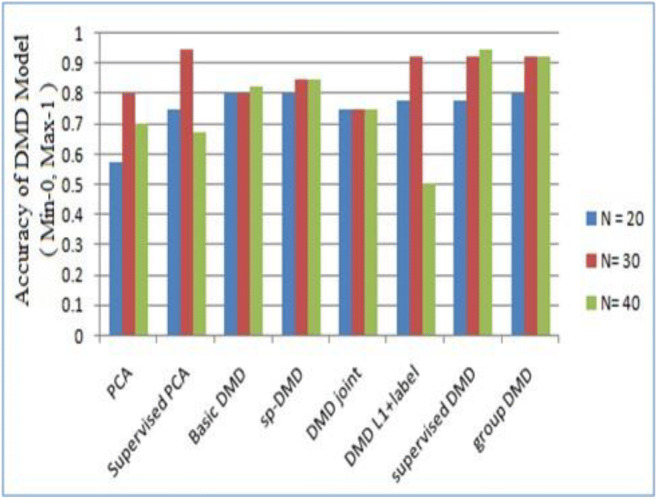
The classification accuracy of dynamic mode decomposition (DMD) methods concerning training frequencies

The discovery of governing partial differential equations

The sparse regression method is capable of discovering PDEs of a given system in the spatial domain by the time-series measurements. Rudy introduced a data-driven sparse regression model that helps us to discover the governing PDEs of a dynamical system (Rudy et al. 2017). The method is efficiently demonstrated on canonical problems that span multiple domains. This research promises to discover physical laws and governing equations. Brunton explores forward deep learning methods for discovering nonlinear PDE (Brunton et al. 2016b). The authors considered noisy and scattered observations in time and space. The methodology helps us to forecast future states of the physical system like Navier-Stokes (Subba Rao et al. 2017; Rao et al. 2018), Schrodinger, and Burger’s equation. Sirignano proposed a DNN algorithm for solving high-dimensional nonlinear PDE (Sirignano and Spiliopoulos 2018). The algorithm is mess-free and DNN is trained with randomly sampled points in space and time. The DNN algorithm is tested on Burger’s equation and results are approximated to the general solution. Raissi introduced a new DNN that is trained to solve governing nonlinear PDE and gives laws of physics (Raissi 2018). The method is demonstrated through some classical examples of physics problems. Long proposed a new DNN called PDE-Net (Rudy et al. 2019a, b). The constraints of PDE-Net are designed by exploiting wavelet theory. This feed-forward PDE-Net is used to predict the dynamics of physical systems and helps to identify the governing partial differential equations.

Raissi leverages the advantages in probabilistic ML to discover governing differential equations (Raissi et al. 2017). The modified Gaussian process priors help to infer parameters from noisy observations. The noise observations come from computer simulations and experiments. Raissi also presented “hidden physics models” that learn PDEs from small data (Raissi and Karniadakis 2018). The planned method is applied to identify the data-driven discovery of PDEs. This method relies on a Gaussian process that enables a balance between data fitting and model complexity. Schaeffer investigated the problem of learning PDE via sparse optimization and data-driven approach (Schaeffer 2017). The authors implemented a learning algorithm via sparse optimization to perform parameter estimation and feature selection and the result shows the ability and capability of performing analytics. Chang investigated surface flow equations (Chang and Zhang 2019) through ML technique of “Least absolute Shrinkage and Selection Operator (LASSO).” The authors discussed the procedure to calculate differential from noise data. The planned LASSO model gives a better outcome for learning equations of surface flow. Berg used ML to discover hidden PDEs in complex data-sets. The authors elaborately discussed the model and its feature selection (Berg and Nyström 2019). The dynamics of second-order nonlinear PDE were accurately described by an ODE that is automatically discovered. The flowchart in Fig. 4 explains the flow of discovery of governing PDEs from available data.

Fig. 4.

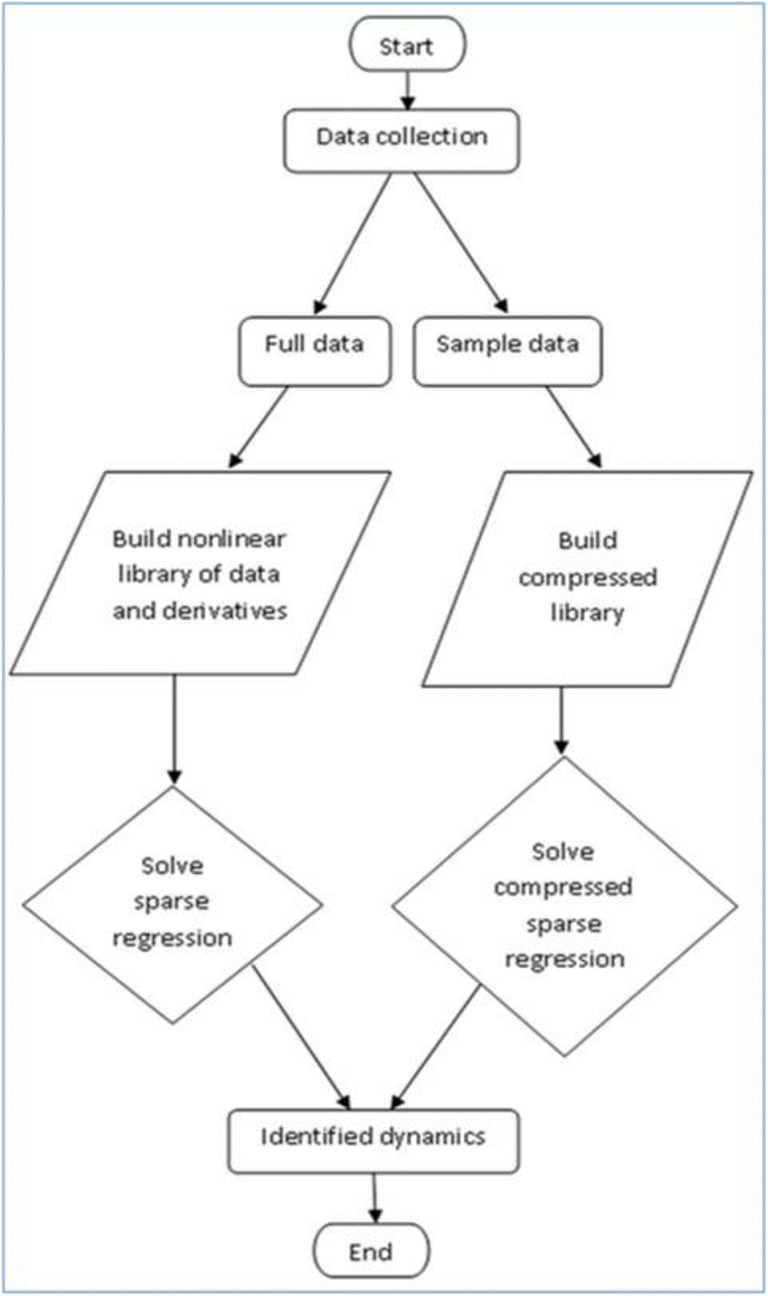
Discovery of governing partial differential equations from available data

Identification of nonlinear dynamical systems

The combined techniques of sparse regression, machine learning, and dynamical systems are used to identify nonlinear PDE entirely from data. Mangan proposed data-driven methods to infer neural networks by using sparse identification of dynamical systems (Mangan et al. 2016). This method succeeds in inferring the metabolic network, regularity network, and enzyme kinetics. Wang proposed Runge-Kutta DNN governed ODE for the identification of dynamical systems (Wang and Lin 1998). Runge-Kutta DNN estimates the rate of the system state in high accuracy. The authors invested two algorithms for Runge-Kutta DNN and proved the convergence of learning algorithms. Mangan developed a methodology for a model selection of dynamical systems (Mangan et al. 2019). This methodology is used for the identification of nonlinear dynamical systems (Rajendra et al. 2019a, b). The authors demonstrated a mass-spring system and the infection’s disease model. Li proposed data-driven methods for identifying time-varying aerodynamics (Li et al. 2019). Aerodynamic systems capture vortex-induced vibrations of a prototype bridge. The simulations of vortex-induced vibrations are in high accuracy with normalized MSE of 0.0023. Josh introduced a method for nonlinear dynamical systems to generate symbolic equations automatically (Bongard and Lipson 2007). The proposed method is applied to nonlinear dynamical systems and demonstrated on 4 simulated and 2 real systems. The model-free symbolic equations play a significant role to know complex systems. Li’s nonlinear system identification through “Proportional (P), Integral (I), and Derivative (D)” neural networks simply called PID neural networks (Li and Liu 2006). The weights in PID neural networks are in tune with the algorithm of backpropagation. The authors demonstrated that the model gives a lesser amount of fault and rapid convergence. Qiao proposed “a self-organizing radial basis function (SORBF) ANN method” to recognize and model the dynamical systems (Qiao and Han 2012). The SORBF performance could be able to achieve through the optimization of parameters. The authors presented the simulation results and effectiveness of the SORBF method. Table 1 explains the regression results of some standard PDE (Burgers, Schrodinger, and Navier-Stokes) identified structure in Brunton’s PDE-FIND (Brunton et al. 2016b).

Table 1.

The regression results of some standard PDE identified structure in Brunton’s PDE-FIND (Brunton et al. 2016b)

Partial differential equation(PDE)	Form of PDE	Approximate error (noise, no noise)
Korteweg–de Vries (KdV)	zt + 6zzx + zxxx = 0	1%, 7%
Burgers Equation	zt + zzx − ϵzxx = 0	0.15%, 0.8%
Schrodinger Equation	${\mathrm{iz}}_{\mathrm{t}}+\frac{1}{2}{\mathrm{z}}_{\mathrm{xx}}-\frac{{\mathrm{x}}^2}{2}\mathrm{z}=0$	0.25%, 10%
Nonlinear Schrödinger equation(NLS)	${\mathrm{iz}}_{\mathrm{t}}+\frac{1}{2}{\mathrm{z}}_{\mathrm{xx}}+\left|{\mathrm{z}}^2\right|\mathrm{z}=0$	0.05%, 3%
Kuramoto–Sivashinsky (KS) equation	zt + zzx + zxx + zxxxx = 0	1.3%, 52%
Reaction Diffusion Equation	zt = 0.1∇2z + λ(A)z − ω(A)w wt = 0.1∇2w + λ(A)w + ω(A)z A2 = z2 + w2, ω = − βA2, λ = 1 − A2	0.02%, 3.8%
Navier-Stokes Equation	${\mathrm{z}}_{\mathrm{t}}+\left(\mathrm{u}.\nabla \right)\mathrm{z}=\frac{1}{Re}{\nabla }^2\mathrm{z}$	1%, 7%

Machine learning of dynamical systems

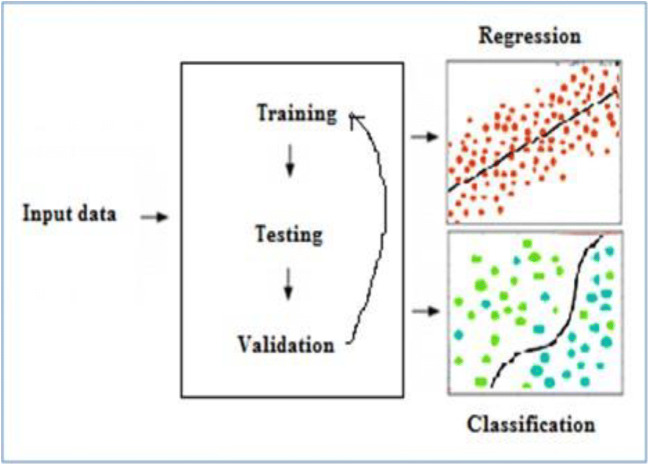
Machine learning is currently being used to extract useful patterns and coherent structures in high-dimensional dynamics of complex systems. Weinan proposed a machine learning algorithm via high-dimensional nonlinear dynamical systems (Weinan 2017). The supervised learning algorithm is developed by consideration of regression problems. This paper concludes that continuous dynamical systems are an alternative way to develop machine learning techniques. Brunton proposed the discovery of a multi-scale model for materials with the help of data-driven methods (Brunton and Kutz 2019). The authors developed a python-based program for sparse identification of high-dimensional dynamical systems called pySINDy. This research demonstrated how to use pySINDy to simulate canonical dynamical systems and perform numerical studies of nonlinear tracking control Regazzoni presented a new data-driven method called “model order reduction” based on machine learning that is applied to nonlinear dynamical systems arising in ODE (Regazzoni et al. 2019). This model formulates the dimensional reduction problem as a probability of maximum likelihood to minimize errors in input-output data pairs. Lee critically examined the main advantages of machine learning (Lee et al. 2018). The authors particularly discussed RNN and its role in decision-making and control problems. This paper also presented the advantages and disadvantages of these methods for the field of energy and process systems engineering. Boots proposed an online spectral algorithm that uses SVD to scale the partial observable nonlinear complex dynamical systems (Boots and Gordon 2011). The authors demonstrated a high bandwidth video mapping and illustrated the behaviors of dynamical systems. Wolfe presented the algorithms for learning the predictive state representation model (Wolfe et al. 2005). The Monte Carlo and temporal difference algorithms were developed to model dynamic systems. The performance and results of these algorithms are compared with existing algorithms. Song extended the Hilbert space embeddings and estimated a kernel to handle conditional distributions (Song et al. 2009). The authors presented a nonparametric method for dynamic system models via conditional embedding and verified the effectiveness of the model in a variety of dynamical systems. Figure 5 visualizes two important problems of regression and classification that arise in data-driven methods.

Fig. 5.

Driven framework used to develop machine learning algorithms

Deep learning of dynamics

Neural networks can be trained for use with dynamical systems, providing an efficient tool for time-stepping and forecasting (Rajendra et al. 2019a, b). Cireşan presented a method of multi-column DNN for the classification of traffic sign recognition (Cireşan et al. 2012). This research paper implements DNN fully on GPU and DNNs are trained on various preprocessed data into MCDNN. This helps us to make the system insensitive and improves reorganization performance. Lusch presented a data-driven DNN method to discover eigenfunctions of nonlinear identification of dynamical systems (Lusch et al. 2018). The author identifies nonlinear coordinate transformation from data. The authors claim that the benefit from DNN and the physical interpretability of universal linear Koopman embeddings. Wu proposed data-driven dynamical models of deep NN that identify signal-noise decomposition (Wu et al. 2018). The authors modeled an unknown vector field with the help of DNN. The authors discussed critical issues that identify signal-noise decomposition. The authors’ discussed the critical issues with the DNN for nonlinear dynamical systems and demonstrated methods showing the robustness to form the predictive models. Atencia proposed a model for parametric estimation and dynamical systems’ identification (Atencia et al. 2005) via the Hopfield Neural Network (HNN). The put forward HNN gives less error and is more efficient compared with gradient estimators. Suzuki proposed a method to model dynamical systems via point attractors (Suzuki et al. 2018). The model comprises CNN autoencoder and time-scale RNN. The method applied to manipulate the soft materials. The result depicts that the robot could perform the job via sensor signals. Qin proposed a scheme for approximating data-driven unknown governing PDEs using DNN (Qin et al. 2019). The residual network, recurrent residual neural network, and recursive residual neural network are demonstrated based on the integral form of dynamical systems. The performances of these methods are discussed in several examples. Table 2 gives the details of DNNs and their associated ODE numerical methods.

Table 2.

List of Deep Neural Networks, their associated Differential Equation Numerical schemes

Deep neural network	Associated differential equation	Numerical scheme
Residual neural network(ResNet)	$\frac{\partial u}{\partial t}=f\left(u\right)$	Euler’s forward
Deep PolyNet	$\frac{\partial u}{\partial t}=f\left(u\right)$	Euler’s backward
Ultra-DNN(FractalNet)	$\frac{\partial u}{\partial t}=f\left(u\right)$	Runga-Kutta(RK)
Reversible Residual Network(RevNet)	$\dot{X}=f(\dot{Y)}\text{and}\dot{Y}=f(\dot{X)}$	Euler’s forward

CNN, RNN, and LSTM of dynamic models

The deep CNN is regularly used in image processing and analysis. Weimer proposed a design configuration of DNN architectures for feature extraction by sequential learning strategies from huge data (Weimer et al. 2016). The developed DNN algorithm automatically generates features in industrial inspection. Trischler proposed a FFNN algorithm that can be trained on datasets of nonlinear dynamical systems (Trischler and D’Eleuterio 2016). Recast the FFNN as RNN that replaces the original nonlinear dynamical systems. The authors claim that the FFNN and RNN operate on continuous data. The unified model MgNet developed (He and Xu 2019) that depends on closed connections between multigrid (MG) and CNN. The concept of data space and feature space is introduced in convolutional neural networks. The result shows better performance compared with other CNN existing models. Chen put forward the ODE neural network (Chen et al. 2018). The derivation of the hidden layer state is parameterized using the ODE-Net. This allows complete training of ordinary differential equations within deep learning models (See Table 3). Kumar planned a diagonal RNN method is similar to the identification of nonlinear unknown dynamics (Kumar et al. 2018). The authors developed a back propagation dynamic algorithm to tune the diagonal RNN model parameters. The method is compared with identification models of radial base functions and feed-forward multilayer neural networks. The diagonal RNN has performed better and robustly in dynamical systems. Zhang constructed a data-driven ANN model (Zhang et al. 2019) by combining CNN and LSTM for the prediction of unmanned surface vehicle roll motion. CNN used the sensor data of the unmanned surface vehicles to extract local time series and relevant features. The planned model on real datasets outperformed compared with other modern methods. Zhu presented an electrocardiogram generation with a generative adversarial network method referred to as BiLSTM-CNN (Zhu et al. 2019) by combining LSTM and CNN. This model includes a generator that employs the BiLSTM network and a discriminator which is based on CNN. The authors compared the recital of their model through RNN-AE and RNN-VAE. The BiLSTM-CNN model converges very fast and generates electrocardiogram data with high accuracy. Lechner designed a learning model to train dynamical systems by gradient descent in the domain of robotics (Lechner et al. 2020). The authors introduced a regularization component for the improvement of systems stability. The scheme evaluated simulated robotic experiments and compared them with linear and nonlinear RNN architectures. The method improves the performance of tests to match the performance of nonlinear RNN.

Table 3.

Performance on MNIST shows test error (Chen et al. 2018)

	Test error	Number of Params	Memory	Time
Multilayer perceptron	1.6%	0.2 M	–	–
Residual neural network	0.4%	0.6 M	Order (L)	Order (L)
RK-Net	0.5%	0.2 M	Order (L)	Order (L)
ODE-Net	0.4%	0.2 M	Order (1)	Order (L)

Data-driven models of dynamical systems

The recent innovations in data-driven models for PDE systems have been highlighted by many re-searchers. Davoudi proposed a vision-based inspection of data-driven models for surface observations of concrete beams (Davoudia et al. 2018). The image dataset containing 862 has been included in a database for reinforced concrete beams. A supervised ML builds predictive models that are useful for estimating internal shear and moment loads. The authors estimated the accuracy of reinforced concrete beams. Suna provided a physics-constrained deep neural network and developed a surrogate model for fluid dynamics (Suna et al. 2020). This model is not dependent on any simulation-based data and it shows good results on the flow field in between deep learning and numerical simulations. Wu presented a data-driven time-dependent PDE framework in modal space using DNNs (Wu and Xiu 2020). The finite-dimensional model is accomplished by training DNN based on ResNet using specified data. The predictive accuracy of models for different PDEs including Burger’s equation is presented to illustrate the error analysis and effectiveness. Pai points out that the frequency-time study is appropriate for parameter and nonparametric of dynamical systems (Frank Pai 2013). The Hilbert-Huang transform is the alliance of Hilbert transform and mode decomposition chosen empirically. The Hilbert-Huang transform provides piece decomposition and precise time-frequency analysis compared with Fourier and Wavelet transforms. The conjugate pair decomposition is used for online frequency tracking. The planned method could provide accurate identification of various nonlinear dynamical systems. Dsilva focuses on applying machine learning methods to spot components in a group of multi-scale data (Dsilva et al. 2016). The authors presented an approach to utilize local geometry and noise dynamics. The analysis of data-driven reduction for multi-scale dynamical systems recovers the underlying slow variables. Schulze presented a data-driven insight for dynamical systems with delay (Schulze and Unger 2016). This approach is validated by different examples. The result shows that the need for preserving the delay formation in the model of dynamical systems. Giannakis developed a scheme for dynamic mode decomposition (Giannakis 2019) and forecasting of ergodic unobserved component modeling systems (Murthy et al. 2018; Narasimha Murthy et al. 2019). This scheme is based on Perron-Frobenius and Koopman groups on an orthogonal basis. The authors established the connection between Laplace-Beltrami and Koopman operators to provide an analysis of diffusion-mapped coordinates for system dynamics. See in Figure 6 the spiral function approximated with a neural ODE (Chen et al. 2018).

Fig. 6.

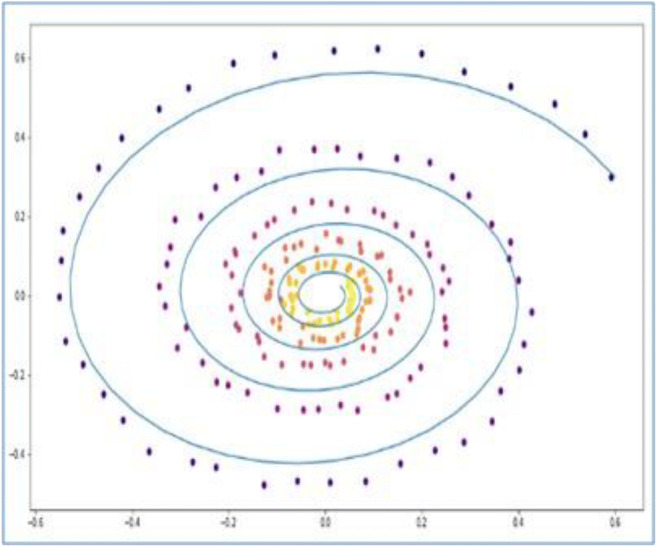
A Neural ODE approximated the spiral function is better than RNN (Chen et al. 2018)

Way forward

The amount of data generated from experiments, simulations, and historical records is exponentially growing at an incredible pace. Simultaneously, the algorithms in deep learning and data science are getting much better. Therefore, we characterize the dynamical systems purely from data. Deep learning provides new and powerful algorithms like CNNs RNNs and reinforcement learning is used in modeling of dynamical systems. Data-driven methods are revolutionizing in science and technology, and most of these methods are applicable to model the complex dynamical systems. These formulation models are facilitated in the future to encompass an incredible range of phenomena, including those observed in classical mechanical systems, electrical circuits, turbulent fluids, climate science, finance, ecology, social systems, neuroscience, epidemiology, and nearly every other system that evolves in time. In the future, these techniques will continue to gain greater relevance, because there are investigations that are working in the process of integrating data, which will allow data of different types to be used and origins, allowing discoveries to be made about the relationships and interactions between the different dynamical systems.