Water Electrolysis in Saturated Phosphate Buffer at Neutral pH

Abstract

Hydrogen production from renewable energy and ubiquitous water has a potential to achieve sustainability, although current water electrolyzers cannot compete economically with the fossil fuel‐based technology. Here, we evaluate water electrolysis at pH 7 that is milder than acidic and alkaline pH counterparts and may overcome this issue. The physicochemical properties of concentrated buffer electrolytes were assessed at various temperatures and molalities for quantitative determination of losses associated with mass‐transport during the water electrolysis. Subsequently, in saturated K‐phosphate solutions at 80 °C and 100 °C that were found to be optimal to minimize the losses originating from mass‐transport at the neutral pH, the water electrolysis performance over model electrodes of IrO_x and Pt as an anode and a cathode, respectively, was reasonably comparable with those of the extreme pH. Remarkably, this concentrated buffer solution also achieved enhanced stability, adding another merit of this electrolyte for water electrolysis.

Keeping it neutral: Determination and analysis of physicochemical properties revealed that phosphate solutions at neutral pH achieved smaller mass‐transport losses during water electrolysis at higher molalities and temperatures. Electrocatalytic testing demonstrated water electrolysis in saturated phosphate solutions to be comparable to that in extreme pH counterparts at elevated temperatures.

1. Introduction

Our future sustainable society would largely rely on the renewable energy, although the low energy density and spatiotemporal fluctuation hamper widespread implementation. The renewable energy can be converted into electricity, which then can be stored in chemical bonds via an electrocatalytic process for subsequent transport to the site of consumption.[ ¹ , ² ] Hydrogen has a high energy density and is a promising substance as the energy carrier.[ ¹ , ³ ] By using water as a reactant, the electrocatalytic water splitting, i. e., water electrolysis process, yields hydrogen in a renewable way if driven by the electric power generated in a renewable manner. However, the hydrogen produced via water electrolysis in current technology fails to compete economically with fossil fuel‐based counterparts, ^[1] which necessitates the development of a cost‐effective and robust water electrolysis system.

Conventional industrial‐scale water electrolyzers operates in the extremely acidic or alkaline pH conditions to maximize the overall cell efficiency by minimizing the kinetic overpotential and ohmic losses under such extreme pH conditions. The available data on the cost‐breakdown of water electrolyzers indicate that the cell stack accounts for half of the capital cost of the alkaline and proton exchange membrane (PEM) water electrolyzers. ^[4] In more details, the half of the stack cost for the alkaline and PEM electrolyzers comprise electrocatalysts and bipolar plates, respectively. ^[4] We remark here that the corrosiveness of the extreme pH conditions requires the use of corrosion‐tolerant materials, e. g., titanium, as the plate in the acidic media, which further increases cost. In this context, near‐neutral pH aqueous medium has emerged as an alternative choice for water electrolyzers,[ ⁵ , ⁶ , ⁷ , ⁸ ] which is less corrosive, and offers a safer operation and broader options for materials. Such a condition is compatible with renewable energy driven systems for home use, e. g., a system that connects photovoltaic cells with an electrolyzer to store excess electricity as hydrogen that functions as a fuel for fuel cells. ^[5]

Significant research efforts have been dedicated to developing electrocatalysts for the half‐reactions of water electrolysis, i. e., the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER). In acidic and alkaline solutions, noble metals such as Pt for the HER and IrO_x and RuO_x for the OER were reported to exhibit the highest activity of water electrolysis, which sit at the top of the “volcano” trend.[ ⁹ , ¹⁰ , ¹¹ ] To develop active yet cost‐effective electrocatalysts, several electrodes composed of earth‐abundant elements have been reported such as NiMo for the HER and NiFeO_x for the OER.[ ¹⁰ , ¹² , ¹³ , ¹⁴ ] When used in near‐neutral pH conditions, however, these electrodes fail to catalyze the reaction at decent overpotential. ^[15] Previous studies using the Pt electrocatalyst reported a HER overpotential as large as >250 mV at −4 mA cm⁻² in solutions of 0.1 M Na₂SO₄ ^[16] and 0.1 M KClO₄ ^[17] at pH 7.0, which is substantially larger than 30 mV at pH 13 in the solutions of 0.1 M NaOH ^[16] and 0.1 M KOH. ^[17] Similarly, the OER overpotential at 0.1 mA cm⁻² of α‐Fe₂O₃ in 0.1 M Na₂SO₄ at pH 7.0 was >700 mV, while that in 0.1 M NaOH at pH 13 was below 450 mV. ^[18] This poor performance reported at the near‐neutral pH to those under extreme pH conditions called for research activity in this direction.

The addition of buffering species such as phosphate was found to be effective in improving the electrocatalytic performance at near‐neutral pH levels.[ ¹⁹ , ²⁰ ] The enhancement was accounted for by the prevention of local pH shift at the surface.[ ²¹ , ²² ] In the absence of the buffering species, the OER under the near‐neutral pH conditions consumes hydroxide ions at a lower reaction rate [Eq. (1)], whereby the reaction switches to the oxidation of the water molecules [Eq. (2)], leading to a substantial acid‐shift of the local pH values: ^[23]

(1)

$${\displaystyle 2{\mathrm{H}}_2\mathrm{O}\overrightarrow{\leftarrow }{\mathrm{O}}_2+4{\mathrm{H}}^{+}+4e^{-}}$$ (2)

Similarly, the HER experiences reactant‐switching from the proton [Eq. (3)] to the water molecule [Eq. (4)],[ ¹⁶ , ¹⁷ ] resulting in an alkali‐shift in the proximity of the electrode surface: ^[22]

$${\displaystyle 2{\mathrm{H}}^{+}+2e^{-}\overrightarrow{\leftarrow }{\mathrm{H}}_2}$$ (3)

$${\displaystyle 2{\mathrm{H}}_2\mathrm{O}+2e^{-}\overrightarrow{\leftarrow }{\mathrm{H}}_2+2\mathrm{O}{\mathrm{H}}^{-}}$$ (4)

In stark contrast, when the buffering species is present, the species maintains the local pH at the electrode surface due to the buffering action: ^[24]

$${\displaystyle \mathrm{HA}\overrightarrow{\leftarrow }{\mathrm{H}}^{+}+{\mathrm{A}}^{-}}$$ (5)

In other words, the presence of the buffering species prevents the formation of a concentration gradient and thus reduces the concentration overpotentials, ^[25] which leads to higher performance than in unbuffered conditions. Fundamentally, such buffering actions become most effective when the pH of a solution is closer to the pKa of the buffer species, where protonated and deprotonated buffer ions equally coexist, setting a primary guideline for the use of the buffer for aqueous electrocatalytic reactions. ^[26]

Notably, further studies on the HER and OER in buffered conditions pointed to another role of buffering species.[ ²⁰ , ²¹ ] Targeting a reaction rate on the order of 10 mA cm⁻², we previously investigated the electrocatalytic HER and OER in buffered solutions at concentrations greater than the typical electrolyte (>0.1 M; hereafter, we use the term “concentrated” for solution more concentrated than 0.1 M). ^[6] Our simulation found that the proton generated via the buffering action quantitatively fails to account for the experimentally achievable HER rate depending on the pKa of the buffering species and pH of the reaction condition. ^[27] Rather, we found that the buffering species most likely functions as the proton carrier and directly participates in the surface reactions. ^[27] Furthermore, a combined experimental and theoretical investigation in this line of study elucidated that the electrocatalytic HER rate was majorly determined by the mass‐transport of the buffering species that functions as a proton carrier. ^[21] The optimization of electrolyte properties to maximize the mass‐transport of the buffering species thus improved the electrocatalytic performance, highlighting the concept of “electrolyte engineering.” ^[25] Further improvement in the performance, however, is retarded by the lack of a comprehensive dataset of physicochemical properties of the aqueous solutions more concentrated than 0.1 mol kg⁻¹. ^[28] In addition, the quantitative rationalization of such concentrated solutions still remains elusive, especially at elevated temperatures compatible with industrially relevant electrolyzer plants that would improve the mass‐transport and kinetics. This gap between the available and the target hampers rational development of water electrolysis in concentrated buffer conditions. Altogether, adding buffer species to solutions at neutral pH and carefully tuning their physicochemical properties at elevating temperatures would increase the system efficiency of water electrolysis in a less corrosive environment, which would pave the way for CO₂‐free hydrogen in a sustainable society.

This study herein addresses the physicochemical properties of concentrated buffer solutions to rationally pin down the optimal electrolyte for water electrolysis at neutral pH. We began with experimental measurement of the solubility, viscosity, and conductivity of concentrated phosphate solutions at various temperatures and then quantitatively analyzed losses associated with diffusion and migration events during water electrolysis. Subsequently, we investigated the water electrolysis at elevated temperatures in optimal electrolytes that minimize the losses at the neutral pH. Using a model Pt‐IrO_x system, our catalytic testing revealed that the concentrated buffer solution achieved performance not only comparable to‐but also more stable than‐extreme pH conditions. This work demonstrates the concentrated buffer solutions as a promising electrolyte for water electrolysis under neutral pH conditions.

2. Results and Discussion

2.1. Experimental determination of physicochemical properties of concentrated buffer electrolyte

Knowing that the existing PEM and alkaline electrolyzers make use of elevated temperatures of ∼80 °C to optimize their efficiency, ^[4] we anticipate an optimum performance of near‐neutral pH water electrolyzers also at elevated temperatures due to the improved kinetics ^[29] and mass‐transport. ^[30] Nevertheless, limited available dataset on the physicochemical properties of buffered solutions hampers the rational optimization with respect to the temperature at near‐neutral pH. This lack of data motivated us to determine the physicochemical properties of various concentrated buffer solutions in a quantitative manner.

In the present study, we limited ourselves to electrolyte pH conditions at neutral, i. e. pH 7 at 25 °C. We considered four criteria when choosing the buffer species: electrochemical stability, pKa, temperature‐tolerance, and solubility. As to the electrochemical stability, a buffer used as an electrolyte for water electrolysis should not irreversibly decompose. In this regard, organic substances such as citrate buffer cannot be used because they are electrochemically oxidized. ^[20] This criterion basically narrows the option of the buffer species suitable for our purpose to inorganic ones.[ ³¹ , ³² , ³³ ] Regarding the pKa, the buffering ions need to be in an environment in which the protonation‐deprotonation reaction of the buffer is fast enough to catch up with the formation of local pH gradient. Such an ability, called the buffering capacity, becomes larger when the pH of the solution is closer to the pKa of the buffer. Among representative inorganic buffers, the pKa value of borate (9.2) and carbonate (10.3 for HCO₃ ⁻/CO₃ ²⁻) deviates from the benchmarking pH 7 by more than 2.2 and 3.3, respectively, while that of phosphate is 7.2. Thirdly, although the bicarbonate solution with H₂CO₃ and HCO₃ ⁻ pair possesses a pKa value of 6.5, the bicarbonate solutions could not be employed in an open environment employed in this study because CO₂ is released from the solution at elevated temperatures and thus the pH of the solution alkali‐shifts (∼pH 10). Lastly, the solubility of phosphate at 25 °C is larger than that of carbonate and borate, ^[28] which would allow for the more concentrated environment with high conductivity than the other buffers. These considerations pinned down phosphate as a suitable electrolyte to investigate water electrolysis at the neutral pH. We hereafter use the term M‐phosphate (M=Li, Na, K, Cs) to denote the phosphate solution at pH 7 for the sake of simplicity. The anionic species in the M‐phosphate solution is H₂PO₄ ⁻ and HPO₄ ²⁻ according to the pKa of phosphate. ^[28]

Figure 1a plots the measured solubilities of M‐phosphate as a function of the temperature, whose pH levels were adjusted to 7 at 25 °C prior to the elevation of temperature. The boiling point elevation in the concentrated solution made possible the determination of solubility at temperatures greater than the boiling point of H₂O, and the highest achievable temperature varied with the identity of the cation. Although the solubility increased with the temperature in all solutions, its sensitivity to the temperature differed depending on the identity of the cation. The Li‐phosphate solution exhibited the lowest solubility of 0.5 mol kg⁻¹ at 25 °C, which slightly increased with temperature and reached 0.7 mol kg⁻¹ at 100 °C. The Cs‐ and K‐phosphate solutions showed greater solubilities of 2.1 and 2.6 mol kg⁻¹ at 25 °C, respectively, which increased monotonically to 4.6 mol kg⁻¹ at 108 °C and 2.7 mol kg⁻¹ at 110 °C. On the other hand, the solubility of Na‐phosphate solution was merely 0.9 mol kg⁻¹ at 25 °C, which sharply increased to 4.0 mol kg⁻¹ at 40 °C, and a further increase in temperature led to only a slight increase to the value of 4.5 mol kg⁻¹ at 112 °C. This unique behavior of the Na‐phosphate solution was likely due to changes in the number of hydrations with temperature: ^[34] e. g., the hydration number for NaH₂PO₄ was 1 below ca. 40–60 °C above which it became zero, while that of KH₂PO₄ remained zero from 0 to 100 °C. ^[34]

Figure 1.

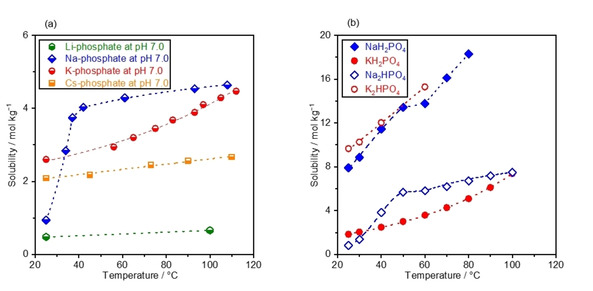
Solubility curves of phosphate solutions. a) The solubility of M‐phosphate (M=Li, Na, K, Cs) was measured at various temperatures. b) The solubility of NaH₂PO₄, KH₂PO₄, Na₂HPO₄, and K₂HPO₄ was plotted as a function of the temperature, adopted from available dataset. ^[28] pH levels of solutions were adjusted to 7.0 at 25 °C prior to the measurements.

Digesting the available data on the solubility of phosphate at different pH levels helped rationalize the solubility curve observed in Figure 1a. The solubility of monobasic phosphate (NaH₂PO₄ and KH₂PO₄) and dibasic phosphate (Na₂HPO₄ and K₂HPO₄) were adopted from the literature ^[28] and are plotted as a function of the temperature in Figure 1b. The monobasic and dibasic phosphate are the predominant phosphate species at the weakly acidic pH of ca. pH 5 and the weakly alkaline pH of ca. 10, respectively. ^[28] Interestingly, Na‐phosphate dissolves more than K‐phosphate when monobasic, while Na‐phosphate dissolves less than K‐phosphate for dibasic ones. Unfortunately, there is a lack of scientific theory to fully describe the solution more concentrated than 0.1 mol kg⁻¹, which prevents rationalization of this varying solubility with identity of phosphate anions. ^[35] Nonetheless, we postulate that this behavior would at least in part originate from the difference of the water affinity of ions.[ ³⁵ , ³⁶ , ³⁷ , ³⁸ ] Generally, ions fall in categories of kosmotropes or chaotropes; kosmotropes dictate the strongly hydrated ions with smaller size and higher surface charge density while chaotropes are the weakly hydrated species. ^[38] The following order was obtained as Hofmeister series in which species on the left and right possess more kosmotropic and chaotropic character, respectively: ^[37]

$${\displaystyle \mathrm{H}{}_2\mathrm{PO}{}_4{}^{-}<\mathrm{HPO}{}_4{}^{2-}}$$ (6)

$${\displaystyle \mathrm{K}{}^{+}<\mathrm{Na}{}^{+}}$$ (7)

Oppositely charged ions with similar water affinity tend to associate with each other, leading to a smaller mean activity coefficient and fewer dissolved ions, while the opposite is true for ion pairs with dissimilar water affinities. ^[38] According to this rule, K⁺ interacts with H₂PO₄ ⁻ more strongly than Na⁺ likely indicating lower solubility of KH₂PO₄ than NaH₂PO₄. Likewise, Na⁺ would associate more with HPO₄ ²⁻ than K⁺, possibly resulting in higher solubility of K₂HPO₄ than Na₂HPO₄. Interestingly, this order of predicted solubilities of both monobasic and dibasic phosphate solutions agrees with Figure 1b, likely validating the view from water affinity in rationalizing the solubility of concentrated buffer solutions. In terms of phosphate solutions at pH 7, in which both H₂PO₄ ⁻ and HPO₄ ²⁻ coexist, interactions among M ⁺, H₂PO₄ ⁻, and HPO₄ ²⁻ are all at play. The complexity might have resulted in the non‐straightforward order of Li⁺<Cs⁺<K⁺<Na⁺ at neutral pH in Figure 1a. Knowing that K‐, Na‐, and Cs‐phosphate solutions have higher solubility than Li‐phosphate by one order of magnitude, we focus hereafter on these three phosphate solutions that allow for the investigation of a wide range of the molality values.

Before describing the mass‐transport event, we first address its theoretical aspect to elucidate the key parameter governing the phenomena in the solution. In general, mass‐transport comprises the diffusion, the migration, and the convection, ^[25] which are theoretically expressed by the Nernst‐Planck equation [Eq. (8)]:

$${\displaystyle J_i\left(x\right)=-D_i\frac{\partial c\left(x\right)}{\partial x}-\frac{z_{i}F}{RT}{D}_{i}c\frac{\partial \varphi \left(x\right)}{\partial x}-cv\left(x\right)}$$ (8)

in which J is the flux, D is the diffusion coefficient, c is the concentration of the solution, z is the charge number, F is the Faraday constant, and v is the velocity of the forces in the solution. ^[27] The first, second, and third terms on the right side of Equation (8) denote the diffusion, migration, and convection, respectively. This expression clearly shows that both the diffusion and migration are a function of the diffusion coefficient, which largely determines the overall mass‐transport flux.

With this formula in mind, we subsequently studied the diffusion coefficient. The diffusion coefficient is theoretically described by the following equation in the framework of the Stokes‐Einstein model, ^[25] without considering the solute‐solvent and solute‐solute interactions: ^[39]

$${\displaystyle D=\frac{kT}{3\pi d\mu }}$$ (9)

in which, k is the Boltzmann constant, d denotes the Stokes diameter (effective diameter of the hydrated ion), and μ represents the viscosity of the solution. The diffusion coefficient in part governs the conductivity σ of the electrolyte: ^[40]

$${\displaystyle \sigma =\frac{F^2{z}^{2}c}{RT}D}$$ (10)

Based on these relationships, below the viscosity and the conductivity of Na‐, K‐, and Cs‐phosphate solutions were measured and discussed.

Figure 2 summarizes the measured viscosity of Na‐, K‐, and Cs‐phosphate solutions at various temperatures. Because excessively large molalities make the difference in the viscosity among various M‐phosphate solutions visibly smaller, we tentatively chose the molality of 2.0 mol kg⁻¹ as the representative (see Table S1 for full dataset of viscosity at various molalities and temperatures). Viscosity of the 2.0 mol kg⁻¹ Na‐phosphate solution below 40 °C could not be measured because of its solubility. Regardless of the identity of the cations, the viscosity decreased with elevating temperatures, consistent with the previously reported empirical law.[ ³⁰ , ⁴¹ ] Comparing the viscosity of M‐phosphate solutions revealed that the viscosity of K‐phosphate was the smallest, followed by Cs⁺ and Na⁺ at 60 °C and lower:

$${\displaystyle \mathrm{K}{}^{+}<\mathrm{Cs}{}^{+}<\mathrm{Na}{}^{+}}$$ (11)

Figure 2.

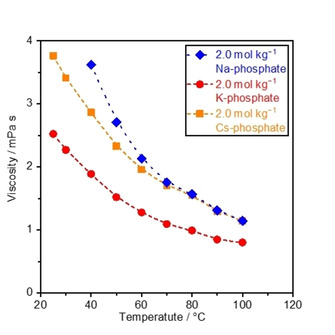
Viscosity of phosphate solutions at the neutral pH. The viscosity of Na‐, K‐, and Cs‐phosphate solutions was measured at various temperatures using a viscometer, and pH levels of solutions were adjusted to 7.0 at 25 °C prior to the measurements. The dotted lines are provided as a visual aid. See Table S1 for the complete data at different molalities and temperatures.

However, the viscosities of Na‐ and Cs‐phosphate solutions became identical above 60 °C. To shed light on this transition, the logarithm of viscosity was plotted as a function of reciprocal of the temperature in Figure S1,[ ³⁰ , ⁴¹ ] as in the Arrhenius expression. The Na‐phosphate solution at >60 °C as well as the K‐ and Cs‐phosphate solutions across the entire temperature regime exhibited identical slopes. In contrast, the slope value for the Na‐phosphate solution below 60 °C was greater than these values, consistent with the transition in the viscosity‐temperature relationship for the Na‐phosphate solutions. The origin of this unique behavior for Na‐phosphate remains unclear at this stage; however, we may postulate that it might have originated from the change of the hydration number for Na‐phosphate solution at varying temperatures as discussed in Figure 1. The hydration number of both NaH₂PO₄ and Na₂HPO₄ decreases at higher temperatures, ^[34] and thus the hydrated size of Na‐phosphate becomes smaller with increasing temperature. The larger phosphate sizes at lower temperatures would hinder the motion of the species, which anticipates a higher sensitivity to the temperature in the lower temperature regime. All in all, since Equation (9) states that the diffusion coefficient is proportional to the reciprocal of the viscosity, the observed lower viscosity of K‐phosphate indicated a larger diffusion flux of phosphate species in the K‐phosphate solution than that in the Na‐ and Cs‐phosphate solutions. Nevertheless, the viscosity of K‐phosphate solution at this molality was found to be substantially larger than 2.2 mPa s of industrially relevant solutions of 7.0 mol kg⁻¹ KOH solution at 25 °C. ^[28]

With increasing molality, the viscosity increased in all phosphate solutions at neutral pH (see Table S1 and Figures S2a and S3). This viscosity‐molality relationship was consistent with the expression below that is applicable at lower molalities (<0.1 mol kg⁻¹):[ ⁴² , ⁴³ , ⁴⁴ ]

$${\displaystyle {\eta }_r=\frac{\eta }{{\eta }_0}=1+A{m}^{1/2}+Bm+D{m}^2}$$ (12)

in which, η _r is relative viscosity, η is viscosity of solution, η ₀ is viscosity of solvent, and m is molality. The A‐coefficient is determined by ion‐ion electrostatic interaction, ^[45] the B‐coefficient is an adjustable parameter which is related to the size of the ions, and the D‐coefficient is likely related to solute‐solute association effects. ^[44] Applying this equation to the concentrated buffer sheds lights on their properties. The A‐coefficient was calculated from the ionic attraction theory by the Falkenhagen‐Vernon equation [Eq. (13)];[ ⁴⁴ , ⁴⁶ ]

$${\displaystyle \mathrm{A}=0.7536\left[\frac{{\lambda }_1^0+{\lambda }_2^0}{4{\lambda }_1^0{\lambda }_2^0}-\frac{({\lambda }_1^0-{\lambda }_2^0{)}^2}{4.41{\lambda }_1^0+{\lambda }_2^0({\lambda }_1^0+{\lambda }_2^0)}\right]}$$ (13)

in which λ is limiting equivalent conductance. The A‐coefficient value is obtainable only at 25 °C because of limited availability of the dataset. ^[28] By fitting the experimental data with Equation (12) using the thus determined A‐coefficient, the B and D‐coefficients at 25 °C were determined ^[44] and listed in Table 1. At 25 °C, all values of A, B and C in Na‐phosphate were larger than that of K and Cs‐phosphate, presumably reflecting the strong electrostatic interaction of ions in the Na‐phosphate solution, the larger hydrated radius of the Na⁺ ion of 3.58 Å versus 3.31 Å of the K⁺ ion and 3.29 Å of the Cs⁺ ion, ^[47] and stronger solute‐solute association effects. These properties of the Na‐phosphate solution anticipate its larger viscosities than the K‐ and Cs‐phosphate solutions, consistent with the measured results in Figure 2 and Table S1 at 25 °C.

Table 1.

The values of A‐, B‐, and D‐coefficient at 25 °C. A‐coefficient calculated with Equation (13).[ ²⁸ , ⁴⁴ ] B‐ and D‐ coefficient obtained by fitting the experimental data with Equation (12).

M	A [104 m−2 S−1 mol]	B [mol−1 kg]	D [mol−2 kg2]
Na	7.8	0.21	0.80
K	6.3	0.17	0.37
Cs	6.1	0.18	0.70

The measured conductivity of the K‐phosphate solutions at various molalities was plotted as a function of the temperature in Figure 3 together with experimentally determined values of saturated Na‐phosphate as well as the reported values of KOH ^[48] as a reference. The figure revealed that the conductivity increased with temperature and molality. The following expression obtained from Equations (9) and (10) helped rationalize the dependence of the conductivity on the temperature:

$${\displaystyle \sigma =\frac{z^{2}ecF}{3\pi d\mu }}$$ (14)

Figure 3.

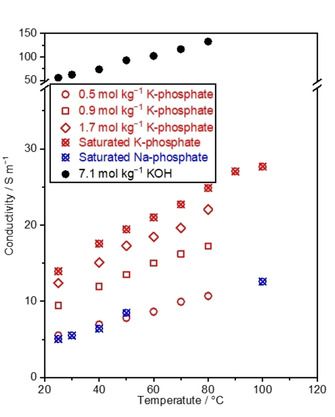
Conductivity of K‐phosphate solutions. Conductivity of the phosphate solutions was assessed by measuring impedance, which was conducted in the 2‐electrode system using two Pt wires, while keeping the distance between Pt wires at 2.0 cm (cell constant, K_cell=0.6 cm⁻¹). The concentration of saturated K‐phosphate was 2.6, 2.8, 2.9, 3.1, 3.3, 3.6, 3.8, and 4.1 mol kg⁻¹ at 25, 40, 50, 60, 70, 80, 90, and 100 °C, respectively, and that of saturated Na‐phosphate was 0.9, 1.8, 3.9, 4.1, 4.6 mol kg⁻¹, respectively, at 25, 30, 40, 50, and 100 °C. The values of KOH were adopted from the literature. ^[55] The pH levels of the phosphate solutions were adjusted to 7.0 at 25 °C prior to the measurements.

in which e denotes the elementary charge. Primarily, the conductivity was proportional to the inverse of the viscosity. Since Figure 2 showed a decreasing viscosity with temperature, the increase in conductivity with temperature shown in Figure 3 agrees with Equation (14).

With increasing molality, the conductivity of both K‐phosphate (Figure 3) and Na‐phosphate (Figure S2a) solutions monotonically increased, which is consistent with the previous report on K₂HPO₄. ^[49] However, one may wonder about the absence of conductivity maxima in the conductivity‐molality relationship, which was previously observed for KH₂PO₄ ^[49] and KOH. ^[48] This apparent dissimilarity was accounted for by the viscosity‐molality relationship. More precisely, Equation (14) predicts that at a given temperature, the conductivity is a function of the molality and the kinematic viscosity as variables in the present condition. The dynamic viscosity of solutions increased with molality as discussed (Figure S2b); however, the extent of the increase differed depending on the identity of ions. At a given molality, K₂HPO₄ exhibited a higher viscosity than KH₂PO₄. Interestingly, the K‐phosphate possessed a viscosity value in‐between K₂HPO₄ and KH₂PO₄ at the molality of our interest, e. g., 1.5 mol kg⁻¹. Such a larger increase of the viscosity for the K₂HPO₄ would lower its conductivity at higher molality, leading to the appearance of a conductivity maximum at a lower molality in the conductivity‐molality relationship. In contrast, the relatively smaller increase in the viscosity for KH₂PO₄ and K‐phosphate solutions shifted their conductivity maximum to appear at higher molalities, which was likely greater than their solubility, resulting in an apparently monotonic increase in the conductivity with molality in experiments.

These variations of the viscosity, and in turn those of the conductivity, with different types of phosphate anions would be rationalized by their distinct sizes. A previous study suggested that the smaller ions would interact more strongly with water molecules and ionic species. ^[50] Accordingly, the mobility of the solution containing smaller ions is lower, making its viscosity large. ^[50] The ionic size of HPO₄ ²⁻ is 2.30 Å, which is smaller than 2.38 Å for H₂PO₄ ⁻. ^[51] Thus, the viscosity of solution with HPO₄ ²⁻ is anticipated to be larger than that with H₂PO₄ ⁻ solutions, consistent with the experimental observation (Figure S2b). The fact that the viscosity of K‐phosphate appeared to be between the value of KH₂PO₄ and K₂HPO₄ indicates the absence of complex interactions between the anionic species impacting the viscosity.

The variation in the viscosity and the conductivity for different cations likely arose also because of distinct effective ion sizes in the hydrated form. Specifically, previous studies suggested that the alkali metal ion interacts more with the surrounding ion as the hydrated ion size along alkali metal increases, which results in the increase of the viscosity.[ ³⁸ , ⁴² ] Given that the Na⁺ ion has a larger hydrated radius of 3.58 Å than 3.31 Å of the K⁺ ion and 3.29 Å of the Cs⁺ ion, ^[47] this suggestion is consistent with the larger viscosity of the Na‐phosphate than the K‐ and Cs‐phosphate solutions in Figure 2. In addition, the larger effective size and the viscosity of Na⁺ would likely lead to smaller conductivity according to Equation (14), which agrees with the conductivity shown in Figure 3 measured in solutions more concentrated than 0.1 mol kg⁻¹.

Finally, we remark on the applicability of existing theory for the dilute solution to solutions more concentrated than 0.1 mol kg⁻¹ in this current work. The concentration described in Equations (9), (10), and (14) is a nominal one and might deviate from the effective concentrations when the molality is greater than 0.1 mol kg⁻¹ because of the decrease in the mean activity coefficient.[ ³⁰ , ³⁵ ] In addition, the effective ion size is a direct function of the hydration number, which would vary with the molality as well.[ ⁴⁷ , ⁵² ] Nevertheless, among the phosphate solutions investigated in Figure 2 and Figure 3, a higher conductivity was observed for solutions with smaller viscosities, indicating that the variation in the mean activity coefficient and the number of hydration were quantitatively smaller than that of viscosity, which makes viscosity be a primary parameter impacting mass‐transport. In fact, the conductivity calculated with Equation (14) using the measured viscosity quantitatively agrees with the experimentally obtained values (Figure S4), which demonstrate the validity and applicability of the employed equation and model in the conditions considered in the present study. Overall, we focused on K‐phosphate solution from this point on as a representative solute that demonstrated higher solubility, smaller viscosity, and larger conductivity among M‐phosphates at pH 7, which all would anticipate a greater mass‐transport flux and in turn improved catalytic performance for water electrolysis.

2.2. Quantitative analysis of losses due to the mass‐transport during water electrolysis

Here, we address the mass‐transport flux of phosphate species in the K‐phosphate solutions using the measured quantities in the previous section. We determine the ohmic loss and concentration overpotential originating from the flux of migration and diffusion, respectively. In the analysis below, calculations were performed at an electrode distance of 0.5 mm, which is the same as that in the alkaline electrolyzer of zero‐gap configuration,[ ⁴³ , ⁵³ ] and on the same order as the thickness of typical membrane used in conventional PEM electrolyzer (0.1 mm). ^[54]

By definition, the ohmic loss, or iR loss, is described by the following equation:

$${\displaystyle R=\frac{1}{\sigma }\times \frac{l}{A}=\frac{K_{cell}}{\sigma }}$$ (15)

in which l and A are the specific length and cross‐sectional area of the electrochemical cell, respectively, ^[39] and l/A is called the cell constant K _cell. Together with Equation (14), we obtain:

$${\displaystyle iRloss=i\times R=i\times K_{cell}\frac{3\pi d\mu }{z^{2}ecF}}$$ (16)

in which i is the electric current. The quantitative determination of the iR‐loss thus requires a quantity of K _cell, which was set to be 0.2 cm⁻¹ as determined by the previously reported relationship between K _cell and electrode‐gap. ^[55]

Regarding the diffusion contribution, we consider a hypothetical extreme condition, in which the diffusion of phosphate species governs the reaction rate and directly participates in the surface reactions[ ²¹ , ²⁵ , ²⁷ ] as the diffusion‐limited condition. The diffusion flux is converted to the concentration overpotential ^[56] that represents an overpotential originating from a concentration gradient. Therefore, the obtained concentration overpotential is the theoretically attainable maximum. In an equation, the concentration overpotential is derived by: ^[56]

$${\displaystyle {\eta }_{Concentration}=\frac{RT}{nF}ln\frac{C_b}{C_s}}$$ (17)

in which n is the number of electrons transferred per unit overall reaction, C _b is the concentration in the bulk of electrolyte, and C _s is the concentration at the surface of electrode. The diffusion‐limited current density is described as follows:

$${\displaystyle j=nF{J}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}=-nFD\frac{C_b-C_s}{\partial x}}$$ (18)

Combing Equations 17 and 18 yields the following formulate:

$${\displaystyle {\eta }_{Concentration}=\frac{RT}{nF}ln\frac{C_b}{C_b+\frac{j}{nFD}\partial x}}$$ (19)

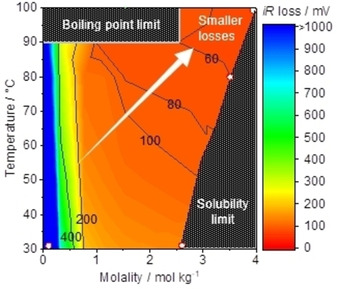
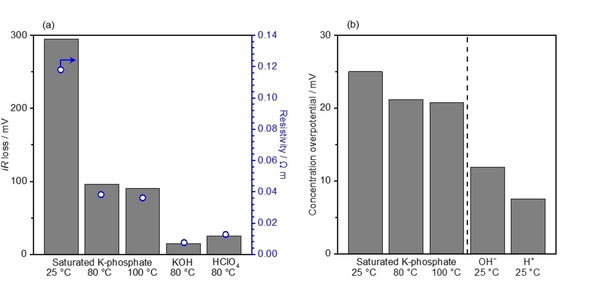
The iR‐loss and the concentration overpotential were computed using Equations (16) and (19), respectively, at 100 mA cm⁻² for electrodes in size of 1 cm² and shown in Figure 4. Figure 4a summarizes the calculated values of iR loss in K‐phosphate solutions of 2.6 mol kg⁻¹ at 25 °C, 3.5 mol kg⁻¹ at 80 °C and 4.1 mol kg⁻¹ at 100 °C, which are the saturated solution at each temperature. The saturated solution was chosen as the model here because the smaller viscosity and in turn larger diffusion coefficient were anticipated at the higher molality. We also show the iR losses of 7.0 mol kg⁻¹ KOH and 7.0 mol kg⁻¹ HClO₄ at 80 °C for comparison as representative alkaline and acidic solutions, respectively. In the figure, the phosphate solution exhibited an iR loss as high as >150 mV at 25 °C, which substantially decreased to ca. 50 mV at elevated temperatures. However, this value was still inferior to that in the 7.0 mol kg⁻¹ KOH solution at 80 °C. Likewise, the value of resistivity in the saturated K‐phosphate solutions decreased with elevating temperatures and reached a value of 0.04 Ω m at 100 °C that was still larger than 0.0075 Ω m of the 7.0 mol kg⁻¹ KOH solution at 80 °C. This larger resistivity and in turn the iR‐losses could be regarded as the limitation of saturated K‐phosphate solution compared with the extreme pH counterparts.

Figure 4.

Analysis of voltage losses due to the mass‐transport at 100 mA cm⁻². (a) iR loss was obtained by multiplying the resistivity of the solution by the cell constants. The resistivity was accessed by impedance spectroscopy, which was conducted in the 2‐electrode system using two Pt wires while keeping the distance between Pt wires at 2.0 cm (cell constant, K _cell=0.6 cm⁻¹) in K‐phosphate (pH 7.0) of 2.6 mol kg⁻¹ at 25 °C, 3.5 mol kg⁻¹ at 80 °C and 4.1 mol kg⁻¹ at 100 °C as well as 7.0 mol kg⁻¹ HClO₄ at 80 °C. The value of 7.1 mol kg⁻¹ KOH was adopted from literature. ^[48] The cell constant at a distance of 0.5 mm between electrodes were extrapolated from the previously reported values, ^[61] which corresponded to 0.2 cm⁻¹. The surface area of the electrode was 1.0 cm². (b) Concentration overpotential, or Nernstian loss, was calculated in a condition of complete depletion of the reactant at the electrode surfaces. Conditions: current density =100 mA cm⁻², the surface area of electrode=1.0 cm², and diffusion layer thickness of=0.5 mm in K‐phosphate (pH 7.0) of 2.6 mol kg⁻¹ at 25 °C, 3.5 mol kg⁻¹ at 80 °C and 4.1 mol kg⁻¹ at 100 °C, and in 1.0 mol kg⁻¹ OH⁻¹ and 1.0 mol kg⁻¹ H⁺.

We remark here that the practical operation would require the use of membrane or diaphragm for separation of gases, and their resistivity adds losses to the system.[ ⁵⁴ , ⁵⁷ ] The Zirfon® diaphragm filled with 30 w % KOH solution and Nafion® membrane (also functioning as solid electrolyte) are used in conventional alkaline and PEM electrolyzers, respectively, whose corresponding resistivities were 0.06 Ω m and 0.09 Ω m.[ ⁵⁴ , ⁵⁸ , ⁵⁹ ] Consequently, this value of 0.06 Ω m for the diaphragm filled with electrolyte becomes responsible for the iR loss in the alkaline electrolyzer, corresponding to the iR loss of 120 mV. The additional use of the diaphragm would also add a resistivity of ca. 0.06 Ω m in the K‐phosphate solution, making the total resistivity amount to approximately 0.1 Ω m. Nevertheless, we argue that the use of the diaphragm could be omitted in concentrated buffer conditions due to the small solubility and diffusion coefficient of gases as well as increased viscosity of the solutions, which all lead to lessened gas crossover as demonstrated previously. ^[49]

Figure 4b compiled the calculated values of concentration overpotential. The concentration overpotential in K‐phosphate solutions decreased with increasing the temperature from 25 mV at 25 °C to 21 mV at 100 °C. The figure contained the concentration overpotential in the hypothetical acidic and alkaline conditions of only 1 mol kg⁻¹ H⁺ and OH⁻ at 25 °C as a reference due to the lack of available diffusion coefficient of these ions at high temperature and high molalities. ^[28] Comparing these values revealed that the concentration overpotential in K‐phosphate was larger than 8 and 12 mV of the acidic and alkaline representatives, respectively. Importantly, we remember here that the concentration overpotential considered herein was the theoretically attainable maximum, in which the reactant (phosphate, proton, and the hydroxide ion) was completely depleted at the surface. In addition, the concentration overpotential in Figure 4b was quantitatively smaller than the iR loss in Figure 4a by one order of magnitude. Therefore, the loss in the electrolysis system using those electrolytes would majorly originates from the migration of ions. Lastly, this quantitatively small concentration overpotential was in line with our previous study, ^[60] which demonstrated that optimization of the electrolyte properties to maximize the mass‐transport flux would result in an improved overall performance. According to Equation (9), the diffusion coefficient was proportional to the temperature and reciprocal of the viscosity. The elevation of the temperature resulted in a decrease in the viscosity (Figure 2), which lead to an increase in diffusion coefficient. Thus, the mass‐transport flux was enlarged, and in turn the concentration overpotential became smaller as demonstrated herein. All things considered, concentrated K‐phosphate solution at elevated temperature is potentially an effective electrolyte for water electrolysis at the neutral pH among M‐phosphate solutions investigated.

2.3. Demonstration of water electrolysis in concentrated buffer solutions at neutral pH

Our study thus far indicated the concentrated K‐phosphate solutions as promising electrolyte, and we now perform catalytic testing of water electrolysis in this electrolyte solution. Chronopotentiometry (CP) was conducted at 10 mA cm⁻² and 80 °C in K‐phosphate solution as well as HClO₄ and KOH solutions as references, using model Pt/Pt mesh and IrO_x/Ti mesh electrodes as the cathode and the anode, respectively (see Figures S5–S7 for surface morphologies). The obtained iR‐free voltages are shown in Figures 5a and 5b (see Figure S8 for the cell geometry and Figure S9 for the performance without iR‐correction). The CP profiles in 7.0 mol kg⁻¹ HClO₄, KOH, and 3.5 mol kg⁻¹ K‐phosphate displayed in the figure were averaged for the two independent experiments (see Figure S10 for raw data). The iR‐corrected voltage increased with time in acidic and alkaline electrolyte solutions (Figure 5a), although the extent of the increment depended on the electrolyte identity and molality. In 0.1 mol kg⁻¹ HClO₄ and KOH, the initial voltage of 1.40 V increased to 1.56 V and >2.0 V, respectively, after testing for 6 h. The more concentrated solutions shown in Figure 5b were employed to mimic the harsh environment of industrial electrolyzer, and the initial voltage was as small as 1.24 V for HClO₄ that rapidly increased with time to reach >2.0 V, while that at alkaline pH was 1.30 V, which also increased with time and ended at >1.60 V. No apparent losses in the performance was observed at the cathode for these experiments, and hence the increase in the overall voltage was most likely accounted for by the degradation of IrO_x as investigated recently.[ ¹⁰ , ⁶¹ , ⁶² ] In fact, the voltages using the IrO_x/Ti mesh‐Pt/Pt mesh eventually matched those using bare Ti mesh‐Pt/Pt mesh in KOH solutions (Figure S11), suggesting that the dissolution of iridium was responsible for the increase in the overall voltage with time. Notably, such a rapid degradation of iridium was not anticipated in the acidic medium, given that the lifetime of PEM electrolyzer using an IrO_x anode was around 60000 h. ^[63] This shorter lifetime in the present study might have originated from the different circumstance, e. g., pure H₂O is supplied to the PEM and the evolved H⁺ is transported through the solid electrolyte, while in our study, the acidic H₂O is directly in contact with the anode. Due to the loss of iridium, the current density observed in the acidic and alkaline pH solutions in Figures 5a and 5b did not therefore entirely originate from the water electrolysis, indicative of a Faradaic efficiency much lower than 100 %.

Figure 5.

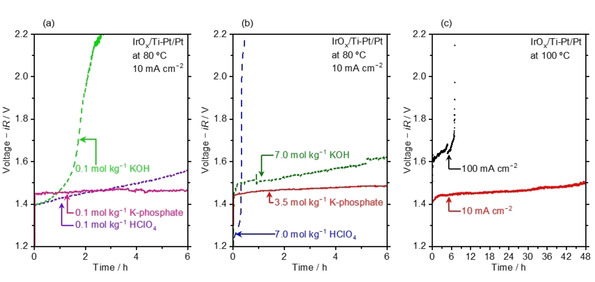
Water electrolysis performance in concentrated buffer solutions. (a) Chronopotentiometry (CP) profile performed at 10 mA cm⁻² and 80 °C in electrolyte solutions of 0.1 mol kg⁻¹ KOH, 0.1 mol kg⁻¹ HClO₄, and 0.1 mol kg⁻¹ K‐phosphate. (b) CP profile performed at 10 mA cm⁻² and 80 °C in electrolyte solutions of 7.0 mol kg⁻¹ KOH, 7.0 mol kg⁻¹ HClO₄, and 3.5 mol kg⁻¹ K‐phosphate. These profiles are the average of the experiments for 3.5 mol kg⁻¹ K‐phosphate, 7.0 mol kg⁻¹ HClO₄, and KOH (see Figure S10 for raw data. (c) Overall water electrolysis performance was accessed by CP at 10 and 100 mA cm⁻² in 4.1 mol kg⁻¹ K‐phosphate solutions at 100 °C. All measurements were performed in the two‐electrode configuration using IrO_x/Ti mesh and Pt/Pt mesh as anode and cathode with a geometric surface area of 1.0 cm², respectively, under Ar bubbling. The voltage displayed in the figure has been iR‐corrected with measured impedance value unless otherwise noted. The pH level of K‐phosphate solutions was adjusted to 7.0 at 25 °C prior to the measurements.

In stark contrast, in 0.1 and 3.5 mol kg⁻¹ K‐phosphate solutions (Figures 5a and b, respectively), an overall voltage of 1.45 and 1.44 V in the beginning increased only by 0.02 and 0.04 V after 6 h of testing at almost 100 % of Faradaic efficiency toward the HER and OER (see Figure S12 for gas quantification). The stability during not only the prolonged operation but also the startup‐shutdown cycling was regarded as a key to the practical implementation.[ ⁶⁴ , ⁶⁵ ] Figure S13 shows the voltage profile obtained by periodically performing CP at 10 mA cm⁻² with an interval of 1 h in 7.0 mol kg⁻¹ KOH and the 3.5 mol kg⁻¹ K‐phosphate solutions at 80 °C. While in the KOH solution, the initial voltage increased with on‐off cycling, the initial voltage in the K‐phosphate solution was unchanged during the testing. These results demonstrated the stable operation made possible by the buffered solution at elevated temperatures, contrasting to the extreme pH counterparts. Hence, the concentrated K‐phosphate solution not only exhibits the fast mass‐transport but also achieves catalytic performance comparable to the extreme pH conditions as well as more stable operation.

At this stage, the origin of the improved stability in the buffered condition with respect to the extreme pH counterparts remains unclear. Nonetheless, provided that the loss of performance in the extreme pH condition originated from the dissolution of iridium, as well as superior stability observed in the K‐phosphate solution (Figures 5a, 5b), we postulate that the phosphate species would prevent its dissolution in the buffered solutions in a manner similar to the self‐healing mechanism claimed previously.[ ⁶ , ⁶⁶ ] In the case of reported Co‐phosphate during the OER catalysis, Co species undergo oxidation from +II to +III and eventually to +IV, which upon the release of O₂ returns back to the original +II state.[ ⁶⁷ , ⁶⁸ ] This Co (+II) state readily dissolves in the solution, which in the presence of phosphate species forms cobalt‐phosphate complex upon dissolution and precipitates on the electrode surface.[ ⁶⁷ , ⁶⁸ , ⁶⁹ ] The re‐deposited Co (+II) species on the electrode surface reacts with Co (+IV) species on the electrode forming +III via disproportionation reaction and hence participates again in the catalytic cycle. ^[68] In the case of iridium, its oxidation state is considered to change from +III to +IV and then to +V that eventually back to +III state upon release of O₂ according to the literature.[ ²³ , ⁶² , ⁷⁰ ] Similarly to the case of Co, the lowest valence state of +III is known to dissolve, ^[49] which can be one route of iridium dissolution leading to performance loss. To the best of our knowledge, the solubility product (K _sp) of iridium (+III) and phosphate has not been determined in any literature. We anticipate similarly low K _sp for Ir‐phosphate to Co‐phosphate, given that they both fall in the same group in the periodic table and therefore have similar character of d‐electrons. Once the Ir (+III) state is redeposited on the electrode surface, this species can be anodically oxidized to deposit on the surface ^[71] and can again take part in the catalytic cycle.

For targeting practical applications, additional catalytic testing was conducted for longer periods of time at 100 °C using model Pt/Pt mesh and IrO_x/Ti mesh electrodes. Figure 5c presents the CP profile at 10 mA cm⁻² for 48 h, in which the initial iR‐free voltage of 1.44 V remained reasonably stable during the operation and ended at 1.50 V. However, the profile largely differed when performed at a higher current density. At 100 mA cm⁻², the voltage was initially ca. 1.6 V that rapidly increased over several hours, reaching >6 V after 6 h. This voltage of >6 V agreed with that using bare Ti mesh anode (Figure S14), indicative of the loss of iridium species. We consider two possible origins of the loss of iridium at higher current densities in the buffered solutions: First, the higher anodic potential of >1.6 V vs. reversible hydrogen electrode (RHE) was reported to drive the overoxidation of iridium into the +VI state at acidic pH levels, which dissolves into the solution as a form of IrO₄ ²⁻, resulting in the loss in the performance. ^[62] This scenario pointed to the use of other anionic species that achieve smaller K _SP with iridium as well as increasing the number of iridium sites to improve stability. Second, the stripping of the catalyst layer could be induced by the physical force of the bubbles, which would be manifested at higher reaction rates. ^[62]

Cyclic voltammetry (CV) was performed in the two‐ and three‐electrode configurations to describe the breakdown of the initial voltage of water electrolysis under neutral pH (see Figure S15 for the Tafel plots of half‐reactions). Figure 6 presents the breakdown in 0.1 mol kg⁻¹ K‐phosphate solution at 80 °C and in 4.2 mol kg⁻¹ K‐phosphate solution at 100 °C. In both cases, the anodic half‐reaction required substantial overpotentials, e. g., 240 mV and 230 mV at 10 mA cm⁻² in 0.1 and 4.5 mol kg⁻¹ K‐phosphate solutions, respectively, even using the IrO_x electrode. Remarkably, the anodic overpotential in the dilute K‐phosphate solution became substantially larger than that in 4.5 mol kg⁻¹ K‐phosphate solutions at higher reaction rates reaching 100 mA cm⁻², presumably because the buffering capacity was insufficient to mitigate the local pH alteration. This observation further emphasizes the value of using the concentrated buffer solution to sustain a higher reaction rate. The voltage during water electrolysis in the highly acidic and alkaline solutions could not be broken‐down because their pH values are below 0 and above 14, which exceeds the range of the pH meter.

Figure 6.

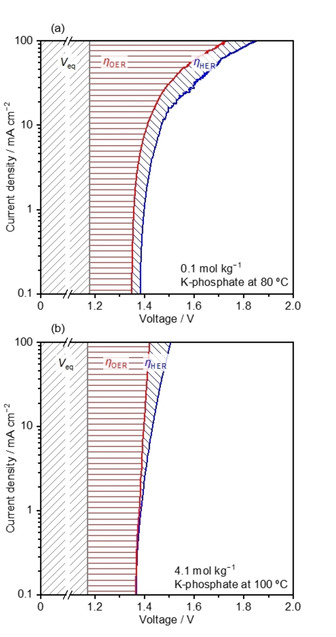
Voltage breakdown of water electrolysis in buffered solutions at neutral pH. a) Voltage breakdown for the water electrolysis at a scan in K‐phosphate of 0.1 mol kg⁻¹ 80 °C, and b) in K‐phosphate of 4.1 mol kg⁻¹ 100 °C determined by electrocatalytic testing for the half‐cell reactions. η_i indicates the overpotential for process i. All measurements were performed in the three‐electrode configuration using IrO_x/Ti mesh, Pt/Pt mesh, and Hg/Hg₂Cl₂ as anode, cathode, and reference electrode, respectively, under Ar bubbling at a scan rate of 10 mV s⁻¹. The voltage displayed in the figure has been iR‐corrected with measured impedance value. The pH levels of K‐phosphate solutions were adjusted to 7.0 at 25 °C prior to the measurements.

The poor stability of IrO_x during the water electrolysis in both acidic and alkaline conditions hampered fair comparison at the steady‐state. To fairly judge the electrolysis performance in the concentrated phosphate, we compare it with those of industrially relevant current‐potential relationship obtained with NiFeO_x anode and NiMo cathode in KOH solutions. Figure 7 shows the cathodic scan of the CV profile obtained in the saturated K‐phosphate solutions of 4.1 mol kg⁻¹ at 100 °C using the Pt cathode and IrO_x anode, as well as that in 30 wt % KOH solution at 73 °C using NiMo cathode and NiFeO_x anode (see Figure S16 for comparison between the CVs in the saturated K‐phosphate solution at 80 °C and 30 wt% KOH solution at 73 °C). The latter was adopted from our previous study, whose performance was almost identical to the best performing electrolyzer in a variety of industrial alkaline electrolyzer with temperature ranging from 70 °C to 90 °C. ^[73] In neutral pH condition, the voltage at 10 mA cm⁻² was 1.44 V, which agreed with the initial value of 1.44 V of the water electrolysis performance (Figure 5c). A current density of 100 mA cm⁻² was achieved at a voltage of 1.49 V at 100 °C, which is comparable to the performance of 1.50 V attained in the alkaline condition at 73 °C.

Figure 7.

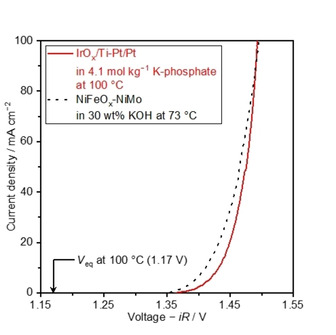
Cyclic voltammograms recorded at a scan rate of 10 mV s⁻¹ in K‐phosphate of 4.1 mol kg⁻¹ 100 °C in the two‐electrode configuration. V _eq denotes equilibrium voltage for water electrolysis. The current‐voltage relationship over the NiFeO_x/Ni foam anode and NiMo/Ni foam cathode in 30 wt% KOH at 73 °C is also presented in the figure, which was adopted from our previous study. ^[73] All measurements were performed in the two‐electrode configuration using IrO_x/Ti mesh and Pt/Pt mesh as anode and cathode, respectively, under Ar bubbling. The voltage displayed in the figure has been iR‐corrected with measured impedance value. The pH level of K‐phosphate solutions was adjusted to 7.0 at 25 °C prior to the measurements.

Seeking for cost‐effective alternative catalysts, we employed NiFeO_x as the anode in 4.1 mol kg⁻¹ K‐phosphate solution, but found that the overall voltage at the neutral pH was as large as 1.76 V at 20 mA cm⁻², which was larger by 200 mV than those at alkaline conditions (Figure S17). Interestingly, its performance at steady‐state was identical with the pristine NiO_x electrode, indicative of loss of NiFeO_x during the OER at the neutral pH. Another previous study consistently reported the dissolution of nickel and iron species from NiFeO_x anode during OER in 0.1 M K‐phosphate solution at pH 7. ^[74] The lack of active and stable electrodes composed of cost‐effective and earth‐abundant elements that catalyze the OER at the near‐neutral pH urge us to develop such electrocatalysts for the production of CO₂‐free hydrogen on a large scale.

All in all, this section demonstrated that model iridium and platinum electrodes have stable operation of water electrolysis in buffered conditions at neutral pH. The performance was found to be comparable with the extreme pH counterparts. The system however was subject to gradual loss in the performance with time at higher reaction rates, e. g., 100 mA cm⁻², presumably due to the dissolution of iridium anode. Such poor stability can be mitigated by the further electrolyte engineering as well as development of active catalyst at higher dispersion, calling for reserach activity in this direction.

3. Conclusions

The physicochemical properties of concentrated phosphate solutions (>0.1 mol kg⁻¹) at neutral pH were investigated for their potential use as an electrolyte for the water electrolysis. The measured solubility of M‐phosphate solutions (M=Li, Na, K, Cs) revealed that Na‐, K‐ and Cs‐phosphate solutions achieved higher molality at elevated temperatures likely owing to the affinity of these alkali metal cation with the phosphate anions present in the solution, namely H₂PO₄ ⁻ and HPO₄ ²⁻. Their viscosity and conductivity were then determined at a variety of temperatures and molalities. At a given molality, the K‐phosphate solution exhibited a smaller viscosity as well as larger conductivity presumably due to its smaller hydrated ion size. Notably, these experimentally determined physicochemical properties were successfully rationalized by the extrapolation of the existing model dealing with the dilute solution. These findings help to rationally select K‐phosphate as the optimal electrolyte at the neutral pH, which can achieve the highest mass‐transport fluxes during the water electrolysis among M‐phosphate solutions. By focusing on this K‐phosphate, the mass‐transport flux during water electrolysis was computed, revealing that the losses due to the mass‐transport in the saturated K‐phosphate solutions (i. e., 3.5 mol kg⁻¹ at 80 °C and 4.1 mol kg⁻¹ at 100 °C) could be potentially comparable with those of existing electrolyzers. Subsequently, using an IrO_x anode and a Pt cathode, the water electrolysis was demonstrated at 10 mA cm⁻² in the K‐phosphate solutions at elevated temperatures. It was observed that the overall voltage was reasonably comparable with the extreme pH counterparts, and remained stable during the hours of operation, contrasting to the acidic and alkaline pH conditions that experienced a rapid deactivation of the anodes. However, the voltage at a higher reaction rate of 100 mA cm⁻² experienced a rapid increase with time in the buffered condition likely because of the deactivation of the IrO_x anode. In addition, voltage breakdown analysis pointed to the largest losses in the performance due to the kinetic overpotentials at the anode. These observations call for the development of electrocatalyst‐electrolyte system to improve the activity and stability at the anode at the neutral pH. Overall, our findings presented in this study demonstrated that the concentrated buffer solutions are a potential electrolyte for water electrolysis at neutral pH. Further developments in anode material functional in such a condition was pointed to as a prerequisite for practical applications.

Experimental Section

The following chemicals were used: H₂Cl₆Pt₆⋅H₂O (99.9 %, FUJIFILM Wako Pure Chemical Corporation), KOH (99.99 %), H₃PO₄ (99.99 %, Sigma‐Aldrich), HClO₄ (assay 70 %, Sigma‐Aldrich), Na₃IrCl₆⋅xH₂O, H₂C₂O₄ (≥99 %, Sigma‐Aldrich), Na₂CO₃⋅H₂O (≥ 99.5 %, Sigma‐Aldrich), H₂PtCl₆ (≥ 99 %, Sigma‐Aldrich), HCl (37 wt% in H₂O, ACS reagent, Sigma‐Aldrich), HNO₃ (69‐70 wt% in H₂O, SAJ first grade, Sigma‐Aldrich), KCl (99.999 %, Sigma‐Aldrich), Ni(NO₃)₂ ⋅ 6H₂O (97.0+%, FUJIFILM Wako Pure Chemical Corporation), Fe(NO₃)₃ ⋅ 9H₂O (99.0+%, FUJIFILM Wako Pure Chemical Corporation), and urea (ACS reagent, 99.0‐100.5 %, Sigma‐Aldrich).

A variety of M‐phosphate solutions (M=Li, Na, K, Cs) were employed as the electrolyte. For the preparation of 500 g of various molality of M‐phosphate solutions at pH 7, 8 mol kg⁻¹ H₃PO₄ solution was firstly diluted with ultrapure water (18.2 MΩ cm) under vigorous stirring to obtain approximately 300 g of the target molality of the solution. The molality in our study was determined to represent that of phosphate ions (the sum of H₂PO₄ ⁻ and HPO₄ ²⁻). Upon adding 7 mol kg⁻¹ NaOH, KOH, CsOH, or 3 mol kg⁻¹ LiOH, the pH value of the solution was adjusted to 7 by simultaneously measuring the pH using a pH meter (D‐71 and 9625, HORIBA). Finally, the total weight was adjusted to 500 g by pouring ultrapure water, and the pH of the resulting solution is referenced throughout this study.

The solubility of M‐phosphate was determined by observing the dissolution of salts at varying temperatures. More specifically, a 5 ml‐sample vial was first filled with 4 ml of the saturated solution with a known total amount of salt. This vial was then placed in an oil‐bath at the target temperature for 30 min. If the precipitates remained after 30 min, then the temperature was raised by 1 °C, and solution was left for another 30 min. This process was repeated until the precipitate disappeared. The concentration was denoted as the solubility at the final temperature.

The conductivity was accessed by measuring the solution resistance of M‐phosphate solutions by electrochemical impedance spectroscopy using a 16‐channel research‐grade potentiostat system (VMP3, BioLogic Science Instruments) at varying molalities and temperatures. The measurement was performed in a two‐electrode system with two Pt wires separated by 2.0 cm. The cell constant of our system was determined by measuring the impedance in 1.0 mol kg⁻¹ KCl solution as a reference. The viscosity of M‐phosphate solutions was measured with a viscometer (SVM3001, Anton Paar) at varying concentrations and temperatures.

The IrO_x electrodes were fabricated by electrochemical deposition following a reported protocol ^[71] with a titanium mesh substrate. The pH level of the deposition bath containing 0.4 mM of Na₃IrCl₆⋅xH₂O and 2 mM of H₂C₂O₄ was adjusted to 10 by adding Na₂CO₃⋅H₂O, which was kept at 35 °C for 4 days prior to the deposition. A Ti mesh (Fuel Cell Store) with a geometric size of 1×1 cm² was washed by immersing in 0.1 mol kg⁻¹ HCl, ultrapure water and ethanol sequentially for 5 min each. The electrochemical deposition was conducted using a three‐electrode configuration with Pt mesh (Nilaco) and Hg/Hg₂Cl₂ (saturated with KCl) as the counter and reference electrodes, respectively. IrO_x was deposited onto the titanium mesh as a working electrode by immersing the mesh in the prepared deposition bath and applying a constant current density of 140 μA cm⁻² for 63 ks. The catalytic activity of the fabricated electrodes was assessed by CV in 0.1 mol kg⁻¹ HClO₄ to confirm the identical properties of the electrodes before catalytic testing.

In addition to IrO_x, a platinized platinum (Pt/Pt mesh) electrode was fabricated by electrochemical deposition following a reported recipe[ ⁷⁵ , ⁷⁶ ] with a Pt mesh (Nilaco) as the substrate. Prior to electrochemical deposition, the Pt mesh was washed by immersion in aqua regia for 1 min. The aqua regia was prepared by mixing HCl and HNO₃ at a volume ratio of 3 : 1. The mesh was then continuously washed with copious amount of ultrapure water. Subsequently, the electrochemical deposition was conducted using a three‐electrode configuration with Pt mesh (Nilaco) and Hg/Hg₂Cl₂ (saturated with KCl) as the counter and reference electrodes, respectively. Platinum was deposited onto the platinum mesh as a working electrode by immersing the mesh in the prepared deposition bath and applying a constant potential of −0.1 V vs. Hg/Hg₂Cl₂ for 15 min. The catalytic activity of the fabricated electrode was assessed by CV in 0.1 mol kg⁻¹ HClO₄ to confirm the identical properties of the electrodes before catalytic testing.

For the fabrication of the NiFeO_x electrode, the hydrothermal synthesis was conducted following a reported procedure. ^[77] Prior to the synthesis, a Ni foam was washed as mentioned earlier by immersing the foam in 0.1 mol kg⁻¹ HCl, ultrapure water, and ethanol sequentially for 5 min each. The Ni foam was then transferred together with 80 mL of solution containing 1 mM of Ni(NO₃)₂ ⋅ 6H₂O, 1 mM of Fe(NO₃)₃ ⋅ 9H₂O, and 5 mM of urea to a 100 mL Teflon‐lined stainless‐steel autoclave and heat‐treated at 120 °C for 12 h. The autoclave was then naturally cooled to room temperature.

Electrocatalytic measurements were conducted using the thus fabricated IrO_x/Ti mesh anode and Pt/Pt mesh cathode in two‐ and three‐electrode systems. Hg/Hg₂Cl₂ (saturated with KCl) was employed as a reference electrode for the measurements in the three‐electrode setup. Before and during all measurements, Ar (99.9999 %), H₂ (99.99999 %) or O₂ (99.9995 %) gas was continuously supplied to the cell. To define the diffusion layer thickness, we did not apply stirring throughout our study. A cell with a diameter of 25 mm and a height of 50 mm (total volume of 24.5 cm³) was employed for our testing, which was filled with electrolyte solution of 12 cm³. In the solution, electrodes with the geometric surface area of 10 mm×10 mm were immersed. To minimize the evaporation of the liquid electrolyte, we introduced 550 mm long glass tubes connected to the cell, which function to reflux. The CV, chronoamperometry (CA), CP and potentiostatic electrochemical impedance spectroscopy measurements were performed at room temperature (25 °C) using the potentiostat system. The cell used in our study at elevated temperatures up to 80 °C was equipped with a jacket (Water‐Jacketed glass cell; BAS Inc.), and its temperature was controlled by an external equipment (NCB‐1210, Eyela). For testing above 80 °C, the temperature was controlled by placing the cell in the oil bath (see Figure S8 for detailed cell configuration). All current densities are expressed in terms of the geometric electrode surface area unless otherwise noted.

The morphology of the electrode surface was characterized by scanning electron microscope (Hitachi, S‐4700) at accelerating voltages of 20 kV equipped with energy dispersive x‐ray spectroscopy (EDS, Horiba).

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

T. Naito, T. Shinagawa, T. Nishimoto, K. Takanabe, ChemSusChem 2020, 13, 5921.