Changes to Carbon Isotopes in Atmospheric CO₂ Over the Industrial Era and Into the Future

Abstract

In this “Grand Challenges” paper, we review how the carbon isotopic composition of atmospheric CO₂ has changed since the Industrial Revolution due to human activities and their influence on the natural carbon cycle, and we provide new estimates of possible future changes for a range of scenarios. Emissions of CO₂ from fossil fuel combustion and land use change reduce the ratio of ¹³C/¹²C in atmospheric CO₂ (δ¹³CO₂). This is because ¹²C is preferentially assimilated during photosynthesis and δ¹³C in plant‐derived carbon in terrestrial ecosystems and fossil fuels is lower than atmospheric δ¹³CO₂. Emissions of CO₂ from fossil fuel combustion also reduce the ratio of ¹⁴C/C in atmospheric CO₂ (Δ¹⁴CO₂) because ¹⁴C is absent in million‐year‐old fossil fuels, which have been stored for much longer than the radioactive decay time of ¹⁴C. Atmospheric Δ¹⁴CO₂ rapidly increased in the 1950s to 1960s because of ¹⁴C produced during nuclear bomb testing. The resulting trends in δ¹³C and Δ¹⁴C in atmospheric CO₂ are influenced not only by these human emissions but also by natural carbon exchanges that mix carbon between the atmosphere and ocean and terrestrial ecosystems. This mixing caused Δ¹⁴CO₂ to return toward preindustrial levels in the first few decades after the spike from nuclear testing. More recently, as the bomb ¹⁴C excess is now mostly well mixed with the decadally overturning carbon reservoirs, fossil fuel emissions have become the main factor driving further decreases in atmospheric Δ¹⁴CO₂. For δ¹³CO₂, in addition to exchanges between reservoirs, the extent to which ¹²C is preferentially assimilated during photosynthesis appears to have increased, slowing down the recent δ¹³CO₂ trend slightly. A new compilation of ice core and flask δ¹³CO₂ observations indicates that the decline in δ¹³CO₂ since the preindustrial period is less than some prior estimates, which may have incorporated artifacts owing to offsets from different laboratories' measurements. Atmospheric observations of δ¹³CO₂ have been used to investigate carbon fluxes and the functioning of plants, and they are used for comparison with δ¹³C in other materials such as tree rings. Atmospheric observations of Δ¹⁴CO₂ have been used to quantify the rate of air‐sea gas exchange and ocean circulation, and the rate of net primary production and the turnover time of carbon in plant material and soils. Atmospheric observations of Δ¹⁴CO₂ are also used for comparison with Δ¹⁴C in other materials in many fields such as archaeology, forensics, and physiology. Another major application is the assessment of regional emissions of CO₂ from fossil fuel combustion using Δ¹⁴CO₂ observations and models. In the future, δ¹³CO₂ and Δ¹⁴CO₂ will continue to change. The sign and magnitude of the changes are mainly determined by global fossil fuel emissions. We present here simulations of future δ¹³CO₂ and Δ¹⁴CO₂ for six scenarios based on the shared socioeconomic pathways (SSPs) from the 6th Coupled Model Intercomparison Project (CMIP6). Applications using atmospheric δ¹³CO₂ and Δ¹⁴CO₂ observations in carbon cycle science and many other fields will be affected by these future changes. We recommend an increased effort toward making coordinated measurements of δ¹³C and Δ¹⁴C across the Earth System and for further development of isotopic modeling and model‐data analysis tools.

Key Points

• Carbon isotopes, ¹⁴C and ¹³C, in atmospheric CO₂ are changing in response to fossil fuel emissions and other human activities

• Future simulations using different SSPs show continued changes in isotopic ratios that depend on fossil fuel emissions and, for ¹³C, BECCS

• Applications using atmospheric ¹⁴C and ¹³C in studies of the carbon cycle or other fields will be affected by future changes

1. Introduction

Carbon isotopes are present in the atmosphere, ocean, and terrestrial biosphere in ratios of approximately 99% ¹²C/C, 1% ¹³C/C, and 1 × 10^{−12 14}C/C. ¹²C and ¹³C are stable isotopes while ¹⁴C is a radioactive isotope called radiocarbon. Radiocarbon is formed naturally in the upper atmosphere from cosmogenic radiation, which produces neutrons that react with atmospheric nitrogen. Because the isotopic composition of carbon is affected by physical, chemical, and biological processes, these ratios are not constant, and they vary across different carbon pools and over time and space. Precise measurements of small differences in these ratios, together with theoretical or empirical models of isotopic fractionation and mixing, enable the investigation of various aspects of the carbon cycle. Observing and analyzing the changes in carbon isotopic composition of atmospheric CO₂ can help to understand the natural carbon cycle's response to human activities.

The notation δ¹³C refers to the deviation of the ratio ¹³C/¹²C in a sample from a standard ratio ¹³C/¹²C, referred to as Vienna Pee Dee Belemnite (VPDB). Typical measurement precision is ±0.01–0.03‰ for atmospheric CO₂. The primary international reference material for δ¹³C is calcite (IAEA‐603 and, formerly, NBS19). Calcite must be converted to CO₂ to implement the VPDB scale at individual laboratories, which has been shown to result in significant laboratory offsets (WMO/IAEA, 2003). Current activities to address measurement compatibility include the distribution of pure CO₂ or CO₂ in whole air reference materials (Brand et al., 2009; Wendeberg et al., 2013; WMO/IAEA, 2018), but achieving long‐term compatibility of δ¹³C measurements in atmospheric CO₂ made at different laboratories remains a challenge, and laboratory offsets must be considered when compiling data (see section 5).

The notation used for ¹⁴C is Δ¹⁴C, which is similar to the definition of δ¹³C in that it refers to deviations from a standard ratio termed “Modern.” The notation Δ¹⁴C includes a correction for radioactive decay in samples of known age and a correction for mass‐dependent fractionation, defined as Δ in Stuiver and Polach (1977). Assuming that any process discriminating against ¹³C will discriminate approximately twice as strongly against ¹⁴C, measurements of δ¹³C in a sample can be used to correct for mass‐dependent fractionation. This enables Δ¹⁴C to uncover effects that are unrelated to simple fractionation processes. Typical measurement precision is ±2–3‰ for atmospheric CO₂. Reference material used for Δ¹⁴C measurements is typically oxalic acid (Stuiver, 1983), but whole air reference materials have also been used for atmospheric measurements (Graven et al., 2012b). Whole air and CO₂ have been used in intercomparisons between radiocarbon laboratories making atmospheric measurements and generally showed compatibility of 2‰ or better (Hammer et al., 2017; Miller et al., 2013), in addition to intercomparison activities using wood cellulose and other materials (e.g., Scott et al., 2010).

In this paper, we review the observed changes in the ¹³C and ¹⁴C isotopic composition of atmospheric CO₂ (δ¹³CO₂ and Δ¹⁴CO₂) over the Industrial Period and the processes driving these changes. We review key applications for atmospheric δ¹³CO₂ and Δ¹⁴CO₂ observations from the literature, with an emphasis on global or large‐scale processes. Then we present new simulations of future changes in atmospheric δ¹³CO₂ and Δ¹⁴CO₂ corresponding to future emission scenarios through 2100. We discuss the impacts of these future changes on applications for atmospheric δ¹³CO₂ and Δ¹⁴CO₂ observations and make recommendations for observational and modeling activities for δ¹³C and Δ¹⁴C.

2. The ¹⁴C and ¹³C Suess Effects

The onset of the Industrial Revolution initiated extensive fossil fuel burning that introduced carbon previously stored in geological reservoirs into the atmosphere. Fossil fuels are completely devoid of ¹⁴C because they have been stored in geological reservoirs for millions of years, much longer than the ¹⁴C half‐life of 5,700 years. This gives fossil fuels a Δ¹⁴C signature of −1,000‰. For ¹³C, the carbon in fossil fuels has an isotopic signature (δ¹³C) that ranges from −44‰ to −19‰ (Andres et al., 2000). The δ¹³C in fossil fuels is lower than the δ¹³C in atmospheric CO₂ (−8.5‰ to −4‰ from the present through the past 65 million years, Graven et al., 2017; Tipple et al., 2010) because fossil fuel carbon originates from plant materials and the photosynthesis process discriminates against ¹³C. There are also geological processes causing further discrimination against ¹³C for some fossil fuels. There is no fractionation during combustion if combustion is complete, but carbonization can produce fractionation (Turney et al., 2006).

As fossil fuels are slightly depleted in ¹³C and entirely depleted in ¹⁴C, the burning of fossil fuels increases ¹²CO₂ at a faster relative rate than ¹³CO₂ and ¹⁴CO₂. This dilution effect, which drives δ¹³C and Δ¹⁴C downward, is termed “The Suess Effect.” In 1955, Hans Suess published the first observations of ¹⁴C dilution using tree ring records of atmospheric CO₂ (Suess, 1955). The “Suess Effect” terminology was also later applied to ¹³C, as the dilution process is similar (Keeling, 1979). Importantly, the decreases observed in atmospheric δ¹³CO₂ and Δ¹⁴CO₂ are governed not only by the amount of fossil fuels burnt but also by other human activities and by natural carbon cycle exchanges and their response to changes in atmospheric composition and climate.

Cement manufacturing also involves “fossil” carbon in that the source material is geological and therefore free of any ¹⁴C. The source material is carbonate rock, which has a δ¹³C of approximately 0‰. The amount of CO₂ produced by cement manufacturing is only a few percent of the CO₂ produced by fossil fuel burning. The global average δ¹³C for all fossil fuel combustion and cement production has been −28‰ to −24‰ (Andres et al., 2016). It has shifted toward more negative values in recent years as the share of combustion from natural gas (δ¹³C ~ −44‰) increases while coal (δ¹³C ~ −24‰) decreases.

Land use changes represent another influence on the carbon cycle from human activities. Land use can have various effects that could impact δ¹³CO₂ and Δ¹⁴CO₂: net transfer of carbon from the biosphere to the atmosphere (or vice versa), changes to the average ¹³C discrimination and its spatial pattern through changes in plant type such as the conversion of forest to pasture, and changes in the residence time of carbon in the biosphere. Overall, land use appears to have had small effects on global mean δ¹³CO₂ and Δ¹⁴CO₂ over the Industrial Period, in part because of responses of natural biospheric and ocean fluxes that compensate for land use effects on δ¹³CO₂ and Δ¹⁴CO₂. However, land use effects could be important regionally and for some applications (Scholze et al., 2008).

3. The Nuclear Bomb Effect for ¹⁴C

In the 1950s and 1960s, nuclear weapons testing produced ¹⁴C in the atmosphere, strongly enriching ¹⁴C and counteracting the Suess Effect. This effect was termed the “Atom Bomb Effect” when first reported by Rafter and Fergusson (1957); we refer to it as the “Nuclear Bomb Effect.” The process for ¹⁴C production was similar to the natural production of ¹⁴C in the atmosphere: Neutrons produced by the hydrogen bomb explosions react with atmospheric nitrogen to produce ¹⁴C. Most of the nuclear explosions and ¹⁴C production took place in the Northern Hemisphere, and most tests and particularly the largest tests occurred shortly before the Partial Test Ban Treaty came into effect in 1963 (Naegler & Levin, 2006).

There is an ongoing production of ¹⁴C by the nuclear industry at nuclear power plants, with the ¹⁴C production varying by type of reactor. The amount of ¹⁴C produced by the nuclear industry and released to the atmosphere is only about 10% of the natural production of ¹⁴C (Graven & Gruber, 2011), so the effects on Δ¹⁴CO₂ are much smaller than the effects from the nuclear weapons testing, which, in contrast, exceeded the rate of natural production by 2 orders of magnitude (Naegler & Levin, 2006). Nuclear power plant emissions ramped up between the 1970s and 1990s as the nuclear industry expanded, but they appear to have recently started to fall (Zazzeri et al., 2018).

4. Natural Carbon Cycle Response to the Suess and Nuclear Bomb Effects

By perturbing the isotopic composition of atmospheric CO₂, the Suess and Nuclear Bomb Effects have also affected all the other carbon reservoirs in the ocean and on land that exchange with atmospheric CO₂ on decadal to centennial timescales (Figures 1 and 2). These exchanges between the atmosphere and other carbon reservoirs have modulated the changes to atmospheric CO₂, effectively mixing the anthropogenic emissions into a larger carbon pool that encompasses atmospheric CO₂ and land and ocean carbon with residence times of about a century or less.

Figure 1.

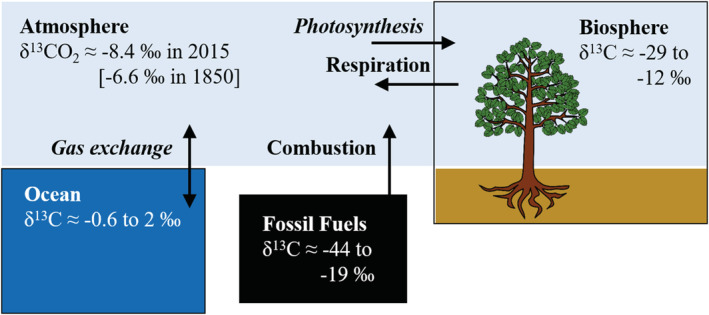
Diagram of ¹³C in the global carbon cycle showing the pools interacting with atmospheric CO₂ on the timescale of the Industrial Period. Typical ranges of δ¹³C are shown for each of the pools (Andres et al., 2000; Bowling et al., 2008; Graven et al., 2017; Olsen et al., 2019). Global average δ¹³CO₂ was −8.4‰ in 2015 and −6.6‰ in 1850. Processes involving significant fractionation are shown in italics; processes without significant fractionation are shown in normal text.

Figure 2.

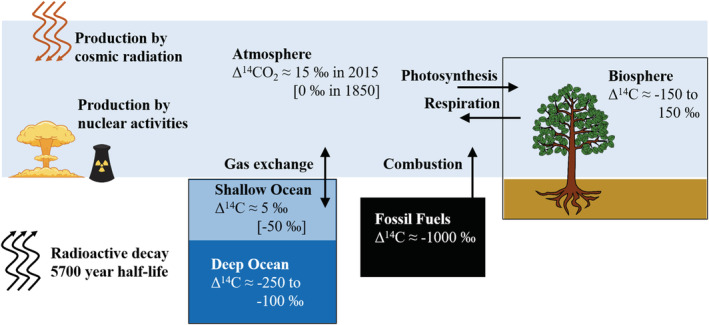
Diagram of ¹⁴C in the global carbon cycle showing the pools interacting with atmospheric CO₂ on the timescale of the Industrial Period. Typical ranges of Δ¹⁴C are shown for each of the pools. Global average Δ¹⁴CO₂ was approximately 15‰ in 2015 and 0‰ in 1850, whereas Δ¹⁴CO₂ in the troposphere was much higher in 1964–1965, 600‰ to 1,000‰ (Figure 3). In the shallow ocean, average Δ¹⁴C was approximately 5‰ in 2015 and −50‰ in 1850. Production of ¹⁴C occurs naturally through cosmic radiation and anthropogenically through nuclear activities. All ¹⁴C undergoes radioactive decay with a half‐life of 5,700 years.

On land, the CO₂ taken up by photosynthesis carries the stable isotopic signature of atmospheric CO₂, modified by fractionation during photosynthesis (Figure 1). Photosynthetic fractionation, also called discrimination, varies by plant type. Most trees are C₃ plants that discriminate more than C₄ plants like grasses, with the δ¹³C of the fixed carbon approximately 18‰ lower in C₃ and 4‰ lower in C₄ plants than in atmospheric CO₂. The CO₂ returned to the atmosphere by respiration carries the isotopic signature of the organic material being respired, which can have a range of ages. Fractionation does not occur during respiration (Lin & Ehleringer, 1997), although there can be differences in δ¹³C between different plant and soil compounds or gradients within plants that can lead to variation in δ¹³C of respiration (Bowling et al., 2008).

Similarly, the CO₂ entering the ocean through air‐sea exchange carries the stable isotopic signature of atmospheric CO₂, modified by fractionation during gas transfer (Figure 2). The CO₂ exiting the ocean carries the isotopic signature of dissolved inorganic carbon (DIC) at the surface, modified by fractionation during gas transfer. Fractionation during gas transfer includes both kinetic and equilibrium effects (Zhang et al., 1995) and results in ocean DIC being ¹³C‐enriched compared to atmospheric δ¹³CO₂. The δ¹³C of ocean waters are also influenced by marine ecosystems such that the net photosynthesis in the surface ocean and net respiration at depth cause δ¹³C to generally decrease with depth (Eide et al., 2017).

The gross fluxes to the atmosphere from the terrestrial biosphere and the ocean, and vice versa, also carry the radiocarbon signature of the respective pool. Because of the fractionation correction used in the Δ¹⁴C notation, the processes involving fractionation do not alter the Δ¹⁴C signature of the carbon leaving one pool and entering another. Differences in the Δ¹⁴C signature of different pools are caused by natural or anthropogenic ¹⁴C production and by radioactive decay. Before the Suess and Nuclear Bomb Effects, Δ¹⁴C in terrestrial and oceanic pools was lower than atmospheric Δ¹⁴C because of radioactive decay, depending on how long the carbon was isolated from the atmosphere. The Δ¹⁴C in new leaves would be nearly the same as atmospheric Δ¹⁴C, whereas the Δ¹⁴C in the deep ocean or in aged soils would be much lower.

The decline in atmospheric δ¹³CO₂ since the Industrial Revolution has resulted in the CO₂ taken up by photosynthesis being lighter than CO₂ returned to the atmosphere by respiration. Similarly, the CO₂ taken up by the ocean is lighter than the CO₂ returned to the atmosphere. Therefore, the net land exchange and net ocean exchange are causing a net flux of ¹³C from the terrestrial biosphere to the atmosphere and from the ocean to the atmosphere that partly counteracts the decline in atmospheric δ¹³CO₂. These are referred to as “disequilibrium fluxes.” In addition, the discrimination against ¹³C that occurs during photosynthesis may be increasing over time (Keeling et al., 2017; Schubert & Jahren, 2012), causing even less ¹³C to be removed by photosynthesis. Discrimination is increasing because of the impact of rising atmospheric CO₂ concentration on photorespiration and mesophyll processes. Individual plants and ecosystems may have also experienced changes in δ¹³C due to variation or trends in climate that influence the strength of ¹³C discrimination. Air‐sea exchange of ¹³C is also influenced by ocean temperature, wind speed, and biological productivity. Changes in these properties may have also caused small influences on the atmospheric δ¹³CO₂ trend over the Industrial Period (Keeling et al., 2017).

The Suess Effect has a similar effect on ¹⁴C, such that decreases in atmospheric Δ¹⁴CO₂ lead to net effluxes of ¹⁴C from the land biosphere and the ocean that partly counteract the decrease in atmospheric Δ¹⁴CO₂ (Stuiver & Quay, 1981). The nuclear weapons tests had the opposite effect. The Nuclear Bomb Effect caused the atmosphere to become highly enriched in ¹⁴C and land and ocean exchanges acted to remove ¹⁴C and decrease Δ¹⁴CO₂ (Levin & Hesshaimer, 2000). Now that several decades have passed since the bomb testing ended, the land and ocean exchanges of ¹⁴C have become more complex. There are both positive and negative influences on Δ¹⁴CO₂. Reservoirs where the carbon is stored for a matter of years quickly became more enriched in ¹⁴C following the atmosphere, but with a lag. Now, as atmospheric Δ¹⁴C is falling, the Δ¹⁴C of these reservoirs is again falling behind the atmosphere trend. These reservoirs, which include carbon in terrestrial vegetation and in the surface waters of subtropical ocean gyres, are now positive influences on Δ¹⁴CO₂, releasing ¹⁴C back to the air (Graven, Gruber, et al., 2012; Randerson, Collatz, et al., 2002). Reservoirs that exchange with the atmosphere on longer timescales, such as the carbon in the surface water of the Southern Ocean, remain lower in Δ¹⁴C and continue to be a negative influence on Δ¹⁴CO₂ today (Graven, Gruber, et al., 2012).

In the simple diagrams in Figures 1 and 2, and in the simple carbon cycle model we present later, we have omitted the conduit of terrestrial carbon to the ocean via rivers, which comprises 0.4 to 0.8 PgC year⁻¹ (Resplandy et al., 2018). The impacts of rivers on atmospheric δ¹³CO₂ and Δ¹⁴CO₂ are likely to be small overall, since the riverine flux is much smaller than the gross fluxes between atmospheric CO₂ and the terrestrial biosphere and ocean, but the carbon in rivers will respond to atmospheric δ¹³CO₂ and Δ¹⁴CO₂ and changing environmental conditions that affect terrestrial and riverine carbon cycling. Radiocarbon measurements have revealed differences in the age of dissolved and particulate organic carbon in rivers that help to identify their sources (Marwick et al., 2015). There is also evidence that land use has altered the age of the terrestrial carbon exported to the ocean, where deforestation increases the transport of aged soil organic carbon in rivers and its subsequent remineralization (Drake et al., 2019).

5. Atmospheric Changes Over the Industrial Period

The changes in atmospheric δ¹³CO₂ and Δ¹⁴CO₂ over the Industrial Period have been quantified using a combination of direct sampling of the atmosphere and records of atmospheric composition from tree rings, ice cores, and firn. Regular observations of δ¹³CO₂ and Δ¹⁴CO₂ have been made by direct measurements of air samples since the 1970s for δ¹³CO₂ (Allison & Francey, 2007; Keeling et al., 2005; Vaughn et al., 2010) and the 1950s for Δ¹⁴CO₂ (Levin et al., 2010; Turnbull et al., 2016). Records of δ¹³CO₂ and Δ¹⁴CO₂ prior to direct measurements have been constructed using measurements of air in ice cores and firn for δ¹³CO₂ (Rubino et al., 2013) and tree ring cellulose and other materials for Δ¹⁴CO₂ (Hogg et al., 2013; Reimer et al., 2013).

Recently, various records have been compiled and harmonized to provide a consistent record of global δ¹³CO₂ and Δ¹⁴CO₂ changes over the Industrial Period, 1850–2015 (Graven et al., 2017) (Figure 3). These compiled records provide annual averages for global δ¹³CO₂ and for Δ¹⁴CO₂ in three zonal bands.

Figure 3.

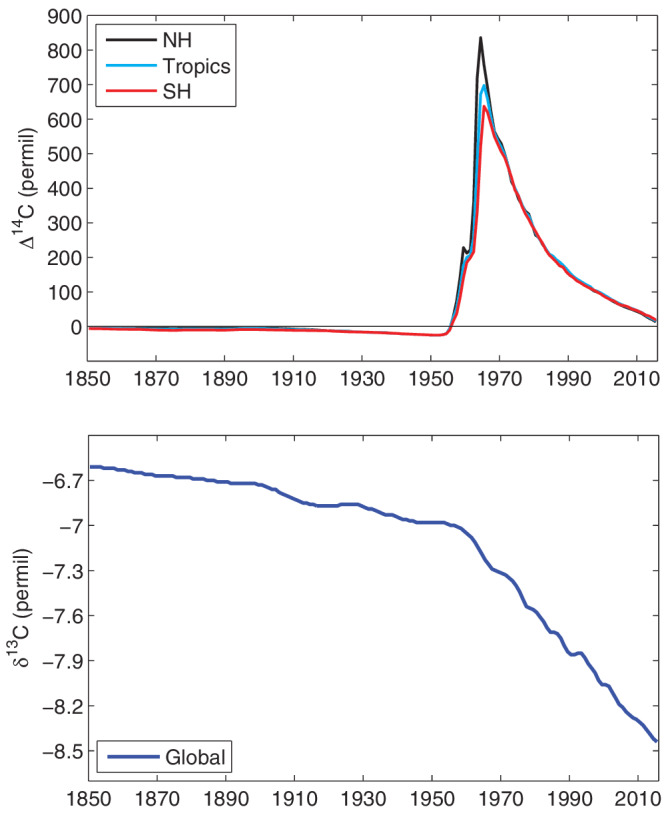
Compiled historical data sets for Δ¹⁴CO₂ (top) and δ¹³CO₂ (bottom) from Graven et al. (2017). Annual mean values of Δ¹⁴C are provided for three zonal bands representing the Northern Hemisphere (30–90°N), the Tropics (30°S to 30°N), and the Southern Hemisphere (30–90°S). Annual mean, global mean values are provided for δ¹³C.

From 1850 to 2015 atmospheric δ¹³CO₂ decreased by 1.8‰, with 1.5% of this drop occurring since 1950 (Figure 3) (Graven et al., 2017; Rubino et al., 2013). The Graven et al. (2017) compilation shows a smaller change in δ¹³CO₂ over the Industrial Period, 1850 to 2015, than in previous estimates. Measurements of δ¹³CO₂ reported by Bauska et al. (2015) and Friedli et al. (1986) between 1850 and 1950 are approximately 0.05‰ and 0.12‰ higher, respectively, than in Graven et al. (2017) so that when combined with recent flask data the change since 1850 appears larger. The difference arises from the methods to convert calcite ¹³C standards into CO₂ and implement the VPDB scale at individual laboratories (Brand et al., 2009). Laboratory offsets can be larger than 0.1‰, much larger than the compatibility goal of ±0.01‰ (WMO/IAEA, 2003, 2018). We expect the data reported by Graven et al. (2017) to be the most robust estimate available of the δ¹³CO₂ change since 1850 because they ensured that the data from both periods were from the same laboratory (CSIRO), while also incorporating recent flask data from other laboratories by quantifying laboratory offsets. Ongoing activities to distribute reference materials of pure CO₂ or CO₂ in whole air show promise for improving measurement compatibility (Wendeberg et al., 2013; WMO/IAEA, 2018).

Atmospheric Δ¹⁴CO₂ decreased by approximately 20‰ between 1850 and 1950 as a result of fossil fuel emissions after the Industrial Revolution (Suess, 1955) (Figure 3). Then Δ¹⁴CO₂ rose rapidly from the mid‐1950s until the mid‐1960s during the period of intense nuclear weapons testing (Rafter & Fergusson, 1957). Tropospheric Δ¹⁴CO₂ reached its highest level in 1964–1965, which was 835‰ in the Northern Hemisphere annual average (Figure 3). After the peak in 1964–1965, Δ¹⁴CO₂ decreased at a nearly exponential rate as the “bomb ¹⁴C” mixed into the ocean and terrestrial biosphere. Initially, large gradients were observed between the Northern and Southern Hemispheres because most of the bomb tests occurred in the Northern Hemisphere (Figure 3) (Nydal & Lövseth, 1983). The large interhemispheric gradients in the atmosphere weakened after a few years through atmospheric mixing. Since the 1990s the decrease of Δ¹⁴CO₂ has been almost linear at about 5‰ year⁻¹, now driven primarily by fossil fuel emissions (Graven et al., 2012b; Levin et al., 2010). The interhemispheric gradient has switched sign: Now Δ¹⁴CO₂ in the Northern Hemisphere is about 5‰ lower than in the Southern Hemisphere. Both the Δ¹⁴CO₂ trend and the interhemispheric gradient are weaker than expected from fossil fuel emissions alone because of the combined influence on Δ¹⁴CO₂ from carbon exchanges with the ocean and land biosphere and by natural ¹⁴C production and ¹⁴C emissions from nuclear power plants.

How would atmospheric Δ¹⁴CO₂ have evolved in response to the Suess Effect, if there had been no bomb tests? And how would the Nuclear Bomb Effect have evolved in the absence of fossil fuel emissions? To demonstrate the different effects of fossil fuel emissions and nuclear weapons testing on Δ¹⁴CO₂, we conducted simulations with a simple carbon cycle model under two hypothetical scenarios (Figure 4). One is a scenario with nuclear weapons testing, but without fossil fuel emissions. The other scenario includes fossil fuel emissions, but no nuclear weapons testing. Details of the simulations are given in Supporting Information Text S1.

Figure 4.

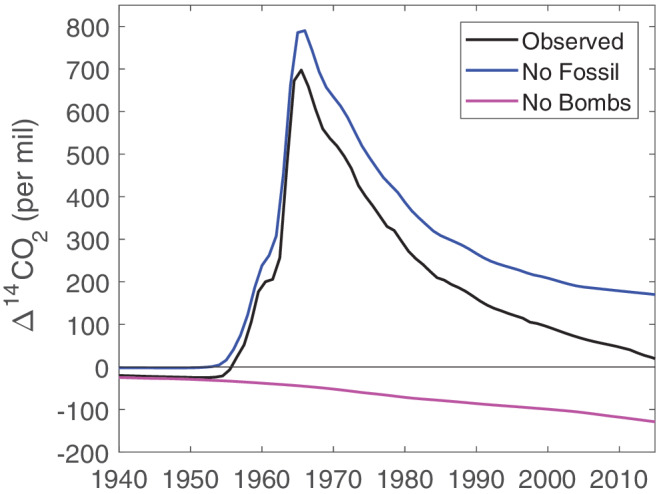
Observed Δ¹⁴CO₂ and simulated Δ¹⁴CO₂ for scenarios without nuclear weapons tests (“No Bombs”) or without fossil fuel burning (“No Fossil”).

Under the scenario without fossil fuel emissions, global atmospheric Δ¹⁴CO₂ peaks at a higher level of 790‰ (compared to the observed value in the tropics in 1965 of approximately 700‰) because, in this case, the bomb‐derived ¹⁴C is mixed into a lower concentration of atmospheric CO₂ (Figure 4). After the peak in Δ¹⁴CO₂, it exponentially declines in a similar way to that observed until around 1990. Then the simulated Δ¹⁴CO₂ decline slows, whereas the observed Δ¹⁴CO₂ decline continues at a nearly steady rate after 1990. This divergence of the simulated and observed Δ¹⁴CO₂ shows how the importance of the Suess Effect has strengthened in the past few decades (Graven et al., 2012b; Levin et al., 2010). Without fossil fuel emissions, Δ¹⁴CO₂ would have been about 150‰ higher than observed in 2015.

Under the scenario without nuclear weapons testing, atmospheric Δ¹⁴CO₂ decreases throughout the period 1850 to 2015, reaching −130‰ in 2015 (Figure 4). Without the addition of ¹⁴C from the weapons tests, the Suess Effect would have reduced Δ¹⁴CO₂ substantially below preindustrial levels by now.

6. Applications of Atmospheric ¹³CO₂ Measurements

Observations of atmospheric δ¹³CO₂ have been used in many applications to investigate carbon fluxes and the functioning of plants. A major application has been the so‐called “double deconvolution” on historical CO₂ and δ¹³CO₂ data to partition CO₂ uptake by the ocean versus the terrestrial biosphere (Keeling et al., 1989). These studies use mass balance equations and model simulations that account for fractionation and changing disequilibrium fluxes. The double deconvolution method has been used with direct atmospheric measurements to attribute interannual variations in CO₂ growth rate to land and ocean sources, concluding that El Niño events are associated with an anomalous terrestrial source of CO₂ (Keeling et al., 1995). The double deconvolution method has also been used with ice core and firn data to investigate centennial‐ to millennial‐scale variations associated with climate variability, indicating that the terrestrial response to temperature is generally stronger than the ocean's response (Trudinger et al., 1999). The double deconvolution suggested that the low CO₂ growth rate in the 1940s was driven by the ocean (Trudinger et al., 2002), although this conclusion remains controversial (Bastos et al., 2016; Rafelski et al., 2009).

Atmospheric inversions have been used to estimate spatially resolved fluxes of carbon and ¹³C based on atmospheric data and models. These operate similarly to the double deconvolution. The first study employed a two‐dimensional atmospheric model and helped to identify the “missing sink” of carbon in the land biosphere and particularly in the Northern Hemisphere (Ciais et al., 1995). Subsequent three‐dimensional studies indicated that land and ocean CO₂ sinks were comparable in magnitude and that CO₂ uptake increased in the Northern Hemisphere after the Pinatubo eruption in 1991, in addition to the interannual variability related to El Niño (Enting et al., 1995; Rayner et al., 1999). A shortcoming of these studies was that variability in plant ¹³C discrimination was not considered. In reality, plant ¹³C discrimination and CO₂ uptake are expected to be correlated, for example, because drought will reduce both productivity and discrimination as plants close their stomata to minimize water loss (Randerson, Enting et al., 2002). Expanding the methodology to estimate discrimination as part of the inversion, Peters et al. (2018) estimated variations in water use efficiency on continental scales and showed that global models underestimated the drought response of plants.

The potential for long‐term trends in plant discrimination had also been neglected in global studies using the double deconvolution. Using historical δ¹³CO₂ data with a simple carbon cycle model, Keeling et al. (2017) found that ¹³C discrimination is likely to have strengthened by 0.7‰ between 1975 and 2005, which is consistent with a dependence on CO₂ concentration that has been found in laboratory and paleo studies and attributed to mesophyll and photorespiration effects (Schubert & Jahren, 2012). Keeling et al. (2017) further argue that the past double deconvolution studies have neglected a mechanistic link between land and ocean isotopic fluxes that means long‐term δ¹³CO₂ data actually do not provide a strong constraint on land and ocean CO₂ sinks. For example, changing the ocean diffusivity in a simple model changes the ocean CO₂ uptake and ¹³C flux, but it creates compensating changes in the ¹³C flux to the land via the residual CO₂ flux needed to maintain mass balance. Therefore, ocean diffusivity (which governs ocean CO₂ uptake) does not have a strong influence on the long‐term δ¹³CO₂ trend.

Atmospheric δ¹³CO₂ measurements are commonly used to investigate terrestrial biosphere activity on local or regional scales by estimating isotopic signatures of photosynthesis or respiration using the “Keeling Plot” approach. The “Keeling Plot” (Keeling, 1958), or alternative formulations such as the “Miller‐Tans Plot” (Miller & Tans, 2003), quantifies the isotopic signature of a CO₂ source or sink by manipulating the CO₂ and ¹³CO₂ mass balance equations so that the isotopic signature is given by the intercept or slope of a regression fit. These studies have revealed a strong link between isotopic fluxes and water availability (Pataki et al., 2003). They have helped to explain the driving factors of water use efficiency by plants, a metric for the amount of productivity per unit water loss, and how these factors affect spatial and temporal patterns of water use efficiency (Bowling et al., 2002). These studies typically sample air in flasks that are subsequently analyzed for δ¹³CO₂ by mass spectrometry in the laboratory, but now optical instruments that measure ¹³CO₂ are increasingly used in the field. These instruments have also enabled eddy covariance measurements of ¹³CO₂ fluxes, uncovering the suppression of daytime respiration (Wehr et al., 2016).

Other studies have measured δ¹³CO₂ in urban areas to investigate fossil fuel emissions. In combination with other tracers such as Δ¹⁴CO₂ or δ¹⁸O of CO₂, δ¹³CO₂ measurements have been useful for determining the proportion of natural gas versus petroleum contributions to fossil fuel CO₂ emissions in urban areas (Newman et al., 2016; Pataki et al., 2007).

Measurements of atmospheric δ¹³CO₂ are also critical to other studies that do not interpret the measurements directly but rather use them for comparison with δ¹³C measured in other materials. In terrestrial ecology, atmospheric δ¹³CO₂ is compared to δ¹³C in tree rings or leaves to investigate spatial patterns and temporal variation in the internal leaf CO₂ concentration and thereby, the response of plant productivity to climate, atmospheric CO₂, and other variables (Frank et al., 2015; Wang et al., 2017). Measurements of δ¹³C in DIC in the ocean have been compared with atmospheric δ¹³CO₂ to estimate anthropogenic CO₂ uptake (Gruber & Keeling, 2001; Quay et al., 2003). Comparisons with atmospheric δ¹³CO₂ are also used in ecological studies of the diet, trophic structure, physiology, and local environment of animals (DeNiro & Epstein, 1978).

7. Applications of Atmospheric ¹⁴CO₂ Measurements

Observations of atmospheric Δ¹⁴CO₂ have been used in many applications to investigate the global carbon cycle (Levin & Hesshaimer, 2000). The Suess (1955) measurement of industrial‐era Δ¹⁴CO₂ via tree ring records comprised some of the first evidence of the strong impact of fossil fuel burning on atmospheric CO₂, predating the start of C. D. Keeling's long‐term CO₂ concentration measurements (Keeling, 1960). The first direct measurements of atmospheric Δ¹⁴CO₂ were made around the same time as the nuclear weapons tests, revealing large spatial gradients caused by the location of the nuclear tests. These observations were used to investigate atmospheric mixing and showed that the interhemispheric exchange time in the troposphere is about 1 year and the mixing between the stratosphere and troposphere has a seasonal variation (Lal & Rama, 1966; Nydal, 1966).

Other studies have investigated ocean or terrestrial biosphere CO₂ fluxes using Δ¹⁴CO₂ measurements. By using Δ¹⁴CO₂ measurements and carbon cycle models to construct an inventory of bomb‐derived ¹⁴C in each of the main carbon reservoirs, Hesshaimer et al. (1994) showed that previous estimates of the ocean ¹⁴C inventory (Broecker et al., 1985) had been too high. This implied that the depth to which bomb‐derived ¹⁴C had penetrated into the ocean and the amount of CO₂ that had been taken up were also overestimated. Several other studies have used oceanic measurements of Δ¹⁴C in DIC to estimate the air‐sea gas exchange velocity (Naegler et al., 2006; Sweeney et al., 2007; Wanninkhof, 2014). Changes in ocean circulation that impact the air‐sea exchange of ¹⁴C have been inferred from Δ¹⁴CO₂ measured on timescales of interannual, El Niño events (Rozanski et al., 1995) and timescales of decades to centuries (Rodgers et al., 2011). The magnitude of net primary production in the terrestrial biosphere has also been estimated (Naegler & Levin, 2009) using Δ¹⁴CO₂ measurements and carbon cycle models to construct an inventory of bomb‐derived ¹⁴C, in a similar approach to Hesshaimer et al. (1994). A few studies have also considered the effect of biospheric carbon fluxes on atmospheric Δ¹⁴CO₂ measurements. Signatures of elevated Δ¹⁴C in respiration were postulated for seasonal cycles of Δ¹⁴CO₂ in North America (LaFranchi et al., 2016) and for the large‐scale meridional gradients of Δ¹⁴CO₂ (Levin & Hesshaimer, 2000).

A major and growing application for atmospheric Δ¹⁴CO₂ measurements is the calculation of local CO₂ added by fossil fuel combustion (ffCO₂). Evidence for a regional Suess Effect had already appeared in comparisons of tree ring data (Tans et al., 1979). Then I. Levin developed the methodology for the calculation of ffCO₂ with atmospheric observations in Europe in the 1980s (Levin et al., 1989). The method attributes regional gradients in Δ¹⁴CO₂ to fossil fuel emissions, while accounting for other regional influences on Δ¹⁴CO₂ from heterotrophic respiration and nuclear power plants (β) (Turnbull et al., 2006):

$$\mathrm{ffC}{\mathrm{O}}_2=C_m\frac{\mathrm{\Delta }\mathit{bg}-\mathrm{\Delta }m}{\mathrm{\Delta }\mathit{bg}+\mathrm{1,000}‰}+\beta$$ (1)

Here C _m is the measured CO₂ concentration, Δm is the measured Δ¹⁴CO₂, and Δbg is the Δ¹⁴CO₂ at a “background” site that is upwind of the region of interest. β represents a correction for nonfossil fuel influences on Δ¹⁴CO₂, which could include heterotrophic respiration or ¹⁴C emissions from nuclear power plants. I. Levin and colleagues have measured Δ¹⁴CO₂ in the city of Heidelberg since 1986, comparing it to measurements from Jungfraujoch in the Swiss Alps to calculate ffCO₂ (Levin et al., 2003, 2011). Their measurements have shown little change in the ffCO₂ present in Heidelberg, similar to reported trends in local emissions. Observing system simulation experiments have demonstrated that Δ¹⁴CO₂ measurements have a strong potential for improving atmospheric observation‐based estimates of not only regional fossil fuel emissions but also biospheric fluxes (Basu et al., 2016; Fischer et al., 2017). In the state of California, USA, measurements of Δ¹⁴CO₂ from a network of towers were combined with a regional atmospheric transport model in an atmospheric inversion to estimate fossil fuel emissions, finding that reported emissions were consistent with Δ¹⁴CO₂ observations (Graven et al., 2018). In an atmospheric inversion applied to Δ¹⁴CO₂ measurements across North America, estimated emissions for the entire United States were consistent with those officially reported but significantly higher than some other commonly used fossil fuel emissions data products (Basu et al., 2020). Some other studies have combined Δ¹⁴CO₂ measurements with CO, a combustion product that can be measured continuously (Turnbull et al., 2015; Vogel et al., 2010).

Applications making use of Δ¹⁴CO₂ measurements for comparison with Δ¹⁴C in other materials are much more numerous than for δ¹³CO₂, and they span a broad range of fields including archaeology, physiology, and forensics (Bronk Ramsey, 2008; Geyh, 2001; Spalding et al., 2005). Within carbon cycle science, Δ¹⁴C measurements are widely used in ecology and soil science to determine the residence time of carbon in different compound classes (Trumbore, 2000).

Some applications combine δ¹³C and Δ¹⁴C to draw more powerful inferences from the combination that was possible with either alone. For example, Keeling et al. (2017) showed that atmospheric δ¹³CO₂ trends could not be matched by a carbon cycle model constrained by radiocarbon data, unless changes in ¹³C discrimination during photosynthesis were included in the model. Krakauer et al. (2006) analyzed spatial patterns in both atmospheric Δ¹⁴CO₂ and δ¹³CO₂ to investigate the air‐sea gas exchange velocity.

8. Projected Future Changes in δ¹³CO₂ and Δ¹⁴CO₂

In the future, atmospheric δ¹³CO₂ and Δ¹⁴CO₂ will continue to evolve in response to fossil fuel emissions and other human activities, and the carbon cycle responses to them. Future simulations of Δ¹⁴CO₂ were first presented by Caldeira et al. (1998) for the IS92a “business‐as‐usual” emission scenario from the first IPCC Assessment Report. They showed that increasing fossil fuel emissions cause Δ¹⁴CO₂ to decrease to lower than −150‰ in 2100. While Δ¹⁴CO₂ decreases strongly, the number of atoms of ¹⁴C in the atmosphere actually increases due to a large efflux of ¹⁴C from the ocean to the atmosphere in response to the changing air‐sea disequilibrium. Graven (2015) ran similar simulations using the Representative Concentration Pathways from the fifth IPCC Report considering not just business‐as‐usual but a range of future scenarios (Meinshausen et al., 2011). She found a range of possible paths for Δ¹⁴CO₂ through this century, with the high fossil fuel emission scenario dropping to less than −230‰ in 2100 but a mitigation scenario in line with limiting global warming below 2°C dropping to about −20‰ in the 2030s and then remaining nearly steady. She made important inferences about the impacts of these different scenarios. The high fossil fuel emission scenario creates ambiguity in the use of radiocarbon dating because at some point during the century “new” materials would have the same radiocarbon age as materials that are up to 2,000 years old, with impacts on archaeology and forgery detection. In contrast, scenarios where Δ¹⁴CO₂ stops decreasing imply that applications in ecology, forensics, and physiology that make use of the Δ¹⁴CO₂ trend as a shorter‐term clock would no longer be viable.

The first simulations of future δ¹³CO₂ were presented by Köhler (2016) using the Representative Concentration Pathways. They showed continued declines in δ¹³CO₂ as fossil fuel emissions grow in high‐emission scenarios, but reversals of δ¹³CO₂ trends for low‐emission scenarios. There was a range of about 5‰ between the high fossil fuel emission and mitigation scenarios in 2100, with the most stringent mitigation scenario reaching a minimum around midcentury and then increasing by several per mil.

The future scenarios being considered for the sixth IPCC Report by the Coupled Model Intercomparison Project (CMIP) are now based on a set of five narratives, called the shared socioeconomic pathways (SSPs) (O'Neill et al., 2014). Scenarios ranging from worlds without climate action to very stringent mitigation scenarios in line with limiting global warming to 1.5°C have been explored for each of these narratives (Riahi et al., 2017; Rogelj et al., 2018). Finally, a selection of SSP‐based scenarios have been identified as the main scenarios to be examined in CMIP6 (O'Neill et al., 2016). The atmospheric CO₂ concentration, fossil fuel emissions, and land use emissions for six of the key SSP‐based scenarios are shown in Figure 5 (Hoesly et al., 2018; Meinshausen et al., 2017). These pathways employ varying amounts of “negative emissions” from deliberate CO₂ removal, and the net fossil fuel emissions including negative emissions are also shown in Figure 5. These SSP‐based scenarios span a larger range of possible future pathways than the RCPs, including a lower‐emission pathway consistent with a maximum end‐of‐century warming of 1.5°C (SSP1‐1.9) as well as a very high emission pathway without controls on greenhouse gas emissions (SSP5‐8.5). There is also an “overshoot” scenario where atmospheric CO₂ concentration rises until midcentury and then decreases rapidly as a result of strong and targeted CO₂ removal activities (SSP5‐3.4os). The process for deliberate CO₂ removal included in the SSP scenarios is Bioenergy with Carbon Capture and Storage (BECCS). In this way, the CO₂ removal is mediated by an initial uptake into the terrestrial biosphere, which has implications for atmospheric δ¹³CO₂ (Köhler, 2016). BECCS acts like an “anti‐Suess Effect,” enriching atmospheric δ¹³CO₂ by preferentially removing ¹²C through photosynthesis and burial of biofuel‐derived CO₂.

Figure 5.

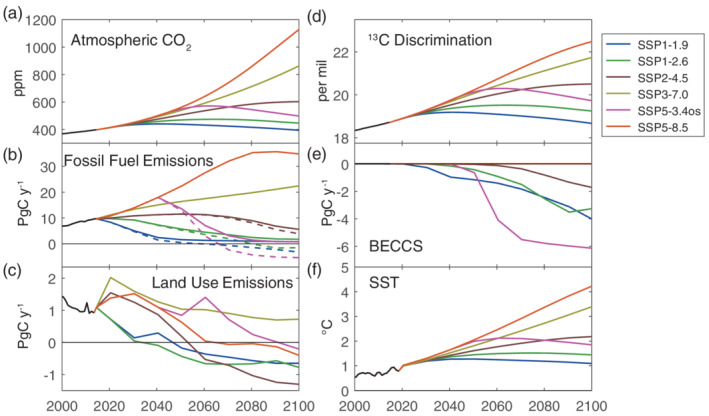
(a) Atmospheric CO₂, (b) fossil fuel emissions, (c) land use emissions, (d) ¹³C discrimination, (e) CO₂ removal by BECCS, and (f) global mean sea surface temperature (SST) used in the future simulations. In (b) the gross fossil fuel emissions are shown with solid lines while dashed lines show net emissions accounting for BECCS. Historical data are shown in black until 2015, and then the six SSP‐based scenario projections are shown for 2015–2100.

We conduct simulations of future atmospheric δ¹³CO₂ and Δ¹⁴CO₂ that consider the change in atmospheric CO₂ concentration, fossil fuel emissions, land use emissions, and BECCS, as well as the response of the carbon cycle to these changes for these six SSP‐based scenarios (Figure 5). In addition, future changes in ¹³C discrimination by land plants are included as a function of atmospheric CO₂ concentration following Schubert and Jahren (2015), and changes in air‐sea fractionation factors are included as a function of sea surface temperature and dissolved carbonate concentration (Orr et al., 2017). Future changes to the δ¹³C in fossil fuel emissions were not included because there was not enough information provided with the SSP‐based scenarios to estimate them. Further details of the future simulations are given in Text S2.

The simulations show that atmospheric Δ¹⁴CO₂ drops below 0‰ within the next few years in all scenarios (Figure 6). In the lowest emission scenario, SSP1‐1.9, where net fossil fuel emissions reach zero around 2050 (Figure 5), Δ¹⁴CO₂ stays around 0‰ for about 10 years and then increases again, remaining at about 10–12‰ for the second half of the century. In this scenario, the effect of a small amount of continued fossil fuel emissions is roughly balanced by other ¹⁴C fluxes. The less ambitious mitigation scenario SSP1‐2.6 reaches a minimum of −38‰ in the 2050s and then rebounds slightly. The simulated Δ¹⁴CO₂ for SSP1‐2.6 is approximately 20‰ lower than the simulated Δ¹⁴CO₂ for RCP2.6 in Graven (2015) due to the different structure of the model biosphere, the different criteria for selecting model parameters, and differences between emissions in SSP1‐2.6 and RCP2.6 (see Text S2).

Figure 6.

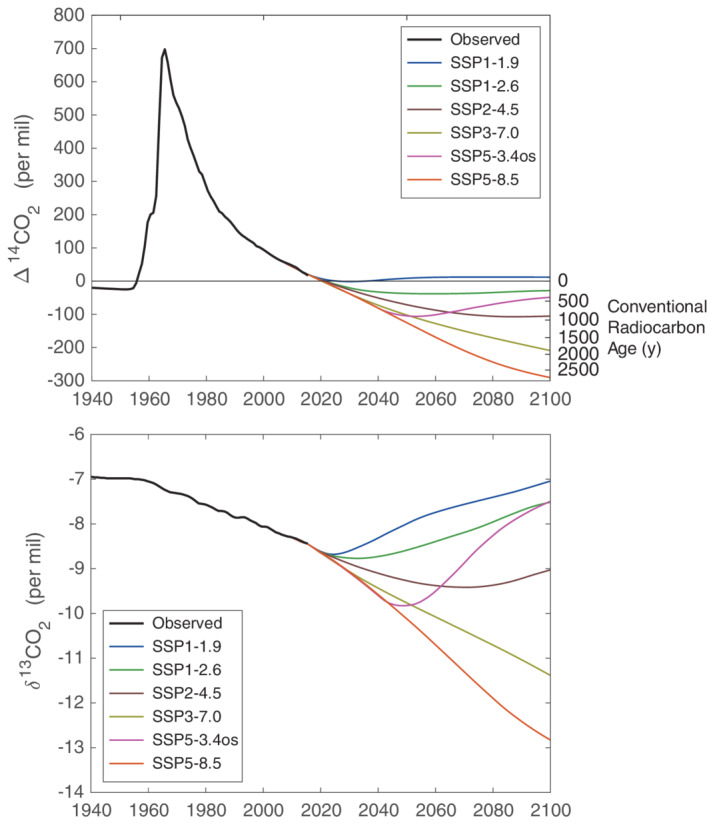
Observed Δ¹⁴CO₂ and δ¹³CO₂ for 1940 to 2015 and simulated Δ¹⁴CO₂ and δ¹³CO₂ for 2015 to 2100 for the six SSP‐based CMIP6 ScenarioMIP scenarios. Colored lines show the midrange values across the 32 sets of parameters used in the simulations. The right axis in the top panel shows the conventional radiocarbon age of a carbon‐containing specimen with the same radiocarbon content, calculated by 8,033 * ln(Δ¹⁴C/1,000‰ + 1).

The scenarios SSP2‐4.5, SSP3‐7.0, and SSP5‐8.5 include the least mitigation of emissions and simulated Δ¹⁴CO₂ declines steadily until late in the century. Atmospheric Δ¹⁴CO₂ reaches −105‰, −209‰, and −290‰ for SSP2‐4.5, SSP3‐7.0, and SSP5‐8.5, respectively. SSP2‐4.5 and SSP3‐7.0 are comparable to RCP4.5 and RCP8.5, which were simulated to reach −80‰ and −254‰ by Graven (2015). In this case the differences in the model structure, calibration, and scenario cause Δ¹⁴CO₂ to be 25‰ lower or 40‰ higher Δ¹⁴CO₂ in 2100. The scenario SSP5‐8.5 has stronger emissions than any of the RCPs and therefore a more negative Δ¹⁴CO₂ in 2100.

In the overshoot scenario SSP5‐3.4os, Δ¹⁴CO₂ is simulated to rebound quickly after 2050 due to the reduction in fossil fuel emissions and the rapid implementation of BECCS. The input of fossil carbon is rapidly reduced, and the removal of lower‐Δ¹⁴C carbon, relative to the carbon in the shallow ocean and terrestrial biosphere, leads to a net efflux of ¹⁴C back to the atmosphere that increases Δ¹⁴CO₂.

Simulated δ¹³CO₂ declines to approximately −8.7‰ in 2025 in all SSP‐based scenarios and then diverges. All scenarios that we explored that reach a peak and then reduce fossil fuel emissions (all but SSP3‐7.0 and SSP5‐8.5) show an inflection in δ¹³CO₂ that is more pronounced than for Δ¹⁴CO₂. In SSP1‐1.9, δ¹³CO₂ is approximately −7‰ in 2100, about the same as it was in 1940. SSP1‐2.6 and SSP5‐3.4os both have δ¹³CO₂ of approximately −7.5‰ in 2100, after a stronger decline and reversal in SSP5‐3.4os compared to SSP1‐2.6. SSP2‐4.5 reaches a minimum of −9.4‰ in 2070 and then returns to −9‰ by 2100. SSP3‐7.0 and SSP5‐8.5 decrease through the century and reach −11.4‰ and −12.8‰, respectively, in 2100.

In Figure 7, we show the individual contributions to the trends in δ¹³CO₂ and Δ¹⁴CO₂ for SSP1‐2.6, SSP5‐3.4os, and SSP5‐8.5. The contributions for SSP1‐1.9, SSP2‐4.5, and SSP3‐7.0 are shown in Figure S1. Over the recent past, 2000–2015, the negative influence of the ocean weakens from about −5‰ year⁻¹ to zero while the negative influence of fossil fuel emissions strengthens slightly. Positive influences from biospheric exchange and from ¹⁴C production by natural cosmogenic radiation and by nuclear power plants have relatively constant positive influences of 3–4‰ year⁻¹ over 2000–2015. Trend contributions of similar magnitudes were found in the early 2000s by Levin et al. (2010) and Graven et al. (2012b).

Figure 7.

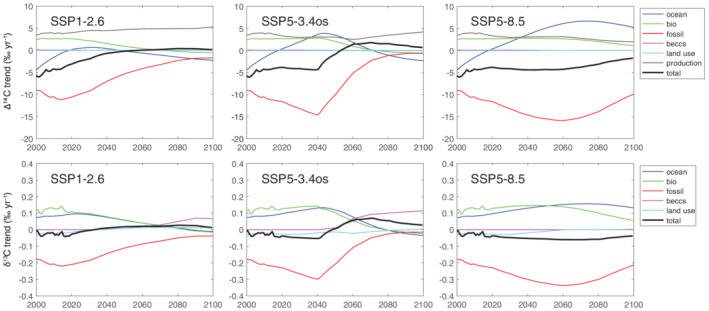
Simulated trend components for Δ¹⁴CO₂ (top row) and δ¹³CO₂ (bottom row) for SSP1‐2.6, SSP5‐3.4os, and SSP5‐8.5. Other SSP‐based scenarios are shown in Figure S1. Colored lines show the midrange values across the 32 sets of parameters used in the simulations. BECCS and land use contributions are uniformly near zero for Δ¹⁴CO₂.

After 2015 the SSP scenarios diverge. The fossil fuel influence weakens in SSP1‐2.6, followed by an inflection in the oceanic and biospheric contributions, which turn negative around midcentury. After this point, the positive influence of ¹⁴C production is approximately balanced by the other influences, and Δ¹⁴CO₂ remains around −30‰ (Figure 6). In these simulations, nuclear power plant ¹⁴C emissions are assumed to stay constant at 2008 values throughout 2100. In reality, these emissions could increase or decrease, depending on the future changes in the nuclear industry. However, nuclear power plant ¹⁴C emissions are only about 10% of natural ¹⁴C production, so their changes are unlikely to have a large impact on these simulations. Even though natural and nuclear power plant ¹⁴C production is constant in the future simulations, its contribution to the Δ¹⁴CO₂ trend varies over time and across different simulations because it depends on the CO₂ concentration in the atmosphere. BECCS and land use have essentially no effect on Δ¹⁴CO₂ in SSP1‐2.6 or in any other SSP‐based scenario assessed here.

For SSP5‐3.4os and SSP5‐8.5, the negative influence of fossil fuel emissions strengthens until 2040 (SSP5‐3.4os) or 2060 (SSP5‐8.5). Over this time, the overall trend in Δ¹⁴CO₂ remains approximately steady at −4‰ year⁻¹, which results from the change in oceanic influence counteracting the strengthening in fossil fuel influence. Other influences remain steady. In 2040, SSP5‐3.4os begins a rapid reduction in fossil fuel emissions (Figure 5). About 10 years later, Δ¹⁴CO₂ starts to increase. The rapid weakening of the fossil fuel influence on Δ¹⁴CO₂ leads to a net positive trend in Δ¹⁴CO₂ starting in the 2050s. This suggests that a rapid decarbonization of the energy system could lead to the first increase in Δ¹⁴CO₂ since the “bomb peak” in 1964–1965. In contrast, the decreasing trend in SSP5‐8.5 remains remarkably steady before weakening in the last few decades of the century. In this scenario, the positive influence of ocean exchange becomes twice as strong as the positive influence of ¹⁴C production. The strong positive influence from the ocean is a major reversal from the preindustrial period when the ocean was the main negative influence counteracting natural ¹⁴C production and from the 20th century period when the ocean was the main sink for bomb ¹⁴C.

In all scenarios, the biospheric influence responds to the change in the atmospheric trend that governs the biospheric disequilibrium. For example, as the Δ¹⁴CO₂ trend slows, the biospheric disequilibrium weakens because Δ¹⁴C of previously assimilated carbon is more similar to present Δ¹⁴CO₂. Sign changes in the Δ¹⁴CO₂ trend lead to sign changes in the biospheric disequilibrium and influence on the Δ¹⁴CO₂ trend. The effect is modulated by the turnover time of carbon in the biosphere, between 36 and 56 years (Text S2, Naegler & Levin, 2009). The oceanic influence responds to changes in the Δ¹⁴CO₂ trend with a longer effective turnover time and with exchanges between many vertical boxes.

For δ¹³CO₂, the positive biospheric and oceanic contributions to the trend nearly balance the negative fossil fuel contribution over 2000–2015. The negative influence from land use is much smaller and similar to the overall trend. In SSP1‐2.6 fossil fuel emissions peak and slowly weaken after 2015, leading to a weaker negative trend in δ¹³CO₂. Interestingly, the fossil fuel emissions in 2030 are not much smaller than 2015, but the overall trend in δ¹³CO₂ is positive. The weakening in the biospheric and oceanic contributions happens more slowly than for the fossil fuel contribution, resulting in an overall positive trend in δ¹³CO₂ despite the continued fossil fuel emissions. This indicates the negative trend in δ¹³CO₂ that has been taken as an indication of the ¹³C Suess Effect is actually dependent not just on the presence of fossil fuel emissions but on the acceleration in fossil fuel emissions or their magnitude. In SSP1‐2.6 the effect of land use switches sign around 2030 but remains small. After 2070, BECCS is the strongest positive contribution to the δ¹³CO₂ trend. The disequilibria in the biosphere and ocean switch sign around 2080 after several decades of increasing δ¹³CO₂.

In SSP5‐3.4os, the patterns are similar to SSP1‐2.6 but more extreme as a result of the rapid drop in fossil fuel emissions and the rapid expansion of BECCS. Between 2040 and 2060, the δ¹³CO₂ trend changes from about −0.05‰ year⁻¹ to more than + 0.05‰ year⁻¹. In SSP5‐8.5, δ¹³CO₂ continues to decrease even after fossil fuel emissions growth stalls in 2080, unlike the other two SSPs where the δ¹³CO₂ trend turned positive after fossil fuel emissions weakened. In SSP5‐8.5, the fossil fuel emissions are large enough that the fossil fuel contribution to the δ¹³CO₂ trend remains dominant.

The simulated future changes in atmospheric δ¹³CO₂ and Δ¹⁴CO₂ span a larger range than previous atmospheric carbon isotope studies (Graven, 2015; Köhler, 2016). This is expected because the SSP‐based scenarios span a larger range in atmospheric CO₂ concentration and fossil fuel emissions than the RCPs. The lowest simulated Δ¹⁴CO₂ in 2100 for SSP5‐8.5 is nearly −300‰ while the highest simulated Δ¹⁴CO₂ in 2100 for SSP1‐1.9 is above 0‰. The range in the RCPs was −250‰ to −20‰ (Graven, 2015). For δ¹³CO₂, the lowest simulated value in 2100 for SSP5‐8.5 is nearly −13‰, while the highest simulated value in 2100 for SSP1‐1.9 is approximately 7‰, similar to what it was in 1950. It is difficult to compare these values with Köhler (2016) because his simulations underestimated δ¹³CO₂ observed over the Industrial Period.

We emphasize that these simulations do not account for all climate change‐related feedbacks to ¹³C and ¹⁴C fluxes. They do account for temperature‐driven changes to solubility and fractionation that affect air‐sea exchanges, but not for other potential changes to ocean or terrestrial biospheric fluxes. For example, Khatiwala et al. (2018) found that simulated changes in ocean circulation affected the air‐sea ¹⁴C fluxes over the 21st century, although these fluxes were still within the range simulated by Graven (2015). Changes to ocean circulation could also affect ¹³C fluxes, and other changes such as wind speed not considered by Khatiwala et al. (2018) could affect both ¹³C and ¹⁴C fluxes through the impact on gas exchange. On land, changes in climate could affect photosynthesis, turnover of biospheric carbon, and permafrost stability with impacts on ¹³C and ¹⁴C fluxes. However, we do expect that the SSP‐driven changes in emissions and atmospheric CO₂ concentration that are included in these simulations will be the dominant influences over this century.

9. Impacts of Predicted Future Changes

The predicted changes in atmospheric δ¹³CO₂ and Δ¹⁴CO₂ have impacts on the way δ¹³CO₂ and Δ¹⁴CO₂ are used in carbon cycle science and other fields. As described in Graven (2015), high‐emission scenarios that cause strong decreases in Δ¹⁴CO₂ provide a continuing atmospheric perturbation that can be tracked to study exchange rates and residence times in different carbon pools. However, these scenarios create problems for applications such as radiocarbon dating because recently produced materials will have the same radiocarbon content as materials produced at some point up to 2,500 years in the past. Figure 6 includes on the right axis the equivalent conventional radiocarbon age. This shows the age of materials with the same ratio of ¹⁴C/C but where the ratio has been reduced because of radioactive decay rather than dilution by fossil carbon. The “age” of the atmosphere in the highest emission scenario is up to 2,500 years in the year 2100, older than for the highest RCP (Graven, 2015). In this scenario, radiocarbon dating would not be able to distinguish newly produced materials from those up to 2,500 years old by the end of this century, and by 2050, radiocarbon dating would give ambiguous results for samples up to nearly 1,500 years old. These periods encompass much of the development of human civilization when radiocarbon dating has been a key tool in archaeology.

Similarly, applications for forgery detection or illegal ivory trading will be affected because newly produced materials will not be so easily distinguished from older ones. Radiocarbon measurements have been used to date the age of ivory (Cerling et al., 2016), with low radiocarbon content below Modern reflecting ivory produced prior to the 1950s that is not subject to legal restrictions or bans. But new ivory will soon also measure below 0‰, eliminating the use of ¹⁴C as a detection tool for illegal ivory. Within carbon cycle science, the high‐emission scenarios reduce the effectiveness of using Δ¹⁴CO₂ to quantify fossil fuel emissions because the sensitivity of Δ¹⁴CO₂ to fossil fuel CO₂ goes down from −2.6‰ ppm⁻¹ presently to −1.6‰ ppm⁻¹ in 2050 for high‐emission scenarios (Graven, 2015). Advances in measurement precision are needed to maintain the detection limit for fossil fuel CO₂, but measurement precision has not improved over the last 10 years.

On the other hand, low‐emission scenarios reduce the impact to these applications above but create different challenges for other applications. Low‐emission scenarios cause Δ¹⁴CO₂ to stabilize in the middle to late 21st century, eliminating the temporal change in Δ¹⁴CO₂ that formed the basis of many applications examining exchange rates and residence times, both in carbon cycle science and other field such as physiology. For example, in physiology the production of different types of cells can be assessed with their radiocarbon content. The age of a person can be matched to the atmospheric “bomb curve” (Figure 3) to determine what the Δ¹⁴C in the cells of interest would be at birth or early in life, and then by comparing the Δ¹⁴C in cells of adults their production rate be estimated (Spalding et al., 2005). If atmospheric Δ¹⁴CO₂ stabilizes, then this application cannot be used because the difference in radiocarbon content of materials produced in different years or decades would drop to very low levels. This type of application is now widely used to examine decadal‐scale carbon turnover in soil science (Trumbore, 2000), and it would be difficult to replace with other methods.

For δ¹³CO₂, the predicted changes also have impacts on applications using atmospheric δ¹³CO₂ measurements. As atmospheric δ¹³CO₂ changes, the disequilibrium between atmospheric CO₂ and the carbon in the terrestrial biosphere and the ocean will also change. Following a low‐emission scenario will result in the atmospheric δ¹³CO₂ trend reversing and the disequilibrium changing sign. For atmospheric inversions interpreting atmospheric δ¹³CO₂, it will be important to accurately estimate the changing disequilibrium flux despite potentially complex changes. Studies of plant activity using tree rings could also be complicated by the reversal of the atmospheric δ¹³CO₂ trend in the low‐emission scenarios, or by the predicted changes in discrimination of several per mil in the high‐emission scenarios (Figure 5). Ocean observations of δ¹³C will also show a more complicated relationship with anthropogenic CO₂ in the low‐emission scenarios, such that it may not be possible to use ocean δ¹³C data to estimate ocean CO₂ uptake as it has been used in the past (Gruber & Keeling, 2001; Quay et al., 2003).

10. Current Status and Future Needs for Observations and Modeling of Carbon Isotopes

Observations of δ¹³C and Δ¹⁴C in atmospheric CO₂ and other carbon reservoirs have enabled important insights on the carbon cycle and on atmospheric and oceanic circulation, as outlined above. The observations from the unique period of the nuclear bomb testing were particularly powerful, and scientific research would have benefitted greatly if an even larger number of observations had been made during that time, across a larger variety of environments, including additional measurements of the atmosphere and ocean as well as the carbon in soils, rivers, and lakes. The geochemist Wally Broecker, who pioneered many radiocarbon applications, used to say, “Instead of publishing papers, we should have just dropped everything and collected samples all over the world.”

Another critical period is now upon us, as Δ¹⁴CO₂ drops below 0‰ and either stabilizes or continues dropping to very low levels. Simulations of future atmospheric changes demonstrate that it is unavoidable that some applications for Δ¹⁴C, and possibly δ¹³C, will become less effective in the future. The specific applications that will be affected depend on the emissions pathway followed. Since the utility of at least some applications is decreasing over time, observations made now will, in general, be more useful than those that will be made in the future. For example, the use of Δ¹⁴C measurements to establish the decadal‐scale turnover of terrestrial carbon pools will disappear in the future if Δ¹⁴CO₂ stabilizes. Therefore, it would be immensely valuable to make concerted, coordinated efforts to conduct more observations of Δ¹⁴C in the Earth System as soon as possible. The sooner we make the observations, the more we will achieve with them.

Currently, observations of atmospheric δ¹³CO₂ and Δ¹⁴CO₂ are conducted by several laboratories operating global or regional networks of stations. Global networks for δ¹³CO₂ are operated by the US National Oceanic and Atmospheric Administration (NOAA), Australia's Commonwealth Scientific and Industrial Research Organisation (CSIRO), and Scripps Institution of Oceanography (SIO). Only one global network for Δ¹⁴CO₂ is currently being operated, by the University of Heidelberg, although other global networks have operated in the past (Graven et al., 2012a; Nydal & Lövseth, 1983). There are regional networks for Δ¹⁴CO₂ and δ¹³CO₂ in Europe as part of the Integrated Carbon Observing System (ICOS) and in North America by NOAA and other laboratories. Urban‐scale networks have also been developed (Turnbull et al., 2015). Most of these observations are publicly available, for example, through the World Data Centre for Greenhouse Gases (https://gaw.kishou.go.jp/) or the ICOS portal (https://www.icos‐cp.eu/).

Little is known about the current atmospheric distribution of Δ¹⁴CO₂ and δ¹³CO₂ away from the surface. There have been some stratospheric observations of Δ¹⁴CO₂ conducted since the late 1980s (Kanu et al., 2016; Nakamura et al., 1994), but these comprise only a handful of vertical profiles. NOAA conducts regular aircraft measurements of Δ¹⁴CO₂ in the troposphere at some sites in North America (Estevan Point, Park Falls, Cape May, and Portsmouth) and at a larger network of sites for δ¹³CO₂ (Miller et al., 2012; Sweeney et al., 2015). Some other aircraft measurements of δ¹³CO₂ have also been made, showing influences of biospheric exchange and atmospheric mixing in the northern free troposphere and influences of the stratosphere in the tropopause region (Assonov et al., 2010; Levin et al., 2002). More observations from aircraft would help to refine our understanding of δ¹³CO₂ and Δ¹⁴CO₂ variations through the atmosphere, with applications for assessing biospheric fluxes, fossil fuel emissions, and atmospheric transport. The implementation of laboratory calibration recommendations and continued intercomparison activities are needed to ensure that data from different labs can be combined (WMO/IAEA, 2016).

In addition to efforts expanding the observations of Δ¹⁴C and δ¹³C across the carbon cycle, efforts to make modeling tools more openly available are needed to optimize the scientific advances that can be made with Δ¹⁴C and δ¹³C observations. We believe that existing observations are underutilized at present because isotopic modeling tools and expertise are not widely available or widely used. Modeling of atmospheric δ¹³CO₂ and Δ¹⁴CO₂ is typically done on a case‐by‐case basis. There is currently a lack of shared atmospheric modeling tools for isotopic simulations. Models are used on global scales and on regional scales, ranging from box models to high‐resolution three‐dimensional transport models (Basu et al., 2016; Keeling et al., 2017; Peters et al., 2018). To simulate atmospheric δ¹³CO₂ and Δ¹⁴CO₂, models or data‐based estimates of the carbon and isotopic fluxes from relevant processes are also needed. Here too, various models and estimates of isotopic fluxes have been used in individual studies, but not many of these are made available for other researchers. To provide modeled isotopic fluxes for use by the community, and to promote isotopic modeling in general, it was recommended that modeling groups in the latest Coupled Model Intercomparison Project activity (CMIP6) simulate carbon isotopes in the land and ocean modules of their Earth System Models using a specified atmospheric boundary condition (Figure 3, Graven et al., 2017; Jones et al., 2016; Orr et al., 2017). Only one model, CESM2, has so far included carbon isotopes in their CMIP6 simulations. It is hoped that the next phase of the CMIP will include more isotopic modeling and that isotopic modeling will be incorporated in other large modeling activities. Simulation of atmospheric δ¹³CO₂ and Δ¹⁴CO₂ in the atmospheric models of Earth System Models has not yet been implemented, so it is currently not possible to do a fully coupled simulation of δ¹³C and Δ¹⁴C using the most state‐of‐the‐art models. Such fully coupled isotopic models would be useful not only for the modern period but also for paleoclimate modeling. Other shared tools enabling atmospheric modeling of δ¹³CO₂ and Δ¹⁴CO₂ would also help to exploit existing and future atmospheric measurements.

To fully develop the use of Δ¹⁴CO₂ observations to monitor regional emissions from fossil fuel combustion, many more observations and better modeling capabilities on regional scales are needed. Studies of regional atmospheric measurement networks combined with high‐resolution atmospheric modeling have only recently been published (Basu et al., 2020; Graven et al., 2018), and best practices are still under development. For example, different studies have constructed atmospheric inversions differently. The methods used in Graven et al. (2018) and Fischer et al. (2017) first calculate fossil fuel‐derived CO₂ (ffCO₂, Equation 1) and biospheric CO₂ and then run an inversion for fossil fuel and biospheric fluxes. In contrast, Basu et al. (2016) set up their inversion to estimate individual ¹⁴CO₂ and CO₂ fluxes across North America, including all the processes that can influence Δ¹⁴CO₂ in the inversion. Other best practices that are still under development include the location and sampling height of observation sites in the network. Sites that have lower sampling heights or that are located closer to emission sources have higher signals in ffCO₂, whereas sites with higher sampling heights or located further from sources have lower signals, but they represent larger regions. Having more than one observation site within a particular region can be important to prevent biases from any unique site characteristics, for example, including both urban and ex‐urban sites that differ not only in their ffCO₂ signals or representation scale but also in the atmospheric model's representation of the transport in different types of regions (Brophy et al., 2019). In some locations, the ¹⁴C emissions from nuclear power plants can cause enrichment of Δ¹⁴CO₂, particularly near to high ¹⁴C‐emitting reactors in the United Kingdom and Canada (Bozhinova et al., 2014; Graven & Gruber, 2011; Vogel et al., 2013). A better understanding of ¹⁴C emissions from nuclear power plants and better ¹⁴C emissions data would enable their effect to be accurately accounted for and improve the utility of Δ¹⁴CO₂ for ffCO₂ quantification in regions with nuclear power plants. Further development of regional networks for Δ¹⁴CO₂ and complementary measurements including satellite observations, as well as the model‐data analysis frameworks for interpreting the observations to constrain ffCO₂ emissions, are needed (Ciais et al., 2015; Fischer et al., 2017).

11. Summary

Since the Industrial Revolution, the carbon isotopic composition of atmospheric CO₂ has undergone dramatic changes as a result of human activities and the response of the natural carbon cycle to them. The relative amount of atmospheric ¹⁴C and ¹³C in CO₂ has decreased because of the addition of ¹⁴C‐ and ¹³C‐depleted fossil carbon, while the nuclear bomb tests increased ¹⁴C in the atmosphere in the 1950s and 1960s. Measurements of Δ¹⁴CO₂ and δ¹³CO₂ have been used to make invaluable contributions to our knowledge of atmospheric mixing, air‐sea gas exchange, plant function, and fossil fuel emissions. As fossil fuel burning continues to grow, the Suess Effect on ¹⁴C and ¹³C in CO₂ continues. However, lower‐emission scenarios would lead to stabilized Δ¹⁴CO₂ and increases in δ¹³CO₂ over this century. The different paths described by the SSP‐based scenarios show that there is a wide range of possible changes to ¹⁴C and ¹³C of CO₂ in the future. Researchers should be aware of the possible changes and their effect on the continued utility of ¹⁴C and ¹³C measurements of CO₂ for scientific applications across various fields. We recommend a concerted effort to increase the number of ¹⁴C and ¹³C measurements across the Earth System and more development of publicly available modeling tools that incorporate ¹⁴C and ¹³C, including Earth System Models.

Supporting information

Supporting Information S1

Table S1

Table S2

Graven, H. , Keeling, R. F. , & Rogelj, J. (2020). Changes to carbon isotopes in atmospheric CO₂ over the industrial era and into the future. Global Biogeochemical Cycles, 34, e2019GB006170 10.1029/2019GB006170

Data Availability Statement

Historical and future atmospheric forcing data sets for Δ¹⁴CO₂ and δ¹³CO₂ can be accessed at input4MIPs (https://esgf‐node.llnl.gov/search/input4mips/). The future Δ¹⁴CO₂ and δ¹³CO₂ data sets are also given in Table S2. SSP‐based emissions scenarios are hosted by the International Institute for Applied Systems Analysis and available online (from https://tntcat.iiasa.ac.at/SspDb/). The simple carbon cycle model is available online (at https://github.com/heathergraven/simplemodel2020).