Quantification of Chaotic Intrinsic Variability of Sea‐Air CO₂ Fluxes at Interannual Timescales

Abstract

Chaotic intrinsic variability (CIV) emerges spontaneously from nonlinear ocean dynamics even without any atmospheric variability. Eddy‐permitting numerical simulations suggest that CIV is a significant contributor to the interannual to decadal variability of physical properties. Here we show from an ensemble of global ocean eddy‐permitting simulations that large‐scale interannual CIV propagates from physical properties to sea‐air CO₂ fluxes in areas of high mesoscale eddy activity (e.g., Southern Ocean and western boundary currents). In these regions and at scales larger than 500 km (~5°), CIV contributes significantly to the interannual variability of sea‐air CO₂ fluxes. Between 35°S and 45°S (midlatitude Southern Ocean), CIV amounts to 23.76 TgC yr⁻¹ or one half of the atmospherically forced variability. Locally, its contribution to the total interannual variance of sea‐air CO₂ fluxes exceeds 76%. Outside eddy‐active regions its contribution to total interannual variability is below 16%.

Key Points

• Interannual chaotic intrinsic (CIV) variability propagates from physical to chemical tracers in areas of strong mesoscale activity

• It contributes significantly to interannual variability of sea‐air CO₂ fluxes over the Southern Ocean and western boundary current systems

• CIV is small outside eddy‐active regions where interannual variability of sea‐air CO₂ fluxes is prominently driven by atmospheric forcing

1. Introduction

Until recently, the variability of the total carbon (C) sink was considered to be dominated by the land biosphere (Ciais et al., 2013; Le Quéré et al., 2018). This view is increasingly challenged by observational studies reporting a substantial variability of the global ocean C uptake at interannual (~0.3 PgC yr⁻¹) (Rödenbeck et al., 2015) to decadal timescales (~0.6 PgC yr⁻¹) (Landschützer et al., 2016). Although the causes of these large fluctuations are still not fully understood (Gruber, Landschützer, et al., 2019), there is scientific consensus that they are driven by the natural variability of the coupled ocean‐atmosphere system (Heinze et al., 2015; Séférian et al., 2013) occurring over the Southern Ocean and the North Atlantic (Landschützer, Gruber, Haumann, et al., 2015; Watson et al., 2009). Both are key regions of the ocean C cycle where anthropogenic C spreads efficiently downward to deep and bottom waters (Gruber, Clement, et al., 2019). The magnitude of these natural fluctuations of the ocean C sink complicates the detection of a potential weakening of the ocean C sink and its attribution to human activities (Séférian et al., 2014). At the same time, because they are associated with atmospheric variability, these fluctuations might be predictable.

While recent studies based on coarse resolution ESMs have demonstrated that natural fluctuations of the ocean C sink are predictable (Li et al., 2016, 2019; Lovenduski et al., 2019; Séférian et al., 2018; Yeager et al., 2018), eddy‐permitting simulations with ocean‐only global models suggest that a significant part of the interannual variability of physical variables emerges spontaneously due to nonlinearities in ocean dynamics, regardless of the atmospheric variability (e.g., Hirschi et al., 2013; Nonaka et al., 2016; O'Kane et al., 2013; Penduff et al., 2011; Sérazin et al., 2015). This chaotic intrinsic variability (CIV) reaches multidecadal and basin scales. Non‐eddying ocean models, hence presumably coarse‐resolution ESMs, tend to strongly underestimate the contribution of CIV to interannual variability (Grégorio et al., 2015; Penduff et al., 2011). By analogy to atmospheric weather prediction, ocean CIV may limit the predictability of oceanic variability up to climate‐relevant scales.

Eddying ensemble simulations initiated with perturbed initial conditions and driven by the same atmospheric reanalysis allow to study oceanic CIV along with the atmospherically forced variability (Bessières et al., 2017). Previous studies focusing on physical variables suggest that the contribution of CIV to interannual variability varies spatially over the ocean. CIV is largest in areas of high kinetic energy such as the Southern Ocean or western boundary current extensions (e.g., Gulf Stream, Kuroshio, and Agulhas Current). Estimates of its contribution to the total interannual variance of sea level anomalies (SLAs) reach up to 80% over large parts of the Southern Ocean in eddy‐permitting ocean models (Penduff et al., 2011). The fraction of interannual variance produced by CIV reaches 50% for the meridional overturning circulation (MOC) in the South Atlantic (Grégorio et al., 2015; Hirschi et al., 2013; Leroux et al., 2018). It also accounts for up to 75% of the variability of the regional Ocean Heat Content in the Southern Ocean (Penduff et al., 2018).

Regions of high CIV also coincide with major CO₂ sink regions (e.g., Southern Ocean). Since oceanic CIV contributes significantly to the total variability of physical properties (e.g., SLAs; sea surface temperature, SST; and AMOC) underlying the variability of sea‐air fluxes of CO₂, we suggest it could also impact the total variability of CO₂ fluxes through the vertical mixing of nutrients and carbon‐related fields in the ocean mixed layer. Predictability assessments of sea‐air CO₂ fluxes derived from coarse‐resolution ESMs might be overestimated in the absence of eddies (Séférian et al., 2018). To the contrary, estimates of the time of emergence of anthropogenic climate change impacts on CO₂ fluxes might be underestimated in the absence of eddies (McKinley et al., 2016). A potential underestimation of the time of emergence was reported for sea level rise where the magnitude of chaotic variability driven by eddying nonlinear processes competes with long‐term trends driven by external anthropogenic forcing (Llovel et al., 2018). As of today, the contribution of CIV to sea‐air CO₂ flux fluctuations at interannual timescales remains to be demonstrated and its magnitude to be evaluated.

In coupled ocean‐atmosphere simulations, it is almost impossible to separate the oceanic fluctuations that are directly forced by the atmosphere, that are due to oceanic CIV, and that emerge from the coupling itself (e.g., ENSO). An ensemble of ocean simulations driven by the same atmospheric variability allows to disentangle the atmospherically forced variability from oceanic CIV using simple ensemble statistics (i.e., ensemble means and standard deviations). This study relies on the analysis of an ensemble of three eddy‐permitting global ocean‐biogeochemical hindcast simulations. Section 2 introduces the model experiments. Section 3 presents the contribution of CIV to the interannual variability of sea‐air CO₂ fluxes and section 4 the drivers of CIV. The limitations of our approach are discussed in section 5.

2. Model Experiments

The 1/4°‐resolution (grid spacing of 28 km at the Equator, decreasing poleward) three‐simulation ensemble is generated through perturbations of physical and biogeochemical initial conditions. The admittingly small size of the ensemble reflects the still high computational cost of coupled physical‐biogeochemical simulations. Simulations are run with the oceanic component of an ESM and include marine biogeochemistry.

2.1. Physical‐Biogeochemical General Circulation Model

In this study, we use a configuration of the Nucleus for European Modeling of the Ocean framework (NEMO 3.2, http://www.nemo‐ocean.eu/) implemented on a global tripolar 1/4° grid. It couples the ocean general circulation model OPA9 (Madec et al., 1998), the sea ice code LIM2 (Fichefet & Maqueda, 1997), and the biogeochemical model PISCESv1 (Aumont & Bopp, 2006). Details on model parameterizations and performance are presented in Barnier et al. (2006). The biogeochemical model PISCES simulates the temporal and spatial evolution of the first levels of the pelagic ecosystem and the carbon cycle with 24 prognostic tracers. It distinguishes two phytoplankton (diatoms and nanophytoplankton) and two zooplankton (microzooplankton and mesozooplankton) functional groups. Phytoplankton growth is limited by the availability of nutrients external to the cell (nitrate, ammonium, silicic acid, phosphate, and iron) and light. Ratios of Fe, Si, and Chl to C are computed as a function of nutrient limitation. Fixed Redfield ratios are imposed for C:N:P (Takahashi et al., 1985) for living and detrital pools. The carbon chemistry is computed following recommendations of Phase 2 of the Ocean Carbon‐Cycle Model Intercomparison Project (OCMIP) (Najjar & Orr, 1999). The model considers three external sources of nutrients: river input, atmospheric deposition, and sediment mobilization for Fe (Terhaar et al., 2018).

2.2. Simulation Protocol

The NEMO/PISCES model is forced from 1958 to 2002 by the DFS4.2 product (Drakkar Forcing Set 4.2) (Brodeau et al., 2010), which is derived from atmospheric reanalysis. Physical and biogeochemical tracer distributions are initialized on 1 January 1958 with output from a 138‐yr‐long run including anthropogenic carbon at 1/2° resolution, described in Bourgeois et al. (2016). The simulations are forced with yearly averaged historical atmospheric CO₂ concentrations reconstructed from ice cores and atmospheric records (Le Quéré et al., 2015). External input of fresh water by major rivers follows Barnier et al. (2006). Two additional members are branched off the reference simulation in 1979 on 1 January. They are restarted with initial conditions of physical and biogeochemical tracer distributions corresponding to the last model time step (restart files) on 31 December of years 1976 and 1980. Except for the difference in restart conditions on 1 January 1979, both simulations and their atmospheric forcing are identical to the reference simulation and run up to year 2002 forced by the corresponding years of atmospheric reanalysis. The selection of the pivotal year (1979) was guided by the analysis of time series of surface ocean fields to verify that tracer distributions had reached an asymptotic quasi‐steady state after 21 years of simulation (1 January 1958 to 31 December 1978) at ¼° resolution. Years for swapping initial conditions were similar in terms of large‐scale distributions based on the comparative analysis of tracer distributions from multiple restart files ±5 years around the pivotal year. Additional details are provided in the supporting information (SI).

2.3. Evaluation Data Sets

Each of the three ensemble members is evaluated against observations in terms of annual climatological mean and standard deviation over the period of analysis (1983–2002). Model evaluation focuses on SST (Locarnini et al., 2013) and sea‐air CO₂ fluxes (Landschützer, Gruber, & Bakker, 2015; Landschützer, Gruber, Haumann, et al., 2015). Data sets and model evaluation are presented in the SI (Figures S4–S7). Zonal means and root mean square errors are provided to quantify model biases with respect to observations.

2.4. Model Output Processing and Statistical Analysis

Model output is interpolated from the model tripolar grid on a regular 1° × 1°‐resolution grid prior to further processing and analysis. Time series of yearly model output are linearly detrended. All analyses are based on yearly anomalies, obtained by removing the 1983–2002 averages of all fields. The results (Figures 1, 2, 3) are not sensitive to the period of analysis: similar results are obtained for the last 10 years (1993–2002). In this study, the forced variability is obtained from the time‐varying ensemble mean fields and corresponds to the variability that is directly driven by the atmospheric reanalysis.

Figure 1.

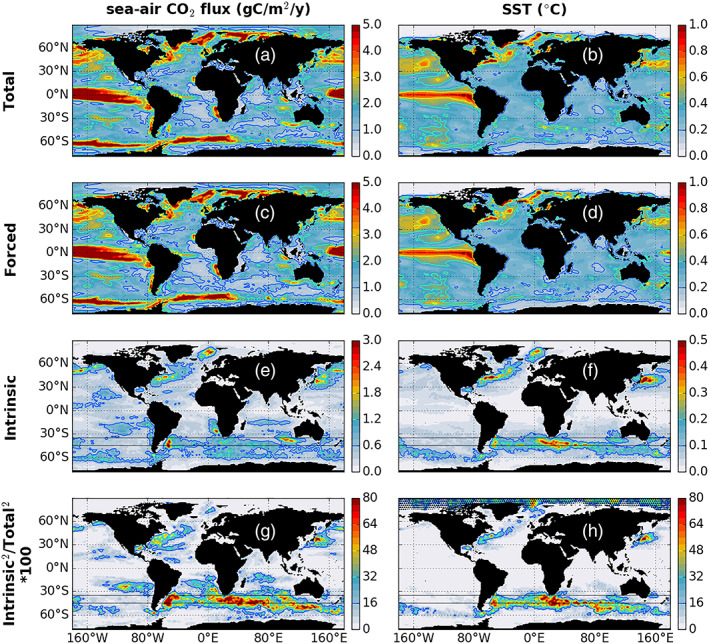
Total interannual variability of (a) sea‐air CO₂ flux and (b) sea surface temperature (SST) and their (c, d) forced and (e, f) intrinsic components. Panels (g) and (h) present the ratios of interannual variances of chaotic intrinsic variability to total variability. Stippling on subplots (g) and (h) highlights areas where total variability is lower than the first level of its respective σ _T color bar in (a) or (b). Gray lines indicate the latitude band used in Figure 3.

Figure 2.

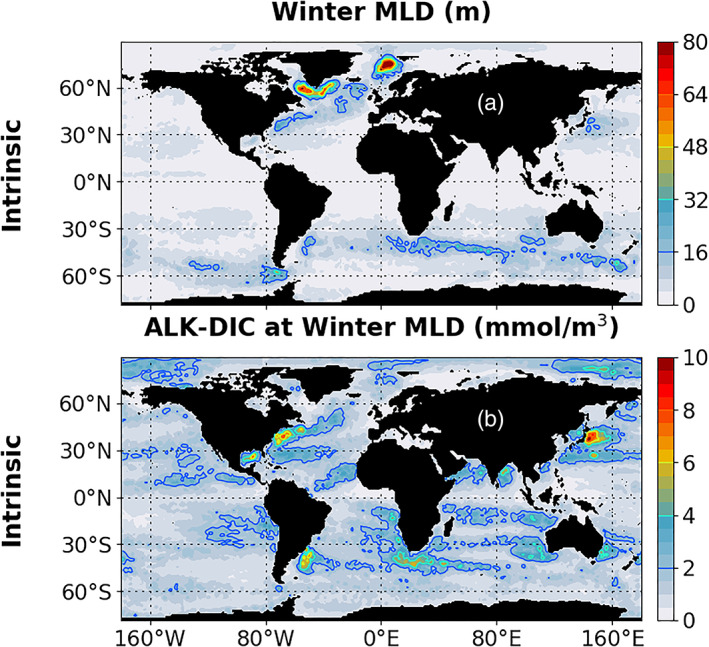
Interannual chaotic intrinsic variability diagnosed for the mean winter mixed layer depth (MLD) (a) and for the carbonate ion concentration approximated by ALK‐DIC at the base of the mean winter MLD mixed layer (b). The mean winter MLD is computed for the three hemispheric winter months.

Figure 3.

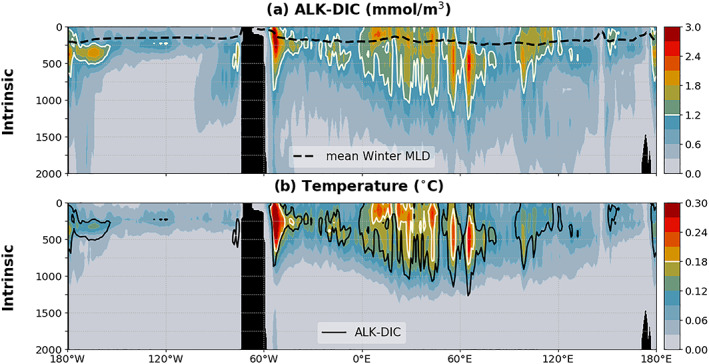
Vertical sections of interannual CIV averaged over 35–45°S, for (a) ALK‐DIC and (b) temperature. The black dashed line in (a) highlights the mean winter MLD. The black solid line in (b) corresponds to the 1.2‐mmol/m³ ALK‐DIC contour superimposed in pale yellow on (a).

Amplitudes of total, forced, and intrinsic variabilities are computed following Leroux et al. (2018) based on yearly‐averaged model fields. Because the analysis focuses on large‐scale signals, a 5° spatial low‐pass filter based on fast Fourier transform is applied to all horizontal fields. Total variability is decomposed in its forced and intrinsic contributions. The amplitudes of these three quantities (total, forced, and intrinsic variabilities) are linked to each other by the sum of their squared standard deviations:

$${\sigma }_{\mathit{\text{forced}}}^2+{\sigma }_{\mathit{\text{intrinsic}}}^2={\sigma }_{\mathit{\text{total}}}^2,$$ (1)

with σ_forced defined as the unbiased temporal standard deviation of the ensemble mean time series and ${\sigma }_{\mathit{\text{intrinsic}}}=\sqrt{\overline{{\epsilon }^2}}$ the square root of the time‐averaged unbiased ensemble variance ε² (i.e., the intermember unbiased variance). Due to the small size of our ensemble (three members), relation 1 is not strictly verified. We define the error associated with estimates of ( ${\sigma }_{\mathit{\text{forced}}}^2+{\sigma }_{\mathit{\text{intrinsic}}}^2$) as

$$e=\sqrt{\left|{\sigma }_{\mathit{\text{total}}}^2-\left({\sigma }_{\mathit{\text{forced}}}^2+{\sigma }_{\mathit{\text{intrinsic}}}^2\right)\right|}.$$ (2)

Our analysis addresses the interannual variability of sea‐air CO₂ fluxes. To identify the mechanisms behind the CIV of sea‐air CO₂ fluxes, we focus on its thermodynamic (SST; sea surface salinity, SSS) and geochemical drivers at the mean depth of the winter mixed layer (dissolved inorganic carbon, DIC; alkalinity, ALK), as well as the variability of mixed layer depth (MLD) for the vertical mixing of these properties. The gas transfer coefficient is not included in the analysis. It is a function of wind speed with a negligible temperature effect through the temperature dependence of the Schmidt number and chemical enhancement (Wanninkhof, 1992). As the wind stress does not depend on surface currents, the air‐sea momentum flux is the same in the three members.

3. Contribution of CIV to the Interannual Variability of Sea‐Air CO₂ Fluxes

The decomposition of the total variability (σ _T) of SST and sea‐air CO₂ fluxes into their forced (σ _F) and intrinsic components (σ _I) identifies σ _F as the major contributor to σ _T for both fields over large areas of the ocean (Figure 1). While σ _T and σ _F have similar spatial distributions, the geographical pattern of σ _I is strikingly different. High values of σ _I are diagnosed over regions of high kinetic energy such as the Southern Ocean, the Gulf Stream, North Atlantic, and Kuroshio currents. The geographical patterns and magnitudes of the ratio of variances (σ _I ²/σ _T ²) are both consistent with those reported by Penduff et al. (2011), although we use a different experimental approach (SI for SLA). With the exception of the northern part of the Zapiola anticyclone, the maximum of σ _I remains smaller than for σ _F. The relative contribution of CIV to the total interannual variance (σ _I ²/σ _T ²) exceeds 50% for SST (Figure 1h) and sea‐air CO₂ fluxes (Figure 1g) over large areas in the Southern Ocean and along the Kuroshio and the Gulf Stream. This ratio locally reaches ~76% for sea‐air CO₂ fluxes, mainly in the 35–45°S latitude band (hereafter referred to as midlatitude Southern Ocean). Estimates of σ _I for sea‐air CO₂ flux locally exceed 2.4 g C m⁻² yr⁻¹ but mostly lie between 0.6 and 1.2 g C m⁻² yr⁻¹ (Figure 1e). The largest values of σ _T and σ _F are reached in the Equatorial Pacific and in the Northern Hemisphere for both SST (Figures 1b and 1d) and sea‐air CO₂ flux (Figures 1a and 1c). Geographical patterns for all three components of variability are thus in good agreement for these two variables. This new result is consistent with the strong control exerted by SST on the solubility of CO₂ and thus on seawater CO₂ partial pressure (pCO₂) and, ultimately, on the CO₂ flux across the sea‐air interface.

Maps of total, forced, and intrinsic variability of sea‐air CO₂ fluxes illustrate that the total variability is dominated by the forced component over most of the global ocean outside eddy‐active regions (Figure 1). This is confirmed by the global integrals (78°S to 90°N; Table 1) of the forced (σ _F = 652.1 TgC yr⁻¹) and intrinsic (σ _I = 158.0 TgC yr⁻¹) components of the total variability of sea‐air CO₂ fluxes (σ _T = 673.5 TgC yr⁻¹). The contribution of CIV to the total variability of sea‐air CO₂ fluxes is higher in eddy‐active regions (Table 1): in the midlatitude Southern Ocean (35°S to 45°S) for instance, σ _T = 52.7 TgC yr⁻¹, σ _F = 47.4 TgC yr⁻¹, and σ_I = 23.8 TgC yr⁻¹. In the three eddy‐active regions analyzed in this study, the ratio of variances of intrinsic to total variability ranges between 16% and 22%, as opposed to only 5.5% over the global ocean.

Table 1.

Estimates of Total (σ _T), Forced (σ _F), and Chaotic Intrinsic Variability (σ _I) of Sea‐Air CO₂ Fluxes Integrated Over the Global Ocean and Over Three Regions With High Eddy Kinetic Energy

Sea‐air CO2 flux (TgC yr−1)	σ T (TgC yr−1)	σ F (TgC yr−1)	σ I (TgC yr−1)	σ I 2/σ T 2 (%)	Error e (TgC yr−1)
Global ocean 78°S to 90°N	673.5	652.1	158.0	5.5	86.3
Midlatitude Southern Ocean 45–35°S	52.7	47.4	23.8	20	13.0
Gulf Stream 70°W, 40°W to 35°N, 50°N	9.91	9.16	3.99	16	2.18
Kuroshio 140°E, 170°E to 30°N, 45°N	10.5	9.46	4.92	22	2.68

Note. The ratio of variances (σ _I ²/σ _T ²) provides a measure of the contribution of CIV to the total variability. The error (e) has been estimated at each grid point of the global ocean following Equation 2 and integrated over the area of interest.

4. Drivers of CIV of Sea‐Air CO₂ Fluxes

Mixed layer deepening and shoaling contributes to the variability of surface ocean carbon properties by upward mixing of cold subsurface waters enriched in DIC and ALK (SI for σ _T, σ _I, and σ _F for DIC and ALK). Changes in ALK and DIC have opposing effects on pCO₂ and sea‐air CO₂ fluxes. Their net outcome can be approximated by the difference between ALK and DIC, which corresponds at first order to the carbonate ion concentration [CO₃ ²⁻] (Dufour et al., 2013). The effect of equal changes in both tracers is close to zero on [CO₃ ²⁻] and hence also on pCO₂. Geographical patterns of CIV of SST (Figure 1f) and [CO₃ ²⁻] (approximated by ALK‐DIC; Figure 2b) are mostly consistent with those computed for mean winter MLD over the Southern Ocean, the Gulf Stream, and Kuroshio extensions (Figure 2a). The subpolar deepwater formation area (Labrador Sea) is a noteworthy exception. In this area σ _I(MLD) reaches ~80 m at interannual timescales, while σ _I(SST) and σ _I(ALK‐DIC) do not exceed background values which might explain the low σ _I values computed for sea‐air CO₂ fluxes. A maximum of σ _I(MLD) of similar magnitude is diagnosed in the Nordic Seas, this time associated with large σ _I for sea‐air CO₂ fluxes and analyzed drivers. These results provide evidence for the spreading of interannual‐to‐decadal CIV from physical variables to sea‐air fluxes of CO₂ but also reveal regional differences in the contribution of the underlying drivers. Estimates of σ _I for SST reach 0.5°C in regions of high eddy kinetic energy, while those of [CO₃ ²⁻] range between 2 and 5 mmol/m³ over these same areas.

The analysis allows a differentiation between thermal (SST) and geochemical (predominantly ALK‐DIC) drivers of CIV of sea‐air CO₂ fluxes. The coherence between σ _I maps of SST and sea‐air exchange of CO₂ points toward the dominant role of SST as a driver of intrinsic variability in CO₂ fluxes. Changes in biogeochemical mixed layer properties, in particular σ _I(ALK‐DIC), driven by σ _I(MLD) further contribute to the CIV of sea‐air CO₂ fluxes. The effect of mixed layer variability on the surface ocean carbon system depends on the vertical gradients of properties (temperature, DIC, ALK, and nutrients) at the base of the mixed layer (Dufour et al., 2013; Mahadevan et al., 2004). However, ALK and temperature, as well as DIC, have opposing effects on surface ocean partial pressure of CO₂ and thus sea‐air CO₂ fluxes. These competing effects give rise to regional differences in the expression of CIV of sea‐air CO₂ fluxes in response to σ _I(MLD).

To deepen the analysis of drivers of CIV of sea‐air CO₂ fluxes, we assess the vertical distributions of CIV for temperature and ALK‐DIC over the midlatitude Southern Ocean. Figure 3b shows that σ_Ι(temperature) peaks around the depth of the thermocline and decreases toward the surface. This pattern is due to the formulation of surface forcing in the ensemble experiment: turbulent air‐sea heat fluxes parameterized through bulk formulae exert in all members an implicit relaxation of SST (Barnier et al., 1995) toward the same equivalent air temperature, which translates into a damping of the spread of SST (Bessières et al., 2017). The surface damping has no direct impact on the temperature spread below the surface, in particular at the thermocline where it reaches its maximum. To the contrary, the forced variability is strongest at the surface and decreases with depth (not shown), allowing σ_Ι(temperature) to reach its strongest contribution to total variability within the upper 500 m of the water column (Figure 3b). High values of CIV for temperature (Figure 3a) and ALK‐DIC (Figure 3b) are associated with the Zapiola anticyclone, a barotropic vortex characterized by strong vertical motions and for which CIV of sea‐air CO₂ fluxes exceeds forced variability (Figure 1). The zonal and vertical structures of σ _Ι(ALK‐DIC) (Figure 3a) resemble those of temperature (Figure 3b), with large signals in the Atlantic and Indian Ocean sectors underlying large surface CIV values (Figures 1 and 2). The close correspondence is consistent with the fact that at first order, these active and passive tracers (measuring the thermal and biogeochemical properties of water masses) are advected by the same currents, whose chaotic character is confirmed by SLA CIV maps (Figure S8g). The identical sensitivity to advection (and mixing) is likely to explain the propagation of CIV from physical to biogeochemical properties, at least where advection dominates their evolution.

These results confirm that σ _I(SST) is a major driver of CIV of sea‐air CO₂ fluxes through its effect on CO₂ solubility and thus ocean pCO₂. Our estimates of CIV of sea‐air CO₂ fluxes must however be considered as lower estimates, since the surface forcing formulation induces a damping of σ _I(SST).

5. Limitations of the Study

The major limitation of this study is the small size of the ensemble, which leads to inaccuracies in the calculation of the terms of Equation 1. The resulting error e (Equation 2) is associated with the sum of the squared contributions of σ _F and σ _I. The individual contributions of σ _F and σ _I to e cannot be separated from the sum of the squared contributions and quantified. The error estimate e should be seen as an upper limit of the error associated with each term (σ _F or σ _I). The error associated with estimates of CIV for sea‐air CO₂ fluxes ranges from 2.18 TgC yr⁻¹ in the Gulf Stream region (σ _I = 3.99 TgC yr⁻¹, σ _F = 9.16 TgC yr⁻¹) to 86.3 TgC yr⁻¹ at global scale (σ _I = 158.0 TgC yr⁻¹, σ _F = 652.1 TgC yr⁻¹), which corresponds to 54.6% of σ _I. It should be mentioned, however, that Hirschi et al. (2013) provided first estimates of the CIV of AMOC with only two ensemble members. These estimates were subsequently confirmed and refined by Leroux et al. (2018) using a larger ensemble of 50 members at the same model resolution. Thus, while future studies with larger ensemble sizes are needed to reduce the error and to refine estimates of σ _I, these are likely to corroborate our key results.

The spatial resolution of the model used here remains modest (¼°), and switching to 1/12° resolution will certainly strengthen mesoscale activity. By analogy with studies focusing on the CIV of SLA (e.g., Sérazin et al., 2015), such an increase in resolution is expected to result in higher CIV of sea‐air CO₂ fluxes without, however, significant changes in spatial patterns (i.e., strongest CIV over areas with high eddy kinetic energy). In addition, the relative contribution of CIV to the total interannual variability of sea‐air CO₂ fluxes (ratio of variances) may not change much at 1/12° since the forced variability is expected to increase as well (Grégorio et al., 2015).

Finally, several different protocols have been proposed to quantify CIV of physical properties, all yielding consistent results (see, e.g., Leroux et al., 2018). For these reasons, and considering that CIV of sea‐air CO₂ fluxes appears to primarily originate in that of physical properties, we expect future studies to qualitatively corroborate our main findings while refining our quantitative estimates.

6. Conclusions

Recent studies suggest that physical CIV is much smaller in coarse‐resolution models than at eddy‐permitting resolution (Grégorio et al., 2015; Penduff et al., 2011), where it emerges in the form of high‐frequency chaotic mesoscale variability that cascades toward larger spatial and temporal scales (Sérazin et al., 2018). CIV is not in phase with the variability of the atmospheric forcing and represents an irreducible source of uncertainty for the forecasting of the physical ocean state and the marine carbon cycle.

The present study highlights that CIV propagates from physical to biogeochemical properties in areas of strong mesoscale activity. It suggests that physical‐biogeochemical coupling generates CIV of ocean carbon fluxes over the same regions, but with a smaller magnitude compared to that of ocean physical variables. Outside these areas, CIV remains small implying that over large parts of the ocean the interannual variability of sea‐air CO₂ fluxes is driven by the atmospheric forcing. Our results lend credit to recently published estimates of the interannual to decadal predictability horizon of ocean carbon fluxes from coarse‐resolution ESMs (Li et al., 2016; Li & Ilyina, 2018; Lovenduski et al., 2019; Séférian et al., 2018) and statistical approaches for detecting the impact of climate change on the ocean carbon sink (e.g., Denvil‐Sommer et al., 2019; Rödenbeck et al., 2015). However, CIV contributes significantly to the total variability of sea‐air CO₂ fluxes over eddy‐active areas such as the Southern Ocean, a key region for the ocean carbon cycle. Over eddy‐active areas, a significant fraction of the interannual variability of sea‐air CO₂ fluxes at large scale could respond to random internally generated physical fluctuations, in particular of temperature.

As CIV cannot be isolated directly from observations, further model simulations and model intercomparisons are required to fully assess the robustness of our results. However, the comparison between our and previous results (e.g., Grégorio et al., 2015; Penduff et al., 2011; Sérazin et al., 2015) highlights consistent regional patterns and magnitude across model systems and approaches for SLA. These and the present results confirm that the ocean alone (i.e., uncoupled to the atmosphere) can spontaneously generate a significant physical and biogeochemical CIV, which is much weaker at coarser resolution. Future climate projections with eddying oceans are thus likely to include a new oceanic source of low‐frequency variability with a random phase, whose impact on the marine carbon cycle and biogeochemistry will need to be quantified.

Conflict of Interest

The authors have no competing interests to declare.

Supporting information

Supporting Information S1

Gehlen, M. , Berthet, S. , Séférian, R. , Ethé, C. , & Penduff, T. (2020). Quantification of chaotic intrinsic variability of sea‐air CO₂ fluxes at interannual timescales. Geophysical Research Letters, 47, e2020GL088304 10.1029/2020GL088304

Data Availability Statement

Observational data sets for this research are included in Locarnini et al. (2013) for SST and Landschützer, Gruber, and Bakker (2015) for air‐sea CO₂ fluxes. Postprocessed model output and the code used to create all figures are available online (at https://climatedata.umr‐cnrm.fr/public/cnrm/articles/Gehlen‐et‐al_GRL_2020/).