Skip to main content
NCBI home page
NASA Author Manuscripts logoLink to NASA Author Manuscripts
. Author manuscript; available in PMC: 2020 Dec 23.
Published in final edited form as: Life Sci Space Res (Amst). 2017 Apr 20;14:64–73. doi: 10.1016/j.lssr.2017.04.001

Comparing HZETRN & SHIELD Transport Codes

John W Norbury a, Tony C Slaba a, Nikolai Sobolevsky b, Brandon Reddell c
PMCID: PMC7757342  NIHMSID: NIHMS1532137  PMID: 28887946

Abstract

For the first time, the American (NASA) and Russian (ROSCOSMOS) space radiation transport codes, HZETRN and SHIELD respectively, are directly compared to each other. Calculations are presented for Galactic Cosmic Ray (GCR) minimum Hydrogen, Oxygen and Iron projectiles incident on a uniform Aluminum cylinder of varying thickness. Comparisons are made for the flux spectra of neutrons, light ions, heavy ions and pions emitted from the back of the Aluminum cylinder. In order to provide more benchmark comparisons, some calculations with the GEANT and FLUKA transport codes are also shown.

Keywords: Space radiation, Radiation transport, HZETRN, SHIELD

1. Introduction

International cooperation in the exploration of space is expected to continue with human missions to Mars. Protection of astronauts from the harmful effects of space radiation is a major factor that needs to be taken into consideration in mission planning. Accurate prediction of expected radiation dose levels that will be encountered by astronauts is of utmost importance. Such predictions are made with space radiation transport codes, and various space agencies typically rely on a particular code that has been developed within their own national space agencies. For example, the HZETRN code (Wilson et al., 2015a, 2015b, 2016; Slaba et al., 2016) is typically used by NASA, the SHIELD code (Dementyev and Sobolevsky, 1999; Hansen et al., 2012) is typically used by the Russian Space Agency, the GEANT code (Agostinelli et al., 2003) is used by the European Space Agency, and the PHITS code (Sato et al., 2006; 2013) is used by the Japanese Space Agency. Other codes that receive significant use are FLUKA (Battistoni et al., 2015) MCNP (McKinney et al., 2006) and HETC-HEDS (Charara et al., 2008; Townsend et al., 2005).

When international partners are planning joint space missions and predicting radiation effects, it is obviously important that the transport codes being used are in reasonable agreement with one another, as well as with measured data. The current special issue of this journal is devoted to comparisons between different codes and data, specifically oriented to a Mars mission. There have been many studies of the comparisons of transport codes with each other in the literature (Matthia et al., 2016; Slaba et al., 2017; Wilson et al., 2014, 2015a, 2015b, 2016; Lin et al., 2012; Heinbockel et al., 2011a; 2011b) and also in the present special issue. However, a significant gap in the literature is a direct comparison of the American and Russian codes HZETRN and SHIELD respectively, with each other. The present paper represents the first such direct comparison of these two important space radiation transport codes.

While the main focus of this paper is to compare the NASA deterministic HZETRN code and the ROSCOSMOS Monte Carlo SHIELD code, some comparisons to the Monte Carlo GEANT and FLUKA codes are also provided to give insight into possible differences between HZETRN and SHIELD. Brief descriptions of the various transport codes are provided below.

2. Description of transport codes

2.1. HZETRN

The HZETRN (High charge (Z) and Energy TRaNsport) code (Wilson et al., 2015a, 2015b, 2016; Slaba et al., 2016) is a deterministic transport code specifically developed by NASA for space radiation transport. It employs numerical solutions to the time-independent, linear Boltzmann equation. It utilizes the continuous slowing down approximation in which discrete atomic interactions are represented by stopping power. The HZETRN code has undergone regular updates with releases in 2010 and 2015 denoted as HZETRN2010 and HZETRN2015. HZETRN2010 was a one-dimensional (1D) code that employed the straight-ahead approximation, in which particles are transported along a single ray (N=1) representing the incident beam direction. HZETRN2010 also allowed for forward-backward (N=2) propagation in which backward moving particles were also propagated along a second ray at 180° relative to the incident beam direction. In contrast, HZETRN2015 allows for three-dimensional (3D) transport in which neutrons and light ions (Z≤2) can be propagated in three-dimensions, with the number of rays N being arbitrary. If one chooses the N=1 option in HZETRN2015, this corresponds to the straight-ahead approximation, while the N=2 option is the forward-backward approximation and N>2 corresponds to 3D transport. HZETRN2015 was utilized in all calculations in the present paper.

The nuclear physics models employed in HZETRN are now briefly described. Further details can be found in the references (Wilson et al., 1991). NUCFRG3 (Adamczyk et al., 2012) is a nuclear fragmentation model, which is used for heavy ion collisions and accounts for both strong and electromagnetic (Adamczyk et al., 2012) interactions. The parametric model of Bertini and Ranft (Wilson et al., 1991) is used for nucleon production from strong interactions, while an electromagnetic dissociation model (Adamczyk et al., 2012) is used for nucleon production from electromagnetic interactions. A semi-empirical model is used for light ion fragmentation and production from targets. Heavy target fragments are not transported, but are accounted for in dose and dose equivalent calculations. Light target fragments from heavy projectiles are not included in the cross section model. Neutrons from heavy projectiles are approximately accounted for in the cross section model.

2.2. SHIELD

The transport codes SHIELD (Sobolevsky, 1970; Barashenkov et al., 1972) and also NMTC/HETC (Nucleon-Meson Transport Code / Heavy ion Transport Code) (Coleman and Armstrong, 1971; Armstrong and Chandler, 1972) were the first transport codes in the modern sense of the word. The SHIELD code (http://www.inr.ru/shield) (Dementyev and Sobolevsky, 1999) allows for the transport of nucleons, pions, kaons, anti-nucleons and muons, as well as nuclei with arbitrary values of proton and mass number at energies up to 1 TeV/n. The lower limit is 1 MeV/n for charged particles and the thermal energy for neutrons. The geometric configuration of a target may be an arbitrary combination of bodies bounded by second order surfaces. The chemical and isotopic composition of materials in each geometric zone of a target is arbitrary. The ionization energy loss of charged particles and ions, fluctuations of ionization loss, the multiple Coulomb scattering and main decay modes of pions and kaons are taken into account.

At the simulation of the hadron cascade in a target, all generations of the secondary particles are taken into account. The sources of secondary particles, such as low energy neutrons (En < 14.5 MeV) as well as gamma-rays, electrons, positrons and neutrinos (as products of meson decays) are formed. All these particles are stored in special arrays with all their individual parameters. After the hadron cascade is completed, the transfer of neutrons with energies below 14.5 MeV from the source array is simulated using the original neutron transport code LOENT (LOw Energy Neutron Transport) (Latysheva and Sobolevsky, 2008) on the basis of a 28-group system of the ABBN (Abagyan, Bazazyants, Bondarenko, Nikolaev) neutron constants (Abagyan et al., 1981; http://www.ippe.ru/podr/abbn/english/index.php). The LOENT code can be used both independently and together with the SHIELD code, with which it has a common geometrical module and a number of common subroutines.

Complete storing of the generated tree of hadron cascades is implemented in the SHIELD code (Sobolevsky, 2015), without any loss of physical information and taking into account all possible correlations. Storing of the tree is carried out in special arrays. The tree is stored in relation to the geometrical configuration of the target. Such organization of computations allows complete separation of the modeling and scoring parts of the code. If necessary, the user can collect trees on an external drive and carry out tree visualization. At the end of modeling of a regular hadron cascade, the tree arrays are cleaned.

The quality of a transport code essentially depends on the generator of inelastic nuclear interactions. The SHIELD code uses the MSDM (Multi-Stage Dynamical Model) generator (Botvina et al., 1997), which includes current versions of well-known Russian models of nuclear reactions. The fast, cascade stage of nuclear reactions at energies below 1 GeV, is modeled using the Dubna intra-nuclear cascade model (Toneev and Gudima, 1983). Above 10 GeV the Quark-Gluon String Model (QGSM) (Amelin et al., 1990a) is used, while in the intermediate range 1 – 10 GeV, some extensions of QGSM (Amelin et al., 1990b) are used. Thus, a consistent description of the fast stage of nuclear reactions in the whole energy range of primary hadrons and nuclei up to 1 TeV/n is provided.

Evolution of the excited residual nucleus towards an equilibrium state is described in terms of the pre-equilibrium model based on the Monte Carlo solution of the corresponding Master equation (Gudima et al., 1983). Further equilibrium de-excitation of the residual nucleus includes several mechanisms. For light nuclei (A < 16), the modified model of Fermi break-up (Botvina et al., 1987) is applied. Medium and heavy nuclei at moderate excitations (E∗ < 2 MeV/n) de-excite themselves by particle evaporation (Botvina et al., 1987). For heavy nuclei, a competition of evaporation and fission is implemented (Adeev et al., 1983). Highly excited nuclei (E∗ > 2 MeV/n) may decay into several excited fragments according to the Statistical Multi-fragmentation Model (SMM) (Bondorf et al., 1995) followed by the emission of particles from fragments. Thus, the MSDM generator provides description of all the stages of a nuclear reaction in the exclusive approach.

Besides the general version of the SHIELD code, there is a special medical version SHIELD – HIT (Heavy Ion Therapy) which is designed for applications to the field of hadron therapy in oncology (Gudowska et al., 2004; Hansen et al., 2012). The medical version uses the same generator of nuclear reactions MSDM, but includes more detailed energy grids, more precise data for the stopping power dE/dx, and improved models of the electromagnetic fluctuations, with the goal of calculating dose fields with the necessary accuracy, where the energy range for charged particles is narrowed to the interval 25 keV/n − 2 GeV/n.

2.3. GEANT

Some calculations using the GEANT (GEometry ANd Tracking) Monte Carlo transport code are also shown in this paper. The GEANT4 version 10.01 (Agostinelli et al., 2003) was used. The software has been developed as a C++ toolkit and users must write an application that utilizes modules from the toolkit. A variety of physics packages are available, with the QGSP-BERT-HP and QMD packages being used in the present work: the Quark Gluon String (QGS) model is used for high energy nucleons, pions and nuclei; the Precompound (P) model handles post-interaction nuclear de-excitation; the Bertini cascade (BERT) is used for interactions below 10 GeV. The Quantum Molecular Dynamics (QMD) is used for heavy ion collisions and the High Precision (HP) neutron database is used for low energy interactions.

2.4. FLUKA

The FLUKA (FLUctuating KAscade) Monte Carlo transport code was also used to make specific comparisons in this study (release version FLUKA2011 Version 2c dated October 2014) (Ferrari et al., 2005; Bohlen et al., 2014). The precision defaults were used, which include three heavy ion event generators, Dual Parton Model and Jets III (DPMJET-III), Relativistic Quantum Molecular Dynamics (RQMD), and the Boltzmann Master Equation (BME) models (Roesler et al., 2001; Sorge et al., 1989a, 1989b; Cerutti et al., 2006). The energy transition used between the DPMJET3/RQMD was set at 10 GeV (note: FLUKA default transition is at 5 GeV/n), where DPMJET3 was used above 10 GeV/n and RQMD was used between 10 GeV/n and 0.1 GeV/n, with the BME model used for energies lower than 0.1 GeV/n. All models are processed by a generalized intra-nuclear cascade followed by a pre-equilibrium stage and then an evaporation-fragmentation-fission stage.

3. Outline of Calculations

A benchmark problem was defined for comparing the transport codes, which consisted of a broad energy spectrum, galactic cosmic ray (GCR) pencil beam boundary condition incident on an aluminum cylinder, as shown in Figure 1. The cylinder radius is set to 5 times the length, to reduce lateral leakage, and mimics a semi-infinite slab geometry. GCR solar minimum and maximum environments were studied, but only the GCR minimum results will be shown. Solar particle event (SPE) boundary conditions have also been studied, but are not reported in the present work. The charge Z = 1, 2, 8, 14, 26 (H, He, O, Si, Fe respectively) components of the GCR spectrum were considered separately and the H, O, and Fe results will be shown. The GCR minimum input spectra comes from the work of Denisov et al. (2011).

Figure 1:

Figure 1:

Open in a new tab

Benchmark problem: GCR minimum particles are incident on an Aluminum cylinder target of varying thickness. Particles exiting the back surface of the target are tracked and flux spectra are calculated.

A variety of cylinder lengths were studied, namely 1, 3.16, 10, 31.6 and 100 g/cm2. Only results from the 1, 10, and 100 g/cm2 cylinders will be shown here. Particles exiting the back surface of the cylinder were tracked and their fluxes were determined. The tracked primary and secondary particles exiting the back slab were neutrons, protons (11H), deuterons (12H), tritons (13H), helions (11H),(23He), alphas (24He), and pions (π±). For GCR 16O projectiles, the ions 816O,714N,612C were also tracked. For GCR 56Fe projectiles, the ions 2656Fe,2554Mn,2452Cr were tracked. (Note that results for 1 g/cm2 provide an almost direct comparison of nuclear models. Results at 100 g/cm2 are dominated by nucleon physics and transport.)

4. Results

4.1. Neutron production

HZETRN2015, SHIELD and GEANT4 results for neutron production are shown in Figures 2 and 3 for H, O and Fe projectiles. (H projectiles are shown in a different figure to O and Fe because H is an elementary projectile, which does not fragment. The heavier projectiles O and Fe are complex, consisting of many nucleons, and undergo fragmentation reactions.) Neutron production is seen to increase significantly as the shield thickness is increased. HZETRN2015 was run in the 3D (arbitrary N) mode. An approximate representation of neutron production from the target following a heavy ion nuclear collision was utilized in this work (Wilson et al., 1991). The rather simple approximation scales the proton-induced differential cross section by A0.4, where A is the mass of the projectile.

Figure 2:

Figure 2:

Open in a new tab

Neutrons (n) exiting Al cylinders exposed to GCR solar minimum 1H projectiles.

Figure 3:

Figure 3:

Open in a new tab

Neutrons (n) exiting Al cylinders exposed to GCR solar minimum for a) 16O and b) 56Fe projectiles.

The codes are generally in good agreement with each other, except in the 100 MeV region for O and Fe projectiles, where HZETRN is lower than SHIELD and GEANT. The differences near 100 MeV are due to nuclear model differences and transport approximation error in HZETRN2015. The 3D transport included in HZETRN2015 relied on the forward/isotropic formalism that does not account for the full angular detail of the neutron production cross section. Such errors are more apparent in the mid energy region where produced particles are neither fully forward nor fully isotropic.

4.2. Light ion production

Results for light ion (isotopes of Hydrogen and Helium) production are shown in Figures 4 - 8 for GCR minimum H, O and Fe projectiles impinging on an Al target of varying thickness.

Figure 4:

Figure 4:

Open in a new tab

Protons (p) exiting Al cylinders exposed to GCR solar minimum 1H.

Figure 8:

Figure 8:

Open in a new tab

Deuterons (d) and alpha (α) particles exiting Al cylinders exposed to GCR solar minimum 56Fe projectiles. A direct knockout model is used for a) and b) and is turned off for c) and d) (KOoff). Deuteron calculations have been scaled by 5 and 100 for 10 g/cm2 and 100 g/cm2 respectively. Alpha calculations have been scaled by 10 and 1000 for 10 g/cm2 and 100 g/cm2 respectively.

4.2.1. Proton production

Proton production from proton (H) projectiles is shown in Figure 4, while Figure 5 shows proton production from O and Fe projectiles. When the projectile is a proton, the high energy proton flux is somewhat attenuated as the depth increases. At low energy the proton flux increases with depth. For O and Fe projectiles, the proton flux increases at all energies as shield thickness is increased.

Figure 5:

Figure 5:

Open in a new tab

Protons (p) exiting Al cylinders exposed to GCR solar minimum for a) 16O and b) 56Fe projectiles.

For proton production from proton projectiles (Figure 4), one sees good agreement between all codes due to the fact that the transport is dominated by stopping power and total cross sections, which are both relatively well-known. For proton production from O and Fe projectiles (Figure 5), there is reasonable agreement between codes, given the differences in nuclear models (especially apparent for 1 g/cm2) and transport methods. HZETRN is missing light target evaporation fragments produced from heavy ions, which accounts for almost all of the observed differences at 1 g/cm2 and 10 g/cm2.

4.2.2. Deuteron and alpha production

Deuteron (2H) and alpha (4He) production results are shown in Figure 6 for H projectiles and in Figures 7 and 8 for O and Fe projectiles. SHIELD and GEANT4 show good agreement, however, with some significant differences around 100 MeV/n and also near the high energy projectile fragmentation peak. Graphs a and b in each figure show HZETRN results using a simplified model of direct light ion knockout from the target (Cucinotta et al., 1996). Graphs c and d in each figure show this model switched off, resulting in better agreement of HZETRN with SHIELD and GEANT4. The codes appear to be in reasonable agreement in the high energy region; however, the plots are in log-scale and the differences are actually factors of two or more at high energies. Differences appear smaller at high energies than they do at low energies, but are still quite substantial due to uncertainties and measurement gaps associated with light ion production from heavy ions. For the lower energy region, where target fragments contribute, there are significant differences between the codes. All three codes include low energy target evaporation, although HZETRN does not include light target evaporation fragments produced from heavy ions. HZETRN also includes the direct-knockout spectrum which extends up to higher energies. It would be worthwhile to see SHIELD results extended to lower energy in future work.

Figure 6:

Figure 6:

Open in a new tab

Deuterons (d) and alpha (α) particles exiting Al cylinders exposed to GCR solar minimum 1H projectiles. A direct knockout model is used for a) and b) and is turned off for c) and d) (KOoff).

Figure 7:

Figure 7:

Open in a new tab

Deuterons (d) and alpha (α) particles exiting Al cylinders exposed to GCR solar minimum 16O projectiles. A direct knockout model is used for a) and b) and is turned off for c) and d) (KOoff). Calculations have been scaled by 5 and 100 for 10 g/cm2 and 100 g/cm2 respectively.

4.3. Heavy ion production

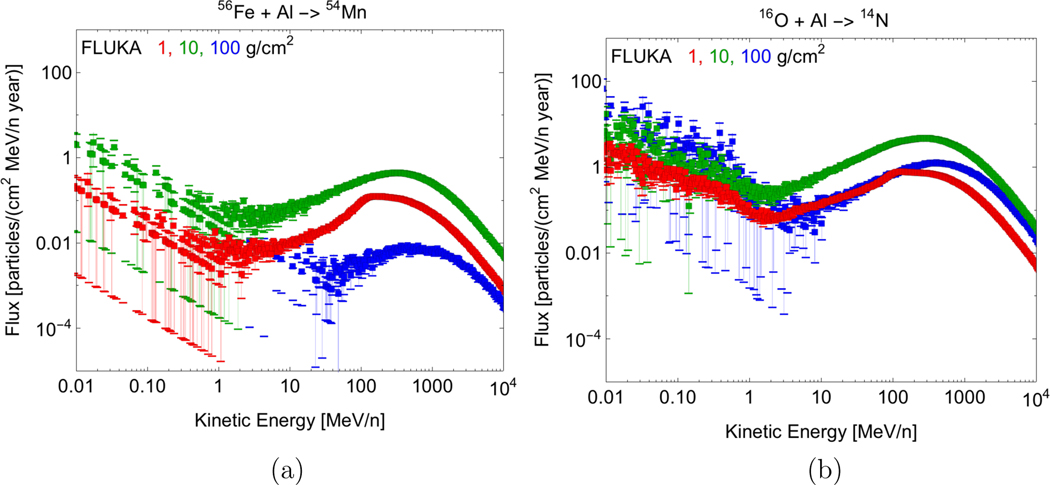
In order to clearly see the fragment production behavior as a function of depth, examples of FLUKA calculations of Fe, Mn, and Cr production from Fe projectiles (Figures 9a, 10a, 11a respectively) and O, N, C production from O projectiles (Figures 9b, 10b, 11b respectively) are shown. Figure 9 shows the Fe and O flux decreasing with depth due to slowing down of the projectiles and attenuation (loss) associated with nuclear interactions. Note that Fe cannot be produced from Al target fragmentation, whereas O can be produced from target fragmentation. The low energy buildup is due to the larger number of slower projectiles and target production of O (but not Fe) fragments.

Figure 9:

Figure 9:

Open in a new tab

FLUKA calculations of a) 56Fe and b) 16O exiting Al cylinders exposed to GCR solar minimum a) 56Fe and b) 16O projectiles.

Figure 10:

Figure 10:

Open in a new tab

FLUKA calculations of a) 54Mn and b) 14N exiting Al cylinders exposed to GCR solar minimum a) 56Fe and b) 16O projectiles.

Figure 11:

Figure 11:

Open in a new tab

FLUKA calculations of a) 52Cr and b) 12C exiting Al cylinders exposed to GCR solar minimum a) 56Fe and b) 16O projectiles.

Figures 10 and 11 show FLUKA calculations for fragment production with one- and two-nucleon removals, respectively. Mn and Cr can be produced from Fe projectile fragmentation, but not Al target fragmentation. C and N can be produced both from O projectile fragmentation and Al target fragmentation. Both figures show fragment production increasing from 1 g/cm2 to 10 g/cm2, with production decreasing again at 100 g/cm2. The decline after ∼10 g/cm2 is due to attenuation associated with nuclear collisions and the diminishing flux of larger mass projectiles serving as the source term for these fragments. (This behavior is not seen in Figure 9, because the projectile fragments are produced elastically.) Again, the low energy buildup is due to the larger number of slower projectiles and target production of N and C (but not Mn or Cr) fragments.

Code comparisons for Fe, Mn and Cr production from Fe projectiles are shown in Figures 12 - 14, respectively for 1, 10, and 100 g/cm2. Recall that Fe, Mn, and Cr fragments can only be produced from Fe projectile fragmentation and cannot be produced from Al target fragmentation. Good agreement for 56Fe production is seen from all codes because transport is dominated by stopping power and total cross sections, which are both relatively well know. Generally, qualitative agreement is seen for Mn and Cr production (with differences of a factor of two or more), although there are insufficient FLUKA statistics and no SHIELD results at low energy. FLUKA and SHIELD show disagreements in the hundreds of Mev/n region, where HZETRN and GEANT agree well, lying between the SHIELD and FLUKA results.

Figure 12:

Figure 12:

Open in a new tab

56Fe exiting Al cylinders exposed to GCR solar minimum 56Fe projectiles as a function of shield depth, a) 1 g/cm2, b) 10 g/cm2, and c) 100 g/cm2.

Figure 14:

Figure 14:

Open in a new tab

52Cr exiting Al cylinders exposed to GCR solar minimum 56Fe projectiles as a function of shield depth, a) 1 g/cm2, b) 10 g/cm2, and c) 100 g/cm2.

Code comparisons for O, N, and C production from O projectiles are shown in Figures 15 - 17, respectively for 1, 10, and 100 g/cm2. These figures show the interesting results where C, N and O fragments can be produced via both O projectile and Al target fragmentation. There is a much more significant rise in the low energy fragment production due to production from the Al target. Overall, good agreement for O production is found from all codes, but with some disagreements with GEANT at low energy. The rise in the low energy portion of GEANT4 results at 100 g/cm2 are associated with nucleon induced target fragmentation. Similar low energy behavior is seen in subsequent plots and differences are consistent with uncertainties in heavy ion fragmentation models.

Figure 15:

Figure 15:

Open in a new tab

16O exiting Al cylinders exposed to GCR solar minimum 16O projectiles as a function of shield depth, a) 1 g/cm2, b) 10 g/cm2, and c) 100 g/cm2.

Figure 17:

Figure 17:

Open in a new tab

12C exiting Al cylinders exposed to GCR solar minimum 16O projectiles as a function of shield depth, a) 1 g/cm2, b) 10 g/cm2, and c) 100 g/cm2.

The low energy target fragmentation bump does not appear for 16O + Al → 16O for thin (1, 10 g/cm2) targets, but it does appear for the thick (100 g/cm2) target case in Figure 15. The low energy rise of the O fragment for thinner shields is simply due to slowing down of the projectile. O can be produced from target fragmentation and one expects more at larger depths. The low energy target fragmentation bump does appear for 16O + Al → 14N and 16O + Al → 12C for all thin and thick targets, because 14N and 12C produced from both projectile and target fragmentation.

4.4. Pion production

Results for pion production are shown in Figures 18 - 20. FLUKA example results are separated (graph a in each figure) in order to clearly show the behavior as a function of depth. As expected, pion production increases with depth for all projectiles. Code comparisons are shown for HZETRN, SHIELD and FLUKA for shield thicknesses of 1, 10, and 100 g/cm2 in graphs b, c, and d of each figure, respectively. Overall, good agreement is seen with the largest disagreements for the thin shield 1 g/cm2, reflecting differences in nuclear models, as noted previously. The SHIELD and FLUKA results are in excellent agreement for all reactions.

Figure 18:

Figure 18:

Open in a new tab

Charged pions (π+ +π−) exiting Al cylinders exposed to GCR solar minimum 1H projectiles. a) FLUKA calculations show flux increasing with increasing depth. b-d) code comparisons as a function of shield depth.

Figure 20:

Figure 20:

Open in a new tab

Charged pions (π+ +π−) exiting Al cylinders exposed to GCR solar minimum 56Fe projectiles. a) FLUKA calculations show flux increasing with increasing depth. b-d) code comparisons as a function of shield depth.

5. Summary and Conclusions

This paper represents the first direct comparisons of the American (NASA) and Russian (ROSCOSMOS) space radiation transport codes, HZETRN and SHIELD. Calculations of the flux spectra of neutrons, light ions, heavy ions and pions were presented for GCR minimum Hydrogen, Oxygen and Iron projectiles incident on a uniform Aluminum cylinder of varying thickness. Some comparison calculations with the GEANT4 and FLUKA transport codes were also shown.

Neutron production calculations showed good agreement between HZETRN, SHIELD and GEANT, with some moderate differences near 100 MeV and also at very low energy. Proton calculations between HZETRN, SHIELD and GEANT showed good agreement for a thick (100 g/cm2) target. SHIELD and GEANT showed good agreement for all thicknesses, with significant differences from HZETRN, especially for the very thin (1 g/cm2) target, reflecting differences in nuclear models, which should all be applicable to these calculations.

Deuteron and alpha production showed qualitative agreement between codes with the largest differences being for the 100 MeV region and for the very thin (1 g/cm2) target, again reflecting differences in nuclear models. Comparison calculations of heavy ion production were made between HZETRN, SHIELD, GEANT and FLUKA. In general, the codes were in reasonable agreement with each other, with some moderate differences at low energy. Comparison calculations of pion production were made between HZETRN, SHIELD and FLUKA, with good agreement between codes.

Overall, this study showed good agreement between HZETRN and SHIELD and also with GEANT and FLUKA. The largest discrepancies were for light ion production from thin targets.

Figure 13:

Figure 13:

Open in a new tab

54Mn exiting Al cylinders exposed to GCR solar minimum 56Fe projectiles as a function of shield depth, a) 1 g/cm2, b) 10 g/cm2, and c) 100 g/cm2.

Figure 16:

Figure 16:

Open in a new tab

14N exiting Al cylinders exposed to GCR solar minimum 16O projectiles as a function of shield depth, a) 1 g/cm2, b) 10 g/cm2, and c) 100 g/cm2.

Figure 19:

Figure 19:

Open in a new tab

Charged pions (π+ +π−) exiting Al cylinders exposed to GCR solar minimum 16O projectiles. a) FLUKA calculations show flux increasing with increasing depth. b-d) code comparisons as a function of shield depth.

6. Acknowledgements

HZETRN2015 calculations were done by J. Norbury, subsequent to previous calculations using HZETRN2010 done by T. Slaba and J. Norbury. SHIELD calculations were done by N. Sobolevsky. GEANT calculations were done by T. Slaba. FLUKA calculations were done by B. Reddell. This work began with a series of joint technical interchange meetings between space radiation scientists from NASA, ROSCOSMOS and other space agencies held in Moscow over the past several years. Support from NASA, ROSCOSMOS and other space agencies is gratefully acknowledged. This work was supported in part by the Human Research Program under the Human Exploration and Operations Mission Directorate of NASA.

References

  1. Abagyan LP, Bazazyants NO, Nikolaev MN, Tsibulya AM, 1981. Group constants for calculations of reactors and shielding. Handbook. Energoizdat, Moscow, 1981 (in Russian). [Google Scholar]
  2. Adamczyk AM, Norman RB, Sriprisan S, Townsend LW, Norbury JW, Blattnig SR, Slaba TC, 2012. NUCFRG3: Light ion improvements to the nuclear fragmentation model. Nuclear Instruments and Methods in Physics Research A 678, 21–32. [Google Scholar]
  3. Adeev GD, Botvina AS, Iljinov AS, Mebel MV, Piscasov NI, Serdyuk OI, 1993. A Method of Calculation of Mass and Energy Distributions of Fission Residuals in Reactions Induced by Intermediate Energy Particles. INR RAS 816/1993, Moscow (in Russian). [Google Scholar]
  4. Agostinelli S, et al. , 2003. Geant – a simulation toolkit. Nucl. Instrum. Meth. Phys. Res. A 506, 250–303. [Google Scholar]
  5. Amelin NS, Gudima KK, Toneev VD, 1990a. Ultrarelativistic Nucleus-Nucleus Collisions within a Dynamical Model of Independent Quark-Gluon strings. Yadernaya Fizika 51, 1730 (in Russian). Preprint GSI-89–52. [Google Scholar]
  6. Amelin NS, Gudima KK, Siviklokov SY, Toneev VD, 1990b. Further Development of the Quark-Gluon Strings Model for Describing High-Energy Collisions with Nuclear Target. Yadernaya Fizika 52, 272. (in Russian) [Google Scholar]
  7. Armstrong TW, Chandler KG, 1972. HETC - A High Energy Transport Code. Nucl. Sci. Eng 49(1972)110–111. [Google Scholar]
  8. Barashenkov VS, Sobolevsky NM, Toneev VD, 1972. Interaction of high-energy radiation with matter. Atomnaya Energiya 32, 123 (in Russian). [Google Scholar]
  9. Battistoni G. et al. , 2015. Overview of the FLUKA code. Ann. Nucl. Energy 82, 10–18. [Google Scholar]
  10. Bohlen TT, Cerutti F, Chin MW, Fasso A, Ferrari A, Ortega PG, Mairani A, Sala PR, Smirnov G, Vlachoudis V, 2014. The FLUKA code: developments and challenges for high energy and medical applications. Nucl. Data Sheets 120, 211214. [Google Scholar]
  11. Bondorf JP, Botvina AS, Iljinov AS, Mishustin IN, Sneppen K, 1995. Statistical multifragmentation of nuclei. Phys. Rep 257, 133–221. [Google Scholar]
  12. Botvina AS, Iljinov AS, Mishustin IN, Bondorf JP, Donangelo R, Sneppen K, 1987. Statistical Simulation of the Break up of Highly Excited Nuclei. Nucl. Phys.A475, 663–686. [Google Scholar]
  13. Botvina AS, Dementyev AV, Smirnova ON, Sobolevsky NM, Toneev VD, 1997. MSDM - Multy Stage Dynamical Model. International Codes and Model Inter-comparison for Intermediate Energy Activation Yields, by R.Michel and P.Nagel, NSC/DOC(97)-1, NEA/P&T No 14, OECD, Paris, 1997, p.307. [Google Scholar]
  14. Cerutti F, Battistoni G, Capezzali G, Colleoni P, Ferrari A, Gadioli E, Mairani A, Pepe A, 2006. Low energy nucleus-nucleus reactions: the BME approach and its interface with FLUKA. Proceedings of the 11th International Conference on Nuclear Reactions Mechanisms, Gadioli E. (editor). Villa Monastero, Varenna, Italy, 12–16 June 2006. [Google Scholar]
  15. Charara YM, Townsend LW, Gabriel TA, Zeitlin CJ, Heilbronn LH, Miller J, 2008. HETC-HEDS code validation using laboratory beam energy loss spectra data. IEEE Trans. Nucl. Sci 55, 3164–3168. [Google Scholar]
  16. Coleman WA, Armstrong TW, 1971. NMTC - A Nucleon-Meson Transport Code. Nucl. Sci. Eng 43, 353–354. [Google Scholar]
  17. Cucinotta FA, Townsend LW, Wilson JW, Shinn JL, Badhwar GD, Dubey RR, 1996. Light ion components of the galactic cosmic rays: nuclear interactions and transport theory. Adv. Space Res 17, 77–86. [DOI] [PubMed] [Google Scholar]
  18. Dementyev AV, Sobolevsky NM, 1999. SHIELD – universal Monte Carlo hadron transport code: scope and applications. Rad. Meas 30, 553–557. [Google Scholar]
  19. Denisov AN Kuznetsov NV, Nymmik RA, Panasyuk MI, Sobolevsky NM, 2011. Assessment of the radiation environment on the Moon. Acta Astro. 68, 1440–1447. [Google Scholar]
  20. Ferrari A, Sala PR, Fasso A, Ranft J, 2005. FLUKA: A Multi-Particle Transport Code CERN 2005–10 / SLAC-R-773 preprint. [Google Scholar]
  21. Gudima KK, Mashnik SG, Toneev VD, 1983. Cascade-Exciton Model of Nuclear Reactions. Nucl. Phys. A401, 329–361. [Google Scholar]
  22. Gudowska I, Sobolevsky N, Andreo P, Belkic D, Brahme A, 2004. Ion Beam Transport in Tissue-Like Media Using the Monte Carlo Code SHIELD-HIT. Phys. Med. Biol 49, 1933–1958. [DOI] [PubMed] [Google Scholar]
  23. Hansen DC, Luhr A, Sobolevsky N, Bassler N, 2012. Optimizing SHIELD-HIT for carbon ion treatment. Phys. Med. Biol 57, 2392–2409. [DOI] [PubMed] [Google Scholar]
  24. Heinbockel JH, Slaba TC, Blattnig SR, Tripathi RK, Townsend LW, Handler T, Gabriel TA, Pinsky LS, Reddell B, Clowdsley MS, Singleterry RC, Norbury JW, Badavi FF, Aghara SK, 2011a. Comparison of transport codes HZETRN, HETC and FLUKA for a solar particle event. Adv. Space Res 47, 1079–1088. [Google Scholar]
  25. Heinbockel JH, Slaba TC, Tripathi RK, Blattnig SR, Norbury JW, Badavi FF, Townsend LW, Handler T, Gabriel TA, Pinsky LS, Reddell B, Aumann AR, 2011b. Comparison of the Transport Codes HZETRN, HETC and FLUKA for galactic cosmic rays. Adv. Space Res 47, 1089–1105. [Google Scholar]
  26. Latysheva LN, Sobolevsky NM, 2008. LOENT - the code for Monte Carlo simulation of neutron transport in complex geometries. INR RAS 1200/2008, Moscow, 2008 (in Russian). [Google Scholar]
  27. Lin ZW, Adams JH, Barghouty AF, Randeniya SD, Tripathi RK, Watts JW, Yepes PP, 2012. Comparisons of several transport models in their predictions in typical space radiation environments. Adv. Space Res 49, 797–806. [Google Scholar]
  28. Matthia D, Ehresmann B, Lohf H, Kohler J, Zeitlin C, Appel J, Sato T, Slaba TC, Martin C, Berger T, Boehm E, Boettcher S, Brinza DE, Burmeister S, Guo J, Hassler DM, Posner A, Rafkin SCR, Reitz G, Wilson JW, Wimmer-Schweingruber RF, 2016. The Martian surface radiation environment - a comparison of models and MSL/RAD measurements. J. Space Weather & Space Climate 6, A13. [Google Scholar]
  29. McKinney GW, Lawrence DJ, Prettyman TH, Elphic RC, Feldman WC, Hagerty JJ, 2006. MCNPX benchmark for cosmic ray interactions with the Moon. J. Geophys. Res 111, E06004. [Google Scholar]
  30. Roesler S, Engel R, Ranft J, 2001. The Monte Carlo event generator DPMJET-III. In: Proceedings of the Monte Carlo 20 0 0 Conference: 1033–1038. [Google Scholar]
  31. Sato T, Niita K, Iwase H, Nakashima H, Yamaguchi Y, Sihver L, 2006. Applicability of particle and heavy ion transport code PHITS to the shielding design of spacecrafts. Radiat. Meas 41, 1142–1146. [Google Scholar]
  32. Sato T, Niita K, Matsuda N, Hashimoto S, Iwamoto Y, Noda S, Ogawa T, Iwase H, Nakashima H, Fukahori T, Okumura K, Kai T, Chiba S, Furuta T, Si-hver L, 2013. Particle and heavy ion transport code system PHITS, version 2.52. J. Nucl. Sci. Technol 50, 913–923. [Google Scholar]
  33. Slaba TC, Wilson JW, Badavi FF, Reddell BD, Bahadori AA, 2016. Solar proton exposure of an ICRU sphere within a complex structure part II: Ray-trace geometry Life Sci. Space Res. 9, 77–83. [DOI] [PubMed] [Google Scholar]
  34. Slaba TC, Bahadori AA, Reddell BD, Singleterry RC, Clowdsley MS, Blattnig SR, 2017. Optimal shielding thickness for galactic cosmic ray environments. Life Sci. Space Res 12, 1–15. [DOI] [PubMed] [Google Scholar]
  35. Sobolevsky NM, 1970. Program of calculation of nucleon-meson cascade in matter by Monte Carlo. JINR, B1–2-5458, Dubna. (in Russian) [Google Scholar]
  36. Sobolevsky NM, 2015. Algorithm for storing of the hadron cascade tree in the SHIELD transport code. INR RAS 1398/2015, Moscow. (in Russian). [Google Scholar]
  37. Sorge H, Stoecker H, Greiner W, 1989a. Poincare invariant Hamiltonian dynamics: Modelling multi-hadronic interactions in a phase space approach. Ann. Phys 192, 266306. [Google Scholar]
  38. Sorge H, Stoecker H, Greiner W, 1989b. Relativistic quantum molecular dynamics approach to nuclear collisions at ultrarelativistic energies. Nucl. Phys. A498, 567c–576c. [Google Scholar]
  39. Toneev VD, Gudima KK, 1983. Particle Emission in Light and Heavy Ion Reactions. Nucl. Phys.A400, 173–189. [Google Scholar]
  40. Townsend LW, Miller TM, Gabriel TA, 2005. HETC radiation transport code development for cosmic ray shielding applications in space. Rad. Prot. Dosim 116, 135–139. [DOI] [PubMed] [Google Scholar]
  41. Wilson JW, Townsend LW, Schimmerling W, Khandelwal GS, Khan F, Nealy JE, Cucinotta FA, Simonsen LC, Shinn JL, Norbury JW, 1991. Transport methods and interactions for space radiations. NASA Reference Publication 1257. [Google Scholar]
  42. Wilson JW, Slaba TC, Badavi FF, Reddell BD, Bahadori AA, 2014. Advances in NASA radiation transport research: 3DHZETRN. Life Sci. Space Res 2, 6–22. [Google Scholar]
  43. Wilson JW, Slaba TC, Badavi FF, Reddell BD, Bahadori AA, 2015a. 3DHZETRN: Shielded ICRU spherical phantom Life Sci. Space Res. 4, 46–61. [DOI] [PubMed] [Google Scholar]
  44. Wilson JW, Slaba TC, Badavi FF, Reddell BD, Bahadori AA, 2015b. 3DHZETRN: Neutron leakage in finite objects Life Sci. Space Res. 7, 27–38. [DOI] [PubMed] [Google Scholar]
  45. Wilson JW, Slaba TC, Badavi FF, Reddell BD, Bahadori AA, 2016. Solar proton exposure of an ICRU sphere within a complex structure Part I: Combinatorial geometry Life Sci. Space Res. 9, 69–76. [DOI] [PubMed] [Google Scholar]

RESOURCES