Technical Note: Film-Based Measurement of Gold Nanoparticle Dose Enhancement for ¹⁹²Ir

Abstract

Purpose

The purpose of this work is to introduce a simple yet accurate technique to measure the dose enhancement factor (DEF) of a citrate-capped gold nanoparticle (GNP) solution using EBT3 film in an ¹⁹²Ir setup.

Methods

DEF is the ratio of absorbed dose in a solution compared to absorbed dose in water, assuming identical irradiation parameters. Citrate-capped GNPs were synthesized. An acrylic apparatus was constructed such that the EBT3 film was placed in charged particle equilibrium within the GNP solution with 0.28%, 0.56%, and 0.77% gold by mass. Sets of 12 dose measurements were collected for each GNP concentration as well as for water. The expected value of DEF was also calculated with the effective mass absorption coefficient of the GNP solution and water for an ¹⁹²Ir spectrum. Furthermore, Burlin cavity correction factors were calculated and experimentally verified. Experimental verification of the cavity correction was performed by measuring DEF using stacks of 1, 3, and 5 sheets of film and extrapolating the DEF to 0 sheets of film.

Results

Experimental cavity corrections agreed with those calculated with the Burlin cavity formalism. The calculated DEF was 1.013, 1.027, and 1.037 for the 0.28%, 0.56%, and 0.77% gold by mass GNP solutions, respectively. The corresponding uncorrected DEF measurement values were 1.013±0.006, 1.024±0.010, and 1.032±0.006, respectively. When applying the Burlin cavity formalism, the final corrected DEF measurement values were 1.016±0.006, 1.029±0.010, and 1.039±0.006, respectively.

Conclusion

The experimental cavity correction results agreed with the theoretical Burlin calculations, which allowed for the Burlin corrections to be performed for all GNP concentrations and measured DEF values. The adjusted DEF values agreed with the theoretical calculations. Thus, these results indicate that a Burlin cavity calculation can be applied to correct film-based DEF measurements for ¹⁹²Ir.

I. INTRODUCTION

Photon beams that are used for radiotherapy treatments are non-discriminatory when interacting with their medium, depositing dose to both cancerous and healthy tissue. For this reason, beam geometry and intensity modulation are used to minimize dose delivery to healthy tissue. However, they do not address the fundamental issue of photons damaging all tissue in their path. Gold nanoparticles (GNPs) can potentially be used to enhance dose to an immediate region, in and around a tumor. This effect is particularly strong for low photon energies, where the high atomic number of gold greatly increases the photoelectric interactions (1,2). Dose enhancement factor (DEF) is a commonly utilized metric for reporting the effect of GNPs and is defined as the ratio of absorbed dose to a GNP solution relative to another medium (water is used as the reference medium in this study).

Monte Carlo (MC) simulations are one of the main tools used to explore GNP dose enhancement (3–12). DEF is greatly dependent on photon energy. Energies ranging from 50 kVp to 6 MV photon sources from linear accelerators were investigated. Published data have shown that higher GNP concentrations and lower photon energies increase DEF values (5,6,8). Cho et al. (6) reported that 18 mg Au/gram tumor produced DEF values of 2.16, 1.92, and 2.08 with ¹²⁵I, 50 kVp, and ¹⁶⁹Yb, respectively, but 1.68, 1.57, and 1.44 DEF with ¹²⁵I, 50 kVp, and ¹⁶⁹Yb with a concentration of 7 mg Au/gram tumor, respectively. Yoon et al. (7) predicted a DEF in a 5% Au by weight GNP solution of 1.11 with ¹⁹²Ir irradiation. Furthermore, Mesbahi et al. (5) calculated that the optimum energy to produce DEF was 90 keV. A summary of these reported enhancements appears in Table 1.

Table 1.

Dose enhancement factors as a function of radiation source and weight percent of gold.

% Gold by mass	Radiation Source	DEF
1.8	I-125	2.16
1.8	50 kVp	1.92
1.8	Yb-169	2.08
0.7	I-125	1.68
0.7	50 kVp	1.57
0.7	Yb-169	1.44
5.0	Ir-192	1.11

The studies reported DEF values as averaged across macroscopic volumes, but MC simulations are also able to calculate the range and microscopic spatial distribution of the dose enhancement (8,10,11). A MC study performed by Jones et al. (10) reported that DEF was 2.0 within 5 µm of the GNPs but was reduced to only 1.05 30 µm from the GNPs. Lin et al. (11) performed a MC study and calculated that DEF was within 1.15 for the first 10 nm from the GNPs for both kVp and MV photons.

Irradiation of cell cultures is another way to measure the enhancement effects of GNPs. Cell culture assays using GNPs vs. a control group determined that the addition of GNPs to radiation therapy decreased the cell survival rate (13–18). Zhang et al. (14) measured cellular uptake in thio-glucose GNPs (Glu-GNP) and sodium citrate GNPs (TGS-GNPs) in conjunction with radiotherapy. A cellular growth inhibition of 30.6% and 46.0% in Glu-GNP and TGS-GNPs, respectively, was measured. Whereas, a growth inhibition of 15.9% was measured with irradiation alone. Liu et al. (15) discovered that the percentage of surviving cells after irradiation decreased by 2–45%, depending on the source and concentration of polyethylene glycol (PEG)ylated-GNPs. Hainfield et al. (19) performed an in vivo study with mice. They discovered that mice treated with radiation therapy in conjunction with GNPs had an 86% 1-year survival rate, compared to a 20% rate for mice with no GNPs supplementing their treatment.

There exists a knowledge gap between MC simulations and in vitro/in vivo studies. If there is a discrepancy between the results, this could either be due to the GNP solution not being accurately represented in simulations or as a result of biological factors such as GNP cell uptake. For this reason, methods to physically measure dose enhancement are useful tools. They can directly measure the component of the GNP radiosensitization coming from the increase in absorbed dose. These measurements can be used to validate MC simulations and theoretical expectations. A discrepancy between physical dose enhancement and simulations would be able to reveal issues with the assumed properties of the GNP solution or errors in the simulation setup.

Gel dosimetry was used to determine DEF values (20–23), but it is a time consuming and an expensive process. The purpose of this work was to develop an easy to replicate and reliable technique for measuring physical dose enhancement, which can serve as a verification for GNP DEF values. The chosen source was ¹⁹²Ir due to its prevalence in radiation oncology clinics and its low average photon energy, which improves dose enhancement. EBT3 radiochromic film along with a Burlin cavity correction was used to measure the DEF (24, 25). This correction formalism was chosen due to its conceptual simplicity, direct applicability to the film-based experimental setup, and the fact that it does not require Monte Carlo simulations. The measured values are benchmarked against theoretical expectations of DEF for the GNP concentration and ¹⁹²Ir spectrum.

II. METHODS AND MATERIALS

II. A. Nanoparticle Synthesis and Characterization

The GNP synthesis was completed at the University of Texas at San Antonio (UTSA). GNPs were synthesized using a citrate reduction method (26). All solutions were prepared using ultrapure deionized water. First, a 12.7 mM aqueous solution of tetrachloroauric acid (HAuCl₄) was prepared. 14.4 mL of this solution was centrifuged in 1.2 mL aliquots for 60 minutes at 14,000g. 1 mL of supernatant was removed from each microcentrifuge tube and reserved, and the remaining 0.2 mL of solution was discarded to remove any aggregates. 12 mL of the HAuCl₄ solution was added to a flask containing 600 mL Milli-Q water. While stirring, the solution was brought to a boil on a hot plate. Next, 8 mL of a 36.5 mM sodium citrate aqueous solution was added to the flask and the resulting solution was boiled for an additional 10 minutes. A color change from clear to dark red indicated successful synthesis of citrate-capped GNPs.

After the GNPs were synthesized, the solution was concentrated by placing 14 mL of the GNP solution into 15 mL centrifuge tubes, which were then centrifuged at 4,000 rpm for 25 minutes. After the GNPs were centrifuged, approximately 13 mL of the supernatant was removed and discarded. Approximately 1 mL of concentrated GNP solution remained and was reserved. These concentrated portions were collected and centrifuged for an additional 25 minutes at 4,000 rpm, and the supernatant was again discarded.

The size of the GNPs was determined via scanning electron microscopy (SEM). GNP solution was drop-cast onto silicon wafers and allowed to dry; the wafers were then rinsed with a copious amount of deionized water. SEM images of the GNPs were acquired using a Hitachi S5500 STEM instrument located in the Kleberg Advanced Microscopy Center, which is located at UTSA. Particle size analysis was carried out using ImageJ and the mean GNP diameter and standard deviation was determined to be 29.8 ± 2.8 nm.

II.B. Theoretical calculations

Theoretical DEF calculations serve as a benchmark for the measurements. This theoretical DEF was determined using Eq. 1, which is valid under the assumption that charged particle equilibrium (CPE) exists (25).

$$DEF=\frac{{\left(\frac{{\mu }_{en}}{\rho }\right)}_{H_{2}O}\cdot f_{H2O}+{\left(\frac{{\mu }_{en}}{\rho }\right)}_{Au}\cdot f_{Au}}{{\left(\frac{{\mu }_{en}}{\rho }\right)}_{H_{2}O}}$$ (1)

The factors ${\frac{{\mu }_{en}}{\rho }}_x$ and $f_x$ represent the mass energy absorption coefficient and fraction of material by weight present in liquid media x, respectively. The effective mass attenuation coefficient was determined from the photon energy spectrum for the microSelectron-v2 HDR source, as described by Taylor et al. (27). Mass energy absorption coefficients for the energy bins of the spectrum were obtained from the National Institute of Standards and Technology (28) and used with Eq. 2 to calculate the expected $\frac{{\mu }_{en}}{\rho }$.

$$<\frac{{\mu }_{en}}{\rho }> =\frac{\int \frac{{\mu }_{en}}{\rho }\cdot E\cdot \varphi dE}{\int E\cdot \varphi dE}$$ (2)

The variables E and ϕ represent the energy and fluence of the photon spectrum, respectively. For each energy bin of the photon spectrum (27), the associated $\frac{{\mu }_{en}}{\rho }$ was interpolated from the NIST data tables (28). The integral in Eq. 2 was then evaluated as a discrete summation over the energy bins using MATLAB. Once the effective $\frac{{\mu }_{en}}{\rho }$ was determined, the theoretical DEF was calculated to be 1.037 for a 0.77% gold by mass solution, based upon the results from Eq. 1 and 2.

II. C. Dose enhancement measurement apparatus

The equations in the previous section require the existence of CPE. For CPE to exist for the film measurements, the range of the ¹⁹²Ir electrons must be shorter than the distance from the boundary of the GNP solution to the analyzed portion of the film. According to the ESTAR database (29), the range of a 0.38 MeV energy electron is 1.2 mm in water. The apparatus was designed to suspend the film within a GNP solution, while ensuring CPE. This film is sandwiched between two pieces of acrylic. Figure 2 shows a labeled photograph and diagram of the GNP apparatus. The solution well has a diameter of 1 cm, there is 3.2 mm of GNP solution backscatter behind the film, and 6.4 mm of GNP solution in front of the film.

Figure 2:

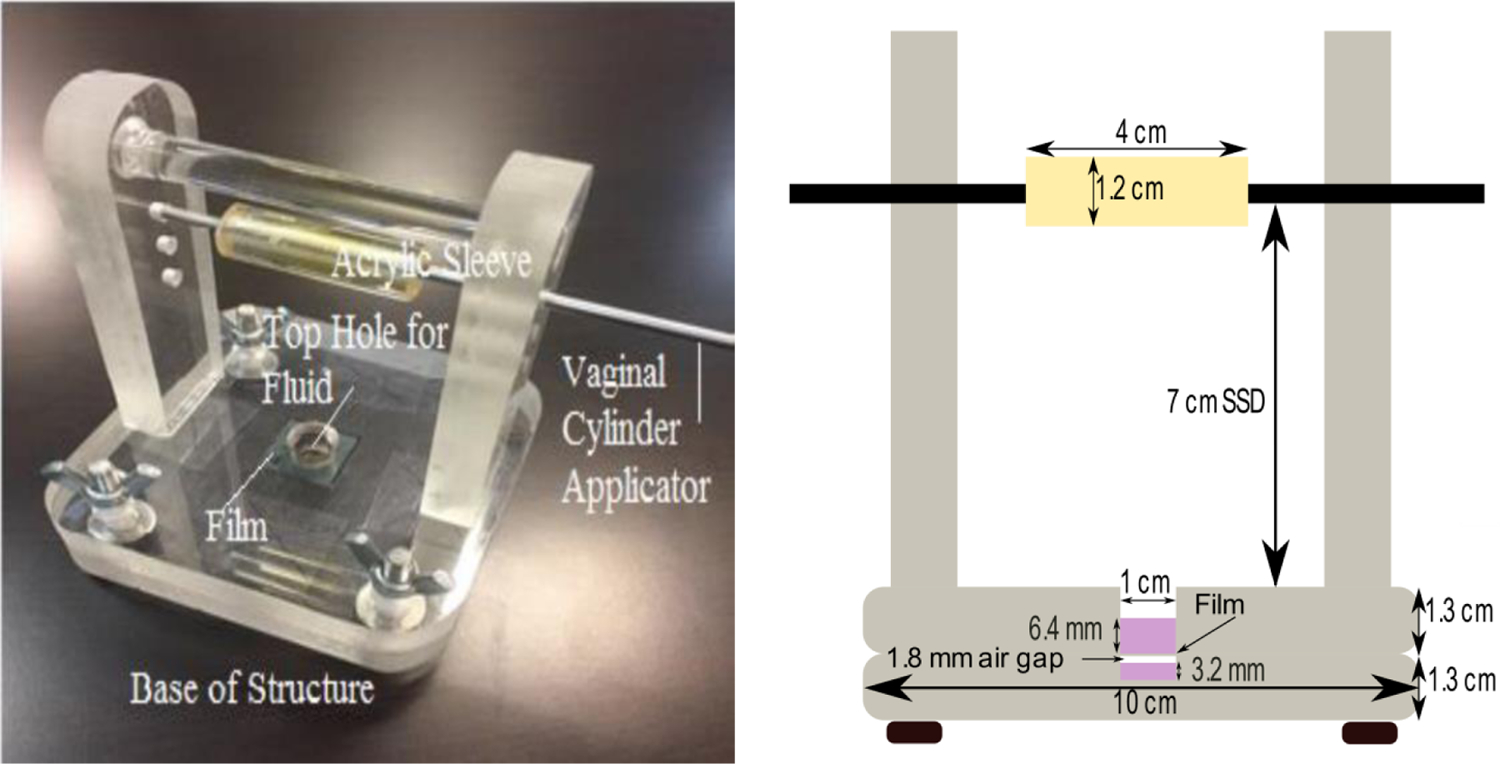
(Left) A labeled photograph of the GNP apparatus. (Right) A cross sectional sketch of the GNP apparatus is displayed. An air gap exists between the bottom of the film and the GNP solution in the lower well. This is described further in the Discussion section.

A vaginal cylinder applicator was placed at a 7 cm distance from the base of the apparatus. This distance was chosen to minimize the effect of positional variation in the source relative to the film. An acrylic sleeve with a diameter of 1.2 cm was fit over the applicator. The acrylic sleeve was designed to remove any beta electrons emanating from the source. The base was constructed by drilling 4 holes at the corner of each acrylic slab, to connect two separate acrylic slabs together with bolts. The size of each acrylic slab was 10 × 10 × 1.3 cm. On the bottom acrylic slab, a 1 cm diameter hole was drilled 0.5 cm deep. The top slab of acrylic had a hole with a diameter of 1 cm drilled all the way through it.

These experiments utilized EBT3 radiochromic film. The film was cut into 2 × 2 cm squares. A circle was drawn around the dosimeter to demarcate the region of the film that was in contact with the fluid used. The parts of the film that were within 1.2 mm of the vessel wall were not included with the analysis here, as these regions would not be within CPE.

II.D. Experimental Execution

The experiment was conducted by delivering 1.75 Gy to the EBT3 film with a microSelectron-v2 ¹⁹²Ir HDR source. Three different GNP solutions with 0.28%, 0.56%, and 0.77% gold by mass were used alongside distilled water, which served as the control group. First, 0.25 mL of the selected fluid was placed at the bottom of the well, located on the bottom slab of the apparatus. Next, the film was placed over the well. Then, the top part of the apparatus was screwed on tightly over the film. Finally, 0.5 mL of the selected fluid was placed on top of the secured film. Once the film was secured and the fluid was inserted, a vaginal cylinder applicator was placed at a 7 cm distance from the base of the apparatus and connected to the HDR afterloader. Twelve measurements were taken for each GNP solution used and distilled water.

After the film was irradiated, the film was scanned using an EPSON Perfection V750 PRO scanner two days after irradiation. The scanning parameters were positive film, 48-bit color, 300 dpi, and the images were exported as .TIFF. A region of interest, the same size as the diameter of the hole in the apparatus, was marked on the film to make data collection easier. Samples of 3 circular ROIs with a diameter of 5 mm were taken from the demarcated region of the film and analyzed on MATLAB using the red color channel. The deposited dose from GNP and water irradiation conditions was determined based upon differences in the red color channel. This color channel was chosen due to it being the most sensitive one in the range of dose measurements made here.

II.E. Burlin Cavity Corrections

The presence of the film perturbs the distribution of radiation throughout the GNP solution. Thus, corrections are required to yield a value of DEF in the absence of the film. Cavity corrections were both measured and calculated. The measurements were made by irradiating stacks of 1, 3, and 5 sheets of film in 0.77% gold by mass GNP solution, in a setup that was identical to that of the GNP DEF experiment. The dose to the film was fit as a function of the number of sheets, and the absorbed dose was extrapolated to 0 pieces of film. The calculated corrections were performed with the Burlin cavity formalism, as displayed in Eq. 3. For the calculations, the plastic was assumed to be compositionally equivalent to polyethylene.

$$\frac{D_a}{D_b}=d\cdot S_b^a+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_b^a$$ (3)

The variable D_x represents the absorbed dose to medium x, $S_b^a$ and ${\left(\frac{{\mu }_{en}}{\rho }\right)}_b^a$ are ratios of medium a and medium b’s stopping power and mass absorption coefficient, respectively, and d is a parameter related to the size of the cavity. The stopping power ratio was approximated by assuming a monoenergetic electron spectrum with an energy of 380 keV. This assumption will be addressed further in the Discussion section. The d factor was calculated using Eq. 4.

$$d=\frac{1-e^{-\beta \cdot L}}{\beta \cdot L}$$ (4)

It is assumed that L represents the depth of the active layer in the film. Thus, half of the film thickness was utilized for L in Eq. 4. The rationale for the exponential term in Eq. 4 is that the electron fluence coming from the wall of a cavity exponentially decays as it traverses the cavity. The value of β is calculated based on knowing the range of electrons (t_max) traversing a cavity. More specifically, as shown in Eq. 5, the remaining fraction of electrons at t_max is assumed to be a small number. A value of 0.04 was utilized in Eq. 5 based on the work of Janssens et al (30), who empirically determined it to provide the most accurate cavity correction data for the exponential function. The value t_max was set as the range of a 0.38 MeV electron (1.2 mm).

$$e^{-\beta \cdot t_{max}}=0.04$$ (5)

The final Burlin cavity correction was determined based upon applying the Burlin cavity formalism, from Eq. 3, for GNP and water setups. Equation 6 displays how the Burlin cavity formalism is used to adjust the absorbed dose measured in film to equal the absorbed dose measured in either the GNP solution or water. The measured absorbed dose is the absorbed dose to the film suspended in either GNP or water.

$$\frac{D_{f,GNP}}{D_{GNP}}=d\cdot S_{GNP}^{film}+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_{GNP}^{film}$$ (6)

The term D_f,GNP is the dose to the film in the GNP solution, and D_GNP is the dose to the GNP solution. Next, the measured DEF is defined in Eq. 7 as the dose to the film in GNP solution divided by the dose to film in water.

$$DE{F}_{measured}=\frac{D_{f, GNP}}{D_{f, water}}=\frac{D_{GNP}\cdot \left(S_{GNP}^{film}+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_{GNP}^{film}\right)}{D_{water}\cdot \left(S_{water}^{film}+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_{water}^{film}\right)}=DEF\cdot \frac{S_{GNP}^{film}+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_{GNP}^{film}}{S_{water}^{film}+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_{water}^{film}}$$ (7)

Rearranging Equation 7 such that the true, corrected DEF is a function of the measured DEF and the Burlin formalism yields Eq. 8.

$$DEF=\frac{D_{f, GNP}}{D_{f, water}}\cdot \frac{S_{water}^{film}+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_{water}^{film}}{S_{GNP}^{film}+\left(1-d\right)\cdot {\left(\frac{{\mu }_{en}}{\rho }\right)}_{GNP}^{film}}= DE{F}_{measured}\cdot Burlin Correction$$ (8)

The mass energy absorption coefficients were evaluated with a discreet summation representation of Eq. 2. The stopping power values were interpolated in MATLAB from the ESTAR database (29) at the energy of 380 keV.

II. F. Uncertainty analysis

DEF was evaluated as a ratio of the average measurements. There were twelve measurements taken with each solution and three dose readings taken per piece of film. These three readings were averaged to produce a single measurement for each piece of film. Uncertainty in the measured data was calculated using Eq. 9.

$$Uncertainty=DEF\cdot \sqrt{{\left(\frac{SE}{\mu }\right)}_{\hspace{0.17em}\hspace{0.17em}GNP}^2+{\left(\frac{SE}{\mu }\right)}_{\hspace{0.17em}\hspace{0.17em}{H}_{2}O}^2}$$ (9)

In Eq. 9, DEF is the measured value for the given concentration, SE is the standard error of the mean for each media investigated, and µ is the mean of all the measurements taken for each media investigated.

III. RESULTS

DEF was measured as a function of GNP concentration. Table 2 displays the theoretical and measured DEF of each concentration investigated, the Burlin cavity correction of each concentration, and the cavity corrected DEF. Figure 3 is a graphical representation of the measured and theoretical DEF. Figure 4 shows the results of the cavity corrected DEF and the theoretical value. Figure 5 displays the experimental cavity correction data. A linear equation, used to fit the experimental Burlin data, was chosen based on the significant p values attained during a coefficient regression analysis. An intercept of 1.041 ± 0.012 (p = 1.50*10⁻¹⁹) and a linear coefficient (relative to the number of sheets of film) of −0.008 ± 0.003 (p = 0.03) were determined to provide the best mathematical representation of the fitted data. The coefficient associated with a second order polynomial was insignificant, so it was not included in the analysis.

Table 2:

A display of DEF and associated uncertainty as a function of GNP concentration

% Gold by mass	DEF (Theoretical)	DEF (Measured)	BC Correction	Cavity Corrected DEF
0.28	1.013	1.013 ± 0.006	1.003	1.016 ± 0.006
0.56	1.027	1.024 ± 0.010	1.005	1.029 ± 0.010
0.77	1.037	1.032 ± 0.006	1.007	1.039 ± 0.006

Figure 3:

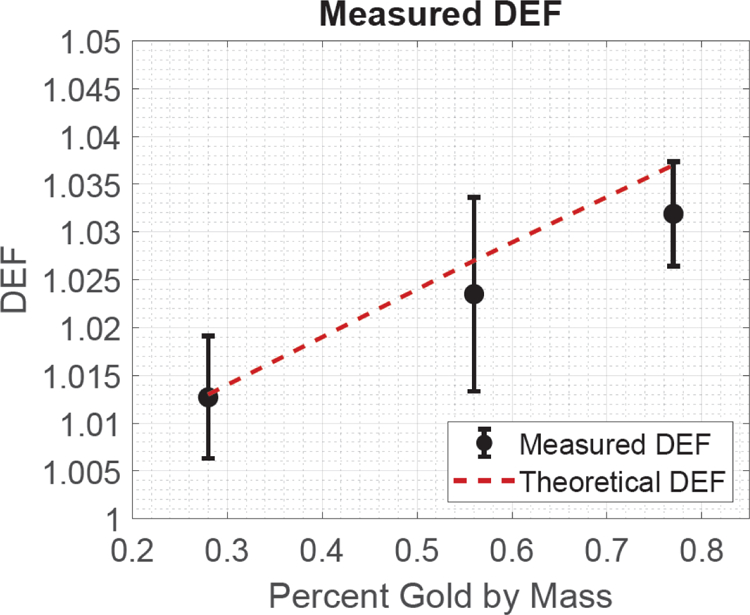
The measured (uncorrected) and theoretical DEF as well as the associated uncertainty as a function of the GNP solution’s percent gold by mass.

Figure 4:

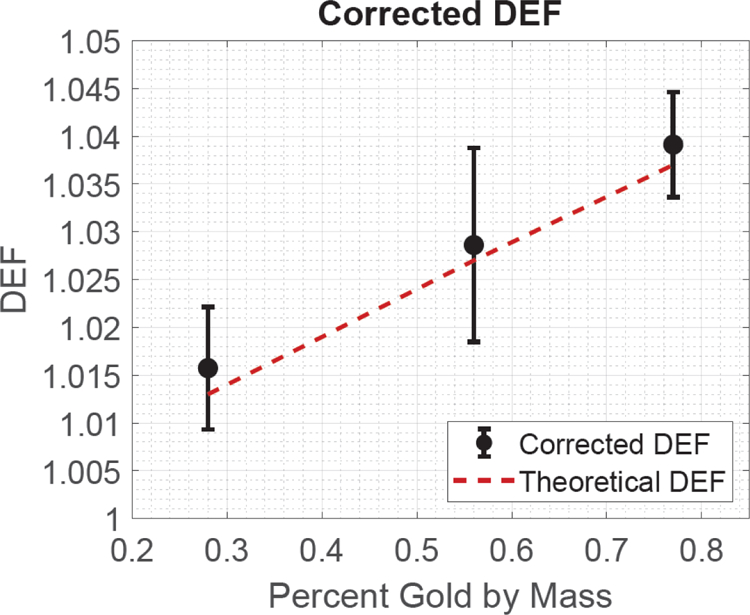
The corrected and theoretical DEF as well as the associated uncertainty as a function of the GNP solution’s percent gold by mass.

Figure 5:

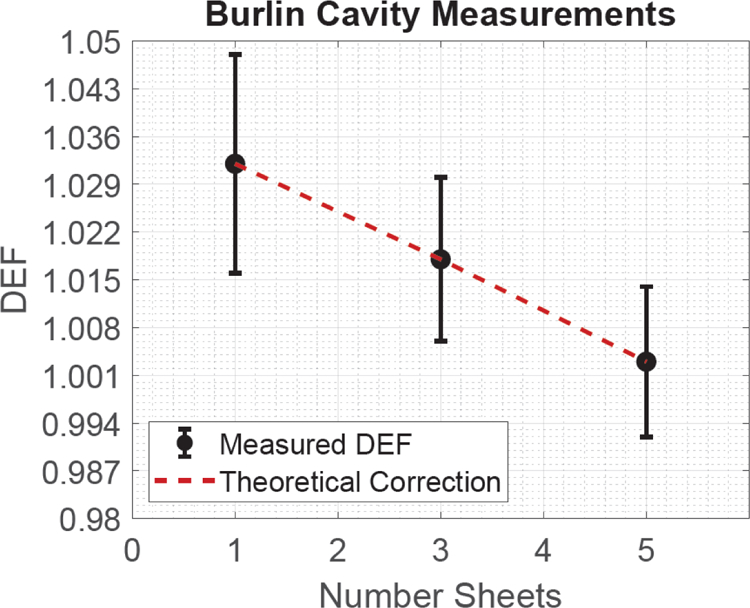
The results of the experimental cavity experiment with associated uncertainty.

The Burlin cavity corrections were compared with the Burlin cavity experiment to validate the efficacy of applying the Burlin cavity correction to the measured DEF values. The result of the Burlin cavity experiment provided an intercept of DEF equal to 1.041 ± 0.012, which was procured by extrapolating the number of sheets of film from the cavity correction experiment (see Fig. 5) to 0. However, the extrapolated DEF required an additional Burlin correction. The Burlin correction we used had a value of d = 1, which led to the Burlin correction being a ratio of the electron stopping powers with a final value of 0.996. Thus, applying this correction to the 0-sheet intercept yields an extrapolated DEF of 1.037±0.012. This can be compared to the result of applying the full Burlin correction to the measured DEF, which is 1.039±0.006. Both values have uncertainties that include the theoretically expected DEF of 1.037.

IV. DISCUSSION

To demonstrate that this DEF measurement approach is valid for different sized nanoparticles, an additional experiment was performed. This measurement utilized 100 nm GNPs, with a 0.44% gold by mass concentration. The same methods presented in this manuscript were used to measure dose enhancement and to calculate the Burlin correction and the theoretically expected DEF. The Burlin-corrected DEF measurement value for the 100 nm GNP solution is 1.025 ± 0.009 and the theoretically expected value is 1.021. These results indicate a similar level of agreement as those seen for the 30 nm GNP solution.

As can be seen in Fig. 2, there is an air gap (1.8 mm) between the bottom of the film and the GNP solution in the lower well of the apparatus. This air gap was left purposely to prevent the GNP solution from flowing between the film and acrylic apparatus via capillary action. The effect of the air gap on the dose measurement can be evaluated relative to the effect of the film plastic coating. While the air gap is 14 times thicker than this coating, its density is roughly 1000 times smaller. Thus, the presence of this air gap should produce perturbations that are significantly smaller than that of the Burlin correction.

A limitation of the cavity corrections was the functional form used to extrapolate the true DEF. Initially, multiple linear regression was applied with DEF versus number of sheets and squared number of sheets. This fit, however, indicated a non-significant p-value associated with the squared coefficient. For this reason, the final fit only applied regression against the number of sheets. This did produce a strong R value of 0.99. Another limitation of the Burlin cavity correction we applied was the assumption that the energy spectral distribution for the stopping power can be approximated by a single mono-energetic beam of 380 keV. A comprehensive calculation of the spectral distribution would involve averaging across the spectrum of secondary electrons during irradiation. However, this can be avoided due to the lack of energy dependence of the stopping power ratio. Table 3 displays the stopping power ratio and effect on the Burlin correction when assuming various monoenergetic electron energies. This includes electrons with the same energy as the lowest and highest photon energies (60 and 885 keV) emanating from the ¹⁹²Ir spectrum. The impact that the electron energies had on the final Burlin correction was not significant relative to our measurement uncertainties. The maximum difference in the final Burlin correction factor is 0.02% between 60 and 885 keV. Thus, a monoenergetic electron spectrum with an energy of 380 keV was assumed here.

Table 3:

The impact that different monoenergetic electron energies have on the stopping power ratio and final Burlin correction factor.

Energy (keV)	$S_{GNP}^{film}$	$S_{H2O}^{film}$	Burlin Correction
60	1.0723	1.0680	1.0147
380	1.0624	1.0584	1.0146
885	1.0484	1.0447	1.0145

The measurements performed in this study can serve as the foundation for future projects involving the measurement of DEF. Currently, citrate-capped GNPs, which were used in this study, precipitate when the percent gold by mass exceeds 0.77%. PEGylated GNPs (PGNPs) can potentially become more concentrated than the citrate-capped GNPs, which would lead to measuring higher DEF values. Furthermore, Burlin cavity corrections could be applied to anthropomorphic phantom measurements to evaluate more clinically relevant GNP setups.

V. CONCLUSION

The Burlin-corrected DEF measurements agree with the theoretically expected values. Additionally, the extrapolated cavity corrections yielded similar values to those calculated. Thus, these results indicate that Burlin cavity calculations can be applied to correct film-based DEF measurements for ¹⁹²Ir.