Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Jul 27.
Published in final edited form as: Phys Med Biol. 2020 Jul 27;65(15):155005. doi: 10.1088/1361-6560/ab8aaa

Monte Carlo track-structure for the radionuclide Copper-64: Characterization of S-values, nanodosimetry and quantification of direct damage to DNA

J Carrasco-Hernández 1, J Ramos-Méndez 2, B Faddegon 2, AR Jalilian 3, M Moranchel 1, MA Ávila-Rodríguez 4,*
PMCID: PMC7757752  NIHMSID: NIHMS1652993  PMID: 32303013

Abstract

TOPAS-nBio was used to simulate, collision-to-collision, the complete trajectories of electrons in water generated during the explicit simulation of 64Cu decay. S-values and direct damage to the DNA were calculated representing the cell (C) and the cell nucleus (N) with concentric spheres of 5 μm and 4 μm in radius, respectively. The considered “target”←“source” configurations, including the cell surface (Cs) and cytoplasm (Cy), were: C←C, C←Cs, N←N, N←Cy and N←Cs. Ionization cluster size distributions were also calculated in a cylinder immersed in water corresponding to a DNA segment of 10 base-pairs in length (diameter 2.3 nm, length 3.4 nm), modeling a radioactive point source moving from the central axis to the edge of the cylinder. For that, the first moment (M1) and cumulative probability of having a cluster size of 2 or more ionizations in the cylindrical volume (F2) were obtained. Finally, the direct damage to the DNA was estimated by quantifying double-strand breaks (DSBs) using the clustering algorithm DBSCAN.

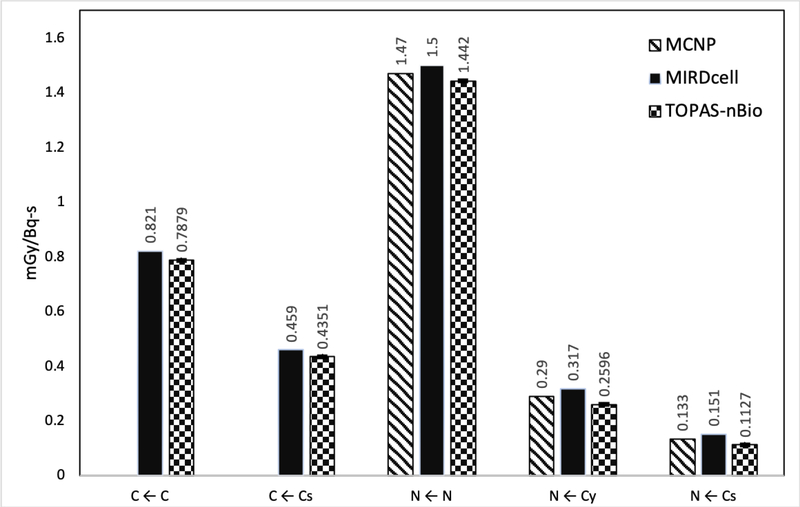
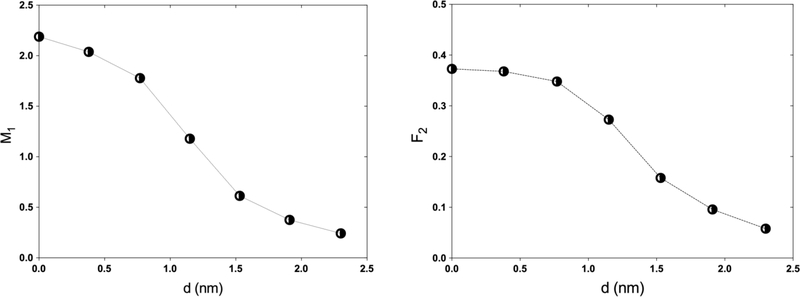
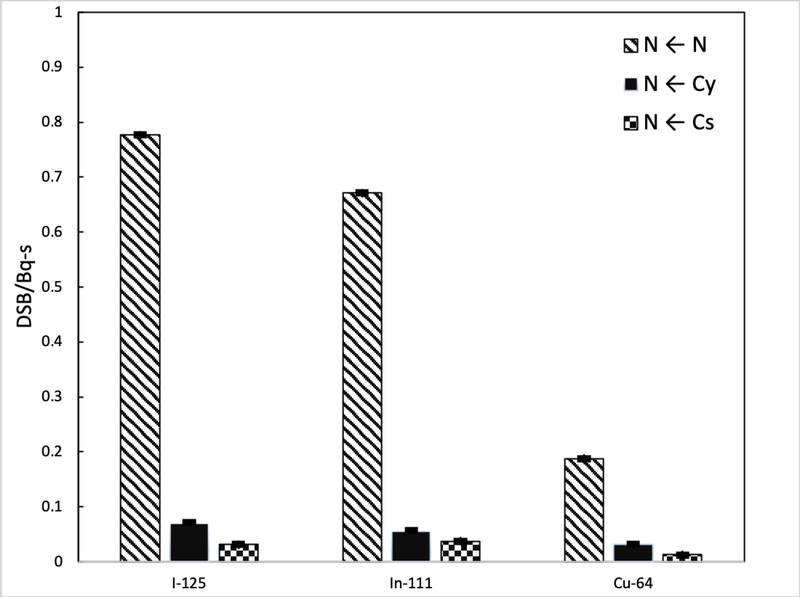
The S-values obtained with TOPAS-nBio for 64Cu were 7.879×10−4±5×10−7, 4.351×10−4±6×10−7, 1.442×10−3±1×10−6, 2.596×10−4±8×10−7, 1.127×10−4±4×10−7 Gy/Bq-s for the configurations C←C, C←Cs, N←N, N←Cy and N←Cs, respectively. The difference of these values, compared with previously reported S-values for 64Cu with the code MNCP and software MIRDCell, ranged from −4% to −25% for the configurations N←N and N←Cs, respectively. On the other hand, F2 was maximum with the source at the center of the cylinder 0.373±0.001, and monotonically decreased until reaching a value of 0.058±0.001 at 2.3 nm. The same behavior was observed for M1 with values ranging from 2.188±0.004 to 0.242±0.002. Finally, the DBSCAN algorithm showed that the mean number of DNA DSBs per decay were 0.187±0.001, 0.0317±0.0005, and 0.0125±0.0002 DSB-(Bq-s)−1 for the configurations N←N, N←Cs, and N←Cy, respectively.

In conclusion, the results of the S-values show that the absorbed dose strongly depends on the distribution of the radionuclide in the cell, the dose being higher when 64Cu is internalized in the cell nucleus, which is reinforced by the nanodosimetric study by the presence of DNA DSBs attributable to the Auger electrons emitted during the decay of 64Cu.

Keywords: Copper-64, Topas-nBio, S-values, nanodosimetry, Auger electrons, DNA-double-strand-breaks

1. Introduction

Copper is an essential element for life. Due to its properties, it is a cofactor in a variety of biological reactions such as respiration, free radical eradication, connective tissue formation, and neurological development, among others. However, in excess, it is toxic and even lethal to the cell since it binds to proteins, interferes with the homeostasis of other metals and generates hydroxyl radicals; so cells have developed sophisticated mechanisms to maintain a critical balance between need and toxicity [Zhou & Gitschier, 1997]. The homeostasis of copper is regulated mainly by the transporter CTR1 that allows its internalization into the cell. Once internalized in the cytoplasm, several chaperones such as Atox1, CCS and COX17 are responsible for transporting the copper within the different intracellular compartments [Lee et al., 2002]. Recently it has been shown that Atox1 contributes to important physiological processes including inflammation, angiogenesis, iron balance, and many others [Hatori & Lutsenko, 2016]. In addition, in a study conducted with mouse embryonic fibroblast cell lines, positive and negative for Atox1, it was identified that this copper chaperone was one of the main proteins responsible for transporting and binding copper to the cell nucleus [Beaino et al., 2014].

Unbalanced homeostasis of copper can lead to a wide variety of diseases, including cancer [Denoyer et al., 2015]. There exists scientific evidence that copper-levels in serum and tumors of cancer patients are aberrantly elevated compared to healthy subjects [Gregoriadis et al., 1983]. Additionally, it has been demonstrated that copper plays an important role in tumor growth, progression and metastasis [Gupte & Mumper, 2009]. This feature can be useful to target copper dependent tumors for theranostic applications using suitable radioisotopes of copper. In this regard, Copper-64 (64Cu) possess unique properties that could serve the dual role of diagnostic and targeted radionuclide therapy (TRNT). It decays with a half-life of T1/2 = 12.7 h, and emits β+ (37.1%) and β− (17.9%) particles, in addition to 43.5% of electron capture that results in the emission of Auger electrons with high linear energy transfer (LET). This enhances the radiobiological effect of this radioisotope, provided its internalization to the cell nucleus.

In recent years, 64Cu in the chemical form of copper dichloride ([64C]CuCl2) has been identified as a potential theranostic agent using the human copper transporter 1 (hCTR1) as a molecular target. Preclinical studies using [64Cu]CuCl2 as a theranostic agent in selected cancer xenograft models in mice had demonstrated its potential as a therapeutic agent [Qin et al., 2014; Ferrari et al., 2015]. To date, no clinical trials have been performed in humans to evaluate the potential of [64Cu]CuCl2 as a theranostic agent. Only case reports in patients with prostate cancer metastasis, uterine cancer, and glioblastoma have been described, with promising results [Valentini et al., 2014; Valentini et al., 2015]. To help explain these promising results, Guerreiro et al (2018) evaluated the nuclear uptake of this tracer in selected prostate cancer (PCa) cell lines and a non-tumorigenic cell line, finding that [64Cu]CuCl2 was taken up preferentially by PCa cells, compared to normal cells. A more complete explanation may require accounting for the therapeutic effect of Auger electrons, which requires the internalization of 64Cu into the cell nucleus.

Recently, Avila-Rodriguez et al (2017) performed PET-based biodistributions and radiation dosimetry calculations for [64Cu]CuCl2 in human healthy volunteers, reporting the liver as the critical organ. Then, Righi et al (2018) calculated the radiation dose in prostate cancer lesions in patients injected with 64CuCl2. A high contrast between the lesions and the healthy tissue was observed one hour after the injection. A dose of 6×10−2 mGy/MBq was determined for the lesions, which is rather low to cause the therapeutic effect of 64CuCl2 previously reported in preclinical studies and the case reports cited above. However, the therapeutic effect of the Auger electrons was not taken into account in either work. It has been shown that when Auger emitters are introduced into the cell nucleus and incorporated into the DNA, the Auger electrons can cause damage similar to heavy particles such as α-particles, as evidenced by cell survival experiments [Humm et al 1994]. This prompted our interest in using the Monte Carlo method to include the contribution of Auger electrons in the dosimetric characterization of 64Cu. The internalization of radioisotopes to the cell nucleus, and the cascade of electrons emitted during the decay of Auger emitters such as 64Cu, can cause DNA double-strand breaks (DSBs) [Cornelissen & Vallis, 2010; McMillan et al., 2015]. This phenomenon requires a study on a nanometer scale to determine the effect of the Auger electrons in the proximity of the DNA molecule.

Given the complex intracellular and nuclear distribution of copper, it is necessary to perform dosimetry at the cellular and subcellular levels. However, it is difficult to make experimental measurements on the nanometer scale in biological media, so, theoretical calculations are needed to estimate the energy deposition [Ftacnikova & Bohm, 2000]. The S-value is the mean absorbed dose to a target region per unit of cumulated activity in a source region [Goddu et al., 1997]. This value represents the key physical quantity for converting administered activity to radiation doses in the MIRD formalism [Loevinger & Berman, 1968; Loevinger et al., 1988; Watson et al., 1993]. In this scheme, the cell consists of the nucleus and surrounding cytoplasm, represented by two homogenous concentric spheres of unit density [Roeske et al., 2008]. There exists a compendium of S-values calculated for a broad variety of radionuclides, but data for 64Cu is not provided [Goddu et al., 1997]. Cai et al. [2017] calculated S-values for 64Cu in different geometries using the condensed-history Monte Carlo method with MCNP [Team, 2003]. They used the spectrum of secondary particles emitted by 64Cu in the configurations (“target” ← “source”): N ← N (nucleus), N ← Cy (cytoplasm) and N ← Cs (cell surface) of a single cell or multiple copies distributed in a regular array. Their results were compared with S-values obtained with the MIRDCell software [Vaziri et al., 2014], reporting differences of 2% for N ← N, 9% for N ← Cy and 12% for N ← Cs. However, S-value calculations performed with MCNP and MIRDCell did not take account of the complete spectra of emitted Auger electrons during the decay of 64Cu, as both used average energies. The explicit simulation of the decay process of 64Cu provides a complete Auger spectrum potentially leading to more accurate simulations. The general-purpose Monte Carlo toolkit Geant4 [Agostinelli et al., 2003] provides, among other processes, with physical processes to simulate radioactive decay of many radionuclei, which have been compared with the ENSDF data for consistency, as reported in Hauf et al. [2013]. In addition, the Geant4-DNA Monte Carlo track-structure extension of Geant4 has been used to calculate S-values for several radionuclides [Moradi & Bidabadi, 2018; Sefl et al., 2015]. However, to our knowledge no simulation with 64Cu has been reported with Geant4 or Geant4-DNA.

The objective of this work was to characterize biologically relevant physical parameters of secondary radiation from 64Cu by simulating its complete decay scheme using the Geant4-DNA based TOPAS-nBio Monte Carlo tool [Schuemann et al., 2018]. For that, we performed the calculation of cellular S-values for 64Cu. In addition, we quantified the ionization detail (ID) [Ramos-Méndez et al., 2018a] through clusters size distributions in a biologically relevant volume by means of the nanodosimetric quantities: first moment (M1) and the cumulative probability of having ionization clusters of size larger or equal than two (F2) [Rollet et al., 2010]. Both quantities have been shown to correlate with inactivation cross-section of cells in [Conte et al., 2017a, 2017b]. Finally, we estimated the direct damage to the DNA through the number of double-strand breaks (DSBs) caused by the decay of 64Cu using the clustering algorithm DBSCAN [Ester et al., 1996]. This algorithm was previously used with Geant4-DNA to estimate the number of single and double strand-breaks in proton therapy [Francis et al., 2011].

2. Materials and methods

2.1. Monte Carlo simulation of track-structure

Simulations were performed using TOPAS (TOol for PArticle Simulation) [Perl et al., 2012] version 3.2 and its extension TOPAS-nBio [Schuemann, 2018]. TOPAS facilitates the use of the physical processes provided by Geant4 version 10.05.p01 [Agostinelli et al., 2003] for simulation using the condensed-history Monte Carlo method. TOPAS-nBio facilitates the use of the physical-chemical processes provided by Geant4-DNA [Incerti et al., 2010; Ramos-Méndez et al., 2018b], and a suite of geometric models and scorers of physical quantities of interest for radiobiology [McNamara et al., 2018]. The physics list G4EmDNAPhysics_opt2 of Geant4-DNA was used to simulate, collision-to-collision, the complete trajectories of electrons in water. The G4RadiactiveDecay module from Geant4 was used for the explicit simulation of 64Cu decay including Auger electron production following electron capture. The number of histories in each simulation for S-values, M1 and F2 were 106, and 1.85×105 for DBSCAN. Each simulation was repeated 10 times using different random seeds to obtain an average value with a statistical uncertainty better than 0.5%, 1 standard deviation (1σ).

2.2. S-Values

To obtain the S-values, the cell model consisted of two homogeneous concentric spheres of liquid water (density = 1 g/cm3). The cell of 5 μm radius containing a nucleus of 4 μm radius was centered in a water cube of 100 μm per side, as shown in Figure 1. The 64Cu radioactivity source was isotropic and uniformly distributed in one of the following volume or surface regions of the cell: the cell (C) itself, the cytoplasm (Cy), consisting of the region between the cell surface and nucleus, the cell surface (Cs) or the nucleus (N). Several “target” ← “source” combinations were used: C ← C, C ← Cs, N ← N, N ← Cy, N ← Cs. Results were compared with published data from MIRD software [Goddu et al., 1997] and MCNP [Cai et al., 2017]. As a means of verification, the S-values for the Auger emitters 125I and 111In were also computed using TOPAS-nBio, and compared with previously reported values obtained with Geant4-DNA and MIRD software from [Šefl et al., 2015; Goddu et al., 1997]. These two radionuclides are well known Auger emitters used in nuclear medicine applications [Humm et al., 1994].

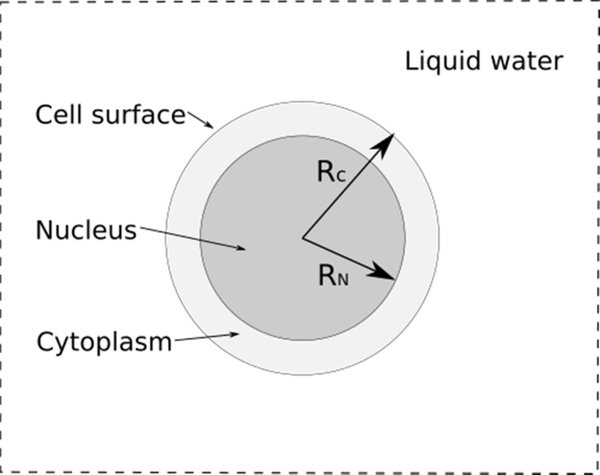
Figure 1.

Figure 1.

Open in a new tab

Spherical model of the cell (radius Rc of 5 μm) consisting of an outer region of cytoplasm and an inner region of cell nucleus (radius RN of 4 μm), in a 100 μm width cube. The full geometry consists entirely of water.

2.3. Clusters

It is known that the complexity of the ID plays a key role in the induction of DNA damage in cells [Rabus & Nettelbeck, 2011]. The number of ionizations produced by a radiation quality, T, in a specific target volume is a stochastic quantity called ionization cluster size, ν. These ionization clusters can be represented by the frequency distributions of clusters sizes, Pν (T), and quantified in terms of its statistical moments (Mk) or cumulative probabilities (Fk) [Grosswendt et al., 2007].

In 1992, it was shown that the clusters of multiple ionizations produced by ionizing radiation in spherical volumes of 2 to 3 nm diameter correlate well with the formation of DSBs [Brenner & Ward, 1992]. Lately, Pν and nanodosimetric quantities M1 and F2 have been shown to correlate with DSBs and cell survival [Garty et al., 2010; Conte et al., 2107a, 2017b]. Hence, we used a cylindrical volume of liquid water of 2.3 nm in diameter and 3.4 nm in length (corresponding to a DNA segment of 10 base-pairs in length) to calculate Pν (T) with TOPAS-nBio. A point source of 64Cu was placed on the plane perpendicular to the cylinder axis at radial distances from the axis of zero to 2.3 nm (Figure 2). The decay process of 64Cu was explicitly simulated. The cumulative probability of having ionization clusters of size 2 or larger, F2, and the mean ionization cluster size (first moment), M1, were obtained from Pν.

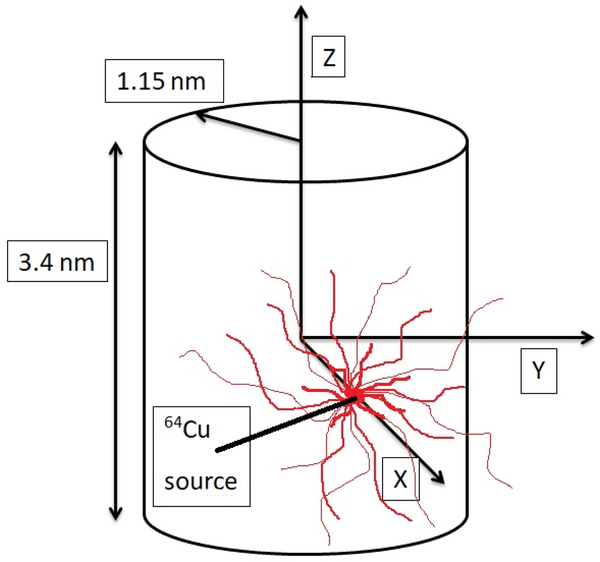
Figure 2.

Figure 2.

Open in a new tab

A water filled cylinder, 2.3 nm in diameter and 3.4 nm in length, was used to represent a DNA segment of 10 base pairs. A 64Cu source was placed at distances up to 2.3 nm from the cylinder axis.

2.4. DBSCAN

Clustering is a technique for extracting information from large amounts of data. The DBSCAN algorithm (Density-Based Spatial Clustering of Applications with Noise) introduced by Ester and coworkers in 1996 [Ester et al., 1996], is an algorithm designed to discover arbitrary forms of spatial clusters. The algorithm requires 2 input parameters: the radius of a neighborhood and the minimum number of points to form a cluster. Francis et al. [2011] adapted this algorithm to calculate DNA damage from the spatial distribution of ionization events scored in water. For this, the algorithm was extended to take into account the energy deposited by ionizing particles, and an adjustable free parameter (SPointsProb) that represents the probability that an ionization event occurring within the sensitive region directly or indirectly (through free radicals produced in the radiolysis process) reaches the DNA. The adjustable free parameter was used as the DBSCAN approach did not consider the geometrical details of a DNA model, and in addition, it provided a faster approach because the detailed transportation of particles through a complex geometry was avoided. The DNA damage calculation using DBSCAN is summarized as follows. First, the spatial position of the ionization events that occurred within a sensitive volume, from individual particle tracks, were filtered using a probability function that depended on the energy deposited. Francis et al [2011] assumed that an interaction within the cell nucleus had a certain probability of causing DNA damage, with the value set to zero at energies below 5 eV, and increased linearly to 1 at an energy equal to or greater than 37.5 eV. The upper energy limit of 37.5 eV was proposed by Friedland et al. [2005] and was obtained by applying a linear model in a sensitive region consisting of a shell of 10 water molecules around a nucleotide, where energy deposition events of this energy are considered as a source of potential DNA damage. Second, a subsequent filtering process was performed by accepting with SPointsProb probability = 0.16 for the remaining ionization events, which are then used by the DBSCAN for clustering analysis. The value of 0.16 was chosen, as it has been shown to reproduce DSB experimental data within uncertainties for protons of 1 MeV and 20 MeV [Francis 2011]. Two types of damage were returned by DBSCAN: single strand breaks (SSBs) and double strand breaks (DBS), the latter formed by two SSBs separated by less than 10 pair-bases or 3.4 nm [Francis et al., 2011]. The DBSCAN algorithm, with the adaptations made by Francis and coworkers, was implemented in TOPAS-nBio [Schuemann et al., 2018]. In this work, TOPAS-nBio with DBSCAN was used to calculate the DSBs produced in the cell nucleus during the decay of 64Cu, as well as for 125I and 111In, for comparison purposes. The 64Cu was uniformly distributed either in the nucleus (N) or cytoplasm (Cy) or on the cell surface (Cs). The geometry used for these calculations was the same used to calculate the S-values (Fig. 1).

3. Results

3.1. S-Values

The S-values calculated with TOPAS-nBio in the five different configurations, for the full spectra of electrons emitted during the explicit decay of the evaluated radionuclides, are shown in Figures 3, 4 and 5, for 125I, 111In and 64Cu, respectively. Typical calculation time was less than 10 min (106 histories, in a single CPU core 3.0 GHz, and 8 GB RAM computer). The results were compared with previously reported values calculated with MIRD software [Goddu et al., 1997], and Geant4-DNA [Šefl et al., 2015] for 125I and 111In, and with MCNP [Cai et al., 2017] for 64Cu. The precise S-values calculated for 64Cu with TOPAS-nBIO, including their statistical error (1 standard deviation), are given in Table 1.

Figure 3.

Figure 3

Open in a new tab

Average S-values for 125I in five different target-source configurations. The statistical errors for the S-values (average of 10 independent simulation runs) calculated in this work were less than 0.5%, 1σ (1 standard deviation).

Figure 4.

Figure 4.

Open in a new tab

Average S-values for 111In in five different target-source configurations. The statistical errors of the S-values (average of 10 independent simulation runs) calculated in this work were less than 0.5%, 1σ (1 standard deviation).

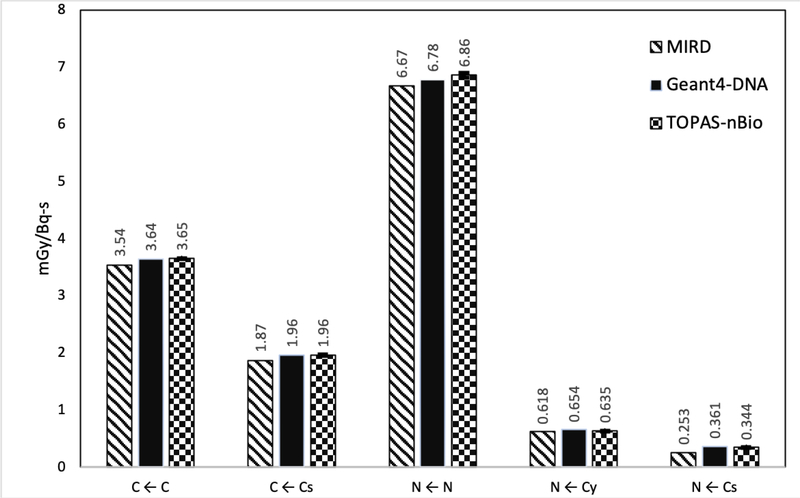
Figure 5.

Figure 5.

Open in a new tab

Average S-Values for 64Cu in five different target-source configurations. The statistical errors for the S-values (average of 10 independent simulaton runs) calculated in this work were less than 0.5%, 1σ (1 standard deviation). If available, MIRDCell and MCNP results are displayed.

Table 1.

S-values for 64Cu obtained with TOPAS-nBIO in this research work (units are given in Gy/Bq-s). Values shown are the average of 10 independent simulations runs with their standard deviation.

Configuration S(C ← C) S(C ← Cs) S(N ← N) S(N ← Cy) S(N ← Cs)
S-value 7.879x10−4±5x10−7 4.351x10−4±6x10−7 1.442x10−3±1x10−6 2.596x10−4±8x10−7 1.127x10−4±4x10−7
Open in a new tab

For 125I and 111In, the difference between TOPAS-nBIO and Geant4-DNA were outside one standard deviation but less than 5% for all evaluated configurations, except for the N ← Cy configuration of 111In that gave a difference of 7%. In the case of TOPAS-nBio and MIRD software, the percentage differences of the configurations C ← C, C ← Cs and N ← N were less than 6% for both radioisotopes, while for N ← Cy the difference was 18% for 111In. For the configuration N ← Cs, differences reached 25% and 36% for 111In and 125I, respectively.

The S values calculated with TOPAS-nBio for 64Cu also resulted in differences when compared with previous calculations. The differences between TOPAS-nBio and MCNP were 3%, 10% and 15% for the configurations N ← N, N ← Cy, and N ← Cs, respectively. When comparing with the values obtained with MIRDCell the differences were less than 5% for the configurations C ← C, C ← Cs and N ← N, while the differences reached −18 and −25% for N ← Cy and N ← Cs, respectively. Results using average energies versus complete electron spectra, are provided as supplemental data which includes Table S1 presenting the average energies of electrons as provided in the MIRD format, and Figure S1 showing the complete electron spectra as provided by Geant4 and used for the simulations in this work.

3.2. Clusters

The typical calculation time to determine M1 and F2 was less than 15 min (106 histories). Figure 6 (left) shows that the first moment M1 depends on the distance of the source to the axis of the cylinder. The mean number of ionizations in the volume (M1) declines monotonically from a maximum of 2.188±0.004 when the source is on the central axis to a value of 0.242±0.002 at a distance of 2.3 nm, twice the radius of the cylinder. Similarly, Figure 6 (right) shows results for the cumulative probability of having clusters of size 2 or larger (F2, which correlates with DSB formation [Grosswendt et al., 2007]) as a function of distance. F2 decreases from 0.373±0.001 at the center of the cylinder to 0.058±0.001 at 2.3 nm.

Figure 6.

Figure 6.

Open in a new tab

First moment of the ionization probability distribution M1 (left) and cumulative probability F2 (right) determined in a cylindrical volume of liquid water of 2.3 nm in diameter and 3.4 nm in length for a point source of 64Cu placed at different distances, d, from the cylinder axis.

3.3. DBSCAN

The typical calculation time for the DBSCAN calculations was around 30 min (1.85×105 histories). Figure 7 shows the DSBs produced in the cell nucleus from the radioactive sources 125I, 111In, and 64Cu, with the source evenly distributed in the nucleus, cytoplasm and on the cell surface. The amount of DSBs that occurs with the configuration N ← Cy and N ← Cs are 8-fold and 16-fold less than the obtained in the configuration N ← N. Note that the nanodosimetric quantities (M1 and F2) and the number of DSBs were calculated considering two different models of the DNA geometry: a cylinder representing a DNA segment of 10 base pairs for the former, and the whole nucleus or a compartment of the cell nucleus for the latter.

Figure 7.

Figure 7.

Open in a new tab

Number of DSB in the nucleus by decay produced by the presence of I-125, In-111 and Cu-64 in the nucleus and cytoplasm and on the surface of the cell. Calculated with TOPAS-nBio using DBSCAN.

4. Discussion

Monte Carlo track-structure simulations are recognized as the most precise theoretical tools for the investigation of the biological effects of ionizing radiation on DNA at subcellular scale [Incerti et al., 2010]. In this study, the absorbed dose at the cellular level of 64Cu was evaluated using TOPAS-nBio. Specifically, cellular S-values were calculated for five different combinations of dose scoring regions and source spatial distributions in the cell, and nanodosimetric quantities were calculated and used to evaluate DNA damage. The S-values of 125I and 111In were calculated as a means of verification of the calculation method, using the explicit decay of these radionuclides with TOPAS-nBio. Results showed reasonable agreement (5% and 6% for 125I and 111In for N ← Cs configuration, respectively) with previously reported values calculated using the electron spectrum of these radionuclides with Geant4-DNA. The differences are attributed to differences in the details of the energy spectrum of Auger electrons used in the simulations from the literature and the current simulations. In this work, simulations using the same energy spectrum were performed (results not shown) and not surprisingly they agreed within 1 standard deviation statistical precision, since TOPAS-nBio uses the radiation transport models of Geant4-DNA. By using the complete decay scheme of 64Cu in the current calculations, the largest differences occurred in configurations where the source was furthest from the target (i.e. the configuration N ← Cs), due mainly to the low energy Auger electrons that are not taken into account in the mean energy used in previous works. The comparison of the 64Cu S-values determined with track-structure TOPAS-nBio using the explicit decay scheme, and the previously reported S-values from the condensed-history MCNP using averaged spectrums, reached differences up to 15% for the configuration N ← Cs. It was not possible to use the same spectrum in both simulations, as the source of the spectrum used in the study with MCNP was not clear. This difference was reduced to 4.5% with TOPAS using condensed-history models (G4EmStandard_option4). A comprehensive study between track-structure and condensed history physical models in Geant4 is given in reference [Kyriakou et al., 2019]. It was concluded from that study, that for 100 nm diameter spheres or bigger, the differences between condensed history and track-structure fall below 15%, our result is within that tolerance. In general, the S-values showed a strong dependence on the cellular distribution in the absorbed dose, being higher for the N ← N configuration and smaller for N ← Cs, which is reasonable due to the relative short range of most Auger electrons, which is lower than 0.5 μm. Then, those electrons created near to the cell surface will be absorbed before they reach the nucleus.

To the best of our knowledge, this is the first study where S-values were obtained for 64Cu using track-structure simulation to simulate collision-to-collision the complete trajectories of all electrons emitted during the explicit decay of 64Cu. Same for the nanodosimetric study with the calculation of M1 and F2 and the quantification of direct damage to DNA caused by the Auger emissions during the decay of this Auger emitting radioisotope. Simulations of DSBs performed in this work with TOPAS-nBio using an average Auger and Coster-Kroning electron spectra of 64Cu [Stepanek et al., 1996] (data not shown), compared with the results obtained by simulating the complete decay scheme, gave similar results for the configuration N ← N (2%), but differences were considerable for the configurations N ← Cs (−75%), and N ← Cy (−30%), pointing out the importance of using the complete decay scheme when performing Monte Carlo Simulations.

The use of ionization cluster size distributions in nanometric volumes is useful because these are closely correlated to the formation of DSBs and with the radiobiological effects induced in cells by the presence of a radionuclide in the proximity of the DNA molecule. Not surprisingly, for the 3 evaluated radioisotopes the configuration where the most DSBs occur is the N ← N, that is, when the radioisotopes are internalized in the cell nucleus. The cumulative probability F2 shows the importance of the proximity of 64Cu with the DNA molecule, since the presence of 2 or more SSBs in a cylinder of the size of 10 base-pairs is maximum when it is inside the cylinder and monotonically decreases as it moves away from this.

It is well known that the intranuclear location, and specifically the proximity of the Auger emitters to the DNA molecule, determines the cytotoxicity of these radionuclides [Cornelissen & Vallis, 2010]. Note that 125I and 111In are two radionuclides used in nuclear medicine applications, both have a high emission of Auger electrons and other suitable properties that could make them useful for the treatment of various types of cancer. At the subcellular level in mammals, it has been shown that 125I (125I-Iodo-2’-deoxyuridine, 125IUdR) produces DSBs in the DNA of cancer cells attributable mainly to the action of energy deposited during their decay [Bodei et al., 2003]. On the other hand, 111In ([111In-DTPA-D-Phe1]-octreotide) has been a good candidate for neuroendocrine tumor therapy, among other things, due to its adequate biological half-life, and also because the internalization of this Auger electron emitting agent occurs virtually in all tumor cells [Bodei et al., 2003]. In a recent publication of cancer therapy with Auger electrons, Ku et al. [2019] review the results of the few clinical trials that have been performed in the last two decades using these two Auger electron emitters. With the DBSCAN algorithm, the direct DSBs were obtained in the cell nucleus, in the cytoplasm and on the surface, for the radionuclides 125I and 111In which, as mentioned above, are radionuclides tested for targeted therapy, and the results were compared with the DSBs produced by 64Cu. Note that the indirect damage caused by the chemical species resulting from the radiolysis process was not included, but it is a subject of future work. Also, DSBs were the result of the whole spectrum of emitted electrons from the radionuclei without separating the individual contributions from Auger and beta particles, as in the simulation they differed only by their initial kinetic energies. Because a DSB could be produced by the simultaneous contribution of Auger and beta particles, separating their contributions may not reflect the actual number of DSBs. However, this study was performed under the same circumstances, varying only the quality of the radiation. It was observed that the amount of DSBs drastically decreases if the radionuclides are found in cytoplasm or on the cell surface, rather than in the nucleus of the cell. When internalized in the nucleus, 64Cu produces 4 less DSBs than 125I and 3 times less than 111In, due to the lower intensity of its electron emissions. Nevertheless, the fast rate of biolocalization of [64Cu]CuCl2 in neoplastic lesions, that reaches its maximum within 1 h after injection, with a mean effective half-life of 9.0±1.2 h (Righi et al., 2018), coupled with the fast clearance of radioactivity from blood, and favorable biodistribution in normal tissues (Avila-Rodriguez et al., 2017), could give important advantages on the therapeutic ratio. Under this rationale, 64Cu in the chemical form of copper dichloride ([64Cu]CuCl2) could provide opportunities for multi-dose deliveries in theranostic applications (Volkert et al. 1991).

The nanodosimetry evaluation and quantification of direct damage to DNA performed in this study, in addition to the promising results obtained in preclinical studies using [64Cu]CuCl2 as a therapeutic agent in animal models and cancer patients, support the therapeutic potential of 64Cu for future theranostic applications.

5. Conclusions

For many years there had been talk about the potential therapeutic effect of radiative emissions from the decay of 64Cu. But to date, no comprehensive evaluation has been performed taking into account all radiative emissions, especially the Auger electron spectra. In this research study, biological relevant physics parameters of secondary radiation were characterized for the first time using a Monte Carlo track-structure tool, simulating the complete decay scheme of 64Cu. It was demonstrated that the use of an average Auger electron spectra, instead of the full decay scheme of 64Cu, can affect the results of S-values up to 15% for the N ← Cs configuration, and the number of DSBs up to 75% for the same configuration. Even when the number of DSBs by direct damage of 64Cu was 4-fold less than other well-known Auger emitters (125I and 111In), the shorter half of 64Cu could improve the therapeutic ratio and dose rate in a multi-dose scheme of targeted radionuclide therapy using [64Cu]CuCl2. This research study is one step in elucidating the potential of 64Cu for theranostic applications. A clinical trial is needed to more fully assess the potential of this tracer as a theranostic agent.

Supplementary Material

TableAndFigure

Acknowledgments

This research was supported by UNAM-DGAPA Grant PAPIIT-IT202518, CONACYT Grants APN-2017-4837, LN-2018-293334, and International Atomic Energy Agency CRP code F22067-RC20569. J.R-M. and B.F were supported by bridge funding grant from the University of California San Francisco School of Medicine and NIH/NCI grant R01CA187003 (TOPAS-nBio, A Monte Carlo tool for radiation biology research).

6 References

  1. Agostinelli S, Allison J, Amako KA, Apostolakis J, Araujo H, Arce P, … & Behner F (2003). GEANT4—a simulation toolkit. Nuclear instruments and methods in physics research section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3), 250–303. [Google Scholar]
  2. Avila-Rodriguez M A, Rios C, Carrasco-Hernandez J, Manrique-Arias J C, Martinez-Hernandez R, García-Pérez F O, Jalilian A R, Martinez-Rodriguez E, Romero-Piña M E and Diaz-Ruiz A (2017) Biodistribution and radiation dosimetry of [64Cu]copper dichloride: first-in-human study in healthy volunteers EJNMMI Res 7(1) 98–7pp [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Beaino W, Guo Y, Chang AJ, & Anderson CJ (2014). Roles of Atox1 and p53 in the trafficking of copper-64 to tumor cell nuclei: implications for cancer therapy. JBIC Journal of Biological Inorganic Chemistry, 19(3), 427–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bodei L, Kassis AI, Adelstein SJ, & Mariani G (2003). Radionuclide therapy with iodine-125 and other auger–electron-emitting radionuclides: Experimental models and clinical applications. Cancer Biotherapy and Radiopharmaceuticals, 18(6), 861–877. [DOI] [PubMed] [Google Scholar]
  5. Brenner DJ, & Ward JF (1992). Constraints on energy deposition and target size of multiply damaged sites associated with DNA double-strand breaks. International journal of radiation biology, 61(6), 737–748. [DOI] [PubMed] [Google Scholar]
  6. Cai Z, Kwon YL, & Reilly RM (2017). Monte Carlo N-Particle (MCNP) modeling of the cellular dosimetry of 64Cu: comparison with MIRDCell S values and implications for studies of its cytotoxic effects. Journal of Nuclear Medicine, 58(2), 339–345. [DOI] [PubMed] [Google Scholar]
  7. Conte V, Selva A, Colautti P, Hilgers G, & Rabus H (2017). Track structure characterization and its link to radiobiology. Radiation Measurements, 106, 506–511. [Google Scholar]
  8. Conte V, Selva A, Colautti P, Hilgers G, Rabus H, Bantsar A, … & Pszona S (2017). Nanodosimetry: towards a new concept of radiation quality. Radiation protection dosimetry, 180(1–4), 150–156. [DOI] [PubMed] [Google Scholar]
  9. Cornelissen B, & A Vallis K (2010). Targeting the Nucleus: An Overview of Auger-Electron Radionuclide Therapy. Current Drug Discovery Technologies, 7(4), 263–279. [DOI] [PubMed] [Google Scholar]
  10. Denoyer D, Masaldan S, La Fontaine S, & Cater MA (2015). Targeting copper in cancer therapy: ‘Copper That Cancer’. Metallomics, 7(11), 1459–1476. [DOI] [PubMed] [Google Scholar]
  11. Ester M, Kriegel HP, Sander J, & Xu X (1996, August). A density-based algorithm for discovering clusters in large spatial databases with noise. In KDD’96 Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (Vol. 96, No. 34, pp. 226–231). [Google Scholar]
  12. Ferrari C, Niccoli Asabella A, Villano C, Giacobbi B, Cocceti D, Panichelli P, & Rubini G (2015). Copper-64 dichloride as theranostic agent for glioblastoma multiforme: a preclinical study. BioMed research international, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Francis Z, Villagrasa C, & Clairand I (2011). Simulation of DNA damage clustering after proton irradiation using an adapted DBSCAN algorithm. Computer methods and programs in biomedicine, 101(3), 265–270. [DOI] [PubMed] [Google Scholar]
  14. Friedland W, Dingfelder M, Jacob P, Paretzke HG (2005). Calculated DNA double- strand break and fragmentation yields after irradiation with He ions. Radiation Physics and Chemistry, 72(2), 279–286, 2005. [Google Scholar]
  15. Ftá_nikova S, & Bohm R (2000). Monte Carlo calculations of energy deposition on cellular, multicellular and organ level for Auger emitters. Radiation Protection Dosimetry 92(4), 279–288. [Google Scholar]
  16. Garty G, Schulte R, Shchemelinin S, Leloup C, Assaf G, Breskin A, & Grosswendt B (2010). A nanodosimetric model of radiation-induced clustered DNA damage yields. Physics in Medicine & Biology, 55(3), 761. [DOI] [PubMed] [Google Scholar]
  17. Guerreiro J, Alves V, Abrunhosa A, Paulo A, Gil O, & Mendes F (2018). Radiobiological characterization of 64CuCl2 as a simple tool for prostate cancer theranostics, Molecules 23(11), 2944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Goddu SM, Howell RW, Bouchet LG, Bolch WE, & Rao DV (1997). MIRD cellular S values. Reston, VA: Society of Nuclear Medicine. [Google Scholar]
  19. Gregoriadis GC, Apostolidis NS, Romanos AN, Paradellis TP (1983). A comparative study of trace elements in normal and cancerous colorectal tissues. Cancer. 52(3), 508–519. [DOI] [PubMed] [Google Scholar]
  20. Grosswendt B, Pszona S, & Bantsar A (2007). New descriptors of radiation quality based on nanodosimetry, a first approach. Radiation protection dosimetry, 126(1–4), 432–444. [DOI] [PubMed] [Google Scholar]
  21. Gupte A, & Mumper RJ (2009). Elevated copper and oxidative stress in cancer cells as a target for cancer treatment. Cancer Treatment Reviews. 35(1), 32–46. [DOI] [PubMed] [Google Scholar]
  22. Hatori Y, & Lutsenko S (2016). The role of copper chaperone Atox1 in coupling redox homeostasis to intracellular copper distribution. Antioxidants, 5(3), 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hauf S, Kuster M, Batič M, Bell ZW, Hoffmann DH, Lang PM, … & Zoglauer A (2013). Radioactive decays in Geant4. IEEE Transactions on Nuclear Science, 60(4), 2966–2983. [Google Scholar]
  24. Humm JL, Howell RW, & Rao DV (1994). Dosimetry of Auger-electron-emitting radionuclides: report no. 3 of AAPM Nuclear Medicine Task Group No. 6. Medical Physics, 21(12), 1901–1915. [DOI] [PubMed] [Google Scholar]
  25. Incerti S, Baldacchino G, Bernal M, Capra R, Champion C, Francis Z, & Nieminen P (2010). The geant4-dna project. International Journal of Modeling, Simulation, and Scientific Computing, 1(02), 157–178. [Google Scholar]
  26. Ku A, Facca VJ, Cai Z, Reilly RM (2019). Auger electrons for cancer therapy – a review. EJNMMI Radiopharmacy and Chemistry, 4:27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kyriakou I, Ivanchenko V, Sakata D, Bordage MC, Guatelli S, Incerti S, Emfietzoglou D (2019). Influence of track structure and condensed history physics models of Geant4 to nanoscale electron transport in liquid water. Phys. Medica 58, 149–54. [DOI] [PubMed] [Google Scholar]
  28. Lee J, Peña MMO, Nose Y, & Thiele DJ (2002). Biochemical characterization of the human copper transporter Ctr1. Journal of Biological Chemistry, 277(6), 4380–4387. [DOI] [PubMed] [Google Scholar]
  29. Loevinger R, Budinger TF, & Watson EE (1988). MIRD primer for absorbed dose calculations. Society of Nuclear Medicine. Publisher: Society of Nuclear Medicine, New York: (1988) [Google Scholar]
  30. Loevinger R, & Berman M (1968). A formalism for calculation of absorbed dose from radionuclides. Physics in Medicine & Biology, 13(2), 205. [DOI] [PubMed] [Google Scholar]
  31. McMillan DD, Maeda J, Bell JJ, et al. (2015). Validation of 64Cu-ATSM damaging DNA via high-LET Auger electron emission. J Radiat Res. 56(5), 784–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. McNamara AL, Ramos-Méndez J, Perl J, Held K, Dominguez N, Moreno E, … & Incerti S (2018). Geometrical structures for radiation biology research as implemented in the TOPAS-nBio toolkit. Physics in Medicine & Biology, 63(17), 175018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Moradi MS, & Bidabadi BS (2018). Micro-dosimetry calculation of Auger-electron-emitting radionuclides mostly used in nuclear medicine using GEANT4-DNA. Applied Radiation and Isotopes, 141, 73–79. [DOI] [PubMed] [Google Scholar]
  34. Perl J, Shin J, Schümann J, Faddegon B, & Paganetti H (2012). TOPAS: an innovative proton Monte Carlo platform for research and clinical applications. Medical physics, 39(11), 6818–6837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Qin C, Liu H, Chen K, Hu X, Ma X, Lan X, & Cheng Z (2014). Theranostics of malignant melanoma with 64CuCl2. J. Nuclear Medicine 55(5), 812–817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Rabus H, & Nettelbeck H (2011). Nanodosimetry: Bridging the gap to radiation biophysics. Radiation Measurements, 46(12), 1522–1528. [Google Scholar]
  37. Ramos-Méndez J, Burigo LN, Schulte R, Chuang C, & Faddegon B (2018) Fast calculation of nanodosimetric quantities in treatment planning of proton and ion therapy. Physics in Medicine and Biology, 63(23), 235015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ramos-Méndez J, Perl J, Schuemann J, McNamara A, Paganetti H, & Faddegon B (2018). Monte Carlo simulation of chemistry following radiolysis with TOPAS-nBio. Physics in Medicine & Biology, 63(10), 105014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Righi S, Ugolini M, Bottoni G, Puntoni M, Iacozzi M, Paparo F, … & Piccardo A (2018). Biokinetic and dosimetric aspects of 64 CuCl 2 in human prostate cancer: possible theranostic implications. EJNMMI research, 8(1), 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Roeske JC, Aydogan B, Bardies M, & Humm JL (2008). Small-scale dosimetry: challenges and future directions. In Seminars in nuclear medicine (Vol. 38, No. 5, pp. 367–383). WB Saunders. [DOI] [PubMed] [Google Scholar]
  41. Rollet S, Colautti P, Grosswendt B, Moro D, Gargioni E, Conte V, & DeNardo L (2010). Monte Carlo simulation of mini TEPC microdosimetric spectra: influence of low energy electrons. Radiation Measurements, 45(10), 1330–1333. [Google Scholar]
  42. Schuemann J, McNamara AL, Ramos-Méndez J, Perl J, Held KD, Paganetti H, … & Faddegon B (2018). TOPAS-nBio: An Extension to the TOPAS Simulation Toolkit for Cellular and Sub-cellular Radiobiology. Radiation research, 191(2), 125–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Šefl M, Incerti S, Papamichael G, & Emfietzoglou D (2015). Calculation of cellular S-values using Geant4-DNA: the effect of cell geometry. Applied Radiation and Isotopes, 104, 113–123. [DOI] [PubMed] [Google Scholar]
  44. Stepanek J, Larsson B, Weinreich R (1996). Auger-Electron Spectra of Radionuclides for Therapy and Diagnostics. Acta Oncologica 35(7), 863–868. [DOI] [PubMed] [Google Scholar]
  45. Team MC (2003). MCNP–A General Purpose Monte Carlo N-Particle Transport Code. Version 5. Technical report, LA-UR-03–1987, Los Alamos National Laboratory; (NM, USA: ). [Google Scholar]
  46. Valentini G, Panichelli P, Villano C, Pigotti G, & Martini D (2014). 64CuCl2: new theranostic agent. Nuclear Medicine and Biology 7(41), 638. [Google Scholar]
  47. Valentini G, Panichelli P, Villano C, Pigotti G, Martini D, Giacobbi B, & Coccetti D (2015). Case report: glioblastoma imaging and therapy with 64CuCl2., J. Nuclear Medicine 56 (S2), 24. [Google Scholar]
  48. Vaziri B, Wu H, Dhawan AP, Du P, Howell RW, Bolch WE, … & Meredith RF (2014). MIRD pamphlet No. 25: MIRDcell V2. 0 software tool for dosimetric analysis of biologic response of multicellular populations. Journal of Nuclear Medicine, 55(9), 1557–1564. [DOI] [PubMed] [Google Scholar]
  49. Volkert WA, Goeckeler WF, Ehrhardt GJ, & Ketring AR (1991). Therapeutic radionucides: production and decay property considerations. Journal of nuclear medicine: official publication, Society of Nuclear Medicine, 32(1), 174–185. [PubMed] [Google Scholar]
  50. Watson EE, Stabin MG, & Siegel JA (1993). MIRD formulation. Medical physics, 20(2), 511–514. [DOI] [PubMed] [Google Scholar]
  51. Zhou B, & Gitschier J (1997). hCTR1: a human gene for copper uptake identified by complementation in yeast. Proceedings of the National Academy of Sciences, 94(14), 7481–7486. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

TableAndFigure
NIHMS1652993-supplement-TableAndFigure.pdf (195.8KB, pdf)

RESOURCES