Random Survival Forests Analysis of Intraoperative Complications as Predictors of Descemet Stripping Automated Endothelial Keratoplasty Graft Failure in the Cornea Preservation Time Study

Key Points

Question

Does random survival forests analysis allow for an improved analytic approach for identifying factors predictive of graft failure and for obtaining adjusted graft survival estimates from the Cornea Preservation Time Study (CPTS)?

Findings

This cohort study using a prediction model found that, of the 50 baseline donor, recipient, and eye bank variables, intraoperative complications of Descemet stripping automated endothelial keratoplasty were highly predictive of graft failure in the CPTS.

Meaning

These findings, while post hoc, support the hypothesis that random survival forests analysis allows for an improved analytic approach for identifying factors predictive of graft failure and for obtaining adjusted graft survival estimates that may be useful for future ophthalmic surgical studies.

Abstract

Importance

A new analytic method can evaluate factors of interest associated with graft failure after Descemet stripping automated endothelial keratoplasty (DSAEK) or more generally in any ophthalmic surgical setting with a time-to-event outcome.

Objective

To reanalyze types of intraoperative complications associated with DSAEK graft failure in the Cornea Preservation Time Study using random survival forests.

Design, Setting, and Participants

This cohort study, initially conceived in April 2019, used a prediction model to conduct a post hoc secondary analysis of data collected in a multicenter, double-masked, randomized clinical trial. Forty US clinical sites with 70 surgeons participated, with donor corneas provided by 23 US eye banks. The study included 1090 participants, representing 1330 eyes, undergoing DSAEK for Fuchs dystrophy (1255 eyes [94.4%]) or pseudophakic or aphakic corneal edema (75 eyes [5.6%]). Enrollment occurred between April 16, 2012, and February 20, 2014, and follow-up ended June 5, 2017. Statistical analysis was performed from July 10, 2019, to May 29, 2020.

Intervention

Descemet stripping automated endothelial keratoplasty with random assignment of a donor cornea with preservation time of 7 days or less or 8 to 14 days.

Main Outcomes and Measures

Ranked variable importance for intraoperative complications among 50 donor, recipient, and eye bank variables and restricted mean survival time through 47 months (1434 days) after DSAEK were examined. Random survival forests, a nonparametric method (with less restrictive model assumptions) that is far more flexible in its ability to model nonlinear effects and interactions, was used to analyze the data.

Results

This study included 1090 participants (663 women [60.8%]; median age, 70 years [range, 42-90 years]), representing 1330 eyes. Random survival forests ranked a DSAEK intraoperative complication as the third most predictive factor of graft failure, after surgeon and eye bank, in the final model with 5 predictors. In the first 47 months after DSAEK, the estimated mean difference in restricted mean survival time for grafts that experienced a DSAEK intraoperative complication vs those that did not was −227 days (99% CI, −352 to −70 days) based on the final RSF model.

Conclusions and Relevance

These findings, while post hoc, support the hypothesis that random survival forests allow for an improved analytic approach for identifying factors predictive of graft failure and for obtaining adjusted graft survival estimates. Random survival forests offer the opportunity to guide the development of future population-based cohort ophthalmic surgical studies, establishing definitive factors for procedural success.

This cohort study reanalyzes types of intraoperative complications associated with Descemet stripping automated endothelial keratoplasty (DSAEK) graft failure in the Cornea Preservation Time Study using random survival forests.

Introduction

Since keratoplasty became widely available in the 1950s with advances in eye banking and surgical technique, there have been numerous studies, mostly retrospective, single-site, and/or registry studies, that have examined the donor, recipient, and operative factors that are associated with graft survival after penetrating keratoplasty (PKP)^1,2,3,4 and, more recently, endothelial keratoplasty, including Descemet stripping automated endothelial keratoplasty (DSAEK)^5,6,7,8 and Descemet membrane endothelial keratoplasty.^7,9 Two notable prospective clinical trials that examined these factors in secondary analyses using standard Kaplan-Meier¹⁰ and Cox proportional regression¹¹ statistical analytic methods were the Cornea Donor Study (CDS) for PKP^12,13,14 and the Cornea Preservation Time Study (CPTS) for DSAEK.^15,16 In the CDS, recipient pseudophakic or aphakic corneal edema and history of glaucoma were found to be associated with lower PKP success¹⁴; donor age, the factor explored through primary analysis, had no effect on PKP success for most donors 34 to 71 years of age.¹⁷ No other donor, recipient, or operative factors were associated with lower PKP graft survival in the CDS. In the CPTS, similarly, pseudophakic corneal edema was associated with lower DSAEK success, while history of glaucoma was not.¹⁶ However, history of diabetes in the donor and the occurrence of any intraoperative complication were also associated with lower DSAEK graft survival in the first 8 weeks after DSAEK¹⁶; preservation time (PT), the factor explored through primary analysis, showed no difference in DSAEK success for up to 11 days of storage.¹⁸ No other donor, recipient, or operative factors were associated with lower DSAEK success in the CPTS.

Random forests, introduced by Breiman¹⁹ for classification and regression tasks, is an increasingly popular machine-learning technique that offers excellent performance and great flexibility in its ability to handle all types of data, including “big data.”²⁰ Random forests average the predictions of many decision trees, each of which asks a series of logical questions of the predictor variables (eg, “Is prelamellar donor corneal dissection thickness >600 μm?”) that split the observations repeatedly to maximize group differentiation with respect to the outcome until a final partition of the data is obtained. Each tree in the forest is grown on 63.2% of the data, and when splitting the data, only a fraction of the predictors are considered at each split of the data. This has the effect of making the trees more distinct from one another so that the collection of trees, known as a forest or an ensemble, provides superior predictive performance to any single tree. Random forests with a survival outcome (eg, graft survival) are known as random survival forests (RSF).²¹ For RSF, cumulative hazard functions are obtained for each tree based on 36.8% of the data that were not used to grow it for greater accuracy and then averaged across trees to produce a final forest cumulative hazard function for each observation. Random survival forests have been used to analyze survival problems with great success (eg, in esophageal cancer staging,^22,23 heart transplant waiting list mortality,²⁴ and prediction of time to incident type 2 diabetes from metabolomics data²⁵). To our knowledge, RSF analysis has been used only in a limited manner in the ophthalmic literature for only 1 study predicting risk of diabetic retinopathy in patients with type 2 diabetes.²⁶

In contrast to standard Kaplan-Meier and Cox proportional hazards regression analyses, RSF analysis requires less-restrictive assumptions and can accommodate many types of predictors and interactions among them.²¹ Random survival forests can also be used to analyze high-dimensional data sets in which there are more predictors than the sample size of the data,^27,28 for which classical methods such as Cox proportional hazards regression fail. An additional strength of RSF modeling is that it provides its own internal generalization error estimate as well as measures of variable importance (VIMP) for each variable included in the model. However, RSF modeling is much more computationally intensive than modeling via Kaplan-Meier or Cox proportional hazards regression, and RSF analysis is not appropriate if there are too few prognostic variables, observations, or events.^29,30

We know from previous analyses that undifferentiated intraoperative complications were associated with graft failure in the CPTS,¹⁶ while the specific types of intraoperative complications associated with this finding were not explored. The purpose of this study was to reanalyze which types of intraoperative complications might be associated with DSAEK graft failure in the CPTS using RSF and adjusting for other important donor, recipient, eye bank, and intraoperative variables. This knowledge may provide additional evidence-based guidelines for clinical decision-making to maximize the success of DSAEK surgery and to allow for more efficient use of donor corneal tissue.

Methods

Details of the CPTS protocol have been previously reported.^15,16,18 The protocol was approved by the institutional review boards governing each investigational site, and individual participants provided written informed consent to participate in the study, with consent requested again to extend follow-up from 36 months to a common study end date. Participants were reimbursed $25 for each protocol visit. Study oversight was provided by an independent data and safety monitoring committee. The research adhered to the tenets of the Declaration of Helsinki.³¹ The protocol was registered and is publicly available (NCT01537393).

Participants were enrolled at 40 clinical sites between April 16, 2012, and February 20, 2014, and donor corneas were provided by 23 eye banks across the United States. The study included 1090 participants, representing 1330 eyes, undergoing DSAEK for Fuchs dystrophy (1255 eyes [94.4%]) or pseudophakic or aphakic corneal edema (75 eyes [5.6%]). Eyes undergoing DSAEK were randomly assigned to receive a donor cornea with PT of 7 days or less or 8 to 14 days in a noninferiority trial; for participants with both eyes eligible, the first eye was assigned randomly to a PT group, and the second eye was assigned to the other PT group. The 1330 eyes completing surgery with a CPTS-assigned cornea were considered the study eyes. Assigned corneas were from donors aged 12 to 75 years (median age, 61 years) with an eye bank–measured central endothelial cell density at the time of screening of at least 2300 cells/mm². Surgeons elected to either receive the lenticule after lamellar dissection by the eye bank or have the tissue shipped for dissection by the surgeon at the time of the DSAEK. The eye bank prospectively recorded all prelamellar and postlamellar dissection observations.^15,32 For the 343 surgeon-prepared eyes, 43 (12.5%) were missing data on prelamellar donor dissection thickness, and 67 (19.5%) were missing data on lenticule thickness.¹⁵ Specific intraoperative complications were tracked, including difficulty with donor lenticule insertion and flipping of the donor lenticule.^15,16,18,32 Follow-up examinations were performed at 1 day, 1 week, and 1, 6, 12, 24, and 36 months postoperatively. Follow-up ended June 5, 2017. Participants consenting to extension of follow-up in the study had visits scheduled at 48 and 60 months postoperatively. Postoperative care was provided according to each investigator’s standard practice.

Graft failure was defined as the occurrence of 1 of the following: (1) regrafting for any reason, (2) a cloudy or equivocally cloudy cornea on the first postoperative day that did not clear within 8 weeks, or (3) a cornea that was initially clear postoperatively but became and remained cloudy for 90 days (late failures).^15,16,18 Grafts that failed during the first 8 postoperative weeks were further classified as primary failures if they occurred in the absence of operative complications or early donor failures if they occurred in the presence of operative complications.

A DSAEK intraoperative complication was defined as the occurrence of the donor lenticule flipping on insertion, difficulty unfolding and positioning without hook, difficulty unfolding and positioning with hook, difficult air fill and retention in positioning, reinsertion of donor after extrusion, or the following write-in operative complications: donor insertion, difficult air fill and retention after extrusion, or retained air in the posterior chamber. Other intraoperative complications noted by the surgeon not associated with the DSAEK procedure included cataract extraction–related complications (ie, broken posterior capsule or vitreous loss), donor-quality surgeon observations (ie, color or excessive folds), and miscellaneous (ie, excessive blood in the anterior chamber or excessive pain) (eTable in the Supplement).

Statistical Analysis

Statistical analysis was performed from July 10, 2019, to May 29, 2020. Candidate variables were selected in accordance with the guidelines provided by Rajeswaran and Blackstone.³³ Fifty donor, recipient, eye bank, and intraoperative variables were considered for inclusion in the final model. The final RSF model used to obtain the direct adjusted survival estimates (ie, marginal effects)^34,35,36 for a DSAEK intraoperative complication consisted of the 4 variables selected as most important, including a DSAEK intraoperative complication, and PT, which we required to be included in the model selection procedure and the final model. To obtain direct adjusted survival curves from the final RSF model, 2 predicted survival curves were obtained for each observation with the actual value of the DSAEK intraoperative complication variable and its counterfactual (ie, yes for no and no for yes), keeping all other covariate values as they were. This resulted in 1330 × 2 predicted survival curves that were then averaged to obtain 2 final survival curves. The restricted mean survival time (RMST) with time horizon τ is defined as the area under the survival curve up to τ and represents the time survived in the first τ time units.³⁷ Thus, the difference in RMST through 47 months (1434 days) after DSAEK between grafts that experienced a DSAEK intraoperative complication and those that did not (adjusted for the 4 other variables in the final model) was calculated as the difference in the areas under these 2 survival curves. Even though graft survival 3 years after DSAEK was chosen prospectively as the primary outcome for the original CPTS analysis, 2 graft failures occurred after the 3-year protocol visit window (1065-1278 days), the latest of which occurred at 1434 days or, equivalently, 47 months. For this reason and in accordance with the secondary post hoc nature of this analysis, we chose 47 months instead of 3 years as the time horizon for RMST.

Our study cohort for the analysis consisted of the 1330 eyes that underwent surgery. Because the effective sample size for this analysis was the number of graft failures (as events provide more information than censored observations)³⁸ and we considered 50 total donor, recipient, eye bank, and intraoperative predictors, we used variable hunting based on VIMP to select the final RSF model,^27,28 requiring PT to be included.

Confidence intervals were constructed by subsampling^39,40,41 the data 50 000 times and growing RSF on each subsample of size 400 to obtain 50 000 subsampling estimates. These estimates were used to construct the 99% pivotal CIs. Subsampling confidence intervals are related to bootstrap confidence intervals except the sampling is without replacement and the number of observations selected is smaller than the total sample size of the data set. The data were prepared using SAS, version 9.4 (SAS Institute Inc) and analyzed using R, version 3.6.3 (R Foundation for Statistical Computing) with the randomForestSRC package.^42,43

Results

This study included 1090 participants (663 women [60.8%]; median age, 70 years [range, 42-90 years]), representing 1330 eyes. Among the 1330 eyes that underwent surgery, 81 experienced graft failure in the first 4 years after DSAEK; of the 240 patients who underwent bilateral surgery, only 1 experienced graft failure in both eyes, and there were no cases in which both corneas recovered from the same donor experienced graft failure. Total follow-up time for the 1330 study eyes was 4114 years.

RSF-Ranked VIMP

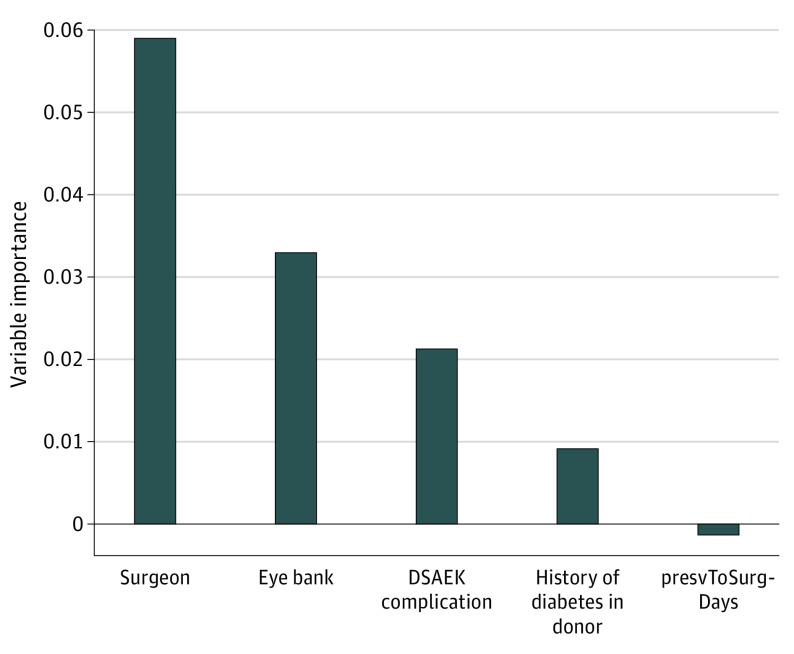
The VIMP plot for the final RSF model, with the variables selected by variable hunting based on VIMP after requiring PT, is displayed in Figure 1. In the final model, a DSAEK intraoperative complication was ranked the third most predictive factor of graft failure, after surgeon and eye bank, in the final RSF model with 5 predictors. The other intraoperative complications (cataract, donor quality, and miscellaneous) (eTable in the Supplement) were ultimately excluded from modeling because they were too infrequent. The Harrell C statistic⁴⁴ for the final RSF model predicting graft failure was 0.71.

Figure 1. Variable Importance Plot for Predicting Graft Failure for the 4 Predictors Selected by Variable Hunting Using Variable Importance After Requiring Preservation Time.

Any predictor with variable importance above the line at 0.00 contributes to the prediction accuracy of the final model. Any variable with variable importance less than 0.00 is a noisy variable in the final model, which is the case with preservation time, which we required to be included. This is consistent with the results of the primary study, which found that graft survival at 3 years was indistinguishable through 11 days of preservation time and the decrement in survival was modest for corneas preserved 12 to 14 days. DSAEK indicates Descemet stripping automated endothelial keratoplasty; and presvToSurgDays, preservation to surgery (in days).

Survival Curves

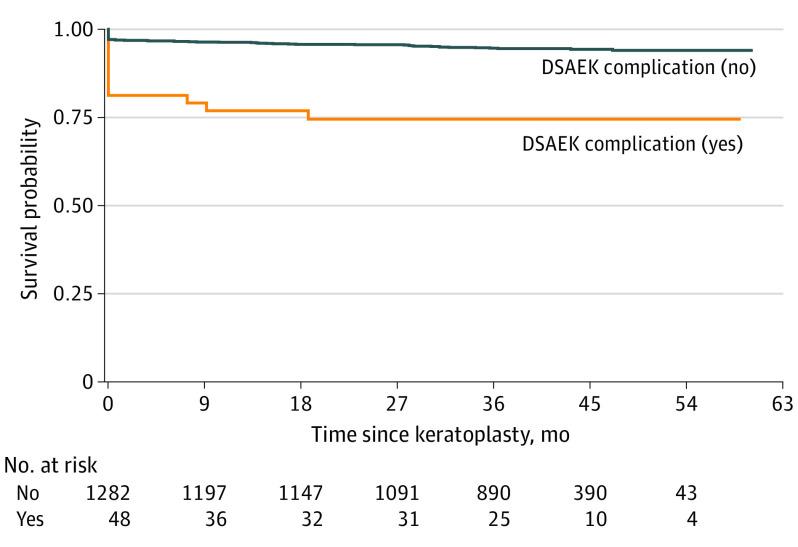
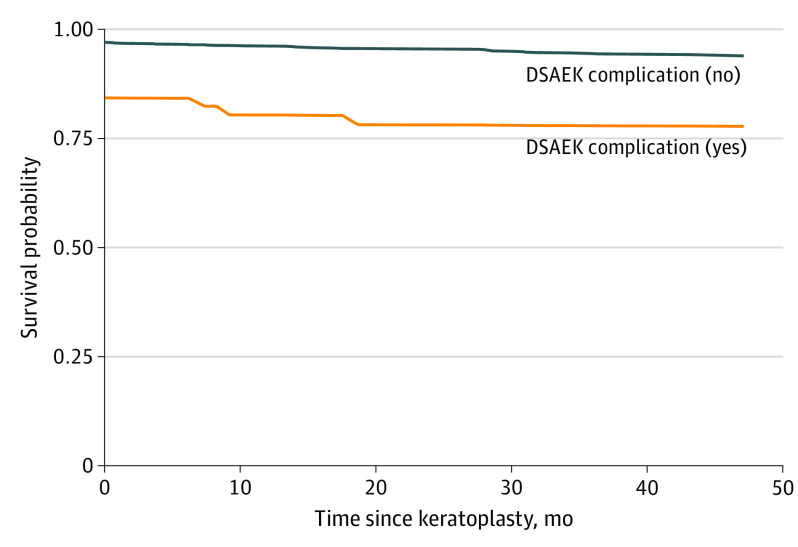
Unadjusted Kaplan-Meier survival curves and eyes at risk over time by DSAEK intraoperative complication (yes or no) are displayed in Figure 2. Direct adjusted survival curves estimated via RSF are displayed in Figure 3. Thus, adjusting for 4 other baseline donor, recipient, eye bank, and intraoperative variables attenuated the estimated differences between grafts that experienced a DSAEK intraoperative complication and those that did not, which suggests that, even though a DSAEK complication was deleterious in and of itself, there were other factors that were also associated with poorer survival of the grafts that experienced a DSAEK intraoperative complication.

Figure 2. Unadjusted Survival Curves for Presence or Absence of a Descemet Stripping Automated Endothelial Keratoplasty (DSAEK) Intraoperative Complication.

The survival curves were estimated nonparametrically via the Kaplan-Meier method (1330 eyes).

Figure 3. Adjusted Survival Curves for Presence or Absence of a Descemet Stripping Automated Endothelial Keratoplasty (DSAEK) Intraoperative Complication .

The survival curves were estimated nonparametrically via random survival forests (1330 eyes).

RMST Analysis

With corneal grafts that experienced no DSAEK intraoperative complication as the comparator for survival, the analysis of the RMST using RSF showed that, in the first 47 months after DSAEK, the estimated mean difference in RMST was –227 days (99% CI, –352 to –70 days) for grafts that experienced a DSAEK intraoperative complication, where negative differences correspond to fewer days of graft survival compared with the reference category. In contrast, when the difference in RMST was calculated via Kaplan-Meier survival curves, the unadjusted difference was –277 (99% CI, –499 to –56 days), which is naturally consistent with what we noted when comparing the Kaplan-Meier and RSF survival curves.

Discussion

Our study, reanalyzing an established prospective data set from the CPTS that examined PT and other donor, recipient, eye bank, and intraoperative factors associated with graft success after DSAEK,¹⁵ will have yielded supportive and more detailed findings, if this post hoc analysis is confirmed in future population-based cohort studies. The RSF analysis was able to model more variables with greater sophistication than the previous analyses using Cox proportional hazards regression with main covariate effects only and a frailty term for surgeon (Figure 1; eFigure in the Supplement). With just 4 variables (PT, recipient diagnosis, donor history of diabetes, and any intraoperative complication), there are 11 possible interaction terms to consider. In contrast, RSF analysis models interactions automatically through its recursive splitting. Our RSF analysis went beyond the previous analysis methods in delineating the association of a specific factor of interest with graft failure, intraoperative complications associated with DSAEK, as opposed to undifferentiated intraoperative complications, adjusted for other important variables, including eye bank, a previously unmodeled source of heterogeneity. With our newly reported RSF analysis, on average in the first 47 months after DSAEK, if a DSAEK intraoperative complication occurred, the graft survived between 70 and 352 fewer days (ie, the upper and lower limits of the 99% CI) compared with corneal grafts that did not experience a DSAEK complication, adjusting for the 4 other variables in the final model. This more granular analysis of DSAEK intraoperative complications associated with graft failure derived from RSF compares with the broader categories of factors associated with DSAEK graft survival analyzed using Kaplan-Meier and Cox proportional hazards regression analyses.^{8,45,46,47,48,49,50,51,52,53}

Strengths and Limitations

This study has some strengths. The CPTS prospectively collected a predetermined number of potential donor, recipient, and operative predictors, as well as eye bank observations at time of donor evaluation and processing, and analyzed their association with graft failure. Our findings are broadly representative because they were obtained from 23 Eye Bank Association of America–certified eye banks and 70 experienced, masked DSAEK surgeons. Finally, this analysis benefited from eschewing survival probabilities or hazard ratios at a specific time horizon as the outcome in favor of RMST. Restricted mean survival time accounts for the entire survival trajectory through the chosen time horizon and produces treatment or exposure differences in units of time, which are more meaningful, readily understood, and actionable than abstract survival probabilities or (especially) hazard ratios.

This study has some limitations. We were unable to model individual intraoperative complications associated with DSAEK because they were too rare when viewed individually. Another possible limitation was that, even though the sample size was large for a randomized clinical trial, there is some evidence that random forests require more events per predictor variable than standard methods,³⁰ and the event rate for the CPTS was quite low (ie, 0.02 failures per eye-year). However, we acted to mitigate the possibility of model optimism by using variable hunting based on VIMP to obtain a parsimonious final RSF model, and we can be confident that a DSAEK intraoperative complication is a strong predictor in the CPTS.

Conclusions

Random survival forests offer a promising alternative to traditional analytic methods for identifying variables at baseline that are most predictive of keratoplasty success when there are many candidate prognostic variables and for providing adjusted graft survival estimates. Kaplan-Meier analysis is nonparametric but is limited in that it can only analyze the association of 1 variable with survival at a time; it cannot adjust for other variables. Cox proportional hazards regression analysis can handle multiple variables but requires that the ratio of hazards for any 2 individuals remains constant over time (ie, proportional). Also, interactions must be prespecified, and correlated predictors and/or too many predictors often pose modeling problems. Finally, the bivariable screening of each candidate predictor and the outcome (combined with forward, backward, or stepwise variable selection, which is common in the presence of many potential predictors) is suboptimal with well-established drawbacks.^{54,55,56,57,58,59,60,61,62} In contrast to Cox proportional hazards regression (or parametric survival models such as Weibull regression), RSF analysis is more flexible in its ability to model nonlinear effects and interactions and requires fewer assumptions. Random survival forest analysis is appropriate for competing risks⁶³ as well as for right-censored survival data and for data sets of all sizes, including those with more prognostic variables than observations, for which standard methods fail. However, RSF analysis is not appropriate if there are too few variables, observations, or events. We acknowledge the importance of demonstrating that any method newly applied to a given field must have clinical relevance and not just theoretical advantages compared with existing methods. Nevertheless, the RSF analysis supported, clarified, and enriched our previous findings from the CPTS that used standard Kaplan-Meier and Cox proportional hazards regression analysis methods.

Supplement.

eFigure. Forest Plot of Hazard Ratios and Associated P Values From Cox Regression Analysis With Bivariable Screening of Candidate Variables and Backward Selection

eTable. List of Variables From the Cornea Preservation Time Study (CPTS) Used in the Random Survival Forests