Swarm-CG: Automatic Parametrization of Bonded Terms in MARTINI-Based Coarse-Grained Models of Simple to Complex Molecules via Fuzzy Self-Tuning Particle Swarm Optimization

Abstract

We present Swarm-CG, a versatile software for the automatic iterative parametrization of bonded parameters in coarse-grained (CG) models, ideal in combination with popular CG force fields such as MARTINI. By coupling fuzzy self-tuning particle swarm optimization to Boltzmann inversion, Swarm-CG performs accurate bottom-up parametrization of bonded terms in CG models composed of up to 200 pseudo atoms within 4–24 h on standard desktop machines, using default settings. The software benefits from a user-friendly interface and two different usage modes (default and advanced). We particularly expect Swarm-CG to support and facilitate the development of new CG models for the study of complex molecular systems interesting for bio- and nanotechnology. Excellent performances are demonstrated using a benchmark of 9 molecules of diverse nature, structural complexity, and size. Swarm-CG is available with all its dependencies via the Python Package Index (PIP package: swarm-cg). Demonstration data are available at: www.github.com/GMPavanLab/SwarmCG.

1. Introduction

In many research fields, innovation passes through the design and development of new types of functional materials and molecular systems with controllable properties. The shape and functions of such complex nanostructures typically originates from the collective behavior of a large number of interacting molecules, as it is the case, for example, in lipid membranes,^1,2 supramolecular polymers,³⁻⁵ crystals,⁶⁻⁸ cages,⁹⁻¹¹ and so forth. The investigation of these molecular systems at a sufficiently high (submolecular) resolution is a tedious task, especially when these are composed of large, soft, and flexible macromolecules in the solution.

Alongside with experimental studies, molecular modeling techniques such as molecular dynamics (MD) or Monte Carlo simulations have turned out to be cornerstone tools to this purpose.¹²⁻²⁰ Recent advances in computational hardware and simulation software have made possible to study and model increasingly larger molecular systems, allowing the investigation of their structural properties with great (atomistic-level) detail. However, the large number of degrees of freedom (DOFs) of these calculations still limits classical all-atom MD simulations (AA-MD) to the study of systems with a maximum of ∼10⁶ atoms (including the solvent, in, e.g., explicit solvent simulations) and within the timescales of nano- to microseconds.^12,13 Furthermore, AA-MD may typically suffer from limited sampling, especially in the simulation of complex molecules, with the risk of entrapment and oversampling of local minima and metastable states.^21,22 As a consequence, AA-MD simulations cannot be practically employed for the observation of many crucial phenomena and molecular events occurring on long characteristic timescales.

A typical approach to overcome these limitations is coarse graining (CG), which consists of simplifying the description of high-resolution molecular models (fine grain, FG), reducing their resolution by grouping several atoms in CG beads (pseudo atoms). The objective of CG modeling is to limit the number of DOFs to be treated in the simulations, while still providing a physically relevant representation of the molecular systems. The way particles are grouped together (mapping scheme) determines which DOFs are either retained or neglected in the CG process²³⁻²⁵ and can be modulated by molecular modelers according to the specific questions of interest. Different CG frameworks have gained popularity by allowing to simulate complex molecular systems, and their dynamical properties, such as solvent and small-molecule mixtures,²⁶⁻³³ polymer melts,³⁴⁻³⁷ lipid bilayers,³⁸⁻⁴⁰ vesicles,^39,41,42 proteins,⁴³⁻⁴⁵ and various types of complex nanomaterials.^14,46−50 Essentially, the CG process can follow two different routes: bottom-up or top-down.

In bottom-up approaches (structure-based CG), parameters of the CG force field are extracted from the reference equilibrium AA-MD simulations. Methods such as inverse Monte Carlo (IMC),⁵¹ iterative Boltzmann inversion (IBI),⁵² multistate IBI,⁵³ force matching,^18,54−56 relative entropy minimization,⁵⁷ the generalized Yvon–Born–Green (g-YBG)⁵⁸ equation, or particle swarm optimization (PSO)^33,34,59,60 can be applied to this end. Their parameter extraction schemes either try to reproduce the pair distribution functions,⁵¹⁻⁵³ to match the forces,^18,54−56 to minimize the information loss in terms of relative entropy,⁵⁷ or to make use of the liquid state theory.⁵⁸ Bottom-up approaches generally allow to capture great details of the interactions of a FG system and benefit from rigorous formalism. On the other hand, the very nature of these structure-based approaches is to rely on equilibrium AA-MD simulation(s) of bulk/condensed systems for calibrating CG force fields, which induces transferability issues: bottom-up CG force fields are rarely accurate in thermodynamic conditions away from those used during parametrization.^61,62 The necessity of disposing of well-equilibrated AA-MD trajectories is also often a nontrivial task, which is important in structure-based CG of heterogeneous systems including large and flexible molecules. Bottom-up CG approaches have been applied mostly to solvent and small-molecule mixtures,²⁶⁻³³ polymer melts,³⁴⁻³⁷ amorphous organic solids,⁶³ lipids,^18,64,65 and peptides.⁶⁶ To date, the number of successful studies involving more structured macromolecular systems⁶⁷⁻⁶⁹ is still limited. Inversely, top-down approaches essentially focus on reproducing key experimental data and thermodynamic properties, while making minimal, indirect, or no use of AA-MD simulations.^12,24,70,71 The main limit in the use of top-down approaches is the need for reliable experimental results to be used as a reference. However, in most cases for which it is of practical interest to develop a CG model, experimental results are often not available (i.e., this is one reason why the development of a CG model is a necessity in order to exhaustively study these systems and to gain a deeper insight into their behavior).

Perhaps one of the most widely used CG framework is MARTINI,⁷² which maps molecular fragments composed of ∼3–5 heavy atoms into predefined CG beads, parametrized according to the partitioning of their associated molecular fragments between aqueous and hydrophobic environments. MARTINI CG beads are distributed in 4 categories: polar (P), nonpolar (N), apolar (C), and charged (Q) bead types, while nonbonded pair interactions (solute–solute and solute–solvent interactions) are represented using nondirectional 12-6 Lennard-Jones potentials. Such top-down approaches enable the modular and additive parametrization of new complex molecules, capitalizing on a relative transferability of the force field, which has proven useful to create CG molecular models for various types of molecules, from biomolecules, such as lipids,⁷³⁻⁷⁵ peptides, and proteins,^76,77 to synthetic molecules, such as polymers^78,79 and fullerenes.^80,81 Moreover, the MARTINI scheme makes this force field, in principle, transferable, which is very useful when one wants to compare and study structural variants or different conditions in the molecular systems. In most cases, however, molecular modelers need to refine their base MARTINI models to more faithfully represent a specific molecular chemistry and architecture.^24,71,82

Bottom-up and top-down approaches each have their drawbacks and in practice many CG-based studies rely on a combination of these two routes. In particular, one of the most challenging tasks in complex molecular systems is to quantify the intramolecular and intermolecular interactions of heterogeneous systems composed of large and flexible molecules, notably exhibiting long-range ordering at low density in the solvent, starting solely from their molecular structures. Combined top-down and bottom-up approaches are particularly useful to this end. For example, previous studies^{14,46−48,50,83,84} have demonstrated the potential of combining MARTINI,⁷² AA-MD simulations, and enhanced sampling methods⁸⁵⁻⁸⁸ for probing the self-assembling capabilities of complex (heterogeneous) molecular systems in a rigorous way. Their general workflow can be summarized as follows, in 3 steps. First, according to the MARTINI framework, a preliminary CG model is built for each molecular species in the system by mapping constitutive molecular fragments to CG beads, which types are opportunely chosen based on the chemical analogy and polarities of the fragments. This allows to quickly set up an initial guess of the nonbonded interactions in the CG system.^24,71 Second, molecular modelers have to parametrize the intramolecular bonded interactions between CG beads, namely, the bond, angle, and dihedral parameters, in terms of equilibrium values and force constants.^70,72 These define the molecular flexibility, shape, and size and are just as important as the nonbonded parametrization for how the molecules will interact between them and their surroundings (also solvent). Best practice is to tune bonded parameters (BPs) in a bottom-up fashion, based on separate well-sampled AA-MD simulations of each molecular species in the solvent at the relevant thermodynamic conditions (temperature, pressure, etc.) using a reliable AA force field.^12,70,72,89 During this step of bonded parametrization, the nonbonded parameters remain constant. Third, the nonbonded parameters can be eventually adjusted to refine the interactions between all pairs of molecular species in the system (while typically BPs remain constant in this phase). For example, to this end, enhanced sampling methods such as umbrella sampling methods such as, for example, umbrella sampling^85,86 or (well-tempered) metadynamics^87,88 have been applied to calculate interaction energies and to compare between the CG versus AA models.^{14,46−48,50,83,84} When available, experimental data can also be used for validation. Finally, it is important to control that BPs have not been affected during the nonbonded parameter refinement. Steps 2 and 3 can be repeated if necessary, allowing to rigorously tune both bonded and nonbonded interactions in concert. Frequently, however, studies relying on top-down CG modeling validate the force field parameters using few experimental data, or simply assume that the nonbonded interaction force field is transferable, which sometimes provide an incomplete picture of the dynamics of the molecular systems.^24,82

For molecules of interest in materials science, soft matter, and modeling of complex molecular systems, usually composed of 20–200 CG beads using fine mapping schemes and including symmetrical, partially symmetrical, flexible, or planar parts, automatic tools for the parametrization of the CG models would be of great help, making the coarse-graining process more robust and reliable.^12,23 While in principle a simultaneous optimization of bonded and nonbonded interactions would be desirable, in many cases this is practically unfeasible. For this reason, in this work, we decided to rely on the widely used MARTINI force field for what pertains to the nonbonded interactions, and we focus exclusively on easing and automatizing the parametrization of the bonded interactions in the context of combined top-down and bottom-up CG modeling approaches. Several software, such as MSCGFM,⁹⁰ VOTCA,²⁶ BOCS,³² Magic,⁹¹ and PyCGTOOL,⁹² implement approaches that can be used for tuning bonded interactions, while the nonbonded ones remain constant, notably direct Boltzmann inversion (DBI),^93,94 IBI,^52,53 IMC,⁵¹ and the g-YBG equation.⁵⁸ The g-YBG equation and DBI are direct approaches, which do not require to run simulations iteratively for refining parameters. Although their direct nature allows a great speed-up of the parametrization process, they are not perfectly suited for handling complex molecules, for which they might provide a relatively poor description of the intramolecular interactions.^25,58,68 IBI,^52,53 IMC,⁵¹ and the iterative version of the g-YBG approach (iter-g-YBG)²⁵ are better suited to this end, relying on iterative simulations to refine the potentials. Iterative approaches then allow to better handle the coupling between DOFs (i.e., the modification of one potential might affect other potentials), notably between bonds, angles, and dihedrals, which is frequently encountered in high-resolution CG models of complex and flexible molecules. However, these typically require extensive sampling for accurately calculating the correction to be applied to the potentials at each iteration, which can become particularly expensive for large and flexible molecules and may cause convergence issues.^25,68,89 Existing software also sometimes lack user-friendliness, they might require manually smoothening the distributions of the reference potentials, choose the fineness of the grid used for calculating potentials (which introduces a trade-off between accuracy and computation time), and their input formats are not very convenient for usage with widely adopted combined top-down and bottom-up approaches, notably making use of MARTINI. In fact, these reasons prompted the recent development of PyCGTOOL,⁹² which simply implements DBI with increased ease-of-use with MARTINI.

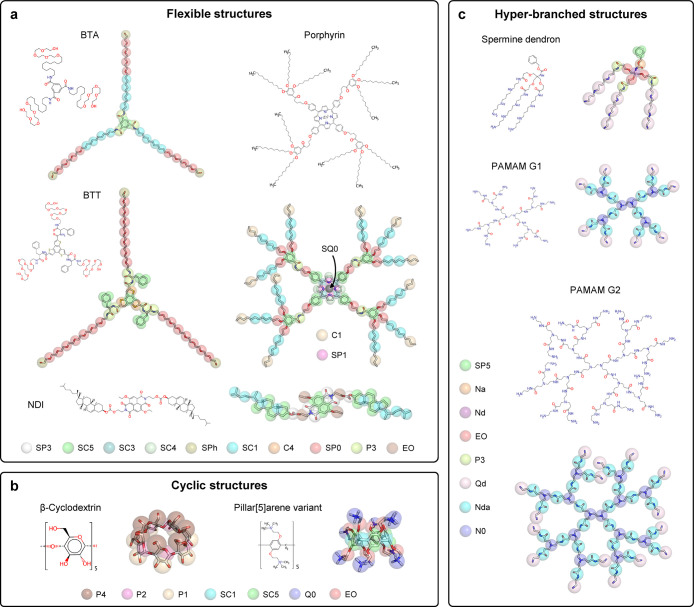
Here, we introduce Swarm-CG, a general and easy-to-use tool that combines DBI^93,94 and fuzzy self-tuning PSO⁹⁵ (FST-PSO) to automatically parametrize bonded interactions in CG models in a bottom-up fashion, within CG frameworks such as MARTINI. The method requires only a reference AA-MD trajectory and a preliminary CG topology of the molecule of interest. Swarm-CG makes a first guess of the equilibrium BPs via DBI, then automatically refines them via iterative CG-MD runs and FST-PSO,⁹⁵ until the distributions of the bonds, angles, and dihedrals in the CG model are in good agreement with those of the AA model. Its scoring function relies on the Earth mover’s distance⁹⁶ (EMD, aka Wasserstein) for simultaneously evaluating the matching of all bond, angle, and dihedral distributions, according to the provided CG topology and bonded potential functions. In particular, the coupling of FST-PSO to the EMD for score evaluation allows to obtain a parameter-free software, requiring only minimalistic input from the user, while the fast-converging PSO variant (FST-PSO)⁹⁵ used here also allows to correctly handle noisy optimization and offers good performances for complex and flexible molecules, even using limited CG sampling during each iteration. To empirically demonstrate the robustness of this approach, we challenged Swarm-CG on a diverse molecular data set, including small to large molecules of different natures and shapes; (i) flexible and symmetric self-assembling monomers generating supramolecular polymers in the solution: water-soluble 1,3,5-benzenetricarboxamide (BTA) with amphiphilic side chains,⁸³ C3-symmetric benzotrithiophene (BTT) decorated by l-phenylalanine and octaethylene glycol side-chains,⁸⁴ naphthalene diimide (NDI),⁴⁷ and Zn-porphyrin based self-assembling monomers,⁵⁰ (ii) cyclic structures: β-cyclodextrin⁹⁷ and pillar[5]arene,⁹⁸ and (iii) complex hyper-branched polymers: a spermine dendron⁹⁹ and poly(amidoamine) dendrimers of generation 1 and 2 (PAMAM G1 and G2)^49,100−102 (Figure 1). Benchmarking results demonstrate that Swarm-CG readily performs comparably to expert molecular modelers and systematically yields CG models that exhibit reliable behavior in the solvent environment, within 4–24 h on standard desktop machines (wall time). Notably, such execution times allow to explore different CG representations of the molecule of interest using different AA-to-CG mappings and topologies. The approach is perfectly suited for building and optimizing CG models based on widely used CG frameworks such as MARTINI. At the same time, Swarm-CG workflow is general and can be applied in principle to any CG framework and any CG passage through scales.

Figure 1.

Molecules used to benchmark Swarm-CG. Each molecule is represented by its molecular structure and AA model with superimposed CG MARTINI bead mapping. (a) Flexible and symmetric molecular structures generating supramolecular polymers: water-soluble BTA with amphiphilic side chains,⁸³ C3-symmetric BTT decorated by l-phenylalanine and octaethylene glycol side-chains,⁸⁴ NDI-based,⁴⁷ and Zn-porphyrin-based molecules.⁵⁰ (b) Examples of cyclic structures: β-cyclodextrin⁹⁷ and a pillar[5]arene.⁹⁸ (c) Complex hyper-branched polymer structures: spermine dendron⁹⁹ and PAMAM G1 and G2.^49,100−102 Each panel indicates the color coding of the CG MARTINI bead types (see Supporting Information for exact mapping data).

2. Algorithm

The algorithm implemented in Swarm-CG is designed to automatically optimize the parameters of the bonded interactions in a CG molecular model, namely, the parameters of the potential functions used by the force field for bonds, angles, and dihedrals in a user-provided CG molecular topology file, in a bottom-up fashion. The software requires to preliminary define the AA-to-CG mapping and the nonbonded interactions force field (e.g., selecting beads types in MARTINI). The functional form of the bonded interaction potentials can generally be described as

1

where the first term is the potential associated to the length l_i of each bond, the second term is the potential of the angles θ_j, and the third term is the potential of the dihedral angles ϕ_k. k_bi, k_aj, and k_dk are, respectively, the bond, angle, and dihedral force constants, l_0i indicates the equilibrium bond lengths, θ_0j is the equilibrium angle values, n_k is the periodicity, and ϕ_0k is the phase shift of each dihedral.

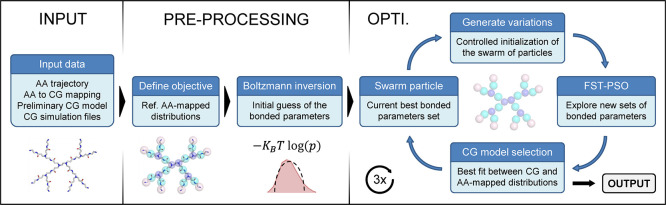
In the bottom-up part of the MARTINI framework, an all-atom trajectory of the target molecule in the solvent, at a chosen thermodynamic state, is mapped to CG particles (hereafter referred to as the “AA-mapped” trajectory) and used as the reference to tune BPs, namely, the parameters in eq 1, and to obtain matching distributions of the bond lengths, angle values, and dihedral torsions (hereafter referred to as “geoms”) in the CG representation. Often the tuning of BPs in the CG models is performed manually, by repeating simulations of the CG system until the agreement between CG and AA-mapped models is deemed satisfactory. Provided that a well-sampled AA-MD reference trajectory is available, the bonded parametrization of CG models is essentially an optimization problem, which requires to iterate CG-MD while the BPs are optimized. To automatically perform this operation with high accuracy and minimal user setup, in particular for complex molecules that include symmetrical, partially symmetrical, flexible, or planar parts, Swarm-CG is built around a state-of-the-art metaheuristic, FST-PSO,⁹⁵ which is employed to iteratively tune the BPs to improve the geometrical features of the CG model throughout successive CG-MD simulations. At each iteration step (i.e., in each successive CG-MD run), a scoring function based on the EMD⁹⁶ evaluates the current and complete set of BPs by comparing the resulting geoms distributions with those of the AA-mapped reference trajectory. After a defined number of iteration steps, the best matching set of BPs is selected. The workflow implemented in Swarm-CG is summarized in Figure 2. The following sections describe the protocol and heuristics implemented in Swarm-CG that allowed to make the software parameter-free and versatile to deal with different modeling requirements and designs.

Figure 2.

General workflow of Swarm-CG. This can be schematized into three phases. (i) Preparation of the input: the software requires a reference AA-MD trajectory, a predefined AA-to-CG mapping and a preliminary CG model, where the nonbonded interactions are predefined (CG bead types and interactions), and (ii) preprocessing: an AA-mapped reference model is built, computing the bond, angle, and dihedral distributions of the reference AA-mapped MD trajectory, and an initial guess of bonded CG parameters is made (to be then optimized). (iii) Optimization process: iterative CG-MD simulations are performed, while at each iteration, Swarm-CG, starting from a “swarm particle” (a set of BPs), changes the BPs to optimize the consistency with the reference AA-MD trajectory. The resulting set of CG bond parameters is then obtained as the output.

2.1. Input

Swarm-CG is currently designed for usage with the GROMACS^103,104 MD engine. In this paper, we demonstrate Swarm-CG performances to optimize CG models built based on the well-known MARTINI force field. However, the workflow of Swarm-CG is general and it can be used for refining basically any CG model, provided that nonbonded parameters and a mapping scheme are defined and a reliable reference AA-MD trajectory is available. The necessary input can be divided in two groups: (i) AA data used to define the target of the optimization and (ii) preliminary CG data used to perform the model optimization.

The AA input data (i) include a well-sampled MD trajectory of the AA molecular model to be used as a reference and its predefined mapping to CG beads. We note that while a few automatic AA-to-CG mapping schemes have been already proposed (e.g., in the MARTINI formalism),^92,105 these typically work only for small molecules. The search of methods suggesting the best CG representation for accurately treating the dynamics and structural features of molecules is a subject of great scientific debate.^106−109 Here, for the sake of a broader practical utility of Swarm-CG, we preferred to leave the AA-to-CG mapping to the user, who is free to choose the preferred CG scheme (the MARTINI force field or other preset schemes),^18,110,111 while the software will optimize the bonded terms accordingly.

Input CG data (ii) include a preliminary CG model, together with its nonbonded force field parameters, and simulation setup for the iterative MD simulations that will be used for the model refinement, i.e., the starting molecular configuration and the MD parameter files (cf.Section 6.1). The starting molecular configuration will be minimized and preprocessed at each iterative MD simulation step using new sets of BPs. The preliminary CG model needs to contain relevant information on the CG beads (e.g., type, charge, and mass), the bonded potential topology, and functional forms (which define the form of eq 1), while equilibrium values and force constants are arbitrarily initialized (e.g., to 0). Symmetries of the CG topology can be specified in the preliminary model file to improve the quality of the reference AA sampling and to reduce the number of free parameters to optimize. To this end, the bonds (or angles, dihedrals) that are structurally equivalent because of their chemical nature or the molecular symmetries can be gathered in “groups” so that: (i) their distributions are averaged in the analysis and (ii) they will share the same BPs in the CG model (cf.Section 6.1). Groups of geoms are directly indicated by the user in the preliminary model file. Swarm-CG provides detailed documentation and uses a set of default file names for easier argument handling.

2.2. Scoring Function

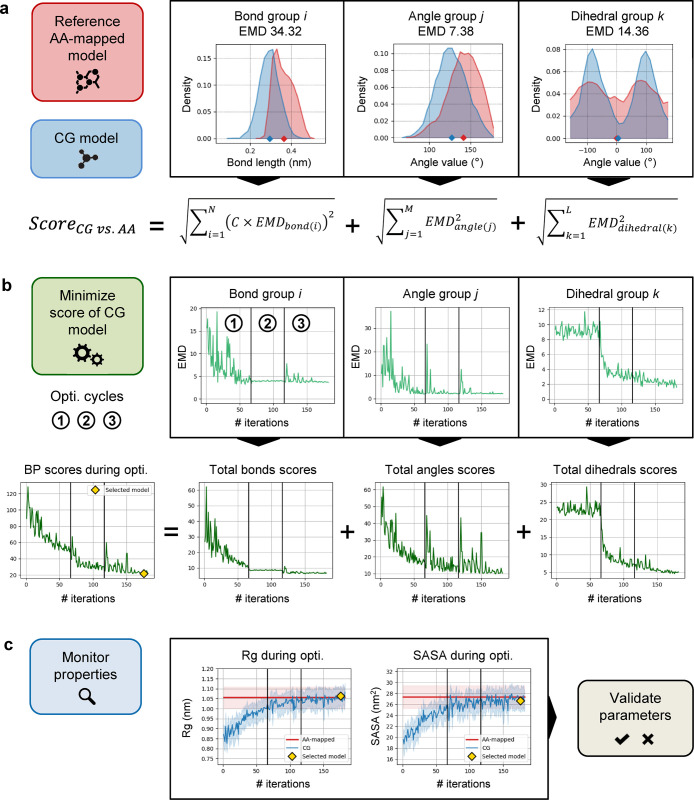
To attribute a score to the BPs set of a CG model (namely, how good/bad this performs compared to the reference AA model), the reference AA trajectory is first mapped to its CG representation to generate a “target/reference” AA-mapped trajectory that the optimized CG model aims at reproducing. In this perspective, the geometrical features of the CG model can be evaluated by comparing the CG-MD trajectory to the AA-mapped, on two scales: (i) “global” structural molecular properties, for example, the radius of gyration (R_g) and solvent accessible surface area (SASA) and (ii) “local” conformation and flexibility, which can be assessed via the distributions of geoms. Because multiple sets of BPs can produce similar R_g or SASA values, it is not possible to directly use such global structural properties as feedback for the optimization process, as the results would be locally inaccurate. Therefore, Swarm-CG uses a scoring function based on the differences between the corresponding geoms distributions obtained from the CG and AA-mapped trajectories (reported in Figure 3a). The differences are evaluated using the EMD,⁹⁶ which solves the optimal transport problem¹¹² to quantify the amount of “work” necessary to transform one distribution into another. The set of BPs selected by Swarm-CG as the outcome of the optimization process is the one that minimizes the scoring function, while R_g and SASA are monitored during the execution and ultimately used for a posteriori model validation.

Figure 3.

Overview of the scoring function and iterative optimization procedure used in Swarm-CG to automatically tune the BPs of a preliminary CG model (using illustrative data). (a) Single model scoring: the scoring function evaluates the matching between pairwise distributions of N groups of bonds, M groups of angles, and L groups of dihedrals from CG vs AA model trajectories using the EMD. C is a scaling factor applied to the EMD of bonds. (b) Iterative model optimization: the procedure generates new sets of BPs to minimize the differences between CG and reference AA-mapped distributions. (c) Quality control: radius of gyration (R_g) and SASA monitored during optimization.

In the present context, using the EMD offers several advantages over other f-divergences. Notably, the EMD: (i) quantifies the difference between geoms distributions in interpretable units (Å, degrees), (ii) is well suited for comparison of multimodal distributions in this application case, and (iii) it allows to correctly handle dihedral distributions by using a periodic distance matrix. A scaling factor C is applied to the EMD obtained for bond distributions to allow comparison with the EMD obtained for angles and dihedrals because units are different.

By default, we set C = 50, meaning that an EMD of 0.4 Å between bond distributions is equivalent to an EMD of 20° between the angle or dihedral distributions. To better penalize large mismatches between distributions and respect the weight of each geom, we do not normalize score components by the number of geoms defined in the topology. Therefore, it is important to note that the scores can be compared exclusively between trajectories of CG models generated in similar conditions (i.e., identical topology and nonbonded interactions parameters, but also simulation parameters) and with respect to a (well-sampled) reference AA-mapped trajectory. The components of the scoring function can be considered separately to exclusively evaluate the matching of bond, angle, or dihedral distributions during the optimization procedure. Swarm-CG performs EMD calculations via PyEMD.^96,113

2.3. Iterative Optimization Procedure

PSO^114,115 is a population-based global optimization algorithm (aka metaheuristic) inspired by the collective movement of birds flocks and fish schools. In PSO, a swarm of individuals (referred to as “particles”, each representing a set of values to be optimized) moves iteratively inside a bounded search space and cooperates to identify the best solution for a problem, according to an objective function. Usually, there are two groups of settings in PSO that control the cooperation within the swarm: (i) social attraction, which favors the collaboration among particles, and (ii) cognitive attraction, which prompts a particle to rely on its individual experience. The swarm of particles can be initialized either randomly or from known approximate solutions. Metaheuristics such as PSO are particularly suited for solving black-box optimization problems and effectively handle noisy data.

To refine BPs of CG models, Swarm-CG relies on FST-PSO,⁹⁵ a recently introduced PSO variant. FST-PSO exploits fuzzy logic to dynamically adjust PSO settings independently for each particle during optimization, making it a more efficient, parameter-free, and versatile PSO variant.⁹⁵ Nonetheless, the performance of all PSO algorithms is greatly affected by the initial positioning of the swarm in the search space.¹¹⁵ If the initial candidate solutions are positioned close to the basin of attraction of a local minimum of the objective function, the swarm might converge prematurely and be unable to move out of that region. To systematically achieve global optimization while minimizing execution times, Swarm-CG uses an iterative procedure that includes 3 successive optimization cycles calibrated to complement each other (Figure 3b).

Notably, BPs of the CG model are optimized from higher to lower geoms vibrational frequencies. Exclusively bonds and angles are tuned in cycle 1. Angles and dihedrals are then optimized in cycle 2. Finally, all parameters are refined altogether in optimization cycle 3 (see Table 1). Accordingly, the scoring function is adapted for each cycle to include relevant components exclusively. Swarm-CG also calibrates each initialization of the swarm of particles to maximize FST-PSO performances. At the start of cycle 1, initialization is performed using DBI (cf.Supporting Information Section S1.1) to guess BPs of the CG model for one swarm particle, which is used as a reference to generate variations and initialize the rest of the swarm. At the start of cycles 2 and 3, the best set of BPs obtained in previous cycles is chosen as a reference particle to generate the rest of the swarm. For each BPs, variations around the reference particle are generated randomly within adaptive ranges, which are decreased as the procedure progresses through optimization cycles (Table 1). Adaptive ranges also take into account the EMD previously obtained for each pairwise CG and AA-mapped geoms distributions, which directs the optimization procedure toward reducing first the largest discrepancies between models (cf.Supporting Information Section S1.2). The two first optimization cycles allow a quick exploration of relevant sets of BPs using short simulation times (10 ns by default), while the third optimization cycle uses longer simulation times to perform a final merging and refinement step (25 ns by default).

Table 1. Default Settings Used to Perform 3 Cycles of BPs Optimization of a CG Model in Swarm-CG.

	geoms optimized
opti. Cycle	bonds	angles	dihedrals	reference swarm particle initialization	variations around reference swarm particle	simulation time of production runsc (ns)
1	yes	yes	nob	BI	large	10
2	noa	yes	yesb	best from cycle 1	medium	10
3	yes	yes	yesb	best from cycle 2	small	25

^aIn cycle 2, bond parameters are fixed to those of the best scored model obtained during cycle 1.

^bDihedral parameters are applied for simulation and optimized only in cycles 2 and 3, if dihedral topologies are provided in the input preliminary CG model.

^cDefault settings, simulation times can be increased by the user for very large molecules.

In all PSO algorithms, the procedure terminates after a pre-defined number of steps or when improvements over the objective function become minimal. To allow a parameter-free usage of Swarm-CG, simple heuristics enable automatic selection of a relevant swarm size and number of swarm iterations to perform in each cycle of optimization. The Swarm size (S_size) is defined according to the dimension (D) of the search space as 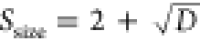and number of swarm iterations (S_iter) as 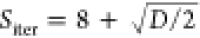. An optimization cycle is terminated prematurely if no improvement occurred within 6 swarm iterations. Default settings readily allow to perform accurate bonded parametrization of virtually any CG model, as long as the provided topology and potential functions are relevant. The accuracy and execution times of Swarm-CG are expected to satisfy molecular modeler requirements for the optimization of up to approximately 100 free parameters,⁹⁵ which represent approximately 50 groups of bonds, angles, and dihedrals (i.e., many more geoms in symmetrical molecules). Beyond that, users can easily access Swarm-CG parameters, for example, to increase the number of optimization steps or add more optimization cycles.

2.4. Execution Modes

The software provides two execution modes, which conform to two different CG modeling philosophies. Using execution mode 1, all equilibrium values (l_0i θ_0j, and ϕ_0k in eq 1) are optimized together with the force constants (k_bi, k_aj, and k_dk in eq 1), for each group of bonds, angles, and dihedrals. This procedure, based on the bottom-up philosophy, allows for a fully automatic and relatively easy usage of the software, which precisely reproduces geoms distributions from an AA-mapped reference trajectory. However, using Swarm-CG in execution mode 1 as a black box may also have undesired effects. For instance, an insufficient conformational sampling in the reference AA-MD trajectory may automatically introduce artifacts in the optimized CG model. Indeed, poor sampling can attribute excessive statistical weight to some molecular conformation, which will affect the resulting CG model and limit its accuracy. For example, the folding of flexible hydrophobic molecules in polar solvents into metastable compact conformations may be typically oversampled in AA-MD simulations. While the folding is a consequence of solvophobic interactions, it may result in a CG model in which the output BPs encode the bending of straight linear chains (e.g., long alkyl groups, formed by a straight chain of CG beads) in the form of spurious angle equilibrium values (different from, e.g., 180°), producing shorter bonds, and so forth. Similarly, limited sampling can affect the modeling of symmetric molecules (e.g., the branched molecules of Figure 1), by enforcing nonsymmetric parameters that emerge by the oversampled local minima, in contradiction with the chemical structure of the molecule. In such cases, this may eventually result into having an “effect” emerging from the AA models and encoded into the BPs of the CG models, which may then affect the way molecules interact between them, their flexibility, transferability across different molecular environments, and so forth. However, Swarm-CG is well equipped to mitigate such spurious effects of limited MD sampling, by averaging in the AA-mapped reference the distributions obtained for structurally symmetric/identical parts of the molecule. It is also worth underlining that such possible issues emerging from using a not properly sampled AA-MD trajectory as the reference is not specific to Swarm-CG but rather a general drawback of the bottom-up approach. Therefore, one should always be careful and check that the AA-MD trajectory is sufficiently well sampled to ensure that the observed properties of the optimized CG models are reliable. While enhanced sampling approaches such as replica exchange MD^116,117 and metadynamics^87,88 may be useful in this sense, said issues can be mitigated by using the second execution mode (mode 2) of Swarm-CG.

Execution mode 2 is identical to mode 1, with the exception that equilibrium values for bonds, angles, and dihedrals can be predefined in the preliminary CG model and conserved during the optimization, while only their force constants are optimized (along with all bond parameters). For example, in the case of flexible molecules containing long solvophobic chains (e.g., alkyl chains in water), execution mode 2 allows to manually predefine chemically relevant equilibrium angle values between the alkyl CG beads (e.g., 180°) and to obtain an accurate folding propensity of the molecule (i.e., the correct folding effect) exclusively by softening angle force constants, without biasing the equilibrium conformation (and without encoding such bias in the optimized CG models). Compared to mode 1, mode 2 requires more experience of the user and some knowledge of the molecular system, as well as an initial hands-on setup.

2.5. Usage

Swarm-CG allows users to quickly verify the setup and progress of an optimization procedure. At the outset of an optimization, Swarm-CG produces a graphical summary of the geoms distributions used as the target for optimization, notably allowing to verify the consistency of the mapping and choice of potential functions. At any point during the iterative execution process, the best identified set of BPs is readily provided as an output in a CG model ITP file, while the progress of the procedure can be monitored by producing a graphical summary similar to the one presented in Figure 3. Separate modules allow to perform these actions independently from the optimization. For manual editing of models, such as further modifying nonbonded interactions (e.g., CG bead types in MARTINI) and evaluating their impact on the bonded parametrization, the routine for model evaluation via scoring function and geoms distributions is also available as a separate module.

3. Results

The following sections describe the results obtained for automatic bonded parametrization of CG models included in the Swarm-CG benchmark (Figure 1), using default settings of the program. Here, we focus on synthetic structures as: (i) being the core activity of our group, we have a good amount of available data to test the performance and accuracy of Swarm-CG and (ii) because it is for the simulation of synthetic molecular systems that the development of de novo AA and CG models from scratch is most often required, while the accuracy of such models is clearly critical for the reliability of the results that these can provide. This can be a time-consuming activity, in which the advantages of an automatic tool such as Swarm-CG combined with a general CG force field such as MARTINI are more evident. The benchmark synthetic molecules that we use herein were selected for their structural diversity in terms of molecular flexibility, symmetry, and complexity (cf.Section 6.2). We first created AA models and generated AA-MD trajectories (up to 1 μs of simulation) for each single molecule in the explicit solvent (while most of the cases studied herein are in water, the approach is versatile to treat molecules in various solvents, as it is shown in the case of the NDI and porphyrin-based structures shown in Figure 1, studied in methyl cyclohexane),⁵⁰ guaranteeing well-sampled references for the automatic bonded parametrization of the CG models. CG models were already available from the literature for 7 of the 9 benchmarking molecules (BTA,⁸³ BTT,⁸⁴ NDI,⁴⁷ Zn-porphyrin-based molecule,⁵⁰ β-cyclodextrin,⁹⁷ and PAMAM dendrimers of generation G1 and G2⁴⁹), which allowed us to challenge Swarm-CG performances with respect to manually parametrized CG models previously developed by expert molecular modelers. To this end, we used the available CG models as provided (notably for what pertains to mapping and nonbonded interactions) and allowed Swarm-CG to modify exclusively the equilibrium values and force constants of each bonded potential function defined in the available CG topology (cf.Section 6.2). For the 2 other molecules (pillar[5]arene⁹⁸ and spermine dendron⁹⁹), CG models were built in the framework of MARTINI and optimized using AA models previously reported by our group (cf.Section 6.2). For all models, bonded parametrizations were evaluated using (i) Swarm-CG scoring function, which assesses the local geometrical features of a CG model, together with (ii) R_g and SASA, which provide a global evaluation of its dynamics.

We first tackle relatively small and flexible molecules forming supramolecular polymers in the solution that we use as examples to discuss in detail the differences between execution mode 1 versus mode 2. Then, we report the results of Swarm-CG for the parametrization of relatively rigid cyclic molecular structures. Finally, we increase molecular complexity by parametrizing complex hyperbranched directional and nondirectional macromolecules, such as dendrons and dendrimers. Because the simulation times used in the optimization runs (10–25 ns by default in the examples reported herein) might be insufficient in some cases to get well-converged R_g and SASA data at each step of the optimization process, R_g and SASA values presented for the selected (i.e., best scored) set of BPs are all issued from 200 ns validation simulations that are conducted at the end of the optimization procedure. This also allowed to verify that all optimized models are stable in CG simulation using a standard integration time step of 20 fs. All average R_g values obtained for optimized CG models using execution mode 1 are summarized in Table 2 and compared to the available manually parametrized CG models. The number of iterative optimization steps used for each model is determined according to the formula previously described in Section 2.3, while execution times are reported in Table 2 (hardware is detailed in Table S2).

Table 2. Average R_g Obtained for CG Models of the Benchmark Optimized Using Execution Mode 1 and Swarm-CG Default Settings, the Reference AA-Mapped Trajectories and Manually Parameterized CG Models from the Literature^a.

		radius of gyration (Rg)
molecule	bond scaling	ref. AA model [Å]	optimized CG model error [ΔÅ] (Δ%)	manually parametrized CG model error [ΔÅ] (Δ%)	optimization wall timeb (h)
BTA	++	9.07	0.37 (4.1%)	0.41 (4.5%)83	6
BTT	++	8.45	0.73 (8.6%)	0.89 (10.5%)84	7
NDI	+++	10.98	0.53 (4.8%)	0.75 (6.8%)47	16.5
porphyrin	++	13.58	0.40 (3.0%)	0.60 (4.4%)50	15.5
β-cyclodextrin	n/a	5.71	0.15 (2.6%)	0.35 (6.1%)97	5
pillar[5]arene	+	6.43	0.07 (1.1%)	n/a	6.5
spermine dendron	+	9.50	0.27 (2.8%)	n/a	12
PAMAM G1	n/a	9.95	0.12 (1.2%)	2.62 (26.3%)49	5
PAMAM G2	n/a	13.61	1.26 (9.3%)	3.32 (24.4%)49	5.5

^aAll data points were obtained in 200 ns simulations. (+) Minimal bond rescaling. (++) Important bond rescaling. (+++) All bonds rescaled.

^bUsing standard desktop machines, see Supporting Information and Table S2 for simulations parameters and hardware specifications.

3.1. Small Flexible Molecules Generating Supramolecular Polymers

Because we have a good benchmark of AA and CG models for (relatively) small and flexible molecules that generate supramolecular polymers in different environments,^{46,47,49,50,83,84,97−99,118} we started from here in showing the potential of Swarm-CG. We chose the examples reported in Figure 1a. These are relatively flexible molecules that generate supramolecular structures in water (BTA and BTT)^83,84 or in organic solvents (BTA, porphyrin, and NDI-based units).^46,47,50,84 These molecules show an intrinsic symmetric character having three (BTA and BTT), two (NDI), or four (porphyrin) structurally identical arms originating from their cores, while NDI and porphyrin also include planar substructures at their core. Thus, these are the typical motifs which may suffer from spurious different parametrizations of identical groups given by insufficient sampling, and in this sense, they represent the ideal ground to test Swarm-CG. For these systems, we compared the results obtained using Swarm-CG execution mode 1 versus mode 2. As previously mentioned (cf.Section 2.4), execution mode 2 allows the user to preset conserved equilibrium values for angles and dihedrals, while Swarm-CG then optimizes the corresponding force constants to have the CG model behaving consistently with the reference AA model.

For the CG modeling of BTA, BTT, NDI, and porphyrin-based motifs, we relied on previously developed AA and CG models, where intramolecular nonbonded interactions were accurately tuned using state-of-the-art enhanced sampling techniques.^{14,46,47,50,83,84} Considering the nonbonded parameters of these CG models as reliable, we used Swarm-CG exclusively to set up their bonded terms.

3.1.1. BTA

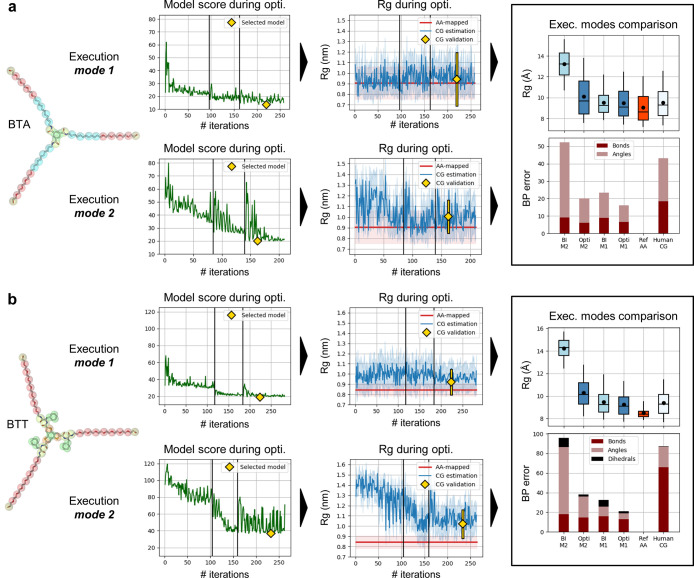
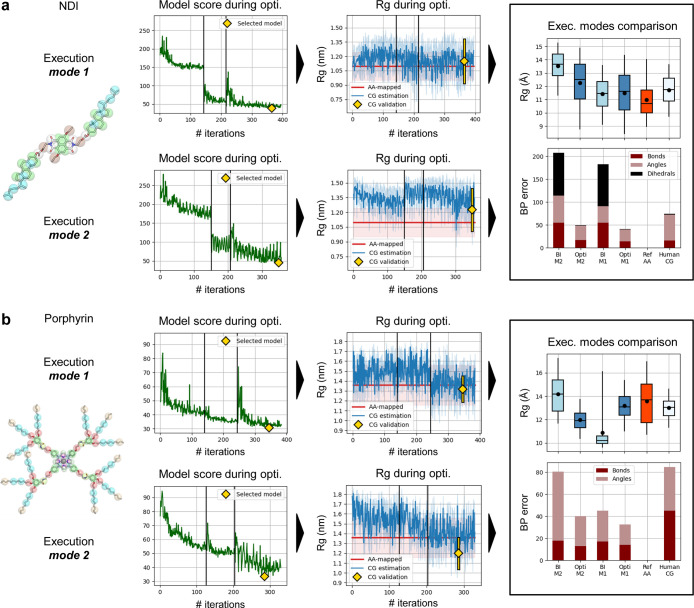
We first comment the optimization case of the CG model of the water-soluble BTA.⁸³ The main results of both execution modes are reported in Figure 4a. Geometrical features of the optimized models are compared to both those calculated from AA-mapped data and from the literature CG model⁴⁶ (cf.Section 6.2).

Figure 4.

Results of Swarm-CG for the optimization of BPs of two C₃-symmetric flexible structures using execution modes 1 (M1) and 2 (M2) with default settings: (a) BTA model.⁸³ (b) BTT model.⁸⁴ From left to right we report: (i) molecular structure and (ii) evolution of the scoring function, where green lines show the score attributed to candidate BPs during optimization. Yellow diamonds indicate the score of the selected model. (iii) the evolution of R_g, in which blue lines show average R_g estimates at each iteration of the CG model optimization (light blue intervals represent ±standard deviation), and red horizontal lines show the average R_g of AA-mapped reference trajectories (light red intervals represent ±standard deviation). Yellow diamonds and lines show averages and standard deviations obtained from 200 ns simulations. (iv) The comparison of R_g and BPs errors in different models in 200 ns simulations (BI: step 1, Opti: selected model). Boxplots and whiskers display percentiles 5, 25, 50, 75, and 95 of R_g values. Black dots show average R_g values. Stacked barplots show each component of the scoring function, the sum of which amounts to the BPs score.

Using execution mode 1, the DBI coupled to distributions averaging within groups of similar geoms yielded an already appropriate set of BPs at the very first step of the optimization process (Figure S2), here also validated in an additional 200 ns of MD simulation. For BTA, which can be considered a structurally (relatively) “simple” case with respect to the rest of the benchmark (i.e., composed of 3 core CG beads, linear side arms, and a 3-fold symmetry), the BI implemented in Swarm-CG with geoms averaging proved very efficient. Optimization still reduced small mismatches in geoms distributions (Figure S4) and BPs scores decreased from 23.3 to 16.1 without modifying the average R_g of the CG model, which was found in good agreement with AA-mapped data for both sets of BPs (i.e., both errors <5%). The set of BPs, which obtained the lowest score during the optimization procedure, is considered as the most relevant (Figure 4a, yellow diamonds), with respect to AA-mapped reference data, and is further validated in a 200 ns simulation. This longer simulation validates that the optimized CG model correctly reproduces both local and global geometrical features calculated from the AA-mapped trajectory. BPs optimization converged within 257 steps (Table 2).

We also tested the manually parametrized CG model of BTA⁸³ in a 200 ns simulation. BPs score and average R_g error for this model were 43.2 and 4.5% with respect to AA-mapped data (Figure 4a, right plots). Both BPs sets obtained via BI and optimization using execution mode 1 fixed small mismatches observed in local geometrical features of the manually parametrized model (Figure S6), without substantially improving the average R_g error.

Using execution mode 2, all equilibrium values for the angles between the CG beads representing the three side chains of the BTA were fixed at 180°. As expected, the BI initially produced an imperfect set of BPs (Figure S3 and cf.Supporting Information Section S1.1), which were quickly tuned as the optimization approached convergence. BPs scores decreased from 52.2 to 20.0. The optimized set of BPs produced more “loosely” adjusted overlaps of the distributions for some angle groups that used equilibrium values at 180° (Figure S5, angle groups 7, 8, and 9), providing increased flexibility of the CG molecular model with respect to the optimized BPs obtained via execution mode 1 and AA-mapped data (i.e., average R_g increased just by 0.65 Å, or 7 points, reaching 10.1 Å). BPs scores first decreased slowly during optimization cycle 1, then only angle distributions were further optimized during cycle 2 and all BPs were refined during cycle 3 using longer simulation times. At the start of cycles 2 and 3, the swarm is reinitialized around the best scored set of BPs obtained in previous cycles, using calibrated variations (cf.Section 2.3) which allowed to escape a local minima of the objective function and produced the fluctuations of BPs scores observed after steps 95 and 160. BPs optimization converged within 209 steps. The selected maximum number of optimization steps is reduced compared to execution mode 1 because equilibrium angle values are provided by the user, reducing the dimensionality of the problem.

It is worth re-underlining that in this case (mode 2) the BTA folding is not pre-encoded in the CG model as the bonded terms, but it is exclusively a consequence of the spontaneous collapse of the molecule in the solvent (hydrophobic effect, bead–bead interactions), which, in a sense, is more physically correct. However, it is also worth noting that such a comparison between mode 1 and mode 2 shows that the two modes work substantially the same in these cases, demonstrating that the behavior of these CG models is mainly controlled by the nonbonded interactions between the CG beads in the models more than by the bonded terms, so that the difference between the 2 execution modes is globally negligible in this case (see Figure 4).

3.1.2. BTT

We then optimized the CG model of the three-branched BTT⁸⁴ motif, again using both execution modes. The main results are reported in Figure 4b. Geometrical features of the optimized models are compared to both those calculated from AA-mapped data and from the literature CG model⁸⁴ (cf.Section 6.2).

Using execution mode 1, the BI again yielded an appropriate set of BPs at the very first step of the optimization process, with essentially a single group of dihedrals for which distributions were not perfectly adjusted (Figure S8). These were fixed during optimization (BPs scores down from 31.7 to 20.8) and allowed to retrieve a correct planar geometry of the core of BTT, along with slightly better adjusted geoms distributions (Figure S10). Notably, the average and spread of R_g values obtained for the optimized CG model are just slightly larger with respect to those of the AA-mapped reference trajectory (Figure 4b: ΔR_g of 0.7 Å). Although the error is substantially negligible, this is consistent with the higher dynamicity of CG models compared to the AA ones¹¹⁹ (this is more evident in BTT, as this motif allows stronger core-to-arms and arms-to-arms interactions compared to, e.g., BTA). BPs optimization converged within 282 steps (Table 2).

We tested the manually parametrized CG model of BTT in a 200 ns simulation. BPs score and average R_g error for this model were 87.4 and 10.5% with respect to AA-mapped data. The set of optimized BPs obtained using execution mode 1 fixed the small mismatches observed in local geometrical features of the manually parametrized model (Figure S12), while producing a very similar average and spread of R_g values.

Using execution mode 2, as expected the BI initially produced an inaccurate set of BPs (Figure S9 and cf.Supporting Information Section S1.1), which was then tuned during optimization. BPs scores decreased from 95.6 to 38.0. Again, the optimized BPs produced more “loosely” adjusted distribution overlaps for angle groups that used equilibrium values at 180° (Figure S11, angle groups 3–8), providing increased flexibility of the CG molecular model with respect to the model optimized via execution mode 1 and AA-mapped data (i.e., average R_g increased by 1.10 Å or 12 points, reaching 10.3 Å). BPs optimization converged within 261 steps.

3.1.3. NDI

We performed the same study for the NDI-based molecules, the results of which are reported in Figure 5a and compared to the CG model available from the literature.⁴⁷ Using execution modes 1 and 2, the initial BIs yielded inappropriate sets of BPs, notably due to the several dihedral potentials used to maintain the planarity of the molecular core (Figures S14 and S15). During optimization with mode 1, BPs scores decreased from 182.2 to 41.3 and allowed to retrieve a correct planar geometry of the core of NDI, with correctly adjusted geoms distributions (Figure S14). The average R_g value of the optimized model is in perfect agreement with the AA-mapped reference trajectory (Figure 5a: ΔR_g = 0.5 Å or 4.8%). BPs optimization converged within 395 steps (Table 2). As a comparison, the manually parametrized CG model of NDI yielded a higher BPs score of 74.42 in a 200 ns simulation, indicating that some geoms distributions could be better adjusted (Figure S18), although average R_g was correct at 11.7 Å (ΔR_g = 0.7 Å or 6.8%).

Figure 5.

Results of Swarm-CG for the optimization of BPs of other symmetric flexible structures in the benchmark, using execution modes 1 (M1) and 2 (M2) with default settings, (a) NDI model.⁴⁷ (b) Porphyrin-based monomer model.⁵⁰ From left to right we report: (i) molecular structure and (ii) evolution of the scoring function, where green lines show the score attributed to candidate BPs during optimization. Yellow diamonds indicate the score of the selected model. (iii) Evolution of R_g, in which blue lines show average R_g estimates at each iteration of the CG model optimization (light blue intervals represent ±standard deviation), and red horizontal lines show the average R_g of AA-mapped reference trajectories (light red intervals represent ±standard deviation). Yellow diamonds and lines show averages and standard deviations obtained from 200 ns simulations. (iv) Comparison of R_g and BPs errors in different models in 200 ns simulations (BI: step 1, opti.: selected model). Boxplots and whiskers display percentiles 5, 25, 50, 75, and 95 of R_g values. Black dots show average R_g values. Stacked barplots show each component of the scoring function, the sum of which amounts to the BPs score.

Using execution mode 2, the BPs scores went down from 350.2 to 52.4 and produced geoms distributions almost indistinguishable from those obtained using mode 1, because only the hinge junctions between the core and arms (Figure S17, angle groups 10 and 11) used angles at 180° and those were already “loosely” adjusted with mode 1 (although Swarm-CG selected an equilibrium value at 120°). In both resulting models, the low force constant associated with the hinge junctions should not restrict the full extension of the arms, and thus is not expected to significantly affect assembly simulations, but these specific flexibilities must be considered carefully. The average R_g was 11.8 Å (ΔR_g = 0.8 Å or 7.8%). BPs optimization converged within 301 steps.

3.1.4. Porphyrin

Lastly, we optimized the CG model of the porphyrin-based molecule, as shown in Figure 5b, which possesses four arms originating from a central core according to a square symmetry, as we did for the previous cases. Again, we compared the geometrical features of the optimized models with those calculated from AA-mapped data and the literature CG model.⁵⁰ Using execution mode 1, the BI initially produced inappropriate BPs, and mismatches between CG and AA-mapped geoms distributions were effectively reduced during optimization (Figure S20), notably allowing to obtain a relevant geometry of the porphyrin core in this more “complicated” case (i.e., nested network of bonds). BPs scores went down from 45.2 to 32.6. The average R_g was also found in good agreement with the AA-mapped trajectory (ΔR_g = 0.4 Å or 3%). The averaging of distributions within groups of similar geoms, coupled to CG modeling, produced a planar geometry of the porphyrin core which reduced the spread of R_g values with respect to AA-mapped data (Figure 5b, boxplots). BPs optimization converged within 392 steps (Table 2). Using execution mode 2, as expected, the BI initially produced an inaccurate set of BPs (Figure S21 and cf.Supporting Information Section S1.1), which was tuned during optimization. BPs scores decreased from 80.6 to 40.2. Once again, optimized BPs produced more “loosely” adjusted distribution overlaps for angle groups that used equilibrium values at 180° (Figure S23, angle group 3 in particular), providing increased flexibility of the CG molecular model with respect to the optimized BPs obtained via execution mode 1 and AA-mapped data. In this case, this allowed the model to adopt more folded conformations in the solvent (i.e., average R_g decreased by 1.20 Å or 10 points, reaching 12 Å). BPs optimization converged within 322 steps.

3.2. Cyclic Structures

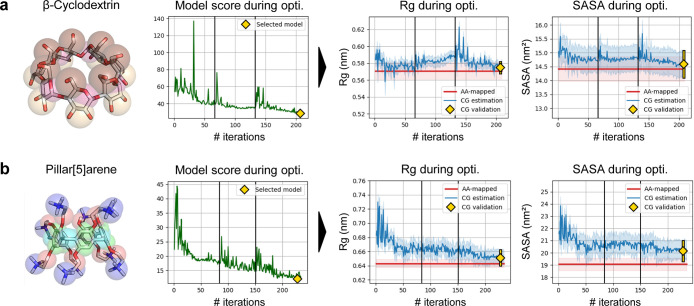
We also challenged Swarm-CG in treating different types of molecular architectures, i.e., cyclic and symmetric molecules with a more rigid architecture, namely, cyclodextrins and pillar[5]arene. In such cases, we report the results of execution mode 1 (as for such relatively simple and rigid motifs, execution mode 2 reported identical results).

3.2.1. β-Cyclodextrin

We first comment the optimization case of the CG model of β-cyclodextrin,⁹⁷ for which the main results are reported in Figure 6a. Geometrical features of the resulting CG model are compared to both those calculated from AA-mapped data and from the CG model available from the literature⁹⁷ (cf.Section 6.2).

Figure 6.

Results of Swarm-CG for the optimization of BPs of two cyclic structures using execution mode 1 with default settings. (a) β-Cyclodextrin model.⁹⁷ (b) Pillar[5]arene model.⁹⁸ From left to right we report: (i) molecular structure and (ii) evolution of the scoring function, where green lines show the score attributed to candidate BPs during optimization. Yellow diamonds indicate the score of the selected model. (iii) Evolution of R_g, in which blue lines show average R_g estimates at each iteration of the CG model optimization. (iv) Evolution of SASA, in which blue lines show average SASA estimates at each iteration of the CG model optimization. Light blue intervals represent ±standard deviation, and red horizontal lines show the average R_g/SASA of AA-mapped reference trajectories (light red intervals represent ±standard deviation). Yellow diamonds and lines show averages and standard deviations obtained from 200 ns simulations.

The mismatches between CG and AA-mapped geoms distributions were effectively reduced during optimization (Figure 6a, green line). However, in the 200 ns validation simulation, geoms distributions of the optimized CG model did not perfectly reproduce those calculated from the AA-mapped trajectory (Figure S27). A small issue in the topology of the model, related to the size of CG beads used in the MARTINI framework, prevents proper closing of angles between P4–P2–P2 beads (i.e., maroon-pink-pink and Figure S27, angle 4) and slightly affects other geoms distributions. These small mismatches in local geometry are acceptable at CG resolution, in the context of this molecular structure. According to the MARTINI framework, fixing them would require modifications such as scaling the bond lengths between P4–P2 beads (i.e., maroon-pink), which would introduce other forms of error in the CG model, notably related to nonbonded parametrization. Nonetheless, the optimization process yielded appropriate BPs in the context of the CG topology provided for β-cyclodextrin, and average R_g and SASA are in very good agreement with the AA-mapped trajectory (i.e., both errors <1%). BPs optimization converged within 206 steps (Table 2).

We tested the manually parametrized CG model of β-cyclodextrin in a 200 ns simulation. Swarm-CG scoring function yielded a BPs score of 71.9 for this model, indicating larger discrepancies in the local geometrical features (Figure S29) compared to the optimized CG model which obtained a BPs score of 28.2, with respect to the AA-mapped reference trajectory. BPs optimization produced marginal improvements on an average R_g error (0.2 Å or 3.5 points) for this small and cyclic molecule, with respect to the available manual bonded parametrization (Table 2).

3.2.2. Pillar[5]arene

Next, we optimized the CG model of a pillar[5]arene, for which the main results are reported in Figure 6b. Geometrical features of the resulting CG model are exclusively compared to those calculated from the AA-mapped data⁹⁸ because no manually parametrized CG model was available from the literature for this molecule. The mismatches between CG and AA-mapped geoms distributions were effectively reduced during optimization (Figure 6b, green line). The optimized CG model was further validated in a 200 ns simulation, in which geoms distributions correctly overlapped with those calculated from the AA-mapped trajectory (Figure S31). Average R_g and SASA values were also found in good agreement (errors: 1 and 5%). Because the CG model of the pillar[5]arene was prepared according to the MARTINI framework, bonds were rescaled between SC5 and EO beads (i.e., cyclic core to arms junctions) and the average R_g of the AA-mapped reference was rescaled accordingly (cf.Supporting Information Section S2.2), while no transformation was applied to its average SASA value. Therefore, the small discrepancy observed between the average SASA of the optimized CG and AA-mapped models is expected, and the rescaled, average R_g is a better reference to assess this model’s bonded parametrization. BPs optimization converged within 230 steps (Table 2).

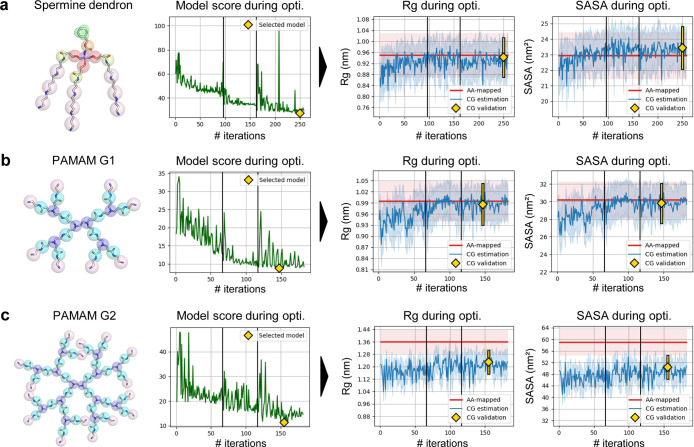
3.3. Complex Hyper-Branched Macromolecules

Finally, we challenged Swarm-CG for the optimization of CG models of complex macromolecules, for which we use, as a case study, a spermine-based dendron (flexible, small, and directional branched macromolecule) and PAMAM dendrimers of generations 1 (G1, symmetric/nondirectional, small, and flexible branched macromolecule), and 2 (G2, large, symmetric/nondirectional and complex branched macromolecule). For these cases, only the results of execution mode 1 are reported, as execution mode 2 provided an analogous picture. Here, as Swarm-CG averages the behavior of the identical/symmetric side branches in both the AA and CG systems, which prevents spurious effects that may arise from insufficient AA-MD sampling.

3.3.1. Directional Dendrons

We first comment the optimization case of the CG model of a spermine-functionalized dendron, as reported in Figure 7a, as an example of a flexible, branched, and directional molecule.^99,118 Geometrical features of the resulting CG model are exclusively compared to those calculated from AA-mapped data because no manually parametrized CG model was available from the literature for this molecule.

Figure 7.

Results of Swarm-CG for the optimization of BPs of three types of hyper-branched macromolecules (i.e., dendrons and dendrimers) using execution mode 1 with default settings. (a) Spermine dendron model.⁹⁹ (b) PAMAM G1 model.⁴⁹ (c) PAMAM G2 model.⁴⁹ From left to right we report: (i) molecular structure and (ii) evolution of the scoring function, where green lines show the score attributed to candidate BPs during optimization. Yellow diamonds indicate the score of the selected model. (iii) Evolution of R_g, in which blue lines show average R_g estimates at each iteration of the CG model optimization. (iv) Evolution of SASA, in which blue lines show average SASA estimates at each iteration of the CG model optimization. Light blue intervals represent ±standard deviation, and red horizontal lines show the average R_g/SASA of AA-mapped reference trajectories (light red intervals represent ±standard deviation). Yellow diamonds and lines show averages and standard deviations obtained from 200 ns simulations.

As depicted by the decreasing scores attributed to candidate sets of BPs during optimization (Figure 7a, green line), the process effectively minimizes mismatches between CG and AA-mapped geoms distributions, which were reduced by a factor of 2 when comparing the initial set of BPs (step 1) to those of the optimized model (step 249). BPs optimization converged within 255 steps (Table 2). The optimized CG model was further validated in a 200 ns simulation. Distributions of the bonds and angles correctly overlap between the optimized CG and AA-mapped models (Figure S34), and, on a larger scale, average R_g and SASA values are also in very good agreement (i.e., both errors <3%). The average SASA of the optimized CG model is slightly increased with respect to that of the AA-mapped, which is due to the scaling of bond lengths between CG beads of the aromatic ring and is inherent to the MARTINI framework (cf.Supporting Information Section S2.2). This scaling has little incidence on R_g values in this model, and the AA-mapped average R_g was calculated without considering any offset.

3.3.2. PAMAM G1 Dendrimer

Next, we optimized the CG model of a G1 PAMAM dendrimer, a small structural variant belonging to a well-known family of dendrimers,^49,101,102 here used as an example of a relatively flexible and small symmetric branched macromolecule, for which the main results are reported in Figure 7b. Notably, a MARTINI CG model for PAMAM G5 is available from the literature⁴⁹ and could be adapted (truncated) to obtain a smaller PAMAM G1. Geometrical features of the resulting CG model are compared to both those calculated from AA-mapped data and from the CG model adapted from the literature⁴⁹ (cf.Section 6.2). We show that Swarm-CG is capable of optimizing the CG parametrization for such types of molecules, which performs even better versus AA models compared to the CG parameters available in the literature (and adapted for smaller dendrimer generations), in terms of behavior of the dendrimer in the solvent (water). In particular, the simple truncation to G1 of the available MARTINI model for G5 PAMAM dendrimers (maintaining the very same bonded and nonbonded literature parameters)⁴⁹ results in an overestimation of the R_g and SASA of the dendrimer in explicit water, which could be somewhat expected considering that Lee and Larson also highlighted similar slight size overestimations for G5 PAMAM when the model was developed.⁴⁹ By providing the same nonbonded terms as an input; however, here we show that Swarm-CG is capable of easily optimizing the CG models to successfully improve the agreement with AA models for these branched macromolecules.

The mismatches between CG and AA-mapped geoms distributions were again reduced by a factor of 2 during optimization, when comparing the initial set of BPs to those of the optimized CG model (Figure 7b, green line). The optimized CG model was further validated in a 200 ns simulation, in which geoms distributions correctly overlapped with those calculated from the AA-mapped trajectory (Figure S37). Average R_g and SASA values were also in perfect agreement (i.e., both errors <2%). BPs optimization converged within 182 steps (Table 2).

We then tested the available manually parametrized CG model of PAMAM G1⁴⁹via a 200 ns CG-MD simulation. The Swarm-CG scoring function yielded a BPs score of 123.7 for this CG model (Figure S38). Noteworthy, the discrepancy in the local geometrical features with respect to the AA-mapped reference MD trajectory is considerably reduced in the optimized CG model produced by Swarm-CG, which yielded a BPs score as low as 9.0 (Figure S37). With respect to manual parametrization, the average R_g error in the optimized CG model provided by Swarm-CG (calculated respect to the AA reference model) is also reduced by 2.5 Å (∼25%) using the optimized set of BPs (see Table 2).

3.3.3. PAMAM G2 Dendrimer

We then optimized the CG model of PAMAM G2, for which the main results are reported in Figure 7c. PAMAM G2 is here used as an example of a more complex, symmetric branched macromolecule. As for PAMAM G1, a MARTINI CG model for PAMAM G2 was adapted from the literature⁴⁹ and used for comparison. Also in this case, we show that Swarm-CG is capable of retrieving a reliable parametrization for such types of molecules, which performs even better versus AA models compared to the existing CG parameters in terms of behavior of the G2 PAMAM dendrimer in the water, obtaining an improvement in the CG model performance in line with those discussed above for G1 PAMAM. Geometrical features of the resulting CG model are compared to both those calculated from AA-mapped data and from the CG model adapted from the literature⁴⁹ (cf.Section 6.2).

The mismatches between CG and AA-mapped geoms distributions were effectively reduced during optimization (Figure 4c, green line). Geoms distributions of the optimized CG model correctly overlapped with those calculated from the AA-mapped trajectory in a 200 ns validation simulation (Figure S41). However, average R_g and SASA values were approximately 1.3 Å (10%) and 8 nm² (16%) lower with respect to the AA-mapped reference (all values are reported in Table 2). In this case, we can safely assume that the CG topology is valid. Thus, as we proved that BPs are correctly tuned according to the reference AA-mapped trajectory, the cause of the residual R_g and SASA offset cannot be directly attributed to errors in the bonded parametrization. In this perspective, this can be imputed: (i) to the nonbonded interaction parameters, which could possibly slightly underestimate interactions of the molecule with the solvent or overestimate intramolecular interactions, or (ii) to sampling limitations in the AA-MD trajectory (oversampling of determined molecular configurations, possible for particularly complex molecules). We also underline that if nonbonded parameters are inadequate or sub-optimal (as in the case of G1 and G2 PAMAM parametrization), Swarm-CG consequently adjusts the bonded terms to reproduce at best in the CG model the geometry described by the AA-MD reference trajectory, exclusively based on geoms distributions. These observations highlight the potential of Swarm-CG as a diagnostic tool for CG modeling, which provides hints for model refinement beyond its primary purpose of automatic bonded parametrization.

We compared the automatically optimized CG model of G2 PAMAM with the manually parametrized one obtained using parameters available from the literature⁴⁹via a 200 ns CG-MD simulation. A Swarm-CG scoring function yielded a BPs score of 123.8 for the manually optimized CG model. Again, the discrepancies in local geometrical features calculated with respect to the AA-reference trajectory were considerably reduced in the Swarm-CG-optimized CG model (Figure S42), which provides a BPs score of 23.0 (Figure S41). With respect to manual CG parametrization, the average R_g error is also reduced by ∼15 points using the optimized set of BPs provided by Swarm-CG (see Table 2). BPs optimization converged within 182 steps (Table 2). The selected maximum number of optimization steps is identical as for the optimization of PAMAM G1, owing to the hyper-branched structures of PAMAM molecules, for which topologies can be considered identical once similar bonds and angles have been grouped together. This is also why the manually parametrized models of PAMAM G1 and G2 obtained very similar BPs scores (123.7 and 123.8), which are not exactly identical only because of the intrinsic statistical variability associated with the MD sampling.

All these results provided for such a diverse set of different molecules, including these branched dendrimers, demonstrate that Swarm-CG has great potential to also treat molecular architectures of considerable complexity in an efficient and reliable way.

4. Methodological Considerations

To ease the development of CG models and increase their physical relevance and accuracy, we used a benchmark of wide structural diversity to demonstrate that Swarm-CG can be employed with default settings for the bottom-up tuning of BPs in CG models of diverse complexity. Swarm-CG systematically yields appropriate sets of BPs in the context of the provided model topology and reference AA trajectory, within wall times compatible with molecular modelers’ requirements. Using execution mode 1, R_g values of the optimized models were systematically in agreement with the reference AA trajectory.

Importantly, Swarm-CG produces sets of BPs via an optimization process, for which the objective function is exclusively based on the user-provided AA reference trajectory. Therefore, the BPs produced by Swarm-CG are optimized exclusively to reproduce the geometrical behavior observed in the AA trajectory for the molecule of interest. The process of averaging distributions within geoms groups does improve the quality of the reference sampling for large symmetrical molecules and yielded particularly accurate BPs in the present benchmark. To this end, the step of defining relevant geoms groups in the preliminary CG model file is crucial. On the other hand, as mentioned before, we highlight the importance of obtaining a sufficiently sampled AA trajectory to be used as a reference for Swarm-CG. In the cases studied herein, 1 μs of AA-MD simulation was proven long enough to guarantee this, but the required sampling may change depending on the system of interest.

For molecules that adopt folded conformations in AA-MD simulations, execution mode 2 typically provides increased flexibility in the optimized CG models, which allows to reproduce the dynamical properties of the molecules as an “effect” rather than a pre-encoded condition in the models. This is particularly important when one may want to develop models for molecules composed of rather flexible groups, which then are supposed to interact between them or with other molecules in the simulations. In fact, this may limit spurious effects arising from too rigidly parametrized BPs (eventually coming from the reduced timescales accessible by common AA-MD simulations) that may then affect how molecules interact between them. Although less automatic, mode 2 has the advantage of not using the software as a black box, but at the same time it requires prior knowledge of the molecular system that is not always accessible. In such a case, the user can always use Swarm-CG in mode 1, which in principle should provide the best accessible bonded parametrization. We included the option to select either usage mode to leave maximum freedom to the user, with a standard or more advanced usage of the software.

All CG models resulting from the present benchmark could be run in 200 ns simulations using time steps of 20 fs. By default, Swarm-CG uses conservative maximum values for force constants, which maximizes the stability of the optimized models for usage in assembly simulations. To this end, the iterative optimization process aims at identifying an appropriate balance of force constants between all the elements of the topology, while reproducing AA-mapped geoms distributions in the CG model. For special needs, all parameters of the software can be modified, notably allowing users to increase the range of the force constants to be explored during optimization, although this might be detrimental to the model stability and should be used carefully. Simulation instabilities in optimized models would most likely be caused by issues in the topology definition (e.g., geoms or bond lengths scaling).

Interestingly, we demonstrated that Swarm-CG can also be used as a diagnostic tool, notably for large molecular structures for which both bonded and nonbonded parametrizations, as well as obtaining sufficient AA-MD sampling to produce a reliable reference trajectory can be particularly complex (cf.Section 3.3.3).

In principle, Swarm-CG can also be employed for tuning BPs in higher-scale CG models (e.g., lower CG resolution, mapping more atoms into each CG bead).^18,120,121 While demonstrating such a usage is outside the scope of this paper, the workflow would remain substantially unchanged, except for: (i) the nonbonded parameters provided, (ii) the mapping file that would group multiple atoms into each larger CG bead, and (iii) the number of CG beads and swarm iterations used for optimization, which could potentially be decreased to minimize execution times, without affecting the accuracy of the results. Moreover, in such a case, the user would not be restricted to using an AA-MD trajectory as the reference, but also a finer CG-MD trajectory would work to this purpose (with the advantage of a speed up in the process and of an overall improved dynamical sampling). In this sense, the successive higher-scale parametrizations (finer-to-coarser CG optimization) would be less computationally expensive than the first one (AA-to-CG), while the user should at the same time consider that approximations intrinsically accompany every CG step and that in multistep approaches accuracy is key to avoid sum of errors. Swarm-CG could also be applied to the bonded parametrization of polarized CG models or elastic networks used in CG models of proteins (e.g., MARTINI).¹²² The code has been developed for immediate usage with the MARTINI CG force field (explicit or implicit solvent environments) and the GROMACS^103,104 MD engine, although developments are underway for extending Swarm-CG to other CG frameworks and MD engines.

Finally, other automatic methods (e.g., IBI, etc.) could be used instead of PSO, which in principle may allow to converge with a better efficiency to the global minimum. However, these lack explorative efficiency compared to PSO.^60,89,123 For this reason, while these are well suited for some types of molecular systems, these would hardly handle the high complexity of the large macromolecular systems studied herein. On the other hand, the good (empirical) convergence demonstrated for the large variety of complex molecular structures explored herein (Figures 4–7) demonstrates that the approach adopted in Swarm-CG guarantees good reliability and robust versatility to efficiently handle a large variety of molecular models.

5. Conclusions

Leveraging FST-PSO,⁹⁵ an efficient and setting-free PSO variant, here we designed Swarm-CG, a software that automatizes the iterative bottom-up parametrization of BPs of CG molecular models, within CG frameworks such as MARTINI. We took particular care to provide a versatile software capable of systematically producing reliable results for virtually any CG model, from simple to complex molecular architectures, using default Swarm-CG settings. The software is versatile and requires minimal input preparation. Swarm-CG can satisfy molecular modelers’ requirements for routine building of CG models composed of up to 200 CG beads (in the MARTINI framework, this corresponds to molecular architectures containing at least ∼600–800 heavy atoms), and possibly more, both in terms of accuracy and execution times. We particularly expect this tool to support the development of new CG molecular models for the study of synthetic molecular systems and their interaction with other (bio/non-bio) molecular targets, as it is becoming increasingly crucial in the various bio- and nanotechnology fields. Swarm-CG is available via the Python Package Index (package: swarm-cg) with all its dependencies. Demonstration data are available at www.github.com/GMPavanLab/SwarmCG.

6. Methods

6.1. Input Details

AA data used to set the target of the optimization procedure include a structure and trajectory files. The AA structure with atom types, connectivity, masses, and charges can be provided via a GROMACS portable topology file (.tpr). The AA trajectory can be provided in any GROMACS format accepted by MDAnalysis^124,125 (.xtc, .trr or else). Periodic boundary conditions (PBC) are handled internally if the trajectory file includes the position and size of the simulation box at each time step. Otherwise, it is assumed PBC have already been handled and a warning is displayed at the start of the program. The AA trajectory is mapped on-the-fly to allow faster experimentation with different mapping schemes. The mapping of atoms to CG beads must be provided as a GROMACS index file (.ndx). The weight of the atoms that would be mapped to multiple CG beads will be split accordingly when performing the mapping and calculating all AA-mapped reference geoms distributions.

The preliminary CG model to be optimized must be provided as a GROMACS topology file (.itp), along with the nonbonded interactions force field to be applied in MD simulations. To better handle sampling in symmetrical molecules, users can easily form groups of bonds, angles, and dihedrals in this topology file (using line returns or comments). AA-mapped distributions will be averaged within groups to create the references used as the target of the optimization procedure, and shared parameters will be used and optimized for the geoms of each group. This also makes the optimization process more efficient by reducing the number of free parameters. For example, grouping 5 angles together reduces the number of associated free parameters from 10 to 2 when using execution mode 1 and GROMACS angle functions 2.

Swarm-CG requires users to provide a GROMACS structure file (.gro) to be used as the starting conformation of each simulation step during the iterative optimization process. This structure will be (i) minimized and (ii) preprocessed before gathering data from the production run (iii), using three user-provided GROMACS MD parameters files (.mdp), one for each step. Only the simulation parameters of the production run will be modified to adapt its number of steps and the number of frames of the output trajectory to be analyzed, according to software parameters (1000 frames by default, within 10 or 25 ns). Although the starting conformation does not have to be perfectly accurate, as it will be minimized and preprocessed at the start of each iteration, this conformation must allow running stable simulations while exploring different sets of BPs. For example, molecular modelers can make use of an initial set of MARTINI bond parameters just stable enough to obtain a preliminary CG model file and a starting conformation to be used for the optimization phase.

The following GROMACS bonded potential functions^103,104 are implemented, which should be necessary and sufficient for building CG models: constraints function 1, bond function 1, angle functions 1 and 2, and dihedral functions 1, 2, 4, and 9. Swarm-CG can effectively optimize parameters for dihedral potential functions with multiplicity greater than one, although these may be used carefully as they are known to easily trigger instabilities in simulations. During optimization, sets of BPs (i.e., particles of the swarm) that cause simulations to terminate abruptly get attributed the worst possible score the scoring function can yield, according to the given topology and geoms domains.

6.2. Benchmarking Data and Models

To compare the performance of Swarm-CG for bonded parametrization with respect to manually parametrized CG models, we first collected several MARTINI models available from the literature and from previous results of our group. We selected the following molecular data set based on CG data availability and structural diversity: BTA⁸³ and BTT decorated by l-phenylalanine and octa-ethylene glycol side-chains,⁸⁴ NDI,⁴⁷ Zn-porphyrin based molecule,⁵⁰ β-cyclodextrin,⁹⁷ and PAMAM G1 and G2.⁴⁹ Their CG topologies, selected bead types and nonbonded interactions force field were used as provided, except for β-cyclodextrin and PAMAM G1 and G2 for which CG topologies were built by truncating the existing CG models of a β-cyclodextrin dimer⁹⁷ and PAMAM G5.⁴⁹ Additionally, two last molecules expand the benchmark and improve its structural diversity; a pillar[5]arene⁹⁸ and spermine-functionalized branched dendron.⁹⁹ For the spermine dendron and pillar[5]arene, we built CG models from scratch in the framework of MARTINI using the CG bead types presented in Figure 1. For the pillar[5]arene and the dendron, there are no previously developed manually optimized CG models to compare with, and the performance of Swarm-CG has been evaluated exclusively with respect to the data from the AA-mapped trajectories in these cases.

For these 9 molecules, we created AA models and generated trajectories for each single molecule in the solvent using time steps of 2 fs and extensive sampling (Table 3 and Supporting Information Section S2.1), which are used as a trusted reference for the bonded parametrization of CG models and benchmarking of Swarm-CG.

Table 3. Data Used for the Benchmarking of Swarm-CG Using Default Settings.

	reference AA trajectory
molecule	simulation time (μs)	number of frames	force field	solvent	nonbonded parametrizationa	used for manual parametrization evaluation
BTA	1	5000	GAFF126+ TIP3P127	Water	MARTINI 2.283	yes
BTT	1	5000	GAFF126+ TIP3P127	Water	MARTINI 2.284	yes
NDI	1	5000	GAFF126	cyclohexane	MARTINI 2.247	yes
porphyrin	1	5000	GAFF126	cyclohexane	MARTINI 2.250	yes
β-cyclodextrin	1	5000	q4md-CD128+ TIP3P127	Water	MARTINI 2.197	yes
pillar[5]arene	1	5000	GAFF126+ TIP3P127	Water	MARTINI 2.2129	no
spermine dendron	1	5000	GAFF126+ TIP3P127	Water	MARTINI 2.2129	no
PAMAM G1	1	5000	GAFF126+ TIP3P127	Water	MARTINI 2.249	yes
PAMAM G2	1	5000	GAFF126+ TIP3P127	Water	MARTINI 2.249	yes

^aWhere present, nonbonded interactions were further tuned as described in the associated literature, starting from the cited force field.

All topologies defined for the CG models of the benchmark use exclusively bonds and angles defined between CG beads that are closely located on the AA molecular graph (i.e., no long-range bonds and angles between CG beads were used to artificially constraint the flexibility of the CG models), except for molecules that contain flat cores and the cyclic structures. For the BTT and porphyrin-based molecular models, longer range angles and dihedrals were defined to obtain flat structures of the cores. For β-cyclodextrin and pillar[5]arene, longer range angles were also used to obtain correct geometries of the central cyclic structures.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c05469.

• Additional details concerning the Swarm-CG algorithm; computational details of the AA-MD and CG-MD simulations; additional setup details for the usage of Swarm-CG in execution modes 1 and 2; details of the molecular AA and CG models, and molecular structures studied in this work; data (e.g., geoms distributions, etc.) generated and used by Swarm-CG in the optimization of the CG models of all molecules in the benchmark (PDF)

The authors declare no competing financial interest.