Machine Learning-Guided Three-Dimensional Printing of Tissue Engineering Scaffolds

Abstract

Various material compositions have been successfully used in 3D printing with promising applications as scaffolds in tissue engineering. However, identifying suitable printing conditions for new materials requires extensive experimentation in a time and resource-demanding process. This study investigates the use of Machine Learning (ML) for distinguishing between printing configurations that are likely to result in low-quality prints and printing configurations that are more promising as a first step toward the development of a recommendation system for identifying suitable printing conditions. The ML-based framework takes as input the printing conditions regarding the material composition and the printing parameters and predicts the quality of the resulting print as either “low” or “high.” We investigate two ML-based approaches: a direct classification-based approach that trains a classifier to distinguish between low- and high-quality prints and an indirect approach that uses a regression ML model that approximates the values of a printing quality metric. Both modes are built upon Random Forests. We trained and evaluated the models on a dataset that was generated in a previous study, which investigated fabrication of porous polymer scaffolds by means of extrusion-based 3D printing with a full-factorial design. Our results show that both models were able to correctly label the majority of the tested configurations while a simpler linear ML model was not effective. Additionally, our analysis showed that a full factorial design for data collection can lead to redundancies in the data, in the context of ML, and we propose a more efficient data collection strategy.

Impact statement

This study investigates the use of Machine Learning (ML) for predicting the printing quality given the printing conditions in extrusion-based 3D printing of biomaterials. Classification and regression methods built upon Random Forests show promise for the development of a recommendation system for identifying suitable printing conditions reducing the amount of required experimentation. This study also gives insights on developing an efficient strategy for collecting data for training ML models for predicting printing quality in extrusion-based 3D printing of biomaterials.

Introduction

Three-dimensional printing technologies offer an unprecedented control over design of constructs with complex architecture.¹ This possibility is particularly advantageous for the design of scaffolds for tissue engineering since both internal and external architecture of such scaffolds play critical roles in their function.^2,3 Among various additive manufacturing techniques available for scaffold fabrication, extrusion-based 3D printing methods have found widespread application due to their low cost and compatibility for processing of a wider range of biomaterials. Successful scaffold fabrication using extrusion-based printing, however, requires optimization of interrelated processing parameters such as speed, pressure, and temperature of the printing process.⁴ This optimization also highly depends on material-related factors such as viscoelastic properties and curing mechanism of the material composition intended for scaffold fabrication.⁵ Accordingly, these combinations of parameters necessitate an optimization process involving time- and labor-intensive experiments, which may hinder progress in this emerging field.

During recent years, various studies have focused on the investigation of printability of existing or novel biomaterials, and the consequent optimization of their 3D printing process.^4–11 Systematic studies such as those involving factorial design approaches¹² have been successful in identifying suitable printing conditions of biomaterials, but at the expense of extensive experimentation. One technology that exhibits a great potential for accelerating the development of printable biomaterials and the optimization of their 3D printing is Artificial Intelligence (AI). Recent studies demonstrate successful use of AI techniques based on Machine Learning (ML) to improve 3D printing of materials.^13–16 ML is a subfield of AI that provides predictions by analyzing underlying behaviors within a given dataset. The three common ways ML has been used in these studies are to (1) predict and optimize printing parameters to maximize the structure's properties,^13,16–22 (2) optimize printability of the material,^23,24 and (3) assess the quality of the prints.^{14,15,25–27}

A hierarchical ML method that leveraged domain knowledge of complex physical systems and statistical learning was developed to optimize 3D printing of a silicone elastomer printed in a support bath based on a freeform reversible embedding setup.¹³ This strategy effectively incorporated advanced physical modeling into an ML algorithm and enabled the determination of optimal printing parameters that delivered more rapid printing of constructs with higher shape fidelity, and provided insight into the impact of different parameters on the printing process. A convolutional neural network (CNN) trained with a database of hundreds of thousands of geometries from finite element analysis was used to design and 3D print composite constructs with superior mechanical properties.¹⁶ In this work, the ML model could identify the geometrical configurations of soft and stiff materials that resulted in the highest toughness and strength when 3D printed as composite structures.

Other studies have used ML to determine material printability.^23,24 Inductive logic programming methodology was employed to predict the printability of various collagen and fibrin mixtures. By establishing a relationship between a rheological property and shape fidelity, the algorithm determines which mixtures would produce a high-quality print.²³

ML has not been limited to preprinting processes and has been investigated to assure print quality during the printing process. A CNN algorithm trained on digital image datasets was developed to detect interlayer imperfections during 3D printing of poly(lactic acid) filaments.¹⁴ The trained ML model in this work could afford a real-time detection of delamination in printed constructs, serving as a self-monitoring tool for 3D printing. Using a similar approach, an autonomous self-correcting system was developed that could detect over-/under-extrusion during 3D printing and adjust the flow rate in real-time to correct the extrusion process at the same or faster rate than a human operator.¹⁵ Despite the high potential of ML methods, these strategies have not been fully adopted for 3D printing of tissue engineering scaffolds.

In this study, we investigated the use of ML for aiding extrusion-based printing of a polymeric biomaterial. To this end, we employed a dataset of printing experiments based on extrusion-based 3D printing of poly(propylene fumarate) (PPF) for fabrication of porous scaffolds for bone tissue engineering, which was previously generated in a full-factorial design study.¹² Based on the obtained measurements of the printing experiments, we characterized the printing quality of each print using two printing quality metrics, machine precision and material accuracy, and explored the use of statistical ML for predicting printing quality for a given printing configuration. We examined whether ML could be used for distinguishing between printing configurations that are likely to result in low-quality prints and printing configurations that are more promising, and assessed the amount of experimental data that was necessary to train an ML-based model to establish a data collection protocol that minimizes experimental work.

Methods

Dataset and printing quality metrics

The dataset employed in this work was generated in a previously reported full-factorial design study, which investigated fabrication of porous scaffolds by means of extrusion-based 3D printing of crosslinked PPF as a model biomaterial.¹² The original study was designed to identify optimal printing conditions and the impact of various processing parameters on the quality of prints using a linear and quadratic full-factorial regression model. Processing variables consisted of material-related (i.e., PPF composition in the printing solution), printing-related (i.e., printing pressure and speed), and design-related (i.e., programmed fiber spacing) factors. For each set of processing parameters, the dataset included mean fiber diameter, mean interfiber spacing, and mean pore size of each printed layer. These measurements were obtained through layer-by-layer imaging and image analysis of the prints, and were used to calculate the % error for machine precision¹² (Eq. 1) and material accuracy¹² (Eq. 2) values for each printing condition. It should be noted that these metrics reflect the deviations of the experimental values from the programmed values and therefore larger values indicate larger errors or “lower” printing quality.

Overall, this dataset covered 72 possible combinations of processing parameters – 2 material compositions (85, 90 wt% PPF), 3 fiber spacings (0.8, 1.0, 1.2 mm), 3 printing speeds (5, 7.5, 10 mm/s), and 4 printing pressures (2, 2.5, 3, 4 bar) – for up to 10 layers per scaffold, and 4 replicates per processing condition. However, not all combinations of processing parameters were printable, and additional speeds were tested for 85 wt% PPF and additional spacings were tested for 90 wt% PPF.¹² The configurations resulting in complete or partial prints are presented in the Supplementary Tables S1 and S2.

ML-based approach for predicting printing quality

We employed statistical ML-based models for predicting the printing quality of a given printing configuration. A printing configuration was characterized by the material composition, printing speed, printing pressure, scaffold layer, and programmed fiber spacing. These parameters were the input features of the ML models.

We explored two different approaches for predicting printing quality: (1) a direct approach where a classification model classifies each input configuration as either “low” or “high” quality, and (2) an indirect regression-based approach that predicts the printing quality metric for a given printing configuration and subsequently applies a threshold to characterize the printing as “low” or “high” quality. Both approaches, classification-based and regression-based are built upon Random Forests.²⁸ A Random Forest is an ensemble model that is built upon a set of tree-like structured models. Random Forests can be used for both classification and regression and are suitable even for training on small-size datasets. We additionally trained a simpler linear regression model, specific to each material composition, as a baseline method. In the following, we describe in detail the three approaches.

• (1)Classification-based Approach

• For the classification-based approach, we labeled the data with binary labels, indicating low-quality and high-quality prints, using given threshold values (see the last paragraph of this section). Subsequently, we trained two Random Forest classifier (RFc) models for classifying a printing configuration as low or high quality based on the labels derived from the machine precision and material accuracy metrics, respectively. Each RFc model predicts a label, that is, low or high quality, for a given printing configuration.

• (2)Regression-based Approach
• In this setting, we investigated an indirect approach to the classification problem which was built upon a regression RF model. More specifically, we trained two Random Forest regressor (RFr) models for predicting the values for machine precision and material accuracy, respectively. The regression models predict a value of the printing quality metric for a given printing configuration and subsequently this predicted value is thresholded to classify the prediction as low or high quality.

• The regression-based approach was developed to circumvent the need for defining a cutoff value for separating the prints into low and high quality for the data-labeling process as it is required in the case of the classification model. If the threshold is applied before training the models, then the learned decision boundaries will depend on the selected threshold value. On the contrary, the regression-based approach does not require the application of a threshold to label the data; however, it assumes that a printing quality metric is available for quantifying the quality of the prints.

• (3)Linear Model

• Finally, we implemented a simpler approach, which was based on a linear regression²⁹ model for predicting material accuracy given printing speed and printing pressure. The linear regression model was used for comparison purposes. Our motivation in this study was to investigate whether a simpler approach using a linear function is sufficient to approximate material accuracy given printing speed and pressure for a fixed material composition as RFs capture nonlinear methodologies.

• We characterized the printing quality as low or high based on the computed values of machine precision and material accuracy. The threshold for each printing quality metric for separating low- and high-quality prints was selected based on expert intuition. For material accuracy, prints with values higher than 50% were considered of low quality while for machine precision this threshold was set to 6%.

Experimental design

Models' specifications

For the RF models and the linear regression model, we used the Scikit-learn library from python.³⁰ For the two RF-based models, we used the data on both material compositions available. In the RF models, the number of trees was set to 100 and the maximum depth tree was set to 6. A larger number of trees results in faster convergence, however, it increases computational complexity. One hundred trees proved to be enough for the accuracy to converge, according to our observations. The depth of trees can be arbitrarily large, however, growing deep trees has the danger of overfitting on the training data undermining performance on unseen data. This can be prevented when setting a maximum value on the depth. The rest of the models' hyperparameters were set to the default values of the sklearn implementation. The linear model has material-specific meaning, as it was trained only on experiments from a single material composition. We chose to train a model specifically for material composition 85 wt% PPF, for which we had a larger number of experimental data.

Printing quality metrics

To characterize printing quality as low or high, we examined the use of two printing quality metrics: machine precision and material accuracy (Eq. 1 and 2). We trained models for each metric and selected the one that resulted in higher performance based on the Evaluation Metrics discussed below.

Evaluation setup

The models were being evaluated following a leave-one-out validation setup. Leave-one-out validation means that if the dataset consists of N data points then N-1 points are being used to train the model and 1 data point is left out for evaluating the model. This process is repeated N times until the model has been evaluated on all data points. Although this setup guarantees that the model is not tested on data instances that the model has seen during training, it can still give misleading results if there are correlations between the data points of the dataset. To detect such dependencies in the data, we analyzed our dataset to understand the effect of each printing parameter in the resulting printing quality as we discuss in Feature Importance. Our analysis revealed that there are correlations between printing configurations that differ either on the scaffold layer or on the fiber spacing. For that purpose, the leave-one-out validation experiment was designed as follows: The left-out configuration to be tested at each iteration is the set of all printing configurations of the dataset that share the same values for the material composition, printing speed, and printing pressure, and differ either in the fiber spacing or in the scaffold layer. Therefore the left-out configuration is defined by the values of the parameters: material composition, printing speed, and printing pressure. In the dataset, there are 16 unique combinations of these 3 parameters and therefore the leave-one-out experiment is repeated 16 times. Note when a combination is left out, all the data points of different fiber spacing and scaffold layers are included in the left-out set.

Evaluation metrics

The models were evaluated for their capacity to correctly classify printing configurations as either low or high. Due to the unique design of the evaluation setup, which sets aside a set of configurations for testing instead of a single configuration, we introduced the Prediction Accuracy score (P.A. score) for evaluating performance.

The P.A. score shows the percentage of the printing configurations of the left-out set that have been correctly classified as low- or high-quality prints based on the reference labels. If the majority of the predictions (P.A. score >0.50) within the left-out set were in agreement with the reference values, then the prediction for the testing configuration was considered correct. For the classification models, the predicted labels were obtained directly from the output of the models. For the regression models, if the predicted value for the printing quality metric exceeded the prespecified threshold, then the predicted label was low. The reference labels were determined after thresholding the experimental values of the printing quality metrics.

Specifically for evaluating the classification-based approach, we additionally obtained the Area Under Receiver Operating Characteristic Curve (AUROC), which is a standard metric for classification modes. The AUC metric³¹ examines the capacity of a classification model to separate the two classes with various thresholds for the predicted probabilities. It takes values from 0 to 1 with 1 indicating perfect classification and 0.5 indicating predictions no better than a random classifier. The AUROC was determined for each left-out set of printing configurations in a leave-one-out validation setting. It is computed taking into account the reference labels, as derived after applying the threshold value onto the printing quality metric, and the predicted probabilities for each configuration falling in each class, as obtained by the RFc model.

Feature importance

The input features for training the ML models were the parameters of each printing configuration (material composition, printing speed, printing pressure, scaffold layer, fiber and spacing). Feature importance was used to assess the effect of each feature on the output of the model. Variations of features with low importance would cause little to no effect on the output of the model. We studied feature importance for two purposes: First, to design the leave-one-out validation strategy avoiding dependencies between the training and testing data as explained in the previous section, and, second, to identify an efficient data collection protocol for future studies.

We studied feature importance by (1) using the RF model itself, and (2) designing different protocols of leave-one-out validation experiments. The RF assessed feature importance, whereas the model was being built to determine the structure of the trees that compose the model. We ranked the features based on their importance using an embedded function in the Scikit-learn implementation of the RF. For this analysis, the RFr regression model was used. In addition to that, we assessed the performance of the models, with a leave-one-out validation setting, excluding each time a specific feature to understand which features are the most important for improving the performance of the models. More specifically, we executed 5 leave-one-out validation experiments, one for each input feature. For each studied feature, the left-out configuration to be tested was selected such that the value of the examined feature had not been seen during training. For example, when examining the importance of printing speed, all training points with the same speed value as the leave-out configuration would be excluded from the training set.

Learning curves

We evaluated the learning curves of the RFr model to understand whether the dataset was sufficient for training and whether there were redundancies in the data. A learning curve is a plot that shows how the accuracy of a model changes when the size of the dataset is increased. Using a leave-one-out validation setting, we plotted the average accuracy on the test set by incrementally varying the size of the training set. In addition to that, we plotted learning curves fixing the fiber spacing and also fixing both fiber spacing and scaffold layer. These two parameters appeared to be noninformative according to the feature importance analysis and we used the learning curves to further test this hypothesis. These three experiments were intended to simulate three scenarios of data collection: full-factorial design; data collected across material/speed/pressure/layer combinations for one spacing; data collected across material/speed/pressure combinations for one spacing and one layer.

Results

Printing quality metrics

Figure 1 shows representative images of low- and high-quality prints based on machine precision or material accuracy as printing quality metrics. Material accuracy proved to be a better metric for characterizing low- and high-quality prints compared with machine precision. More specifically, when material accuracy was used as a printing quality metric for labeling the data, the RFc and RFr models achieved accuracies 74% and 75%, respectively. When the dataset was labeled using machine precision, the RFc and RFr models achieved accuracies 62% and 63%, respectively. Based on these results, material accuracy is the printing quality metric that was used in all subsequent experiments for labeling the data. Results from using machine precision for labeling the data are presented in the Supplementary Table S3. Moreover, the code is included in the GitHub repository https://github.com/KavrakiLab/bioMateriaLs.

FIG. 1.

Representative images of low- (A) and high-quality (C) prints based on machine precision (of machine precision of 9.80% and 2.65%, and material accuracy of 3.20% and 32.58%, respectively), and low- (B) and high-quality (D) prints based on material accuracy (of machine precision of 1.75% and 4.90%, and material accuracy of 70.56% and 3.86%, respectively). The printing configurations (layer, material composition, printing pressure, printing speed, programmed spacing) for the images are as follows: (A) layer 6, 85 wt% PPF, 2.5 bar, 7.5 mm/s, 1.2 mm, (B) layer 3, 85 wt% PPF, 2.5 bar, 20 mm/s, 1.2 mm, (C) layer 3, 85 wt% PPF, 2 bar, 10 mm/s, 1.2 mm, and (D) layer 4, 85 wt% PPF, 2 bar, 5 mm/s, 1.2 mm. Scale bar = 1 mm. PPF, poly(propylene fumarate).

Comparison between the classification- and the regression-based approach

We trained the two models, RFc and RFr, using material accuracy for characterizing printing quality. We evaluated the two models using the P.A. score in a leave-one-out validation setting. We recall that at each iteration of the leave-one-validation, the set of all configurations that share the same values of material composition, printing speed, and pressure are being tested and the P.A. score is reported. If the P.A. score is larger than 0.5, then the prediction is considered to be correct. Table 1 summarizes the results for the 16 tested printing configurations as well as the average P.A. score over all 16 tested configurations. According to the results, both models correctly labeled all tested combinations for material composition of 85 wt% PPF, whereas the tested configurations for material composition of 90 wt% PPF were challenging for both models. This can be justified by the fact that the largest portion of the experimental data was obtained from printing experiments using material with composition 85 wt% PPF. The models were trained on a dataset that included printing experiments using two different material compositions and, hence are not expected to generalize across different materials as also indicated by the poor predictions of material composition of 90 wt% PPF. For the classification model RFc we additionally report the AUROC in Table 2. The average AUROC value across all tested configurations was 0.71 indicating the capability of the model to predict correct labels for the majority of the tested configurations.

Table 1.

Evaluation of Random Forest Classifier and Random Forest Regressor Models Using Prediction Accuracy Score

wt% PPF	85	85	85	85	85	85	85	85	85	85	85	85	90	90	90	90	avg
Pressure (bar)	2.0	2.0	2.0	2.0	2.5	2.5	2.5	2.5	2.5	3.0	3.0	3.0	2.5	3.0	3.0	4.0
Speed (mm/s)	5.0	7.5	10.0	15.0	5.0	7.5	10.0	15.0	20.0	5.0	7.5	10.0	5.0	5.0	7.5	5.0
RFc (P.A. score)	0.98	0.99	0.82	0.54	0.99	0.99	0.99	0.62	0.68	0.93	0.95	0.97	0.27	0.41	0.77	0.00	0.74
RFc correct prediction	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	×	×	✓	×
RFr (P.A. score)	0.98	0.99	0.82	0.75	1.00	1.00	1.00	0.63	0.74	0.93	0.92	0.97	0.27	0.04	1.0	0.00	0.75
RFr correct prediction	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	×	×	✓	×

The P.A. scores are given across all leave-one-out configurations (PPF composition-pressure-speed) and the average is included. The correct/incorrect predictions are noted (correct if P.A. score is higher than 0.5).

RFc, random forest classifier; RFr, random forest regressor; P.A. score, prediction accuracy score; PPF, poly(propylene fumarate).

Table 2.

AUROC Evaluation of Random Forest Classifier Model

wt% PPF	85	85	85	85	85	85	85	85	85	85	85	85	90	90	90	90	avg
Pressure (bar)	2.0	2.0	2.0	2.0	2.5	2.5	2.5	2.5	2.5	3.0	3.0	3.0	2.5	3.0	3.0	4.0
Speed (mm/s)	5.0	7.5	10.0	15.0	5.0	7.5	10.0	15.0	20.0	5.0	7.5	10.0	5.0	5.0	7.5	5.0
RFc (AUROC)	0.97	0.95	0.75	0.62	0.92	0.96	0.92	0.58	0.60	0.59	0.3	0.92	0.41	0.98	0.77	0.13	0.71

The AUROC is presented across all leave-one-out configurations (PPF composition-pressure-speed) and the average is included.

Feature importance

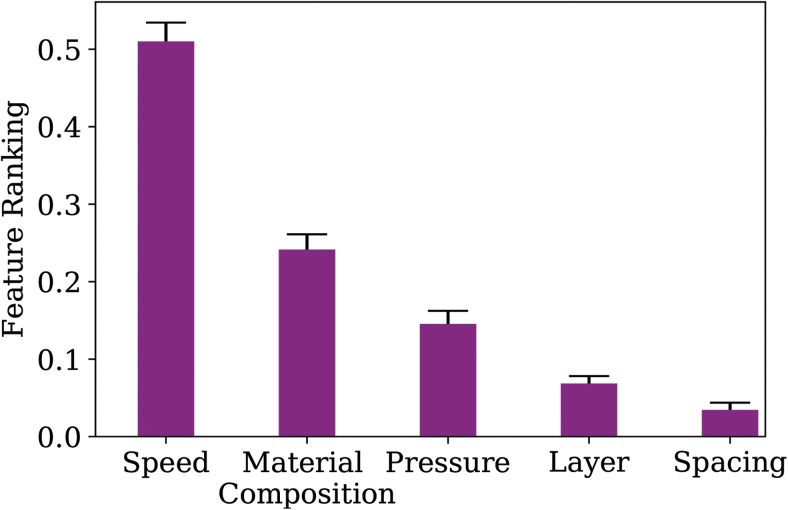
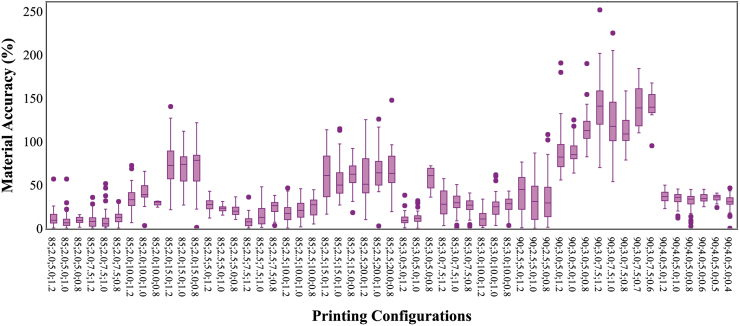
The ranking of the features, regarding their effect on the predicted value, based on the feature importance function of Scikit-learn is shown in Figure 2. This analysis shows that printing speed, material composition, and printing pressure are the most important factors for differentiating between low-quality and high-quality prints. Fiber spacing and scaffold layer seem to be less informative features. Figure 3, which shows the material accuracy for all printing configurations, confirms this observation, as printing configurations that differ only on the fiber spacing have similar values of material accuracy.

FIG. 2.

Ranking of the features (printing parameters), as obtained from the RFr model, based on their importance for affecting printing quality. RFr, random forest regressor;

FIG. 3.

Material accuracy is plotted for the whole dataset of printable configurations. Data points that share the same material composition, printing speed, printing pressure, and programmed spacing are combined in a box plot. Material accuracy values are shown on the y-axis. Printing configuration of data points is shown on the x-axis (material composition (wt% PPF); printing pressure (bar); printing speed (mm/s); programmed spacing (mm), respectively).

We further examined feature importance by running a leave-one-out validation experiment for each feature in which the left-out configuration for testing had a value for the examined feature that the model had not seen during training. For example, when doing a leave-one-speed-out experiment for speed 5 mm/s then all configurations with speed 5 mm/s are excluded from the training set. Our intention here was to understand how sensitive the model is when it is tested on unseen values for each feature. The average accuracies over all printing configurations are presented in Table 3. The material composition is not studied in this analysis since there are only two different compositions in the dataset. The experiments that examine the accuracy on unseen values of scaffold layer and fiber spacing obtained the highest accuracy. This means that although the model has not seen the same values for scaffold layer or fiber spacing during training, it still makes very accurate predictions. This further reinforces our observations that prints with varying values of either fiber spacing or scaffold layer are correlated and therefore are redundant cases for our training set. Table 3 shows that when the model is tested on unseen values of speed or pressure then the accuracy significantly drops. These observations can be helpful for future data collection experiments. Variations of features that appear to be less important in our analysis, such as scaffold layer and fiber spacing, may not be examined in detail.

Table 3.

Random Forest Regressor Models Were Evaluated and the Average Accuracy Is Reported

Leave-one-X-out setup	Average RFr accuracy
Layer	0.93
Spacing	0.96
Speed	0.75
Pressure	0.36
Speed-pressure	0.75

Models were trained in different leave-one-out settings. The test set was developed to contain one layer, spacing, speed, pressure value, and speed-pressure value combination.

Learning curves

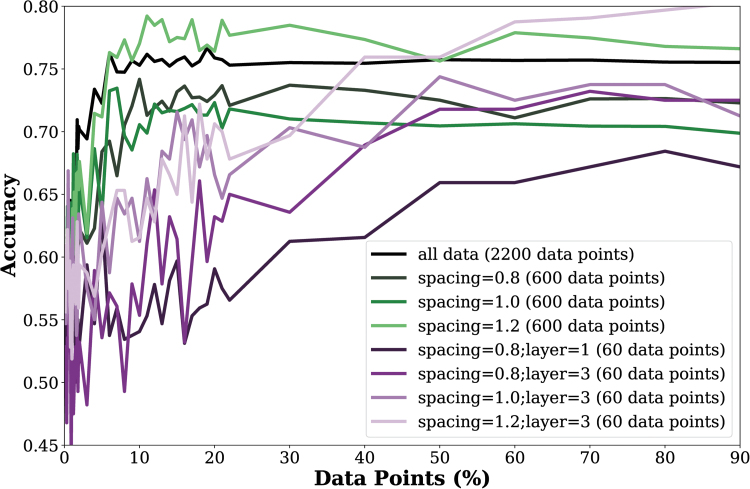
Figure 4 shows the learning curves for three different experimental setups: First, the entire dataset was used as the training set (excluding the testing configuration following a leave-one-out validation setting). Second, the value of the spacing was fixed and only the printing experiments with that value of fiber spacing were retained in the training set. Finally, we fixed both, fiber spacing and scaffold layer, and we preserved only the printing configurations with the specific combination of fiber spacing and scaffold layer in the training set. The plot shows that there is redundant data in the training set as the maximum accuracy is reached when less than 20% of the data was used for training. When the repetitions of the printing experiments with varying values of either fiber spacing or scaffold layer were removed from the dataset the accuracy was not compromised. This result demonstrates that the source of the redundancy was the repetitions of the experiments with varying values of either fiber spacing or scaffold layer.

FIG. 4.

Test accuracy of the RFr model as a function of the size of the training set for: full factorial design; data collected across material-speed-pressure-layer combinations for one spacing; data collected across material-speed-pressure combinations for one spacing and one layer.

We finally compared two training scenarios that reflect two different data collection strategies: First, the entire dataset was used to train the RFr model and, second, the fiber spacing was set to a specific value and all training configurations with different values were removed from the training set. With this experiment, we investigated whether removing these data would cause any decrease in the accuracy. The results are presented in Table 4. The results show that the removal of the experiment repetitions across spacing did not negatively affect the accuracy of the model proving that they are actually redundant data.

Table 4.

Prediction Accuracy Scores Are Reported for Random Forest Regressor Models Across All Leave-One-Out Configurations and the Correct/Incorrect Prediction (Correct If Prediction Accuracy Score Is Higher Than 0.5) Is Noted

wt% PPF	85	85	85	85	85	85	85	85	85	85	85	85	90	90	90	90
Pressure (bar)	2.0	2.0	2.0	2.0	2.5	2.5	2.5	2.5	2.5	3.0	3.0	3.0	2.5	3.0	3.0	4.0
Speed (mm/s)	5.0	7.5	10.0	15.0	5.0	7.5	10.0	15.0	20.0	5.0	7.5	10.0	5.0	5.0	7.5	5.0
Full dataset	0.98	0.99	0.82	0.75	1.00	1.00	1.00	0.63	0.74	0.93	0.92	0.97	0.27	0.04	1.00	0.00
Correct prediction	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	×	×	✓	×
Fixed spacing	0.98	1.00	0.85	0.88	1.00	1.00	1.00	0.55	0.53	1.00	0.98	1.00	0.60	1.00	1.00	1.00
Correct prediction	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓

The models were trained on a full dataset and on a dataset with fixed spacing (1.2 mm).

Linear model

The capability of a linear model to label the tested printing configuration is presented in Table 5. We used sklearn's linear regression with default parameters. With this experiment we investigated whether a linear model is sufficient to approximate material accuracy when a single material is considered. Again, we used material accuracy as the metric indicating printing quality. Printing speed and pressure were selected as the input features as they were the most informative features again according to our analysis from the RF models. We averaged the values of material accuracy over all repetitions of fiber spacing and scaffold layer. According to the results in Table 5, the material-specific linear model does not achieve better accuracy than the RFr, which considers material composition as a feature. Therefore, developing a linear model per material composition does not seem to provide any additional benefit compared with a nonlinear model, which covers a larger number of materials.

Table 5.

Linear Model Is Evaluated

wt% PPF	85	85	85	85	85	85	85	85	85	85	85	85
Pressure (bar)	2.0	2.0	2.0	2.0	2.5	2.5	2.5	2.5	2.5	3.0	3.0	3.0
Speed (mm/s)	5.0	7.5	10.0	15.0	5.0	7.5	10.0	15.0	20.0	5.0	7.5	10.0
Linear model prediction	✓	✓	✓	×	✓	✓	✓	✓	✓	×	×	×

Correct/incorrect prediction is reported for all printing configurations (PPF composition, pressure, speed respectively) in “leave-one-configuration-out.”

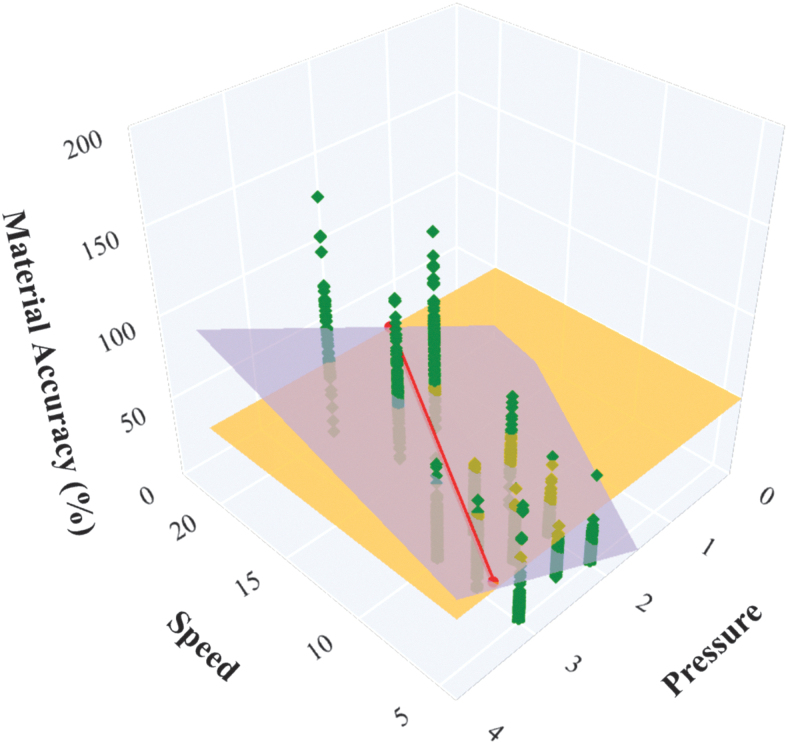
The linear model was trained using two input features and therefore it is possible to examine the function learned by the model along with the data points. A visualization of the line that is obtained by fitting the data is provided in Figure 5, which can be useful to analyze the relationship between the material accuracy of points with different input parameters. The purple plane represents the learned function while the yellow one is set at the threshold value of 50%. It is clear that the function will predict all the speed/pressure combinations on the right side or the red line (plane intersection) as high-quality prints, while the combinations to the left will be predicted as low-quality prints. From practice we know that any extreme combination of values (e.g., pressure 0 bar and speed 0 mm/s) will not really give high-quality prints, although the learned function suggests so. This highlights the inefficiency of a linear boundary and a linear model to characterize the given data.

FIG. 5.

Three dimensional visualization of the relationship between material accuracy and the two printing parameters: printing speed and pressure for material composition 85 wt% PPF. The actual values are shown in green with each pillar containing configurations with the same speed-pressure value and different values of layer and spacing. The yellow plane represents the threshold of 50% material accuracy. The purple plane shows the function learned by the linear regression model. The red line represents the intersection between these two planes.

Discussion

This study investigated the use of ML for predicting printing quality in extrusion-based printing of a polymeric biomaterial. ML has the potential to be used as the core of a recommendation system for identifying suitable printing parameters, thus reducing experimentation. We investigated two metrics for labeling the data based on the resulting printing quality: material accuracy and machine precision.¹² The use of material accuracy for training of the models resulted in more accurate predictions and was selected as a more indicative metric to characterize printing quality. We examined two ML-based approaches for predicting printing quality. The first approach utilizes a classification model that classifies each printing configuration as a low- or high-quality print. The second approach is based on a regression model that predicts the material accuracy for each printing configuration. This value is thresholded to classify the print as low or high quality. Both models are built upon Random Forests. The classification approach assumes the availability of a clear cutoff value for separating low- from high-quality prints, which in practice may be challenging to define. The decision boundary that is learned from the classification model is sensitive to the selection of the value of the threshold. On the other side, the regression-based approach does not require a cutoff for the printing quality and the function that the regression model approximates does not depend on the selection of the threshold. However, the regression model assumes the existence of a printing quality metric. Despite these differences, both models performed equally well for the material composition, which was well represented in the data (85 wt% PPF). Regarding the material composition with significantly fewer experimental data (90 wt% PPF), both models had poor performance.

We also investigated feature importance to get insights on which printing parameters are mostly influencing the printing quality and define an efficient protocol for collecting data for future studies. Features that impact printing quality, such as material composition, need to be carefully examined while other features that may not be influencing the printing outcome may lead to data redundancies. The dataset we used was collected with a factorial design covering a large number of combinations of printing conditions. Our analysis showed that the material composition, printing speed, and printing pressure are the most important parameters affecting the quality of a print. Fiber spacing and scaffold layer appeared to be uninformative features. This suggests that further experimentation can focus on collecting data with larger coverage of printing speed and pressure and on examining a larger variety of material compositions. Such additional data would improve ML approaches. As a final point, in this study, the dataset included printing data from two different material compositions of which one was under-represented in the dataset (i.e., 90 wt% PPF). This dataset does not allow us to investigate whether the trained models can generalize across different material compositions. However, in principle, employing the presented ML methodologies with more material compositions, could produce models that generalize across unseen material compositions. Experiment repetitions with varying values of fiber spacing or scaffold layers appeared to be redundant according to our analysis. Fixing the values of those parameters in the data collection process would significantly reduce the number of required experiments.

There are a plethora of ML methods available. This study investigated a direct classification-based approach and an indirect approach that uses a regression ML model. Both models were built upon Random Forests. The choice of the methods used was made after examining the amount of experimental data that was available. The choice was also guided by the desire to analyze the existing experimental dataset without expert physical modeling. Clearly, there are several ML methods that could be used.²⁹ Our results indicate that nonlinear models will be needed but a further investigation of linear models such as Ridge or Lasso²⁹ may also yield some insight. This study establishes, however, the potential of ML to form the core of a recommendation system for identifying suitable printing parameters, thus reducing experimentation.

Conclusions

This study investigated the use of ML methodologies for distinguishing between printing configurations that are likely to result in low-quality prints and printing configurations that are more promising. Our work did not use any expert physical modeling. The analysis established that simple linear models are not sufficient for predicting printing quality even within a single material composition. The use of a statistical ML model, the Random Forest, proved worthwhile. RF is suitable for training on small datasets such as the one available for this work. The models we trained predicted the printing quality for a given printing configuration accurately for the material for which enough data points were available, and our work identified which parameters mostly affect the printing quality. Focusing experimental work on varying those parameters could guide experimentation and also allow for the collection of additional data to further train the ML models with the ultimate goal of producing recommendation systems.

Disclosure Statement

No competing financial interests exist.

Funding Information

We acknowledge support toward 3D printing of tissue engineering scaffolds from the National Institutes of Health (P41 EB023833) (AGM) and Rice University Funds (LEK). We also acknowledge support from a National Science Foundation Graduate Research Fellowship (MRP) and a Rubicon postdoctoral fellowship from the Netherlands Organization for Scientific Research (Project No. 019.182EN.004) (MD).

Supplementary Material

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3