Nonlinear ICA of fMRI reveals primitive temporal structures linked to rest, task, and behavioral traits

Abstract

Accumulating evidence from whole brain functional magnetic resonance imaging (fMRI) suggests that the human brain at rest is functionally organized in a spatially and temporally constrained manner. However, because of their complexity, the fundamental mechanisms underlying time-varying functional networks are still not well understood. Here, we develop a novel nonlinear feature extraction framework called local space-contrastive learning (LSCL), which extracts distinctive nonlinear temporal structure hidden in time series, by training a deep temporal convolutional neural network in an unsupervised, data-driven manner. We demonstrate that LSCL identifies certain distinctive local temporal structures, referred to as temporal primitives, which repeatedly appear at different time points and spatial locations, reflecting dynamic resting-state networks. We also show that these temporal primitives are also present in task-evoked spatiotemporal responses. We further show that the temporal primitives capture unique aspects of behavioral traits such as fluid intelligence and working memory. These results highlight the importance of capturing transient spatiotemporal dynamics within fMRI data and suggest that such temporal primitives may capture fundamental information underlying both spontaneous and task-induced fMRI dynamics.

1. Introduction

Functional magnetic resonance imaging (fMRI) of the human brain during the resting-state (rfMRI) has shown that spontaneous brain activity works in a spatially and temporally constrained manner, instead of evolving randomly, even though there is no imposed task or stimulation in resting state.

One well-known phenomenon during resting-state is the existence of resting-state networks (RSNs), which represent sets of possibly remote regions which are co-activated with high temporal correlation (functional connectivity, FC; Biswal (2012); Fox et al. (2005); Power et al. (2011); Raichle (2015); Thomas Yeo et al. (2011)). Although some well-known RSNs consistently obtained from an analysis of the whole resting-state acquisition (with duration of 5–15 minutes), recent studies have shown that FCs are not constant, but rather dynamically modulated within a relatively short time span (Calhoun et al., 2014; Hutchison et al., 2013; Preti et al., 2017).

The aforementioned studies highlighted the importance of incorporating time into the modeling of the networks, to understand the time-varying functional networks of the brain measured by rfMRI. Hidden Markov models (HMM) have been commonly used for modeling brain dynamics by assuming that the brain activity can be described by a sequence of a finite number of spatial patterns (states) (Taghia et al., 2017; Vidaurre et al., 2017, 2018; Zhang et al., 2019). Other studies have shown that specific sequences of frames re-occur over the resting-state acquisitions (Guidotti et al., 2015; Majeed et al., 2011; Mitra et al., 2015; Takeda et al., 2016). Such patterns are possibly related to recurrent instantaneous (short-time) spatial co-activation patterns (CAP) (Karahanoğlu and Van De Ville, 2015; Liu and Duyn, 2013; Liu et al., 2018). Despite these findings, less is known about the fundamental mechanisms which might explain those phenomena of rfMRI in a unified framework.

In this study, we propose a novel nonlinear feature extraction framework which extracts hidden nonlinear temporal structures repeatedly appearing in the data, and using this approach we show that rfMRI data are composed of a set of distinctive (nonlinear) temporal structures, which we call temporal primitives. The proposed method is a novel framework of nonlinear spatial independent component analysis (sICA), called local space-contrastive learning (LSCL), which is an extension of the recently proposed nonlinear sICA method referred to as SCL (Morioka et al., 2018), see Fig. 1. The method extracts distinctive local (short time-range) nonlinear temporal structures from data so as to decompose it into independent components (spatial patterns, or networks), by training a nonlinear feature extractor in an unsupervised, data-driven manner. As with SCL, LSCL assumes spatial nonstationarity (time courses in different voxels are have different statistical properties) and a nonlinear observation model of the data (Fig. 1a). In contrast to SCL, LSCL assumes a temporally local generative model, i.e. the components generating the time series can be different for each short temporal window. LSCL then trains a nonlinear feature extractor which outputs a set of feature values from a temporally-windowed input time series, so as to optimize the classification performance of a multinomial logistic regression (MLR) classifier which predicts the parcel label of the input (Fig. 1b). Based on such training, the feature extractor is supposed to learn spatially specific local nonlinear temporal structures within a limited number of components, and output feature values representing the original spatial components. Applying the method to the human-connectome project (HCP) rfMRI dataset (Essen et al., 2013), LSCL identifies a new kind of primitive, local temporal structures which we call temporal primitives. These primitives appear recurrently and consistently across the whole dataset. Our analyses show that the temporal primitives are strongly temporally modulated at each occurrence, and the nonlinearity of the feature extractor (deep convolutional neural network; CNN) contributes to extract the fundamental temporal structures underlying such modulating patterns. This may be impossible to achieve via linear feature extractors. We also show that the temporal primitives recurrently (repeatedly) appear at different time points and spatial locations, leading to a spatial organization of the co-activations of rfMRI signals, including well-known RSNs. The same temporal primitives are also found in fMRI during task conditions (tfMRI) underlying task-induced responses. The obtained results indicate that the temporal primitives are the fundamental elements organizing the dynamics of both rfMRI and tfMRI signals. We further show that each of the temporal primitives correlate with some specific individual behavioral traits, which suggests that each primitive might be based on different biological substrates.

Figure 1:

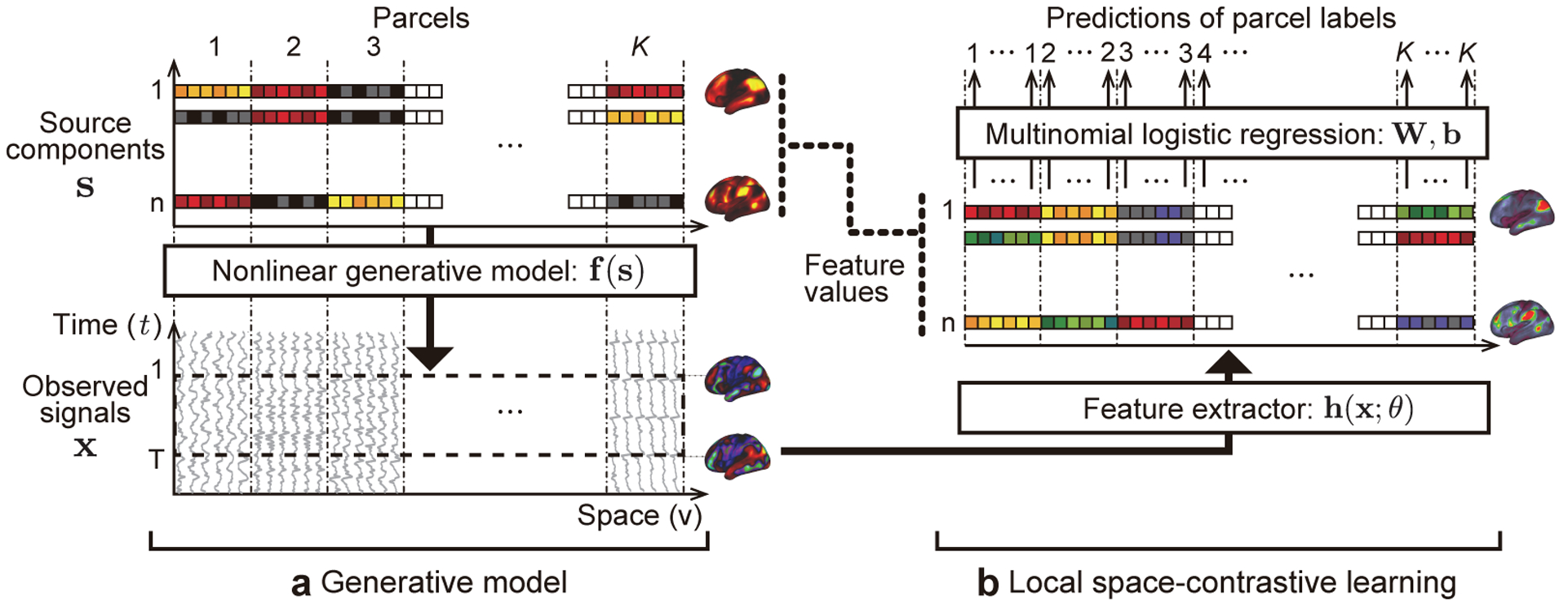
The concept of local space-contrastive learning (LSCL). (a) The generative model is basically a nonlinear version of sICA. The source components are spatial patterns which are spatially (conditionally) mutually independent. The observed time series are given by a nonlinear transformation of the components for each location. Different from ordinary sICA, the components have spatial-parcel-wise stationarity, i.e. different statistics in different parcels, and spatial-parcel-wise independence, which does not necessary mean marginal independence generally assumed in sICA. In addition, LSCL assumes that the components generating the time series can be different for each short temporal window (dotted rectangle on the observed signals), which is in contrast to ordinary sICA, which assumes that the whole time series are generated from the common components. (b) In LSCL, we attempt to find the original components by training a feature extractor to be sensitive to the spatial nonstationarity of the data by using a multinomial logistic regression. The feature extractor is given a short fragment of time series randomly picked from the whole time series at a location as an input, and the logistic regression attempts to predict the parcel label (1, …, K) corresponding to it from the output of the feature extractor (feature values). This framework makes the feature extractor learn component-specific local nonlinear temporal structures, referred to as temporal primitives. See Inline Supplementary Fig. 5 for the detailed procedures to obtain the feature values, which are described in Section 2.5.

2. Material and methods

2.1. Space-contrastive learning

Space-contrastive learning (SCL) is a novel nonlinear spatial ICA (sICA) method (Morioka et al., 2018), which is based on the recently-proposed nonlinear temporal ICA framework, time-contrastive learning (TCL) (Hyvärinen and Morioka, 2016).

TCL theory provided the first identifiability proof for nonlinear ICA by assuming nonstationary independent components. In general, nonlinear ICA assumes a generative model

$$x(t)=f(s(t)),$$ (1)

where x(t) is the observed n-dimensional data point at time point t, f is an invertible and smooth mixing function, and s(t) is the n-dimensional vector of independent components s_i(t). The time series s_i are assumed to be mutually independent. While nonlinear ICA is an ill-defined problem in general (Hyvärinen and Pajunen, 1999), the starting point in TCL is to assume that each s_i(t) is nonstationary, which makes the problem well-defined. Merely for mathematical convenience, the nonstationarity is assumed to be much slower than the sampling rate; in other words, the time series can be divided into segments in each of which the distributions are approximately constant; but crucially, the distribution is different across segments because of the nonstationarity. Accordingly, TCL assumes conditional (segment-wise) independence, instead of marginal independence assumed in ordinary ICA. It was proven that such temporal structure, called time-segment-wise stationarity, enables the estimation of the source signals up to component-wise nonlinearities (Hyvärinen and Morioka, 2016). The learning proceeds by dividing the data into time segments, and then training a feature extractor and a multinomial logistic regression (MLR) so as to predict which segment each observed data point came from. The feature extractor is followed by linear ICA, which is applied to disentangle the linear indeterminacy left by the feature extractor part of TCL, finally giving the estimates the independent components up to point-wise nonlinearities such as squaring.

SCL is basically a “transposed” version of TCL, and thus is a nonlinear equivalent of the sICA framework widely-used in resting-state fMRI analyses (Mckeown et al., 1998). That is, SCL estimates independent components as spatial patterns, which have spatial (parcel-wise) mutual independence and nonstationarity, based on observed time series which are nonlinear mixtures of the components for each location. Notably, the index t (data point) in the generative model (Eq. (1)) is now a 2D or 3D index of spatial location, and x(t) is the observed time series of length n at the location. As with TCL, we assume that the spatial resolution of the nonstationarity is lower than the sampling resolution. We call such spatial structure spatial-parcel-wise stationarity; it can be found in many kinds of data sets including fMRI, where it is widely known that brain activities are functionally localized. Accordingly, SCL assumes conditional (spatial-parcel-wise) independence, instead of marginal independence generally assumed in sICA. The learning procedure in SCL is the same as in TCL except for the transpose of the data matrix; we divide spatial locations into parcels (parcellation), and then train a feature extractor and a MLR so as to predict the parcel labels corresponding to the observed time series. Notably, the feature extractor now takes a single time series at a location as an input, and then estimates activities of independent components generating the time series at that location.

Since SCL is a nonlinear version of sICA, it attempts to find some distinctive nonlinear temporal patterns to decompose data into components. What this means in practice is that, in SCL, the time series corresponding to one component (spatial pattern or network) do not need to be the same across different spatial locations. This is in stark contrast to linear sICA, in which a single network (component) has a single, global time course. Instead, in SCL, the locations in one component are assumed to have common nonlinear temporal structures behind their time series (e.g., nonlinear AR models). Such potential for a wider class of temporal patterns allows us to extract a wider class of networks compared to the ordinary linear sICA.

In this study, we extend SCL to a new sICA framework called LSCL. In contrast to ordinary sICA and SCL, LSCL assumes a temporally local generative model (Fig. 1), i.e., the components generating the time series can be different for each short temporal window. Based on this model, the feature extractor is supposed to learn spatially specific local nonlinear temporal structures within a limited number of components, and output feature values representing the original spatial components. As with SCL, LSCL assumes spatial-parcel-wise independence instead of marginal independence. We will describe LSCL in detail in Section 2.5, after describing data and the drawback of SCL to analyze it.

2.2. Dataset

We used publicly available rfMRI data from the HCP 1200-subject data release (https://db.humanconnectome.org), collected on a 3 T Siemens Skyra scanner with gradients customized for the HCP (Essen et al., 2013). All subjects gave informed consent consistent with policies approved by the Washington University Institutional Review Board. We analyzed 1,003 subjects whose full four 15-min (1,200 data points; TR=0.72s) rfMRI runs were available. The data were preprocessed based on the HCP’s preprocessing pipeline; briefly, 1) spatial processing was applied using the procedure described in Glasser et al. (2016), 2) areal-feature-based surface registration was applied (MSMAll HCP pipeline) (Glasser et al., 2016), and 3) structured artifacts were removed by ICA-FIX (independent component analysis followed by FM-RIB’s ICA-based X-noiseifier) (Griffanti et al., 2014; Salimi-Khorshidi et al., 2014). The rfMRI data were then represented as a time series on the registered grayordinates space, a combination of cortical surface vertices and subcortical standard-space voxels. We discarded the subcortical voxels, and used only the cortical surface vertices (in total 59,412 vertices) for our analyses. We also discarded the initial 300 data points (3.6 minutes) and the final 100 data points (1.2 minutes), and used the remaining middle 800 data points of all runs for the further analyses to avoid unsettled conditions of the brain (see Inline Supplementary Fig. 11 for the potential temporal nonstationarity of rfMRI data found by LSCL). We used two resting-runs of session-1 of all subjects for the main analysis, and the remaining two resting-runs of session-2 for evaluating the generalization accuracy of the trained model. Phase encoding was counterbalanced to have both of right-to-left (RL) and left-to-right (LR) directions for each session.

For the evaluation of the model trained from the rfMRI data, we also used task fMRI data (tfMRI) from the same HCP data release. tfMRI data were acquired with identical pulse sequence settings while subjects performed 7 tasks (Barch et al., 2013); Working Memory (WM; 405 frames), Gambling (253), Relational (232), Emotion (176), Social (274), Motor (284), and Language (316). Each task was comprised of a pair of runs with different phase encoding directions (RL and LR), both used for the analysis. We only used the subjects who had complete tfMRI runs.

2.3. Preprocessing

Since our method is based on spatial parcel-wise stationarity, it requires prior information about a functional parcellation which guarantees spatial stationarity of source components within each parcel. For such parcellation, we here simply divided the 59,412 cortical surface vertices into regular similar-sized small regions (1,833 parcels), using the following procedures: 1) We located centers of parcels by creating a new cortical sphere model containing a smaller number of vertices (1,002) separately for each hemisphere, whose vertices represent the centers of parcels, with unique parcel labels (“-surface-create-sphere” command in the HCP’s Connectome Workbench software, with the setting of the desired number of vertices of 1,000). 2) Each vertex on the original spherical surface was assigned to one of the new parcel labels by searching for the nearest parcel center. Each parcel thus contained 32.4±1.1 vertices, whose area was approximately 28.3 mm² on the midthickness surface model. 3) We excluded parcels which were located on or close to the medial wall and thus containing none or very few vertices on the cortices (smaller than half of average number). Eventually, 1,833 parcels were kept (916 on the left, and 917 on the right hemisphere) for the further analyses. Although this method is simply based on the assumption that spatially proximal locations have similar functional brain activities and does not consider actual functional similarities across regions unlike conventional parcellation studies (Glasser et al., 2016), the parcellation will still satisfy the spatial nonstationarity if we choose the parcel size to be reasonably small. However, since a too small parcel size can complicate the training of the classifier due to the large number of parcels and a small number of data points in each, the parcel size has to be chosen as a compromise.

For multi-subject analyses, the run data were temporally concatenated across all subjects as with ordinary sICA. (data size: number of time point × runs × subjects × vertices = 800 × 2 × 1, 003 × 59, 412.)

2.4. Feature extractor

We used a temporal CNN as the feature extractor which takes a single time series as an input and nonlinearly extracts component activity. Several studies have already shown that such a convolutional network can automatically learn hierarchical structures in data such as images (He et al., 2015; Krizhevsky et al., 2012; Szegedy et al., 2015) and audio (van den Oord et al., 2016).

The network consists of concatenated convolutional hidden layers, each followed by batch-normalizations (Ioffe and Szegedy, 2015) and nonlinear activation units (Table 1). For the nonlinear units, we used a type of gated activation:

$$z=\text{max}(0,W_1*x+b_1)\odot \sigma (W_2*x+b_2)$$ (2)

where x is the input to the layer, * denotes a temporal convolutional operator, ⊙ denotes an element-wise multiplication operator, max(·, ·) is an element-wise max function, σ(·) is an element-wise sigmoid function; W₁, W₂, b₁, and b₂ are learnable convolutional parameters. The first term in this product is the widely used rectified linear unit (ReLU) (Nair and Hinton, 2010), and its activations are modulated by the gating function (sigmoid) in the second term which controls the information passing through the layer. The network also includes two down-sampling layers, which downsample the temporal dimension in half in an invertible way (Jacobsen et al., 2018); i.e., the input to the layer was separated into two time series by picking time points with the stride size of two, with one temporal shift between them, and then they are concatenated across channels (the dimension of channel was doubled). This temporal down-sampling roughly preserves the information coming from the lower layer, and likewise preserves the temporal ordering. In addition, the first layer of the network is a temporal normalization layer which standardizes the input to have mean of 0 and std of 1 for each sample.

Table 1:

Network architecture of CNN and MLR

Layer name	Output size time × channel	Description
Input	46 × 1	Cropped time series (fragment)
Normalize	46 × 1	Temporal normalization
Conv1	32 × 16	Convolutional layer; [15,16] × 2
Conv2	30 × 16	Convolutional layer; [3,16] × 2
Conv3	28 × 16	Convolutional layer; [3,16] × 2
DownSample1	14 × 32	Down-sampling (split time-series into channels)
Conv4	12 × 32	Convolutional layer; [3, 32] × 2
Conv5	10 × 32	Convolutional layer; [3, 32] × 2
DownSample2	5 × 64	Down-sampling (split time-series into channels)
Conv6	3 × 64	Convolutional layer; [3, 64] × 2
Conv7 (feature)	1 × 5	Convolutional layer; [3, 5] × 2
MLR	1 × 1, 833	Fully connected layer; [5 × 1, 833]

The outputs of the feature extractor (Conv7) are called feature values, and they represent the activities of the components. The MLR follows the feature extractor. Its goal is to predict parcel labels from the activities of components extracted by the feature extractor.

Notably, the network does not have temporal pooling structures for down-sampling as ordinary CNNs do (Krizhevsky et al., 2012; Szegedy et al., 2015). Instead, we restricted the input size to be the same as the width of the receptive field of the network (46), which was determined by the network structure (Table. 1), so as to constrain the temporal dimension of the feature values (Conv7) to be 1. That is, this network performs convolutions on a shorter window (46) than the original time series. We explain this window-cropping scheme in detail in the next section.

To show the advantage of using a nonlinear model, we also perform the experiments with a simple linear model which is comprised of a single convolutional layer and has the same number of components and same width of the receptive field as those of the nonlinear model. The convolutional layer was followed by the ReLU nonlinearity, which is necessary to represent nonstationarity (of variance, for example, see Hyvärinen and Morioka (Hyvärinen and Morioka, 2016)) similarly to the nonlinear model.

2.5. Extension to LSCL and its training

The network (feature extractor and the MLR) is trained by stochastic gradient descent (SGD) based on back-propagation, which is commonly used in deep learning studies.

In basic SCL, one training sample is a time series on a spatial location t in the parcel, together with the parcel label. However, since the data matrix here has a much smaller number of spatial data points (59,412) compared with the temporal dimension (800 × 2 × 1, 003 = 1, 604, 800 time points), the training based on this basic framework would be difficult.

In order to enhance the training, we propose a more efficient strategy called local SCL (LSCL); instead of using a whole time series, we use a combination of multiple short cropped fragments as one sample. Specifically, for each training sample, 1) we crop several short fragments (contiguous time series), whose length is equal to the width of the receptive field (46), from random subjects/runs/vertices/timings in a target parcel (fragments are picked not to span multiple subjects/runs), 2) feed them into the feature extractor and extract feature values separately for each fragment, and then we 3) take the average of the obtained feature values. The averaged feature value is then fed into the MLR, and the whole network is updated by back-propagation based on its prediction error. This cropping method virtually increases the number of data points from the original one, and the averaging increases the training accuracy by reducing the variability of (averaged) feature values across samples. We fixed the number of fragments in one sample to 128.

In addition to the stabilization of the training, this training strategy has some important implications which make the ensuing LSCL fundamentally different from ordinary sICA. Firstly, since different fragments are treated as different data points, every component can be computed from different fragments picked from the locations, giving rise to different spatial patterns in the output. Thus, the components do not have a single spatial pattern unlike in linear sICA. Secondly, since the feature extractor is given temporally cropped short time series as inputs instead of whole time series like in ordinary sICA, it has to learn local temporal structures specific to the components. In particular, each component can be interpreted as detecting one short temporal primitive, which we define as the local temporal structure corresponding to one component.

LSCL needs additional linear sICA after the training of the feature extractor to disentangle the linear indeterminacy, as with TCL (Hyvärinen and Morioka, 2016) and SCL. We applied fastICA (Hyvärinen, 1999) to the learned feature values. The input to the linear sICA is based on the reproduction of the input to the MLR during the training phase, i.e., random-crop-averaged feature values. More precisely, one sample is a five-dimensional vector obtained by taking an average of each of the five components at 128 randomly selected subjects/runs/vertices/timings from a specific parcel. We collected 10,000 samples for each of 1,833 parcels; i.e., input data size is 5 × 18, 330, 000. Importantly, we performed parcel-wise-demean for each component of the input data before applying fastICA because 1) linear ICA assumes that the data is stationary (whether temporally or spatially), and the non-stationarity created by different means in different parcels would violate the basic assumptions and lead to very poor demixing results, while 2) LSCL assumes parcel-wise-independence which is not affected by the parcel-wise-bias (change of origin for each parcel) of the components, which are expected to emerge due to parcel-wise modulation of the components. The estimated 5 × 5 demixing matrix is applied to the component-axis of the feature values to disentangle the linear indeterminacy across components. See Inline Supplementary Fig. 5 for the visualization of the procedure. Considering potential linear demixing by the feature extractor to some extent, we selected the demixing matrix which was the most close to the identity matrix (after permutation), by repeating the estimation 1,000 times with different random initial values.

In this study, we further applied a spatial averaging within each parcel in order to decrease computational complexity while increasing signal-to-noise ratio (data size: number of time points × runs × subjects × parcels = 800 × 2 × 1, 003 × 1, 833), followed by subject-run-wise temporal normalization to have zero mean and unit standard deviation. Note that this procedure decreases spatial resolution for later analyses. Although this data matrix itself does not satisfy the spatial-parcel-wise-stationarity because it has only one (concatenated) time series in each parcel, LSCL framework can still make its analysis feasible because the cropping strategy mentioned above treats observations at different timings as different data points, which virtually increases the number of data points in a parcel.

The other training parameters of LSCL are set as follows: Initial learning rate of 0.1, momentum of SGD of 0.9, mini-batch size of 128. The initial weights of each layer were randomly drawn from a uniform distribution. The training was performed only from the session-1 of rfMRI dataset; the session-2 of rfMRI and the task-runs of tfMRI were used to evaluate the generalizability of the trained network.

The LSCL toolbox (Python) is available from the authors upon request, which fundamental part is based on that of TCL (https://github.com/hirosm/TCL).

2.6. Extraction of whole feature values

For evaluating the resulting components, we extracted feature values from the dataset (time series × runs × subjects × parcels) by applying the trained feature extractor to short time series of length 46, sliding-windowed with stride 4 from the time series of each run, subject, and parcel (number of features: number of time points × runs × subjects × parcels × components = 189 × 2 × 1, 003 × 1, 833 × 5). The extracted feature values were followed by the linear sICA. Compared to the data matrix, the feature values have the additional dimension of components computed from the original data. Note that the temporal dimension of the feature values now represents the timing (temporal index) of the sliding windows corresponding to the obtained feature values, and its temporal resolution is 4 times smaller than the input because of the stride size of the sliding windows. The following analyses are based on visualizing this matrix and its relations to the input data.

2.7. Chance level of the feature values

To see how frequently the temporal primitives appeared in the data, we computed the chance level of the feature values. The chance level was estimated by inputting surrogate time series which follow a Gaussian AR model fit to the original data (autoregressive randomization; ARR) (Liégeois et al., 2017). The order of AR was selected to be the same as the width of the receptive field (i.e., 46). Since the feature extractor takes one dimensional time series as an input, we used a univariate (one dimensional) AR model instead of a multivariate model. The AR coefficients were assumed to be the same across regions, but estimated separately for each subject and run. Exceeding this chance level means that the feature extractor was significantly activated by any property not included by this AR model, such as nonlinearity, non-Gaussianity, non-stationarity, or region-specificity of the input time series. The significance level α was here selected as 0.001.

We call those time series fragments whose feature values achieved statistical significance realizations of the temporal primitives. For further comparison, we also obtained feature values from temporally shuffled time series (random shuffle; RS), in which the temporal structure was completely broken.

2.8. Representative patterns of the temporal primitives

Next we computed temporal patterns that best represent the computations in each component. Such representative temporal patterns of the temporal primitives were obtained by taking an average of the input signals which led to the highest activity for the component. That means those patterns represent the most fundamental temporal structures representing each of the components learned by the feature extractor. Importantly, since CNN generally has the well-known property of shift-invariance in its input space, there should be some amount of temporal shifts between those time series, which can make a simple sample average less interpretable. In order to compensate for this, we temporarily shifted each of the time series so as to maximize their cross correlations to the one which has the highest-activity, before taking their average. The relationship between those temporal shifts applied to the inputs and the corresponding feature values are later evaluated to see the shift-invariance learned by the feature extractor (Fig. 4a). The averaged temporal patterns within a window, whose length is the same as the width of the receptive field of the feature extractor (about 32 s) and has the highest number of overlaps of the shifted time series inside, are hereafter called representative temporal patterns. In preliminary experiments, we checked the averaged temporal patterns with changing the threshold of the feature values, and found that they were not so sensitive to the threshold values (Inline Supplementary Fig. 1). Considering a trade-off between sharpness and stability of the averaged patterns, we decided to use top 0.0001% (695) sliding-windowed time series for obtaining the representative patterns.

Figure 4:

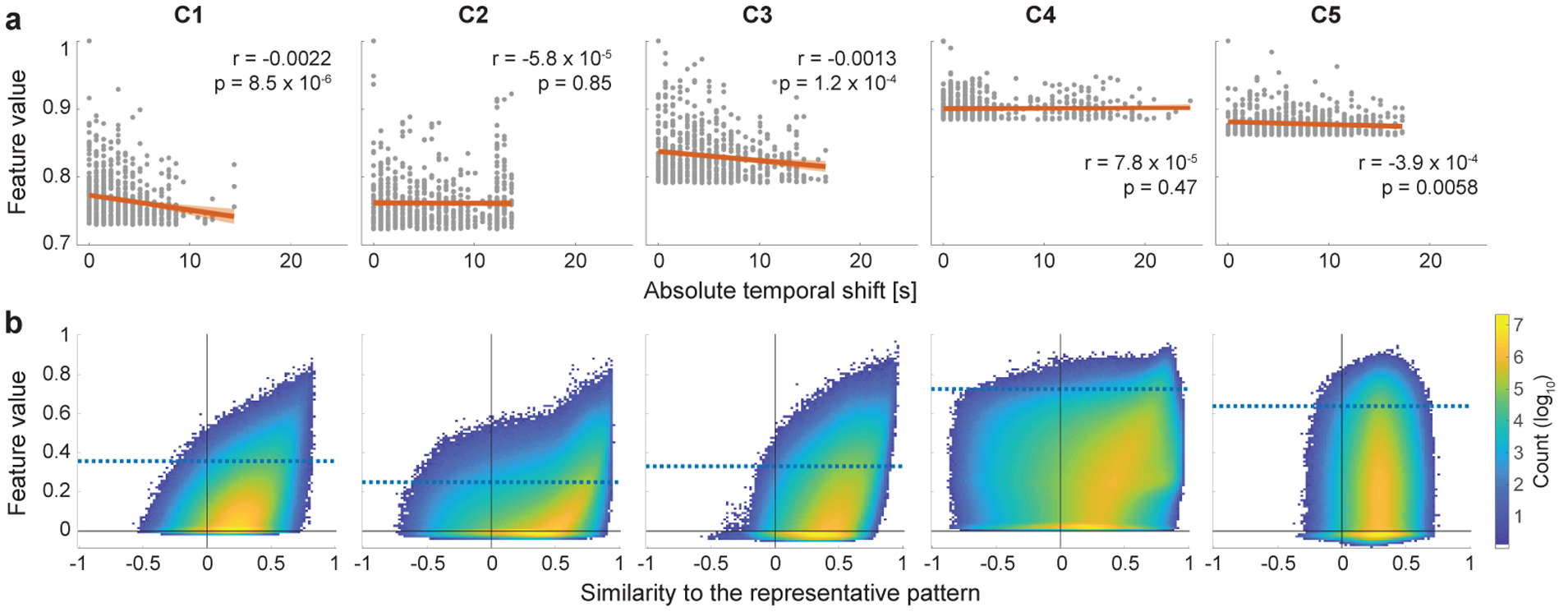
Invariance of the feature extractor against temporal modulations of the temporal primitives. (a) The robustness of the feature extractor to the temporal shifts of the realizations. Each panel shows the relationship between the feature values and the (absolute) temporal shifts that were applied to their inputs for alignment to reference signal in Fig. 2a. Each point corresponds to one of the top time series shown in Fig. 2a (n = 695). The feature values were normalized to have maximum value of 1 for each component. The red lines are the estimated least-square fits, and colored bands indicate 95% confidence bounds. Although the slopes are significant in some of the components, they are quite small, which illustrates the shift-invariance of the feature extractor. (b) Two-dimensional histogram showing the relationship between feature values and the similarities of their inputs to the representation patterns (Fig. 2a). To evaluate only the modulations different from the temporal shifts shown in a, the similarities (Pearson correlation) were measured after compensating their temporal shifts relative to the representative patterns (see Section 2.8 for the temporal-shift alignment). Blue horizontal lines are the chance levels same with those shown in Fig. 3a. Note that the colorbar is log-scale.

2.9. t-SNE analysis of the realizations of the temporal primitives

Next we attempted to visualize some nonlinear aspects of the temporal primitives of the independent components. We discard here the shift-invariance which the primitives have by construction. To visualize the nonlinear processing (modulation) of the temporal primitives, for each component, we embedded their realizations (as defined above) into a two-dimensional space by t-SNE (van der Maaten and Hinton, 2008) based on the similarities (Pearson correlation) between them. To compensate for the modulation related to the temporal shift investigated above, we temporally shifting the realizations so as to maximize their cross correlation to the representative pattern obtained above, before measuring the similarity. To make the amount of the overlap between time series after the temporal shifts consistent, the time series outside of the temporal extent of the realizations were also considered for the shifting, and cropped later at the same window as that of the reference patterns. Those data were fed into the t-SNE algorithm implemented in the MATLAB Statistics and Machine Learning Toolbox with Pearson correlation distance metric and perplexity 100 (the other parameters are the default values), and then embedded into a two-dimensional space. To decrease computational complexity, we reduced the number of realizations of C2 and C3 into a tenth by thinning out them.

2.10. Frequency analysis of the realizations of the temporal primitives

We performed frequency analysis on the temporal primitives to see their frequency characteristics. The temporally adjusted realizations were used for the analysis (see Section 2.9) to make the temporal patterns in the analysis window consistent across the realizations. The power spectral density (PSD) was estimated for each of the realizations by discrete Fourier transform with hanning window, after standardizing it to have zero-mean and unit variance. The average of the PSDs corresponding to the highest feature values (top 0.0001%) of a component is called representative frequency spectrum of the component.

2.11. Visualization of the spatial co-occurrence of the temporal primitives

Since the feature extractor learns local temporal structures without out putting their precise timings, the learned temporal primitives could have appeared at different time points and spatial locations across the realizations. That means the spatial co-occurrence (co-activation) patterns of the temporal primitives, which are represented by the spatial patterns of the feature values, can be different across time. To visualize the variety of the spatial co-occurrence patterns, we showed their distribution by embedding them into a two-dimensional space by tSNE. We fed the feature values into the tSNE algorithm by treating the spatial axis as variables representing the spatial patterns (1,833 dimensions), and the other axes (timings, subjects, and runs) as observations. To decrease computational complexity, we reduced the number of samples into half by temporal striding. The similarity was measured by Pearson correlation, and the perplexity was set to 100.

2.12. Timing of event-related temporal primitives

To facilitate interpretation of the temporal primitives, we investigated the timing and location of their realizations during task blocks in the task data. Firstly, we extracted feature values from the tfMRI data by applying the feature extractor and the linear sICA matrix trained from the rfMRI data (Section 2.5) for each task run, through temporal sliding-window with stride 1 (see Section 2.6). We then picked realizations which appeared during the task blocks of all subjects and runs (excluding Motor-CUE condition). Considering the temporal invariance of the feature extractor, for each realization, we estimated the timings of the realizations relative to the representative pattern by temporally matching them. Then, the reference point of the (shifted) representative pattern (0 s in Fig. 2a) was used as the actual timing of the realization. The realizations corresponding to a specific timing can be plotted by showing the input time series assigned to that timing. We also counted the number of the timing-specific realizations for each region, then plotted as a spatial pattern to show their spatial preferences.

Figure 2:

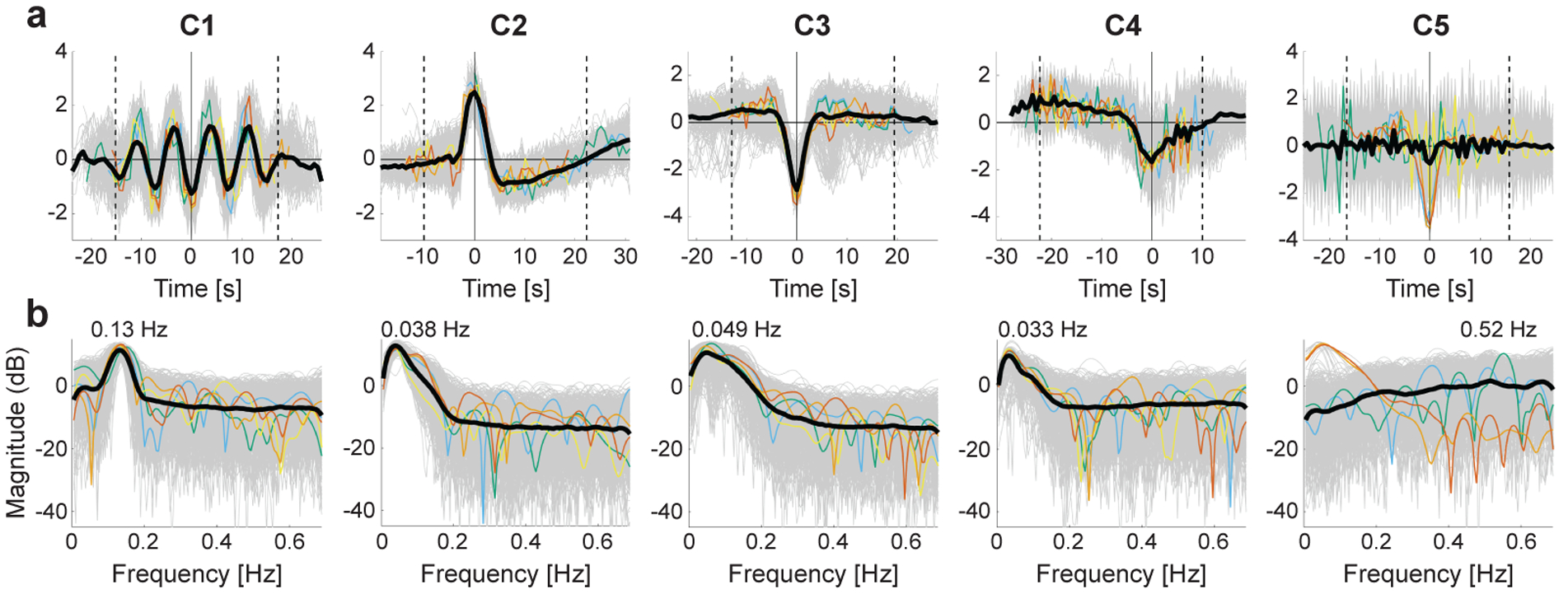
(a) Visualization of the representative temporal patterns (the most important temporal characteristics) of temporal primitives, which are component-specific spatio-temporally-local nonlinear temporal structures learned by the nonlinear feature extractor (CNN). They were represented by taking an average of time fragments whose (unmixed) feature values were very large at each component dimension. Gray thin lines are the individual input time series which produced the top-0.0001% highest component activities in the whole dataset. The colored thin lines indicate the samples with the very highest activations (1st–5th: red, orange, yellow, green, and blue). Considering the well-known property of shift-invariance of CNNs (see Fig. 4a for further evaluation), all samples were temporally shifted so as to maximize their cross correlations to the reference signal, i.e. the one with the highest activity (red sample). The black thick line shows their sample average after the temporal shifting. Two dotted vertical lines indicate the edges of a temporal window whose width is the same as the width of the receptive field of the feature extractor (~ 32 s); the (absolute) peak point inside the window was selected as the reference point (0 s). We can see that the average temporal patterns inside the windows show clear differences across components, and are hereafter used as the representative temporal patterns of the temporal primitives. (b) The representative frequency spectra of the temporal primitives. The spectrum was estimated for each of shift-adjusted inputs corresponding to those in a (see Section 2.9 for the shift-adjustment). As with a, the gray thin lines are the individual plots, the colored thin lines indicate the samples with the very highest activations, and the black thick line shows their average. The peak frequency of the average spectrum was displayed on the line.

2.13. Relationship between temporal primitives and behavioral traits

To see possible contribution of the temporal primitives to the behavioral traits of the subjects, we investigated which traits were correlated with the components activities. We only considered traits related to intelligence and the response accuracies during tfMRI acquisitions: episodic memory (age-adjusted), cognitive flexibility (age-adjusted), inhibitory control (age-adjusted), fluid intelligence accuracy, fluid intelligence speed, reading (age-adjusted), vocabulary (age-adjusted), processing-speed (age-adjusted), spatial orientation, attention true positive (TP), attention true negative (TN), verbal episodic memory, working memory (age-adjusted), emotion recognition, WM tfMRI accuracy (WM_Task_Acc), Language tfMRI accuracy (Language_Task_Acc), Social tfMRI accuracy (Social_Task_TOM_Perc_TOM), Relational tfMRI accuracy (Relational_Task_Acc), and Emotion tfMRI accuracy (Emotion_Task_Acc). The subject-representative value of the component was obtained by taking an average of the whole feature values of the subject (across time, parcels, and runs) for each component. To avoid possible bias across acquisition days, the averaging was performed across session-1 and session-2; the feature values of session-2 were obtained by applying the feature extractor trained from session-1 to the data of session-2. Head motion, gender, and age were regressed out as confounds from both of the averaged feature values and the traits. We then calculated Spearman correlation between the feature values and the behavioral traits, and evaluated the significance (two-sided, permutation test). We also evaluated the spatial distribution of the relationship by calculating the average feature value and evaluating the correlation separately for each parcel.

2.14. Linear sICA

For comparison, we also analyzed the data by a conventional linear sICA analysis. The dataset preprocessed above (parcel-averaged, 800 time points in each run) was at first processed by group-PCA (Smith et al., 2014) to reduce the dimensionality to 800. The output was then fed into group-ICA using FSL’s MELODIC tool (Hyvärinen, 1999; Beckmann and Smith, 2004) to estimate the spatially independent components. We here set the number of components to 15, considering the similarity of the estimated components to the spatial co-occurrence patterns of the temporal primitives.

3. Results

3.1. Representative patterns of the temporal primitives

In the LSCL framework, the feature extractor learns component-specific, spatiotemporally localized elements which we call temporal primitives, so as to demix the rfMRI data into nonlinear components (see Section 2 for details). The learning is based on logistic regression in a “self-supervised” scheme where class labels of time series fragments are defined based on spatial locations.

The training (on session-1 of rfMRI) and testing (on session-2 of rfMRI) accuracies after the learning procedure were 4.3 % and 3.9 % respectively, both of them were much higher than the chance level (0.055 %). The similarity of the training and testing accuracies further implies that the extracted temporal primitives are not the artifacts caused by overfitting to the training dataset.

To understand what kind of temporal structure was learned from data, we first visualized their representative temporal patterns for each component (Fig. 2a). These patterns were represented by an average of the time fragments from the whole dataset (all subjects, runs, parcels, and timings), whose (unmixed) feature values were very large at each component dimension. That means those representative patterns show the most important characteristics representing the component learned by the feature extractor. We also showed representative frequency spectra of the temporal primitives (Fig. 2b) (see Inline Supplementary Fig. 6a for the global average spectra of all realizations, and Fig. 6b for the subject-wise-average spectra). The obtained representative patterns are clearly distinctive across components (Fig. 2a): Component 1 (C1) has an oscillatory pattern (ripple) made of repetitive sine-like waves of about 0.13 Hz (Fig. 2b). Each sample followed the oscillation for a few cycles, and then was unlocked from it. C2 is a transient pattern similar to the hemodynamic response function (HRF), and the respiration response function (RRF) evoked by a deep breath (Birn et al., 2008), which consists of an early overshoot followed by a later undershoot peaking at approximately 16 s, similarly to HRF. The conventional HRF has been proposed to be decomposable to at least two different components, and C3 seems to be similar to one of them, the stimulus-related component (Cardoso et al., 2012; Herman et al., 2017; Lima et al., 2014), which is represented by a transient negative blood-oxygen-level dependent (BOLD) response (NBR). C4 has a long plateau with a weak negative trend followed by a sharper slope (and a positive rebound), which looks relevant to the task-block BOLD response with an adaptation (negative slope) followed by an undershoot. C5 responded to high frequency (noisy) temporal patterns, which can be also seen from its flat spectrum at high frequency range over 0.2 Hz (Fig. 2b), which implies that C5 represents high frequency artifacts in fMRI data. The average spectrum (Inline Supplementary Fig. 6a) has a small peak around 0.52 Hz, which may be related to the previously reported head position spectra (0.55 Hz) specific to this dataset (Power et al., 2019). Those distinctive patterns across components support our claim that LSCL makes the feature extractor learn component-specific temporal structures to decompose the data into components.

Figure 6:

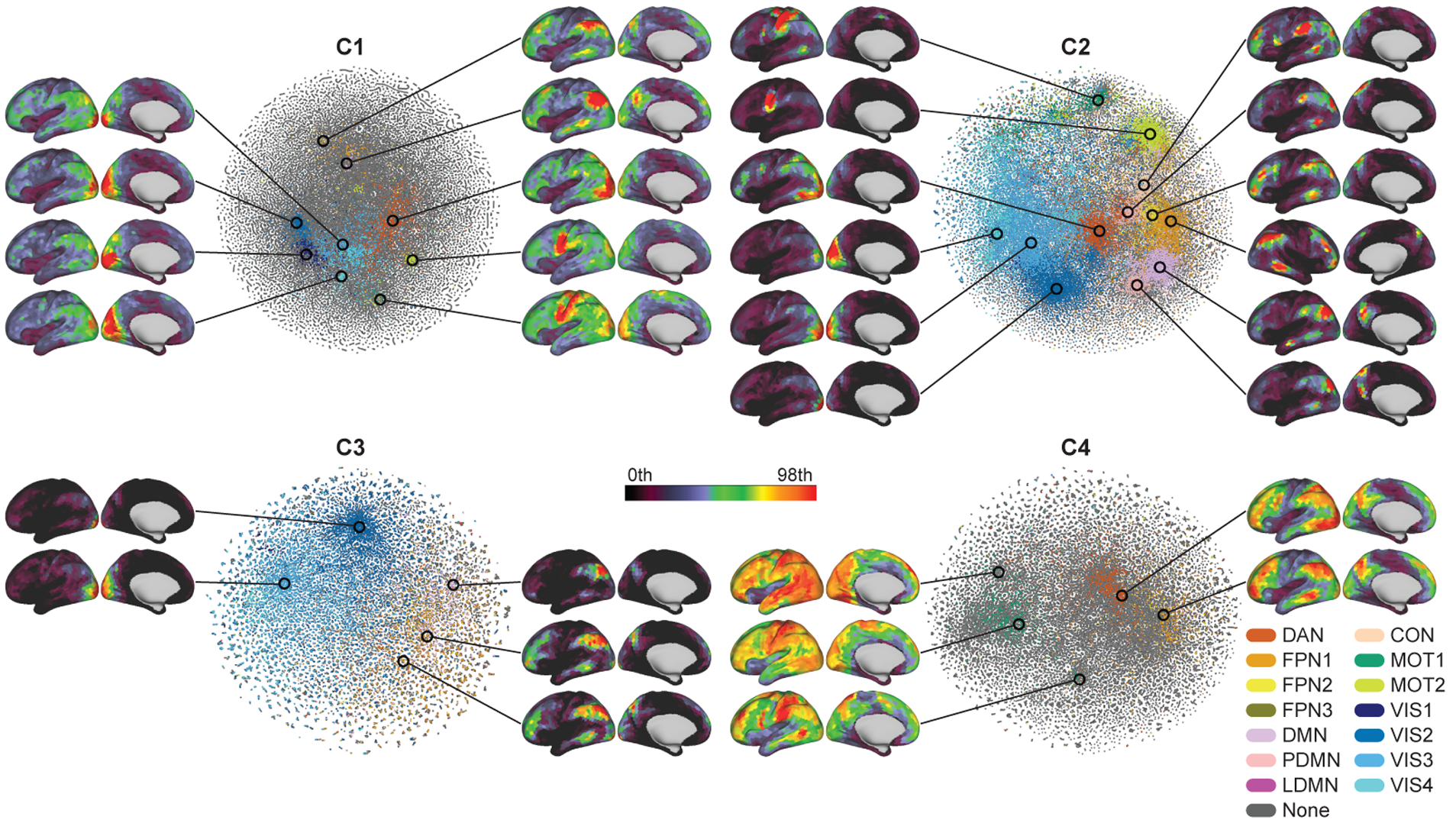
The spontaneous spatial co-occurrence patterns of the temporal primitives. Scatter plots show two-dimensional t-SNE embeddings of the spatial co-occurrence patterns of the temporal primitives during the resting-states (see Section 2.11 for t-SNE analysis details). The color indicates the most similar RSN obtained by conventional linear sICA (see Inline Supplementary Fig. 3); DAN (dorsal attention network), FPN (fronto-parietal network), DMN (default mode network), PDMN (posterior DMN), LDMN (lateral DMN), CON (cingulo-opercular network), MOT (motor and somatosensory network), and VIS (visual network). The similarities were measured by Pearson correlation, and thresholded by 0.35; the gray points have similarities to the RSNs less than 0.35. The spatial patterns show some examples of the co-occurrence patterns on the embedded space, obtained by taking local average of 500 data points on some locations. Only left hemispheres are shown, except for the FPN of C2 because it showed right dominant pattern.

To show that those representative patterns were not biased to a small number of subjects, we counted how many subjects were included in the 695 time fragments for each component; (C1) 397, (C2) 217, (C3) 227, (C4) 484, (C5) 461). Although those numbers were significantly smaller than the case of completely random selections from the all subjects with the same probability (α = 0.05, permutation test, not corrected), they were reasonably distributed over many subjects, without overfitting to a small subset of them.

3.2. Occurrence ratios of the temporal primitives

Fig. 3a shows the histogram of the feature values. Comparing with surrogate data (see Section 2.7 for the surrogate data generation), the feature values had significantly higher values compared to chance level: Proportions of 0.28%, 1.4%, 1.3%, 0.10%, and 0.43%, respectively, exceeded the threshold of α = 0.001 (not corrected). This implies local time series contained temporal structure, related to the temporal primitives, which is rarely observed in the surrogate data. The significantly occurring time series are hereafter called realizations of the temporal primitives. C2 and C3 have especially high proportions of the realizations relative to the others, indicating they comprise a relatively larger part of the rfMRI time series. The difference of the sensitivities to the surrogate data also indicates some distinctive characteristics of the temporal primitives; e.g., C5 was more strongly activated by the random shuffle surrogate data than the actual data, which seems to indicate C5 captures high frequency noises in the data, but is different from C1 even though C1 also represents relatively high frequency temporal pattern (Fig. 2).

Figure 3:

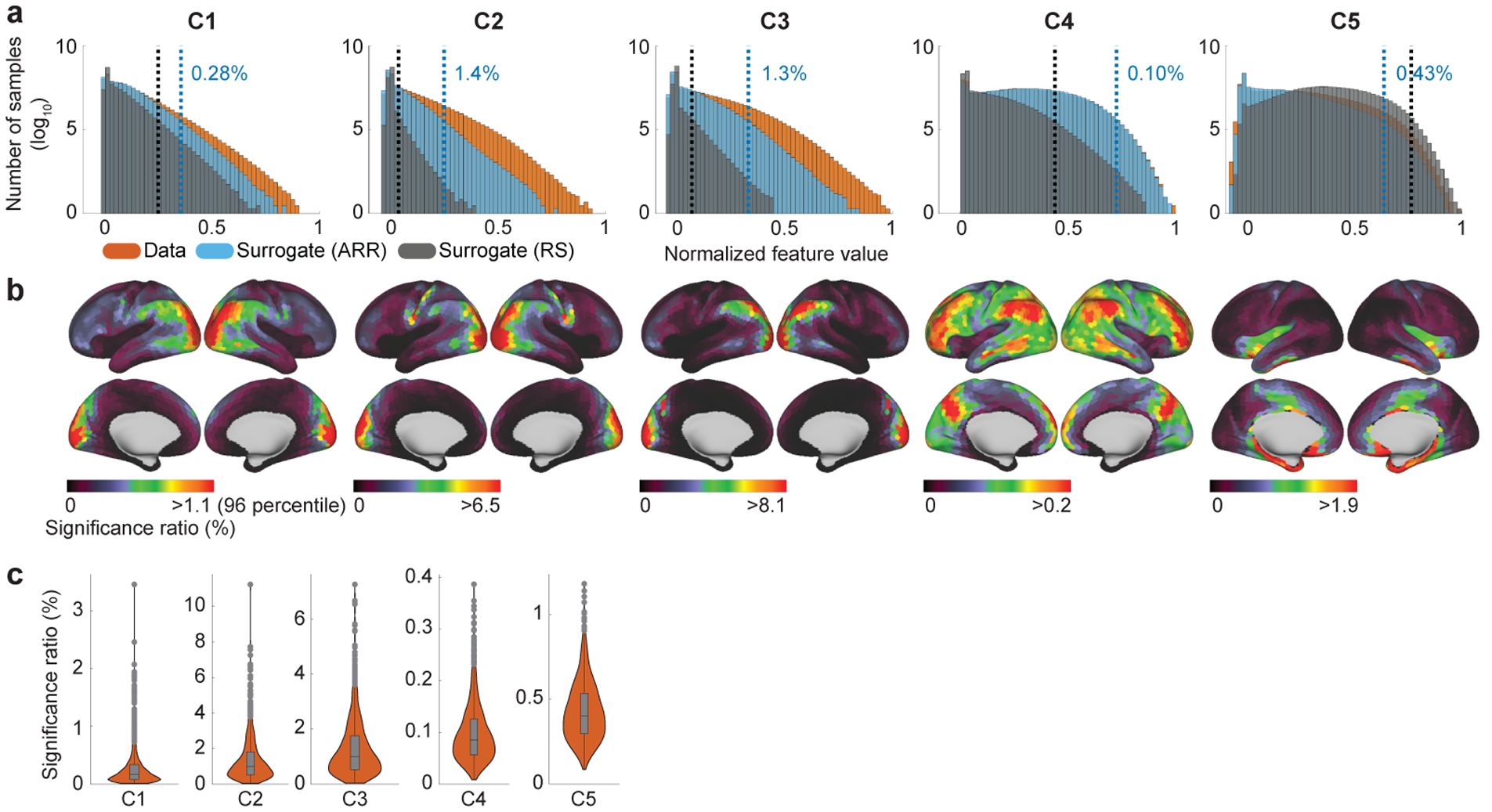
(a) Histogram (log-scale) of the feature values obtained from the whole dataset (orange), and its comparison to those from the surrogate data (blue: autoregressive randomization (ARR); grey: random shuffle (RS)). The scale of the feature values were normalized to have the maximum value of 1 for each component. Blue vertical lines show the chance levels of the feature values estimated from the ARR surrogate data (α = 0.001; not corrected). 0.28%, 1.4%, 1.3%, 0.10%, and 0.43% of the feature values were over the chance level. For comparison, black verticals show the threshold estimated from the RS surrogate data (α = 0.001; not corrected). The difference of the sensitivities to the surrogate data across components indicates some characteristics of the temporal primitives; e.g., the higher feature values of C5 in the RS surrogate data seems to indicate that it captures high frequency (possibly physiological) artifacts in the data, which tend to lack temporal structures as with RS surrogate data. (b) Location-wise visualizations of the significance ratios of the feature values show spatial nonstationarity and component-specificity of the the realizations. The chance level is the same with a. Importantly, those spatial distributions do not indicate co-activation networks, as explained in the text. (c) Between subject variability of the significant ratios. A data point in the boxplot represents the ratio of the realizations in a subject. The box is drawn between the 25 and 75 percentiles, with a line indicating the median. Whiskers indicate 1.5 times the interquartile range.

The location-wise visualization of the realization ratios shows clear spatial nonstationarity for each component (Fig. 3b), which is consistent with the assumption of LSCL. The distributions are also distinct, though there is a large amount of overlap. In particular, C1, C2, and C3 have similar distributions, especially around visual cortex, inferior parietal lobule (IPL), and a part of middle temporal gyrus (MTG). However, they have some differences: C2 has large values around somatomotor/sensory regions, C3 has large values around parieto-occipital sulcus (POS). C4 is more broadly distributed than the others; its pattern seems to be a combination of the task-positive network and the default-mode network (DMN). C5 has large activities in noise-susceptible regions such as inferior temporal lobe (Simmons et al., 2009). It should be noted that these spatial distributions do not represent spatial co-occurrence (networks) of the temporal primitives (see Fig. 6) because those plots were obtained by counting the number of realizations for each parcel without considering their timings (see Inline Supplementary Fig. 5 for the procedure), while the spatial co-occurrence patterns can be actually different across time in LSCL (see Section 2.5 and Fig. 6).

The distribution of the subject-wise realization ratios shows that none of the temporal primitives is subject-specific (Fig. 3c), though some subjects seem to lack the realizations of some components.

3.3. Nonlinear modulations of the temporal primitives

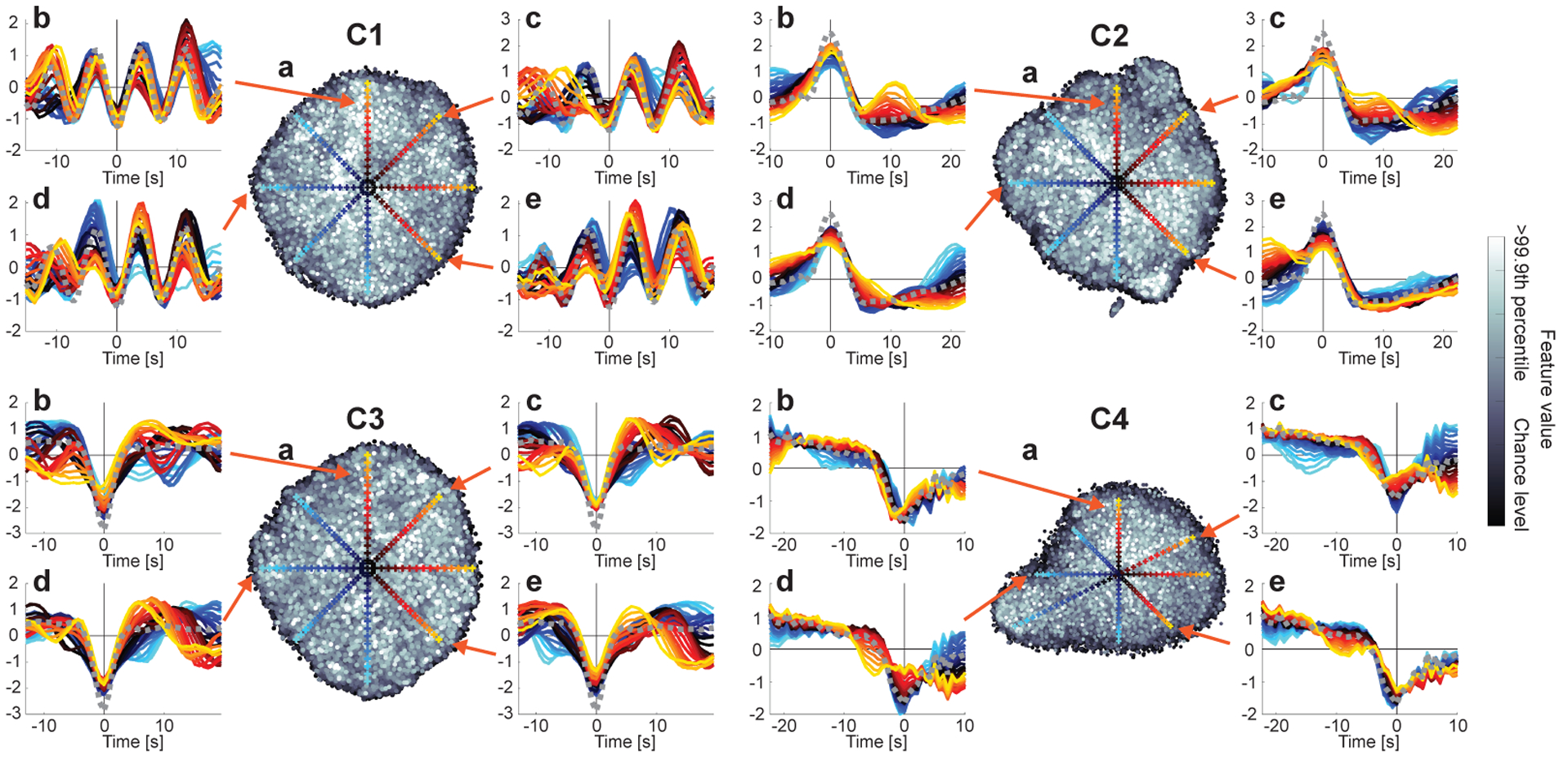
The visualization of the representative patterns (Fig. 2a) is intuitive, but just the first step in understanding the nonlinear computations in LSCL. In fact such patterns do not in themselves describe the nonlinear nature of the components. We next further analyze the nonlinear modulation observed in the realizations of the temporal primitives.

The most fundamental nonlinearity in our framework is invariance to temporal shifts. This is partly because the input samples are obtained from data randomly cropped from the data matrix without considering the actual timing of the brain activities; it is also worth noting that rfMRI data do not have any task design. Shift-invariance is also enforced by construction because we use CNNs which have the well-known property of learning shift-invariant features due to their convolutional nature. As shown in Fig. 4a, such temporal shifts were indeed quite common, and the components learned some shift-invariance, as seen from the small slope of the linear regression analysis.

To evaluate the amount of nonlinear modulation other than the temporal shifts shown above, we plotted relationships between the feature values and the similarities of their inputs to the representative patterns after compensating for their temporal shifts (Fig. 4b). Basically, the histograms illustrate that the feature extractor is sensitive to temporal patterns resembling the representative patterns (except for C5); in other words, it is deactivated when the input includes fewer occurrences, resulting in sparseness of the feature values (except for C5). However, the relationship does not appear to be linear; the histograms have wider horizontal distributions compared to a linear model (results for linear model are shown in Inline Supplementary Fig. 2), which indicates that the nonlinear feature extractor has wide range of modulations to which the feature values are invariant, thanks to its nonlinearity. We hereafter omit C5 from the further analyses because our analyses above suggests that it represents fMRI noise.

To intuitively visualize the nonlinear modulations of the realizations, we plotted their distribution by embedding them into a two-dimensional space based on their similarities (Fig. 5a). Firstly, we see that the scatter plots do not show clear relationship between feature values (grayscale colors) and their embedded locations. This again implies that the feature extractor has strong invariance against the modulations of the component-specific patterns. In contrast, a linear feature extractor would show maximum activation for one input pattern, and weaker activations for anything deviating from it. Secondly, the distribution did not show a clear clustering structure, which suggests the variability was not structural, and not easy to further classify within a component. That implies that the components were properly divided into structurally specific components, without being contaminated by the other potentially distinctive ones.

Figure 5:

Visualization of the modulations of the temporal primitives. (a) two-dimensional t-SNE embedding of the realizations (see Section 2.9 for t-SNE analysis details). Each point corresponds to one of the realizations. The grayscale color indicates the feature value. Their chance levels (the lower bounds of the realizations) are the same as Fig. 3. (b–e) Each panel illustrates the temporal patterns of some local realizations, which were shown by gradually changing the location on a line on the embedded space. The colored cross on the t-SNE space indicates the sampling location, and the temporal pattern plotted with the same color in the corresponding panel shows the temporal pattern given by a local average of the 100 closest points around the location. The gray dotted line is the representative pattern obtained in Fig. 2a, which were used as a reference for compensating the temporal shifts of the realizations. Those differences of the temporal patterns in the embedded space illustrate the modulations of the realizations.

The other in-set panels show the temporal patterns in selected locations on the embedded space. While the basic shape of the temporal primitives seems to be preserved across realizations, if we take a closer look, the shapes are clearly variable. For example, C1 sometimes has smaller number of cycles and/or slightly different frequencies of the cycles (see C1b for example), and C4 sometimes shows a different length of the plateau before the strong negative slope (C4b). These results illustrate the nonlinear invariance of the CNN feature extraction operating on the input space.

3.4. Spatial co-occurrence of the temporal primitives

To show that the temporal primitives are fundamental elements underlying the intrinsic time-varying co-activations of the rfMRI signals, we visualized the distributions of their spatial co-occurrence patterns during the resting-state, by embedding them into a two-dimensional space for each component (see Section 2.11 for more details) (Fig. 6). To show their relationship to the well-known RSNs, the embedded patterns were colored based on their similarities to the RSNs obtained by the conventional linear sICA analysis on the same dataset; they represent default-mode network (DMN), posterior-DMN (PDMN), lateral-DMN (LDMN), dorsal attention network (DAN), fronto-parietal network (FPN), cingulo-opercular network (CON), motor (MOT), and visual (VIS) networks (Inline Supplementary Fig. 3). Firstly, C2 showed especially wide variety of co-occurrence patterns, and large proportion of them were similar to the RSNs. This reveals that C2 temporally modulates the co-occurrence patterns during the resting-states, and the well-known RSNs, which are usually represented by functional connectivities (or co-activations) on remote regions, are mostly driven by its occasional co-occurrences on the regions. Next, the co-occurrence patterns of C3 were less distributed than C2, and mainly located on FPN and VIS (and occasionally on DMN). This indicates that C3 represents the activities of the fronto-parietal control network and visual network, which observed as NBR on the regions. The spatial patterns of C4 were dominantly task-positive patterns (DAN, MOT, FPN), and also showed larger DMN than the other components. Together with its temporal pattern, C4 seems to represent task-relevant activations (or effortful deactivations) persisting for some duration, rather than the transient activities represented by C2 and C3. Notably, such persisting task-relevant activities appeared during resting-states even without any imposed tasks. Lastly, C1 showed wide variety of co-occurrence patterns relevant to RSNs as in C2 though they were less spatially focused compared to C2. Overall, the overlaps of some co-occurrence patterns across components imply that the temporal pattern corresponding to a single network is not always the same, but rather modulated by other underlying brain activities, which again attests to the nonlinearity of the processing.

3.5. Task-induced temporal primitives

To further investigate the temporal primitives, we evaluated the timings and spatial locations of their realizations induced by task conditions (Figs. 7 and 8), by applying the feature extractor trained from the rfMRI to the task-fMRI data (tfMRI). We found that their timings and locations were consistent in many task conditions, though some tasks have distinctive patterns (especially Motor and Language) possibly because of their distinctive block designs.

Figure 7:

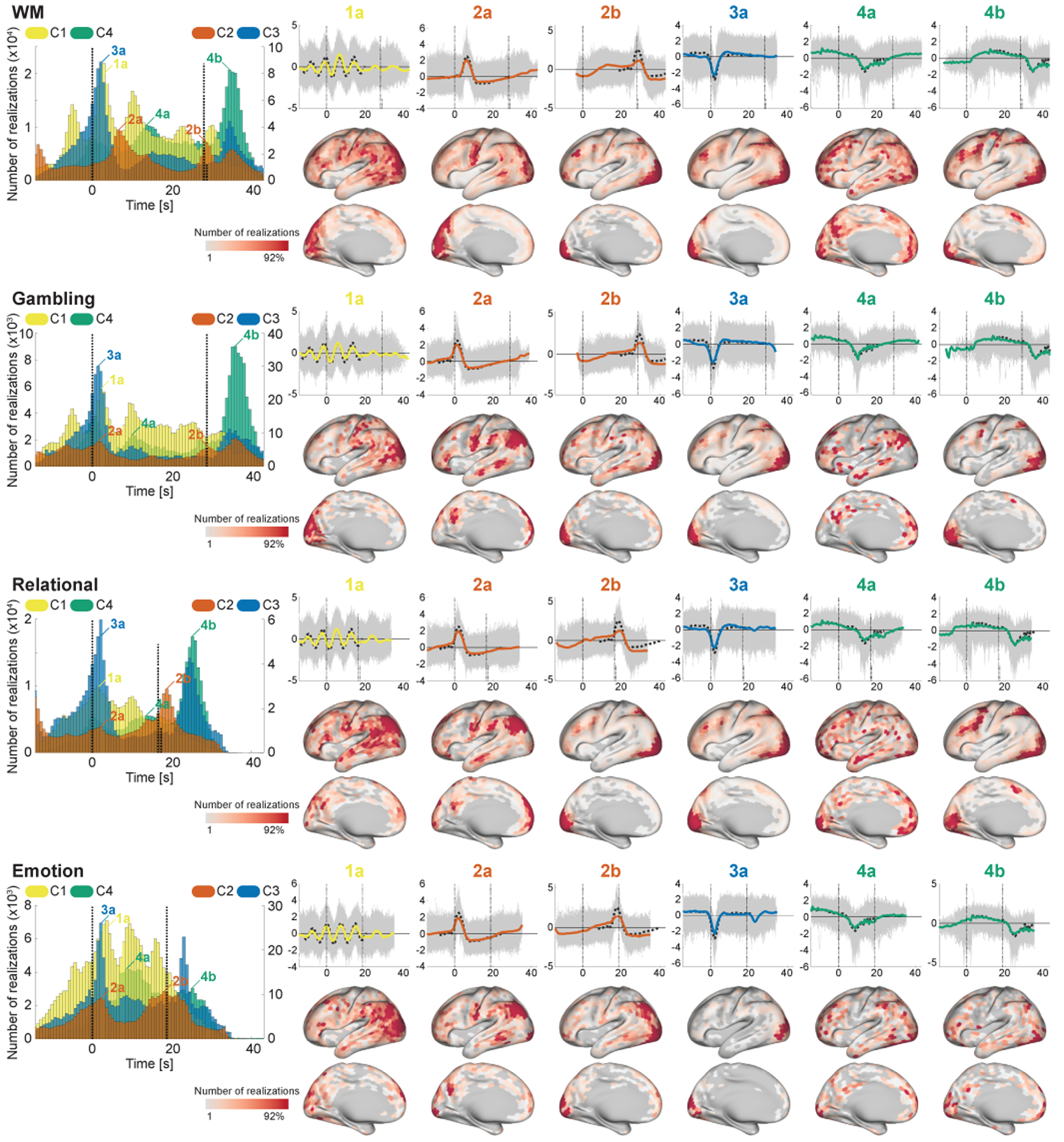
The timings and spatial locations of the realizations during the task conditions (WM, Gambling, Relational, and Emotion; see the remaining task conditions in Fig. 8). We discarded C5 here because of the lack of temporal preferences. (Left) Histogram of the timings of the realizations of the components (see Section 2.12 for more details). One temporal bin corresponds to one volume. Although there are some sub-conditions for each task, we mixed all of their realizations as the same task (Motor-CUE condition was excluded). The vertical line at 0 s indicates the onset of the task block, and the other vertical lines show the end of the task blocks. The length of the vertical lines indicates the number (ratio) of blocks ended at the timing. Note that the width of the receptive field of the feature extractor (about 32 s) is longer than the length of task blocks. (Right-upper) Temporal patterns of the realizations corresponding to some peaks on the histograms. Grey thin lines show the realizations corresponding to the timing, and the colored thick line is their sample average. Black dotted line shows the representative pattern obtained in Fig. 2a and used as a reference for estimating the timings. (Right-lower) Spatial histogram of the realizations on the specific timing given in the upper part.

Figure 8:

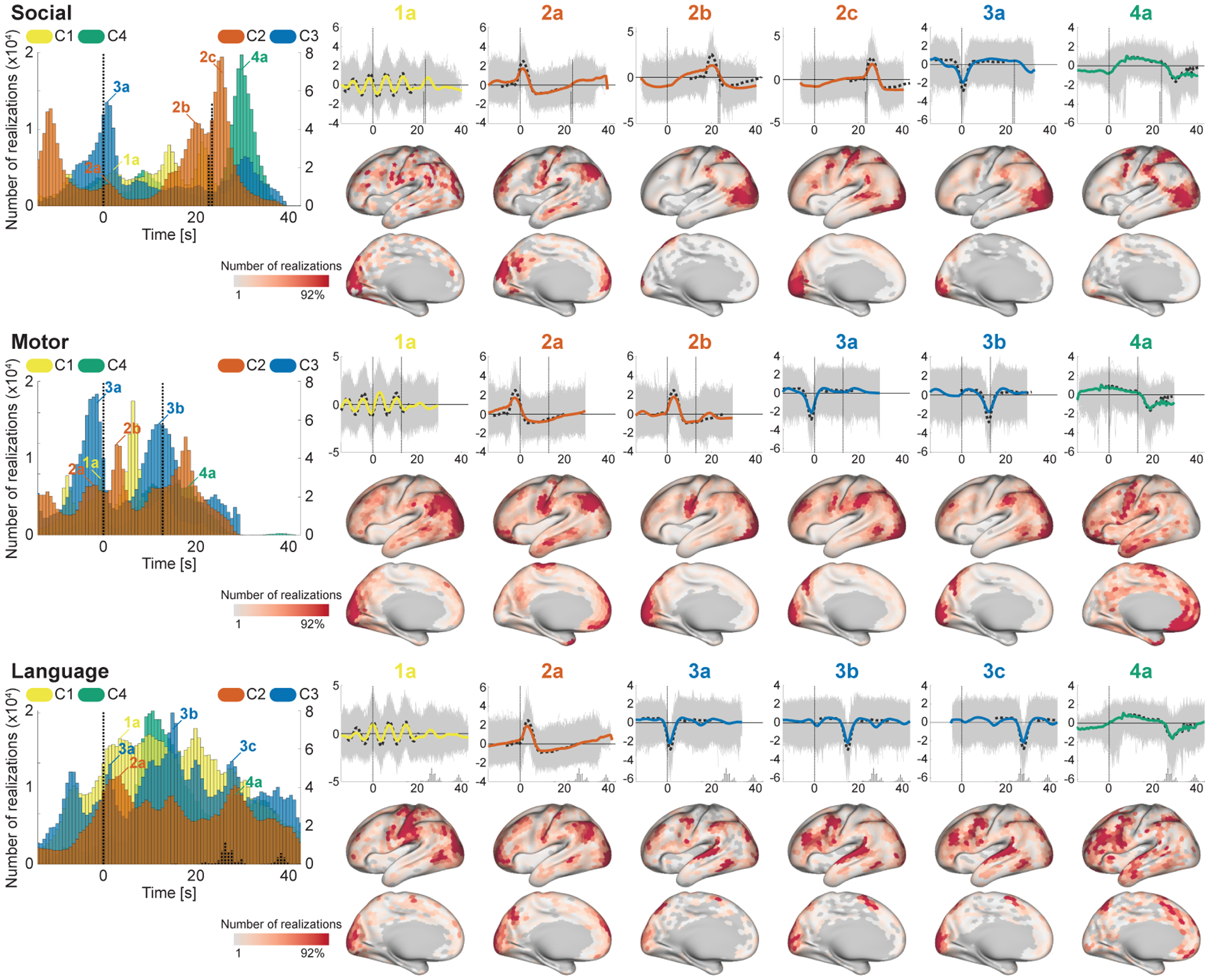
The timings and spatial locations of the realizations during the task conditions (Social, Motor, and Language). See Fig. 7 for the details.

C4 consistently appeared at two relatively distinctive timings across tasks; 10.9 ± 2.1 s (15.1 ± 2.9 volumes) after the onset, and 6.4 ± 1.9 s (8.8 ± 2.6 volumes; excluding Language) after the end of task blocks (the latter peak in Language task was not clear because of the large variance of the block length). The realizations on the both peaks showed long plateau with slight negative trend, which was similar to the well-known BOLD-response induced by block design paradigm. Their spatial locations on the latter peak have clear similarity to the effect size maps of the corresponding tasks (see Inline Supplementary Fig. 4 for the effect size maps), while those on the earlier peak were scattered on the other (task-irrelevant) regions. Those results indicate that C4 represents BOLD responses induced by sustaining tasks on the task-relevant regions, and also extended/effortful deactivations from the baseline on the other task-irrelevant regions.

C3 consistently appeared 1.7 ± 0.6 s (2.3 ± 0.8 volumes; excluding Motor, which was always preceded by the CUE condition) after the onsets of the task conditions. The spatial locations were less task-specific compared to C4, and mainly located on FPN and visual area, which were consistent with the co-occurrence patterns during the resting-states (Fig. 6) (except for the language-related areas in the Language task). Those results reveal that, during tfMRI, C3 organizes negative BOLD activities of FPN, and the stimulus-evoked hemodynamic responses on the stimulus-relevant regions, on task onsets. The spatial overlap of C3 (3a; deactivation) and C4 (4b; activation) on visual areas might be explained by the modulation of the balance between stimulus- and task-related components of the HRF (Cardoso et al., 2012) across blocks; i.e., C3 (stimulus-related) was dominant there in some blocks, while C4 (task-related) was dominant in other blocks.

C2 also has consistent peaks across many tasks. Firstly, it appeared around the end of the task block (2b in Figs. 7 and 8); the temporal patterns and the spatial patterns being similar to the effect size map indicates that they represent the transient activities appeared at the end of the block responses on the task-relevant regions. C2 also has another peak just after the onset in many task conditions (2a in Figs. 7 and 8), which temporal patterns were similar to RRF (Birn et al., 2008). The spatial locations were consistent across tasks; DMN-related regions, motor, and visual area; many of those regions were reported to coincide with the respiration-variation-induced signals (Birn et al., 2006; Power et al., 2017). Those results indicates that C2 represents both of the neural-activity-related responses (2b) and the respiration artifacts (2a) phase-locked to the stimulus onsets (Huijbers et al., 2014).

Although C1 looked less timing-specific, the realizations clearly showed cyclic peaks around the onsets of the blocks in many tasks. The interval of the peaks was about 7.2 s (10 volumes), which was consistent with the period of the cycles of the representative pattern of C1. That implies that C1 appeared at many time points during task blocks, being slightly phase-locked to the onsets of the blocks and gradually unlocked from it later. The spatial locations of the corresponding realizations were widely scattered on task-irrelevant regions, which suggests its less task-type-relevant biological substrate.

3.6. Relationship between temporal primitives and behavioral traits

To investigate the possible contribution of the temporal primitives to the individual differences of the behavioral traits, we measured correlation between subject-average component activities and some of the individual traits, especially intelligence measures and the performances during tfMRI (Fig. 9a). Although the correlations were not strong, some traits showed significant relationship with the components. C1 was preferentially correlated with working memory-related traits. C2 and C3 were correlated with fluid intelligence measure; C3 was also correlated with the language performance.

Figure 9:

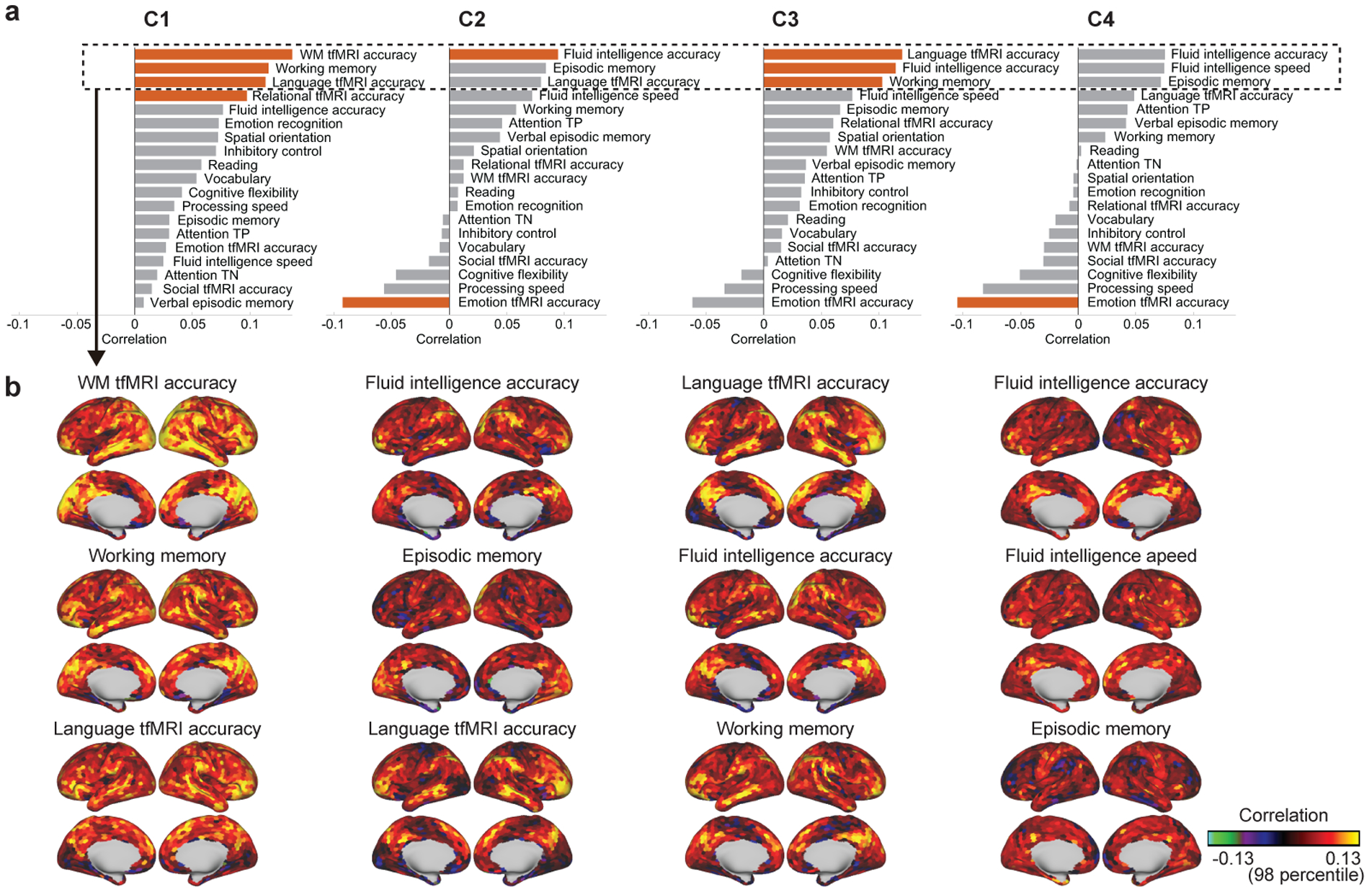
The relationship of the temporal primitives to the behavioral traits of the subjects. (a) Spearman correlation coefficient between subject-average component activities and 19 behavioral traits related to intelligence and response-accuracies during tfMRI. Red bars indicate significant relationship (p < 0.05; 100,000 times permutation test, with FDR correction for multiple comparisons). (b) The spatial distribution of the relationship between subject-parcel-average component activities and some traits corresponding to the top-3 highest correlation in a for each component (column).

Figure 9b shows the parcel-wise relationship of each component to the behavioral traits which had the highest positive correlations in Fig. 9a. Their spatial nonstationarity indicates that the component activities representing the deferences of the behavioral traits are not whole-brain-wide, but rather concentrated on some specific regions. In addition, such distinctive regions look consistent across components and traits; middle temporal gyrus (MTG), intraparietal sulcus (IPS), posterior cingulate cortex (PCC), Brodmann area 40, ventrolateral prefrontal cortex (VLPFC), and orbitofrontal cortex (OFC).

4. Discussion

We proposed a novel nonlinear sICA framework called LSCL, and showed that resting-state data are composed of some recurrent, local, and nonlinear temporal structures called temporal primitives. The temporal primitives were extracted by training a nonlinear feature extractor (CNN) from resting-state data in an unsupervised, data-driven manner, so as to demix it into components whose temporal statistics are spatially nonstationary. The feature extractor then automatically identified some particularly distinctive local temporal structures, which appeared frequently and consistently during the resting-state acquisitions. Our analyses revealed that these temporal primitives are fundamental elements of both spontaneous and task-induced fMRI signals. Here, we set the number of components to five, and the learned components had distinctive characteristics: C1 captures less task-specific transient phenomena (ripple), recurrently appears during resting and task conditions, and slightly phase-locked to task-onsets. C2 represents a transient neural-activity-related response (HRF) and a respiration-variation-related artifact (RRF), and organizes well-known RSNs by its co-occurrence in remote regions during resting-state. The distinction between HRF and RRF during resting-state is challenging because of the similarity of their temporal patterns, their some spatial overlap (see Fig. 6 and 2a in Figs. 7 and 8), and non-periodic nature of their appearances. However, the time-varying spatial co-occurrences (Fig. 6) implies that C2 represents not only RRF-relevant artifacts, but also some amount of neuronal-relevant activities. C3 represents a NBR on FPN and the stimulus-evoked component of HRF on the corresponding regions, which were also appearing during resting-state without any explicit external triggers. C4 captures state-persistent brain activities induced on the state-relevant regions, conventionally captured by GLM-based analysis in tfMRI data, and here found to appear in both of resting and task conditions. C5 captures high frequency noise in fMRI data; considering its flat (non-peaky) spectrum over 0.2 Hz, C5 especially seems to have captured physiologically originated artifacts (e.g., respiration around 0.2–0.4 Hz, and aliased cardiac pulsation around 1 Hz), which have some variability across subjects/timings. Some subjects show a peak around 0.038 Hz in C5 (Inline Supplementary Fig.6b), which may be because of the occasional contamination of the other components in the same temporal window. Considering temporally and spatially structured artifacts were supposed to have been already removed by ICA-FIX (Section 2.2), C5 captured temporally unstructured artifacts, which spatial co-occurrence patterns were not always the same.

Our results showed that the temporal primitives appeared with a large variety of nonlinear modulations for each realization (Fig. 5), highlighting the importance of the nonlinearity of the feature extractor. To further illustrate the importance of the nonlinearity, we conducted the same analyses using a linear feature extractor (Inline Supplementary Fig. 2). Compared to the nonlinear model, the linear model extracted only two reasonable components, which have slower trends than those of the nonlinear model (the other components seem to represent just noises). We assume this is because the linear model cannot recognize the wide variety of realizations generated from a single temporal primitive as a single component because of its weak invariance, as seen from the narrower horizontal distributions (higher sensitivity) of the representative-pattern-specificity histogram (Inline Supplementary Fig. 2b) compared to those of the nonlinear model (Fig. 4b). Those results illustrate how nonlinearity in the feature extractor is important to achieve robustness against the various modulations of the temporal primitives.

Our results showed that the temporal primitives organize the time varying networks during resting states by spatially co-occurring at remote regions. The functional networks during resting-state (RSNs) are conventionally characterized by functional connectivities (FCs) across regions (Biswal et al., 1995), or spatial co-activations (tICA, sCIA, CAP, HMM) (Liu and Duyn, 2013; Mckeown et al., 1998; Smith et al., 2012; Vidaurre et al., 2017). Recent studies have shown that the FCs are not constant, but rather temporally modulated (dynamic FC, dFC) (Allen et al., 2012; Leonardi et al., 2013; Preti et al., 2017). C2 showed a particularly wide variety of spatial co-occurrence patterns during the resting-state, and many of them were related to well-known RSNs. This indicates that C2 may be the main underlying factor generating the observed temporal correlation or co-activations between remote regions by the conventional analyses. Although it may be counterintuitive in the context of sICA to see similar co-occurrence patterns across different components (Fig. 6), it is actually allowed in LSCL, as far as the spatial patterns are distinctive across components on temporal average (Fig. 3b) and different primitives do not appear at the same timing and parcel consistently (basically, if it is the case, those components would have correlation on fragment-average feature values (input samples to MLR for training; see Section 2.5) within the parcels, which contradicts the assumption of the spatial-parcel-wise independence of LSCL.). This is one of the interesting consequences of LSCL.

The duration of the temporal primitives were about 30 s, which might explain why the sliding window FC approach requires 30–60 s of window length to successfully capture dFCs (Leonardi and Ville, 2015; Zalesky and Breakspear, 2015). Some studies have shown that HMM analysis reveals state-transition dynamics of RSNs (Vidaurre et al., 2017), which is consistent with the clusters of the co-occurrence patterns of C2 (Fig. 6). Although the other temporal primitives also exhibited spatial co-occurrences during the resting-states, their patterns were more region-specific compared to C2: C3 is mainly related to FPN and VIS, and C4 represents task-relevant brain activities (DAN, FPN, MOT) persisting for a short time, or extended/effortful deactivation on DMN.

Although the temporal primitives were extracted from resting-state data, they also appeared during task conditions, and were found to generate, at least to some extent, the task-induced BOLD responses. C4 seems to represent the persisting patterns of the BOLD responses, usually extracted by the conventional GLM analyses in task-based fMRI studies. C3 captures the stimulus-evoked component of HRF on the corresponding regions, and NBR on FPN at the onsets of the task blocks, which could be related to the functional role of the FPN as a flexible hub in cognitive control and adaptive implementation of task demands (Cole et al., 2013). C2 captures transient activities occurred at the end of task blocks, and respiration-related artifacts at the onset of task blocks. On the other hand, the fact that the task-relevant patterns also appeared during the resting-state is consistent with the previous findings of the task-relevant activities of being embedded in a subspace of resting-states activities (Kenet et al., 2003; Luczak et al., 2009; Smith et al., 2009). We also trained the feature extractor only from the tfMRI data (Inline Supplementary Fig. 10). The extracted patterns did not have much variety compared to those from rfMRI, and most of them seemed to be relevant to the task design matrix convolved by HRF. Considering the similarity of those patterns to the temporal primitives from rfMRI (especially C3 and c4), the temporal primitives would be sufficient to capture the task-induced patterns and their variability to some extent.

The distinctive relationship of the temporal primitives to some of the cognitive traits suggest that they may have different biological substrates, and capture important individual variations. The correlation of C2 and C3 with fluid intelligence indicates their contributions to the flexible functional organization of the brain. C3 also has significant correlation with the language performance, which may be related to the appearance of C3 at the language-related areas during the Language task (Fig. 8). C1 had distinctive correlation to the working-memory-related measures, which suggests its specific biological substrates, such as memory consolidation, though it will require further study to conclude. Although those correlations were significant, the effect sizes were rather small. However, this would not be surprising because the temporal primitives were extracted in unsupervised, data-driven manner, that is, without any explicit use of subjects traits, unlike the previous studies which explicitly used the traits to find a feature space which represents the relationship between the brain activities and the traits in supervised manner (Dubois et al., 2018; Finn et al., 2015; He et al., 2019; Kashyap et al., 2019; Noble et al., 2017; Perry et al., 2017; Smith et al., 2015).

Since C1 had especially intriguing and less-known temporal pattern, we conducted some additional analyses based on its frequency characteristics to see its possible subject-specificity and physiological origin. At first, we found a subtle difference of the subject-median peak frequencies of the PSDs of the realizations (0.12 ± 0.0068 Hz). To evaluate the potential physiological factors causing the variability, we computed the correlation between the peak frequencies and the behavioral traits of the subjects (see Section 2.13 for the basic analysis). For comprehensive findings, we here considered all of the traits obtained by HCP (https://db.humanconnectome.org), except for some unstable ones, in which 1) fewer than 250 subjects had valid measures, 2) over 75% of subjects had the same value, or 3) very extreme outliers were contained (if max(y) > 100 × mean(y), where y = (x − median(x))², and x is a vector containing trait values of subjects). Those rejection criteria were based on Smith et al. (2015), but the thresholds were selected to be severer; 450 traits remained in total. As a result, systolic blood pressure (r = 0.13) and some FreeSurfer measures (intra-cranial volume, r = −0.12; right precentral average thickness, r = −0.12; and left entorhinal surface area, r = −0.11) had significant correlation with the peak frequency (p < 0.05; 100,000 times permutation test, with FDR corrected), which implies a possible physiological origin of C1 instead of the systemic noise common across subjects. A recent study suggested that respirations induce 0.12 Hz artifacts on head position traces, though they did not show their clear appearance on fMRI signals (Power et al., 2019). Although C1 has a peak frequency close to this, the time-varying locations of C1 (Fig. 6) imply that C1 is not simply related to the global artifacts caused by body motion.

Previous studies have already shown that rfMRI data are made of repetitive events of some spatial co-activation patterns (CAP) (Chen et al., 2015; Liu and Duyn, 2013; Liu et al., 2013), spatio-temporal patterns (Majeed et al., 2011; Guidotti et al., 2015; Takeda et al., 2016), or lag threads (Mitra et al., 2015). However, the extracting one dimensional (nonlinear) temporal patterns as we did here, without considering their spatial co-occurrence, seems to be conceptually new. Although LSCL and the methods cited above are looking at different dimensions (time, space, or time-space), they are possibly capturing the same phenomena. For example, CAP studies (Liu and Duyn, 2013; Karahanoğlu and Van De Ville, 2015) found spatial co-activations of BOLD signals condensed in events of short periods (4–8 s), and showed that those time-varying events generated the fluctuations of dFCs. Considering the short durations of the peaks of C2 and C3, CAPs are possibly related to the spatial co-occurrence of those temporal primitives. Majeed et al. (2011) extracted a recurrent spatio-temporal pattern with the window length of about 20 s, referred to as the template, within which DMN and attention network were opposed in activity levels, and gradually reverted sign with a cycle of duration of about 20 s. C2 and C4 may be related to such a template because they tend to appear in both of DMN and task-positive regions, though their temporal patterns are not clearly consistent with the cyclic pattern of the template (Fig. 2a). That may be because we extracted several components, and the template was thus divided into several components.

To show the potential contribution of the temporal primitives to those repetitive events, we applied CAP analysis (Liu and Duyn, 2013) to the feature values of C2, which showed a particularly wide variety of spatial co-occurrence patterns (Fig. 6), as follows; 1) the parcels included in a part of PCC (31pd and 31pv in Glasser et al. (2016)) were used as a seed region, 2) the frames (co-occurrence patterns) where the seed-average feature values exceeded a threshold (85 percentile of all frames) were obtained, and 3) k-means clustering with k = 8 were applied to them. The result showed that the PCC-relevant co-occurrence patterns of C2 (C2-CAPs) were mainly classified into three groups (Inline Supplementary Fig. 7); task-negative networks (C2-CAPs 6 and 7, related to DMN-MFG and DMN-SFG in Liu and Duyn (2013) respectively), motor networks (C2-CAPs 2 and 8), and visual networks (C2-CAPs 1, 3, and 4). Basically, the decomposition was similar to the CAPs from rfMRI (fMRI-CAPs; Liu and Duyn (2013)), except that 1) motor and visual C2-CAPs were more dominant and had higher consistency compared to the task-negative networks, which was opposite in fMRI-CAPs, and 2) we did not see subcortex-relevant DMNs (caudate nucleus and hippocampus) shown in Liu and Duyn (2013) because we excluded subcortical regions from the analysis. Such time varying C2-CAPs and their consistency to the fMRI-CAPs supports our claim that the temporal primitives (especially C2) are driving the local repetitive events such as CAPs, which are observed as dynamic functional connectivity during resting-state.

To evaluate the reproducibility of the temporal primitives, we split the training data in half (502 and 501 subjects each), and trained a feature extractor individually from each of them (Inline Supplementary Fig. 8). Although some components seemed to be failed to be decomposed (see similarity of C5 to C3 in the subset 2), many of the components were similar across the subsets, and to Fig. 2, which implies the reproducibility of the temporal primitives across subjects.

Importantly, in LSCL (and SCL), the assumption of spatial independence is not the same as that of ordinary sICA; LSCL assumes parcel-conditional spatial independence given parcel labels, instead of marginal spatial independence usually assumed by sICA. Since LSCL does not impose independence across parcels, the spatial patterns of the components, which are determined by parcel-wise modulation parameters, can look similar to each other (see the similarities of the spatial patterns of C1, C2, and C3 in Fig. 3b). Although the LSCL components can be marginally independent if the modulation parameters are also independent (Hyvärinen and Morioka, 2016), that does not seem to happen here.

Since LSCL is based on the assumption of spatial-parcel-wise stationarity and independence, it requires pre-defined spatial functional parcellation which satisfies the assumption at least approximatively. In this study, we used a simple parcellation which divides cortices into small similar-sized parcels, and showed that even such simple method was sufficient for LSCL. Although more sophisticated parcellations explicitly considering functional similarities could increase the classification performance, we would assume that the learned temporal primitives might not be very different as far as we use a parcellation with similar or higher spatial resolution. This is because the spatial patterns of the components have much wider distributions than the parcel-size (Fig. 3b), and thus contaminations of some neighbor regions would not have a lot of influence on the learning of the model.

As with many other ICA algorithms, the selection of the number of components is challenging in LSCL. In preliminary experiments, we tried some values and found that on the one hand, if we increase the number of components, some components get similar temporally and/or spatially each other (see Inline Supplementary Fig. 9 for the representative patterns in 6 components case; C1–C5 were consistent with Fig. 2a, but C6 was similar to C2); and on the other hand, if we decrease the number of components, some components disappear or are mixed together with other components. The experiments implies that the setting n = 5 was reasonable, considering that the components were properly demixed without being contaminated by different temporal primitives. As we can see from Fig. 5, the temporal patterns of the realizations looked qualitatively consistent for each component even after the nonlinear modulations. However, the best setting can be different across datasets. For example, different TR of rfMRI would lead to a different number of distinctive components; slower TR would complicate the detection of high frequency patterns such as C1, on the other hand, faster TR may allow us to decompose C5 into some distinctive components, which were considered as high frequency artifacts in this study. The best setting would be also dependent on the duration of the temporal pattern of interest.

Training of the feature extractor (CNN) by LSCL took about 25 hours (Intel Xeon 3.5GHz 8 core CPUs, 128 GB Memory, NVIDIA Tesla P100 GPU). After the training, the feature value extraction from fMRI data through sliding-window took about 2 s for each resting-run.

LSCL (and SCL) frameworks can be applied not only to rfMRI data, but to many kinds of multidimensional time series which satisfy the assumption of spatial-parcel-wise stationarity, such as calcium imaging, videos, and so on. Compared to SCL, LSCL has a wide applicability because it treats different timings as different data points in addition to the spatial data points; it could be applied to data with much lower spatial dimension, e.g., electroencephalography (EEG), magnetoencephalography (MEG), electrocorticography (ECoG), where sICA is usually considered inadequate because of a small number of spatial locations. We think this is an important avenue for future work.

The key appealing points of LSCL are the nonlinearity, unsupervised learning, and the extraction of local dynamics. Since nonlinearity is thought to be intrinsic in many of real dynamics including the brain, its explicit consideration would give us a new insight into the hidden phenomena of the dynamics, which are not visible by the conventional linear frameworks such as linear sICA (Mckeown et al., 1998). Such nonlinear models generally need a lot of data for learning (He et al., 2015; Krizhevsky et al., 2012; Szegedy et al., 2015), and thus unsupervised learning nature of LSCL is advantageous because unlabeled data are generally easier to obtain compared to the labeled data, which is especially the case in brain imaging data. Extraction of local and repetitive dynamics is a novel concept. Although many dynamical systems are inherently nonstationary, they may be temporally repeating a finite number of sequences (Ikegaya et al., 2004; Liu and Duyn, 2013; Majeed et al., 2011; Mitra et al., 2015; Van De Ville et al., 2010) rather than moving completely randomly. LSCL has a potential to extract such local events composing the nonstationary data. On the other hand, some extensions can be helpful depending on the type of the dynamics. One of the fundamental limitation (property) of LSCL is that it extracts temporal (one dimensional) structures rather than spatio-temporal (two dimensional) structures. Since some studies already found spatio-temporal patterns in brain imaging data (Ikegaya et al., 2004; Majeed et al., 2011; Mitra et al., 2015), some additional post-analyses to extract nonlniear spatio-temporal structures would be an interesting future direction. However, since the interpretation of such nonlinear spatio-temporal patterns would be more complicated, more intuitive visualization methods would be also required.

5. Conclusion

In this study, we proposed a novel nonlinear feature extraction framework called local space-contrastive learning (LSCL), which extracts distinctive nonlinear temporal structure hidden in brain imaging data, by training a deep temporal convolutional neural network in an unsupervised, data-driven manner. By applying to the HCP’s fMRI dataset obtained from over 1,000 subjects, we demonstrate that: 1) LSCL identified certain distinctive local temporal structures, referred to as temporal primitives, which repeatedly appeared at different time points and spatial locations, reflecting dynamic resting-state networks, 2) these temporal primitives were also present in task-evoked spatiotemporal responses, and 3) the temporal primitives captured unique aspects of behavioral traits. In addition to these findings underlying fMRI data, our newly-developed feature extraction framework can provide a novel general tool to find out fundamental information from various kinds of imaging modalities, and give us new insight into the complex dynamics of the brain.